The Impact of Future Offshore Wind Farms on Wind Power Generation in Great Britain

Abstract

In the coming years the geographical distribution of wind farms in Great Britain is expected to change significantly. Following the development of the “round 3” wind zones (circa 2025), most of the installed capacity will be located in large offshore wind farms. However, the impact of this change in wind-farm distribution on the characteristics of national wind generation is largely unknown. This study uses a 34-year reanalysis dataset (Modern-Era Retrospective Analysis for Research and Applications (MERRA) from National Aeronautics and Space Administration, Global Modeling and Assimilation Office (NASA-GMAO)) to produce a synthetic hourly time series of GB-aggregated wind generation based on: (1) the “current” wind farm distribution; and (2) a “future” wind farm distribution scenario. The derived data are used to estimate a climatology of extreme wind power events in Great Britain for each wind farm distribution. The impact of the changing wind farm distribution on the wind-power statistics is significant. The annual mean capacity factor increased from 32.7% for the current wind farm distribution to 39.7% for the future distribution. In addition, there are fewer periods of prolonged low generation and more periods of prolonged high generation. Finally, the frequency and magnitude of ramping in the nationally aggregated capacity factor remains largely unchanged. However, due to the increased capacity of the future distribution, in terms of power output, the magnitude of the ramping increases by a factor of 5.

1. Introduction

Under the EU 2008 Renewables Directive, the UK is expected to produce 15% of its total energy consumption from renewable sources by 2020 [1]. Due to the excellent wind resources available, offshore wind has been identified as the main technology for achieving this target [2,3]. The development of offshore wind in the UK has been managed in three rounds defined by the Crown Estate. Round 1 started in 2000 and led to the installation of 1.2 GW of capacity across 12 farms. More recently, a number of the projects outlined in Round 2 have been built, increasing the installed capacity to 3.6 GW (approximately 35% of the total UK wind capacity). This growth looks set to continue over the next few years; in addition to a further 4.7 GW of capacity from Round 2 which is either under construction or in the planning stage, the third round of developments (launched in 2009) identified a number of offshore zones which could increase the installed capacity by up to 26 GW [4,5]. As a result the amount of electricity generated by wind has increased from 650 GWh (less than 1% of total consumption) in 2003 to 28.4 TWh (approximately 9% of total consumption) in 2013.

As the penetration of wind power increases, extreme events such as prolonged periods of low or high generation and rapid changes (ramps) in generation are of growing concern to National Grid, the system operator. It is not possible to assess the frequency of these events directly from generation records as they do not extend back far enough to accurately determine the representative return periods [6]. This is due to inter-annual variability in the wind speed as well as the changing geographical distribution of the wind capacity [7]. In response to these challenges, a number of studies have used surface based wind observations [8,9,10,11], or meteorological reanalysis data [12] to estimate the long term power characteristics based on current or recent historical wind farm distributions.

Following the development of the Round 3 offshore wind zones, however, most of the GB wind capacity will be located offshore, in clusters of very large wind farms. To successfully prepare for the impact of increased future wind penetration on the electricity transmission system in Great Britain (GB), it is necessary to understand the impact of this change in wind-farm distribution on the operational characteristics of national wind generation. There are two aspects of the change in wind farm distribution that could particularly affect the overall characteristics of the wind power resource. Firstly, offshore wind speeds are generally higher and more consistent than onshore wind speeds [13,14]. The authors of [15] suggest that due to the increased wind resource, offshore wind farms could operate at capacity factors of up to 40%. As onshore wind farms typically operate at capacity factors of around 25%–30% [16], a significant increase in the proportion of offshore capacity can therefore be expected to lead to an increase in the nationally aggregated capacity factor [8]. Secondly, the change in the geographical distribution of wind capacity could alter the degree of smoothing between different sites. In particular, the concentration of large amounts of wind capacity close together in offshore zones could increase the variability in the total wind power resource and thus reverse the smoothing previously gained through the geographical dispersion of wind farms.

In this paper, we investigate the impact of increasing the penetration of offshore wind capacity on the statistical characteristics of the wind power resource. Great Britain has been selected as a case study as it currently has the largest capacity of offshore wind, which is expected to increase significantly over the next few years. In particular, the potential changes in the magnitude and frequency of extreme wind power generation events are assessed. These events pose considerable challenges for the efficient and secure operation of the power system. To achieve this, a 34-year reanalysis dataset (MERRA from NASA-GMAO, [17]) is used to produce a synthetic hourly time series of GB-aggregated wind generation for a variety of wind farm distributions (details of this method are given in Section 2). The generation characteristics of different wind farm distributions, including the present and proposed future distributions, are then presented in Section 3, where the implications of the results for power system management are also discussed. Finally, conclusions are presented in Section 4.

2. Estimating the Long Term Power Output of a Defined Wind Farm Distribution

This study uses the method described in [12] to derive an hourly time series of the GB-aggregated wind power generation for a 34 year period (1980–2013) based on: (1) the “current” wind farm distribution and (2) a “future” wind farm distribution scenario. The derived hourly time series are used to estimate a climatology of extreme wind power events in Great Britain for each wind farm distribution. To investigate the impacts of the change in wind farm distribution in more detail, two additional scenarios will also be considered. The “current + onshore” scenario includes all of the current wind farms plus the future onshore projects only. The “current + offshore” scenario includes all of the current wind farms plus the future offshore projects only. To allow for the proper comparison of each scenario, the same 34 years of wind speed data is used. This implicitly assumes that decadal changes in wind speed are small relative to higher frequency variability (such as inter-annual or seasonal changes). As discussed in Section 4, research to quantify the effect of longer term variability and climate change on the wind resource is ongoing.

After assessing some long term capacity factor statistics, two types of extreme event are analysed in detail: (1) persistent wind events, defined as a prolonged period of time with low or high GB aggregated wind power generation; and (2) ramping events, defined as the maximum change in the GB-aggregated capacity factor that occurs during a defined period of time.

2.1. The GB-Aggregated Capacity Factor Time Series

Following [12], an hourly time series of GB-aggregated wind power generation spanning the period 1980–2013 is derived for each of the scenarios using a 34-year reanalysis dataset (MERRA from NASA-GMAO. Firstly, the horizontally gridded 2 m, 10 m and 50 m altitude winds are bi-linearly interpolated to each wind farm location. These winds are then vertically interpolated to a representative turbine hub height, assuming a logarithmic change in wind speed with altitude. These hub-height winds are converted to wind farm power output using the transform function (power curve) shown in Figure 1. This power curve is based on empirical comparisons between forecasted wind speeds and recorded wind farm power output (analysis by National Grid), and was adjusted by [12] for use with MERRA data. Finally, the power output of each wind farm is then summed over all wind farms to estimate produce an hourly time-series of GB-aggregated wind power generation.

The performance of this methodology has been extensively validated using historical distributions of wind-farms and recorded GB wind-power output data [12]. These authors showed that whilst there were deficiencies in the model at small spatiotemporal scales (for example, hourly variability at a single site) the reanalysis can accurately reproduce near-surface wind variability on spatiotemporal scales greater than around 300 km and 6 h, without dynamical downscaling. When used to produce an hourly time series of GB-aggregated wind power generation, the results were highly correlated with recorded GB hourly generation data from National Grid (with a linear correlation coefficient of 0.96). In addition, the variability in the MERRA derived GB-aggregated capacity factor was well correlated with measured data for time intervals greater than 6 h.

Figure 1. Transformation function used to convert the hub-height wind speed to power output (the “adjusted” curve from [12]).

Figure 1. Transformation function used to convert the hub-height wind speed to power output (the “adjusted” curve from [12]).

The validation of the wind-power climatology in [12] was performed using a current-day wind-farm distribution (i.e., is dominated by onshore sites) whereas the future GB wind farm capacity distribution is likely to be dominated by offshore farms. To confirm that the MERRA derived estimates remain applicable in future offshore-dominated scenarios, it has been validated against the hourly aggregated capacity factor of three offshore wind farms for the period 1 October 2012 to 19 June 2013. While this data does not consider the summer period, it can be considered to capture the majority of the variability at the site. Figure 2a shows the derived hourly data are well correlated with metered data (with a correlation coefficient, r = 0.89). Consequently, the estimated long-term mean capacity factor, 39.7%, is in good agreement with the metered value, 40.3%. Furthermore, Figure 2b shows the cumulative frequency distribution for the MERRA derived data is very similar to that of the measured data. However, there is a small positive bias at moderate capacity factors.

Figure 2. A comparison of MERRA derived data and measured data from a cluster of offshore wind farms: (a) the hourly capacity factor aggregated across the three farms; (b) the cumulative distribution of the capacity factor.

Figure 2. A comparison of MERRA derived data and measured data from a cluster of offshore wind farms: (a) the hourly capacity factor aggregated across the three farms; (b) the cumulative distribution of the capacity factor.

2.2. Wind Farm Distributions

As of April 2014, the installed capacity of wind power in Great Britain was approximately 10.2 GW spread across 317 wind farms (hereafter referred to as the current wind farm distribution, this is not the same distribution as that used in [12]). Figure 3 shows the majority of this capacity is located onshore (approximately 7 GW), of which most is located in northern England and south west Scotland. In addition, due to a large number of new offshore wind farms there is a significant amount of capacity located off the coast of East Anglia and in the Thames estuary.

To represent the future wind farm distribution, a number of assumptions have been made:

• All Round 3 zones are developed to full capacity (details provided in Table 1).
• All onshore wind farms under construction or with planning permission are fully commissioned.
• All existing farms remain generating at their current capacity. It therefore does not consider the decline in wind turbine performance with age, which is on average 1.6 ± 0.2 of their output per year [18].

Table 1. Details of the Round 3 offshore wind zones.

Farm	Size (MW)	Median distance from coastline (km)
Moray Firth	1116	28
Firth of Forth	3465	54
Dogger Bank	7200	160
Hornsea 1 (Heron & Njord)	1200	112
East Anglia	7200	56
Rampion	665	50
Navitus Bay Wind Park	970	21
Celtic Array	4185	30

Table 1. Details of the Round 3 offshore wind zones.

Farm	Size (MW)	Median distance from coastline (km)
Moray Firth	1116	28
Firth of Forth	3465	54
Dogger Bank	7200	160
Hornsea 1 (Heron & Njord)	1200	112
East Anglia	7200	56
Rampion	665	50
Navitus Bay Wind Park	970	21
Celtic Array	4185	30

These assumptions lead to approximately 50 GW of wind capacity distributed across 515 farms in Great Britain (as shown in Figure 3). Offshore wind becomes significantly more dominant with 75% of the capacity (in comparison to 35% for the current distribution). Much of this 37.5 GW of capacity is located in clusters of wind farms in the North Sea. The growth in the offshore wind capacity is consistent with that of the “Gone Green” scenario outlined in the future energy scenarios report produced by the system operator [19].

Figure 3. The wind farm distribution and capacity of April 2014 (a) and a future scenario (b).

Figure 3. The wind farm distribution and capacity of April 2014 (a) and a future scenario (b).

For each distribution, the spatial dispersion of the capacity has been quantified in terms of the mean separation per unit capacity, s, calculated as:

$$s={\displaystyle \sum _{i=1:N}\frac{c_i}{C_T}\left({\displaystyle \sum _{j=1:N}\frac{c_j{d}_{ij}}{C_T}}\right)}$$

(1)

where c_j is the wind farm capacity, d_ij is the distance between wind farms, N is the number of wind farms and C_T is the total installed capacity. Despite the clustering of turbines in offshore wind zones, overall the capacity is more spatially dispersed in the future distribution. The mean distance between each MW unit of capacity, D, increases from 420 km for the current distribution to 460 km for the future distribution. This is a result of the large distances between the Round 3 wind zones and the coastline (given in Table 1). If the future distribution did not include any of the Round 3 offshore projects, there would be a small reduction in the spatial dispersion of the capacity (D = 410 km). In contrast, if the future capacity did not include any new onshore projects (only offshore), the capacity would become more spatially dispersed than the current distribution D = 450 km, but not as dispersed as the assumed future distribution which includes a combination of new onshore and offshore farms.

Where available, the hub height of the turbines in each of the future wind farms has been taken from planning documents published by the farm developer. For the onshore farms where this is not available, a hub height of 65 m has been assumed. This equates to approximately the median hub height of the onshore wind farms constructed in the last five years. For the Round 3 offshore wind farms, the developers have proposed a range of possible hub heights, which reflects the range in possible turbine designs. For these farms, the median hub height has been selected (this value ranges from 110 to 160 m).

3. Results and Discussion

In this section, the current and future GB-aggregated capacity factor time series (Section 2) will be used to assess and compare the statistical characteristics of a future wind power resource with greatly increased offshore wind penetration. Firstly, the long term characteristics such as the annual-mean capacity factor and the frequency distribution of hourly capacity factor values are compared (Section 3.1). Following this, the frequency (and thus return period) of extreme persistence and ramping events are investigated (Section 3.2 and Section 3.3).

3.1. GB-Aggregated Capacity Factor: Long Term Statistics

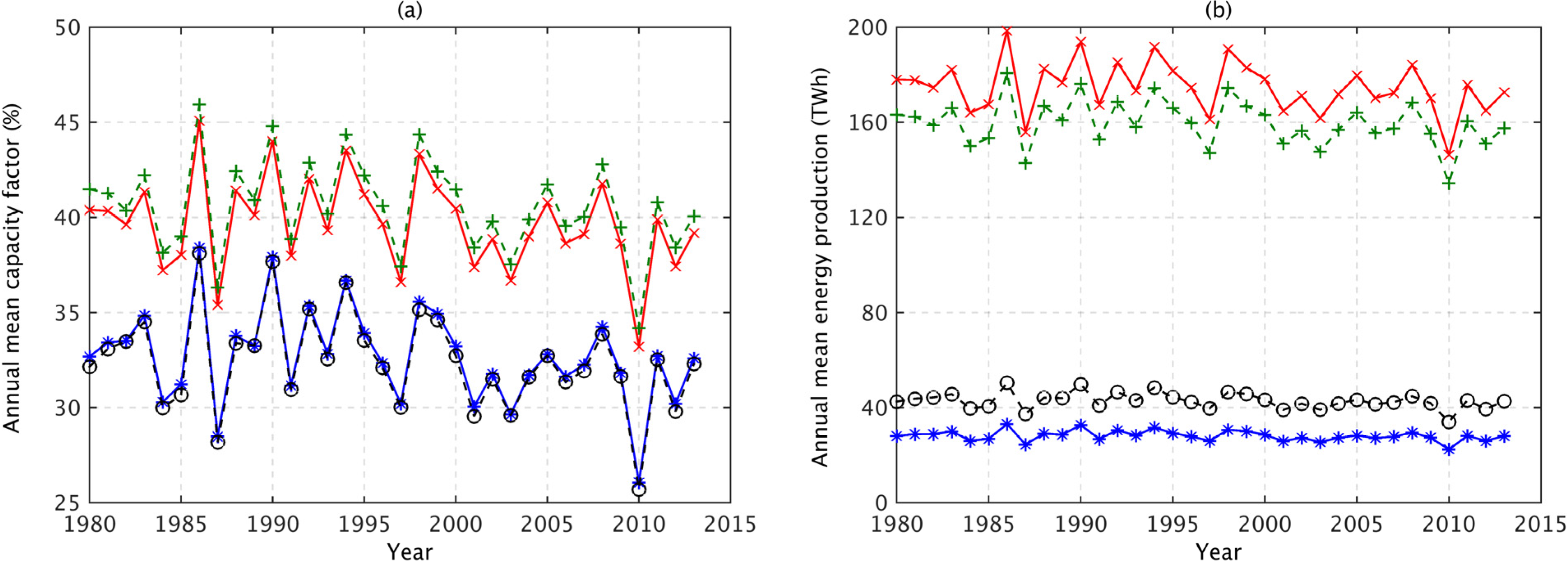
The hourly GB-aggregated capacity factor time series described in Section 2.1 has been used to analyse the annual mean capacity factor that would have been produced between 1980 and 2013, if the wind farm distributions described in Section 2.2 had been present. Figure 4a shows that for both the current and future wind farm distributions there is large year to year variability in the capacity factor. For the current wind farm distribution, the annual capacity factor varies from 25.7% to 38.4% with a mean value of 32.7% (blue line). This is slightly greater than previous long term estimates such as in [8], who derived a capacity factor of 30% based on speed records for a period of 33 years (1970–2003) from onshore sites only. The annual capacity factor of the future wind farm distribution is consistently larger, with a range of 33.2%–45.0% and a mean value of 39.7% (red line). With the future wind farm distribution, it is therefore very unlikely that the annual GB capacity factor will be as low as the current mean value, even in a very low wind speed year. It is even less likely that the annual capacity factor will fall below 30%. This could lead to an increase in the capacity credit of wind generation, and thus smaller back-up costs [20].

Figure 4. (a) The annual mean capacity factor and (b) the annual mean energy production derived using different wind distribution scenarios; current (blue), future (red), current + onshore (black) and current + offshore (green).

Figure 4. (a) The annual mean capacity factor and (b) the annual mean energy production derived using different wind distribution scenarios; current (blue), future (red), current + onshore (black) and current + offshore (green).

Figure 4b shows the annual mean energy production for each of the wind farm distributions. Over the 34-year period, the estimated energy production of the future wind farm distribution is a factor of 6.2 times greater than that for the current distribution. While, the addition of only the onshore wind farms slightly decreases the GB capacity factor, the increased capacity means that the energy production still increases by a factor of 1.5. In comparison, the addition of only the offshore wind farms increases the energy production by a factor of 5.7.

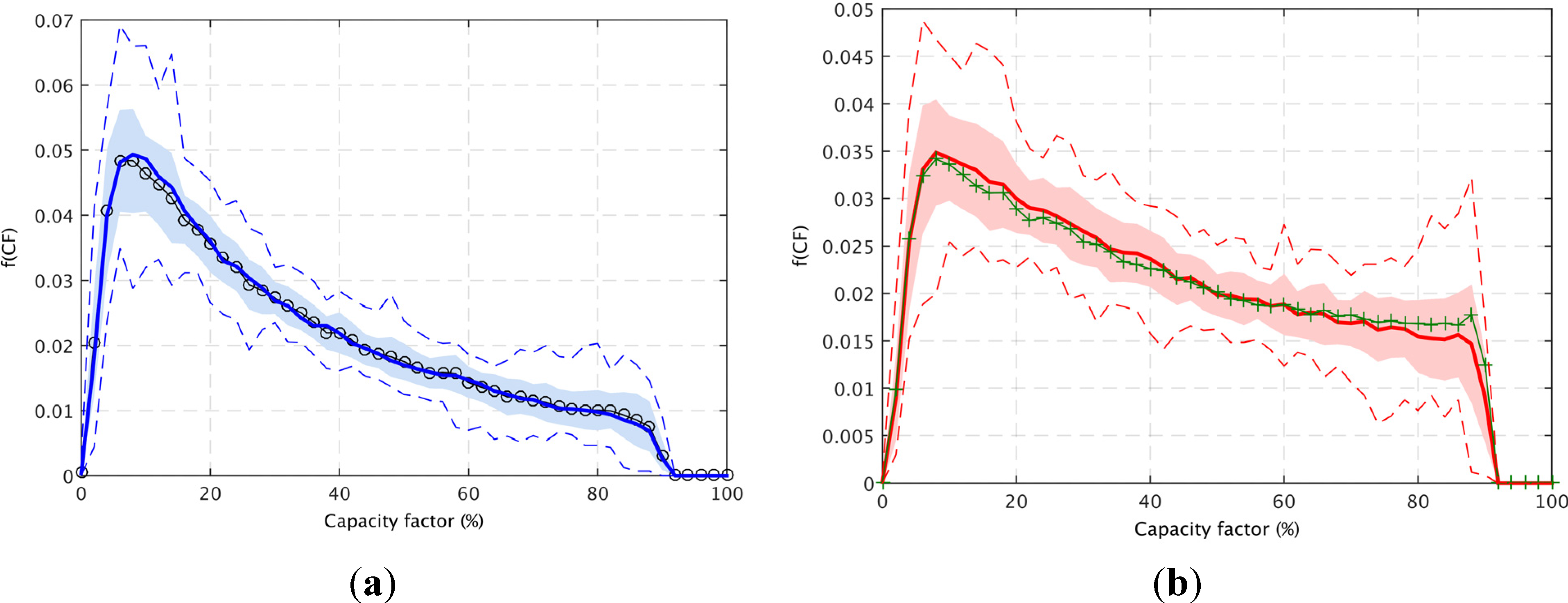
Further analysis of the hourly GB-aggregated capacity factor time series shows that for the current wind farm distribution, the frequency distribution is skewed towards low values (Figure 5a); the 25th, 50th and 75th percentile values have mean capacity factors of 12%, 25% and 48% respectively. In comparison, for the future wind farm distribution there is a shift to higher capacity factors, thus the capacity factor values are more evenly distributed (Figure 5b) and the 25th, 50th and 75th percentile values have mean capacity factors of 18%, 36% and 60% respectively.

Figure 5. The frequency density distribution of the hourly GB-aggregated capacity factor derived from the full (1980–2013) time series for (a) the “current” wind farm distribution (blue) along with the “current + onshore” distribution (black, circles); and (b) the “future” wind farm distribution (red) along with the “current + offshore” distribution (green, crosses). The plot shows the mean value for each capacity factor bin (bin size 1%) across the 34 years and the shaded areas represent ±1 standard deviation from the mean (solid) and the dashed lines indicate the minimum and maximum annual frequencies.

Figure 5. The frequency density distribution of the hourly GB-aggregated capacity factor derived from the full (1980–2013) time series for (a) the “current” wind farm distribution (blue) along with the “current + onshore” distribution (black, circles); and (b) the “future” wind farm distribution (red) along with the “current + offshore” distribution (green, crosses). The plot shows the mean value for each capacity factor bin (bin size 1%) across the 34 years and the shaded areas represent ±1 standard deviation from the mean (solid) and the dashed lines indicate the minimum and maximum annual frequencies.

In addition to the current and future scenarios, Figure 4 and Figure 5 also show results from two additional scenarios that consider the addition of future onshore and offshore wind farms separately. These results suggest that the improved performance of the future distribution is due almost entirely to the addition of offshore wind capacity. Figure 5a shows that if only the planned onshore wind projects were added to the current distribution, there is very little change in the frequency distribution of the GB-aggregated capacity factor and the 34-year mean GB-aggregated capacity factor would decrease slightly to 32.4%. In contrast, if only the offshore wind farms were added, the frequency distribution of the GB-aggregated capacity factor is shifted to the higher values and is very similar to the results for the future wind farm distribution, in this case the mean capacity factor increases to 40.6%.

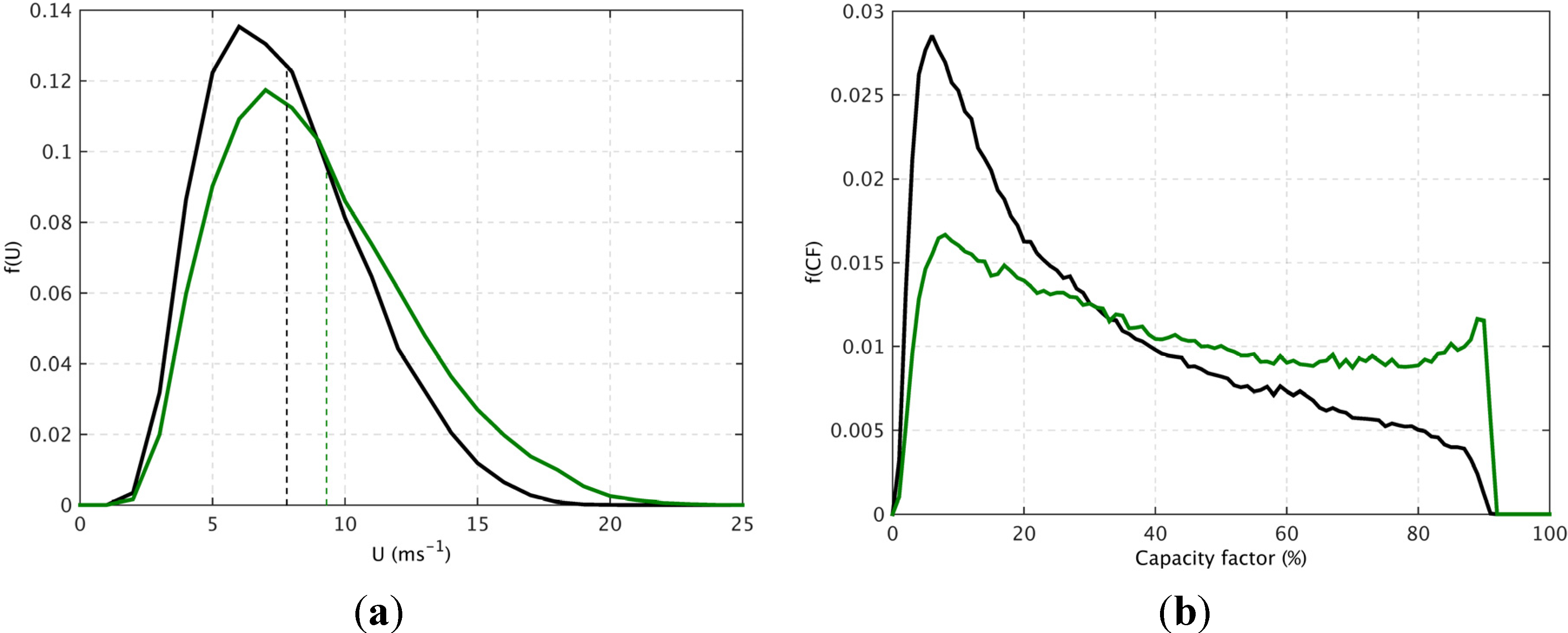
To analyse these differences in more detail, Figure 6a shows that (as expected) the offshore wind farms are more likely to experience higher wind speeds than the onshore farms. The capacity weighted 34-year mean wind speed for all of offshore wind farms in the future distribution is 9.3 ms⁻¹, compared to 7.8 ms⁻¹ for all onshore farms. As a result, the frequency distribution of hourly capacity factor values for offshore wind farms is relatively flat, while the onshore frequency distribution is clearly skewed towards low capacity factor values (Figure 6b). The 34-year mean capacity factor for the onshore farms is 31.6%, compared to 42% for the offshore farms. The latter result is broadly in agreement with that for the Danish offshore wind fleet [21]. However, it is significantly larger than the observed values from current offshore wind farms in GB. For the period 2004–2007, the Round 1 wind farms achieved a mean capacity factor of 29.5% [22]. For the same period, the mean capacity factor of the Round 1 offshore wind farms derived from the MERRA data is 33%. The difference in these values is likely to be attributable to the relatively low availability of the offshore turbines in the Round 1 wind farms. For onshore farms, the annual turbine availability is typically above 97%, however for the UK Round 1 offshore wind farms this figure is reduced to just 80% [22]. This difference is largely due to increased difficulty in accessing offshore turbines for repair or maintenance. The power curve used in this study is predominantly based on onshore wind turbines, and therefore does not take into account this reduced availability. Consequently, the capacity factors estimated in this study for the future wind farm distribution assume that the availability of offshore turbines in the larger Round 3 projects will approach the levels of availability currently found at onshore turbines.

Figure 6. A comparison of (a) the frequency distribution of the hourly capacity weighted GB mean wind speed, the dashed lines represent the capacity weighted mean wind speeds; and (b) the frequency distribution of the hourly GB-aggregated capacity factor, for the future wind farm scenario. Statistics for the onshore (black) and offshore (green) wind farms are plotted separately.

Figure 6. A comparison of (a) the frequency distribution of the hourly capacity weighted GB mean wind speed, the dashed lines represent the capacity weighted mean wind speeds; and (b) the frequency distribution of the hourly GB-aggregated capacity factor, for the future wind farm scenario. Statistics for the onshore (black) and offshore (green) wind farms are plotted separately.

3.2. A 34 Year Climatology of Persistent Low or High Wind Generation

Persistent low generation events can have serious implications for the security of supply, particularly if they coincide with periods of high demand. In contrast, as the penetration of wind capacity increases, periods of persistent high generation could lead to the deliberate curtailment of wind to ensure local load balancing. This is an inefficient use of the available resource and can lead to significant costs for the system operator [23,24]. This section uses the hourly GB-aggregated capacity factor time series to determine the magnitude and frequency of persistent low and high generation events for both the current and future wind farm distributions.

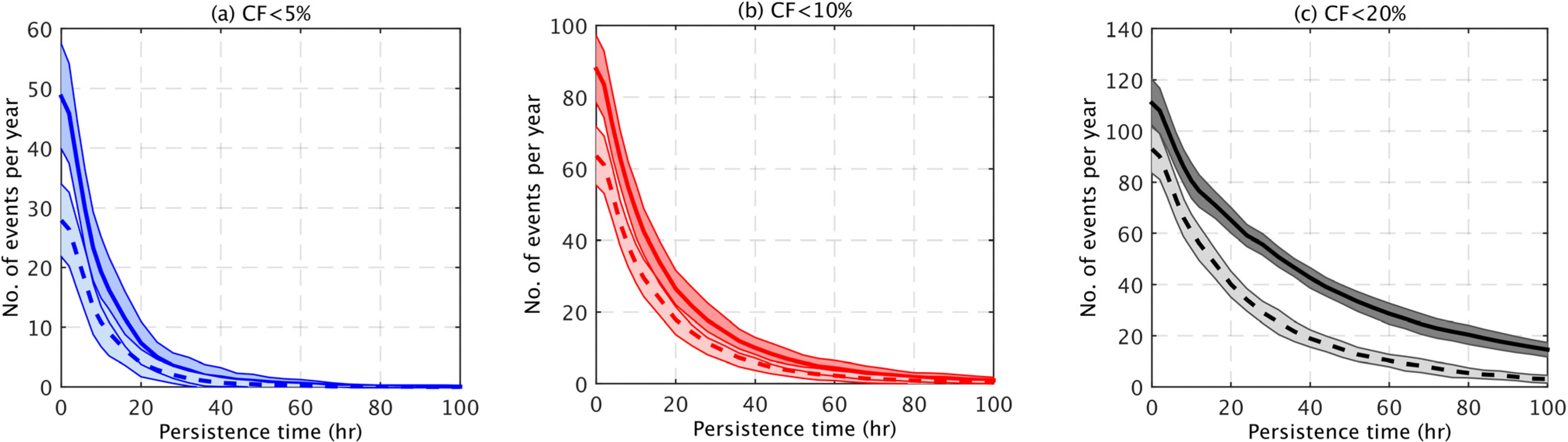
The mean frequency with which persistent low generation events occur is presented in Figure 7a–c as a function of the length of time for which the GB-aggregated capacity factor remains below a given threshold (5%, 10% and 20%). The frequency of persistent low generation events reduces as the capacity factor threshold is decreased or the persistence time increases. The figure shows the mean number of events per year for the 34 years ±1 standard deviation, as well as the minimum and maximum number of events in any one year. As in Figure 4 and Figure 5, there is large inter-annual variability in the frequency of persistence events. For example, for the current wind farm distribution the GB-aggregated capacity factor remains below 20% for at least 10 h, between 65 and 92 times per year, depending on the year.

Figure 7. The frequency of persistent low generation events for the current (solid lines) and future (dashed lines) wind farm distributions for three capacity factor thresholds: (a) 5%; (b) 10%; (c) 20%. All panels show the mean number of events per year for all 34 years ±1 standard deviation (shaded areas).

Figure 7. The frequency of persistent low generation events for the current (solid lines) and future (dashed lines) wind farm distributions for three capacity factor thresholds: (a) 5%; (b) 10%; (c) 20%. All panels show the mean number of events per year for all 34 years ±1 standard deviation (shaded areas).

Figure 7a–c also show that there are fewer persistent low generation events for the future wind farm distribution. For example, for the current distribution there are 16 occasions per year on average in which the GB-aggregated capacity factor is below 5% for at least 12 h, compared with only nine occasions for the future distribution. For the capacity thresholds of 5% and 10%, the difference between the current and future scenarios decreases as the persistence time increases. However, for the 20% capacity factor threshold, the difference between the current and future scenarios initially widens as the persistence time increases, reaching a maximum when the persistence time equals 30 h, before decreasing as the persistence time increases further.

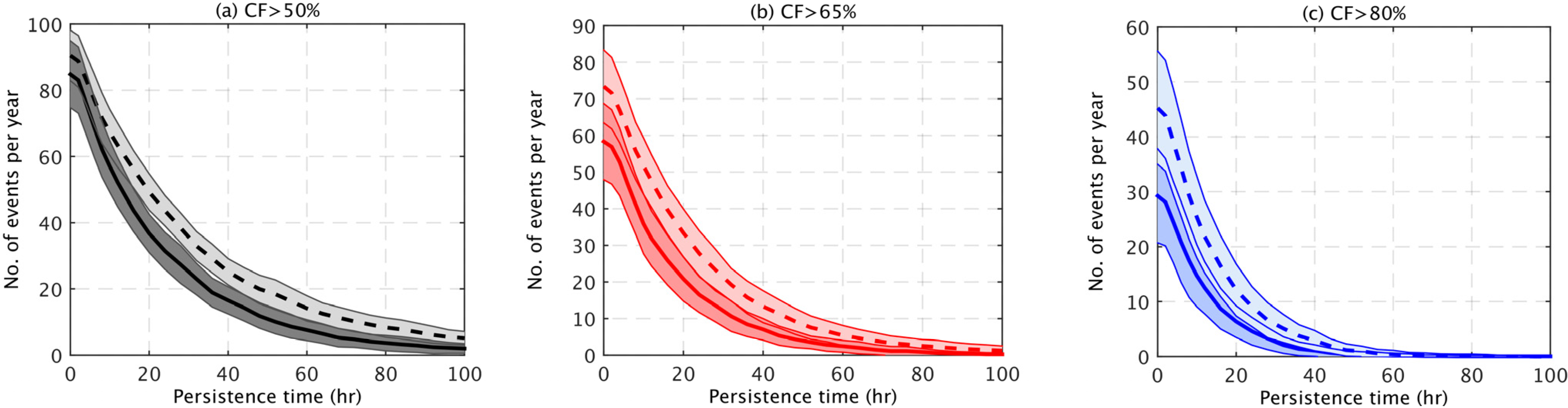
In contrast, there are a greater number of periods of persistent high generation for the future distribution than there are for the current distribution. Figure 8a–c show the mean frequency with which persistent high capacity factor events occur as a function of the length of time for which the GB-aggregated capacity factor remains above a given threshold (50%, 65% and 80%). The frequency of these events decreases as the threshold or the persistence time increases. For the current wind farm distribution, the capacity factor remains above 65% for at least 24 h 16 times a year on average, compared with 27 times per year for the future distribution.

Figure 8. The frequency of persistent high generation events for the current (solid lines) and future (dashed lines) wind farm distributions for three capacity factor thresholds: (a) 50%; (b) 65%; (c) 80%. All panels show the mean number of events per year for all 34 years ±1 standard deviation (shaded areas).

Figure 8. The frequency of persistent high generation events for the current (solid lines) and future (dashed lines) wind farm distributions for three capacity factor thresholds: (a) 50%; (b) 65%; (c) 80%. All panels show the mean number of events per year for all 34 years ±1 standard deviation (shaded areas).

The changes in the frequency of persistent generation events in Figure 7 and Figure 8 are almost entirely due to the addition of the offshore wind farms, the addition of onshore farms has very little impact. This is shown by considering the results of the “current + onshore” and “current + offshore” scenarios, which are almost identical to the results of the current and future scenarios respectively. The increased offshore capacity leads to a shift in the frequency distribution of the hourly GB-aggregated capacity factor towards higher values (Figure 5). As a consequence of this shift, the overall proportion of time for which the capacity factor is below the 5%, 10% and 20% thresholds is reduced from 6%, 20% and 42% for the current wind farm distribution to just 3%, 12% and 29% for the future distribution. In contrast, the overall proportion of time for which the GB-aggregated capacity factor exceeds the 50%, 65% and 80% thresholds is increased from 22%, 12% and 3% for the current distribution to 35%, 20% and 8% for the future distribution.

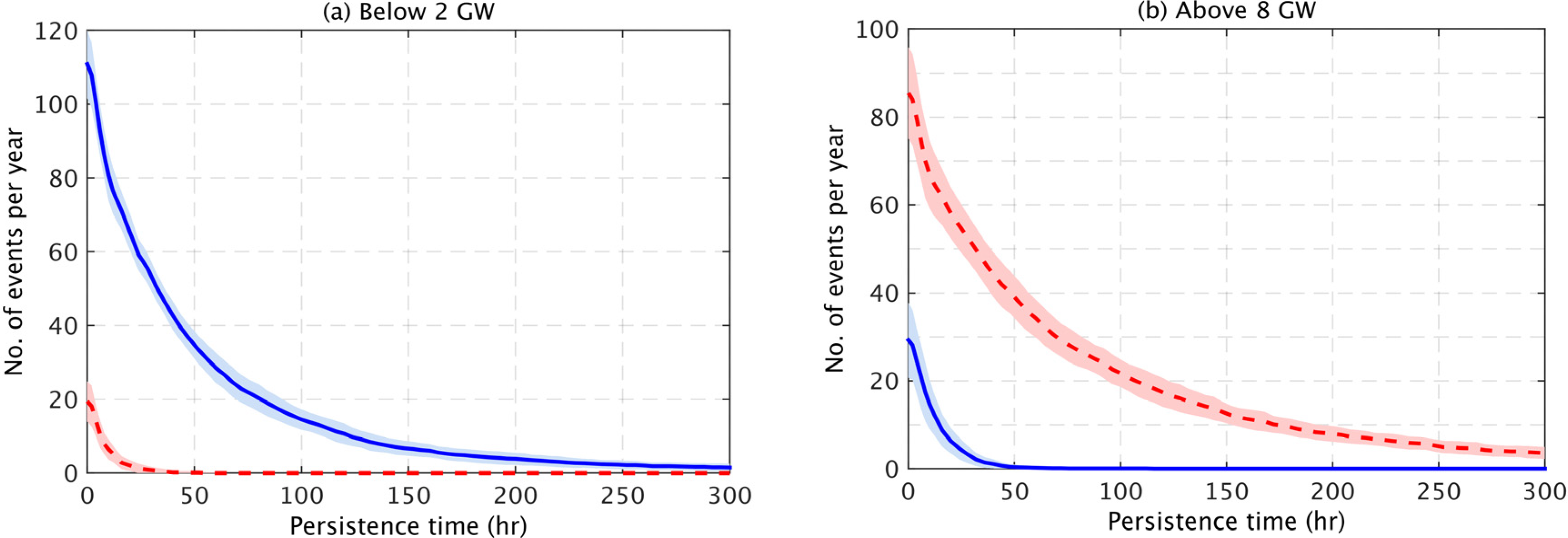
Given the difference in the capacity between the current (10.2 GW) and future distributions (50 GW) it is also important to consider the persistence of events defined by a fixed power output threshold. Figure 9a shows that for the future distribution, there are very few ocassions in a year where the GB mean power output is persistently below 2 GW, for any period of time. In contrast, for the current distribution, the power output falls below this threshold more frequently. For example, for the future distribution there is an average of only one event per year when the power output is below 2 GW for a period of 24 h, in comparison to 59 events per year for the current distribution. Figure 9b shows that for the current distribution, there are few events where the GB mean power output is persistently greater than 8 GW. In contrast, for the future distribution this corresponds to a capacity factor of only 16% and therefore such events occur more frequently. For example, for the current distribution the GB power output is greater than 8 GW for a period of 24 h on only five occasions per year on average, in comparison to 55 events per year for the future distribution.

Figure 9. The frequency of events for which: (a) the GB mean power output is persistently below 2 GW; and (b) the GB mean power output is persistently above 8 GW. Both panels show the mean value for the current (blue) and future (red) distributions ±1 standard deviation.

Figure 9. The frequency of events for which: (a) the GB mean power output is persistently below 2 GW; and (b) the GB mean power output is persistently above 8 GW. Both panels show the mean value for the current (blue) and future (red) distributions ±1 standard deviation.

3.3. A 34 Year Climatology of Ramping Events

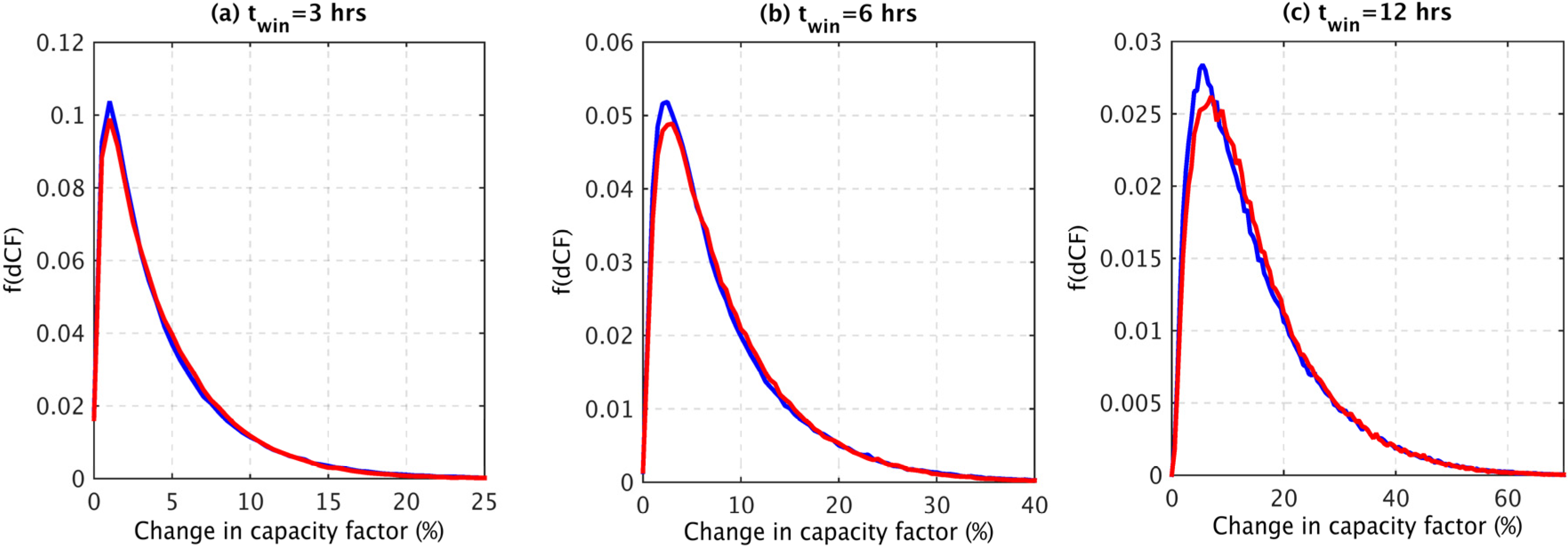
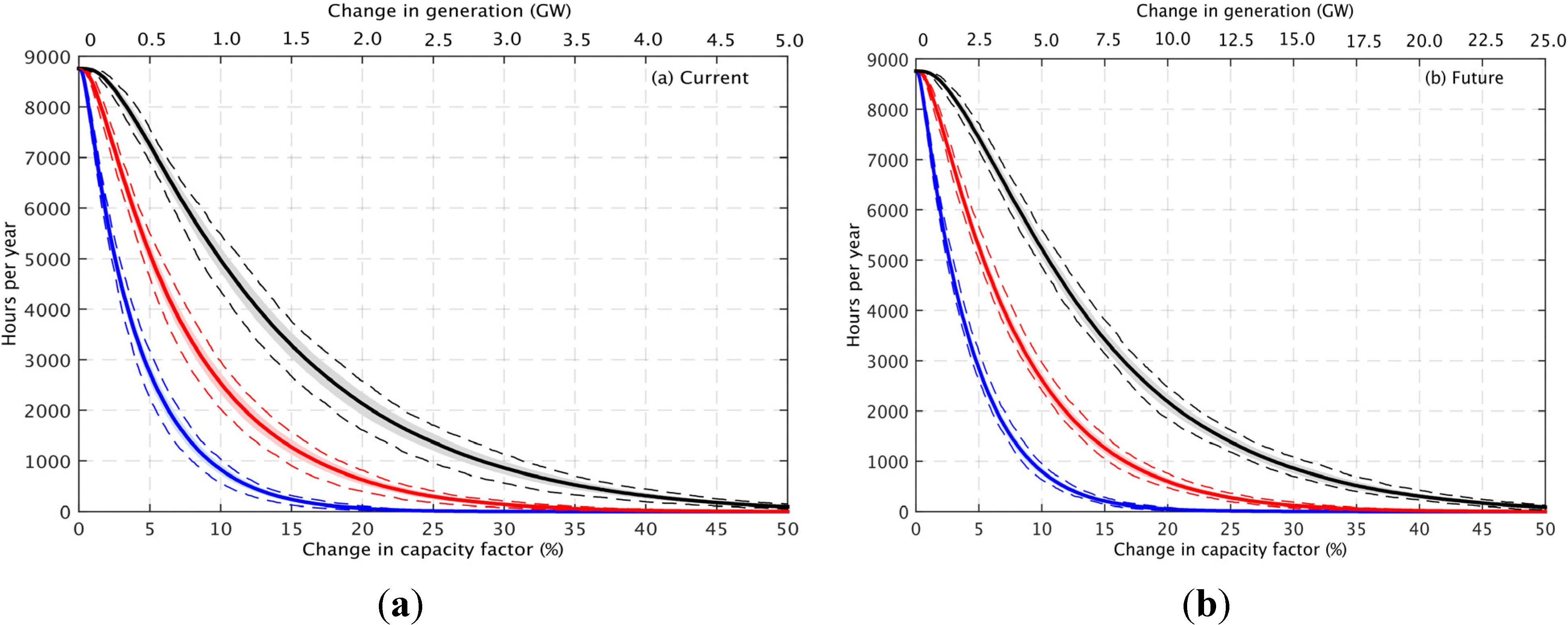
Ramping events are a major concern for power system operators as they can lead to large forecast errors which can have significant implications for the cost of balancing the system. As the penetration of wind increases, the implications of these errors will become greater. Figure 10a–c show the frequency distribution of current and future ramping events within three time windows: Δt = 3, 6 and 12 h. The figures suggest that, despite the fact that the offshore wind farms typically experience higher wind speeds than those onshore and therefore operate in a different region of the power curve, the frequency and magnitude of ramping events is largely insensitive to the change in wind farm distribution. Nevertheless, as the capacity of the future wind farm distribution is significantly greater than the current distribution, a similar change in capacity factor equates to a change in power which is approximately five times greater for the future distribution (Figure 11). For example, for the current distribution a swing of 2.5 GW within 3 h (corresponding to a capacity factor of 25%) occurs on 14 occasions in an average year. However, for the future distribution a similar swing (2.5 GW within 3 h) corresponds to only a 5% swing in capacity factor and occurs much more frequently (for 2900 occasions in an average year).

Figure 10. The frequency distribution of ramping events for the current (blue) and future (red) wind farm distributions for three time windows: (a) t_win = 3 h; (b) t_win = 6 h; and (c) t_win = 12 h.

Figure 10. The frequency distribution of ramping events for the current (blue) and future (red) wind farm distributions for three time windows: (a) t_win = 3 h; (b) t_win = 6 h; and (c) t_win = 12 h.

Figure 11. The frequency distribution of ramping events for the (a) current and (b) future wind farm distribution. The figures show the mean number of hours per year for which there is a subsequent ramp of at least ΔCF (also expressed as ΔP) within different time windows t_win = 3 (blue), 6 (red) and 12 (black) h. The shaded area represents ±1 standard deviation, and the dashed lines represent the minimum and maximum numbers for any one year.

Figure 11. The frequency distribution of ramping events for the (a) current and (b) future wind farm distribution. The figures show the mean number of hours per year for which there is a subsequent ramp of at least ΔCF (also expressed as ΔP) within different time windows t_win = 3 (blue), 6 (red) and 12 (black) h. The shaded area represents ±1 standard deviation, and the dashed lines represent the minimum and maximum numbers for any one year.

These results suggest that whilst the swings in capacity factor in the future will be similar to those currently experienced, the increased future capacity implies that the system operator will need to frequently manage much larger power swings than are experienced at present.

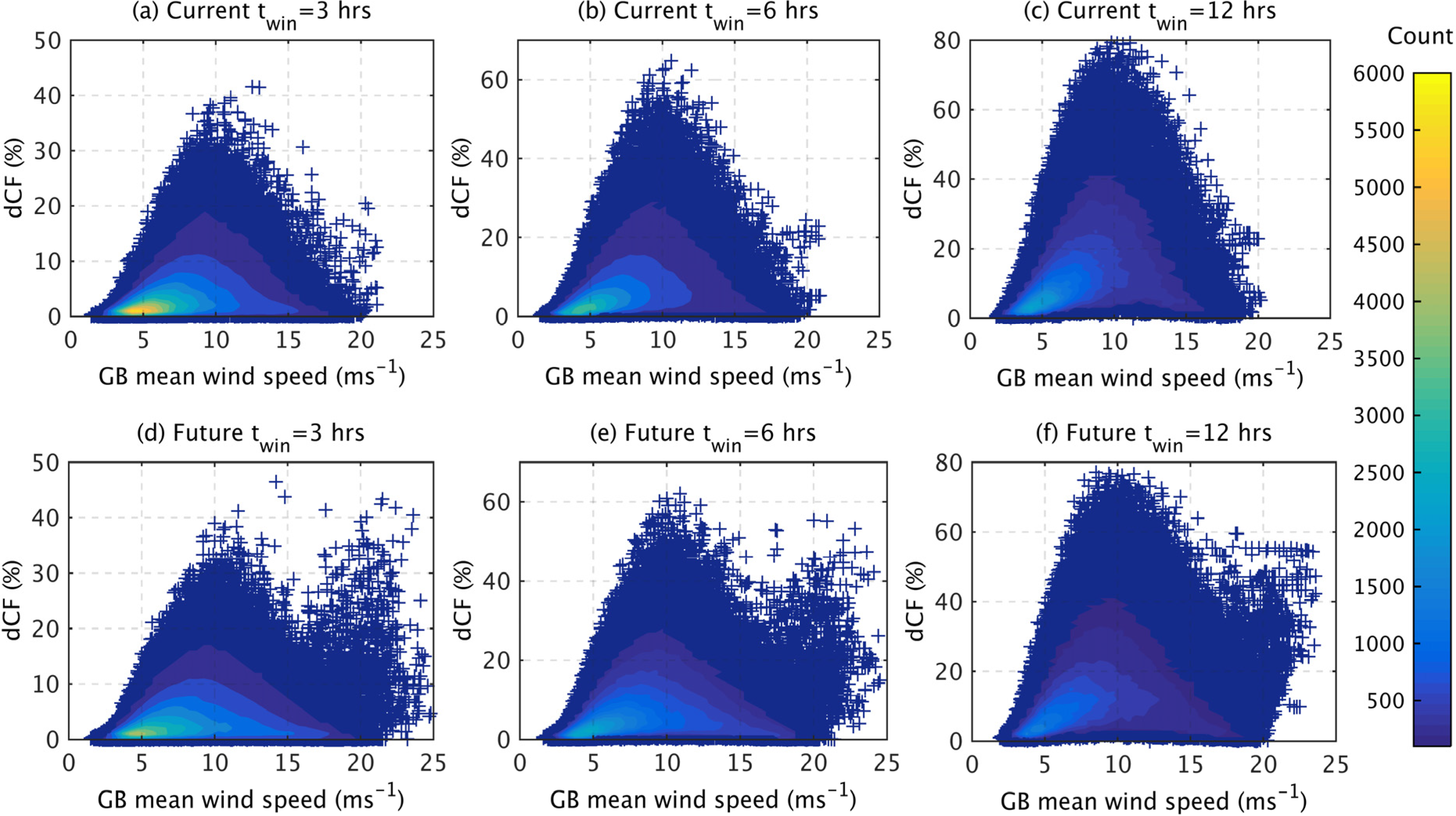
While the overall frequency distribution of the ramping events is largely unchanged (Figure 10), it should be noted that for individual cases the ambient meteorological conditions can sometimes elicit very different ramping responses from the current and future wind fleets. To investigate this, Figure 12 shows the frequency of different ramp magnitudes as a function of the GB capacity weighted mean wind speed. In general, the shape of the distributions is very similar for the current and future wind fleets, with the majority of the large ramping events occurring at moderate GB mean wind speeds. However, for the future distribution a second peak emerges at high wind speeds (approx. 20 ms⁻¹), which can be attributed to turbine cut-out. These events are very rare and only occur on approximately 800 occasions (less than 0.25% of the time), but nonetheless need to managed by the system operator.

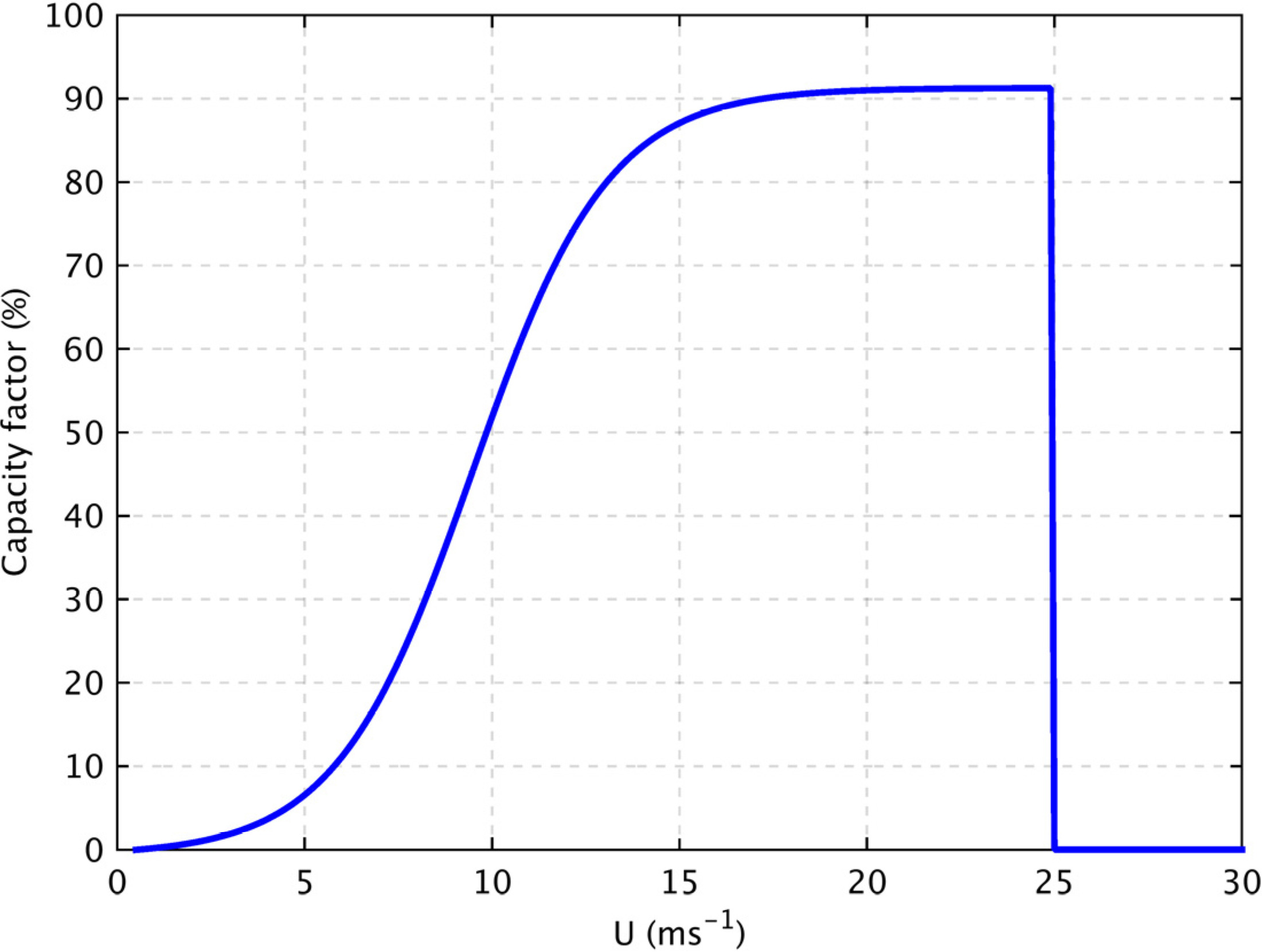
During some high wind events, a lot of wind farms in the current distribution operate at or just below their rated power, where a change in wind speed induces only a small change in power output (Figure 1). For the future distribution, a lot of wind farms are located offshore and thus experience higher wind speeds. In such cases, an increase in wind speed can lead to very large power swings as large offshore farms cut-out (Figure 1). This suggests that in the current scenario, cut-out events rarely contribute to the highest national ramping events, but with the move offshore, the cut-out events become more prominent and can contribute to the highest national ramps. These events are however very rare and of similar magnitude to moderate wind speed events (U_GB = 7.5–12.5 ms⁻¹). Further analysis has shown that for both distributions and all time windows, over 80% of these events occur in the winter months (December to February) and none occur in the summer months (June to August).

Figure 12. The frequency of ramping events as a function of the magnitude in the ramp (expressed as a change in GB-aggregated capacity factor) and the GB capacity weighted mean wind speed. The analysis has been completed for three time windows t_win = 3 h, t_win = 6 h and t_win = 12 h for the current (a–c) and future (d–f) wind farm distributions. The individual points show the full dataset, while the contours detail the density of the points in wind speed bins of 0.25 ms⁻¹ and ΔCF of 1% (above 100 occurrences).

Figure 12. The frequency of ramping events as a function of the magnitude in the ramp (expressed as a change in GB-aggregated capacity factor) and the GB capacity weighted mean wind speed. The analysis has been completed for three time windows t_win = 3 h, t_win = 6 h and t_win = 12 h for the current (a–c) and future (d–f) wind farm distributions. The individual points show the full dataset, while the contours detail the density of the points in wind speed bins of 0.25 ms⁻¹ and ΔCF of 1% (above 100 occurrences).

4. Conclusions

This paper assesses the potential impact of a large increase in offshore wind capacity on the characteristics of national wind power in Great Britain (GB). While the results in this paper are specifically relevant to Great Britain, the impact of the change in wind farm distribution on the variability of the generation is likely to impact other parts of the world, particularly in regions which are planning significant proportions of offshore capacity.

Following the method outlined in [12], a state-of-the-art reanalysis data set is used to derive hourly time series of the GB-aggregated wind power generation for a 34 year period (1980–2013), assuming particular fixed distributions of wind farms. To assess the impact of potential future changes in the wind power resource, results using two primary distributions are compared: (1) a “current” wind farm distribution from April 2014; and (2) a “future” scenario including a large amount of additional offshore wind capacity. This “future” distribution includes the development of the Round 3 offshore zones and corresponds to the “Gone Green” post-2025 scenario outlined by the system operator [19]. The performance of this method for offshore sites is validated using recorded wind power output from a cluster of offshore wind farms in South East England.

The future long term mean wind energy yield is estimated to be around 6.2 times larger than that generated by the current wind fleet. Most of this increase is due to the increase in total wind capacity (from 10.15 GW to 50 GW). As offshore wind farms tend to experience higher wind speeds however, there is also an increase in the long term mean GB-aggregated capacity factor (from 32.7% to 39.7%). The corresponding shift in the frequency distribution towards higher values means that there are fewer instances of low generation, implying that the low-yield experienced nationally in 2010 would become very unlikely in this future scenario. These results assume that the availability of offshore turbines in the Round 3 projects will approach the average availability observed with the “current” (mostly onshore) wind fleet.

Extreme events, such as persistent periods of low or high generation and large ramps in generation, are of particular concern to power system operators. The number of persistent low generation events decreases substantially in the “future” scenario, with a corresponding, but smaller increase in the number of persistent high generation events. This is due to both the increase in GB capacity and the shift in the frequency distribution of capacity factor towards higher values. The magnitude of ramps in power output increases by around a factor of 5 between the “current” and “future” scenarios. However, there is very little difference in the number of ramping events when considered as a change in GB-aggregated capacity factor. Detailed examination of these results suggests there is potential for an increase in the number of ramping events associated with high wind speed cut-out in the “future” scenario. In the “current” scenario, cut-out events do occur but rarely contribute to the largest national ramping events. With the move offshore, the cut-out events become more prominent and form a significant component of the largest national ramps. However, it should be noted that the magnitude of these ramps remains within the range observed for the current wind farm distribution. Design stage attention to the cut-out level of future offshore wind farms could therefore improve the operability of the envisaged future power system and further research is recommended.

The results show an expected large year to year variability in the wind generation; the annual capacity factor varies from 33.2% to 45.0% for the future wind farm distribution. While the 34-year time series used in this study is able to characterise most of the present day inter-annual variability of the wind resource, the potential for longer term variations in the resource, in terms of both its “average” and extreme characteristics, is a subject which deserves much greater research attention. Significant inter-annual and inter-decadal variations in wind-speed have been shown to occur across the 20th Century [7,10,25], and would have had significant impacts on wind-power resources [25,26]. Progress on assessing long-term variations and the potential for future trends ([e.g., [27]), can continue to be made through a thorough combination of long-term meteorological reanalyses and appropriate use of well-calibrated high-quality global climate model simulations.