Application of Machine Learning Algorithms to Predict Gas Sorption Capacity in Heterogeneous Porous Material
Abstract
1. Introduction
2. Methods
2.1. Aims and Workflow
2.2. Machine Learning Base Models
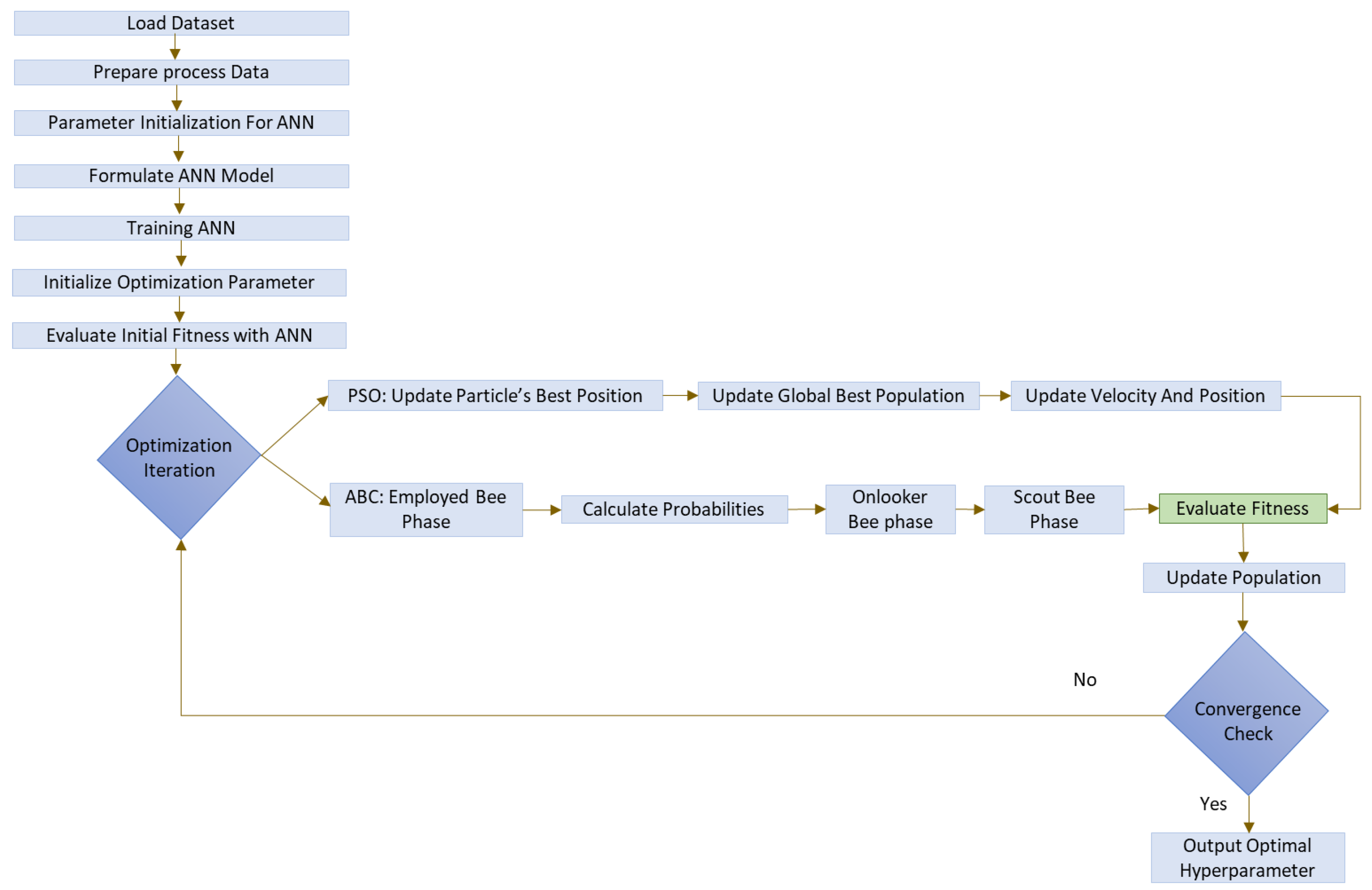
2.2.1. Artificial Neural Network (ANN)
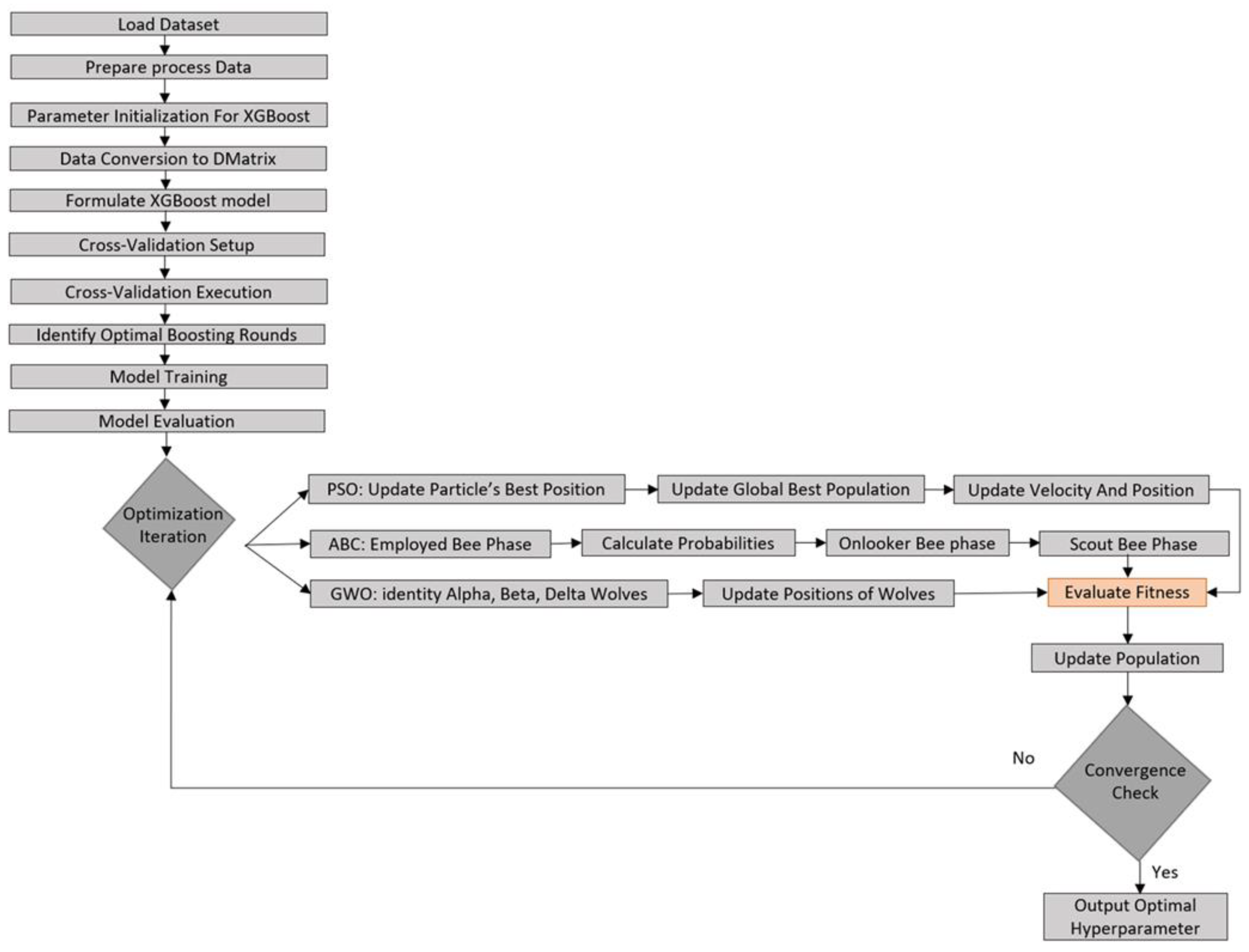
2.2.2. Extreme Gradient Boosting (XGBoost)
2.2.3. Artificial Bee Colony (ABC) Optimization
2.2.4. Particle Swarm Optimization (PSO)
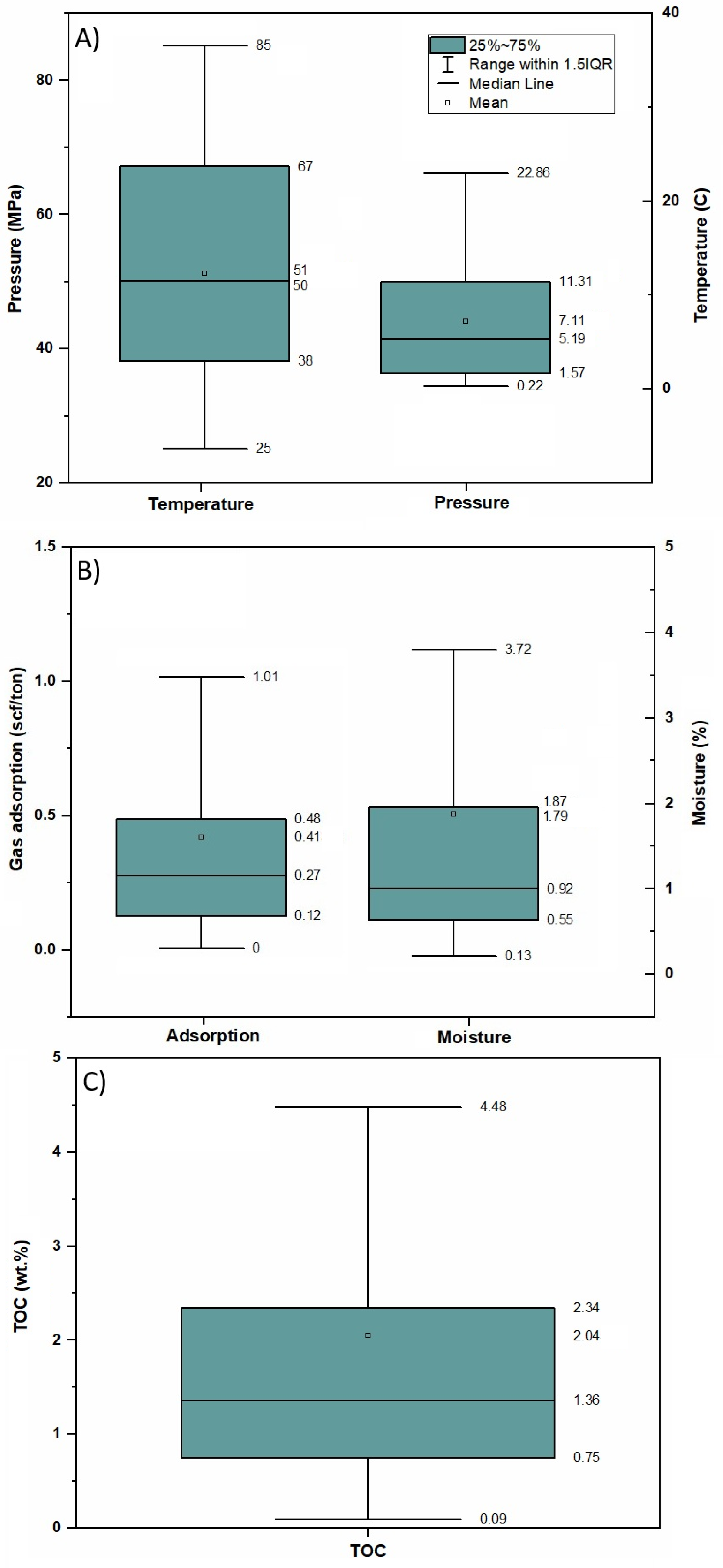
2.3. Data Acquisition
3. Results and Discussion
3.1. Numerical Model for Shale Gas in Heterogeneous Porous Material
3.1.1. Input Variables and Output
- -
- Total organic carbon (TOC, wt%).
- -
- Temperature (T, °C or K).
- -
- Pressure (P, MPa).
- -
- Moisture content (M, wt%).
- -
- Output (Y): Methane sorption capacity (MSC, mmol/g).
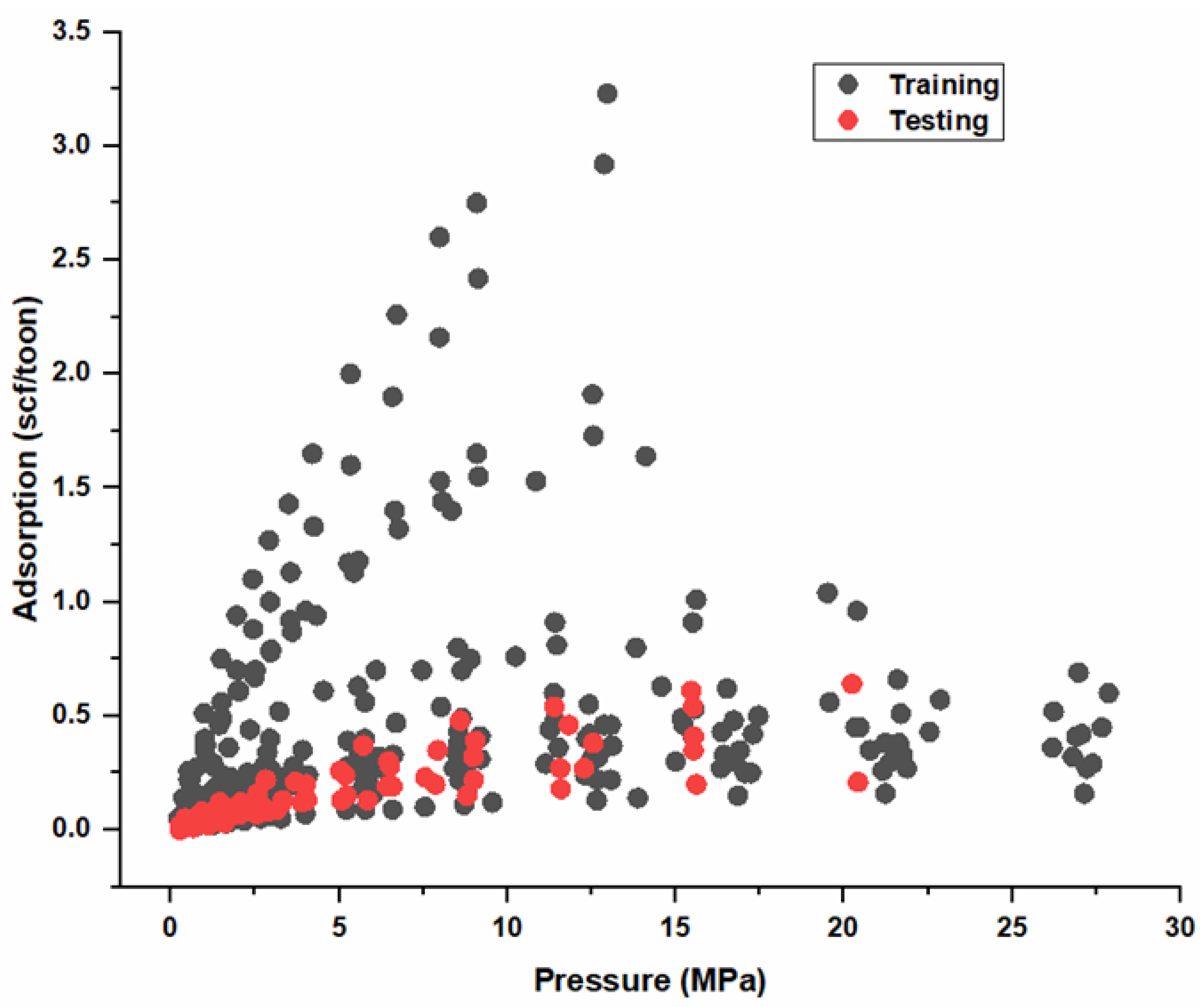
3.1.2. Data Preprocessing
3.1.3. Machine Learning Models
- XGBoost Model:
- ANN Model:
- -
- Input layer: 4 neurons (TOC, T, P, M).
- -
- Hidden layers: (28, 50) neurons (ABC) or (41, 88) neurons (PSO).
- -
- Output layer: 1 neuron (MSC).
- -
- Activation: ReLU for hidden layers, linear for output.
- -
- Loss Function: MSE.
- -
- PSO: Updates weights by minimizing MSE via particle swarm dynamics.
- -
- ABC: Adjusts weights using bee colony foraging behavior.
3.1.4. Optimization Algorithms
- Particle Swarm Optimization (PSO):
- -
- (w): Inertia weight; (c1, c2): Learning factors; (r1, r2): Random numbers.
- Artificial Bee Colony (ABC)
3.1.5. Performance Metrics
- -
- R2 (Coefficient of Determination):
- -
- RMSE (Root Mean Squared Error):
3.2. Hyperparameter Optimization
3.2.1. Optimization of ANN with PSO and ABC
3.2.2. Optimization of XGBoost with PSO and ABC
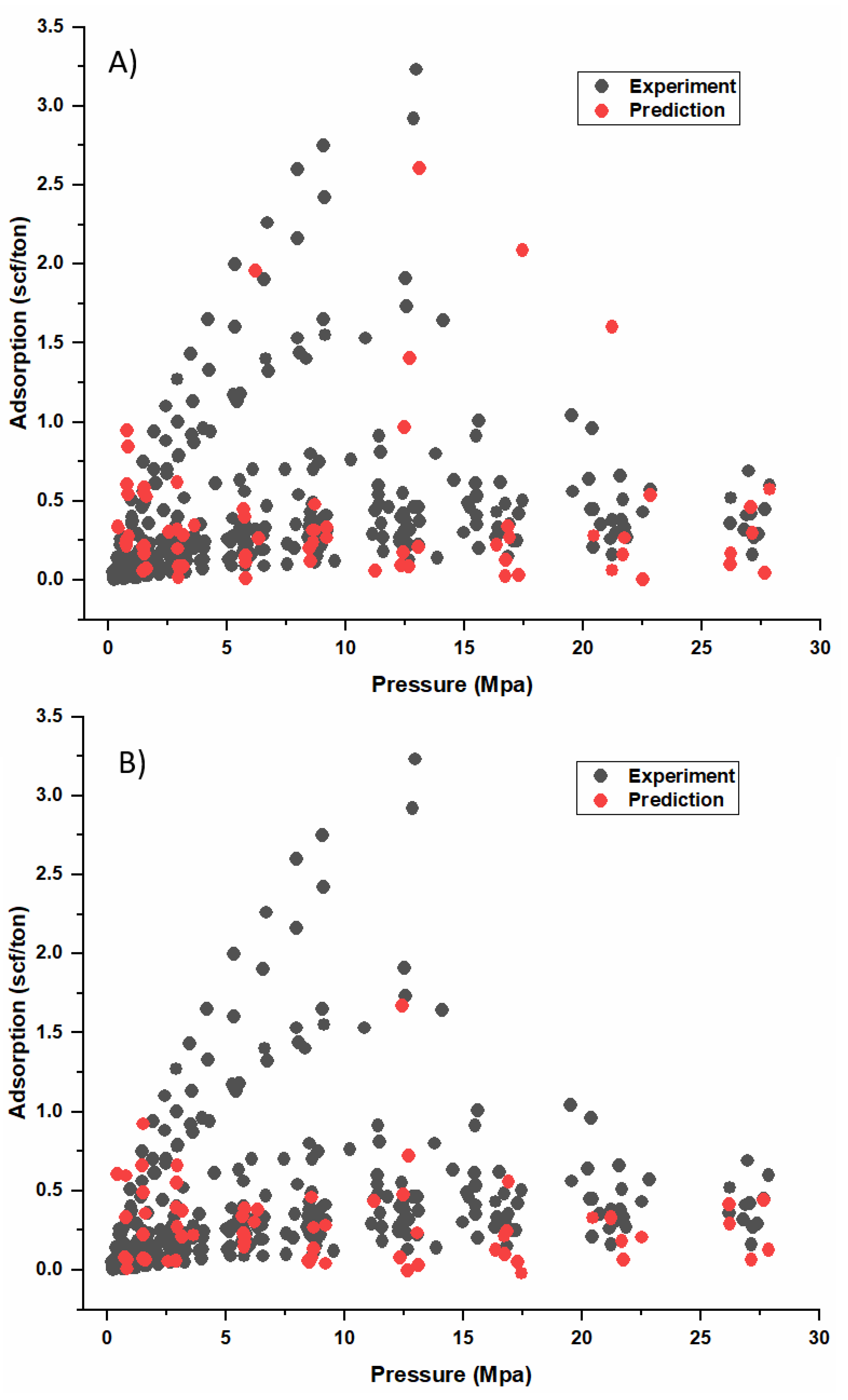
3.3. Model Calibration, Validation, and Performance Evaluation
3.4. Comparison of Proposed ML Model with Previous Model
3.4.1. Learning Approach and Model Complexity
3.4.2. Performance Comparison and Prediction Accuracy
3.4.3. Computational Efficiency and Accuracy
4. Conclusions
- Hybrid XGBoost models underperform, likely due to the incompatibility of boosting algorithms with ABC and PSO optimization techniques.
- The hybrid ANN-ABC and ANN-PSO models in this study outperform traditional ML models by enhancing prediction accuracy through SI optimization and improving adaptability to diverse shale gas reservoir conditions.
- This study offers a reliable numerical modeling framework for predicting methane sorption in heterogeneous shale formations by integrating XGBoost and ANN optimized by PSO and ABC. The models efficiently capture nonlinear interactions among geochemical and thermodynamic factors, giving greater accuracy for gas-in-place predictions in shale gas reservoirs.
- The findings in this work represent an advanced approach to MSC prediction, leveraging the strengths of deep learning and SI for improved accuracy, efficiency, and scalability.
- The petroleum industry can utilize this model in commercial software to predict the amount of producible gas in shale reservoirs and make it easier for these reservoirs to operate.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| XGBoost | Extreme gradient boosting |
| ANN | Artificial neural network |
| ABC | Artificial bee colony |
| PSO | Particle swarm optimization |
| GPR | Gaussian Process Regression |
| GEP | Gene expression programming |
| GWO | Gray wolf optimizer |
| SVM | Support vector machine |
| SVR | Support vector regression |
| SSA | Sparrow search algorithm |
| GIP | Gas-in-place |
| MSC | Methane sorption capacity |
| ML | Machine learning |
| TOC | Total organic carbon |
| SI | Swarm intelligence |
References
- Zhang, W.; Chen, W.; Wang, T.; Yuan, Y. A self-similarity mathematical model of carbon isotopic flow fractionation during shale gas desorption. Phys. Fluids 2019, 31, 112005. [Google Scholar]
- Gu, J.; Liu, G.; Gao, F.; Hu, Y.; Ye, D. Multiple seepage model and gas production simulation of shale with power law fracture distribution. Phys. Fluids 2023, 35, 11. [Google Scholar]
- Middleton, R.S.; Gupta, R.; Hyman, J.D.; Viswanathan, H.S. The shale gas revolution: Barriers, sustainability, and emerging opportunities. Appl. Energy 2017, 199, 88–95. [Google Scholar]
- Huang, H.; Sun, W.; Xiong, F.; Chen, L.; Li, X.; Gao, T.; Jiang, Z.; Ji, W.; Wu, Y.; Han, J. A novel method to estimate subsurface shale gas capacities. Fuel 2018, 232, 341–350. [Google Scholar]
- Huang, H.; Li, R.; Jiang, Z.; Li, J.; Chen, L. Investigation of variation in shale gas adsorption capacity with burial depth: Insights from the adsorption potential theory. J. Nat. Gas Sci. Eng. 2020, 73, 103043. [Google Scholar]
- Tang, X.; Ripepi, N.; Stadie, N.P.; Yu, L.; Hall, M.R. A dual-site Langmuir equation for accurate estimation of high pressure deep shale gas resources. Fuel 2016, 185, 10–17. [Google Scholar]
- Fan, L.; Liu, S. A novel experimental system for accurate gas sorption and its application to various shale rocks. Chem. Eng. Res. Des. 2021, 165, 180–191. [Google Scholar]
- Middleton, R.S.; Carey, J.W.; Currier, R.P.; Hyman, J.D.; Kang, Q.; Karra, S.; Jiménez-Martínez, J.; Porter, M.L.; Viswanathan, H.S. Shale gas and non-aqueous fracturing fluids: Opportunities and challenges for supercritical CO2. Appl. Energy 2015, 147, 500–509. [Google Scholar]
- International Energy Agency (IEA). World Energy Outlook 2022; International Energy Agency (IEA): Paris, France, 2022. [Google Scholar]
- Tang, H.; Yu, Y.; Sun, Q. Progress, Challenges, and Strategies for China’s Natural Gas Industry Under Carbon-Neutrality Goals. Processes 2024, 12, 1683. [Google Scholar]
- Rivard, C.; Lavoie, D.; Lefebvre, R.; Séjourné, S.; Lamontagne, C.; Duchesne, M. An overview of Canadian shale gas production and environmental concerns. Int. J. Coal Geol. 2014, 126, 64–76. [Google Scholar]
- Wang, Q.; Li, R. Research status of shale gas: A review. Renew. Sustain. Energy Rev. 2017, 74, 715–720. [Google Scholar]
- Hays, J.; Finkel, M.L.; Depledge, M.; Law, A.; Shonkoff, S.B.C. Considerations for the development of shale gas in the United Kingdom. Sci. Total Environ. 2015, 512, 36–42. [Google Scholar]
- Negi, B.S.; Pandey, K.K.; Sehgal, N. Renewables, shale gas and gas import-striking a balance for India. Energy Procedia 2017, 105, 3720–3726. [Google Scholar]
- Costa, D.; Neto, B.; Danko, A.S.; Fiúza, A. Life Cycle Assessment of a shale gas exploration and exploitation project in the province of Burgos, Spain. Sci. Total Environ. 2018, 645, 130–145. [Google Scholar]
- Ibad, S.M.; Padmanabhan, E. Methane sorption capacities and geochemical characterization of Paleozoic shale Formations from Western Peninsula Malaysia: Implication of shale gas potential. Int. J. Coal Geol. 2020, 224, 103480. [Google Scholar] [CrossRef]
- Ibad, S.M.; Padmanabhan, E. Inorganic geochemical, mineralogical and methane sorption capacities of Paleozoic shale formations from Western Peninsular Malaysia: Implication of shale gas potential. Appl. Geochem. 2022, 140, 105269. [Google Scholar] [CrossRef]
- Davenport, J.; Wayth, N. Statistical Review of World Energy; Energy Institute: London, UK, 2023. [Google Scholar]
- Lin, X.; Liu, C.; Wang, Z. The influencing factors of gas adsorption behaviors in shale gas reservoirs. Front. Earth Sci. 2023, 10, 1021983. [Google Scholar]
- Hu, K.; Zhang, Q.; Liu, Y.; Thaika, M.A. A developed dual-site Langmuir model to represent the high-pressure methane adsorption and thermodynamic parameters in shale. Int. J. Coal Sci. Technol. 2023, 10, 59. [Google Scholar]
- Chen, L.; Zuo, L.; Jiang, Z.; Jiang, S.; Liu, K.; Tan, J.; Zhang, L. Mechanisms of shale gas adsorption: Evidence from thermodynamics and kinetics study of methane adsorption on shale. Chem. Eng. J. 2019, 361, 559–570. [Google Scholar]
- Meng, M.; Zhong, R.; Wei, Z. Prediction of methane adsorption in shale: Classical models and machine learning based models. Fuel 2020, 278, 118358. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhao, L.; Zhang, D. Study of adsorption behavior in shale reservoirs under high pressure. J. Nat. Gas. Sci. Eng. 2018, 49, 275–285. [Google Scholar]
- Curtis, J.B. Fractured shale-gas systems. Am. Assoc. Pet. Geol. Bull. 2002, 86, 1921–1938. [Google Scholar]
- Li, Q.; Li, Q.; Cao, H.; Wu, J.; Wang, F.; Wang, Y. The Crack Propagation Behaviour of CO2 Fracturing Fluid in Unconventional Low Permeability Reservoirs: Factor Analysis and Mechanism Revelation. Processes 2025, 13, 159. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, S. Review of shale gas sorption and its models. Energy Fuels 2020, 34, 15502–15524. [Google Scholar]
- Razavi, R.; Bemani, A.; Baghban, A.; Mohammadi, A.H.; Habibzadeh, S. An insight into the estimation of fatty acid methyl ester based biodiesel properties using a LSSVM model. Fuel 2019, 243, 133–141. [Google Scholar]
- Dashti, A.; Raji, M.; Alivand, M.S.; Mohammadi, A.H. Estimation of CO2 equilibrium absorption in aqueous solutions of commonly used amines using different computational schemes. Fuel 2020, 264, 116616. [Google Scholar]
- Daneshfar, R.; Bemani, A.; Hadipoor, M.; Sharifpur, M.; Ali, H.M.; Mahariq, I.; Abdeljawad, T. Estimating the heat capacity of non-Newtonian ionanofluid systems using ANN, ANFIS, and SGB tree algorithms. Appl. Sci. 2020, 10, 6432. [Google Scholar]
- Nabipour, N.; Daneshfar, R.; Rezvanjou, O.; Mohammadi-Khanaposhtani, M.; Baghban, A.; Xiong, Q.; Li, L.K.; Habibzadeh, S.; Doranehgard, M.H. Estimating Biofuel Density Via a Soft Computing Approach Based Intermolecular interactions. Renew. Energy 2020, 152, 1086–1098. [Google Scholar]
- Karkevandi-Talkhooncheh, A.; Rostami, A.; Hemmati-Sarapardeh, A.; Ahmadi, M.; Husein, M.M.; Dabir, B. Modeling minimum miscibility pressure during pure and impure CO2 flooding using hybrid of radial basis function neural network and evolutionary techniques. Fuel 2018, 220, 270–282. [Google Scholar]
- Rostami, A.; Hemmati-Sarapardeh, A.; Shamshirband, S. Rigorous prognostication of natural gas viscosity: Smart modeling and comparative study. Fuel 2018, 222, 766–778. [Google Scholar]
- Daneshfar, R.; Keivanimehr, F.; Mohammadi-Khanaposhtani, M.; Baghban, A. A neural computing strategy to estimate dew-point pressure of gas condensate reservoirs. Pet. Sci. Technol. 2020, 38, 706–712. [Google Scholar]
- Vanani, M.B.; Daneshfar, R.; Khodapanah, E. A novel MLP approach for estimating asphaltene content of crude oil. Pet. Sci. Technol. 2019, 37, 2238–2245. [Google Scholar]
- Najafi-Marghmaleki, A.; Tatar, A.; Barati-Harooni, A.; Arabloo, M.; Rafiee-Taghanaki, S.; Mohammadi, A.H. Reliable modeling of constant volume depletion (CVD) behaviors in gas condensate reservoirs. Fuel 2018, 231, 146–156. [Google Scholar]
- Syah, R.; Naeem, M.H.T.; Daneshfar, R.; Dehdar, H.; Soulgani, B.S. On the prediction of methane adsorption in shale using grey wolf optimizer support vector machine approach. Petroleum 2022, 8, 264–269. [Google Scholar] [CrossRef]
- Zhou, Y.; Hui, B.; Shi, J.; Shi, H.; Jing, D. Machine learning method for shale gas adsorption capacity prediction and key influencing factors evaluation. Phys. Fluids 2024, 36, 016604. [Google Scholar]
- Chinamo, D.S.; Bian, X.; Liu, Z.; Cheng, J.; Huang, L. Estimation of Adsorption Gas in Shale Gas Reservoir by Using Machine Learning Methods. SSRN 4885195. 2024. Available online: https://www.ijfmr.com/papers/2024/5/27082.pdf (accessed on 16 April 2025).
- Beaton, A.P.; Pawlowicz, J.G.; Anderson, S.D.A.; Berhane, H.; Rokosh, C.D. Rock eval, total organic carbon and adsorption isotherms of the Duvernay and Muskwa formations in Alberta: Shale gas data release. Energy Resour. Conserv. Board. 2010, 4, 33. [Google Scholar]
- Beaton, A.P.; Pawlowicz, J.G.; Anderson, S.D.A.; Rokosh, C.D. Rock eval, total organic carbon, isotherms and organic petrography of the Colorado Group: Shale gas data release. Energy Resour. Conserv. Board. 2008, 11, 88. [Google Scholar]
- Brownlee, J. XGBoost with Python: Gradient Boosted Trees with XGBoost and Scikit-Learn; Machine Learning Mastery: San Juan, Puerto Rico, 2016. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Bemani, A.; Baghban, A.; Mohammadi, A.H.; Andersen, P.Ø. Estimation of adsorption capacity of CO2, CH4, their binary mixtures in Quidam shale using LSSVM: Application in CO2 enhanced shale gas recovery CO2 storage. J. Nat. Gas Sci. Eng. 2020, 76, 103204. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Raji, M.; Dashti, A.; Alivand, M.S.; Asghari, M. Novel prosperous computational estimations for greenhouse gas adsorptive control by zeolites using machine learning methods. J. Environ. Manag. 2022, 307, 114478. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A.; Optimizer, G.W. Advances in engineering software. Renew. Sustain. Energy Rev. 2014, 69, 46–61. [Google Scholar]
- Najari, S.; Gróf, G.; Saeidi, S.; Gallucci, F. Modeling and optimization of hydrogenation of CO2: Estimation of kinetic parameters via Artificial Bee Colony (ABC) and Differential Evolution (DE) algorithms. Int. J. Hydrogen Energy 2019, 44, 4630–4649. [Google Scholar] [CrossRef]
- Meng, M.; Qiu, Z.; Zhong, R.; Liu, Z.; Liu, Y.; Chen, P. Adsorption characteristics of supercritical CO2/CH4 on different types of coal a machine learning approach. Chem. Eng. J. 2019, 368, 847–864. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization. Technical Report-tr06. 2005. Available online: https://abc.erciyes.edu.tr/pub/tr06_2005.pdf (accessed on 14 April 2025).
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar]
- Panigrahi, B.K.; Shi, Y.; Lim, M.-H. Handbook of Swarm Intelligence: Concepts, Principles and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 8. [Google Scholar]
- Onwunalu, J.E.; Durlofsky, L.J. Application of a particle swarm optimization algorithm for determining optimum well location and type. Comput. Geosci. 2010, 14, 183–198. [Google Scholar]
- Sharma, A.; Onwubolu, G. Hybrid particle swarm optimization and GMDH system. In Hybrid Self-Organizing Modeling Systems; Springer: Berlin/Heidelberg, Germany, 2009; pp. 193–231. [Google Scholar]
- Amar, M.N.; Larestani, A.; Lv, Q.; Zhou, T.; Hemmati-Sarapardeh, A. Modeling of methane adsorption capacity in shale gas formations using white-box supervised machine learning techniques. J. Pet. Sci. Eng. 2022, 208, 109226. [Google Scholar]
- Mao, F. Research on Influencing Factors and Prediction Methods of Shale Gas Content Based on Machine Learning Algorithm. Open Access Libr. J. 2023, 10, 1–16. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Volume 1. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95, Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Williams, C.K.I.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings World Congress on Computational Intelligence (Cat. No. 98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Snelson, E.; Ghahramani, Z. Sparse Gaussian processes using pseudo-inputs. In Proceedings of the 19th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 5–8 December 2005; Volume 18. [Google Scholar]
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Quinonero-Candela, J.; Rasmussen, C.E. A unifying view of sparse approximate Gaussian process regression. J. Mach. Learn. Res. 2005, 6, 1939–1959. [Google Scholar]
- Hsu, C.-W.; Chang, C.-C.; Lin, C.-J. A Practical Guide to Support Vector Classification. 2003. Available online: https://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf (accessed on 21 April 2025).
- Zhang, Y.; Wang, S.; Ji, G. A comprehensive survey on particle swarm optimization algorithm and its applications. Math. Probl. Eng. 2015, 2015, 931256. [Google Scholar] [CrossRef]



| Model | Hyperparameter |
|---|---|
| ANN with ABC | Hidden layer sizes = (28, 50); Activation = ReLU (hidden), Linear (output); Learning rate = 0.0354 Colony size = 30 (10 employed, 10 onlooker, 10 scout); Max cycles = 100; Abandonment limit = 50 |
| ANN with PSO | Hidden layer sizes = (41, 88); Activation = ReLU (hidden), Linear (output); Learning rate = 0.0077 Swarm size = 30; Max iterations = 100; Inertia weight (w) = 0.7; c1 = 1.5, c2 = 1.5 |
| XGBoost with ABC | Max depth = 4; n_estimators = 443; Learning rate = 0.0074 Colony size = 30; Max cycles = 100; Abandonment limit = 50 |
| XGBoost with PSO | Max depth = 3; n_estimators = 342; Learning rate = 0.0100 Swarm size = 30; Max iterations = 100; Inertia weight (w) = 0.7; c1 = 1.5, c2 = 1.5 |
| Studies | Model | R2 | RMSE |
|---|---|---|---|
| [22] | XGBoost | 0.978 | 0.005 |
| ANN | 0.918 | 0.300 | |
| RF | 0.908 | 0.060 | |
| SVM | 0.841 | 0.131 | |
| [36] | GWO-SVM | 0.982 | 0.050 |
| [37] | GPR | 0.970 | 0.030 |
| [38] | PSO-SVR | 0.960 | 0.099 |
| GWO-SVR | 0.952 | 0.109 | |
| SSA-SVR | 0.936 | 0.126 | |
| XGBoost | 0.960 | 0.099 | |
| [54] | GEP | 0.983 | |
| [55] | CatBoost | 0.986 | 0.022 |
| Current work | ANN-ABC | 0.991 | 0.045 |
| ANN-PSO | 0.995 | 0.042 | |
| XGBoost-ABC | 0.944 | 0.146 | |
| XGBoost-PSO | 0.762 | 0.092 |
| ML Model | Description | Key Input Parameters | Accuracy/Performance | Reference |
|---|---|---|---|---|
| XGBoost | Ensemble learning method that improves prediction accuracy by minimizing bias and variance. | Total organic carbon (TOC), temperature, pressure, porosity, clay content | High accuracy compared to traditional models. | [22] |
| GWO-SVM | SI technique that replicates the hierarchical relationships and hunting behavior of gray wolves in the wild. | Temperature, pressure, TOC, moisture, and gas content | Provides a better prediction of the adsorbed gas than models that have been suggested before. | [36] |
| GPR | Probabilistic model that provides uncertainty estimates in predictions. | TOC, moisture, temperature, pressure, gas composition | Predicts adsorption with an error margin < 3%. | [37] |
| PSO-SVR | Swarm intelligence (SI) and vector regression to improve prediction accuracy and computational efficiency. | Temperature, TOC, vitrinite reflectance, pressure, and volume | PSO-SVR model performed better than other models used in this study. | [38] |
| GEP | Mimics brain neurons to capture complex nonlinear relationships in adsorption data. | TOC, porosity, mineral composition, reservoir pressure | Outperforms conventional Langmuir models. | [54] |
| CatBoost | Tree-structure-based integrated learning model that uses the boosting technique. | TOC and pore-specific surface area | The model achieved an accuracy of 98.6% in predicting shale gas content, outperforming conventional prediction methods. | [55] |
| ANN-ABC ANN-PSO | Improving model performance by leveraging SI and bee colony behavior. | TOC, temperature, pressure, moisture content, and gas content | Gives an excellent prediction of the adsorbed gas compared to previously proposed models. | This study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibad, T.; Ibad, S.M.; Tsegab, H.; Jaffari, R. Application of Machine Learning Algorithms to Predict Gas Sorption Capacity in Heterogeneous Porous Material. Resources 2025, 14, 80. https://doi.org/10.3390/resources14050080
Ibad T, Ibad SM, Tsegab H, Jaffari R. Application of Machine Learning Algorithms to Predict Gas Sorption Capacity in Heterogeneous Porous Material. Resources. 2025; 14(5):80. https://doi.org/10.3390/resources14050080
Chicago/Turabian StyleIbad, Tasbiha, Syed Muhammad Ibad, Haylay Tsegab, and Rabeea Jaffari. 2025. "Application of Machine Learning Algorithms to Predict Gas Sorption Capacity in Heterogeneous Porous Material" Resources 14, no. 5: 80. https://doi.org/10.3390/resources14050080
APA StyleIbad, T., Ibad, S. M., Tsegab, H., & Jaffari, R. (2025). Application of Machine Learning Algorithms to Predict Gas Sorption Capacity in Heterogeneous Porous Material. Resources, 14(5), 80. https://doi.org/10.3390/resources14050080






