Is Everything Lost? Recreating the Surface Water Temperature of Unmonitored Lakes in Poland
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Objects
2.2. Materials
2.3. Methods
2.3.1. Air2Water
- The calibration was carried out using data from the first 70% of the observation period.
- The validation was carried out for the remaining 30% of the time series, where the observed LSWT was compared with the model’s predictions.
2.3.2. Statistical Metrics
2.3.3. Trend Analysis
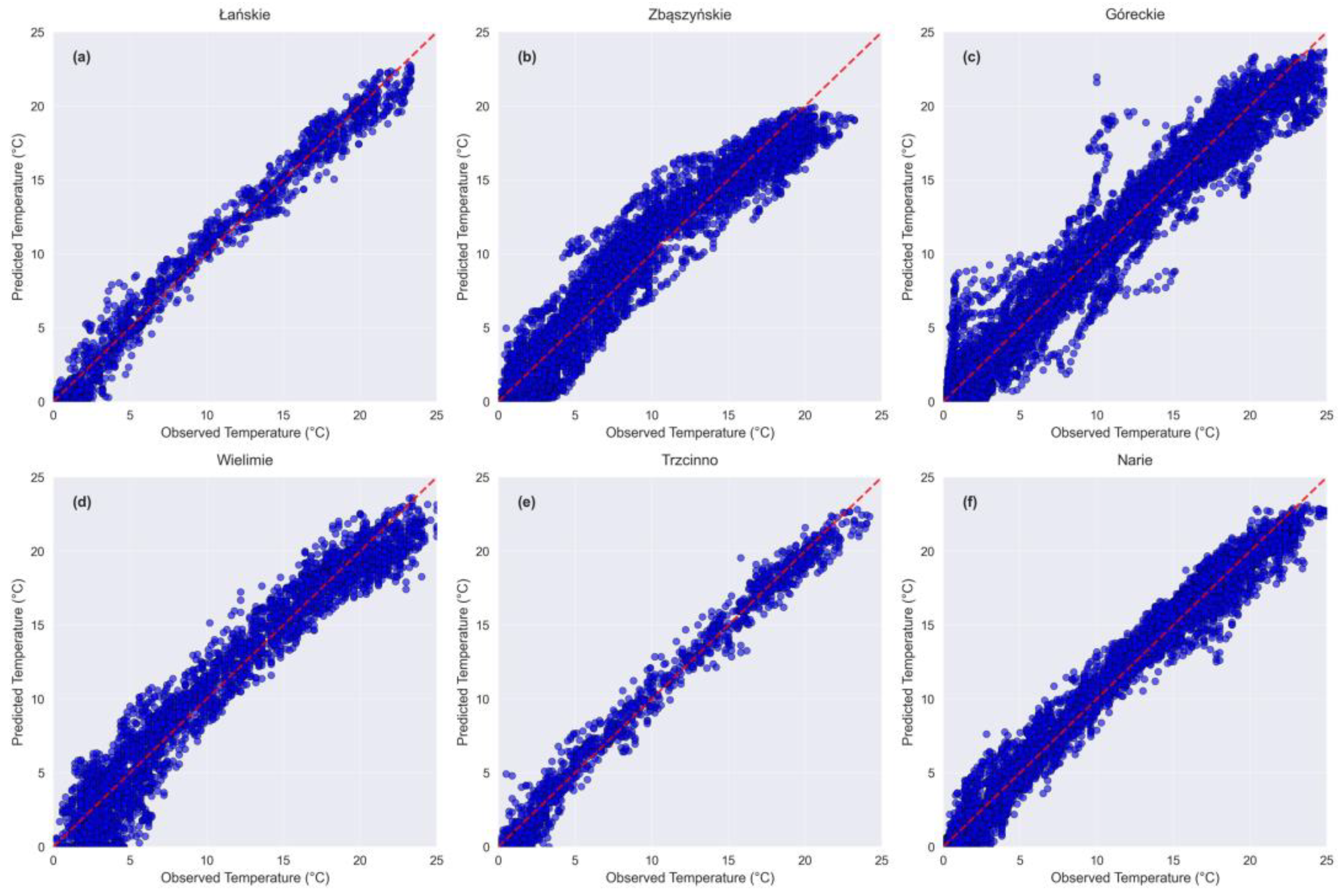
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huttula, T.; Peltonen, A.; Bilaletdin, Ä.; Saura, M. The effects of climatic change on lake ice and water temperature. Aqua Fenn. 1992, 22, 129–142. [Google Scholar]
- Koinig, K.; Schmidt, R.; Woegrath, S.; Tessadri, R.; Psenner, R. Climate Change as the primary cause for pH shifts in a high alpine lake. Water Air Soil Pollut. 1998, 104, 167–180. [Google Scholar] [CrossRef]
- Shcherbak, V.I.; Semenyuk, N.Y.; Yakushin, V.M. Phytoplankton structural and functional organization in a large lowland reservoir under conditions of global climate change (case-study of Kaniv Reservoir). Hydrobiol. J. 2022, 58, 3–27. [Google Scholar] [CrossRef]
- Salk, K.R.; Venkitswaran, J.J.; Couture, R.; Higgins, S.N.; Paterson, M.J.; Schiff, S.L. Warming combined with experimental eutrophication intensifies lake phytoplankton blooms. Limnol. Oceanogr. 2021, 67, 147–158. [Google Scholar] [CrossRef]
- Li, D.; Dorber, M.; Barbarossa, V.; Verones, F. Global characterization factors for quantifying the impacts of increasing water temperature on freshwater fish. Ecol. Indic. 2022, 142, 109201. [Google Scholar] [CrossRef]
- Ducharne, A. Importance of stream temperature to climate change impact on water quality. Hydrol. Earth Syst. Sci. 2008, 12, 797–810. [Google Scholar] [CrossRef]
- Detmer, T.M.; Parkos, J.J.; Wahl, D.H. Long-term data show effects of atmospheric temperature anomaly and reservoir size on water temperature, thermal structure, and dissolved oxygen. Aquat Sci. 2022, 84, 3. [Google Scholar] [CrossRef]
- Ptak, M.; Sojka, M.; Graf, R.; Choiński, A.; Zhu, S.; Nowak, B. Warming Vistula River—The effects of climate and local conditions on water temperature in one of the largest rivers in Europe. J. Hydrol. Hydromech. 2022, 1, 1–11. [Google Scholar] [CrossRef]
- Carvalho, L.; Kirika, A. Changes in shallow lake functioning: Response to climate change and nutrient reduction. Hydrobiologia 2003, 506, 789–796. [Google Scholar] [CrossRef]
- Attiah, G.; Kheyrollah Pour, H.K.; Scott, K.A. Four decades of lake surface temperature in the Northwest Territories, Canada, using a lake-specific satellite-derived dataset. J. Hydrol. Reg. Stud. 2023, 50, 101571. [Google Scholar] [CrossRef]
- Echavarría-Caballero, C.; Domínguez-Gómez, J.A.; González-García, C.; Domínguez-Perez, R.; García-García, M.J. Warming inland water in peninsular Spain revealed by landsat 5 analysis. Geocarto Int. 2024, 39, 2371923. [Google Scholar] [CrossRef]
- Woolway, R.I.; Dokulil, M.T.; Marszelewski, W.; Schmid, M.; Bouffard, D. Warming of Central European lakes and their response to the 1980s climate regime shift. Clim. Chang. 2017, 42, 505–520. [Google Scholar] [CrossRef]
- Ptak, M.; Sojka, M.; Nowak, B. Effect of climate warming on a change in thermal and ice conditions in the largest lake in Poland—Lake Śniardwy. J. Hydrol. Hydrodyn. 2020, 68, 260–270. [Google Scholar] [CrossRef]
- Bal, G.; de Eyto, E. Simple Bayesian reconstruction and forecasting of stream water temperature for ecologists—A tool using air temperature, optionally flow, in a time series decomposition approach. PLoS ONE 2023, 18, e0291239. [Google Scholar] [CrossRef]
- Sivakumar, B.; Jayawardena, A.W.; Li, W.K. Hydrologic complexity and classification: A simple data reconstruction approach. Hydrol. Process. 2007, 21, 2713–2728. [Google Scholar] [CrossRef]
- Lehmann, A.; Giuliani, G.; Ray, N.; Rahman, K.; Abbaspour, K.; Nativi, S.; Craglia, M.; Cripe, D.; Quevauviller, P.; Beniston, M. Reviewing innovative Earth observation solutions for filling science-policy gaps in hydrology. J. Hydrol. 2014, 518, 267–277. [Google Scholar] [CrossRef]
- Noori, R.; Woolway, R.I.; Jun, C.; Bateni, S.M.; Naderian, D.; Partani, S.; Maghrebi, M.; Pulkkanen, M. Multi-decadal change in summer mean water temperature in Lake Konnevesi, Finland (1984–2021). Ecol. Inform. 2023, 78, 102331. [Google Scholar] [CrossRef]
- Zhu, S.; Ptak, M.; Choiński, A.; Wu, S. Exploring and quantifying the impact of climate change on surface water temperature of a high mountain lake in Central Europe. Environ. Monit. Assess. 2020, 192, 7. [Google Scholar] [CrossRef]
- Herrick, C.; Steele, B.G.; Brentrup, J.A.; Cottingham, K.L.; Ducey, M.J.; Lutz, D.A.; Palace, M.W.; Thompson, M.C.; Trout-Haney, J.V.; Weathers, K.C. lakeCoSTR: A Tool to Facilitate Use of Landsat Collection 2 to Estimate Lake Surface Water Temperatures. Ecosphere 2023, 14, e4357. [Google Scholar] [CrossRef]
- Kim, H.I.; Kim, D.; Salamattalab, M.M.; Mahdian, M.; Bateni, S.M.; Noori, R. Machine learning-based modeling of surface water temperature dynamics in arctic lakes. Environ. Sci. Pollut. Res. 2024, 31, 59642–59655. [Google Scholar] [CrossRef]
- Joynt, E.H., III; Wolfe, A.P. Paleoenvironmental inference models from sediment diatom assemblages in Baffin Island lakes (Nunavut, Canada) and reconstruction ofsummer water temperatures. Can. J. Fish. Aquat. Sci. 2001, 58, 1222–1243. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, K.; Frassl, M.A.; Boehrer, B. Reconstructing Six Decades of Surface Temperatures at a Shallow Lake. Water 2020, 12, 405. [Google Scholar] [CrossRef]
- Willard, J.D.; Read, J.S.; Topp, S.; Hansen, G.J.A.; Kumar, V. Daily surface temperatures for 185,549 lakes in the conterminous United States estimated using deep learning (1980–2020). Limnol. Oceanogr. Lett. 2022, 7, 287–301. [Google Scholar] [CrossRef]
- Jia, T.F.; Yang, K.; Peng, Z.Q.; Tang, L.F.; Duan, H.M.; Luo, Y. Review on the Change Trend, Attribution Analysis, Retrieval, Simulation, and Prediction of Lake Surface Water Temperature. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6324–6355. [Google Scholar] [CrossRef]
- Song, S.; Yang, J.; Liu, L.; Bai, G.; Zhou, J.; McKay, D. Lake surface water temperature in China from 2001 to 2021 based on GEE and HANTS. Ecol. Inform. 2024, 84, 102903. [Google Scholar] [CrossRef]
- Piccolroaz, S.; Healey, N.; Lenters, J.; Schladow, S.; Hook, S.; Sahoo, G.; Toffolon, M. On the predictability of lake surface temperature using air temperature in a changing climate: A case study for Lake Tahoe (USA). Limnol. Oceanogr. 2018, 63, 243–261. [Google Scholar] [CrossRef]
- Heddam, S.; Ptak, M.; Zhu, S. Modelling of Daily Lake Surface Water Temperature from Air Temperature: Extremely Randomized Trees (ERT) versus Air2Water, MARS, M5Tree, RF and MLPNN. J. Hydrol. 2020, 588, 125130. [Google Scholar] [CrossRef]
- Jia, T.; Luo, Y. Using Air2water Model to Predict the Water Temperature of Fuxian Lake. In Climate Change and Environmental Sustainability, Advances in Science, Technology & Innovation; He, B.J., Prasad, D., Pignatta, G., Jupesta, J., Eds.; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Nowak, B.; Dumieński, G. Znaczenie jezior w gospodarce kraju. Gospod. Wodna 2020, 8, 8–14. [Google Scholar]
- Ptak, M.; Sojka, M.; Choiński, A.; Nowak, B. Effect of environmental conditions and morphometric parameters on surface water temperature in Polish lakes. Water 2018, 10, 580. [Google Scholar] [CrossRef]
- Choiński, A. Katalog Jezior Polski; Wydawnictwo Naukowe UAM: Poznań, Poland, 2006. [Google Scholar]
- Piccolroaz, S.; Toffolon, M.; Majone, B. A simple lumped model to convert air temperature into surface water temperature in lakes. Hydrol. Earth Syst. Sci. 2013, 17, 3323–3338. [Google Scholar] [CrossRef]
- Piccolroaz, S. Prediction of lake surface temperature using the air2water model: Guidelines, challenges, and future perspectives. Adv. Oceanogr. Limnol. 2016, 7, 36–50. [Google Scholar] [CrossRef]
- He, Y. Air2waterpy: Python Implementation of the Air2Water Model. GitHub. Available online: https://github.com/he134543/air2waterpy (accessed on 3 January 2025).
- Piccolroaz, S.; Toffolon, M.; Majone, B. The role of stratification on lakes’ thermal response: The case of L ake S uperior. Water Resour. Res. 2015, 51, 7878–7894. [Google Scholar] [CrossRef]
- Toffolon, M.; Piccolroaz, S.; Majone, B.; Soja, A.M.; Peeters, F.; Schmid, M.; Wüest, A. Prediction of surface temperature in lakes with different morphology using air temperature. Limnol. Oceanogr. 2014, 59, 2185–2202. [Google Scholar] [CrossRef]
- Thiery, W.; Stepanenko, V.M.; Fang, X.; Jöhnk, K.D.; Li, Z.; Martynov, A.; Perroud, M.; Subin, Z.M.; Darchambeau, F.; Mironov, D.; et al. LakeMIP Kivu: Evaluating the representation of a large, deep tropical lake by lake models. Tellus A Dyn. Meteorol. Oceanogr. 2014, 66, 21390. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Kettle, H.; Thompson, R.; Anderson, N.J.; Livingstone, D.M. Empirical modeling of summer lake surface temperatures in southwest Greenland. Limnol. Oceanogr. 2004, 49, 271–282. [Google Scholar] [CrossRef]
- Toffolon, M.; Piccolroaz, S. A hybrid model for river water temperature as a function of air temperature and discharge. Environ. Res. Lett. 2015, 10, 114011. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Kendall, M.G.; Stuart, A. The Advanced Theory of Statistics, 3rd ed.; Charles Griffin Ltd.: Cheshire, UK, 1968. [Google Scholar]
- Gilbert, R.O. Statistical Methods for Environmental Pollution Monitorin; Van Nos-trand Reinhold, Co.: New York, NY, USA,, 1987. [Google Scholar]
- Pettitt, A.N. A non-parametric approach to the changepoint problem. Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Patakamuri, S.K.; O’Brien, N. Modified Versions of Mann Kendall and Spearman’s Rho Trend Tests, Version 1.6; 2022. Available online: https://cran.r-project.org/web/packages/modifiedmk/modifiedmk.pdf (accessed on 10 January 2025).
- Pohlert, T. Non-Parametric Trend Tests and Change-Point Detection, Version 1.1.6; 2023. Available online: https://cran.r-project.org/web/packages/trend/vignettes/trend.pdf (accessed on 10 January 2025).
- Yang, Y.-C.; Lu, C.-Y.; Huang, S.-J.; Yang, T.-Z.; Chang, Y.-C.; Ho, C.-R. On the Reconstruction of Missing Sea Surface Temperature Data from Himawari-8 in Adjacent Waters of Taiwan Using DINEOF Conducted with 25-h Data. Remote Sens. 2022, 14, 2818. [Google Scholar] [CrossRef]
- Huang, F.; Qian, B.; Ochoa, C.G. Long-term river water temperature reconstruction and investigation: A case study of the Dongting Lake Basin, China. J. Hydrol. 2023, 616, 128857. [Google Scholar] [CrossRef]
- Ptak, M.; Zhu, S.; Amnuaylojaroen, T.; Li, H.; Szyga-Pluta, K.; Jiang, S.; Wang, L.; Sojka, M. Utilizing Multi-Source datasets for the Reconstruction and Prediction of water temperature in Lake Miedwie (Poland). Remote Sens. 2024, 16, 2753. [Google Scholar] [CrossRef]
- Sharaf, N.; Prats, J.; Reynaud, N.; Tormos, T.; Bruel, R.; Peroux, T.; Danis, P.-A. A long-term dataset of simulated epilimnion and hypolimnion temperatures in 401 French lakes (1959–2020). Earth Syst. Sci. Data 2023, 15, 5631–5650. [Google Scholar] [CrossRef]
- Yu, S.J.; Ryu, I.G.; Park, M.J.; Im, J.K. Long-term relationship between air and water temperatures in Lake Paldang, South Korea. Environ. Eng. Res. 2021, 26, 200177. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, Z.; Luo, J.; Liu, W.; Chen, M.; Niu, F.; Wang, Y.; Shang, Y. Simulation and Prediction of Thermokarst Lake Surface Temperature Changes on the Qinghai–Tibet Plateau. Remote Sens. 2024, 16, 4645. [Google Scholar] [CrossRef]
- Virdis, S.G.P.; Kongwarakom, S.; Juneng, L.; Padedda, B.M.; Shrestha, S. Historical and projected response of Southeast Asian lakes surface water temperature to warming climate. Environ. Res. 2024, 247, 118412. [Google Scholar] [CrossRef]
- Duan, H.; Shang, C.; Yang, K.; Luo, Y. Dynamic Response of Surface Water Temperature in Urban Lakes under Different Climate Scenarios—A Case Study in Dianchi Lake, China. Int. J. Environ. Res. Public Health 2022, 19, 12142. [Google Scholar] [CrossRef]
- Shi, Y.; Huang, A.; Wu, Y.; Lazhu Wen, L. Trends of Summer Lake Surface Water Temperature on the Tibetan Plateau and Their Response to Climate Change. Earth Space Sci. 2024, 11, e2024EA003910. [Google Scholar] [CrossRef]
- Brkić, Ž. Increasing water temperature of the largest freshwater lake on the Mediterranean islands as an indicator of global warming. Heliyon 2023, 9, e19248. [Google Scholar] [CrossRef]
- Tavares, M.H.; Cardoso, M.A.; Motta Marques, D.; Bonnet, M.-P.; Fragoso, C.R. High Spring Warming Rates in an Extensive Subtropical Shallow Lakes System Detected Using MODIS Imagery. ACS EST Water 2024, 4, 1518–1530. [Google Scholar] [CrossRef]
- Ptak, M.; Nowak, B. Variability of oxygen-thermal conditions in selected lakes in Poland. Ecol. Chem. Eng. S 2016, 23, 639–650. [Google Scholar] [CrossRef]
- Sharabian, M.N.; Ahmad, S.; Karakouzian, M. Climate Change and Eutrophication: A Short Review. Eng. Technol. Appl. Sci. Res. 2018, 8, 3668–3672. [Google Scholar] [CrossRef]
- Gajewska, M.; Plichta, K. Nowe metody rekultywacji wód powierzchniowychna przykładzie jezior w Polsce. Inżynieria Morska I Geotechnika 2009, 1, 1. [Google Scholar]
- Ptak, M.; Choiński, A.; Strzelczak, A.; Targosz, A. Disappearance of Lake Jelenino since the end of the XVIII century as an effect of anthropogenic transformations of the natural environment. Pol. J. Environ. Stud. 2013, 22, 191–196. [Google Scholar]
- Informatyczny System Osłony Kraju, Hydroportal. Available online: https://hydroportal.pl/ (accessed on 10 February 2025).
- Ptak, M.; Amnuaylojaroen, T.; Sojka, M. Seven decades of surface temperature changes in central European lakes. What’s next? Resources 2024, 13, 149. [Google Scholar] [CrossRef]
- Tanentzap, A.J.; Morabito, G.; Volta, P.; Rogora, M.; Yan, N.D.; Manca, M. Climate warming restructures an aquatic food web over 28 years. Glob. Chang. Biol. 2020, 26, 6852–6866. [Google Scholar] [CrossRef]
- Goyer, K.; Bertolo, A.; Pépino, M.; Magnan, P. Effects of lake warming on behavioural thermoregulatory tactics in a cold-water stenothermic fish. PLoS ONE 2014, 9, e92514. [Google Scholar] [CrossRef]
- Jabbari, A.; Boegman, L.; Molot, L.A. Modeling future dissolved oxygen and temperature profiles in small temperate lake trout lakes. Aquat. Sci. 2025, 87, 8. [Google Scholar] [CrossRef]
- Kangur, K.; Tammiksaar, E.; Pauly, D. Using the “mean temperature of the catch” to assess fish community responses to warming in a temperate lake. Environ. Biol. Fish. 2022, 105, 1405–1413. [Google Scholar] [CrossRef]
- Wilkońska, H. The effect of heated water discharge in the Konin lakes (Poland) on their ichtiofauna. Ekol. Pol. 1988, 36, 145–164. [Google Scholar]
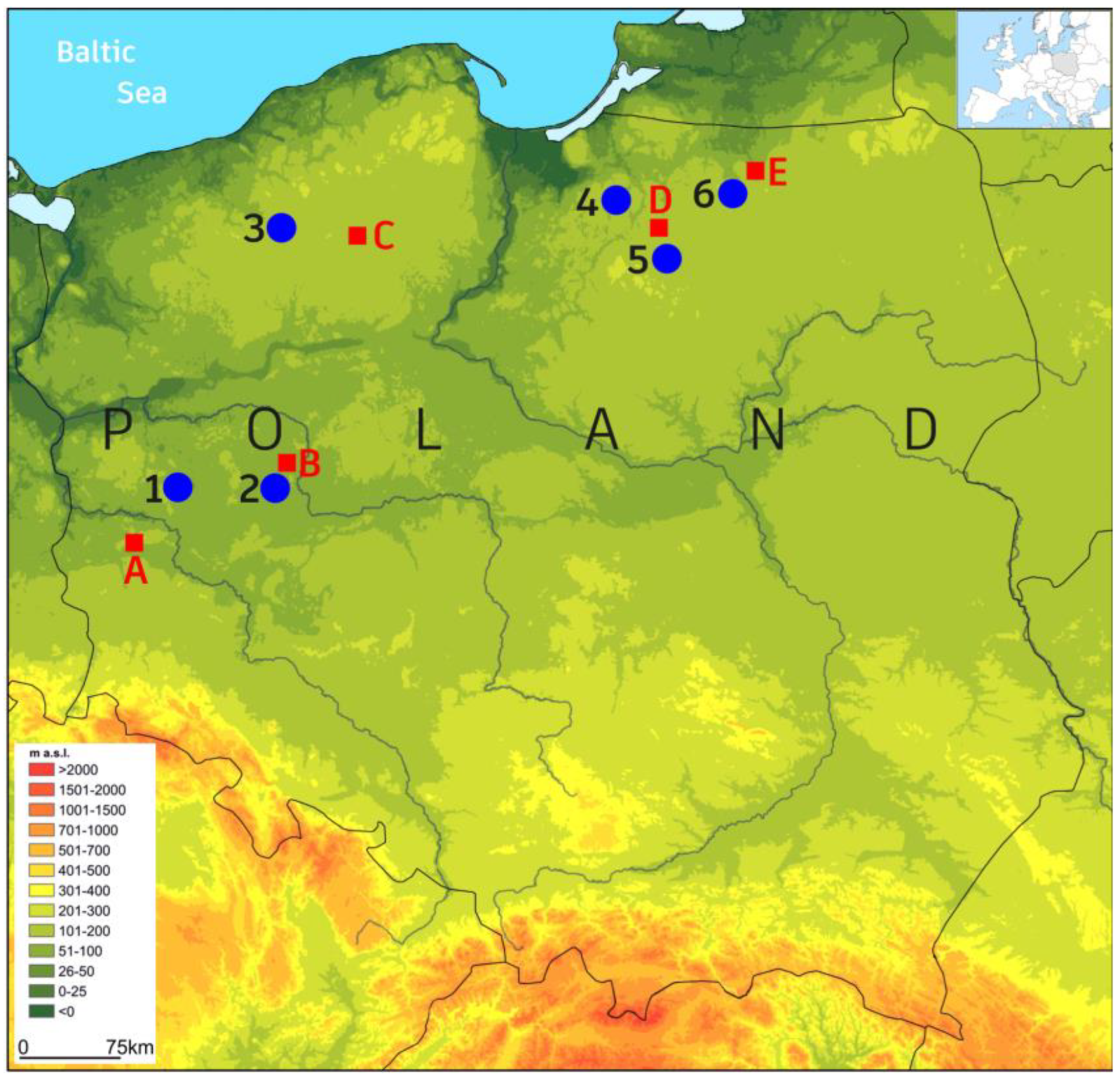


| Lake | Area [ha] | Depth [m] | Volume [Million m3] | m a.s.l. | In Situ Measurements LSWT | ||
|---|---|---|---|---|---|---|---|
| Max | Mean | ||||||
| 1 | Zbąszyńskie | 742.5 | 9.6 | 3.5 | 26.1 | 52.8 | 1973–1990 |
| 2 | Góreckie | 104.1 | 17.2 | 9.0 | 9.3 | 66.3 | 1972–1992 |
| 3 | Wielimie | 1754.6 | 5.5 | 2.2 | 40.1 | 132.7 | 1973–1983 |
| 4 | Łańskie | 1042.0 | 53.0 | 16 | 168.0 | 134.7 | 1972–1976 |
| 5 | Narie | 1240.0 | 43.0 | 9.8 | 124.0 | 104.0 | 1972–1992 |
| 6 | Trzcinno | 32.3 | 32.2 | 10.5 | 3.0 | 109.0 | 1972–1976 |
| Lake | ||||||
|---|---|---|---|---|---|---|
| Metric | Zbąszyńskie | Góreckie | Narie | Trzcinno | Wielimie | Łańskie |
| MAE | 1.286 | 1.23 | 0.846 | 0.763 | 1.32 | 0.812 |
| MSE | 2.652 | 2.838 | 4.547 | 0.943 | 2.737 | 1.097 |
| RMSE | 1.62 | 1.68 | 2.13 | 0.97 | 1.65 | 1.04 |
| rRMSE (%) | 18.83 | 15.88 | 22.51 | 10.46 | 15.46 | 11.21 |
| R2 | 0.941 | 0.952 | 0.922 | 0.982 | 0.944 | 0.979 |
| Correlation | 0.970 | 0.976 | 0.961 | 0.991 | 0.972 | 0.990 |
| p-value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Bias | −0.098 | −0.039 | −0.071 | −0.083 | −0.075 | −0.048 |
| NSE | 0.952 | 0.922 | 0.982 | 0.944 | 0.979 | |
| IOA | 0.988 | 0.98 | 0.995 | 0.986 | 0.995 | |
| Lake | Period | S | Tau | Z-Value | p-Value | Sen’s Slope (°C.Decade−1) | Lake | Period | S | Tau | Z-Value | p-Value | Sen’s Slope (°C.Decade−1) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zbąszyńskie | Jan | 88 | 0.217 | 1.63 | 0.103 | 0.10 | Góreckie | Jan | 84 | 0.207 | 1.56 | 0.119 | 0.28 |
| Feb | 25 | 0.062 | 0.45 | 0.653 | 0.04 | Feb | 24 | 0.059 | 0.43 | 0.666 | 0.09 | ||
| Mar | 98 | 0.241 | 1.82 | 0.069 | 0.18 | Mar | 88 | 0.217 | 1.63 | 0.103 | 0.26 | ||
| Apr | 28 | 0.069 | 0.51 | 0.613 | 0.10 | Apr | 32 | 0.079 | 0.58 | 0.561 | 0.10 | ||
| May | −48 | −0.118 | −0.88 | 0.378 | −0.07 | May | −14 | −0.034 | −0.24 | 0.807 | −0.04 | ||
| Jun | 150 | 0.369 | 2.79 | 0.005 | 0.30 | Jun | 160 | 0.394 | 2.98 | 0.003 | 0.41 | ||
| Jul | 130 | 0.320 | 2.42 | 0.016 | 0.23 | Jul | 131 | 0.323 | 2.44 | 0.015 | 0.23 | ||
| Aug | 66 | 0.163 | 1.22 | 0.223 | 0.13 | Aug | 118 | 0.291 | 2.19 | 0.028 | 0.26 | ||
| Sep | 132 | 0.325 | 2.46 | 0.014 | 0.27 | Sep | 146 | 0.360 | 2.72 | 0.007 | 0.32 | ||
| Oct | 64 | 0.158 | 1.18 | 0.237 | 0.18 | Oct | 100 | 0.246 | 1.86 | 0.063 | 0.25 | ||
| Nov | 168 | 0.414 | 3.13 | 0.002 | 0.31 | Nov | 178 | 0.438 | 3.32 | 0.001 | 0.41 | ||
| Dec | 90 | 0.222 | 1.67 | 0.095 | 0.16 | Dec | 96 | 0.236 | 1.78 | 0.075 | 0.30 | ||
| Yearly mean | 182 | 0.448 | 3.40 | 0.001 | 0.17 | Yearly mean | 204 | 0.502 | 3.81 | 0.000 | 0.25 | ||
| Wielimie | Jan | 76 | 0.187 | 1.41 | 0.159 | 0.47 | Narie | Jan | 90 | 0.222 | 1.67 | 0.095 | 0.17 |
| Feb | 32 | 0.079 | 0.58 | 0.561 | 0.16 | Feb | 14 | 0.034 | 0.24 | 0.807 | 0.04 | ||
| Mar | 87 | 0.214 | 1.61 | 0.107 | 0.39 | Mar | 88 | 0.217 | 1.63 | 0.103 | 0.34 | ||
| Apr | 42 | 0.103 | 0.77 | 0.442 | 0.12 | Apr | 36 | 0.089 | 0.66 | 0.511 | 0.12 | ||
| May | −21 | −0.052 | −0.38 | 0.707 | −0.08 | May | −4 | −0.010 | −0.06 | 0.955 | −0.02 | ||
| Jun | 132 | 0.325 | 2.46 | 0.014 | 0.53 | Jun | 134 | 0.330 | 2.49 | 0.013 | 0.45 | ||
| Jul | 57 | 0.140 | 1.05 | 0.293 | 0.18 | Jul | 70 | 0.172 | 1.29 | 0.196 | 0.27 | ||
| Aug | 52 | 0.128 | 0.96 | 0.339 | 0.23 | Aug | 126 | 0.310 | 2.34 | 0.019 | 0.37 | ||
| Sep | 100 | 0.246 | 1.86 | 0.063 | 0.38 | Sep | 118 | 0.291 | 2.19 | 0.028 | 0.45 | ||
| Oct | 78 | 0.192 | 1.44 | 0.149 | 0.33 | Oct | 76 | 0.187 | 1.41 | 0.159 | 0.28 | ||
| Nov | 176 | 0.433 | 3.28 | 0.001 | 0.64 | Nov | 158 | 0.389 | 2.95 | 0.003 | 0.50 | ||
| Dec | 72 | 0.177 | 1.33 | 0.183 | 0.43 | Dec | 62 | 0.153 | 1.14 | 0.253 | 0.30 | ||
| Yearly mean | 180 | 0.443 | 3.36 | 0.001 | 0.30 | Yearly mean | 206 | 0.507 | 3.85 | 0.000 | 0.26 | ||
| Łańskie | Jan | 70 | 0.172 | 1.29 | 0.196 | 0.23 | Trzcinno | Jan | 75 | 0.185 | 1.39 | 0.165 | 0.22 |
| Feb | 18 | 0.044 | 0.32 | 0.750 | 0.04 | Feb | 38 | 0.094 | 0.69 | 0.488 | 0.13 | ||
| Mar | 84 | 0.207 | 1.56 | 0.119 | 0.31 | Mar | 92 | 0.227 | 1.71 | 0.088 | 0.42 | ||
| Apr | 34 | 0.084 | 0.62 | 0.536 | 0.15 | Apr | 28 | 0.069 | 0.51 | 0.613 | 0.09 | ||
| May | 6 | 0.015 | 0.09 | 0.925 | 0.03 | May | −3 | −0.007 | −0.04 | 0.970 | −0.01 | ||
| Jun | 140 | 0.345 | 2.61 | 0.009 | 0.50 | Jun | 126 | 0.310 | 2.34 | 0.019 | 0.47 | ||
| Jul | 62 | 0.153 | 1.14 | 0.253 | 0.24 | Jul | 58 | 0.143 | 1.07 | 0.285 | 0.22 | ||
| Aug | 122 | 0.300 | 2.27 | 0.023 | 0.41 | Aug | 112 | 0.276 | 2.08 | 0.037 | 0.36 | ||
| Sep | 130 | 0.320 | 2.42 | 0.016 | 0.46 | Sep | 130 | 0.320 | 2.42 | 0.016 | 0.52 | ||
| Oct | 76 | 0.187 | 1.41 | 0.159 | 0.30 | Oct | 90 | 0.222 | 1.67 | 0.095 | 0.30 | ||
| Nov | 164 | 0.404 | 3.06 | 0.002 | 0.54 | Nov | 134 | 0.330 | 2.49 | 0.013 | 0.54 | ||
| Dec | 72 | 0.177 | 1.33 | 0.183 | 0.35 | Dec | 72 | 0.177 | 1.33 | 0.183 | 0.34 | ||
| Yearly mean | 212 | 0.522 | 3.96 | 0.000 | 0.30 | Yearly mean | 222 | 0.547 | 4.15 | 0.000 | 0.29 |
| No | Lake | 1994–2012 | 2013–2023 | ||
|---|---|---|---|---|---|
| Sen’s Slope (°C per Decade) | p-Value | Sen’s Slope (°C per Decade) | p-Value | ||
| 1 | Zbąszyńskie | 0.13 | 0.198 | 0.05 | 0.858 |
| 2 | Góreckie | 0.20 | 0.069 | 0.06 | 1.000 |
| 3 | Wielimie | 0.18 | 0.225 | 0.03 | 0.858 |
| 4 | Łańskie | 0.24 | 0.034 | 0.02 | 0.858 |
| 5 | Narie | 0.26 | 0.034 | 0.00 | 1.000 |
| 6 | Trzcinno | 0.34 | 0.009 | 0.20 | 0.721 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ptak, M.; Sojka, M.; Szyga-Pluta, K.; Baloch, M.Y.J.; Amnuaylojaroen, T. Is Everything Lost? Recreating the Surface Water Temperature of Unmonitored Lakes in Poland. Resources 2025, 14, 67. https://doi.org/10.3390/resources14040067
Ptak M, Sojka M, Szyga-Pluta K, Baloch MYJ, Amnuaylojaroen T. Is Everything Lost? Recreating the Surface Water Temperature of Unmonitored Lakes in Poland. Resources. 2025; 14(4):67. https://doi.org/10.3390/resources14040067
Chicago/Turabian StylePtak, Mariusz, Mariusz Sojka, Katarzyna Szyga-Pluta, Muhammad Yousuf Jat Baloch, and Teerachai Amnuaylojaroen. 2025. "Is Everything Lost? Recreating the Surface Water Temperature of Unmonitored Lakes in Poland" Resources 14, no. 4: 67. https://doi.org/10.3390/resources14040067
APA StylePtak, M., Sojka, M., Szyga-Pluta, K., Baloch, M. Y. J., & Amnuaylojaroen, T. (2025). Is Everything Lost? Recreating the Surface Water Temperature of Unmonitored Lakes in Poland. Resources, 14(4), 67. https://doi.org/10.3390/resources14040067









