Biomass Gasification for Waste-to-Energy Conversion: Artificial Intelligence for Generalizable Modeling and Multi-Objective Optimization of Syngas Production
Abstract
1. Introduction
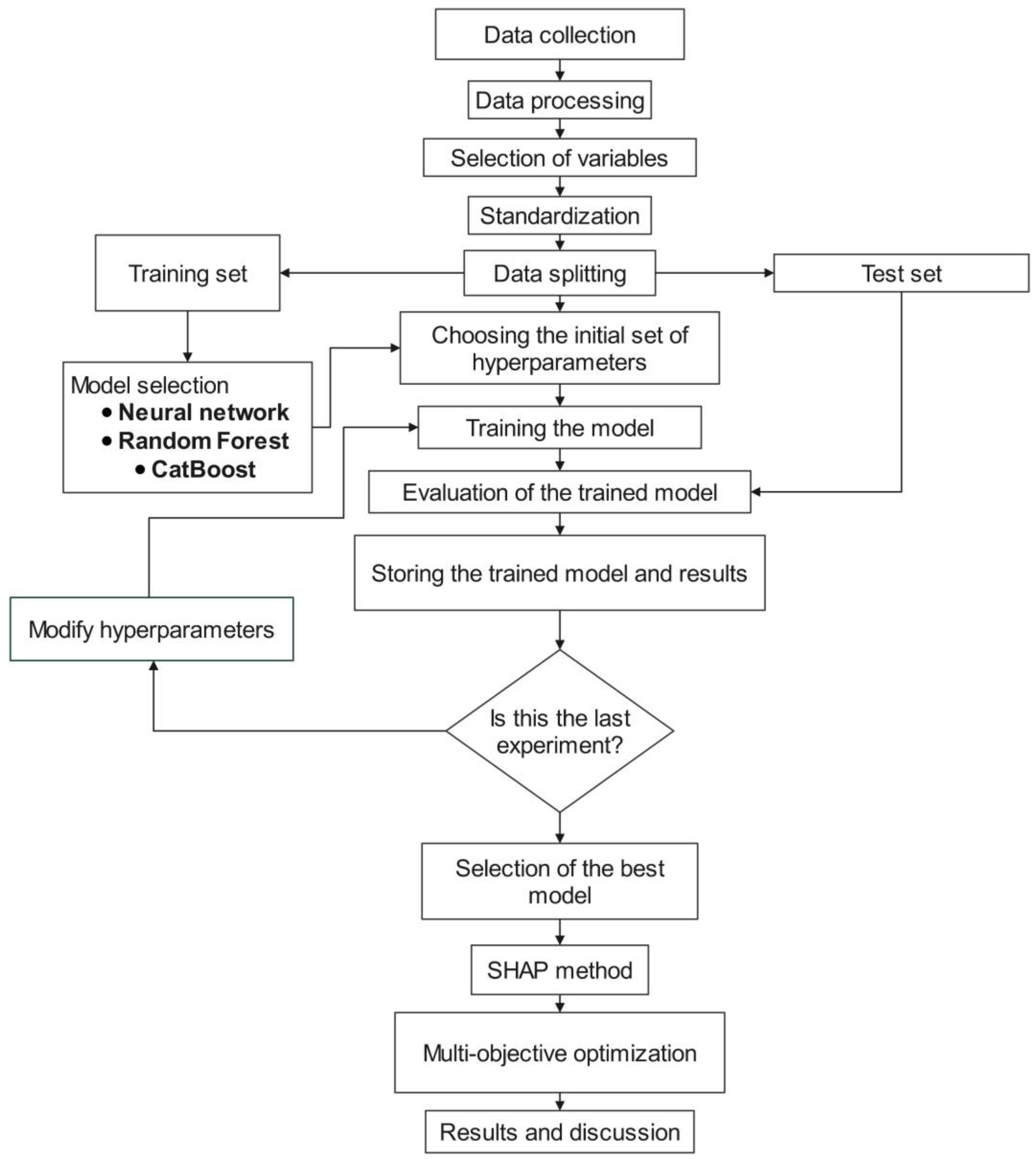
2. Methodology
2.1. Database
2.2. Machine Learning
2.2.1. Model Evaluation
2.2.2. Hyperparameter Optimization
2.3. Multi-Objective Optimization
3. Results and Discussions
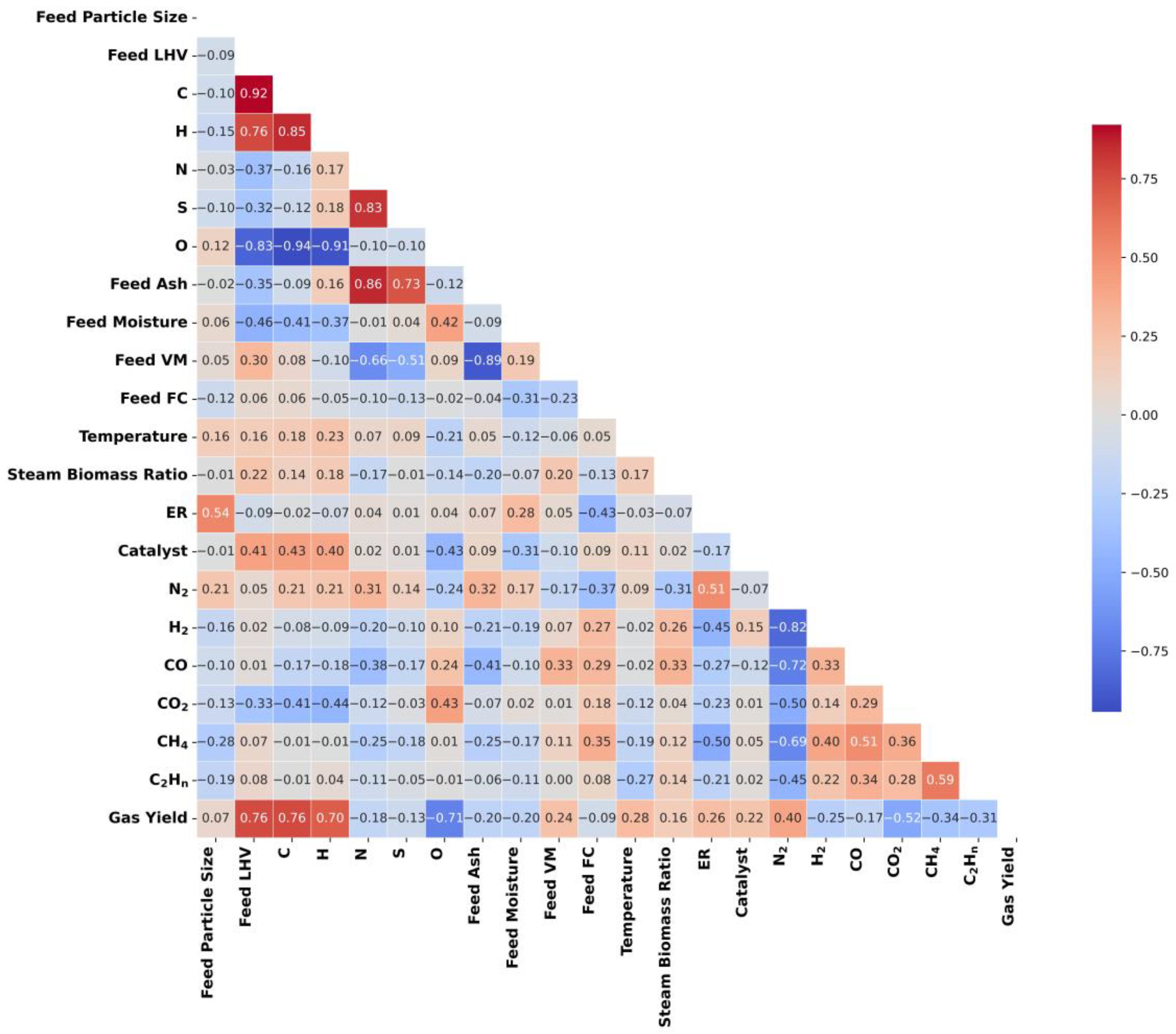
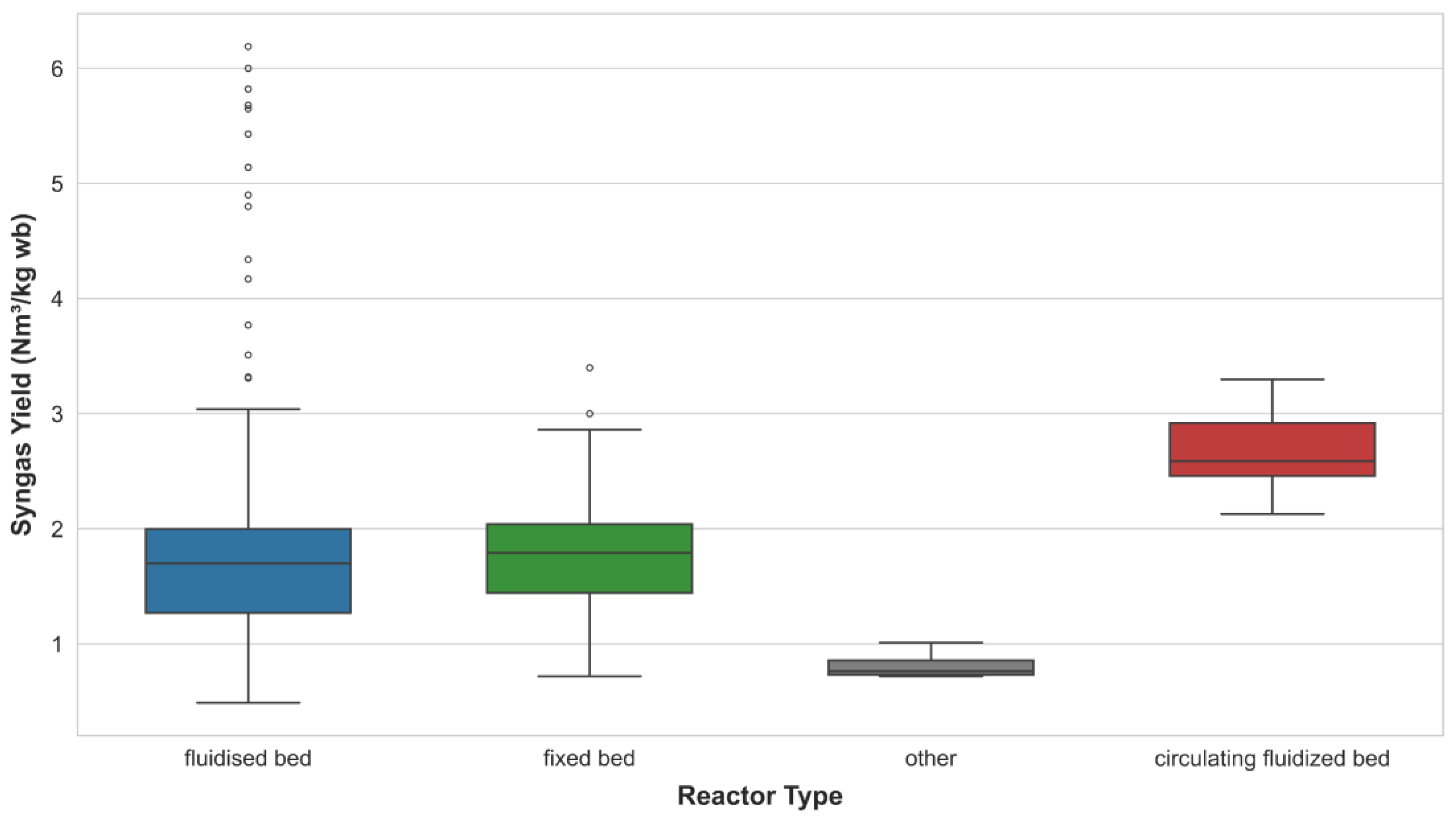
3.1. Exploratory Analysis
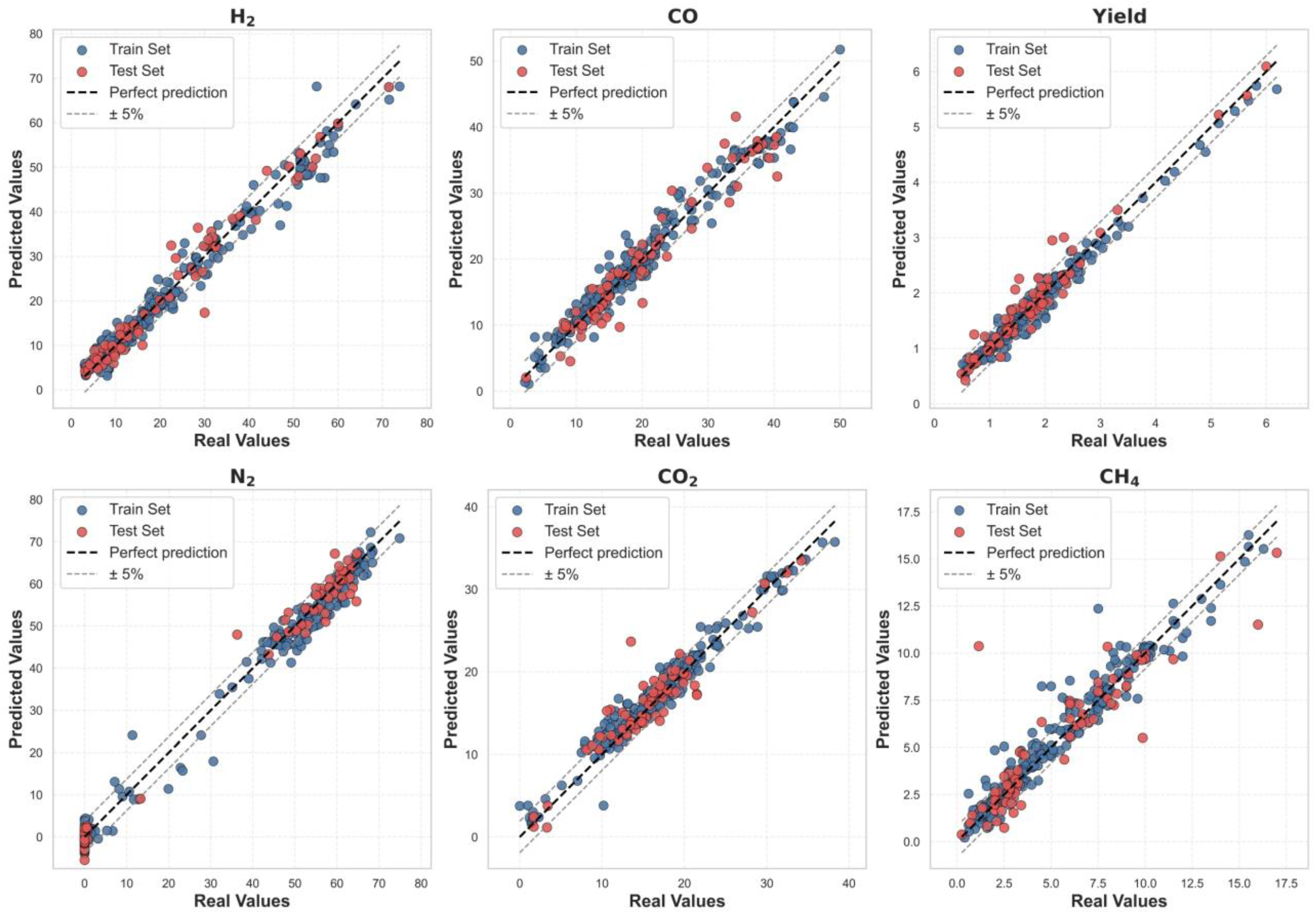
3.2. Machine Learning Results
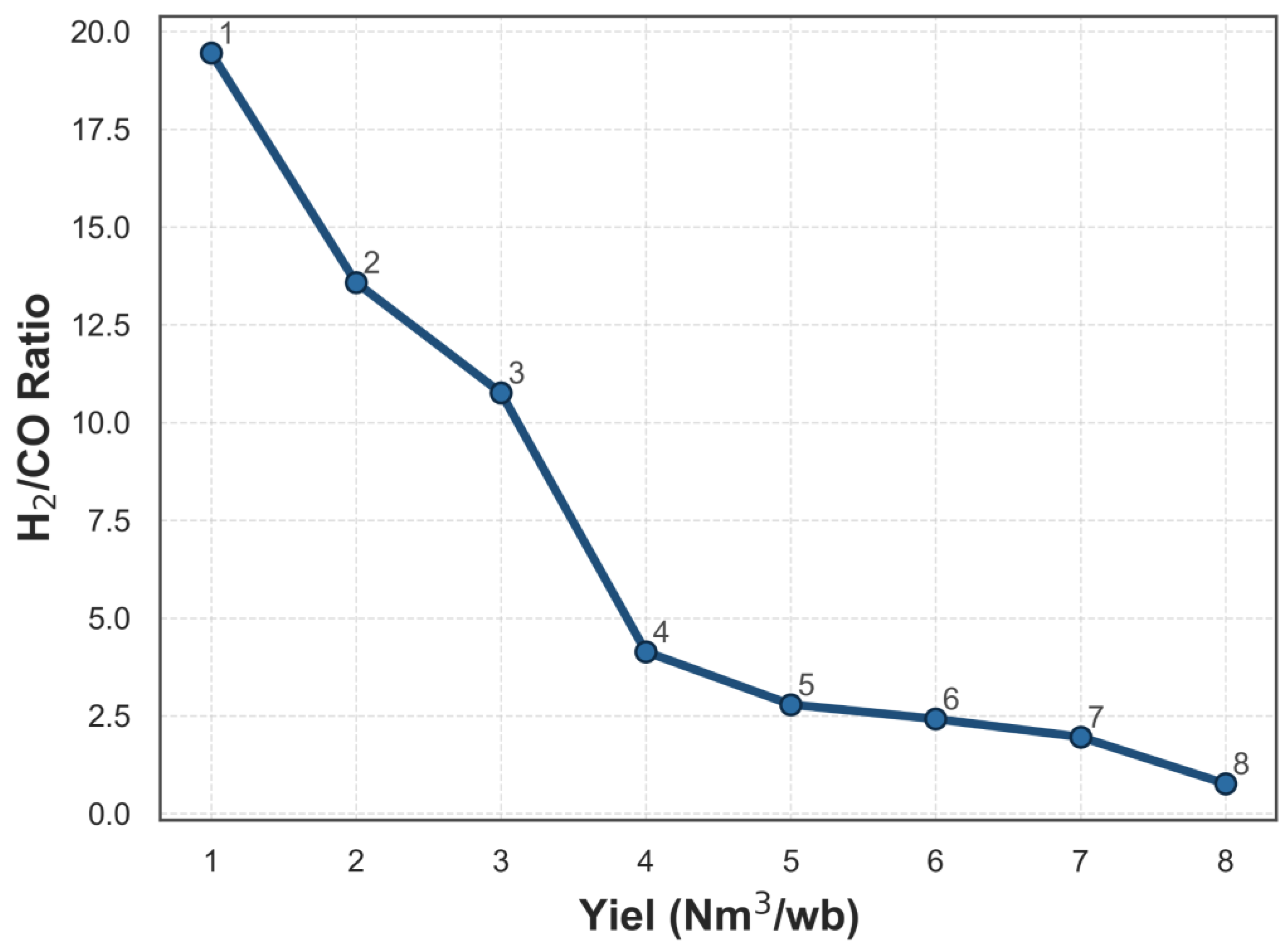
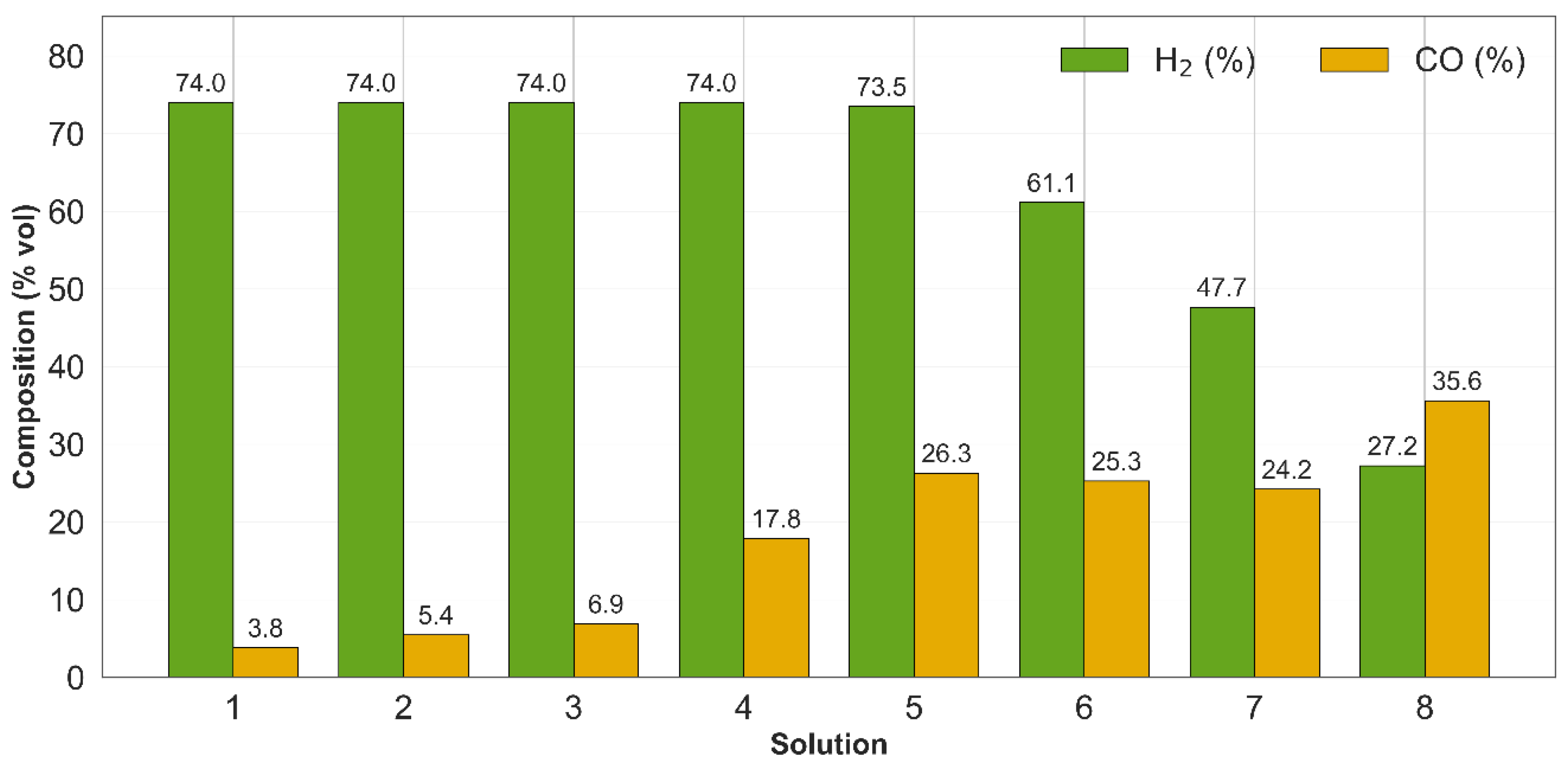
3.3. Multi-Objective Optimization Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network |
| daf | Dry and ash-free |
| db | Dry basis |
| ER | Equivalence ratio |
| FC | Fixed carbon |
| FT | Fischer–Tropsch |
| LHV | Lower heating value |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| MILP | Mixed-integer linear programming |
| ML | Machine learning |
| MLP | Multi-layer perceptron |
| MSW | Municipal solid waste |
| NLP | Nonlinear programming |
| OF | Objective function |
| OMLT | Optimization and machine learning toolbox |
| R2 | Correlation coefficient |
| ReLU | Rectified linear unit |
| RMSE | Root mean square error |
| SHAP | Shapley additive explanations |
| Tanh | Hyperbolic tangent |
| TPE | Tree-structured Parzen Estimator |
| VM | Volatile matter |
| wb | Wet basis |
| wt | Weight |
| ε | Minimum acceptable syngas yield |
References
- Fernando, S.; Adhikari, S.; Chandrapal, C.; Murali, N. Biorefineries: Current Status, Challenges, and Future Direction. Energy Fuels 2006, 20, 1727–1737. [Google Scholar] [CrossRef]
- UNEP. Beyond an Age of Waste: Turning Rubbish into a Resource. In Global Waste Management Outlook; UNEP: Nairobi, Kenya, 2024; ISBN 978-92-807-4129-2. [Google Scholar]
- World Must Move beyond Waste Era and Turn Rubbish into Resource: UN Report. Available online: https://www.unep.org/news-and-stories/press-release/world-must-move-beyond-waste-era-and-turn-rubbish-resource-un-report (accessed on 12 August 2025).
- Gao, Y.; Wang, M.; Raheem, A.; Wang, F.; Wei, J.; Xu, D.; Song, X.; Bao, W.; Huang, A.; Zhang, S.; et al. Syngas Production from Biomass Gasification: Influences of Feedstock Properties, Reactor Type, and Reaction Parameters. ACS Omega 2023, 8, 31620–31631. [Google Scholar] [CrossRef]
- Ascher, S.; Sloan, W.; Watson, I.; You, S. A Comprehensive Artificial Neural Network Model for Gasification Process Prediction. Appl. Energy 2022, 320, 119289. [Google Scholar] [CrossRef]
- López-Flores, F.J.; Ochoa-Barragán, R.; Raya-Tapia, A.Y.; Ramírez-Márquez, C.; Ponce-Ortega, J.M. (Eds.) Chapter 17–Challenges and Future Scope. In Machine Learning Tools for Chemical Engineering; Elsevier: Amsterdam, Netherlands, 2025; pp. 591–598. ISBN 978-0-443-29058-9. [Google Scholar]
- Daoutidis, P.; Lee, J.H.; Rangarajan, S.; Chiang, L.; Gopaluni, B.; Schweidtmann, A.M.; Harjunkoski, I.; Mercangöz, M.; Mesbah, A.; Boukouvala, F.; et al. Machine Learning in Process Systems Engineering: Challenges and Opportunities. Comput. Chem. Eng. 2024, 181, 108523. [Google Scholar] [CrossRef]
- Baruah, D.; Baruah, D.C.; Hazarika, M.K. Artificial Neural Network Based Modeling of Biomass Gasification in Fixed Bed Downdraft Gasifiers. Biomass Bioenergy 2017, 98, 264–271. [Google Scholar] [CrossRef]
- Xiao, G.; Ni, M.; Chi, Y.; Jin, B.; Xiao, R.; Zhong, Z.; Huang, Y. Gasification Characteristics of MSW and an ANN Prediction Model. Waste Manag. 2009, 29, 240–244. [Google Scholar] [CrossRef] [PubMed]
- Serrano, D.; Golpour, I.; Sánchez-Delgado, S. Predicting the Effect of Bed Materials in Bubbling Fluidized Bed Gasification Using Artificial Neural Networks (ANNs) Modeling Approach. Fuel 2020, 266, 117021. [Google Scholar] [CrossRef]
- Elmaz, F.; Yücel, Ö.; Mutlu, A.Y. Predictive Modeling of Biomass Gasification with Machine Learning-Based Regression Methods. Energy 2020, 191, 116541. [Google Scholar] [CrossRef]
- Kardani, N.; Zhou, A.; Nazem, M.; Lin, X. Modelling of Municipal Solid Waste Gasification Using an Optimised Ensemble Soft Computing Model. Fuel 2021, 289, 119903. [Google Scholar] [CrossRef]
- López-Flores, F.J.; Ramírez-Márquez, C.; Ponce-Ortega, J.M. Process Systems Engineering Tools for Optimization of Trained Machine Learning Models: Comparative and Perspective. Ind. Eng. Chem. Res. 2024, 63, 13966–13979. [Google Scholar] [CrossRef]
- Ceccon, F.; Jalving, J.; Haddad, J.; Thebelt, A.; Tsay, C.; Laird, C.D.; Misener, R. OMLT: Optimization & Machine Learning Toolkit. arXiv 2022, arXiv:2202.02414. [Google Scholar] [CrossRef]
- Turner, M.; Chmiela, A.; Koch, T.; Winkler, M. PySCIPOpt-ML: Embedding Trained Machine Learning Models into Mixed-Integer Programs. arXiv 2024, arXiv:2312.08074. [Google Scholar]
- Dowson, O.; Parker, R.B.; Bent, R. MathOptAI.Jl: Embed Trained Machine Learning Predictors into JuMP Models. arXiv 2025, arXiv:2507.03159. [Google Scholar]
- López-Flores, F.J.; Lira-Barragán, L.F.; Rubio-Castro, E.; El-Halwagi, M.M.; Ponce-Ortega, J.M. Hybrid Machine Learning-Mathematical Programming Approach for Optimizing Gas Production and Water Management in Shale Gas Fields. ACS Sustain. Chem. Eng. 2023, 11, 6043–6056. [Google Scholar] [CrossRef]
- Hou, S.; Duque, E.M.S.; Palensky, P.; Vergara, P.P. A Constraint Enforcement Deep Reinforcement Learning Framework for Optimal Energy Storage Systems Dispatch. arXiv 2023, arXiv:2307.14304. [Google Scholar] [CrossRef]
- Bugosen, S.I.; Laird, C.D.; Parker, R.B. Process Flowsheet Optimization with Surrogate and Implicit Formulations of a Gibbs Reactor. arXiv 2024, arXiv:2310.09307. [Google Scholar] [CrossRef]
- Jalving, J.; Ghouse, J.; Cortes, N.; Gao, X.; Knueven, B.; Agi, D.; Martin, S.; Chen, X.; Guittet, D.; Tumbalam-Gooty, R.; et al. Beyond Price Taker: Conceptual Design and Optimization of Integrated Energy Systems Using Machine Learning Market Surrogates. Appl. Energy 2023, 351, 121767. [Google Scholar] [CrossRef]
- López-Flores, F.J.; Ramírez-Márquez, C.; Rubio-Castro, E.; Ponce-Ortega, J.M. Solar Photovoltaic Panel Production in Mexico: A Novel Machine Learning Approach. Environ. Res. 2024, 246, 118047. [Google Scholar] [CrossRef]
- Padilla-Esquivel, C.A.; López-Flores, F.J.; Hernández-Pérez, L.G.; Rubio-Castro, E.; Ponce-Ortega, J.M. Optimizing Green Urea Production: Integration of Process Simulation, Artificial Intelligence, and Sustainable Technologies. J. Clean. Prod. 2025, 501, 145371. [Google Scholar] [CrossRef]
- Mansaray, K.G.; Ghaly, A.E.; Al-Taweel, A.M.; Hamdullahpur, F.; Ugursal, V.I. Air Gasification of Rice Husk in a Dual Distributor Type Fluidized Bed Gasifier. Biomass Bioenergy 1999, 17, 315–332. [Google Scholar] [CrossRef]
- De Andrés, J.M.; Narros, A.; Rodríguez, M.E. Air-Steam Gasification of Sewage Sludge in a Bubbling Bed Reactor: Effect of Alumina as a Primary Catalyst. Fuel Process. Technol. 2011, 92, 433–440. [Google Scholar] [CrossRef]
- Lv, P.M.; Xiong, Z.H.; Chang, J.; Wu, C.Z.; Chen, Y.; Zhu, J.X. An Experimental Study on Biomass Air–Steam Gasification in a Fluidized Bed. Bioresour. Technol. 2004, 95, 95–101. [Google Scholar] [CrossRef]
- Fremaux, S.; Beheshti, S.-M.; Ghassemi, H.; Shahsavan-Markadeh, R. An Experimental Study on Hydrogen-Rich Gas Production via Steam Gasification of Biomass in a Research-Scale Fluidized Bed. Energy Convers. Manag. 2015, 91, 427–432. [Google Scholar] [CrossRef]
- Sarker, S.; Nielsen, H.K. Assessing the Gasification Potential of Five Woodchips Species by Employing a Lab-Scale Fixed-Bed Downdraft Reactor. Energy Convers. Manag. 2015, 103, 801–813. [Google Scholar] [CrossRef]
- Lv, P.; Chang, J.; Xiong, Z.; Huang, H.; Wu, C.; Chen, Y.; Zhu, J. Biomass Air−Steam Gasification in a Fluidized Bed to Produce Hydrogen-Rich Gas. Energy Fuels 2003, 17, 677–682. [Google Scholar] [CrossRef]
- Miccio, F.; Piriou, B.; Ruoppolo, G.; Chirone, R. Biomass Gasification in a Catalytic Fluidized Reactor with Beds of Different Materials. Chem. Eng. J. 2009, 154, 369–374. [Google Scholar] [CrossRef]
- Li, X.T.; Grace, J.R.; Lim, C.J.; Watkinson, A.P.; Chen, H.P.; Kim, J.R. Biomass Gasification in a Circulating Fluidized Bed. Biomass Bioenergy 2004, 26, 171–193. [Google Scholar] [CrossRef]
- Narváez, I.; Orío, A.; Aznar, M.P.; Corella, J. Biomass Gasification with Air in an Atmospheric Bubbling Fluidized Bed. Effect of Six Operational Variables on the Quality of the Produced Raw Gas. Ind. Eng. Chem. Res. 1996, 35, 2110–2120. [Google Scholar] [CrossRef]
- Baratieri, M.; Pieratti, E.; Nordgreen, T.; Grigiante, M. Biomass Gasification with Dolomite as Catalyst in a Small Fluidized Bed Experimental and Modelling Analysis. Waste Biomass Valorization 2010, 1, 283–291. [Google Scholar] [CrossRef]
- Sarker, S.; Bimbela, F.; Sánchez, J.L.; Nielsen, H.K. Characterization and Pilot Scale Fluidized Bed Gasification of Herbaceous Biomass: A Case Study on Alfalfa Pellets. Energy Convers. Manag. 2015, 91, 451–458. [Google Scholar] [CrossRef]
- Biagini, E.; Barontini, F.; Tognotti, L. Development of a Bi-Equilibrium Model for Biomass Gasification in a Downdraft Bed Reactor. Bioresour. Technol. 2016, 201, 156–165. [Google Scholar] [CrossRef]
- Dutta, P.P.; Pandey, V.; Das, A.R.; Sen, S.; Baruah, D.C. Down Draft Gasification Modelling and Experimentation of Some Indigenous Biomass for Thermal Applications. Energy Procedia 2014, 54, 21–34. [Google Scholar] [CrossRef]
- Loha, C.; Chattopadhyay, H.; Chatterjee, P.K. Energy Generation from Fluidized Bed Gasification of Rice Husk. J. Renew. Sustain. Energy 2013, 5, 043111. [Google Scholar] [CrossRef]
- Zhang, Z.; Pang, S. Experimental Investigation of Biomass Devolatilization in Steam Gasification in a Dual Fluidised Bed Gasifier. Fuel 2017, 188, 628–635. [Google Scholar] [CrossRef]
- Song, T.; Wu, J.; Shen, L.; Xiao, J. Experimental Investigation on Hydrogen Production from Biomass Gasification in Interconnected Fluidized Beds. Biomass Bioenergy 2012, 36, 258–267. [Google Scholar] [CrossRef]
- Karatas, H.; Akgun, F. Experimental Results of Gasification of Walnut Shell and Pistachio Shell in a Bubbling Fluidized Bed Gasifier under Air and Steam Atmospheres. Fuel 2018, 214, 285–292. [Google Scholar] [CrossRef]
- Liu, H.; Hu, J.; Wang, H.; Wang, C.; Li, J. Experimental Studies of Biomass Gasification with Air. J. Nat. Gas Chem. 2012, 21, 374–380. [Google Scholar] [CrossRef]
- Gai, C.; Dong, Y. Experimental Study on Non-Woody Biomass Gasification in a Downdraft Gasifier. Int. J. Hydrogen Energy 2012, 37, 4935–4944. [Google Scholar] [CrossRef]
- Arena, U.; Zaccariello, L.; Mastellone, M.L. Fluidized Bed Gasification of Waste-Derived Fuels. Waste Manag. 2010, 30, 1212–1219. [Google Scholar] [CrossRef]
- Arena, U.; Di Gregorio, F. Gasification of a Solid Recovered Fuel in a Pilot Scale Fluidized Bed Reactor. Fuel 2014, 117, 528–536. [Google Scholar] [CrossRef]
- Kaewluan, S.; Pipatmanomai, S. Gasification of High Moisture Rubber Woodchip with Rubber Waste in a Bubbling Fluidized Bed. Fuel Process. Technol. 2011, 92, 671–677. [Google Scholar] [CrossRef]
- Lahijani, P.; Zainal, Z.A. Gasification of Palm Empty Fruit Bunch in a Bubbling Fluidized Bed: A Performance and Agglomeration Study. Bioresour. Technol. 2011, 102, 2068–2076. [Google Scholar] [CrossRef]
- Ruoppolo, G.; Ammendola, P.; Chirone, R.; Miccio, F. H2-Rich Syngas Production by Fluidized Bed Gasification of Biomass and Plastic Fuel. Waste Manag. 2012, 32, 724–732. [Google Scholar] [CrossRef] [PubMed]
- Khan, Z.; Yusup, S.; Ahmad, M.M.; Chin, B.L.F. Hydrogen Production from Palm Kernel Shell via Integrated Catalytic Adsorption (ICA) Steam Gasification. Energy Convers. Manag. 2014, 87, 1224–1230. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, G.; You, Y.; Xiao, B.; Liu, S.; He, P.; Guo, D.; Guo, X.; Zhang, G. Hydrogen-Rich Gas Production by Steam Gasification of Municipal Solid Waste (MSW) Using NiO Supported on Modified Dolomite. Int. J. Hydrogen Energy 2012, 37, 6503–6510. [Google Scholar] [CrossRef]
- Iovane, P.; Donatelli, A.; Molino, A. Influence of Feeding Ratio on Steam Gasification of Palm Shells in a Rotary Kiln Pilot Plant. Experimental and Numerical Investigations. Biomass Bioenergy 2013, 56, 423–431. [Google Scholar] [CrossRef]
- Erkiaga, A.; Lopez, G.; Amutio, M.; Bilbao, J.; Olazar, M. Influence of Operating Conditions on the Steam Gasification of Biomass in a Conical Spouted Bed Reactor. Chem. Eng. J. 2014, 237, 259–267. [Google Scholar] [CrossRef]
- Yin, R.; Liu, R.; Wu, J.; Wu, X.; Sun, C.; Wu, C. Influence of Particle Size on Performance of a Pilot-Scale Fixed-Bed Gasification System. Bioresour. Technol. 2012, 119, 15–21. [Google Scholar] [CrossRef]
- Huynh, C.V.; Kong, S.-C. Performance Characteristics of a Pilot-Scale Biomass Gasifier Using Oxygen-Enriched Air and Steam. Fuel 2013, 103, 987–996. [Google Scholar] [CrossRef]
- Carpenter, D.L.; Bain, R.L.; Davis, R.E.; Dutta, A.; Feik, C.J.; Gaston, K.R.; Jablonski, W.; Phillips, S.D.; Nimlos, M.R. Pilot-Scale Gasification of Corn Stover, Switchgrass, Wheat Straw, and Wood: 1. Parametric Study and Comparison with Literature. Ind. Eng. Chem. Res. 2010, 49, 1859–1871. [Google Scholar] [CrossRef]
- Herguido, J.; Corella, J.; Gonzalez-Saiz, J. Steam Gasification of Lignocellulosic Residues in a Fluidized Bed at a Small Pilot Scale. Effect of the Type of Feedstock. Ind. Eng. Chem. Res. 1992, 31, 1274–1282. [Google Scholar] [CrossRef]
- Luo, S.; Zhou, Y.; Yi, C. Syngas Production by Catalytic Steam Gasification of Municipal Solid Waste in Fixed-Bed Reactor. Energy 2012, 44, 391–395. [Google Scholar] [CrossRef]
- López-Flores, F.J.; Ochoa-Barragán, R.; Raya-Tapia, A.Y.; Ramírez-Márquez, C.; Ponce-Ortega, J.M. (Eds.) Chapter 9—Deep Learning. In Machine Learning Tools for Chemical Engineering; Elsevier: Amsterdam, Netherlands, 2025; pp. 241–291. ISBN 978-0-443-29058-9. [Google Scholar]
- Taud, H.; Mas, J.F. Multilayer Perceptron (MLP). In Geomatic Approaches for Modeling Land Change Scenarios; Camacho Olmedo, M.T., Paegelow, M., Mas, J.-F., Escobar, F., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 451–455. ISBN 978-3-319-60801-3. [Google Scholar]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random Forests. In Ensemble Machine Learning: Methods and Applications; Zhang, C., Ma, Y., Eds.; Springer: New York, NY, USA, 2012; pp. 157–175. ISBN 978-1-4419-9326-7. [Google Scholar]
- Genuer, R.; Poggi, J.-M. (Eds.) Random Forests. In Random Forests with R; Springer International Publishing: Cham, Switzerland, 2020; pp. 33–55. ISBN 978-3-030-56485-8. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. arXiv 2019, arXiv:1706.09516. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A Comparative Analysis of Gradient Boosting Algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Zhou, Y.; Cahya, S.; Combs, S.A.; Nicolaou, C.A.; Wang, J.; Desai, P.V.; Shen, J. Exploring Tunable Hyperparameters for Deep Neural Networks with Industrial ADME Data Sets. J. Chem. Inf. Model. 2019, 59, 1005–1016. [Google Scholar] [CrossRef]
- Agrawal, T. (Ed.) Optuna and AutoML. In Hyperparameter Optimization in Machine Learning: Make Your Machine Learning and Deep Learning Models More Efficient; Apress: Berkeley, CA, USA, 2021; pp. 109–129. ISBN 978-1-4842-6579-6. [Google Scholar]
- Gridin, I. (Ed.) Hyperparameter Optimization. In Automated Deep Learning Using Neural Network Intelligence: Develop and Design PyTorch and TensorFlow Models Using Python; Apress: Berkeley, CA, USA, 2022; pp. 31–110. ISBN 978-1-4842-8149-9. [Google Scholar]
- Zol, S.; Chandodkar, H.; Ahmed, M.; Haider, M.B.; Kumar, K.D.P.L.; Naidu, B.N.; Kumar, R.; Viswanadham, N. Multi-Objective Optimization of Syngas Production from Bio-Glycerol: A Bi-Reforming Approach Using NSGA-II. J. Environ. Chem. Eng. 2025, 13, 116186. [Google Scholar] [CrossRef]
- Huang, H.; Ramaswamy, S. Modeling Biomass Gasification Using Thermodynamic Equilibrium Approach. Appl. Biochem. Biotechnol. 2009, 154, 14–25. [Google Scholar] [CrossRef] [PubMed]
- Várhegyi, G.; Wang, L.; Skreiberg, Ø. Empirical Kinetic Models for the CO2 Gasification of Biomass Chars. Part 1. Gasification of Wood Chars and Forest Residue Chars. ACS Omega 2021, 6, 27552–27560. [Google Scholar] [CrossRef] [PubMed]
- Silva, I.P.; Lima, R.M.; Santana, H.E.; Silva, G.F.; Ruzene, D.S.; Silva, D.P. Development of a Semi-Empirical Model for Woody Biomass Gasification Based on Stoichiometric Thermodynamic Equilibrium Model. Energy 2022, 241, 122894. [Google Scholar] [CrossRef]
- Aentung, T.; Patcharavorachot, Y.; Wu, W. Co-Gasification of Plastic Waste Blended with Biomass: Process Modeling and Multi-Objective Optimization. Processes 2024, 12, 1906. [Google Scholar] [CrossRef]
- Molochas, C.; Tsiakaras, P. Carbon Monoxide Tolerant Pt-Based Electrocatalysts for H2-PEMFC Applications: Current Progress and Challenges. Catalysts 2021, 11, 1127. [Google Scholar] [CrossRef]
- Rauch, R.; Hrbek, J.; Hofbauer, H. Biomass Gasification for Synthesis Gas Production and Applications of the Syngas. In Advances in Bioenergy; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2016; pp. 73–91. ISBN 978-1-118-95784-4. [Google Scholar]
- Lögdberg, S. Development of Fischer-Tropsch Catalysts for Gasified Biomass; School of Chemical Science and Engineering, Royal Institute of Technology: Stockholm, Sweden, 2007; ISBN 978-91-7178-698-2. [Google Scholar]



| Min | Max | Mean | SD | |
|---|---|---|---|---|
| Feedstock information | ||||
| Type | Pine sawdust, Woody biomass, Herbaceous biomass, Sewage sludge, Municipal solid waste, Other | |||
| Shape | Pellets, Fibers, Dust, Particles, Other | |||
| Particle Size (mm) | 0.25 | 70.00 | 4.47 | 6.52 |
| LHV [MJ/kg wb] | 11.50 | 42.90 | 18.48 | 6.43 |
| Ultimate Analysis | ||||
| C [%daf] | 40.07 | 86.03 | 51.31 | 8.83 |
| H [%daf] | 3.79 | 14.23 | 6.82 | 1.91 |
| N [%daf] | 0 | 7.32 | 0.99 | 1.79 |
| S [%daf] | 0 | 1.61 | 0.33 | 0.43 |
| O [%daf] | 0 | 53.40 | 39.93 | 10.41 |
| Proximate Analysis | ||||
| Ash [%db] | 0.27 | 44.00 | 6.89 | 11.51 |
| Moisture [%db] | 0 | 27.00 | 8.42 | 5.47 |
| Volatile Matter [%db] | 56.00 | 89.11 | 77.75 | 8.72 |
| Fixed carbon [%db] | 9.07 | 23.82 | 15.71 | 3.06 |
| Lignocellulosic Composition | ||||
| Cellulose [% db] | 29.60 | 46.20 | 38.84 | 5.15 |
| Hemicellulose [%db] | 14.00 | 29.60 | 21.30 | 4.52 |
| Lignin [%db] | 13.60 | 33.00 | 24.14 | 5.87 |
| Gasifier Conditions and Information | ||||
| Temperature [°C] | 553.00 | 1050.00 | 796.00 | 79.61 |
| Operation Mode | Batch, Continuous | |||
| Residence Time [min] | 1.93 | 403.00 | 87.72 | 96.60 |
| Steam/Biomass [wt/wt] | 0.00 | 4.04 | 1.09 | 0.76 |
| ER | 0.09 | 0.87 | 0.29 | 0.10 |
| Gasifying Agent | Air, Air + Steam, Oxygen, Steam, Air + Oxygen, Other | |||
| Reactor Type | Fluidized Bed, Fixed Bed, Circulating Fluidized Bed | |||
| Bed Material | Olivine, Silica, Dolomite, Alumina, Olivine Sand, Calcium Oxide | |||
| Catalyst | Present, Not present | |||
| Scale | Lab, Pilot | |||
| Min | Max | Mean | SD | |
|---|---|---|---|---|
| N2 [vol.%db] | 0.00 | 74.90 | 35.38 | 27.04 |
| H2 [vol.%db] | 3.00 | 73.85 | 22.42 | 16.88 |
| CO [vol.%db] | 2.20 | 50.00 | 20.12 | 10.11 |
| CO2 [vol.%db] | 0.00 | 38.25 | 16.28 | 6.21 |
| CH4 [vol.%db] | 0.25 | 17.00 | 5.32 | 3.43 |
| C2Hn [vol.%db] | 0 | 9.50 | 2.09 | 1.48 |
| Syngas yield [Nm3/kg wb] | 0.49 | 6.19 | 1.79 | 0.94 |
| Model | Hyperparameter | Variable Type | Min | Max |
|---|---|---|---|---|
| Random Forest | Bootstrap | Categorical | True, False | |
| Max features | Categorical | None, sqrt, log2 | ||
| N estimators | Integer | 10 | 500 | |
| Max depth | Integer | 2 | 24 | |
| Min samples split | Integer | 2 | 20 | |
| Min samples leaf | Integer | 1 | 20 | |
| CatBoost | Bootstrap type | Categorical | Bayesian, Bernoulli, MVS | |
| Learning rate | Float | 0.01 | 0.8 | |
| Depth | Integer | 2 | 16 | |
| N estimators | Integer | 10 | 500 | |
| L2 leaf reg | Float | 1 | 50 | |
| ANN | Hidden layers | Integer | 1 | 6 |
| Neurons per layer | Integer | 12 | 200 | |
| Learning Rate | Log | 1 × 10−5 | 1 × 10−1 | |
| Batch size | Integer | 1 | 10 | |
| Regularization parameter (L2) | Log | 1 × 10−4 | 1 × 10−1 | |
| Model | Hyperparameter | Variable Type | Optimal Value | Average Time |
|---|---|---|---|---|
| Random Forest | Bootstrap | Categorical | yes | 1 h |
| Max features | Categorical | - | ||
| N estimators | Integer | 26 | ||
| Max depth | Integer | 14 | ||
| Min samples split | Integer | 4 | ||
| Min samples leaf | Integer | 1 | ||
| CatBoost | Bootstrap type | Categorical | - | 8 h |
| Learning rate | Float | 0.4348 | ||
| Depth | Integer | 4 | ||
| N estimators | Integer | 447 | ||
| Reg hoja L2 | Float | 30.6249 | ||
| ANN | Hidden layers | Integer | 5 | 15 h |
| Neurons per layer | Integer | 167 | ||
| Integer | 16 | |||
| Integer | 148 | |||
| Integer | 35 | |||
| Integer | 36 | |||
| Learning Rate | Log | 0.0002 | ||
| Batch size | Integer | 6 | ||
| Regularization parameter (L2) | Log | 0.0003 |
| Output Variables | RMSE | MAE | R2 | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std (±) | Mean | Std (±) | Mean | Std (±) | Mean | Std (±) | |
| N2 | 0.1806 | 0.0647 | 0.1207 | 0.7771 | 0.9638 | 0.0288 | 0.9440 | 0.0323 |
| H2 | 0.2475 | 0.0726 | 0.1750 | 0.7347 | 0.9379 | 0.0241 | ||
| CO | 0.3454 | 0.1646 | 0.2419 | 0.6246 | 0.8713 | 0.0707 | ||
| CO2 | 0.3748 | 0.0926 | 0.2642 | 0.3341 | 0.8573 | 0.0634 | ||
| CH4 | 0.3803 | 0.0668 | 0.2505 | 0.0775 | 0.8355 | 0.0430 | ||
| C2Hn | 0.6275 | 0.1781 | 0.3970 | 0.0728 | 0.6317 | 0.1009 | ||
| Syngas Yield | 0.2838 | 0.0873 | 0.2099 | 0.0490 | 0.9171 | 0.0458 | ||
| Model/Metrics | RMSE | MAE | MAPE | R2 |
|---|---|---|---|---|
| N2 | ||||
| Random Forest | 0.0310 | 0.0845 | 0.1535 | 0.9704 |
| CatBoost | 0.0165 | 0.1025 | 0.1458 | 0.9843 |
| RNA | 0.0146 | 0.0871 | 0.1757 | 0.9860 |
| H2 | ||||
| Random Forest | 0.0304 | 0.1202 | 0.9408 | 0.9698 |
| CatBoost | 0.0330 | 0.1354 | 0.9832 | 0.9672 |
| RNA | 0.0297 | 0.1187 | 1.6501 | 0.9705 |
| CO | ||||
| Random Forest | 0.0855 | 0.1949 | 2.4344 | 0.9149 |
| CatBoost | 0.0667 | 0.2011 | 1.9675 | 0.9335 |
| RNA | 0.06233 | 0.1857 | 1.6714 | 0.9380 |
| CO2 | ||||
| Random Forest | 0.0874 | 0.2107 | 1.4399 | 0.9016 |
| CatBoost | 0.1162 | 0.2532 | 1.4494 | 0.8692 |
| RNA | 0.1078 | 0.2114 | 1.8687 | 0.8787 |
| CH4 | ||||
| Random Forest | 0.2741 | 0.2640 | 0.3583 | 0.7557 |
| CatBoost | 0.1953 | 0.2480 | 0.3549 | 0.8258 |
| RNA | 0.1922 | 0.2343 | 0.3553 | 0.8286 |
| C2Hn | ||||
| Random Forest | 0.4738 | 0.4018 | 0.8234 | 0.6190 |
| CatBoost | 0.4721 | 0.4300 | 0.7823 | 0.6204 |
| RNA | 0.5038 | 0.4022 | 0.7233 | 0.5949 |
| Syngas Yield | ||||
| Random Forest | 0.1048 | 0.2185 | 0.7983 | 0.9181 |
| CatBoost | 0.1029 | 0.2395 | 1.3467 | 0.9197 |
| RNA | 0.0687 | 0.1746 | 1.0693 | 0.9463 |
| Solution 1 | Solution 2 | Solution 6 | Solution 7 | Solution 8 | |
|---|---|---|---|---|---|
| Feed LHV | 11.5 | 14.79 | 42.90 | 42.90 | 42.90 |
| C | 40.79 | 43.81 | 44.99 | 54.91 | 52.43 |
| H | 4.46 | 7.283 | 14.23 | 14.23 | 14.23 |
| N | 5.742598 | 1.746 | 0.00 | 0.422 | 0.00 |
| S | 0.739873 | 0.221 | 0.52 | 0.00 | 0.00 |
| O | 0.00 | 31.87 | 0.00 | 3.01 | 24.92 |
| Feed ash | 5.53 | 0.27 | 0.27 | 0.27 | 0.27 |
| Feed moisture | 1.32 | 7.07 | 0.04 | 0.00 | 0.00 |
| Feed VM | 88.75 | 78.83 | 89.11 | 89.11 | 89.11 |
| Feed FC | 22.15 | 16.94 | 9.20 | 9.07 | 9.07 |
| Temperature | 928.12 | 762.59 | 925.56 | 872.97 | 813.46 |
| Operating condition | Continuous | Continuous | Continuous | Continuous | Continuous |
| Steam/biomass ratio | 2.14 | 1.73 | 0.85 | 0.70 | 1.05 |
| ER | 0.10 | 0.21 | 0.60 | 0.67 | 0.80 |
| Gasifying agent | Air + steam | Steam | Steam | Other | Other |
| Reactor type | Fixed bed | Fluidized bed | Fluidized bed | Fluidized bed | Fluidized bed |
| Bed material | Calcium oxide | Calcium oxide | Calcium oxide | Calcium oxide | Dolomite |
| Catalyst | Present | Present | Present | Present | Present |
| Scale | Pilot | Pilot | Pilot | Pilot | Pilot |
| H2/CO ratio | 19.45 | 13.58 | 2.41 | 1.96 | 0.76 |
| Yield (Nm3/wb) | 1 | 2 | 6 | 7 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Báez-Barrón, G.; Lopéz-Flores, F.J.; Rubio-Castro, E.; Ponce-Ortega, J.M. Biomass Gasification for Waste-to-Energy Conversion: Artificial Intelligence for Generalizable Modeling and Multi-Objective Optimization of Syngas Production. Resources 2025, 14, 157. https://doi.org/10.3390/resources14100157
Báez-Barrón G, Lopéz-Flores FJ, Rubio-Castro E, Ponce-Ortega JM. Biomass Gasification for Waste-to-Energy Conversion: Artificial Intelligence for Generalizable Modeling and Multi-Objective Optimization of Syngas Production. Resources. 2025; 14(10):157. https://doi.org/10.3390/resources14100157
Chicago/Turabian StyleBáez-Barrón, Gema, Francisco Javier Lopéz-Flores, Eusiel Rubio-Castro, and José María Ponce-Ortega. 2025. "Biomass Gasification for Waste-to-Energy Conversion: Artificial Intelligence for Generalizable Modeling and Multi-Objective Optimization of Syngas Production" Resources 14, no. 10: 157. https://doi.org/10.3390/resources14100157
APA StyleBáez-Barrón, G., Lopéz-Flores, F. J., Rubio-Castro, E., & Ponce-Ortega, J. M. (2025). Biomass Gasification for Waste-to-Energy Conversion: Artificial Intelligence for Generalizable Modeling and Multi-Objective Optimization of Syngas Production. Resources, 14(10), 157. https://doi.org/10.3390/resources14100157






