Abstract
The standardized methods used in carbon markets require measurement of the biomass and carbon stored in trees, which can be quantified through allometric equations. The objective of this study was to analyze aboveground biomass estimates with allometric models in three mangrove species and compare them with those used by the Climate Action Reserve (CAR) standard. The mangrove forest in Tabasco, Mexico, was certified with the Forest Protocol for Mexico Version 2.0 (FPM) of the CAR standard. Allometric equations for mangrove species were reviewed to determine the most suitable equation for the calculation of biomass. The predictions of the allometric equations of the FPM were analyzed with data from Tabasco from the National Forest and Soil Inventory 2015–2020, and the percentages of trees within the ranges of diameters of the FPM equations were determined. The FPM equations generated higher biomass values for Rhizophora mangle and lower values for Avicennia germinans than the seven equations with which they were compared. In the mangrove swamp of Ejido Úrsulo Galván, Tabasco, 81.8% of the biomass of A. germinans, 34.4% of Laguncularia racemosa and 24.0% of R. mangle were within the diameter range of the FPM equations, and in Tabasco, 28.5% of A. germinans, 16.7% of L. racemosa and 5.7% of R. mangle were within the diameter range. For A. germinans and R. mangle, we recommend using the equation that considers greater maximum diameters. The allometric equations of the FPM do not adequately predict a large percentage of the biomass.
1. Introduction
Mangrove forests represent a type of ecosystem dominated by arboreal or shrubby plant species called mangroves, supporting saline soils that are flooded for most of the year. They are considered a type of coastal wetland since they are found at the mouths of rivers, coastal lagoons and estuaries and are influenced by saltwater from the sea and fresh water from runoff from hydrological basins through rivers [1].
To estimate a part of the carbon stored in trees, the weight of the biomass must be known. Various methods have been developed to estimate the biomass of forests. There are three main methods: the harvest method, the middle tree method and the allometric method [2]. The most accurate method to estimate biomass weight and subsequently determine the amount of carbon is to destructively analyze tree samples divided into constituent components (stem, branches, leaves, flowers, fruits, and roots). However, cutting down forest trees often runs counter to the objective of conserving forests. An alternative approach is to use established allometric equations to estimate biomass and then calculate biomass carbon as a fraction of this value [3]. Allometry is a powerful tool for estimating tree weight from independent variables, such as trunk diameter and height, which are quantifiable in the field [4].
Site-specific aboveground biomass models estimate biomass with greater precision since they have been generated for a specific species and in a specific area; however, to reduce the error in the estimates, these models must be applied for that particular species and in the region of the study area where the model was generated or a very similar area [5,6]. In addition, given the physiographic and muddy soil conditions in which mangroves are located, the equations reported in the literature were developed on the basis of measuring the diameter of the trees [5].
The use of preexisting allometric equations, instead of specific site equations, is an important source of uncertainty in the determination of biomass and carbon. When the use of preexisting equations is necessary, multiple potentially applicable equations should be used to determine plausible ranges of aboveground biomass. Species and physical characteristics vary from one site to another, and the applicability of equations developed in different places may also be limited, even if the equations are specific to a certain species [3]. The use of species-specific equations over general equations is recommended since the species have structural differences [3,7], and in addition, the general equations overestimate the aboveground biomass in comparison with the specific species equations [6]. The general equations are recommended only when they contain the density of wood measured at the site as a predictor variable and when they are adjusted with trees that grow in environmental conditions similar to the area in which the estimation is made, since these environmental variables control the growth of trees and anatomical characteristics associated with wood density [6,8]. When general equations are used, it is essential to verify that the species present are similar to those used to develop the original equations [3].
In Mexico, equations have been developed for Rhizophora mangle, Avicennia germinans and Laguncularia racemosa in Laguna de Terminos, Campeche [9] and L. racemosa in Marismas Nacionales, Nayarit [10]. The low number of allometric equations in Mexico and the high structural variation in mangroves in Mexico underscore the need for the development of new and different species-specific allometric equations to reduce the uncertainty associated with the use of external data and their inappropriate use in the estimation of plant biomass [3,8].
Studies such as that of Rahman et al. [6] note that the choice of an appropriate allometric model is essential for reducing uncertainties in the estimation of aboveground biomass. Furthermore, their use outside the minimum and maximum diameter range from which they were developed results in significant errors [5], which tend to increase as the diameter increases [6]. In addition, different allometric equations applied to the same species can generate very different results [3,5]. For example, standards such as the Climate Action Reserve (CAR) apply a single allometric equation to estimate the biomass of a species throughout Mexico without considering the range of diameters that can be observed in different physiographic regions [11]. Therefore, it is appropriate to evaluate the models applied by a standard such as CAR, examine the differences in these estimates with different allometric models, determine the influence of the diameter in which they were developed in the biomass estimates and select the most adequate allometric model.
The objective of this study was to analyze various models for the determination of aboveground biomass in mangrove species in Tabasco in comparison with the equations applied by the Forest Protocol for Mexico Version 2.0 of the CAR standard used for payment for environmental services. The results provide a better understanding of the estimation of biomass in these ecosystems and the precise determination of the carbon stored in trees for fair payment in carbon credits.
2. Materials and Methods
2.1. Study Area
The study area is located at Ejido Úrsulo Galván, Jalpa de Méndez, Tabasco, in southeastern Mexico. The geographical location is 18°20′32.12″ and 18°24′25.21″ north latitude and 93°3′56.86″ and 92°59′56.05″ west longitude. It is located in the Grijalva–Mezcalapa delta system in the eastern part of the Mecoacán Lagoon [12]. The climate in the municipality of Jalpa de Méndez is hot-humid, with abundant rains in summer. The precipitation ranges between 1500 and 2000 mm per year, and the average annual temperature is between 24 and 26 °C. The soils of the study area, according to the map of major groups of soils of the state of Tabasco [13], are Histosols. Furthermore, Domínguez-Domínguez et al. [14] included Solonchak soil in mangrove areas. Mangrove soils are generally rich in organic matter and nutrients; however, they have severe limitations due to flooding, the water table, salinity and sodicity, so they do not have the capacity for agricultural use [14,15].
2.2. Sampling Design
The methodology used to determine aboveground biomass is based on the Forest Protocol for Mexico Version 2.0 (FPM) published by the CAR [11].
The forest inventory was conducted by dividing the study area (930 ha) into a grid of 25 × 25 m plots with the open access program QGIS and identifying the coordinates of each plot [11]. A total of 130 grid cells with mangrove vegetation were randomly selected using the randomization tool of the software CALCBOSK (version 2.0, a database application developed by the FPM (Bohemia, NY, USA)). Nested design plots were established in the selected grids using the threshold DBH values proposed by the FPM, which are used for all forest types in Mexico. Given the randomness of plot selection, the average distance between plots varied. Some plots were situated close to the water, while others were located farther away within the inventory grid. Consequently, no criteria related to distance to water were considered when establishing the plots. To conduct the inventory, in each plot with a fixed radius of 11.28 m (area = 439 m2), trees with a diameter at breast height (DBH) ≥ 30 cm and height ≥ 3 m were measured. Within the large plots, a smaller plot with a fixed radius of 5.64 m (area = 100 m2) was located for the purpose of inventorying smaller trees, which can provide information on biomass and carbon increase. In the small plot, all trees with DBHs ≥ 5 and <30 cm were measured. The inventoried trees were those with more than 50% of their main stem within the circumference of the plot. The DBH of A. germinans and L. racemosa was measured at a height of 1.30 m from the stem. For R. mangle, the measurement was made 30 cm above the last aerial root. Trees with forked stems below the diameter measurement height were considered to be two individual trees, while trees with forked stems above the diameter measurement height were considered to be a single tree.
The total number of plots, , was obtained with Equation (1) [5].
where test statistic of the Student’s t distribution, known standard deviation of previous data, error obtained by multiplying the average carbon pool by the desired precision. The size of the estimation error adjusted by the finite population correction factor at 95% confidence was obtained with Equation (2):
where S.E. represents the standard error, is the size of the population and is the sample size. Since was less than 0.05, the correction factor for the finite population did not represent a significant adjustment in the average estimated biomass.
2.3. Allometric Equations Available for Mangrove Species
The aboveground biomass of the mangrove was determined via the allometric equations proposed in the Forest Protocol for Mexico Version 2.0 (FPM V2.0) published by the CAR [11]. The equations used to determine the aboveground biomass of R. mangle and L. racemosa were developed and validated by Day et al. [9] in the mangroves of Campeche, Mexico, and the equation for A. germinans was developed by Smith and Whelan [16] in the mangroves of Florida, USA.
Initially, the range of DBH considered in the equations proposed by the FPM V2.0 was reviewed and compared with those obtained in the mangroves of the UMA to determine if they were within the range used by the protocol for the entire country. A literature review was conducted on the allometric equations available for the species R. mangle, A. germinans and L. racemosa under conditions similar to those used in this study. For each allometric equation, the range of diameters in which they were developed was analyzed. Equations that use the DBH were revised to compare them with those used by the FPM V2.0, omitting the equations that use the height because of the difficulty of measuring this parameter in the field [5]. According to Rodríguez-Zúñiga et al. [8], in mangroves, the measurement of height has a sampling error of 10–15%, so the use of equations that use the normal diameter is recommended.
The aboveground biomass of each tree in the nested plot was calculated by dividing the biomass in Mg by the total number of plots (n = 130). Subsequently, to convert the biomass in Mg to Mg ha−1, the biomass of the trees in the largest plot (DBH ≥ 30 cm) was multiplied by 25 (area = 0.04 ha), and the biomass of the trees in the small plot was multiplied by 100 (area = 0.01 ha).
2.4. Determination of Variables
The equations of Imbert and Rollet [17], Fromard et al. [18], Gomes and Schaeffer-Novelli [19], Komiyama et al. [4], Chave et al. [20], Medeiros and Sampaio [21] and Yepes et al. [22] were applied to the results of the UMA Úrsulo Galván inventory. The equations applied for the mangrove species were developed for countries in Latin America and Asia under similar climate conditions, with temperatures ranging from 20 to 30 °C and annual rainfall ranging from 1000 to 3000 mm year−1.
The aboveground biomass of the trees was calculated within the range of diameters of each of the equations mentioned above. For this, the biomass of all individual trees with diameters within the range was summed. Since diameters greater than the range of diameters of these equations were obtained, the biomass outside these ranges was also estimated to calculate the amount of biomass that the equation does not determine with precision (Table 1). According to Kauffman et al. [5] and Yuen et al. [3], the estimates of an allometric equation outside the maximum diameter that was used for its development had significant errors. On the other hand, the biomass was calculated with the inclusion of the data of the maximum DBH of the range of diameters of each equation proposed by FPM V2.0, and the results were compared with those obtained with equations of other authors obtained from the bibliographic review, which consider larger diameters.

Table 1.
Allometric equations were applied to the species A. germinans, L. racemosa and R. mangle.
2.5. Applicability of the Allometric Equations of FPM V2.0
To obtain a broader database than that of the UMA, the applicability of the allometric equations of the FPM V2.0 was tested. In a state context, the database of the species R. mangle, A. germinans and L. racemosa of the National Forest and Soil Inventory 2015–2020 [23] was used for the state of Tabasco. For this purpose, the average diameter was calculated, and the maximum DBH was obtained, in addition to the percentage of trees within the range of diameters of the FPM V2.0 equations.
3. Results
3.1. Comparison of the Applied Allometric Equations
From the literature, 16 allometric equations were selected and compared with the equations proposed by the Forest Protocol for Mexico Version 2.0, of which six applied to the R. mangle species, four to the L. racemosa species and four to A. germinans and two were common equations (Table 1). The equations of Day et al. [9] proposed by FPM V2.0 for R. mangle and L. racemosa were developed for very small trees (maximum 10 cm DBH), whereas the Yepes et al. [22] equation was developed for trees up to 42.5 cm. The Smith and Whelan equation [16] for A. germinans is applicable to trees up to 21.5 cm, while the Imbert and Rollet equation [17] presents the largest range of DBHs, with a maximum of 40.7 cm. The general equation of Komiyama et al. [4] was developed for various mangrove species with a maximum DBH of 48.9 cm, and that of Chave et al. [20] was generated for the three species included in this study with DBHs up to 42 cm. In the use of common or multispecies equations, it is essential to verify that the species present are similar to those used to develop the original equations. The equations analyzed present different adjustments due to the dimensions of the diameters of the trees and the density of the wood, which are variables that control biomass. These variables are strongly affected by site-specific geographic characteristics, such as soil properties, land use history, altitude, and climatic variables, such as temperature and rainfall [3]. The equations reflect the variability in the volume and biomass of different ecological zones, tree species, ages, types of management and sites [7].
The biomass predictions of the allometric equations applied to A. germinans are presented in Figure 1. Of the allometric equations, the Smith and Whelan equation [16] used by the Forest Protocol for Mexico Version 2.0 generated the lowest biomass values within the same range of DBH. The application of the Komiyama et al. equation [4] to A. germinans generated the highest biomass values within the same DBH range. Komiyama et al. [4] developed the equation for Avicennia alba, which belongs to the same genus as A. germinans. Higher biomass values were generated than would be obtained using the density of A. alba (0.6987 g cm−3) since the density of A. germinans wood (0.8116 g cm−3) was applied in the equation.
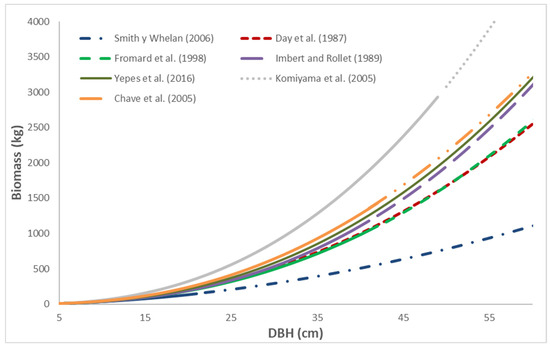
Figure 1.
Predictions of the allometric equation of Smith and Whelan [16] were applied to A. germinans and compared with the predictions of equations developed by other authors. Source of the equations: Smith y Whelan (2006) [16], Day et al. (1987) [9], Fromard et al. (1998) [18], Imbert and Rollet (1989) [17], Yepes et al. (2016) [22], Komiyama et al. (2005) [4], Chave et al. (2005) [20].
In general, when the equations were applied to diameter ranges outside of those for which they were constructed, the differences between the predictions of the equations increased. According to Vorster et al. [24], large trees are a common problem for biomass allometry because they have the greatest amount of biomass and the greatest variation in the form of growth but they are rarely measured because they are the most difficult and expensive to sample. Additionally, in many cases, it is desirable to conserve and hence not carry out destructive sampling with them, resulting in difficulty in predicting outside the diameter range of the sampled trees. This practice is common in biomass assessments because there are few alternatives for most species and because accessing sampling sites is difficult. The diameter and height are influenced by environmental conditions, whereas the density of wood varies between trees of the same species because of the variability of environmental conditions [25]. Estimates can be erroneous, even when equations are applied for similar species, due to diverse environmental settings [3].
The biomass predictions of each allometric equation for L. racemosa are presented in Figure 2. The Smith and Whelan equation [16] generates the lowest biomass values. The Day et al. equation [9] used by FPM V2.0 predicts conservative biomass values compared with the other allometric equations. The Komiyama et al. equation [4] generates the highest biomass values within the same DBH range.
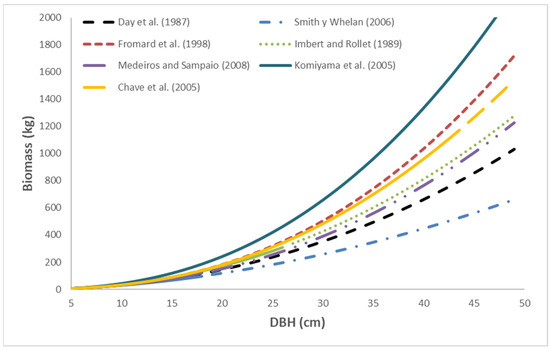
Figure 2.
Predictions of the allometric equation of Day et al. [9] were applied to L. racemosa and compared with the predictions of equations developed by other authors. Source of the equations: Day et al. (1987) [9], Smith y Whelan (2006) [16], Fromard et al. (1998) [18], Imbert and Rollet (1989) [17], Medeiros and Sampaio (2008) [21], Komiyama et al. (2005) [4], Chave et al. (2005) [20].
The biomass predictions of each allometric equation for R. mangle are presented in Figure 3. The Smith and Whelan equation [16] generates the lowest biomass values of the equations within the same DBH. The Day et al. equation [9] used by FPM V2.0 predicts the highest biomass values of the allometric equations. The Komiyama et al. equation [4] generates intermediate values within the same range of DBHs, despite having been developed for Rhizophora mucronata and R. apiculata, which are different botanical species.
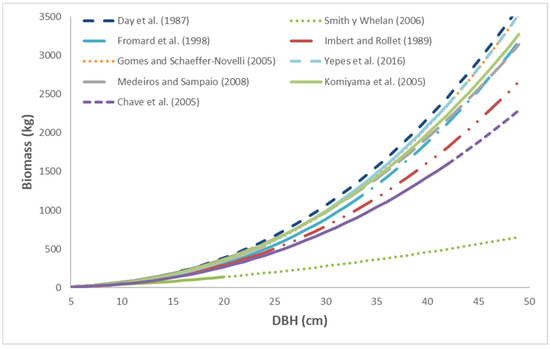
Figure 3.
Predictions of the allometric equation of Day et al. [9] were applied to R. mangle and compared with the predictions of equations developed by other authors. Source of the equations: Day et al. (1987) [9], Smith y Whelan (2006) [16], Fromard et al. (1998) [18], Imbert and Rollet (1989) [17], Gomes and Schaeffer-Novelli (2005) [19], Yepes et al. (2016) [22], Medeiros and Sampaio (2008) [21], Komiyama et al. (2005) [4], Chave et al. (2005) [20].
3.2. Mangrove Biomass Analysis with Allometric Equations in the Study Area
Considering the mangrove tree diameter data of the forest inventory of the UMA, 90% of the diameters of the A. germinans trees are within the range of diameters of the Smith and Whelan equation [16] proposed by FPM V2.0. A total of 68.8% of the L. racemosa trees and 65.9% of the R. mangle trees are within the range of diameters of the equations proposed by Day et al. [9]. For an equation to be applied with a greater margin of adjustment, the size of the trees for which the equation was generated must be taken into consideration since the estimates may be affected if the equations are applied to diameter ranges outside of those used to generate them [3].
The biomass data obtained for the A. germinans trees in the 130 plots via the different equations are presented in Figure 4. The biomass of A. germinans predicted by the FPM V2.0 equation is 0.70 Mg ha−1, of which 0.57 Mg ha−1 is within the range of diameters of the equation and 0.12 Mg ha−1 is outside the range (18.2%). The equations of Fromard et al. [18], Imbert and Rollet [17] and Yepes et al. [22] generate very similar biomass values, where all the trees were within the ranges of diameters of these equations. The general Komiyama et al. equation [4] generates values that are more than double those of the FPM V2.0 equation.
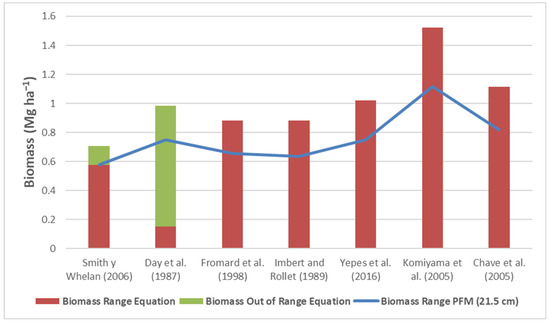
Figure 4.
Biomass of A. germinans obtained via different allometric equations within the ranges of diameters. The solid line represents the biomass obtained at 21.5 cm in diameter according to the Smith and Whelan equation [16]. Source of the equations: Smith y Whelan (2006) [16], Day et al. (1987) [9], Fromard et al. (1998) [18], Imbert and Rollet (1989) [17], Yepes et al. (2016) [22], Komiyama et al. (2005) [4], Chave et al. (2005) [20].
The biomass contributed by A. germinans to the total biomass of the study area was very small compared to that of L. racemosa and R. mangle, due to the limited number of individuals of that species present in the study area. The discrepancy in the number of trees is evident in the distribution per diameter class (Figure S1 in the Supplementary Material), which accounts for the considerable variability in the standard error.
In the species A. germinans, the allometric equation proposed by the protocol includes 90% of the trees; however, the equation generates the lowest biomass values of the equations analyzed. The low biomass values of this equation could be due to the fact that it was developed for mangroves in Florida, USA, which has average temperatures of 23 °C and annual precipitation of 1300 mm year−1 [26], different from Tabasco, which has average temperatures of 28 °C and annual rainfall of 1940 mm year−1 [27]. Yuen et al. [3] mentioned that the specific geographic characteristics of the site, such as the soil properties, land use history, altitude and climatic variables, such as temperature and rainfall, greatly modify the dimensions of the trees and the wood density.
The range of diameters of an allometric equation is determined by the range of diameters in which the equation was developed, and within this range, it has the greatest precision. Not including A. germinans trees that are outside the range of diameters of the FPM V2.0 equation, which in this case is 10%, would mean 0.12 Mg ha−1 (18.2%) biomass would be missed. Therefore, using the Yepes et al. equation [22] is recommended since it was developed considering a greater range of diameters (62.5 cm) and provides conservative predictions of the biomass results. The Yepes et al. equation [22] yields higher biomass values (1.0 Mg ha−1) than the FPM V2.0 equation (0.7 Mg ha−1). Additionally, the equations of Fromard et al. [18] and Imbert and Rollet [17] cover 100% of the diameter range of the mangrove trees present in the study area and yield acceptable predictions. On the other hand, the Chave et al. equation [20] is general. Likewise, although the Komiyama et al. equation [4] accommodates a wide range of diameters, its use is not recommended because this equation generates very high values compared with the rest of the allometric equations, representing overvaluations. Finally, the Day et al. equation [9] does not accommodate an acceptable range of diameters.
The biomass values obtained for the L. racemosa trees via the different equations are presented in Figure 5. The biomass of L. racemosa calculated with the FPM V2.0 equation is 103.45 Mg ha−1, of which 35.58 Mg ha−1 are within the range of diameters of the equation and 67.86 Mg ha−1 are outside the range (65.6%). The equations of Fromard et al. [18], Imbert and Rollet [17] and Chave et al. [20] yield very similar biomass values; however, with the Fromard et al. equation [18], 70.06% of the biomass was outside its diameter range, whereas the Chave et al. equation [20] is a general equation obtained for various mangrove species. The general equation of Komiyama et al. [4] produces 40.78 Mg ha−1 more biomass than that proposed by FPM V2.0.
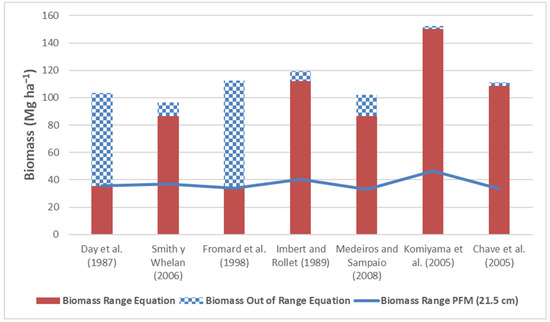
Figure 5.
Biomass of L. racemosa obtained with various allometric equations within the ranges of diameters. The solid line represents the biomass obtained at a diameter of 10 cm via the equation of Day et al. [9]. Source of the equations: Day et al. (1987) [9], Smith y Whelan (2006) [16], Fromard et al. (1998) [18], Imbert and Rollet (1989) [17], Medeiros and Sampaio (2008) [21], Komiyama et al. (2005) [4], Chave et al. (2005) [20].
For L. racemosa, although the FPM V2.0 equation predicts conservative biomass values compared with the other allometric equations, a high percentage of the biomass is not calculated accurately because of the small range of diameters of the equation. Not including R. mangle trees outside the range of diameters in which the equation was developed (34.1%) would mean that 67.86 Mg ha−1 (65.6%) of biomass would be missed. The use of the Imbert and Rollet equation [17] is recommended because this equation was developed with a greater range of diameters than the other specific equations for L. racemosa. The Imbert and Rollet equation [17] results in higher biomass values (119.55 Mg ha−1) than the FPM V2.0 equation (103.45 Mg ha−1), which positively impacts the total number of carbon credits. The Chave et al. equation [20] is an alternative in other places where trees with larger diameters are present since this equation exhibits intermediate behavior compared with the rest of the allometric equations. The use of the general equation of Komiyama et al. [4] is not recommended since despite being developed with the largest range of diameters of the available equations, it generates very different values from the rest of the allometric equations. Rodríguez-Zúñiga et al. [8] recommend the use of specific equations for each species over general equations since species have structural variations among themselves. This criterion is important for estimating the biomass of species of the genus Rhizophora, whose aerial roots are incorporated into the estimated biomass and contribute up to 17% of the total biomass of the tree. The use of general equations underestimates the contribution of the biomass of species with aerial roots to the total biomass of the ecosystem.
The biomass data obtained for the R. mangle trees via the various equations are presented in Figure 6. The biomass of R. mangle calculated with the FPM V2.0 equation is 22.04 Mg ha−1, of which 5.29 Mg ha−1 are within the range of diameters of the equation and 16.75 Mg Mg ha−1 are outside the range (75.98%). The equations of Fromard et al. [18], Imbert and Rollet [17], Yepes et al. [22] and Gomes and Schaeffer-Novelli [19] generate very similar biomass values, of which the Gomes and Schaeffer-Novelli equation [19] results in only 3.81% of the biomass being outside the range of diameters. The general equation of Komiyama et al. [4] generates biomass values similar to those of the FPM V2.0 equation.
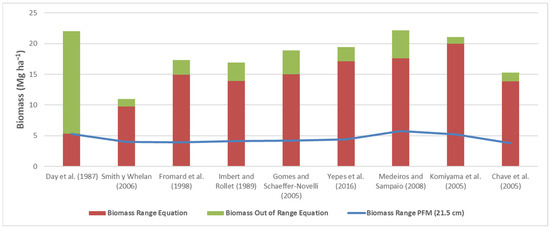
Figure 6.
Biomass of R. mangle obtained with various allometric equations within the ranges of diameters. The solid line represents the biomass obtained at a diameter of 10 cm via the equation of Day et al. [9]. Source of the equations: Day et al. (1987) [9], Smith y Whelan (2006) [16], Fromard et al. (1998) [18], Imbert and Rollet (1989) [17], Gomes and Schaeffer-Novelli (2005) [19], Yepes et al. (2016) [22], Medeiros and Sampaio (2008) [21], Komiyama et al. (2005) [4], Chave et al. (2005) [20].
The FPM V2.0 equation for R. mangle generates the highest biomass values of the allometric equations, and only 65.9% of the R. mangle are within the range of diameters of the equation. Not including the R. mangle trees that are outside the range of diameters (31.2%) would mean that 16.75 Mg ha−1 (75.98%) of biomass would be missed, which would impact the amount of carbon calculated. The Yepes et al. equation [22] is recommended since it was developed based on the largest range of diameters (42.5 cm), excluding the general equation of Komiyama et al. [4], which has a range of 48.9 cm. The Yepes et al. equation [22] yields lower biomass values (19.45 Mg ha−1) than the FPM V2.0 equation (22.04 Mg ha−1). The rest of the allometric equations do not have acceptable diameter ranges.
The results indicate that the FPM V2.0 methodology is limited by the use of allometric equations that are not suitable for the study area and the evaluated species. The use of these equations will result in errors in the actual amount of biomass and carbon credits calculated. Modifications to the standard are necessary so that alternative allometric equations that are more suitable for a particular species can be applied. In FPM V3.0 [28], no changes have been made in the equations applied for the determination of aboveground biomass, so it is suggested that future versions of the FPM analyze the available equations of the species present in the study area. Yuen et al. [3] reported that when preexisting equations are needed, multiple potentially applicable equations should be used to determine plausible ranges of aboveground biomass.
We propose comparing all the existing equations available, verifying the range of diameters of the equations and calculating the biomass with each of them. We suggest choosing the allometric equation that presents a better fit of diameters; that is, discarding equations that are very different, both those that generate very low biomass values and those that generate very high values. Finally, among the possible equations, we advise choosing the one with the largest range of diameters.
3.3. National Forest Inventory 2015–2020 for Tabasco
An analysis of the information from the National Forest and Soil Inventory 2015–2020 for Tabasco [23] is presented in Figure 7. The results indicate that the average DBH for L. racemosa is 12.27 ± 1.15 cm, with a maximum DBH of 44.9 cm. The species A. germinans has an average DBH of 18.18 ± 2.23 cm, with a maximum of 53.2 cm, whereas R. mangle has an average diameter of 14.50 ± 0.69 cm and a maximum of 56.9 cm. The maximum diameters for A. germinans, L. racemosa and R. mangle are outside the range of diameters of the equations proposed by FPM V2.0 for these species in Tabasco. A total of 76.7% of the A. germinans trees inventoried in Tabasco are within the diameter range; however, this percentage represents only 28.5% of the total biomass of the species. For L. racemosa, 48% of the trees are within the range of diameters and constitute 16.7% of the total biomass of the species, whereas for R. mangle, only 26.8% of the trees are within the range of diameters, which comprises 5.7% of the total biomass of R. mangle. The results indicate that it is necessary to develop new allometric equations based on a greater range of maximum diameters.
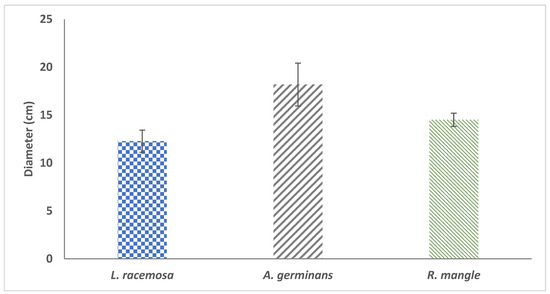
Figure 7.
Average diameters of A. germinans, L. racemosa and R. mangle according to the National Forest and Soil Inventory 2015–2020 CONAFOR for Tabasco.
In future evaluations of mangroves in Tabasco, the development of specific allometric equations that consider broader ranges of diameters is suggested. This is because, in Tabasco, many of the A. germinans, L. racemosa and R. mangle trees have diameters greater than the range of diameters of the allometric equations proposed by FPM V2.0. Rodríguez-Zúñiga et al. [8] reiterate that it is necessary to generate equations on a regional scale to incorporate the existing structural heterogeneity in each country’s regions.
3.4. Evaluation of the FPM Methodology
The FPM V2.0 methodology ensures the veracity of the quantified and reported greenhouse gas removals, ensuring that they meet the strict permanence criteria for projects [11]. Furthermore, the implementation of standardized methodologies should eliminate much of the subjectivity and facilitate the generation of accurate results [29].
Biomass estimation is a critical factor in accounting for carbon stocks in accordance with established standards, where the most accurate method for this purpose is the use of destructive samples of trees [3]. However, mangrove species are considered threatened under Mexican legislation, and thus the destructive methodology cannot be recommended in their case. Allometric equations represent an alternative methodology for estimating biomass [4]. However, their application outside the diameter range for which they were developed has been shown to produce significant errors and high levels of variability [5,30]. The findings of this study illustrate that the allometric equations proposed by the FPM did not contemplate the full range of tree diameters present in the study area. Consequently, the assertion by the standard that it ensures accurate results lacks credibility.
The findings of this study illustrate the importance of employing allometric equations correctly when quantifying biomass. Our results are important for future projects in Mexico that utilize the FPM, especially when the diameter of the trees in the study area exceeds the range for which the allometric equation was developed. We propose the use of the equations of Yepes et al. [22] for A. germinans and R. mangle, and those of Imbert and Rollet [17] for L. racemosa, since these are the allometric equations available that include the greatest maximum diameters. Moreover, similar research is required for the species Conocarpus erectus, which was not present in our study area but does occur in other sites in Mexico.
We recommend that semi-destructive methodologies, such as that proposed by Picard et al. [31], be employed to develop allometric equations that take greater maximum diameters into account to produce more accurate results of biomass in mangroves worldwide. This methodology employs semi-destructive measurement techniques that combine the direct weighing of specific parts of the tree, such as the branches, as well as measurement of trunk volume and wood density. Moreover, pruned portions of the tree can be used to measure biomass [32]. Further research is necessary to develop more accurate non-destructive methodologies to estimate the biomass of study sites. Methodologies such as the use of terrestrial laser scanning (TLS), based on light detection and ranging (LiDAR), have the potential to serve as a substitute for destructive sampling, facilitating the creation of allometric equations [32]. Non-destructive methodologies represent a viable approach for the calculation of carbon in mangroves, particularly given the status of the trees that occur there as protected species, which limits the use of destructive methodologies. Nevertheless, standards such as the CAR still necessitate their use.
The FPM methodology establishes random plot locations, which is an acceptable approach given the importance of avoiding bias in selecting the location of sampling points [5]. However, the inflexibility of the FPM methodology for plot location selection may result in inaccuracies due to site-specific conditions such as elevation, temperature, precipitation and soil properties. Such variables have the potential to influence tree density and growth (diameter, height), as well as the wood density present at a given site. This can result in a modification of the total biomass of the site. The FPM does not allow these inaccuracies to be resolved with the use of alternative methodologies not considered in the same protocol. We suggest adopting a systematic plot selection when it is deemed that some parts of the study area present more carbon than others. This approach, as proposed by Kauffman et al. [5] has been shown to yield more precise data than those obtained through random selection. Furthermore, the FPM stipulates the use of plots of a predetermined size, which must be designed with data accuracy and forest inventory efficiency in mind [5]. Finally, up to version 3.0 [28], it should be noted that the FPM does not account for soil carbon, which consequently excludes this pool from the payment of carbon credits. This represents a considerable disadvantage given that, depending on site quality [15], soil carbon constitutes 50% to 90% of the total carbon in mangrove ecosystems [33,34]. In Mexico, subterranean carbon stocks exceed those of the aboveground biomass. In this sense, Herrera-Silveira et al. [35] report that the mean subterranean Corg (soil + roots) represents approximately 77% of the total Corg, (subterranean and aboveground in live standing trees), not including dead trees.
4. Conclusions
In Mexico, it is necessary to develop allometric equations for mangroves applicable to a wider diametric range because the equations available in the country for R. mangle and L. racemosa and proposed by FPM V2.0 were developed for very small trees (maximum 10 cm DBH), which generate higher biomass predictions than the equations developed by other authors. On the other hand, the FPM V2.0 equation for A. germinans was developed in Florida in the USA and predicts lower biomass values than the equations of other authors.
In the UMA Úrsulo Galván, a high percentage of the inventoried trees are outside the range of diameters of the equations proposed by the FPM V2.0, which means that a high percentage of biomass is not adequately predicted and that a limitation of the FPM V2.0 methodology is the use of inappropriate allometric equations for the study area and the evaluated species.
In Tabasco, the range of diameters of the FPM V2.0 equations includes 76.7% of A. germinans trees, 48% L. racemosa trees and 26.8% R. mangle trees; however, these percentages represent a small fraction of the total biomass of the inventoried trees.
The foregoing highlights the need to modify the Forest Protocol for Mexico to incorporate allometric equations that include the diametric range observed in the country to obtain the aboveground forest biomass.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/resources13090129/s1, Figure S1: Distribution of diameter classes of mangrove trees in the study area.
Author Contributions
C.R.Á.-A.: research, methodology, data curation, writing of the original draft, formal analysis and visualization. M.D.-D.: conceptualization, resources, revision of writing and editing, supervision and acquisition of funds. C.J.V.-N., R.G.A.-P. and P.M.-Z.: formal analysis, writing review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
We thank the National Council of Science and Technology (CONACYT) for the doctorate scholarship awarded to the first author, No. 441771 (CVU).
Data Availability Statement
The data that support this study are available from the corresponding author upon reasonable request. The data are not publicly available due to privacy concerns.
Acknowledgments
We thank the Postgraduate College, Campus Tabasco, for the opportunity to carry out postgraduate studies and the ejidatarios of the UMA Úrsulo Galván for their support in the mangrove forest inventory.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Velázquez-Salazar, S.; Rodríguez-Zúñiga, M.T.; Alcántara-Maya, J.A.; Villeda-Chávez, E.; Valderrama-Landeros, L.; Troche-Souza, C.; Vázquez-Balderas, B. Manglares de México. Actualización y Análisis de los Datos 2020; Comisión Nacional para el Conocimiento y Uso de la Biodiversidad: Ciudad de México, Mexico, 2021; ISBN 978-607-8570-50-8.
- Komiyama, A.; Eong, O.J.; Poungparn, S. Allometry, biomass, and productivity of mangrove forests: A review. Aquat. Bot. 2008, 89, 128–137. [Google Scholar] [CrossRef]
- Yuen, J.Q.; Fung, T.; Ziegler, A.D. Review of allometric equations for major land covers in SE Asia: Uncertainty and implications for above- and below-ground carbon estimates. For. Ecol. Manag. 2016, 360, 323–340. [Google Scholar] [CrossRef]
- Komiyama, A.; Poungparn, S.; Kato, S. Common allometric equations for estimating the tree weight of mangroves. J. Trop. Ecol. 2005, 21, 471–477. [Google Scholar] [CrossRef]
- Kauffman, J.B.; Donato, D.; Adame, M.F. Protocolo Para la Medición, Monitoreo y Reporte de la Estructura, Biomasa y Reservas de Carbono de los Manglares; Documento de Trabajo 117; Cifor: Bogor, Indonesia, 2013. [Google Scholar] [CrossRef]
- Rahman, M.S.; Donoghue, D.N.M.; Bracken, L.J.; Mahmood, H. Biomass estimation in mangrove forests: A comparison of allometric models incorporating species and structural information. Environ. Res. Lett. 2021, 16, 124002. [Google Scholar] [CrossRef]
- Henry, M.; Picard, N.; Trotta, C.; Manlay, R.J.; Valentini, R.; Bernoux, M.; Saint-André, L. Estimating tree biomass of sub-Saharan African forests: A review of available allometric equations. Silva Fenn. 2011, 45, 477–569. [Google Scholar] [CrossRef]
- Rodríguez-Zúñiga, M.T.; Villeda-Chávez, E.; Vázquez-Lule, A.D.; Bejarano, M.; Cruz-López, M.I.; Olguín, M.; Villela Gaytán, S.A.; Flores, R. Métodos Para la Caracterización de los Manglares Mexicanos: Un Enfoque Espacial Multiescala; Comisión Nacional para el Conocimiento y Uso de la Biodiversidad: Ciudad de México, Mexico, 2018; ISBN 978-607-8570-03-4.
- Day, J.W., Jr.; Conner, W.H.; Ley-Lou, F.; Day, R.H.; Machado-Navarro, A. The productivity and composition of mangrove forests, Laguna de Términos, México. Aquat. Bot. 1987, 27, 267–284. [Google Scholar] [CrossRef]
- Valdez, J.I. Manejo forestal de un manglar al sur de Marismas Nacionales, Nayarit. Maderas Bosques 2004, 2, 93–104. [Google Scholar]
- Protocolo Forestal para México Versión 2.0. Climate Action Reserve. Available online: https://www.climateactionreserve.org/how/protocols/mexico-forest/ (accessed on 27 January 2022).
- Tovilla-Hernández, C.; Infante-Mata, D.M.; Ovalle-Estrada, F.; De la Presa-Pérez, J.C.; García-Alfaro, J.R.; De la Cruz-Montes, G. Informe: Inventario del Manglar y Avance de la Intrusión Salina en el Ejido Úrsulo Galván, Municipio de Jalpa de Méndez, Tabasco, México; Fondo Institucional de Fomento Regional para el Desarrollo Científico, Tecnológico y de Innovación, El Colegio de la Frontera Sur; Consejo Nacional de Ciencia y Tecnología: Tapachula, Mexico, 2013.
- Palma-López, D.J.; Jiménez-Ramírez, R.; Zavala-Cruz, J.; Bautista-Zúñiga, F.; Gavi-Reyes, F.; Palma-Cancino, D.Y. Actualización de la clasificación de suelos de Tabasco, México. Rev. Agro Product. 2017, 10, 29–35. [Google Scholar]
- Domínguez-Domínguez, M.; Zavala-Cruz, J.; Rincón-Ramírez, J.A.; Martínez-Zurimendi, P. Management Strategies for the Conservation, Restoration and Utilization of Mangroves in Southeastern Mexico. Wetlands 2019, 39, 907–919. [Google Scholar] [CrossRef]
- Domínguez-Domínguez, M.; Zavala-Cruz, J.; Martínez-Zurimendi, P. Manejo Forestal Sustentable de los Manglares de Tabasco; Secretaría de Recursos Naturales y Protección Ambiental, Colegio de Postgraduados: Villahermosa, Mexico, 2011. [Google Scholar]
- Smith, T.J., III; Whelan, K.R.T. Development of allometric relations for three mangrove species in South Florida for use in the Greater Everglades Ecosystem restoration. Wetl. Ecol. Manag. 2006, 14, 409–419. [Google Scholar] [CrossRef]
- Imbert, D.; Rollet, B. Phytmassaerienne et production primaire dans la mangrove du Grand Cul-de-sac Marine (Guadeloupe, Antilles francaises). Bull. Ecol. 1989, 20, 27–39. [Google Scholar]
- Fromard, F.; Puig, H.; Mougin, E.; Marty, G.; Betoulle, J.L.; Cadamuro, L. Structure, above ground biomass and dynamics of mangrove ecosystems: New data from French Guiana. Oecologia 1998, 115, 39–53. [Google Scholar] [CrossRef] [PubMed]
- Gomes, S.M.L.; Schaeffer-Novelli, Y. Above-ground biomass of mangrove species. I. Analysis of models. Estuar. Coast. Shelf Sci. 2005, 65, 1–18. [Google Scholar]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Folster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
- Medeiros, T.C.C.; Sampaio, E.V.S.B. Allometry of aboveground biomasses in mangrove species in Itamaracá, Pernambuco, Brazil. Wetl. Ecol. Manag. 2008, 16, 323–330. [Google Scholar] [CrossRef]
- Yepes, A.; Zapata, M.; Bolivar, J.; Monsalve, A.; Espinosa, S.M.; Sierra-Correa, P.C.; Sierra, A. Ecuaciones alométricas de biomasa aérea para la estimación de los contenidos de carbono en manglares del Caribe Colombiano. Rev. Biol. Trop. 2016, 64, 913–926. [Google Scholar] [CrossRef] [PubMed]
- Inventario Nacional Forestal y de Suelos 2015–2020. Comisión Nacional Forestal. Available online: https://snmf.cnf.gob.mx (accessed on 13 December 2022).
- Vorster, A.G.; Evangelista, P.H.; Stovall, A.E.L.; Ex, S. Variability and uncertainty in forest biomass estimates from the tree to landscape scale: The role of allometric equations. Carbon Balance Manag. 2020, 15, 8. [Google Scholar] [CrossRef]
- Daba, D.E.; Soromessa, T. The accuracy of species-specific allometric equations for estimating aboveground biomass in tropical moist montane forests: Case study of Albizia grandibracteata and Trichilia dregeana. Carbon Balance Manag. 2019, 14, 18. [Google Scholar] [CrossRef]
- Krauss, K.W.; Doyle, T.W.; Twilley, R.R.; Rivera-Monroy, V.H.; Sullivan, J.K. Evaluating the relative contributions of hydroperiod and soil fertility on growth of south Florida mangroves. Hydrobiologia 2006, 569, 311–324. [Google Scholar] [CrossRef]
- Anuario Estadístico de Tabasco 2009. Instituto Nacional de Estadística y Geografía. Available online: https://www.inegi.org.mx/contenidos/productos/prod_serv/contenidos/espanol/bvinegi/productos/historicos/2104/702825200930/702825200930_1.pdf (accessed on 30 January 2024).
- Protocolo Forestal para México Versión 3.0. Climate Action Reserve. Available online: https://www.climateactionreserve.org/how/protocols/ncs/mexico-forest/ (accessed on 20 June 2024).
- Métodos Estandarizados de VCS: Ampliando la Escala en Reducción de GEI. Verified Carbon Standard. Available online: https://verra.org/wp-content/uploads/2016/05/FactSheet-STAMAS-2013-FINAL_ESP-v3_PT_PM_0.pdf (accessed on 25 August 2024).
- Phan, S.M.; Nguyen, H.T.T.; Nguyen, T.K.; Lovelock, C. Modelling above ground biomass accumulation of mangrove plantations in Vietnam. For. Ecol. Manag. 2019, 432, 376–386. [Google Scholar] [CrossRef]
- Picard, N.; Saint-André, L.; Henry, M. Manual de Construcción de Ecuaciones Alométricas para Estimar el Volumen y la Biomasa de los Árboles: Del Trabajo de Campo a la Predicción; Las Naciones Unidas para la Alimentación y la Agricultura y el Centre de Coopération Internationale en Recherche Agronomique pour le Développement: Rome, Italy, 2012; ISBN 978-92-5-307347-4. [Google Scholar]
- Feliciano, E.A.; Wdowinski, S.; Potts, M.D. Assessing Mangrove Above-Ground Biomass and Structure using Terrestrial Laser Scanning: A Case Study in the Everglades National Park. Wetlands 2014, 34, 955–968. [Google Scholar] [CrossRef]
- Donato, D.C.; Kauffman, J.B.; Murdiyarso, D.; Kurnianto, S.; Stidham, M.; Kanninen, M. Mangroves among the most carbon-rich forests in the tropics. Nat. Geosci. 2011, 4, 293–297. [Google Scholar] [CrossRef]
- Kauffman, J.B.; Heider, C.; Cole, T.G.; Dwire, K.A.; Donato, D.C. Ecosystem carbon stocks of Micronesian mangrove forests. Wetlands 2011, 31, 343–352. [Google Scholar] [CrossRef]
- Herrera Silveira, J.A.; Camacho, R.A.; Pech, E.; Pech, M.; Ramírez, R.J.; Teutli, H.C. Dinámica del carbono (almacenes y flujos) en manglares de México. Terra Latinoam 2016, 34, 61–72. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).