Chemical Leasing (Ch.L.) and the Sherwood Plot
Abstract
1. Introduction
2. Materials and Methods
2.1. The Sherwood Plot (SP)
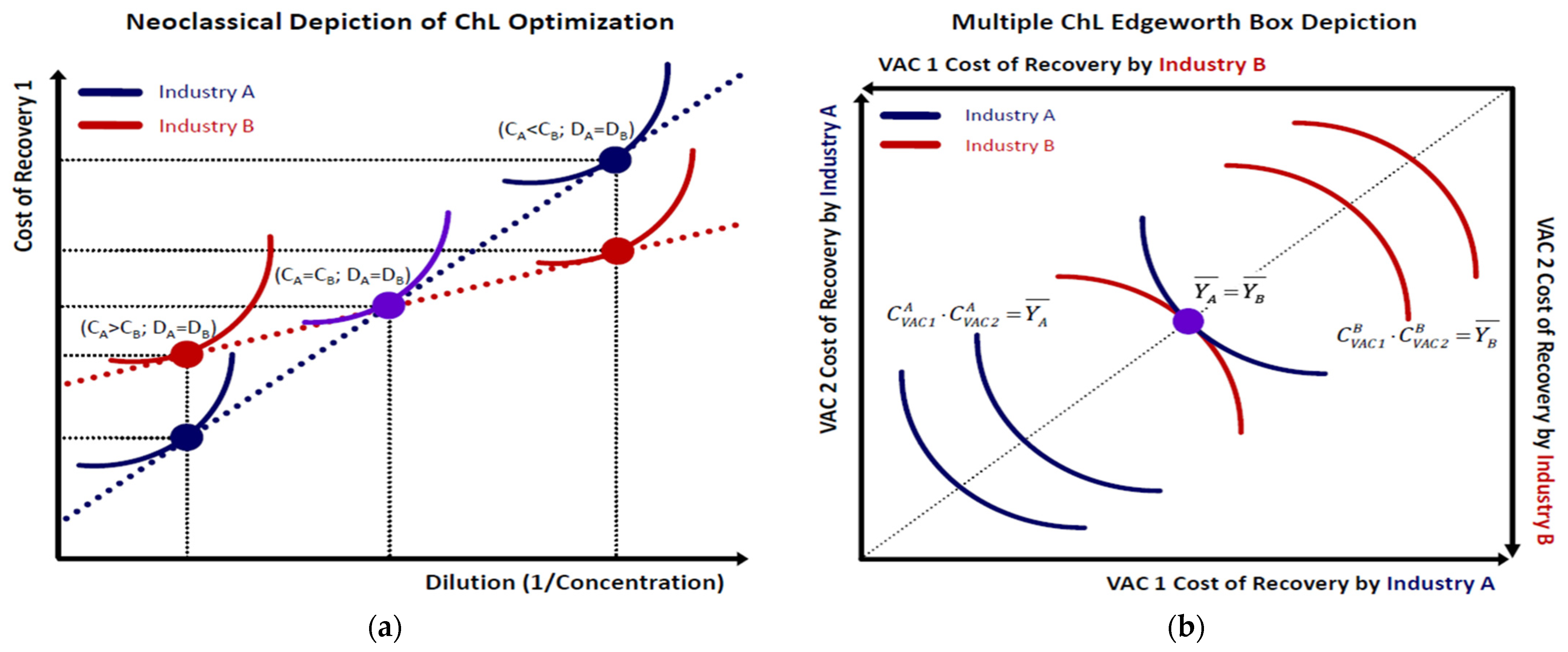
2.2. Microeconomics of VAC Recovery Synergies
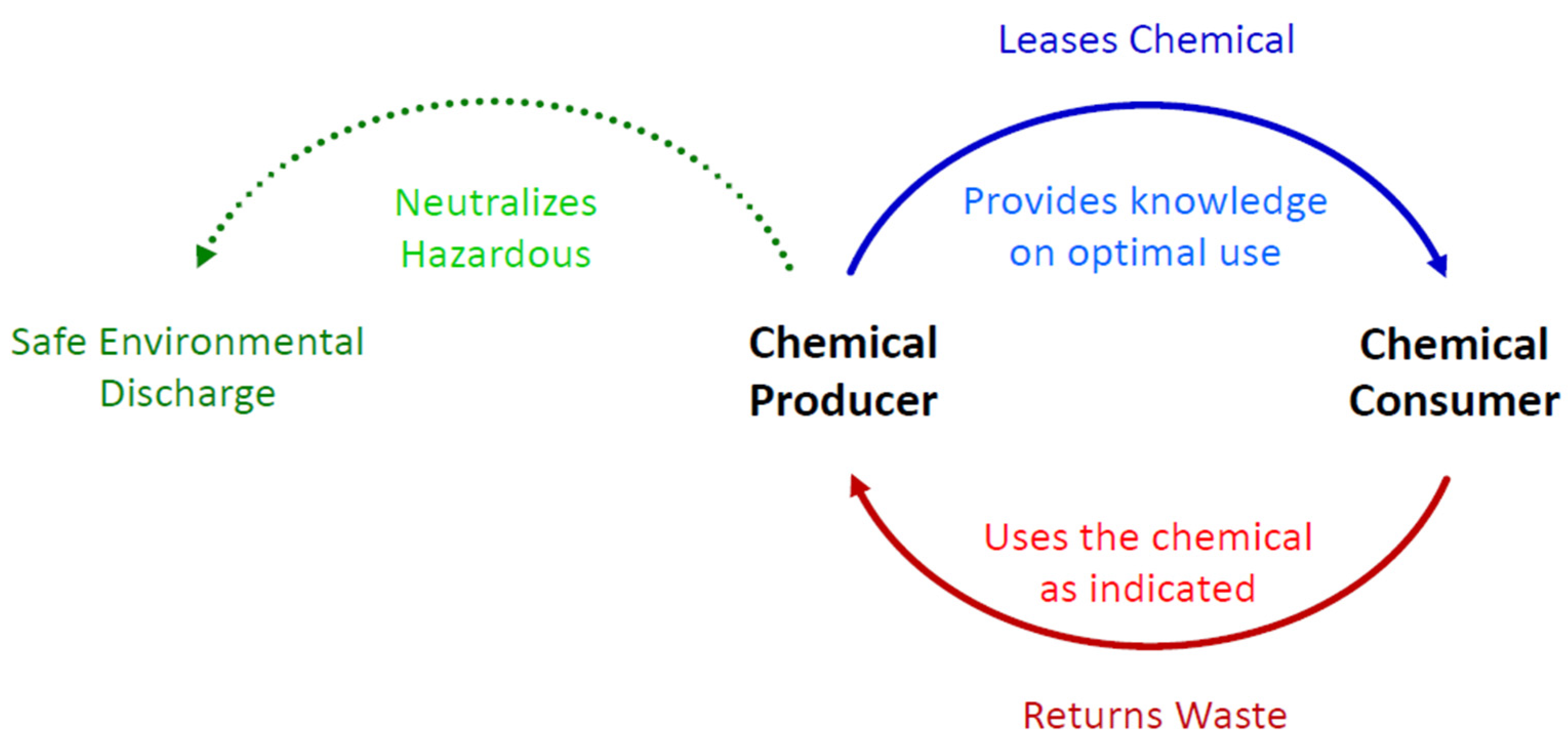
2.3. Chemical Leasing (ChL)
3. Results
3.1. ChL Financial Engineering
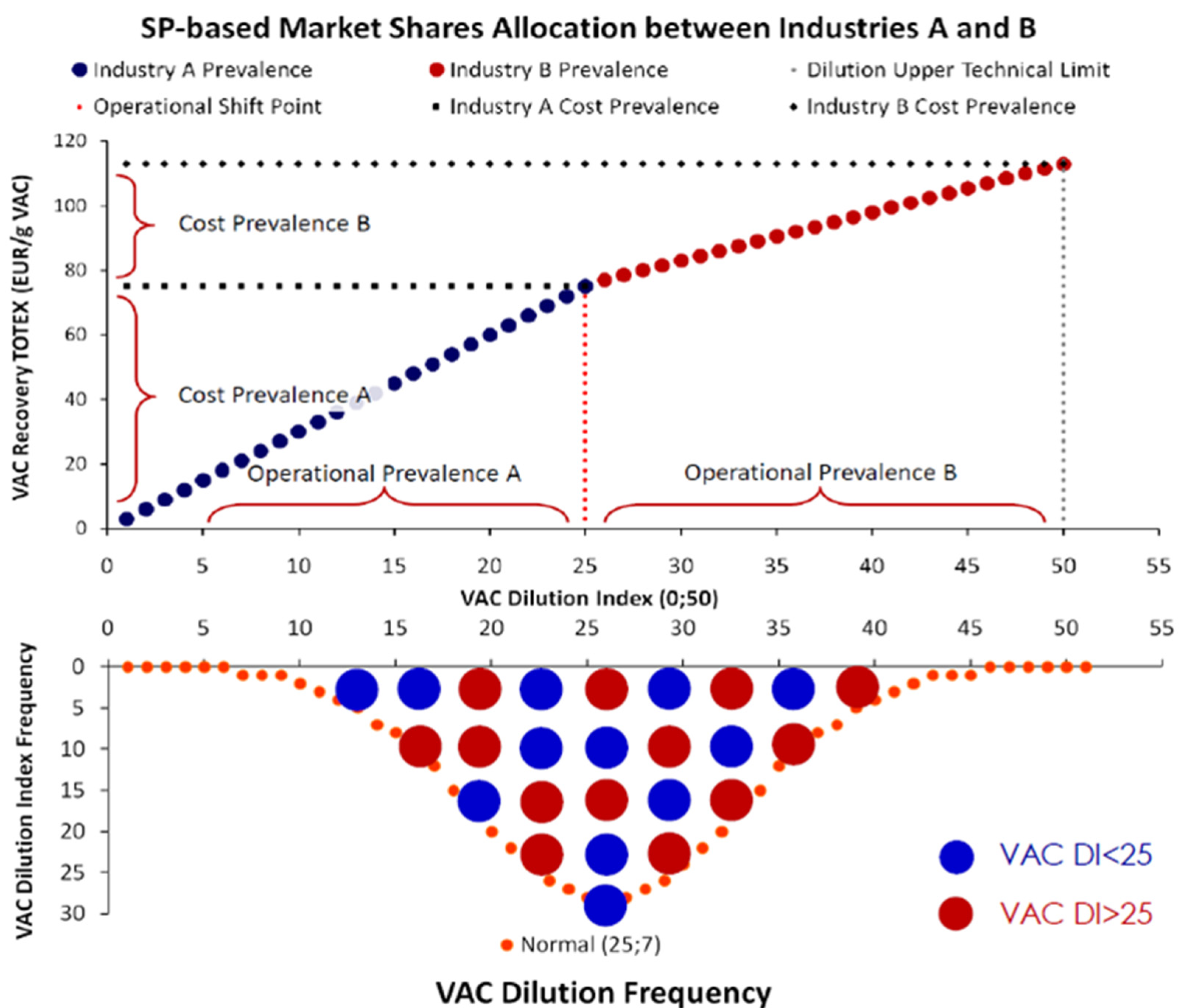
3.2. ChL Market Typology
3.2.1. Complete Information
3.2.2. Incomplete Information
3.3. ChL Pricing and Profitability
3.3.1. Mean ChL Pricing (MEANP)
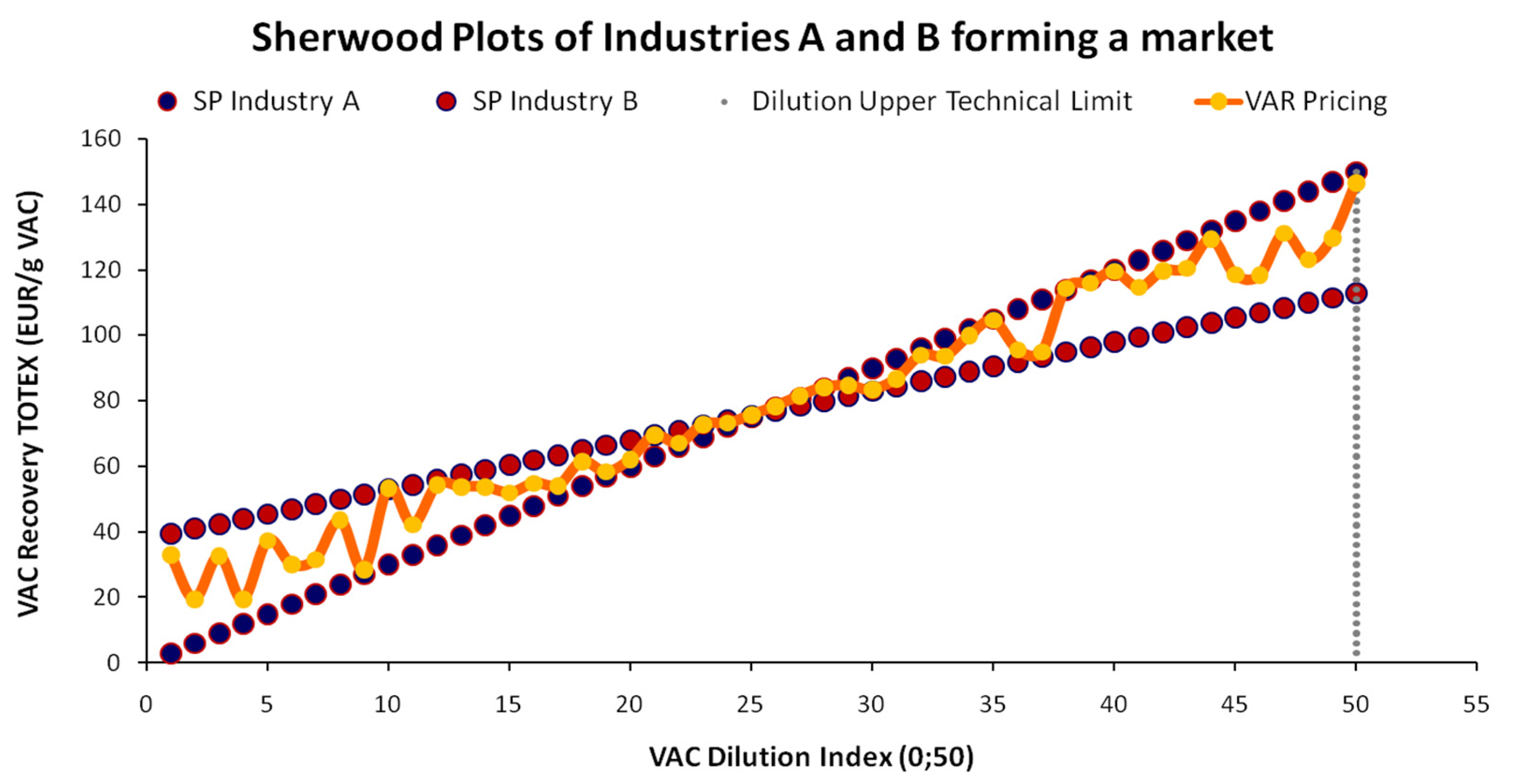
3.3.2. Variable ChL Pricing (VAR)
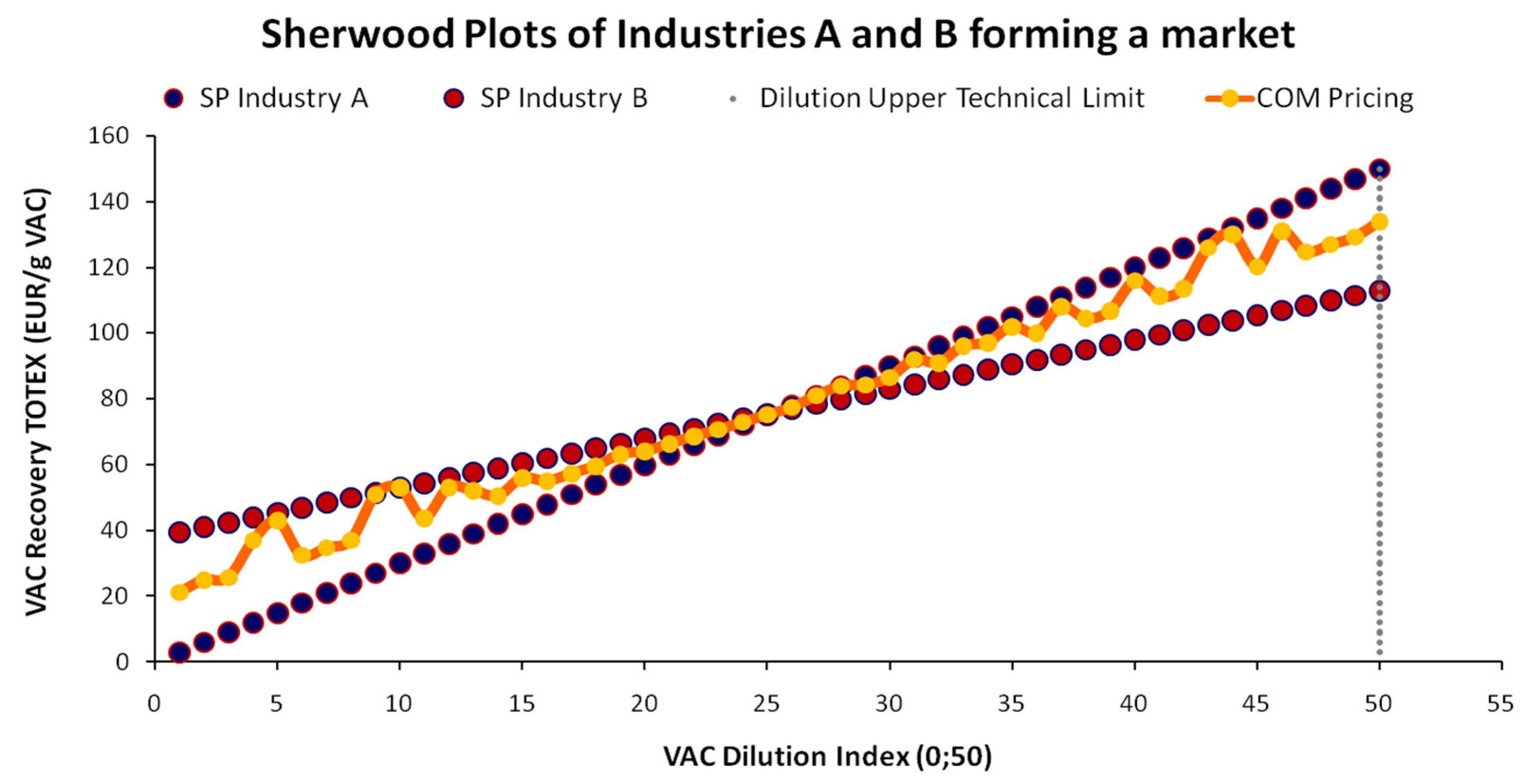
3.3.3. Composite ChL Pricing (COM)
4. Discussion and Extensions
4.1. Institutional Shifts and Circular Economy Finance (CEF)
4.2. Environmental Goods Accounting and Pricing
4.3. Entropy and Industrial Symbiosis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. ChL Contracts for Full and Partial VAC Recovery
Appendix A.1. Full VAC Recovery
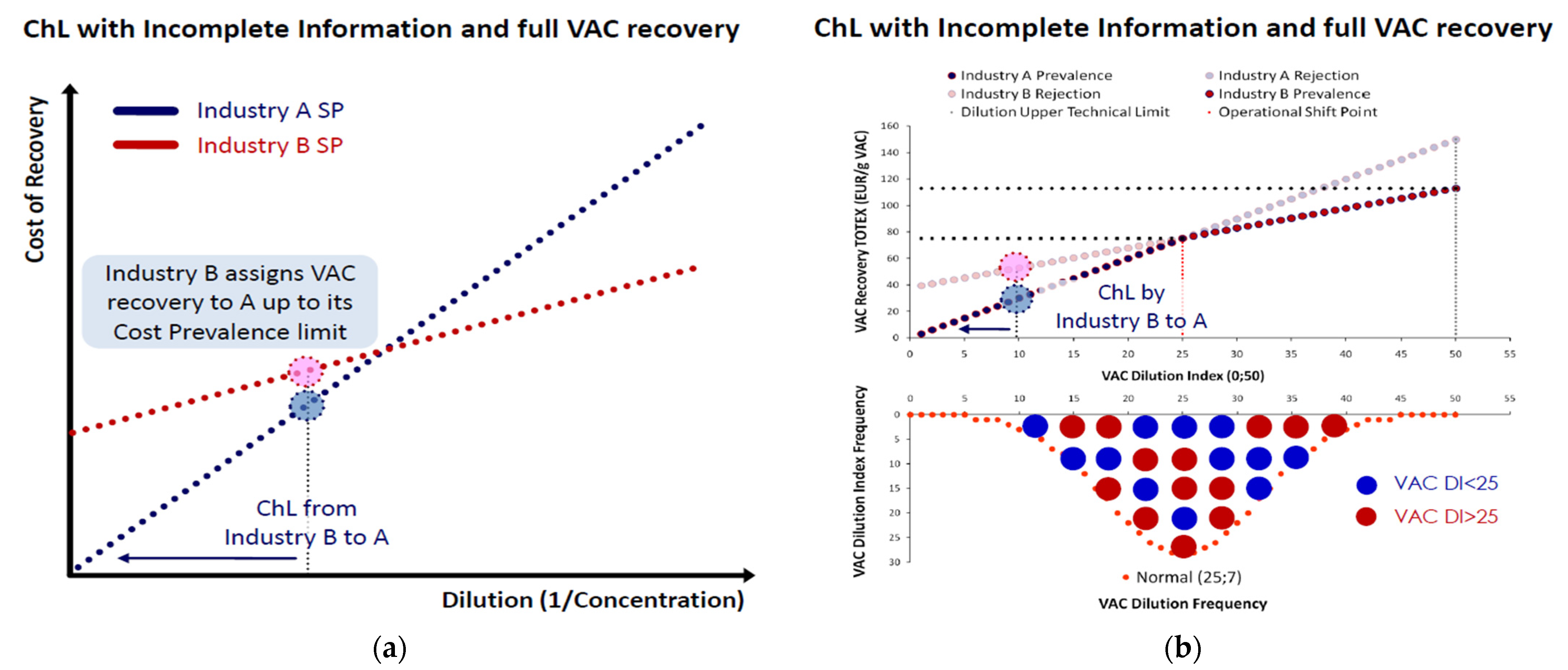
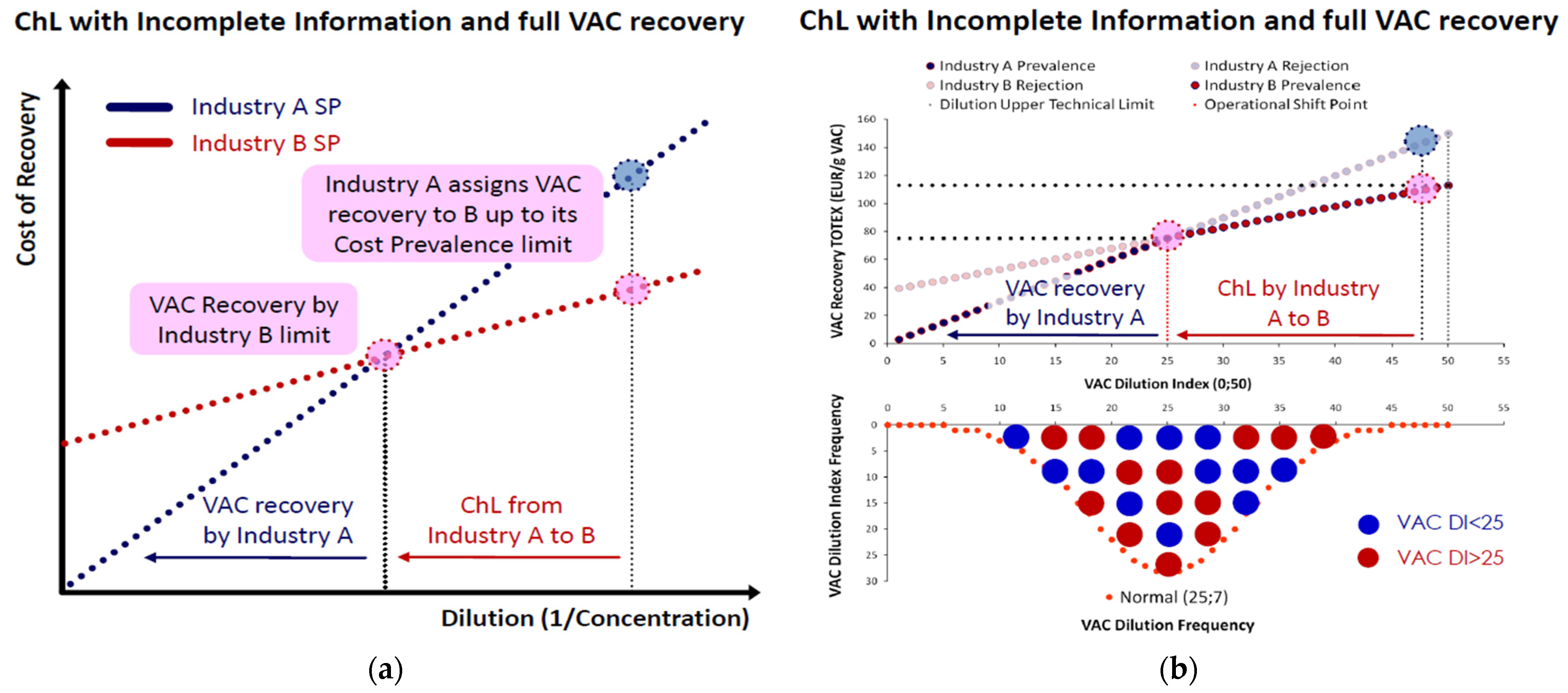
Appendix A.2. Partial VAC Recovery
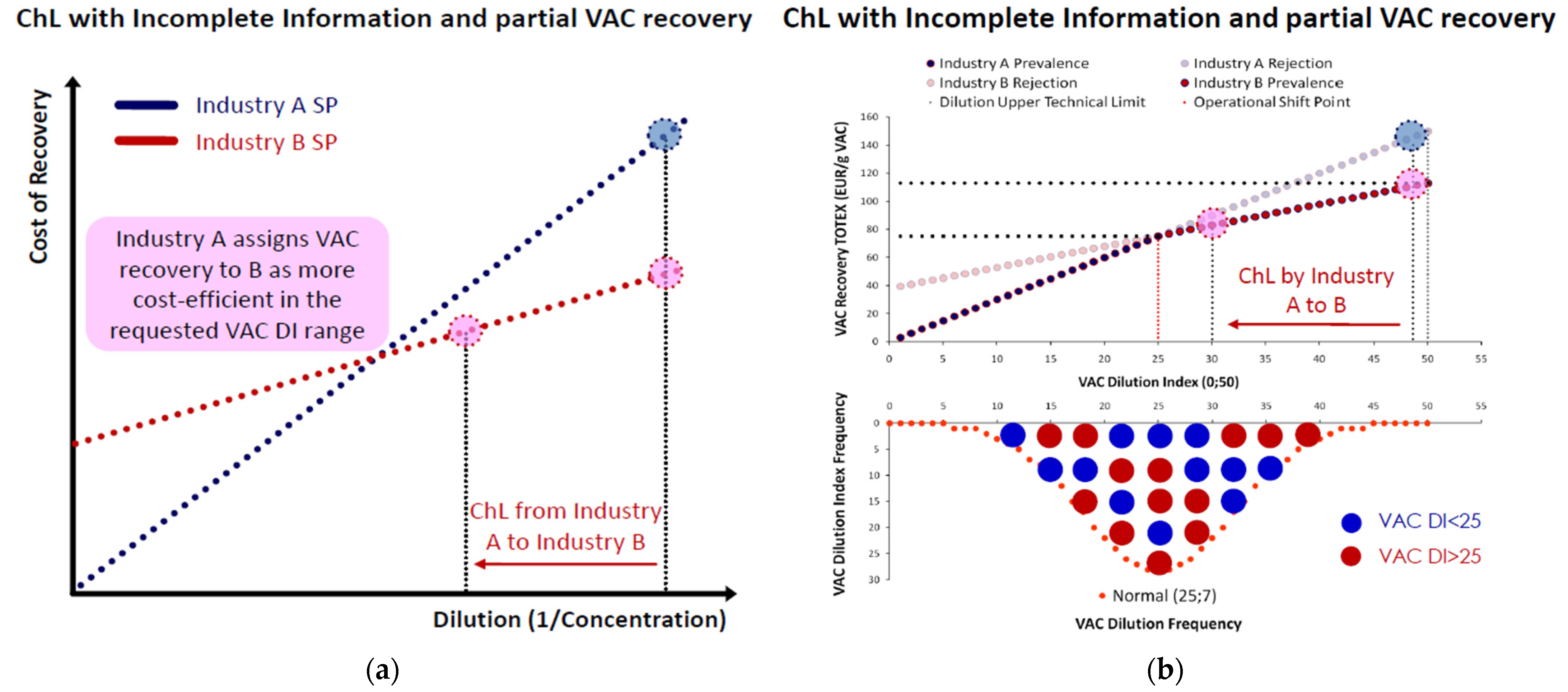
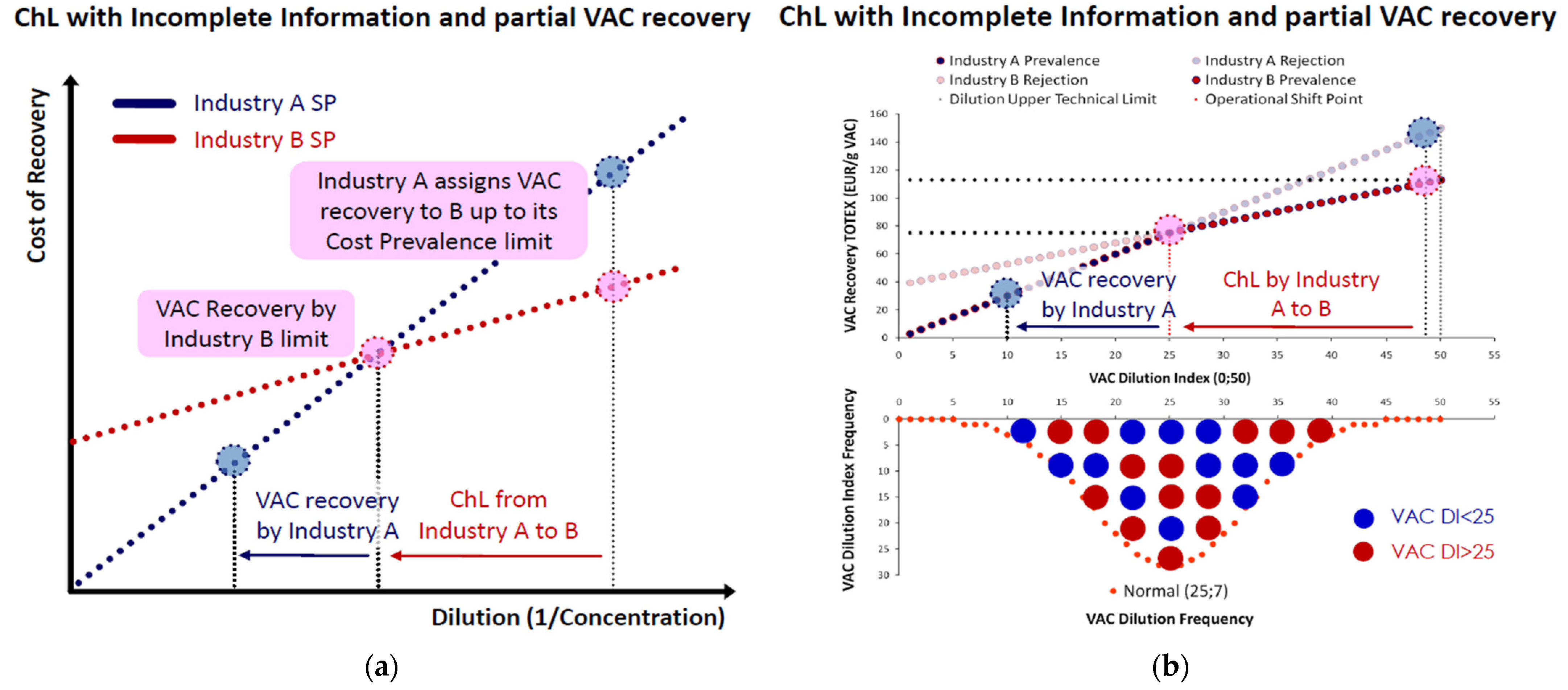
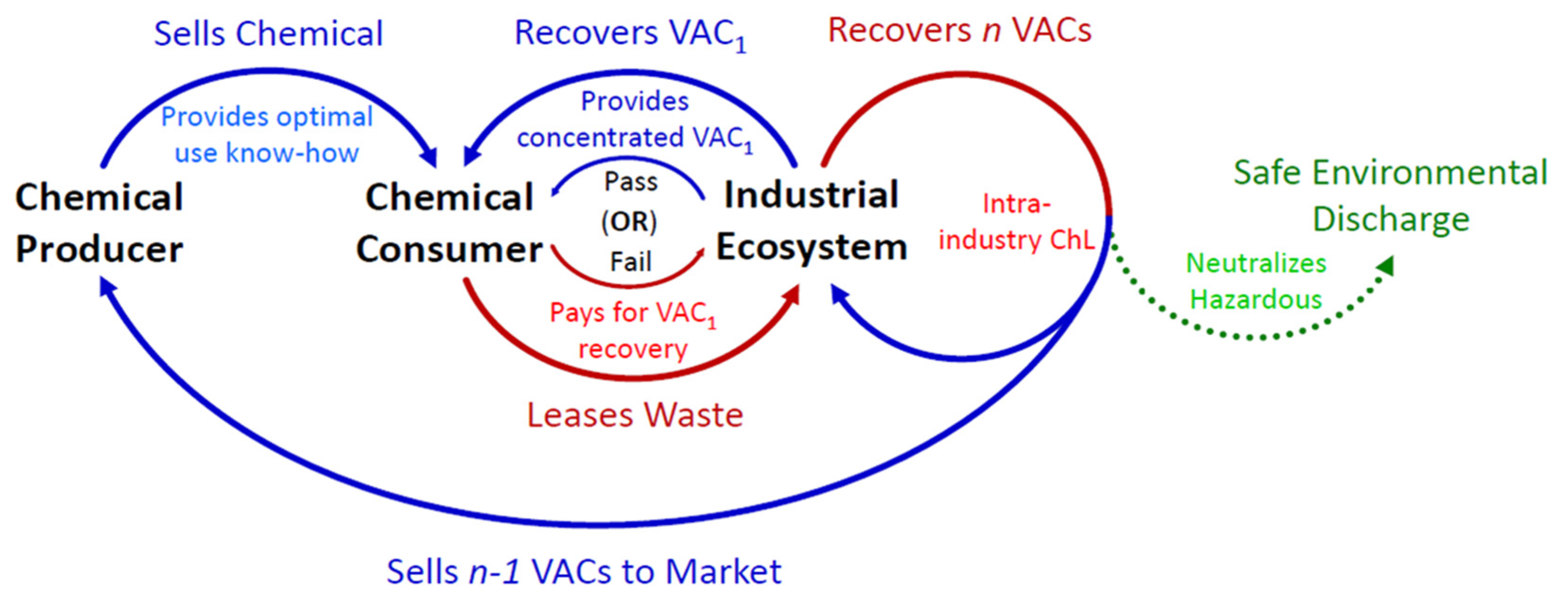
Appendix B. Industrial Symbiosis Markets and ChL Micro-Structural Modeling
Appendix B.1. ChL and Industrial Symbiosis Markets
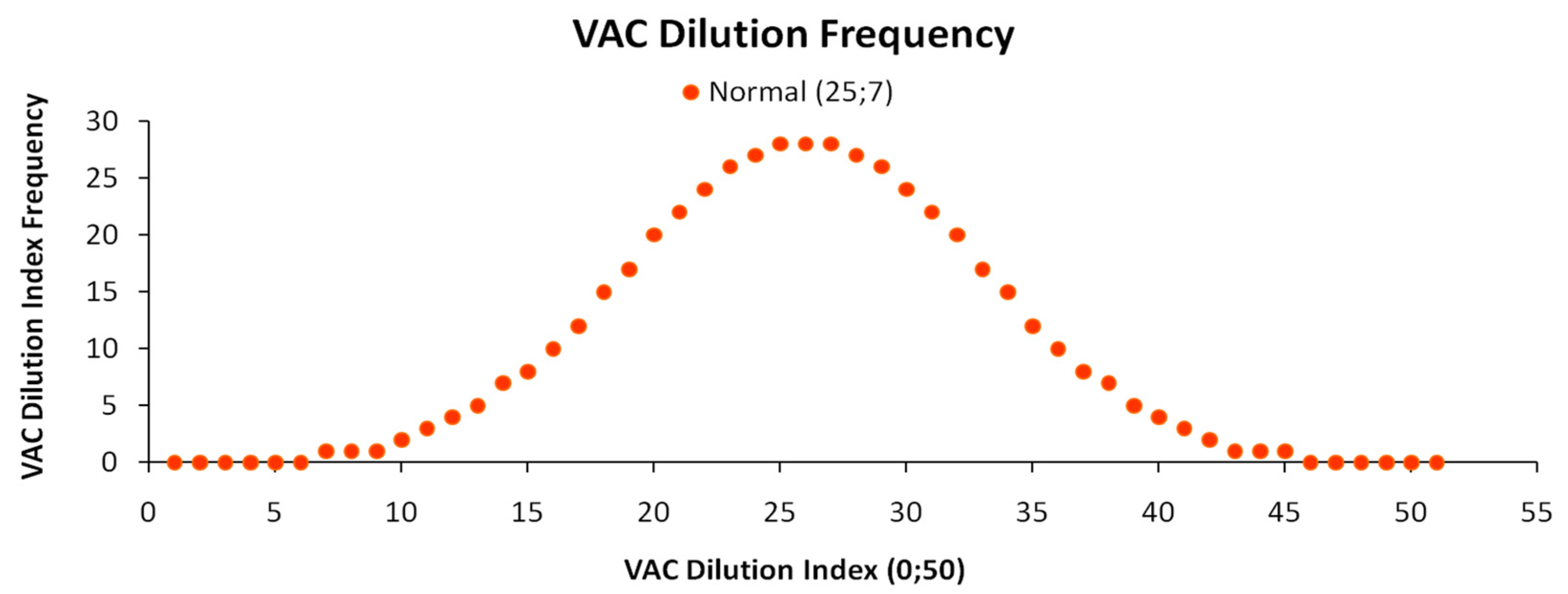
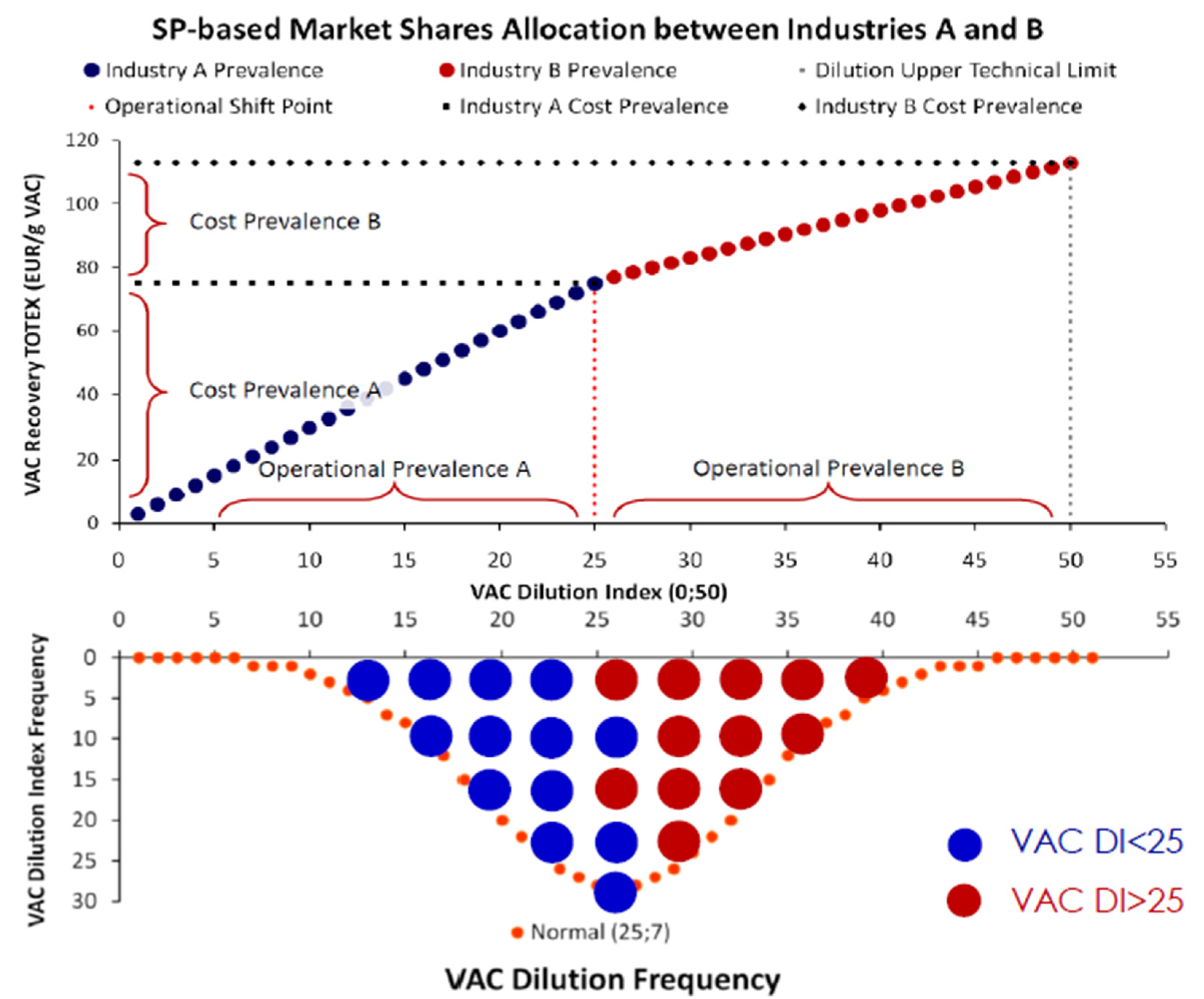
Appendix B.2. VAC Supply and Demand Micro-Structure
Appendix B.2.1. Constrained VAC Recovery
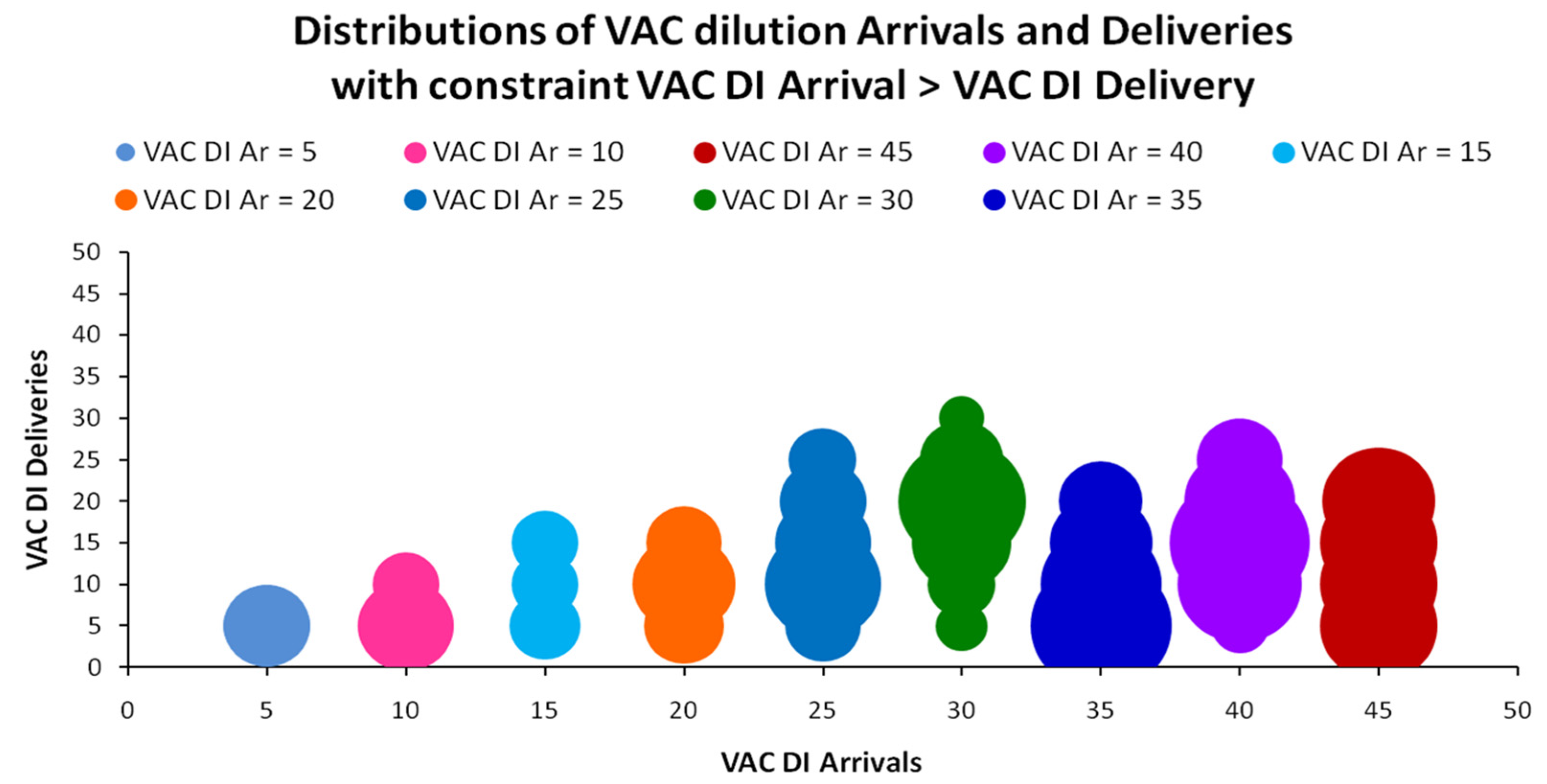
Appendix B.2.2. Unconstrained VAC Recovery
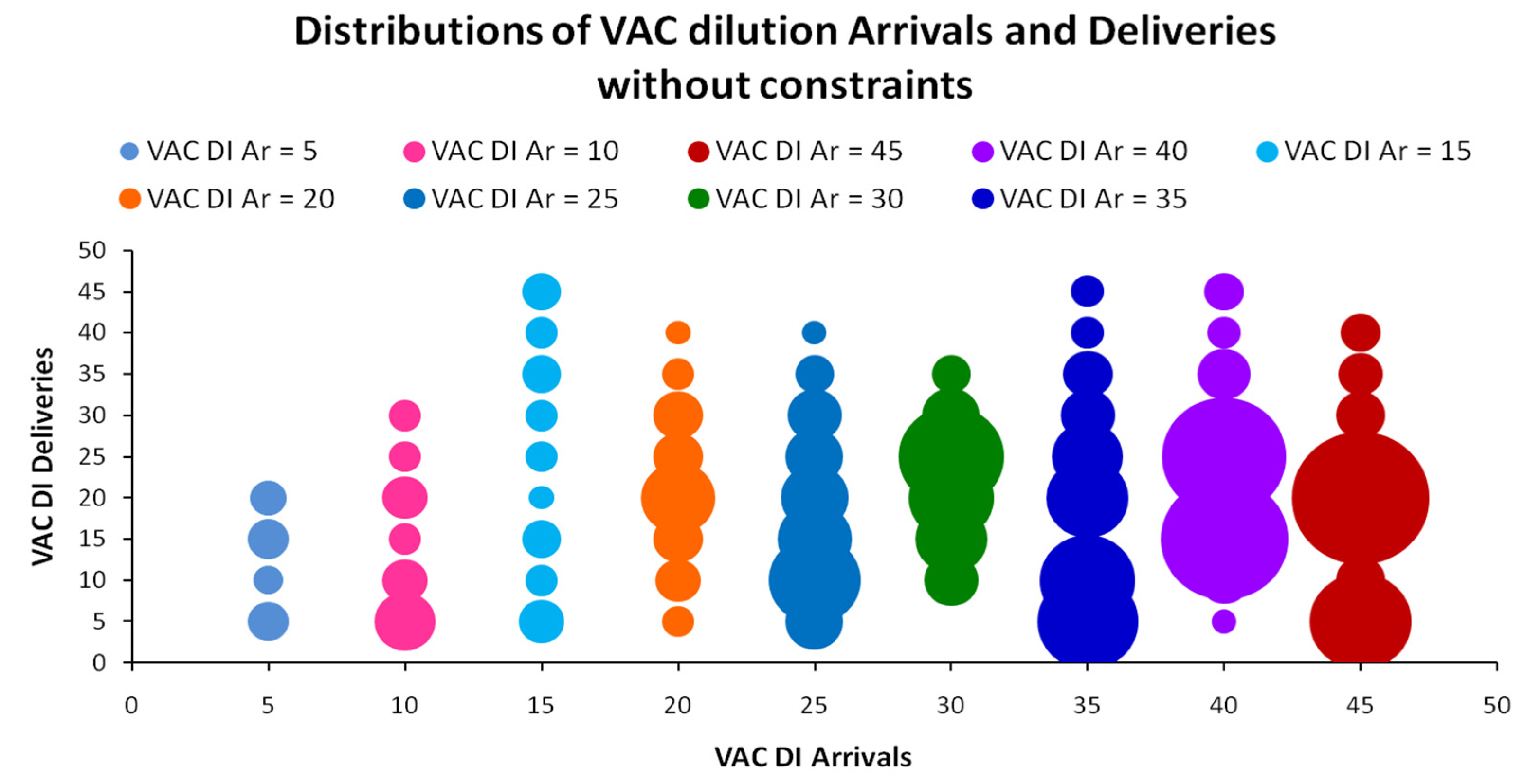
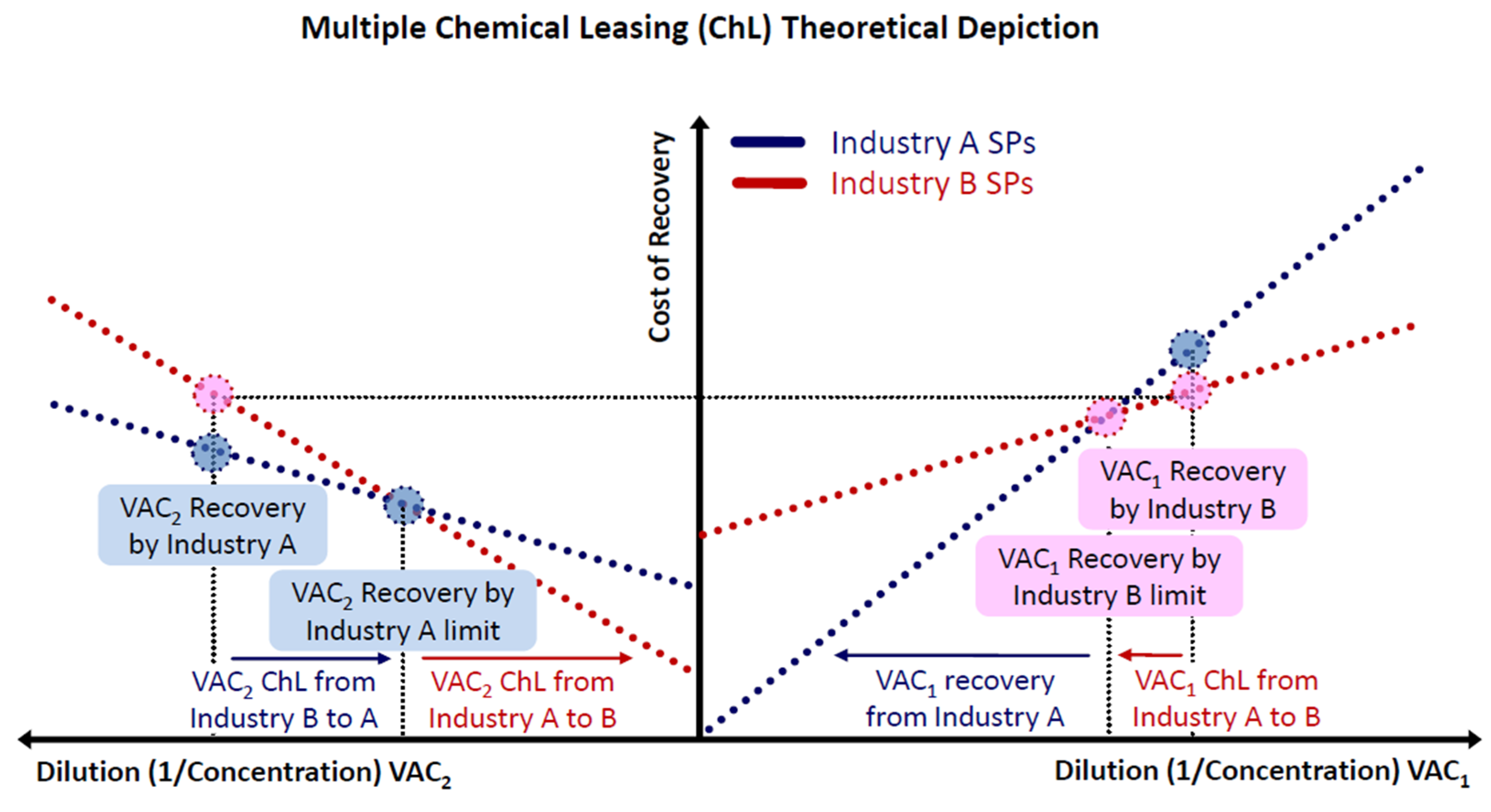
Appendix B.3. Multiple VAC Recovery and Chemical Swaps (Ch.S.)
References
- European Investment Bank (EIB). EIB Group: Climate Bank Roadmap 2021–2025; European Investment Bank: Luxembourg, 2020; ISBN 978-92-861-4908-5. [Google Scholar] [CrossRef]
- Mont, O.; Singhal, O.; Fadeeva, Z. Chemical Management Services in Sweden and Europe: Lessons for the Future. J. Ind. Ecol. 2006, 10, 279–292. [Google Scholar] [CrossRef]
- United Nations Industrial Development Organization (UNIDO). Chemical Leasing in Practice: About the Model. Available online: https://chemicalleasing.com/chemical-leasing-in-practice/ (accessed on 5 March 2024).
- Karakatsanis, G.; Makropoulos, C. Resource Recovery and the Sherwood Plot. Entropy 2023, 25, 4. [Google Scholar] [CrossRef] [PubMed]
- EU Technical Expert Group (TEG) on Sustainable Finance. EU Green Bond Standard Usability Guide. 2020. Available online: https://ec.europa.eu/info/files/200309-sustainable-finance-teg-green-bond-standard-usability-guide_en (accessed on 5 March 2024).
- Sherwood, T.K.; Woertz, B.B. Mass Transfer between Phases. Ind. Eng. Chem. 1939, 31, 1034–1041. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering and Medicine. Separation and Purification: Critical Needs and Opportunities; The National Academies Press: Washington, DC, USA, 1987. [Google Scholar] [CrossRef]
- National Academy of Engineering. The Greening of Industrial Ecosystems; The National Academies Press: Washington, DC, USA, 1994. [Google Scholar] [CrossRef]
- Walter, N.; Snyder, C. Microeconomic Theory: Basic Principles and Extensions, 10th ed.; Thomson South-Western: Mason, OH, USA, 2007; ISBN 13:978-0-324-42162-0. [Google Scholar]
- United Nations Industrial Development Organization (UNIDO). Chemical Leasing: Redefining the Sustainable Management of Chemicals. 2013. Available online: https://www.unido.org/sites/default/files/2013-10/Chemical_Leasing_0.pdf (accessed on 5 March 2024).
- Lozano, R.; Carpenter, A.; Satric, V. Fostering green chemistry through a collaborative business model: A Chemical Leasing case study from Serbia. Resour. Conserv. Recycl. 2013, 78, 136–144. [Google Scholar] [CrossRef]
- EUROSTAT. Energy Statistics—An Overview (Data Extracted: 16 February 2022; Planned article update: 31 May 2023). Statistics Explained 2022. Available online: https://ec.europa.eu/eurostat/statistics-explained/SEPDF/cache/29046.pdf (accessed on 5 March 2024).
- EUROSTAT. Energy Efficiency Statistics (Data Extracted: 16 December 2022; Planned Article Update: 18 December 2023). Statistics Explained 2022. Available online: https://ec.europa.eu/eurostat/statistics-explained/SEPDF/cache/19548.pdf (accessed on 5 March 2024).
- Moser, F.; Jakl, T. Chemical leasing—A review of implementation in the past decade. Environ. Sci. Pollut. Res. 2014, 22, 6325–6348. [Google Scholar] [CrossRef]
- Joas, R.; Abraham, V.; Joas, A. Chemical Leasing: A Business Model to Drive Resource Efficiency in the Supply Chain. In Factor X: Challenges, Implementation Challenges and Examples for a Sustainable Use of Natural Resources; Lehmann, H., Ed.; Springer International Publishing: Cham, Switzerland, 2018; Volume 32, pp. 395–403, Eco-efficiency in Industry and Science; ISBN 978-3-319-50079-9. [Google Scholar] [CrossRef]
- Moser, F.; Karavezyris, V.; Blum, C. Chemical leasing in the context of sustainable chemistry. Environ. Sci. Pollut. Res. 2014, 22, 9. [Google Scholar] [CrossRef]
- Lozano, R.; Carpenter, A.; Lozano, F.J. Critical reflections on the Chemical Leasing concept. Resour. Conserv. Recycl. 2014, 86, 53–60. [Google Scholar] [CrossRef]
- Weerakkody, M.P.; Edirisinghe, L.G.L.M.; Sivashankar, P. Farmers’ attitude towards chemical leasing for sustainability and environmental protection. Curr. Res. Environ. Sustain. 2022, 4, 100175. [Google Scholar] [CrossRef]
- Moser, F.; Jakl, T.; Joas, R.; Dondi, F. Chemical Leasing business models and corporate social responsibility. Environ. Sci. Pollut. Res. 2014, 21, 12445–12456. [Google Scholar] [CrossRef]
- United Nations Industrial Development Organization (UNIDO). Chemical Leasing within Industrial and Service Sector Cleaning Operations: A Viable Business Model to Reduce Chemical Use and Negative Environmental Impacts; UNIDO: Vienna, Austria, 2015; Available online: https://chemicalleasing.com/wp-content/uploads/2021/04/9_UNIDO_Sector_study-cleaning_operation.pdf (accessed on 5 March 2024).
- Schwager, P.; Dunjic, B.; Kaltenegger, I. Success and failure of the chemical leasing model in addressing sustainability challenges: Evidence from practice. Curr. Opin. Green Sustain. Chem. 2017, 8, 14–17. [Google Scholar] [CrossRef]
- Jakl, T.; Schwager, P. Chemical Lasing Goes Global. Selling Services Instead of Barrels: A Win-Win Business Model for Environment and Industry; Springer: Vienna, Austria, 2008; ISBN 978-3-211-73751-4. [Google Scholar]
- Keyhani, M.; Abbaspour, A.; Bahadori-Jahromi, A.; Mylona, A.; Janbey, A.; Godfrey, P.; Zhang, H. Whole Life Carbon Assessment of a Typical UK Residential Building Using Different Embodied Carbon Data Sources. Sustainability 2023, 15, 5115. [Google Scholar] [CrossRef]
- United Nations (UN). System of Environmental Economic Accounting (SEEA) 2012: Central Framework; United Nations: New York, NY, USA, 2014; ISBN 987-92-1-161563-0. Available online: https://unstats.un.org/unsd/envaccounting/seearev/seea_cf_final_en.pdf (accessed on 5 March 2024).
- United Nations; European Commission; International Monetary Fund; Organization for Economic Cooperation & Develop-ment; World Bank. Handbook of Integrated Environmental & Economic Accounting; Studies in Methods, Handbook of National Accounting, Series F, No.61, Rev.1 (ST/ESA/STAT/SER.F/61/Rev.1); United Nations: New York, NY, USA. 2003. Available online: https://unstats.un.org/unsd/environment/seea2003.pdf (accessed on 5 March 2024).
- Karakatsanis, G.; Mamassis, N. Entropy, Recycling and Macroeconomics of Water Resources; European Geosciences Union (EGU) General Assembly: Vienna, Austria, 2014. [Google Scholar] [CrossRef]
- Karakatsanis, G.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Entropy and reliability of water use via a statistical approach of scarcity. In Proceedings of the Facets of Uncertainty: 5th EGU Leonardo Conference-Hydrofractals 2013-STAHY 2013, EGU, IAHS and IUGG, Kos, Greece, 17–19 October 2013. [Google Scholar] [CrossRef]
- Dosi, G. Finance, innovation and industrial change. J. Econ. Behav. Organ. 1990, 13, 299–319. [Google Scholar] [CrossRef]
- Castelnuovo, E.; Galeotti, M.; Gambarelli, G.; Vergalli, S. Learning by-Doing vs. Learning by Researching in a model of climate change policy analysis. Ecol. Econ. 2005, 54, 261–276. [Google Scholar] [CrossRef]
- Greco, M.; Grimaldi, M.; Cricelli, L. An analysis of the open innovation effect on firm performance. Eur. Manag. J. 2016, 34, 1–16. [Google Scholar] [CrossRef]
- Ehrenfeld, J.; Gertler, N. Industrial Ecology in Practice: The evolution of interdependence at Kalundborg. J. Ind. Ecol. 1997, 1, 67–79. [Google Scholar] [CrossRef]
- Keckler, S.E.; Allen, D.T. Material Reuse Modeling: A Case Study of Water Reuse in an Industrial Park. J. Ind. Ecol. 1998, 2, 79–92. [Google Scholar] [CrossRef]
- Hummer, B. Chemical Substitution in the Nepal Carpet Industry. J. Ind. Ecol. 2008, 2, 7–9. [Google Scholar] [CrossRef]
- Barile, M.; Weisstein, E.W. Galton Board. From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/GaltonBoard.html (accessed on 5 March 2024).
- Ahmed, J.; Chumley, T.; Cook, S.; Cox, C.; Grant, H.; Petela, N.; Rothrock, B.; Xhafaj, R. Dynamics of the no-slip Galton board (v1). arXiv 2022, arXiv:2208.07790v1. [Google Scholar] [CrossRef]
- Liakopoulou, A.; Makropoulos, C.; Nikolopoulos, D.; Monokrousou, K.; Karakatsanis, G. An Urban Water Simulation Model for the Design, Testing and Economic Viability Assessment of Distributed Water Management Systems for a Circular Economy. Environ. Sci. Proc. 2020, 2, 14. [Google Scholar] [CrossRef]
- Marin, P. Public-Private Partnerships for Urban Water Utilities: A Review of Experiences in Developing Countries; The World Bank: Washington, DC, USA, 2009; ISBN 978-0-8213-7957-8. Available online: https://openknowledge.worldbank.org/server/api/core/bitstreams/0dea9db2-e7ec-5beb-9a1a-5e7b2d351f59/content (accessed on 5 March 2024).
- Makropoulos, C.; Rozos, E.; Tsoukalas, I.; Plevri, A.; Karakatsanis, G.; Karagiannidis, L.; Makri, E.; Lioumis, C.; Noutsopoulos, C.; Mamais, D. Sewer-mining: A water reuse option supporting circular economy, public service provision and entrepreneurship. J. Environ. Manag. 2017, 216, 285–298. [Google Scholar] [CrossRef]
- Artola, I.; Domenech, T.; Doranova, A.; Roman, L.; Smith, M. Cooperation Fostering Industrial Symbiosis: Market Potential, Good Practice and Policy Actions: Final Report; European Commission, Directorate-General for Internal Market, Industry, Entrepreneurship and SMEs Publications Office: Luxembourg, 2018; ISBN 978-92-79-74679-6. Available online: https://data.europa.eu/doi/10.2873/346873 (accessed on 5 March 2024).
- Gorgels, S.; Muller, P.; Ladher, R.; Booth, J.; Sabah, M.; Priem, M. Annual Report on European SMEs 2021/2022: SMEs and Environmental Sustainability; Publications Office of the European Union: Luxembourg, 2022; ISBN 978-92-9469-296-2. [Google Scholar] [CrossRef]
- Institute of Energy for South-East Europe (IENE). Green Bonds and IENE. An IENE Advisory Note (No 2). 2021. Available online: https://www.iene.eu/articlefiles/inline/green%20bonds%20brochure_3.pdf (accessed on 5 March 2024).
- European Bank for Reconstruction and Development (EBRD). EBRD Invests in Mytilineos Green Eurobond Issuance. 2021. Available online: https://www.ebrd.com/news/2021/ebrd-invests-in-mytilineos-green-eurobond-issuance.html (accessed on 5 March 2024).
- European Bank for Reconstruction and Development (EBRD). EBRD Invests in Debut Issue of Green Bonds by a Greek Bank. 2020. Available online: https://www.ebrd.com/news/2020/ebrd-invests-in-debut-issue-of-green-bonds-by-a-greek-bank-.html (accessed on 5 March 2024).
- European Bank for Reconstruction and Development (EBRD). EBRD invests in PPC’s Sustainability-Linked Bond Issue in Greece. 2021. Available online: https://www.ebrd.com/news/2021/ebrd-invests-in-ppcs-sustainabilitylinked-bond-issue-in-greece.html (accessed on 5 March 2024).
- European Bank for Reconstruction and Development (EBRD). EBRD to Invest in Lamda’s Green Bond in Greece. 2022. Available online: https://www.ebrd.com/news/2022/ebrd-to-invest-in-lamdas-green-bond-in-greece.html (accessed on 5 March 2024).
- European Commission. Proposal for a Directive of the European Parliament and of the Council on Energy Efficiency (Recast); 2021. COM/2021/558. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:52021PC0558 (accessed on 5 March 2024).
- International Energy Agency (IEA). A 10-Point Plan to Reduce the European Union’s Reliance on Russian Natural Gas. 2022. Available online: https://iea.blob.core.windows.net/assets/1af70a5f-9059-47b4-a2dd-1b479918f3cb/A10-PointPlantoReducetheEuropeanUnionsRelianceonRussianNaturalGas.pdf (accessed on 5 March 2024).
- Bolton, P.; Despres, M.; Pereira Da Silva Luiz, A.; Samama, F.; Svartzman, R. The Green Swan: Central Banking and Financial Stability in the Age of Climate Change; Bank of International Settlements (BIS): Basel, Switzerland, 2020; ISBN 978-92-9259-326-1. Available online: https://www.bis.org/publ/othp31.pdf; (accessed on 5 March 2024).
- Taleb, N.N. The Black Swan: The Impact of the Highly Improbable; Random House Publishing Group: New York, NY, USA, 2007; ISBN 978-1-4000-6351-2. [Google Scholar]
- European Central Bank (ECB). ECB Presents Action Plan to Include Climate Change Considerations in Its Monetary Policy Strategy Annex: Detailed Roadmap of Climate Change-Related Actions; Press Release. 2021. Available online: https://www.ecb.europa.eu/press/pr/date/2021/html/ecb.pr210708_1_annex~f84ab35968.en.pdf (accessed on 5 March 2024).
- European Banking Authority (EBA). Draft Implementing Standards on Prudential Disclosures on ESG Risks in Accordance with Article 449a CRR. Consultation Paper Draft It Prudential Disclosures ESG Risks EBA/CP/2021/06. 2021. Available online: https://www.eba.europa.eu/sites/default/documents/files/document_library/Publications/Consultations/2021/Consultation%20on%20draft%20ITS%20on%20Pillar%20disclosures%20on%20ESG%20risk/963621/Consultation%20paper%20on%20draft%20ITS%20on%20Pillar%203%20disclosures%20on%20ESG%20risks.pdf (accessed on 5 March 2024).
- The Nature Conservancy. Reducing Emissions from Deforestation and Degradation (REDD): A Casebook of On-the-Ground Experience; Conservation International and Wildlife Conservation Society: Arlington, VA, USA, 2010; Available online: https://www.nature.org/media/climatechange/redd-casebook-tnc-ci-wcs.pdf (accessed on 5 March 2024).
- Bank for International Settlements (BIS). Climate-Related Financial Risks—Measurement Methodologies; BIS, Basel Committee on Banking Supervision: Basel, Switzerland, 2021; ISBN 978-92-9259-471-8. [Google Scholar]
- Stern, N.H. The Economics of Climate Change: The Stern Review; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Bolton, R. Integrating Economic and Environmental Models: Some Preliminary Considerations. Socio-Econ. Plan. Sci. 1989, 23, 25–37. [Google Scholar] [CrossRef]
- Bartelmus, P. Accounting for sustainable growth and development. Struct. Change Econ. Dyn. 1992, 3, 241–260. [Google Scholar] [CrossRef]
- Vellinga, N.; Withagen, C. On the concept of Green National Income. Oxf. Econ. Pap. 1996, 48, 499–514. [Google Scholar] [CrossRef]
- Odum Howard, T. Environmental Accounting: Emergy and Environmental Decision Making; John Wiley & Sons: New York, NY, USA, 1996; ISBN 0-471-11442-1. [Google Scholar]
- United Nations Statistics Division. Global Assessment of Environment Statistics and Environmental-Economic Accounting. Committee of Experts on Environmental-Economic Accounting (UNCEEA), Statistical Commission. 2007. Available online: https://unstats.un.org/unsd/statcom/doc07/Analysis_SC.pdf (accessed on 5 March 2024).
- Roussis, D.; Karakatsanis, G.; Makropoulos, C. A macroeconomic model of water capital conservation. In Proceedings of the 4th International Conference of Water Economics, Statistics and Finance, Livorno, Italy, 4–5 April 2017. [Google Scholar] [CrossRef]
- Zampori, L.; Pant, R. Suggestions for Updating the Product Environmental Footprint (PEF) Method; EUR 29682 EN; Publications Office of the European Union: Luxembourg, 2019; ISBN 978-92-76-00653-4. Available online: https://publications.jrc.ec.europa.eu/repository/handle/JRC115959 (accessed on 5 March 2024).
- European Commission. Commission Recommendation (EU) 2021/2279 of 15 December 2021 on the Use of the Environmental Footprint Methods to Measure and Communicate the Life Cycle Environmental Performance of Products and Organisations. 2021, C/2021/9332. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A32021H2279 (accessed on 5 March 2024).
- European Commission. Delivering the European Green Deal. 2021. Available online: https://ec.europa.eu/info/strategy/priorities-2019-2024/european-green-deal/delivering-european-green-deal_en (accessed on 5 March 2024).
- S&P Dow Jones Indices. Dow Jones Sustainability Indices (DJSI) Methodology; A Division of S&P Global. 2023. Available online: https://www.spglobal.com/spdji/en/documents/methodologies/methodology-dj-sustainability-indices.pdf (accessed on 5 March 2024).
- Cohen, J.L.; Newman, C.M. When will a large complex system be stable? J. Theor. Biol. 1985, 113, 153–156. [Google Scholar] [CrossRef]
- Karakatsanis, G.; Mamassis, N. Energy, Trophic Dynamics and Ecological Discounting. Land 2023, 12, 1928. [Google Scholar] [CrossRef]
- McVittie, A.; Hussain, S.S. The Economics of Ecosystems and Biodiversity Valuation Database Manual. 2013. Available online: https://www.teebweb.org/wp-content/uploads/2014/03/TEEB-Database-and-Valuation-Manual_2013.pdf (accessed on 5 March 2024).
- Grafton, R.Q.; Jotzo, F.; Wasson, M. Financing sustainable development: Country Undertakings and Rights for Environmental Sustainability CURES. Ecol. Econ. 2004, 51, 65–78. [Google Scholar] [CrossRef]
- Dittrich, M. Green finance in emerging markets. Glob. Solut. J. 2020, 156–167. Available online: https://www.global-solutions-initiative.org/wp-content/uploads/2020/04/GSJ5_Dittrich.pdf (accessed on 5 March 2024).
- Kahsay, H.T. Financial Development and Economic Growth Nexus: Evidence from Ethiopia (Johnson Approach to Co-Integration). Int. J. Sci. Res. 2015, 4, 2319–7064. Available online: https://www.ijsr.net/archive/v4i4/SUB153620.pdf (accessed on 5 March 2024).
- European Commission. Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions: A New Circular Economy Action Plan for a Cleaner and More Competitive Europe. 2020. COM/2020/98 Final. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?qid=1583933814386&uri=COM:2020:98:FIN (accessed on 5 March 2024).
- Council of Europe. Fit for 55’: Council and Parliament Reach Provisional Deal on EU Emissions Trading System and the Social Climate Fund. 18 December 2022. Available online: https://www.consilium.europa.eu/en/press/press-releases/2022/12/18/fit-for-55-council-and-parliament-reach-provisional-deal-on-eu-emissions-trading-system-and-the-social-climate-fund/ (accessed on 5 March 2024).
- United Nations Environmental Program Financial Initiative (UNEP FI). Principles for Responsible Banking (PRB) to Strengthen Climate Ambition to Meet Increased Expectations. Available online: https://www.unepfi.org/industries/banking/principles-for-responsible-banking-to-strengthen-climate-ambition-to-meet-increased-expectations/ (accessed on 5 March 2024).
- Chapagain, A.K.; Hoekstra, A.Y.; Savenije, H.H.J. Saving Water through Global Trade. UNESCO-IHE, Institute for Water Education 2005, Research Report Series No 17. Available online: https://ris.utwente.nl/ws/portalfiles/portal/5150405/Vreman-1.868333.pdf (accessed on 5 March 2024).
- Karakatsanis, G.; Mamassis, N. Energy and the Macrodynamics of Agrarian Societies. Land 2023, 12, 1603. [Google Scholar] [CrossRef]
- Karakatsanis, G.; Roussis, D.; Moustakis, Y.; Gournari, P.; Parara, I.; Dimitriadis, P.; Koutsoyiannis, D. Energy, variability and weather finance engineering. Energy Procedia 2017, 125, 389–397. [Google Scholar] [CrossRef]
- Mochaourab, R.; Jorswieck, E.A. Exchange Economy in Two-User Multiple-Input Single-Output Interference Channels (v3). IEEE J. Sel. Top. Signal Process. 2012, 6, 151–164. [Google Scholar] [CrossRef]
- Tsur, Y.; Zemel, A. Growth, Scarcity and R&D. AgEcon Search 2002; Discussion Paper 14994. [CrossRef]
- Boggia, A.; Massei, G.; Paolotti, L.; Rocchi, L.; Schiavi, F. A model for measuring the environmental sustainability of events. J. Environ. Manag. 2018, 206, 836–845. [Google Scholar] [CrossRef] [PubMed]






| Assumption # | Assumption Description | Assumption Substantiation |
|---|---|---|
| 1 | 100% material efficiency of VAC recovery | There are no material losses across the VAC’s recovery; the requested quantity is exactly delivered |
| 2 | Homogeneity of wastewater matrices | The composition of each wastewater matrix is the same, differentiating only by VAC dilution |
| 3 | Common operational range of industries | Technologically, all industries are equivalent and can recover a VAC at any dilution level (0%→100%) |
| 4 | Delivered VACs are of the same quality | Industries recover VACs with no quality differences; the delivered VAC is qualitatively the same |
| 5 | Industries can process any wastewater quantity | Industries’ capacity can process any amount of wastewater to extract VACs without constraints |
| 6 | Industries implement full-cost accounting | Each industry applies the System of Environmental Economic Accounting (SEEA) [24,25] |
| 7 | Customers’ cost composition indifference | Customers are indifferent on each industry’s prevailing cost factor (constant, variable, environmental, etc.) |
| 8 | Customers lack industrial alternatives | Geographical or other barriers prevent Customers from assigning their wastewater matrices elsewhere |
| 9 | Recovered VACs are delivered immediately | When the VAC is recovered, all industries deliver it to the customer at the requested time with no delays |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karakatsanis, G.; Makropoulos, C. Chemical Leasing (Ch.L.) and the Sherwood Plot. Resources 2024, 13, 65. https://doi.org/10.3390/resources13050065
Karakatsanis G, Makropoulos C. Chemical Leasing (Ch.L.) and the Sherwood Plot. Resources. 2024; 13(5):65. https://doi.org/10.3390/resources13050065
Chicago/Turabian StyleKarakatsanis, Georgios, and Christos Makropoulos. 2024. "Chemical Leasing (Ch.L.) and the Sherwood Plot" Resources 13, no. 5: 65. https://doi.org/10.3390/resources13050065
APA StyleKarakatsanis, G., & Makropoulos, C. (2024). Chemical Leasing (Ch.L.) and the Sherwood Plot. Resources, 13(5), 65. https://doi.org/10.3390/resources13050065







