Elastic Wave Propagation in a Stainless-Steel Standard and Verification of a COMSOL Multiphysics Numerical Elastic Wave Toolbox
Abstract
:1. Introduction
2. Methodology
2.1. Sample Description
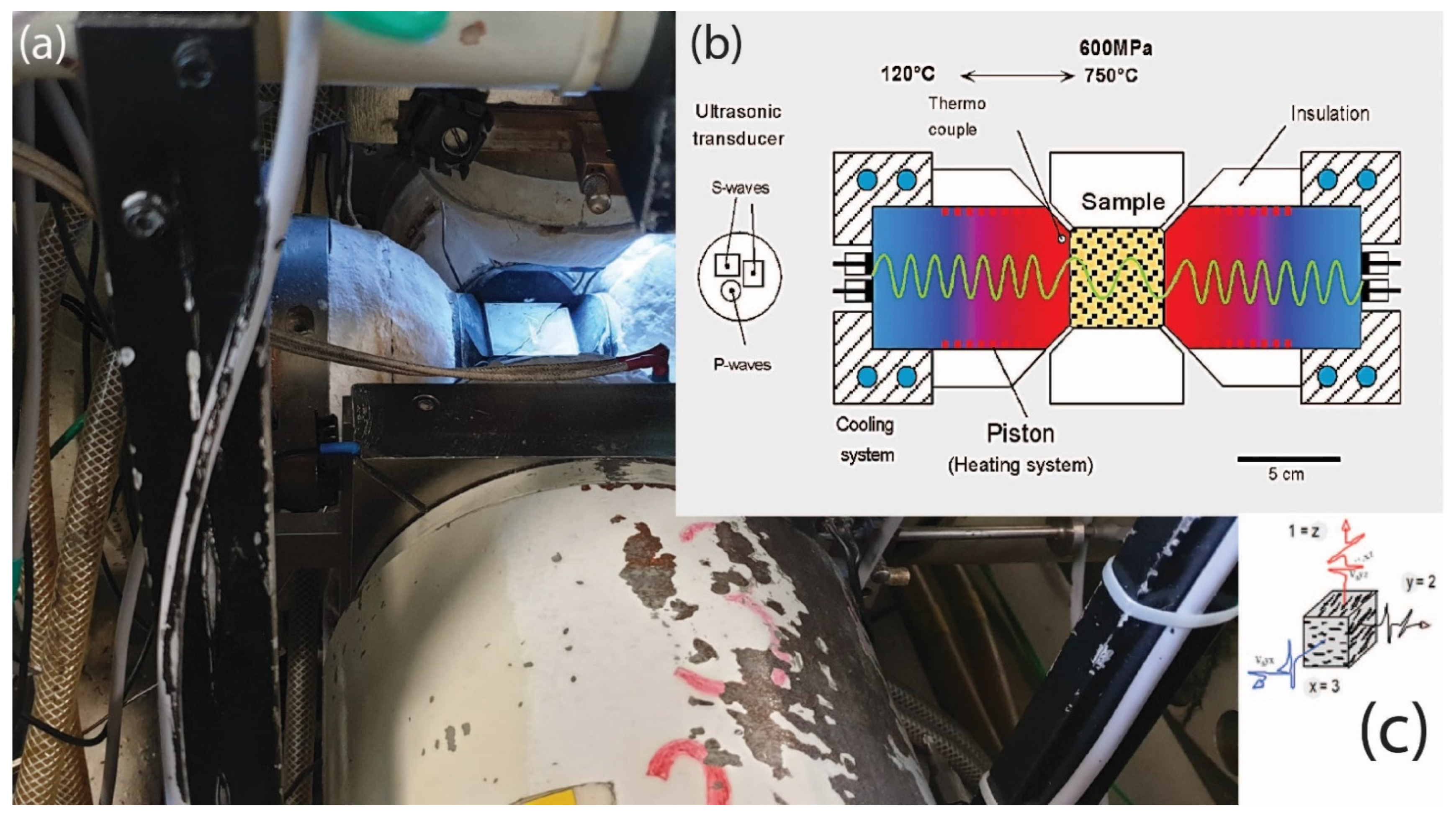
2.2. Experimental Setup
2.3. Numerical Methodology
Governing Equations and Constitutive Laws
3. Results
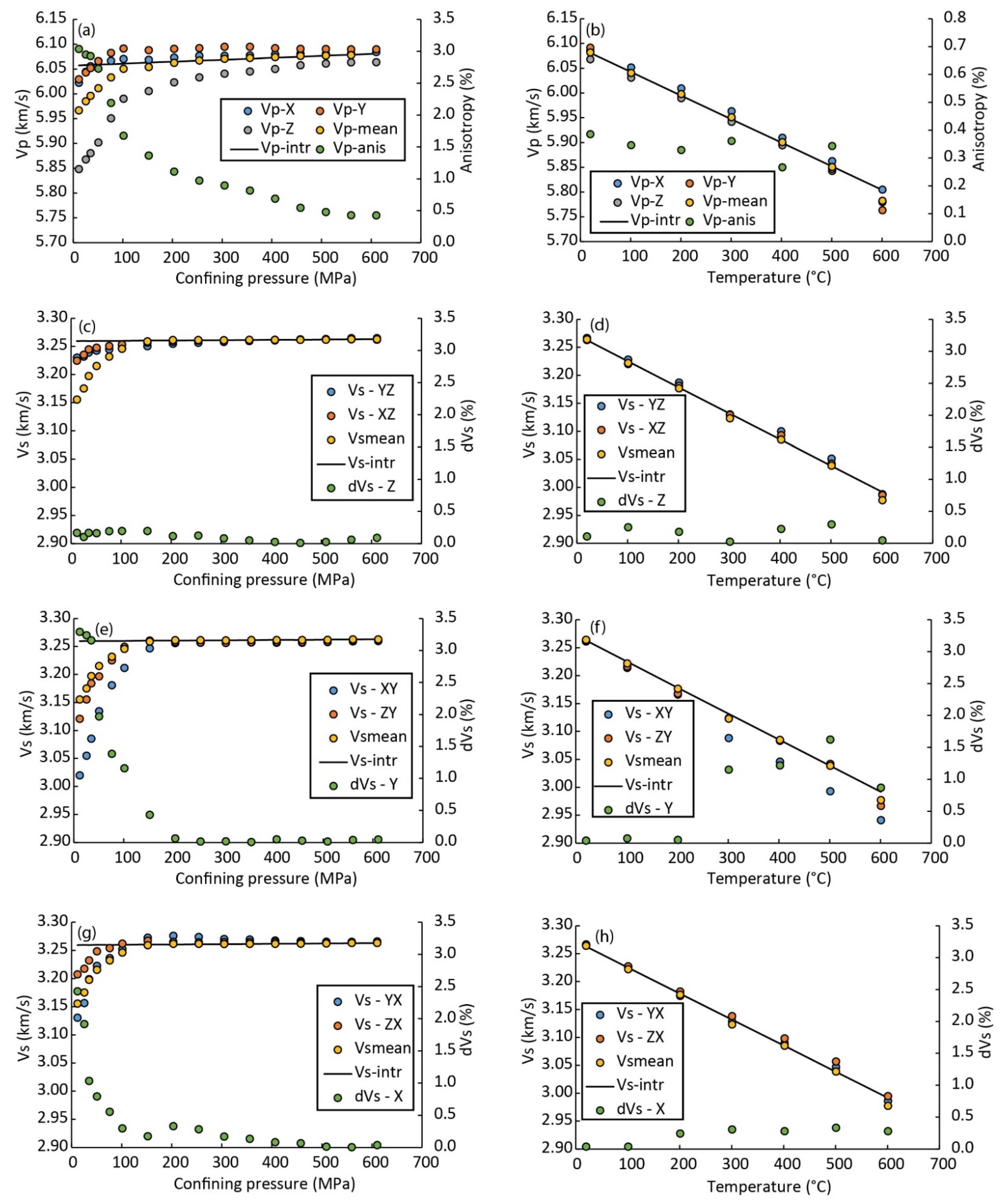
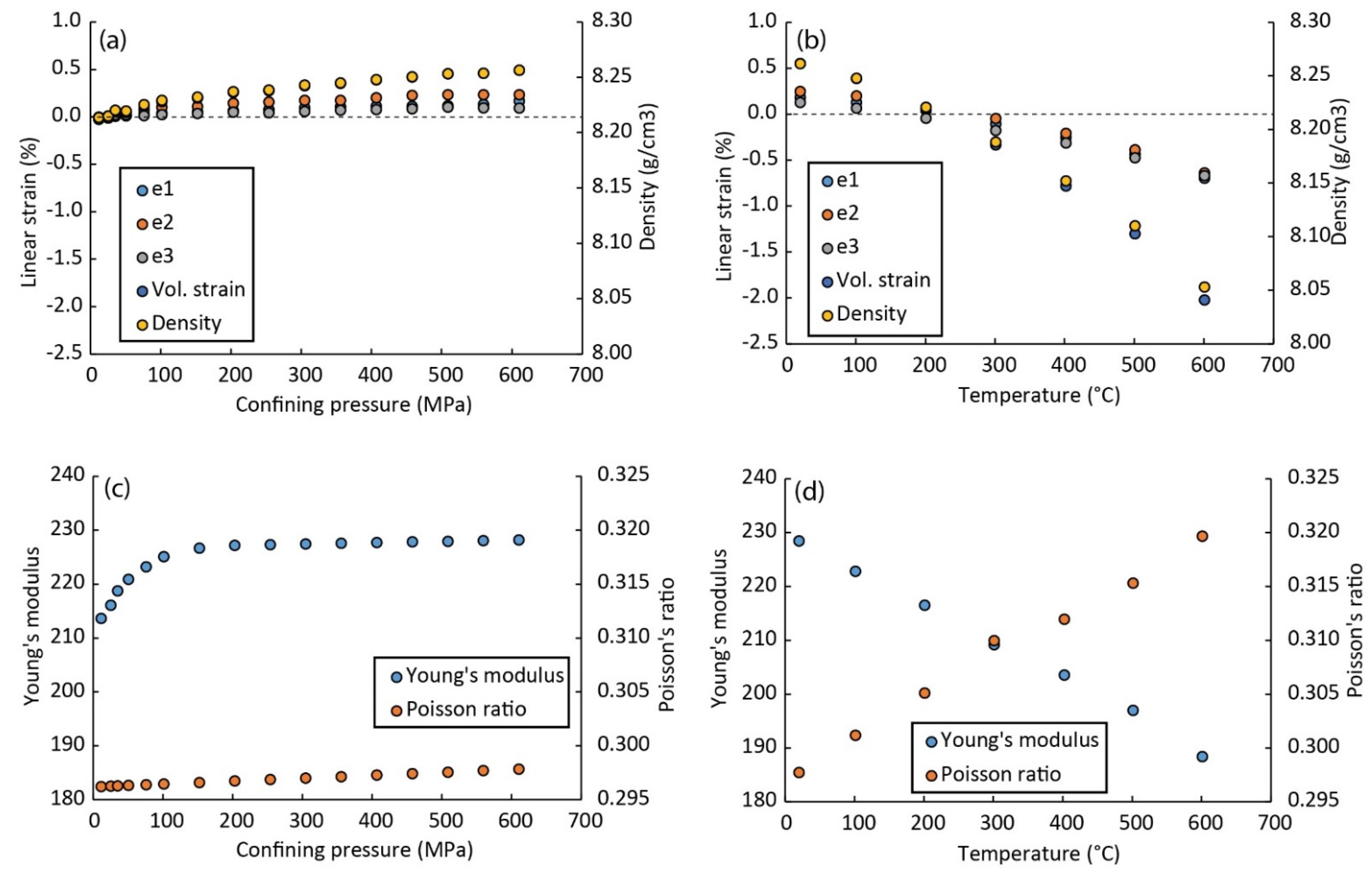
3.1. Laboratory Measurements of Ultrasonic Wave Velocities and Dynamic Elastic Properties
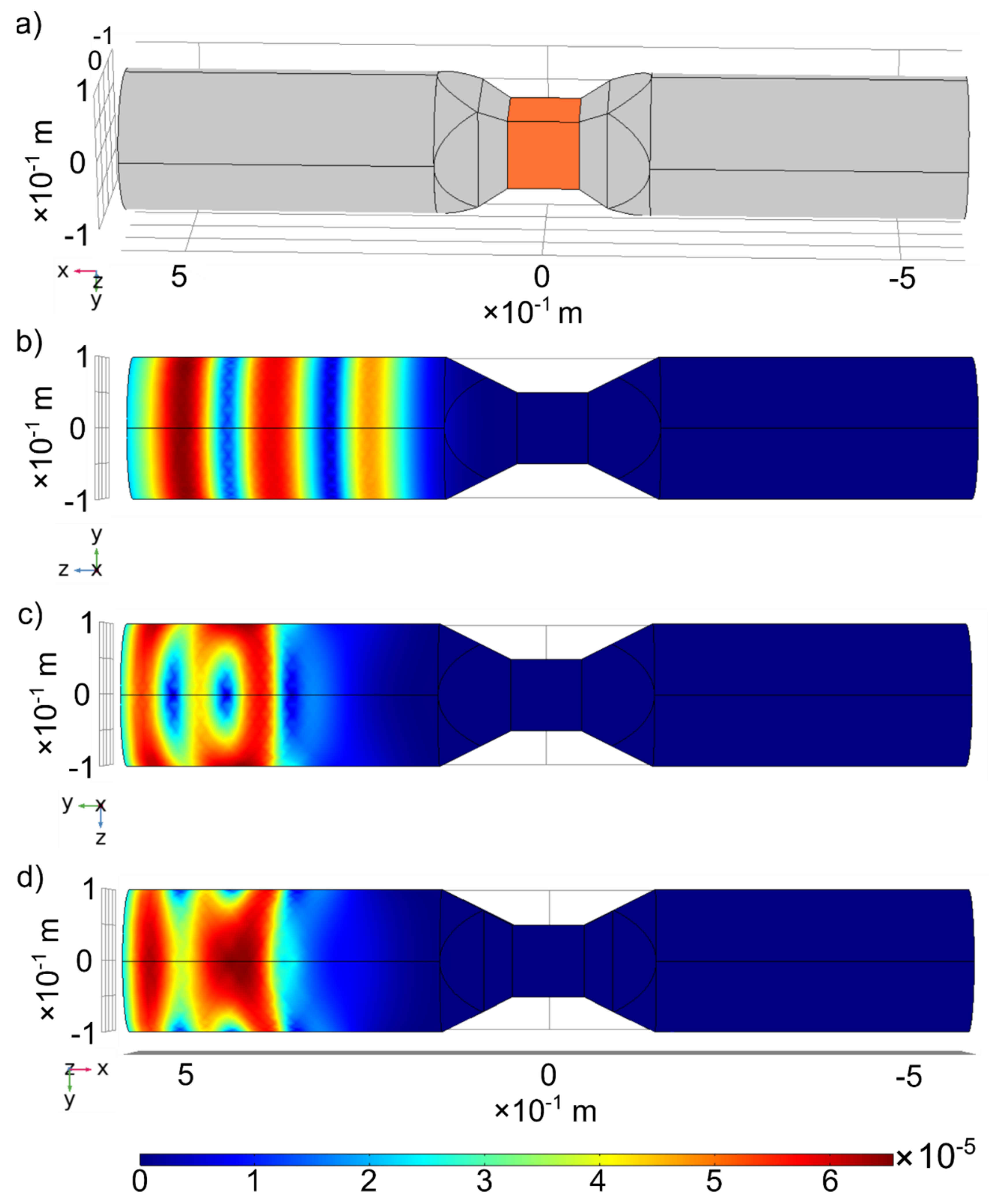
3.2. Numerical Modelling Results
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Birch, F. The velocity of compressional waves in rocks to 10 kilobars: 1. J. Geophys. Res. Earth Surf. 1960, 65, 1083–1102. [Google Scholar] [CrossRef]
- Birch, F. The velocity of compressional waves in rocks to 10 kilobars: 2. J. Geophys. Res. Earth Surf. 1961, 66, 2199–2224. [Google Scholar] [CrossRef]
- Christensen, N.I. Compressional wave velocities in metamorphic rocks at pressures to 10 kilobars. J. Geophys. Res. Earth Surf. 1965, 70, 6147–6164. [Google Scholar] [CrossRef]
- Christensen, N.I. Elasticity of ultrabasic rocks. J. Geophys. Res. 1966, 71, 5921–5931. [Google Scholar] [CrossRef]
- Bazargan, M.; Broumand, P.; Motra, H.; Almqvist, B.; Hieronymus, C.; Piazolo, S. A Numerical Toolbox to Calculate the Seismic Properties of Micro Sized Isotropic and Anisotropic Minerals. In Proceedings of the Mineral Exploration Symposium, Virtual Event, 17–18 September 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Bazargan, M.; Motra, H.B.; Almqvist, B.; Piazolo, S.; Hieronymus, C. Pressure, temperature and lithological dependence of seismic and magnetic susceptibility anisotropy in amphibolites and gneisses from the central Scandinavian Caledonides. Tectonophysics 2021, 820, 229113. [Google Scholar] [CrossRef]
- Christensen, N.I. Compressional wave velocities in rocks at high temperatures and pressures, critical thermal gradients, and crustal low-velocity zones. J. Geophys. Res. Earth Surf. 1979, 84, 6849–6857. [Google Scholar] [CrossRef]
- Kern, H.; Burlini, L.; Ashchepkov, I. Fabric-related seismic anisotropy in upper-mantle xenoliths: Evidence from measurements and calculations. Phys. Earth Planet. Inter. 1996, 95, 195–209. [Google Scholar] [CrossRef]
- Kern, H.; Gao, S.; Liu, Q.-S. Seismic properties and densities of middle and lower crustal rocks exposed along the North China Geoscience Transect. Earth Planet. Sci. Lett. 1996, 139, 439–455. [Google Scholar] [CrossRef]
- Kern, H. Measuring and Modeling of P- and S-Wave Velocities on Crustal Rocks: A Key for the Interpretation of Seismic Reflection and Refraction Data. Int. J. Geophys. 2011, 2011, 530728. [Google Scholar] [CrossRef] [Green Version]
- Scheu, B.; Kern, H.; Spieler, O.; Dingwell, D. Temperature dependence of elastic P- and S-wave velocities in porous Mt. Unzen dacite. J. Volcanol. Geotherm. Res. 2006, 153, 136–147. [Google Scholar] [CrossRef]
- Kern, H.; Popp, T.; Gorbatsevich, F.; Zharikov, A.; Lobanov, K.; Smirnov, Y. Pressure and temperature dependence of VP and Vs in rocks from the superdeep well and from surface analogues at Kola and the nature of velocity anisotropy. Tectonophysics 2001, 338, 113–134. [Google Scholar] [CrossRef]
- Kern, H. The effect of high temperature and high confining pressure on compressional wave velocities in quartz-bearing and quartz-free igneous and metamorphic rocks. Tectonophysics 1978, 44, 185–203. [Google Scholar] [CrossRef]
- Kern, H. Effect of high-low quartz transition on compressional and shear wave velocities in rocks under high pressure. Phys. Chem. Miner. 1979, 4, 161–171. [Google Scholar] [CrossRef]
- Kern, H.; Tubia, J. Pressure and temperature dependence of P- and S-wave velocities, seismic anisotropy and density of sheared rocks from the Sierra Alpujata massif (Ronda peridotites, Southern Spain). Earth Planet. Sci. Lett. 1993, 119, 191–205. [Google Scholar] [CrossRef]
- Almqvist, B.; Cyprych, D.; Piazolo, S.; Bazargan, M. Contributions of microstructure and crystallographic preferred orientation to seismic anisotropy in the lower continental crust, European Geoscience Union. In Proceedings of the EGU General Assembly Conference, Vienna, Austria, 8–13 April 2018; p. 13249. [Google Scholar]
- Almqvist, B.S.; Cyprych, D.; Piazolo, S. Seismic anisotropy of mid crustal orogenic nappes and their bounding structures: An example from the Middle Allochthon (Seve Nappe) of the Central Scandinavian Caledonides. Tectonophysics 2021, 819, 229045. [Google Scholar] [CrossRef]
- Bazargan, M.; Almqvist, B.S.G.; Hieronymus, C.; Piazolo, S. Employing Finite Element Method using COMSOL multiphysics to predict seismic velocity and anisotropy: Application to lower crust and upper mantle rocks. In Proceedings of the 20th EGU General Assembly, EGU2018, Vienna, Austria, 4–13 April 2018; European Geoscience Union: Munich, Germany, 2018; p. 17139. [Google Scholar]
- Bazargan, M.; Almqvist, B.S.G.; Hieronymus, C.; Piazolo, S. Experimental investigation and numerical modelling of elastic wave propagation in meta-morphic rocks. In In Proceedings of the IGSC 2019, Uppsala, Sweden, 21–24 October 2019. [Google Scholar]
- Bazargan, M.; Hem, M.B.; Almqvist, B.S.G.; Hieronymus, C.; Piazolo, S. Elastic wave anisotropy in amphibolites and paragneisses from the Swedish Caledonides measured at high pressures (600 MPa) and temperatures (600 °C). In Proceedings of the 21th EGU General Assembly, EGU2019, Vienna, Austria, 7–12 April 2018; European Geoscience Union: Munich, Germany, 2019; p. 14397. [Google Scholar]
- Bazargan, M.; Hem, M.B.; Almqvist, B.S.G.; Hieronymus, C.; Piazolo, S. Numerical and Experimental Investigations of Elastic Wave Anisotropy in Monomineral and Polymineral Rocks, In Proceedings of the EGU 2020, Vienna, Austria, 3–8 May 2020.
- Ferri, F.; Burlini, L.; Cesare, B.; Sassi, R. Seismic properties of lower crustal xenoliths from El Hoyazo (SE Spain): Experimental evidence up to partial melting. Earth Planet. Sci. Lett. 2007, 253, 239–253. [Google Scholar] [CrossRef]
- Hughes, D.S.; Maurette, C. Variation of elastic wave velocities in basic igneous rocks with pressure and temperature. Geophysics 1957, 22, 23–31. [Google Scholar] [CrossRef]
- Almqvist, B.S.; Misra, S.; Klonowska, I.; Mainprice, D.; Majka, J. Ultrasonic velocity drops and anisotropy reduction in mica-schist analogues due to melting with implications for seismic imaging of continental crust. Earth Planet. Sci. Lett. 2015, 425, 24–33. [Google Scholar] [CrossRef]
- Almqvist, B.S.G.; Mainprice, D. Seismic properties and anisotropy of the continental crust: Predictions based on mineral texture and rock microstructure. Rev. Geophys. 2017, 55, 367–433. [Google Scholar] [CrossRef] [Green Version]
- Mainprice, D. A FORTRAN program to calculate seismic anisotropy from the lattice preferred orientation of minerals. Comput. Geosci. 1990, 16, 385–393. [Google Scholar] [CrossRef]
- Mainprice, D.; Bachmann, F.; Hielscher, R.; Schaeben, H.; Lloyd, G. Calculating anisotropic piezoelectric properties from texture data using the MTEX open source package. Geol. Soc. Spéc. Publ. 2014, 409, 223–249. [Google Scholar] [CrossRef] [Green Version]
- Mainprice, D. Seismic anisotropy of the deep Earth from a mineral and rock physics perspective. In Treatise in Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Oxford, UK, 2015; Volume 2, pp. 487–539. [Google Scholar]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook, 3rd ed.; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar] [CrossRef]
- Vel, S.S.; Cook, A.C.; Johnson, S.; Gerbi, C. Computational homogenization and micromechanical analysis of textured polycrystalline materials. Comput. Methods Appl. Mech. Eng. 2016, 310, 749–779. [Google Scholar] [CrossRef] [Green Version]
- Valcke, S.L.; Casey, M.; Lloyd, G.E.; Kendall, J.-M.; Fisher, Q.J. Lattice preferred orientation and seismic anisotropy in sedimentary rocks. Geophys. J. Int. 2006, 166, 652–666. [Google Scholar]
- Zhong, X.; Frehner, M.; Kunze, K.; Zappone, A. A novel EBSD-based finite-element wave propagation model for investigating seismic anisotropy: Application to Finero Peridotite, Ivrea-Verbano Zone, Northern Italy. Geophys. Res. Lett. 2014, 41, 7105–7114. [Google Scholar] [CrossRef] [Green Version]
- Zhong, X.; Frehner, M.; Kunze, K.; Zappone, A.S. A numerical and experimental investigation on seismic anisotropy of Finero peridotite, Ivrea-Verbano Zone, Northern Italy. IOP Conf. Series Mater. Sci. Eng. 2015, 82, 12072. [Google Scholar] [CrossRef] [Green Version]
- Walsh, J.B. The effect of cracks on the compressibility of rock. J. Geophys. Res. Earth Surf. 1965, 70, 381–389. [Google Scholar] [CrossRef]
- Naus-Thijssen, F.M.J.; Goupee, A.J.; Vel, S.S.; Johnson, S. The influence of microstructure on seismic wave speed anisotropy in the crust: Computational analysis of quartz-muscovite rocks. Geophys. J. Int. 2011, 185, 609–621. [Google Scholar] [CrossRef]
- Bazargan, M.; Almqvist, B.G.; Motra, H.B.; Klein, L.; Broumand, P.; Schmiedel, T.; Piazolo, S.; Hieronymus Ch, F. (In-Review), An Experimental and Numerical Investigation of Grain Size Effects on Ultrasonic Wave Velocities in Gabbro. Available online: https://www.diva-portal.org/smash/record.jsf?pid=diva2%3A1644695&dswid=-5596 (accessed on 10 May 2022).
- Malvern, L. Introduction to the Mechanics of a Continuous Medium; Prentice-Hill: Englewood Cliffs, NJ, USA, 1969. [Google Scholar]
- Wyllie, M.R.J.; Gregory, A.R.; Gardner, L.W. Elastic wave velocities in heterogeneous and porous media. Geophys. Soc. Explor. Geophys. 1956, 21, 41–70. [Google Scholar] [CrossRef]
- Wyllie, M.R.J.; Gregory, A.R.; Gardner, G.H.F. An experimental investigation of factors affecting elastic wave velocities in porous media. Geophysics 1958, 23, 459–493. [Google Scholar] [CrossRef]
- Takei, Y. Effects of Partial Melting on Seismic Velocity and Attenuation: A New Insight from Experiments. Annu. Rev. Earth Planet. Sci. 2017, 45, 447–470. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Maudlin, P.J.; Tomé, C.N. Viscoplastic Selfconsistent Modelling of the Anisotropic Behavior of Voided Polycrystals. AIP Conf. Proc. 2004, 712, 1771–1776. [Google Scholar] [CrossRef]
- Tome, C.; Lebensohn, R.A. Material Modeling with the Visco-Plastic Self-Consistent (VPSC) Approach: Theory and Practical Applications, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2022; ISBN 9780128207130. [Google Scholar]
- Kim, D.; Lekić, V.; Ménard, B.; Baron, D.; Taghizadeh-Popp, M. Sequencing seismograms: A panoptic view of scattering in the core-mantle boundary region. Science 2020, 368, 1223–1228. [Google Scholar] [CrossRef] [PubMed]
- Lebedev, T.S.; Burtnij, P.A.; Korčin, V.A. Behaviour of the pore space in Gabbros and its relationship with elastic wave velocities and high pressures. Gerl. Beitr. Z. Geophys. S. 1974, 83, 170–180. [Google Scholar]

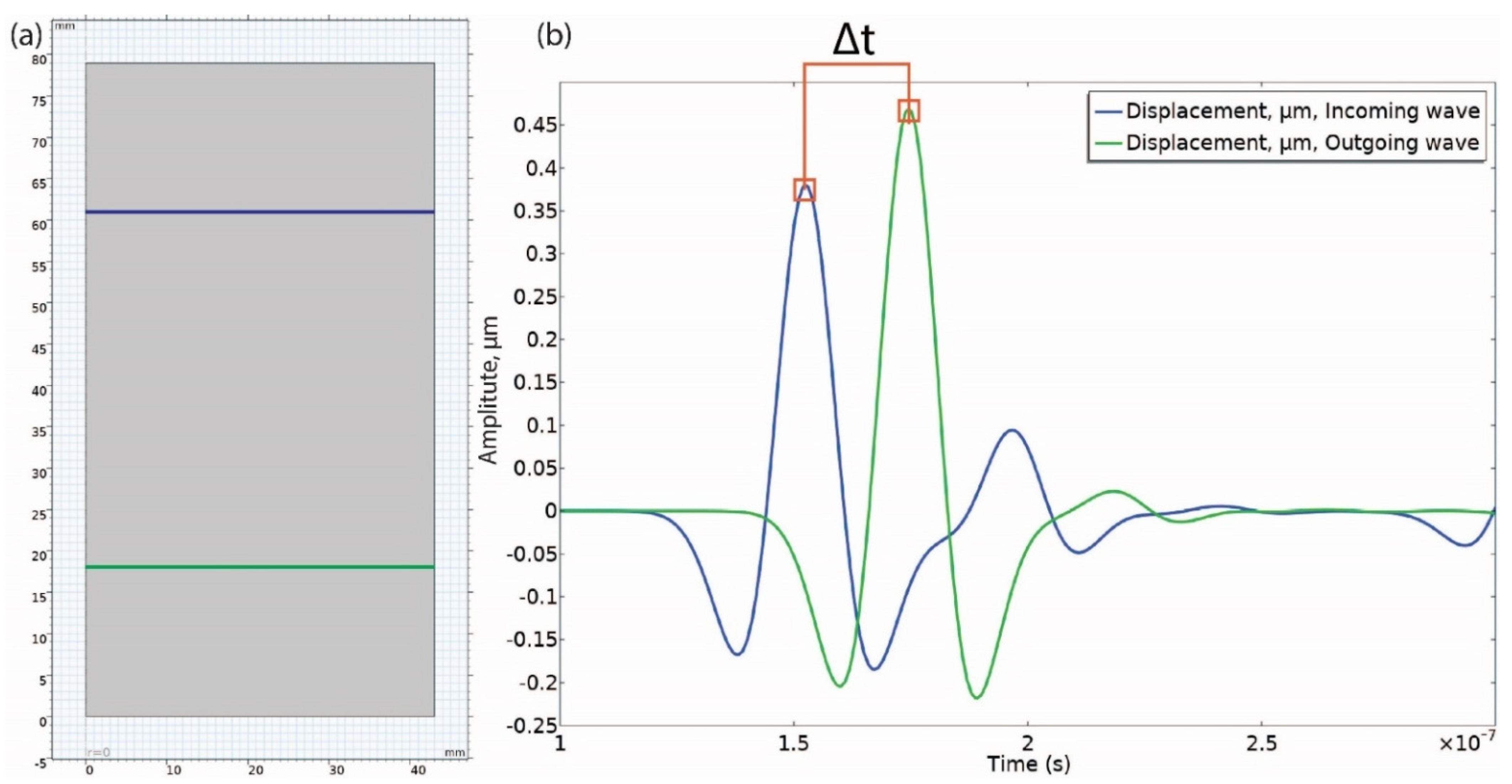
| Young’s Modulus (GPa) | Poisson’s Ratio | Density (kg/m3) | Vp (km/s) | Vs (km/s) | |
|---|---|---|---|---|---|
| Laboratory experiment | 228 | 0.298 | 8256 | 6.03 | 3.26 |
| Numerical results 2D/3D | 228 | 0.298 | 8256 | 6.1 | 3.3 |
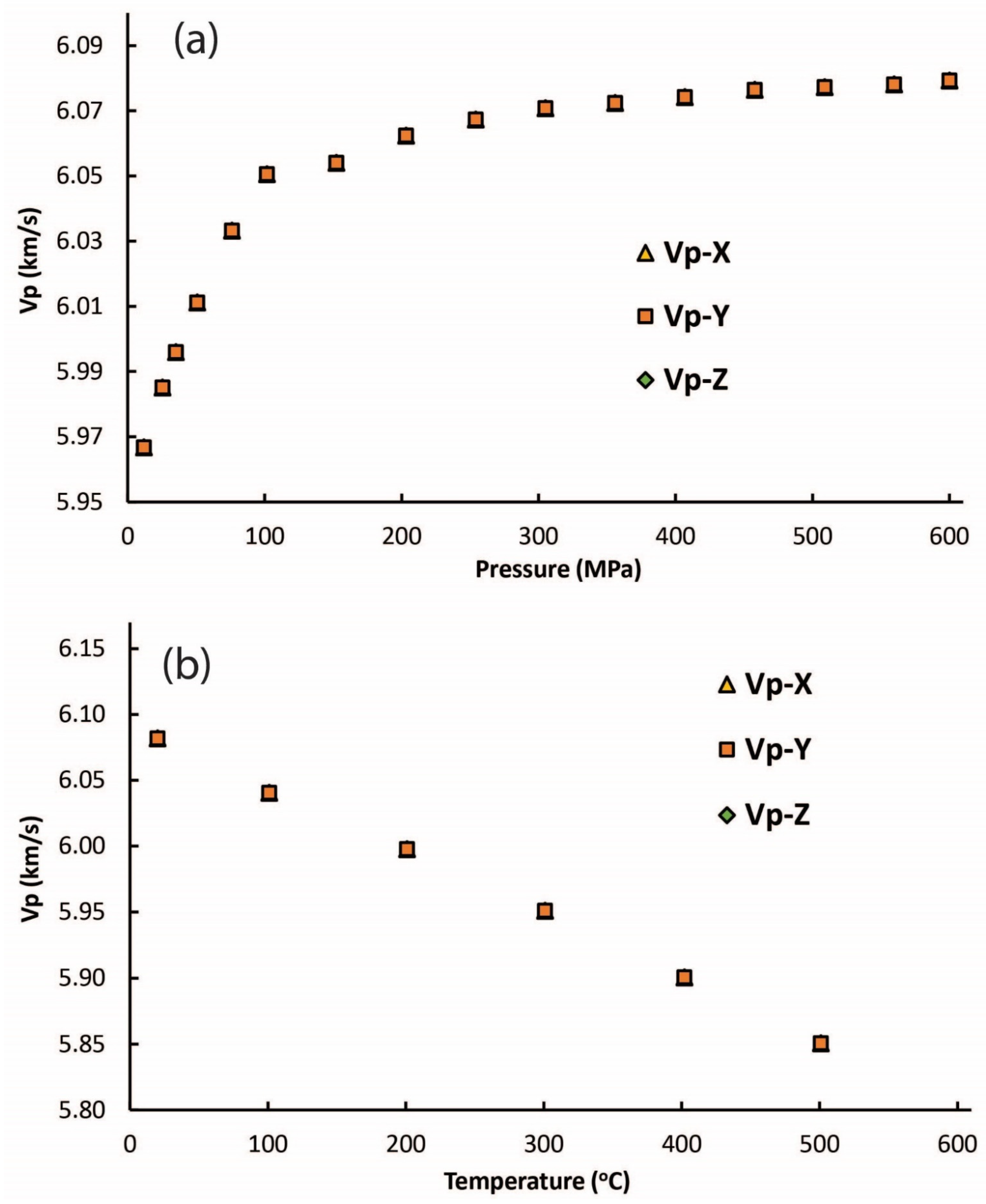
| Laboratory | Numerical | dVp (VpL-VpN) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Temp. | Pc | Vp-Z | Vp-Y | Vp-X | Vp-Z | Vp-Y | Vp-X | dVp-Z | dVp-Y | ΔVp-X | Vp Mean |
| (°C) | (MPa) | (km/s) | (km/s) | (km/s) | (km/s) | (km/s) | (km/s) | (km/s) | (km/s) | (km/s) | (km/s) |
| 20 | 12 | 5.85 | 6.03 | 6.02 | 5.967 | 5.967 | 5.967 | −0.12 | 0.06 | 0.06 | 5.967 |
| 20 | 25 | 5.87 | 6.04 | 6.04 | 5.985 | 5.985 | 5.985 | −0.12 | 0.06 | 0.06 | 5.985 |
| 20 | 35 | 5.88 | 6.05 | 6.06 | 5.996 | 5.996 | 5.996 | −0.12 | 0.06 | 0.06 | 5.996 |
| 20 | 51 | 5.9 | 6.07 | 6.07 | 6.011 | 6.011 | 6.011 | −0.11 | 0.05 | 0.05 | 6.011 |
| 20 | 76 | 5.95 | 6.08 | 6.07 | 6.033 | 6.033 | 6.033 | −0.08 | 0.05 | 0.03 | 6.033 |
| 20 | 102 | 5.99 | 6.09 | 6.07 | 6.051 | 6.051 | 6.051 | −0.06 | 0.04 | 0.02 | 6.051 |
| 20 | 152 | 6.01 | 6.09 | 6.07 | 6.054 | 6.054 | 6.054 | −0.05 | 0.03 | 0.01 | 6.054 |
| 20 | 203 | 6.02 | 6.09 | 6.07 | 6.062 | 6.062 | 6.062 | −0.04 | 0.03 | 0.01 | 6.062 |
| 20 | 254 | 6.03 | 6.09 | 6.08 | 6.067 | 6.067 | 6.067 | −0.03 | 0.02 | 0.01 | 6.067 |
| 20 | 305 | 6.04 | 6.09 | 6.08 | 6.071 | 6.071 | 6.071 | −0.03 | 0.02 | 0.01 | 6.071 |
| 20 | 356 | 6.05 | 6.09 | 6.08 | 6.072 | 6.072 | 6.072 | −0.03 | 0.02 | 0 | 6.072 |
| 20 | 407 | 6.05 | 6.09 | 6.08 | 6.074 | 6.074 | 6.074 | −0.02 | 0.02 | 0.01 | 6.074 |
| 20 | 458 | 6.06 | 6.09 | 6.08 | 6.076 | 6.076 | 6.076 | −0.02 | 0.01 | 0 | 6.076 |
| 20 | 509 | 6.06 | 6.09 | 6.08 | 6.077 | 6.077 | 6.077 | −0.02 | 0.01 | 0 | 6.077 |
| 20 | 560 | 6.06 | 6.09 | 6.08 | 6.078 | 6.078 | 6.078 | −0.01 | 0.01 | 0 | 6.078 |
| 20 | 600 | 6.06 | 6.09 | 6.08 | 6.079 | 6.079 | 6.079 | −0.02 | 0.01 | 0.01 | 6.079 |
| 20 | 600 | 6.07 | 6.09 | 6.09 | 6.082 | 6.082 | 6.082 | −0.01 | 0.01 | 0 | 6.082 |
| 101 | 600 | 6.03 | 6.04 | 6.05 | 6.04 | 6.04 | 6.04 | −0.01 | 0 | 0.01 | 6.04 |
| 201 | 600 | 5.99 | 5.99 | 6.01 | 5.998 | 5.998 | 5.998 | −0.01 | 0 | 0.01 | 5.998 |
| 301 | 600 | 5.94 | 5.95 | 5.96 | 5.951 | 5.951 | 5.951 | −0.01 | 0 | 0.01 | 5.951 |
| 402 | 600 | 5.89 | 5.9 | 5.91 | 5.901 | 5.901 | 5.901 | −0.01 | 0 | 0.01 | 5.901 |
| 501 | 600 | 5.85 | 5.84 | 5.86 | 5.851 | 5.851 | 5.851 | 0 | −0.01 | 0.01 | 5.851 |
| 601 | 600 | 5.78 | 5.76 | 5.8 | 5.783 | 5.783 | 5.783 | 0 | −0.02 | 0.02 | 5.783 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bazargan, M.; Almqvist, B.S.G.; Motra, H.B.; Broumand, P.; Schmiedel, T.; Hieronymus, C.F. Elastic Wave Propagation in a Stainless-Steel Standard and Verification of a COMSOL Multiphysics Numerical Elastic Wave Toolbox. Resources 2022, 11, 49. https://doi.org/10.3390/resources11050049
Bazargan M, Almqvist BSG, Motra HB, Broumand P, Schmiedel T, Hieronymus CF. Elastic Wave Propagation in a Stainless-Steel Standard and Verification of a COMSOL Multiphysics Numerical Elastic Wave Toolbox. Resources. 2022; 11(5):49. https://doi.org/10.3390/resources11050049
Chicago/Turabian StyleBazargan, Mohsen, Bjarne S. G. Almqvist, Hem Bahadur Motra, Pooyan Broumand, Tobias Schmiedel, and Christoph F. Hieronymus. 2022. "Elastic Wave Propagation in a Stainless-Steel Standard and Verification of a COMSOL Multiphysics Numerical Elastic Wave Toolbox" Resources 11, no. 5: 49. https://doi.org/10.3390/resources11050049
APA StyleBazargan, M., Almqvist, B. S. G., Motra, H. B., Broumand, P., Schmiedel, T., & Hieronymus, C. F. (2022). Elastic Wave Propagation in a Stainless-Steel Standard and Verification of a COMSOL Multiphysics Numerical Elastic Wave Toolbox. Resources, 11(5), 49. https://doi.org/10.3390/resources11050049









