A 10 V-to-1 V Double Step-Down Buck Converter Using Time-Based Current Mode Control with Minimum Delay Frequency Difference Phase Adder for 1 MHz Operation

Abstract

An extreme step-down ratio buck converter is proposed using a double step-down (DSD) buck converter architecture and a single time-based current mode PWM controller able to generate two non-overlapping control signal phases. Current sampling for two inductors is implemented with a multiplexer and a pair of VCOs only, which treats the two inductors as one inductor operating at double the frequency. This is achieved without the use of any large external passive components in the controller while remaining stable. The type-II time-based controller uses a VCO, a frequency difference phase adder (FDPA), and a phase detector, generating a control signal with fully integrated components with minimum area. FDPA for proportional control also significantly limits the signal delay of the high gain controller, allowing the use of time-based control technique at <10 MHz, which improves converter efficiency. The proposed time-based current mode controller DSD buck converter is simulated in 130 nm BCD technology operating at 1 MHz for 10 V to 1 V conversion. The simulated peak efficiency is 82.2% at 0.4 A, and recovers from a 1.8 A loading and unloading current step in 5.75 $\mathrm{\mu }$s and 9.9 $\mathrm{\mu }$s, respectively.

1. Introduction

With the increasing electrification of infrastructure, the demand for better improvements in power delivery systems continue to grow. Particularly, power regulators are expected to take up less space, respond faster, consume less power, and power an increasingly wide voltage range as electrification develops in your pocket, on the road, and in the clouds. The most tried-and-true methods of pulse width modulation (PWM) control of switching converters are strained in being used to address such necessities. In analog PWM control, the need for a high power error amplifier to fulfill high gain bandwidth product (GBWP) requirement, and bulky passives to compensate said error amplifier, has a large power consumption and space economy overhead. As well, its typical half-bridge power stage implementation limits the voltage range that can be generated while maintaining an adequate power efficiency [1]. Other control schemes have been developed to overcome the shortcomings of the analog PWM controlled half-bridge buck converter. In particular, time-based control shows significant promise as an alternative control scheme that overcomes many of the issues present in analog PWM control, while also bringing some interesting features of its own. In addition, the time-based control scheme provides a unique advantage to alternative power stage architectures that allow for more extreme voltage down-conversion steps.

In time-based control, the feedback voltage from the power regulator output is applied to a voltage-controlled oscillator (VCO) and compared with a reference oscillator, and the phase difference between the two, computed using a phase detector into a PWM signal, are used to control the power regulator. The voltage-to-time/phase conversion scheme significantly reduces the silicon area required to implement the controller without the need for bulky passives and high GBWP error amplifiers [2,3,4,5,6]. This trait of time-based control makes it ideal for control of integrated power regulators, wherein a high level of integration improves its board space economy, efficiency, and transient response by reducing the distance and number of wirebonding between the power regulator and load. This high level of integration is of particular interest to distributed point-of-load power regulation in extreme step-down buck converters for electric vehicles, cloud computing, and data centers, where the large volume of loads of diverse voltage domains from 48 V high-power macro systems to 1 V low-power digital processing necessitates the use of extreme voltage down-conversions steps of 48 V to 1 V.

Time-based controllers also allow for other unique, sometimes necessary, PWM controller features for switching regulators without added controller complexity, like spread spectrum frequency compensation [7], light load adaptation using variable frequency [8,9], single-input multi-output regulators [10], and current mode control [11,12,13,14,15,16]. However, time-based controllers tend to operate at high frequencies of greater than 10 MHz, which are incompatible with extreme down-conversion steps. This high speed limitation stems from the implementation of its type-II or type-III control scheme. To generate the proportional or derivative response in a time-based controller, which computes the error signals as phase differences, the VCO output has to be delayed differentially. The typical implementation of this is a voltage-controlled delay line (VCDL), which varies the time delay applied to the VCO input based on the voltage difference. To achieve this, conventional VCDLs rely on a fixed center delay at zero error, which is then altered based on the error voltage. The higher the required proportional/derivative response gain for stable phase margin, the larger this center delay will need to be. For time-based controllers operating at higher frequencies, this fixed center delay has only a minor effect on the frequency response of the control loop, with very short time delay required to achieve enough phase difference, largely maintaining the stability of the system. As operating frequency decreases, however, the fixed center delay lengthens significantly, to be able to generate a commensurate proportional/derivative response gain for the desired operating frequency. At 1 MHz, this causes the closed loop to become unstable, as the phase margin severely deteriorates with increased delay. As such, time-based control of power regulators has largely been restricted to voltage regulators of relatively minor voltage conversion ratios, where higher frequency can safely be used without compromising efficiency. For more extreme voltage conversion ratios, however, operating frequency of the power regulator will need to be slowed down, to accommodate the fine-tuned control required.

While time-based regulators operating at lower frequencies have been proposed with alternative proportional gain generation schemes [13,14], these solutions end up reintegrating capacitors into the control loop, thereby forfeiting the advantage of space economy afforded by the time-based control scheme. As such, a method to generate the proportional phase error response with adequate gain and minimal time delay at below 10 MHz operating frequency is required, to be able to implement the extreme voltage down-conversion step using time-based control.

Some of that requirement can also be addressed by a different power regulator architecture, such as the double step-down (DSD) buck converter, which doubles the PWM duty cycle required for larger down-conversion steps [17], which facilitates the use of higher-frequency controllers without severely compromising efficiency [18]. The DSD buck converter, which requires a multiphase controller, is also uniquely synergistic with time-based control, whose use of ring oscillators containing phases with clear oscillator phase differences across its stages has been implemented in multiphase voltage regulators [3].

This paper proposes a DSD buck converter using time-based current mode control for an integrated point-of-load switching power regulator, using a minimal delay phase adder for proportional response gain at low operating frequency. This controller is built to accommodate the non-overlapping alternating charging stages of the DSD buck converter, using a phase-slip-conscious phase detector, as well as a high proportional gain, minimal delay phase adder to generate PWM control that is fast and stable. The buck converter operates at 1 MHz to maximize power efficiency for the extreme 10 V-to-1 V voltage conversion step, while retaining a speedy transient response. The type-II controller, with current mode control added for enhanced speed and stability, is all implemented without addition of large passives within the controller structure, thereby reducing required board space. This paper is organized as follows: Section 2 goes into detail of the design decisions made in using the double step-down architecture, current mode time-based control, to arrive at the optimal combination of power and space efficiency, in addition to response time. Section 3 explains the operating principles of the proposed time-based controller, including the current control loop, minimal delay phase adder, and the phase-slip-conscious non-overlapping phase detector. Section 4 details the simulation results of the proposed buck converter, with Section 5 summarizing the findings of this research and concluding the paper.

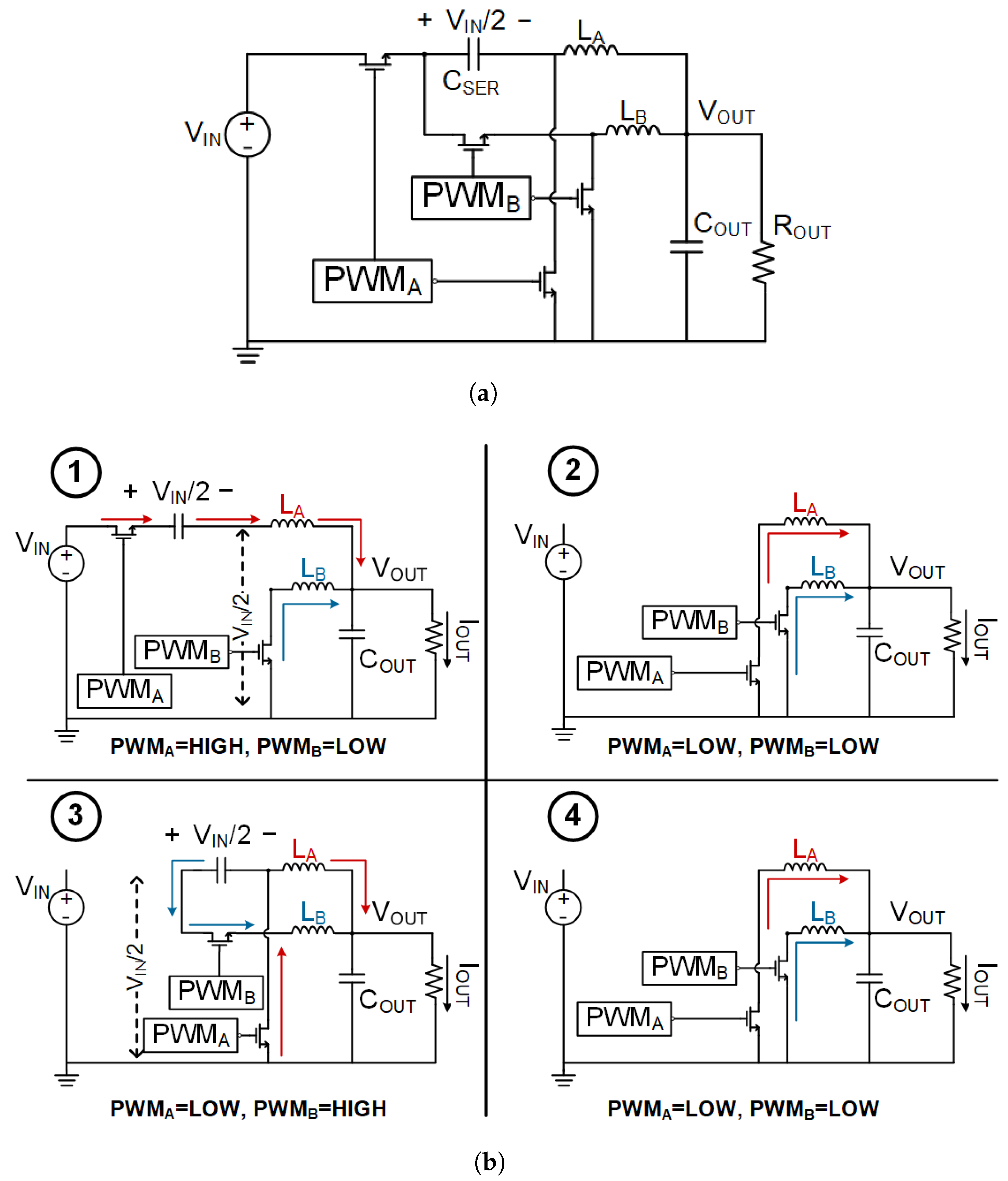
2. Double Step-Down Buck Converter Using Time-Based Control

2.1. Conventional Controller for Double Step-Down Buck Converter

There are various alternative power stage architectures using multi-stage and multiphase control schemes that improve efficiency of a buck converter executing an extreme voltage down-conversion step [18,19]. Of the architectures explored, the DSD architecture stands out as both highly efficient and highly scalable [20]. While the double series capacitor architecture (DSC) in [21] edges out the DSD architecture in terms of efficiency, it uses one more external series connected capacitor, increasing the board space it occupies.

The DSD buck converter works as follows: by adding a single capacitor in series with the top switch going into one output stage inductor in a two-phase, two inductor buck converter, the input voltage ${\mathrm{V}}_{\mathrm{IN}}$ is allowed to first step down to half its original value before converting down to the target output voltage ${\mathrm{V}}_{\mathrm{OUT}}$. Figure 1a shows the model of a DSD buck converter architecture, with the four phases of its switching mode control scheme in Figure 1b. The control scheme can be split into ${\mathrm{PWM}}_{\mathrm{A}}$ and ${\mathrm{PWM}}_{\mathrm{B}}$ sub-converters. In phase 1, the sub-converter for ${\mathrm{PWM}}_{\mathrm{A}}$ is high and ${\mathrm{PWM}}_{\mathrm{B}}$ is low, causing inductor ${\mathrm{L}}_{\mathrm{A}}$ to charge and ${\mathrm{L}}_{\mathrm{B}}$ to discharge. The series capacitor ${\mathrm{C}}_{\mathrm{SER}}$ is charged up to ${\mathrm{V}}_{\mathrm{IN}}/2$ in steady state, and discharges its bottom plate through ${\mathrm{L}}_{\mathrm{A}}$ while its top plate holds at ${\mathrm{V}}_{\mathrm{IN}}$, thus holding its voltage and maintaining the ${\displaystyle \frac{{\mathrm{V}}_{\mathrm{IN}}}{2}}-{\mathrm{V}}_{\mathrm{OUT}}$ voltage across ${\mathrm{L}}_{\mathrm{A}}$. Meanwhile, ${\mathrm{L}}_{\mathrm{B}}$ is discharged through the low side switch controlled by ${\mathrm{PWM}}_{\mathrm{B}}$ to hold $-{\mathrm{V}}_{\mathrm{OUT}}$ across ${\mathrm{L}}_{\mathrm{B}}$. In phase 3, the ${\mathrm{PWM}}_{\mathrm{A}}$ goes low instead while ${\mathrm{PWM}}_{\mathrm{B}}$ goes high, causing ${\mathrm{L}}_{\mathrm{A}}$ to discharge while ${\mathrm{L}}_{\mathrm{B}}$ charges. Here, ${\mathrm{L}}_{\mathrm{A}}$ is discharged to ground, holding $-{\mathrm{V}}_{\mathrm{OUT}}$ across ${\mathrm{L}}_{\mathrm{A}}$, while ${\mathrm{L}}_{\mathrm{B}}$ is charged through the top plate of ${\mathrm{C}}_{\mathrm{SER}}$, previously charged to ${\mathrm{V}}_{\mathrm{IN}}/2$ in phase 1, maintaining ${\displaystyle \frac{{\mathrm{V}}_{\mathrm{IN}}}{2}}-{\mathrm{V}}_{\mathrm{OUT}}$ across ${\mathrm{L}}_{\mathrm{B}}$. On phases 2 and 4, both ${\mathrm{L}}_{\mathrm{A}}$ and ${\mathrm{L}}_{\mathrm{B}}$ discharge. This control scheme allows the input voltage to first be halved at the inductor inputs. The input–output voltage regulation in the DSD control scheme is controlled by on-time by

$${\displaystyle \frac{{\mathrm{V}}_{\mathrm{OUT}}}{{\mathrm{V}}_{\mathrm{IN}}}}=2\times {\mathrm{T}}_{\mathrm{ON}}\times {\mathrm{f}}_{\mathrm{PWM}}$$

(1)

where ${\mathrm{f}}_{\mathrm{PWM}}$ is the switching frequency of the controller and ${\mathrm{T}}_{\mathrm{ON}}$ is the on-time of high side switches of a single control phase. The effective on-time for a given control frequency is effectively quadrupled, as the on-time is doubled for the halved input voltages of two control phases in the DSD buck converter, when compared to the conventional half-bridge buck converter control scheme. The extended effective on-time allows the DSD buck converter to operate at a much higher frequency while mitigating the overall switching power loss associated with a shorter on-time.

Figure 1. (a) The double step-down buck converter architecture and (b) its 4 control phases, with red and blue arrows indicating ${\mathrm{PWM}}_{\mathrm{A}}/{\mathrm{L}}_{\mathrm{A}}$ and ${\mathrm{PWM}}_{\mathrm{B}}/{\mathrm{L}}_{\mathrm{B}}$ sub-converter current flow respectively.

However, the four phase control scheme of the DSD buck converter sets up a restriction on the ${\mathrm{PWM}}_{\mathrm{A}}$ and ${\mathrm{PWM}}_{\mathrm{B}}$ sub-converters. Since the DSD buck converter relies on the alternating charging and discharging of the series capacitor ${\mathrm{C}}_{\mathrm{SER}}$ to enable the on-time extension, the on-times of the sub-converters cannot overlap [18]. Overlapping on-times of the sub-converters would also cause destructive voltage stress on the circuit, potentially destroying lower voltage switches used, and shorting ${\mathrm{V}}_{\mathrm{IN}}$ to the inductors and surging the voltage at the output, which could destroy the load circuitry [22,23,24]. In addition, the autonomous operation of the sub-converter stages is especially precarious in current mode control, as two inductors with no interdependence would need to be measured for their individual currents. Figure 2a shows a peak current mode (PCM) controller used in a DSD buck converter. ${\mathrm{PWM}}_{\mathrm{A}}$ and ${\mathrm{PWM}}_{\mathrm{B}}$ are controlled by two clock frequencies ${\mathrm{CLK}}_{\mathrm{A}}$ and ${\mathrm{CLK}}_{\mathrm{B}}$ with 180° phase separation, turning on the high side switch of the ${\mathrm{PWM}}_{\mathrm{A}}$ and ${\mathrm{PWM}}_{\mathrm{B}}$ sub-converters, respectively, allowing either ${\mathrm{L}}_{\mathrm{A}}$ or ${\mathrm{L}}_{\mathrm{B}}$ to charge up and push current into ${\mathrm{V}}_{\mathrm{OUT}}$, causing the voltage to rise. ${\mathrm{V}}_{\mathrm{OUT}}$ is compared with a reference voltage ${\mathrm{V}}_{\mathrm{REF}}$ through an error amplifier (EA) to generate the error voltage ${\mathrm{V}}_{\mathrm{error}}$, which is then compared with the inductor currents converted to voltages ${\mathrm{V}}_{\mathrm{sense},\mathrm{LA}}$ and ${\mathrm{V}}_{\mathrm{sense},\mathrm{LB}}$, with a slope compensation voltage ${\mathrm{V}}_{\mathrm{slope}}$ added on for stability, for the respective ${\mathrm{PWM}}_{\mathrm{A}}$ and ${\mathrm{PWM}}_{\mathrm{B}}$ sub-converters. As ${\mathrm{V}}_{\mathrm{OUT}}$ rises, once ${\mathrm{V}}_{\mathrm{error}}$ exceeds either inductor signals, the comparator swings high, resetting the SR latch, turning off the high side switch of the respective sub-converter and turning on the low side switch to allow the inductor to discharge and ${\mathrm{V}}_{\mathrm{OUT}}$ to fall. As the two inductors are measured separately and can be conducting different current levels concurrently, there is no mechanism to prevent one sub-converter from turning on while the other sub-converter is still on due to ${\mathrm{V}}_{\mathrm{error}}$ not reaching the sensed inductor current. Figure 2b shows the controller waveform and the ${\mathrm{V}}_{\mathrm{error}}$, ${\mathrm{V}}_{\mathrm{sense},\mathrm{LA}}$, and ${\mathrm{V}}_{\mathrm{sense},\mathrm{LB}}$ readings. Due to current mismatch, ${\mathrm{V}}_{\mathrm{error}}$ is unable to reach ${\mathrm{V}}_{\mathrm{sense},\mathrm{LA}}$ before ${\mathrm{CLK}}_{\mathrm{B}}$ turns ${\mathrm{PWM}}_{\mathrm{B}}$ on, causing phase overlap. This shows the inherent issue with applying current mode control to the DSD architecture DC–DC converter through conventional means. As current across the two inductors have to be separately measured, two controllers are necessary to control each sub-converter. In addition to that, when considering the silicon or board capacity for the PWM controller, complex circuitry is required to convert the inductor voltage into an accurate current reading. Since

$${\mathrm{I}}_{\mathrm{L}}={\displaystyle \frac{1}{\mathrm{L}}}\int {\mathrm{V}}_{\mathrm{L}}\mathrm{dt}$$

(2)

an integral process is required to obtain an accurate read of the inductor current, and any variations in the operating conditions of the DC–DC converter could cause inaccuracies in the integration process.

Figure 2. (a) Peak current mode (PCM) control of DSD buck converter using 2 autonomous sub-converters and (b) phase overlap from current mismatch.

A DSD current mode buck converter using a master–slave adaptive-on adaptive-off time control is proposed in [23] to counter this, by probing the current of the inductor in sub-converter ${\mathrm{PWM}}_{\mathrm{B}}$, and cloning the on- and off-time to sub-converter ${\mathrm{PWM}}_{\mathrm{A}}$ at exactly 180° phase offset. This method leverages the inherent negative feedback loop in the DSD buck converter associated with the alternating charge–discharge cycle of the series capacitor ${\mathrm{C}}_{\mathrm{SER}}$, wherein any current discrepancy between inductors would be directly countered a voltage difference between the two inductors in the opposite direction [25], though designs have incorporated further current balancing measures such as insurance, predicting controller unreliability and other external circumstances [26,27]. Since any current discrepancy between the inductors would be naturally corrected, it stands to reason that the current through ${\mathrm{L}}_{\mathrm{A}}$ would be an accurate representation of the current through ${\mathrm{L}}_{\mathrm{B}}$ [23], with discrepancy from load transients, supply transients, or changes in operating conditions notwithstanding, as such discrepancies would be quickly corrected by the DSD architecture itself so long as both sub-converters continue conducting during transients. Of course, a controller that can provide a full picture of circuit operations at any given moment, transient or not, would serve as a more ideal controller. However, such a controller would need to probe both inductors without resorting to separate controllers for the individual sub-converters.

2.2. Time-Based Current Mode Controller for Double Step-Down Buck Converter

For a full picture of the inductor currents for both sub-converters in the DSD buck converter, a time-based current mode controller is proposed as in Figure 3a. ${\mathrm{V}}_{\mathrm{OUT}}$ is fed into two voltage-controlled oscillators (VCOs), represented in the diagram as a voltage sum and an oscillator. The first VCO ${\mathrm{VCO}}_{\mathrm{RES}}$ generates its frequency from the error between ${\mathrm{V}}_{\mathrm{OUT}}$ and ${\mathrm{V}}_{\mathrm{L}+}$, the latter being the output of a multiplexer with signal inputs ${\mathrm{V}}_{\mathrm{LA}+}$ and ${\mathrm{V}}_{\mathrm{LB}+}$ and selector input ${\mathrm{VCO}}_{\mathrm{SET}}$, multiplied by its voltage-to-frequency ${\mathrm{K}}_{\mathrm{RES}}$. The second VCO ${\mathrm{VCO}}_{\mathrm{SET}}$ generates its frequency from the voltage error between ${\mathrm{V}}_{\mathrm{REF}}$ and ${\mathrm{V}}_{\mathrm{OUT}}$ multiplied by the voltage-to-frequency gain ${\mathrm{K}}_{\mathrm{SET}}$. This difference is also used in a phase adder for the output signal of ${\mathrm{VCO}}_{\mathrm{SET}}$, where the phase of the oscillator signals is shifted based on the error voltage. The oscillator signals are compared in a non-overlapping phase detector to generate for the buck converter signals. The PWM signal S and R controls the ${\mathrm{PWM}}_{\mathrm{A}}$ sub-converter, and the $\overline{\mathrm{S}}$ and $\overline{\mathrm{R}}$ signals controls the ${\mathrm{PWM}}_{\mathrm{B}}$ sub-converter.

Figure 3. Time-based DSD buck converter architecture in (a), and (b) ${\mathrm{V}}_{\mathrm{L}+}$ combination inductor feedback using inductor.

The time-based current mode converter compounds the two inductor currents into one controller by effectively summing the inductor currents together to treat them as a single inductor, facilitated by the specific operational features of both the DSD buck converter and time-based current mode control. Figure 3b shows the voltages of ${\mathrm{V}}_{\mathrm{L}+}$, ${\mathrm{V}}_{\mathrm{LA}+}$, and ${\mathrm{V}}_{\mathrm{LB}+}$ in steady state. ${\mathrm{V}}_{\mathrm{L}+}$ serves as an approximation of the sum of ${\mathrm{V}}_{\mathrm{LA}+}$ and ${\mathrm{V}}_{\mathrm{LB}+}$ and can be expressed as

$$\begin{array}{cc}\hfill {\mathrm{V}}_{\mathrm{L}+}\left(t\right)& ={\mathrm{V}}_{\mathrm{LA}+}\left(\mathrm{t}\right)\mathrm{for}\mathrm{t}=0\mathrm{to}\mathrm{t}={\displaystyle \frac{\mathrm{T}}{2}}\hfill \\ \hfill & ={\mathrm{V}}_{\mathrm{LB}+}\left(\mathrm{t}\right)\mathrm{for}\mathrm{t}={\displaystyle \frac{\mathrm{T}}{2}}\mathrm{to}\mathrm{t}=\mathrm{T}\hfill \end{array}$$

(3)

where T is the period of ${\mathrm{VCO}}_{\mathrm{SET}}$. ${\mathrm{VCO}}_{\mathrm{SET}}$ dictates which inductor voltage is being read by the current mode controller. While ${\mathrm{VCO}}_{\mathrm{SET}}$ is high, ${\mathrm{PWM}}_{\mathrm{A}}$ goes high and ${\mathrm{V}}_{\mathrm{LA}+}$ charges, and vice versa for ${\mathrm{PWM}}_{\mathrm{B}}$ and ${\mathrm{V}}_{\mathrm{LB}+}$ while ${\mathrm{VCO}}_{\mathrm{SET}}$ is low. The multiplexer ensures that ${\mathrm{V}}_{\mathrm{L}+}$ selection will always correspond to the on-phase of the corresponding sub-converter. Due to the non-overlapping on-time requirement of the DSD buck converter, there will be no point where both ${\mathrm{V}}_{\mathrm{LA}+}$ and ${\mathrm{V}}_{\mathrm{LB}+}$ are charging at the same time. This means, unless there is critical failure in the controller to prevent on-time overlap, the maximum sum of ${\mathrm{V}}_{\mathrm{LA}+}$ and ${\mathrm{V}}_{\mathrm{LB}+}$ at any given point is simply the voltage of whichever inductor is charging at the moment. Conversely, the off-times of the two sub-converters could overlap. However, the voltage of either inductor remains so close to ground as to be negligible in the sum of the inductor voltages, when compared to ${\mathrm{V}}_{\mathrm{IN}}/2$. As such, the sum of inductor voltages closely corresponds to the voltage of either inductor during their respective charging phases, making ${\mathrm{V}}_{\mathrm{L}+}$ effectively the combined positive terminal voltage of ${\mathrm{L}}_{\mathrm{A}}$ and ${\mathrm{L}}_{\mathrm{B}}$. In addition, since both inductors terminate at ${\mathrm{V}}_{\mathrm{OUT}}$ on the negative terminal, the voltage error between ${\mathrm{V}}_{\mathrm{L}+}$ and ${\mathrm{V}}_{\mathrm{OUT}}$ can accurately represent the sum of the voltages across ${\mathrm{L}}_{\mathrm{A}}$ and ${\mathrm{L}}_{\mathrm{B}}$. Next, ${\mathrm{VCO}}_{\mathrm{RES}}$ is controlled by the above stated error, making the frequency output of ${\mathrm{VCO}}_{\mathrm{RES}}$ the phase representation of the total inductor voltage. In [12], a time-based current mode buck converter is implemented by feeding the positive terminal voltage of the inductor directly to the VCO of the time-based controller. This control paradigm, which computes the controller signal through phase differences between the VCO signals, converts the voltage error into frequency difference in the VCO input stage. The phase of the VCO signal corresponds with the integral of the frequency. Hence, the phase of ${\mathrm{VCO}}_{\mathrm{RES}}$ can be understood as the following integration:

$$\begin{array}{cc}\hfill {\mathrm{\Phi }}_{\mathrm{RES}}\left(t\right)& =\int [{\omega }_{\mathrm{RES}}+{\mathrm{K}}_{\mathrm{RES}}\times ({\mathrm{V}}_{\mathrm{L}+}-{\mathrm{V}}_{\mathrm{OUT}})]\mathrm{dt}\hfill \\ \hfill & ={\omega }_{\mathrm{RES}}\times \mathrm{t}+{\mathrm{K}}_{\mathrm{RES}}\times \int ({\mathrm{V}}_{\mathrm{LA}+}-{\mathrm{V}}_{\mathrm{OUT}})+({\mathrm{V}}_{\mathrm{LB}+}-{\mathrm{V}}_{\mathrm{OUT}})\mathrm{dt}\hfill \\ \hfill & ={\omega }_{\mathrm{RES}}\times \mathrm{t}+{\mathrm{I}}_{\mathrm{LA}}+{\mathrm{I}}_{\mathrm{LB}}\hfill \end{array}$$

(4)

where ${\omega }_{\mathrm{RES}}$ is the free-running frequency of ${\mathrm{VCO}}_{\mathrm{RES}}$. The frequency of ${\mathrm{VCO}}_{\mathrm{RES}}$ hence represents the total inductor current across ${\mathrm{L}}_{\mathrm{A}}$ and ${\mathrm{L}}_{\mathrm{B}}$, acting as the current loop of the controller, with greater inductor current corresponding with higher ${\mathrm{VCO}}_{\mathrm{RES}}$ frequency. Meanwhile, the frequency of ${\mathrm{VCO}}_{\mathrm{SET}}$ is controlled by the voltage error between ${\mathrm{V}}_{\mathrm{REF}}$ and ${\mathrm{V}}_{\mathrm{OUT}}$, serving as the integral response of the voltage loop of the controller, with greater voltage error (or lower ${\mathrm{V}}_{\mathrm{OUT}}$) corresponding with higher ${\mathrm{VCO}}_{\mathrm{SET}}$ frequency. Next, the phase adder for ${\mathrm{VCO}}_{\mathrm{SET}}$ is also controlled by the ${\mathrm{V}}_{\mathrm{REF}}-{\mathrm{V}}_{\mathrm{OUT}}$ error voltage, and adds phase to the input frequency corresponding to the voltage error multiplied with the voltage-to-phase gain of the phase adder ${\mathrm{K}}_{\mathrm{P}+}$, serving as the proportional response for the voltage loop. The open loop gain of the controller can be expressed as a combination of the current and voltage loops, given by

$$\begin{array}{c}\hfill {\mathrm{H}}_{\mathrm{OL}}\left(\mathrm{s}\right)={\displaystyle \frac{{\widehat{\mathrm{v}}}_{\mathrm{i}}}{{\widehat{\mathrm{v}}}_{\mathrm{v}}}}={\mathrm{H}}_{\mathrm{i}}\left(\mathrm{s}\right)\times {\mathrm{H}}_{\mathrm{v}}\left(\mathrm{s}\right)\end{array}$$

(5)

where ${\widehat{\mathrm{v}}}_{\mathrm{i}}$ is the small signal response of the regulator due to the current loop, ${\widehat{\mathrm{v}}}_{\mathrm{v}}$ is the small signal response of the regulator due to the voltage loop, and ${\mathrm{H}}_{\mathrm{i}}\left(\mathrm{s}\right)$ and ${\mathrm{H}}_{\mathrm{v}}\left(\mathrm{s}\right)$ are the open loop gains of the current and voltage loops, respectively. They can each be expressed as

$$\begin{array}{c}\hfill {\mathrm{H}}_{\mathrm{v}}\left(\mathrm{s}\right)={\displaystyle \frac{{\widehat{\mathrm{\Phi }}}_{\mathrm{SET}}}{{\widehat{\mathrm{v}}}_{\mathrm{v}}}}={\mathrm{H}}_{\mathrm{PI}}\left(\mathrm{s}\right)=({\mathrm{K}}_{\mathrm{P}+}+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{SET}}}{\mathrm{s}}})\end{array}$$

(6)

$$\begin{array}{c}\hfill {\mathrm{H}}_{\mathrm{i}}\left(\mathrm{s}\right)={\displaystyle \frac{{\widehat{\mathrm{v}}}_{\mathrm{i}}}{{\widehat{\mathrm{\Phi }}}_{\mathrm{SET}}\times {\mathrm{H}}_{\mathrm{LC}}\left(\mathrm{s}\right)}}={\displaystyle \frac{\mathrm{s}\times {\mathrm{K}}_{\mathrm{PD}}}{\mathrm{s}+{\mathrm{K}}_{\mathrm{PD}}\times {\mathrm{K}}_{\mathrm{RES}}\times (1+{\mathrm{H}}_{\mathrm{LC}}\left(\mathrm{s}\right))}}\end{array}$$

(7)

$$\begin{array}{c}\hfill {\mathrm{H}}_{\mathrm{LC}}\left(\mathrm{s}\right)={\displaystyle \frac{{\mathrm{R}}_{\mathrm{OUT}}\times (1+{\mathrm{sC}}_{\mathrm{OUT}}{\mathrm{R}}_{\mathrm{esr}})}{{\mathrm{s}}^2{\mathrm{L}}_{\mathrm{A}+\mathrm{B}}{\mathrm{C}}_{\mathrm{OUT}}({\mathrm{R}}_{\mathrm{OUT}}+{\mathrm{R}}_{\mathrm{esr}})+\mathrm{s}({\mathrm{C}}_{\mathrm{OUT}}({\mathrm{R}}_{\mathrm{esr}}(1+{\mathrm{R}}_{\mathrm{DC}})+{\mathrm{R}}_{\mathrm{OUT}})}}\end{array}$$

(8)

where ${\mathrm{R}}_{\mathrm{DC}}$ and ${\mathrm{R}}_{\mathrm{esr}}$ are the parasitic resistances of the inductors ${\mathrm{L}}_{\mathrm{A}}$ and ${\mathrm{L}}_{\mathrm{B}}$ and the equivalent series resistance of the capacitor ${\mathrm{C}}_{\mathrm{OUT}}$, respectively, and ${\mathrm{L}}_{\mathrm{A}+\mathrm{B}}={\displaystyle \frac{{\mathrm{L}}_{\mathrm{A}}+{\mathrm{L}}_{\mathrm{B}}}{2}}$, with the multiplexer in the current loop in Figure 3a allowing for the two inductors to be averaged in the small signal analysis. In steady state, it can be assumed that ${\mathrm{L}}_{\mathrm{A}+\mathrm{B}}={\mathrm{L}}_{\mathrm{A}}={\mathrm{L}}_{\mathrm{B}}$ because of the current sharing property of the DSD buck converter. In the small signal analysis of the closed loop frequency response, the two sub-converters of the DSD buck converter can be effectively treated as a single half-bridge converter with no significant deviation in its performance. The dual loop control can be better understood with Figure 4 below.

Figure 4. Small signal model of the dual loop control scheme.

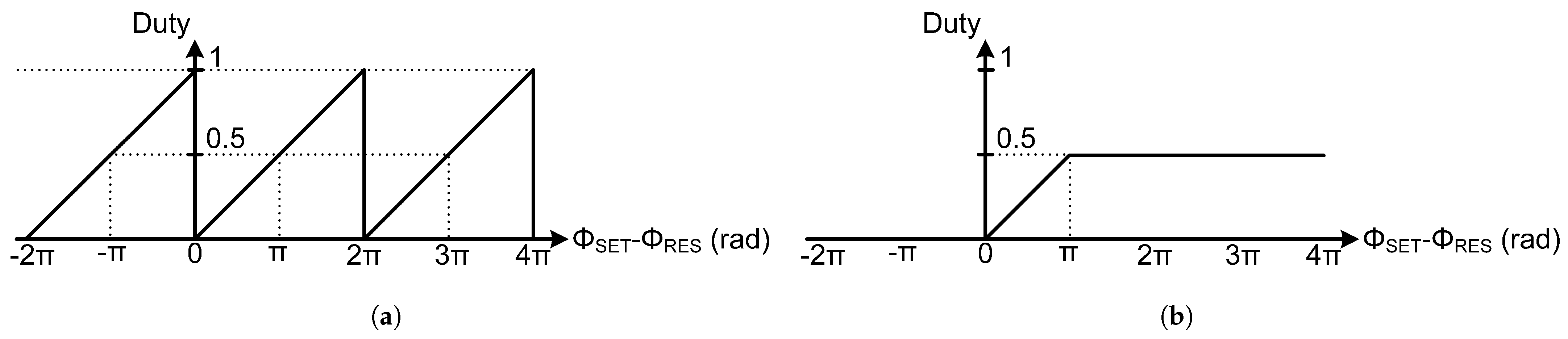
2.3. Conventional VCDL for Proportional Gain Response

In prior articles using time-based control for DC–DC converters, the VCDL is used to generate the proportional phase gain [2,3,5,6,7,8,12]. The VCDL generates a phase difference between the ${\mathrm{VCO}}_{\mathrm{SET}}$ and ${\mathrm{VCO}}_{\mathrm{RES}}$ frequencies by applying a time delay to both signals with a difference in delay in proportion to the voltage error between ${\mathrm{V}}_{\mathrm{FB}}$ and ${\mathrm{V}}_{\mathrm{REF}}$, using a chain of current-starving inverter cells, controlling the propagation delay between frequency input and output. Figure 5 shows the input-to-output effect of the differential VCDLs on the VCO signals with and without an error voltage. A fixed time delay ${\mathrm{t}}_{\mathrm{fixed}}$ is universally applied to both VCO frequencies in both cases, where a delay error of $\mathrm{\Delta }t$ between the frequencies is generated in response to some positive voltage error by delaying ${\mathrm{VCO}}_{\mathrm{SET}}$ by ${\mathrm{t}}_{\mathrm{fixed}}-\mathrm{\Delta }\mathrm{t}/2$, and delaying ${\mathrm{VCO}}_{\mathrm{RES}}$ by ${\mathrm{t}}_{\mathrm{fixed}}+\mathrm{\Delta }\mathrm{t}/2$. The fixed delay bounds the phase gain of the VCDL, where the maximum possible delay error between the VCO frequencies is

$$\begin{array}{c}\hfill \mathrm{\Delta }{\mathrm{t}}_{\max }=2\times {\mathrm{t}}_{\mathrm{fixed}}\end{array}$$

(9)

$\mathrm{\Delta }{\mathrm{t}}_{\max }$ is generally smaller than (9) purports in real VCDLs, as inverters have a minimum propagation delay. As such, should a time-based controller require a large proportional gain response to adequately compensate its closed loop, a fixed time delay of more than half the maximum delay error would be used, severely impacting the response time of the controller to transients, where a slow controller response would cascade into destabilizing the DC–DC converter, as the PWM duty cycle produced is responding to an output voltage state from multiple cycles ago rather than its current state. Time-based controllers in [2,3,12] mitigate this issue by operating the controller at high frequencies of 10 MHz to 25 MHz, where the required time delay for large proportional phase gain is much shorter. This restricts the application of time-based control to small, low-power, and minimal voltage conversion ratio applications, as switching losses are kept minimal when operating power regulators at high switching frequency in those applications. For slower switching frequency DC–DC converters, reference [14] introduced an infinite phase delay line to keep the time delay to a maximum of one oscillator cycle, and delays exceeding that simply skip that oscillator cycle entirely. This method, however, is incompatible with the DSD architecture as its current sharing feature [25] is only active when the controller consistently switches between the two sub-converter phases, allowing the series capacitor to share the stored charged between the two stages when current imbalances occur, and cycle skipping would compromise that during transient conditions. Hence, a proportional phase gain controller is introduced in this paper as a replacement to the VCDL, where the VCO signals are pulled forward differentially rather than delayed in proportion to the error voltage, so as to minimize the propagation delay between feedback and PWM signal.

Figure 5. VCDL phase delay (a) without voltage error and (b) with voltage error.

3. Circuit Implementation

In contrast with the modeled time-based converter in Figure 3, ${\mathrm{VCO}}_{\mathrm{SET}}$ and ${\mathrm{VCO}}_{\mathrm{RES}}$ are controlled differentially as shown in Figure 6, with both voltage and current loop inputs applied to both VCOs as transconductors (OTAs), with transconductance gains of ${\mathrm{G}}_{\mathrm{M},\mathrm{VI}}$ and ${\mathrm{G}}_{\mathrm{M},\mathrm{I}}$, respectively, controlling two current-controlled oscillators (CCOs). This is to maximize the control range of the control loop overall with the double-ended effect of differential feedback, as well as to share a common center frequency between the two VCOs, which prevents frequency mismatch over time. The differential phase adders utilize a second set of identical VCOs, as a pair of CCOs controlled by an OTA with ${\mathrm{G}}_{\mathrm{M},\mathrm{VP}}$ transconductance gain, with a cycle slip detector (CSD) that detects whether the ${\mathrm{CCO}}_{\mathrm{P}+}$ frequency leads or lags the ${\mathrm{CCO}}_{\mathrm{P}-}$ frequency. The resulting signals from both the differential VCOs and the phase adder are divided down with divide-by-32 frequency dividers before having their phase compared with a non-overlapping anti-slip phase detector (NOASPD) that generates complementary PWM signals ${\mathrm{PWM}}_{\mathrm{A}}$ and ${\mathrm{PWM}}_{\mathrm{B}}$ for the DSD buck converter. Because ${\mathrm{V}}_{\mathrm{LA}+}$ and ${\mathrm{V}}_{\mathrm{LB}+}$ can swing from ${\displaystyle \frac{{\mathrm{V}}_{\mathrm{IN}}}{2}}$, the feedback signals have to be divided by 10 using a resistive voltage divider to minimize the voltage swing detected by the current control loop, bounding the frequency range of the VCO pair and thus keeping the frequency deviation of the VCOs under control during one PWM switching cycle, allowing the NOASPD to keep accurate track of the VCO pair phase difference.

Figure 6. Differential time-based current mode control DSD buck converter.

3.1. Differential VCOs

Figure 7 shows the setup for the VCO input pair. Two CCOs made up of six current-starving differential inverter stages are used, with each stage consisting of twp main inverters and two complement-enforcing inverters. The CCO pair is current-starved using a pair of OTAs, tracking the ${\mathrm{V}}_{\mathrm{REF}}-{\mathrm{V}}_{\mathrm{FB}}$ voltage error for the voltage loop feedback and the ${\mathrm{V}}_{\mathrm{FB}}-{\mathrm{V}}_{\mathrm{L}+}$ voltage error for the current loop feedback. As current-starving frequency control throttles the voltage range of the frequency output, the VCO outputs are level shifted to swing from $V_{DD}$ to ground using an inverter. The VCOs operate at a 32 MHz center frequency, between 16 MHz and 66 MHz. The current mode frequency gain is set to 3.2 MHz/V, while the voltage mode frequency gain is 32 MHz/V.

Figure 7. Differential ring oscillators ${\mathrm{VCO}}_{\mathrm{SET}}$ and ${\mathrm{VCO}}_{\mathrm{RES}}$.

In using the combined current and voltage loop feedback in the differential VCOs, the current mode control is applied as such: the positive voltage error ${\mathrm{V}}_{\mathrm{REF}}-{\mathrm{V}}_{\mathrm{FB}}$ generates a frequency error between ${\mathrm{VCO}}_{\mathrm{SET}}$ and ${\mathrm{VCO}}_{\mathrm{RES}}$. This error causes phase error to build up between the VCO signals, resulting in larger PWM duty ratios. The PWM duty ratio translates to a positive increase in average voltage error between ${\mathrm{V}}_{\mathrm{FB}}$ and ${\mathrm{V}}_{\mathrm{L}+}$ during each switching cycle, modulating ${\mathrm{VCO}}_{\mathrm{SET}}$ and ${\mathrm{VCO}}_{\mathrm{RES}}$ to reduce in frequency error. This allows the voltage loop and current loop errors to converge and stabilize the output voltage. During load transients, a load current step up translates to an increase in frequency error due to the voltage loop, building up phase in the PWM duty ratio. The current loop then responds to push down the frequency error and converge the voltage loop error to correspond to the current demand.

This control paradigm means the controller converges the VCO frequencies not to minimize the output voltage error from the reference voltage, but rather to match the output voltage error to the prevailing load current. The control loop mismatch degrades the load regulation of the current mode controller. As such, the current mode gain in this circuit (3.2 MHz/V) has been minimized in relation to the voltage mode integral gain (32 MHz/V) while keeping it significant enough where the current loop is still observable in the controller dynamics. This mitigates the load regulation issue by keeping the voltage-error-to-load-current ratio adequately in relation to the expected load current range, such that a significant voltage error is not observed in the regular operation of the buck converter.

3.2. Frequency Difference Phase Adder (FDPA)

Figure 8 shows the model of the frequency difference phase adder (FDPA) circuit for proportional response gain. A pair of VCOs, ${\mathrm{VCO}}_{\mathrm{P}+}$ and ${\mathrm{VCO}}_{\mathrm{P}-}$, are identical to the integral/current loop VCOs. In this circuit, all 12 oscillator clock phases of the six-stage phase adder VCOs are used, converting their rising edges to pulses and compared in the cycle slip detector circuit, seen in Figure 9. The cycle slip detector consists of two sets of four D-latches, which are tasked with detecting when the phase difference between ${\mathrm{PULSE}}_{\mathrm{P}+}$ and ${\mathrm{PULSE}}_{\mathrm{P}-}$ goes above $2\pi$ radians or under $-2\pi$ radians, resulting in a LEAD or LAG signal being produced for each, respectively. LEAD swings to high whenever at least two simultaneous ${\mathrm{PULSE}}_{\mathrm{P}+}$ pulses are detected after one ${\mathrm{PULSE}}_{\mathrm{P}-}$ pulse before the next one is detected, while LAG swings to high whenever at least two simultaneous ${\mathrm{PULSE}}_{\mathrm{P}-}$ pulses are detected after one ${\mathrm{PULSE}}_{\mathrm{P}+}$ pulse is detected instead. In the case of the phase adder, the cycle slip detector is used on all 12 phases of the VCO stages, effectively checking for phase differences exceeding the $-{\displaystyle \frac{\pi }{6}}$ radian to ${\displaystyle \frac{\pi }{6}}$ radian range instead. Following the detection of a LEAD or LAG signal, a pulse is generated to be added to the frequency divider corresponding to ${\mathrm{VCO}}_{\mathrm{SET}}$ or ${\mathrm{VCO}}_{\mathrm{RES}}$, respectively, producing the ${\mathrm{DIV}}_{\mathrm{SET}}$ and ${\mathrm{DIV}}_{\mathrm{RES}}$ signals, with a center frequency of 1 MHz after frequency division.

Figure 8. Frequency difference phase adder (FDPA).

Figure 9. Cycle slip detector.

Phase is added to ${\mathrm{DIV}}_{\mathrm{SET}}$ and ${\mathrm{DIV}}_{\mathrm{RES}}$ by pulling forward the frequency division process of the respective VCOs using the cycle slip detector pulses. In Figure 10, the phase adder process is shown for the ${\mathrm{V}}_{\mathrm{REF}}-{\mathrm{V}}_{\mathrm{FB}}=0$ and ${\mathrm{V}}_{\mathrm{REF}}-{\mathrm{V}}_{\mathrm{FB}}>0$ conditions for the ${\mathrm{DIV}}_{\mathrm{SET}}$ frequency divider and its complementary signal. With zero voltage error in Figure 10a, the frequency divider detects no pulses from ${\mathrm{PULSE}}_{\mathrm{P}+}$ and so counts 16 ${\mathrm{VCO}}_{\mathrm{SET}}$ pulses before swinging ${\mathrm{DIV}}_{\mathrm{SET}}$ to high, and counts another 16 pulses before sending ${\mathrm{DIV}}_{\mathrm{SET}}$ back to low. The period of ${\mathrm{DIV}}_{\mathrm{SET}}$ is 32 times the period of ${\mathrm{VCO}}_{\mathrm{SET}}$, dividing the ${\mathrm{VCO}}_{\mathrm{SET}}$ frequency by 32. In the positive voltage error condition in Figure 10b, ${\mathrm{PULSE}}_{\mathrm{LEAD}}$ pulses are added to the frequency divider as well. After ${\mathrm{DIV}}_{\mathrm{SET}}$ goes low at the start of the count, four pulses are detected from ${\mathrm{PULSE}}_{\mathrm{LEAD}}$, moving the ${\mathrm{DIV}}_{\mathrm{SET}}$ rising edge up to $12\times {\mathrm{t}}_{\mathrm{VCO}}$ after the initial falling edge. Similarly for the complementary signal $\overline{{\mathrm{DIV}}_{\mathrm{SET}}}$, after its initial falling edge, another four pulses from ${\mathrm{PULSE}}_{\mathrm{LEAD}}$ are detected, similarly moving its rising edge up to $12\times {\mathrm{t}}_{\mathrm{VCO}}$. For the ${\mathrm{VCO}}_{\mathrm{RES}}$ to ${\mathrm{DIV}}_{\mathrm{RES}}$ division process, pulses from ${\mathrm{PULSE}}_{\mathrm{LAG}}$ will pull forward the rising edge of ${\mathrm{DIV}}_{\mathrm{RES}}$ during negative voltage error conditions instead.

Figure 10. Frequency difference phase adder operation during (a) no voltage error and (b) positive voltage error.

Figure 11 depicts the selector used to allocate the ${\mathrm{PULSE}}_{\mathrm{LEAD}}$ and ${\mathrm{PULSE}}_{\mathrm{LAG}}$ to the frequency dividers for the base or complementary signals. An initial pair of divide-by-32 frequency dividers using only the ${\mathrm{VCO}}_{\mathrm{SET}}$ and ${\mathrm{VCO}}_{\mathrm{RES}}$ generates ${\mathrm{CTRL}}_{\mathrm{SET}}$ and ${\mathrm{CTRL}}_{\mathrm{RES}}$ control signals and their respective complementary signals. Another four frequency dividers, using both the VCO and cycle slip detector pulses to perform frequency division, are controlled by the control signals. Taking the set signals as an example, while ${\mathrm{CTRL}}_{\mathrm{SET}}$ is high, the divider it controls is cleared, setting its output to low and barring it from counting any pulse. In the meantime, $\overline{{\mathrm{CTRL}}_{\mathrm{SET}}}$ is low, thus allowing it to accept either the ${\mathrm{VCO}}_{\mathrm{SET}}$ or ${\mathrm{PULSE}}_{\mathrm{LEAD}}$ signals, allowing it to start counting pulses up to 16. Once the total pulses from either add up to 16, $\overline{{\mathrm{DIV}}_{\mathrm{SET}}}$ is able to flip to high as the divider output goes high, and it remains high as $\overline{{\mathrm{CTRL}}_{\mathrm{SET}}}$ goes high to clear the divider output for $\overline{{\mathrm{DIV}}_{\mathrm{SET}}}$ due to the OR gate. It goes low only when $\overline{{\mathrm{CTRL}}_{\mathrm{SET}}}$ switches back to low, re-enabling the divider for $\overline{{\mathrm{DIV}}_{\mathrm{SET}}}$ to resume counting pulses. The reset signals would operate similarly, with ${\mathrm{VCO}}_{\mathrm{RES}}$ generating ${\mathrm{CTRL}}_{\mathrm{RES}}$ and $\overline{{\mathrm{CTRL}}_{\mathrm{RES}}}$ as control signals through the primary frequency divider, controlling the secondary frequency dividers that pull the ${\mathrm{DIV}}_{\mathrm{RES}}$ and $\overline{{\mathrm{DIV}}_{\mathrm{RES}}}$ signals forward based on ${\mathrm{VCO}}_{\mathrm{RES}}$ and ${\mathrm{PULSE}}_{\mathrm{RES}}$ pulses.

Figure 11. Pulse allocation circuit for phase addition to ${\mathrm{DIV}}_{\mathrm{SET}}$ or ${\mathrm{DIV}}_{\mathrm{RES}}$.

Applying proportional phase gain to the VCO signals using this frequency divider phase adder method allows the phase difference to be generated between VCO signals in proportion to the output voltage error without incurring any significant signal propagation delay, unlike the conventional VCDL method. In addition, by allocating the pulse calculation to opposite frequency dividers based on complementary control signals generated from the base VCO frequencies, the complementary divided signals for the sub-converters in the DSD buck converter can be generated concurrently, allowing the sub-converters to be controlled simultaneously through the same proportional phase gain controller. With this method, a proportional phase gain of $50\pi$ radians/V can be achieved to compensate the 1 MHz time-based controller with minimum signal propagation delay.

3.3. Non-Overlapping Anti-Slip Phase Detector

Figure 12 shows the non-overlapping anti-slip phase detector (NOASPD) used to generate the control signals for the eventual PWM output. It performs three main purposes: using ${\mathrm{DIV}}_{\mathrm{SET}}$ and $\overline{{\mathrm{DIV}}_{\mathrm{SET}}}$ signals to allocate the set and reset signals to ${\mathrm{PWM}}_{\mathrm{A}}$ and ${\mathrm{PWM}}_{\mathrm{B}}$ respectively; locking the PWM signals to full cycle on-time or full cycle off-time when the phase difference range is exceeded; and minimizing any possible overlap between the switching signals of the individual sub-converters. For the first task, ${\mathrm{DIV}}_{\mathrm{SET}}$ and $\overline{{\mathrm{DIV}}_{\mathrm{SET}}}$ are inputs for an SR latch with STATE and $\overline{\mathrm{STATE}}$ output, as ${\mathrm{DIV}}_{\mathrm{SET}}$, $\overline{{\mathrm{DIV}}_{\mathrm{SET}}}$, ${\mathrm{DIV}}_{\mathrm{RES}}$, and $\overline{{\mathrm{DIV}}_{\mathrm{RES}}}$ have their rising edges converted to pulses ${\mathrm{PULSE}}_{\mathrm{SET}}$ and ${\mathrm{PULSE}}_{\mathrm{RES}}$. When STATE is high, ${\mathrm{PULSE}}_{\mathrm{SET}}$ and ${\mathrm{PULSE}}_{\mathrm{RES}}$ control ${\mathrm{PWM}}_{\mathrm{A}}$, while they control ${\mathrm{PWM}}_{\mathrm{B}}$ when $\overline{\mathrm{STATE}}$ is high. This way, the switching frequencies of both sub-converters are controlled by the complementary ${\mathrm{DIV}}_{\mathrm{SET}}$, facilitating phase recovery during transients as the phase difference between set and reset signals fluctuate. This allows for consistent control of the ${\mathrm{V}}_{\mathrm{L}+}$ input from Figure 3a, where the charging phases of both inductors are aligned with the rising edges of ${\mathrm{DIV}}_{\mathrm{SET}}$ and $\overline{{\mathrm{DIV}}_{\mathrm{SET}}}$.

Figure 12. Non-overlapping anti-slip phase detector.

For the second task, the cycle slip detector from the phase adder circuit is once again used, this time to detect the phase difference between the ${\mathrm{DIV}}_{\mathrm{SET}}$ and ${\mathrm{DIV}}_{\mathrm{RES}}$ signals to ensure they do not exceed the $0<{\mathrm{\Phi }}_{\mathrm{SET}}-{\mathrm{\Phi }}_{\mathrm{RES}}<\pi$ range. Figure 13 shows the phase detector outputs of a typical phase detector in (a) alongside this NOASPD in (b). In typical phase detectors, when the phase difference between ${\mathrm{\Phi }}_{\mathrm{SET}}$ and ${\mathrm{\Phi }}_{\mathrm{RES}}$ goes below 0 radians or above 2$\pi$ radians, the phase detector loops around to the other side to 2$\pi$ radians and 0 radians, respectively. This would destabilize the PWM controller for the DC–DC converter, which relies on the accurate tracking of overall phase difference regardless of cycle slip. In addition, for the DSD buck converter, phase difference cannot exceed even $\left|\pi \right|$, since the PWM generated for either sub-converter would overlap. Hence, the NOASPD has a cycle slip detector with pulsed inputs of the rising edges of both base and complementary signals of ${\mathrm{DIV}}_{\mathrm{SET}}$ and ${\mathrm{DIV}}_{\mathrm{RES}}$, such that a slip detected would indicate phase difference exceeding $\pi$ radians.

Figure 13. Phase difference to duty ratio transfer function for phase detector (a) without slip detection and (b) with slip detection at $\pi$ radians.

Figure 14 depicts the cycle slip detector and $STATE/\overline{STATE}$ pulse allocation for both $+\pi$ radians and $-\pi$ radians cycle slip conditions. In (a), as two simultaneous ${\mathrm{PULSE}}_{\mathrm{SET}}$ are detected before the next ${\mathrm{PULSE}}_{\mathrm{RES}}$, the phase difference exceeds $+\pi$ radians, setting $1\pi$ to high, which locks ${\mathrm{PWM}}_{\mathrm{A}}$ and ${\mathrm{PWM}}_{\mathrm{B}}$ signals to ${\mathrm{PULSE}}_{\mathrm{SET},\mathrm{A}}$ and ${\mathrm{PULSE}}_{\mathrm{SET},\mathrm{B}}$ frequency, ensuring a maximum phase difference of $\pi$ radians between them. As the frequencies converges and the phase difference recovers, two simultaneous ${\mathrm{PULSE}}_{\mathrm{RES}}$ are detected before the next ${\mathrm{PULSE}}_{\mathrm{SET}}$, setting $>1\pi$ back down to low and PWM signals return below $\pi$ radian phase difference. Conversely, in (b), the two simultaneous ${\mathrm{PULSE}}_{\mathrm{RES}}$ detected before the next ${\mathrm{PULSE}}_{\mathrm{SET}}$ indicate phase difference slipping below $0\pi$, setting $<0\pi$ to high and stopping PWM signals from propagating altogether. After some time, two simultaneous ${\mathrm{PULSE}}_{\mathrm{SET}}$ are detected before the next ${\mathrm{PULSE}}_{\mathrm{RES}}$, indicating phase difference recovery, setting $<0\pi$ back to low, and PWM signals to propagate again.

Figure 14. Cycle slip detector behaviour when (a) phase difference exceeds 1 $\pi$ and (b) phase detector falls below 0 $\pi$

Finally, to enforce the non-overlapping requirement for ${\mathrm{PWM}}_{\mathrm{A}}$ and ${\mathrm{PWM}}_{\mathrm{B}}$ on-times, a dead time generator is applied at the end of the NOASPD, allowing time for either PWM signal to transition to low before the next PWM signal to transition from low to high. At the end of the NOASPD, ${\mathrm{PWM}}_{\mathrm{A}}$ and ${\mathrm{PWM}}_{\mathrm{B}}$ signals are inverted for control for the low side switches.

4. Post-Layout Simulation Results

This circuit is simulated in 130 nm BCD process in Cadence Virtuoso, with the time-based controller designed in the 1 V low-voltage domain and the power switches operating at 10 V ${\mathrm{V}}_{\mathrm{IN}}$. The power stage is simulated, with layout parasitic data extracted for the low-voltage domain controller and the DSD power stage switches, while the output filter is modeled using two $2.2$$\mathrm{\mu }$H inductors with 12 m$\mathrm{\Omega }$ DC resistance for the two sub-converter stages, a 22$\mathrm{\mu }$F output filter capacitor with 20 m$\mathrm{\Omega }$ equivalent series resistance, and three resistive voltage dividers of 50 k$\mathrm{\Omega }$ each, dividing the ${\mathrm{V}}_{\mathrm{LA}+}$, ${\mathrm{V}}_{\mathrm{LB}+}$, and ${\mathrm{V}}_{\mathrm{OUT}}$ by 10 for the VCO feedback. The active area is 1.068 mm × 0.402 mm, or 0.412 mm², as shown in Figure 15.

Figure 15. Active area of time-based control 10 V-to-1 V DSD buck converter, area of 0.412 mm².

Per the Figure 16 graph, the peak efficiency of the DSD buck converter is 82.2% at 0.4 A, when simulated across a range of 0.1 A to 2 A. The load regulation across that same load current range is 19.5 mV/A.

Figure 16. Efficiency and load regulation of DSD buck converter.

Figure 17 shows the frequency response of the unified DSD buck converter control loop. The control scheme used provides a unity gain bandwidth (UGBW) of 330 kHz and phase margin of 55.5 at ${\mathrm{R}}_{\mathrm{OUT}}=5$$\mathrm{\Omega }$.

Figure 17. Frequency response of the time-based controller.

Figure 18a,b show the transient response of the time-based DSD buck converter during loading and unloading steps of 0.2 A to 2.0 A loading and 2.0 A to 0.2 A unloading, respectively. During the 1.8 A current loading step in (a), voltage output experiences a 103.7 mV undershoot before settling to within 1% of the starting voltage level in 5.75 $\mathrm{\mu }$s, while during the 1.8 A current unloading step in (b), voltage output overshoots by 126.7 mV and settles in 9.9 $\mathrm{\mu }$s. The performance of the time-based current mode 10 V-to-1 V DSD buck converter is compared with similar time-based controller buck converters. Despite the tenfold reduction in switching frequency of the proposed time-based controller, along with the commensurate reduction in frequency response bandwidth as a result, the transient response of the DSD buck converter keeps within a similar <10 $\mathrm{\mu }$s response time for both loading and unloading step response seen in prior articles, while managing a significantly larger output LC filter with two inductors, a much larger current load, and an extreme 0.1 times voltage down-conversion step. Table 1 shows the performance of this voltage regulator in comparison with other time-based voltage regulators, while Table 2 compares its performance against other voltage regulators with extreme down-conversion steps. In comparison to other time-based voltage regulators, it can be seen that the transient response of this voltage regulator design is able to match the recovery time of regulators operating at much higher frequencies and with much smaller current steps. Meanwhile, its comparison against other extreme down-conversion voltage regulators show marked improvements in active area consumption, while managing to achieve the lower end of efficiency range of prior attempts in this area.

Figure 18. Simulated 1.8 A loading and unloading transients. (a) UP 0.2 A to 2.0 A; (b) DN 2.0 A to 0.2 A.

Table 1. Performance comparison (time-based controllers).

		JSSC 2015 [2]	TPE 2024 [6]	JSSC 2019 [12]	ESSCIRC 2023 [14]	This Work
Controller		Time-based Voltage Mode	Time-based Voltage Mode	Time-based Current Mode	Time-based Current Mode	Time-based Current Mode
Process		180 nm CMOS	180 nm BCD	65 nm CMOS	180 nm CMOS	130 nm BCD
Proportional Controller		VCDL	VCDL	VCDL	IPSDL	FDPA
${\mathrm{V}}_{\mathrm{IN}}$ (V)		1.8	5 to 36	1.8	3.3	10
${\mathrm{V}}_{\mathrm{OUT}}$ (V)		0.6 to 1.5	3.3	0.15 to 1.69	0.4 to 2.3	1
Step-Down Ratio		0.333 to 0.833	0.0917 to 0.66	0.0833 to 0.939	0.121 to 0.697	0.1
Switching Frequency (MHz)		11–25	1.5	10	2.5	1
Inductor/s ($\mathrm{\mu }$H)		0.22	4.7	0.22	1	2.2  ×  2
Output Capacitor ($\mathrm{\mu }$F)		4.7	30	4.7	4.7	22
Max $I_{load}$ (mA)		0.6	1	0.6	1	2
Transient Response	Current Step (A)	0.5	1	0.48	0.95	1.8
	UP Settling Time ($\mathrm{\mu }$s)	3	17	3.5	1.8	5.75
	DN Settling Time ($\mathrm{\mu }$s)	3.5	18	3.5	15.6	9.9

Table 2. Performance comparison (extreme step-down voltage regulators).

		JSSC 2022 [28]	TCAS-II 2022 [29]	JSSC 2020 [23]	JSSC 2021 [30]	APEC 2016 [31]	This Work
Architecture		DSD	DIHC	DSD	DIHC	Half-Bridge	DSD
Process		180 nm BCD	180 nm BCD	GaN HEMT	180 nm BCD + GaN HEMT	350 nm BCD	130 nm BCD
${\mathrm{V}}_{\mathrm{IN}}$ (V)		12	48	48	48	24	10
${\mathrm{V}}_{\mathrm{OUT}}$ (V)		1	1	1	1	1.2	1
Switching Frequency (MHz)		1	1	2	2.5	5	1
Inductor ($\mathrm{\mu }$H)		2 × 1.8	2 × 0.11	2 × 0.9	NA	0.68	2 × 2.2
Output Capacitor ($\mathrm{\mu }$F)		10	47	22	NA	18	22
Series Capacitors ($\mathrm{\mu }$F)		2.2	9 × 1	1	NA	NA	1
Peak Efficiency (%)		83.5	90.6	56.8	90.2	89.8	82.2
Active Area (mm2)		9.6	22	1.46	18.3	2.6	0.412
Transient Response	Current Step (A)	3	NA	1	5	1.8	1.8
	UP Settling Time ($\mathrm{\mu }$s)	1.6	NA	8.2	NA	5.1	5.75
	DN Settling Time ($\mathrm{\mu }$s)	NA	NA	8.4	NA	5.3	9.9

5. Conclusions

In this paper, a 10 V-to-1 V buck converter is presented, using a current mode controller operating in the time domain, implemented with only two pairs of VCOs, one pair used in an FDPA, an NOASPD, and a multiplexer, making the entire controller fully integratable in a silicon die with no large passives, on silicon or on board. By using the DSD architecture, the narrow on-time requirement of a buck converter performing a 0.1 times voltage step is extended, allowing the use of a moderately fast switching 1 MHz controller, improving the efficiency and transient response speed of the converter. The combination of VCO current mode feedback with the DSD buck converter architecture allows for the effective summation of two inductor currents for current mode control using only a multiplexer, massively simplifying current mode feedback of a two-phase two inductor buck converter. The proportional phase gain control is implemented using a minimum delay FDPA, with zero dependency on using signal delay to generate a phase difference for the PWM signal, improving transient response. By using an NOASPD, a maximum 50% duty cycle is enforced for both sub-converters of the DSD buck converter and phase detector cycle slip past the maximum/minimum phase is prevented, ensuring the stability of the buck converter. This circuit simulated in 130 nm BCD process is able to regulate a 1 V output voltage from a 10 V supply, at peak efficiency of 82.2% at 0.4 A load current, while having a maximum load current of 2 A. The DSD buck converter is able to recover from 1.8 A loading and unloading current steps in 5.75 $\mathrm{\mu }$s and 9.9 $\mathrm{\mu }$s, respectively.