Digital Twin-Enabled Decision Support in Mission Engineering and Route Planning
Abstract
:1. Introduction
Specific Contribution
2. Background and Literature Review
2.1. Digital Twin
2.2. Mission Engineering
2.3. Mission Planning
2.4. Model-Based Systems Engineering and Digital Twin
2.5. MagicGrid
2.6. UAS for Last Mile Delivery
2.7. Developing a System Model through Multi-Attribute Utility Theory
2.8. Route Selection Criteria
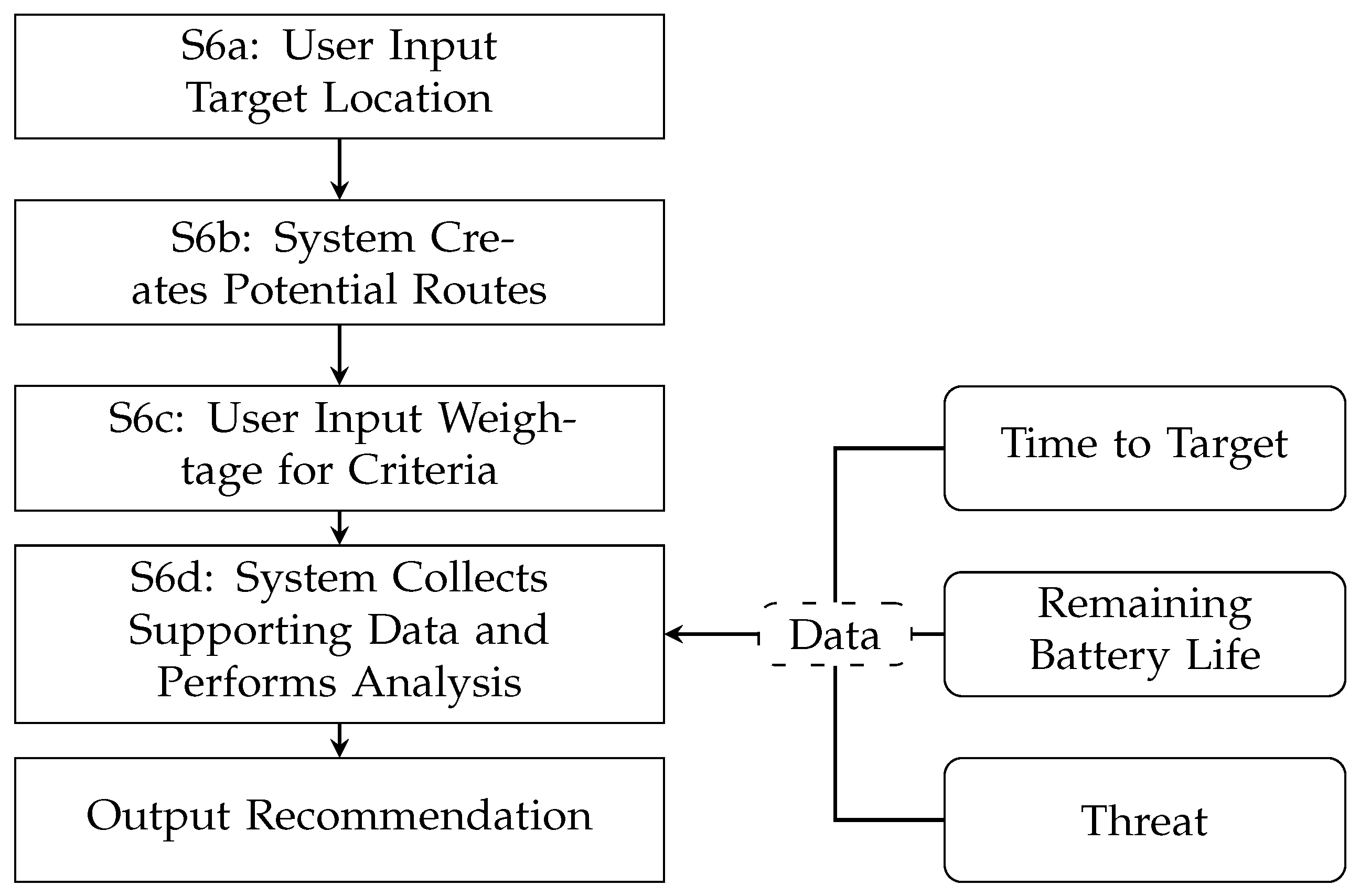
2.8.1. Time to Target
2.8.2. Probability of Hit
2.8.3. Remaining Battery life
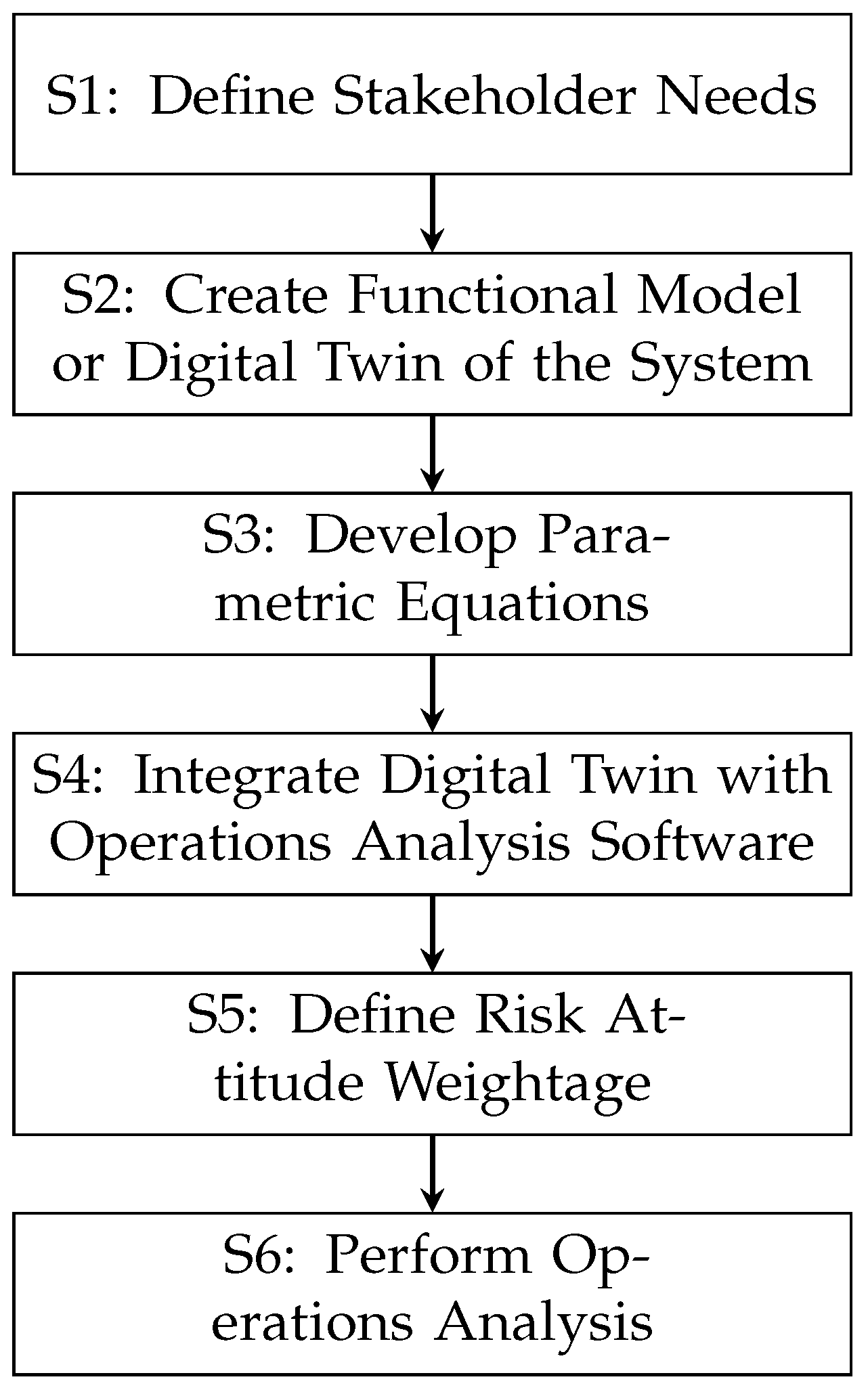
3. Method for the Development of a DT for Route Selection Decision Support
3.1. Step 1: Define Stakeholder Needs
3.2. Step 2: Create a Digital Twin of the System
3.3. Step 3: Develop Parametric Equation(s) for the Variable(s) of Interest
3.4. Step 4: Integration with Operations Analysis Software
3.5. Step 5: Define Risk Attitude Weightage
3.6. Step 6: Perform Operations Analysis
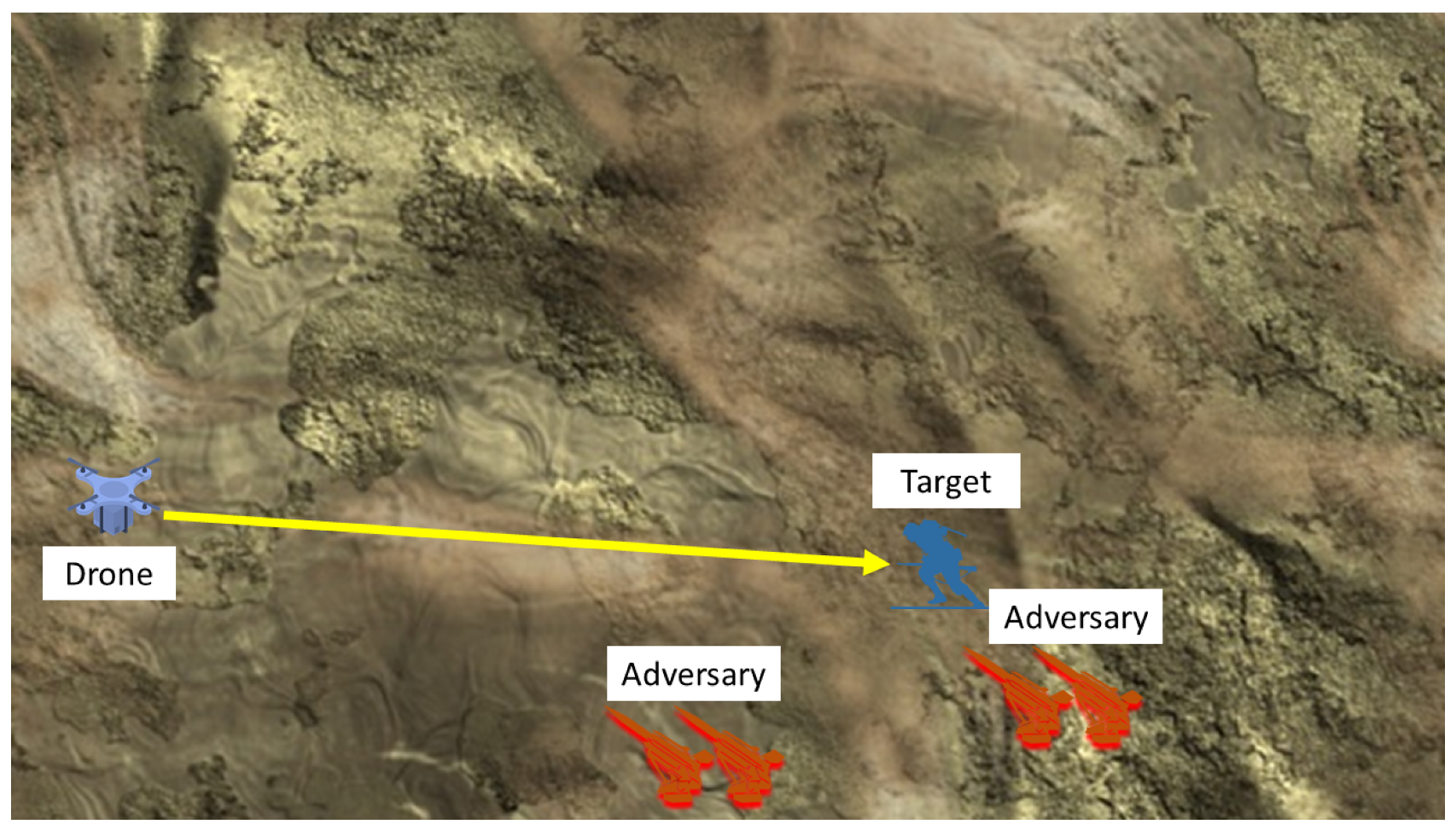
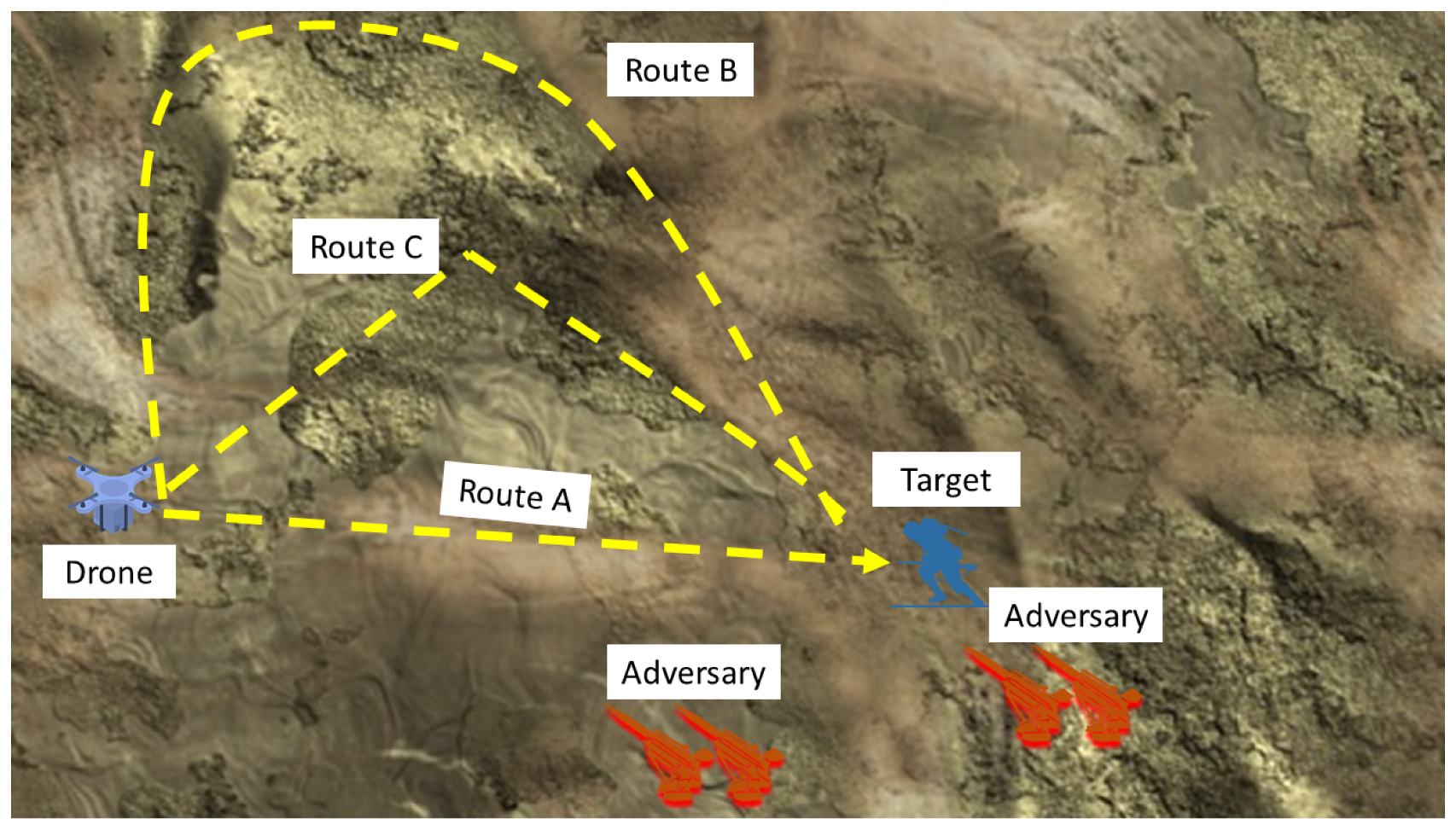
4. Case Study Model Development
5. Results
5.1. Step 1: Define Stakeholder Needs
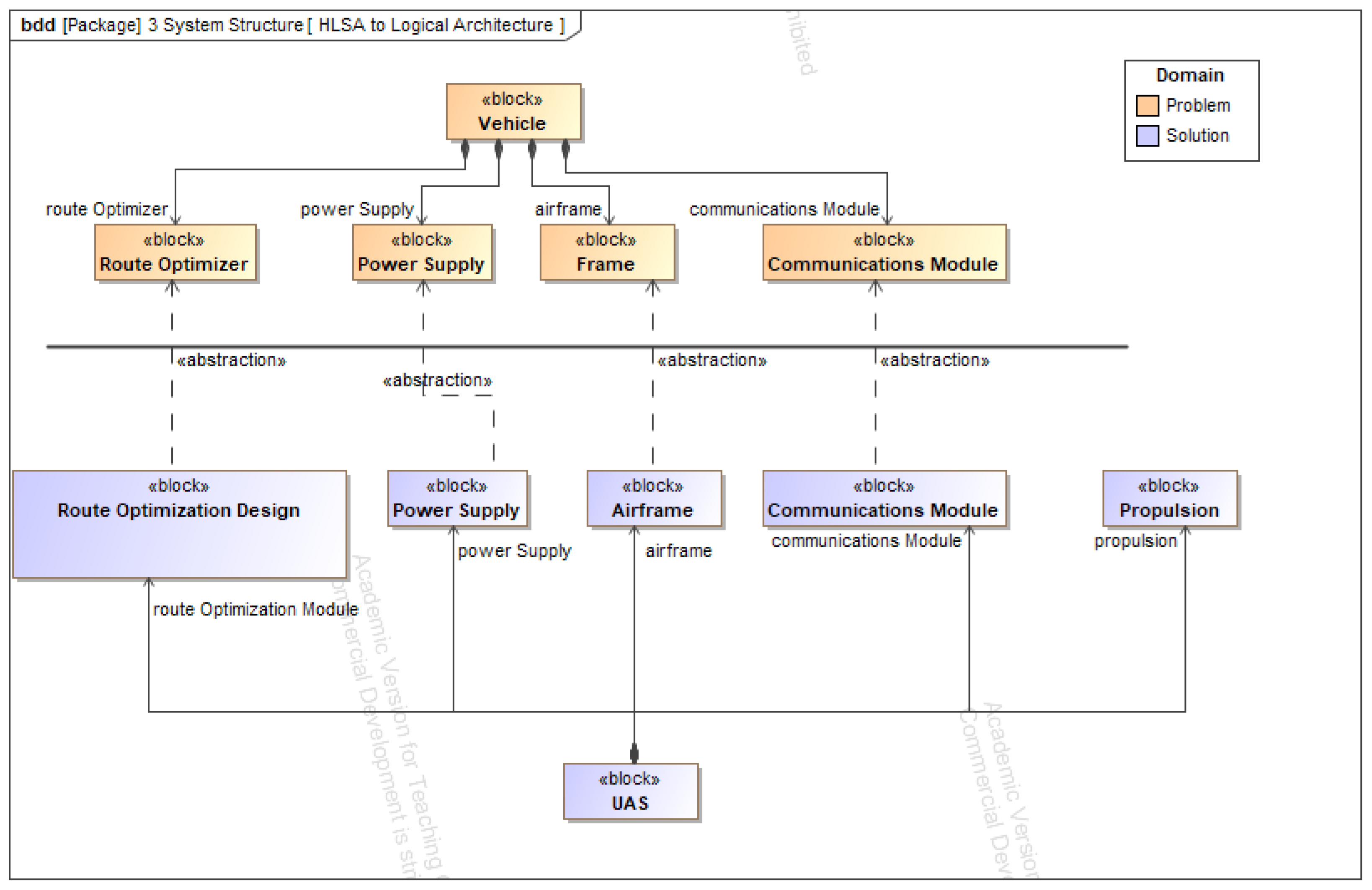
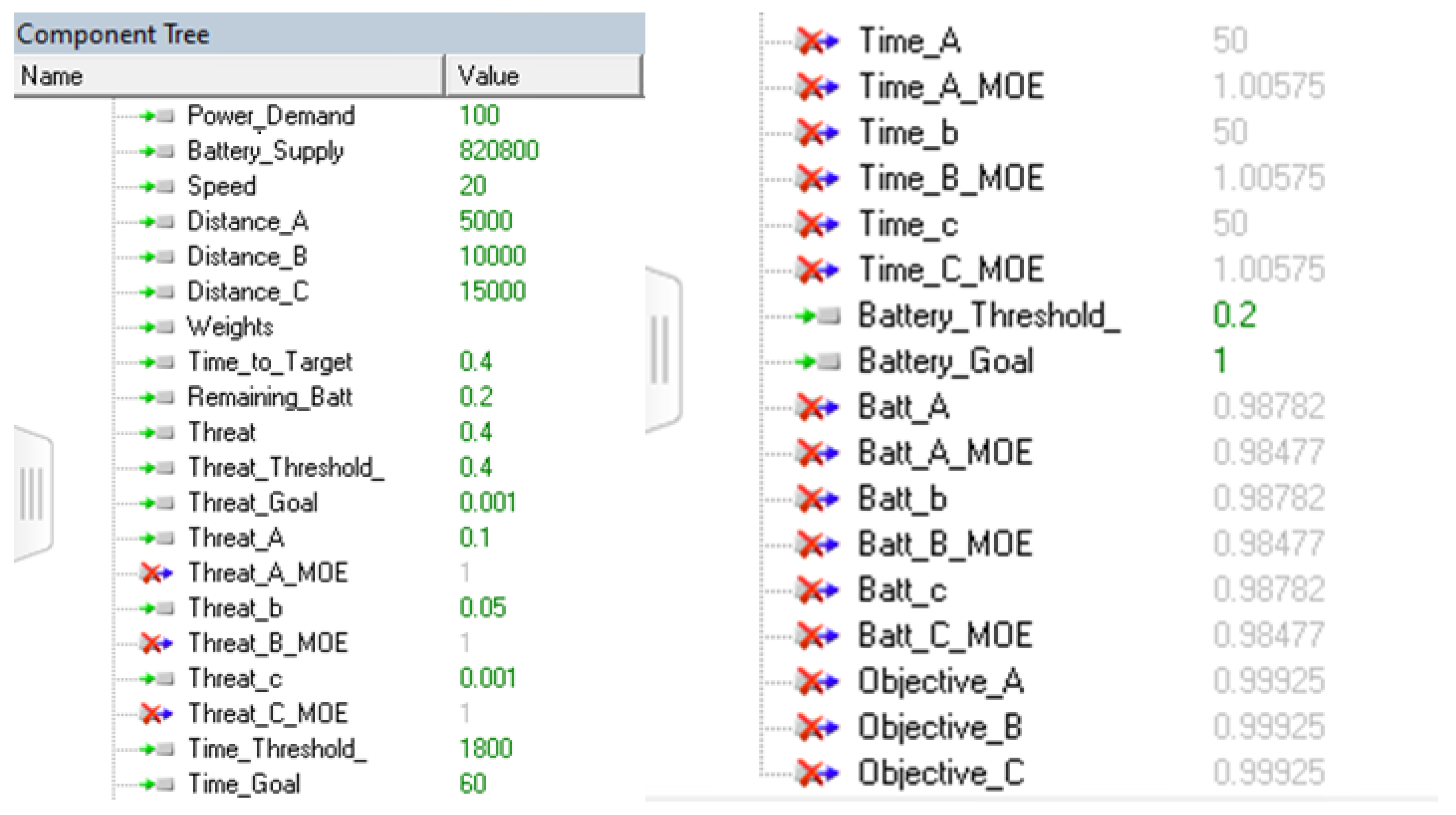
5.2. Step 2: Create a Digital Twin of the System
5.3. Step 3: Develop Parametric Equation(s) for the Variable(s) of Interest
5.4. Step 4: Integration with Operations Analysis Software
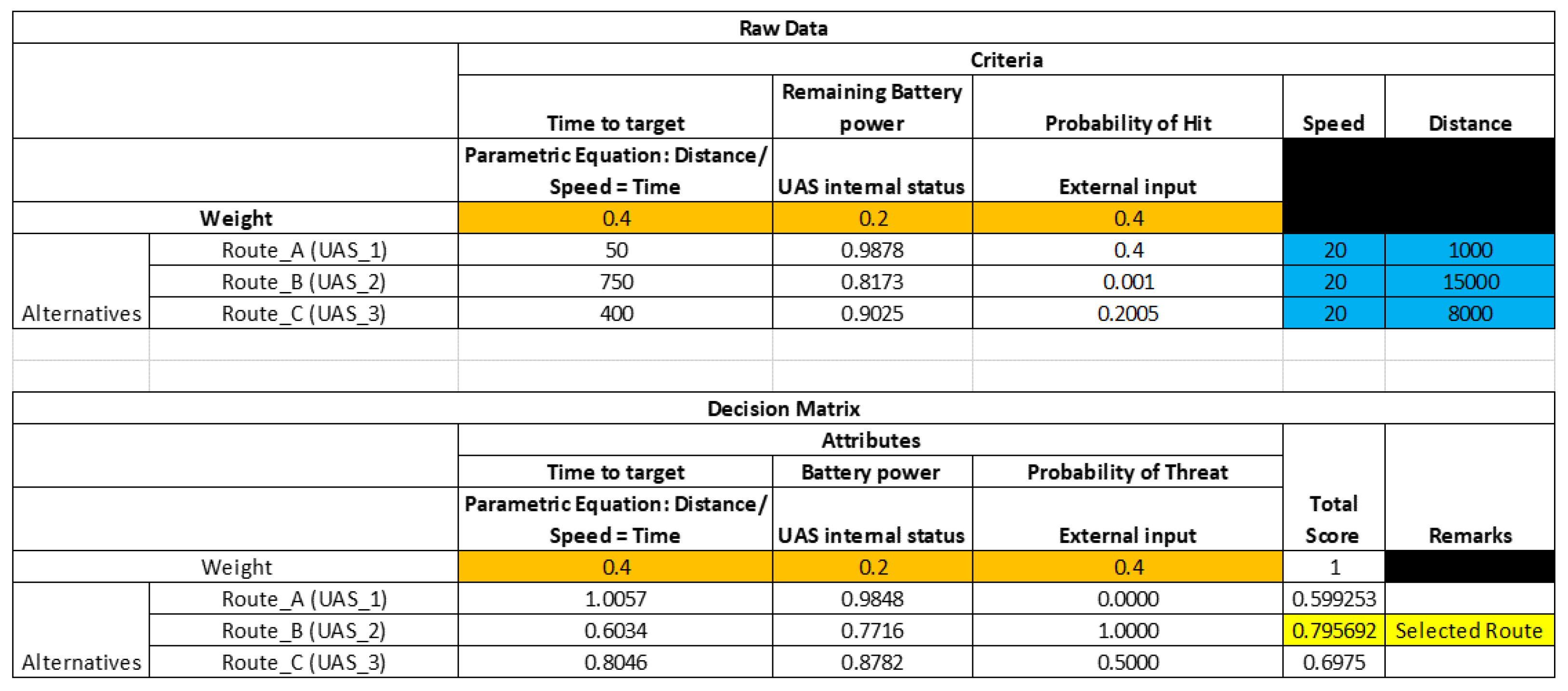
5.5. Step 5: Define Risk Attitude Weightage
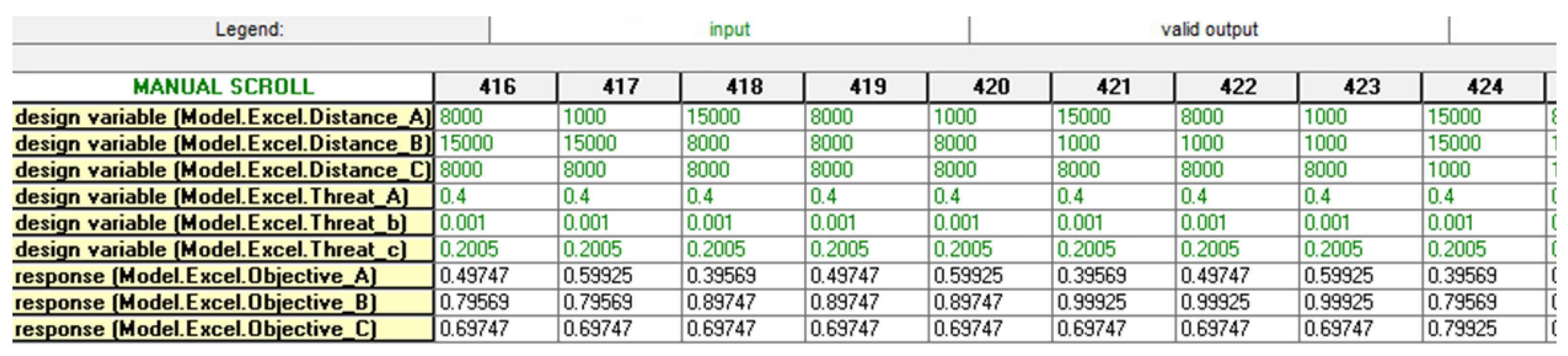
5.6. Step 6: Perform Operations Analysis
6. Discussion
Future Work
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations and Glossary
| AI | Artificial Intelligence is software that attempts to act rationally and mimic human responses [74]. In some communities, machine learning is preferred over artificial intelligence unless speaking about a general artificial intelligence that passes the Turing test [75]. |
| AIAA | American Institute of Aeronautics and Astronautics |
| AoA | Analysis Of Alternatives is defined by Georgiadis et al. as “… an analytical comparison of multiple alternatives to be completed prior to committing and investing costly resources to one project or decision” [76]. |
| DARPA | Defense Advanced Research Projects Agency |
| DoD | Department of Defense |
| DSTL | Defence Science and Technology Laboratory |
| DT | Digital Twin is a digital representation of a system, either under development or deployed, that can be used for many purposes throughout a system’s lifecycle [10]. See Section 2.1 for a detailed discussion of DT. |
| I4.0 | 4th Industrial Revolution is a convergence of digital, biological, and physical innovation. It can be seen as the blurring of boundaries between these domains, and spurs the proliferation of a wide array of technologies including IOT and AI among others [1,2,3]. |
| INCOSE | International Council on Systems Engineering |
| IOT | Internet-of-Things is defined by Atzori et al as “ a conceptual framework that leverages on the availability of heterogeneous devices and interconnection solutions, as well as augmented physical objects providing a shared information base on global scale, to support the design of applications involving at the same virtual level both people and representations of objects” [77]. |
| LMD | Last Mile Delivery in a military context is the distribution of supplies from the last point of bulk disaggregation to dispersed forces in the theater of operations [47]. |
| MAUT | Multiple Attribute Utility Theory is a method for decision-makers to compare performance metrics and to determine trade-offs between them [48]. As discussed by Dyer [49], MAUT provides an axiomatic foundation for decisions that involves several criteria. The axioms impart rationale for quantitative analysis of alternatives. The MAUT additive value model is widely used by practitioners when conducting multi-objective decision analysis [50]. |
| MBSE | Model-Based Systems Engineering is defined by INCOSE as “the formalized application of modelling to support system requirements, design, analysis, verification and validation activities beginning in the conceptual design phase and continuing throughout development and later life cycle phases” [38]. |
| MDMP | Military Decision Making Process is an analytical process that uses time-sensitive logical sequences to analyze a tactical situation to develop a range of potential options, compare the options, and down-select to the best option for the tactical situation. The selected option then becomes the tactical plan a commander implements via arranging forces (both people and machines such as UAS) both in time and space [53,78]. |
| ME | Mission Engineering is defined as the deliberate planning, analyzing, organizing, and integrating of current and emerging operational and system capabilities to achieve desired mission effects (warfighting, space mission scientific return, etc.) [23,24]. |
| MOE | Measure of Effectiveness is a way of establishing how well a system achieves its intended purpose and the system’s needs statement. Generally, an MOE looks at how a system performs externally. [79]. |
| MOP | Measure of Performance is a way of how well a system achieves internal performances characteristics [79]. |
| NASA | National Aeronautics and Space Administration |
| ODTF | Operationalized Digital Twin Framework is a proposed framework that categorizes critical phases of the DT architecting process into: (1) concept exploration, (2) preliminary design, (3) detailed design, (4) implementation, (5) test and evaluation, and (6) operations and maintenance [10]. |
| OMG | Object Management Group |
| OPM | Object Process Methodology is a method and modeling language to represent systems [80]. |
| PHM | Prognostic and Health Management is an approach to managing maintenance for a system using system data from embedded sensors and other system data streams, and algorithms to detect, assess, and monitor degrading health of a system; and predicts failure progression before it occurs so that condition-based maintenance can be scheduled [16,81]. |
| RTS | Returns To Scale is a mathematical description of long-run returns as the scale of production increases [82]. |
| SE | Systems Engineering |
| SOS | System of Systems is two or more systems that work together in some manner to achieve a common goal or mission [83]. |
| SysML | Systems Modeling Language is a modeling language and method derived from UML to represent systems especially for SE processes [84]. |
| UAS | Unmanned Aerial System is a flying system such as a quad copter, a fixed wing propeller driven aircraft, or other machine capable of sustained flight that is unmanned and generally contains some degree of autonomy. |
| UK | United Kingdom |
| UML | Unified Modeling Language is a modeling language used to represent systems (primarily software) [85]. |
| US | United States |
References
- Schwab, K. The Fourth Industrial Revolution; World Economic Forum: Geneva, Switzerland, 2016. [Google Scholar]
- Zoldan, A. The Fourth Revolution: Its Challenges For Businesses and Individuals. Forbes 2021. pp. 1–5. Available online: https://www.forbes.com/sites/forbesbusinesscouncil/2021/05/03/the-fourth-revolution-its-challenges-for-businesses-and-individuals/?sh=484b22db49bc (accessed on 1 August 2021).
- Li, G.; Hou, Y.; Wu, A. Fourth Industrial Revolution: Technological Drivers, Impacts and Coping Methods. Chin. Geogr. Sci. 2017, 27, 626–637. [Google Scholar] [CrossRef] [Green Version]
- Farrell, T.; Terriff, T. The Source of Military Change; Lynne Rienner Publishers: Boulder, CO, USA, 2002. [Google Scholar]
- Hoadley, D.S. Artificial Intelligence and National Security; Congressional Research Service: Washington, DC, USA, 2020.
- Barno, D.; Bensahel, N. War in the Fourth Industrial Revolution. War on the Rocks. 19 June 2018. Available online: https://warontherocks.com/2018/06/war-in-the-fourth-industrial-revolution/ (accessed on 1 August 2021).
- Green, M.D. Digital Engineering Strategy; Office of the Deputy Assistant Secretary: Washington, DC, USA, 2018.
- Dyer, J.S. MAUT—Multiattribute utility theory. In Multiple Criteria Decision Analysis: State of the Art Surveys; Springer: Berlin/Heidelberg, Germany, 2005; pp. 265–292. [Google Scholar]
- Aleksandraviciene, A.; Morkevicius, A. MagicGrid Book of Knowledge; Vitae Litera: Kaunas, Lithuania, 2018. [Google Scholar]
- Bickford, J.; Van Bossuyt, D.L.; Beery, P.; Pollman, A. Operationalizing digital twins through model-based systems engineering methods. Syst. Eng. 2020, 23, 724–750. [Google Scholar] [CrossRef]
- Glaessgen, E.H.; Stargel, D. The Digital Twin Paradigm for Future NASA and U.S. Air Force Vehicles. In Proceedings of the 53rd Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2012; pp. 1–14. [Google Scholar] [CrossRef] [Green Version]
- AIAA Digital Engineering Integration Committee. Digital Twin: Definition & Value. AIAA and AIA Position Paper. 2020. Available online: https://www.aia-aerospace.org/report/digital-twin-paper/ (accessed on 1 August 2021).
- Digital Twin Consortium. The Definition of a Digital Twin. Available online: https://www.digitaltwinconsortium.org/hot-topics/the-definition-of-a-digital-twin.htm (accessed on 1 August 2021).
- Boschert, S.; Heinrich, C.; Rosen, R. Next Generation Digital Twin. In Proceedings of the TMCE 2018, Las Palmas de Gran Canaria, Spain, 7–11 May 2018; pp. 209–218. [Google Scholar]
- Buchholz, S.; Briggs, B. Tech Trends 2020. Deloitte Insights, 7 January 2020. [Google Scholar]
- L’Her, G.; Van Bossuyt, D.L.; O’Halloran, B. Prognostic systems representation in a function-based Bayesian model during engineering design. Int. J. Progn. Health Manag. 2017, 8, 1–24. [Google Scholar] [CrossRef]
- Bachelor, G.; Brusa, E.; Ferretto, D.; Mitschke, A. Model-Based Design of Complex Aeronautical Systems Through Digital Twin and Thread Concepts. IEEE Syst. J. 2020, 14, 1568–1579. [Google Scholar] [CrossRef]
- Madni, A.M.; Madni, C.C.; Lucero, S.D. Leveraging Digital Twin Technology in Model-Based Systems Engineering. Systems 2019, 7, 7. [Google Scholar] [CrossRef] [Green Version]
- Kunath, M.; Winkler, H. Integrating the Digital Twin of the manufacturing system into a decision support system for improving the order management process. Procedia Cirp 2018, 72, 225–231. [Google Scholar] [CrossRef]
- West, S.; Stoll, O.; Meierhofer, J.; Züst, S. Digital Twin Providing New Opportunities for Value Co-Creation through Supporting Decision-Making. Appl. Sci. 2021, 11, 3750. [Google Scholar] [CrossRef]
- Hofmann, W.; Branding, F. Implementation of an IoT-and cloud-based digital twin for real-time decision support in port operations. IFAC-PapersOnLine 2019, 52, 2104–2109. [Google Scholar] [CrossRef]
- Korth, B.; Schwede, C.; Zajac, M. Simulation-ready digital twin for realtime management of logistics systems. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 4194–4201. [Google Scholar]
- Mission Engineering Guide; Office of the Deputy Director for Engineering; Office of the Under Secretary of Defense for Research and Engineering: Washington, DC, USA, 2020. Available online: https://ac.cto.mil/wp-content/uploads/2020/12/MEG-v40_20201130_shm.pdf (accessed on 5 July 2021).
- Eller, E. A mission operations and data analysis workforce model to aid mission engineering. In Proceedings of the Space Programs and Technologies Conference, Huntsville, AL, USA, 26–28 September 1995; p. 3820. [Google Scholar]
- Beam, D.F. Systems Engineering and Integration as a Foundation for Mission Engineering; NPS: Washington, DC, USA, 2015; pp. 1–63.
- Tulum, K.; Durak, U.; Yder, S.K. Situation aware UAV mission route planning. In Proceedings of the 2009 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–12. [Google Scholar]
- Biswas, S.; Anavatti, S.G.; Garratt, M.A. Multiobjective Mission Route Planning Problem: A Neural Network-Based Forecasting Model for Mission Planning. IEEE Trans. Intell. Transp. Syst. 2021, 22, 430–442. [Google Scholar] [CrossRef]
- Thompson, F.; Guihen, D. Review of mission planning for autonomous marine vehicle fleets. J. Field Robot. 2018, 36, 333–354. [Google Scholar] [CrossRef]
- Lamont, G.B.; Slear, J.N.; Melendez, K. UAV swarm mission planning and routing using multi-objective evolutionary algorithms. In Proceedings of the 2007 IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making, Honolulu, HI, USA, 1–5 April 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 10–20. [Google Scholar]
- Short, A.R.; Hodge, R.D.; Van Bossuyt, D.L.; DuPont, B. Active mission success estimation through functional modeling. Res. Eng. Des. 2018, 29, 565–588. [Google Scholar] [CrossRef]
- Short, A.R.; Van Bossuyt, D.L. Risk attitude informed route planning in a simulated planetary rover. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, MA, USA, 2–5 August 2015; American Society of Mechanical Engineers: New York, NY, USA,, 2015; Volume 57052, p. V01BT02A048. [Google Scholar]
- Sharma, S. Military route planning in battle field simulations for a multi-agent system. J. Comput. Methods Sci. Eng. 2010, 10, S97–S105. [Google Scholar] [CrossRef]
- Bate, S.; Stanley, K. Heuristic route planning: An application to fighter aircraft. In Proceedings of the IEEE 1988 National Aerospace and Electronics Conference, Dayton, OH, USA, 23–27 May 1988; IEEE: Piscataway, NJ, USA, 1988; pp. 1114–1120. [Google Scholar]
- Barth, C.D. Composite Mission Variable Formulation For Real-Time Mission Planning. Master’s Thesis, Massachusetts Institute Of Technology, Cambridge, MA, USA, 2001. [Google Scholar]
- Bruni, S.; Schurr, N.; Cooke, N.; Riordan, B.; Freeman, J. Designing a mixed-initiative decision-support system for multi-uas mission planning. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting, Las Vegas, NV, USA, 19–23 September 2011; SAGE Publications: Los Angeles, CA, USA, 2011; Volume 55, pp. 21–25. [Google Scholar]
- Tillman, F.; Lie, C.; Hwang, C. Simulation model of mission effectiveness for military systems. IEEE Trans. Reliab. 1978, 27, 191–194. [Google Scholar] [CrossRef]
- Machovina, B.J. Susceptibility Modeling and Mission Flight Route Optimization in a Low Threat, Combat Environment. Ph.D. Thesis, University of Denver, Denver, CO, USA, 2010. [Google Scholar]
- Object Management Group Wiki. Available online: https://www.omgwiki.org/MBSE/doku.php (accessed on 9 June 2021).
- McDermott, T.; Van Aken, E.; Hutchison, N.; Blackburn, M.; Clifford, M.; Zhongyuan, Y.; Chen, N.; Salado, A.; Henderson, K. Digital Engineering Metrics; Technical Report SERC-2020-TR-002; Stevens Institute of Technology: Hoboken, NJ, USA, 2020. [Google Scholar]
- Liu, M.; Fang, S.; Dong, H.; Xu, C. Review of digital twin about concepts, technologies, and industrial applications. J. Manuf. Syst. 2021, 58, 346–361. [Google Scholar] [CrossRef]
- Kalvit, K. Application of an Innovative MBSE (SysML-1D) Co-simulation in Healthcare. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 2018. [Google Scholar]
- Object Management Group. OMG Systems Modeling Language (OMG SysML) Version 1.6; Technical Report formal/19-11-01; Object Management Group: Needham, MA, USA, 2018. [Google Scholar]
- Menshenin, Y.; Mordecai, Y.; Crawley, E.F.; Cameron, B.G. Model-Based System Architecting and Decision-Making. In Handbook of Model-Based Systems Engineering; Springer: New York, NY, USA, 2021. [Google Scholar]
- ISO/IEC 15288. Systems and Software Engineering—System Life Cycle Processes; International Organization for Standardization: Geneva, Switzerland, 2015. [Google Scholar]
- Walden, D.D.; Roedler, G.J.; Forsberg, K.J.; Hamelin, R.D.; Shortell, T.M. (Eds.) INCOSE Systems Engineering Handbook: A Guide for System Life Cycle Processes and Activities; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Kapurch, S.J. NASA Systems Engineering Handbook; Diane Publishing: Collingdale, PA, USA, 2010. [Google Scholar]
- Thornton, S.; Gallasch, G.E. Swarming logistics for tactical last-mile delivery. In Proceedings of the International Conference on Science and Innovation for Land Power, Adelaide, Australia, 4–6 September 2018; Volume 2018. [Google Scholar]
- Youngblood, A.D.; Collins, T.R. Addressing Balanced Scorecard Trade-off Issues Between Performance Metrics Using Multi-Attribute Utility Theory. Eng. Manag. J. 2015, 15, 11–17. [Google Scholar] [CrossRef]
- Figueira, J.; Greco, S.; Ehrgott, M. Multiple Criteria Decision Analysis:State of the Art Surveys; Springer Science + Business Media, Inc.: New York, NY, USA, 2005. [Google Scholar]
- Parnell, G.S.; Trainor, T.E. Using the Swing Weight Matrix to Weight Multiple Objectives. In Proceedings of the INCOSE International Symposium, San Francisco, CA, USA, 31 January–3 February 2009; pp. 1–18. [Google Scholar] [CrossRef]
- Buede, D.M. The Engineering Design of Systems; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Figliozzi, M.A.; Tucker, C.; Polikakhina, P. Drone Deliveries Logistics, Efficiency, Safety and Last Mile Trade-offs. In Proceedings of the 7th International Conference on Information Systems, Logistics and Supply Chains, Lyon, France, 8–11 July 2018; pp. 1–12. [Google Scholar]
- Reese, P.P. Military Decision Making Process; Center for Army Lessons Learned: Fort Leavenworth, KS, USA, 2009. [Google Scholar]
- Harney, R.C. Combat Systems; NPS: Washington, DC, USA, 2004.
- Clamo, J. System Suitability. Syst. Surviv.-Slides 2021, 9, 1–30. [Google Scholar]
- Chan, C.W.; Kam, T.Y. A procedure for power consumption estimation of multi-rotor unmanned aerial vehicle. J. Phys. Conf. Ser. 2020, 1509, 012015. [Google Scholar] [CrossRef]
- Beery, P.; Paulo, E. Application of Model-Based Systems Engineering Concepts to Support Mission Engineering. Systems 2019, 7, 44. [Google Scholar] [CrossRef] [Green Version]
- Crawley, E.; Cameron, B.; Selva, D. System Architecture; Pearson Education Limited: Harlow, UK, 2016. [Google Scholar]
- Van Bossuyt, D.L.; O’Halloran, B.; Beery, P.T.; Hernandez, A. The Naval Postgraduate School’s Department of Systems Engineering Approach to Mission Engineering Education through Capstone Projects. Systems 2019, 7, 38. [Google Scholar] [CrossRef] [Green Version]
- Kaslow, D.; Soremekun, G.; Kim, H.; Spangelo, S. Integrated Model-Based Systems Engineering (MBSE) Applied to the Simulation of a CubeSat Mission. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2014; pp. 1–14. [Google Scholar]
- Chen, Y.C.; Graham, I. Rethinking the multi-attribute utility approach based procurement route selection technique. Constr. Manag. Econ. 2002, 20, 275–284. [Google Scholar] [CrossRef]
- Bonanne, K.H. A Model-Based Approach to System-of-Systems Engineering via the Systems Modeling Language. Master’s Thesis, Purdue University, Lafayette, IN, USA, 2014; pp. 1–12. [Google Scholar]
- Chadzynski, P.Z.; Willemsen, P.; Brown, B. Enhancing Automated Trade Studies using MBSE, SysML and PLM. In Proceedings of the 28th Annual INCOSE International Symposium, Washington, DC, USA, 7–12 July 2018; pp. 1–10. [Google Scholar]
- Arrow, K.J. A difficulty in the concept of social welfare. J. Political Econ. 1950, 58, 328–346. [Google Scholar] [CrossRef]
- Hazelrigg, G.A. The Implications of Arrow’s Impossibility Theorem on Approaches to Optimal Engineering Design. J. Mech. Des. 1996, 118, 161–164. [Google Scholar] [CrossRef]
- Scott, M.J.; Antonsson, E.K. Arrow’s theorem and engineering design decision making. Res. Eng. Des. 1999, 11, 218–228. [Google Scholar] [CrossRef]
- Mimlitz, Z.; Short, A.; Van Bossuyt, D.L. Toward Risk-Informed Operation of Autonomous Vehicles to Increase Resilience in Unknown and Dangerous Environments. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 50084, p. V01BT02A013. [Google Scholar]
- Short, A.R.; Mimlitz, Z.; Van Bossuyt, D.L. Autonomous system design and controls design for operations in high risk environments. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 50107, p. V02AT03A008. [Google Scholar]
- Seal, D. The Model-Based Engineering (MBE) Diamond: A Framework for Digital Transformation. In Proceedings of the ICOSE International Workshop, Torrance, CA, USA, 25–28 January 2020. [Google Scholar]
- Mordecai, Y.; Dori, D. Conceptual Modeling of System-Based Decision-Making. In Proceedings of the INCOSE International Symposium, Las Vegas, NV, USA, 30 June–3 July 2014; Wiley Online Library: Hoboken, NJ, USA, 2014; Volume 24, pp. 463–478. [Google Scholar]
- Struss, P. Model-Based Decision Support Systems-Conceptualization and General Architecture. In Proceedings of the International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, Kitakyushu, Japan, 21–24 July 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 588–600. [Google Scholar]
- Levi-Soskin, N.; Shaoul, R.; Kohen, H.; Jbara, A.; Dori, D. Model-based diagnosis with FTTell: Assessing the potential for pediatric failure to thrive (FTT) during the perinatal stage. In Proceedings of the EuroSymposium on Systems Analysis and Design, Gdansk, Poland, 19 September 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 37–47. [Google Scholar]
- Kohen, H.; Dori, D. Incorporating hardware-in-the-loop simulation into object-process methodology. In Proceedings of the 2020 IEEE International Systems Conference (SysCon), Montreal, QC, Canada, 24 August–20 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–8. [Google Scholar]
- Kok, J.N.; Boers, E.J.; Kosters, W.A.; Van der Putten, P.; Poel, M. Artificial intelligence: Definition, trends, techniques, and cases. Artif. Intell. 2009, 1, 270–299. [Google Scholar]
- Copeland, B.J. The turing test. Minds Mach. 2000, 10, 519–539. [Google Scholar] [CrossRef]
- Georgiadis, D.R.; Mazzuchi, T.A.; Sarkani, S. Using multi criteria decision making in analysis of alternatives for selection of enabling technology. Syst. Eng. 2013, 16, 287–303. [Google Scholar] [CrossRef]
- Atzori, L.; Iera, A.; Morabito, G. Understanding the Internet of Things: Definition, potentials, and societal role of a fast evolving paradigm. Ad Hoc Netw. 2017, 56, 122–140. [Google Scholar] [CrossRef]
- Marr, J.J. The Military Decision Making Process: Making Better Decisions Versus Making Decisions Better; Technical Report; Army Command and General Staff Coll Fort: Leavenworth, KS, USA, 2001. [Google Scholar]
- Sproles, N. Formulating measures of effectiveness. Syst. Eng. 2002, 5, 253–263. [Google Scholar] [CrossRef]
- Dori, D. Object-process methodology. In Encyclopedia of Knowledge Management, 2nd ed.; IGI Global: Hershey, PA, USA, 2011; pp. 1208–1220. [Google Scholar]
- Sheppard, J.W.; Kaufman, M.A.; Wilmering, T.J. IEEE standards for prognostics and health management. In Proceedings of the 2008 IEEE Autotestcon, Salt Lake City, UT, USA, 8–11 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 97–103. [Google Scholar]
- Soleimani-Damaneh, M. On a basic definition of returns to scale. Oper. Res. Lett. 2012, 40, 144–147. [Google Scholar] [CrossRef]
- Van Bossuyt, D.L.; O’Halloran, B.M.; Arlitt, R.M. A method of identifying and analyzing irrational system behavior in a system of systems. Syst. Eng. 2019, 22, 519–537. [Google Scholar] [CrossRef]
- Hause, M. The SysML modelling language. In Proceedings of the Fifteenth European Systems Engineering Conference, Valencia, Spain, 13–15 September 2006; Volume 9, pp. 1–12. [Google Scholar]
- Fowler, M. UML Distilled: A Brief Guide to the Standard Object Modeling Language; Addison-Wesley Professional: Boston, MA, USA, 2004. [Google Scholar]




| Systems Engineering Process | ODTF Process | MagicGrid Process |
|---|---|---|
| Concept Exploration | Identify primary purpose | Stakeholder needs |
| Identify DT algorithm Identify DT data input types Identify location of DT | System requirements Component requirements | |
| Preliminary Design | Define DT architecture Define DT digital thread Integrate DT requirement into physical design | Use cases Functional analysis Component behavior System context Logical subsystem comms Component structure |
| Identify source data Identify data storage requirement | Not specifically covered | |
| Not specifically covered | Measure of Effectiveness Component parameter |
| Criteria | Risk-Attitude Weightage |
|---|---|
| Time to Target | 0.4 |
| Remaining battery power | 0.2 |
| Probability of Hit | 0.4 |
| Sum | 1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, E.B.K.; Van Bossuyt, D.L.; Bickford, J.F. Digital Twin-Enabled Decision Support in Mission Engineering and Route Planning. Systems 2021, 9, 82. https://doi.org/10.3390/systems9040082
Lee EBK, Van Bossuyt DL, Bickford JF. Digital Twin-Enabled Decision Support in Mission Engineering and Route Planning. Systems. 2021; 9(4):82. https://doi.org/10.3390/systems9040082
Chicago/Turabian StyleLee, Eugene Boon Kien, Douglas L. Van Bossuyt, and Jason F. Bickford. 2021. "Digital Twin-Enabled Decision Support in Mission Engineering and Route Planning" Systems 9, no. 4: 82. https://doi.org/10.3390/systems9040082
APA StyleLee, E. B. K., Van Bossuyt, D. L., & Bickford, J. F. (2021). Digital Twin-Enabled Decision Support in Mission Engineering and Route Planning. Systems, 9(4), 82. https://doi.org/10.3390/systems9040082






