A Method to Account for Personnel Risk Attitudes in System Design and Maintenance Activity Development
Abstract
1. Introduction
Specific Contributions
2. Background and Related Research
2.1. System Availability
2.2. System Reliability
2.3. Maintenance Strategies
2.4. Supportability
2.5. Risk Attitudes of SOMs
2.6. Utility Theory
2.7. Contextualizing this Research within the Systems Engineering Process
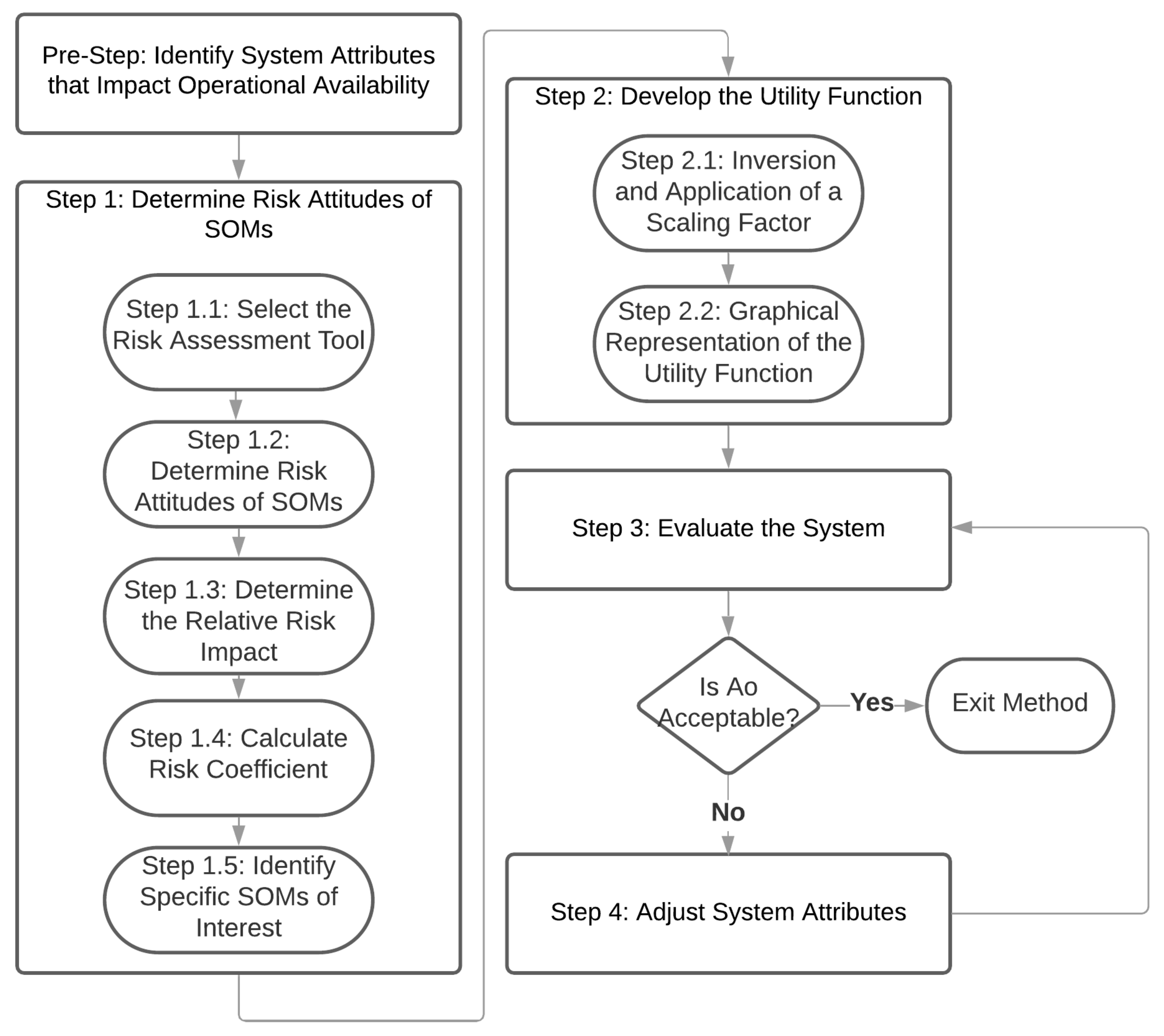
3. Methodology
3.1. Pre-Step: Identify System Attributes that Impact Operational Availability
3.2. Step 1: Determine Risk Attitudes of SOMs
3.2.1. Step 1.1: Select the Risk Assessment Tool
3.2.2. Step 1.2: Determine Risk Attitudes of SOMs
3.2.3. Step 1.3: Determine the Relative Risk Impact
3.2.4. Step 1.4: Calculate Risk Coefficient
3.2.5. Step 1.5: Identify Specific SOMs of Interest
3.3. Step 2: Develop the Utility Function
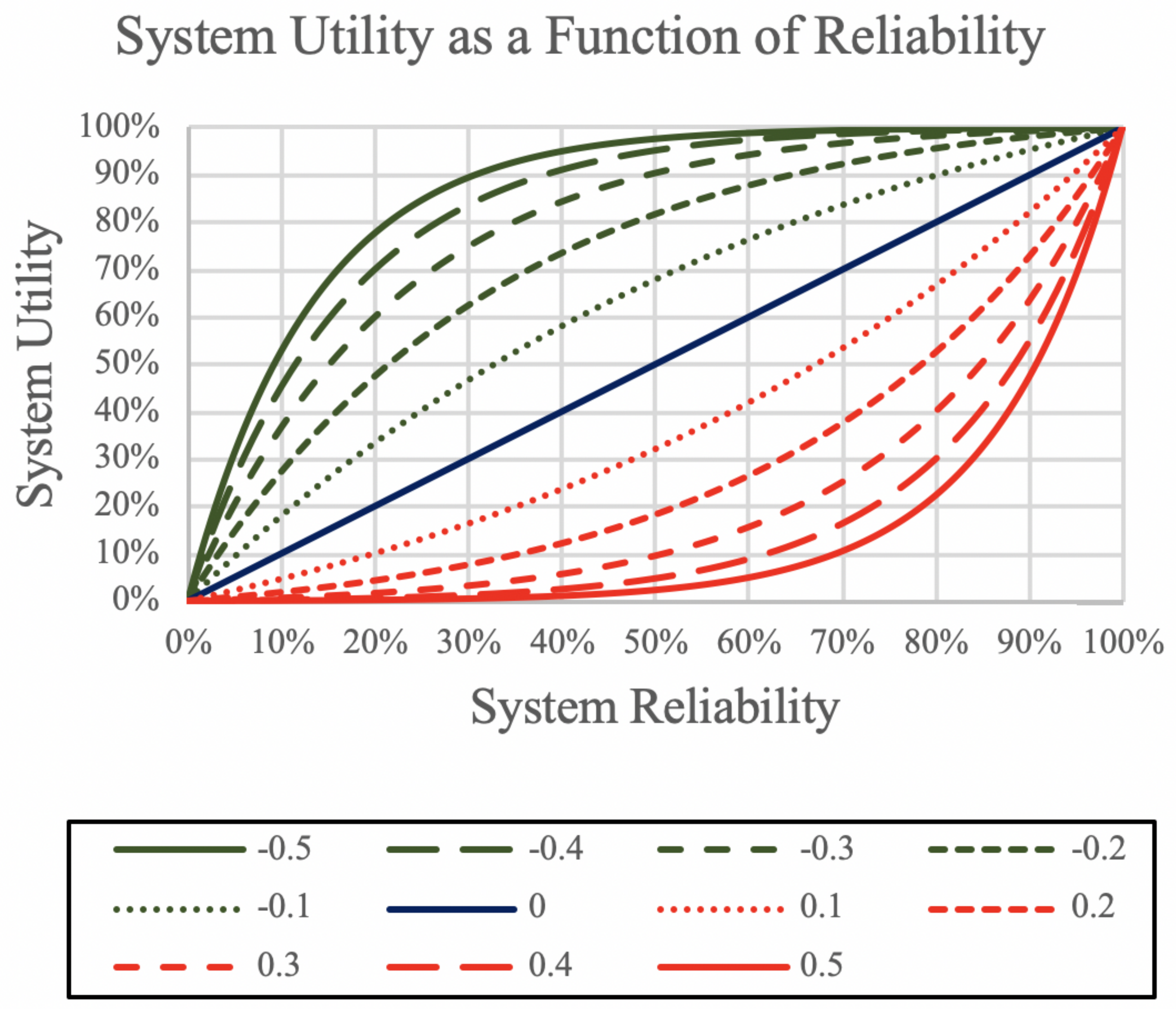
3.3.1. Step 2.1: Inversion and Application of a Scaling Factor
3.3.2. Step 2.2: Graphical Representation of the Utility Function
3.4. Step 3: Evaluate the System
3.5. Step 4: Adjust System Attributes
4. Example Implementation
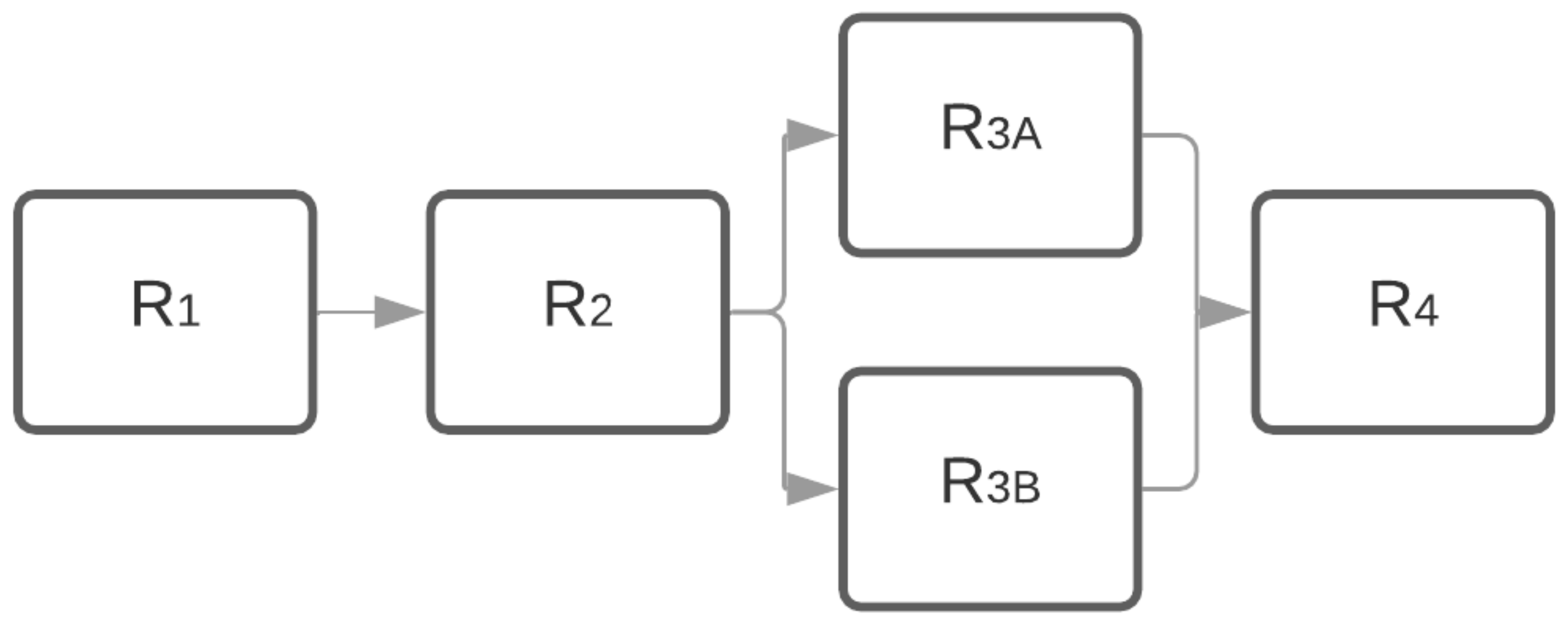
4.1. Pre-Step: Identify System Attributes that Impact Operational Availability
4.2. Step 1: Determine Risk Attitudes of SOMs
Step 1.1: Select the Risk Assessment Tool
4.3. Steps 1.2–1.5: A Summary
4.4. Step 2: Develop the Utility Function
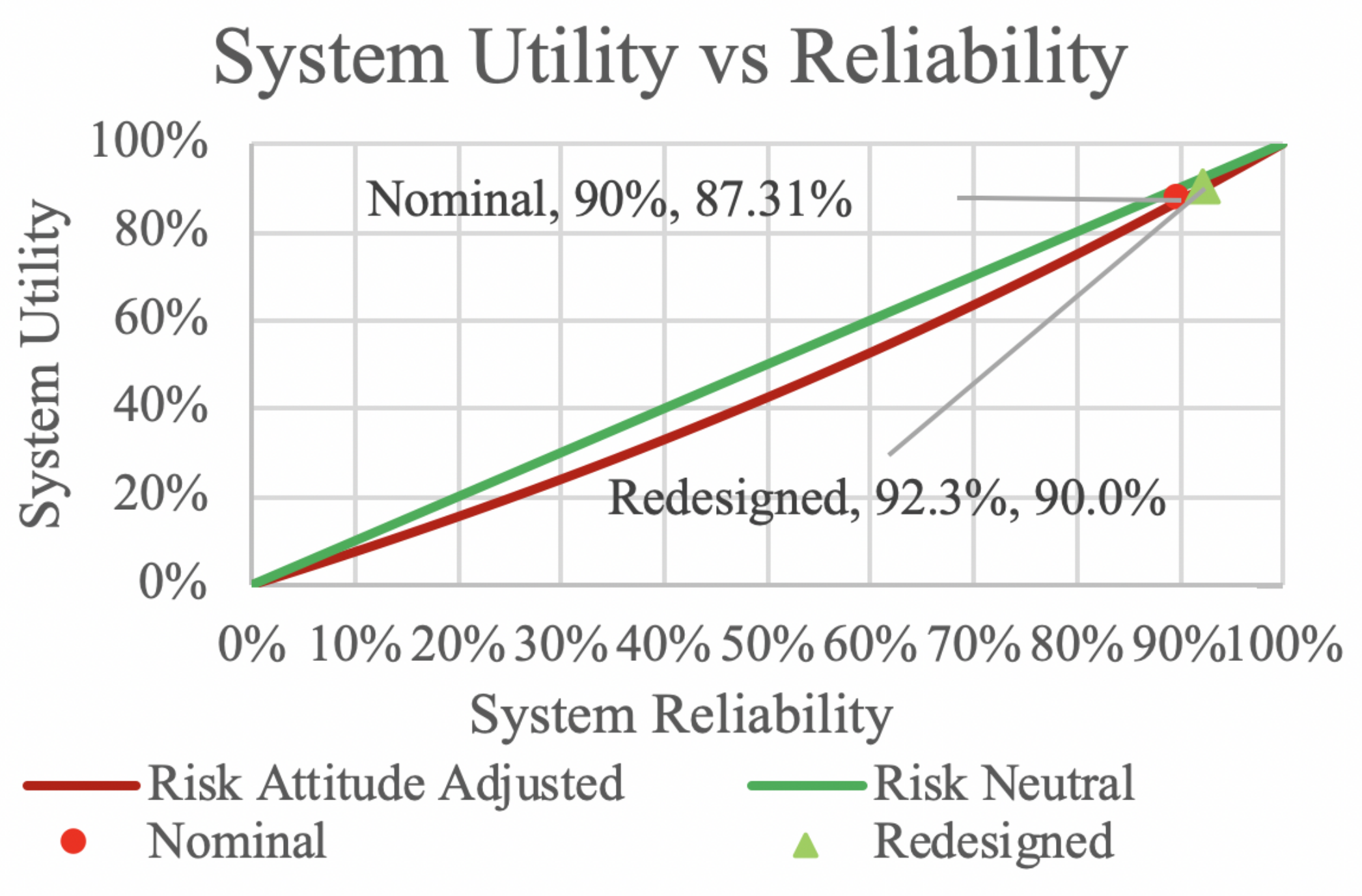
4.5. Step 3: Evaluate the System
4.6. Step 4: Adjust System Attributes
5. Discussion
6. Conclusions and Future Work
Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Waeyenbergh, G.; Pintelon, L. A framework for maintenance concept development. Int. J. Prod. Econ. 2002, 77, 299–313. [Google Scholar] [CrossRef]
- Rahman, A.; Kuswoyo, A.; Prabowo, A.R.; Suharyo, O.S. Developing strategy of maintenance, repair and overhaul of warships in support of navy operations readiness. J. ASRO 2020, 11, 146–151. [Google Scholar]
- Risk Management—Vocabulary; Guide; International Organization for Standardization: Geneva, Switzerland, 2009.
- University, D.A. Operational Availability Handbook: Introduction to Operational Availability; Technical Report; Reliability Analysis Center: Rome, NY, USA, 2001. [Google Scholar]
- Walden, D.D.; Roedler, G.J.; Forsberg, K.J.; Hamelin, R.D.; Shortell, T.M. (Eds.) INCOSE Systems Engineering Handbook: A Guide for System Life Cycle Processes and Activities, 4th ed.; Wiley: Hoboken, NJ, USA, 2015; ISBN 978-1118999400. [Google Scholar]
- Blanchard, B.; Fabrycky, W. Systems Engineering and Analysis; Prentice-Hall International Series in Industrial and Systems Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Pryor, G.A. Methodology for estimation of operational availability as applied to military systems. Int. Test Eval. Assoc. J. 2008, 29, 420–428. [Google Scholar]
- Pryor, G.A. Methodology for Estimation of Operational Availability as Applied to Military Systems; Technical Report; U.S. Army Training and Doctrine Command: Fort Leonard Wood, MO, USA, 2008. [Google Scholar]
- Manov, M.; Kalinov, T. Augmentation of ship’s operational availability through innovative reconditioning technologies. J. Phys. Conf. Ser. 2019, 1297, 012002. [Google Scholar] [CrossRef]
- Pham, H. Handbook of Reliability Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Whitelock, L. Methods used to improve reliability in military electronics equipment. In Papers and Discussions Presented at the Dec. 8–10, 1953, Eastern Joint AIEE-IRE Computer Conference: Information Processing Systems—Reliability and Requirements; Association for Computing Machinery: New York, NY, USA, 1953; pp. 31–33. [Google Scholar]
- Wang, W.; Loman, J.; Vassiliou, P. Reliability importance of components in a complex system. In Proceedings of the Annual Symposium Reliability and Maintainability, 2004-RAMS, Los Angeles, CA, USA, 26–29 January 2004; pp. 6–11. [Google Scholar]
- Guo, H.; Yang, X. A simple reliability block diagram method for safety integrity verification. Reliab. Eng. Syst. Saf. 2007, 92, 1267–1273. [Google Scholar] [CrossRef]
- Coit, D.W. Cold-standby redundancy optimization for nonrepairable systems. Iie Trans. 2001, 33, 471–478. [Google Scholar] [CrossRef]
- Amari, S.V.; Dill, G. Redundancy optimization problem with warm-standby redundancy. In Proceedings of the 2010 Proceedings-Annual Reliability and Maintainability Symposium (RAMS), San Jose, CA, USA, 25–28 January 2010; pp. 1–6. [Google Scholar]
- Hong, H.P.; Zhou, W.; Zhang, S.; Ye, W. Optimal condition-based maintenance decisions for systems with dependent stochastic degradation of components. Reliab. Eng. Syst. Saf. 2014, 121, 276–288. [Google Scholar] [CrossRef]
- Swanson, L. Linking maintenance strategies to performance. Int. J. Prod. Econ. 2001, 70, 237–244. [Google Scholar] [CrossRef]
- Fleischer, J.; Weismann, U.; Niggeschmidt, S. Calculation and optimisation model for costs and effects of availability relevant service elements. In Proceedings of the 13th CIRP International Conference on Life Cycle Engineering, Leuven, Belgium, 31 May–2 June 2006; pp. 675–680. [Google Scholar]
- Modarres, M.; Kaminskiy, M.P.; Krivtsov, V. Reliability Engineering and Risk Analysis: A Practical Guide; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Monga, A.; Zuo, M.J.; Toogood, R.W. Reliability-based design of systems considering preventive maintenance and minimal repair. Int. J. Reliab. Qual. Saf. Eng. 1997, 4, 55–71. [Google Scholar] [CrossRef]
- Gordon, S.; Merchant, G.S.; Crognale, S.J. Integrated Logistics Support Guide, 2nd ed.; Defense Systems Management College Press: Fort Belvior, VA, USA, 1994. [Google Scholar]
- Richardson, J.M. A design for maintaining maritime superiority. Nav. War Coll. Rev. 2016, 69, 4. [Google Scholar]
- Lynch, O. Reducing Logistics Delays Using the Supply Chain Criticality Index: A Diagnostic Approach. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2020. [Google Scholar]
- Kumar, U.D.; Knezevic, J. Supportability-critical factor on systems’ operational availability. Int. J. Qual. Reliab. Manag. 1998, 15, 366–376. [Google Scholar] [CrossRef]
- Van Bossuyt, D.L.; Dong, A.; Tumer, I.Y.; Carvalho, L. On measuring engineering risk attitudes. J. Mech. Des. 2013, 135. [Google Scholar] [CrossRef]
- Van Bossuyt, D.L.; Beery, P.; O’Halloran, B.M.; Hernandez, A.; Paulo, E. The Naval Postgraduate School’s Department of Systems Engineering Approach to Mission Engineering Education through Capstone Projects. Systems 2019, 7, 38. [Google Scholar] [CrossRef]
- Booher, H.R.; Minninger, J. Human systems integration in army systems acquisition. In Handbook of Human Systems Integration; John Wiley Sons: Hoboken, NJ, USA, 2003; pp. 663–698. [Google Scholar]
- Perrow, C. The organizational context of human factors engineering. Adm. Sci. Q. 1983, 28, 521–541. [Google Scholar] [CrossRef]
- Dhillon, B.S. Human Reliability, Error, and Human Factors in Engineering Maintenance: With Reference to Aviation and Power Generation; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Gertman, D.; Blackman, H.; Marble, J.; Byers, J.; Smith, C. The SPAR-H human reliability analysis method. US Nucl. Regul. Comm. 2005, 230, 35. [Google Scholar]
- Wickens, C.D.; Hollands, J.G.; Banbury, S.; Parasuraman, R. Engineering Psychology and Human Performance; Psychology Press: Hove, UK, 2015. [Google Scholar]
- Van Bossuyt, D.; Hoyle, C.; Tumer, I.Y.; Dong, A. Risk attitudes in risk-based design: Considering risk attitude using utility theory in risk-based design. AI EDAM 2012, 26, 393–406. [Google Scholar] [CrossRef]
- Blais, A.R.; Weber, E.U. A domain-specific risk-taking (DOSPERT) scale for adult populations. Judgm. Decis. Mak. 2006, 1, 33–47. [Google Scholar]
- Masclet, D.; Colombier, N.; Denant-Boemont, L.; Loheac, Y. Group and individual risk preferences: A lottery-choice experiment with self-employed and salaried workers. J. Econ. Behav. Organ. 2009, 70, 470–484. [Google Scholar] [CrossRef]
- Highhouse, S.; Nye, C.D.; Zhang, D.C.; Rada, T.B. Structure of the Dospert: Is there evidence for a general risk factor? J. Behav. Decis. Mak. 2017, 30, 400–406. [Google Scholar] [CrossRef]
- Pennings, J.M.; Smidts, A. Assessing the construct validity of risk attitude. Manag. Sci. 2000, 46, 1337–1348. [Google Scholar] [CrossRef]
- Van Bossuyt, D.L.; Tumer, I.Y.; Wall, S.D. A case for trading risk in complex conceptual design trade studies. Res. Eng. Des. 2013, 24, 259–275. [Google Scholar] [CrossRef]
- Roberts, K.H. Managing high reliability organizations. Calif. Manag. Rev. 1990, 32, 101–113. [Google Scholar] [CrossRef]
- Watson, J. Hundreds of Sailors Fight to Save U.S.S. Bonhomme Richard Before Fire Reaches Fuel Tanks. 2020. Available online: https://time.com/5866576/uss-bonhomme-richard-fire-damage/ (accessed on 25 July 2020).
- Youssef, N.A. With USS Bonhomme Richard Fire Extinguished, Navy Turns to Inquiry of Blaze’s Spread. 2020. Available online: https://www.wsj.com/articles/with-uss-bonhomme-richard-fire-extinguished-navy-turns-to-inquiry-of-blazes-spread-11594938399 (accessed on 25 July 2020).
- Vanden Brook, T. Fire Extinguished Aboard USS Bonhomme Richard after Raging for 4 Days. 2020. Available online: https://www.usatoday.com/story/news/politics/2020/07/16/fire-extinguished-navys-bonhomme-richard-after-four-days/5453829002/ (accessed on 25 July 2020).
- Associated Press. Man Who Set Fire to Nuclear Submarine Gets 17 Years. 2013. Available online: https://www.usatoday.com/story/news/nation/2013/03/15/nuclear-submarine-fire/1990663/ (accessed on 25 July 2020).
- Maritime Training Advisory Board (US); United States Maritime Administration; Robert J. Brady Company; National Maritime Research Center (US). Marine Fire Prevention, Firefighting and Fire Safety: A Comprehensive Training and Reference Manual; DIANE Publishing: Darby, PA, USA, 1994. [Google Scholar]
- History.com Editors. The Normandie Catches Fire. 2009. Available online: https://www.history.com/this-day-in-history/the-normandie-catches-fire (accessed on 25 July 2020).
- Larter, D.B. After the US Navy’s Bonhomme Richard Catastrophe, a Far-Reaching Crackdown on Fire Safety. 2020. Available online: https://www.defensenews.com/naval/2020/07/25/after-the-us-navys-bonhomme-richard-catastrophe-a-far-reaching-crackdown-on-fire-safety/ (accessed on 25 July 2020).
- Fishburn, P.C. Utility Theory for Decision Making; Technical Report; Research Analysis Corp.: McLean, VA, USA, 1970. [Google Scholar]
- Kirkwood, C.W. Notes on Attitude toward Risk Taking and the Exponential Utility Function; Technical Report; Arizona State University: Tempe, AZ, USA, 1997. [Google Scholar]
- Keeney, R.L.; Raiffa, H. Decisions with Multiple Objectives: Preferences and Value Trade-Offs; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Berhold, M.H. The use of distribution functions to represent utility functions. Manag. Sci. 1973, 19, 825–829. [Google Scholar] [CrossRef]
- Lindley, D. A class of utility functions. Ann. Stat. 1976, 4, 1–10. [Google Scholar] [CrossRef]
- Armstrong, J.S.; Overton, T.S. Estimating nonresponse bias in mail surveys. J. Mark. Res. 1977, 14, 396–402. [Google Scholar] [CrossRef]
- Fisher, R.J. Social desirability bias and the validity of indirect questioning. J. Consum. Res. 1993, 20, 303–315. [Google Scholar] [CrossRef]
- Fisher, R.J.; Tellis, G.J. Removing social desirability bias with indirect questioning: Is the cure worse than the disease? ACR N. Am. Adv. 1998, 25, 563–567. [Google Scholar]
- Lusk, J.L.; Norwood, F.B. Direct versus indirect questioning: an application to the well-being of farm animals. Soc. Indic. Res. 2010, 96, 551–565. [Google Scholar] [CrossRef]
- Moshagen, M.; Hilbig, B.E.; Erdfelder, E.; Moritz, A. An experimental validation method for questioning techniques that assess sensitive issues. Exp. Psychol. 2014, 61, 48. [Google Scholar] [CrossRef]
- Valkonen, A.; Glisic, B. Measurement of individual risk preference for decision-making in SHM. In Proceedings of the 12th International Workshop on Structural Health Monitoring: Enabling Intelligent Life-Cycle Health Management for Industry Internet of Things (IIOT), IWSHM 2019, Stanford, CA, USA, 10–12 September 2019; pp. 1487–1495. [Google Scholar]
- Momen, N.; Taylor, M.K.; Pietrobon, R.; Gandhi, M.; Markham, A.E.; Padilla, G.A.; Miller, P.W.; Evans, K.E.; Sander, T.C. Initial validation of the military operational risk taking scale (MORTS). Mil. Psychol. 2010, 22, 128–142. [Google Scholar] [CrossRef]
- Zanakis, S.H.; Solomon, A.; Wishart, N.; Dublish, S. Multi-attribute decision making: A simulation comparison of select methods. Eur. J. Oper. Res. 1998, 107, 507–529. [Google Scholar] [CrossRef]
- Liu, Y.z.; Xu, D.P.; Jiang, Y.C. Method of adaptive adjustment weights in multi-attribute group decision-making. Syst. Eng. Electron. 2007, 29, 45–48. [Google Scholar]
- Howard, R.A. Decision analysis: Practice and promise. Manag. Sci. 1988, 34, 679–695. [Google Scholar] [CrossRef]
- Mac Namee, P.; Celona, J. Decision Analysis with Supertree; Scientific Press: South San Francisco, CA, USA, 1990. [Google Scholar]
- Rolison, J.J.; Hanoch, Y.; Wood, S.; Liu, P.J. Risk-taking differences across the adult life span: A question of age and domain. J. Gerontol. Ser. B Psychol. Sci. Soc. Sci. 2014, 69, 870–880. [Google Scholar] [CrossRef] [PubMed]
- Van Bossuyt, D.L.; Dean, J. Toward Customer Needs Cultural Risk Indicator Insights for Product Development. In Proceedings of the ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, MA, USA, 2–5 August 2015. [Google Scholar]
- Igleski, J.R.; Van Bossuyt, D.L.; Reid, T. The Application of Retrospective Customer Needs Cultural Risk Indicator Method to Soap Dispenser Design for Children in Ethiopia. In Proceedings of the ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016. [Google Scholar]
| Risk Domain | Value (Nominal) | Risk Attitude |
|---|---|---|
| Ethics | −0.2 | Risk Averse |
| Finance | 0.2 | Risk Seeking |
| Health/Safety | 0.1 | Risk Seeking |
| Recreation | 0 | Risk Neutral |
| Social | −0.3 | Risk Averse |
| Risk Domain | Relative Impact |
|---|---|
| Ethics | 1.2 |
| Finance | 1.1 |
| Health/Safety | 1.5 |
| Recreation | 0.2 |
| Social | 1.35 |
| Component | MTBF (Hrs) | Failure Rate | Reliability |
|---|---|---|---|
| 1 | 14,000 | 0.000071 | 0.964916 |
| 2 | 16,500 | 0.000061 | 0.970152 |
| 3 | 8000 | 0.000125 | 0.939413 |
| 4 | 15,000 | 0.000067 | 0.967216 |
| Risk Domain | Raw Risk Attitude | Adj Risk Attitude | Risk Impact |
|---|---|---|---|
| Ethics | 0.8021 | 0.8021 | 1.2 |
| Finance | −0.7397 | 0.0000 | 1.1 |
| Health/Safety | 0.8750 | 0.8750 | 1.5 |
| Recreation | −0.3131 | 0.0000 | 0.5 |
| Social | 0.5581 | 0.5581 | 1.35 |
| 0.447 | 0.606 | −1.651 | 1 |
| Standard Configuration | |||
|---|---|---|---|
| Component | MTBF (hrs) | Lambda | Reliability |
| 1 | 14,000 | 0.000071 | 0.964916 |
| 2 | 16,500 | 0.000061 | 0.970152 |
| 3 | 8000 | 0.000125 | 0.939413 |
| 4 | 15,000 | 0.000067 | 0.967216 |
| System Reliability | 0.90210155 | ||
| Improved Maintenance Concept | |||
| Component | MTBF (hrs) | Lambda | Reliability |
| 1 | 21,000 | 0.000048 | 0.976472 |
| 2 | 24,750 | 0.000040 | 0.980001 |
| 3 | 12,000 | 0.000083 | 0.959189 |
| 4 | 22,500 | 0.000044 | 0.978023 |
| System Reliability | 0.93435329 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rathwell, B.W.; Van Bossuyt, D.L.; Pollman, A.; Sweeney, J., III. A Method to Account for Personnel Risk Attitudes in System Design and Maintenance Activity Development. Systems 2020, 8, 26. https://doi.org/10.3390/systems8030026
Rathwell BW, Van Bossuyt DL, Pollman A, Sweeney J III. A Method to Account for Personnel Risk Attitudes in System Design and Maintenance Activity Development. Systems. 2020; 8(3):26. https://doi.org/10.3390/systems8030026
Chicago/Turabian StyleRathwell, Benjamin W., Douglas L. Van Bossuyt, Anthony Pollman, and Joseph Sweeney, III. 2020. "A Method to Account for Personnel Risk Attitudes in System Design and Maintenance Activity Development" Systems 8, no. 3: 26. https://doi.org/10.3390/systems8030026
APA StyleRathwell, B. W., Van Bossuyt, D. L., Pollman, A., & Sweeney, J., III. (2020). A Method to Account for Personnel Risk Attitudes in System Design and Maintenance Activity Development. Systems, 8(3), 26. https://doi.org/10.3390/systems8030026





