Discrete Competitive Lotka–Volterra Model with Controllable Phase Volume
Abstract
1. Introduction
2. Materials and Methods
2.1. Competitive Lotka–Volterra Model
2.2. Finite-Difference Models with Controllable Symmetry
2.2.1. Semi-Implicit Integration as a Tool to Obtain Adaptive Discrete Systems
2.2.2. Discrete CLVM Model with Controllable Symmetry
3. Results
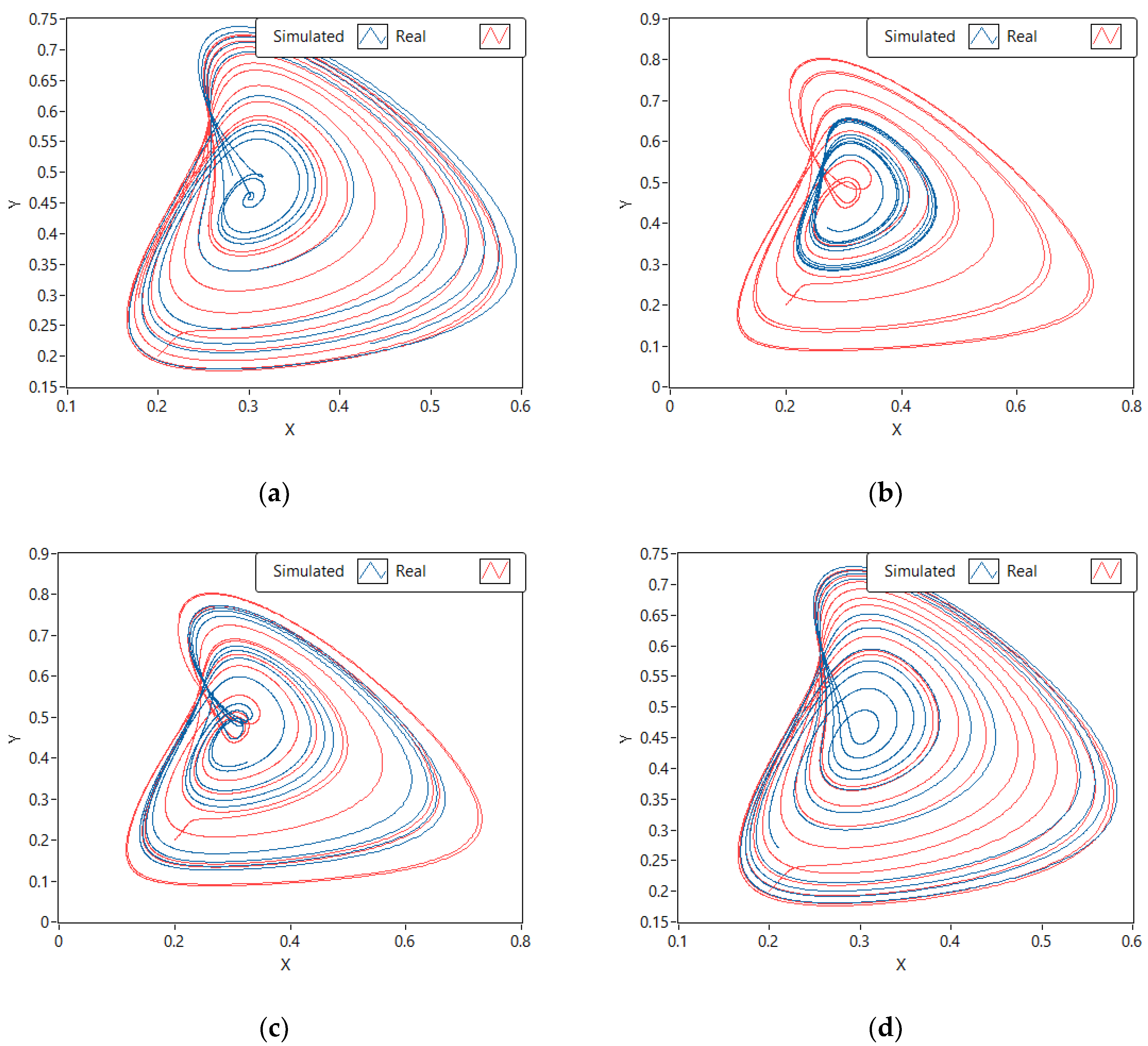
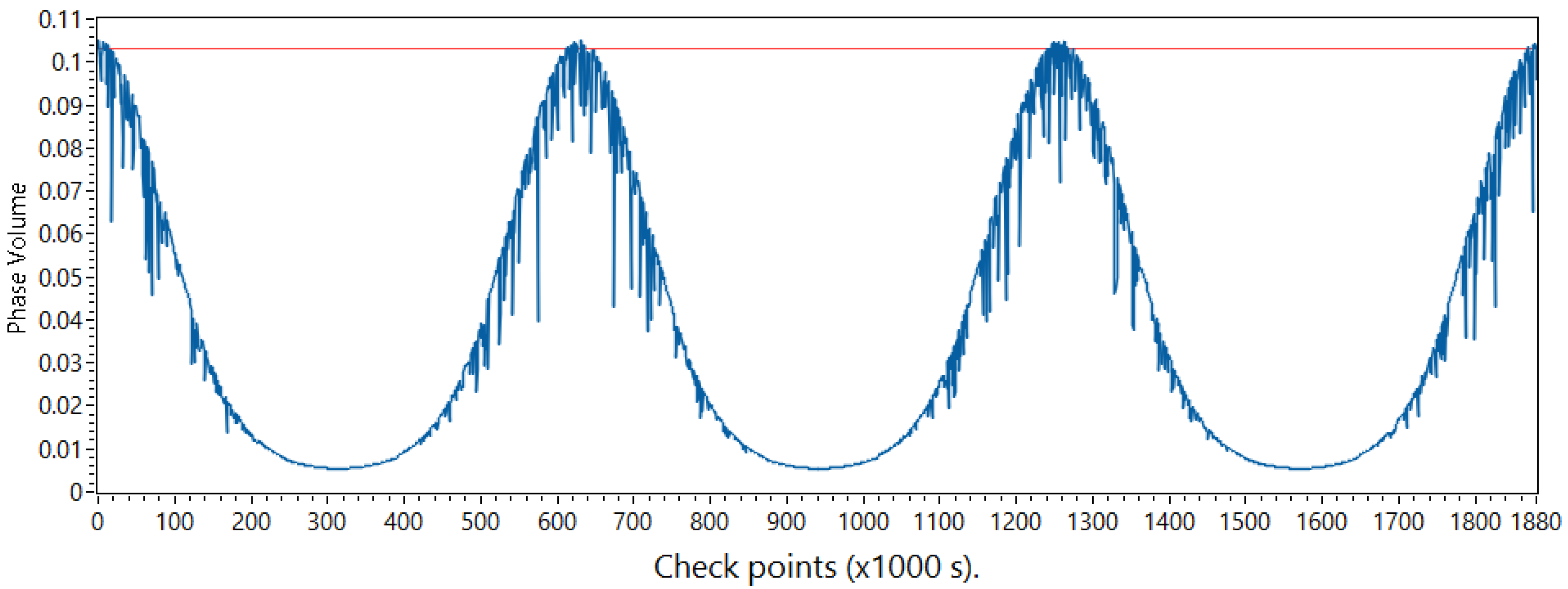
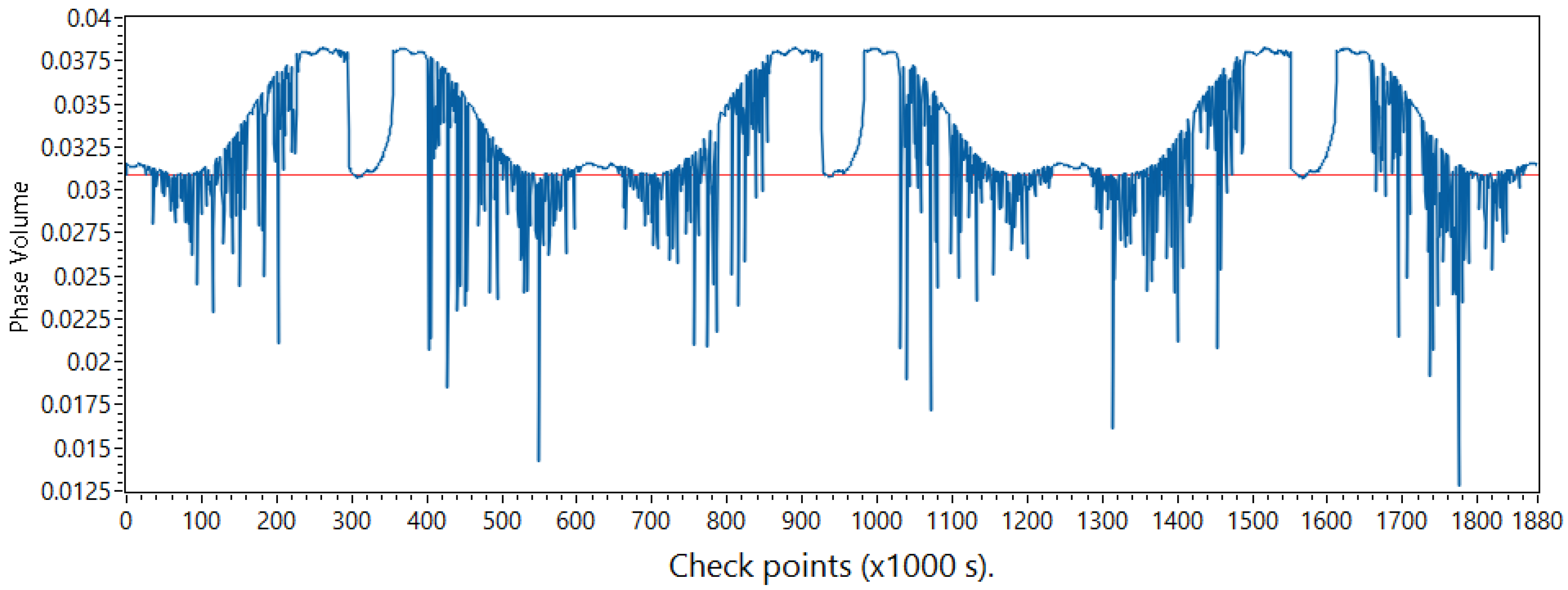
3.1. Phase Space Analysis
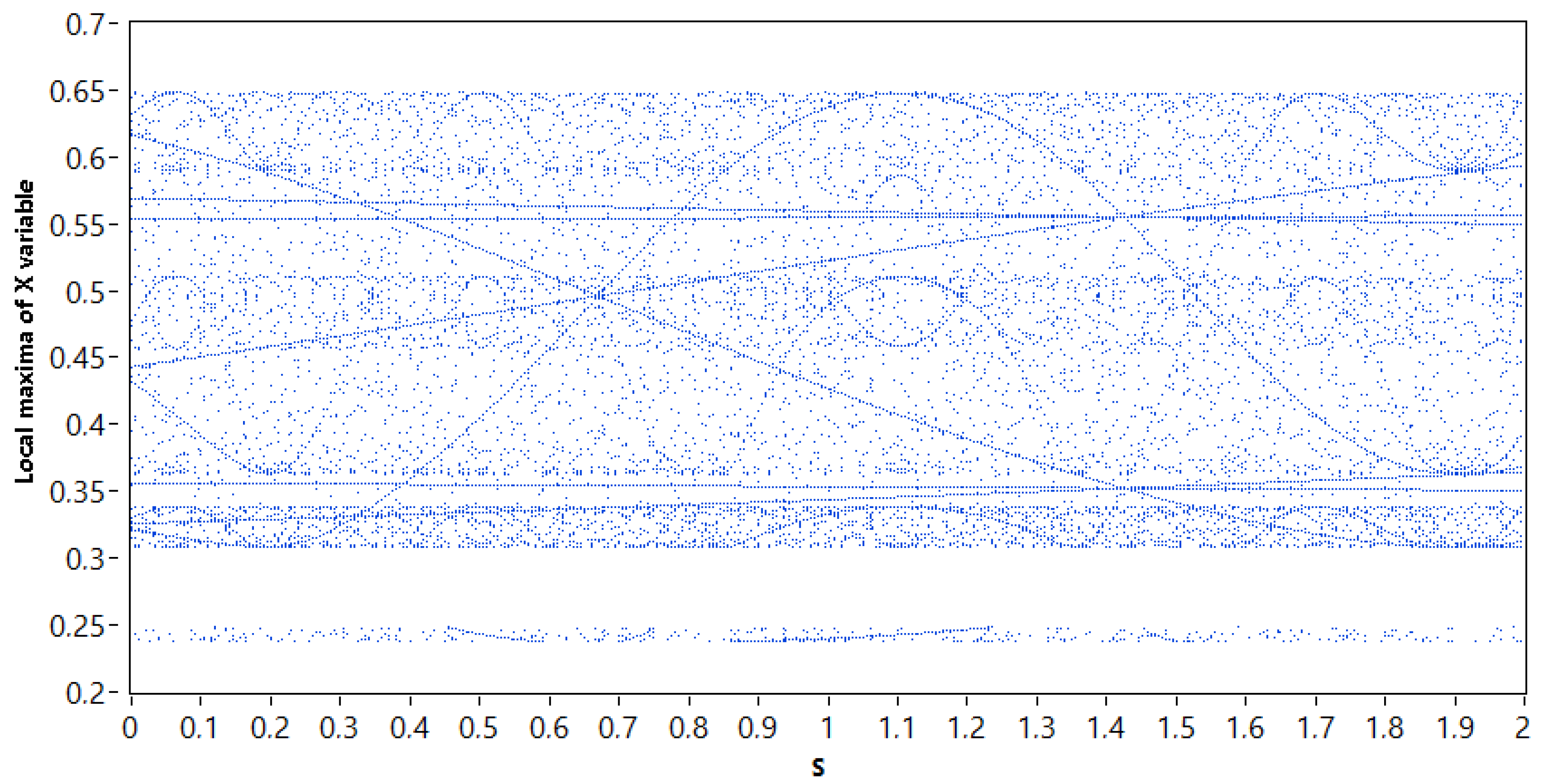
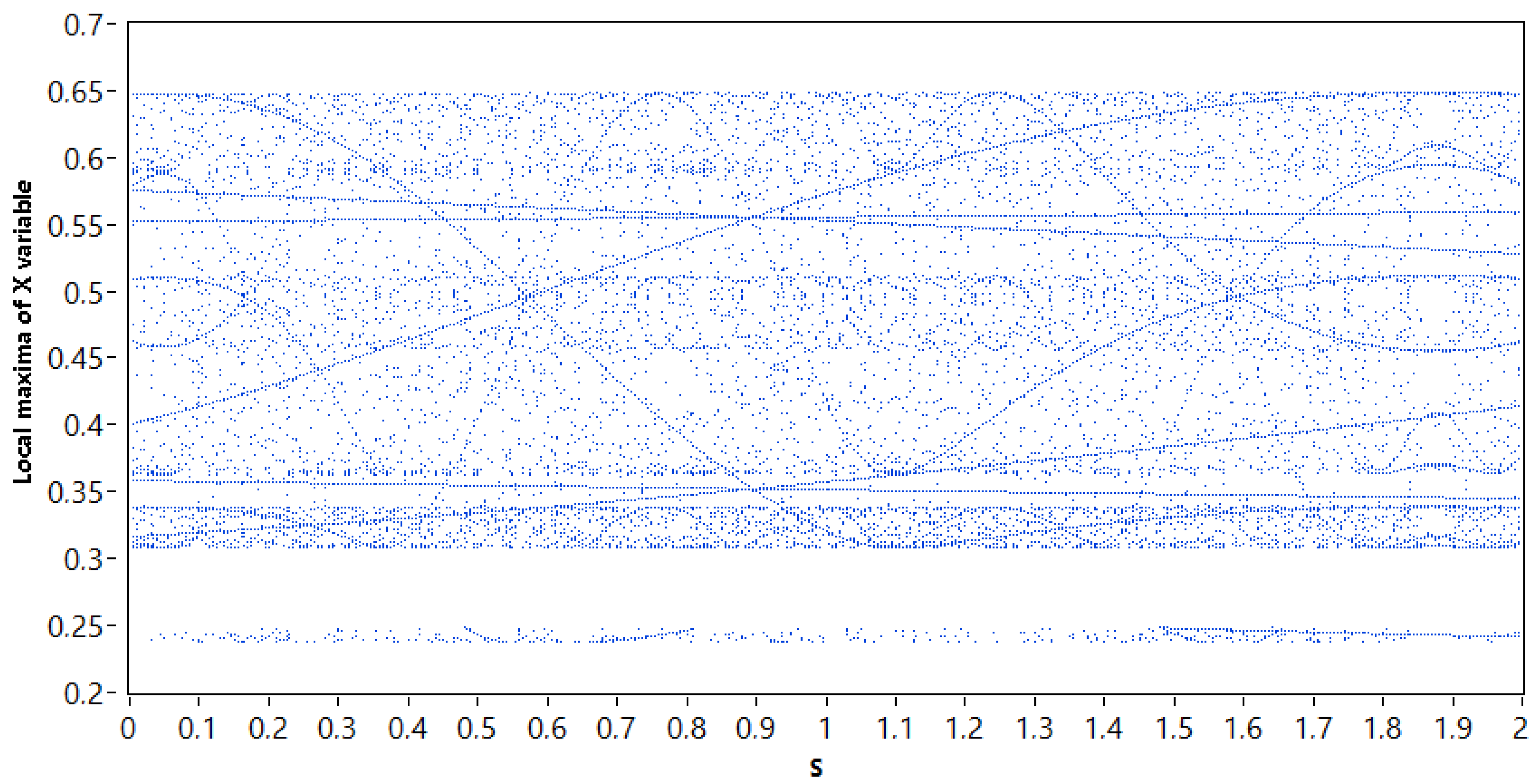
3.2. Bifurcation Analysis
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Knuth, D.E. Stable Marriage and Its Relation to Other Combinatorial Problems: An Introduction to the Mathematical Analysis of Algorithm; The American Mathematical Society: Providence, RI, USA, 1996. [Google Scholar]
- Lotka, A.J. Contribution to the Theory of Periodic Reaction. J. Phys. Chem. 1910, 14, 271–274. [Google Scholar] [CrossRef]
- Lotka, A.J. Analytical Note on Certain Rhythmic Relations in Organic Systems. Proc. Natl. Acad. Sci. USA 1920, 6, 410–415. [Google Scholar] [CrossRef]
- Volterra, V. Variazioni e fluttuazioni del numero d’individui in specie animali conviventi. Mem. Acad. Lincei Roma 1926, 2, 31–113. [Google Scholar]
- Titov, V.A.; Veynberg, R.R. Dynamic analysis of existing models based on Lotka-Volterra equation “predator-prey”. Fundamental’nye Issled. 2016, 8, 409–413. [Google Scholar]
- Solomon, S. Generalized Lotka-Volterra (GLV) models of stock markets. Appl. Simul. Soc. Sci. 2000, 3, 301–322. [Google Scholar] [CrossRef]
- Modis, T. Technological Forecasting at the Stock Market. Technol. Forecast. Soc. Chang. 1999, 62, 173–202. [Google Scholar] [CrossRef]
- Liu, H.C. When one stock share is a biological individual: A stylized simulation of the population dynamics in an order-driven market. Decis. Econ. Financ. 2020. [Google Scholar] [CrossRef]
- Ganguly, S.; Neogi, U.; Chakrabarti, A.S.; Chakraborti, A. Reaction-Diffusion Equations with Applications to Economic Systems. In Econophysics and Sociophysics: Recent Progress and Future Directions; Springer: Cham, Switzerland, 2017; pp. 131–144. [Google Scholar]
- Wei, T.; Li, Y.; Song, C. The Competition Model of High-Tech Industry Clusters with Limited Innovation Resources on Lotka-Volterra Model. In 2013 International Conference on Information System and Engineering Managemen; IEEE: Washington, DC, USA, 2013; pp. 741–744. [Google Scholar]
- Guidolin, M.; Guseo, R.; Mortarino, C. Regular and promotional sales in new product life cycles: Competition and forecasting. Comput. Ind. Eng. 2019, 130, 250–257. [Google Scholar] [CrossRef]
- Khan, N.T.; Jung, G.; Kim, J.; Kim, Y.B. Evolving competition between low-cost carriers and full-service carriers: The case of South Korea. J. Transp. Geogr. 2019, 74, 1–9. [Google Scholar] [CrossRef]
- Kaszkurewicz, E.; Bhaya, A. Modeling market share dynamics under advertising effort and word-of-mouth interactions between customers. IEEE Trans. Comput. Soc. Syst. 2018, 5, 382–390. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, H. Testing the trade relationships between China, Singapore, Malaysia and Thailand using Grey Lotka-Volterra competition model. Kybernetes 2016, 45, 931–945. [Google Scholar] [CrossRef]
- Bernardo, G.; D’Alessandro, S. Systems-dynamic analysis of employment and inequality impacts of low-carbon investments. Environ. Innov. Soc. Transit. 2016, 21, 123–144. [Google Scholar] [CrossRef]
- Kamann, D.-J.F.; Nijkamp, P. Technogenesis: Incubation and Diffusion; Research Memorandum: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Assumma, V.; Bottero, M.; Datola, G.; De Angelis, E.; Monaco, R. Dynamic models for exploring the resilience in territorial scenarios. Sustainability 2020, 12, 3. [Google Scholar] [CrossRef]
- Nam, T. The broken promises of democracy: Protest-repression dynamics in Korea 1990–1991. Mobilization 2006, 11, 427–442. [Google Scholar] [CrossRef]
- Marasco, A.; Romano, A. Deterministic modeling in scenario forecasting: Estimating the effects of two public policies on intergenerational conflict. Qual. Quant. 2018, 52, 2345–2371. [Google Scholar] [CrossRef]
- Gao, Y.; Li, Z.; Khan, K. Effect of cognitive variables and emotional variables on urban residents’ recycled water reuse behavior. Sustainability 2019, 11, 2208. [Google Scholar] [CrossRef]
- Phochanikorn, P.; Tan, C. An integrated multi-criteria decision-making model based on prospect theory for green supplier selection under uncertain environment: A case study of the thailand palm oil products industry. Sustainability 2019, 11, 1872. [Google Scholar] [CrossRef]
- Dominioni, G.; Marasco, A.; Romano, A. A mathematical approach to study and forecast racial groups interactions: Deterministic modeling and scenario method. Qual. Quant. 2018, 52, 1929–1956. [Google Scholar] [CrossRef]
- Ditzen, J. Cross-country convergence in a general Lotka–Volterra model. Spat. Econ. Anal. 2018, 13, 191–211. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Holly, S.; Mur, J. Contemporary developments in the theory and practice of spatial econometrics. Spat. Econ. Anal. 2018, 13, 139–147. [Google Scholar] [CrossRef]
- Trubetskov, D.I. Phenomenon of Lotka-Volterra mathematical model and similar models. Izv. Vuzov. Prikl. Nelinejnaya Din. 2011, 2, 69–87. [Google Scholar]
- Christodoulakis, N. Conflict dynamics and costs in the Greek civil war 1946–1949. Def. Peace Econ. 2016, 27, 688–717. [Google Scholar] [CrossRef]
- Yoshikazu, H.; Yoshiteru, I. Stable Marriage Problem Mapped to Lotka-Volterra Model: Stable Equilibria Mapped from Stable Matchings. Procedia Comput. Sci. 2014, 35, 1398–1406. [Google Scholar]
- Voroshilova, A. Identification of parental labour motivational factors by future parents. In Proceedings of the 11th International Days of Statistics and Economics MSED-2017: Conference Proceedings, Prague, Czech Republic, 14–16 September 2017; pp. 1800–1807. [Google Scholar]
- Butusov, D.N.; Karimov, A.I.; Pyko, N.S.; Pyko, S.A.; Bogachev, M.I. Discrete chaotic maps obtained by symmetric integration. Physica A 2018, 509, 955–970. [Google Scholar] [CrossRef]
- Tutueva, A.V.; Nepomuceno, E.G.; Karimov, A.I.; Andreev, V.S.; Butusov, D.N. Adaptive chaotic maps and their application to pseudo-random numbers generation. Chaos Solitons Fractals 2020, 133, 109615. [Google Scholar] [CrossRef]
- Butusov, D.N.; Karimov, A.I.; Andreev, V.S. Computer simulation of chaotic systems with symmetric extrapolation methods. In Proceedings of the XVIII International Conference on Soft Computing and Measurements (SCM), Saint Petersburg, Russia, 19–21 May 2015; pp. 78–80. [Google Scholar]
- Butusov, D.N.; Ostrovskii, V.Y.; Karimov, A.I.; Andreev, V.S. Semi-explicit composition methods in memcapacitor circuit simulation. Int. J. Embed. Real-Time Commun. Syst. (IJERTCS) 2019, 10, 37–52. [Google Scholar] [CrossRef]
- Smale, S. On the differential equations of species in competition. J. Math. Biol. 1976, 3, 5–7. [Google Scholar] [CrossRef]
- Vano, J.A.; Wildenberg, J.C.; Anderson, M.B.; Noel, J.K.; Sprott, J.C. Chaos in low-dimensional Lotka–Volterra models of competition. Nonlinearity 2006, 19, 2391. [Google Scholar] [CrossRef]
- Butusov, D.N.; Karimov, A.I.; Tutueva, A.V. Symmetric extrapolation solvers for ordinary differential equations. In Proceedings of the NW Russia Young Researchers in Electrical and Electronic Engineering Conference (EIConRusNW), Saint Petersburg, Russia, 2–3 February 2016; pp. 162–167. [Google Scholar]
- Butusov, D.N.; Tutueva, A.V.; Ostrovskii, V.Y. Simulation of Dynamical Systems Based on Parallel Numerical Integration Methods. In Proceedings of the 2015 IEEE North West Russia Section Young Researchers in Electrical and Electronic Engineering Conference, Saint Petersburg, Russia, 2–4 February 2015; pp. 56–60. [Google Scholar]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Butusov, D.; Karimov, A.; Tutueva, A.; Kaplun, D.; Nepomucheno, E.G. The Effects of Padé Numerical Integration in Simulation of Conservative Chaotic Systems. Entropy 2019, 21, 362. [Google Scholar] [CrossRef]
- Houkes, W.; Zwart, S.D. Transfer and templates in scientific modelling. Stud. Hist. Philos. Sci. Part A 2019, 77, 93–100. [Google Scholar] [CrossRef]
- Abramson, G.; Zanette, D.H. Globally coupled maps with asynchronous updating. Phys. Rev. E 1998, 58, 4454–4460. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voroshilova, A.; Wafubwa, J. Discrete Competitive Lotka–Volterra Model with Controllable Phase Volume. Systems 2020, 8, 17. https://doi.org/10.3390/systems8020017
Voroshilova A, Wafubwa J. Discrete Competitive Lotka–Volterra Model with Controllable Phase Volume. Systems. 2020; 8(2):17. https://doi.org/10.3390/systems8020017
Chicago/Turabian StyleVoroshilova, Anzhelika, and Jeff Wafubwa. 2020. "Discrete Competitive Lotka–Volterra Model with Controllable Phase Volume" Systems 8, no. 2: 17. https://doi.org/10.3390/systems8020017
APA StyleVoroshilova, A., & Wafubwa, J. (2020). Discrete Competitive Lotka–Volterra Model with Controllable Phase Volume. Systems, 8(2), 17. https://doi.org/10.3390/systems8020017




