Agent-Based Simulation of Hardware-Intensive Design Teams Using the Function–Behavior–Structure Framework
Abstract
1. Introduction
2. Results
2.1. Literature Review
2.1.1. Agent-Based Modeling and Simulation
2.1.2. Models of Designers
2.1.3. Design Synthesis Process
2.1.4. Agile Processes
2.2. Methods
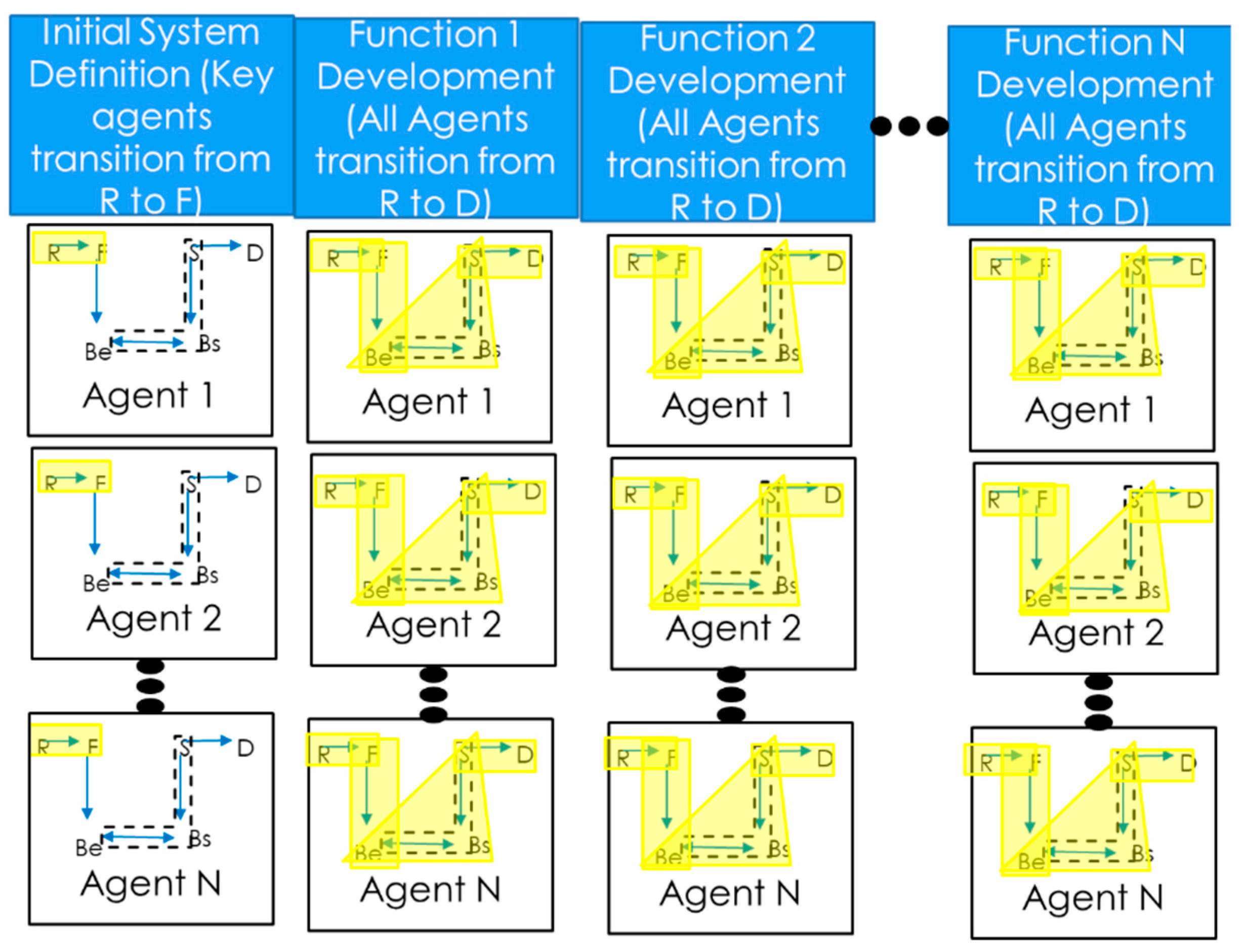
2.3. Modeling and Simulation of Design Teams Performing Agile and Waterfall Development
2.3.1. The Agent Model
2.3.2. Waterfall Simulation
- System requirements review (SRR);
- System functional review (SFR);
- Preliminary design review (PDR);
- Critical design review (CDR).
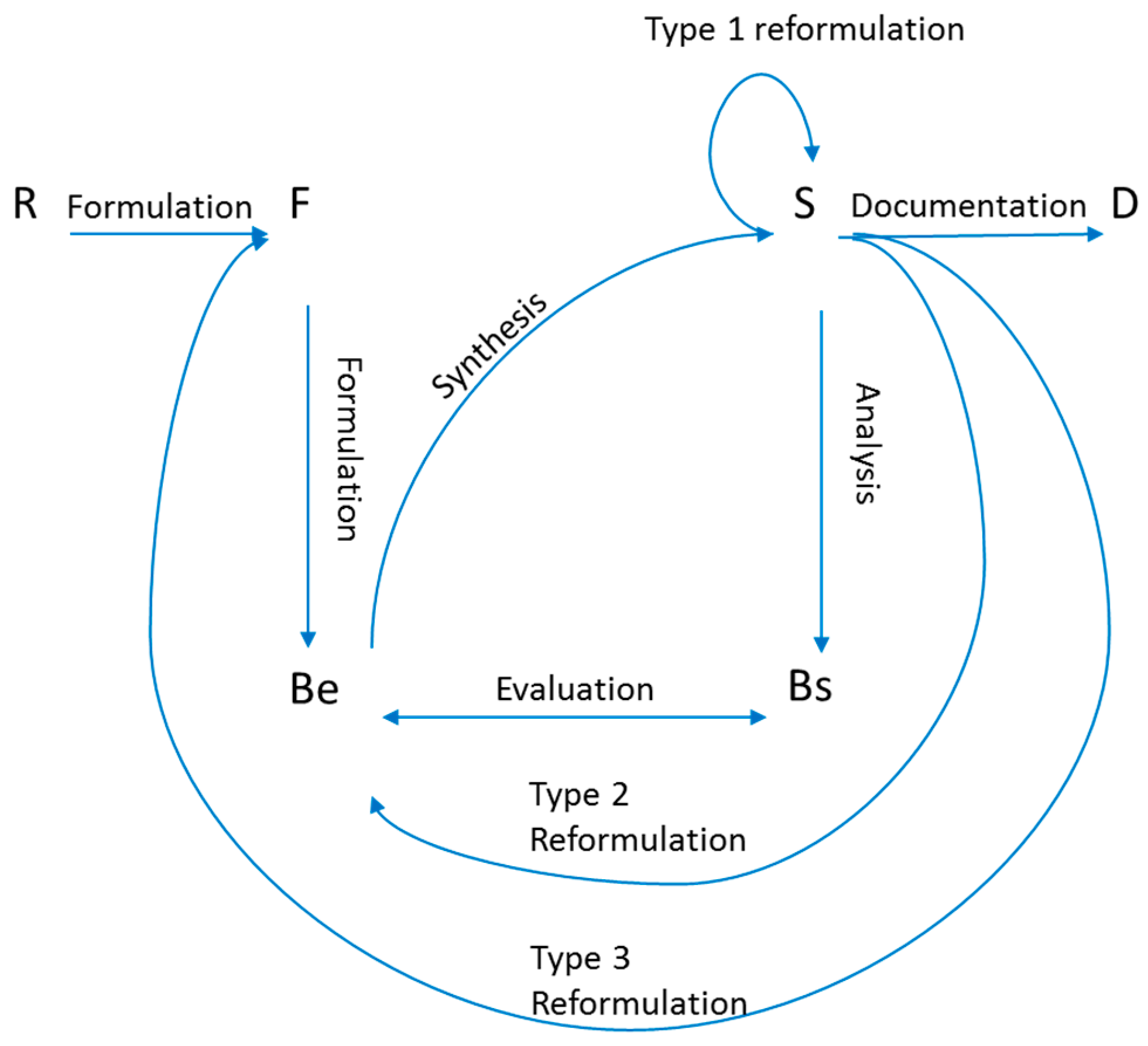
- SRR—corresponds to the transition from R to F
- ○
- A goal of SRR is to translate customer requirements into system-specific functions [23]. This aligns well with the FBS transition of formulation where functions are formulated from requirements.
- SFR—corresponds to the transition from F to Be
- ○
- A goal of SFR is to create a design approach that performs in such a way as to accomplish required functions [23]. This aligns well with the FBS transition of creating expected behavior from functions.
- PDR—corresponds to the transition from Be to S
- ○
- PDR is meant to show that the detailed design approach for the system satisfies functions [23]. The Be to S transition is meant to achieve this as the expected behavior (low-level functions) is used to derive the design.
- CDR—corresponds to the transition from S to D
- ○
- CDR is meant to show that the total system design is complete, meets requirements, and is ready to be built or coded [23]. This is represented by the transition from structure to documentation. In order to make this transition, the design must be complete, which is met by completing the structure phase; it must meet requirements, which is met by completing the Bs to Be comparison (part of the structure phase in the implemented FBS model); and the design must be ready to be created, which is represented by completing the documentation, which is where the design is handed off to manufacturing or coders to be created.
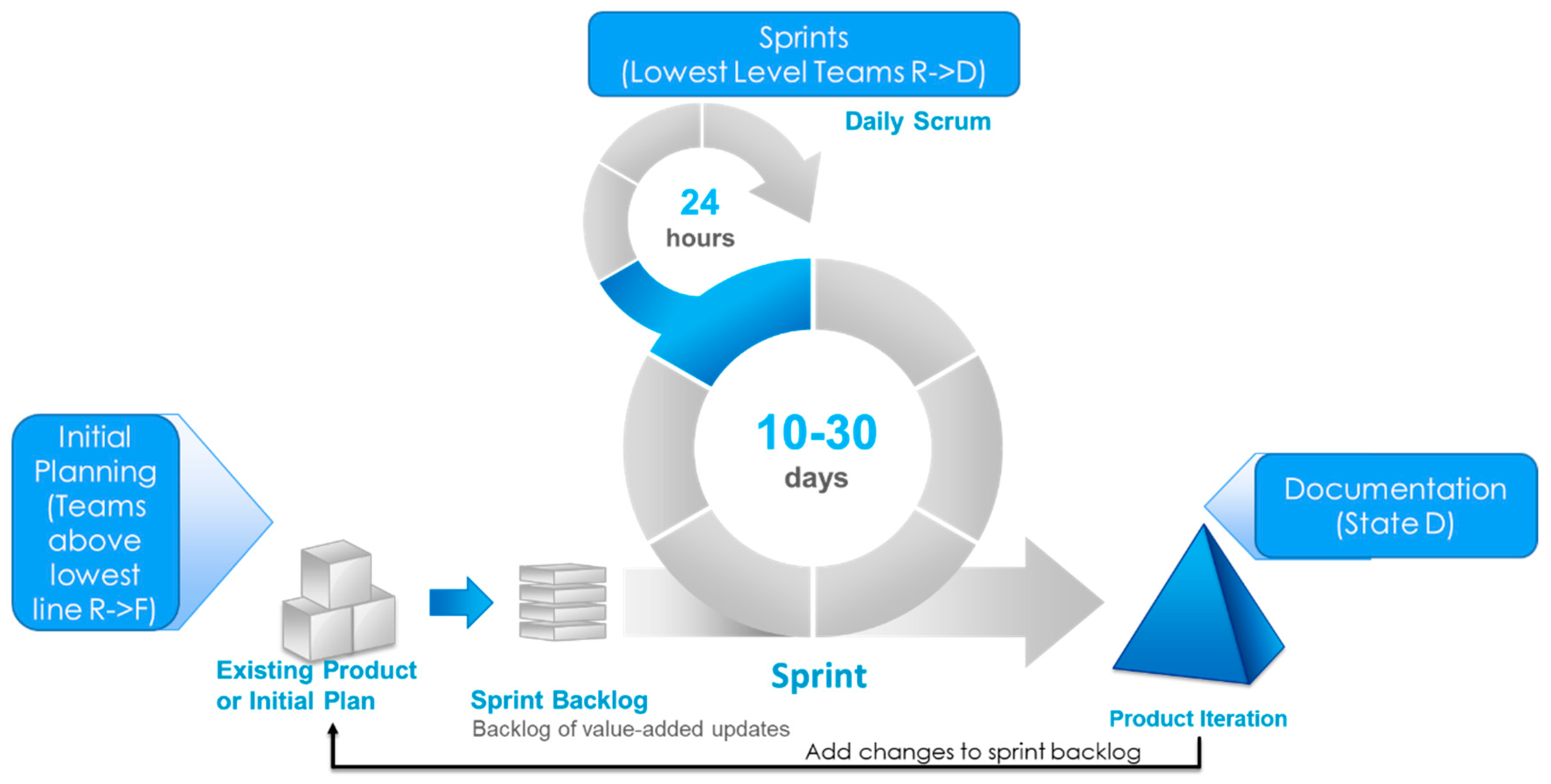
2.3.3. Agile Simulation
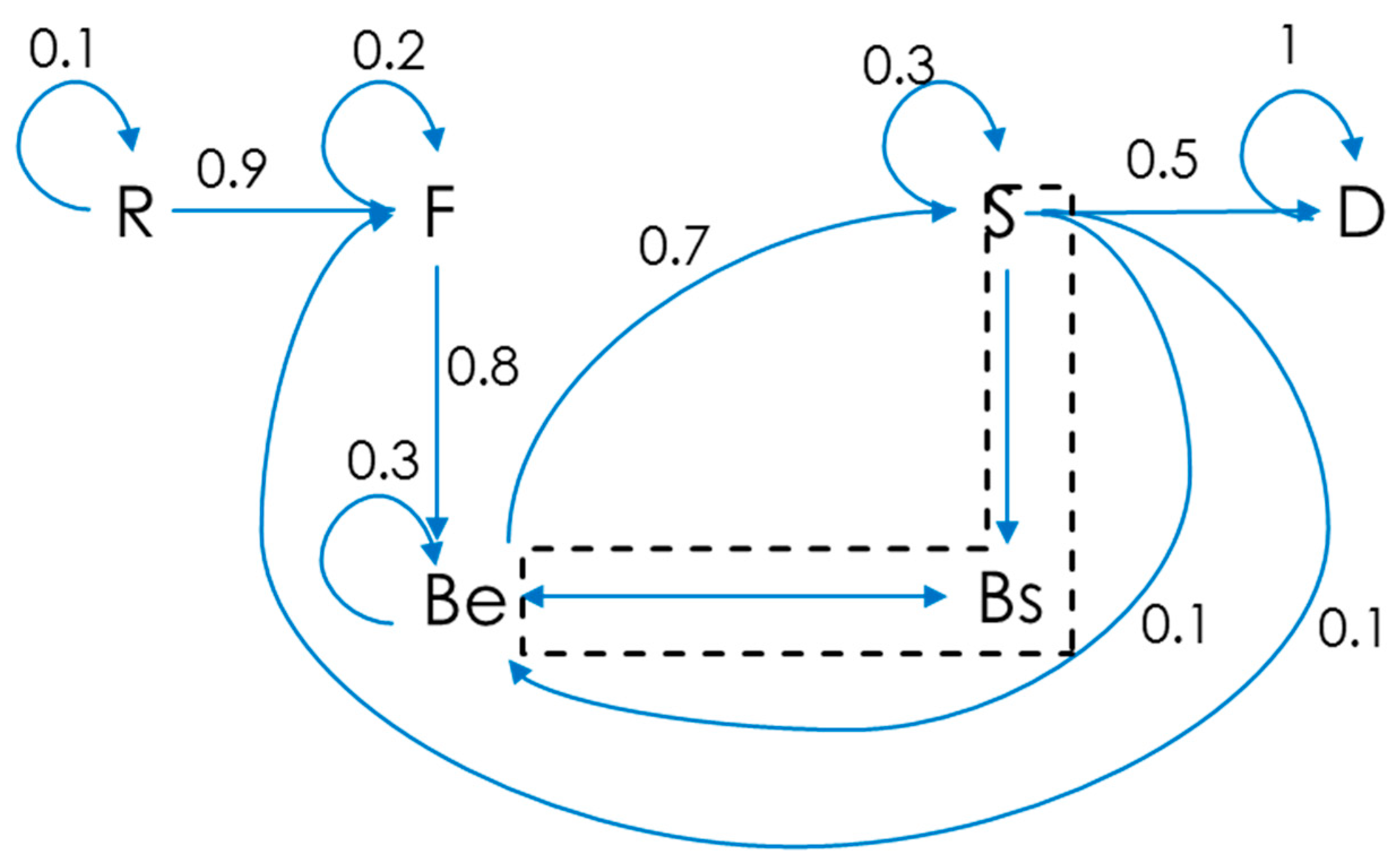
2.3.4. FBS Model Calibration
2.3.5. Simulation Design
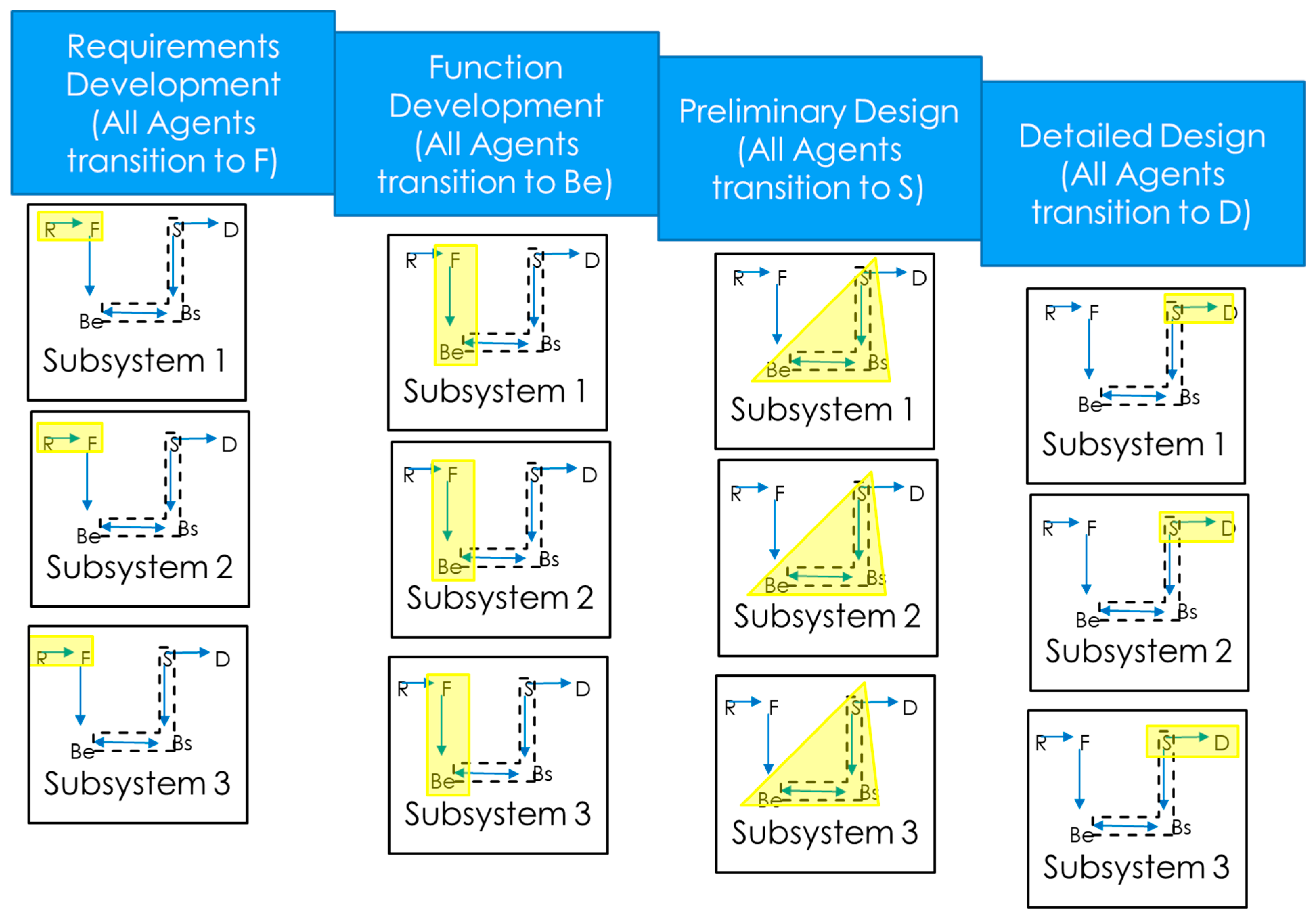
Waterfall Simulation Design
- Requirements development (R→F);
- Function development (F→ Be);
- Preliminary design (Be→S);
- Detailed design (S→D).
Agile Simulation Design
2.3.6. Assumptions
- Designers can be represented by the FBS model. The FBS model is an abstracted model of designers. While it does not represent all aspects of designers, it contains enough information to represent the states that the designers go through during the design process [17].
- The synthesis, analysis, and evaluation activities were combined into a single activity. This was necessary so that the FBS model could be represented by a first-order Markov process.
- The system being designed is unprecedented. The designers do not know a priori the optimal design solution.
- Design teams work in parallel. Teams do not wait for other teams to perform their work before starting.
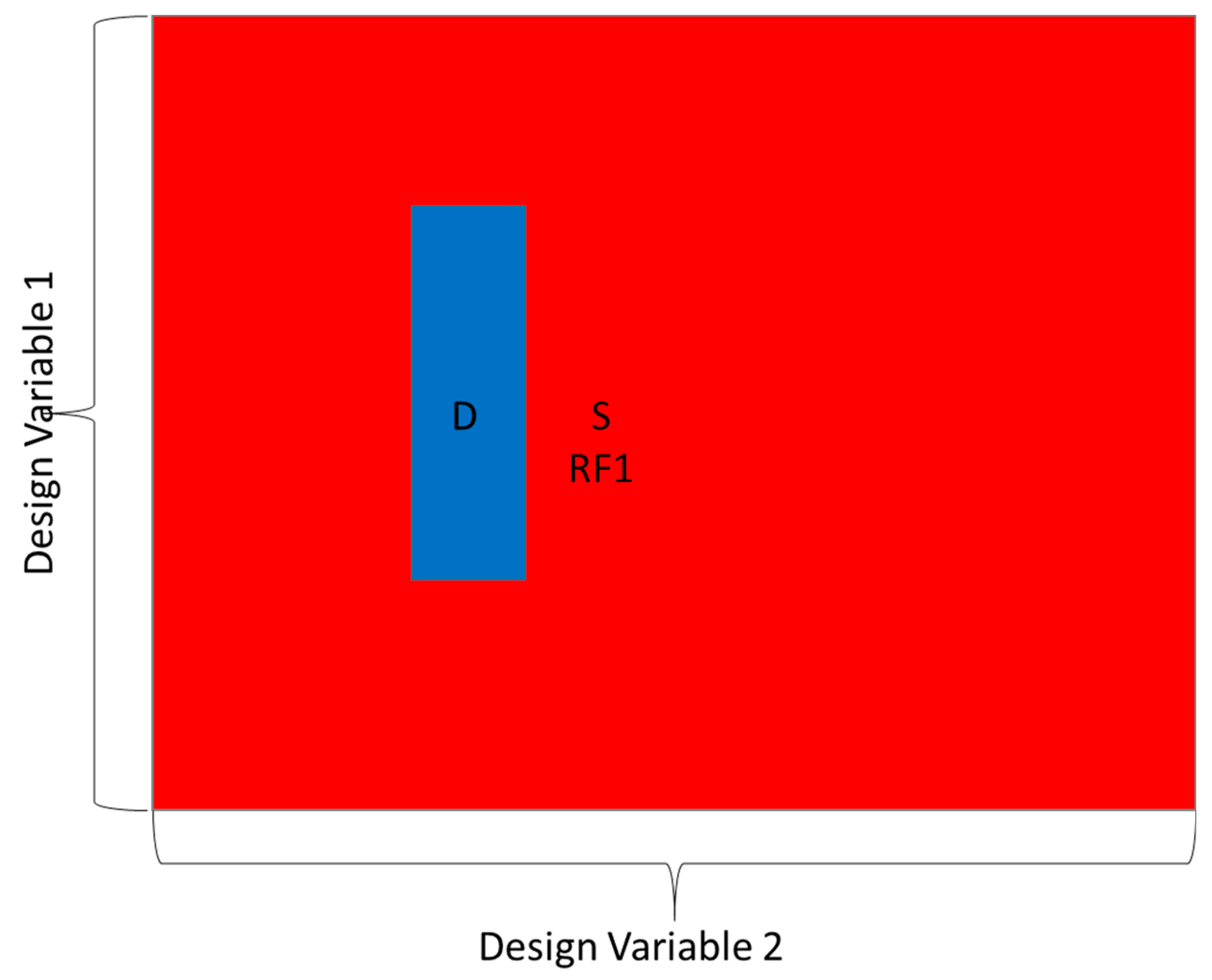
- Reformulations caused by design incompatibility are type I reformulations. It was assumed that these types of reformulations are caused by incompatibility in the structure of two different parts of the design.
- The simulation was designed assuming that the agents interact with one another through a model of the system they are developing. Communication between the agents was not modeled due to this assumption. Rather, agents learn of the design decisions and implications of those decisions on the system as soon as their peer agents learn them. Thus, information learned about the design of the system is given to agents with zero time lag.
- Team leaders do not contribute to design work. This was done to represent the roles of these leaders primarily in the planning of the design through requirements and function derivation.
- Idle time was not modeled. It was assumed that agents that complete their work early have other projects they can work on and their idle time does not count towards the total number of effort hours needed to complete the design.
- Agents understand the coupling in a design. When coupling forces redesigns of subsystems, the minimum number of subsystems are redesigned.
- The software and launch vehicle systems are simple versions of these types of systems. This assumption was needed to ensure that the simulation development effort was tractable as a fully defined development process for these large and complex systems which are difficult to define and fully simulate. This makes the simulation results not necessarily representative of real-world performance outright. They are still considered valid for comparison purposes, which is the primary objective of this research.
2.3.7. Software Program Development Simulation
2.3.8. Launch Vehicle Development Simulation
- Stage 1 thrust—determined by the Stage 1 rocket engine team;
- Stage 1 propellant mass—determined by the Stage 1 tank team;
- Stage 1 structure mass—determined by the Stage 1 structural team;
- Stage 1 diameter—determined by the Stage 1 mechanical team;
- Stage 2 thrust—determined by the Stage 2 rocket engine team;
- Stage 2 propellant mass—determined by the Stage 2 tank team;
- Stage 2 structure mass—determined by the Stage 2 structural team;
- Stage 2 diameter—determined by the Stage 2 mechanical team;
- Payload mass—determined by the systems analysis team.
2.4. Verification and Validation
2.4.1. Model Validation
2.4.2. Model Parameter Validation
2.4.3. Validation of Simulation Output against Case Studies
3. Discussion
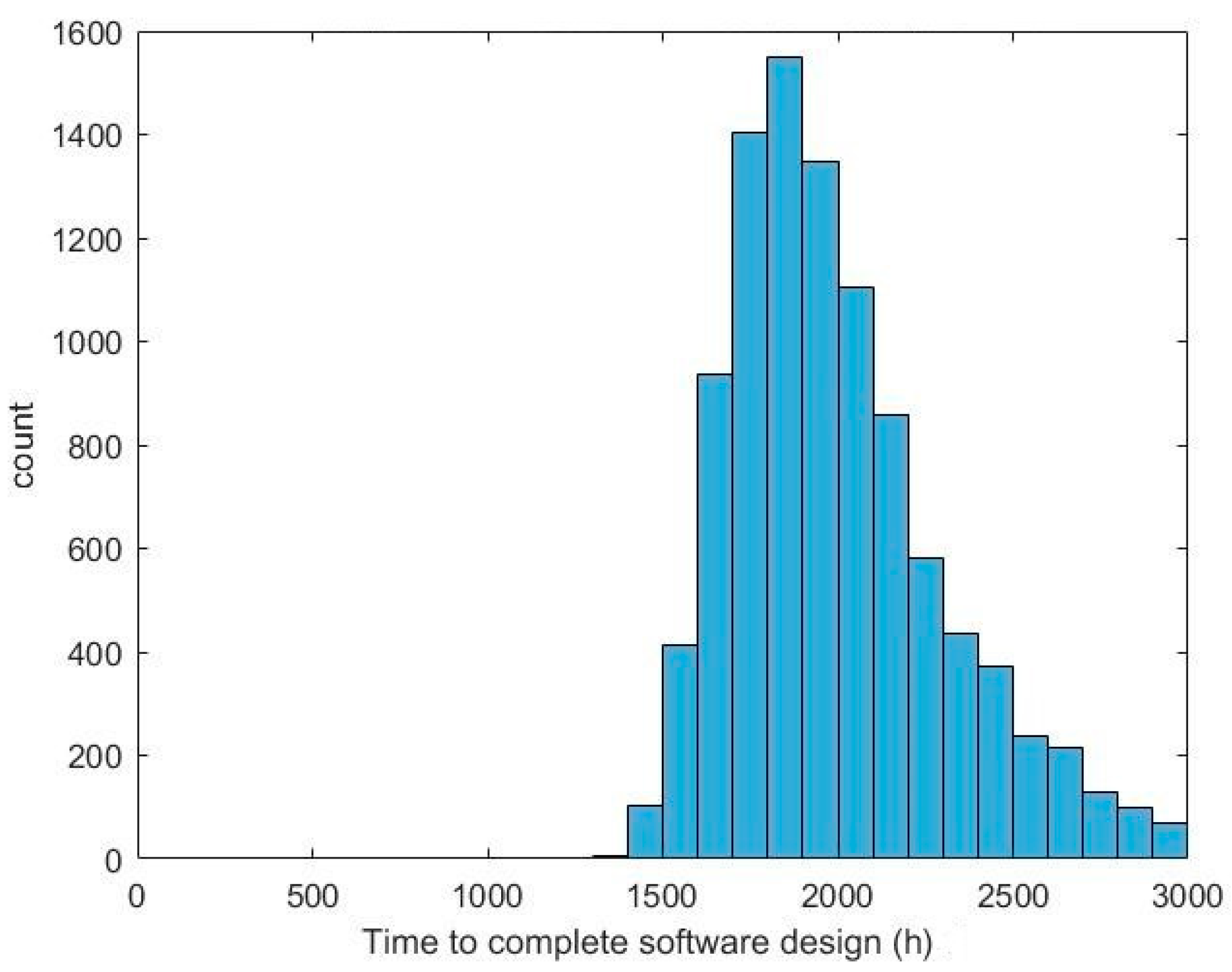
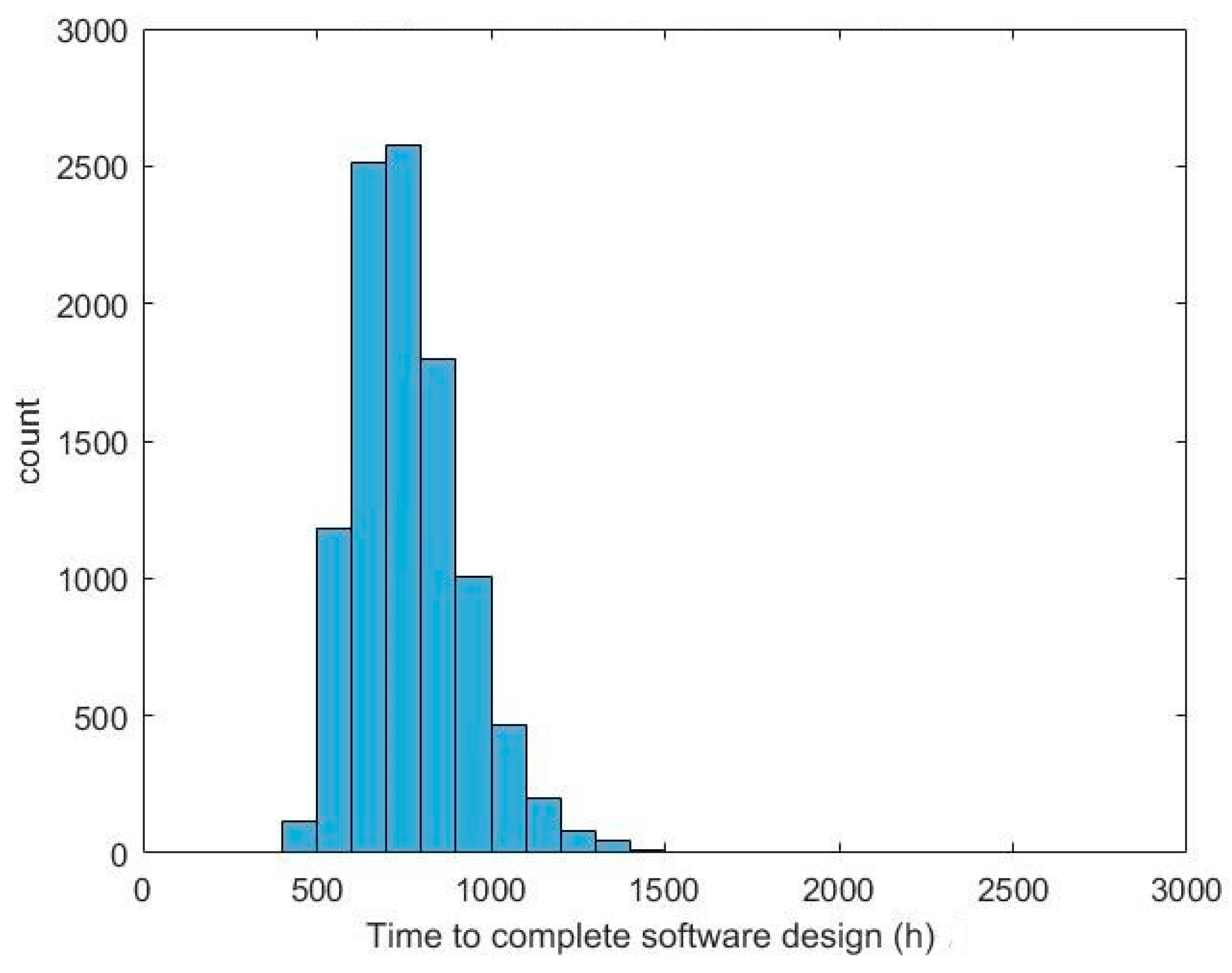
3.1. Software Development Simulation Results Analysis
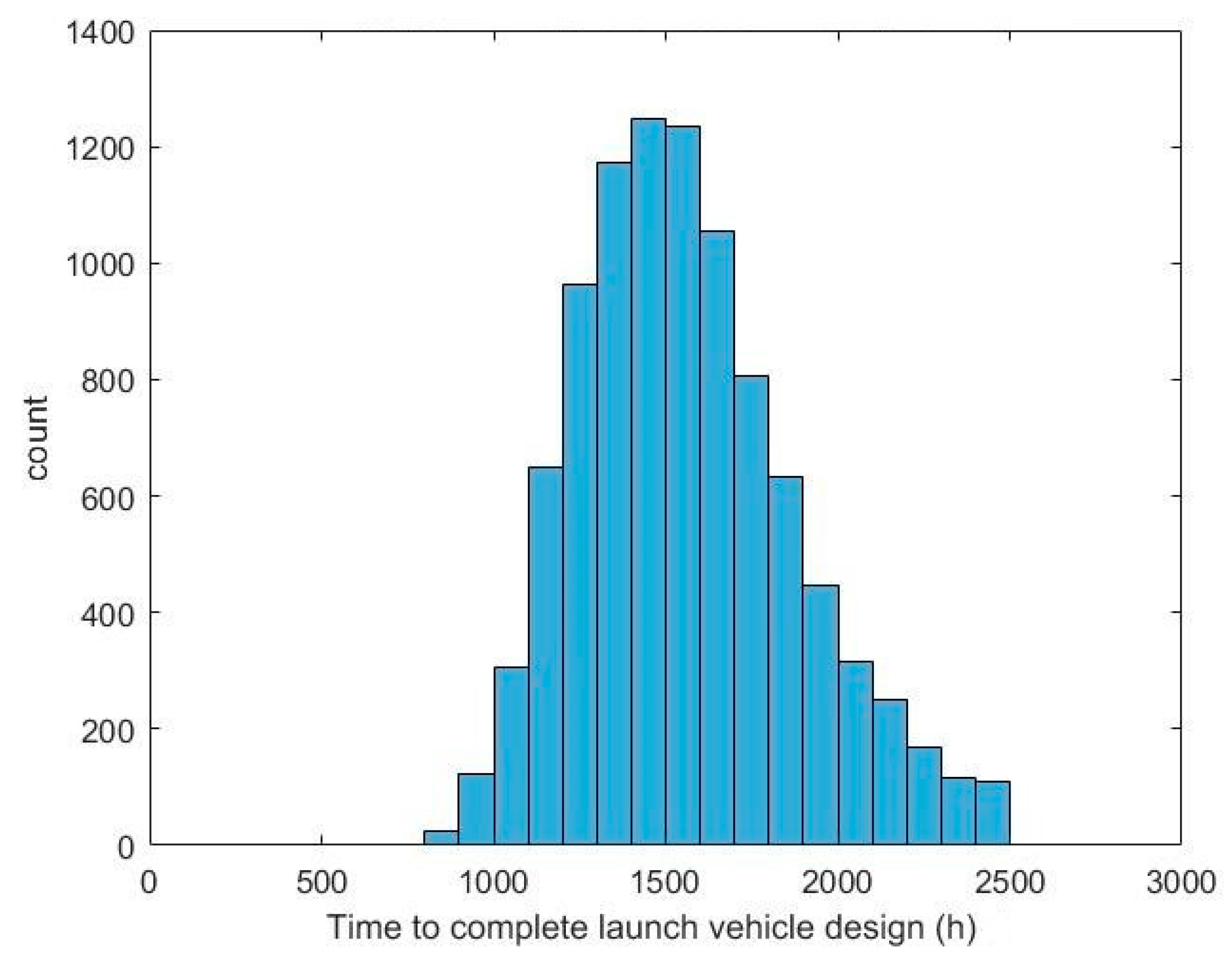
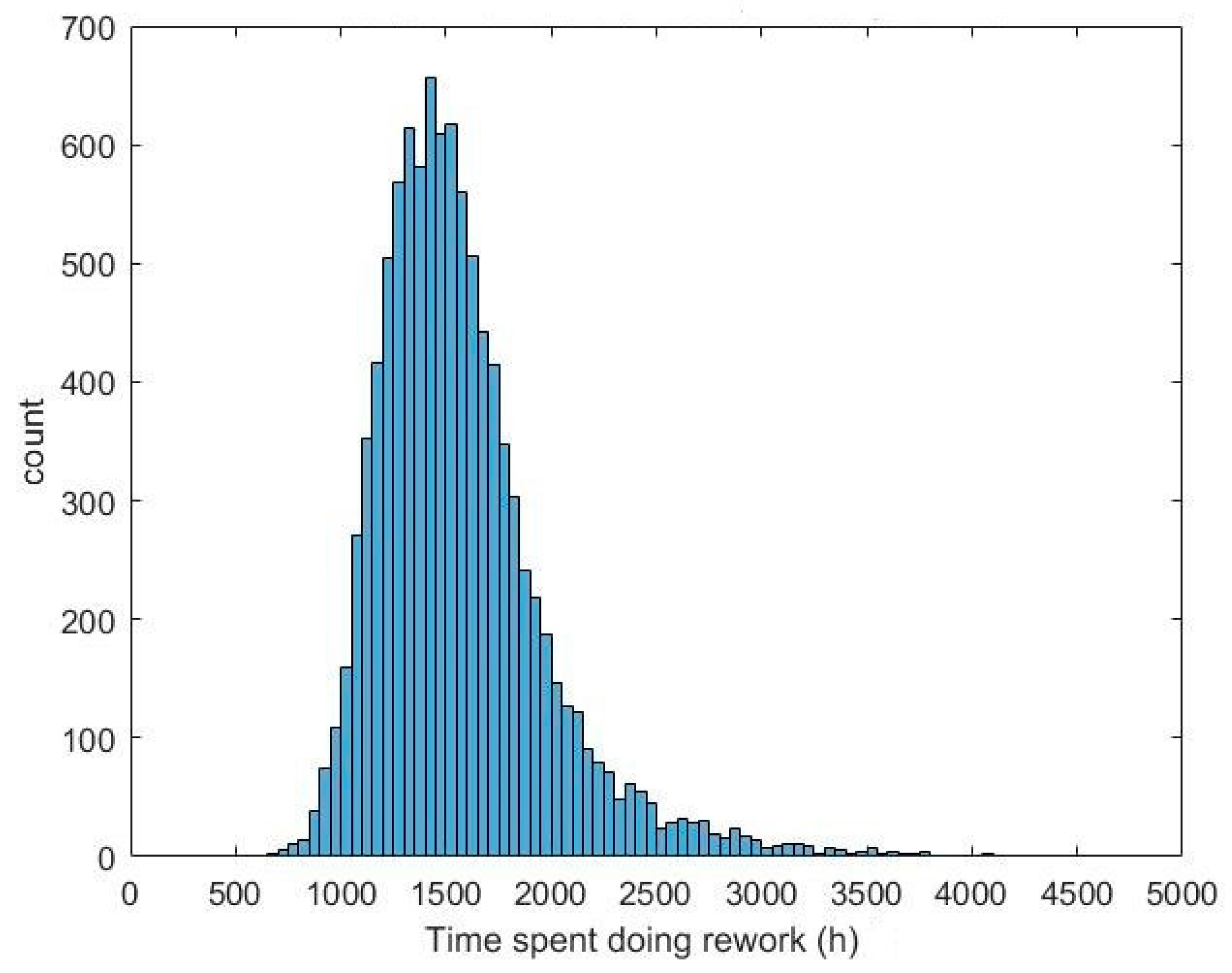
3.2. Launch Vehicle Development Simulation Results Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mesmer, B.L. Incorporation of Decision and Game Theories in Early-Stage Complex Product Design to Model End-Use; The University at Buffalo, State University of New York: New York, NY, USA, 2012. [Google Scholar]
- van Dam, K.H.; Nikolic, I.; Lukszo, Z. Agent-Based Modelling of Socio-Technical Systems; Springer Science & Business Media: Dordrecht, Germany, 2012; ISBN 978-94-007-4933-7. [Google Scholar]
- Perrone, L.F. Tutorial on Agent-Based Modeling and Simulation Part II: How to Model with Agents. In Proceedings of the 2006 Winter Simulation Conference, Monterey, CA, USA, 3–6 December 2006. [Google Scholar]
- Beck, K.; Beedle, M.; van Bennekum, A.; Cockburn, A.; Cunningham, W.; Fowler, M.; Grenning, J.; Highsmith, J.; Hunt, A.; Jeffries, R.; et al. Principles behind the Agile Manifesto. Available online: http://www.agilemanifesto.org/principles.html (accessed on 7 June 2016).
- Hazelrigg, G.A. Fundamentals of Decision Making for Engineering Design and Systems Engineering; Neils Corp: Portland, OR, USA, 2012; ISBN 978-0-9849976-0-2. [Google Scholar]
- Otto, K.N. Imprecision in Engineering Design; Antonsson, E., Ed.; Engineering Design Research Laboratory, Division of Engineering and Applied Science, California Institute of Technology: Pasadena, CA, USA, 2001. [Google Scholar]
- Mori, T.; Cutkosky, M.R. Agent-based collaborative design of parts in assembly. In Proceedings of the 1998 ASME Design Engineering Technical Conference, Atlanta, GA, USA; 1998; pp. 13–16. [Google Scholar]
- Levitt, R.E.; Thomsen, J.; Christiansen, T.R.; Kunz, J.C.; Jin, Y.; Nass, C. Simulating Project Work Processes and Organizations: Toward a Mocro-Contingency Theory of Organizational Design. Manag. Sci. 1999, 45, 1479–1495. [Google Scholar] [CrossRef]
- Jin, Y.; Levitt, R.E. The virtual design team: A computational model of project organizations. Comput. Math. Organ. Theory 1996, 2, 171–195. [Google Scholar] [CrossRef]
- Gero, J.S.; Kannengiesser, U. The function-behaviour-structure ontology of design. In An Anthology of Theories and Models of Design; Springer: Berlin/Heidelberg, Germany, 2014; pp. 263–283. [Google Scholar]
- Dorst, K.; Vermaas, P.E. John Gero’s Function-Behaviour-Structure model of designing: A critical analysis. Res. Eng. Des. 2005, 16, 17–26. [Google Scholar] [CrossRef]
- Vermaas, P.E.; Dorst, K. On the conceptual framework of John Gero’s FBS-model and the prescriptive aims of design methodology. Des. Stud. 2007, 28, 133–157. [Google Scholar] [CrossRef]
- Gero, J.S. Prototypes: A Basis for Knowledge-Based Design. In Knowledge Based Systems in Architecture; Acta Polytechnica Scandinavica: Helsinki, Finland, 1988; pp. 3–8. [Google Scholar]
- Gero, J.S.; Jiang, H. Exploring the Design Cognition of Concept Design Reviews Using the FBS-Based Protocol Analysis. In Analyzing Design Review Conversations; Purdue University Press: West Lafayette, IN, USA, 2015; p. 177. [Google Scholar]
- Gero, J.S. Design prototypes: A knowledge representation schema for design. AI Mag. 1990, 11, 26. [Google Scholar]
- Kan, J.W.; Gero, J.S. Using Entropy to Measure Design Creativity. Available online: https://pdfs.semanticscholar.org/ee51/228e545f46a083a5f2a23cc6f1e8bea0fb6c.pdf (accessed on 4 July 2016).
- Kan, J.W.; Gero, J.S. A generic tool to study human design activities. In Proceedings of the 17th International Conference on Engineering Design, Stanford, CA, USA, 24–27 August 2009. [Google Scholar]
- Indian Institute of Science. Research into design: Supporting sustainable product development. In Proceedings of the 3rd International Conference on Research into Design (ICoRD’11), Bangalore, India, 10–12 January 2011. [Google Scholar]
- Gero, J.S.; Jiang, H.; Dobolyi, K.; Bellows, B.; Smythwood, M. How do Interruptions during Designing Affect Design Cognition? In Design Computing and Cognition’14; Springer: Berlin/Heidelberg, Germany, 2015; pp. 119–133. [Google Scholar]
- Lewis, K.E.; Collopy, P.D. The Role of Engineering Design in Large-Scale Complex Systems; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012. [Google Scholar]
- Poleacovschi, C.; Collopy, P. A Structure for Studying the Design of Complex Systems; International Astronautical Federation: Naples, Italy, 2012. [Google Scholar]
- ISO/IEC/IEEE 15288:2015, Systems and Software Engineering—System Life Cycle Processes; International Organization for Standardization: Geneva, Switzerland, 2015.
- MIL-STD-499B. 1993. Available online: http://everyspec.com/MIL-STD/MIL-STD-0300-0499/MIL-STD-499B_DRAFT_24AUG1993_21855/ (accessed on 20 July 2017).
- Reich, Y. A critical review of general design theory. Res. Eng. Des. 1995, 7, 1–18. [Google Scholar] [CrossRef]
- Royce, W.W. Managing the development of large software systems. In Proceedings of the IEEE WESCON, Los Angeles, CA, USA, 25–28 August 1970; Volume 26, pp. 1–9. [Google Scholar]
- Schneider, S.A.; Schick, B.; Palm, H. Virtualization, Integration and Simulation in the Context of Vehicle Systems Engineering. In Proceedings of the Embedded World 2012 Exhibition & Conference, Numberg, Germany, 13 June 2012. [Google Scholar]
- Douglass, B.P. Agile Systems Engineering; Morgan Kaufmann: Burlington, MA, USA, 2015; ISBN 978-0-12-802349-5. [Google Scholar]
- Dependencies (DCMA Point 4—“Relationship Types” Assessment). Available online: http://www.ssitools.com/helpandsuport/ssianalysishelp/dependencies__dcma_point_4____relationship_types__assessment_.htm?ms=IQAgAg==&mw=MjQw&st=MA==&sct=MjMw (accessed on 21 February 2017).
- Cocco, L. Complex System Simulation: Agent-Based Modeling and System Dynamics. 2013. Available online: https://iris.unica.it/retrieve/handle/11584/266241/344640/Cocco_PhD_Thesis.pdf (accessed on 18 July 2019).
- Sutherland, J.; Schwaber, K. The Scrum Papers; Scrum: Paris, France, 2007. [Google Scholar]
- Dingsøyr, T.; Nerur, S.; Balijepally, V.; Moe, N.B. A decade of agile methodologies: Towards explaining agile software development. J. Syst. Softw. 2012, 85, 1213–1221. [Google Scholar] [CrossRef]
- SAFe 4.0 Introduction; Scaled Agile Inc.: Boulder, CO, USA, 2016.
- Scaled Agile Framework—SAFe for Lean Software and System Engineering. Available online: http://v4.scaledagileframework.com/ (accessed on 2 October 2017).
- Case Study—Scaled Agile Framework. Available online: https://www.scaledagileframework.com/case-studies/ (accessed on 20 April 2016).
- Lam, J. SKHMS: SAFe Adoption for Chip Development. Available online: https://www.scaledagileframework.com/hynix-case-study/ (accessed on 20 April 2016).
- Thomas, L.D. System Engineering the International Space Station. Available online: https://www.researchgate.net/publication/304212685_Systems_Engineering_the_International_Space_Station (accessed on 23 July 2019).
- Rigby, D.K.; Sutherland, J.; Takeuchi, H. Embracing agile. Harv. Bus. Rev. 2016, 94, 40–50. [Google Scholar]
- Szalvay, V. Complexity Theory and Scrum. blogs.collab.net 2006. Available online: http://blogs.collab.net/agile/complexity-theory-and-scrum (accessed on 5 November 2015).
- Dyba, T.; Dingsøyr, T. Empirical studies of agile software development: A systematic review. Inf. Softw. Technol. 2008, 50, 833–859. [Google Scholar] [CrossRef]
- D’Ambros, M.; Lanza, M.; Robbes, R. On the Relationship between Change Coupling and Software Defects. In Proceedings of the 2009 16th Working Conference on Reverse Engineering, Lille, France, 13–16 October 2009; pp. 135–144. [Google Scholar]
- Schwaber, K. Scrum development process. In Business Object Design and Implementation; Springer: Berlin/Heidelberg, Germany, 1997; pp. 117–134. [Google Scholar]
- Bott, M.; Mesmer, B.L. Determination of Function-Behavior-Structure Model Transition Probabilities from Real-World Data; AIAA: San Diego, CA, USA, 2019. [Google Scholar]
- Mascagni, M.; Srinivasan, A. Parameterizing parallel multiplicative lagged-Fibonacci generators. Parallel Comput. 2004, 30, 899–916. [Google Scholar] [CrossRef]
- Binder, K.; Heermann, D.; Roelofs, L.; Mallinckrodt, A.J.; McKay, S. Monte Carlo Simulation in Statistical Physics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Box, G.E.P. Science and Statistics. J. Am. Stat. Assoc. 1976, 71, 791–799. [Google Scholar] [CrossRef]
- Coupling (Computer Programming). Available online: https://en.wikipedia.org/w/index.php?title=Coupling_(computer_programming)&oldid=787318124 (accessed on 16 October 2017).
- Cho, G.E.; Meyer, C.D. Markov chain sensitivity measured by mean first passage times. Linear Algebra Appl. 2000, 316, 21–28. [Google Scholar] [CrossRef]
- Petty, M.D. Verification, validation, and accreditation. In Modeling Simulation Fundamentals. Theoretical Underpinnings Practical Domains; Wiley: Hoboken, NJ, USA, 2010; pp. 325–372. [Google Scholar]
- Gero, J.S.; Kannengiesser, U. Modelling expertise of temporary design teams. J. Des. Res. 2004, 4, 1–13. [Google Scholar] [CrossRef]
- Gero, J.S.; Kannengiesser, U. The situated function–behaviour–structure framework. Des. Stud. 2004, 25, 373–391. [Google Scholar] [CrossRef]
- Ferrenberg, A.M.; Swendsen, R.H. Optimized Monte Carlo Data Analysis. Comput. Phys. 1989, 3, 101–104. [Google Scholar] [CrossRef]






| Metric | Expected Result | Software Program Simulation Result | Launch Vehicle Simulation Result |
|---|---|---|---|
| Productivity | 36%–50% Gain | 42% Gain | 1% Gain |
| Time to Market | 30%–70% Faster | 62% Faster | 12% Faster |
| Reduction in Defects | ~50% Fewer | 57% Fewer | 3% More |
| Metric | Waterfall Simulation | Agile Simulation | Difference in Waterfall and Agile Means | Expected Result |
|---|---|---|---|---|
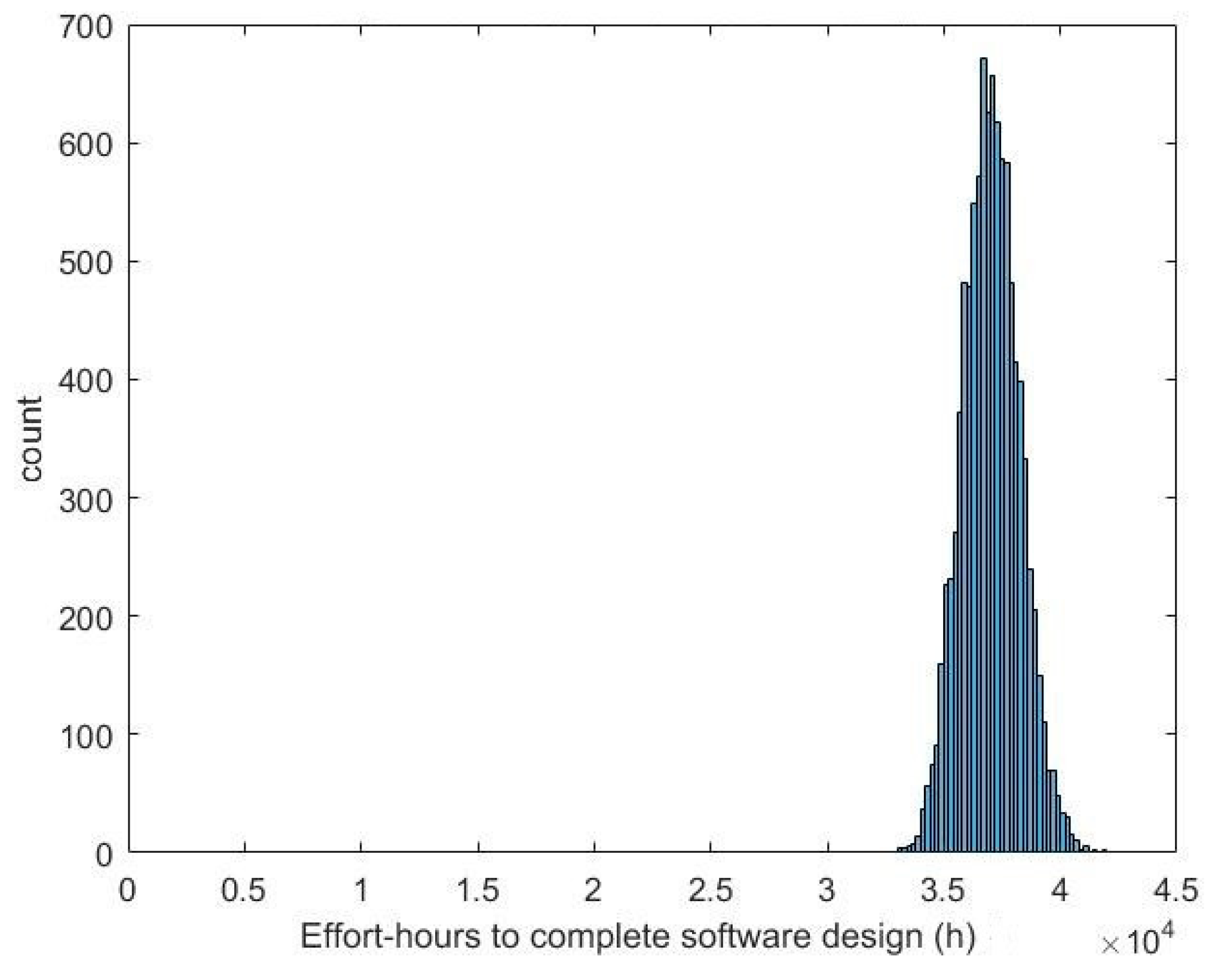
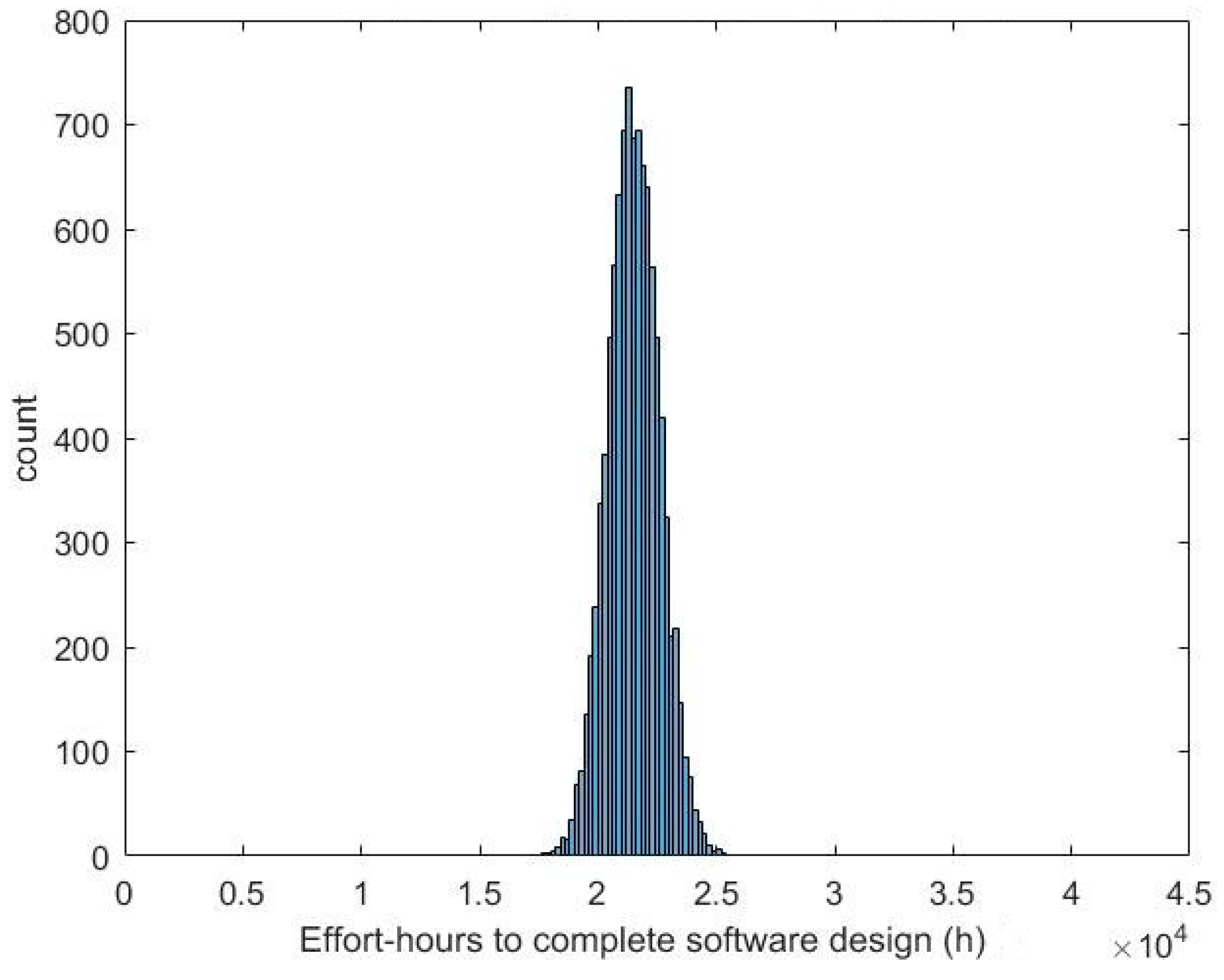
| Effort hours | Mean: 37,038 h SD: 1225 h | Mean: 21,518 h SD: 1091 h | 42% less time in Agile mean | 36%–50% less |
| Total time expended | Mean: 2012 h SD: 337 h | Mean: 765 h SD: 157 h | 62% less time in Agile mean | 30%–70% less |
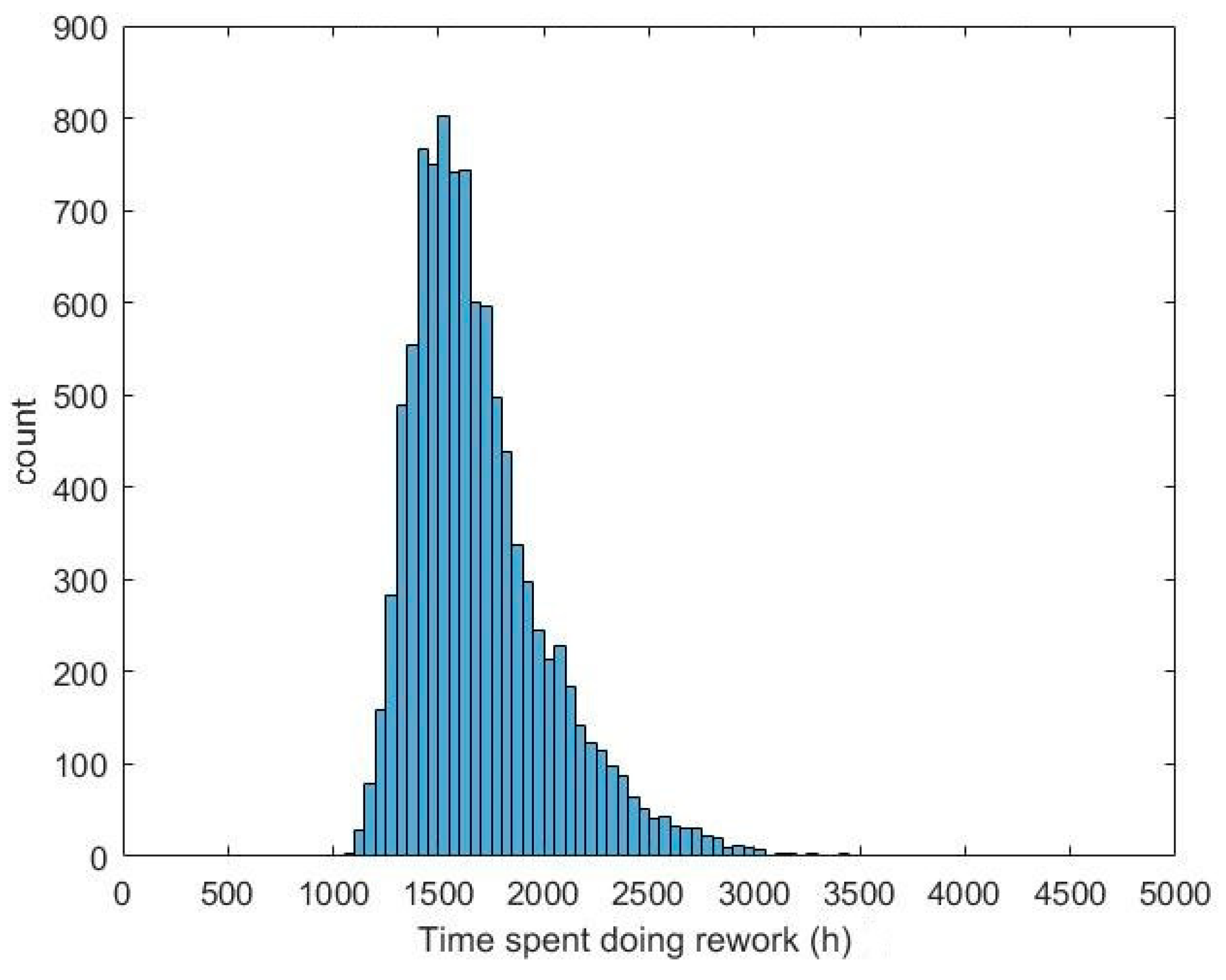
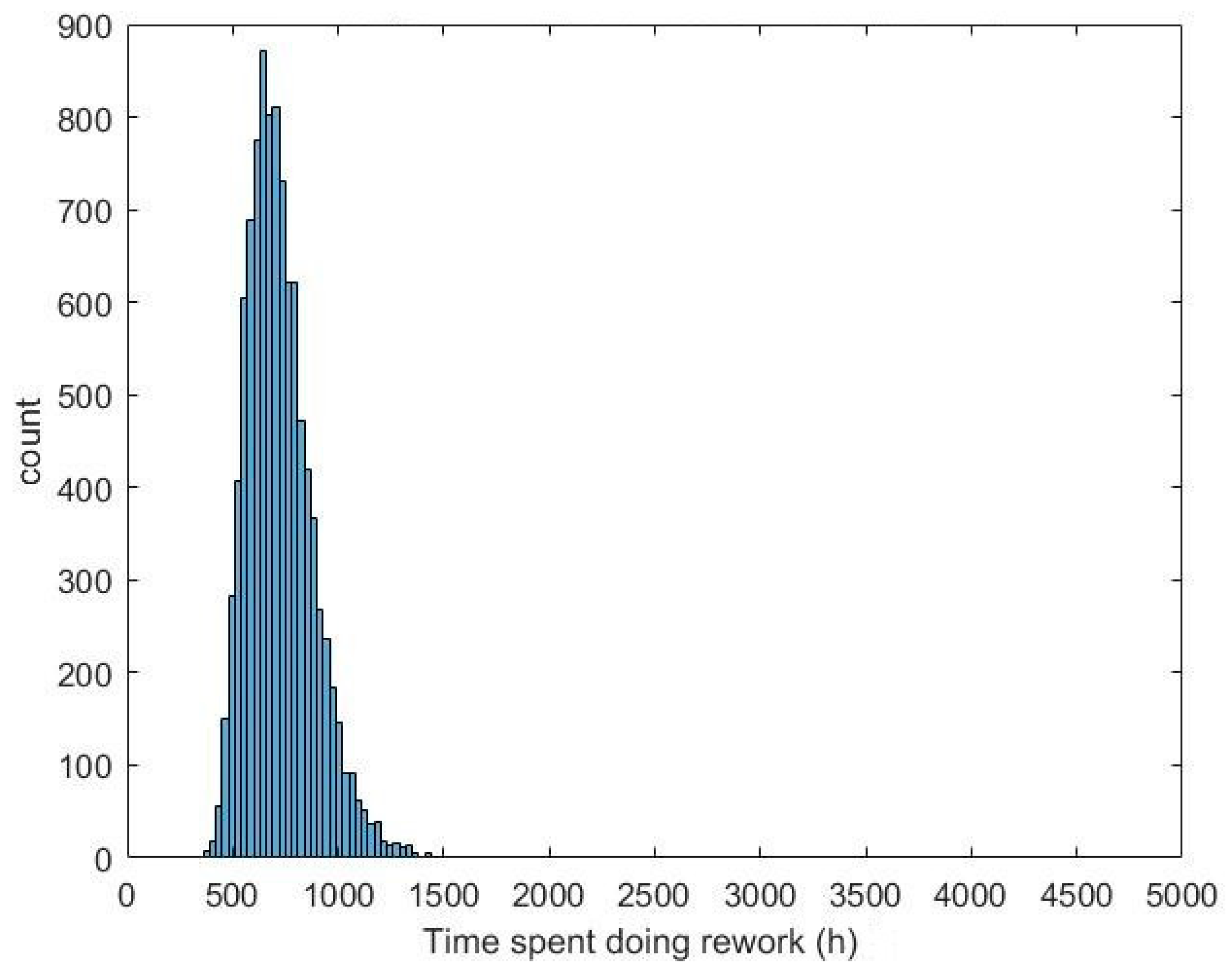
| Time spent in rework | Mean: 1693 h SD: 332 h | Mean: 724 h SD: 157 h | 57% less time in Agile mean | ~50% less |
| Metric | Waterfall Simulation | Agile Simulation | Difference in Waterfall and Agile Means |
|---|---|---|---|
| Effort-Hours | Mean: 22,846 h SD: 1693 h | Mean: 22,672 h SD: 1724 h | 1% fewer hours in Agile mean |
| Total time expended | Mean: 1836 h SD: 405 h | Mean: 1608 h SD: 407 h | 12% fewer hours in Agile mean |
| Time spent in rework | Mean: 1519 h SD: 402 h | Mean: 1569 h SD: 407 h | 3% more hours in Agile mean |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bott, M.; Mesmer, B. Agent-Based Simulation of Hardware-Intensive Design Teams Using the Function–Behavior–Structure Framework. Systems 2019, 7, 37. https://doi.org/10.3390/systems7030037
Bott M, Mesmer B. Agent-Based Simulation of Hardware-Intensive Design Teams Using the Function–Behavior–Structure Framework. Systems. 2019; 7(3):37. https://doi.org/10.3390/systems7030037
Chicago/Turabian StyleBott, Mitch, and Bryan Mesmer. 2019. "Agent-Based Simulation of Hardware-Intensive Design Teams Using the Function–Behavior–Structure Framework" Systems 7, no. 3: 37. https://doi.org/10.3390/systems7030037
APA StyleBott, M., & Mesmer, B. (2019). Agent-Based Simulation of Hardware-Intensive Design Teams Using the Function–Behavior–Structure Framework. Systems, 7(3), 37. https://doi.org/10.3390/systems7030037






