Abstract
The basic processes that bring about living systems are conventionally represented in the framework of chemical reaction networks. Recently, it has been proposed that this framework can be exploited for studying various other phenomena. Reaction networks are specially suited for representing situations where different types of entities interact in contextual ways leading to the emergence of meta-structures. At an abstract level, a reaction network represents a universe whose evolution corresponds to the transformation of collections of entities into other collections of entities. Hence, we propose that systems correspond to the sub-networks that are stable enough to be observed. In this article, we discuss how to use reaction networks for representing systems. Namely, we introduce the different representational levels available (relational, stoichiometric, and kinetic), we show how to identify observable systems in the reaction network, discuss some relevant systemic notions such as context, emergence, and meta-system, and present some examples.
1. Introduction
Systems theory (ST) focuses on the properties, laws, principles and phenomena that different kinds of systems share. Particularly, the founders of systems theory emphasized the importance of studying the structural isomorphism between systems of different domains of reality, which are studied by different scientific disciplines. Consistently, mathematical modeling was proposed as the main interdisciplinary tool of systems theory due to its suitability to represent and handle the formal structure of systems independently of the nature of their components [1,2].
The mathematical modeling of systems has considered a variety of frameworks, usually different when changing from one area of knowledge to another. In general, there is a tradeoff between how precise is the description of the system and its properties, and the number of entities and types of interaction. For example, when an ecological system of only a few species is considered, differential equations are used and exact knowledge of the system can be gathered. However, this approach is not scalable to large ecological systems because the equations involved are too complex and thus the dynamics cannot be computed. In such cases, alternative frameworks such as network or agent-based models are used. These frameworks can simulate some aspects of the dynamics of large systems, but important features that can be studied using differential equations such as the sensitivity to perturbations and the dependence on the system’s parameters are lost [3].
Moreover, although well-grounded philosophical and structural principles have been developed for systemic thinking, and although the importance of integrating different areas of knowledge in the mathematical representations has been constantly stressed [4,5], interdisciplinary scientists have had a hard time trying to develop formal representations of systems that integrate diverse areas of knowledge. As a consequence of this, we can conclude that systemic thinking lacks a formal language to express the full scope of systemic thoughts [6].
In conclusion, one of the big challenges in ST is developing a language that allows for putting multiple perspectives into play, but at the same time is mathematically well-grounded so large scale interdisciplinary models can be developed and tested.
In various biochemistry-related areas such as systems biology, bioinformatics, and chemical computing, reaction networks are the mainstream language of representation [7,8,9]. Interestingly, the language of reaction networks allows for three levels of representation: relational, stoichiometric, and kinetic, respectively. These three levels are increasingly richer in their mathematical structure. On the relational level, one can represent simple structural properties such as connectivity and cycles, and is mainly used for visualization purposes [10,11]. On the stoichiometric level, one can analyze quantitative structural properties of the processes occurring in a reaction network such as elementary flux-modes and self-maintainance [12], and, on the kinetic level, one can compute the time-evolution of the reaction network and perform a detailed study of it [13].
A recent advance of the reaction network formalism is Chemical Organization Theory (COT) [14]. In COT, a reaction network can be associated with a set of organizations, which represent the sustainable subnetworks of the reaction network, and can be computed relatively easily. In fact, the study of biochemical reaction networks can hardly be developed using traditional system dynamical tools for large reaction networks [15]. However, organizations have been proven to provide a landscape of the long-term dynamics, and thus characterize the observable systems emerging from a reaction network. Hence, COT is a language that helps to bridge the gap between precision of the representation and size of the system. COT has been applied to study several metabolic and other biochemical systems [16,17,18], and has been proposed as a framework for chemical computation [19] and model checking [20].
Formalisms mathematically equivalent to the language of reaction networks have emerged, rather unexpectedly, in areas outside biology. Namely, formalisms in the early times of parallel computation such as Vector Addition Systems [21] and Petri Nets [22], and, in Linguistics, a formalism known as commutative grammars [23], have been proven to be mathematically equivalent to reaction networks [24,25]. The discovery of these equivalences has led to important cross-fertilizations between biology and computer science [26]. Moreover, since traditional networks are a special type of reaction networks, where only one-to-one relations are allowed, the network-based models in areas such as ecology and social science [27,28] can also be understood as mathematical representations using a simplified version of the language of reaction networks.
Why have reaction networks emerged as a representational language in seemingly different areas of knowledge? The reason is simple but profound. Reaction networks (or any language mathematically equivalent to it) entail a natural way to represent universes where the interactions among entities are of transformational nature.
Hence, thinking of reaction networks not as a framework for representing biochemical interactions, but as a language for representing processes of transformation, proposes an interesting way to understand and represent systems as processes that are self-maintaining, and thus stable enough to be observed in time [29,30]. Representing systems by reaction networks not only permits the incorporation of different perspectives into play but also the possibility to represent and study the long-term dynamics of systems with a large number of entities and interactions. Attempts of modeling systems using reaction networks beyond the biochemical domain have been developed in political, decision-making, and economical systems [31,32,33]. Remarkably, these applications have been carried out combining scholars in various fields including social science, bioinformatics, and mathematics. Hence, these works entail a truly formal interdisciplinary dialogue.
In this paper, we discuss how reaction networks can serve as both a framework-for-thinking-about and a language-for-modeling systems. In Section 2, we introduce the three levels of description available to represent reaction networks and introduce some relevant properties. In Section 3, we present COT, in Section 4, we discuss how to model systems using reaction networks and present some systemic relevant notions in our framework, in Section 5, we present examples of non biochemical systems modeled using reaction networks, and we present our conclusions and future perspectives in Section 6.
2. Reaction Networks
We introduce the notions of the reaction network formalism that are necessary to understand the relational, stiochiometric and dynamical levels of representation, and to introduce COT. Most of the material of this section, with the exception of the identification of different layers of representation, is standard material in the reaction networks literature. For a comprehensive treatment of the reaction network formalism, we refer to [9,34]. From now on, let be a set of m species that can react with each other according to a set of n reactions. Reactions describe how certain collections of species transform into other collections of species. For a given reaction , the species to be transformed, i.e., consumed by r, are called reactants of r, and the species to be created by this transformation are called products. Together, the set of species and the set of reactions are called reaction network .
In general, some reactions in might occur more often than others. A particular specification of the occurrence of reactions within the reaction network is called reaction process, or simply process (In reaction network modeling, is usually called flux vector. We are introducing a slightly more general notion because our aim lies beyond the modeling of biochemical systems) and denoted by .
Before proceeding with a more detailed description of how reaction networks and processes are represented, note that, for any set of species , we find a unique maximal set of reactions , defined as the set of all reactions whose reactants are in X. Thus, each set X induces a sub-network . Hence, a process applied to X can only contain reactions from .
Note that implies . Thus, a process applied to X can always be applied to . On the contrary, if is a process applied to , can be applied to X only if considers reactions in only.
In this section, we will be concerned with the structure of a set . To do so, we will introduce three (increasingly more complex) ways to represent a process, and define some properties related to the consumption and production of species. Since we focus on a set , we assume that contain reactions in only.
2.1. Relational Descriptions
Relational descriptions are the simplest form of representation of reactions and processes. Reactions is specified by a set of consumed species, and a set of produced species, and denoted by , and a process is simply a set of reactions.
Definition 1.
X is closed w.r.t. iff . If X closed w.r.t. the process , we say that X is structurally closed.
The notion of closure formalizes the fact that no new species are created by a process. For structurally closed sets, no process can create new species. Note that, although X can be closed for certain processes, such as the (trivial) empty process, if X is not structurally closed, the processes for which X is not closed might change its structure. Indeed, when X is not structurally closed, some reactions are such that is not a subset of X. Therefore, at least one species is not in X. Hence, whenever such reactions occur in a process applied to X, new species are added. As a consequence, reactions that are in but not in might become available for further processes that, in turn, might add new species. This mechanism can continue until no new species can be added by any process, i.e., when a structurally closed set has been reached.
Lemma 1.
For all X, the structurally closed set of minimal cardinality that contains X is unique [14].
Definition 2.
X is semi-self-maintaining w.r.t. if and only if . If X is semi-self-maintaining w.r.t. , we say that X is structurally semi-self-maintaining.
Similarly to structural closure, the evolution of a reaction network generally leads to a structural semi-self-maintaining network. Indeed, if a set X is not structurally semi-self-maintaining, then, for some processes, we have that the reactants consumed by the reactions in the process are not being produced by any reaction in the process. Therefore, such species that are not produced are going to be consumed by the processes occurring in the reaction network, until a structurally semi-self-maintaining set is obtained.
Definition 3.
Two species are directly-connected w.r.t. X if and only if there exist a reaction such that . We say are connected w.r.t. X if and only if there is a sequence of species such that , is directly-connected to and .
The connected relation is a generalization of connectivity for traditional networks. In particular, it allows for decomposing a reaction network into a collection of non-interacting subnetworks. In fact, note that every reaction consumes/produces species that are directly-connected to the reactants, and when two species and are not connected, we have that none of the species connected to are connected to any of the species connected to and vice-versa. From here, it is easy to deduce that any process applied to X can be partitioned into a list of disjoint sub-processes, and that each of these sub-processes in turn correspond to disjoint subsets of species of X. From now on, we will assume that all species in X are connected.
2.2. Stoichiometric Description
Note that, in a relational description, reactions provide information about the type of species transformed only, but not about how many species of each type are transformed by the reaction. A stoichiometric description provides a new level of information on how reactions and processes are represented. A reaction is represented by
with , and , and .
The number denotes the number of reactants of type of the i-th reaction. Together, these numbers form a reactant matrix . Analogously, the number denominates the number of products of type of the i-th reaction. Together, these numbers form a product matrix . From here, we can encode the way in which species are consumed and produced by the reactions in the stoichiometric matrix .
Since the stoichiometric description counts the amount of each type of species involved in the reactions, processes can be extended to specify the number of times that each reaction occurs. Thus, a process corresponds to a vector .
We can also represent the state of a reaction network by a vector of non-negative coordinates such that corresponds to the number of species of type in the reaction network, . Moreover, we can compute the state of the reaction network associated to a state and a process by the following equation:
For simplicity, we have assumed that the coordinates of are large enough for the reactions in to take place in any order (The study of processes where the number of species is small has been profoundly studied in the context of Petri Nets using the notion of deadlock state [22]. See also [35].).
From here, we can define some relevant quantitative roles for the species participating in a process. For simplicity, we will assume that X is a closed set (When this condition is not satisfied, the definitions below require minor modifications that are not relevant for the purposes of this article.), and that a process applied to X is such that if then .
Definition 4.
A species is a catalizer w.r.t. X if and only if implies .
A catalizer is not affected by the action of a process in the reaction network. There are two interesting facts about catalizers. First, if s is a catalizer w.r.t. X, then s is a catalizer with respect to all , but not necessarily with respect to . Second, catalizers w.r.t. X correspond to a row of zeroes in the stoichiometric matrix associated to , and thus are easy to compute.
Lemma 2.
A species is a catalizer w.r.t. X if and only if for all process applied to X, we have that .
Definition 5.
Let be a non-null process vector applied to X such that does not have negative coordinates. If , we say that is overproduced by in X.
Overproduced species have the potential to unlimitedly increase their amount by repeating the process which overproduces them. Therefore, overproduced species can be considered as an unlimited resource in the reaction network. Interestingly, an overproduced species by in X is also overproduced by in any . Moreover, if two species and in X are overproduced by the processes and , respectively, it is trivial that overproduces the set in X.
Both overproduced species and catalizers can be used to refine the notion of connectivity (see Definition 3), and thus help to provide a much more elegant decomposition of the reaction network into dynamically independent sub-networks. For the sake of simplicity, we will not elaborate on this issue here, but refer the reader to [36] for an elaborated exposition of these results.
Moreover, the notion of (structural) semi-self-maintaining networks can be extended in the stoichiometric description, leading to a quantitative definition of sustainable reaction network.
Definition 6.
Let be a non-null process. X is weak-self-maintaining with respect to if and only if , . If, additionally, such process satisfies if and only if , we say X self-maintaining.
Lemma 3.
If X is self-maintaining, then X is structurally semi-self-maintaining.
For a weak-self-maintaining set X, there are processes that lead to a non-negative production of all the species involved in the process. These processes, however, might not use all the reactions in . For self-maintaining sets, we can find processes such that every reaction in occurs, and the result of the process does not lead to the consumption of any species. Therefore, self-maintaining sets entail the parts of the reaction network where self-sustainable processes, at a quantitative level of description, can occur.
2.3. Kinetic Description
In order to quantify the overall transformation of species derived from a process occurring in time, we represent the state vector as a function of time , where encodes the number of species at time t.
Suppose that the process occurs between times and . Therefore, we can obtain from , and as follows:
This equation provides a formal description for the change of the number of species driven by a process [37].
By setting the diffenence between and infinitely small, Equation (3) becomes the differential equation
with initial conditions specified by .
In this case, the process vector is a function of time. Usually, is conceived as a function of time t, the state vector , and a vector of parameters associated to the reactions and given by the dynamical rules of the system. The common case of continuous dynamics is the mass-action kinetic law [13], where the state vector represents the concentration of species in the reaction network at time t, and the process vector function is defined by:
for and is a strictly positive vector whose coordinates are called reaction rate constants.
For (discrete or continuous) probabilistic dynamics, the process vector represents the probability of occurrence of the reactions in the network.
A reaction network together with the discrete/continuous and deterministic/probabilistic kinetic law is called a reaction system. A reaction system is the most refined description of a reaction network because it describes how the local dynamics evolve.
3. Connecting the Description Levels: Chemical Organization Theory
The relational, stoichiometric and kinetic levels of representation present three increasingly precise ways of representing a reaction network and its processes. However, the gain in precision is compensated with an increase in the computational resources required to identify the properties of the reaction network. In Table 1, we summarize some important structural features and the computational resources required for identifying such structures at each level of representation.

Table 1.
Table of scalability of properties depending on the level of representation. Each property is either not computable, or a level or scalability is associated. A property is more scalable if it can be computed for larger networks. Hence, Full, Moderate, and Hard scalability represent three levels of increasingly more complex computation, respectively.
Namely, the relational description is capable of identifying connectivity-related properties in the network by means of simple set-like operations, but is unable to describe properties of quantitative nature. The stoichiometric description allows for describing properties of quantitative nature by means of matrix algebra operations (which are computationally tractable for moderately large networks), but it is unable to describe the influence of kinetic parameters and the precise time-evolution of a reaction network. The kinetic description is able to fully represent the influence of parameters and the time-evolution of a reaction network, but such description requires solving a highly coupled and nonlinear system of (either discrete, stochastic, or differential) equations. These equations do not have an analytic solution in most cases. Hence, the exploration of the dynamics of a reaction network requires numerical solutions that become intractable for large reaction networks.
Since a full-featured understanding of the dynamics of a reaction network is intractable at the kinetic level, COT proposes that certain structural properties at the kinetic level can be traced at the relational or stoichiometric levels, and thus at a computationally affordable cost. Such structural traces are, technically speaking, necessary conditions for the desired properties of the reaction system. In particular, COT focuses on the connection between structural properties at the relational and stoichiometric levels with the long-term behavior of the reaction system.
To this end, COT introduces the crucial notion of organization:
Definition 7.
X is a (semi-)organization if and only if X is closed and (semi-)self-maintaining.
An organization satisfies simultaneously the relational-level property of closure and the stoichiometric-level property of self-maintaining. By combining these two requirements, COT identifies the structural footprint of stable dynamics. Namely, a closed set of species entails a subnetwork whose processes do not produce new species, and within these closed dynamics, there are processes that allow self-maintenance of the quantity of species in the system. Therefore, as long as self-maintaining processes occur, the subnetwork will be preserved in time.
In order to connect the notion of organization with the dynamical level, we introduce the following notions.
Definition 8.
Let be the power set of and
For a state , the set is the abstraction of . For a given set of species , a state is an instance of X if and only if its abstraction equals X.
The notions of abstraction and instance connect the representations of the reaction network with the reaction system, and organizations represent the abstractions of all the possible stable instances:
Theorem 1.
If is a fixed-point of the ODE (4), i.e., , then the abstraction is an organization [33].
Fixed points entail the simplest dynamically stable instances of a reaction system, and are crucial for determining most important features of the dynamics of a system [38]. Thus, Theorem 1 provides a link between the long-term behavior of a reaction system and its underlying reaction network. In simple words, it proves that a necessary condition to be a fixed point at the kinetic level is to be an organization at the stoichiometric level (and thus a a semi-organization at the relational level). Moreover, in [39], Theorem 1 is extended to other stable asymptotic behaviors such as periodic orbits and limit cycles. In addition to these results, necessary conditions for the existence of adequate flux vectors are explored in [40], and algorithmic studies concerning the computation of the organizations of a reaction network are presented in [41,42,43].
4. Discussion: Reaction Networks and the Modeling of Systems
We now discuss some general aspects about using reaction networks as a language for the modeling of systems.
4.1. Reaction Networks as Universes and Organizations as Systems
In the reaction network formalism, we define species and reactions to specify how the entities we consider interact and transform. Therefore, it is important to stress that we do not start from the idea of a pre-existing system to be modeled. On the contrary, we start from a set of relevant entities, which can be of any nature (physical, cognitive, economic, etc.), and we determine a set of rules that specify how combinations of these entities transform into new combinations. Since, for a system, it is generally assumed that it is, to some extent, stable in time so it can be observed, and it holds certain properties that entail its qualitative identity, we propose that the more adequate notion of system is a subnetwork such that X is an organization. Therefore, systems are conceived as self-maintaining entities that emerge from the universe of interactions [29,44]. This explains the notion of qualitative identity of a system from a dynamic perspective. Namely, a system is continuously changing its inner components and sub-processes, but the qualitative identity and unity are secured as long as the reaction network is structurally closed and its inner processes are self-maintaining. Hence, the reaction network plays the role of universe of existence and interaction, and the organizations play the role of potentially observable systems in this universe.
The latter view allows for a recursive representation of the systems in a universe [45]. In case the whole reaction universe is an organization, we conceive it as the largest possible system, if not, several largest systems might exist. By looking inside the largest systems, we find smaller systems that are contained in the largest systems, and continue recursively until we arrive to the smallest organizations, which play the role of minimal observable entities.
Since we are free to chose our basic entities and processes, a fundamental step when modeling with reaction networks is to choose a basic representational ontology which includes the fundamental entities in the transformational universe, and then define the transformation rules among these basic entities. Next, we can extend the representation of such universe by incorporating either new entities and new reactions, or by replacing existing entities and reactions by a deeper or fine-grained representation of the replaced entities.
4.2. Inner and External Contexts
In the reaction network formalism, we identify two fundamentally different notions of context. The first is the epistemic (or external) context that corresponds to the choice of the subnetwork to be considered. The external context specifies what entities and interactions we consider. In this approach, we start from our universe and analyze specific external contexts represented by subnetworks . The choice of an external context constrains the entities to be found and the transformations allowed to occur.
The second context operates within the external context. This behavioral (or inner) context specifies what processes are allowed to occur and how they occur. The inner context determines whether a subnetwork is self-maintaining, and thus an organization. If the inner context forbids the occurrence of self-maintaining processes, we have that will not be stable in time, and thus not observable.
The previous observation implies an interesting dichotomy between structure (external context) and dynamics (inner context) in the study of systems. The importance of this dichotomy has not been widely acknowledged by the biochemistry-related community working with reaction networks models. It occurs for two main reasons. First, in most biochemical cases, the reaction network is meant to model a predefined system, thus the notion of external context is of virtual nature only. Secondly, biochemical processes are governed by deterministic physical laws. Hence, the inner context of the reaction network is fixed by deterministic principles of the biochemical domain [13].
However, by considering reaction networks as a language for modeling systems, species might not be biochemical or even physical entities. Hence, processes might not necessarily obey any determined set of rules, and thus external and inner contexts might become relevant and influence each other.
4.3. The Emergence of Systems and Meta-Systems
In the reaction network approach, the emergence of a stable system is a natural consequence of the dynamics. In fact, Theorem 1 states that stable dynamical regimes correspond to organizations in the reaction network. This is equivalent to say that the systems we observe are observable because they are stable enough in time to be observed, and that this stability is the consequence of a dynamical process. Therefore, systems are stable structures of processes emerging from the transformational interactions, i.e., dynamics, occurring in the universe.
In COT, a reaction network is represented as a hierarchy of subnetworks. At the lowest level, we have the empty reaction network (0 species), and each subsequent level has subnetworks having more species. At the highest level, we find the set . This representation is known as the Hasse diagram (see Figure 1).
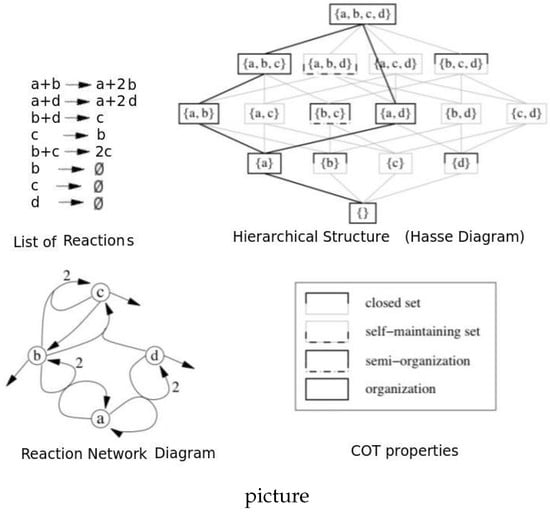
Figure 1.
Example of hierarchy of reaction networks and their properties in COT. Inspired from [14].
This setting is convenient for explaining not only the emergence of systems from the interaction of species, but also the emergence of meta-systems from the interaction of systems. Since we conceive organizations as systems, we note that when two or more organizations interact, a new reaction network is formed. Since the new reaction network can have reactions that are not in any of the former organizations, the union of two (or more) organizations may or may not be an organization. In the example in Figure 1, we see that both and are organizations, but when they combine to become , the new reaction becomes active. Therefore, is not closed and thus is not an organization, but its closure is closed and self-maintaining, and thus an organization. This simple example illustrates that organizations form a hierarchy, and that this hierarchy can be used to explain how meta-systems can non-trivially emerge by the interaction of systems.
4.4. The Lack of Identity Problem and the Membrane Solution
One important drawback of the reaction network formalism is that the species do not have individual identity. This means that given a certain species type s, we have that all the species of this type are equivalent in the reaction network. This has proven to be problematic for modeling systems where species represent entities having mechanisms of memory or recognition [32]. Moreover, there is a way to construct virtual cells of interaction in an extended reaction network formalism known as membrane or P-systems [46]. In the P-systems framework, we allow different reaction networks to exist, and each of these reaction networks is enclosed in a membrane and thus is allowed to evolve separately from the other reaction networks. However, each reaction network is also allowed to exchange species with other reaction networks by means of a common space. Therefore, indirect communication between reaction networks is possible.
The use of membranes brings a new modeling dimension because we can attribute agency properties to reaction networks, and since membranes can be recursively defined, we can assign recursive layers of individual identity within an agent. Moreover, by properly labeling species according to the compartment they belong to, we can model interactions where mechanisms of recognition and even memory operate. Remarkably, it has been shown that when, for even the simplest cases where two reaction networks interact, it is possible that both networks co-stabilize in an organization, even though the two reaction networks are not stable on their own [40].
4.5. Resilience and Other Modern Systemic Notions
The reaction network approach provides a suitable landscape of concepts to formalize some modern systemic notions. As an example, we will elaborate on the notion of resilience. Resilience has been defined as the ability of a system to cope with change (There is a large number of definitions for the concept of resilience [47]. We use this definition due to its simplicity and generality.). By ‘cope’, authors generally mean ‘to be able to maintain its qualitative identity’, and ‘change’ means ‘a perturbation.’ However, the notion of qualitative identity, as well as the notion of perturbation, are generally applied in a non-formal manner. This leads to multiple interpretations of the notion of resilience. In our approach, the notions behind resilience can be properly defined. In fact, the qualitative identity of a system in this setting corresponds to an organization together with a self-maintaining process occurring in it, and the perturbation corresponds to three different types of change. The first is a change of state, and this means increasing or decreasing the values of the coordinates of the vector . The second is a change of the inner context, and this means changing the set of possible processes that can occur in the system. The third is a change of the external context, and this means adding or eliminating species and/or reactions in the system.
Since the notion of identity and change are properly defined, resilience can be formally studied using reaction networks. In a similar way, we propose that other notions introduced in the system theory literature such as robustness, adaptivity, etc. can be formalized using structural properties of a reaction network. We will not elaborate on the details of these notions here, but refer to [36] for a mathematical framework to formalize such notions.
5. Examples
We now overview three cases of non-biochemical systems that have been modeled using reaction networks.
5.1. Social System: Political Structure
The use of reaction networks as a language for modeling political systems was inspired by Luhmann’s approach to sociology [48]. Luhmann introduced the notion of communication as the basis of societies’ structuring and ordering [49]. The concept of communication is defined as the flow produced by the exchange of social-symbols. These symbols belong to different social structures. For example, for simple economical, legal and political structures, the communication flow is done through money, justice and power, respectively. In a general case, all of these structures overlap, and, hence, communications in one system may affect the others. Therefore, a social system emerges from these structures of communication.
In [31], Dittrich and Winter developed a reaction network that represents a toy-model of the political system based on Luhmann’s concept of communication. They define 13 communication species, e.g., social movement demands ‘’ (acronym from the German: Soziale Bewegung Forderung), social movement members ‘’ (Soziale Bewegung Mitglieder), potential collective binding decisions ‘’ (Potenzielle Kollectiv Verbindliche Entscheidungen), etc., and a set of 20 reactions to model the interactions among these communications. For example, the reaction ‘’ models that Demands from social movements can be stimulated by potential collectivly binding decisions. The species ‘’ corresponds to a social movement demand decision (e.g., do not increase the tax), that may be expressed as a protest, or by other actions, ‘’ might correspond to a potential law such as increase the tax, and ‘’ corresponds to the communications that the social movement members discuss or spread (for example within social networks). For simplicity, we will not present the full set of species and reactions, but provide a diagram of the topology of the network and the hierarchy of organizations in Figure 2.
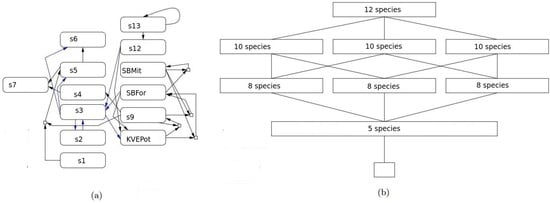
Figure 2.
(a) Topology of the reaction network model of the political system. Labelled boxes represent species and arrows represent reactions. (b) The hierarchy of organizations.
In this network, the simplest organization represents a political system where there is formal political power of high and low levels, public opinion, thematic conflicts, and public force. The dynamics of self-maintaining networks is given by how public opinion influences thematic conflicts and how they get resolved by the political power. It resembles a monarchy-like system. More complex organizations in the hierarchy involve either social movements and social demands, political parties and their programs, or collectively binding decisions and their implementation. Further levels combine these structures in different ways, and the highest level at the hierarchy is the conjunction of all these cases together.
5.2. Decision System: Evolutionary Game Theory
In a game theoretical setting, an agent interacts with another agent by deciding a certain action on the basis of a set of possible actions and the payoffs of these actions. The payoffs depend on the decision of both agents, but no agent knows the decision of the other agent. For example, if we consider cooperative C and defecting D decisions, we have that a cooperative interaction requires two cooperative agents generating payoff for the cooperative payoff specified by by the reaction , while the interaction of a cooperative decision with a defecting decision, , generates payoff for the defecting decision only.
In the evolutionary game theory setting, agents are allowed to interact several times. They can eventually recognize and remember other agents as well as their past actions. From here, each agent develops a ‘strategy’ that sets how agents interact with each other depending on past interactions.
Since the interactions in evolutionary game theory are between agents, agent-based modeling is the dominant paradigm to represent these systems [50]. Unfortunately, it is very difficult to develop analytic results for agent-based models, and performing simulations to explore the parameter space is computationally very expensive when several strategies are in play. As an alternative, in [32], a reaction network model was developed to represent the evolutionary game theoretical setting of the prisoner’s dilemma, and, in particular, the evolution of cooperation problem [51]. Species play the role of decisions and payoffs, and a reaction network is built from the payoff matrix of decisions (see Figure 3).
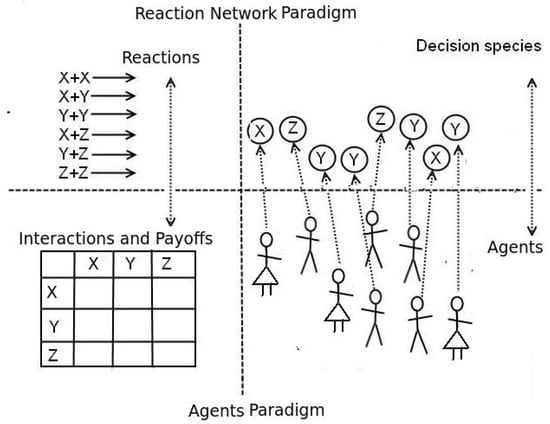
Figure 3.
Paradigm change from agent-based (bottom) to reaction network (top) modeling. The interaction among agents corresponds to a vessel of decision species interacting, and the payoff matrix corresponds to a set of reactions which consumes a pair of decisions to produce the payoff of each decision and two new decisions determined by the strategies.
The reaction network model is able to fully reproduce the results obtained using agents for the evolutionary prisoner’s dilemma. Interestingly, a formula that explains when cooperation is evolutionarily stable is obtained [32]. This formula is equivalent to the famous result obtained by Nowak in [52].
5.3. Ecological Systems
Ecological interactions among biological species can be modeled using reaction networks. As an example, Table 2 provides a simple model of a list of ecological interactions using reaction networks.

Table 2.
Reactions associated to most common ecological interactions.
Since, in this setting, interactions are many-to-many directed relations, reaction networks allow a more complex representation of ecological interactions than traditional network models. Moreover, a more detailed account of the ecological concepts can be developed in certain ecosystems. For example, consider the mutualistic interaction between mychorrizae and plants [53]. Namely, plants y feed from mycelium to grow roots ( in Equation (6)), mycorrhizae x feeds from the roots to produce mycelium ( in Equation (6)), and contributes to the production of mycelium ( in Equation (6)), which, in turn, increments the absorption capacities of plants y ( in Equation (6)). Therefore, the following set of reactions:
provides a more complex model of a mutualistic relation than the one shown in Figure 2.
Therefore, reaction networks can be used to model the mechanisms of ecological interactions. Remarkably, COT provides a suitable conceptual landscape to formalize ecological notions. For example, organizations can be understood as sustainable ecosystems, and invasion of a particular ecological species x in an eco-system E can be modeled by adding species and reactions that represent the interaction mechanisms of the species x with the ecological species in the ecosystem E [30].
6. Conclusions
In this paper, we have proposed the language of reaction networks, and particularly its COT implementation, as a representational framework for systemic modeling. In particular, we focused on crucial notions in a system’s theory such as the notion of the system itself, context, meta-system, resilience, etc., and presented a reaction network model for a political, agent-decision, and ecological systems.
Remarkably, this framework does not require the choice of a particular point of view, or field of knowledge, that serves as a reference for representing a system. On the contrary, it is required to identify a set of entities, that can be, in principle, of any nature (physical, biological, social, economical, etc.), and define a set of interactions of transformational nature (reactions) among them. The set of interactions is understood as a universe of basic processes, i.e., a reaction network. From here, a system corresponds to a sub-network such that its structural properties ensure its qualitative identity (closed) and observability (self-maintaining), i.e., organizations in the COT sense. Technically speaking, organizations characterize the global invariants of the local dynamics, and can be computed at a computationally tractable cost.
Since reactions are allowed to combine entities of different nature (see, for example, the interactions combining payoffs and decisions in Section 5.2), this approach is a priori interdisciplinary.
In order to advance the modeling of systems using COT, we envisage various challenges. First, this perspective requires proving its usefulness beyond the toy-model studies. We believe that a model of an ecological universe of interactions, extending the toy-model presented in Section 5.3, is a good option. Second, COT is still at an early stage of mathematical development. Several advances can be made applying lattice theoretical notions [54] to the hierarchy of organizations [14], and more profound studies in the topology of reaction networks could provide a more rich structure that the one presented in this paper. Such a richer structure could be used not only to better understand how systems emerge and combine, but also for improving algorithms regarding the computation of organizations [41]. In this vein, we present some advances in this issue [36].
Last but not least, we believe that it is fundamental to develop a semi-formal methodology that ensures that interdisciplinary reaction networks can be designed by combining the expertise from different fields. Indeed, previous reaction networks models of non-biochemical systems required an extensive dialogue among the disciplines involved in the problem in question (e.g., sociologist, economist, and biologist). The aim of such dialogue was to find an ontology (set of species) and the interaction mechanisms (sets of reactions) that combine the different perspectives into play. This exhaustive dialogue has been carried out due to the motivation of the members involved in the respective studies. However, a methodology to advance on such a dialogue could foster the application of this formalism at a wider scale.
We suggest two ways in which this potentially divergent process can be improved. The first is to provide semantic tools to construct the ontology given by the set of species. Researchers can be aided by current powerful language taxonomies and semantic tools that can help them to identify misunderstandings and ambiguous meanings. The second is the possibility to visualize the output of the COT analysis of a reaction network (e.g., see Figure 1b). In this way, researchers can modify in real-time the structure of the reaction network and observe how the structural properties of the reaction network depend on the local interactions.
The ultimate goal of using reaction networks as a language for modeling systems is to bring systemic thinking closer to the real world. We aim at not only scholars, but also decision-makers and the general public contributing with their knowledge and expertise, so multiple perspectives can be integrated in a single framework that brings forward a broader understanding of the emergent consequences of our local actions.
Acknowledgments
This work has been supported by the FONDECYT Grant 1150229 and the FONDECYT Postdoctoral Scholarship 3170122.
Author Contributions
All authors contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bogdanov, A. Essays in Tektology: The General Science of Organization; Intersystems Publications: Seaside, CA, USA, 1984. [Google Scholar]
- Von Bertalanffy, L. General Systems Theory; George Braziller: New York, NY, USA, 1968; Volume 41973, p. 40. [Google Scholar]
- Vemuri, V. Modeling of Complex Systems: An Introduction; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Ashby, W.R. An Introduction to Cybernetics; Chapman & Hall: London, UK, 1956. [Google Scholar]
- Laszlo, E.; Clark, J.W. Introduction to Systems Philosophy; Gordon and Breach: New York, NY, USA, 1972. [Google Scholar]
- Goertzel, B. Chaotic Logic: Language, Thought, and Reality from the Perspective of Complex Systems Science; Springer Science & Business Media: Berlin, Germany, 2013; Volume 9. [Google Scholar]
- Dittrich, P.; Ziegler, J.; Banzhaf, W. Artificial chemistries—A review. Artif. Life 2001, 7, 225–275. [Google Scholar] [CrossRef]
- Kitano, H. Systems biology: A brief overview. Science 2002, 295, 1662–1664. [Google Scholar] [CrossRef] [PubMed]
- Steuer, R.; Junker, B.H. Computational models of metabolism: Stability and regulation in metabolic networks. Adv. Chem. Phys. 2009, 142, 105–251. [Google Scholar]
- Albrecht, M.; Kerren, A.; Klein, K.; Kohlbacher, O.; Mutzel, P.; Paul, W.; Schreiber, F.; Wybrow, M. On Open Problems in Biological Network Visualization; International Symposium on Graph Drawing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 256–267. [Google Scholar]
- Lee, D.Y.; Yun, H.; Park, S.; Lee, S.Y. MetaFluxNet: The management of metabolic reaction information and quantitative metabolic flux analysis. Bioinformatics 2003, 19, 2144–2146. [Google Scholar] [CrossRef] [PubMed]
- Schuster, S.; Fell, D.A.; Dandekar, T. A general definition of metabolic pathways useful for systematic organization and analysis of complex metabolic networks. Nat. Biotechnol. 2000, 18, 326–332. [Google Scholar] [CrossRef] [PubMed]
- Feinberg, M.; Horn, F.J. Dynamics of open chemical systems and the algebraic structure of the underlying reaction network. Chem. Eng. Sci. 1974, 29, 775–787. [Google Scholar] [CrossRef]
- Dittrich, P.; Di Fenizio, P.S. Chemical organisation theory. Bull. Math. Biol. 2007, 69, 1199–1231. [Google Scholar] [CrossRef] [PubMed]
- Klamt, S.; Gagneur, J.; von Kamp, A. Algorithmic approaches for computing elementary modes in large biochemical reaction networks. IEE Proc. Syst. Biol. 2005, 152, 249–255. [Google Scholar] [CrossRef]
- Matsumaru, N.; Centler, F.; di Fenizio, P.S.; Dittrich, P. Chemical organization theory applied to virus dynamics (Theorie chemischer organisationen angewendet auf infektionsmodelle). IT Inf. Technol. 2006, 48, 154–160. [Google Scholar] [CrossRef]
- Kreyssig, P.; Escuela, G.; Reynaert, B.; Veloz, T.; Ibrahim, B.; Dittrich, P. Cycles and the qualitative evolution of chemical systems. PLoS ONE 2012, 7, e45772. [Google Scholar] [CrossRef] [PubMed]
- Centler, F.; Dittrich, P. Chemical organizations in atmospheric photochemistries—A new method to analyze chemical reaction networks. Planet. Space Sci. 2007, 55, 413–428. [Google Scholar] [CrossRef]
- Matsumaru, N.; Centler, F.; di Fenizio, P.S.; Dittrich, P. Chemical organization theory as a theoretical base for chemical computing. In Proceedings of the 2005 Workshop on Unconventional Computing: From Cellular Automata to Wetware; Luniver Press: Beckington, UK, 2005; pp. 75–88. [Google Scholar]
- Kaleta, C.; Richter, S.; Dittrich, P. Using chemical organization theory for model checking. Bioinformatics 2009, 25, 1915–1922. [Google Scholar] [CrossRef] [PubMed]
- Karp, R.M.; Miller, R.E. Parallel program schemata. J. Comput. Syst. Sci. 1969, 3, 147–195. [Google Scholar] [CrossRef]
- Murata, T. Petri nets: Properties, analysis and applications. IEEE Proc. 1989, 77, 541–580. [Google Scholar] [CrossRef]
- Crespi-Reghizzi, S.; Mandrioli, D. Commutative grammars. Calcolo 1976, 13, 173–189. [Google Scholar] [CrossRef]
- Heiner, M.; Koch, I.; Voss, K. Analysis and simulation of steady states in metabolic pathways with Petri nets. In Proceedings of the Workshop and Tutorial on Practical Use of Coloured Petri Nets and the CPN Tools (CPN’01), Aarhus, Denmark, 29–31 August 2001; pp. 15–34.
- Veloz González, T.I. A Computational Study of Algebraic Chemistry. Master Thesis, Universidad de Chile, Santiago, Chile, 2010. [Google Scholar]
- Heiner, M.; Gilbert, D.; Donaldson, R. Petri nets for systems and synthetic biology. In International School on Formal Methods for the Design of Computer, Communication and Software Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 215–264. [Google Scholar]
- Pascual, M.; Dunne, J.A. Ecological Networks: Linking Structure to Dynamics in Food Webs; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Borgatti, S.P.; Mehra, A.; Brass, D.J.; Labianca, G. Network analysis in the social sciences. Science 2009, 323, 892–895. [Google Scholar] [CrossRef] [PubMed]
- Razeto-Barry, P. Autopoiesis 40 years later. A review and a reformulation. Orig. Life Evol. Biosph. 2012, 42, 543–567. [Google Scholar] [CrossRef] [PubMed]
- Veloz, T. Teoría de organizaciones químicas: Un lenguaje formal para la autopoiesis y el medio ambiente. In Autopoiesis: Un Concepto Vivo; Universitas Nueva Civilización: Santiago, Chile, 2014. (In Chile) [Google Scholar]
- Dittrich, P.; Winter, L. Chemical organizations in a toy model of the political system. Adv. Complex Syst. 2008, 11, 609–627. [Google Scholar] [CrossRef]
- Veloz, T.; Razeto-Barry, P.; Dittrich, P.; Fajardo, A. Reaction networks and evolutionary game theory. J. Math. Biol. 2014, 68, 181–206. [Google Scholar] [CrossRef] [PubMed]
- Dittrich, P.; Winter, L. Reaction networks as a formal mechanism to explain social phenomena. In Proceedings of the 4th Iternational Workshop on Agent-Based Approaches in Economics and Social Complex Systems (AESCS 2005), Tokyo, Japan, 9–13 July 2005; pp. 9–13.
- Feinberg, M. Lectures on Chemical Reaction Networks; Notes of lectures given at the Mathematics Research Center; University of Wisconsin: Madison, WI, USA, 1979. [Google Scholar]
- Kreyssig, P.; Wozar, C.; Peter, S.; Veloz, T.; Ibrahim, B.; Dittrich, P. Effects of small particle numbers on long-term behaviour in discrete biochemical systems. Bioinformatics 2014, 30, i475–i481. [Google Scholar] [CrossRef] [PubMed]
- Veloz, T.; Razeto-Barry, P. Studying Structural Changes of a System using Reaction Networks. Systems submitted for publication. 2016. [Google Scholar]
- Horn, F.; Jackson, R. General mass action kinetics. Arch. Ration. Mech. Anal. 1972, 47, 81–116. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Westview Press: Boulder, CO, USA, 2014. [Google Scholar]
- Peter, S.; Dittrich, P. On the relation between organizations and limit sets in chemical reaction systems. Adv. Complex Syst. 2011, 14, 77–96. [Google Scholar] [CrossRef]
- Peter, S.; Veloz, T.; Dittrich, P. Feasibility of Organizations—A Refinement of Chemical Organization Theory with Application to P Systems. In Proceedings of the 11th International Conference on Membrane Computing (CMC11), Jena, Germany, 24–27 August 2010; p. 369.
- Centler, F.; Kaleta, C.; di Fenizio, P.S.; Dittrich, P. Computing chemical organizations in biological networks. Bioinformatics 2008, 24, 1611–1618. [Google Scholar] [CrossRef] [PubMed]
- Centler, F.; Kaleta, C.; di Fenizio, P.S.; Dittrich, P. A parallel algorithm to compute chemical organizations in biological networks. Bioinformatics 2010, 26, 1788–1789. [Google Scholar] [CrossRef] [PubMed]
- Veloz, T.; Reynaert, B.; Rojas, D.; Dittrich, P. A decomposition theorem in chemical organizations. In Proceedings of the European Conference in Artificial Life, Paris, France, 8–12 August 2011.
- Maturana, H.; Varela, F. Autopoiesis and Cognition: The Realization of the Living; Springer: Dordrecht, The Netherlands, 1985. [Google Scholar]
- Mesarovic, M.D.; Macko, D.; Takahara, Y. Theory of Hierarchical, Multilevel, Systems; Elsevier: Amsterdam, The Netherlands, 2000; Volume 68. [Google Scholar]
- Păun, G. Computing with membranes. J. Comput. Syst. Sci. 2000, 61, 108–143. [Google Scholar] [CrossRef]
- Folke, C. Resilience: The emergence of a perspective for social–ecological systems analyses. Glob. Environ. Chang. 2006, 16, 253–267. [Google Scholar] [CrossRef]
- Luhmann, N. The Differentiation of Society; Columbia University Press: New York, NY, USA, 1983. [Google Scholar]
- Razeto-Barry, P.; Cienfuegos, J. La paradoja de la probabilidad de lo improbable y el pensamiento evolutivo de Niklas Luhmann. Convergencia 2011, 18, 13–38. [Google Scholar]
- Axelrod, R. The Complexity of Cooperation; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Axelrod, R.M. The Evolution of Cooperation; Basic Books: New York, NY, USA, 2006. [Google Scholar]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Harley, J.L. The Biology of Mycorrhiza; Leonard Hill (Books) Ltd.: London, UK, 1959. [Google Scholar]
- Birkhoff, G.; Birkhoff, G.; Birkhoff, G.; Mathématicien, E.U.; Birkhoff, G. Lattice Theory; American Mathematical Society: New York, NY, USA, 1948; Volume 25. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).