Abstract
After having outlined the essential differences between non-complex systems and complex systems we briefly recall the conceptual approaches considered by the pre-complexity General Systems Theory introduced by Von Bertalanffy in 1968 and those of the science of complexity and post-Bertalanffy General Systems Theory. In this context, after outlining the concept of completeness, we consider cases of incompleteness in various disciplines to arrive at theoretical incompleteness. The latter is clarified through several cases of different natures and by approaches in the literature, such as logical openness, the Dynamic Usage of Models (DYSAM), and the principle of uncertainty in physics. The treatment and the contrast between completeness and incompleteness are introduced as a conceptual and cultural context, as knowledge to manage the knowledge society in analogy, for example, with the transition from the logic of certainty to that of uncertainty introduced by De Finetti. The conceptual framework of completeness is not appropriate for dealing with complexity. Conversely, the conceptual framework of incompleteness is consistent and appropriate with interdisciplinary complexity.
1. Introduction
This article introduces conceptual specifications regarding the concepts of completeness and incompleteness. The latter concept is treated by distinguishing between (a) incompleteness of a phenomenological nature (given, for instance, by non-proceduralizability; non-completability; incompleteness of constraints, of degrees of freedom or representation; approximation; and by indefiniteness) and (b) theoretical incompleteness (given, for instance, by non-decidability; principles of uncertainty; non-computable uncertainty; non-complete, non-explicit and non-univocal modeling). The theme of theoretical incompleteness has been treated in the literature in correspondence to, or negation of, meanings of completeness in various disciplines [1], such as logic and mathematics, where examples include Russell’s paradox [2] and the incompleteness theorems introduced by Gödel [3].
This paper focuses on concepts appropriate for modeling complex systems, such as social systems [4,5,6]. It attempts to outline conceptual invariants relating to theoretical incompleteness and its disciplinary transversality, therefore, being suitable for generalizations not based on genericity, but being suitable for methodologies, approaches, and representations for problems, typically related to complex systems [7,8], (see Section 2) represented, for instance, as networks [9].
Such problems and representations showing how incompleteness, or better, assumptions of completeness, turn out to be completely or partially ineffective and inadequate [10] are explored. This is done by using procedures and analytical models based on finite representations and logically closed systems (see Section 6.1).
We emphasize the search for meaning, cross-usability of the philosophical concept of incompleteness and of theoretical incompleteness. This should really be a cultural process involving all of the concepts of the post-Bertalanffy Theory of General Systems [11,12,13] such as logical openness (see Section 6.1) as a multiplicity of modeling; coherence; emergence as continuous and unpredictable, but coherent, acquisition of multiple properties; equivalence/non-equivalence of models and evolutionary paths; theoretical principles of uncertainty and indeterminacy; individuality to break equivalences; induction of properties, rather than prescriptions of solutions; overall conceptual interdependence, non-separability from the environment; irreversibility as the price for uniqueness; multiplicity, multiple systems set dynamically by the same components; observed in terms of the observer; networks and properties of networks, such as small worldness and their topological properties; simultaneity; and overlapping. These, considering the fact that properties and problems of complex systems, particularly social systems, are still dealt with using the concepts of classical Bertalanffy General Systems Theory [14], such as anticipation; openness as permeability of system barriers to matter and energy; equilibrium; functioning, as for devices possessing and not acquiring properties; optimal and computable organization; optimization always being possible and positive in principle; predictability and repeatability; adjustability; feedback; and reversibility.
When dealing with social systems such a distinction, between Bertalanffy and post-Bertalanffy General Systems Theory, is combined with, or even corresponds to, the knowledge to be used to manage. That is, conceive, make emergent, and change properties, and induce processes in business, culture, and economics, within cooperation and assimilation, fashion, food uses, interactions, professions, customs, and general usage.
The post-industrial society [15], or knowledge society [16], is where examples of sources of complexity are properties, such as knowledge-intensive products and services; delocalization and globalization; duplicability; general highly-networked interconnections; high virtuality; importance of individuality; coherences rather than equilibrium; interchangeability; online actions; reduced time between design, implementation, and marketing; generally short product lifespan; technological innovations and solutions rapidly creating new problems; non-linearity; and large amounts of data. Conversely, social systems are often managed, i.e., conceived as non-complex systems, by still using the knowledge of pre-complexity [17].
This is not simply to update methods, but to vary and structurally adapt the general culture. This article is meant to be a contribution towards social development processes in areas such as education and the management of enterprises and social institutions [18,19]. Here, the word ‘management’ takes for granted the directivity of social systems, in a pre-complexity systemic vision. In reality, the aim is to induce the emergence of properties to be acquired by the Social Systems (as complex systems) and not to adjust or impose them. Giving orders to a complex system is inadequate and ineffective. Management of complex systems, which social systems are, requires multiple strategies and approaches, such as action on the environment, adding suitable perturbations, making energetic variations, acting upon the relations with the outside world and on learning processes by interacting with other systems. It is to change constraints and provide perturbations to be processed by the system to orient and not to decide. This could include changes in the use of resources, language, organizational approaches, prices, or rates. Probably the word management is now misleading after years of being synonymous with directive and invasive approaches.
The work objectives are based on considering theoretical incompleteness as one of the properties characterizing complex systems amongst others well-known in the literature [20] (see Section 2).
Theoretical incompleteness should be suitably represented, modeled, used, activated or de-activated, graduated, replicated, avoided, and combined in different forms. The assumption of theoretical incompleteness as a negative property which must be reduced to incompleteness to be completed as the only possible strategy is very ineffective when dealing with complex systems.
We may consider a possible analogy between the mesoscopic level of representation and theoretical incompleteness. In physics, mesoscopic variables, when not relating to the quantum level, relate to an intermediate level between the micro and the macro. At this level the micro is not completely neglected as when adopting the macro levels (see, for instance, [21,22,23,24]).
The approach based on considering mesoscopic variables relies on the philosophy of the ‘middle way’ as introduced in [25].
Simple examples of mesoscopic variables are:
- In car traffic, when considering the instantaneous number of cars, or clusters, which cannot accelerate. Simultaneously we consider cars blocked in a queue, cars which are decelerating, and cars with constant speed;
- In a building, one can consider the instantaneous number of people, or clusters, using the elevator or stairs, going either up or down; and
- In a flock we may consider the instantaneous number of birds, or clusters, having the same speed, whatever their direction or altitude.
The mesoscopic level is the place of continuous negotiations between the micro and the macro, where a large variety of mesoscopic representations are possible allowing an undefined number of possible clusters.
On the other hand, the conceptual analogy of the mesoscopic case with theoretical incompleteness lies in the fact that such incompleteness may apply in several different ways as the place of those continuous negotiations between completeness and incompleteness. In this case, instead of clusters, there are different levels, graduations, and approximations of completeness and incompleteness referring to different variables describing the case.
Theoretical incompleteness may be intended as the place where phenomena are incomplete enough to allow emergence [26] of dynamical coherences [27], e.g., multiple synchronizations [28], as for the emergence of complex systems (see Section 2) rather than iterations of the same complete rules and properties. This is the case of logically open systems, introduced in Section 6, of which their evolution is not driven by the same complete rules, but by dynamically changing coherent rules.
One interesting future research issue relates to the possibility of considering theoretical incompleteness as a necessary, or even, in specific cases, a sufficient condition for the establishment of processes of emergence.
The purpose of this paper is to underline and support approaches for the usages of incompleteness as a property rather than to avoid it as a negative property, in principle. This relates to complex systems in general, with special attention to social systems.
We conclude by stressing the extreme interdisciplinary nature of this way of understanding theoretical incompleteness to be elaborated by disciplines relevant for dealing with social systems in their post-industrial phase, or knowledge societies intended as those based upon scientific and theoretical knowledge as their main resource (see Section 7). Examples of such disciplines are communication sciences; economics; education; political sciences; psychology; and sociology.
2. Non-Complex and Complex Systems
Non-complex systems are intended as those based on the properties cited in the Introduction and which are related to classical Bertalanffy General Systems Theory. Non-complex systems acquire over time the same property due to their functioning (such as the working of powered electronic devices when, for instance, they are transformed from a structured set of components to a device acquiring the property of being a radio or some other end-user device). Elementary examples include machinery, electronic devices, and feedback-regulated devices, systems that do not learn, having fixed rules, or otherwise low-parametric variability. It is a matter of decidable systems, represented completely, whose evolutionary paths can reach a finite, or in any case, a numerable number of states. Their possible openness involves finite and precise modalities to process external environmental input [14]. Into this category fall systems that have probabilistic, but computable, evolutionary behavioral paths (see the difference between computable and non-computable uncertainty [29] as introduced below). Examples of such systems include automata (mechanical and electronic systems), transportation systems, housing systems, telecommunication systems, security systems, energy management systems, and fuzzy systems [30].
Complex systems do not acquire, over time, the same systemic property, but comprise continuous processes of structural changes (see Section 5.1, Section 5.4, and Section 5.8), such as phase transition [31,32], with self-organization (when the sequence of new properties acquired in a phase transition-like manner, has regularities and repetitiveness, for example a swarm around a light, the formation of queues, or synchronizations [33,34,35,36,37] and emergence (when the sequence of new properties is not regular, not repetitive, but coherent, i.e., having multiple different synchronisations and correlations, for example a flock having multiple and changing shapes, density and direction but maintaining scale invariance) [38,39,40] taking place, acquiring over time coherent sequences of new properties [41,42]. Examples of complex systems without cognitive systems include cellular automata; double pendulum; dissipative structures [43,44], e.g., whirlpools in fluid dynamics and chaotic systems (see below). Examples include the climate system; protein chains and their withdrawal; cells and bacteria; objects on vibrating surfaces that tend to make consistent variations; autonomous lighting networks that tend to adopt coherent variations (such as communities of fireflies); and traffic signals (Internet). We may consider examples of complex systems consisting of coherent communities of living systems provided with cognitive systems, i.e., autonomous systems that are able to decide their behavior not only in an algorithmic way. In these cases the decision of behaviors cannot be reduced to compute optimizations, but it is a process of emergence from a wide variety of aspects. In a nutshell, a cognitive system is to be understood as a system of interactions between activities such as those related to attention, perception, language, the affective and emotional sphere, memory and inferential system, logical activity. Examples include swarms; flocks; industrial clusters; industrial district networks; markets; and social systems, such as cities, schools, hospitals, companies, families, and temporary communities, such as passengers, audiences, and telephone networks.
Complex systems have characterizing properties. Some of them are listed below.
- Scale invariance when patterns, shapes, and morphological properties are independent of dimensions (e.g., spatial properties, number of components) [45];
- Validity of power laws among variables characterizing the system. Power laws are given by a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event, e.g., its size, the frequency is said to follow a power law [46].
- The evolutionary paths of the system fall within the basin of an attractor, see Figure 1 and Section 5.7, [47,48,49,50]. Evolutionary paths are robust to perturbations. This is the case of chaotic systems which are very sensitive to initial conditions, e.g., smoke diffusion and weather [51,52,53].
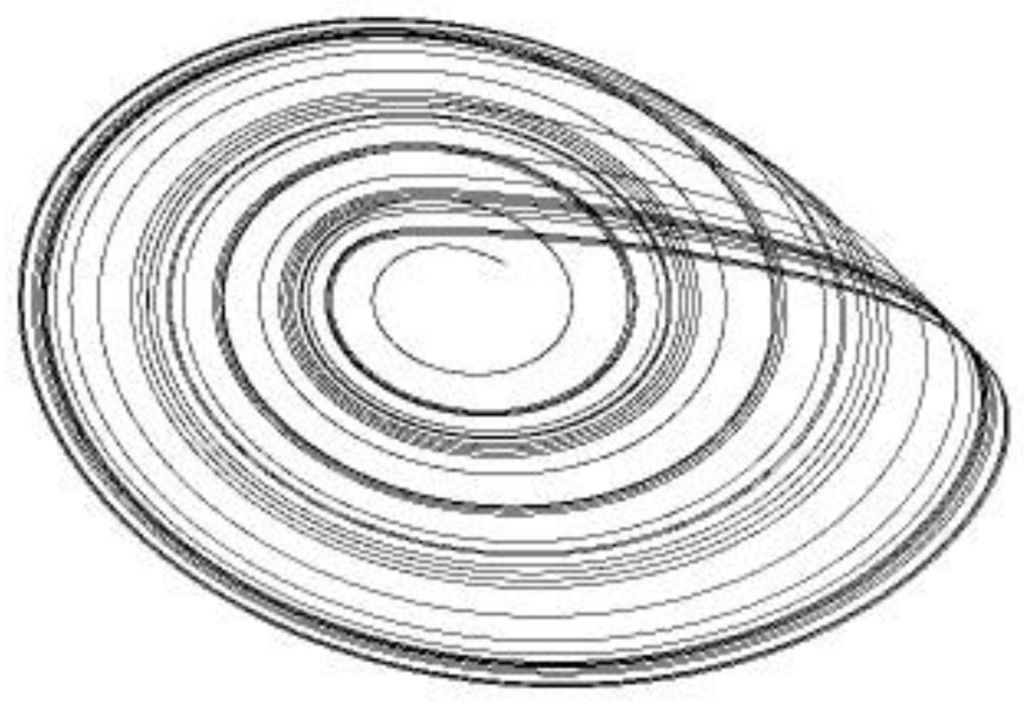 Figure 1. Generic graphic representation of evolutionary paths around an attractor, a single point in this case.
Figure 1. Generic graphic representation of evolutionary paths around an attractor, a single point in this case. - Properties based on Network Science [54,55,56,57,58]. We consider properties of a network representing a complex system, such as being scale-free (when the network has a high number of nodes possessing few links, and a small number of nodes possessing a high number of links. In other words, in scale-free networks the probability that a node selected at random will possess a particular number of links follows a power law). Furthermore networks can have the property to be small-world when most nodes are not neighbors of one another, but most nodes can be reached from every other node via a small number of intermediate links. Other properties relate to the degree of sequence distribution, cluster coefficient, topology of the network, and fitness (the way the links between nodes change over time depends on the ability of nodes to attract links) [59,60,61,62]. Several representations of social systems based on networks are available in the literature (see, for instance, [63,64]).
Other properties which may be considered include their explicit analytical intractability (their behavior cannot be zipped nor exhaustively represented with analytical formulae). In such cases systems are modeled using non-ideal models, such as neural networks and cellular automata.
We are considering here theoretical incompleteness as a candidate property of complex systems.
For an overview on properties of complex systems see, for instance, [65,66,67,68].
3. Meaning
Definitions are supposed to provide, at the highest levels of precision, formal descriptions of properties and limits with the vocation for completeness or exhaustiveness. That is, we cannot add to it. Examples in mathematics are geometrical axioms. Other generic examples relate to fiscal properties, such as taxation or safety procedures in the workplace.
An incomplete definition is intended to overlook some aspects which would tend to make it only partially usable.
Without going into theoretical specificity treated by semiotics and philosophy, we consider here the meanings of terms as given at different levels of contextuality and sensitivity to usage, suitable for different levels of generalization. The completeness of a definition is in these cases dampened by metaphorical usage, analogies, and extrapolations accepting generic contextuality. For instance, this occurs when one has to specify concepts which need to include all possible negations of a definition (absolute incompleteness as opposed to completeness). This is the concept of incompleteness which is not reducible to multiple negations of completeness.
4. Notes on the Concept of Completeness
Considering the topic of this article, there are several ways to indicate the meaning of completeness. For instance, a list may be considered complete when it contains all, and possibly only, the references to the entities under consideration. Of course, the number of elements is usually expected to be finite and limited, even though the definition is conceptually extendable to different cases. The reference is to be exhaustive, with complete information considered and without overlooking any detail that is deemed to be significant.
“Complete” has the meaning of being the maximum, to finish, end, close, reaching the purpose, considering even equi-finality starting from different initial conditions in open systems [14]. Completeness can refer to a process which, over time, reaches its final, possibly more than one, state, equivalent or not.
Completeness may be understood as corresponding to the fact that a system or a process has a finite number of degrees of freedom (fully described by a finite number of variables), and a finite number of constraints (values of min and max which may be adopted by variables). An endless completeness may be considered to correspond with incompleteness.
Completeness can also conceptually relate to processes and functionalities assumed as complete. For example, as they are self-consistent and autonomous, able to find resources to maintain a property, such as life, or to perform autopoietic reproduction. This is the case of systems which are incomplete (for example, with a number of states being assumed as being undefined), but autonomous, that is capable of reacting, for example in a stochastic manner or by learning, to specific inputs.
A related concept is that of completability, in general; that is, the possibility of making complete what is not yet complete. In general, in the non-complexity conceptual context, the assumption of completability as potential is assumed valid.
In mathematics, completeness can refer to the properties of a mathematical entity to be contained within another larger entity of the same type. Furthermore, in mathematical logic completeness refers to the fact that a set of axioms is sufficient to prove all the truths of a theory. Based on this it is, therefore, possible to decide the truth or falsity of any statement formulated in the language of the theory. In this context, the conceptual space of completeness would be well defined by considering it as consisting of:
- Decidability. As introduced by Alan Turing (1912–1954) a problem is decidable if there is an algorithm that produces the corresponding solution in finite time for each instance of the input data (the equivalent of having a complete, calculable model of the behavior of systems having that problem and subjected to an external intervention). This is the concept of effective computability [69].A problem is “undecidable” if there is no algorithm which produces the corresponding solution in finite time for each instance of the input data (equivalent to the fact that an algorithm cannot produce the solution in finite time). In mathematical logic, the concept of undecidability refers to the fact that a given formalized theory T is not decidable, i.e., there is no algorithm able to mechanically determine for each formula whether or not it is a theorem of T (see Section 5.1 and Section 5.7). The reference is to the Turing machine, an ideal finite states machine. This machine processes, using a predetermined set of rules defined exhaustively by reading and writing symbols, the data contained on an ideal tape for input and having potentially infinite length. The process of such an abstract model defines computability, the concept of algorithm in general [69].
- Deduction, instead of induction or abduction. Validity of deduction is assumed when, for example, (a) this box contains red balls; (b) these balls are from that box; (c) the balls are all red. If the premises are true, the conclusions cannot be that true. Whereas induction has a probabilistic nature as in the case that (a) the balls are from that box; (b) these balls are red; (c) the more they pull out and if they are all red one might conclude that all the balls in the box are red.In the case of abduction, introduced by Sanders Peirce (1839–1914), it is matter of the invention of hypotheses, which can also be understood as a choice amongst the most effective available. For example, when observing facts of type B, a rule such as: if A then B may explain B. So, if at the time no other hypothesis can explain B better, we may assume the validity of A [70]. This is related to creativity, as in second order cybernetics, focusing upon inventing a new game rather than playing an existing game [71].
- Certainty. Essentially this is a matter of reducing, or even cancelling, uncertainty. In the logic of certainty [72,73], it is not conceptually considered to maximize probabilities, but to have computable levels of certainty. However, probabilities relate to configurations of events, conditional probabilities as considered by the observer.The assumption that events can be considered as isolated, separated by configurations to which they belong should be considered as reductionist simplifications. On the other hand, configurations are not objectivistic but rather depend upon the cognitive approach taken by the observer.
These configurations are inalienably constructivist [74,75,76,77,78,79], created by the observer, the generator of cognitive reality rather than of relativism, as introduced by De Finetti (1906–1985) [80]. The cognitive strategy expressed by cognitivism is well-expressed through the distinction between:
- ▪
- Trying to understand how something really is, and
- ▪
- How it is more effective to think of it (which model to adopt).
Note that the former is a particular case of the latter. Objectivism leads to the inevitable phenomenological acceptance of becoming. From the moment we wonder what happened..., how it happened ... by involving cognitive abilities, constructivism intervenes. We assume then descriptive and interpretative models of the phenomena detected (detection needs a model itself...), generators, in their turn, of new configurations to be modelled. Something happened in what our cognitive system calls outside and we adopt a strategy to make models for acting, interacting, and abstracting using the cognitive system we have. Science does this and cognitive science studies this process. There is a vast literature on this subject (see, for instance, [81,82,83,84]). For example, is it more effective to think of a social problem as being military or political, a mathematical problem as being geometrical or algebraic, the problem of corruption as being cultural or legal (See Section 5.2 and Section 5.3). Effectiveness may increase by suitably considering options in combined and not only exclusive ways (assuming only the “or” option), e.g., biological and psychological. Non-computable uncertainty refers to those contexts having, as a component, the environment with its turbulence, processes of emergence, and autonomous processes [85,86]. Section 5.5 covers incompleteness and non-predictability.
5. Incompleteness
Below is a partial list, in no specific order, illustrating concepts and cases related to incompleteness, considered as constituting examples of dynamic and theoretically-incomplete sets (see Section 6) of cases of phenomenological incompleteness.
The property of incompleteness may refer to one or more specific properties; may have different levels or may be general; that is, valid for any properties in general or for any property of a specific entity; may be intended as not yet complete or uncompletable or chronically not-completable, in principle. The property of incompleteness should be considered in combination with one or more levels of description and scales.
5.1. Non-Proceduralizable
The prototype of the concept of procedure is the concept of the algorithm intended as a program for a Turing Machine as an ideal programmable machine (see Section 4 on decidability). The general idea is to have approaches well-defined through step-by-step methods indicating what and when to do something mechanically applicable to families of problems, such as those related to construction, health, maintenance, and security. A procedure is intended as that being well-described in instruction manuals.
However, the plurality of degrees of freedom of complex systems; their structural change (change of rules rather than of parameters of only the same rule, variability, and unpredictability) make procedural approaches ineffective because they consider fixed and abstract variables in the face of phenomena whose variables change, form, and combine in multiple and unpredictable ways, i.e., they are emergent [89,90]. The procedures may cover areas, aspects of a problem, and provide, for example, the basic behavioral claims in cases of emergency, e.g., health, and ensure legal cover for those who carefully followed the prescribed procedure.
However, the procedures to deal with a problem can increase so much that it becomes impossible or paralyze an appropriate intervention for situations with features of uniqueness (complex emergent systems are made of coherent uniqueness). Such procedures often have as their purpose the prevention of unauthorized actions or personal responsibilities. Examples include actions to tackle environmental disasters or criminal acts, and interventions in the face of irrational, unexpected behavior with predictable, nefarious outcomes.
There are also cases where complexity prevents the adoption of procedures to be considered as exhaustive. For example, the management of safety at work is not reducible to rules, due to the complexity inevitably introduced by the human operator [91].
In mathematics, this issue concerns the non-reducibility of general computation to Turing computability as for emerging and natural computing [92]).
5.2. Uncompletable
In geometry, an axiom of order introduced by David Hilbert (1862–1943) states that if A and C are two points, then there always exists at least a point B on the line AC, such that C lies between A and B, see Figure 2.

Figure 2.
There always exists at least a point between two points.
It is a theoretical generator of points between two points.
In this case, a hypothetical list of points between two points is uncompletable (because of the non-finite number).
In a metaphorical or conceptually similar way, the knowledge, i.e., representations and models, of a complex problem is not limited to the formulation of lists having finite numbers of recommended procedures to be followed (the classical instructions for use). Rather, in the case of social systems, it is a question of cognitive, context-sensitive processing, always variable depending, for example, upon experience, or new information or new knowledge, as considered by logical openness (see Section 6.1).
Since the classical instructions for use cannot exhaust the possibilities of actual use, modern products and services are presented with appropriate designs to induce adequate but any usage by the generic user.
In the management of public safety any procedure is uncompletable as any type of events can change the context, such as the use of technologies, environmental impact, or unexpected situations, in general.
5.3. Incompleteness and Uniqueness
Completeness can be understood to reflexively possess repeatability of the action of completing in the face of the improbable uniqueness of the action of completing, for instance, by applying the same procedure. The action of completing may be assumed to be identically repeatable, for example, because of the sameness of what is to be completed: either a procedure or the mathematical fractal filling curves of Peano and Hilbert [93]. There is conceptual negation of uniqueness, i.e., an assumption of repeatability of the same procedure to deal with the same category of problems. Processes of completion intended as unique, for one-off, non-repeatable, cases contrasts with the iterative, procedural aspect of completion.
In a parallel way, incompleteness can be understood as the non-repeatability of any completion. This may occur, for example, because what is to be completed is considered never equal to itself, e.g., on suitably different scales, or because of the dependence of the process of completing based on different initial conditions. There is conceptual correspondence with the concept of uniqueness.
Strategies and approaches to manage repeatability are inadequate for the possible uniqueness of incompleteness; as for emergent properties, unique and incomplete, not completely definable in an analytical way.
5.4. Undefined and Uncompleted
Indefiniteness can be considered as being due to insufficient levels of accuracy in defining (perhaps as desired or possibly upgradeable until achieving definiteness). The vague lines of the impressionist painters constructively leave the observer to mentally build his/her line at that time. Indefiniteness, imprecision, and incompleteness can be understood to constitute a constructivist freedom.
In turn, it is possible to consider indefinability as being given, for example, by structural dynamics for which entities or processes, on a suitable scale and level of description, change fundamental structural properties and identity. For example, structural dynamics apply to the structural autonomy of processes of emergence which cannot be completely, explicitly, and univocally defined (they are logically open, see Section 6.1). A flock is always different over time, but it keeps its identity as a flock in that it maintains, for instance, sufficient levels of coherence and scale invariance. Furthermore, appropriate levels of vagueness and incompleteness are areas of potentiality for processes which adopt corresponding levels of uniqueness (e.g., oneness of people, fingerprints, medical patients, or snowflakes). Moreover, there are various (even infinite) ways to comply with constraints. Variables considered as representing a specific entity can take on different values while respecting the constraints, e.g., constantly close to the minimum or maximum values of the constraints or oscillating in regular or stochastic ways.
Another example of indefiniteness and incompleteness is given in baroque music by the practice of the basso continuo, a historically improvised accompaniment, so that the score does not completely indicate the chords to play along with the low notes, but only numbers (or code words, as the word BACH) which give clues on how the instrumentalist should improvise.
5.5. Incompleteness and Non-Predictability
It is possible to consider incompleteness as being combined with non-predictability. We distinguish between at least two types of probabilities which represent predictability. Certain probability is intended here as computable probability intended as identifying significant possible extremes e.g., maximum-minimum, to the phenomenological becoming of any process, which is free to happen within these extremes, such as, for example, computed through the Bayes’ theorem. In short, the theorem states that if P(A) and P(B) are the independent probabilities of A and B, and P(A | B) is the probability (conditional probability) of observing event A given that B is true, than P(B | A) is the probability of observing event B given that A is true, see also Section 4. Uncertain probability is intended here as non-computable probability referring to the non-predictability of processes, for example, of emergence which cannot be completely, explicitly, and uniquely defined.
The property of incompleteness of events or processes may be predictable or not, such as the induction of a self-organizing process which could have non-predictable aspects, for example, in producing the Belousov-Zhabotinski reaction [94,95] consisting of an oscillating chemical reaction in which the periodic variation of concentrations is indicated by striking color variations and the formation of convective patterns called Rayleigh-Bénard cells [96] in a liquid evenly heated from below. The occurrence of such processes is predictable but in incomplete ways, e.g., details of patterns and directions of convective patterns are not predictable. On the other hand, aspects of unpredictability, as in processes of emergence, owe their unpredictability to their being constantly incomplete, which makes them unique.
5.6. Multiple and Dynamic Incompleteness
Depending upon the level of description, incompleteness may relate to various aspects of a phenomenon, such as completely owning a property, but at different times (both with and without regularity); with different modes (e.g., intensity); or relating to different properties.
In the scientific literature, multiple and dynamic incompleteness may be intended as being expressed by the concept of quasiness where, for example, quasicrystals are a particular solid form in which the atoms are arranged in a deterministic but not repetitive structure, which is not periodic, as in the case of normal crystals, honeycombs, and beehives. Quasicrystals have almost periodic patterns for which the local arrangement of the material is fixed and regular, but not periodic throughout the material, i.e., the property is incompletely respected in multiple possible ways [97].
5.7. Incompleteness and Undecidability
A typical problem of undecidability (see Section 4) is the classic halting problem for the Turing machine. Turing showed [69] that a Turing machine which decides, i.e., stops in some state, whether another Turing machine processing an input w will stop in some state or will continue indefinitely, cannot exist.
In this regard, in mathematical logic Kurt Gödel (1906–1978) proved two theorems about the incompleteness of mathematics [3]. One of these states that, in any consistent formalization of mathematics, sufficiently powerful to allow axiomatization of the elementary theory of natural numbers (that is, define the structure of natural numbers with the operations of sum and product) it is possible to construct a formally-correct proposition that can be neither proven nor disproved within the same system.
This is logically equivalent to the construction of a logical formula that denies its own provability. The second states that if one considers a coherent mathematical theory sufficient to contain arithmetic (e.g., the arithmetic based on the Peano axioms: 1-there exists a natural number 0; 2-every natural number has a natural number successor; 3-different numbers have different successors; 4-zero is not the successor of any natural number; 5-each subset of natural numbers which contains 0 and the successor of each element coincides with the entire set of natural numbers (axiom of induction), it is not possible to prove the coherence of the theory within the theory itself. The result can be extended to any theory that can be represented recursively (by recursive functions and predicates), and for which it is possible to arithmetize the syntax of the theory. A generalization consists in the fact that it is not possible to use a coherent system to demonstrate its own coherence.
Incompleteness concerns indecisiveness as a characteristic of a given problem; for example, the non-theoretical availability of an algorithm able to answer questions related to the problem.
As will be shown below when dealing with theoretical incompleteness (see Section 6), incompleteness as undecidability also concerns the conceptual impossibility of identifying solutions and, in particular, optimal solutions to complex problems which require, instead, systems of dynamical and non-equivalent approaches (as with DYSAM and logical openness as introduced in Section 6.1 and Section 6.2) to intervene effectively on properties acquired continuously rather than being possessed by complex systems.
Of the same nature is the concept of optimization which, for complex systems, does not concern the acquisition of the best value, but of permissible values through the dynamics of variable configurations within dynamic constraints ensuring coherence at least as synchronization (for example, in biology ensuring sustainability and permissible values of vital parameters) or permissible evolutionary trajectories in the vicinity of an attractor. In short sn attractor is a set of numerical values, e.g., a single point or a finite set of points, a curve, and a manifold, toward which a dynamical system, starting from any variety of initial conditions tends to evolve. Evolutionary paths of the system, when close enough to the attractor, remain close even if perturbed (the Lorenz butterfly attractor is a celebrated example, [52,53]).
5.8. Systemic Incompleteness
Systems can be considered as complete or incomplete.
For example, systems can be considered complete when they are fully described by a finite number of variables and models (presumably the same throughout the entire developmental period). Yet a system can be considered complete when all of the evolutionary-reachable states are of a finite and limited number. This is the case of logical closure (see Section 6.1) as opposed to logic openness.
Systems can be considered incomplete when their complexity in acquiring properties and their structural dynamics are such that a single model is not sufficient for their representation. More non-equivalent models are needed, not only in an indefinite number, but variable in different combinations to be abductively, constructively invented by the observer (as in the case of DYSAM introduced in Section 6.2).
Moreover, a system can be considered incomplete when the set of reachable evolutionary states is undefined or, better, its finiteness is undecidable.
5.9. Incompleteness of Constraints
As mentioned in Section 5.9 the incompleteness of the constraints is the fact that nothing is said about how to comply with such constraints and the actual use that a single system makes. Systems with the same constraints may have had different evolutionary paths.
For example, as mentioned above in Section 5.4, the values between the maximum and minimum constraints are all authorized, but they may be acquired by systems in different ways over time, for example, close to the maximum or close to the minimum, or oscillating with regularity, or randomly oscillating.
The mode of use of the constraints (that is, the modes respecting the constraints) allows systems to be considered as structurally equivalent, but actually different, with regard to aspects of their evolutionary process and whereby paths between the constraints represent specific trajectories having specific properties.
The use of the constraints is not prescribable and in this aspect lays the incompleteness.
5.10. Incompleteness and Freedom
We only mention how the concept of freedom refers to the possibility of building new degrees of freedom rather than the extension, both in number and for allowable values, of those already available.
6. Theoretical Incompleteness
The concept of theoretical incompleteness is typically studied in mathematics, as mentioned in Section 4 and Section 5.7. In general, the concept of theoretical incompleteness refers to incompleteness in principle, intrinsically, as a possible property possessed by systems, theories, phenomena, or processes, and their properties themselves. Regarding systems, this corresponds, for example, to the concept of logical openness.
6.1. The Case of Logical Openness
We recall that closed systems refer to the fact of being isolated, without exchange of neither matter nor energy with the outside world and reaching their final state uniquely determined by the initial conditions. Examples are ideally thermally-insulated machines.
The concept of the logically closed model is suitable to describe the evolution of such thermodynamically closed systems.
More precisely, we define a model as logically closed when:
- a full, formal description of the relations between the state variables of the model is available;
- a complete and explicit, i.e., analytically describable, description of the interaction between the system and its environment is available; and
- knowledge from the previous two points allows deduction of all possible states which the system can take together with its structural characteristics.
For example, a simple temperature control system with a thermostat can be considered logically closed and complete since the influence of the environment is reduced to its possible variations of temperature to which the thermostat reacts.
A system is intended as logically open when there is violation of the three points above (see Table 1). Logical openness [10,87,88,98], ([99], pp. 111–112) can be considered as the non-depleting or infinite number of degrees of freedom when the system includes the environment (in principle independent), thus making the system incomplete as regards the environment and its influence. In complex systems, as introduced in Section 1 and Section 2, the degrees of freedom (system variables) are not only in an imprecise and variable number, but can be continuously acquired. In complex systems processes of emergence occur for which the system acquires n-sequences of new non-equivalent properties to be dealt with by adopting n-different levels of description to be treated with corresponding n-different models and combinations (as with DYSAM, introduced below). The n-levels of modeling are based on n-levels of representation by:
- ▪
- constructively creating suitable possible correspondences between levels,
- ▪
- adopting a strategy to move between levels, and
- ▪
- considering, simultaneously, more than one level.

Table 1.
A schematic comparison between aspects of logically closed systems and logically open systems.
The incompleteness of logical openness is given both by usage of a variable number of models and by the indefiniteness of n due to the fact that models and representations are abductively and constructively generated by the observer [99].
It is possible to consider logical openness for autonomous systems provided with cognitive systems which process input and decide case by case, each in a possibly different way from the other (a) the behavior to be taken; (b) the degrees of freedom in unknown number, variable and continually acquired. This is the case for human behavior where assumptions of rationality and optimization are simplistic and inadequate (for example, to model the behavior of market customers by adopting decisions based on optimizing the trade-off between price and quality) as is the assumption of complete respect for procedures or repeatability over time.
In the case of logical openness for systems with cognitive systems, one may consider the following examples of levels of logical openness.
- A first level can be considered as being given by thermodynamic openness to which we have referred, for which matter and energy are able to cross the boundaries of the system. For example, the system is able to send and receive signals, but nothing is said about their processing or attribution or the processing of their meaning. This is the case for two computers physically exchanging “strings of bits’’ and for the moves of two opponents who are playing against each other.
- A second level can be considered where received and transmitted signals are processed in the hypothesis of an absolute semantics, predetermined, and equal for all. In this case there is the assumption that the meaning of the messages is identical and constant between transmitter and receiver, as with the formal language of operating systems for computers: in the interactions with the user it is the latter which must adapt and understand the pre-established meanings.
- A third level can be considered where one system generates a model of the other, and communication takes place between the respective models. For example, two systems exchange messages whose meanings are constructed by using each other’s models. The problem of user modeling in computer science involves these issues. Moreover, mutual modeling takes place through learning activities and it is refined over time, such as relations between teacher and pupil, or between companions in a sports team and within families.
- A fourth level can be considered where a system in the communication process sends not only the message but also the context (as an extension, a completion, of the message itself) in which it takes the meaning which the sender wants to transmit, providing the receiver with the ability to generate the context, inducing it (for example the relationship between two or more subjects during a negotiation). In this process, the use of examples and redundancy can be expected precisely to induce the generation of a certain meaning of that message.
- A fifth level can be considered where a system can use the previous levels of openness and decide how to act: either as a closed system or an open one at various levels. The ability to decide on the level of openness can be understood as the maximum expression of openness. For example, during a conversation, the system can decide to refuse to understand or pay attention, or be active interacting with interlocutors; sending examples even without the guarantee they will be used; or sending confusing, ambiguous examples, on purpose.
Logical closure is complete by definition (see above). Logical openness is incomplete on principle, as negation of logical closure.
6.2. The Case of the DYnamic uSAge of Models (DYSAM)
Logical openness has resulted in approaches such as the use of Dynamic Usage of Models (DYSAM) [99] (pp. 64–75), based on established approaches in the literature, such as ensemble learning [100,101] and Evolutionary Game Theory [102].
From an objectivist conception the dynamics consist of the temporal representation through a model which is expected to be the best existing one, in principle, and which should only be implemented with an appropriate research activity. We distinguish here, however, between dynamic models having time in their equations and the dynamics of models as methods and strategies to use more models over time. This is to cope with the multitude of properties acquired by complex systems over time.
Examples are given by considering and using non-equivalent models simultaneously as the biochemical and psychological aspects in medicine; the economic, cultural, and religious aspect in sociology; in childhood, where a child uses the five senses, not with the purpose of choosing the one which feels best, but to learn how to use them simultaneously in a coherent manner; in physics, to decide when it is more appropriate to use classical and quantum models.
However, the problem is not only to model dynamic systems which change their evolution over time, but complex systems which change themselves by acquiring new properties. The dynamics refer not only to how the same system changes parameters, but also to how the system acquires several aspects simultaneously and non-equivalent properties (not linearly convertible one to another), and continually transforms itself coherently, requiring models based on logical openness. This is the case, for example, for Multiple Systems and Collective Beings [99] (pp. 97–134) constituted by the same elements interacting in different ways to accommodate the acquisition of various diverse properties.
In Multiple Systems the same component elements (a) play interchangeable, multiple and overlapping roles (that is, an action, a position, the value of a variable have different meanings depending on the respective systems they establish); and (b) simultaneously or sequentially interact in various ways, dynamically constituting sequences of different systems. Examples of Multiple Systems are given, for example, by co-operative and multiple roles of programs and nodes of the Internet, in electrical networks, by the values of sensors constituting, at one and the same time, safety and regulatory systems.
Multiple Systems are called Collective Beings when the constituent elements are autonomous, possessing cognitive systems which allow them to decide their behavior and mode of interaction. Examples of Collective Beings are given, for example, by people and families who can simultaneously form corporate systems, traffic, markets, and users of telephone networks.
DYSAM refers to the logically open use of multiple strategies and approaches not to solve, but to induce, for instance, by using redundancies to confirm the same meaning of the intervention, but in multiple coherent ways.
This can be done, for example, by acting on the environment, inserting suitable perturbations, making energetic variations, acting on external relations, acting on communication processes, learning by interacting with other systems, and by inserting attractors of meaning with repetitions and reformulations. Thus, perturbations are processed by the system to orient it and not to decide its destiny.
DYSAM makes sense in cases of incompleteness; otherwise there would be instructions for use.
6.3. Uncertainty Principles
Theoretical incompleteness is closely related to the uncertainty principles in physics for which, in certain phenomena, the search for increasing accuracy in knowing the value of one variable correspondingly involves reduction in knowing the value taken by another. It is the measurement of homologous components, such as position and momentum (the product of the mass of an object and its speed). This is the well-known Uncertainty Principle [103] introduced in 1927 by Werner Heisenberg (1901–1976). One must also consider the related Complementarity Principle introduced by Neils Bohr (1885–1962) in 1928 [104] for which the corpuscular and wave aspects of a physical phenomenon will never occur simultaneously. The experimental observation of one prevents observation of the other.
Finally, from a generic point of view, the property of incompleteness can be general or refer to a specific property or several properties; have different levels; mean not yet complete; mean uncompletable or chronically uncompletable; and theoretically non-completable as for procedures (see Section 5.1).
7. Handling Incompleteness
All of this should help us to recognize incompleteness situations against which approaches based on negative extensions, or iterations, or combinations of those used for completeness are inadequate, both theoretically and practically.
As outlined above, when it is not about abstract problems, as in mathematics, incompleteness matches complexity as a property. This is true across disciplines.
In general, the issue concerns the inadequacy of dealing with problems and complex phenomena using classical General Systems Theory, as mentioned in the introduction. An example of such inadequacy is given by the management of properties of the post-industrial society (knowledge society) using criteria and approaches typical of the industrial society instead of using the principles and approaches of post-Bertalanffy General Systems Theory.
In particular, as outlined above, multiplicity, non-equivalence, concurrent and dynamic contextualities, cognitive skills, such as abduction, coherence, and the ability to induce, have to be used. Learning abilities are not considered for obtaining repeatability or the equilibrium of situations, but for selecting and creating strategies, models, and approaches in the face of unpredictability and non-repeatability of complexity. Examples include logical openness and DYSAM.
In social systems, this regards their formation, emergence, and management processes. This requires modeling based on principles beyond classical ones moving, for example, from stratified differentiation to functional differentiation [105,106], which leads to ineffectiveness when considering roles and structures to be replaced with other functionals. One has to rethink the concept of management and of value, for example, with respect to the independence of economics and finance. The management of companies modeled as autopoietic, emerging, distributed, and incomplete has nothing to do with that of companies considered as structurally stable, in which the non-emergent aspect is considered to be absolutely dominant.
In social systems, it also involves their processes of education previously considered as dispensing knowledge, divided into disciplines and focusing on events and places (school terms and places like schools) when the environment was stable, as was the role of education. In the knowledge society, education processes are multiple, interdisciplinary, non-explicit, non-complete, non-unique, and non-equivalent, even with different and dynamic coherences (a typical situation of logical openness).
8. Conclusions
The transition from the logic of certainty to the logic of uncertainty is a matter of transition from research with the assumption of completeness to that of incompleteness; from equilibrium and regulation to coherence; from the search for the solution to the inducement of the acquisition of properties, as considered by post-Bertalanffy General Systems Theory. Incompleteness is not formulated as a possibly temporary theoretical limit, but as the intrinsic foundations of logical openness.
We must face the balance between completeness and incompleteness, as limit and opportunity.
It is not simply to replace previously-accepted concepts and approaches relating to completeness with others relating to incompleteness, but to use both of them properly, depending on the context, and also simultaneously using a DYSAM-like approach. In the first case, related to replacing completeness, there seems to be a reassuring relativism, able to make algorithmic processes of choice for the best approach. In the second case, however, the possible simultaneous use of approaches of different natures is dynamic, braided with incompleteness and completeness, suitable for complexity. Dealing with complexity, the usage of algorithms, removing responsibilities and always tending to guarantee the optimal objective choice, is inconceivable. Incompleteness represents this situation by making explicit the responsibility of choosing between various currently equivalent possibilities, with particular regard to various kinds of problems, such as social, medical and scientific for which choices are irreducible to optimizations. The focus on incompleteness not only makes explicit the impossibility to choose algorithmically, it also opens the way for various cultural reflections of a different nature, such as the role of unintended effects [107] in social emergence [108] of social dynamics [109]. Such reflections should be useful to move from considering complexity as “inaccurate machinery”, not fully understood (but this is precisely the perspective), to carry out research, to represent the multiplicity of incompleteness and dynamic coherence as an irreducible conceptual space (with its own properties), for which it is theoretically impossible to zip them into complete, analytical representations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Carrier, M. The Completeness of Scientific Theories; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Godehard, L. One Hundred Years of Russell’s Paradox: Mathematics, Logic, Philosophy; Gruyter: Berlin, Germany, 2004. [Google Scholar]
- Gödel, K. On Formally Undecidable Propositions of Principia Mathematica and Related Systems; Dover Publications Inc.: Mineola, NY, USA, 1962. [Google Scholar]
- Castellani, B.; Hafferty, F.W. Sociology and Complexity Science: A New Field of Inquiry; Springer-Verlag: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Estrada, E. The Structure of Complex Networks: Theory and Applications; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Rouse, W.B. Modeling and Visualization of Complex Systems and Enterprises; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hooker, C. (Ed.) Philosophy of Complex Systems; Elsevier: Oxford, UK, 2011.
- Bellomo, N.; Ajmone Marsan, G.; Tosin, A. Complex Systems and Society: Modeling and Simulation; Springer: New York, NY, USA, 2013. [Google Scholar]
- Barabási, A.L. Linked: The New Science of Networks; Perseus Publishing: Cambridge, MA, USA, 2002. [Google Scholar]
- Licata, I. Logical openness in cognitive models. Epistemologia 2008, 31, 177–191. [Google Scholar]
- Minati, G.; Abram, M.; Pessa, E. (Eds.) Towards a Post-Bertalanffy Systemics; Springer: New York, NY, USA, 2016.
- Minati, G. General System(s) Theory 2.0: A brief outline. In Towards a Post-Bertalanffy Systemics, Proceedings of the Sixth National Conference of the Italian Systems Society, Rome, Italy, 21–22 November 2014; Minati, G., Abram, M., Pessa, E., Eds.; Springer: New York, NY, USA, 2016; pp. 211–219. [Google Scholar]
- Minati, G.; Pessa, E. Special Issue on Second Generation General System Theory. Systems 2014. Available online: http://www.mdpi.com/journal/systems/special_issues/second-generationgeneral-system-theory (accessed on 13 July 2016). [Google Scholar]
- Von Bertalanffy, L. General System Theory: Foundations, Development, Applications; George Braziller: New York, NY, USA, 1968. [Google Scholar]
- Kumar, K. From Post-Industrial to Post-Modern Society: New Theories of the Contemporary World; Blackwell Publishers: Oxford, UK, 2004. [Google Scholar]
- Haunss, S. Conflicts in the Knowledge Society; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Minati, G. Some new theoretical issues in Systems Thinking relevant for modelling corporate learning. Learn. Organ. 2007, 14, 480–488. [Google Scholar]
- Minati, G. Knowledge to manage the Knowledge Society. Learn. Organ. 2012, 19, 352–370. [Google Scholar] [CrossRef]
- Minati, G. Special Issue: Knowledge to manage the Knowledge Society. Learn. Organ. 2012, 19, 296–382. [Google Scholar] [CrossRef]
- Boccara, N. Modeling Complex Systems; Springer: New York, NY, USA, 2010. [Google Scholar]
- Altshuler, B.L.; Lee, P.A.; Webb, R.A. (Eds.) Mesoscopic Phenomena in Solids; North Holland: Amsterdam, The Netherlands, 1991.
- Haken, H. Information and Self-Organization. A macroscopic approach to complex systems; Springer: Berlin, Germany, 1988. [Google Scholar]
- Imry, Y. Physics of Mesoscopic Systems. In Directions in Condensed Matter Physics; Grinstein, G., Mazenko, G., Eds.; World Scientific: Singapore, 1986; pp. 101–163. [Google Scholar]
- Liljenstrom, H.; Svedin, U. (Eds.) Micro, Meso, Macro: Addressing Complex Systems Couplings; World Scientific: Singapore, 2005.
- Laughlin, R.B.; Pines, D.; Schmalian, J.; Stojkovic, B.P.; Wolynes, P. The Middle Way. PNAS 2000, 97, 32–37. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, J. Emergence as a Construct: History and Issues. Emergence 1999, 1, 49–72. [Google Scholar] [CrossRef]
- Mikhailov, A.S.; Calenbuhr, V. From Cells to Societies. Models of Complex Coherent Actions; Springer: Berlin, Germany, 2002. [Google Scholar]
- Boccaletti, S. The Synchronized Dynamics of Complex Systems; Elsevier: Oxford, UK, 2008. [Google Scholar]
- Licata, I. Living with Radical Uncertainty. The Exemplary case of Folding Protein. In Crossing in Complexity: Interdisciplinary Application of Physics in Biological and Social Systems; Licata, I., Sakaji, A., Eds.; Nova Science: New York, NY, USA, 2010; pp. 1–9. [Google Scholar]
- Zadeh, L.A.; Klir, G.J.; Yuan, B. (Eds.) Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi A. Zadeh; World Scientific: Singapore, 1996.
- Pessa, E. Phase Transitions in Biological Matter. In Physics of Emergence and Organization; Licata, I., Sakaji, A., Eds.; World Scientific: Singapore, 2008; pp. 165–228. [Google Scholar]
- Nishimori, H. Elements of Phase Transitions and Critical Phenomena; Oxford University Press: New York, NY, USA, 2015. [Google Scholar]
- Nagaev, R.F. Dynamics of Synchronising Systems; Springer-Verlag: Berlin, Germany, 2002. [Google Scholar]
- Ashby, W.R. Principles of the Self-Organizing Dynamic System. J. Gen. Psychol. 1947, 37, 125–128. [Google Scholar] [CrossRef] [PubMed]
- De Wolf, T.; Holvoet, T. Emergence Versus Self Organisation: Different Concepts but Promising when Combined. In Engineering Self-Organising Systems: Methodologies and Applications; Brueckner, S.A., Di Marzo Serugendo, G., Karageorgos, A., Eds.; Springer: New York, NY, USA, 2005; pp. 1–15. [Google Scholar]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.L.; Zhouc, C.S. The synchronization of chaotic systems. Phys. Rep. 2002, 366, 1–98. [Google Scholar] [CrossRef]
- Buck, J.; Buck, E. Biology of synchronous flashing of fireflies. Nature 1966, 211, 562–564. [Google Scholar] [CrossRef]
- Baas, N.A. Emergence, Hierarchies, and Hyperstructures. In Alife III, Santa Fe Studies in the Sciences of Complexity; Langton, C.G., Ed.; Addison-Wesley: Redwood City, CA, USA, 1994; pp. 515–537. [Google Scholar]
- Ryan, A.J. Emergence is Coupled to Scope, not Level. Complexity 2006, 67, 67–77. [Google Scholar] [CrossRef]
- Emmeche, C.; Koppe, S.; Stjernfelt, F. Explaining Emergence: Towards an Ontology of Levels. J. Gen. Philos. Sci. 1997, 28, 83–119. [Google Scholar] [CrossRef]
- Minati, G.; Licata, I. Meta-Structural properties in Collective Behaviours. Int. J. Gen. Syst. 2012, 41, 289–311. [Google Scholar] [CrossRef]
- Minati, G.; Licata, I. Emergence as Mesoscopic Coherence. Systems 2013, 1, 50–65. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order through Fluctuations; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Prigogine, I. From Being to Becoming: Time and Complexity in the Physical Sciences; W.H. Freeman & Co.: New York, NY, USA, 1981. [Google Scholar]
- Stanley, H.E.; Amaral, L.A.N.; Gopikrishnan, P.; Ivanov, P.C.; Keitt, T.H.; Plerou, V. Scale invariance and universality: Organizing principles in complex systems. Phys. A Stat. Mech. Its Appl. 2000, 281, 60–68. [Google Scholar] [CrossRef]
- Schroeder, M. Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise; Dover Publications Inc.: New York, NY, USA, 2009. [Google Scholar]
- Bunde, A.; Havlin, S. Fractals and Disordered Systems; Springer: New York, NY, USA, 2012. [Google Scholar]
- Ruelle, D. Chaotic Evolution and Attractors; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Grassberger, P.; Procaccia, I. Measuring the Strangeness of Strange Attractors. Phys. D 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Liu, C.; Liu, T.; Liu, L.; Liu, K. A new chaotic attractor. Chaos Solitons Fractals 2004, 22, 1031–1038. [Google Scholar] [CrossRef]
- Giuliani, A.; Zbilut, J. The Latent Order of Complexity; NovaScience: New York, NY, USA, 2008. [Google Scholar]
- Lorenz, E. Deterministic Non Period Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Sparrow, C. The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors; Springer-Verlag: New York, NY, USA, 2013. [Google Scholar]
- Lewis, T.G. Network Science: Theory and Applications; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Motter, A.E.; Albert, R. Networks in motion. Phys. Today 2012, 65, 43–48. [Google Scholar] [CrossRef]
- Valente, T.W. Network Interventions. Science 2012, 337, 49–53. [Google Scholar] [CrossRef] [PubMed]
- Dorogovtsev, S.N.; Goltsev, A.V.; Mendes, J.F.F. Critical phenomena in complex networks. Rev. Mod. Phys. 2008, 80, 1275–1335. [Google Scholar] [CrossRef]
- Baker, A. Complexity, Networks, and Non-Uniqueness. Found. Sci. 2013, 18, 687–705. [Google Scholar] [CrossRef]
- Newman, M. Networks: An Introduction; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Cohen, R.; Havlin, S. Complex Networks: Structure, Robustness and Function; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Giuliani, A. Networks as a Privileged Way to Develop Mesoscopic Level Approaches in Systems Biology. Systems 2014, 2, 237–242. [Google Scholar] [CrossRef]
- Kohestani, H.; Giuliani, A. Organization principles of biological networks: An explorative study. Biosystems 2016, 141, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Kadushin, C. Understanding Social Networks: Theories, Concepts, and Findings; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]
- Missaoui, R.; Sarr, I. Social Network Analysis—Community Detection and Evolution; Springer: New York, NY, USA, 2015. [Google Scholar]
- Johnson, S. Emergence: The Connected Lives of Ants, Brains, Cities and Software; Touchstone: New York, NY, USA, 2002. [Google Scholar]
- Kauffman, S. At Home in the Universe: The Search for the Laws of Self-Organization and Complexity; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Gros, C. Complex and Adaptive Dynamical Systems; Springer: New York, NY, USA, 2013. [Google Scholar]
- Hong, H.; Park, H.; Choi, M.Y. Collective synchronization in spatially extended systems of coupled oscillators with random frequencies. Phys. Rev. E 2005, 72, 036217. [Google Scholar] [CrossRef] [PubMed]
- Turing, A. On computable numbers, with an application to the Entscheidungs problem. Proc. Lond. Math. Soc. 1936, 42, 230–265. [Google Scholar]
- Magnani, L. Abduction, Reason and Science: Processes of Discovery and Explanation; Springer: New York, NY, USA, 2001. [Google Scholar]
- Von Foerster, H. Cybernetics of Cybernetics. In Communication and Control in Society; Krippendorff, K., Ed.; Gordon and Breach: New York, NY, USA, 1979; pp. 5–8. [Google Scholar]
- Hacking, I. The Emergence of Probability: A Philosophical Study of Early Ideas about Probability Induction and Statistical Inference; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Liu, B. Uncertainty Theory; Springer-Verlag: Berlin, Germany, 2014. [Google Scholar]
- Gash, H. Constructing constructivism. Constr. Found. 2014, 9, 302–327. [Google Scholar]
- Gergen, K.J. An Invitation to Social Construction; Sage Publications: London, UK, 2015. [Google Scholar]
- Gash, H. Systems and Beliefs. Found. Sci. 2016, 21, 177–187. [Google Scholar] [CrossRef]
- Butts, R.; Brown, J. (Eds.) Constructivism and Science; Kluwer: Dordrecht, The Netherlands, 1989.
- Segal, L. The Dream of Reality: Heinz Von Foerster’s Constructivism; Springer-Verlag: New York, NY, USA, 2013. [Google Scholar]
- Von Glasersfeld, E. Radical Constructivism: A Way of Knowing and Learning; Falmer Press: London, UK, 1995. [Google Scholar]
- Galavotti, M.C. (Ed.) Bruno de Finetti Radical Probabilist; College Publications: London, UK, 2008.
- Friedenberg, J.D.; Silverman, G.W. Cognitive Science: An Introduction to the Study of Mind; SAGE Publications Inc.: Los Angeles, CA, USA, 2015. [Google Scholar]
- Cecconi, F. (Ed.) New Frontiers in the Study of Social Phenomena: Cognition, Complexity, Adaptation; Springer: New York, NY, USA, 2016.
- Nescolarde-Selva, J.A.; Usó-Doménech, J.-L. Gash A theorical point of view of reality, perception, and language. Complexity 2014, 20, 27–37. [Google Scholar] [CrossRef]
- Usó-Doménech, J.L.; Nescolarde-Selva, J.; Gash, H. Guest editorial: Belief systems and science. Cybern. Syst. 2015, 46, 379–389. [Google Scholar] [CrossRef]
- Lee, M.D. Bayesian Cognitive Modeling; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- De Finetti, B. Theory of Probability—A Critical Introductory Treatment; John Wiley & Sons: London, UK, 1975. [Google Scholar]
- Licata, I. Seeing by models: Vision as adaptive epistemology. In Methods, Models, Simulations and Approaches towards a General Theory of Change; Minati, G., Abram, M., Pessa, E., Eds.; World Scientific: Singapore, 2012; pp. 385–400. [Google Scholar]
- Minati, G.; Penna, M.P.; Pessa, E. Thermodynamic and Logical Openness in General Systems. Syst. Res. Behav. Sci. 1998, 15, 131–145. [Google Scholar] [CrossRef]
- Manrubia, S.C.; Mikhailov, A.S. Emergence of Dynamical Order: Synchronization Phenomena in Complex Systems; World Scientific: Singapore, 2004. [Google Scholar]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Bonometti, P. Improving safety, quality and efficiency through the management of emerging processes: The TenarisDalmine experience. Learn. Organ. 2012, 19, 299–310. [Google Scholar]
- Mac Lennan, B.J. Natural computation and non-Turing models of computation. Theor. Comput. Sci. 2004, 317, 115–145. [Google Scholar] [CrossRef]
- Bader, M. Space-Filling Curves: An Introduction with Applications in Scientific Computing; Springer-Verlag: Berlin, Germany, 2013. [Google Scholar]
- Tyson, J.J. The Belousov-Zhabotinskii Reaction; Springer: Berlin, Germany, 1976. [Google Scholar]
- Kinoshita, S. (Ed.) Pattern Formations and Oscillatory Phenomena &Belousov-Zhabotinsky Reaction; Elsevier: Amsterdam, The Netherlands, 2013.
- Getling, A.V. Rayleigh-Bénard Convection: Structures and Dynamics; World Scientific: Singapore, 1998. [Google Scholar]
- Janot, C. Quasicrystals: A Primer; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Licata, I.; Minati, G. Creativity as Cognitive design-The case of mesoscopic variables in Meta-Structures. In Creativity: Fostering, Measuring and Contexts; Corrigan, A.M., Ed.; Nova Publishers: New York, NY, USA, 2010. [Google Scholar]
- Minati, G.; Pessa, E. Collective Beings; Springer: New York, NY, USA, 2006. [Google Scholar]
- Hinton, G.E.; Van Camp, D. Keeping neural networks simple by minimizing the description length of the weights. In Proceedings of the Sixth Annual Conference on Computational Learning Theory; Pitt, L., Ed.; ACM Press: New York, NY, USA, 1993; pp. 5–13. [Google Scholar]
- Zhou, Z.-H. Ensemble Methods: Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Vincent, T.L. Evolutionary Game Theory, Natural Selection, and Darwinian Dynamics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Heisenberg, W. Physics and Beyond; Harper & Row: New York, NY, USA, 1971. [Google Scholar]
- Bohr, N. The Quantum Postulate and the Recent Development of Atomic Theory. Nature 1928, 121, 580590. [Google Scholar] [CrossRef]
- Luhmann, N. How Can the Mind Participate in Communication? In Theories of Distinction: Redescribing the Descriptions of Modernity; Rasch, W., Ed.; Stanford University Press: Stanford, CA, USA, 2002; pp. 169–184. [Google Scholar]
- Luhmann, N. Limits of Steering in Theory. Cult. Soc. 1997, 14, 41–57. [Google Scholar] [CrossRef]
- Usó-Doménech, J.L.; Nescolarde-Selva, J.; Lloret-Climent, M. “Unintended effects”: A theorem for complex systems. Complexity 2015, 21, 342–354. [Google Scholar] [CrossRef]
- Sawyer, R.K. Social Emergence: Societies as Complex Systems; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Skyrms, B. Social Dynamics; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).