Building the Observer into the System: Toward a Realistic Description of Human Interaction with the World
Abstract
:The theory of the Black Box is merely the theory of real objects or systems, when close attention is given to the question, relating object and observer, about what information comes from the object, and how it is obtained.— W. Ross Ashby, 1956 ([1], p. 110)
1. Introduction
2. The Black Box Model
2.1. Systems and Separability
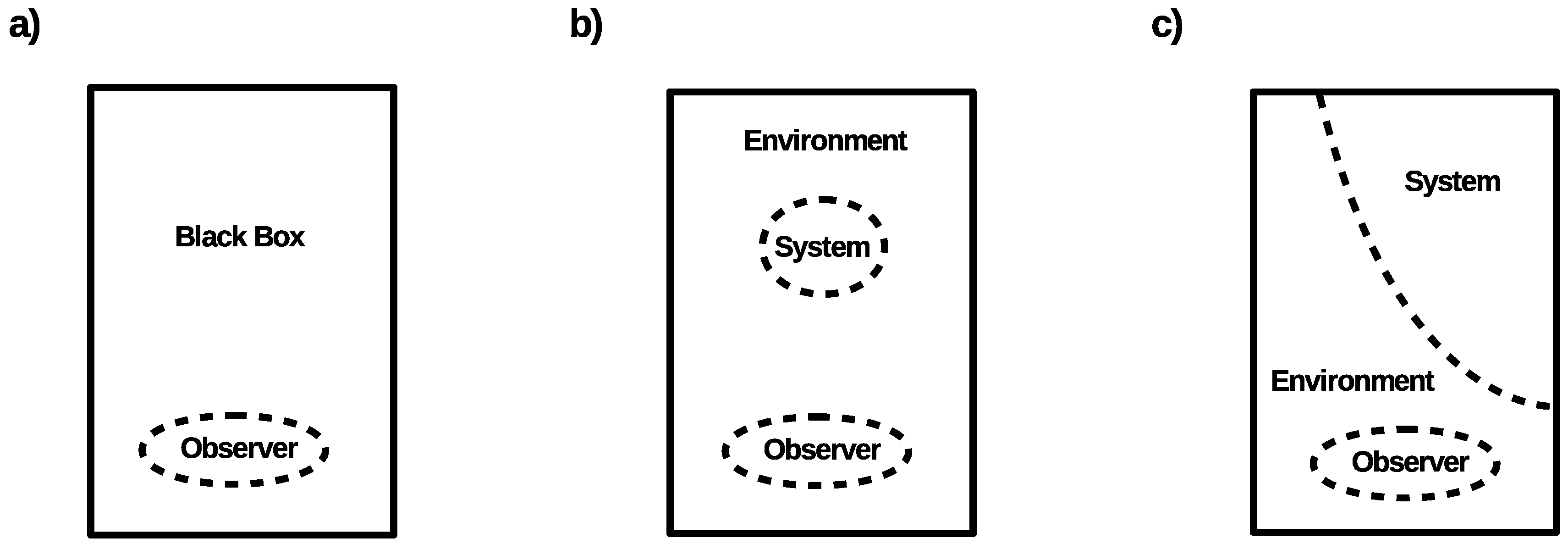
2.2. Definition of the Black Box
2.3. The Black Box as a Model of Physical Systems
2.4. The Epistemic Cut and Decompositional Equivalence
2.5. Observer Dependence and “Subjectivity”
3. No-Go Theorems for Black Boxes
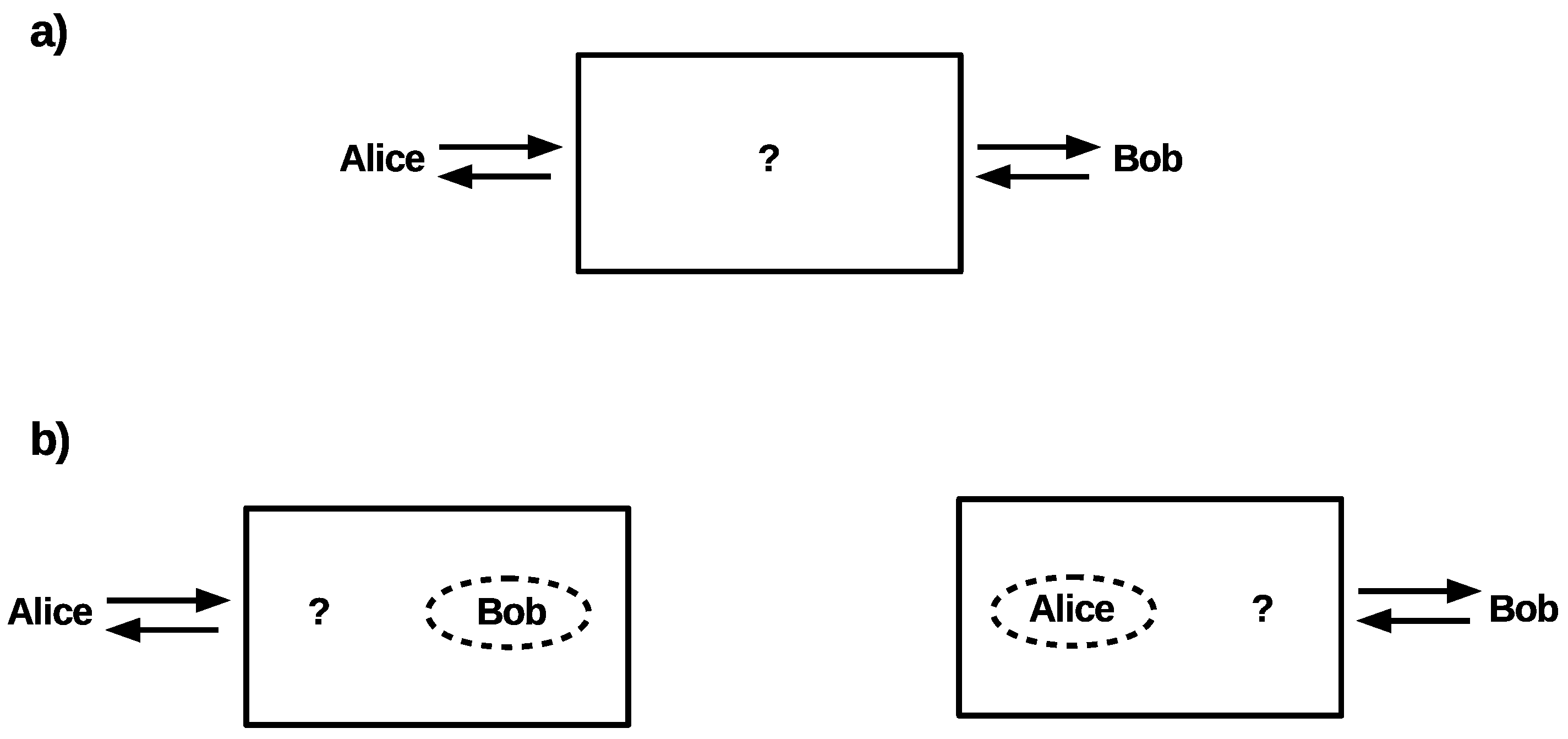
3.1. Moore’s Theorem (1956)
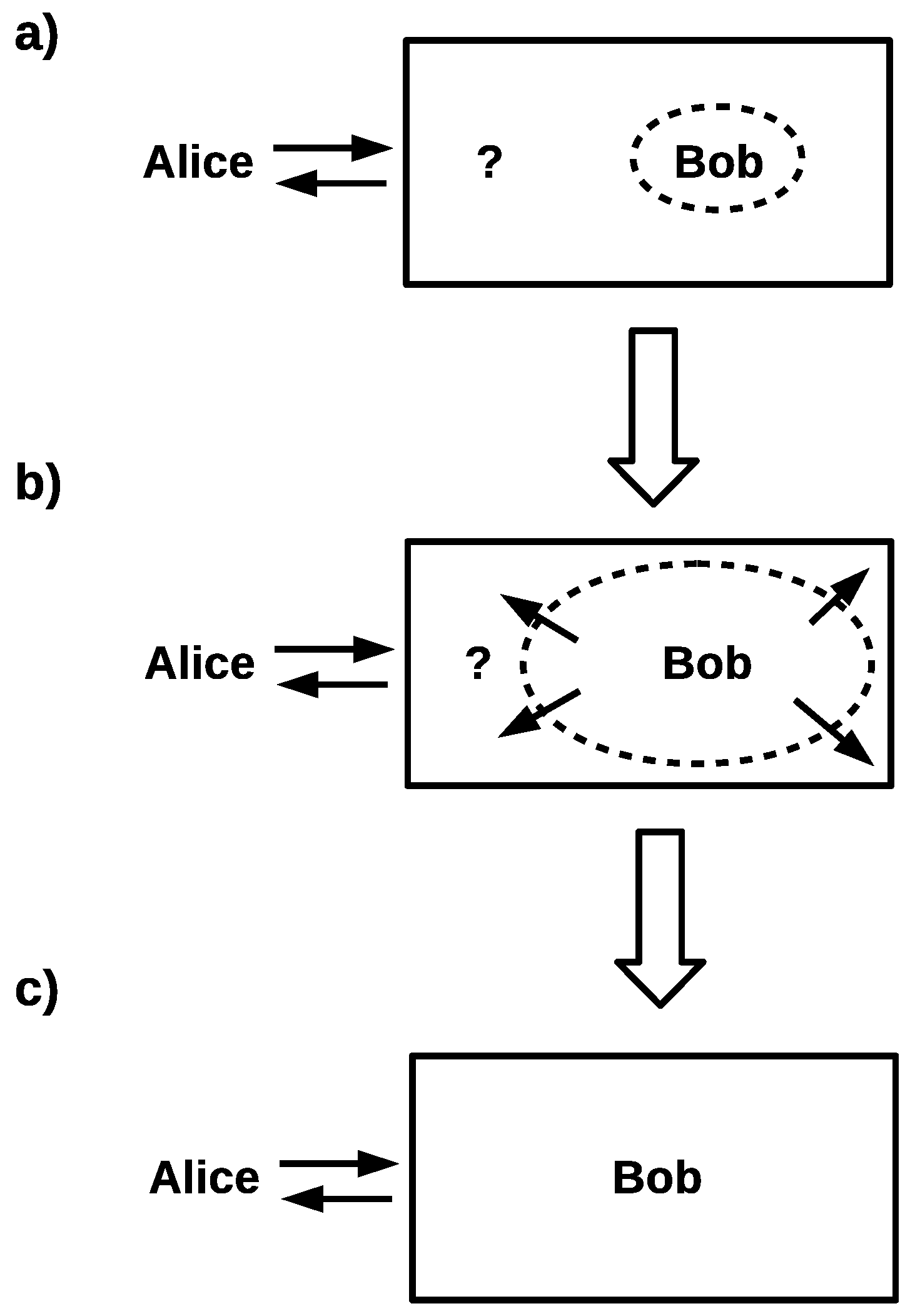
3.2. A Black Box Cannot Be Bounded
3.3. Corollaries
3.4. What is Physics about?
4. “Objects” within a Black Box
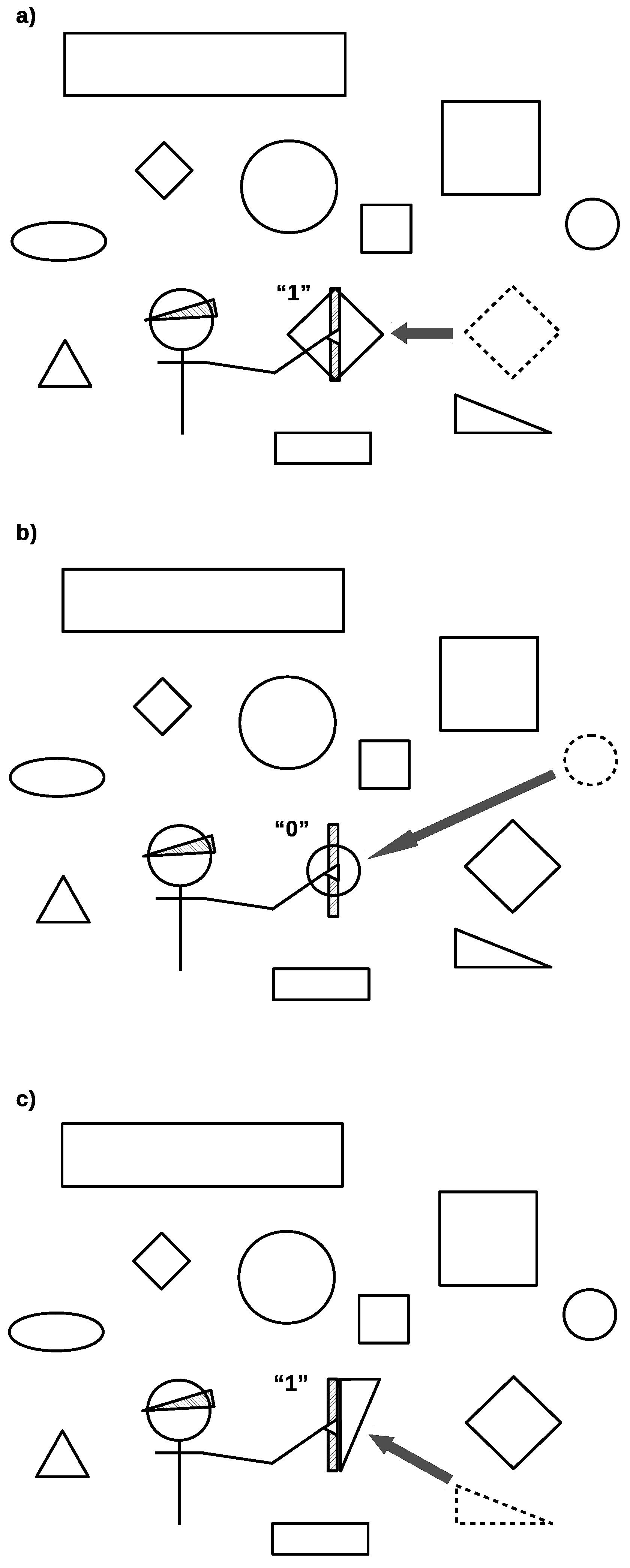
4.1. Object Identification in Practice
- simultaneously accessible to many observers,
- who are able to find out what it is without prior knowledge about the system of interest, and
- who can arrive at a consensus about it without prior agreement.”
4.2. Superpositions Encode the Unresolvable Ambiguity of Object Identification
4.3. Objects as Internal Reference Frames
5. The Black Box as a Cross-Disciplinary Paradigm
5.1. Formal Semantics, Device Independence and Virtual Machines
5.2. Cognitive Science and AI
5.3. Evolution and Development
6. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial intelligence |
| FAPP | For all practical purposes |
| ITP | Interface theory of perception |
| LOCC | Local observations, classical communication |
| SGP | Symbol grounding problem |
References
- Ashby, W.R. Introduction to Cybernetics; Chapman and Hall: London, UK, 1956. [Google Scholar]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–195. [Google Scholar] [CrossRef]
- Landauer, R. Information is a physical entity. Phys. A 1999, 263, 63–67. [Google Scholar] [CrossRef]
- Bennett, C.H. Notes on Landauer’s Principle, reversible computation, and Maxwell’s Demon. Stud. Hist. Philos. Mod. Phys. 2003, 34, 501–510. [Google Scholar] [CrossRef]
- Bacciagalupi, G.; Valenti, A. Quantum Theory at the Crossroads: Reconsidering the 1927 Solvay Conference; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Landsman, N.P. Between classical and quantum. In Handbook of the Philosophy of Science: Philosophy of Physics; Butterfield, J., Earman, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 417–553. [Google Scholar]
- Wallace, D. Philosophy of quantum mechanics. In The Ashgate Companion to Contemporary Philosophy of Physics; Rickles, D., Ed.; Ashgate: Aldershot, UK, 2008; pp. 16–98. [Google Scholar]
- Norsen, T.; Nelson, S. Yet another snapshot of foundational attitudes toward quantum mechanics. 2013; preprint. arXiv:1306.4646v2. [Google Scholar]
- Schlosshauer, M.; Kofler, J.; Zeilinger, A. A snapshot of foundational attitudes toward quantum mechanics. Stud. Hist. Philos. Mod. Phys. 2013, 44, 222–223. [Google Scholar] [CrossRef]
- Sommer, C. Another survey of foundational attitudes towards quantum mechanics. 2013; preprint. arXiv:1303.2719v1. [Google Scholar]
- Fuchs, C. QBism, the perimeter of Quantum Bayesianism. 2010; preprint. arxiv:1003.5201v1. [Google Scholar]
- Cabello, A. Interpretations of quantum theory: A map of madness. 2015; preprint. arXiv:1509.04711v1. [Google Scholar]
- Bell, J.S. Against measurement. Phys. World 1990, 3, 33–41. [Google Scholar] [CrossRef]
- Fuchs, C. On participatory realism. 2016; preprint. arxiv:1601.04360v1. [Google Scholar]
- Wheeler, J.A. Law without law. In Quantum Theory and Measurement; Wheeler, J.A., Zurek, W.H., Eds.; Princeton University Press: Princeton, NJ, USA, 1983; pp. 182–213. [Google Scholar]
- Von Uexküll, J. A stroll through the worlds of animals and men. In Instinctive Behavior; Schiller, C., Ed.; van Nostrand Reinhold: New York, NY, USA, 1957; pp. 5–80. [Google Scholar]
- Von Foerster, H. Objects: Tokens for (eigen-) behaviors. ASC Cybern. Forum 1976, 8, 91–96. [Google Scholar]
- Kampis, G. Explicit epistemology. Revue de la Pensee d’Aujourd’hui 1996, 24, 264–275. [Google Scholar]
- Koenderink, J. The all-seeing eye. Perception 2014, 43, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Rössler, O.E. Endophysics. In Real Brains—Artificial Minds; Casti, J., Karlquist, A., Eds.; North-Holland: New York, NY, USA, 1987; pp. 25–46. [Google Scholar]
- Von Neumann, J. The Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Pattee, H.H. The physics of symbols: Bridging the epistemic cut. Biosystems 2001, 60, 5–21. [Google Scholar] [CrossRef]
- Kauffman, S.A.; Gare, A. Beyond Descartes and Newton: Recovering life and humanity. Prog. Biophys. Mol. Biol. 2015, 119, 219–244. [Google Scholar] [CrossRef] [PubMed]
- Kitto, K. A contextualised general systems theory. Systems 2014, 2, 541–565. [Google Scholar] [CrossRef]
- Tipler, F.J. Quantum nonlocality does not exist. Proc. Natl. Acad. Sci. USA 2014, 111, 11281–11286. [Google Scholar] [CrossRef] [PubMed]
- Bohm, D.; Hiley, B.J.; Kaloyerou, P.N. An ontological basis for the quantum theory. Phys. Rep. 1987, 144, 321–375. [Google Scholar] [CrossRef]
- Rosen, R. On information and complexity. In Complexity, Language, and Life: Mathematical Approaches; Casti, J.L., Karlqvist, A., Eds.; Springer: Berlin, Germany, 1986; pp. 174–196. [Google Scholar]
- Polanyi, M. Life’s irreducible structure. Science 1968, 160, 1308–1312. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Bohr, N. Causality and complementarity. Philos. Sci. 1937, 4, 289–298. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory; Pergamon: Oxford, UK, 1977. [Google Scholar]
- Mermin, D. What’s wrong with this pillow? Phys. Today 1989, 42, 9–11. [Google Scholar] [CrossRef]
- Zeh, D. On the interpretation of measurement in quantum theory. Found. Phys. 1970, 1, 69–76. [Google Scholar] [CrossRef]
- Zeh, D. Toward a quantum theory of observation. Found. Phys. 1973, 3, 109–116. [Google Scholar] [CrossRef]
- Zurek, W.H. Pointer basis of the quantum apparatus: Into what mixture does the wave packet collapse? Phys. Rev. D 1981, 24, 1516–1525. [Google Scholar] [CrossRef]
- Zurek, W.H. Environment-induced superselection rules. Phys. Rev. D 1982, 26, 1862–1880. [Google Scholar] [CrossRef]
- Joos, E.; Zeh, D. The emergence of classical properties through interaction with the environment. Z. Phys. B Condens. Matter 1985, 59, 223–243. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection and the existential interpretation (the rough guide). Philos. Trans. R. Soc. A 1998, 356, 1793–1821. [Google Scholar]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Schlosshauer, M. Decoherence and the Quantum to Classical Transition; Springer: Berlin, Germany, 2007. [Google Scholar]
- Ollivier, H.; Poulin, D.; Zurek, W.H. Objective properties from subjective quantum states: Environment as a witness. Phys. Rev. Lett. 2004, 93, 220401. [Google Scholar] [CrossRef] [PubMed]
- Ollivier, H.; Poulin, D.; Zurek, W.H. Environment as a witness: Selective proliferation of information and emergence of objectivity in a quantum universe. Phys. Rev. A 2005, 72, 042113. [Google Scholar] [CrossRef]
- Blume-Kohout, R.; Zurek, W.H. Quantum Darwinism: Entanglement, branches, and the emergent classicality of redundantly stored quantum information. Phys. Rev. A 2006, 73, 062310. [Google Scholar] [CrossRef]
- Zurek, W.H. Quantum Darwinism. Nat. Phys. 2009, 5, 181–188. [Google Scholar] [CrossRef]
- Riedel, C.J.; Zurek, W.H. Quantum Darwinism in an everyday environment: Huge redundancy in scattered photons. Phys. Rev. Lett. 2010, 105, 020404. [Google Scholar] [CrossRef] [PubMed]
- Riedel, C.J.; Zurek, W.H.; Zwolak, M. The rise and fall of redundancy in decoherence and quantum Darwinism. New J. Phys. 2012, 14, 083010. [Google Scholar] [CrossRef]
- Zwolak, M.; Riedel, C.J.; Zurek, W.H. Amplification, redundancy, and quantum Chernoff information. Phys. Rev. Lett. 2014, 112, 140406. [Google Scholar] [CrossRef] [PubMed]
- Chiribella, G.; D’Ariano, G.M. Quantum information becomes classical when distributed to many users. Phys. Rev. Lett. 2006, 97, 250503. [Google Scholar] [CrossRef] [PubMed]
- Korbicz, J.K.; Horodecki, P.; Horodecki, R. Objectivity in a noisy photonic environment through quantum state information broadcasting. Phys. Rev. Lett. 2014, 112, 120402. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, R.; Korbicz, J.K.; Horodecki, P. Quantum origins of objectivity. Phys. Rev. A 2015, 91, 032122. [Google Scholar] [CrossRef]
- Brandão, F.G.S.L.; Piani, M.; Horodecki, P. Generic emergence of classical features in quantum Darwinism. Nat. Commun. 2015, 6, 7908. [Google Scholar] [CrossRef] [PubMed]
- Fields, C. Quantum Darwinism requires an extra-theoretical assumption of encoding redundancy. Int. J. Theor. Phys. 2010, 49, 2523–2527. [Google Scholar] [CrossRef]
- Fields, C. Classical system boundaries cannot be determined within quantum Darwinism. Phys. Essays 2011, 24, 518–522. [Google Scholar] [CrossRef]
- Schlosshauer, M. Experimental motivation and empirical consistency of minimal no-collapse quantum mechanics. Ann. Phys. 2006, 321, 112–149. [Google Scholar] [CrossRef]
- Everett, H., III. “Relative state” formulation of quantum mechanics. Rev. Mod. Phys. 1957, 29, 454–462. [Google Scholar] [CrossRef]
- Ghirardi, G.C.; Rimini, A.; Weber, T. Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D 1986, 34, 470–491. [Google Scholar] [CrossRef]
- Penrose, R. On gravity’s role in quantum state reduction. Gen. Relativ. Gravit. 1996, 28, 581–600. [Google Scholar] [CrossRef]
- Weinberg, S. Collapse of the state vector. Phys. Rev. A 2012, 85, 062116. [Google Scholar] [CrossRef]
- Jordan, T.F. Fundamental significance of tests that quantum dynamics is linear. Phys. Rev. A 2010, 82, 032103. [Google Scholar] [CrossRef]
- Wiseman, H. Quantum physics: Death by experiment for local realism. Nature 2015, 526, 649–650. [Google Scholar] [CrossRef] [PubMed]
- Swingle, B. Entanglement renormalization and holography. Phys. Rev. D 2012, 86, 065007. [Google Scholar] [CrossRef]
- Saini, A.; Stojkovic, D. Radiation from a collapsing object is manifestly unitary. Phys. Rev. Lett. 2015, 114, 111301. [Google Scholar] [CrossRef] [PubMed]
- Susskind, L. Computational complexity and black hole horizons. Fortschr. Phys. 2016, 64, 24–43. [Google Scholar] [CrossRef]
- Fields, C. If physics is an information science, what is an observer? Information 2012, 3, 92–123. [Google Scholar] [CrossRef]
- Fields, C. A model-theoretic interpretation of environment-induced superselection. Int. J. Gen. Syst. 2012, 41, 847–859. [Google Scholar] [CrossRef]
- Fields, C. On the Ollivier-Poulin-Zurek definition of objectivity. Axiomathes 2014, 24, 137–156. [Google Scholar] [CrossRef]
- Fields, C. Decompositional equivalence: A fundamental symmetry underlying quantum theory. Axiomathes 2016, 26, 279–311. [Google Scholar] [CrossRef]
- Zanardi, P. Virtual quantum subsystems. Phys. Rev. Lett. 2001, 87, 077901. [Google Scholar] [CrossRef] [PubMed]
- Zanardi, P.; Lidar, D.A.; Lloyd, S. Quantum tensor product structures are observable-induced. Phys. Rev. Lett. 2004, 92, 060402. [Google Scholar] [CrossRef] [PubMed]
- Dugić, M.; Jeknić, J. What is “system”: Some decoherence-theory arguments. Int. J. Theor. Phys. 2006, 45, 2249–2259. [Google Scholar] [CrossRef]
- Dugić, M.; Jeknić-Dugić, J. What is “system”: The information-theoretic arguments. Int. J. Theor. Phys. 2008, 47, 805–813. [Google Scholar] [CrossRef]
- De la Torre, A.C.; Goyeneche, D.; Leitao, L. Entanglement for all quantum states. Eur. J. Phys. 2010, 31, 325–332. [Google Scholar] [CrossRef]
- Harshman, N.L.; Ranade, K.S. Observables can be tailored to change the entanglement of any pure state. Phys. Rev. A 2011, 84, 012303. [Google Scholar] [CrossRef]
- Thirring, W.; Bertlmann, R.A.; Köhler, P.; Narnhofer, H. Entanglement or separability: The choice of how to factorize the algebra of a density matrix. Eur. Phys. J. D 2011, 64, 181–196. [Google Scholar] [CrossRef]
- Dugić, M.; Jeknić-Dugić, J. Parallel decoherence in composite quantum systems. Pramana 2012, 79, 199–209. [Google Scholar] [CrossRef]
- Rovelli, C. Relational quantum mechanics. Int. J. Theor. Phys. 1996, 35, 1637–1678. [Google Scholar] [CrossRef]
- Moore, E.F. Gedankenexperiments on sequential machines. In Autonoma Studies; Shannon, C.W., McCarthy, J., Eds.; Princeton University Press: Princeton, NJ, USA, 1956; pp. 129–155. [Google Scholar]
- Popper, K. Conjectures and Refutations: The Growth of Scientific Knowledge; Routledge & Kegan Paul: London, UK, 1963. [Google Scholar]
- Fuchs, C.A.; Stacey, B.C. Some negative remarks on operational approaches to quantum theory. 2014; preprint. arxiv:1401.7254v1. [Google Scholar]
- Bell, J.S. On the Einstein-Podolsky-Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar]
- Aspect, A.; Dalibard, J.; Roger, G. Experimental test of Bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 1982, 49, 1804–1807. [Google Scholar] [CrossRef]
- Fields, C. Bell’s theorem from Moore’s theorem. Int. J. Gen. Syst. 2013, 42, 376–385. [Google Scholar] [CrossRef]
- Kochen, S.; Specker, E.P. The problem of hidden variables in quantum mechanics. J. Math. Mech. 1967, 17, 59–87. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Jennings, D.; Leifer, M. No return to classical reality. Contemp. Phys. 2016, 57, 60–82. [Google Scholar] [CrossRef]
- Peres, A.; Terno, D.R. Quantum information and relativity theory. Rev. Mod. Phys. 2004, 76, 93–123. [Google Scholar] [CrossRef]
- Chitambar, E.; Leung, D.; Mančinska, L.; Ozols, M.; Winter, A. Everything you always wanted to know about LOCC (but were afraid to ask). Commun. Math. Phys. 2014, 328, 303–326. [Google Scholar] [CrossRef]
- Bartlett, S.D.; Rudolph, T.; Spekkens, R.W. Reference frames, superselection rules, and quantum information. Rev. Mod. Phys. 2007, 79, 555–609. [Google Scholar] [CrossRef]
- Roederer, J.G. Information and Its Role in Nature; Springer: Berlin, Germany, 2005. [Google Scholar]
- Roederer, J.G. Pragmatic information in biology and physics. Philos. Trans. R. Soc. A 2016, 374, 20150152. [Google Scholar] [CrossRef] [PubMed]
- Asaro, P.M. From mechanisms of adaptation to intelligence amplifiers: The philosophy of W. Ross Ashby. In The Mechanical Mind in History; Husbands, P., Holland, O., Wheeler, M., Eds.; MIT/Bradford: Cambridge, MA, USA, 2008. [Google Scholar]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Harlow, D.; Hayden, P. Quantum computing vs. firewalls. J. High Energy Phys. 2013, 2013, 85. [Google Scholar] [CrossRef]
- Conway, J.; Kochen, S. The free will theorem. Found. Phys. 2006, 36, 1441–1473. [Google Scholar] [CrossRef]
- Fields, C. A whole box of Pandoras: Systems, boundaries and free will in quantum theory. J. Exp. Theor. Artif. Intell. 2013, 25, 291–302. [Google Scholar] [CrossRef]
- Wang, Q.; Schoenlein, R.W.; Peteanu, L.A.; Mathies, R.A.; Shank, C.V. Vibrationally coherent photochemistry in the femtosecond primary event of vision. Science 1994, 266, 422–424. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, J.A. Information, physics, quantum: The search for links. In Complexity, Entropy, and the Physics of Information; Zurek, W.H., Ed.; Westview: Boulder, CO, USA, 1990; pp. 3–28. [Google Scholar]
- Clifton, R.; Bub, J.; Halvorson, H. Characterizing quantum theory in terms of information-theoretic constraints. Found. Phys. 2003, 33, 1561–1591. [Google Scholar] [CrossRef]
- D’Ariano, G.M. Physics as Information Processing. In Proceedings of the Physics Education Research Conference, Omaha, NE, USA, 3–4 August 2011; Volume 1327, pp. 7–18.
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P. Informational derivation of quantum theory. Phys. Rev. A 2011, 84, 012311. [Google Scholar] [CrossRef]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P. Quantum theory, namely the pure and reversible theory of information. Entropy 2012, 14, 1877–1893. [Google Scholar] [CrossRef]
- Hardy, L. Reconstructing quantum theory. Fund. Theor. Phys. 2015, 181, 223–248. [Google Scholar]
- Müller, M.P.; Masanes, L. Information-theoretic postulates for quantum theory. Fund. Theor. Phys. 2015, 181, 139–170. [Google Scholar]
- Knuth, K.H. Information-based physics: An observer-centric foundation. Contemp. Phys. 2014, 55, 12–32. [Google Scholar] [CrossRef]
- Deutsch, D.; Marletto, C. Constructor theory of information. Proc. R. Soc. A 2015, 471, 20140540. [Google Scholar] [CrossRef] [PubMed]
- Höhn, P.A.; Wever, C.S.P. Quantum theory from questions. 2015; preprint. arxiv:1511.01120v2. [Google Scholar]
- Grinbaum, A. How device-independent approaches change the meaning of physical theory. 2015; preprint. arxiv:1512.01035v3. [Google Scholar]
- Zimmer, H.D.; Ecker, U.K.D. Remembering perceptual features unequally bound in object and episodic tokens: Neural mechanisms and their electrophysiological correlates. Neurosci. Biobehav. Rev. 2010, 34, 1066–1079. [Google Scholar] [CrossRef] [PubMed]
- Fields, C. The very same thing: Extending the object token concept to incorporate causal constraints on individual identity. Adv. Cognit. Psychol. 2012, 8, 234–247. [Google Scholar] [CrossRef]
- Harrison, E.R. Standard model of the early universe. Annu. Rev. Astron. Astrophys. 1973, 11, 155–186. [Google Scholar] [CrossRef]
- Fields, C. Visual re-identification of individual objects: A core problem for organisms and AI. Cognit. Process. 2016, 17, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Arkani-Hamed, N.; Trnka, J. The amplituhedron. J. High-Energy Phys. 2014, 10, 030. [Google Scholar] [CrossRef]
- Krechmer, K. Relational measurements and uncertainty. Measurement 2016. [Google Scholar] [CrossRef]
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, L. Eigenforms—Objects as tokens for eigenbehaviors. Cybern. Hum. Knowing 2003, 10, 73–90. [Google Scholar]
- Kauffman, L. EigenForm. Kybernetes 2005, 34, 129–150. [Google Scholar] [CrossRef]
- Dietrich, E.; Fields, C. Science generates limit paradoxes. Axiomathes 2015, 25, 409–432. [Google Scholar] [CrossRef]
- Wittgenstein, L. Tractatus Logico-Philosophicus; Kegan Paul, Trench, Trubner: London, UK, 1922. [Google Scholar]
- Tarski, A. The semantic conception of truth and the foundations of semantics. Philos. Phenomenol. Res. 1944, 4, 341–376. [Google Scholar] [CrossRef]
- Turing, A.R. On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 1936, 442, 230–265. [Google Scholar]
- Quine, W.V.O. On what there is. Rev. Metaphys. 1948, 2, 21–38. [Google Scholar]
- Tanenbaum, A.S. Structured Computer Organization; Prentice Hall: Upper Saddle River, NJ, USA, 1976. [Google Scholar]
- Smith, J.E.; Nair, R. The architecture of virtual machines. IEEE Comput. 2005, 38, 32–38. [Google Scholar] [CrossRef]
- Partridge, D. The Seductive Computer; Springer: London, UK, 2010. [Google Scholar]
- Chomsky, N. Review of B. F. Skinner, Verbal Behavior. Language 1959, 35, 26–58. [Google Scholar] [CrossRef]
- Harnad, S. The symbol grounding problem. Phys. D 1990, 42, 335–346. [Google Scholar] [CrossRef]
- Taddeo, M.; Floridi, L. Solving the symbol grounding problem: A critical review of fifteen years of research. J. Exp. Theor. Artif. Intell. 2005, 17, 419–445. [Google Scholar] [CrossRef]
- Fields, C. Equivalence of the symbol grounding and quantum system identification problems. Information 2014, 5, 172–189. [Google Scholar] [CrossRef]
- Fodor, J.A. Methodological solipsism considered as a research strategy in cognitive science. Behav. Brain Sci. 1980, 3, 63–73. [Google Scholar] [CrossRef]
- Clark, A.; Chalmers, D. The extended mind. Analysis 1998, 58, 7–19. [Google Scholar]
- Anderson, M.L. Embodied cognition: A field guide. Artif. Intell. 2003, 149, 91–130. [Google Scholar] [CrossRef]
- Cangelosi, A.; Schlesinger, M. Developmental Robotics: From Babies to Robots; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Hommel, B. Event files: Feature binding in and across perception and action. Trends Cognit. Sci. 2004, 8, 494–500. [Google Scholar] [CrossRef] [PubMed]
- Eichenbaum, H.; Yonelinas, A.R.; Ranganath, C. The medial temporal lobe and recognition memory. Annu. Rev. Neurosci. 2007, 30, 123–152. [Google Scholar] [CrossRef] [PubMed]
- Cubek, R.; Ertel, W.; Palm, G. A critical review on the symbol grounding problem as an issue of autonomous agents. Lect. Notes Comput. Sci. 2015, 9324, 256–263. [Google Scholar]
- Mark, J.T.; Marion, B.B.; Hoffman, D.D. Natural selection and veridical perceptions. J. Theor. Biol. 2010, 266, 504–515. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, D.D.; Singh, M.; Prakash, C. The interface theory of perception. Psychon. Bull. Rev. 2015, 22, 1480–1506. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, D.D.; Prakash, C. Objects of consciousness. Front. Psychol. 2014, 5, 577. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J. Functional and effective connectivity: A review. Brain Connect. 2011, 1, 13–36. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.; Levin, M.; Sengupta, B.; Pezzulo, G. Knowing one’s place: A free-energy approach to pattern regulation. J. R. Soc. Interface 2015, 12, 20141383. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. Life as we know it. J. R. Soc. Interface 2013, 10, 20130475. [Google Scholar] [CrossRef] [PubMed]
- Lawson, R.P.; Rees, G.; Friston, K.J. An aberrant precision account of autism. Front. Hum. Neurosci. 2014, 8, 302. [Google Scholar] [CrossRef] [PubMed]
- Bostom, N. Are we living in a computer simulation? Philos. Quart. 2003, 53, 243–255. [Google Scholar] [CrossRef]


© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fields, C. Building the Observer into the System: Toward a Realistic Description of Human Interaction with the World. Systems 2016, 4, 32. https://doi.org/10.3390/systems4040032
Fields C. Building the Observer into the System: Toward a Realistic Description of Human Interaction with the World. Systems. 2016; 4(4):32. https://doi.org/10.3390/systems4040032
Chicago/Turabian StyleFields, Chris. 2016. "Building the Observer into the System: Toward a Realistic Description of Human Interaction with the World" Systems 4, no. 4: 32. https://doi.org/10.3390/systems4040032
APA StyleFields, C. (2016). Building the Observer into the System: Toward a Realistic Description of Human Interaction with the World. Systems, 4(4), 32. https://doi.org/10.3390/systems4040032





