Improved Time Response of Stabilization in Synchronization of Chaotic Oscillators Using Mathematica
Abstract
:1. Introduction
2. Synchronization Using LAC
2.1. Description of the Models
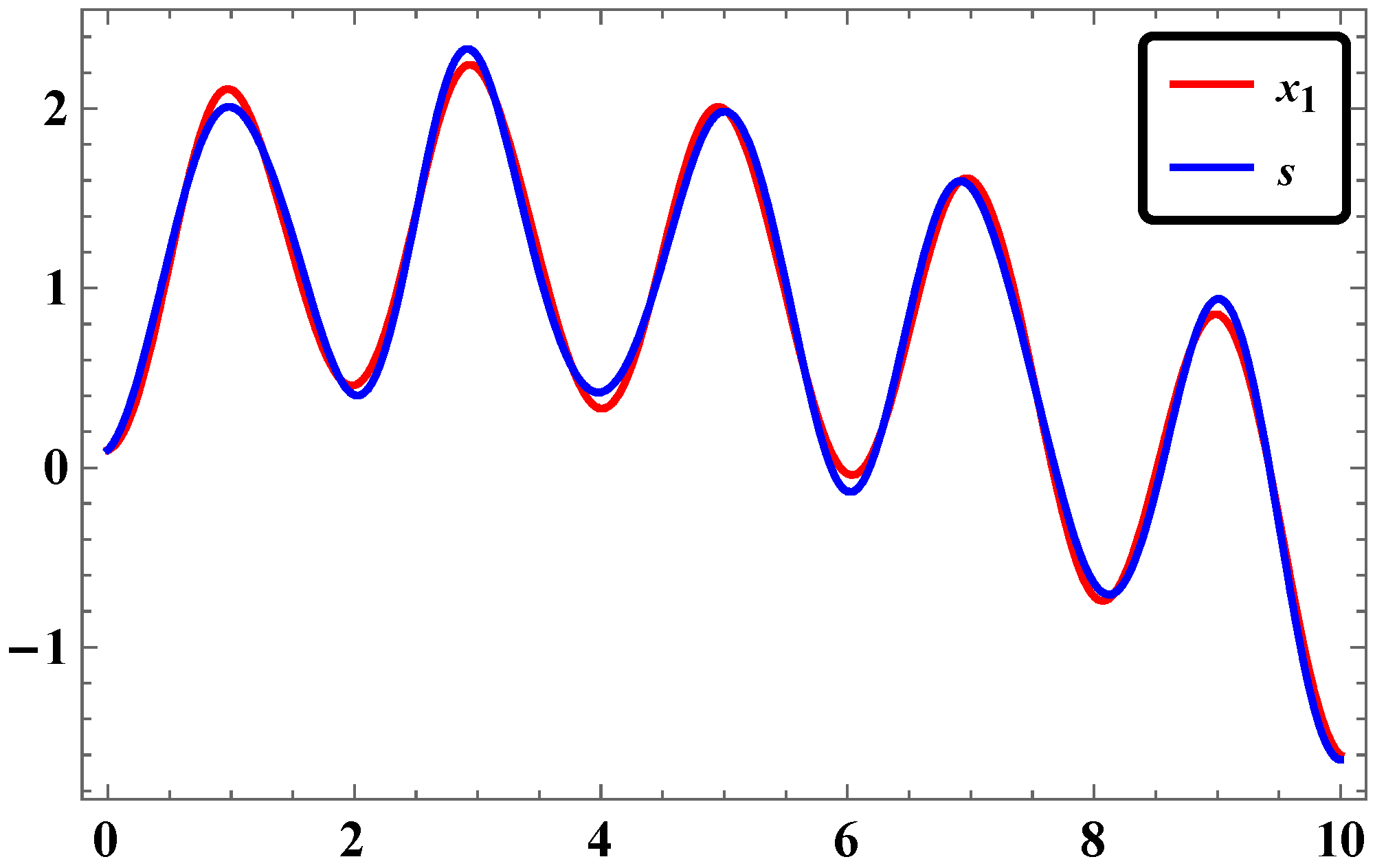
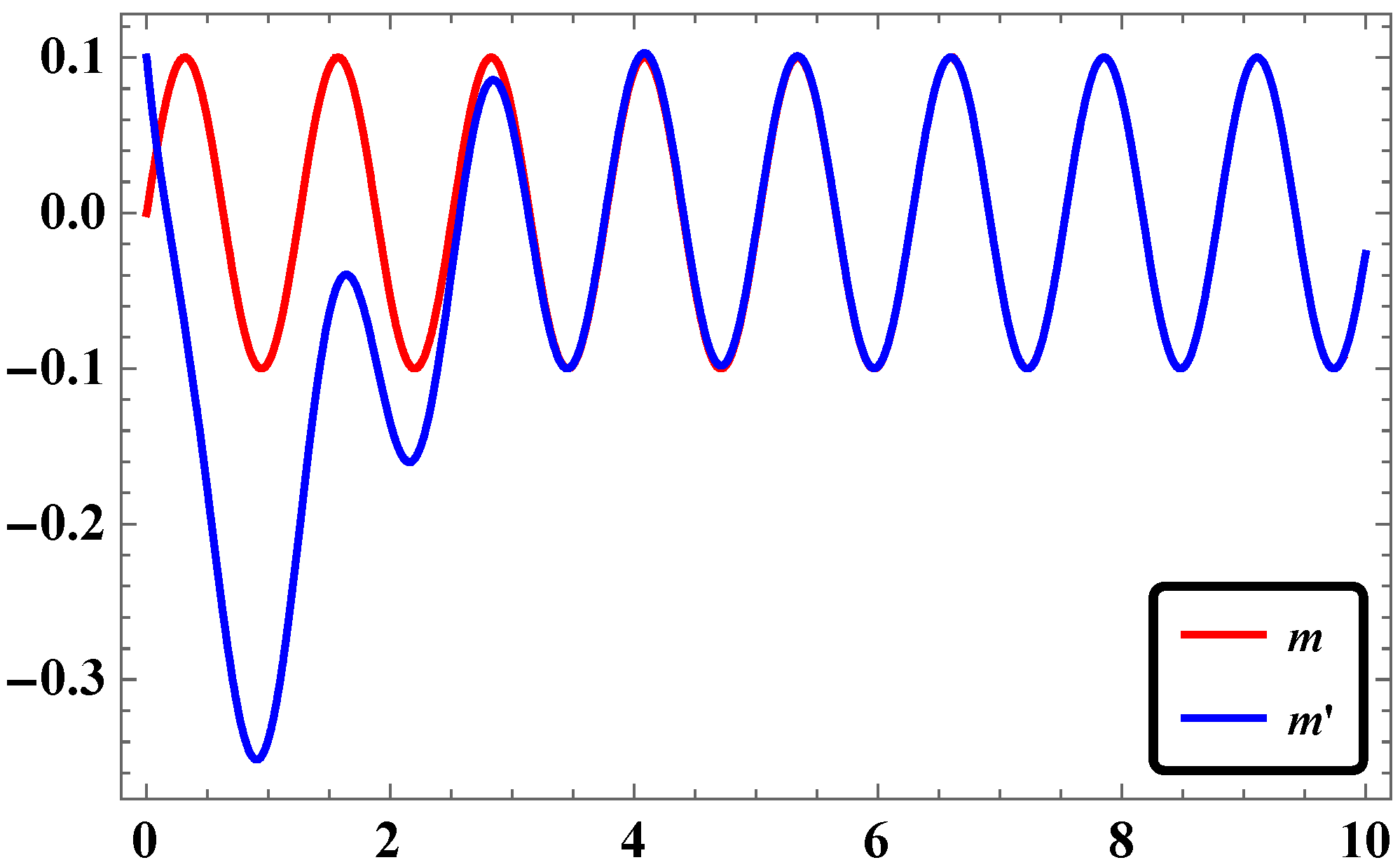
2.2. Synchronization of Two Identical Φ6—VDPO Oscillators via LAC
2.3. Synchronization for Two Identical Φ6—DO via LAC
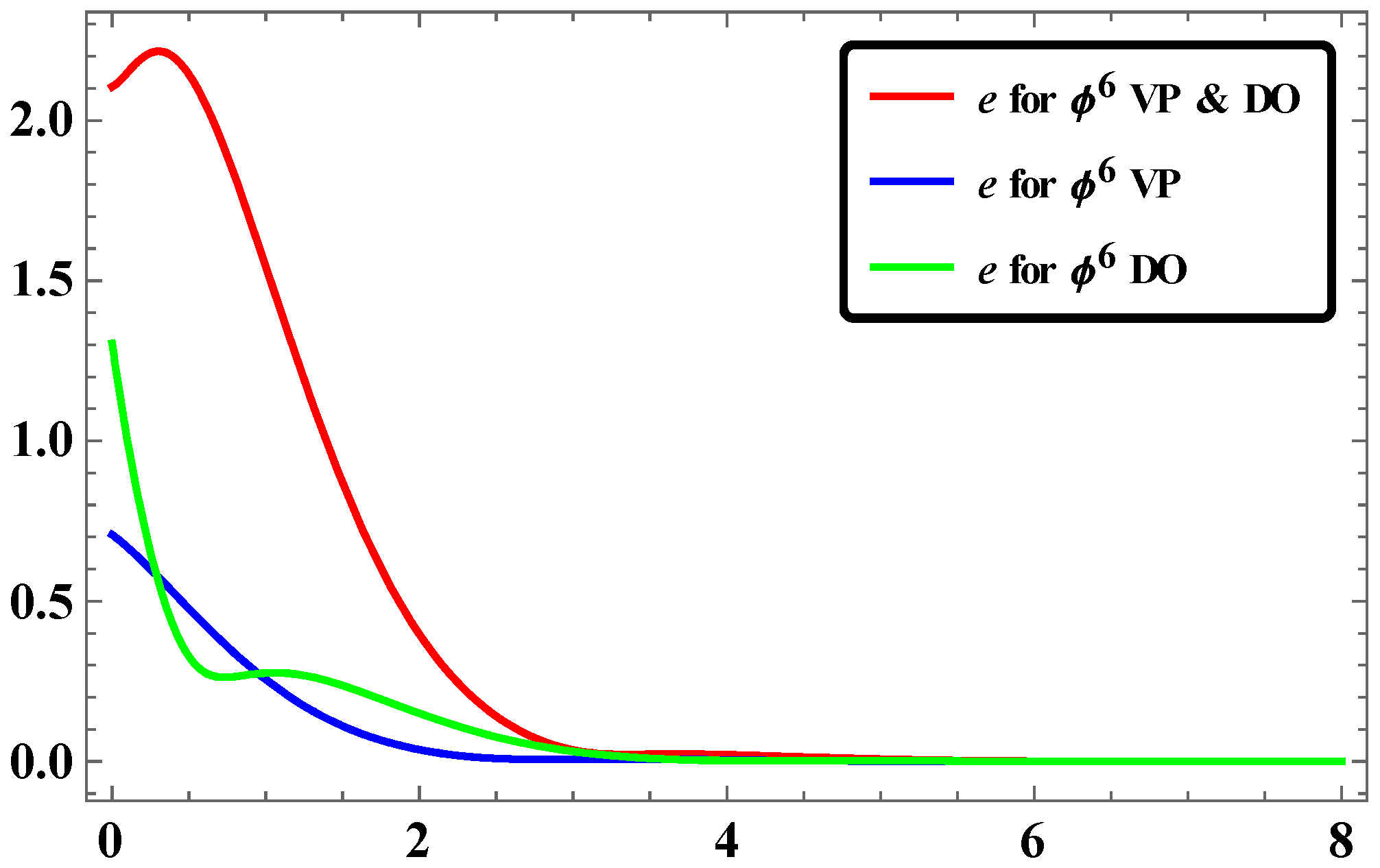
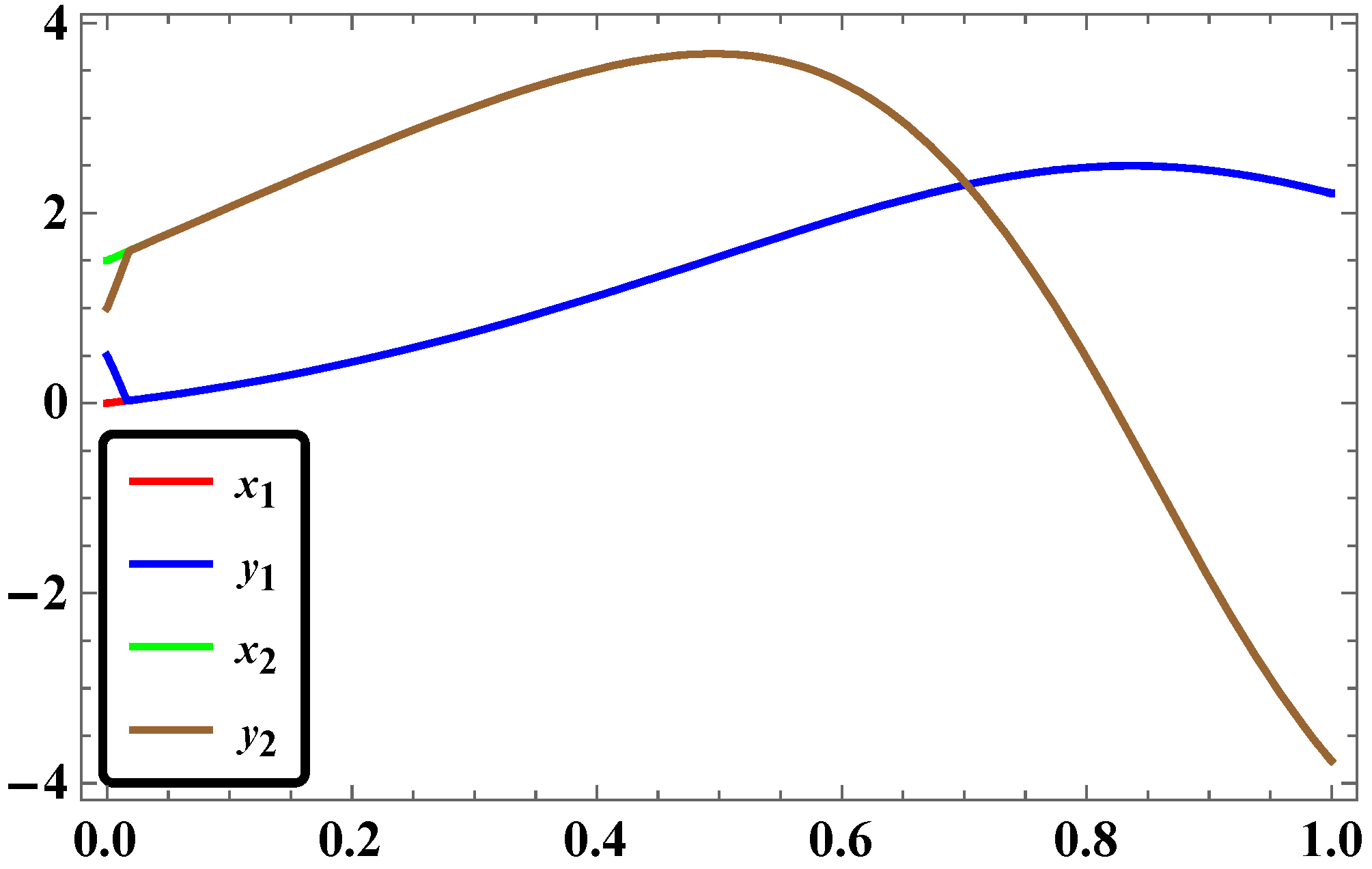
2.4. Synchronization for Φ6—VDPO and DO via LAC
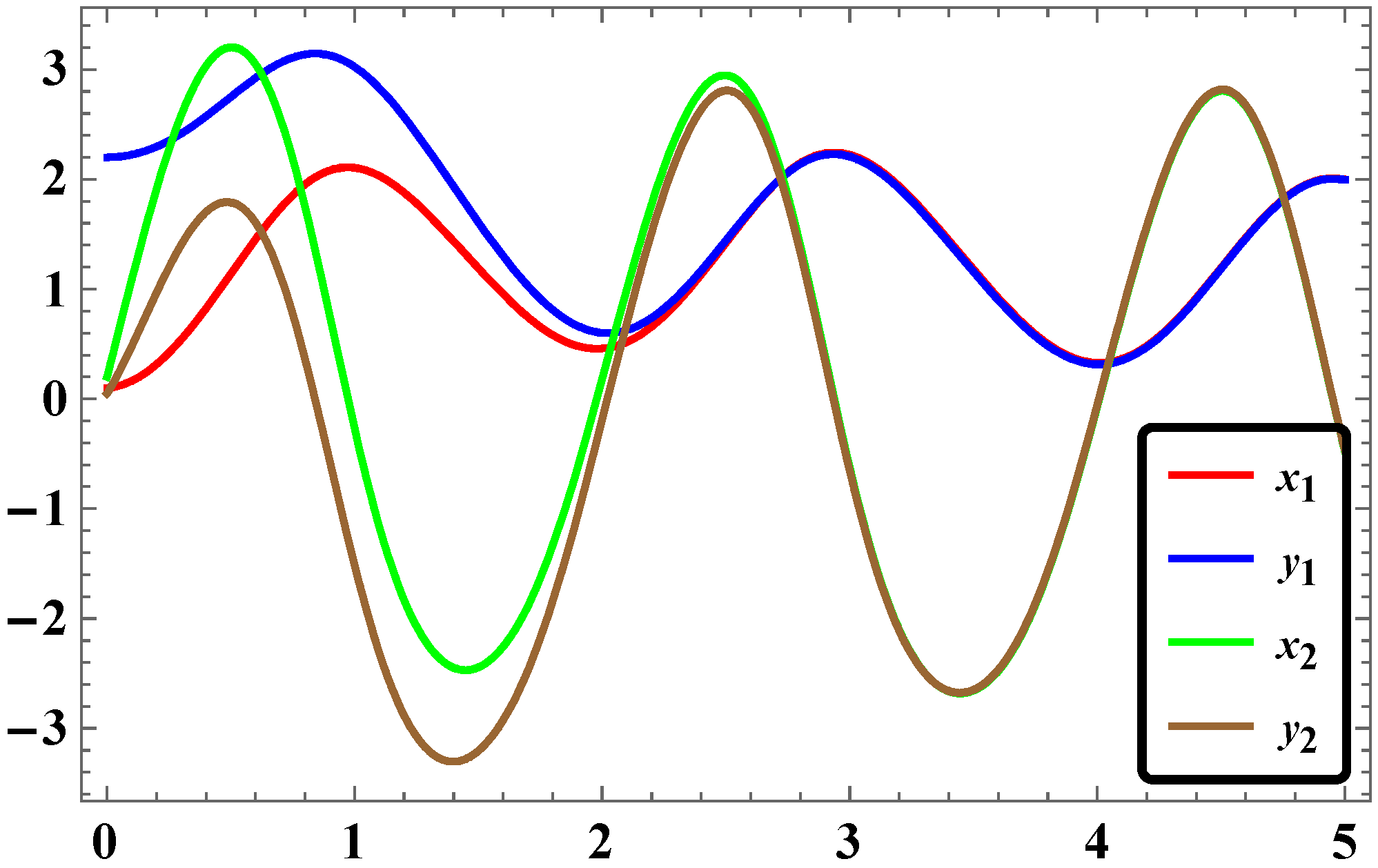
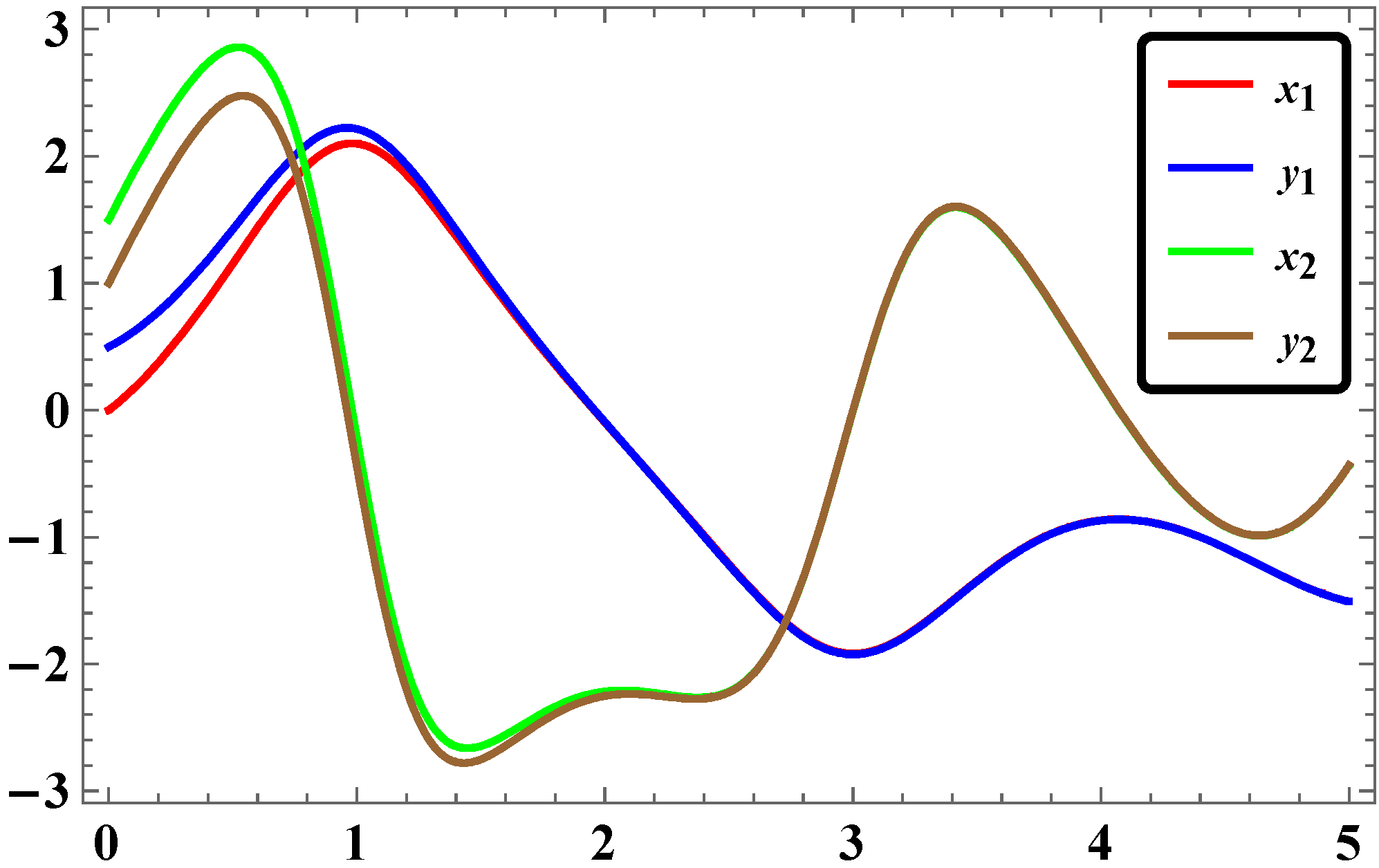
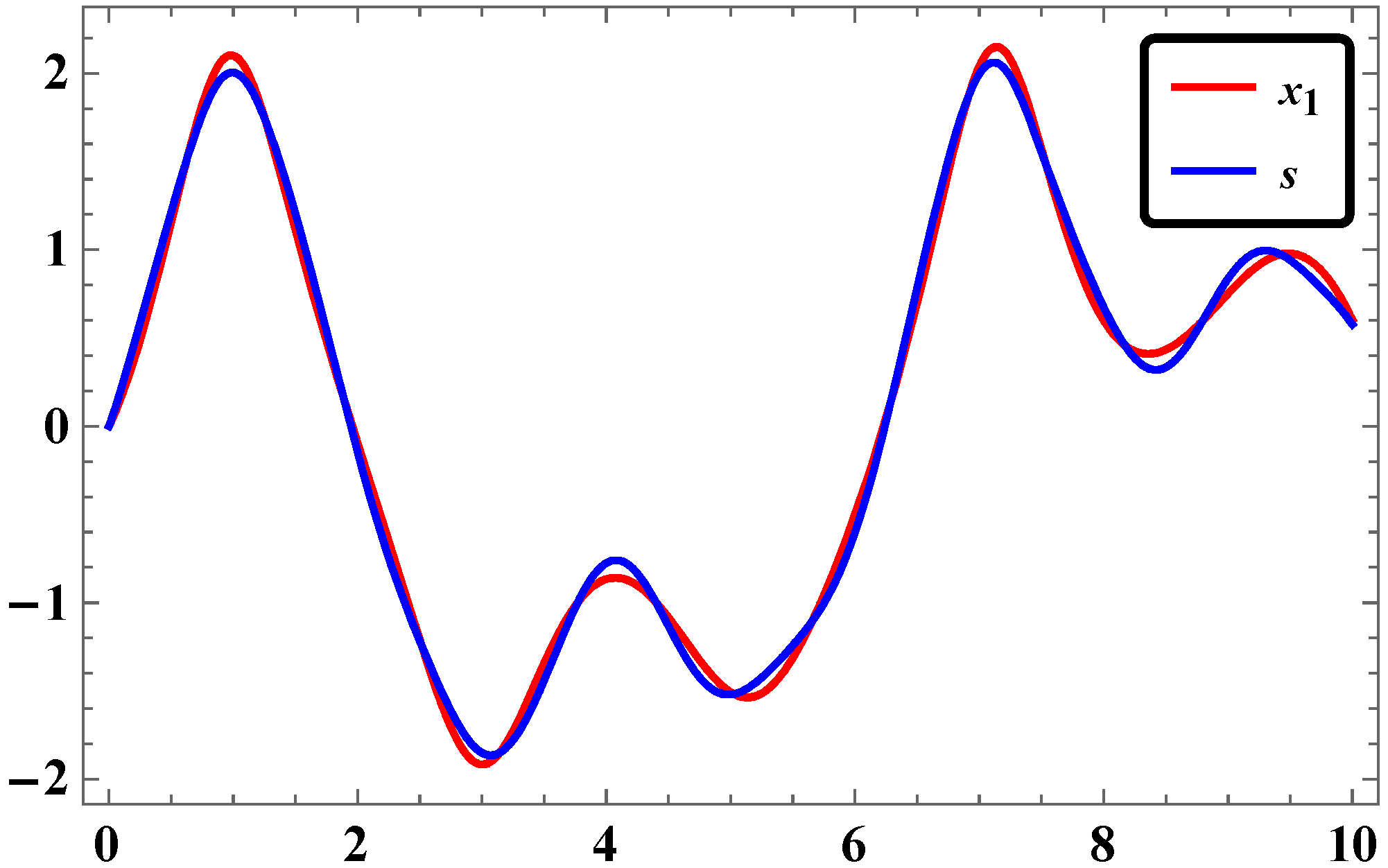
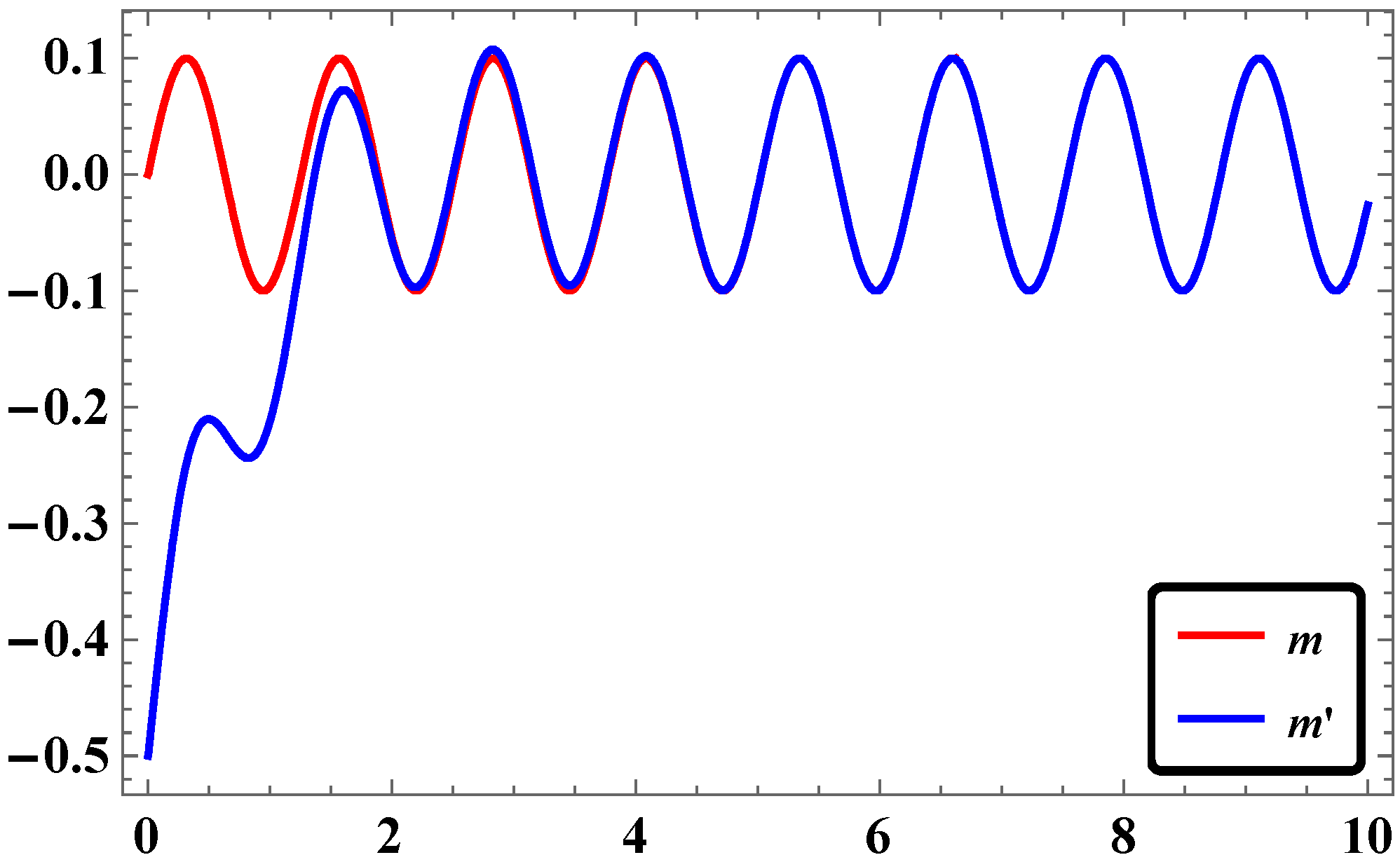
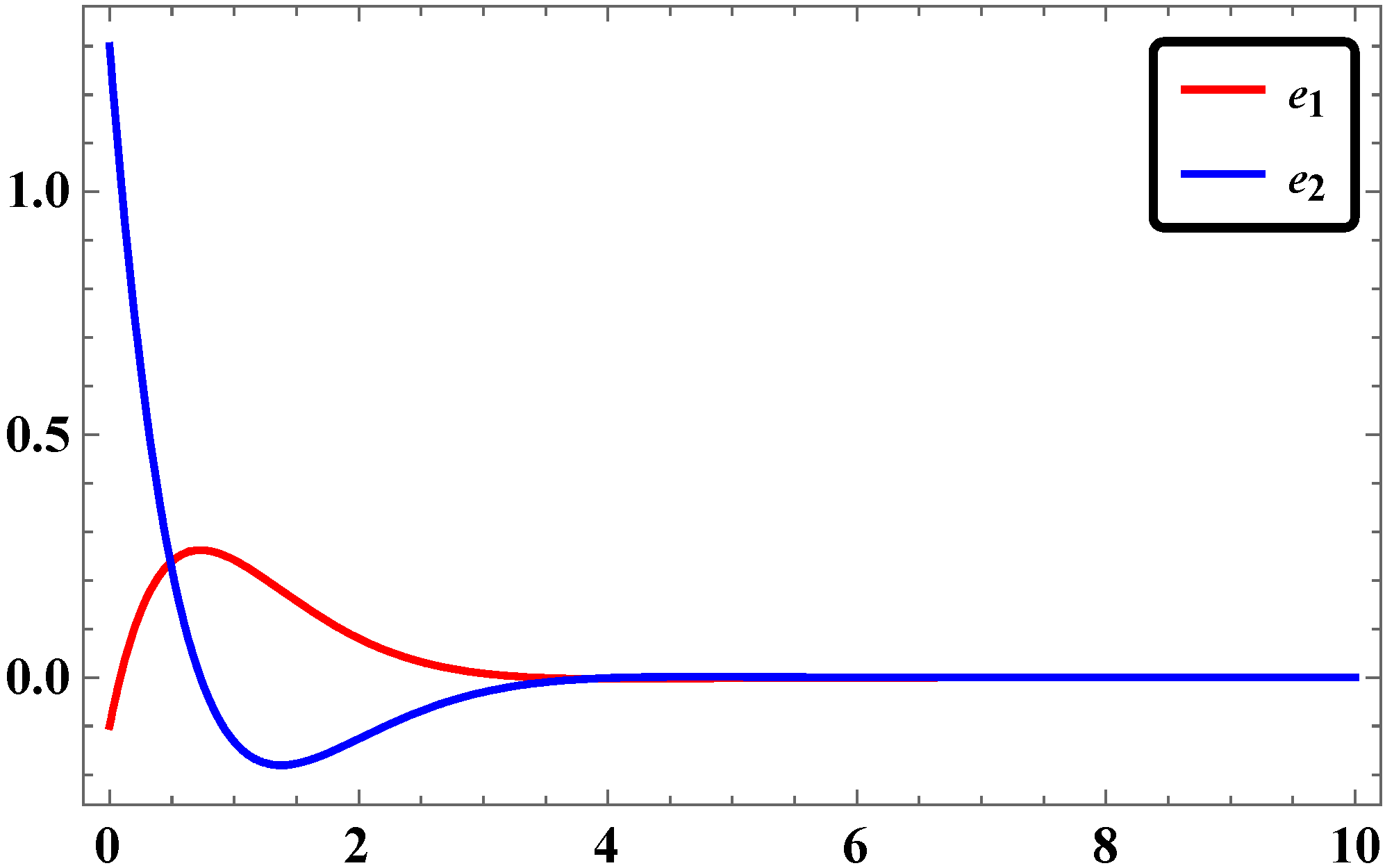
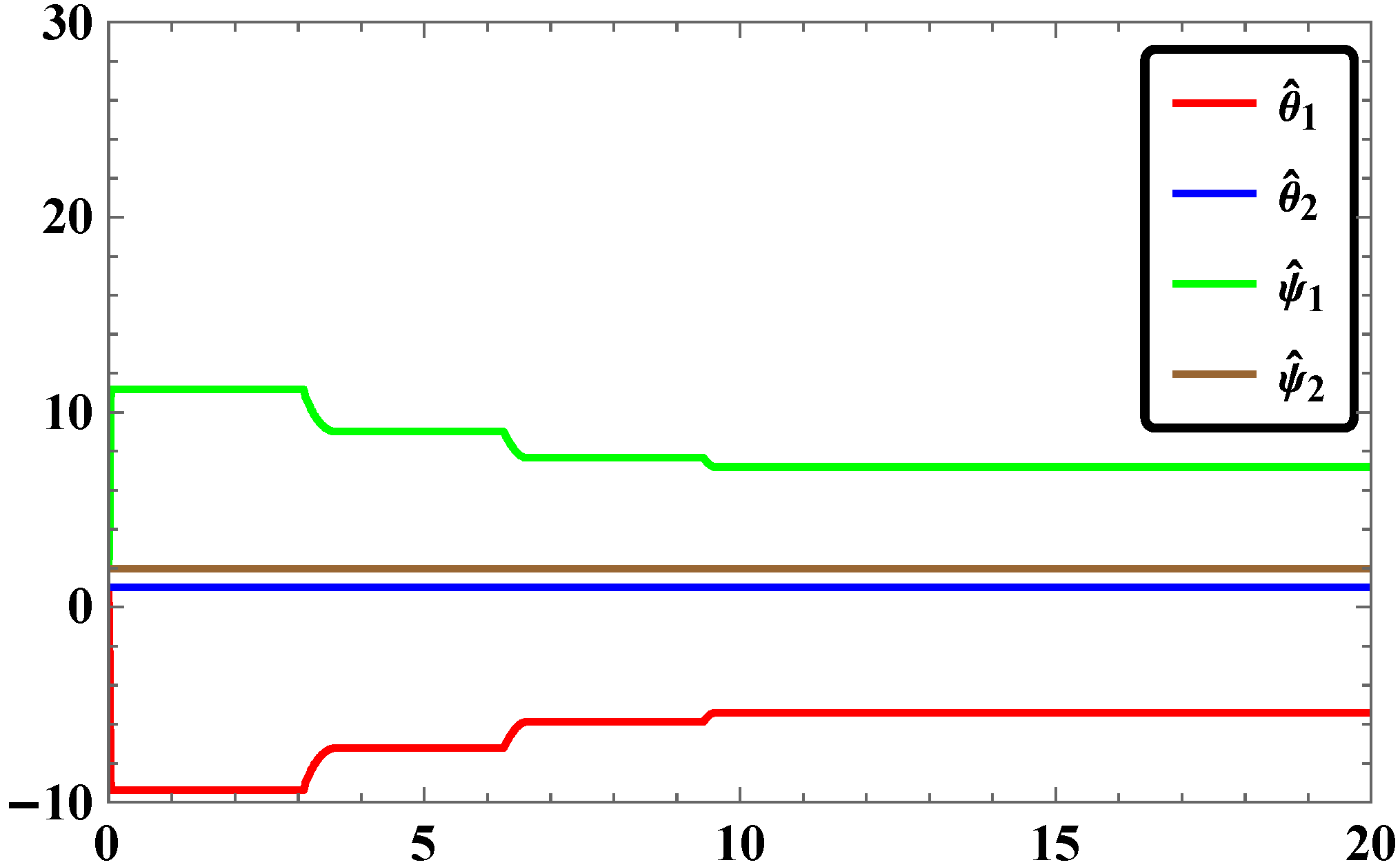
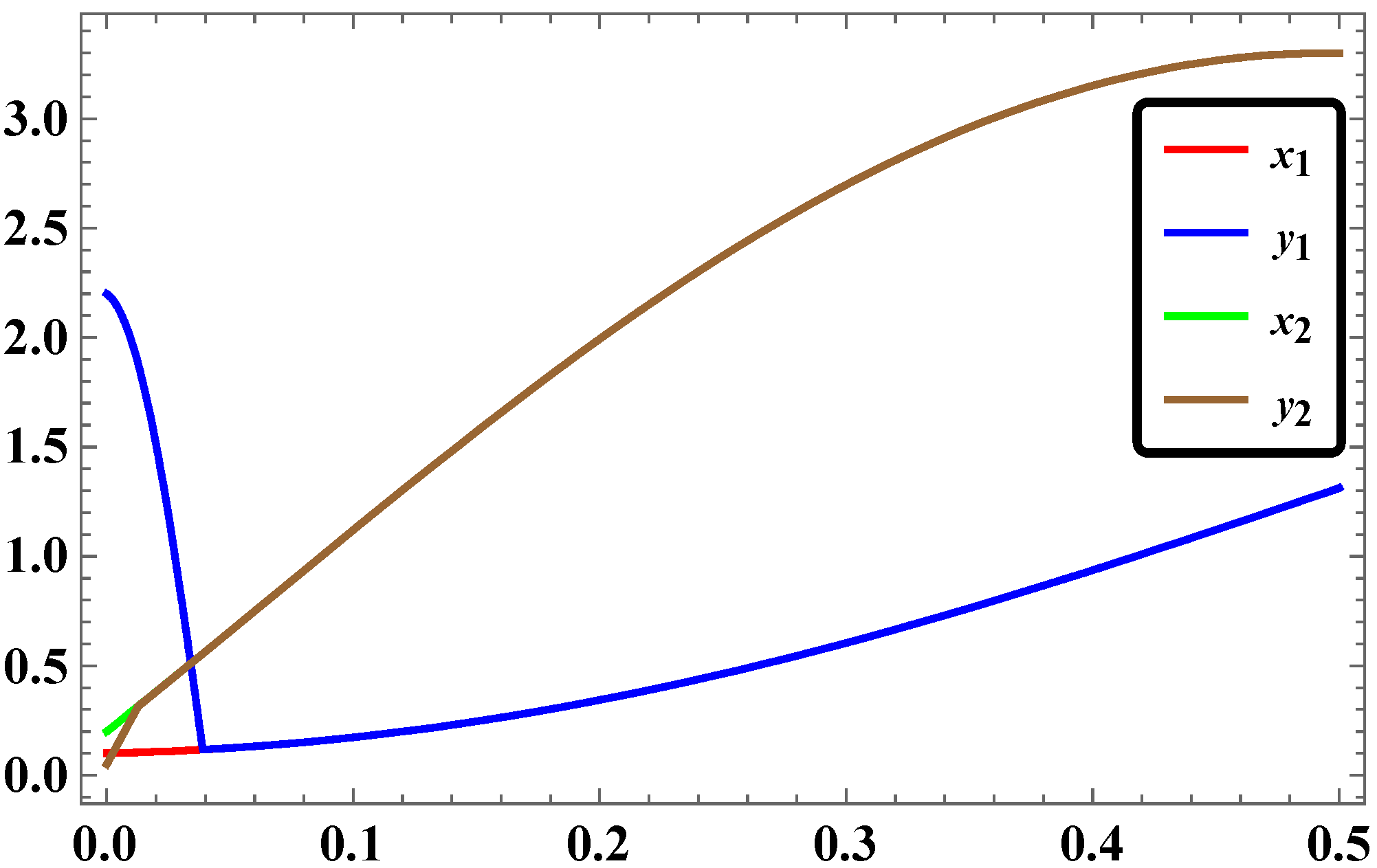
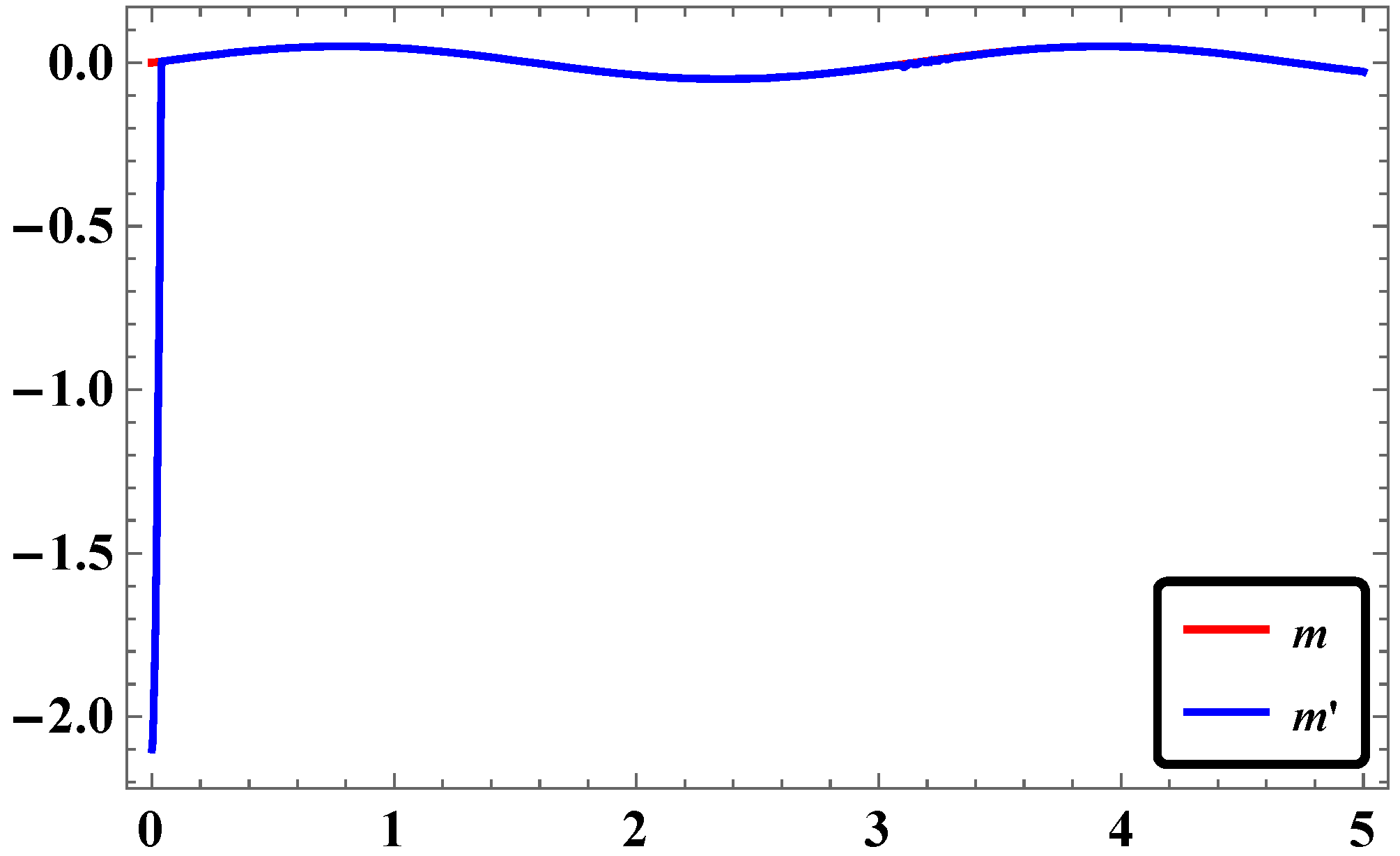
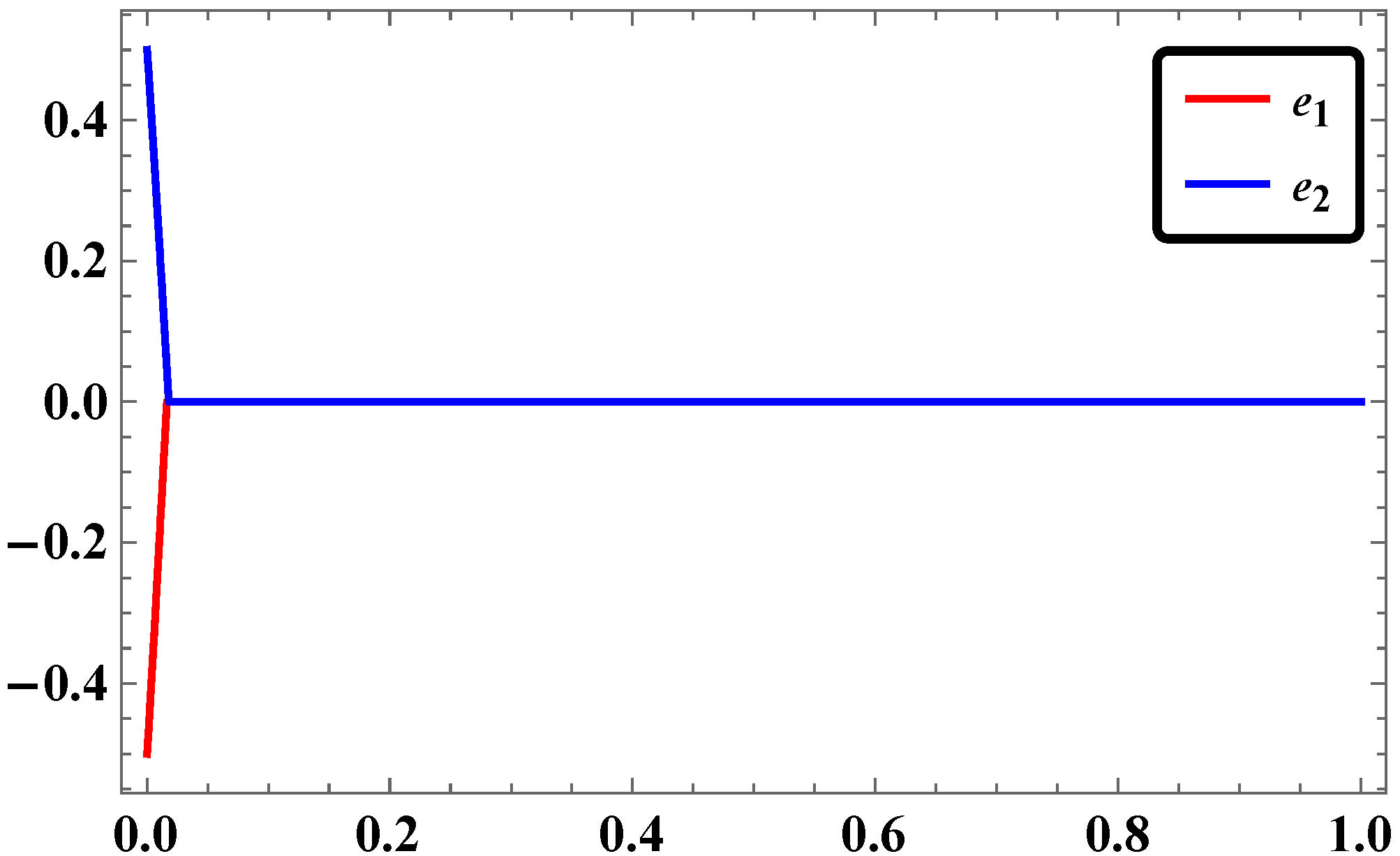
2.5. Results and Discussions
3. Synchronization Using RASMC
3.1. Description of RASMC
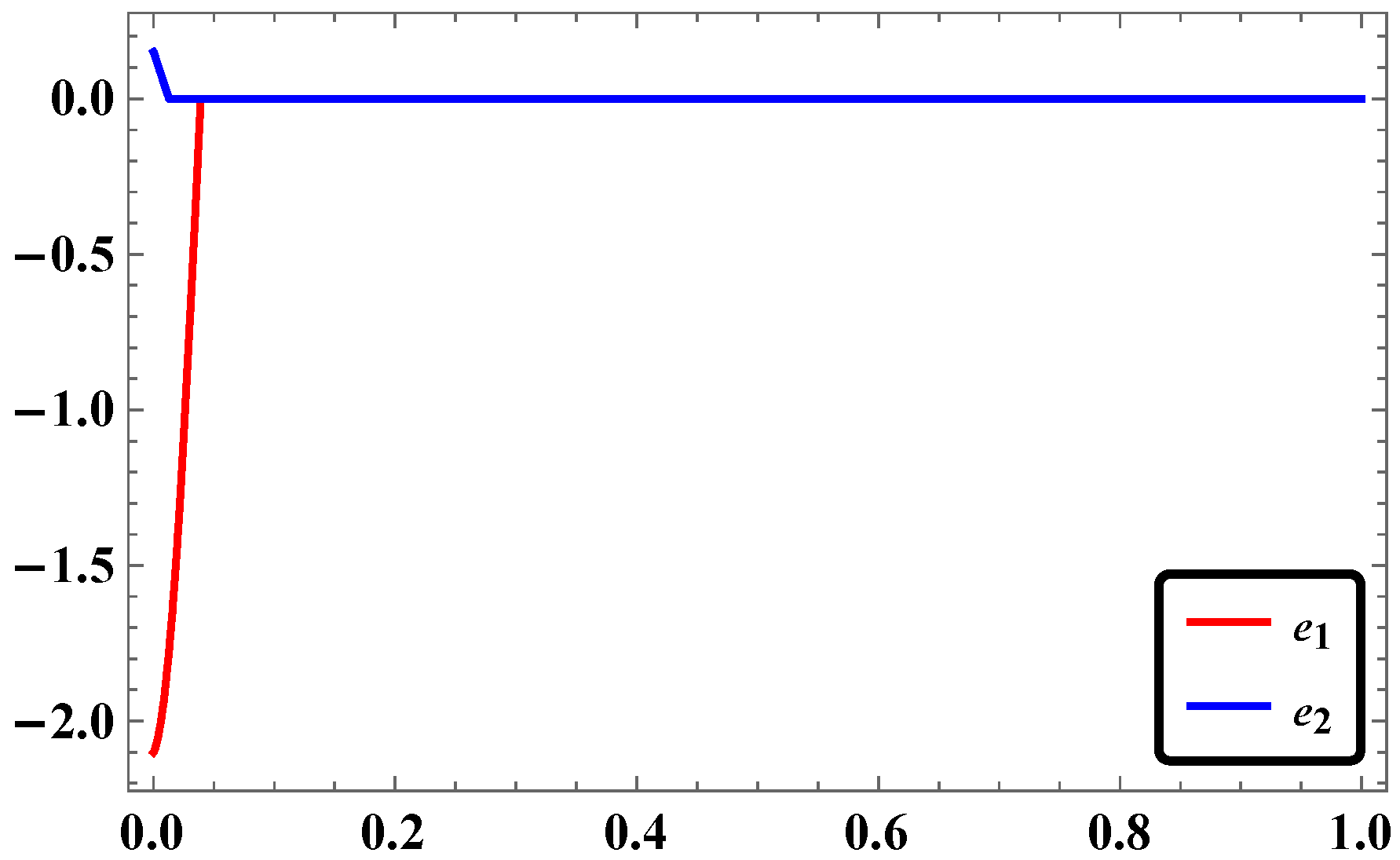
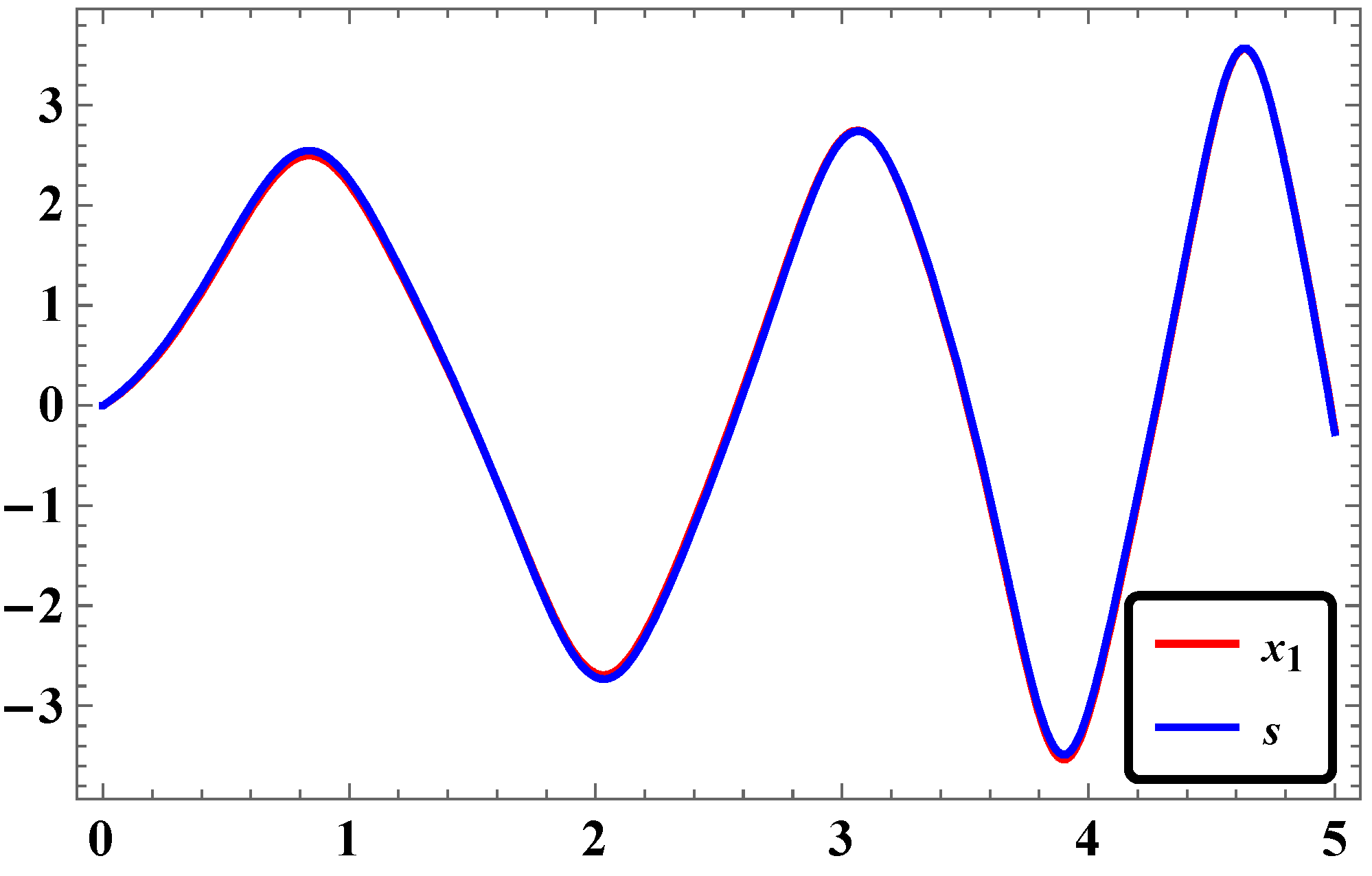
3.2. Synchronization of Two Identical Φ6—VDPO Using RASMC
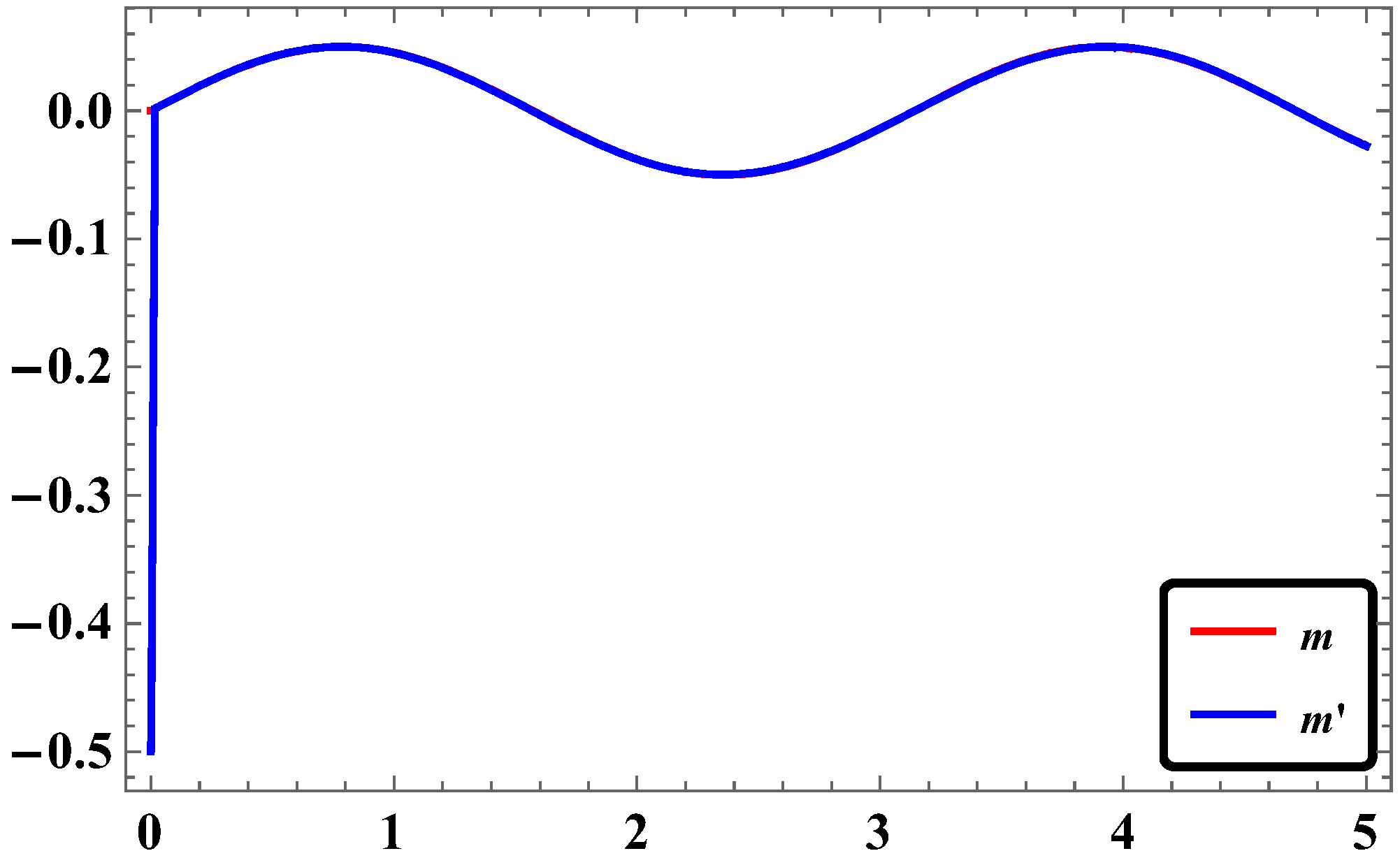
3.3. Synchronization of Two Identical Φ6—DO Using RASMC
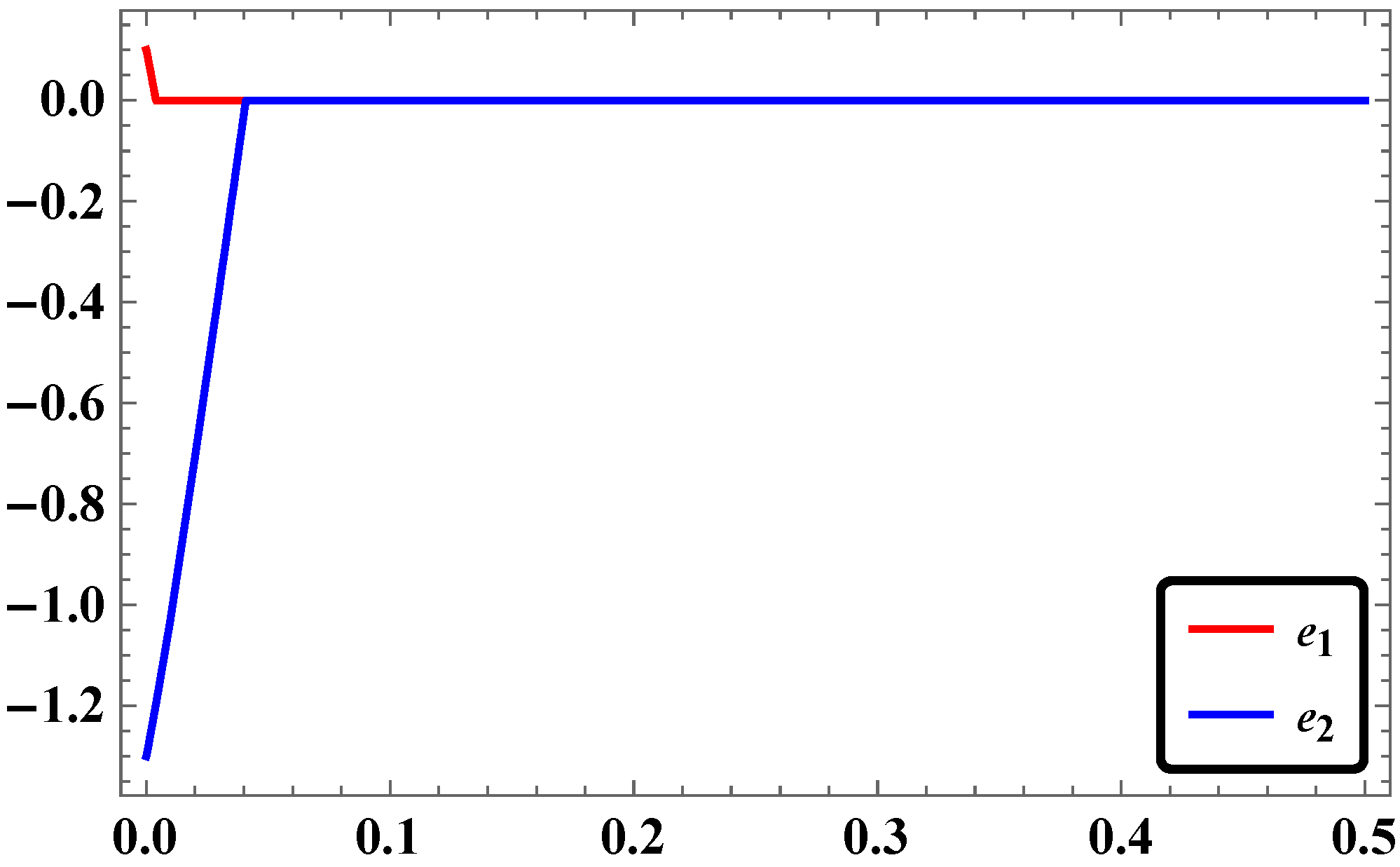
3.4. Synchronization of Φ6—VDPO and DO Using RASMC
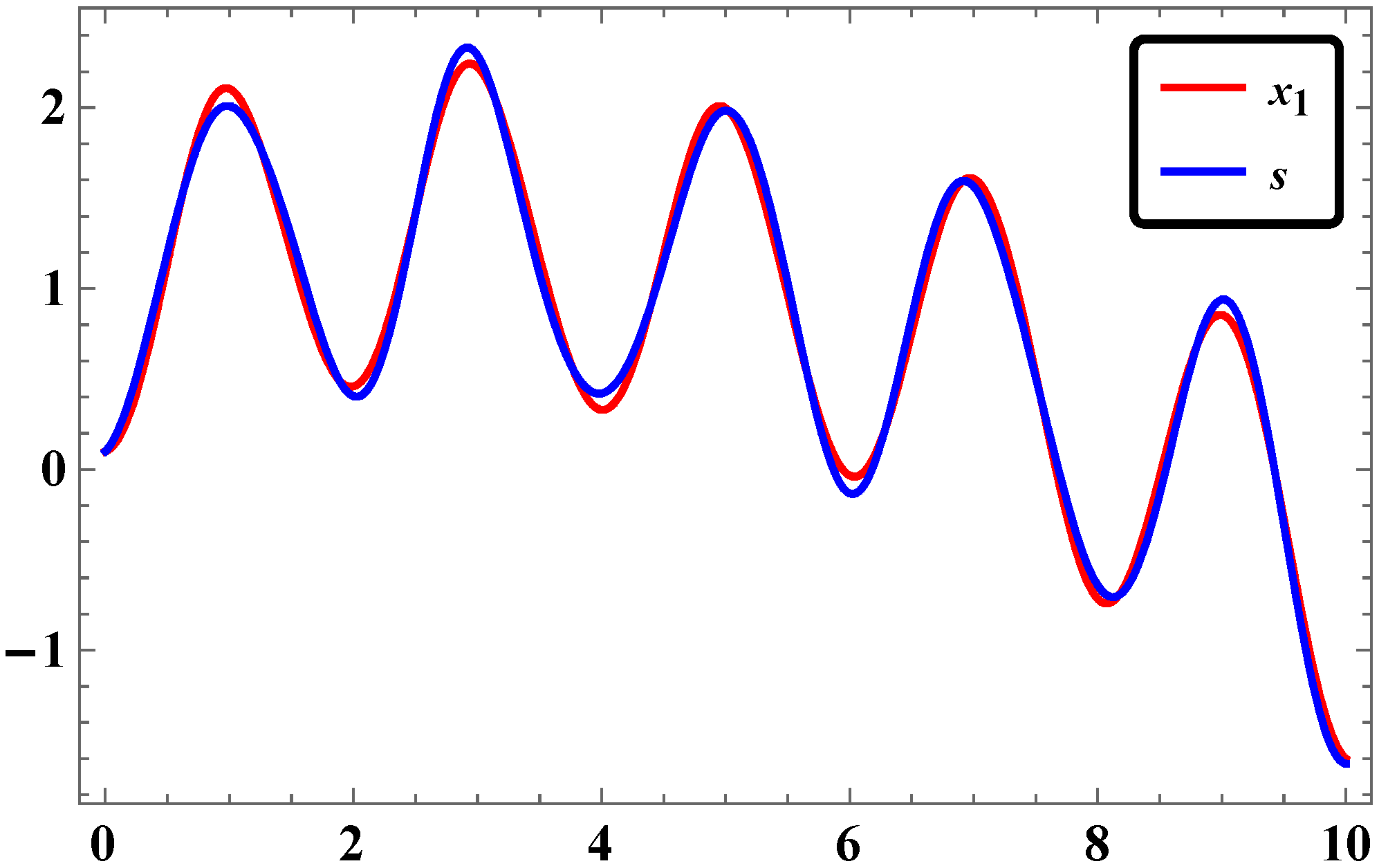
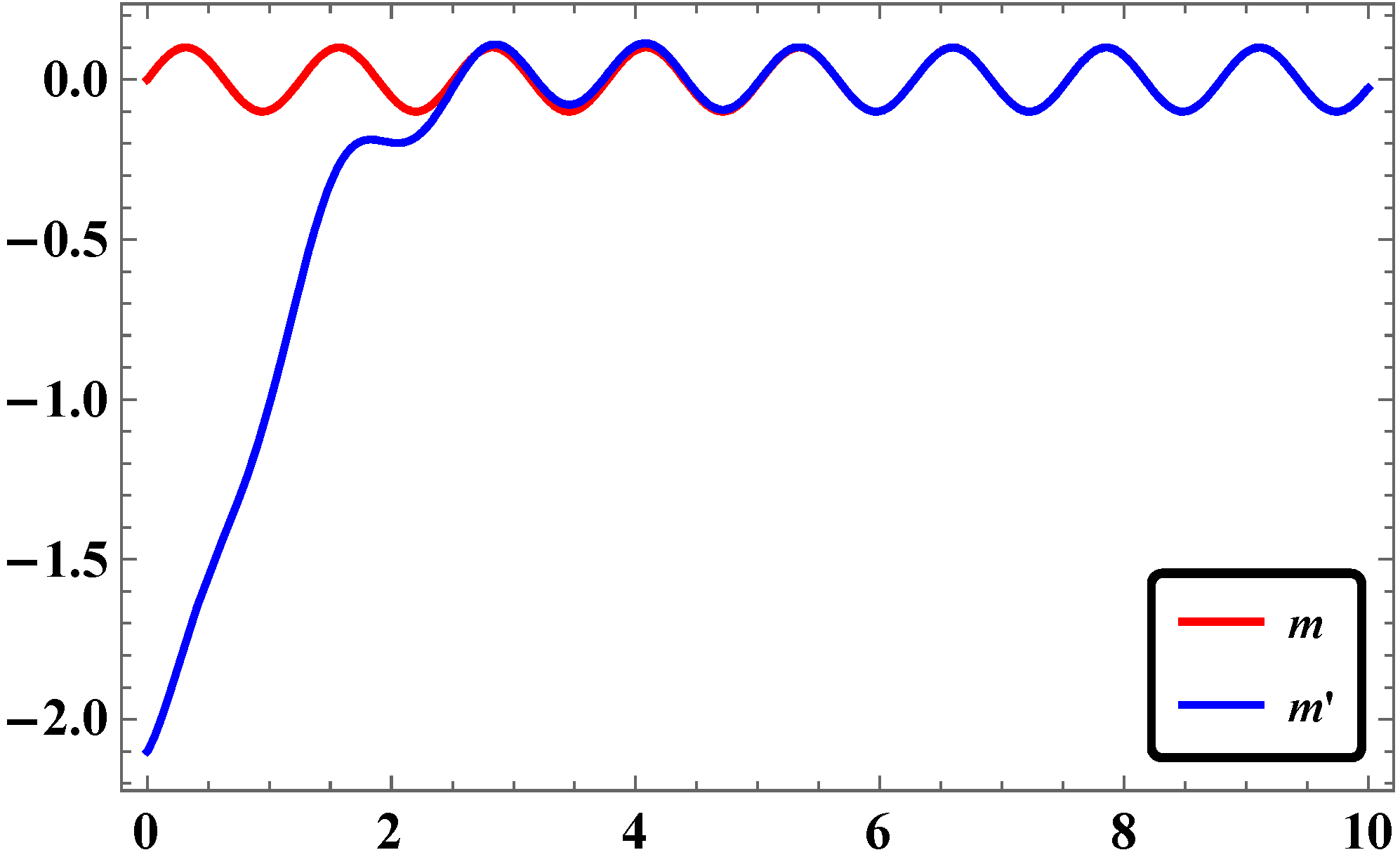
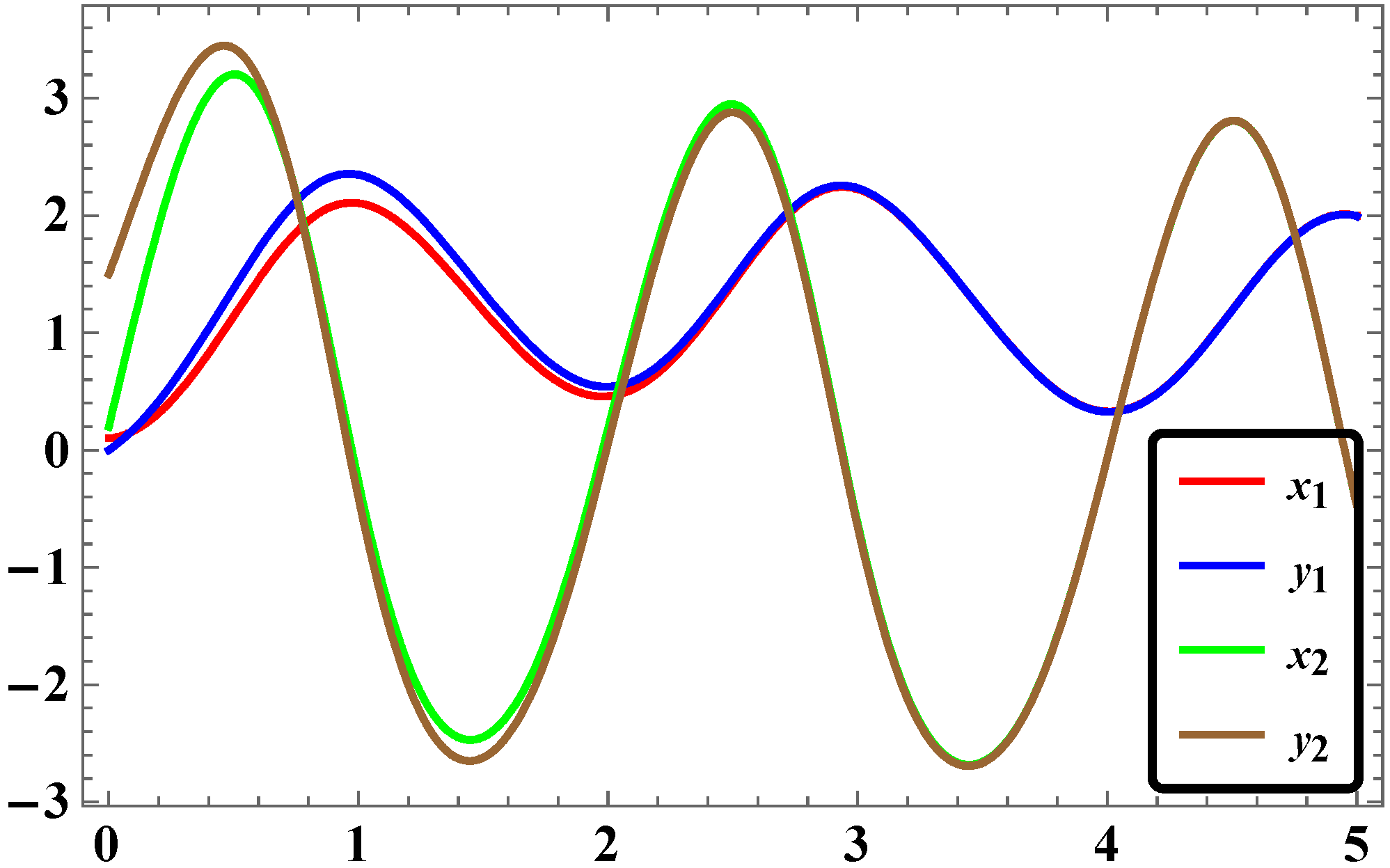
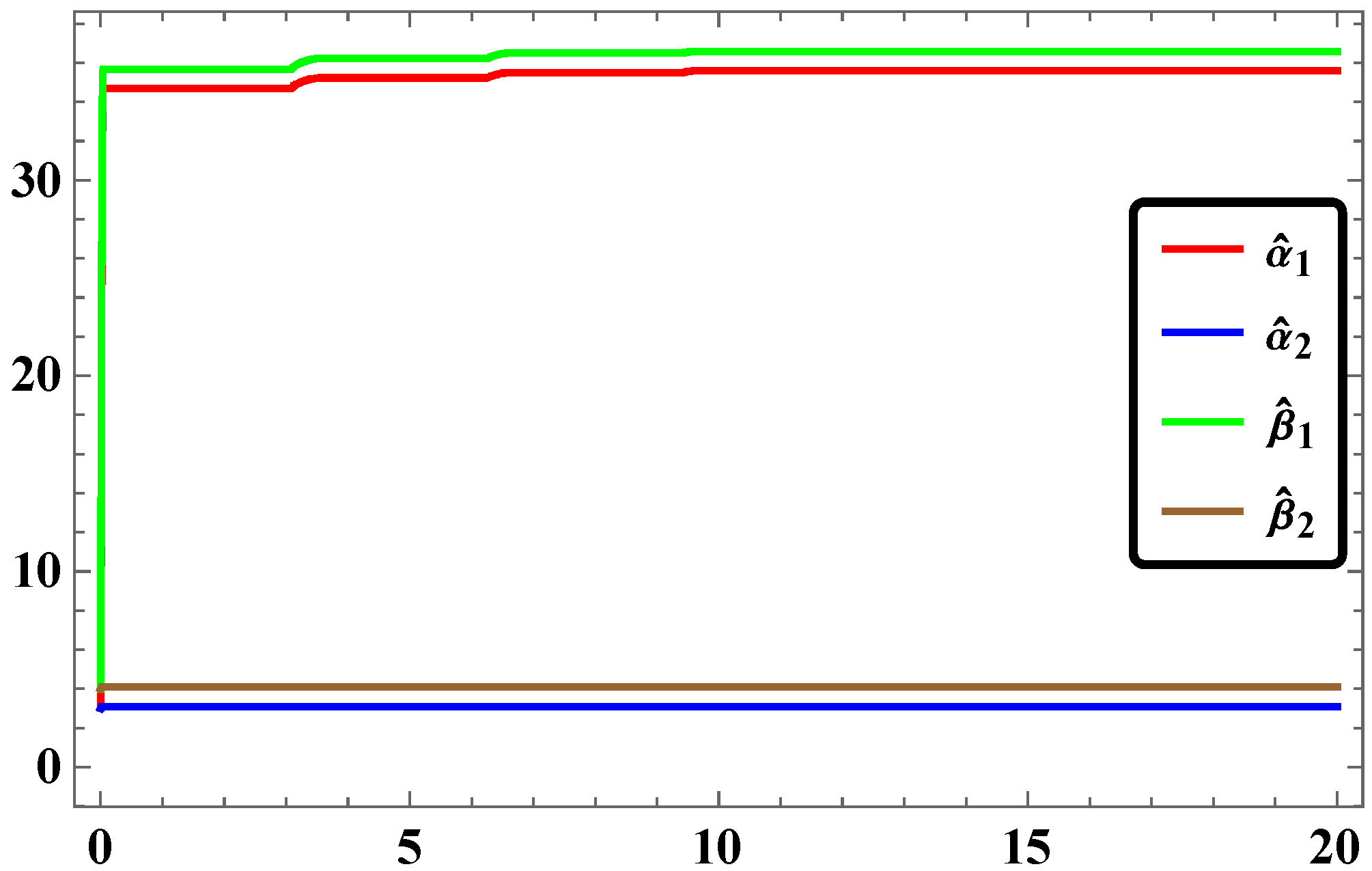
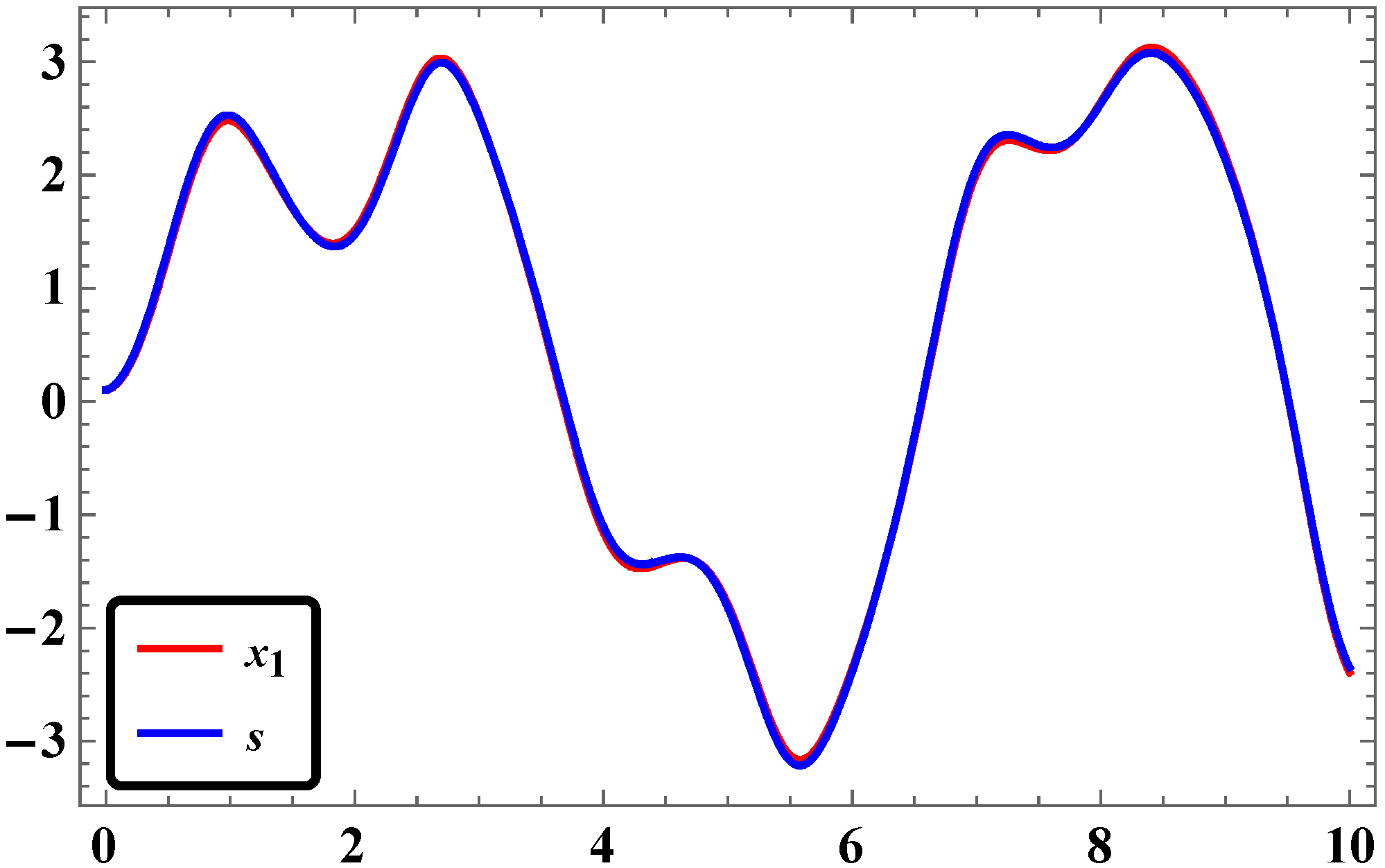
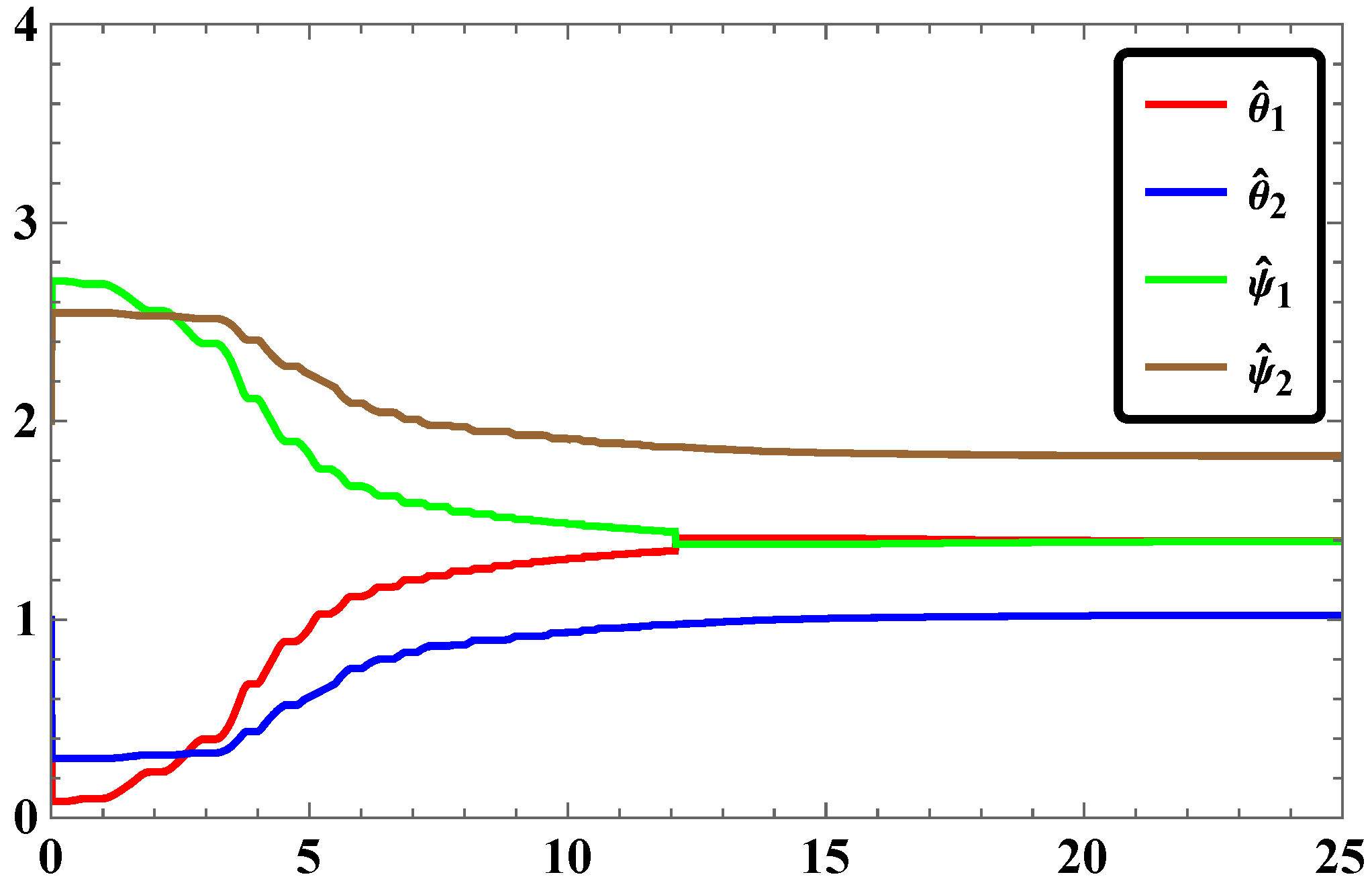
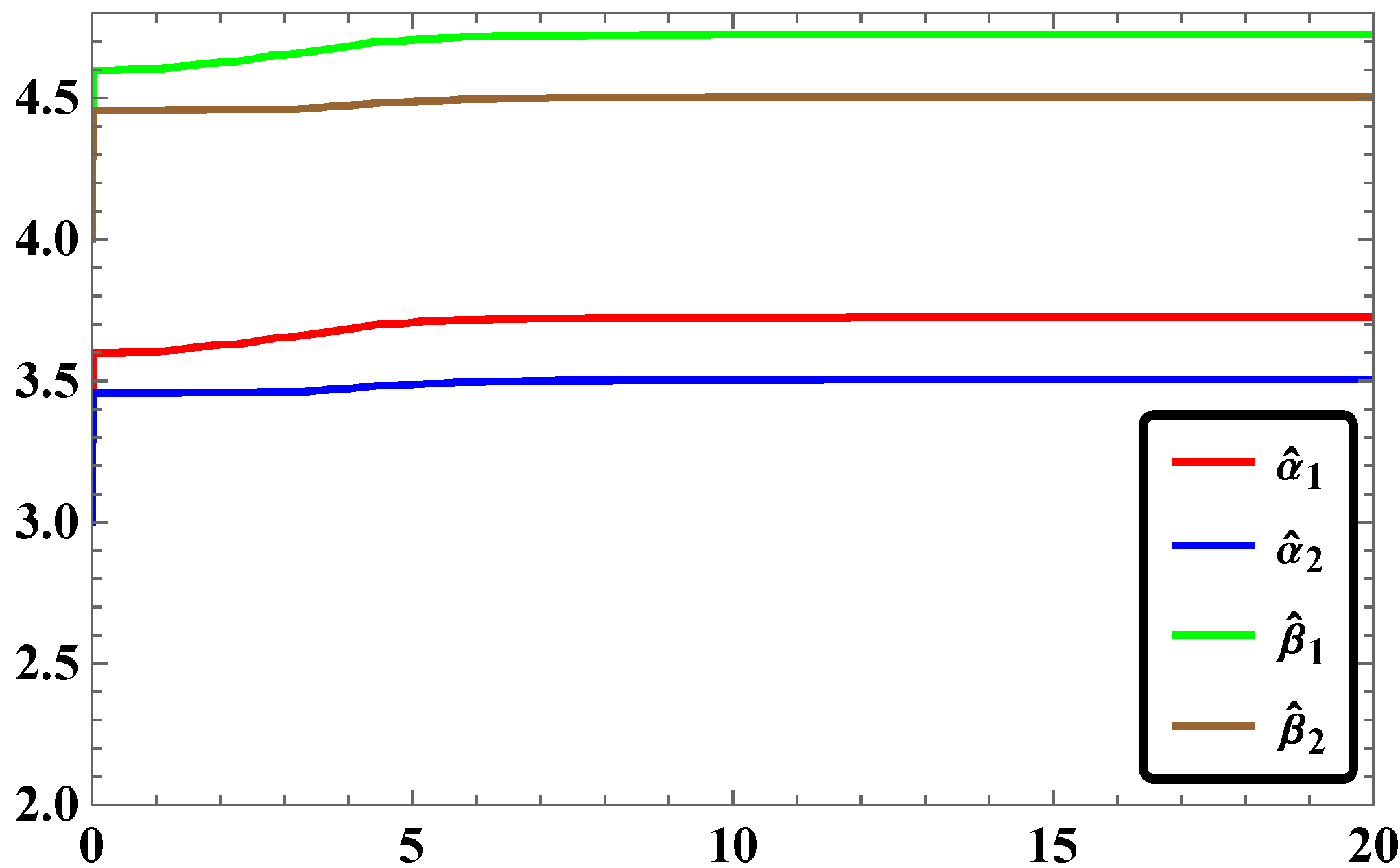
3.5. Numerical Simulations and Discussion
4. Conclusions
- (1)
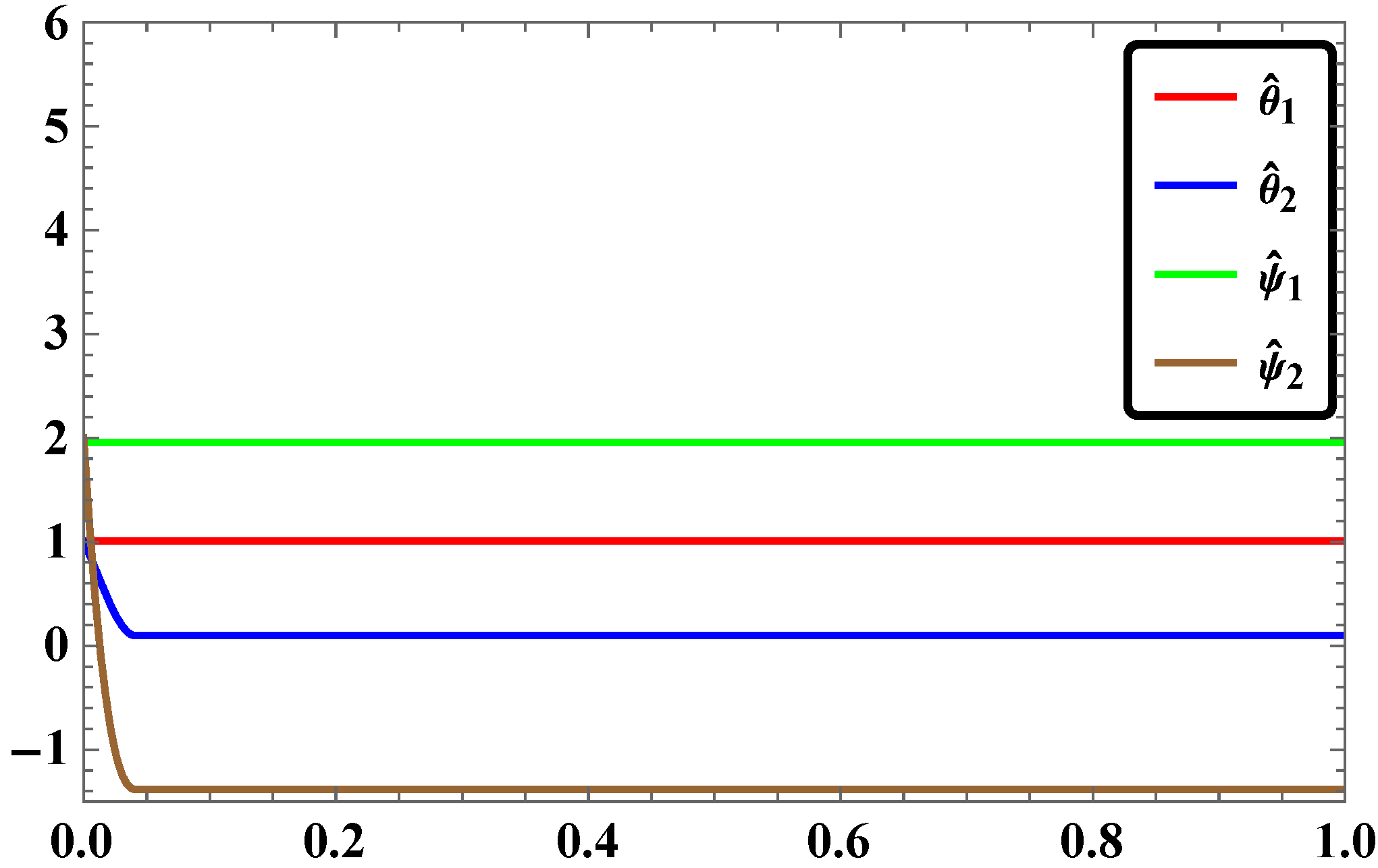
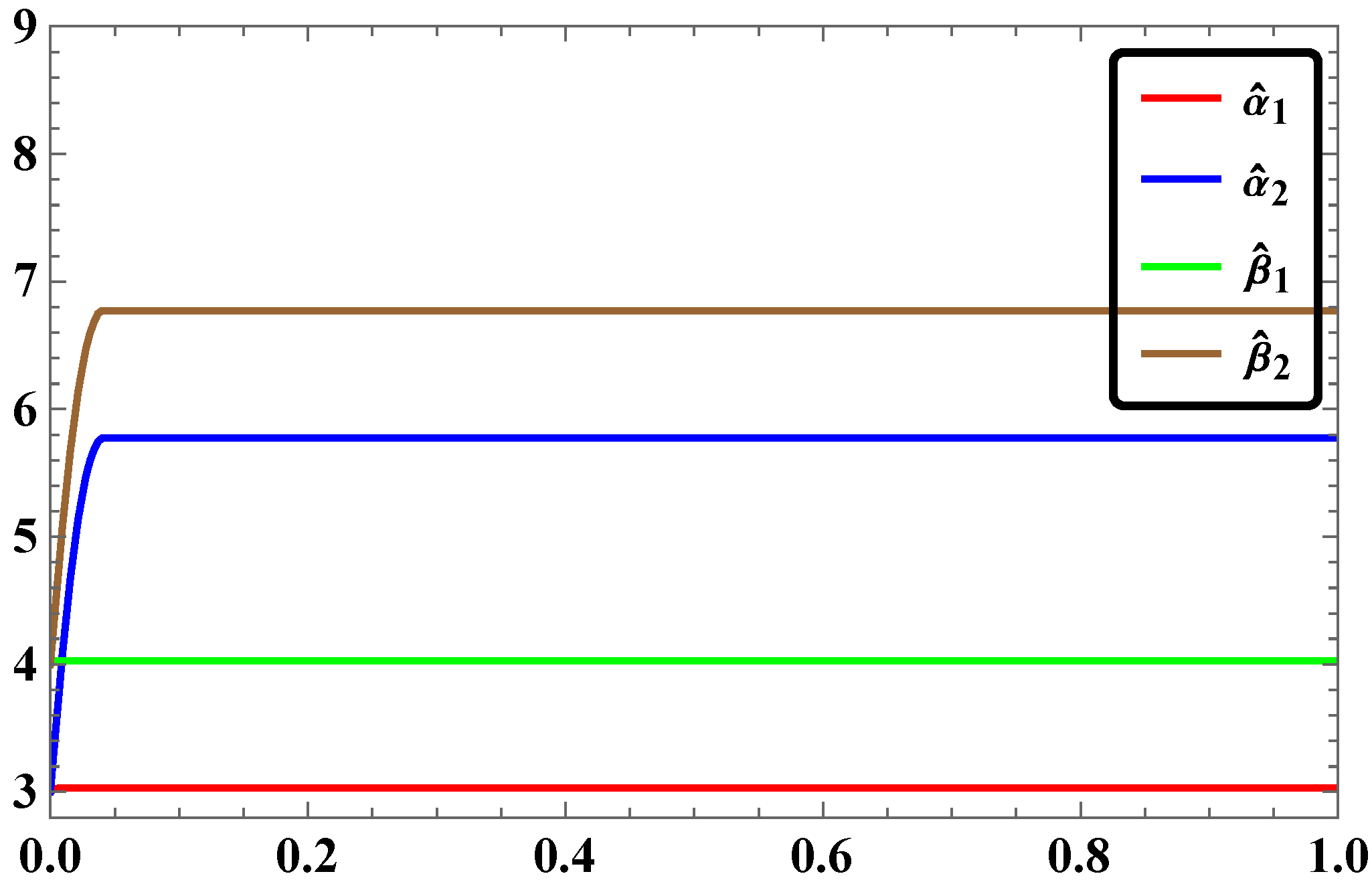
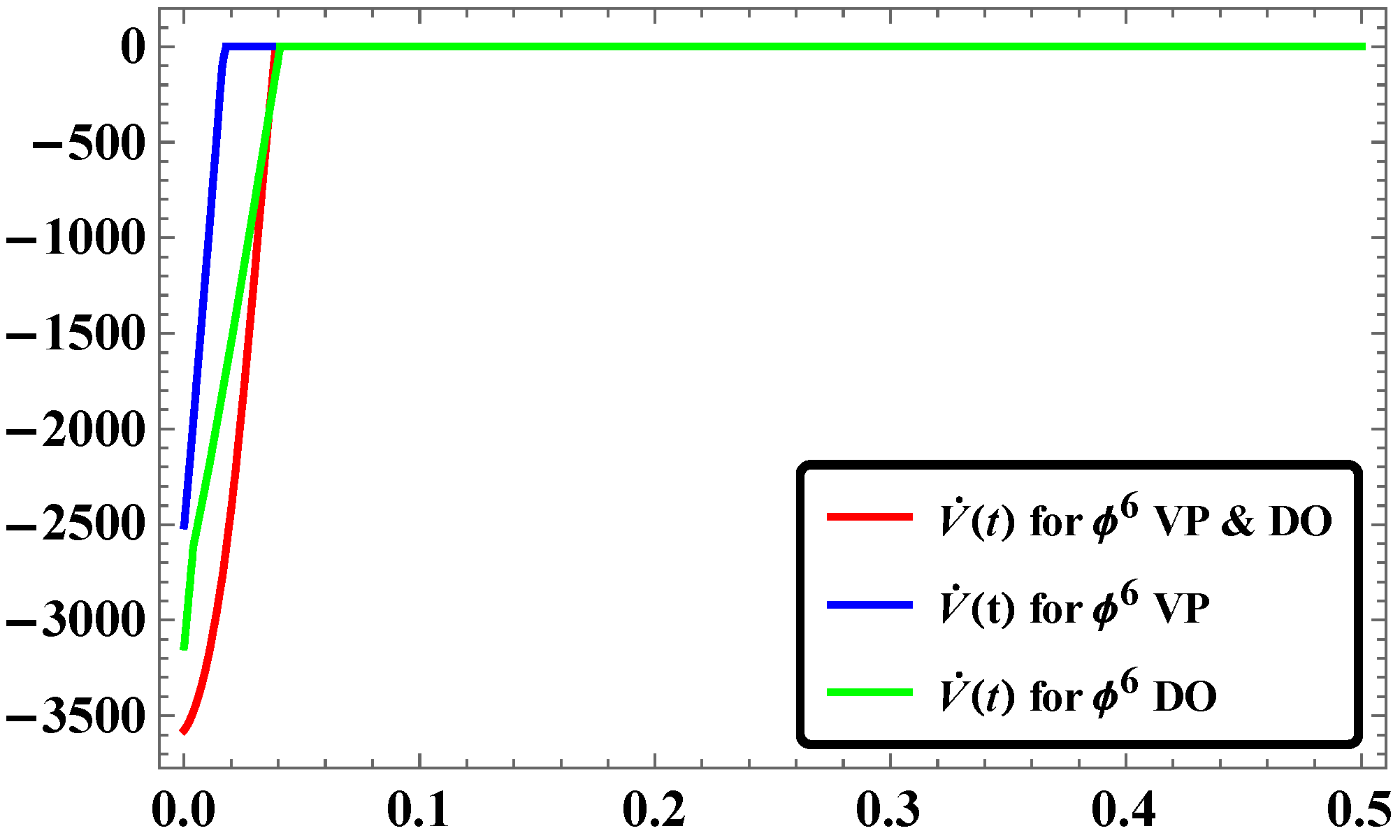
- The time response of stabilization of synchronization for LAC in our study was found to occur with rapid convergence if simulation is done with Mathematica.
- (2)
- For the same pairs of master and slave systems considered in our study, the RASMC is found to be more effective in terms of time response of stabilization of synchronization.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shahzad, M.; Pham, V.T.; Ahmad, M.A.; Jafari, S.; Hadaeghi, F. Synchronization and circuit design of a chaotic system with coexisting hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1637–1652. [Google Scholar] [CrossRef]
- Yao, L.; Cai, G. Chaos Synchronization of a New Hyperchaotic Finance System Via a Novel Chatter Free Sliding Mode Control Strategy. Int. J. Nonlinear Sci. 2014, 17, 176–181. [Google Scholar]
- Mobayen, S. A Novel Global Sliding Mode Control Based on Exponential Reaching Law for a Class of under Actuated Systems with External Disturbances. J. Comput. Nonlinear Dyn. 2015, 11, 021011–021019. [Google Scholar] [CrossRef]
- Azar, A.T.; Zhu, Q. Advances and Applications in Sliding Mode Control Systems; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Shahzad, M.; Raziuddin, M. Synchronization Of Three Dimensional Cancer Model With Rosslar System Using A Robust Adaptive Sliding Mode Controller. Int. J. Math. Arch. 2015, 6, 123–132. [Google Scholar]
- Shahzad, M.; Saaban, A.B.; Ibrahim, A.B.; Ahmad, I. Adaptive control to synchronise and anti-synchronise two identical time delay Bhalekar-Gejji chaotic systems with unknown parameters. Int. J. Autom. Control 2015, 9, 211–227. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, A.; Xia, Y.; Zhang, L. Optimize design of adaptive synchronization controllers and parameter observers in different hyperchaotic systems. Appl. Math. Comput. 2010, 215, 3318–3326. [Google Scholar] [CrossRef]
- Lin, C.; Peng, Y.; Lin, M. CMAC-based adaptive backstepping synchronization of uncertain chaotic systems. Chaos Soliton Fract. 2009, 42, 981–988. [Google Scholar] [CrossRef]
- Bai, E.W.; Lonngren, K.E. Synchronization of two Lorenz system using Active control. Phys. Rev. Lett. 1997, 64, 1199–1196. [Google Scholar] [CrossRef]
- Vincent, U.E. Synchronization of Identical and Nonidentical 4-D Chaotic Systems using Active Control. Chaos Solitons Fract. 2008, 37, 1065–1075. [Google Scholar] [CrossRef]
- Njah, A.N. Synchronization and Anti-synchronization of double hump Duffing-Van der Pol Oscillators via Active Control. J. Inf. Comput. Sci. 2009, 4, 243–250. [Google Scholar]
- Njah, A.N. Synchronization via active control of parametrically and externally excited Φ6—Van der Pol and duffing oscillators and application to secure communications. J. Vib. Cont. 2011, 17, 493–504. [Google Scholar] [CrossRef]
- Shahzad, M.; Ahmad, I. Experimental study of synchronization & Anti-synchronization for spin orbit problem of Enceladus. Int. J. of Cont. Sci. Eng. 2013, 3, 41–47. [Google Scholar]
- Pisarchik, A.N.; Arecchi, F.T.; Meucci, R.; Garbo, A.D. Synchronization of Shilnikov Chaos in CO2 Laser with Feedback. Laser Phys. 2014, 11, 1235–1239. [Google Scholar]
- Hammami, S. State feedback-based secure image cryptosystem hyperchaotic synchronization. ISA Trans. 2015. [Google Scholar] [CrossRef] [PubMed]
- Rafikov, M.; Balthazar, J.M. On control and synchronization in chaotic and hyperchaotic systems via linear feedback control. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 1246–1255. [Google Scholar] [CrossRef]
- Luo, R.Z.; Zhang, F. Finite-Time Modified Projective Synchronization of Unknown Rossler and Coullet Systems. Commun. Control Sci. Eng. 2013, 1, 51–56. [Google Scholar]
- Cai, N.; Jing, Y.; Zhang, S. Modified projective synchronization of chaotic systems with disturbances via active sliding mode control. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1613–1620. [Google Scholar] [CrossRef]
- Fu, G. Robust adaptive modified function projective synchronization of different hyperchaotic systems subject to external disturbance. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2602–2608. [Google Scholar] [CrossRef]
- Ahmad, I.; Saaban, A.; Ibrahim, A.; Shahzad, M. A Research on the Synchronization of Two Novel Chaotic Systems Based on a Nonlinear Active Control Algorithm. Eng. Tech. Appl. Sci. Res. 2015, 5, 739–747. [Google Scholar]
- Singh, P.P.; Singh, J.P.; Roy, B.K. Synchronization and anti-synchronization of Lu and bhalekar-Gejji chaotic systems using nonlinear active control. Chaos Solitons Fract. 2014, 69, 31–39. [Google Scholar] [CrossRef]
- Ahmad, I.; Saaban, A.B.; Ibrahim, A.B.; Shahzad, M. On Globally Exponential Stable Complete Synchronization of Nearly Identical Hyperchaotic Systems via Linear Active Control. Ciênc. Téc. Vitiviníc. Sci. Technol. J. 2015, 30, 141–154. [Google Scholar]
- Shahzad, M. The Improved Results with Mathematica and Effects of External Uncertainty & Disturbances on Synchronization using a Robust Adaptive Sliding Mode Controller: A Comparative Study. Nonlinear Dyn. 2015, 79, 2037–2054. [Google Scholar]
- Pourmahmood, M.; Khanmohammadi, S.; Alizadeh, G. Synchronization of two different uncertain chaotic systems with unknown parameters using a robust adaptive sliding mode controller. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2853–2868. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Rasappan, S. Global Chaos Synchronization for WINDMI and Coullet Chaotic Systems Using Active Control. J. Cont. Eng. Tech. 2013, 3, 69–75. [Google Scholar]
- Ahmad, I.; Saaban, A.B.; Ibrahim, A.B.; Shahzad, M. A Research on Active Control to Synchronize a New 3D Chaotic System. Systems 2016, 4. [Google Scholar] [CrossRef]
- Ahmad, I.; Saaban, A.B.; Ibrahim, A.B.; Shahzad, M.; Naveed, N. The Synchronization of Chaotic Systems with Different Dimensions by a Robust Generalized Active Control. Int. J. Light Electron. Opt. 2016, 127, 4859–4871. [Google Scholar] [CrossRef]
- Ahmad, I.; Saaban, A.; Ibrahim, A.; Shahzad, M. Global Chaos Identical and Nonidentical Synchronization of a New Chaotic System Using Linear Active Control. Complexity 2014. [Google Scholar] [CrossRef]
- Siewe, S.M.; Moukam, K.F.M.; Tchawoua, C.; Woafo, P. Bifurcation and chaos in triple-well Φ6—Van der Pol oscillator driven by external and parametric excitations. Phys. A 2005, 357, 383–396. [Google Scholar] [CrossRef]
- Tchoukuegno, R.; Nbendjo, B.R.N.; Woafo, P. Resonant oscillations and fractal basin boundaries of a particle in a Φ6 potential. Phys. A 2002, 304, 362–368. [Google Scholar] [CrossRef]
- Tchoukuegno, R.; Nbendjo, B.R.N.; Woafo, P. Linear feedback and parametric controls of vibrations and chaotic escape in a Φ6 potential. Int. J. Nonlinear Mech. 2003, 38, 531–541. [Google Scholar] [CrossRef]
- Li, W.; Chang, K. Robust synchronization of drive-response chaotic systems via adaptive sliding mode control. Chaos Soliton Fract. 2009, 39, 2086–2092. [Google Scholar] [CrossRef]
- Yan, J.; Hung, M.; Chiang, T.; Yang, Y. Robust synchronization of chaotic systems via adaptive sliding mode control. Phys. Lett. A 2006, 356, 220–225. [Google Scholar] [CrossRef]
- Aghababa, M.P.; Heydari, A. Chaos synchronization between two different chaotic systems with uncertainties, external disturbances, unknown parameters and input nonlinearities. Appl. Math. Model. 2012, 36, 1639–1652. [Google Scholar] [CrossRef]
- Aghababa, M.P.; Akbari, M.E. A chattering-free robust adaptive sliding mode controller for synchronization of two different chaotic systems with unknown uncertainties and external disturbances. Appl. Math. Comput. 2012, 218, 5757–5768. [Google Scholar] [CrossRef]
- Khan, A.; Shahzad, M. Synchronization of circular restricted three body problem with Lorenz hyper chaotic system using a robust adaptive sliding mode controller. Complexity 2013, 18, 58–64. [Google Scholar] [CrossRef]





© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahzad, M.; Ahmad, I.; Saaban, A.B.; Ibrahim, A.B. Improved Time Response of Stabilization in Synchronization of Chaotic Oscillators Using Mathematica. Systems 2016, 4, 25. https://doi.org/10.3390/systems4020025
Shahzad M, Ahmad I, Saaban AB, Ibrahim AB. Improved Time Response of Stabilization in Synchronization of Chaotic Oscillators Using Mathematica. Systems. 2016; 4(2):25. https://doi.org/10.3390/systems4020025
Chicago/Turabian StyleShahzad, Mohammad, Israr Ahmad, Azizan Bin Saaban, and Adyda Binti Ibrahim. 2016. "Improved Time Response of Stabilization in Synchronization of Chaotic Oscillators Using Mathematica" Systems 4, no. 2: 25. https://doi.org/10.3390/systems4020025
APA StyleShahzad, M., Ahmad, I., Saaban, A. B., & Ibrahim, A. B. (2016). Improved Time Response of Stabilization in Synchronization of Chaotic Oscillators Using Mathematica. Systems, 4(2), 25. https://doi.org/10.3390/systems4020025





