Abstract
This research proposes a hierarchical aggregation approach using Data Envelopment Analysis (DEA) and Analytic Hierarchy Process (AHP) for indicators. The core logic of the proposed approach is to reflect the hierarchical structures of indicators and their relative priorities in constructing composite indicators (CIs), simultaneously. Under hierarchical structures, the indicators of similar characteristics can be grouped into sub-categories and further into categories. According to this approach, we define a domain of composite losses, i.e., a reduction in CI values, based on two sets of weights. The first set represents the weights of indicators for each Decision Making Unit (DMU) with the minimal composite loss, and the second set represents the weights of indicators bounded by AHP with the maximal composite loss. Using a parametric distance model, we explore various ranking positions for DMUs while the indicator weights obtained from a three-level DEA-based CI model shift towards the corresponding weights bounded by AHP. An illustrative example of road safety performance indicators (SPIs) for a set of European countries highlights the usefulness of the proposed approach.
1. Introduction
Individual indicators are multidimensional measures that can assess the relative positions of entities (e.g., countries) in a given area [1]. A Composite indicator (CI) is a mathematical aggregation of individual indicators into a single score. Two simple but popular aggregation methods in the context of multi-criteria decision-making (MCDM) are the weighted sum (WS) method and the weighted product (WP) method [2]. Some researchers have recently pointed out that the WP method may have some advantages over the WS method in CI construction [3,4,5]. However, the assignment of weights to indicators is still a main source of difficulty in the application of these methods. Fortunately, the recent methodological advances in operations research and management science (OR/MS) have provided us with two powerful tools, namely data envelopment analysis (DEA) and analytic hierarchy process (AHP), which can be used as weighting and aggregation tools in CI construction.
Data Envelopment Analysis is a nonparametric method to assess the relative efficiency of a group of DMUs based on their distance from the best-practice frontier. In this method each DMU can freely choose its own weights to maximize its performance [6].
The standard DEA models are formulated using multiple inputs and multiple outputs of DMUs. The application of this group of models in CI construction can be found in [7,8,9]. However, in recent years much more attention has been focused on the application of a new group of DEA models in the field of composite indicators which is known as the “benefit of the doubt” (BOD) approach. In the BOD approach, all indicators are treated as outputs without explicit inputs, i.e., the property of “the larger is the better” [10,11,12].
In light of the possibility of neglecting the priority of various indicators, some critics have questioned the validity and stability of CIs obtained via DEA. Decision makers (DMs), in some contexts, have value judgments concerning the relative priority of indicators that should be taken into account in CI construction.
Alternatively, AHP is a systematic MCDM method to generate the true or approximate weights based on the well-defined mathematical structures of pairwise comparison metrics.
The application of AHP in CI construction provides a priori information about the relative priority of indicators [13,14,15]. AHP usually involves three basic functions: structuring complexities, measuring on a ratio-scale and synthesizing [16]. One of the advantages of AHP is its high flexibility to be combined with the other OR/MS techniques [17]. AHP can be combined with DEA in different ways. The most common approach is the estimation of parameters of weight restrictions on the DEA models. AHP estimates the appropriate values for the parameters in the absolute weight restrictions [18], relative weight restrictions [19,20,21,22,23], virtual weight restrictions [24,25] and restrictions on changes of input (output) units [26].
There are a number of other methods that do not necessarily apply additional restrictions to a DEA model. Such as converting the qualitative data in DEA to the quantitative data using AHP [27,28,29,30,31,32,33,34], ranking the efficient/inefficient units in DEA models using AHP in a two stage process [35,36,37], weighting the efficiency scores obtained from DEA using AHP [38], weighting the inputs and outputs in the DEA structure [39,40,41,42], constructing a convex combination of weights using AHP and DEA [43] and estimating missing data in DEA using AHP [44].
The recent studies by Pakkar [45,46,47,48,49,50] demonstrate the effects of imposing weight bounds on the different variants of DEA models using AHP. To this end, AHP has been applied in single-level DEA models [47,48,49,50] and two-level DEA models [45,46]. Due to the complexity of the hierarchical structures of indicators, this paper applies AHP into an additive three-level DEA model in the context of CI construction. Theoretically, the approach proposed in this paper may also be considered as the additive form of the multiplicative three-level DEA-based CI approach to constructing CIs proposed by [51]. In a three-level hierarchy, the indicators of similar characteristics can be grouped into sub-categories and further into categories. A three-level DEA model entirely reflects the characteristics of a generalized multiple level DEA model developed in [52,53]. Since the proposed approach uses AHP in an additive three-level DEA-based model, it contributes to the set of methods currently available for CI construction.
2. Methodology
This research has been organized to proceed along the following stages (Figure 1):
- Computing the composite value of each DMU using one-level DEA-based CI model (4). The computed composite values are applied in three-level DEA-based CI model (6).
- Computing the priority weights of indicators for all DMUs using AHP, which impose weight bounds into model (6).
- Obtaining an optimal set of weights for each DMU using three-level DEA-based CI model (6) (minimum composite loss η).
- Obtaining an optimal set of weights for each DMU using model (6) bounded by AHP (maximum composite loss κ). Note that if the AHP weights are added to model (6), we obtain model (10).
- Measuring the performance of each DMU in terms of the relative closeness to the priority weights of indicators. For this purpose, we develop parameter-distance model (11). Increasing a parameter in a defined range of composite loss we explore how much a DM can achieve its goals. This may result in various ranking positions for a DMU in comparison to the other DMUs.
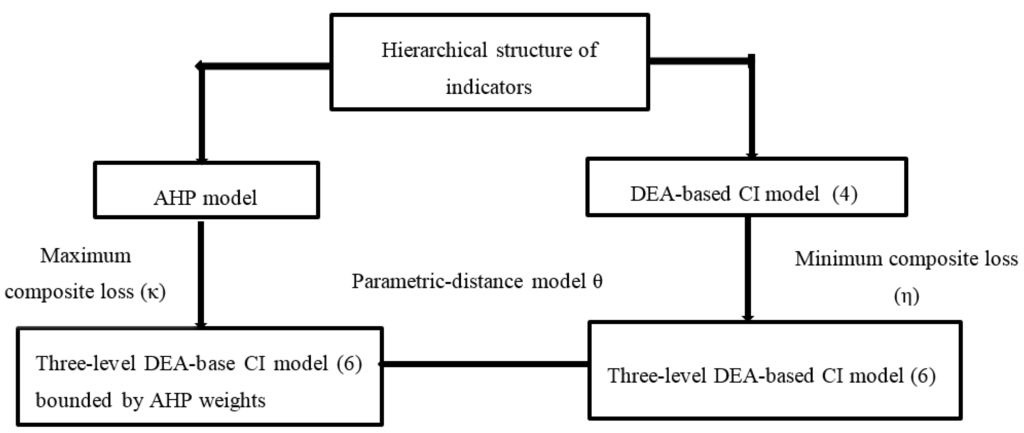
Figure 1.
A hierarchical aggregation approach for indicators using a three-level Data Envelopment Analysis (DEA) and Analytic Hierarchy Process (AHP).
2.1. DEA-Based CI Model
A DEA-based CI model can be formulated similar to a classical DEA model in which all data are treated as outputs without explicit inputs [54]. In the following, and in line with the more common CI terminology, we will often refer to outputs as “indicators”. In order to eliminate the scale differences between all (output) indicators, and moreover, to ensure that all of them are in the same direction of change the normalized counterparts of indicators, using the distance to reference method, are computed as follows [1]:
where is the normalized value of (output) indicator () for DMU (j = 1, 2,…, n). Now assume that all DMUs have unit input (). Then the fractional CCR-DEA model can be developed as follows [55]:
where is the composite indicator of DMU under assessment. is the index for the DMU under assessment where ranges over 1, 2,…, . and are the weights of input i () and (output) indicator r (). The first set of constraints assures that if the computed weights are applied to a group of DMUs, (), they do not attain a composite score of larger than 1. The second set of constraints indicates the non-negative conditions for the model variables. Introducing the constraint and performing the operation of substitution, an equivalent linear model can be formulated as follows:
Model (4) looks like a DEA model without inputs that extends the standard DEA methodology to the field of CI construction.
2.2. Three-Level DEA-Based CI Model
We develop a three-level DEA model to aggregate the performance of indicators under the (sub) category they belong to by a weighted-average method (Figure 2). Let be the value of indicator () of sub-category of category for DMU () after normalizing the original data. Let be the internal weight of indicator of sub-category of category while . Then the value of sub-category of category for the DMU is defined as . Let be the internal weight of sub-category of category while . Then the value of category is defined as . Let be the weight of category . To develop a linear model, the new multiplier of indicator of sub-category of category is defined as: . Similarly, the new multiplier of sub-category of category is defined as: . Consequently, a linear three-level DEA model for indicators can be developed as follows:
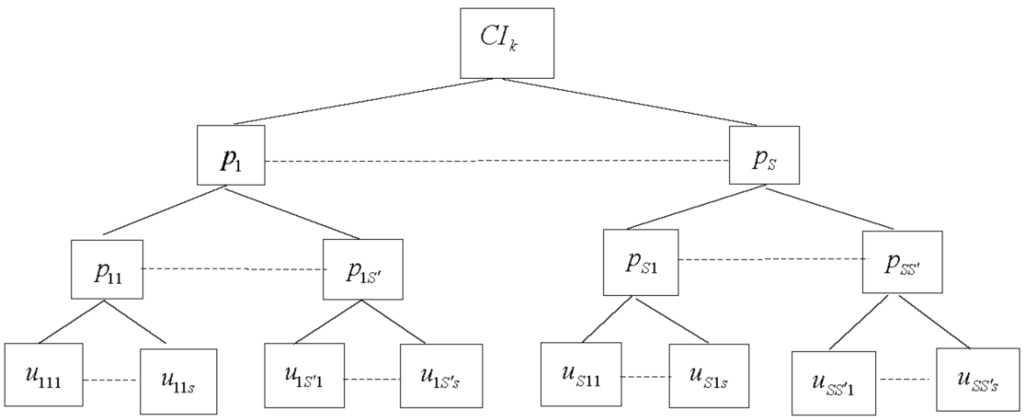
Figure 2.
A three-level DEA framework for hierarchical indicators.
We develop our formulation based on the generalized distance model [56,57] in such a way that the hierarchical structures of indicators, using a weighted-average approach, are taken into consideration [52,53]. Let () be the best attainable composite value for the DMU under assessment, calculated from model (4). We want the composite value , calculated from the set of weights , to be closest to . The degree of closeness between and is measured as with , where is a distance measure and represents the distance parameter. Our definition of “closest” is that the largest distance is at its minimum. On the other hand, the largest distance completely dominates when . For , the distance measure is reduced to . Hence we choose the form of the minimax model: to minimize a single deviation which is equivalent to the following linear model:
Model (6) identifies the minimum composite loss (eta) needed to arrive at an optimal set of weights. The first constraint ensures that each DMU loses no more than of its best attainable composite value, . The second set of constraints satisfies that the composite values of all DMUs are less than or equal to their upper bound of .
Two sets of constraints are added to model (6): and , where are indicator multipliers. This implies that the sum of weights under each (sub-) sub-category equals to the weight of that (sub-) sub-category. It should be noted that the original (or internal) weights used for calculating the weighted averages are obtained as and .
2.3. Prioritizing Indicator Weights Using AHP
Model (6) identifies the minimum composite loss (eta) needed to arrive at a set of weights of indicators by the internal mechanism of DEA. On the other hand, the priority weights of indicators, and the corresponding (sub) categories are defined out of the internal mechanism of DEA by AHP (Figure 3).
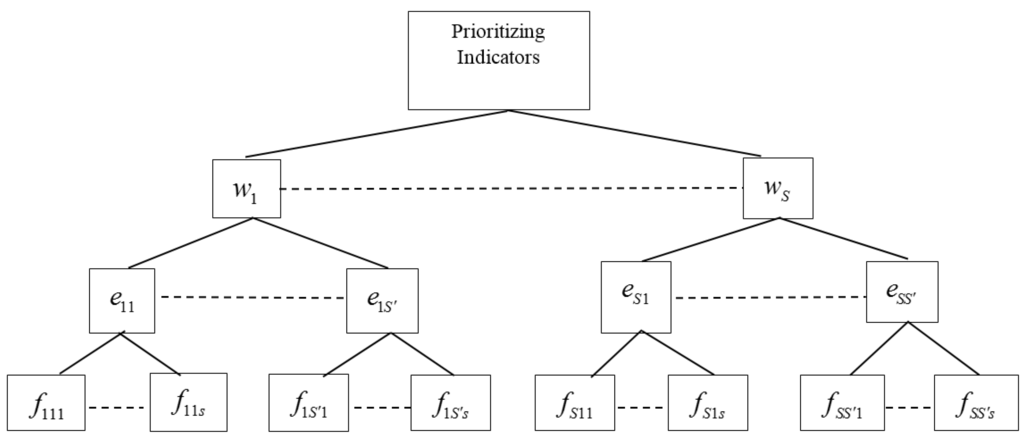
Figure 3.
The AHP model for prioritizing indicators.
In order to more clearly demonstrate how AHP is integrated into the three-level DEA-based CI model, this research presents an analytical process in which indicator weights are bounded by the AHP method. The AHP procedure for imposing weight bounds may be broken down into the following steps:
Step 1: A decision maker makes a pairwise comparison matrix of different criteria, denoted by , with the entries of . The comparative importance of criteria is provided by the decision maker using a rating scale. Saaty [16] recommends using a 1–9 scale.
Step 2: The AHP method obtains the priority weights of criteria by computing the eigenvector of matrix (Equation (7)), , which is related to the largest eigenvalue, .
To determine whether or not the inconsistency in a comparison matrix is reasonable the random consistency ratio, , can be computed by the following equation:
where is the average random consistency index and is the size of a comparison matrix. In a similar way, the priority weights of (sub-) sub-criteria under each (sub-) criterion can be computed. To obtain the weight bounds for indicator weights in the three-level DEA-based CI model, this study aggregates the priority weights of three different levels in AHP as follows:
where is the priority weight of criterion () in AHP, is the priority weight of sub-criterion under criterion and is sub-sub-criterion () under sub-criterion .
In order to estimate the maximum composite loss (kappa) necessary to achieve the priority weights of indicators for each DMU the following linear program is proposed:
The first sets of constraints change the AHP computed weights to weights for the new system by means of a scaling factor . The scaling factor is added to avoid the possibility of contradicting constraints leading to infeasibility or underestimating the relative composite scores of DMUs [58]. The optimal solution to model (10) produces a set of weights for indicators that are used to compute the performance of DMUs.
It should be noted that incorporating absolute weight bounds, using AHP, for indicator weights in a DEA-based CI model is consistent with the common practice of constructing composite indicators. According to this practice, the priority weights of indicators can be used directly in an aggregation function to synthetize indicators’ values into composite values [1]. In addition, this form of placing restrictions on indicator weights simply allows us to identify a specific range of variation between two systems of weights obtained from models (6) and (10).
2.4. A Parametric Distance Model
We can now develop a parametric distance model for various discrete values of parameter such that . Let be the weights of indicators for a given value of parameter , where indicators are under sub-category of category (). Let be the priority weights of indicators under sub-category of category , obtained from model (10). Our objective is to minimize the total deviations between and with the shortest Euclidian distance measure subject to the following constraints:
Because the range of deviations computed by the objective function is different for each DMU, it is necessary to normalize it by using relative deviations rather than absolute ones [59]. Hence, the normalized deviations can be computed by:
where is the optimal value of the objective function for . We define as a measure of closeness which represents the relative closeness of each DMU to the weights obtained from model (10) in the range [0, 1]. Increasing the parameter , we improve the deviations between the two systems of weights obtained from models (6) and (10) which may lead to different ranking positions for each DMU in comparison to the other DMUs. It should be noted that in a special case where the parameter , we assume = 1.
3. A Numerical Example: Road Safety Performance Indicators
In this section we present the application of the proposed approach to assess the road safety performance of a set of 13 European countries (or DMUs): Austria (AUT), Belgium (BEL), Finland (FIN), France (FRA), Hungary (HUN), Ireland (IRL), Lithuania (LTU), Netherlands (NLD), Poland (POL), Portugal (PRT), Slovenia (SVN), Sweden (SWE) and Switzerland (CHE). The data for eleven hierarchical indicators that compose SPIs for these countries have been adopted from [52]. The eight SPIs related to alcohol and speed are undesirable indicators while the three SPIs related to protective systems are desirable ones. The resulting normalized data based on Equations (1) and (2) are presented in Table 1.
Taking the percentage of speed limit violation on rural roads as an example, Slovenia performs the best (1.000) while Poland the worst (0.014) and all other countries’ values lie within this interval.
The results of the AHP model for prioritizing hierarchical SPIs as constructed by the author in Expert Choice software are presented in Table 2. One can argue that the priority weights of SPIs must be judged by road safety experts. However, since the aim of this section is just to show the application of the proposed approach on numerical data, we see no problem to use our judgment alone.

Table 1.
Normalized data on the eleven hierarchical safety performance indicators (SPIs).
| Countries | Alcohol | Speed | Protective Systems | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| % of Drivers above Legal Alcohol Limit In Roadside Police Tests | % of Alcohol Related Fatalities | Mean Speed | Speed Limit Violation (%) | Seat Belt | Child Restraint | ||||||
| Motorways | Rural Roads | Urban Roads | Motorways | Rural Roads | Urban Roads | Daytime Seatbelt Wearing Rate in Front Seats of Light Vehicles (%) | Daytime Seatbelt Wearing Rate in Rear Seats of Light Vehicles (%) | Daytime Usage Rate of Child Restraints (%) | |||
| AUT | 0.116 | 0.463 | 0.938 | 0.781 | 0.802 | 0.766 | 0.051 | 0.254 | 0.904 | 0.699 | 0.863 |
| BEL | 0.068 | 0.654 | 0.846 | 0.743 | 0.768 | 0.348 | 0.029 | 0.222 | 0.799 | 0.488 | 0.729 |
| FIN | 0.593 | 0.136 | 0.963 | 0.729 | 0.907 | 0.409 | 0.023 | 0.323 | 0.911 | 0.922 | 0.716 |
| FRA | 0.263 | 0.123 | 0.933 | 0.787 | 0.838 | 0.505 | 0.037 | 0.318 | 1.000 | 1.000 | 0.937 |
| HUN | 0.279 | 0.283 | 0.955 | 0.793 | 0.817 | 0.362 | 0.033 | 0.230 | 0.727 | 0.501 | 0.433 |
| IRL | 0.237 | 0.119 | 0.945 | 0.762 | 0.724 | 1.000 | 0.032 | 0.223 | 0.901 | 0.914 | 0.857 |
| LTU | 0.555 | 0.321 | 1.000 | 0.713 | 0.714 | 0789 | 0.025 | 0.318 | 0.609 | 0.366 | 0.404 |
| NLD | 0.081 | 1.000 | 0.899 | 0.740 | 0.881 | 0.454 | 0.020 | 0.234 | 0.959 | 0.890 | 0.758 |
| POL | 0.091 | 0.438 | 0.806 | 0.697 | 0.647 | 0.290 | 0.015 | 0.165 | 0.799 | 0.589 | 0.905 |
| PRT | 0.137 | 0.610 | 0.847 | 0.618 | 0.919 | 0.302 | 0.014 | 0.360 | 0.881 | 0.574 | 0.591 |
| SVN | 0.122 | 0.078 | 0.964 | 1.000 | 0.713 | 0.480 | 1.000 | 0.163 | 0.874 | 0.551 | 0.672 |
| SWE | 1.000 | 0.357 | 0.883 | 0.717 | 0.870 | 0.241 | 0.019 | 0.259 | 0.973 | 0.927 | 1.000 |
| CHE | 0.277 | 0.230 | 0.943 | 0.757 | 1.000 | 0.710 | 0.043 | 1.000 | 0.887 | 0.805 | 0.895 |

Table 2.
The AHP hierarchical model for SPIs.
| Objective Level | Criteria Level | Sub-Criteria Level | Sub-Sub-Criteria Level |
|---|---|---|---|
| Prioritizing road user behavior | Alcohol 0.2727 | % of drivers above legal alcohol limit 0.333 | % of drivers above legal alcohol limit 1.000 |
| % of alcohol-related fatalities 0.667 | % of alcohol-related fatalities 1.000 | ||
| Speed 0.5454 | Mean speed 0.60 | Mean speed of vehicles on motorways 0.081 | |
| Mean speed of vehicles on rural roads, 0.342 | |||
| Mean speed of vehicles on urban roads, 0.577 | |||
| Speed limit violations 0.40 | % of vehicles exceeding the speed limit on motorways 0.081 | ||
| % of vehicles exceeding the speed limit on rural roads 0.342 | |||
| % of vehicles exceeding the speed limit on urban roads 0.577 | |||
| Protective systems 0.1818 | Seat belt 0.40 | Daytime seatbelt wearing rate in front seats of light vehicles (%) 0.60 | |
| Daytime seatbelt wearing rate in rear seats of light vehicles (%) 0.40 | |||
| Child Restraint 0.60 | Daytime usage rate of child restraints (%) 1.000 |
Solving model (6) for the country under assessment, we obtain an optimal set of weights with minimum composite loss . Since the raw data are normalized, the weights obtained from this model are meaningful and have an intuitive explanation. As a result, we can later set meaningful bounds on the weights in terms of the relative priority of indicators. Taking Austria as an example in Table 3, with the composite value of one obtained from model (4), we can observe that the alcohol-related fatality rate is 26 times less important than the mean speed of vehicles on motorways and about 3.2 times less important than the daytime usage rate of child restraints. Clearly, the other indicators are ignored in this assessment by assigning zero weights which are equivalent to excluding those indicators from the analysis. This kind of situation can be remedied by including the opinion of experts in defining the relative priority of indicators.

Table 3.
Optimal weights of hierarchical SPIs obtained from model (6) for Austria.
| Weights of Categories | Weights of Sub-Categories | Weights of Sub-Sub-Categories |
|---|---|---|
| 0.0361 | 0.0000 | 0.0000 |
| 0.0361 | 0.0361 | |
| 0.9415 | 0.9415 | 0.9415 |
| 0.0000 | ||
| 0.0000 | ||
| 0.0000 | 0.0000 | |
| 0.0000 | ||
| 0.0000 | ||
| 0.1160 | 0.0000 | 0.0000 |
| 0.0000 | ||
| 0.1160 | 0.1160 | |
It should be noted that the composite value of all countries calculated from model (6) is identical to that calculated from model (4). Therefore, the minimum composite loss for the country under assessment is (Table 4). This implies that the measure of relative closeness to the AHP weights for the country under assessment is . On the other hand, solving model (10) for the country under assessment, we adjust the priority weights of hierarchical SPIs obtained from AHP in such a way that they become compatible with the weights’ structure in the three level DEA-based CI models. Table 5 presents the optimal weights of hierarchical SPIs as well as its scaling factor for all countries.

Table 4.
Minimum and maximum losses in composite values for each country.
| Countries | η | κ | |
|---|---|---|---|
| AUT | 1.000 | 0.000 | 0.158 |
| BEL | 0.938 | 0.000 | 0.127 |
| FIN | 1.000 | 0.000 | 0.173 |
| FRA | 1.000 | 0.000 | 0.184 |
| HUN | 1.000 | 0.000 | 0.284 |
| IRL | 1.000 | 0.000 | 0.254 |
| LTU | 1.000 | 0.000 | 0.270 |
| NLD | 1.000 | 0.000 | 0.023 |
| POL | 0.955 | 0.000 | 0.224 |
| PRT | 0.978 | 0.000 | 0.139 |
| SVN | 1.000 | 0.000 | 0.208 |
| SWE | 1.000 | 0.000 | 0.040 |
| CHE | 1.000 | 0.000 | 0.000 |

Table 5.
Optimal weights of hierarchical SPIs obtained from model (10) for all countries.
| Weights of Categories | Weights of Sub-Categories | Weights of Sub-Sub-Categories |
|---|---|---|
| 0.4089 | 0.1362 | 0.1362 |
| 0.2727 | 0.2727 | |
| 0.8178 | 0.4907 | 0.0397 |
| 0.1678 | ||
| 0.2831 | ||
| 0.3271 | 0.0265 | |
| 0.1119 | ||
| 0.1888 | ||
| 0.2726 | 0.1090 | 0.0654 |
| 0.0436 | ||
| 0.1636 | 0.1636 | |
| 1.4993 | ||
Note that the priority weights of AHP used for incorporating weight bounds on indicator weights in model (10) are obtained as . Similarly, the priority weights of AHP at criteria level can be obtained as while and . In addition, The priority weights of AHP at sub-criteria and sub-sub-criteria levels can be obtained as and , respectively.
The maximum composite loss for each country to achieve the corresponding weights in model (10) is equal to (Table 4). As a result, the measure of relative closeness to the priority weights of SPIs for the country under assessment is = 1. Going one step further to the solution process of the parametric distance model (11), we proceed to the estimation of total deviations from the AHP weights for each country while the parameter is . Table 6 represents the ranking position of each country based on the minimum deviation from the priority weights of indicators for . It should be noted that in a special case where the parameter we assume

Table 6.
The ranking position of each country based on the minimum distance to priority weights of SPIs.
| Countries | Rank | |
|---|---|---|
| AUT | 0.332 | 6 |
| BEL | 0.705 | 11 |
| FIN | 0.438 | 9 |
| FRA | 0.338 | 7 |
| HUN | 0.591 | 10 |
| IRL | 0.331 | 5 |
| LTU | 0.381 | 8 |
| NLD | 0.021 | 2 |
| POL | 0.718 | 12 |
| PRT | 0.782 | 13 |
| SVN | 0.166 | 4 |
| SWE | 0.035 | 3 |
| CHE | 0.000 | 1 |
Table 6 shows that Switzerland (CHE) is the best performer in terms of the value and the relative closeness to the priority weights of indicators in comparison to the other countries. Nevertheless, increasing the value of from 0 to has two main effects on the performance of the other countries: improving the degree of deviations and reducing the value of composite indicator. This, of course, is a phenomenon, one expects to observe frequently. The graph of versus , as shown in Figure 4, is used to describe the relation between the relative closeness to the priority weights of indicators and composite loss for each country. This may result in different ranking positions for each country in comparison to the other countries (Appendix A).
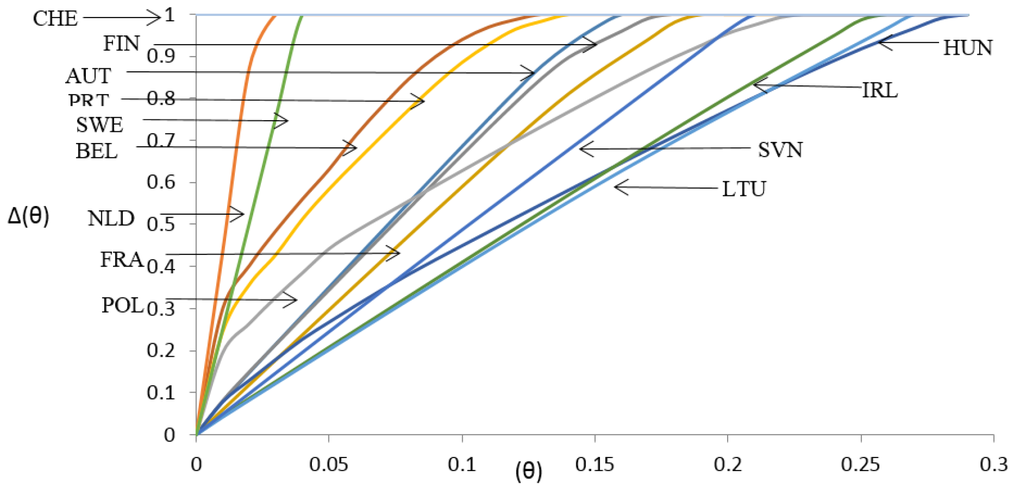
Figure 4.
The relative closeness to the priority weights of indicators [∆(θ)], versus composite loss (θ) for each country.
In order to clearly discover the effect of composite loss on the countries’ ranking as shown in Appendix A, we performed a Kruskal-Wallis test. The Kruskal-Wallis test compares the medians of rankings to determine whether there is a significant difference between them. The result of the test reveals that its p-value is quite smaller than 0.01. Therefore, we conclude that increasing composite loss in the whole range [0.0, 0.29] changes the countries’ ranking significantly. Note that at the countries can be ranked based on from the closest to the furthest from the priority weights of SPIs. For instance, at , Sweden, Ireland and Austria with composite values of one, are ranked in 3rd, 5th and 6th places, respectively, while Belgium, Poland and Portugal with composite values of less than one are ranked in 11th, 12th and 13th places, respectively (Table 4 and Table 6). However, with a small composite loss at , Belgium, Poland and Portugal take 3rd, 6th and 5th places in the rankings, respectively. Using this example, as a guideline, it is relatively easy to rank the countries in terms of distance to the priority weights of SPIs. At , Sweden moves up into 3rd place again while Belgium drops into 4th place. It is clear that both measures, and , are necessary to explain the ranking position of a country.
4. Conclusions
We develop a hierarchical aggregation approach based on DEA and AHP methodologies to construct composite indicators. We define two sets of weights of indicators in a three-level DEA framework. All indicators are treated as benefit type. The first set represents the weights of indicators with minimum composite loss. The second set represents the corresponding priority weights of hierarchical indicators, using AHP, with maximum composite loss. We assess the performance of each DMU in comparison to the other DMUs based on the relative closeness of the first set of weights to the second set of weights. Improving the measure of relative closeness in a defined range of composite loss, we explore the various ranking positions for the DMU under assessment in comparison to the other DMUs. To demonstrate the effectiveness of the proposed approach, we apply it to construct a composite road safety performance index for eleven hierarchical indicators that compose SPIs for 13 European countries.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
The measure of relative closeness to the priority weights of hierarchical SPIs [ ] vs. composite loss [θ] for each country.
| θ | AUT | BEL | FIN | FRA | HUN | IRL | LTU | NLD | POL | PRT | SVN | SWE | CHE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 |
| Rank | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | 1 |
| 0.01 | 0.0788 | 0.3002 | 0.0808 | 0.0595 | 0.0784 | 0.0450 | 0.0419 | 0.4367 | 0.1951 | 0.2454 | 0.0492 | 0.2521 | 1.0000 |
| Rank | 8 | 3 | 7 | 10 | 9 | 12 | 13 | 2 | 6 | 5 | 11 | 4 | 1 |
| 0.02 | 0.1479 | 0.4018 | 0.1497 | 0.1190 | 0.1295 | 0.0863 | 0.0823 | 0.8733 | 0.2640 | 0.3572 | 0.0983 | 0.5041 | 1.0000 |
| Rank | 8 | 4 | 7 | 10 | 9 | 12 | 13 | 2 | 6 | 5 | 11 | 3 | 1 |
| 0.03 | 0.2160 | 0.4852 | 0.2148 | 0.1784 | 0.1793 | 0.1269 | 0.1223 | 1.0000 | 0.3268 | 0.4286 | 0.1473 | 0.7562 | 1.0000 |
| Rank | 7 | 4 | 8 | 10 | 9 | 12 | 13 | 1 | 6 | 5 | 11 | 3 | 1 |
| 0.04 | 0.2838 | 0.5605 | 0.2797 | 0.2378 | 0.2272 | 0.1675 | 0.1624 | 1.0000 | 0.3845 | 0.5133 | 0.1963 | 1.0000 | 1.0000 |
| Rank | 7 | 4 | 8 | 9 | 10 | 12 | 13 | 1 | 6 | 5 | 11 | 1 | 1 |
| 0.05 | 0.3512 | 0.6312 | 0.3444 | 0.2970 | 0.2679 | 0.2081 | 0.2023 | 1.0000 | 0.4418 | 0.5846 | 0.2452 | 1.0000 | 1.0000 |
| Rank | 7 | 4 | 8 | 9 | 10 | 12 | 13 | 1 | 6 | 5 | 11 | 1 | 1 |
| 0.06 | 0.4185 | 0.7113 | 0.4091 | 0.3562 | 0.3073 | 0.2486 | 0.2422 | 1.0000 | 0.4832 | 0.6491 | 0.2941 | 1.0000 | 1.0000 |
| Rank | 7 | 4 | 8 | 9 | 10 | 12 | 13 | 1 | 6 | 5 | 11 | 1 | 1 |
| 0.07 | 0.4857 | 0.7813 | 0.4736 | 0.4152 | 0.3454 | 0.2891 | 0.2819 | 1.0000 | 0.5195 | 0.7121 | 0.3428 | 1.0000 | 1.0000 |
| Rank | 7 | 4 | 8 | 9 | 10 | 12 | 13 | 1 | 6 | 5 | 11 | 1 | 1 |
| 0.08 | 0.5527 | 0.8464 | 0.5379 | 0.4740 | 0.3818 | 0.3296 | 0.3215 | 1.0000 | 0.5556 | 0.7739 | 0.3913 | 1.0000 | 1.0000 |
| Rank | 7 | 4 | 8 | 9 | 11 | 12 | 13 | 1 | 6 | 5 | 10 | 1 | 1 |
| 0.09 | 0.6196 | 0.8991 | 0.6019 | 0.5325 | 0.4163 | 0.3699 | 0.3609 | 1.0000 | 0.5915 | 0.8331 | 0.4397 | 1.0000 | 1.0000 |
| Rank | 6 | 4 | 7 | 9 | 11 | 12 | 13 | 1 | 8 | 5 | 10 | 1 | 1 |
| 0.1 | 0.6861 | 0.9396 | 0.6655 | 0.5906 | 0.4497 | 0.4102 | 0.4001 | 1.0000 | 0.6273 | 0.8858 | 0.4879 | 1.0000 | 1.0000 |
| Rank | 6 | 4 | 7 | 9 | 11 | 12 | 13 | 1 | 8 | 5 | 10 | 1 | 1 |
| 0.11 | 0.7520 | 0.9692 | 0.7283 | 0.6481 | 0.4829 | 0.4504 | 0.4391 | 1.0000 | 0.6628 | 0.9290 | 0.5358 | 1.0000 | 1.0000 |
| Rank | 6 | 4 | 7 | 9 | 11 | 12 | 13 | 1 | 8 | 5 | 10 | 1 | 1 |
| 0.12 | 0.8166 | 0.9869 | 0.7896 | 0.7046 | 0.5160 | 0.4905 | 0.4778 | 1.0000 | 0.6980 | 0.9645 | 0.5833 | 1.0000 | 1.0000 |
| Rank | 6 | 4 | 7 | 8 | 11 | 12 | 13 | 1 | 9 | 5 | 10 | 1 | 1 |
| 0.13 | 0.8777 | 1.0000 | 0.8476 | 0.7596 | 0.5490 | 0.5304 | 0.5161 | 1.0000 | 0.7328 | 0.9838 | 0.6309 | 1.0000 | 1.0000 |
| Rank | 14 | 1 | 15 | 16 | 19 | 20 | 21 | 1 | 17 | 11 | 18 | 1 | 1 |
| 0.14 | 0.9271 | 1.0000 | 0.8967 | 0.8115 | 0.5818 | 0.5701 | 0.5540 | 1.0000 | 0.7669 | 1.0000 | 0.6784 | 1.0000 | 1.0000 |
| Rank | 14 | 1 | 15 | 16 | 19 | 20 | 21 | 1 | 17 | 1 | 18 | 1 | 1 |
| 0.15 | 0.9681 | 1.0000 | 0.9289 | 0.8577 | 0.6145 | 0.6096 | 0.5913 | 1.0000 | 0.8007 | 1.0000 | 0.7260 | 1.0000 | 1.0000 |
| Rank | 14 | 1 | 15 | 16 | 19 | 20 | 21 | 1 | 17 | 1 | 18 | 1 | 1 |
| 0.16 | 1.0000 | 1.0000 | 0.9592 | 0.8998 | 0.6468 | 0.6489 | 0.6279 | 1.0000 | 0.8340 | 1.0000 | 0.7735 | 1.0000 | 1.0000 |
| Rank | 14 | 1 | 15 | 16 | 20 | 19 | 21 | 1 | 17 | 1 | 18 | 1 | 1 |
| 0.17 | 1.0000 | 1.0000 | 0.9896 | 0.9409 | 0.6789 | 0.6880 | 0.6635 | 1.0000 | 0.8665 | 1.0000 | 0.8211 | 1.0000 | 1.0000 |
| Rank | 1 | 1 | 7 | 8 | 12 | 11 | 13 | 1 | 9 | 1 | 10 | 1 | 1 |
| 0.18 | 1.0000 | 1.0000 | 1.0000 | 0.9820 | 0.7104 | 0.7269 | 0.6987 | 1.0000 | 0.8973 | 1.0000 | 0.8687 | 1.0000 | 1.0000 |
| Rank | 1 | 1 | 1 | 8 | 12 | 11 | 13 | 1 | 9 | 1 | 10 | 1 | 1 |
| 0.19 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.7415 | 0.7655 | 0.7335 | 1.0000 | 0.9253 | 1.0000 | 0.9162 | 1.0000 | 1.0000 |
| Rank | 1 | 1 | 1 | 1 | 12 | 11 | 13 | 1 | 9 | 1 | 10 | 1 | 1 |
| 0.2 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.7724 | 0.8036 | 0.7677 | 1.0000 | 0.9538 | 1.0000 | 0.9638 | 1.0000 | 1.0000 |
| Rank | 1 | 1 | 1 | 1 | 12 | 11 | 13 | 1 | 10 | 1 | 9 | 1 | 1 |
| 0.21 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.8029 | 0.8408 | 0.8015 | 1.0000 | 0.9736 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Rank | 1 | 1 | 1 | 1 | 12 | 11 | 13 | 1 | 10 | 1 | 1 | 1 | 1 |
| 0.22 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.8329 | 0.8772 | 0.8349 | 1.0000 | 0.9919 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Rank | 1 | 1 | 1 | 1 | 13 | 11 | 12 | 1 | 10 | 1 | 1 | 1 | 1 |
| 0.23 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.8621 | 0.9136 | 0.8681 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Rank | 1 | 1 | 1 | 1 | 13 | 11 | 12 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.24 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.8905 | 0.9501 | 0.9013 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Rank | 1 | 1 | 1 | 1 | 13 | 11 | 12 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.25 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9180 | 0.9865 | 0.9345 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Rank | 1 | 1 | 1 | 1 | 13 | 11 | 12 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.26 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9432 | 1.0000 | 0.9677 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Rank | 1 | 1 | 1 | 1 | 13 | 1 | 12 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.27 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9669 | 1.0000 | 0.9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Rank | 1 | 1 | 1 | 1 | 13 | 1 | 12 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.28 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9906 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Rank | 1 | 1 | 1 | 1 | 13 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.29 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Rank | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
References
- OECD. Organisation for Economic Co-operation and Development (OECD). In Handbook on Constructing Composite Indicators: Methodology and User Guide; OECD Publishing: Paris, France, 2008. [Google Scholar]
- San Cristobal Mateo, J.R. Multi-Criteria Analysis in the Renewable Energy Industry; Springer: London, UK, 2012. [Google Scholar]
- Ebert, U.; Welsch, H. Meaningful environmental indices: A social choice approach. J. Environ. Econ. Manag. 2004, 47, 270–283. [Google Scholar] [CrossRef]
- Munda, G.; Nardo, M. Noncompensatory/nonlinear composite indicators for ranking countries: A defensible setting. Appl. Econ. 2009, 41, 1513–1523. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W. Comparing MCDA aggregation methods in constructing composite indicators using the Shannon-Spearman measure. Soc. Indic. Res. 2009, 94, 83–96. [Google Scholar] [CrossRef]
- Cooper, W.W.; Seiford, L.M.; Zhu, J. Handbook on Data Envelopment Analysis; Kluwer Academic Publishers: Norwel, MA, USA, 2004. [Google Scholar]
- Chaaban, J.M. Measuring youth development: A nonparametric cross-country “youth welfare index”. Soc. Indic. Res. 2009, 93, 351–358. [Google Scholar] [CrossRef]
- Murias, P.; de Miguel, J.C.; Rodriguez, D. A composite indicator for university quality assessment: The case of Spanish higher education system. Soc. Indic. Res. 2008, 89, 129–146. [Google Scholar] [CrossRef]
- Murias, P.; Martinez, F.; de Miguel, C. An economic wellbeing index for the Spanish provinces: A data envelopment analysis approach. Soc. Indic. Res. 2006, 77, 395–417. [Google Scholar] [CrossRef]
- Cherchye, L.; Moesen, W.; Rogge, N.; van Puyenbroeck, T.; Saisana, M.; Saltelli, A.; Liska, R.; Tarantola, S. Creating composite indicators with DEA and robustness analysis: The case of the technology achievement index. J. Oper. Res. Soc. 2008, 59, 239–251. [Google Scholar] [CrossRef]
- Cherchye, L.; Moesen, W.; Rogge, N.; van Puyenbroeck, T. An introduction to “benefit of the doubt” composite indicators. Soc. Indic. Res. 2007, 82, 111–145. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W.; Poh, K.L. A mathematical programming approach to constructing composite Indicators. Ecol. Econ. 2007, 62, 291–297. [Google Scholar] [CrossRef]
- Arora, A.; Arora, A.S.; Palvia, S. Social media index valuation: Impact of technological, social, economic, and ethical dimensions. J. Promot. Manag. 2014, 20, 328–344. [Google Scholar] [CrossRef]
- Dedeke, N. Estimating the weights of a composite index using AHP: Case of the environmental performance index. Br. J. Arts Soc. Sci. 2013, 11, 199–221. [Google Scholar]
- Singh, R.K.; Murty, H.R.; Gupta, S.K.; Dikshit, A.K. Development of composite sustainability performance index for steel industry. Ecol. Indic. 2007, 7, 565–588. [Google Scholar] [CrossRef]
- Saaty, T.S. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Vaidya, O.S.; Kumar, S. Analytic hierarchy process: An overview of applications. Eur. J. Oper. Res. 2006, 169, 1–29. [Google Scholar] [CrossRef]
- Entani, T.; Ichihashi, H.; Tanaka, H. Evaluation method based on interval AHP and DEA. Cent. Eur. J. Oper. Res. 2004, 12, 25–34. [Google Scholar]
- Kong, W.; Fu, T. Assessing the performance of business colleges in Taiwan using data envelopment analysis and student based value-added performance indicators. Omega 2012, 40, 541–549. [Google Scholar] [CrossRef]
- Lee, A.H.I.; Lin, C.Y.; Kang, H.Y.; Lee, W.H. An integrated performance evaluation model for the photovoltaics industry. Energies 2012, 5, 1271–1291. [Google Scholar] [CrossRef]
- Liu, C.M.; Hsu, H.S.; Wang, S.T.; Lee, H.K. A performance evaluation model based on AHP and DEA. J. Chin. Inst. Ind. Eng. 2005, 22, 243–251. [Google Scholar] [CrossRef]
- Takamura, Y.; Tone, K. A comparative site evaluation study for relocating Japanese government agencies out of Tokyo. Socio-Econ. Plan. Sci. 2003, 37, 85–102. [Google Scholar] [CrossRef]
- Tseng, W.; Yang, C.; Wang, D. Using the DEA and AHP methods on the optimal selection of IT strategic alliance partner. In Proceedings of the 2009 International Conference on Business and Information (BAI 2009), Kuala Lumpur, Malaysia, 23–30 June 2009; Academy of Taiwan Information Systems Research (ATISR): Taipei, Taiwan, 2009; Volume 6, pp. 1–15. [Google Scholar]
- Premachandra, I.M. Controlling factor weights in data envelopment analysis by Incorporating decision maker’s value judgement: An approach based on AHP. J. Inf. Manag. Sci. 2001, 12, 1–12. [Google Scholar]
- Shang, J.; Sueyoshi, T. Theory and Methodology—A unified framework for the selection of a Flexible Manufacturing System. Eur. J. Oper. Res. 1995, 85, 297–315. [Google Scholar]
- Lozano, S.; Villa, G. Multiobjective target setting in data envelopment analysis using AHP. Comput. Oper. Res. 2009, 36, 549–564. [Google Scholar] [CrossRef]
- Azadeh, A.; Ghaderi, S.F.; Izadbakhsh, H. Integration of DEA and AHP with computer simulation for railway system improvement and optimization. Appl. Math. Comput. 2008, 195, 775–785. [Google Scholar] [CrossRef]
- Ertay, T.; Ruan, D.; Tuzkaya, U.R. Integrating data envelopment analysis and analytic hierarchy for the facility layout design in manufacturing systems. Inf. Sci. 2006, 176, 237–262. [Google Scholar] [CrossRef]
- Jyoti, T.; Banwet, D.K.; Deshmukh, S.G. Evaluating performance of national R & D organizations using integrated DEA-AHP technique. Int. J. Product. Perform. Manag. 2008, 57, 370–388. [Google Scholar]
- Korpela, J.; Lehmusvaara, A.; Nisonen, J. Warehouse operator selection by combining AHP and DEA methodologies. Int. J. Product. Econ. 2007, 108, 135–142. [Google Scholar] [CrossRef]
- Lin, M.; Lee, Y.; Ho, T. Applying integrated DEA/AHP to evaluate the economic performance of local governments in china. Eur. J. Oper. Res. 2011, 209, 129–140. [Google Scholar] [CrossRef]
- Ramanathan, R. Supplier selection problem: Integrating DEA with the approaches of total cost of ownership and AHP. Supply Chain Manag. 2007, 12, 258–261. [Google Scholar] [CrossRef]
- Raut, R.D. Environmental performance: A hybrid method for supplier selection using AHP-DEA. Int. J. Bus. Insights Transform. 2011, 5, 16–29. [Google Scholar]
- Yang, T.; Kuo, C. A hierarchical AHP/DEA methodology for the facilities layout design problem. Eur. J. Oper. Res. 2003, 147, 128–136. [Google Scholar] [CrossRef]
- Ho, C.B.; Oh, K.B. Selecting internet company stocks using a combined DEA and AHP approach. Int. J. Syst. Sci. 2010, 41, 325–336. [Google Scholar] [CrossRef]
- Jablonsky, J. Measuring the efficiency of production units by AHP models. Math. Comput. Model. 2007, 46, 1091–1098. [Google Scholar] [CrossRef]
- Sinuany-Stern, Z.; Mehrez, A.; Hadada, Y. An AHP/DEA methodology for ranking decision making units. Int. Trans. Oper. Res. 2000, 7, 109–124. [Google Scholar] [CrossRef]
- Chen, T.Y. Measuring firm performance with DEA and prior information in Taiwan’s banks. Appl. Econ. Lett. 2002, 9, 201–204. [Google Scholar] [CrossRef]
- Cai, Y.; Wu, W. Synthetic financial evaluation by a method of combining DEA with AHP. Int. Trans. Oper. Res. 2001, 8, 603–609. [Google Scholar] [CrossRef]
- Feng, Y.; Lu, H.; Bi, K. An AHP/DEA method for measurement of the efficiency of R & D management activities in universities. Int. Trans. Oper. Res. 2004, 11, 181–191. [Google Scholar]
- Kim, T. Extended Topics in the Integration of Data Envelopment Analysis and the Analytic Hierarchy Process in Decision Making. Ph.D. Thesis, Louisiana State University, Baton Rouge, LA, USA, 2000. [Google Scholar]
- Pakkar, M.S. Using the AHP and DEA methodologies for stock selection. In Business Performance Measurement and Management; Charles, V., Kumar, M., Eds.; Cambridge Scholars Publishing: Newcastle upon Tyne, UK, 2014; pp. 566–580. [Google Scholar]
- Liu, C.; Chen, C. Incorporating value judgments into data envelopment analysis to improve decision quality for organization. J. Am. Acad. Bus. 2004, 5, 423–427. [Google Scholar]
- Saen, R.F.; Memariani, A.; Lotfi, F.H. Determining relative efficiency of slightly non-homogeneous decision making units by data envelopment analysis: A case study in IROST. Appl. Math. Comput. 2005, 165, 313–328. [Google Scholar] [CrossRef]
- Pakkar, M.S. An integrated approach based on DEA and AHP. Comput. Manag. Sci. 2015, 12, 153–169. [Google Scholar] [CrossRef]
- Pakkar, M.S. Using data envelopment analysis and analytic hierarchy process for multiplicative aggregation of financial ratios. J. Appl. Oper. Res. 2015, 7, 23–35. [Google Scholar]
- Pakkar, M.S. Measuring the efficiency and effectiveness of decision making units by integrating the DEA and AHP methodologies. In Business Performance Measurement and Management; Charles, V., Kumar, M., Eds.; Cambridge Scholars Publishing: Newcastle upon Tyne, UK, 2014; pp. 552–565. [Google Scholar]
- Pakkar, M.S. Using DEA and AHP for ratio analysis. Am. J. Oper. Res. 2014, 4, 268–279. [Google Scholar] [CrossRef] [Green Version]
- Pakkar, M.S. Using data envelopment analysis and analytic hierarchy process to construct composite indicators. J. Appl. Oper. Res. 2014, 6, 174–187. [Google Scholar]
- Pakkar, M.S. An integrated approach to the DEA and AHP methodologies in decision making. In Data Envelopment Analysis and Its Applications to Management; Charles, V., Kumar, M., Eds.; Cambridge Scholars Publishing: Newcastle upon Tyne, UK, 2012; pp. 136–149. [Google Scholar]
- Pakkar, M.S. Using DEA and AHP for multiplicative aggregation of indicators. Am. J. Oper. Res. 2015, 5, 327–336. [Google Scholar] [CrossRef]
- Shen, Y.; Hermans, E.; Brijs, T.; Wets, G. Data envelopment analysis for composite indicators: A multiple layer model. Soc. Indic. Res. 2013, 114, 739–756. [Google Scholar] [CrossRef]
- Shen, Y.; Hermans, E.; Ruan, D.; Wets, G.; Brijs, T.; Vanhoof, K. A generalized multiple layer data envelopment analysis model for hierarchical structure assessment: A case study in road safety performance evaluation. Expert Syst. Appl. 2011, 38, 15262–15272. [Google Scholar] [CrossRef]
- Liu, W.B.; Zhang, D.Q.; Meng, W.; Li, X.X.; Xu, F. A study of DEA models without explicit inputs. Omega 2011, 39, 472–480. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the Efficiency of Decision Making Units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Hashimoto, A.; Wu, D.A. A DEA-compromise programming model for comprehensive ranking. J. Oper. Res. Soc. Jpn. 2004, 47, 73–81. [Google Scholar]
- Mavi, R.K.; Mavi, N.K.; Mavi, L.K. Compromise programming for common weight analysis in data envelopment analysis. Am. J. Sci. Res. 2012, 45, 90–109. [Google Scholar]
- Podinovski, V.V. Suitability and redundancy of non-homogeneous weight restrictions for measuring the relative efficiency in DEA. Eur. J. Oper. Res. 2004, 154, 380–395. [Google Scholar] [CrossRef]
- Romero, C.; Rehman, T. Multiple Criteria Analysis for Agricultural Decisions, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).