Multi-Objective Combinatorial Optimization for Dynamic Inspection Scheduling and Skill-Based Team Formation in Distributed Solar Energy Infrastructure
Abstract
1. Introduction
2. Literature Review
2.1. Photovoltaic System Degradation and Fault Detection
2.2. Maintenance Strategies in Renewable Energy Systems
2.3. Machine Learning and Artificial Intelligence in PV Systems
2.4. Optimization Techniques for Maintenance Scheduling
2.5. Vehicle Routing and Scheduling Problems
2.6. Team Formation and Workforce Optimization
2.7. Applications in Renewable Energy Maintenance
2.8. Research Gaps
3. Methodology
3.1. Problem Overview and Multi-Objective Coordination Framework for Distributed Solar Infrastructures Inspection Scheduling and Team Formation
3.2. Mathematical Modeling
3.2.1. Multi-Objective Job Scheduling: Problem Description and Mathematical Modeling
3.2.2. Bi-Objective Team Formation: Problem Description and Mathematical Modeling
3.3. Optimization Algorithms
3.3.1. Job Scheduling Algorithms
3.3.2. Proposed Team Formation Algorithm: HMOO-AOS
| Algorithm 1: Hybrid Multi-Objective Optimization with Adaptive Operator Selection (HMOO-AOS). |
 |
| Algorithm 2: Apply Operator function. |
 |
| Component | Time Complexity | Space Complexity |
|---|---|---|
| Population Initialization | ||
| Fitness Evaluation | ||
| Non-dominated Sorting | ||
| Crowding Distance | ||
| Operator Application | ||
| AOS Update | ||
| Overall |
3.4. Datasets Development and Experimental Setup
3.4.1. Datasets Design and Expert Knowledge Integration for Solar Plants Inspection
3.4.2. Datasets Design and Expert Knowledge Integration for Team Formation
3.5. Experimental Setup
4. Experimental Results
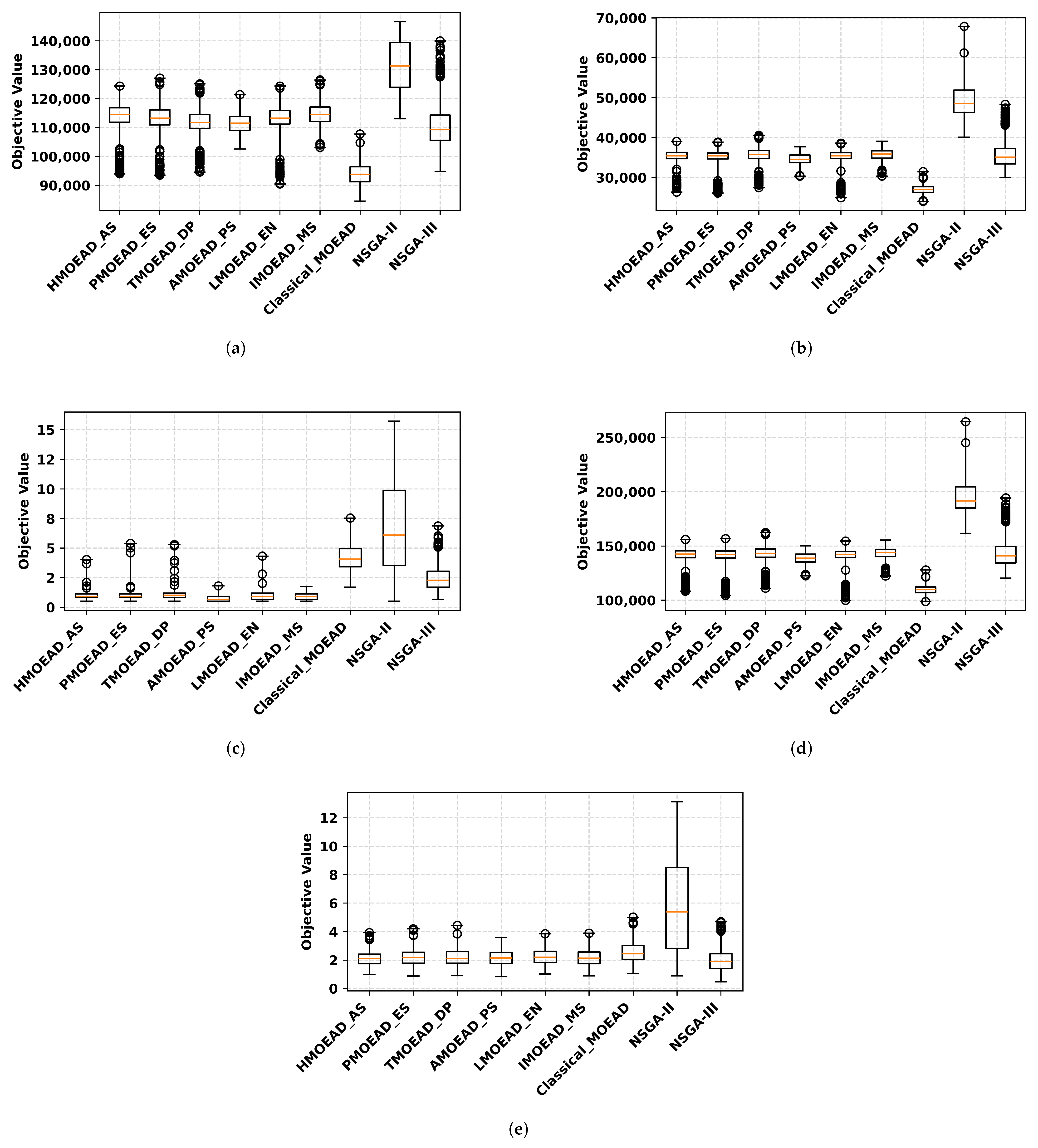
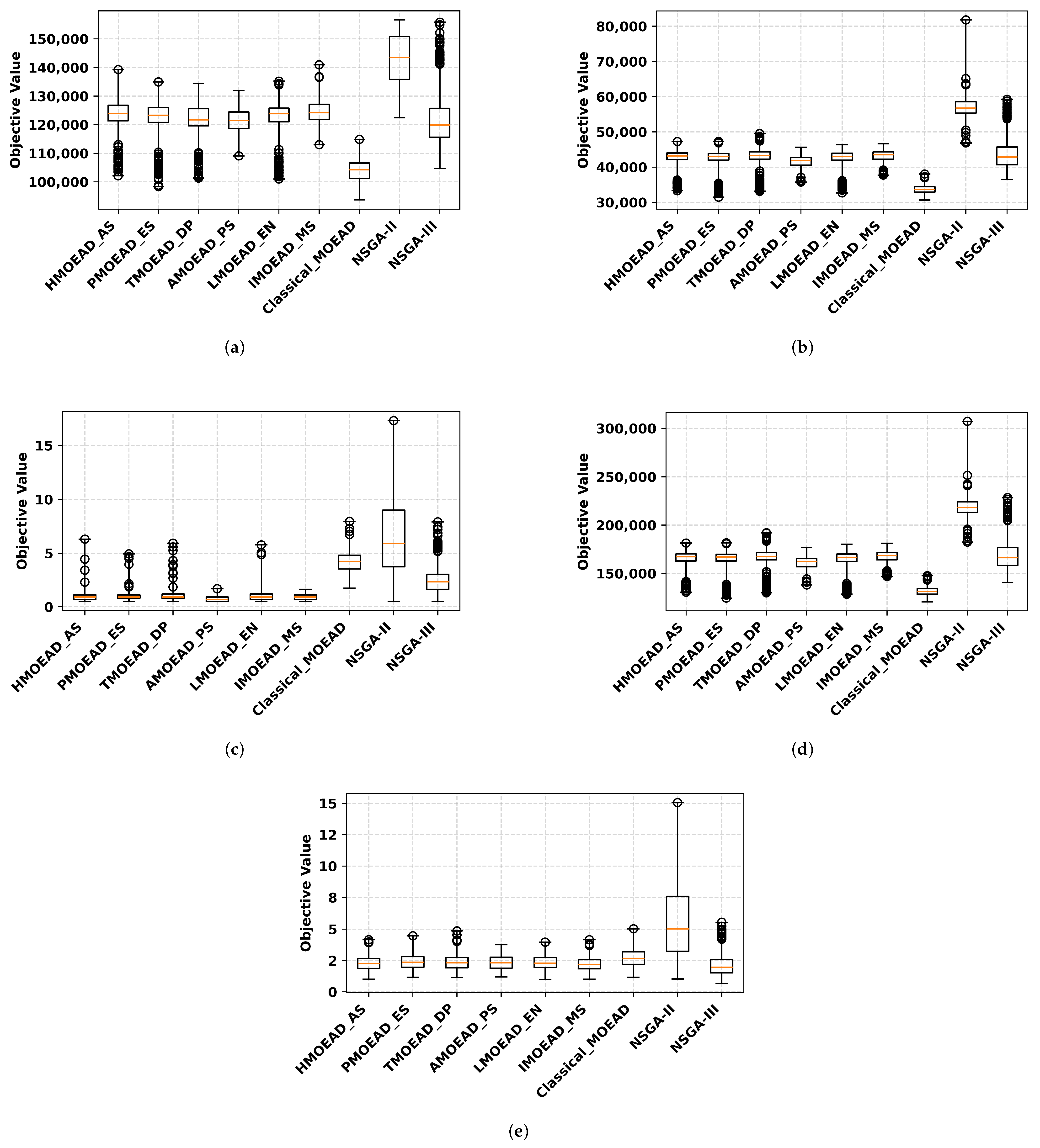
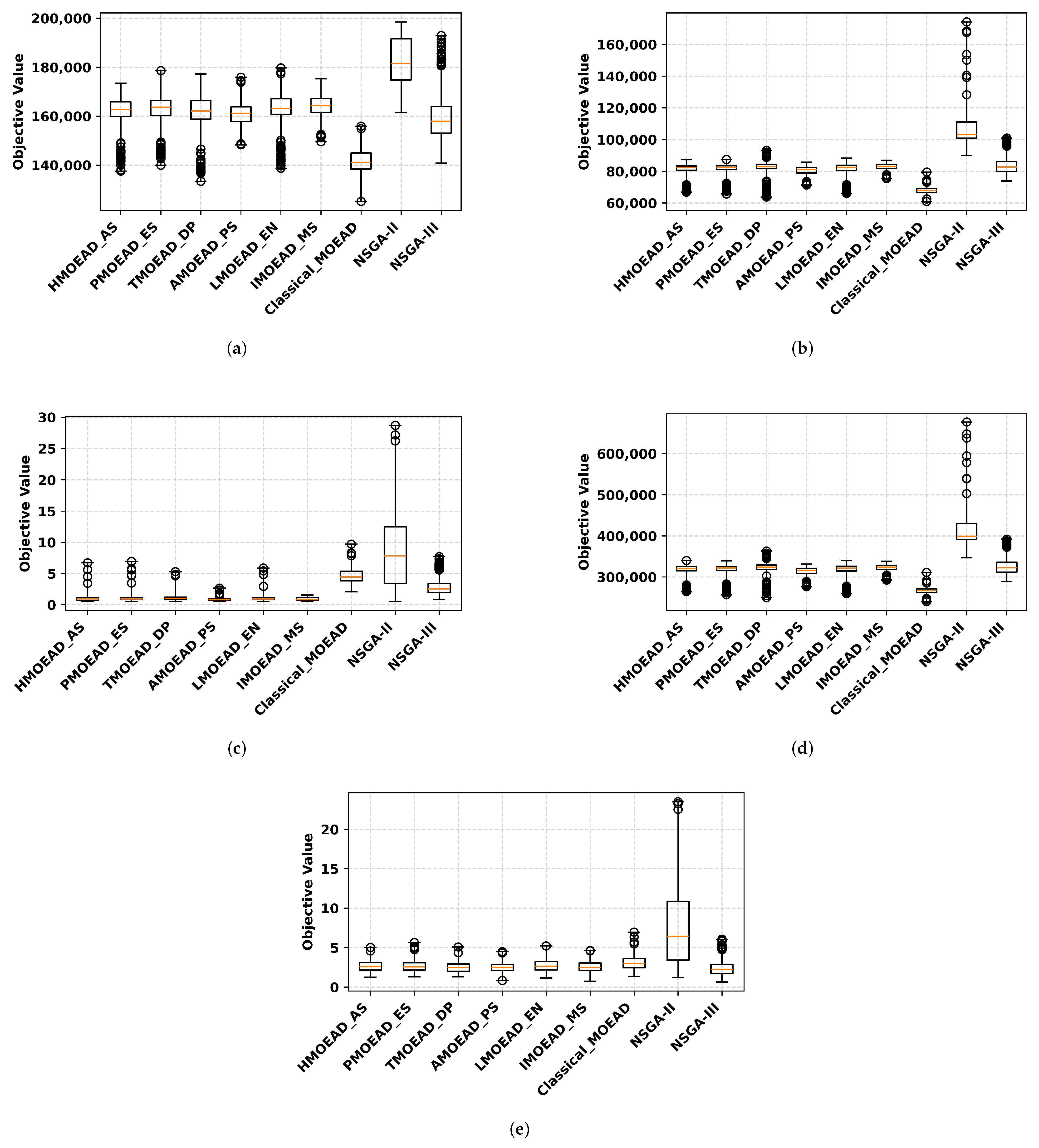
4.1. Performance Comparison of Job Scheduling Algorithms
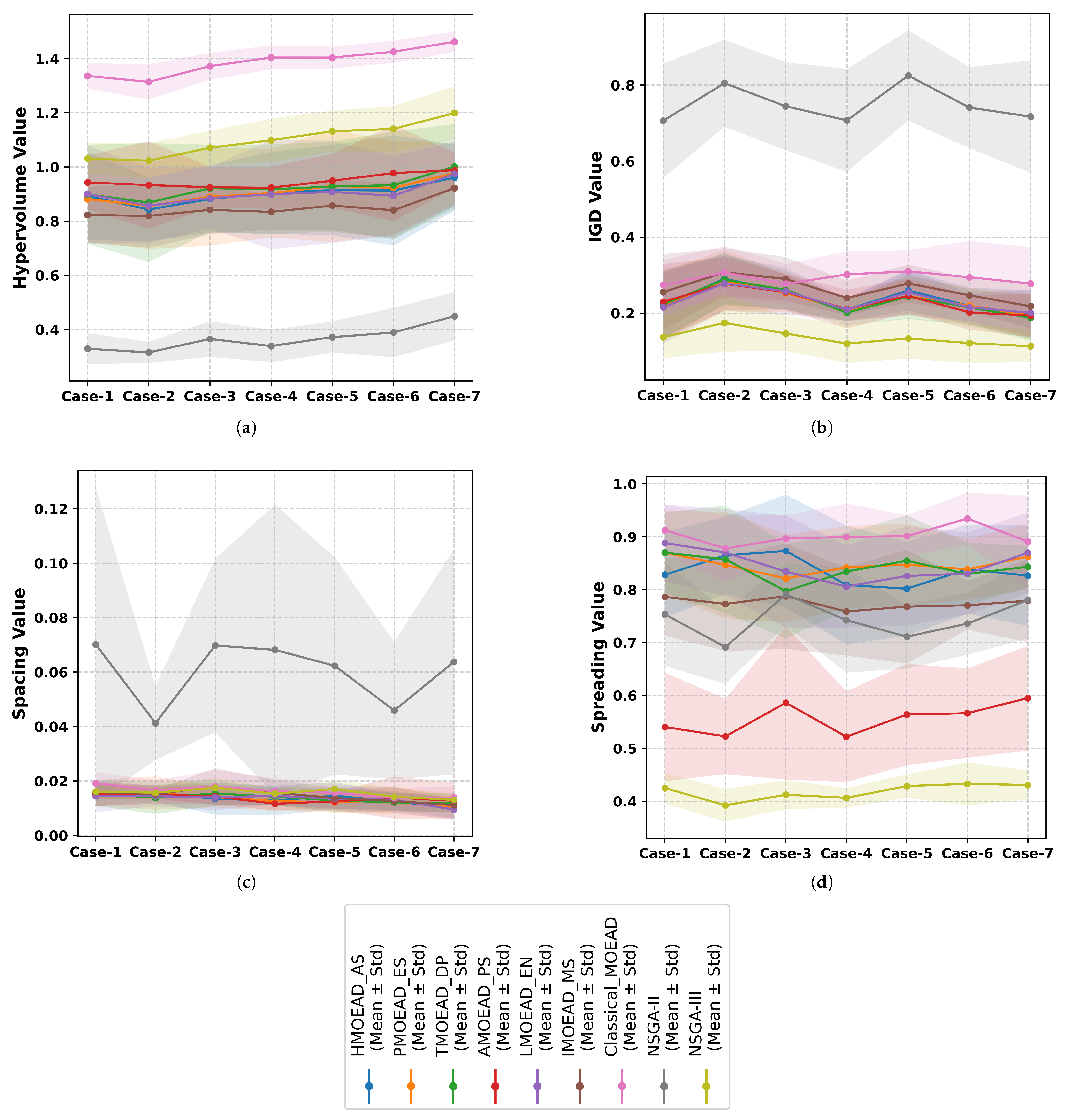
4.1.1. Comparative Analysis of Multi-Objective Performance Indicators
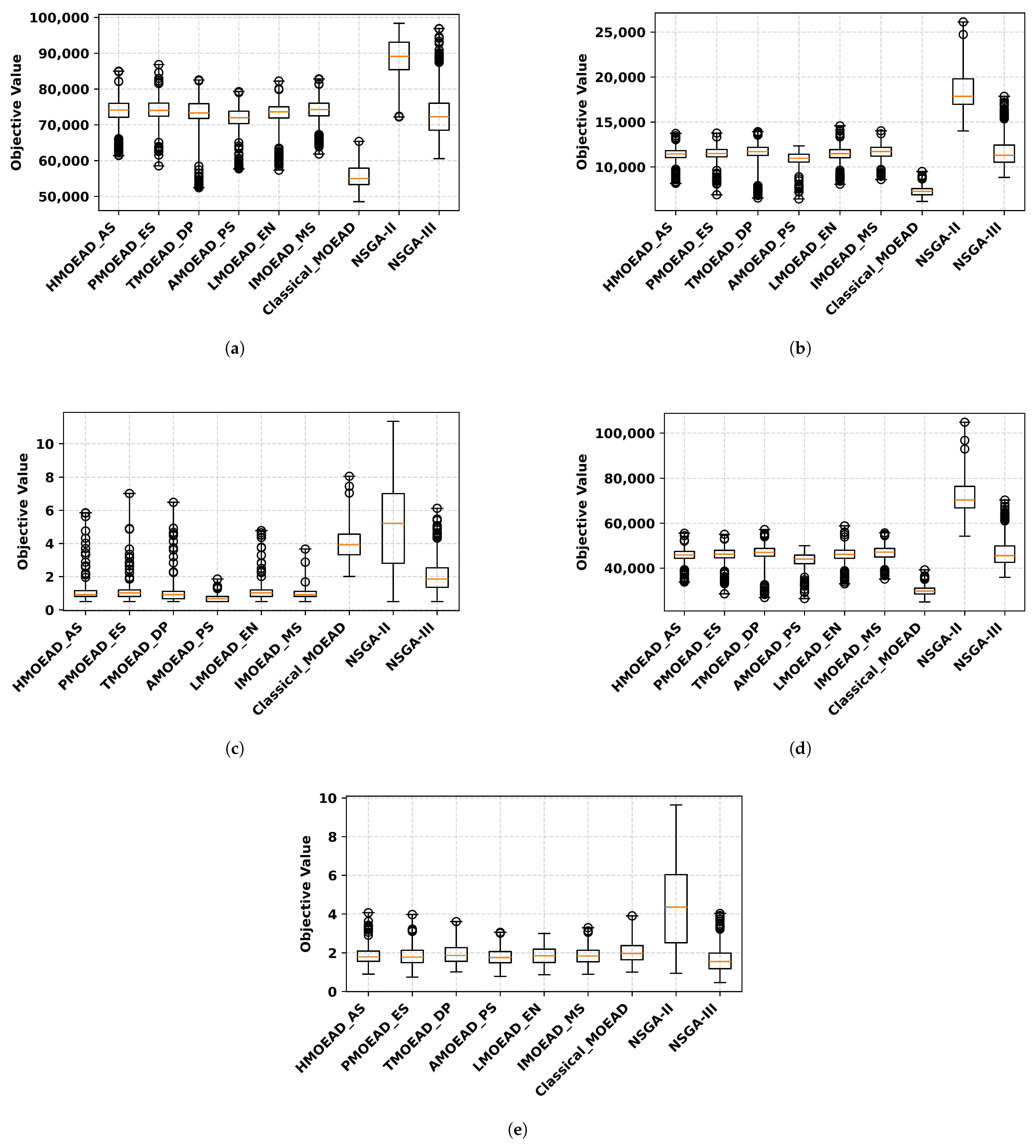
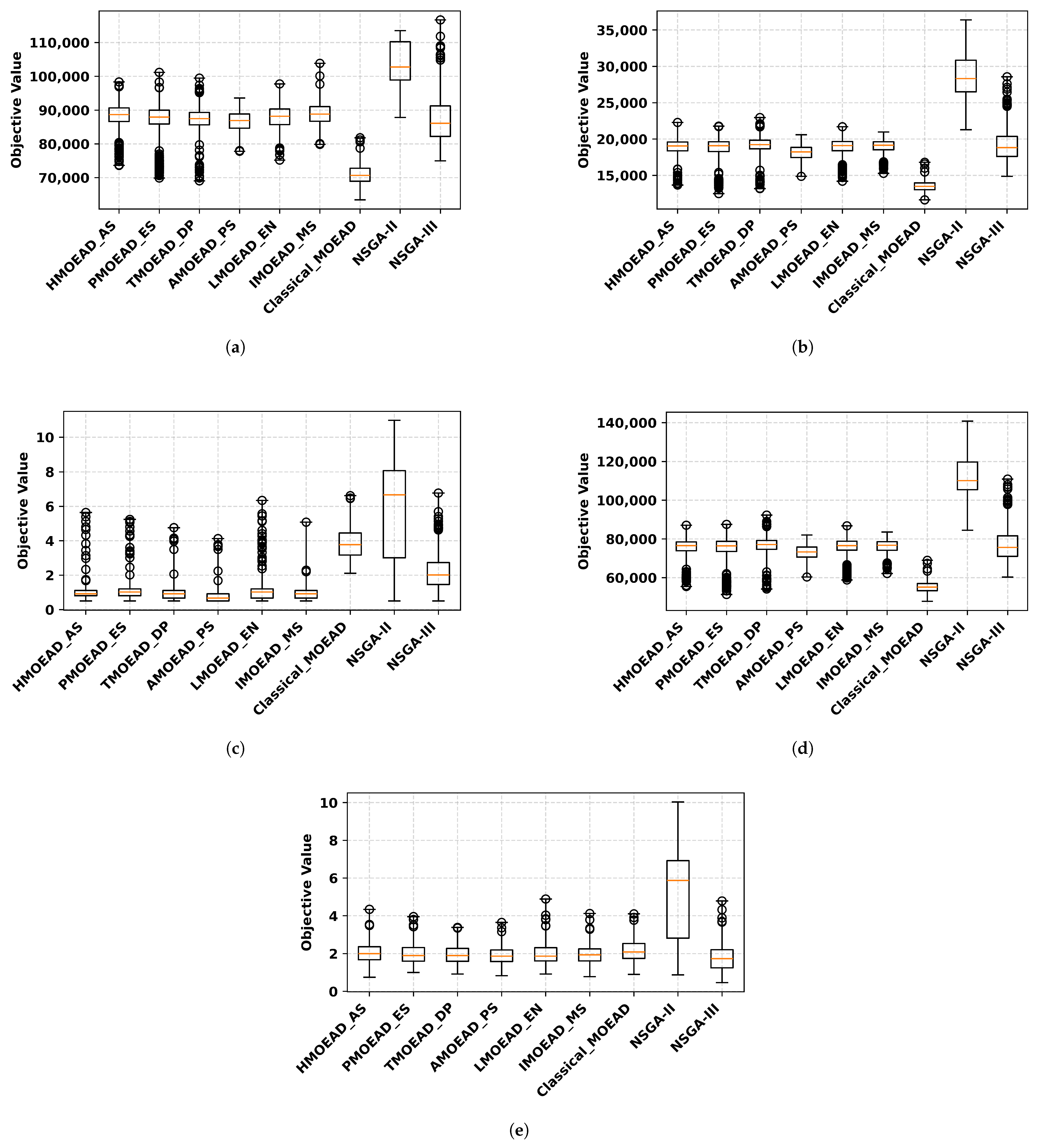
4.1.2. Algorithm’s Solutions Quality Comparison
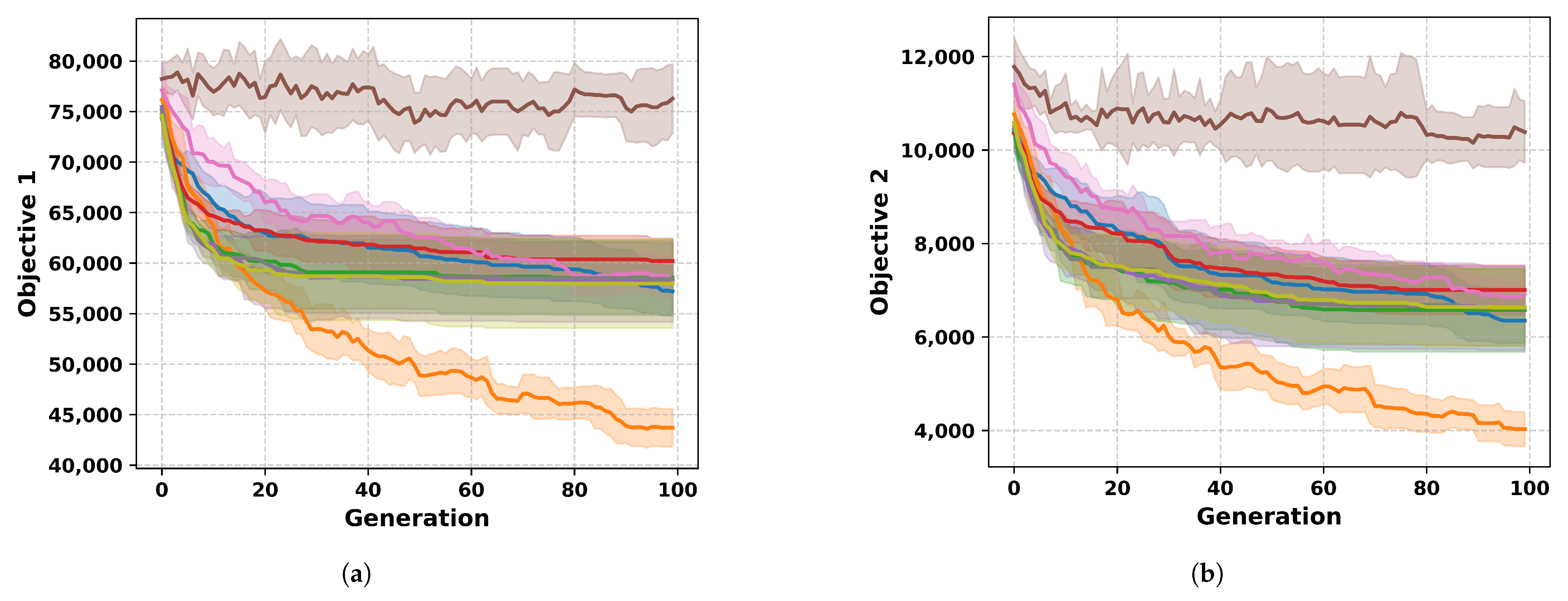
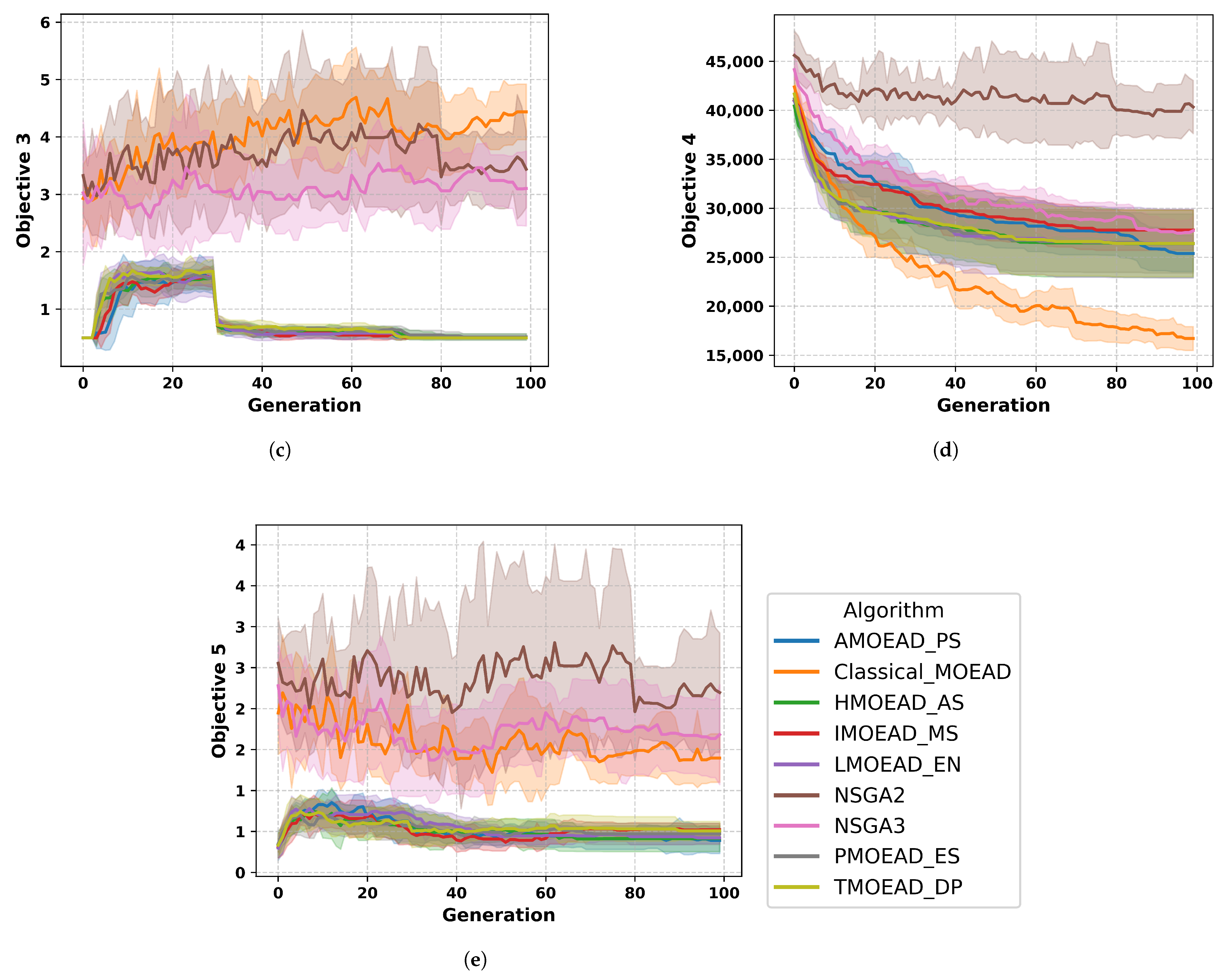
4.1.3. Convergence Characteristics of Multi-Objective JS Algorithms
4.1.4. Runtime Comparison Analysis
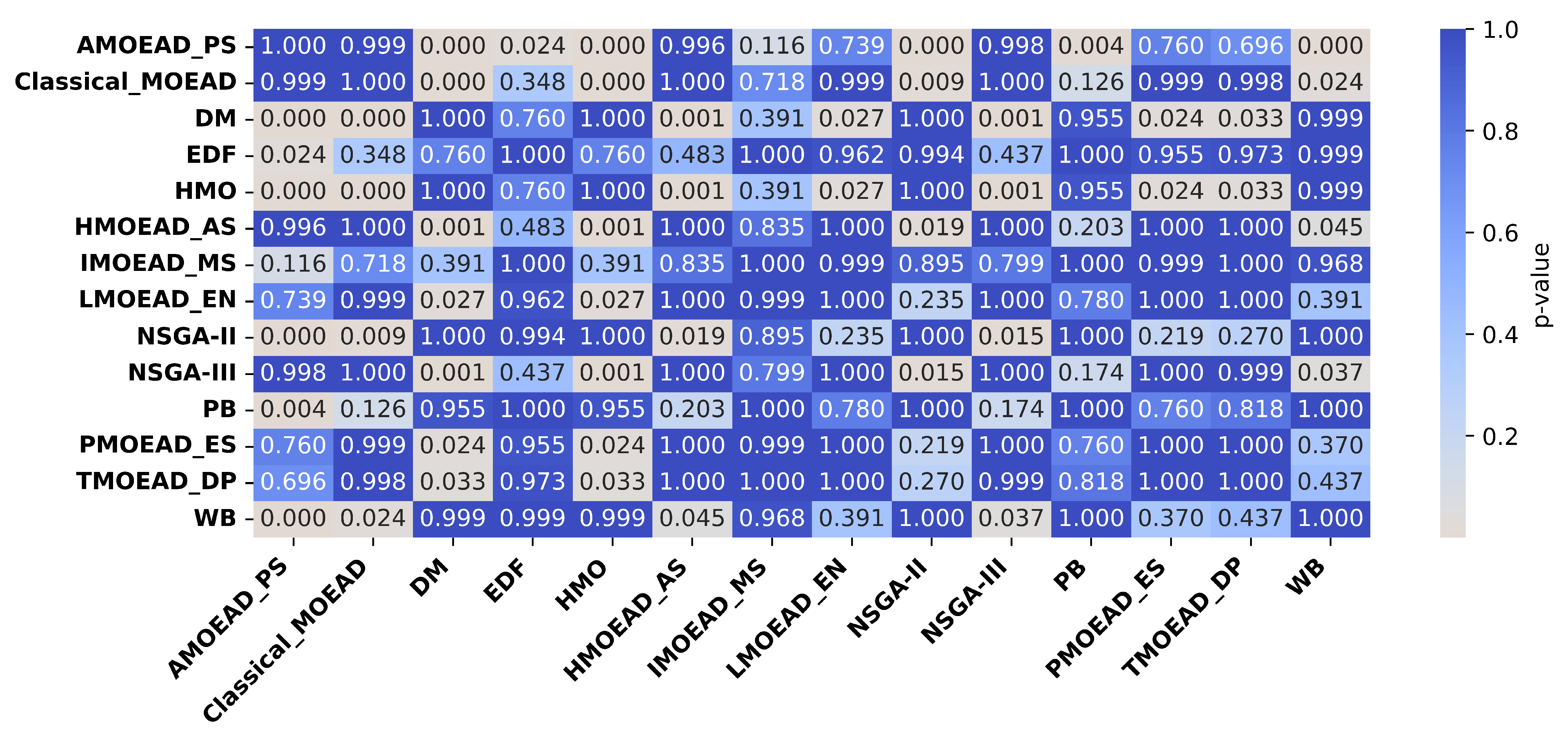
4.1.5. Performance Ranking and Statistical Significance
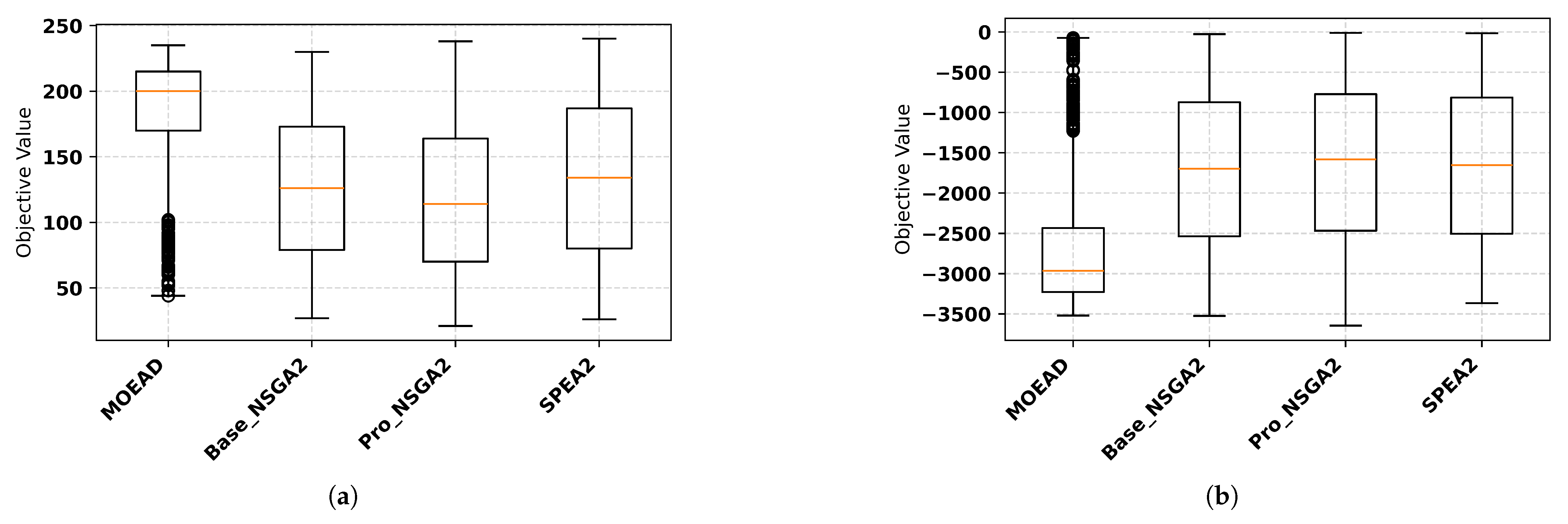
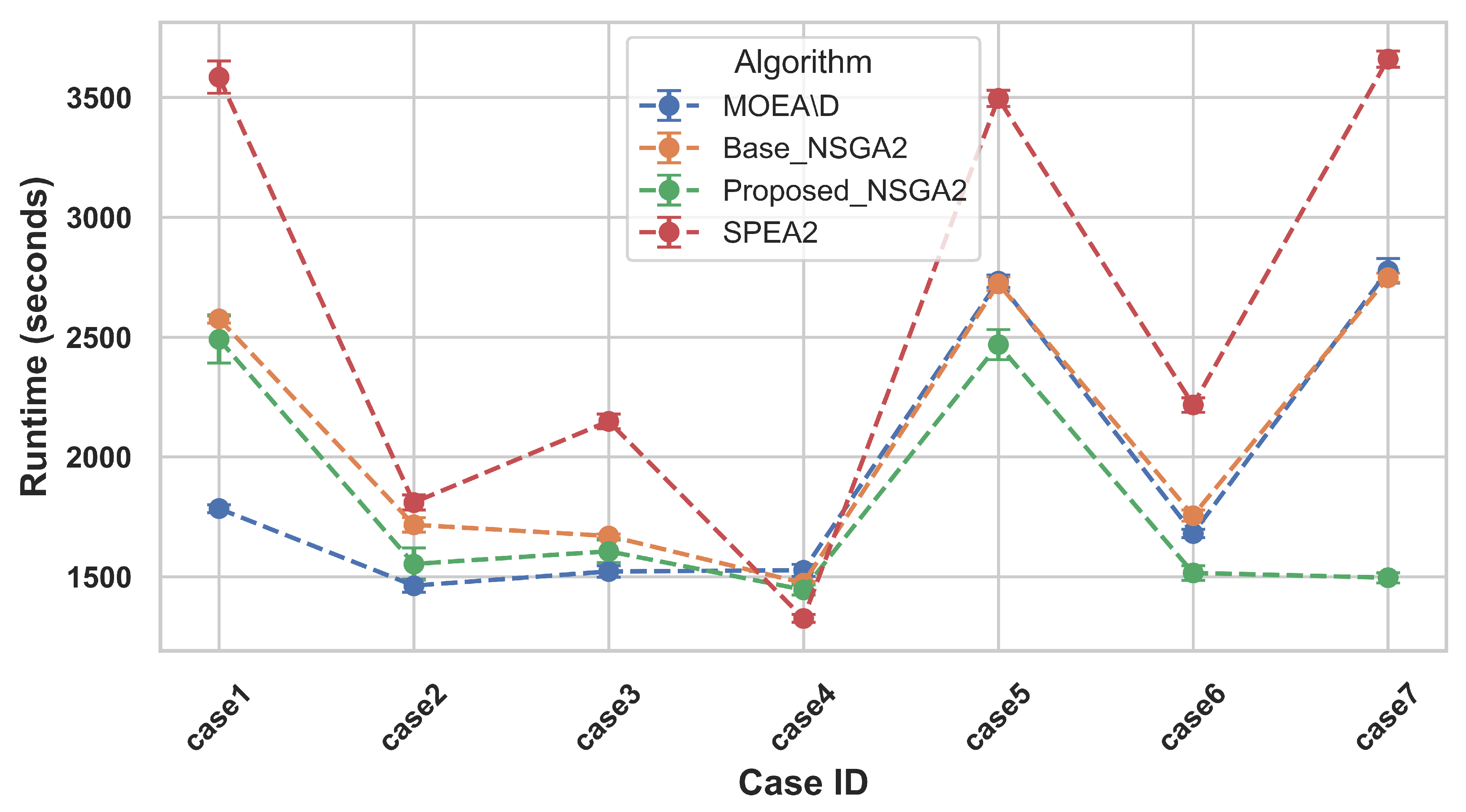
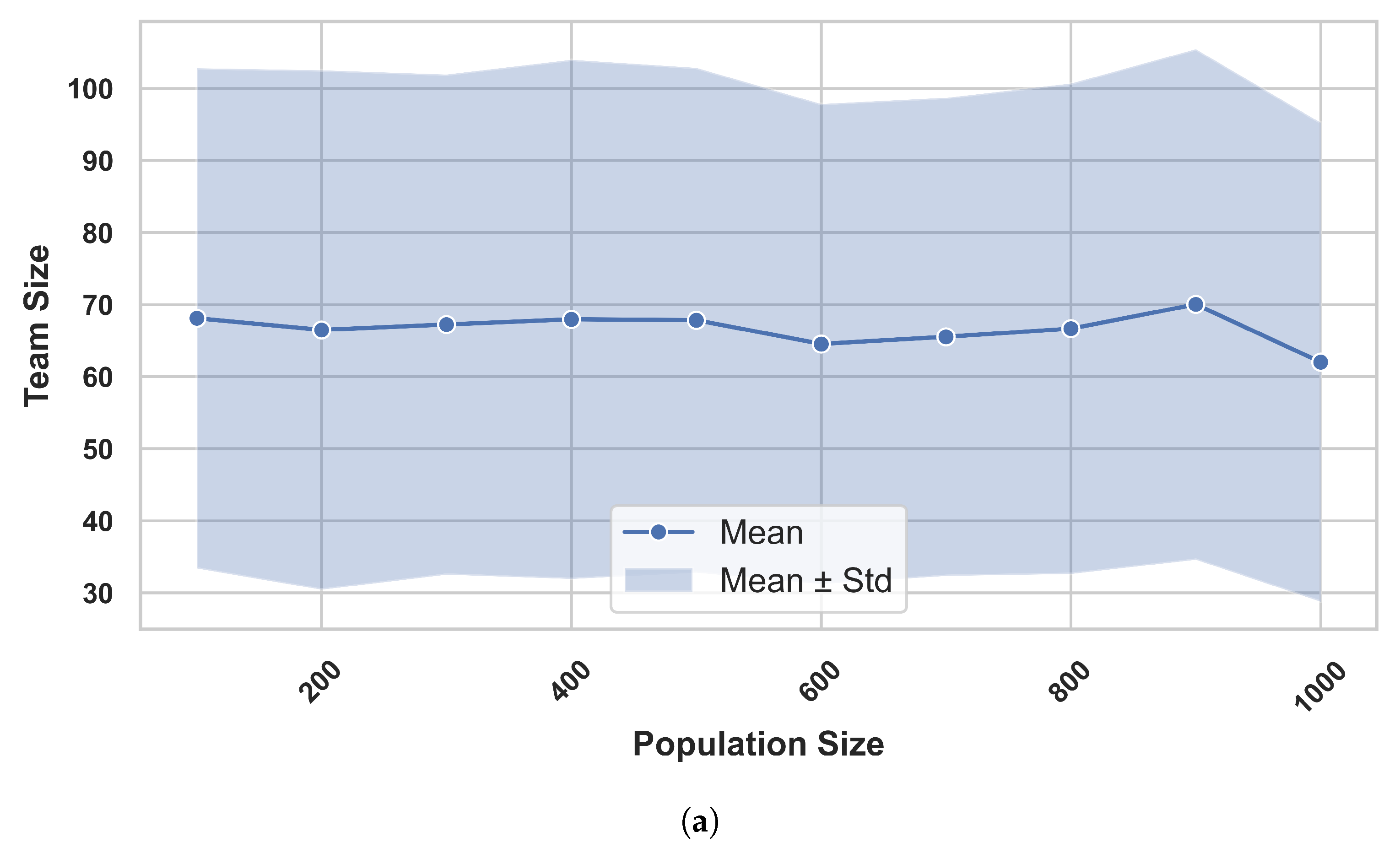
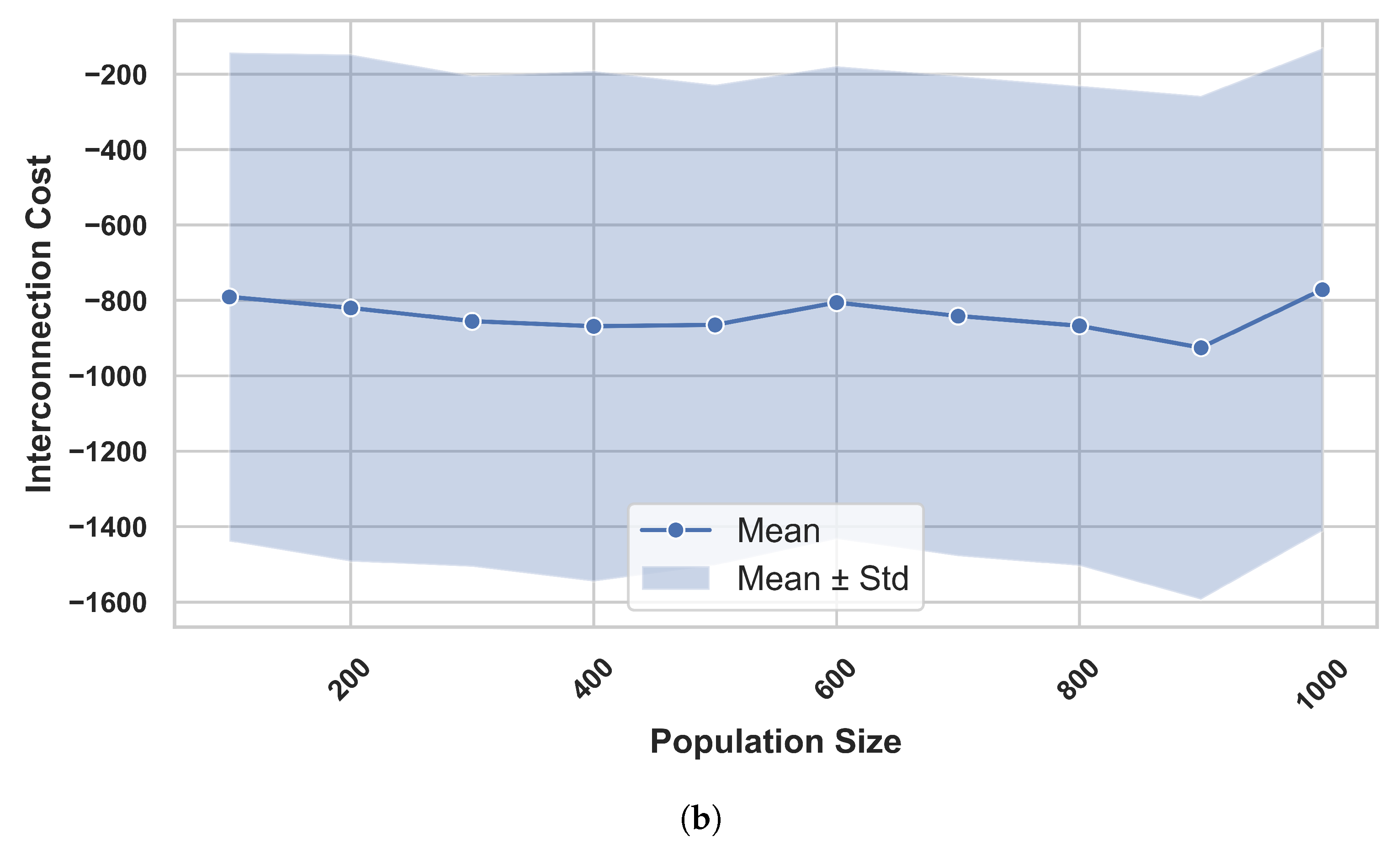
4.2. Team Formation Algorithm (TFA) Performances
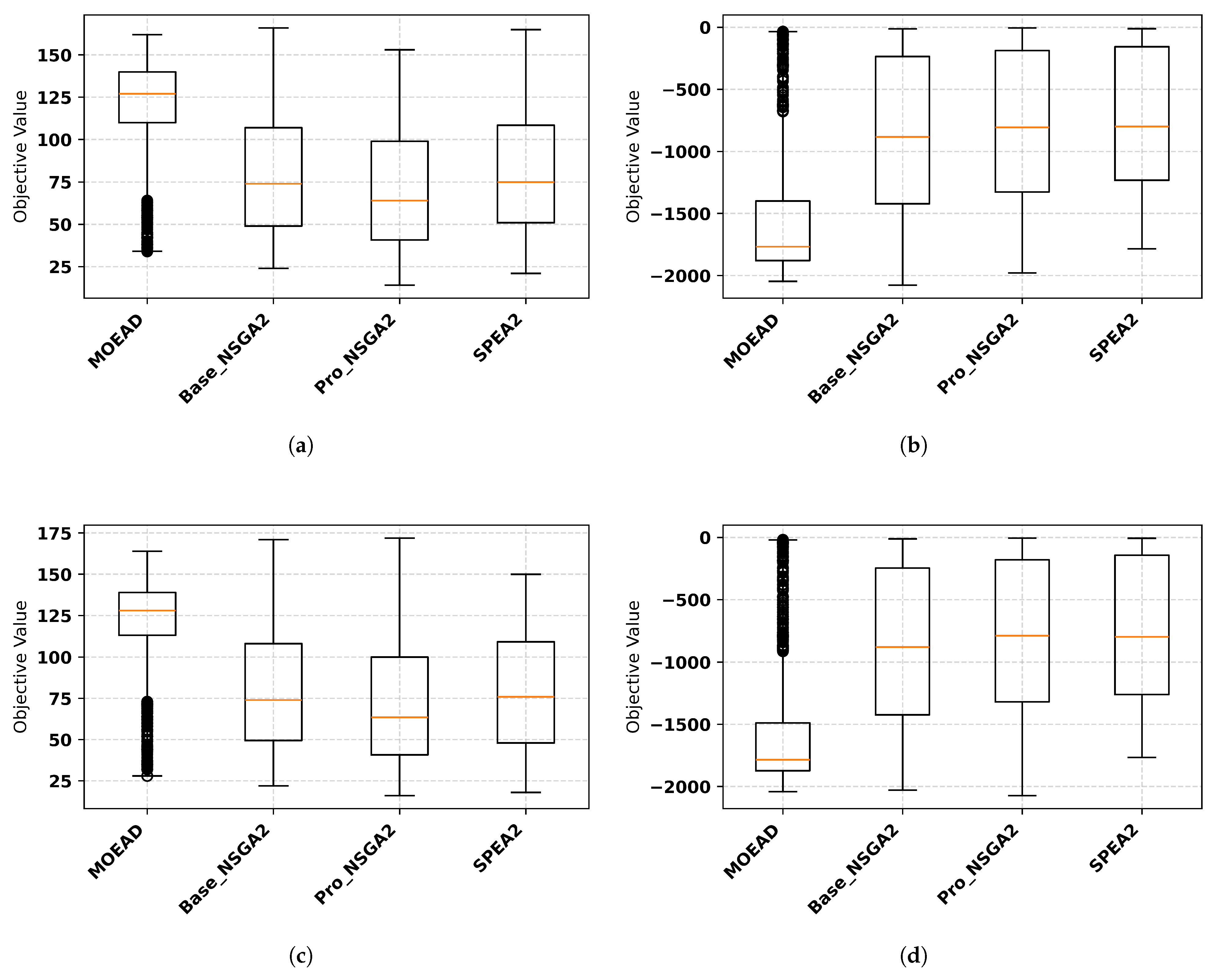
4.2.1. Comparative Analysis of Multi-Objective TFA Performance
4.2.2. Convergence Characteristics of Multi-Objective TF Algorithms
4.2.3. Runtime Comparison Analysis
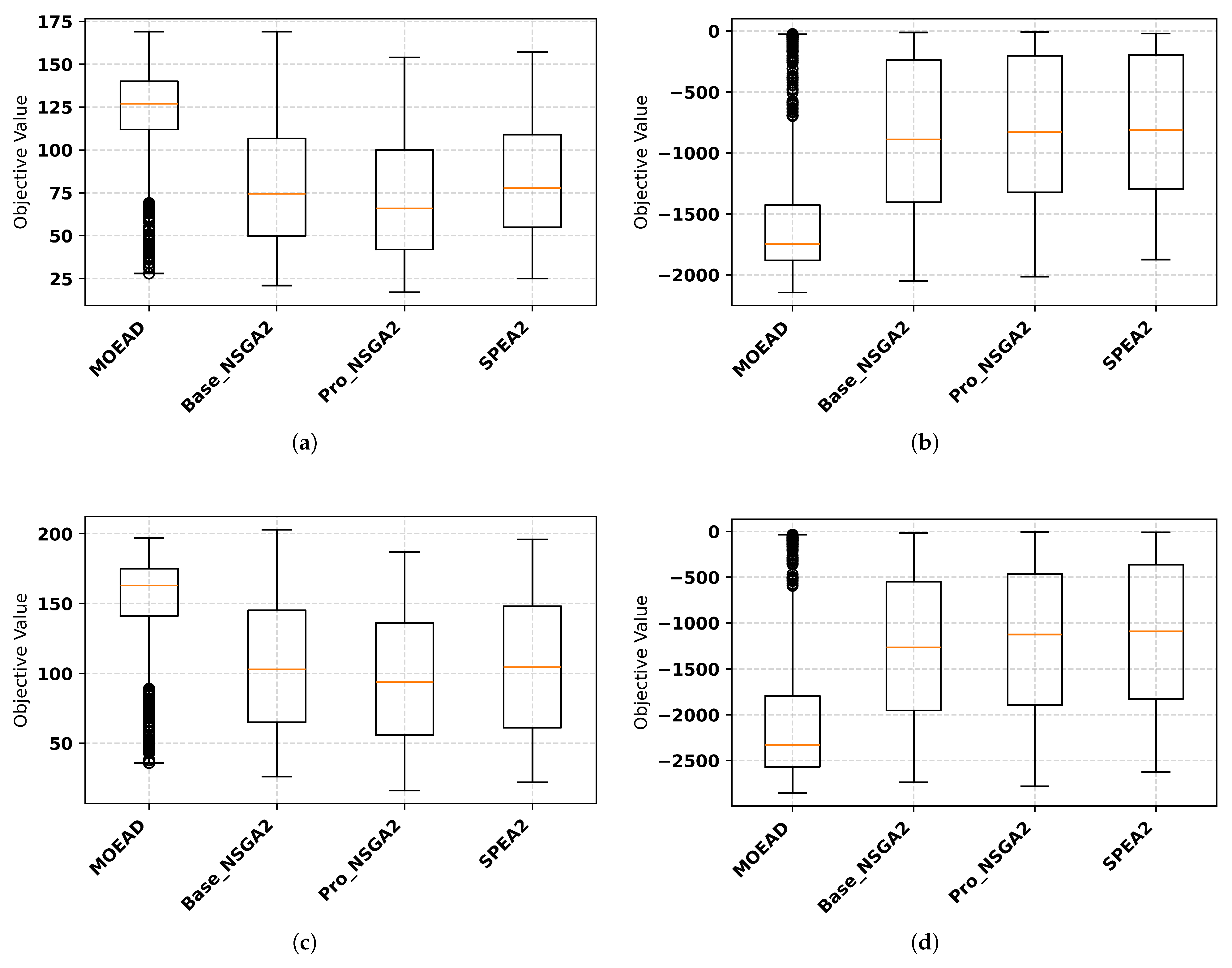
4.2.4. Impact of Population Size on Algorithm Performance
5. Conclusions and Future Work
Funding
Data Availability Statement
Conflicts of Interest
References
- Obaideen, K.; Olabi, A.G.; Al Swailmeen, Y.; Shehata, N.; Abdelkareem, M.A.; Alami, A.H.; Rodriguez, C.; Sayed, E.T. Solar Energy: Applications, Trends Analysis, Bibliometric Analysis and Research Contribution to Sustainable Development Goals (SDGs). Sustainability 2023, 15, 1418. [Google Scholar] [CrossRef]
- Orosz, T.; Rassõlkin, A.; Arsénio, P.; Poór, P.; Valme, D.; Sleisz, Á. Current Challenges in Operation, Performance, and Maintenance of Photovoltaic Panels. Energies 2024, 17, 1306. [Google Scholar] [CrossRef]
- Hacke, P.; Terwilliger, K.; Smith, R.; Glick, S.; Pankow, J.; Kempe, M.; Bennett, S.K.I.; Kloos, M. System voltage potential-induced degradation mechanisms in PV modules and methods for test. In Proceedings of the 2011 37th IEEE Photovoltaic Specialists Conference, Seattle, WA, USA, 19–24 June 2011; pp. 000814–000820. [Google Scholar] [CrossRef]
- Pingel, S.; Frank, O.; Winkler, M.; Daryan, S.; Geipel, T.; Hoehne, H.; Berghold, J. Potential Induced Degradation of solar cells and panels. In Proceedings of the 2010 35th IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010. [Google Scholar] [CrossRef]
- Sarver, T.; Al-Qaraghuli, A.; Kazmerski, L.L. A comprehensive review of the impact of dust on the use of solar energy: History, investigations, results, literature, and mitigation approaches. Renew. Sustain. Energy Rev. 2013, 22, 698–733. [Google Scholar] [CrossRef]
- Jordan, D.C.; Kurtz, S.R. Photovoltaic Degradation Rates—An Analytical Review. Prog. Photovolt. Res. Appl. 2011, 21, 12–29. [Google Scholar] [CrossRef]
- Waqar Akram, M.; Li, G.; Jin, Y.; Chen, X. Failures of Photovoltaic modules and their Detection: A Review. Appl. Energy 2022, 313, 118822. [Google Scholar] [CrossRef]
- Mellit, A.; Tina, G.; Kalogirou, S. Fault detection and diagnosis methods for photovoltaic systems: A review. Renew. Sustain. Energy Rev. 2018, 91, 1–17. [Google Scholar] [CrossRef]
- Bosman, L.B.; Leon-Salas, W.D.; Hutzel, W.; Soto, E.A. PV System Predictive Maintenance: Challenges, Current Approaches, and Opportunities. Energies 2020, 13, 1398. [Google Scholar] [CrossRef]
- Manno, D.; Cipriani, G.; Ciulla, G.; Di Dio, V.; Guarino, S.; Lo Brano, V. Deep learning strategies for automatic fault diagnosis in photovoltaic systems by thermographic images. Energy Convers. Manag. 2021, 241, 114315. [Google Scholar] [CrossRef]
- Michail, A.; Livera, A.; Tziolis, G.; Carús Candás, J.L.; Fernandez, A.; Antuña Yudego, E.; Fernández Martínez, D.; Antonopoulos, A.; Tripolitsiotis, A.; Partsinevelos, P.; et al. A comprehensive review of unmanned aerial vehicle-based approaches to support photovoltaic plant diagnosis. Heliyon 2024, 10, e23983. [Google Scholar] [CrossRef]
- Nascimento, A.; de Souza Ribeiro, L.A.; Oliveira, H.; de Matos, J.G.; Da Silva Santos, O. Development of communication to control photovoltaic system in a microgrid by using Programmable Automation Controller, Raspberry-Pi and open-source software. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 6284–6288. [Google Scholar] [CrossRef]
- Syamsuddin, A.; Adhi, A.C.; Kusumawardhani, A.; Prahasto, T.; Widodo, A. Predictive maintenance based on anomaly detection in photovoltaic system using SCADA data and machine learning. Results Eng. 2024, 24, 103589. [Google Scholar] [CrossRef]
- Amiri, A.F.; Kichou, S.; Oudira, H.; Chouder, A.; Silvestre, S. Fault Detection and Diagnosis of a Photovoltaic System Based on Deep Learning Using the Combination of a Convolutional Neural Network (CNN) and Bidirectional Gated Recurrent Unit (Bi-GRU). Sustainability 2024, 16, 1012. [Google Scholar] [CrossRef]
- Badran, G.; Dhimish, M. Potential Induced Degradation in Photovoltaic Modules: A Review of the Latest Research and Developments. Solar 2023, 3, 322–346. [Google Scholar] [CrossRef]
- Nam, W.; Choi, J.; Kim, G.; Hyun, J.; Ahn, H.; Park, N. Predicting Photovoltaic Module Lifespan Based on Combined Stress Tests and Latent Heat Analysis. Energies 2025, 18, 304. [Google Scholar] [CrossRef]
- Wohlgemuth, J.; Cunningham, D.; Monus, P.; Miller, J.; Nguyen, A. Long Term Reliability of Photovoltaic Modules. In Proceedings of the 2006 IEEE 4th World Conference on Photovoltaic Energy Conference, Waikoloa, HI, USA, 7–12 May 2006; pp. 2050–2053. [Google Scholar] [CrossRef]
- Kempe, M. Modeling of rates of moisture ingress into photovoltaic modules. Sol. Energy Mater. Sol. Cells 2006, 90, 2720–2738. [Google Scholar] [CrossRef]
- Liu, F.; Jiang, L.; Yang, S. Ultra-violet degradation behavior of polymeric backsheets for photovoltaic modules. Sol. Energy 2014, 108, 88–100. [Google Scholar] [CrossRef]
- Julien, S.E.; Kim, J.H.; Lyu, Y.; Miller, D.C.; Gu, X.; Wan, K.T. Cohesive and adhesive degradation in PET-based photovoltaic backsheets subjected to ultraviolet accelerated weathering. Sol. Energy 2021, 224, 637–649. [Google Scholar] [CrossRef]
- Ilse, K.; Micheli, L.; Figgis, B.W.; Lange, K.; Daßler, D.; Hanifi, H.; Wolfertstetter, F.; Naumann, V.; Hagendorf, C.; Gottschalg, R.; et al. Techno-Economic Assessment of Soiling Losses and Mitigation Strategies for Solar Power Generation. Joule 2019, 3, 2303–2321. [Google Scholar] [CrossRef]
- Baltacı, O.; Kıral, Z.; Dalkılınç, K.; Karaman, O. Thermal Image and Inverter Data Analysis for Fault Detection and Diagnosis of PV Systems. Appl. Sci. 2024, 14, 3671. [Google Scholar] [CrossRef]
- Saha, A.; Nipu, N.N.; Khan, M.F. Effect of Partial Shading on the Performance of Solar PV Module and Impact of Bypass Diode in Performance Enhancement. In Proceedings of the 2019 5th International Conference on Advances in Electrical Engineering (ICAEE), Dhaka, Bangladesh, 26–28 September 2019; pp. 891–896. [Google Scholar] [CrossRef]
- Dhanraj, J.A.; Mostafaeipour, A.; Velmurugan, K.; Techato, K.; Chaurasiya, P.K.; Solomon, J.M.; Gopalan, A.; Phoungthong, K. An Effective Evaluation on Fault Detection in Solar Panels. Energies 2021, 14, 7770. [Google Scholar] [CrossRef]
- Brinkhaus, M.; Jarosch, D.; Kapischke, J. All year power supply with off-grid photovoltaic system and clean seasonal power storage. Sol. Energy 2011, 85, 2488–2496. [Google Scholar] [CrossRef]
- Dolara, A.; Lazaroiu, G.C.; Leva, S.; Manzolini, G. Experimental investigation of partial shading scenarios on PV (photovoltaic) modules. Energy 2013, 55, 466–475. [Google Scholar] [CrossRef]
- Aghaei, M.; Fairbrother, A.; Gok, A.; Ahmad, S.; Kazim, S.; Lobato, K.; Oreski, G.; Reinders, A.; Schmitz, J.; Theelen, M.; et al. Review of degradation and failure phenomena in photovoltaic modules. Renew. Sustain. Energy Rev. 2022, 159, 112160. [Google Scholar] [CrossRef]
- Sohani, A. Time-dependent energy, economic, and environmental assessment of a PV-hydrogen integrated power system. Int. J. Hydrogen Energy 2025, 144, 964–976. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). PVPS Task 13: Analytical Monitoring of Photovoltaic Systems; IEA PVPS Task 13 Report; IEA: Paris, France, 2020. Available online: https://iea-pvps.org/research-tasks/performance-operation-and-reliability-of-photovoltaic-systems// (accessed on 1 March 2025).
- Ali, A.; Abdelhadi, A. Condition-Based Monitoring and Maintenance: State of the Art Review. Appl. Sci. 2022, 12, 688. [Google Scholar] [CrossRef]
- Kabashkin, I.; Perekrestov, V.; Pivovar, M. AI-Driven Fault Detection and Maintenance Optimization for Aviation Technical Support Systems. Processes 2025, 13, 666. [Google Scholar] [CrossRef]
- Khan, U.; Cheng, D.; Setti, F.; Fummi, F.; Cristani, M.; Capogrosso, L. A Comprehensive Survey on Deep Learning-based Predictive Maintenance. ACM Trans. Embed. Comput. Syst. 2025, 24, 1–36. [Google Scholar] [CrossRef]
- Hamza, A.; Ali, Z.; Dudley, S.; Saleem, K.; Uneeb, M.; Christofides, N. A multi-stage review framework for AI-driven predictive maintenance and fault diagnosis in photovoltaic systems. Appl. Energy 2025, 393, 126108. [Google Scholar] [CrossRef]
- Salazar-Peña, N.; Tabares, A.; González-Mancera, A. Performance assessment and dynamic fault detection in photovoltaic systems using artificial intelligence. Energy 2025, 330, 136759. [Google Scholar] [CrossRef]
- Triki-Lahiani, A.; Bennani-Ben Abdelghani, A.; Slama-Belkhodja, I. Fault detection and monitoring systems for photovoltaic installations: A review. Renew. Sustain. Energy Rev. 2018, 82, 2680–2692. [Google Scholar] [CrossRef]
- de Oliveira, A.K.V.; Aghaei, M.; Rüther, R. Automatic Inspection of Photovoltaic Power Plants Using Aerial Infrared Thermography: A Review. Energies 2022, 15, 2055. [Google Scholar] [CrossRef]
- Gerd Imenes, A.; Saad Noori, N.; Andreas Nesvag Uthaug, O.; Kroni, R.; Bianchi, F.; Belbachir, N. A Deep Learning Approach for Automated Fault Detection on Solar Modules Using Image Composites. In Proceedings of the 2021 IEEE 48th Photovoltaic Specialists Conference (PVSC), Fort Lauderdale, FL, USA, 20–25 June 2021; pp. 1925–1930. [Google Scholar] [CrossRef]
- Addabbo, P.; Angrisano, A.; Bernardi, M.L.; Gagliarde, G.; Mennella, A.; Nisi, M.; Ullo, S.L. UAV system for photovoltaic plant inspection. IEEE Aerosp. Electron. Syst. Mag. 2018, 33, 58–67. [Google Scholar] [CrossRef]
- Voutsinas, S.; Mandourarakis, I.; Koutroulis, E.; Karolidis, D.; Voyiatzis, I.; Samarakou, M. Control and communication for smart photovoltaic arrays. In Proceedings of the 26th Pan-Hellenic Conference on Informatics, PCI 2022, Athens, Greece, 25–27 November 2022; pp. 139–144. [Google Scholar] [CrossRef]
- Xu, H.; Ma, K.; Shen, B.; Yang, A.; Zhou, Y.; Li, J.; Han, C.; Mu, H. Research on an IoT-based Smart Monitoring System for Distribution Transformers in Solar PV Plants. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023; pp. 2377–2381. [Google Scholar] [CrossRef]
- Magalhães, R.; Costa, L.; Martin-Lopez, S.; Gonzalez-Herraez, M.; Braña, A.F.; Martins, H.F. Long-Range Distributed Solar Irradiance Sensing Using Optical Fibers. Sensors 2020, 20, 908. [Google Scholar] [CrossRef]
- Sun, T.; Shan, M.; Rong, X.; Yang, X. Estimating the spatial distribution of solar photovoltaic power generation potential on different types of rural rooftops using a deep learning network applied to satellite images. Appl. Energy 2022, 315, 119025. [Google Scholar] [CrossRef]
- Fazai, R.; Abodayeh, K.; Mansouri, M.; Trabelsi, M.; Nounou, H.; Nounou, M.; Georghiou, G. Machine learning-based statistical testing hypothesis for fault detection in photovoltaic systems. Sol. Energy 2019, 190, 405–413. [Google Scholar] [CrossRef]
- Harrou, F.; Dairi, A.; Taghezouit, B.; Sun, Y. An unsupervised monitoring procedure for detecting anomalies in photovoltaic systems using a one-class Support Vector Machine. Sol. Energy 2019, 179, 48–58. [Google Scholar] [CrossRef]
- Bounabi, M.; Azmi, R.; Chenal, J.; Diop, E.B.; Ebnou Abdem, S.A.; Adraoui, M.; Hlal, M.; Serbouti, I. Smart PV Monitoring and Maintenance: A Vision Transformer Approach within Urban 4.0. Technologies 2024, 12, 192. [Google Scholar] [CrossRef]
- Sarkar, B.; Paul, R.K. AI-Driven Manufacturing Processes. In AI for Advanced Manufacturing and Industrial Applications; Springer Nature Switzerland: Cham, Switzerland, 2025; pp. 19–59. [Google Scholar] [CrossRef]
- Shadi, M.R.; Mirshekali, H.; Shaker, H.R. Explainable artificial intelligence for energy systems maintenance: A review on concepts, current techniques, challenges, and prospects. Renew. Sustain. Energy Rev. 2025, 216, 115668. [Google Scholar] [CrossRef]
- IEC 61215-1; Terrestrial Photovoltaic (PV) Modules—Design Qualification and Type Approval—Part 1: Test Requirements. International Electrotechnical Commission: Geneva, Switzerland, 2021.
- IEC 61730-1; Photovoltaic (PV) Module Safety Qualification—Part 1: Requirements for Construction. IEC: Geneva, Switzerland, 2023.
- IEC 61730-2; Photovoltaic (PV) Module Safety Qualification—Part 2: Requirements for Testing. IEC: Geneva, Switzerland, 2023.
- Ma, H.; Ning, J.; Zheng, J.; Zhang, C. A Decomposition-Based Evolutionary Algorithm with Neighborhood Region Domination. Biomimetics 2025, 10, 19. [Google Scholar] [CrossRef]
- Guo, X. A Survey of Decomposition Based Evolutionary Algorithms for Many-Objective Optimization Problems. IEEE Access 2022, 10, 72825–72838. [Google Scholar] [CrossRef]
- Zhan, Z.; Hu, Y.; Xia, P.; Ding, J. Multi-Objective Optimization in Construction Project Management Based on NSGA-III: Pareto Front Development and Decision-Making. Buildings 2024, 14, 2112. [Google Scholar] [CrossRef]
- Cerda-Flores, S.C.; Rojas-Punzo, A.A.; Nápoles-Rivera, F. Applications of Multi-Objective Optimization to Industrial Processes: A Literature Review. Processes 2022, 10, 133. [Google Scholar] [CrossRef]
- Coello, C. Evolutionary multi-objective optimization: Current state and future challenges. In Proceedings of the Fifth International Conference on Hybrid Intelligent Systems (HIS’05), Rio de Janeiro, Brazil, 6–9 November 2005; p. 1. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Sutter, T.; Van Parys, B.P.G.; Kuhn, D. A Pareto Dominance Principle for Data-Driven Optimization. Oper. Res. 2024, 72, 1976–1999. [Google Scholar] [CrossRef]
- Praveen, V.; Keerthika, D.; Sivapriya, G.; Sarankumar, A.; Bhasker, B. Vehicle Routing Optimization Problem: A Study on Capacitated Vehicle Routing Problem. Mater. Today Proc. 2022, 64, 670–674. [Google Scholar] [CrossRef]
- Carchiolo, V.; Dio, F.D.; Longheu, A.; Mangioni, G.; Trapani, N.; Malgeri, M.; Romeo, A. Pick-up &; Deliver in Maintenance Management of Renewable Energy Power Plants. In Proceedings of the 2020 Federated Conference on Computer Science and Information Systems, Sofia, Bulgaria, 6–9 September 2020; Volume 21, pp. 579–585. [Google Scholar] [CrossRef]
- Pekel, E. Solving technician routing and scheduling problem using improved particle swarm optimization. Soft Comput. 2020, 24, 19007–19015. [Google Scholar] [CrossRef]
- Gao, X.; Peng, D.; Yang, Y.; Huang, F.; Yuan, Y.; Tan, C.; Li, F. Two-stage graph attention networks and Q-learning based maintenance tasks scheduling. Appl. Intell. 2025, 55, 331. [Google Scholar] [CrossRef]
- Takai, S.; Esterman, M. Towards a Better Design Team Formation: A Review of Team Effectiveness Models and Possible Measurements of Design-Team Inputs, Processes, and Outputs. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Cleveland, OH, USA, 6–9 August 2017. [Google Scholar] [CrossRef]
- Beauchamp, M.R.; McEwan, D.; Waldhauser, K.J. Team building: Conceptual, methodological, and applied considerations. Curr. Opin. Psychol. 2017, 16, 114–117. [Google Scholar] [CrossRef]
- Selvarajah, K.; Zadeh, P.M.; Kobti, Z.; Palanichamy, Y.; Kargar, M. A unified framework for effective team formation in social networks. Expert Syst. Appl. 2021, 177, 114886. [Google Scholar] [CrossRef]
- Yasmine, A.; Yassine, O.; Farouk, Y.; Hicham, C. Workload balancing for the nurse scheduling problem: A real-world case study from a French hospital. Socio-Econ. Plan. Sci. 2024, 95, 102046. [Google Scholar] [CrossRef]
- Szwarc, E.; Golińska-Dawson, P.; Bocewicz, G.; Banaszak, Z. Robust Scheduling of Multi-Skilled Workforce Allocation: Job Rotation Approach. Electronics 2024, 13, 392. [Google Scholar] [CrossRef]
- Bronicki, J.; Nowak, P. Standard and RL-Controled Tabu Search Algorithms Comparison in Capacitated Vehicle Routing Problem Solving. In Advances in Dependable Systems and Networks; Springer Nature Switzerland: Cham, Switzerland, 2025; pp. 32–40. [Google Scholar] [CrossRef]
- Eltoukhy, A.E.E.; Hashim, H.A.; Hussein, M.; Khan, W.A.; Zayed, T. Sustainable vehicle route planning under uncertainty for modular integrated construction: Multi-trip time-dependent VRP with time windows and data analytics. Ann. Oper. Res. 2025, 348, 863–898. [Google Scholar] [CrossRef]
- Lv, H.; Liu, R.; Li, J. A multitasking ant system for multi-depot pick-up and delivery location routing problem with time window. Complex Intell. Syst. 2025, 11, 159. [Google Scholar] [CrossRef]
- Vargas-Quintero, A.; Morillo-Torres, D.; Escobar, J.W. Two-stage linear stochastic programming formulations for the Stochastic Vehicle Routing Problem with Backhauls and Time Windows. Int. J. Syst. Sci. Oper. Logist. 2025, 12, 2451223. [Google Scholar] [CrossRef]
- Souleymane, B.; Oussama, D.; Fatima Ezzahra, A.; Fouad, R. A Time Window Assignment Strategy for Dynamic Vehicle Routing Problem. Transp. Res. Procedia 2025, 84, 169–176. [Google Scholar] [CrossRef]
- Yu, X.; He, C. An Improved Large Neighborhood Search Algorithm for the Comprehensive Container Drayage Problem with Diverse Transport Requests. Appl. Sci. 2025, 15, 5937. [Google Scholar] [CrossRef]
- Alagumathi, M.; Thangavelu, S. A Multi-objective Evolutionary Algorithm Based on Decomposition—Dynamic Resource Allocation with Mixture Model. In Advances in Data-Driven Computing and Intelligent Systems; Springer Nature Singapore: Singapore, 2024; pp. 457–469. [Google Scholar] [CrossRef]
- Pon Ragothama Priya, P.; Baskar, S.; Tamil Selvi, S.; Babulal, C.K. Optimal Allocation of Hybrid Renewable Distributed Generation with Battery Energy Storage System Using MOEA/D-DRA Algorithm. Int. Trans. Electr. Energy Syst. 2023, 2023, 1–18. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, J.; Luo, T.; Zhou, J. Mcaaco: A multi-objective strategy heuristic search algorithm for solving capacitated vehicle routing problems. Complex Intell. Syst. 2025, 11, 211. [Google Scholar] [CrossRef]
- Wang, L.; Song, C.; Sun, Y.; Lu, C.; Chen, Q. A Neural Multi-Objective Capacitated Vehicle Routing Optimization Algorithm Based on Preference Adjustment. Electronics 2023, 12, 4167. [Google Scholar] [CrossRef]
- Vombatkere, K.; Gionis, A.; Terzi, E. Forming coordinated teams that balance task coverage and expert workload. Data Min. Knowl. Discov. 2025, 39, 19. [Google Scholar] [CrossRef]
- Anagnostopoulos, A.; Becchetti, L.; Castillo, C.; Gionis, A.; Leonardi, S. Online team formation in social networks. In Proceedings of the WWW 2012: 21st World Wide Web Conference 2012, Lyon, France, 16–20 April 2012; pp. 839–848. [Google Scholar] [CrossRef]
- Chen, L.; Bai, Q. Optimization in Decision Making in Infrastructure Asset Management: A Review. Appl. Sci. 2019, 9, 1380. [Google Scholar] [CrossRef]
- Munir, Y.; Umer, Q.; Faheem, M.; Akram, S.; Jaffar, A. Developer Recommendation and Team Formation in Collaborative Crowdsourcing Platforms. IEEE Access 2025, 13, 63170–63185. [Google Scholar] [CrossRef]
- Blanco-Fernández, D.; Leitner, S.; Rausch, A. Interactions between dynamic team composition and coordination: An agent-based modeling approach. Rev. Manag. Sci. 2024, 19, 1–37. [Google Scholar] [CrossRef]
- Eftekhar, M.; Ronaghi, F.; Saberi, A. Team Formation Dynamics: A Study Using Online Learning Data. In Proceedings of the 2015 ACM on Conference on Online Social Networks, COSN’15, Palo Alto, CA, USA, 2–3 November 2015; pp. 257–267. [Google Scholar] [CrossRef]
- Lv, B.; Jiang, J.; Wu, L.; Zhao, H. Team formation in large organizations: A deep reinforcement learning approach. Decis. Support Syst. 2024, 187, 114343. [Google Scholar] [CrossRef]
- Merizalde, Y.; Hernández-Callejo, L.; Duque-Perez, O.; Alonso-Gómez, V. Maintenance Models Applied to Wind Turbines. A Comprehensive Overview. Energies 2019, 12, 225. [Google Scholar] [CrossRef]
- Wang, T.; Hu, G.; Cho, S.; Tan, S.W.; Chiang, K.L. A reliability-centered maintenance process for equipment in distribution grids based on extended virtual age model. Energy 2025, 328, 135998. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, M.; Wu, S. Multi-Objective Vehicle Routing Problem for Waste Classification and Collection with Sustainable Concerns: The Case of Shanghai City. Sustainability 2022, 14, 11498. [Google Scholar] [CrossRef]
- Agudelo Zapata, A.A.; Suarez, E.G.; Villegas Florez, J.A. Application of VRP Techniques to the Allocation of Resources in an Electric Power Distribution System. J. Comput. Sci. 2019, 35, 102–109. [Google Scholar] [CrossRef]
- Ssekajja, G. The inter-community domain of commons governance: A framework for analyzing collaborative management of shared environmental resources. J. Environ. Manag. 2025, 389, 126086. [Google Scholar] [CrossRef]
- Fan, S.; Wang, S.; Mbanyele, W.; Zhang, Y. Dual-Path Model of Team Communication and Shared Mental Models in Entrepreneurial Education: Enhancing Team Efficacy in Higher Education Using PLS-SEM. Systems 2025, 13, 536. [Google Scholar] [CrossRef]
- Han, J.; Watanabe, S. A New Hyper-Heuristic Multi-Objective Optimisation Approach Based on MOEA/D Framework. Biomimetics 2023, 8, 521. [Google Scholar] [CrossRef]
- Zheng, W.; Tan, Y.; Fang, X.; Li, S. An Improved MOEA/D with Optimal DE Schemes for Many-Objective Optimization Problems. Algorithms 2017, 10, 86. [Google Scholar] [CrossRef]
- Babor, M.; Pedersen, L.; Kidmose, U.; Paquet-Durand, O.; Hitzmann, B. Application of Non-Dominated Sorting Genetic Algorithm (NSGA-II) to Increase the Efficiency of Bakery Production: A Case Study. Processes 2022, 10, 1623. [Google Scholar] [CrossRef]
- Zou, Y.; Chen, Z.; Zhu, S.; Li, Y. NSGA-III-Based Production Scheduling Optimization Algorithm for Pressure Sensor Calibration Workshop. Electronics 2024, 13, 2844. [Google Scholar] [CrossRef]
- Sinha, A.; Malo, P.; Deb, K. A Review on Bilevel Optimization: From Classical to Evolutionary Approaches and Applications. IEEE Trans. Evol. Comput. 2018, 22, 276–295. [Google Scholar] [CrossRef]
- Colson, B.; Marcotte, P.; Savard, G. An overview of bilevel optimization. Ann. Oper. Res. 2007, 153, 235–256. [Google Scholar] [CrossRef]
- Camacho-Vallejo, J.F.; Corpus, C.; Villegas, J.G. Metaheuristics for bilevel optimization: A comprehensive review. Comput. Oper. Res. 2024, 161, 106410. [Google Scholar] [CrossRef]
- Deb, K.; Sinha, A. An Efficient and Accurate Solution Methodology for Bilevel Multi-Objective Programming Problems Using a Hybrid Evolutionary-Local-Search Algorithm. Evol. Comput. 2010, 18, 403–449. [Google Scholar] [CrossRef]
- Talbi, E.-G. Metaheuristics for Bi-Level Optimization; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Chen, T.Y.; Chen, W.N.; Hao, J.K.; Wang, Y.; Zhang, J. Multi-Agent Evolution Strategy with Cooperative and Cumulative Step Adaptation for Black-Box Distributed Optimization. IEEE Trans. Evol. Comput. 2025; Early Access. [Google Scholar] [CrossRef]
- Yin, S.; Xiang, Z. Adaptive operator selection with dueling deep Q-network for evolutionary multi-objective optimization. Neurocomputing 2024, 581, 127491. [Google Scholar] [CrossRef]
- Sun, J.; Yu, S.; Chu, J.; Liu, R. Maritime Rescue Task Allocation and Sequencing Using MOEA/D with Adaptive Operators and Idle-Time-Aware Decoding Strategy. J. Mar. Sci. Eng. 2025, 13, 1518. [Google Scholar] [CrossRef]
- Zheng, W.; Liu, Y.; Doerr, B. A First Mathematical Runtime Analysis of the Non-dominated Sorting Genetic Algorithm II (NSGA-II). Proc. AAAI Conf. Artif. Intell. 2022, 36, 10408–10416. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Sakane, Y.; Tsukamoto, N.; Nojima, Y. Evolutionary many-objective optimization by NSGA-II and MOEA/D with large populations. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 1758–1763. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, F.; Wu, A. Research on Multi-Objective Process Parameter Optimization Method in Hard Turning Based on an Improved NSGA-II Algorithm. Processes 2024, 12, 950. [Google Scholar] [CrossRef]
- Amador-Larrea, S.; Quiroz-Castellanos, M.; Ramos-Figueroa, O. An Experimental Study of Strategies to Control Diversity in Grouping Mutation Operators: An Improvement to the Adaptive Mutation Operator for the GGA-CGT for the Bin Packing Problem. Math. Comput. Appl. 2025, 30, 31. [Google Scholar] [CrossRef]
- Cao, T.S.; Nguyen, T.T.T.; Nguyen, V.S.; Truong, V.H.; Nguyen, H.H. Performance of Six Metaheuristic Algorithms for Multi-Objective Optimization of Nonlinear Inelastic Steel Trusses. Buildings 2023, 13, 868. [Google Scholar] [CrossRef]
- Pang, L.M.; Ishibuchi, H.; Shang, K. NSGA-II With Simple Modification Works Well on a Wide Variety of Many-Objective Problems. IEEE Access 2020, 8, 190240–190250. [Google Scholar] [CrossRef]
- Mei, Z.; Lu, Y.; Lv, L. Research on Multi-Objective Low-Carbon Flexible Job Shop Scheduling Based on Improved NSGA-II. Machines 2024, 12, 590. [Google Scholar] [CrossRef]
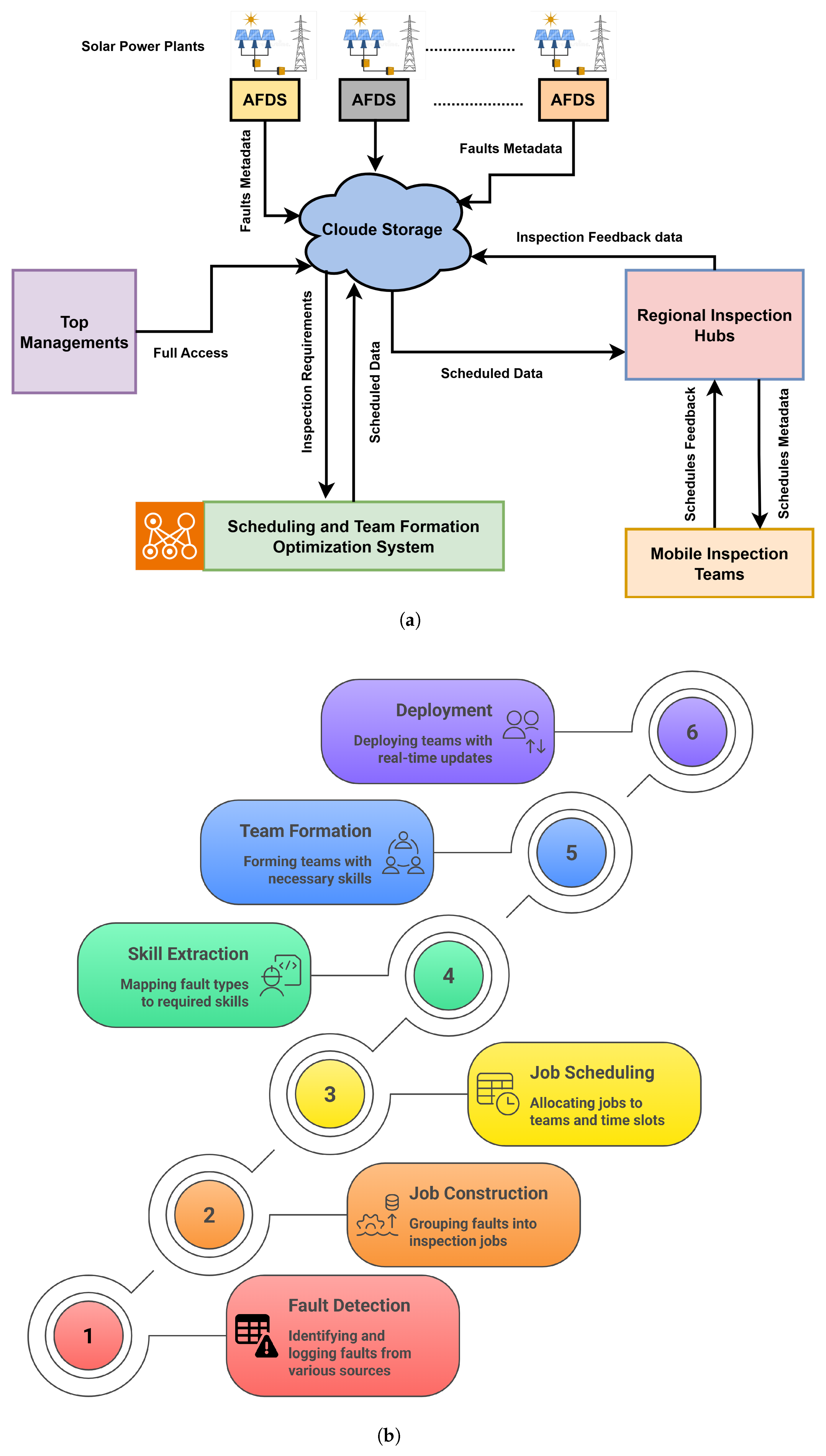





| Algorithm | Category | Optimization Strategy |
|---|---|---|
| Distance Minimization | Heuristic | Minimizes total travel distance |
| Workload Balancing | Heuristic | Distributes workload evenly among teams |
| Priority Based | Heuristic | Schedules tasks based on priority levels |
| Hybrid Multi-Objective | Heuristic | Combines multiple heuristic rules for trade-offs |
| Earliest Deadline First | Heuristic | Schedules tasks according to earliest deadlines |
| HMOEA/D-AS | Decomposition-based Hybrid MOEA | Adaptive scalarization + hybrid variation operators |
| PMOEA/D-ES | Decomposition-based MOEA | PBI scalarization + enhanced neighborhood search |
| TMOEA/D-DP | Decomposition-based MOEA | Tchebycheff scalarization with dynamic parameter control |
| AMOEA/D-PS | Adaptive MOEA | Self-tuning of parameters during search |
| LMOEA/D-EN | Scalable MOEA | Large population + extended neighborhood scope |
| IMOEA/D-MS | Hybrid MOEA | Multi-strategy operators (e.g., SBX, DE, mutation) |
| MOEA/D | Decomposition-based MOEA | Scalar subproblem decomposition |
| NSGA-II | Pareto-based MOEA | Fast non-dominated sorting + crowding distance |
| NSGA-III | Reference-point MOEA | Reference-point based diversity preservation |
| Case Number | Numbers of Jobs | Average Number of Faults Allocated for Each Team | Average Number of Skills Required for Each Team |
|---|---|---|---|
| Case 1 | 155 | 12.7 | 501.3 |
| Case 2 | 175 | 14.3 | 438.6 |
| Case 3 | 205 | 17.3 | 499.4 |
| Case 4 | 255 | 20.8 | 502.6 |
| Case 5 | 275 | 22.4 | 505.6 |
| Case 6 | 305 | 24.0 | 563.4 |
| Case 7 | 355 | 28.3 | 624.2 |
| Algorithm | Population Size | Max. Generation | Mutation Rate | Crossover Rate | Others | |
|---|---|---|---|---|---|---|
| Job Scheduling | Basic MOEAD | 200 | 100 | 0.1 | 0.9 | Neighbor Size = 20 Replacement Limit = 2 |
| MOEAD Variants | 200 | 100 | 0.1 | 0.9 | Neighbor Size = 20 Replacement Limit = 2 No. Division = 5 Theta = 0.5 Delta = 0.9 | |
| NSGA-II | 200 | 100 | 0.1 | 0.9 | Tournament Size = 2 Elite Size = 5 | |
| NSGA-III | 200 | 100 | 0.1 | – | Tournament Size = 2 No. Division = 5 | |
| Team Formation | MOEAD | 200 | 200 | 0.1 | 0.9 | – |
| HMOO-AOS (Proposed) | 200 | 200 | 0.1 | 0.9 | – | |
| NSGA-II (Base) | 200 | 200 | 0.1 | 0.9 | – | |
| SPEA-2 | 200 | 200 | 0.1 | 0.9 | – | |
| Algorithm | Objective | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | Case 7 |
|---|---|---|---|---|---|---|---|---|
| AMOEAD-PS | Total Distance Travel | 60,214.56 ± 3794.51 | 71,564.38 ± 3888.83 | 86,750.55 ± 3161.93 | 111,534.24 ± 3503.28 | 121,097.77 ± 4409.33 | 135,190.42 ± 7533.07 | 160,685.94 ± 4902.91 |
| Total Tardiness (Hours) | 7142.04 ± 828.22 | 10,805.37 ± 1003.67 | 18,174.38 ± 975.35 | 34,539.95 ± 1346.40 | 41,477.07 ± 1807.28 | 53,859.54 ± 3759.42 | 79,965.45 ± 3459.32 | |
| Job Load (std) | 0.83 ± 0.52 | 0.73 ± 0.23 | 0.84 ± 0.57 | 0.77 ± 0.25 | 0.79 ± 0.27 | 0.79 ± 0.24 | 0.82 ± 0.31 | |
| Priority Weighted Tardiness (Hours) | 28,569.02 ± 3148.43 | 43,441.84 ± 3939.21 | 73,197.56 ± 3830.47 | 138,672.21 ± 5202.42 | 160,668.60 ± 6943.44 | 208,567.92 ± 14,167.74 | 311,668.86 ± 13,214.71 | |
| Station Days (std) | 1.74 ± 0.46 | 1.80 ± 0.45 | 1.91 ± 0.48 | 2.17 ± 0.54 | 2.33 ± 0.59 | 2.35 ± 0.61 | 2.50 ± 0.59 | |
| Classical-MOEAD | Total Distance Travel | 47,429.89 ± 3105.76 | 55,587.39 ± 3239.78 | 70,907.73 ± 3025.10 | 93,758.68 ± 3903.39 | 104,060.76 ± 3877.92 | 118,460.16 ± 4499.31 | 141,494.27 ± 4548.28 |
| Total Tardiness (Hours) | 4627.84 ± 466.35 | 7297.01 ± 545.39 | 13,499.30 ± 736.39 | 26,966.35 ± 1017.49 | 33,655.39 ± 1166.56 | 44,887.10 ± 1468.58 | 67,852.85 ± 1987.73 | |
| Job Load (std) | 3.72 ± 0.90 | 4.02 ± 0.99 | 3.87 ± 0.92 | 4.23 ± 1.11 | 4.25 ± 1.03 | 4.48 ± 1.12 | 4.64 ± 1.18 | |
| Priority Weighted Tardiness (Hours) | 18,924.48 ± 1810.53 | 29,976.09 ± 2213.97 | 55,093.28 ± 2934.64 | 109,564.91 ± 4009.22 | 131,295.55 ± 4518.87 | 174,867.58 ± 5568.85 | 266,333.77 ± 7536.64 | |
| Station Days (std) | 1.83 ± 0.48 | 2.03 ± 0.51 | 2.18 ± 0.59 | 2.57 ± 0.76 | 2.71 ± 0.71 | 2.89 ± 0.78 | 3.06 ± 0.86 | |
| DM | Total Distance Travel | 85,636.44 ± 0 | 96,598.42 ± 0 | 111,864.17 ± 0 | 136,213.03 ± 0 | 145,582.12 ± 0 | 160,531.82 ± 0 | 184,364.74 ± 0 |
| Total Tardiness (Hours) | 244,130.40 ± 0 | 313,318.44 ± 0 | 433,433.11 ± 0 | 673,661.94 ± 0 | 783,481.31 ± 0 | 964,400.06 ± 0 | 1,308,375.14 ± 0 | |
| Job Load (std) | 46.50 ± 0 | 52.50 ± 0 | 61.50 ± 0 | 76.50 ± 0 | 82.50 ± 0 | 91.50 ± 0 | 106.50 ± 0 | |
| Priority Weighted Tardiness (Hours) | 864,597.26 ± 0 | 1,135,409.75 ± 0 | 1,596,836.88 ± 0 | 2,531,486.67 ± 0 | 2,873,370.76 ± 0 | 3,547,763.55 ± 0 | 4,875,754.69 ± 0 | |
| Station Days (std) | 42.00 ± 0 | 47.40 ± 0 | 55.20 ± 0 | 68.10 ± 0 | 72.90 ± 0 | 81.00 ± 0 | 93.90 ± 0 | |
| EDF | Total Distance Travel | 85,193.89 ± 0 | 96,288.34 ± 0 | 111,805.61 ± 0 | 142,186.04 ± 0 | 154,210.40 ± 0 | 169,690.14 ± 0 | 193,302.60 ± 0 |
| Total Tardiness (Hours) | 12,114.60 ± 0 | 17,079.91 ± 0 | 26,466.80 ± 0 | 46,339.56 ± 0 | 55,330.55 ± 0 | 70,624.48 ± 0 | 100,947.77 ± 0 | |
| Job Load (std) | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | |
| Priority Weighted Tardiness (Hours) | 47,862.36 ± 0 | 68,054.83 ± 0 | 105,419.27 ± 0 | 185,074.42 ± 0 | 214,126.89 ± 0 | 272,464.55 ± 0 | 392,417.27 ± 0 | |
| Station Days (std) | 1.11 ± 0 | 1.17 ± 0 | 1.40 ± 0 | 1.56 ± 0 | 1.56 ± 0 | 2.05 ± 0 | 2.59 ± 0 | |
| HMO | Total Distance Travel | 99,249.80 ± 0 | 110,547.62 ± 0 | 129,953.20 ± 0 | 164,646.29 ± 0 | 177,829.09 ± 0 | 196,533.21 ± 0 | 230,722.09 ± 0 |
| Total Tardiness (Hours) | 201,424.46 ± 0 | 267,038.78 ± 0 | 382,108.22 ± 0 | 620,640.89 ± 0 | 731,721.49 ± 0 | 915,200.65 ± 0 | 1,266,979.50 ± 0 | |
| Job Load (std) | 40.22 ± 0 | 46.21 ± 0 | 55.21 ± 0 | 70.20 ± 0 | 76.19 ± 0 | 85.19 ± 0 | 100.19 ± 0 | |
| Priority Weighted Tardiness (Hours) | 715,631.78 ± 0 | 972,338.15 ± 0 | 1,414,351.72 ± 0 | 2,342,499.19 ± 0 | 2,688,523.38 ± 0 | 3,372,558.80 ± 0 | 4,731,033.56 ± 0 | |
| Station Days (std) | 38.94 ± 0 | 44.33 ± 0 | 53.03 ± 0 | 67.72 ± 0 | 73.42 ± 0 | 81.52 ± 0 | 95.02 ± 0 | |
| HMOEAD-AS | Total Distance Travel | 62,069.14 ± 5157.77 | 73,751.45 ± 3907.37 | 88,126.94 ± 4245.25 | 113,185.19 ± 6398.13 | 123,078.10 ± 5984.80 | 137,519.02 ± 7309.69 | 161,416.52 ± 7192.54 |
| Total Tardiness (Hours) | 7273.28 ± 1209.19 | 11,322.12 ± 889.22 | 18,702 ± 1551.17 | 34,825.89 ± 2543.55 | 42,480.70 ± 2708.03 | 54,925.44 ± 3746.45 | 80,969.78 ± 4427.12 | |
| Job Load (std) | 1.20 ± 0.81 | 1.09 ± 0.74 | 1.06 ± 0.69 | 0.97 ± 0.38 | 0.99 ± 0.52 | 0.98 ± 0.45 | 0.98 ± 0.59 | |
| Priority Weighted Tardiness (Hours) | 29,079.65 ± 4709.26 | 45,508.63 ± 3427.34 | 75,182.57 ± 5953.68 | 139,840.03 ± 9945.50 | 164,721.96 ± 10,148.19 | 212,651.54 ± 14,407.95 | 315,930.77 ± 16,736.02 | |
| Station Days (std) | 1.73 ± 0.45 | 1.86 ± 0.47 | 2.05 ± 0.51 | 2.12 ± 0.49 | 2.30 ± 0.59 | 2.43 ± 0.61 | 2.65 ± 0.67 | |
| IMOEAD-MS | Total Distance Travel | 64,168.32 ± 2970.32 | 73,884.61 ± 3721.53 | 88,802.62 ± 3778.71 | 114,531.94 ± 4131.77 | 124,476.66 ± 4198.67 | 140,964.09 ± 4265.54 | 164,082.78 ± 4708.81 |
| Total Tardiness (Hours) | 7813.73 ± 668.93 | 11,623.70 ± 903.47 | 18,917.25 ± 1120.24 | 35,603.96 ± 1609.16 | 43,132.39 ± 1734.26 | 56,580.73 ± 1673.13 | 82,727.12 ± 2175.08 | |
| Job Load (std) | 0.97 ± 0.46 | 0.94 ± 0.31 | 0.94 ± 0.34 | 0.93 ± 0.27 | 0.91 ± 0.27 | 0.97 ± 0.48 | 0.89 ± 0.27 | |
| Priority Weighted Tardiness (Hours) | 31,123.29 ± 2659.65 | 46,672.89 ± 3496.45 | 75,937.53 ± 4280.50 | 142,932.42 ± 6178.19 | 167,102.51 ± 6595.22 | 218,889.95 ± 6267.20 | 322,491.06 ± 8338.28 | |
| Station Days (std) | 1.69 ± 0.39 | 1.86 ± 0.43 | 1.98 ± 0.50 | 2.17 ± 0.55 | 2.24 ± 0.55 | 2.33 ± 0.59 | 2.58 ± 0.67 | |
| LMOEAD-EN | Total Distance Travel | 62,730.87 ± 4621.42 | 72,730.98 ± 4360.26 | 87,957.41 ± 4066.43 | 112,578.11 ± 5865.97 | 122,078.90 ± 6920.10 | 137,730.61 ± 5636.44 | 162,305.77 ± 7743.63 |
| Total Tardiness (Hours) | 7569.80 ± 929.11 | 11,414.41 ± 993.11 | 18,819.18 ± 1388.08 | 34,973.46 ± 2386.30 | 42,174.44 ± 2980.78 | 55,345.27 ± 2778.23 | 81,059.51 ± 4681.90 | |
| Job Load (std) | 1.07 ± 0.60 | 1.09 ± 0.65 | 1.22 ± 0.99 | 0.97 ± 0.37 | 1 ± 0.54 | 1.02 ± 0.55 | 1.01 ± 0.55 | |
| Priority Weighted Tardiness (Hours) | 30,233.11 ± 3575.48 | 45,849.96 ± 3898.12 | 75,641.57 ± 5308.92 | 140,321.12 ± 9500.82 | 163,420.18 ± 11,444.04 | 214,131.85 ± 10,554.80 | 315,957.51 ± 17,757.29 | |
| Station Days (std) | 1.71 ± 0.45 | 1.88 ± 0.46 | 1.99 ± 0.57 | 2.23 ± 0.55 | 2.35 ± 0.57 | 2.46 ± 0.65 | 2.73 ± 0.70 | |
| NSGA-II | Total Distance Travel | 77,647.53 ± 5716.87 | 88,934.42 ± 5873.15 | 102,838.48 ± 6769 | 131,195.67 ± 8749.76 | 142,609.63 ± 9347.82 | 156,810.84 ± 9262.29 | 182,134.01 ± 9657.12 |
| Total Tardiness (Hours) | 13,397.55 ± 2734.53 | 18,300.59 ± 2301.07 | 28,378.21 ± 3008.83 | 49,192.22 ± 4307.33 | 57,011.36 ± 3921.29 | 73,903.09 ± 6392.49 | 108,071.42 ± 15,267.13 | |
| Job Load (std) | 4.58 ± 2.76 | 4.97 ± 2.70 | 5.55 ± 3.10 | 6.63 ± 3.87 | 6.06 ± 3.44 | 7.20 ± 4.36 | 8.84 ± 6.40 | |
| Priority Weighted Tardiness (Hours) | 52,181.42 ± 10,783.18 | 71,723.79 ± 8680.47 | 111,180.28 ± 10,888.26 | 194,877.57 ± 16,415.16 | 218,825.19 ± 14,414.59 | 28,3479.77 ± 24,175.24 | 418,379.93 ± 58,269.42 | |
| Station Days (std) | 3.92 ± 2.25 | 4.28 ± 2.12 | 4.93 ± 2.48 | 5.78 ± 3.16 | 5.38 ± 2.76 | 6.31 ± 3.45 | 7.75 ± 5.13 | |
| NSGA-III | Total Distance Travel | 64,179.73 ± 5810.10 | 72,900.47 ± 5852.52 | 87,345.50 ± 6620.55 | 110,459.11 ± 7108.17 | 121,356.41 ± 8188.82 | 135,493.99 ± 8275.31 | 159,071.89 ± 8411.66 |
| Total Tardiness (Hours) | 8025.76 ± 1257.39 | 11,617.28 ± 1489.50 | 19,185.52 ± 2139.22 | 35,658.22 ± 3009.53 | 43,562.55 ± 3832.77 | 56,678.67 ± 4096.28 | 83,471.01 ± 4927.85 | |
| Job Load (std) | 1.87 ± 0.79 | 2.02 ± 0.87 | 2.17 ± 0.93 | 2.43 ± 0.99 | 2.47 ± 1.08 | 2.52 ± 1.05 | 2.77 ± 1.14 | |
| Priority Weighted Tardiness (Hours) | 32,067.70 ± 4782.51 | 46,701.08 ± 5736.46 | 77,089.03 ± 8217.13 | 143,184.54 ± 11,594.11 | 168,883.71 ± 14,393.17 | 219,339.34 ± 15,366.82 | 325,480.85 ± 18,578.66 | |
| Station Days (std) | 1.45 ± 0.54 | 1.62 ± 0.59 | 1.78 ± 0.67 | 1.97 ± 0.74 | 2.08 ± 0.78 | 2.12 ± 0.80 | 2.36 ± 0.87 | |
| PB | Total Distance Travel | 85,193.89 ± 0 | 96,288.34 ± 0 | 111,805.61 ± 0 | 142,186.04 ± 0 | 154,210.40 ± 0 | 169,690.14 ± 0 | 193,302.60 ± 0 |
| Total Tardiness (Hours) | 12,114.60 ± 0 | 17,079.91 ± 0 | 26,466.80 ± 0 | 46,339.56 ± 0 | 55,330.55 ± 0 | 70,624.48 ± 0 | 100,947.77 ± 0 | |
| Job Load (std) | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | |
| Priority Weighted Tardiness (Hours) | 47,862.36 ± 0 | 68,054.83 ± 0 | 105,419.27 ± 0 | 185,074.42 ± 0 | 214,126.89 ± 0 | 272,464.55 ± 0 | 392,417.27 ± 0 | |
| Station Days (std) | 1.11 ± 0 | 1.17 ± 0 | 1.40 ± 0 | 1.56 ± 0 | 1.56 ± 0 | 2.05 ± 0 | 2.59 ± 0 | |
| PMOEAD-ES | Total Distance Travel | 62,696.40 ± 3981.14 | 73,931.61 ± 3799.94 | 86,835.12 ± 6012.71 | 112,296.34 ± 6483.35 | 121,931.41 ± 7125.77 | 138,173.25 ± 6344.05 | 162,215.36 ± 7180.61 |
| Total Tardiness (Hours) | 7628.80 ± 803.62 | 11,438.51 ± 954.87 | 18,498.32 ± 1968.89 | 34,714.13 ± 2722.60 | 42,122.04 ± 3211.84 | 55,569.26 ± 3293.32 | 81,108.98 ± 4402.45 | |
| Job Load (std) | 1.21 ± 0.81 | 1.08 ± 0.67 | 1.13 ± 0.78 | 0.99 ± 0.50 | 0.99 ± 0.48 | 1.02 ± 0.59 | 1.05 ± 0.70 | |
| Priority Weighted Tardiness (Hours) | 30,478.50 ± 3131.06 | 45,864.58 ± 3745.68 | 74,408.44 ± 7680.63 | 139,338.34 ± 10,636.73 | 163,343.13 ± 11,974.92 | 214,821.29 ± 12,552.76 | 316,179.07 ± 16,774.99 | |
| Station Days (std) | 1.78 ± 0.48 | 1.84 ± 0.49 | 2 ± 0.55 | 2.22 ± 0.58 | 2.42 ± 0.60 | 2.49 ± 0.62 | 2.67 ± 0.70 | |
| TMOEAD-DP | Total Distance Travel | 62,201.81 ± 5750.51 | 72,948.29 ± 5657.72 | 86,921.57 ± 4761.33 | 111,464.05 ± 5422.44 | 121,559.17 ± 6145.46 | 137,021.05 ± 6385.76 | 161,319.04 ± 7833.41 |
| Total Tardiness (Hours) | 7492.65 ± 1110.58 | 11,525.62 ± 1304.95 | 19,038.61 ± 1663.80 | 35,402.34 ± 2491.06 | 42,803.11 ± 3004.39 | 56,142.21 ± 3693.25 | 82,460.16 ± 4864.25 | |
| Job Load (std) | 1.11 ± 0.77 | 1.05 ± 0.70 | 1.01 ± 0.57 | 1.02 ± 0.51 | 1.04 ± 0.61 | 1.01 ± 0.48 | 1.02 ± 0.58 | |
| Priority Weighted Tardiness (Hours) | 29,899.50 ± 4341.17 | 46,299 ± 5086.77 | 76,430.65 ± 6348.45 | 142,059.67 ± 9771.22 | 165,913.89 ± 11,351.88 | 217,302.96 ± 13,975.76 | 321,448.54 ± 18,369.01 | |
| Station Days (std) | 1.80 ± 0.44 | 1.93 ± 0.47 | 1.98 ± 0.52 | 2.20 ± 0.57 | 2.37 ± 0.61 | 2.48 ± 0.61 | 2.55 ± 0.66 | |
| WB | Total Distance Travel | 85,193.89 ± 0 | 96,288.34 ± 0 | 111,805.61 ± 0 | 142,186.04 ± 0 | 154,210.40 ± 0 | 169,690.14 ± 0 | 193,302.60 ± 0 |
| Total Tardiness (Hours) | 12,114.60 ± 0 | 17,079.91 ± 0 | 26,466.80 ± 0 | 46,339.56 ± 0 | 55,330.55 ± 0 | 70,624.48 ± 0 | 100,947.77 ± 0 | |
| Job Load (std) | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | 0.50 ± 0 | |
| Priority Weighted Tardiness (Hours) | 47,862.36 ± 0 | 68,054.83 ± 0 | 105,419.27 ± 0 | 185,074.42 ± 0 | 214,126.89 ± 0 | 272,464.55 ± 0 | 392,417.27 ± 0 | |
| Station Days (std) | 1.11 ± 0 | 1.17 ± 0 | 1.40 ± 0 | 1.56 ± 0 | 1.56 ± 0 | 2.05 ± 0 | 2.59 ± 0 |
| Case | AMOEAD PS | Classical MOEAD | HMOEAD AS | IMOEAD MS | LMOEAD EN | NSGA2 | NSGA3 | PMOEAD ES | TMOEAD DP |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 264.51 | 113.87 | 264.92 | 259.76 | 245.87 | 144.36 | 1499.07 | 278.40 | 208.59 |
| 2 | 294.71 | 125.11 | 293.53 | 288.72 | 273.89 | 155.14 | 1679.77 | 309.06 | 237.99 |
| 3 | 364.82 | 136.76 | 368.15 | 358.27 | 339.15 | 168.58 | 1767.57 | 382.69 | 303.88 |
| 4 | 393.52 | 165.50 | 390.72 | 384.94 | 361.46 | 195.12 | 1326.71 | 409.21 | 339.30 |
| 5 | 346.58 | 176.93 | 346.48 | 343.01 | 320.27 | 209.91 | 2153.68 | 362.47 | 299.16 |
| 6 | 430.91 | 205.17 | 431.00 | 425.29 | 397.24 | 246.00 | 2167.69 | 445.08 | 376.76 |
| 7 | 488.38 | 224.99 | 495.20 | 489.68 | 453.29 | 263.87 | 2510.93 | 505.94 | 433.51 |
| Algorithm | Metric | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | Case 7 |
|---|---|---|---|---|---|---|---|---|
| Base NSGA2 | Hypervolume | 0.73 ± 0.02 | 0.78 ± 0.04 | 0.73 ± 0.02 | 0.74 ± 0.02 | 0.75 ± 0.03 | 0.72 ± 0.02 | 0.72 ± 0.03 |
| MOEA/D | Hypervolume | 0.68 ± 0.02 | 0.73 ± 0.04 | 0.68 ± 0.02 | 0.69 ± 0.02 | 0.71 ± 0.02 | 0.68 ± 0.02 | 0.67 ± 0.03 |
| Pro. NSGA2 | Hypervolume | 0.77 ± 0.02 | 0.82 ± 0.03 | 0.77 ± 0.02 | 0.78 ± 0.02 | 0.78 ± 0.03 | 0.75 ± 0.02 | 0.74 ± 0.02 |
| SPEA2 | Hypervolume | 0.66 ± 0.02 | 0.68 ± 0.03 | 0.64 ± 0.01 | 0.65 ± 0.02 | 0.66 ± 0.04 | 0.66 ± 0.02 | 0.67 ± 0.03 |
| Base NSGA2 | Igd | 0.03 ± 0.01 | 0.05 ± 0.01 | 0.03 ± 0.01 | 0.03 ± 0.01 | 0.03 ± 0.01 | 0.02 ± 0.01 | 0.02 ± 0.00 |
| MOEA/D | Igd | 0.05 ± 0.01 | 0.05 ± 0.01 | 0.05 ± 0.02 | 0.05 ± 0.01 | 0.04 ± 0.01 | 0.04 ± 0.01 | 0.04 ± 0.01 |
| Pro. NSGA2 | Igd | 0.02 ± 0.02 | 0.04 ± 0.02 | 0.02 ± 0.02 | 0.01 ± 0.01 | 0.02 ± 0.02 | 0.01 ± 0.01 | 0.01 ± 0.01 |
| SPEA2 | Igd | 0.07 ± 0.02 | 0.11 ± 0.02 | 0.09 ± 0.02 | 0.07 ± 0.02 | 0.08 ± 0.02 | 0.06 ± 0.01 | 0.04 ± 0.01 |
| Base NSGA2 | Spacing | 0.01 ± 0.00 | 0.02 ± 0.00 | 0.02 ± 0.00 | 0.02 ± 0.00 | 0.02 ± 0.01 | 0.01 ± 0.00 | 0.01 ± 0.00 |
| MOEA/D | Spacing | 0.01 ± 0.00 | 0.01 ± 0.00 | 0.01 ± 0.00 | 0.01 ± 0.00 | 0.01 ± 0.00 | 0.01 ± 0.00 | 0.01 ± 0.00 |
| Pro. NSGA2 | Spacing | 0.01 ± 0.00 | 0.02 ± 0.01 | 0.01 ± 0.00 | 0.01 ± 0.01 | 0.01 ± 0.01 | 0.01 ± 0.00 | 0.01 ± 0.00 |
| SPEA2 | Spacing | 0.03 ± 0.00 | 0.03 ± 0.01 | 0.03 ± 0.01 | 0.03 ± 0.01 | 0.02 ± 0.01 | 0.02 ± 0.00 | 0.02 ± 0.00 |
| Base_NSGA2 | Spreading | 0.55 ± 0.08 | 0.59 ± 0.06 | 0.55 ± 0.04 | 0.58 ± 0.08 | 0.55 ± 0.05 | 0.49 ± 0.05 | 0.50 ± 0.03 |
| MOEA/D | Spreading | 1.48 ± 0.08 | 1.51 ± 0.09 | 1.47 ± 0.05 | 1.49 ± 0.05 | 1.50 ± 0.03 | 1.41 ± 0.07 | 1.38 ± 0.08 |
| Pro. NSGA2 | Spreading | 0.55 ± 0.07 | 0.65 ± 0.04 | 0.54 ± 0.05 | 0.57 ± 0.06 | 0.57 ± 0.04 | 0.51 ± 0.04 | 0.54 ± 0.04 |
| SPEA2 | Spreading | 0.58 ± 0.08 | 0.67 ± 0.05 | 0.64 ± 0.07 | 0.64 ± 0.09 | 0.59 ± 0.07 | 0.54 ± 0.07 | 0.56 ± 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alahmadi, M. Multi-Objective Combinatorial Optimization for Dynamic Inspection Scheduling and Skill-Based Team Formation in Distributed Solar Energy Infrastructure. Systems 2025, 13, 822. https://doi.org/10.3390/systems13090822
Alahmadi M. Multi-Objective Combinatorial Optimization for Dynamic Inspection Scheduling and Skill-Based Team Formation in Distributed Solar Energy Infrastructure. Systems. 2025; 13(9):822. https://doi.org/10.3390/systems13090822
Chicago/Turabian StyleAlahmadi, Mazin. 2025. "Multi-Objective Combinatorial Optimization for Dynamic Inspection Scheduling and Skill-Based Team Formation in Distributed Solar Energy Infrastructure" Systems 13, no. 9: 822. https://doi.org/10.3390/systems13090822
APA StyleAlahmadi, M. (2025). Multi-Objective Combinatorial Optimization for Dynamic Inspection Scheduling and Skill-Based Team Formation in Distributed Solar Energy Infrastructure. Systems, 13(9), 822. https://doi.org/10.3390/systems13090822







