Incentives, Constraints, and Adoption: An Evolutionary Game Analysis on Human–Robot Collaboration Systems in Construction
Abstract
1. Introduction
2. Literature Review
2.1. Challenges of HRC Systems in the Construction Industry
2.2. HRC in Construction Supply Chain Systems
2.3. The Mechanism of Regulations and Incentives of Government on Technological Innovation in the Construction Industry
2.4. The Evolutionary Game Theory in Construction
2.5. Knowledge Gap
3. Model Assumptions and Formulation
3.1. Analysis of Game-Theoretic Participants
3.2. Basic Assumptions and Parameter Settings
3.3. Model Formulation
4. Evolutionary Game Model Stability Analysis
4.1. Stability Analysis of Government Supervision Strategies
4.2. Stability Analysis of the Contractor’s Adoption Strategy
4.3. Stability Analysis of the On-Site Team’s Collaboration Strategy
4.4. Stability Analysis of Equilibria in the Tripartite Game System
5. Numerical Simulation
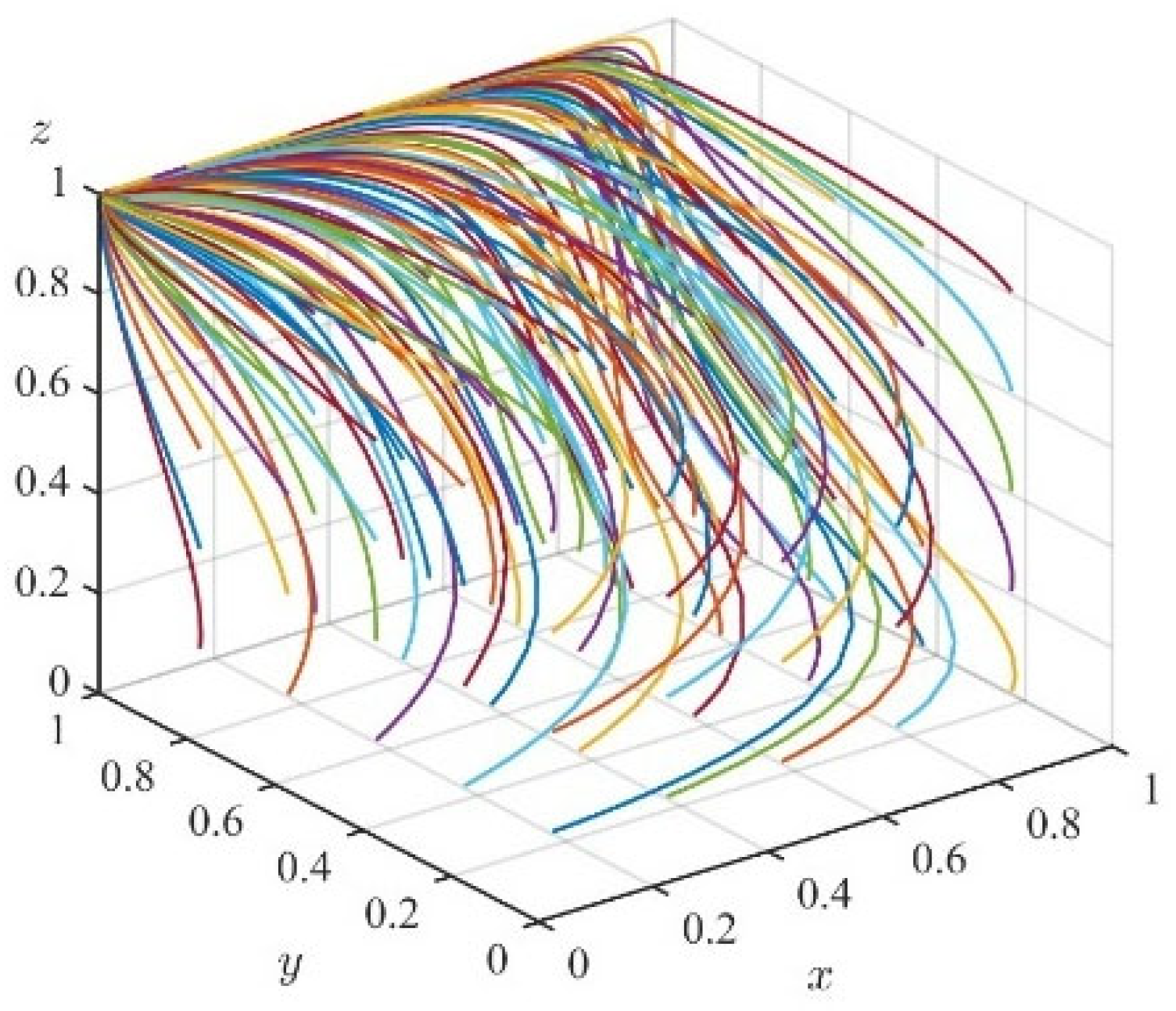
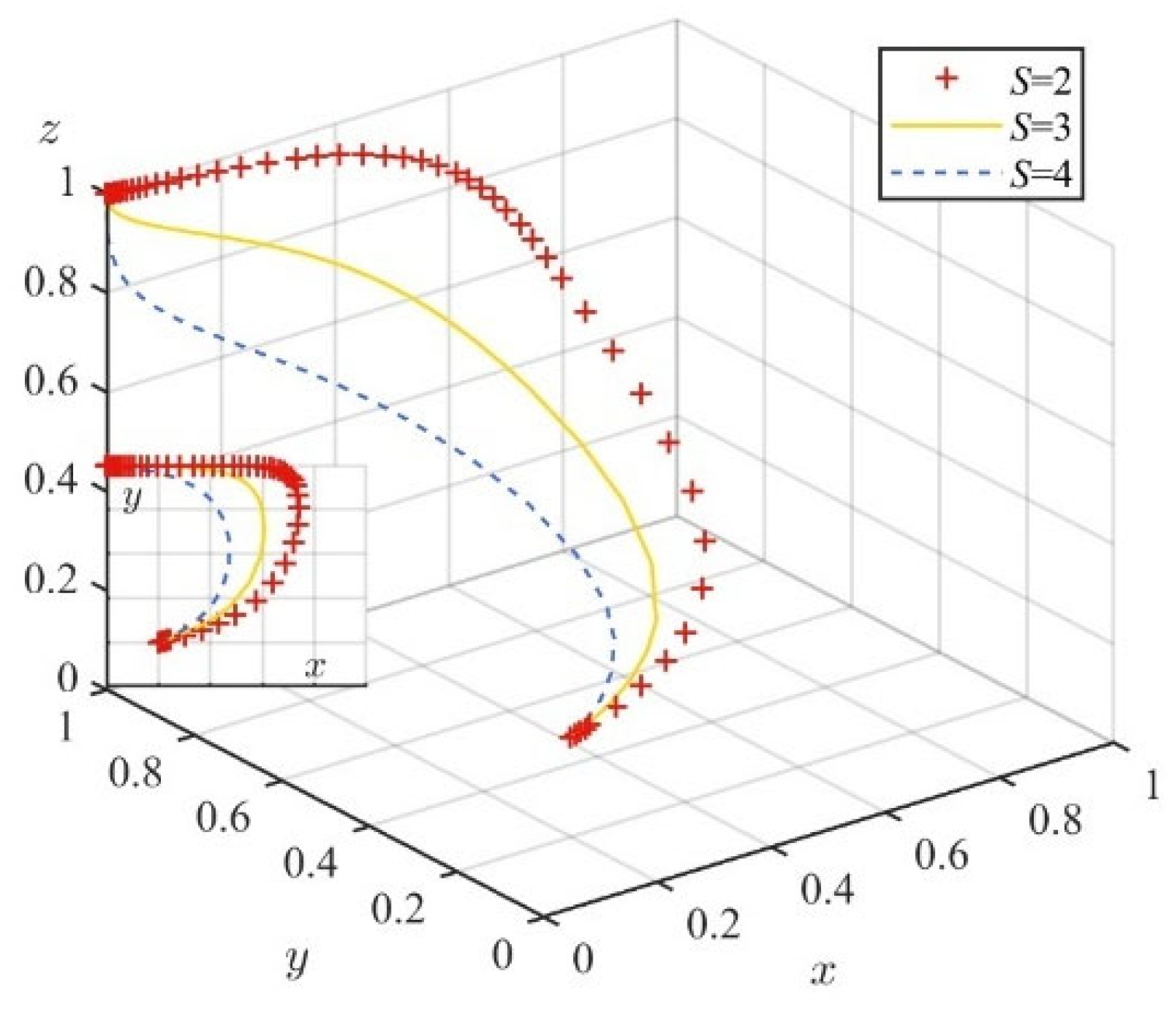
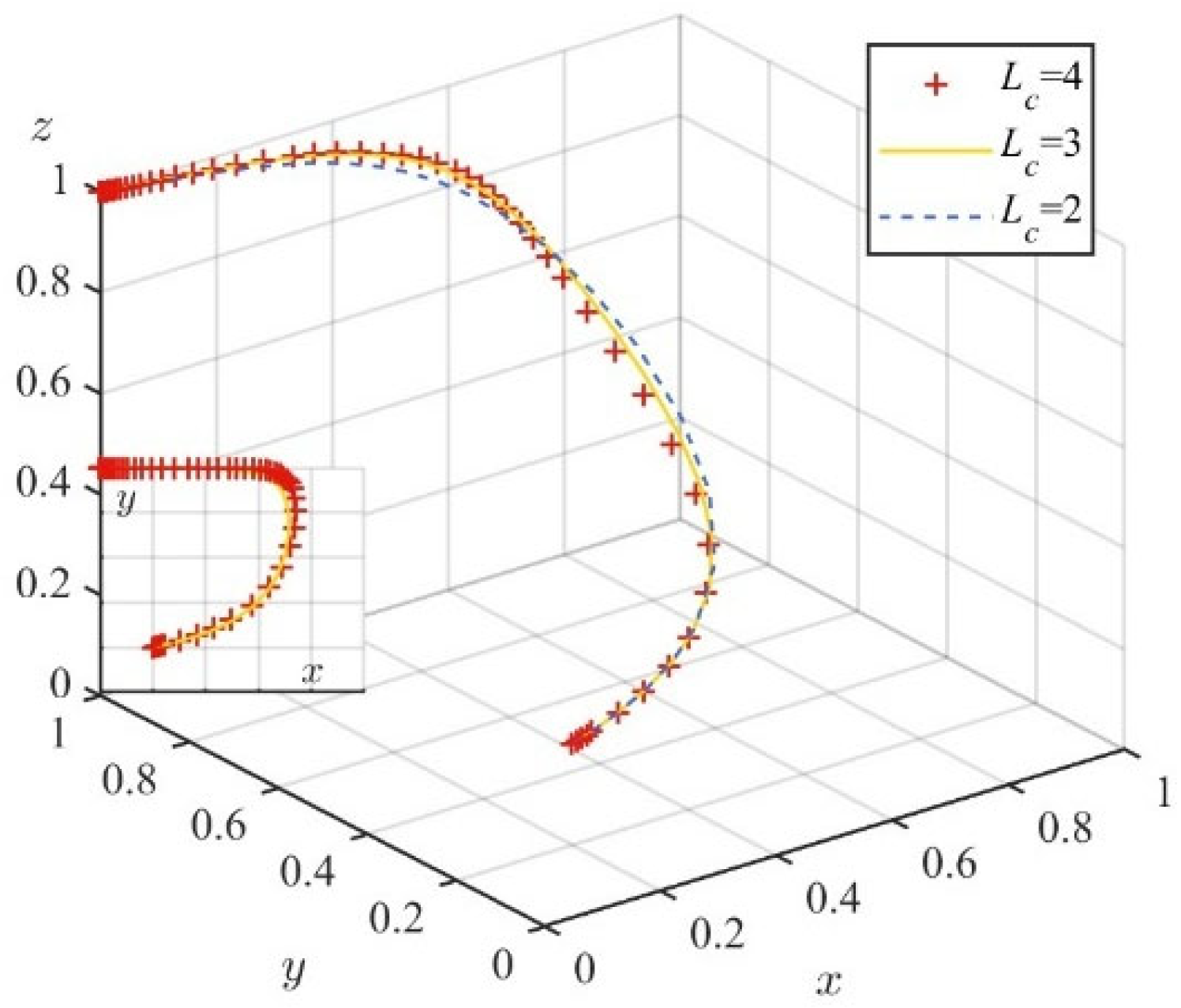
5.1. System Stability Test
5.2. Influence of Relevant Parameters on the Evolution of Stakeholder Behavior
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BIM | Building Information Modeling |
| HRC | Human–Robot Collaboration |
References
- Skibniewski, M.J. The Present and Future of Smart Construction Technologies. Engineering 2025, 44, 21–23. [Google Scholar] [CrossRef]
- Vararean-Cochisa, D.; Crisan, E.-L. The digital transformation of the construction industry: A review. IIM Ranchi J. Manag. Stud. 2024, 4, 3–16. [Google Scholar] [CrossRef]
- Rinchen, S.; Banihashemi, S.; Alkilani, S. Driving digital transformation in construction: Strategic insights into building information modelling adoption in developing countries. Proj. Leadersh. Soc. 2024, 5, 100138. [Google Scholar] [CrossRef]
- Liang, C.-J.; Wang, X.; Kamat Vineet, R.; Menassa Carol, C. Human–Robot Collaboration in Construction: Classification and Research Trends. J. Constr. Eng. Manag. 2021, 147, 03121006. [Google Scholar] [CrossRef]
- Brosque, C.; Galbally, E.; Khatib, O.; Fischer, M. Human-Robot Collaboration in Construction: Opportunities and Challenges. In Proceedings of the 2020 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Ankara, Turkey, 26–28 June 2020; pp. 1–8. [Google Scholar]
- Wu, M.; Lin, J.-R.; Zhang, X.-H. How human-robot collaboration impacts construction productivity: An agent-based multi-fidelity modeling approach. Adv. Eng. Inform. 2022, 52, 101589. [Google Scholar] [CrossRef]
- Burden, A.G.; Caldwell, G.A.; Guertler, M.R. Towards human–robot collaboration in construction: Current cobot trends and forecasts. Constr. Robot. 2022, 6, 209–220. [Google Scholar] [CrossRef]
- Olukanni, E.; Akanmu, A.; Jebelli, H.; Ammar, A.; Okunola, A. Competencies for human–robot collaboration in the construction industry: Perspectives from academia and industry. Constr. Robot. 2025, 9, 15. [Google Scholar] [CrossRef]
- Davila Delgado, J.M.; Oyedele, L.; Ajayi, A.; Akanbi, L.; Akinade, O.; Bilal, M.; Owolabi, H. Robotics and automated systems in construction: Understanding industry-specific challenges for adoption. J. Build. Eng. 2019, 26, 100868. [Google Scholar] [CrossRef]
- Liu, J.; Wang, X.; Liu, T. Behavior Choice Mechanisms and Tax Incentive Mechanisms in the Game of Construction Safety. Buildings 2022, 12, 1078. [Google Scholar] [CrossRef]
- Feng, Q.; Wang, K.; Feng, Y.; Shi, X.; Rao, Y.; Wei, J. Incentives for Promoting Safety in the Chinese Construction Industry. Buildings 2023, 13, 1446. [Google Scholar] [CrossRef]
- Gurgun, A.P.; Koc, K.; Kunkcu, H. Exploring the adoption of technology against delays in construction projects. Eng. Constr. Archit. Manag. 2022, 31, 1222–1253. [Google Scholar] [CrossRef]
- Ji, L.; Liu, W.; Zhang, Y. Research on the Tournament Incentive Mechanism of the Safety Behavior for Construction Workers: Considering Multiple Heterogeneity. Front. Psychol. 2021, 12, 796295. [Google Scholar] [CrossRef]
- Li, J.; Greenwood, D.; Kassem, M. Blockchain in the Construction Sector: A Socio-technical Systems Framework for the Construction Industry. In Advances in Informatics and Computing in Civil and Construction Engineering; Springer: Cham, Switzerland, 2019; pp. 51–57. [Google Scholar]
- Jin, X.; Shen, G.Q.P.; Ekanayake, E.M.A.C. Improving Construction Industrialization Practices from a Socio-Technical System Perspective: A Hong Kong Case. Int. J. Environ. Res. Public Health 2021, 18, 9017. [Google Scholar] [CrossRef]
- Edmondson, D.L.; Kern, F.; Rogge, K.S. The co-evolution of policy mixes and socio-technical systems: Towards a conceptual framework of policy mix feedback in sustainability transitions. Res. Policy 2019, 48, 103555. [Google Scholar] [CrossRef]
- Edmondson, D.L.; Rogge, K.S.; Kern, F. Zero carbon homes in the UK? Analysing the co-evolution of policy mix and socio-technical system. Environ. Innov. Soc. Transit. 2020, 35, 135–161. [Google Scholar] [CrossRef]
- Liu, Y.; Zuo, J.; Pan, M.; Ge, Q.; Chang, R.; Feng, X.; Fu, Y.; Dong, N. The incentive mechanism and decision-making behavior in the green building supply market: A tripartite evolutionary game analysis. Build. Environ. 2022, 214, 108903. [Google Scholar] [CrossRef]
- Yuan, R.; Zhang, B. An Evolutionary Game Study on the Collaborative Mechanism for Construction Digitalization Among Governments, Contractors, and Service Providers. Buildings 2025, 15, 1933. [Google Scholar] [CrossRef]
- Su, Y.; Zhang, Z. Evolutionary Game Analysis on the Promotion of Green Buildings in China Under the “Dual Carbon” Goals: A Multi-Stakeholder Perspective. Buildings 2025, 15, 1392. [Google Scholar] [CrossRef]
- Yang, C.; Xiong, F.; Hu, Q.; Liu, R.; Li, S. Incentive Mechanism of BIM Application in Prefabricated Buildings Based on Evolutionary Game Analysis. Buildings 2023, 13, 1162. [Google Scholar] [CrossRef]
- Wang, Q.; Guo, W.; Xu, X.; Deng, R.; Ding, X.; Chen, T. Analysis of Carbon Emission Reduction Paths for the Production of Prefabricated Building Components Based on Evolutionary Game Theory. Buildings 2023, 13, 1557. [Google Scholar] [CrossRef]
- Feng, T.; Tai, S.; Sun, C.; Man, Q. Study on Cooperative Mechanism of Prefabricated Producers Based on Evolutionary Game Theory. Math. Probl. Eng. 2017, 2017, 1676045. [Google Scholar] [CrossRef]
- Gurevich, U.; Sacks, R. Longitudinal Study of BIM Adoption by Public Construction Clients. J. Manag. Eng. 2020, 36, 05020008. [Google Scholar] [CrossRef]
- Qin, X.; Shi, Y.; Lyu, K.; Mo, Y. Using a TAM-TOE model to explore factors of Building Information Modelling (BIM) adoption in the construction industry. J. Civ. Eng. Manag. 2020, 26, 259–277. [Google Scholar] [CrossRef]
- Li, X.-J. Research on investment risk influence factors of prefabricated building projects. J. Civ. Eng. Manag. 2020, 26, 599–613. [Google Scholar] [CrossRef]
- Shi, Q.; Wang, Z.; Zhu, J. Developing Collaborative Driving Mechanism of Prefabricated Buildings Using Multiagent Stochastic Evolutionary Game. J. Constr. Eng. Manag. 2024, 150, 04024050. [Google Scholar] [CrossRef]
- Park, S.; Yu, H.; Menassa, C.C.; Kamat, V.R. A Comprehensive Evaluation of Factors Influencing Acceptance of Robotic Assistants in Field Construction Work. J. Manag. Eng. 2023, 39, 04023010. [Google Scholar] [CrossRef]
- Okonkwo, C.; Liang, X.; Rasheed, U.; Awolusi, I.; Cai, J.; Wibranek, B. Construction Worker Workload Assessment for Human-Human versus Human-Robot Collaboration in Wood Assembly. In Proceedings of the Computing in Civil Engineering 2023, Corvallis, OR, USA, 25–28 June 2023; pp. 322–330. [Google Scholar]
- Wang, X.; Veeramani, D.; Dai, F.; Zhu, Z. Context-aware hand gesture interaction for human–robot collaboration in construction. Comput.-Aided Civ. Infrastruct. Eng. 2024, 39, 3489–3504. [Google Scholar] [CrossRef]
- Wu, G.; Yang, R.; Li, L.; Bi, X.; Liu, B.; Li, S.; Zhou, S. Factors influencing the application of prefabricated construction in China: From perspectives of technology promotion and cleaner production. J. Clean. Prod. 2019, 219, 753–762. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, L.; Li, Y.; Chen, C.; Zhuang, J. Incentive strategy of safe and intelligent production in assembled steel plants from the perspective of evolutionary game. Sci. Rep. 2023, 13, 15. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, C.; Wang, S.; Yuan, J.; Li, Q. Evolutionary Game Analysis of Construction Workers’ Unsafe Behaviors Based on Incentive and Punishment Mechanisms. Front. Psychol. 2022, 13, 907382. [Google Scholar] [CrossRef]
- Xing, M.; Cao, J.; Cao, D. Impacts of Policy Mix Comprehensiveness on BIM Implementation: Moderating Effects of Environmental State and Response Uncertainty. J. Constr. Eng. Manag. 2023, 149, 04022171. [Google Scholar] [CrossRef]
- An, X.; Ren, S.; Wang, L.; Huang, Y. Evolutionary game analysis of collaborative application of BIM platform from the perspective of value co-creation. Eng. Constr. Archit. Manag. 2024, 32, 4458–4474. [Google Scholar] [CrossRef]
- Si, Y.; Yang, Y.; Shao, Z. Green Building Design and Sustainable Development Optimization Strategy Based on Evolutionary Game Theory Model. Sustainability 2025, 17, 2649. [Google Scholar] [CrossRef]
- Chen, W.; Yang, Z.; Yan, H.; Zhao, Y. How to reduce construction risks in rural areas: An evolutionary game analysis. Eng. Constr. Archit. Manag. 2024, 32, 4495–4521. [Google Scholar] [CrossRef]
- Wan, X.; Liu, J.; Zhao, S. Evolutionary game study on the governance and development of online car-hailing based on blockchain technology. Sci. Rep. 2022, 12, 9388. [Google Scholar] [CrossRef]
- Pi, B.; Deng, L.J.; Feng, M.; Perc, M.; Kurths, J. Dynamic Evolution of Complex Networks: A Reinforcement Learning Approach Applying Evolutionary Games to Community Structure. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 1–18, Early Access. [Google Scholar] [CrossRef] [PubMed]
- Sehwag, U.M.; McAvoy, A.; Plotkin, J.B. Collective artificial intelligence and evolutionary dynamics. Proc. Natl. Acad. Sci. USA 2025, 122, e2505860122. [Google Scholar] [CrossRef]
- Gokhale, C.S.; Traulsen, A. Evolutionary Multiplayer Games. Dyn. Games Appl. 2014, 4, 468–488. [Google Scholar] [CrossRef]
- Cheng, L.; Peng, P.; Lu, W.; Sun, J.; Wu, F.; Shi, M.; Yuan, X.; Chen, Y. The evolutionary game equilibrium theory on power market bidding involving renewable energy companies. Int. J. Electr. Power Energy Syst. 2025, 167, 110588. [Google Scholar] [CrossRef]
- Fontaneda, I.; Camino López, M.A.; González Alcántara, O.J.; Greiner, B.A. Construction Accidents in Spain: Implications for an Aging Workforce. BioMed Res. Int. 2022, 2022, 9952118. [Google Scholar] [CrossRef]
- Hasan, A.; Baroudi, B.; Elmualim, A.; Rameezdeen, R. Factors affecting construction productivity: A 30 year systematic review. Eng. Constr. Archit. Manag. 2018, 25, 916–937. [Google Scholar] [CrossRef]
- Jian, F.; Liu, Q.; Feng, C.; Hu, Q.; Yu, Q.; Guo, Q. Critical Factors Affecting Construction Labor Productivity: A Systematic Review and Meta-Analysis. Buildings 2025, 15, 2463. [Google Scholar] [CrossRef]
- Marinelli, M. From industry 4.0 to construction 5.0: Exploring the path towards human–robot collaboration in construction. Systems 2023, 11, 152. [Google Scholar] [CrossRef]
- Albeaino, G.; Gheisari, M.; Issa, R.R. Human-drone interaction (HDI): Opportunities and considerations in construction. In Automation and Robotics in the Architecture, Engineering, and Construction Industry; Springer: Cham, Switzerland, 2022; pp. 111–142. [Google Scholar]
- Ekanayake, B.; Wong, J.K.-W.; Fini, A.A.F.; Smith, P. Computer vision-based interior construction progress monitoring: A literature review and future research directions. Autom. Constr. 2021, 127, 103705. [Google Scholar] [CrossRef]
- Reja, V.; Pradeep, M.; Varghese, K. A systematic classification and evaluation of automated progress monitoring technologies in construction. In Proceedings of the ISARC International Symposium on Automation and Robotics in Construction, Bogotá, Colombia, 13–15 July 2022; pp. 120–127. [Google Scholar]
- Wu, Z.; Liao, Q.; Chen, K.; Antwi-Afari, M.F.; Chen, Y.; Bao, Z. A systematic review of digital auxiliary technologies enabling human-robot collaboration in construction. Eng. Constr. Archit. Manag. 2025. [Google Scholar] [CrossRef]
- Wei, H.-H.; Zhang, Y.; Sun, X.; Chen, J.; Li, S. Intelligent robots and human-robot collaboration in the construction industry: A review. J. Intell. Constr. 2023, 1, 1–12. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, Y.; Zhou, X.; Hao, S.; Li, J. Identifying the risk factors and their interactions of human–robot collaboration implementation during engineering project construction: Evidence from China. Eng. Constr. Archit. Manag. 2022, 30, 3073–3094. [Google Scholar] [CrossRef]
- Saka, N.; Olanipekun, A.O.; Omotayo, T. Reward and compensation incentives for enhancing green building construction. Environ. Sustain. Indic. 2021, 11, 100138. [Google Scholar] [CrossRef]
- Giel, B.K.; Issa, R.R.A. Return on Investment Analysis of Using Building Information Modeling in Construction. J. Comput. Civ. Eng. 2013, 27, 511–521. [Google Scholar] [CrossRef]
- Zhang, G.; Luo, X.; Zhang, L.; Li, W.; Wang, W.; Li, Q. A Framework of Indicators for Assessing Team Performance of Human–Robot Collaboration in Construction Projects. Buildings 2025, 15, 2734. [Google Scholar] [CrossRef]
- Siegele, D.; Emig, J.; Slongo, C.; Matt, D.T. Advancing Construction Efficiency Through Collaborative Robotics: A Scalable Multi-agent-Based Logistics Solution. In Construction Logistics, Equipment, and Robotics; Springer: Cham, Switzerland, 2024; pp. 176–183. [Google Scholar]
- Garcia, R.B. Establishing an On-Site Construction Pilot for Collaboration Between Humans and Heavy-Duty Robots. In Proceedings of the 3rd Future of Construction Workshop at the International Conference on Robotics and Automation (ICRA 2024), Yokohama, Japan, 13–17 May 2024; pp. 1–4. [Google Scholar]
- Eriksson, T.; Poulsen, A.; Villeval, M.C. Feedback and incentives: Experimental evidence. Labour Econ. 2009, 16, 679–688. [Google Scholar] [CrossRef]
- Zhao, N.; Hong, J.; Lau, K.H. Impact of supply chain digitalization on supply chain resilience and performance: A multi-mediation model. Int. J. Prod. Econ. 2023, 259, 108817. [Google Scholar] [CrossRef]
- Jia, C.; Zhang, R.; Wang, D. Evolutionary Game Analysis of BIM Adoption among Stakeholders in PPP Projects. Complexity 2021, 2021, 5553785. [Google Scholar] [CrossRef]
- Gosling, J.; Naim, M.; Towill, D. Identifying and Categorizing the Sources of Uncertainty in Construction Supply Chains. J. Constr. Eng. Manag. 2013, 139, 102–110. [Google Scholar] [CrossRef]
- Childerhouse, P.; Towill, D.R. Reducing uncertainty in European supply chains. J. Manuf. Technol. Manag. 2004, 15, 585–598. [Google Scholar] [CrossRef]
- Aitken, J.; Childerhouse, P.; Deakins, E.; Towill, D. A comparative study of manufacturing and service sector supply chain integration via the uncertainty circle model. Int. J. Logist. Manag. 2016, 27, 188–205. [Google Scholar] [CrossRef]
- Towill, D.R.; Childerhouse, P.; Disney, S.M. Integrating the automotive supply chain: Where are we now? Int. J. Phys. Distrib. Logist. Manag. 2002, 32, 79–95. [Google Scholar] [CrossRef]
- Zhang, N.; Lu, K.B. The evolutionary game and simulation of key players in the green supply chain of construction industry. Mod. Supply Chain. Res. Appl. 2022, 4, 223–237. [Google Scholar] [CrossRef]
- Liu, J.; Ma, G. Study on incentive and supervision mechanisms of technological innovation in megaprojects based on the principal-agent theory. Eng. Constr. Archit. Manag. 2020, 28, 1593–1614. [Google Scholar] [CrossRef]
- Xiang, Q.; Jing, Z.; Ruwen, T.; Minjiu, Y. Incentive Regulation of Construction Waste Resource Recycling: Subsidy and Tax Incentive. Math. Probl. Eng. 2022, 2022, 8333438. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, L.; Zhuang, J.; Li, Y. Research on Excessive Revenue Distribution and Incentive Mechanism of Transportation PPP Projects from the Perspective of Fairness Preference. J. Transp. Econ. Policy 2024, 58, 99–126. [Google Scholar]
- Wang, Y.; Hu, Y.; Zhuang, J.; Xu, H. Tripartite Evolution Game of Intelligent Carbon Reduction Transformation in the Construction Industry: A Comparative Analysis of Carbon-Tax Incentives and Financial Subsidies. J. Constr. Eng. Manag. 2025, 151, 04025137. [Google Scholar] [CrossRef]
- Sun, C.; Wang, M.; Man, Q.; Wan, D. Research on the BIM Application Mechanism of Engineering-Procurement-Construction Projects Based on a Tripartite Evolutionary Game. J. Constr. Eng. Manag. 2023, 149, 04022182. [Google Scholar] [CrossRef]
- Meng, Q.; Liu, Y.; Li, Z.; Wu, C. Dynamic reward and penalty strategies of green building construction incentive: An evolutionary game theory-based analysis. Environ. Sci. Pollut. Res. 2021, 28, 44902–44915. [Google Scholar] [CrossRef]
- Jiang, X.; Sun, H.; Lu, K.; Lyu, S.; Skitmore, M. Using evolutionary game theory to study construction safety supervisory mechanism in China. Eng. Constr. Archit. Manag. 2022, 30, 514–537. [Google Scholar] [CrossRef]
- Wu, F.; Xu, H.; Sun, K.-S.; Hsu, W.-L. Analysis of Behavioral Strategies of Construction Safety Subjects Based on the Evolutionary Game Theory. Buildings 2022, 12, 313. [Google Scholar] [CrossRef]
- Villena, M.G.; Villena, M.J. Evolutionary Game Theory and Thorstein Veblen’s Evolutionary Economics: Is EGT Veblenian? J. Econ. Issues 2004, 38, 585–610. [Google Scholar] [CrossRef]
- Hou, Y.; Ong, Y.S.; Feng, L.; Zurada, J.M. An Evolutionary Transfer Reinforcement Learning Framework for Multiagent Systems. IEEE Trans. Evol. Comput. 2017, 21, 601–615. [Google Scholar] [CrossRef]
- Falniowski, F.; Mertikopoulos, P. On the discrete-time origins of the replicator dynamics: From convergence to instability and chaos. Int. J. Game Theory 2025, 54, 7. [Google Scholar] [CrossRef]
- Gao, Y.; Jia, R.; Yao, Y.; Xu, J. Evolutionary Game Theory and the Simulation of Green Building Development Based on Dynamic Government Subsidies. Sustainability 2022, 14, 7294. [Google Scholar] [CrossRef]
- Liu, Q. Asymmetric Evolutionary Game Analysis of Building Information Modeling (BIM) Technology Diffusion. Adv. Civ. Eng. 2021, 2021, 4464737. [Google Scholar] [CrossRef]
- Dou, Y.; Sun, X.; Ji, A.; Wang, Y.; Xue, X. Development strategy for prefabricated construction projects: A tripartite evolutionary game based on prospect theory. Eng. Constr. Archit. Manag. 2021, 30, 105–124. [Google Scholar] [CrossRef]
- Yuan, M.; Li, Z.; Li, X.; Li, L.; Zhang, S.; Luo, X. How to promote the sustainable development of prefabricated residential buildings in China: A tripartite evolutionary game analysis. J. Clean. Prod. 2022, 349, 131423. [Google Scholar] [CrossRef]
- Wang, Y.; Zhuang, J.; Lai, R.; Chen, L. A Tripartite Governance Strategy for Infrastructure REITs Considering Tax Incentives and Antiavoidance Regulations. J. Constr. Eng. Manag. 2024, 150, 13. [Google Scholar] [CrossRef]
- Chen, Y.; Zeng, Q.; Zheng, X.; Shao, B.; Jin, L. Safety supervision of tower crane operation on construction sites: An evolutionary game analysis. Saf. Sci. 2022, 152, 105578. [Google Scholar] [CrossRef]
- Narbaev, T.; Hazır, Ö.; Agi, M. A Review of the Use of Game Theory in Project Management. J. Manag. Eng. 2022, 38, 03122002. [Google Scholar] [CrossRef]
- Li, X. Evolutionary Game Analysis of Green Building Development Dynamic System under Government Regulation: From the Perspective of the Contractor. Math. Probl. Eng. 2022, 2022, 1987229. [Google Scholar] [CrossRef]
- Xue, Y.; Liu, F.; Wang, G.; Shao, J. Research on Strategy Evolution of Contractor and Resident in Construction Stage of Old Community Renovation Project. Sustainability 2023, 15, 1650. [Google Scholar] [CrossRef]
- Huang, Z.; Fan, H. A Novel Quantitative Model for Determining Subsidy Levels to Accelerate the Replacement of In-Use Construction Equipment for Emissions Reduction. J. Manag. Eng. 2022, 38, 04021100. [Google Scholar] [CrossRef]
- Khalid, U.; Sagoo, A.; Benachir, M. Safety Management System (SMS) framework development—Mitigating the critical safety factors affecting Health and Safety performance in construction projects. Saf. Sci. 2021, 143, 105402. [Google Scholar] [CrossRef]
- Hanna Awad, S.; Taylor Craig, S.; Sullivan Kenneth, T. Impact of Extended Overtime on Construction Labor Productivity. J. Constr. Eng. Manag. 2005, 131, 734–739. [Google Scholar] [CrossRef]
- Johari, S.; Jha Kumar, N. Interrelationship among Belief, Intention, Attitude, Behavior, and Performance of Construction Workers. J. Manag. Eng. 2020, 36, 04020081. [Google Scholar] [CrossRef]
- Madeira, J. Overtime Labor, Employment Frictions, and the New Keynesian Phillips Curve. Rev. Econ. Stat. 2014, 96, 767–778. [Google Scholar] [CrossRef]
- Geng, X.; Lv, L.; Wang, Y.; Sun, R.; Wang, X. Evolutionary Game Research on Green Construction Considering Consumers’ Preference under Government Supervision. Int. J. Environ. Res. Public Health 2022, 19, 16743. [Google Scholar] [CrossRef]
- Feng, D.; Klaus, B. Preference revelation games and strict cores of multiple-type housing market problems. Int. J. Econ. Theory 2022, 18, 61–76. [Google Scholar] [CrossRef]
- Li, J.; Kendall, G.; John, R. Computing Nash Equilibria and Evolutionarily Stable States of Evolutionary Games. IEEE Trans. Evol. Comput. 2016, 20, 460–469. [Google Scholar] [CrossRef]
- Cheng, B.; Wei, Y.; Zhang, W.; Zhou, X.; Chen, H.; Huang, L.; Huang, J.; Kang, X. Evolutionary Game Simulation on Government Incentive Strategies of Prefabricated Construction: A System Dynamics Approach. Complexity 2020, 2020, 8861146. [Google Scholar] [CrossRef]
- Liu, K.; Liu, Y.; Zhou, H.; Kou, Y.; Ji, Q.; Li, D. Evolutionary game and numerical simulation of participants’ collaborative behavior in integrated project delivery project. Alex. Eng. J. 2021, 60, 373–385. [Google Scholar] [CrossRef]
- Zhang, Y.; Yi, X.; Li, S.; Qiu, H. Evolutionary game of government safety supervision for prefabricated building construction using system dynamics. Eng. Constr. Archit. Manag. 2022, 30, 2947–2968. [Google Scholar] [CrossRef]
- Zhang, R.; Li, L. Research on Evolutionary Game and Simulation of Information Sharing in Prefabricated Building Supply Chain. Sustainability 2023, 15, 9885. [Google Scholar] [CrossRef]
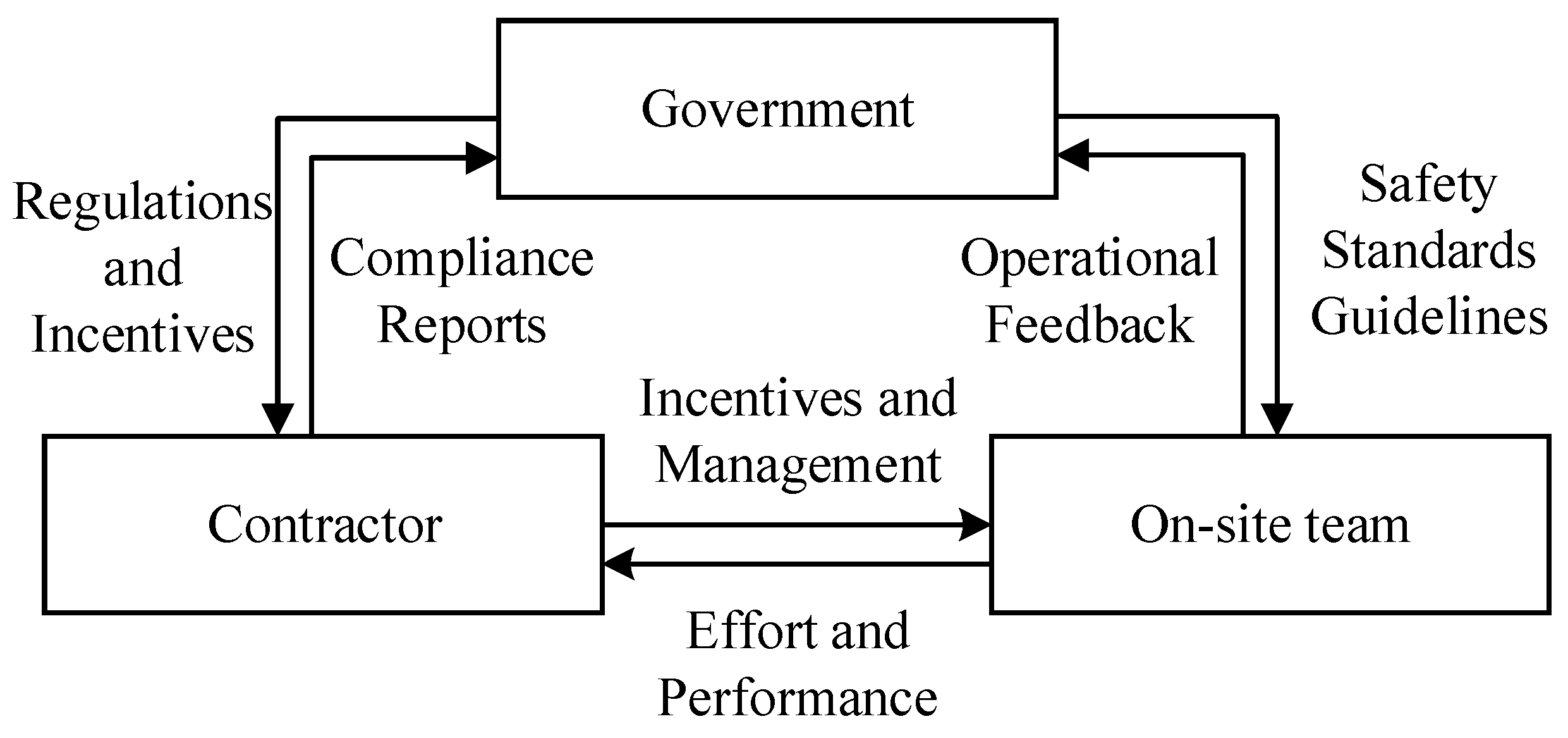
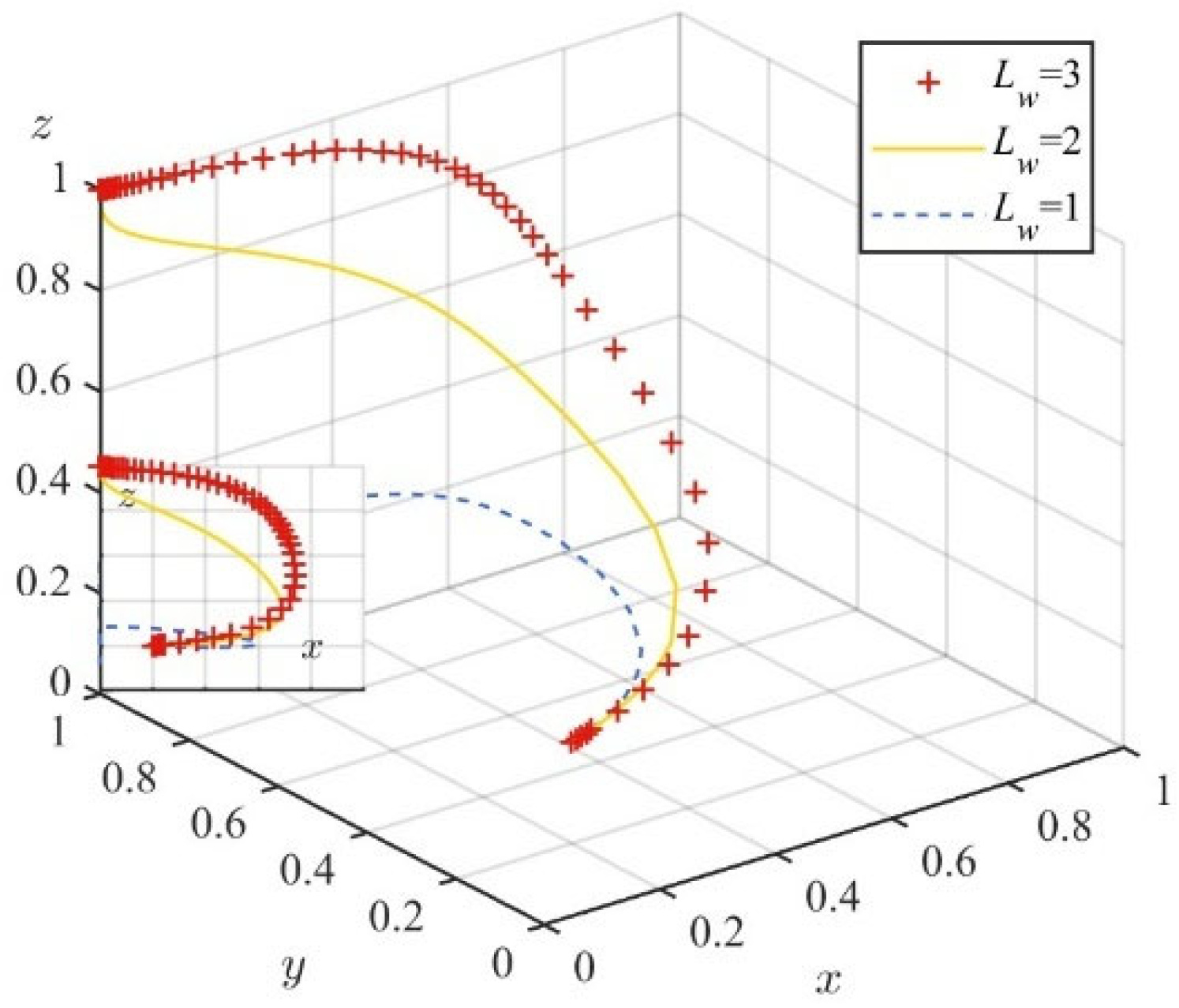
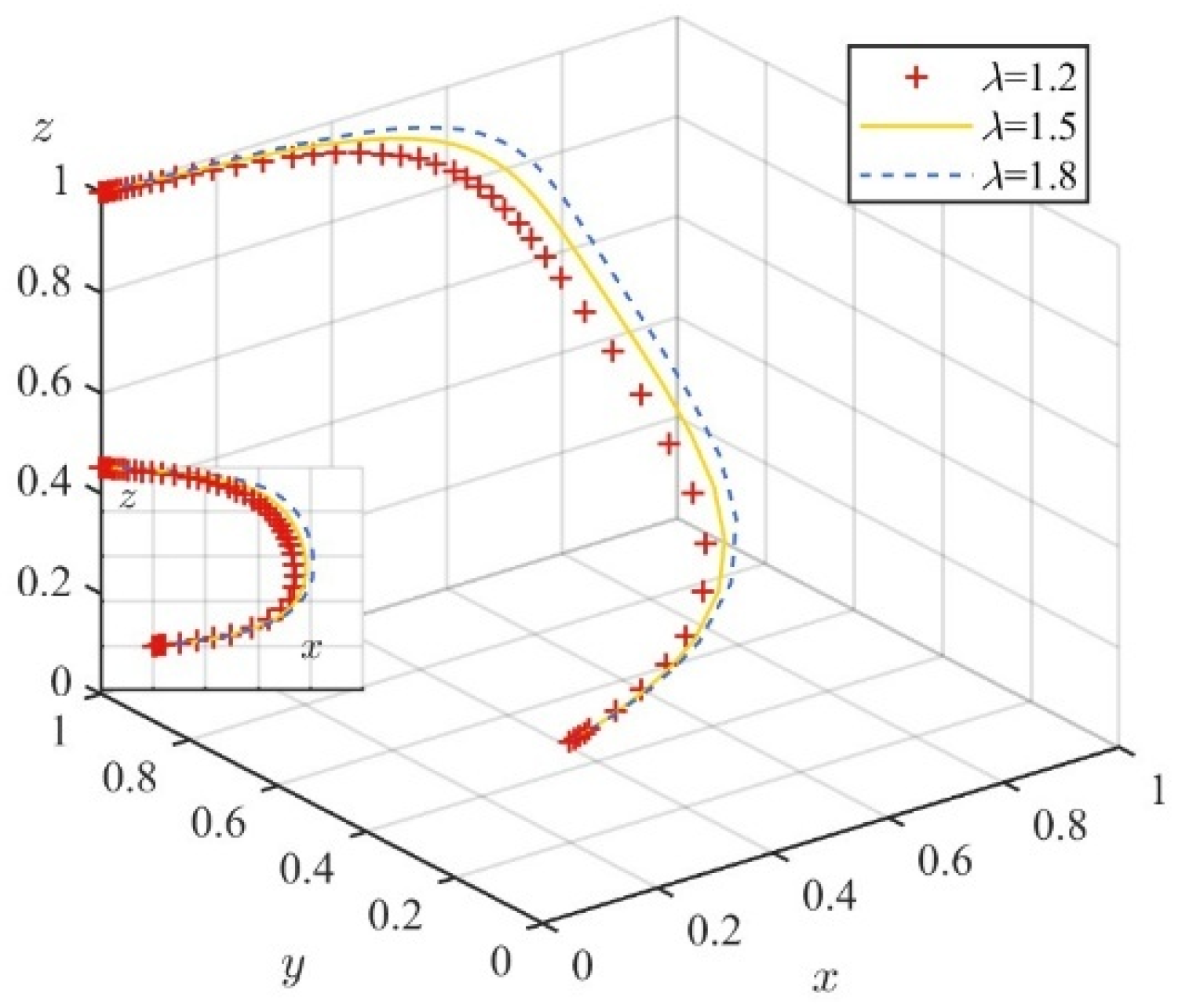
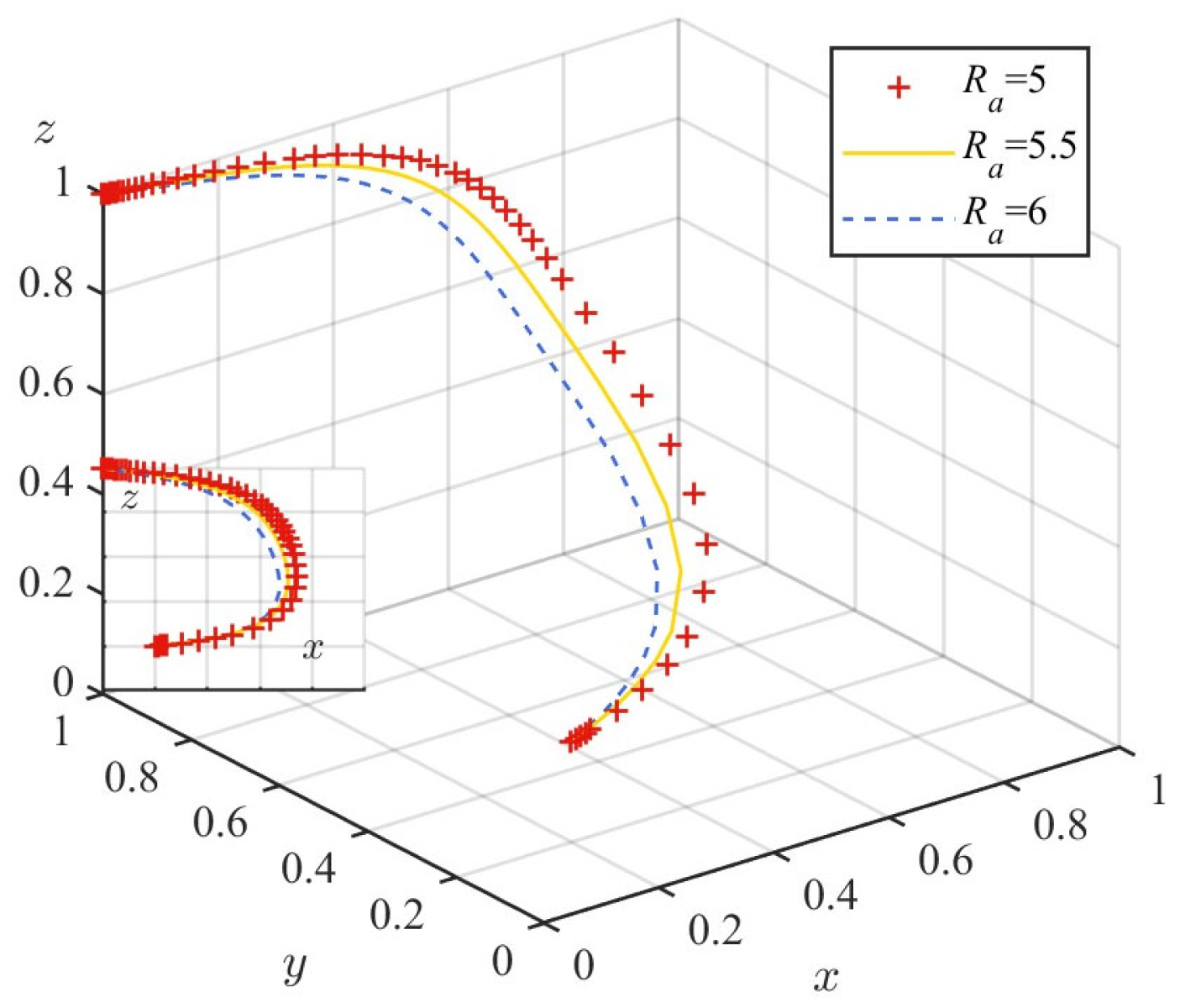
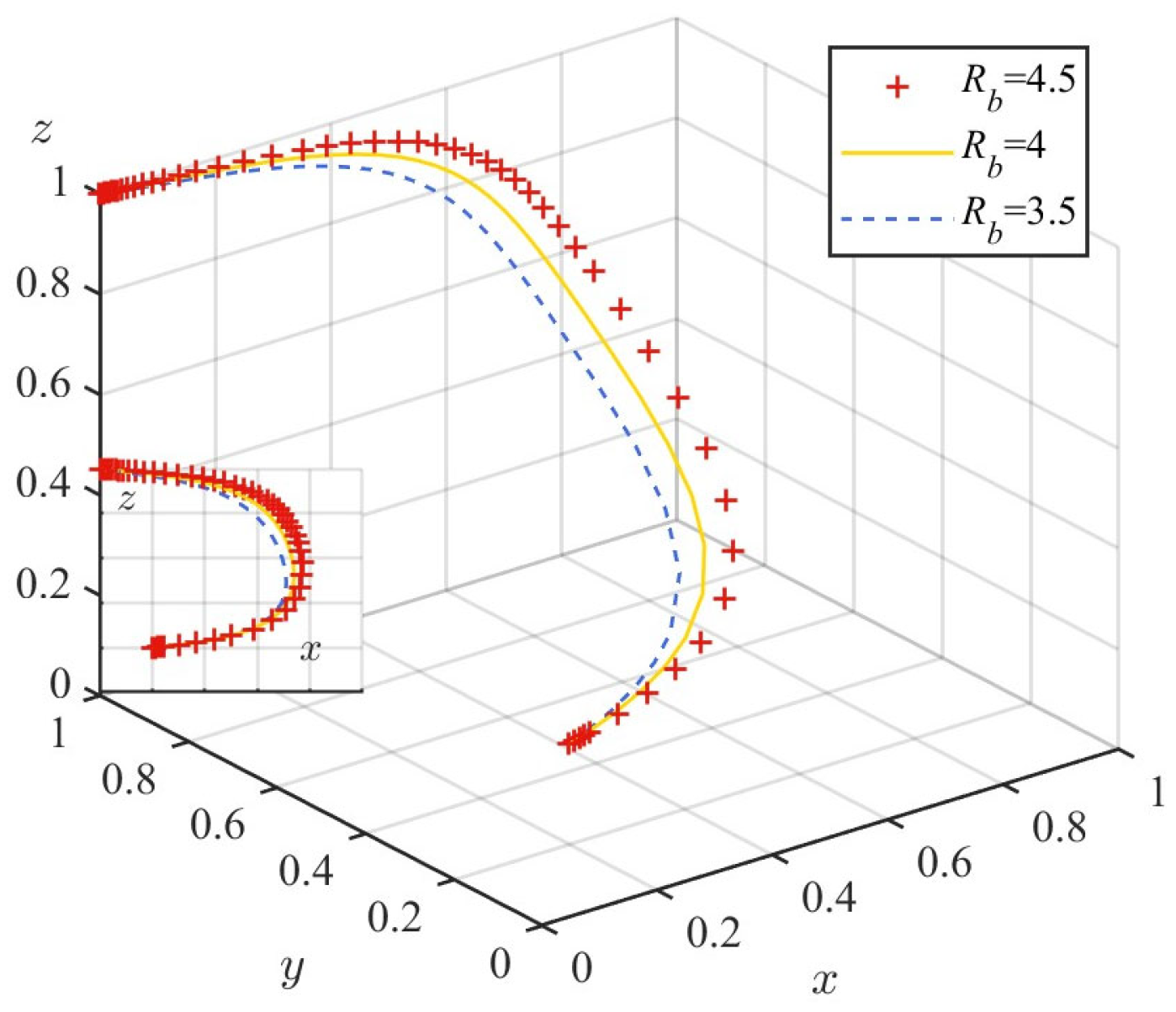
| Contractor (P2) | On-Site Team (P3) | Government (P1) | |
|---|---|---|---|
| Rigid Regulation () | Flexible Regulation () | ||
| Deep adoption () | High-effort collaboration () | ||
| Low-effort collaboration () | |||
| Symbolic adoption () | High-effort collaboration () | ||
| Low-effort collaboration () | |||
| Equilibrium Point | Eigenvalue | Eigenvalue | Eigenvalue | Stability | Degree of Desirability |
|---|---|---|---|---|---|
| Condition 1 | Least desirable | ||||
| Condition 2 | Least desirable | ||||
| Condition 3 | Undesirable | ||||
| Condition 4 | Undesirable | ||||
| Condition 5 | Undesirable | ||||
| Condition 6 | Undesirable | ||||
| Condition 7 | Most desirable | ||||
| Unstable | Desirable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Chen, L.; Luo, X.; Li, W.; Zhang, L.; Li, Q. Incentives, Constraints, and Adoption: An Evolutionary Game Analysis on Human–Robot Collaboration Systems in Construction. Systems 2025, 13, 790. https://doi.org/10.3390/systems13090790
Zhang G, Chen L, Luo X, Li W, Zhang L, Li Q. Incentives, Constraints, and Adoption: An Evolutionary Game Analysis on Human–Robot Collaboration Systems in Construction. Systems. 2025; 13(9):790. https://doi.org/10.3390/systems13090790
Chicago/Turabian StyleZhang, Guodong, Leqi Chen, Xiaowei Luo, Wei Li, Lei Zhang, and Qiming Li. 2025. "Incentives, Constraints, and Adoption: An Evolutionary Game Analysis on Human–Robot Collaboration Systems in Construction" Systems 13, no. 9: 790. https://doi.org/10.3390/systems13090790
APA StyleZhang, G., Chen, L., Luo, X., Li, W., Zhang, L., & Li, Q. (2025). Incentives, Constraints, and Adoption: An Evolutionary Game Analysis on Human–Robot Collaboration Systems in Construction. Systems, 13(9), 790. https://doi.org/10.3390/systems13090790







