Drone-Assisted Order Picking Problem: Adaptive Genetic Algorithm

Abstract

This study tries to make some improvements in the order picking operations by offering a novel mathematical model and efficient solution algorithm. Accordingly, the order picking policies are examined to allow for picking more orders by reducing the collection time/distance of order pickers. Batching orders for the pick are included in the order picking process as it could enable the order picker to collect more orders. Since the most labor-intensive movement in the order picking function in a high-level shelf layout is the retrieval of products from upper shelves and placing them onto the collection vehicle in the picker-to-part system, the use of drones is preferred to eliminate this costly movement. Drones assist humans in the order picking process by retrieving products from upper levels, thus reducing the order picking time. Here, a Vehicle Routing Problem (VRP) is formulated to deal with drone routing which is then solved based on the Order Picking Problem (OPP) framework. Consequently, an integrated OPP involving both order pickers and drones is addressed and formulated using a Mixed-Integer Linear Programming (MILP) model. To cope with the complexity of the problem, an Adaptive Genetic Algorithm (AGA) is designed which is able to yield superior results compared to the classical Genetic Algorithm (GA). Finally, a sensitivity analysis is performed to assess the behavior of the model against real-world fluctuations. The main reason for this research is to speed up the order picking process in warehouses by taking advantage of the tools brought by the technology age. According to the research results, when the results of the drone-assisted order picking process are compared to the order picking process without drone support, an improvement of 29.68% is observed. The theoretical contribution of this work is that it initially mathematically defines the drone-aided OPP in the literature and proposes a solution with the help of the AGA. As a practical contribution, it provides a solution with the capacity to reduce operational costs by accelerating the order picking operation in warehouses and a practical optimization framework for logistics managers. In addition, warehouse managers, senior company managers, and researchers working on order picking processes can benefit from this study.

1. Introduction

The term “Unmanned Aerial Vehicle (UAV)” refers to a remote-controlled, autonomous, or guided aircraft that is not occupied by humans [1]. Originally developed for military purposes, UAVs, commonly known as drones, possess the ability to navigate without the need for traditional infrastructure, making them capable of accessing hazardous locations. Moreover, due to the absence of passengers, UAVs do not require cockpit and environmental systems, resulting in space and energy efficiency [2]. Owing to their exceptional mobility and functionality, drones find applications across various industries such as logistics, defense, surveillance, agriculture, healthcare, search and rescue, and entertainment [3,4,5]. For instance, following Hurricane Katrina in 2008, drones began to be utilized for humanitarian purposes alongside their military applications in the United States [6]. This event marked a shift in perception, with drones increasingly recognized as tools for serving humanity beyond their military functions. Subsequently, in 2010, Parrot introduced a drone with image and video recording capabilities that could be operated via smartphone [7]. The idea of drone delivery systems was pioneered by Amazon in 2013 as the world’s largest online retailer [8]. Drones were first employed for visual transmissions by film, television, and production companies in 2014 [9]. In 2017, Facebook embarked on the development of solar-powered drones to provide internet access to remote areas lacking connectivity [10]. Furthermore, in 2018, the Indian government implemented a security system utilizing drones to safeguard elephant populations in forests. Consequently, the utilization of drones has proliferated across diverse domains, accompanied by advancements in technology.

From 2023 to 2030, the market for commercial drones is projected to grow at a compound annual growth rate of 13.9%, reaching an estimated value of USD 19.89 billion [11]. The company, consumer, public safety, logistics, and passenger market segments all contribute to the overall size of the drone industry. Among these segments, businesses are expected to experience the fastest growth rate until 2025, after which logistics is predicted to grow at the fastest pace [12]. According to forecasts, this growth is expected to be at a Compound Annual Growth Rate of 20.8% from 2022 to 2031 [13]. These statistics indicate an increasing utilization of drones in the logistics industry, demonstrating ongoing evolution and improvement in drone technology.

Order picking and management operations have had a large transformation since the industrial revolution. Conventional order picking techniques employed manpower, but they consumed time and resources and hence were operationally inefficient. In the middle of the 20th century, applications like belt conveyor systems, barcode scanners, and computer-based automated Warehouse Management Systems (WMSs) proliferated in order to deliver efficiency and speed in warehouse operations. The rapid growth of Industry 4.0 innovations and e-commerce has accelerated the adoption of autonomous vehicles and robot systems in warehouses and accentuated human–machine collaboration-based solutions in order picking. Today, drones and Artificial Intelligence (AI)-based optimization algorithms are widely used to bring order picking processes to be faster, cheaper, and more flexible.

There are two main areas of drone use in logistics: indoor and outdoor. Drone use outside the warehouse is associated with the logistics distribution function, where drones are employed to deliver products from warehouses to customers [14]. Drone use within a warehouse operation is referred to as indoor drone use. Inventory management, intra-logistics, and inspection and surveillance constitute the three primary groups for indoor applications [15,16]. The primary objective of inventory management is to maintain products safely in the warehouse under appropriate conditions until they are ready for distribution to customers. Drones can perform various functions in this regard, including inventory audit, cycle counting, buffer stock maintenance, stocktaking, and item search within the warehouse [15,16]. Operations involving intra-logistics can also benefit from drone usage, where drones transport items or goods from warehouses to other locations. However, operating drones within a warehouse presents challenges due to their capability to transport objects but difficulty in handling them, leading to certain limitations in this area [15,16,17]. In warehouse settings, drones can be utilized for surveillance and inspection purposes, allowing for immediate observation of inventory on shelves, warehouse conditions, pallet positioning, and temperature monitoring. Routine drone observation can also deter theft and undesired behavior in the facility, making it a practical approach to reducing costs and improving warehouse operations.

Companies aiming to adapt to technological advancements are exploring various strategies to achieve this transition. While the integration of drones in product distribution yields profitability for companies, their utilization within warehouses also proves lucrative. This study endeavors to elucidate these benefits to researchers and industry experts. Employing drones in the order picking process is proposed herein to minimize the time and distance traveled by order pickers. To address the challenge, a novel mixed-integer programming model is developed, alongside the proposal of an Adaptive Genetic Algorithm (AGA) as a metaheuristic solution. The main reason for utilizing AGA is that it is an algorithm that exceeds the limits of GA. GA is quite successful in optimization problems but has some limits; AGA, which is proposed as an algorithm that exceeds these limits, was applied in this research to achieve better results. In addition, the seed algorithm, which is a grouping algorithm in particular, was integrated into AGA and used so that AGA can produce better results.

New test data are generated and applied within the solution algorithm. The study posits several research questions within this framework, seeking to provide insights into these inquiries:

• RQ1: Can drones be effectively utilized alongside order pickers in warehouse order picking operations? If so, what is the optimal formulation of this problem?
• RQ2: Can the formulated problem be effectively solved? Furthermore, how can maximum efficiency be achieved in the order picking process with drone assistance (by Order Batching Problem)?
• RQ3: What are the comparative results between the classical Genetic Algorithm (GA) and the AGA in solving this problem?
• RQ4: How can we analyze the sensitivity of the developed model against the fluctuations of key parameters?

The findings of this research are of particular interest to company managers in the field. This work explains how to reduce the time and effort spent on order picking, which is the costliest process in warehouses, and therefore serves as a guide for researchers. It also has theoretical contributions as well as contributions to the field as mentioned. For example, in the studies conducted so far in the related literature, the order picking process in general has only been handled with either order pickers or robots. Since there is no research in the literature where drones are used to assist order pickers, this work is the first to fill this gap. Moreover, it is the first study to use the seed algorithm within the AGA metaheuristic.

The structure of the remaining sections is as follows: Section 2 provides a brief theoretical framework for the problem. Section 3 examines the problem description and presents the mathematical model. Section 4 defines the solution methods employed in this research. The numerical experiments and computational analysis are presented in Section 5. Section 6 discusses the practical implications and managerial insights. Final considerations and recommendations for future studies are provided in Section 7.

2. Background

The use of drones in logistics has gained unprecedented speed over the past decade. Most present research works primarily segregate into two broad categories: external logistics (outbound logistics) and internal warehousing activities (intra-logistics). Drones have been thoroughly studied in outbound logistics, particularly delivery and transportation operations, but relatively less work has been carried out on their applications in intra-logistics [18,19,20,21,22,23].

Some studies discuss the application of drones in outbound logistics, in which they are primarily employed for delivering products to customers. Such applications tend to focus on solving the Drone Routing Problem (DRP) as well as improving delivery efficiency [21,24,25,26,27]. Drones are particularly useful in exactly localizing coordinate systems and independently navigating routes to deliver goods, saving significant operational expenses [28,29]. Researchers have also indicated that the cost advantages of drone logistics are likely to outweigh the cost of establishing the infrastructure [23,24].

In comparison to external logistics, intra-logistics uses of drones are less addressed but hold immense potential. Intra-logistics encompasses activities such as inventory management, warehouse monitoring, inspection, and material handling. Multiple studies have examined the application of drones in warehouse inventory control. Researchers have investigated where to place drones for proper positioning within warehouses to enhance efficiency [30]. Studies ventured into drone-based solutions for scanning items’ barcodes and inventory database management through advanced sample-based algorithms [31,32]. Others have proposed new inventory models where drones scan shelves within warehouses to identify open slots [33]. Drones have also found applications in warehouse security and infrastructure monitoring. Drones have been utilized for enhancing warehouse surveillance and operational control [34]. Few research works investigated the application of drones in thermal inspection of factory equipment, e.g., injection molding machines in factories [35].

While intra-logistics literature is limited, attempts have been made to address its issues. Drones have been proposed as a mode of transportation of raw materials and products between different areas of a facility, with heuristic-based scheduling algorithms increasing efficiency [36,37]. Drones have been researched for application in picking up orders from customers, reducing travel distance, and optimizing warehouse layout [38,39]. In spite of promising developments, a number of challenges face the extensive use of drones in logistics, especially intra-logistics. In contrast to robotic arms, drones cannot physically handle and move products prior to shipping [15,16,17]. Factors affecting drone adoption in digital and smart warehouses have been examined in studies, such as battery constraints, collision avoidance, and system integration issues [15]. Malang et al. [40] performed a systematic review of drone use in warehousing, examining how recent developments overcome current barriers. Although drones have shown considerable advantage in outbound logistics, internal warehousing uses are not yet well explored. Follow-up research should focus on designing advanced manipulation technology enabling drones to manipulate and relocate objects more efficiently, advancing AI-driven drone navigation systems for autonomous operation in cluttered warehouse environments, combining drones with warehouse robots to develop hybrid systems for efficient material handling and inventory management, and analyzing cost–benefit trade-offs to increase understanding of the economic feasibility of warehouse-scale drone deployment.

2.1. Motivation of the Study

Especially the logistics sector must keep pace with technological advancements. With Industry 4.0, various innovations have emerged in the business world, compelling companies to adapt. The driving force behind this alignment is their pursuit of increased profits through technological advancements. This pursuit has led companies to utilize drones in the logistics industry, making the use of drones in this sector inevitable. This study emerged from this necessity to employ drones in logistics activities. Upon observation of the relevant field and scanning the pertinent literature, it was noted that relatively less attention had been given to the utilization of drones in warehouse functions, prompting a need for focus.

2.2. Research Gaps

According to the literature examination with regard to the research questions, the following research gaps are identified:

• No study has analyzed the usage of drones with order pickers in the order picking operations in the warehouse to minimize the total time and traveling distance;
• No study has proposed AGA integrated with seed algorithms for the Order Picking Problem (OPP).

2.3. Contributions of the Study

As previously noted, the utilization of drones in warehouse operations remains relatively limited. Existing studies in the literature often overlook specific challenges related to integrating drones using mathematical models and proposing solutions. In this work, a drone-assisted order picking system is designed and formulated using a novel Mixed-Integer Linear Programming (MILP) model. Furthermore, an AGA is offered to treat the complexity of the problem. The primary aim of this study is to guide researchers interested in implementing drones within warehouse environments where orders are particularly picked by batching. Therefore, this research makes the following novel contributions to the literature in three categories:

1.

Proposal and Modeling of the Problem

• Proposing a solution to the OPP using metaheuristic methods while considering the utilization of drones with a mathematical model.

2.

Algorithm Design

• Utilizing AGA together with seed algorithms for the OPP for the first time.

3.

Computational and Managerial Analysis

• Analyzing the usage of drones with order pickers in order picking operations within the warehouse to minimize the total traveling distance.
• Conducting a sensitivity analysis to study the behavior of the model against the possible changes in key parameters.

3. Problem Description

This research explores an OPP where drones assist order pickers. The concept involves employing drones to pick products at higher levels, which would otherwise be time-consuming for human order pickers. By integrating drones into the order picking process, the goal is to enhance efficiency by reducing both distance and time spent on order picking tasks.

The novelty of this study lies in addressing an OPP with drone assistance, a topic not previously explored in the literature. In the scenario examined, there is one drone and multiple order pickers, each starting their routes simultaneously from a common starting point with their respective order picking lists. As they collect products, the order pickers deposit them at designated pick-up and drop-off points. Each order picker’s route is treated as a group, and these groups are arranged in order upon product collection. To prevent confusion, the drone places finished groups back in their designated row at the collection point.

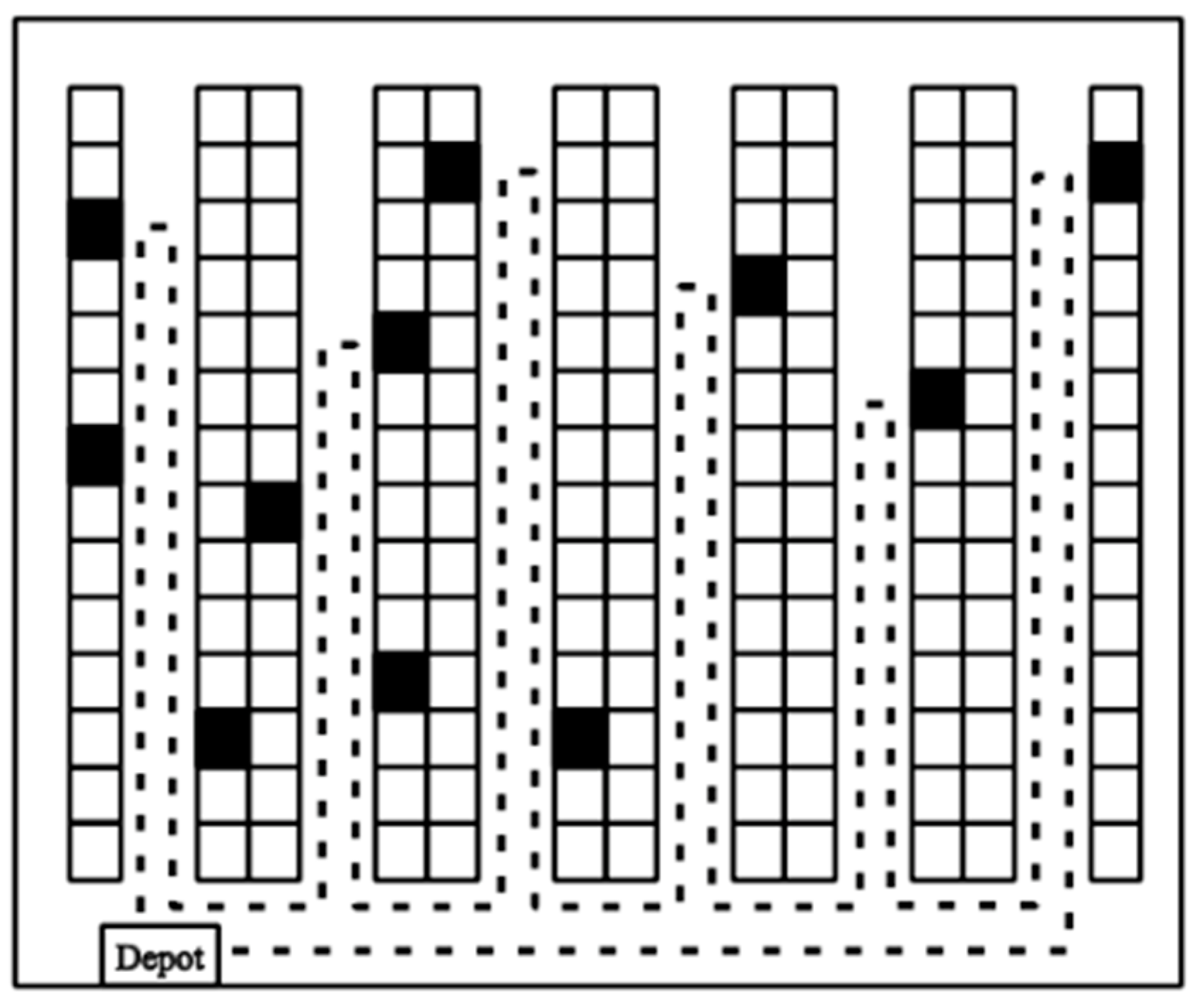
To tackle this problem, a new mixed integer programming model is developed. When devising a solution, various order routing methods are considered. Although the literature offers different approaches for order picking within warehouses [41], this work assumes the use of the return heuristic method, where order pickers enter and exit the same aisle after completing their picking tasks [41]. The experimental design for this study involves a hypothetical single-block warehouse layout, with the depot situated in front of the leftmost aisle, as depicted in Figure 1.

Furthermore, the drone’s route is determined using the Vehicle Routing Problem (VRP). While metaheuristic solutions are employed to decide which products would be picked in each batch for the drone, no information is provided regarding how the drone would navigate among these products—specifically, which products it would visit and in what sequence. Hence, a VRP arises at this stage, which is addressed using GA. Subsequent subsections present an example of this problem and the corresponding mathematical model developed.

3.1. Illustrative Example

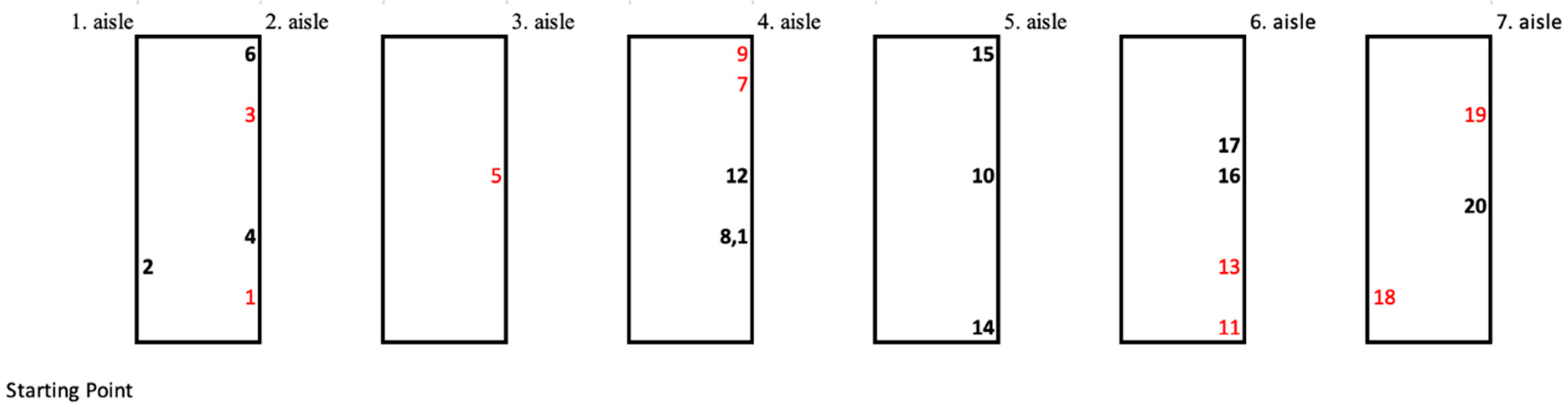
To clarify the problem more easily, we provide an example. In this example, the warehouse consists of 7 aisles, and there are 20 products ordered by 10 customers.

Table 1. Data of the given example.

Customer	Products	Total Weight (kg)
1	1, 2, 3	16 (5 + 7 + 4)
2	4, 5	15 (7 + 8)
3	6	9
4	7	4
5	8, 9, 10	21 (9 + 4 + 8)
6	11	6
7	12, 13, 14	16 (8 + 5 + 3)
8	15	5
9	16, 17, 18	20 (7 + 7 + 6)
10	19, 20	18 (8 + 19)

presents the customers, their respective orders, and the weights of these orders. The drone’s capacity is 25 kg, while the order picker can carry up to 40 kg. Additionally, each aisle has a width of 5 m, and each rack is 2 m wide.

In the given example, there are 7 aisles, each containing 10 storage slots, as illustrated in Figure 2. The products picked by the drones are 1, 3, 5, 7, 9, 11, 13, 18, and 19 (highlighted in red in Figure 2), while the products picked by the order picker are 2, 4, 6, 8, 10, 12, 14, 15, 16, 17, and 20. Moreover, the maximum vertical distance dataset is given in

Table 2. Maximum vertical distance dataset for the illustrative example (order number/aisle number).

	1	2	3	4	5	6	7
1	3	0	0	0	0	0	0
2	0	4	0	0	0	0	0
3	0	10	0	0	0	0	0
4	0	0	0	0	0	0	0
5	0	0	0	4	6	0	0
6	0	0	0	0	0	0	0
7	0	0	0	5	1	0	0
8	0	0	0	0	10	0	0
9	0	0	0	0	0	6	0
10	0	0	0	0	0	0	4

, which refers to what must be traveled in the aisles to collect the products in the orders, depending on the products. In the given example, the order number and customer number can be considered equivalent. Because each customer can only place one order and these orders can contain different products, the order codes from customers are called order numbers which may contain a single product or different products. The aisle number refers to the corridor numbers in the warehouse. Therefore, the rows in Table 2 refer to the order number and the columns refer to the aisle number. Accordingly, the first order has a 3 m distance in the first aisle.

The following solution is proposed wherein the orders are divided into two batches for picking. The products in the first batch are 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10. As a result, the orders of the first five customers are allocated to the first batch, while the orders of the remaining five customers are allocated to the second batch. This approach ensures optimal efficiency for both the order pickers and the drone, allowing them to work at full capacity.

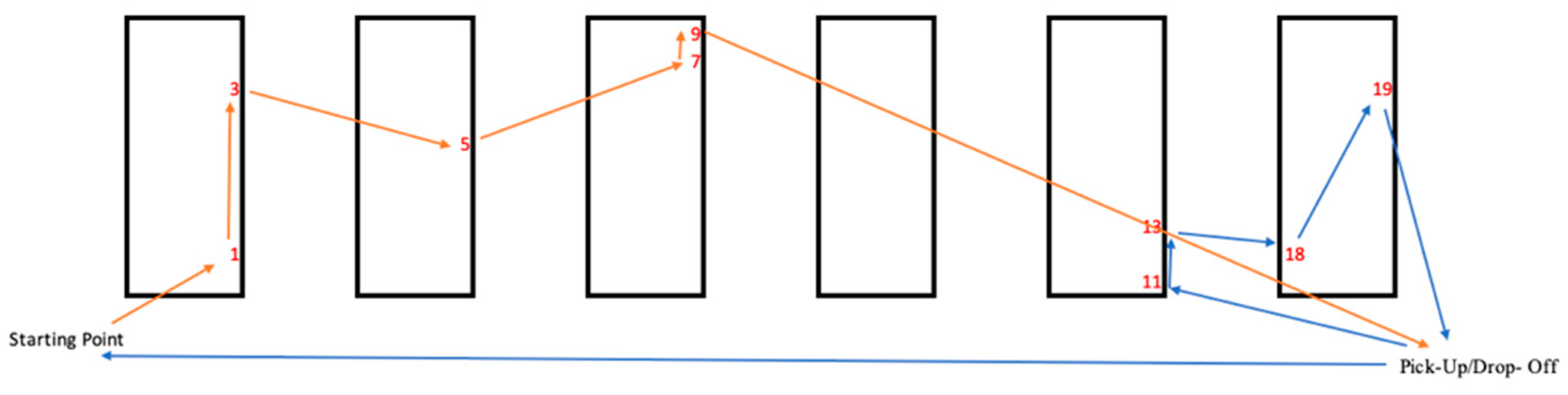
We need to calculate the distances traveled by both the order pickers and the drone according to the provided solution. The routes are determined based on this solution. For the drone’s first route, the sequence is 1, 3, 5, 9, 7, and for the second route, it is 11, 13, 18, 19. The distances traveled by the drones should be calculated using Euclidean distances, considering the coordinates as parameters. Upon calculating the distances of the drone routes, we find 68 m for the first batch and 49 m for the second batch, resulting in a total distance of 117 m for the drone.

Regarding the order pickers, the first picker travels a distance of 102 m, while the second picker covers 120 m. Thus, the total distance traveled by the order pickers is 222 m. Consequently, the total distance required to pick up the orders is calculated as 339 m.

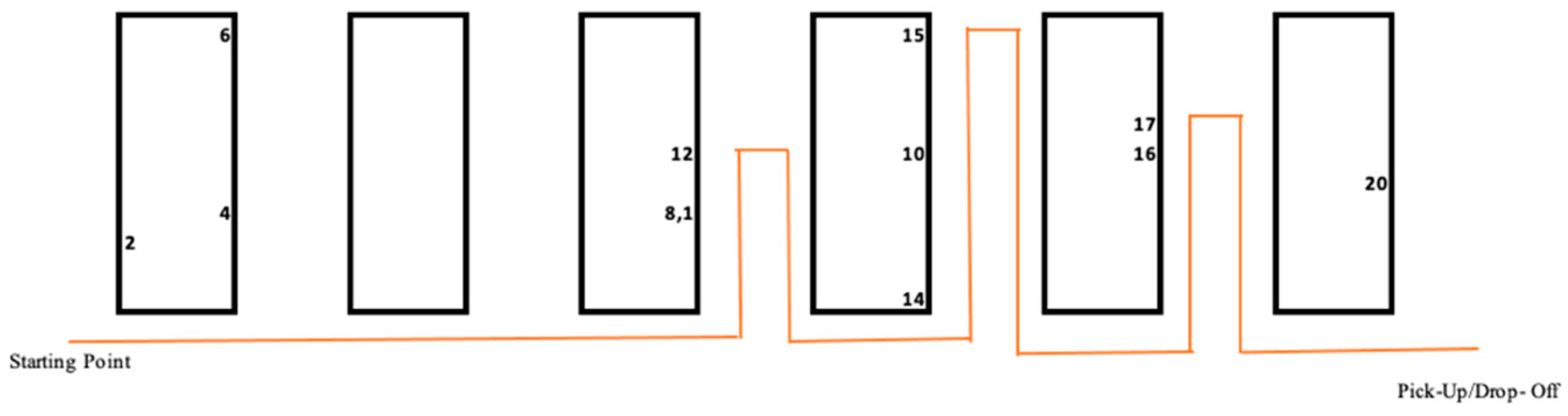
Furthermore, the drone routes are depicted in Figure 3. The route marked with orange arrows represents the path followed by the drone while collecting the first group, and the route shown with blue arrows represents the path followed while collecting the second group. The drone starts its movement from the starting point, moves towards the product codes indicated in red to collect them, and thus collects the specified products, and drops them off at the pick-up/drop-off point. This route is the first route of the drone that is shown with orange arrows in the figure. Then, it starts its second route from its current location to collect the second group, and after collecting the specified products, drops them off at the pick-up/drop-off point, then returns to the starting point. As a consequence, the second route of the drone ends.

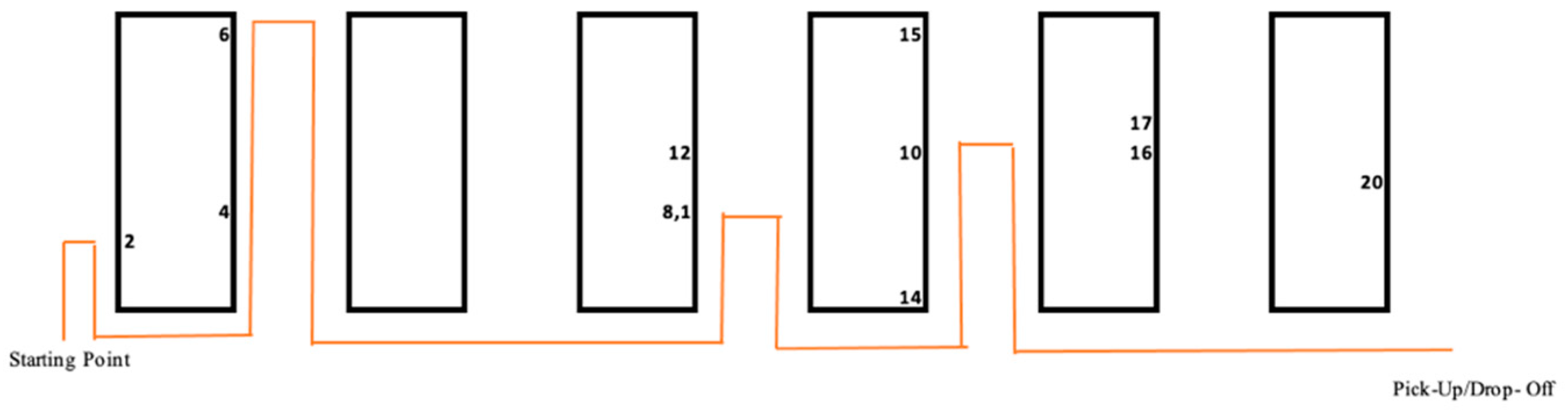
As for the order pickers, the route for picking the first batch is shown in Figure 4, and the route for picking the second batch is depicted in Figure 5. Each route begins from the starting point and concludes at the pick-up/drop-off point.

In addition, to better highlight the problem-solving procedure, the solution (without drone assistance) is discussed as follows. Solving the OPP problem without drones in this study means that the order pickers must pick up all the orders themselves. Therefore, the products are not collected in two different clusters; all the products must be on the order picker’s list. In the first solution, orders are collected by drone and there are two rounds for the drone and two rounds for the order picker. In addition, the order picker and the drone work simultaneously. In the second solution, there is no drone, and since the order picker collects all the products, there are four batches in total, so the order picker needs to make four rounds. According to this calculation, the distance required for the picker to collect all the products is 378 m in total. In the first solution, this total distance is 339 m. Thus, if we consider the objective function only as distance, there is a total improvement of 10.3%. However, it would be more realistic to add the order picking distances to the objective function. When calculating order picking times, the assumed speed and transportation times based on the distances covered, as well as the time it takes to pick up the products from the shelves, must be calculated together. The necessary calculations are given below, and the results are presented in

Table 3. Results of the illustrative example.

	Total Distance (meter)	Total Time (second)
Solution with drone	339	255
Solution without drone	378	485
Efficient rate (%)	10.3	47.42

.

Let us assume that the speed of the drone is 10 km/h and the speed of the order picker is 10 km/h. In the example, there are 9 products that can be picked by the drone and 11 products that can be picked by the order picker. If we assume that the order picking process is performed only with the order picker, the time it takes for the picker to pick the product from the upper shelves is 10 s and the time it takes to pick the product from the lower shelves is 5 s.

• For the solution without drone assistance
  Time to pick up the product from the upper shelves = 9 × 10 = 90 s,
  Time to pick up the product from the normal shelves = 11 × 5 = 55 s,
  Order picker transportation time = 340 s,
  Total time = 90 + 55 + 340 = 485 s.
• For the solution with drone assistance
  Drone order picking time = 42 s,
  Picker order transportation time = 200 s,
  Normal product picking time from shelves = 11 ∗ 5 = 55 s,
  Total time = max (42, 200) + 55 = 255 s

3.2. Mathematical Model

The model’s underlying assumptions are detailed as follows, and the notation utilized in the model is outlined in

Table 4. Notations.

Indices and Sets
$i,j$	Products that can be picked with an order picker
$m,n$	Products that can be picked with the drone
$a\in A$	Order pickers
$p\in P$	Aisles
$o\in O$	Orders
$b\in B$	Batches
$\phi \in \Phi$	Sequences of the drone
$N_i$	Set of all products that can be picked with an order picker
$N_m$	Set of all products that can be picked with the drone
Binary Decision Variables
$y_{mn}^{\phi }$	1, if the drone is going to nth product after mth product in $\phi$th sequence, 0 otherwise
$z_{oba}$	1 if oth order is assigned to bth batch and ath order picker, 0 otherwise
${\propto }_{bpa}$	1 if pth aisle travels in bth batch in ath order picker, 0 otherwise
${\beta }_{ao}^{ib}$	1 if ith product of oth order assigned to bth batch and ath order picker, 0 otherwise
Continuous Decision Variables
$h_{ba}$	Horizontal distance that must be covered to put together bth batch ath order picker
$s_{bpa}$	Maximum distance traveled along with pth aisle for bth batch ath order picker
$y_m$	Sub-tour elimination variable
Parameters
$e_{mo}$	A matrix representing whether oth order includes mth product
$r_{op}$	Maximum vertical distance that goes along the pth aisle starting from the front aisle for the oth order
$v$	Distance between the aisles
${ d}_{mn}$	Euclidian distance between the products
$c$	Capacity of the order picker
$C$	Capacity of the drone
$w_i$	Weight of the ith product
N	Very big number

. Throughout the development of the programming model, certain constraint sets were referenced from existing papers [41,43]. The main consumptions of the model are described below:

• At the pick-up and drop-off point, the groups are placed side by side. However, when calculating the total distance traveled by the drone and the order picker, the distance covered while dropping off the collected products was disregarded due to its insignificance.
• Each customer can place only one order.
• An order may contain multiple products.
• Orders must be collected in groups, and the products within an order cannot be separated; hence, all products in an order must be collected together in the same group.
• The velocities of drones and order pickers are fixed and known.
• Order pickers have the flexibility to pick up orders in both directions.
• The storage locations of the Stock Keeping Units (SKUs) are predetermined and known.
• Order pickers in the warehouse follow the return heuristic when picking orders.

Now, the model is developed as follows:

$$\begin{gathered} \mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} (\sum _a\sum _b{2h}_{ba}+\sum _a\sum _b\sum _p{2s}_{bpa})+\sum _{\phi }\sum _m\sum _n{d}_{mn}{y}_{mn}^{\phi } \\ \mathrm{subject} \mathrm{to} \end{gathered}$$

(1)

$${z_{oba}e}_{mo}\le \sum _n\sum _{\phi }{y}_{mn}^{\phi } \forall m,o,a,b,$$

(2)

$$\sum _n{y}_{mn}^{\phi }-\sum _n{y}_{nm}^{\phi }=0 \forall m,\phi ,$$

(3)

$$\sum _n{y}_{0n}^{\phi }-\sum _n{y}_{n0}^{\phi }=|B| \forall \phi ,$$

(4)

$$\sum _n\sum _o\sum _m{{y_{mn}^{\phi }w}_{m}e}_{mo}\le C \forall \phi ,$$

(5)

$$y_m\ge y_m+1-N\left(1-\sum _{\phi }{y}_{mn}^{\phi }\right) \forall m,n,$$

(6)

$$\sum _a\sum _b{z}_{oba}=1 \forall o,$$

(7)

$$z_{oba}{e}_{io}={\beta }_{ao}^{ib} \forall o,b,i,a,$$

(8)

$$x_{o\phi }{e}_{mo}=\sum _n{y}_{mn}^{\phi } \forall o,m,\phi ,$$

(9)

$$\sum _i\sum _o{\beta }_{ao}^{ib}{w}_i\le c \forall b,a,$$

(10)

$${\propto }_{bpa}\le \sum _o{r}_{op}{z}_{oba}\le M{\propto }_{bpa} \forall p,b,a,$$

(11)

$${v\propto }_{bpa}\le h_{ba} \forall b,p,a,$$

(12)

$${r_{op} z}_{oba}\le s_{bpa} \forall o,b,p,a,$$

(13)

$$d_{mn}=\sqrt{{(n_x-m_x)}^2+{(n_y-m_y)}^2} \forall m,n,$$

(14)

$$y_{mn}^{\phi }\in \left\{\mathrm{0,1}\right\} \forall m,n,\phi ,$$

(15)

$$z_{oba}\in \left\{\mathrm{0,1}\right\} \forall o,b,a,$$

(16)

$$h_{ba}\ge 0 \forall b,a,$$

(17)

$$s_{bpa}\ge 0 \forall b,p,a,$$

(18)

$${\propto }_{bpa}\ge 0 \forall b,p,a,$$

(19)

$$y_m\ge 0 \forall m.$$

(20)

Objective Function (1) consists of two terms. The first term takes into consideration the order picker’s traveled distance. The second term shows the traveled distance by the drone. The order picker distance is calculated as the addition of the motion in vertical and horizontal axes. According to the Manhattan distance formula, the sum of these two distances is the total distance covered by the order picker. This expression was constructed in this way because it is aimed at calculating the minimum distance while performing the order picking.

Constraints are also classified as follows:

I

Constraints Related to the DRP

Constraint (2) guarantees that all products in a single order are selected at the same time. Orders cannot be fragmented, hence products can be dispatched in the same shipment. Constraint (3) defines the route flow in the drone’s route. It provides the correct representation of the VRP problem through indicating vehicle movements between different products. Constraint (4) states the starting and ending points of every drone. Each drone must begin from the specified distribution center and must also end at the same point. Constraint (5) expresses the capacity constraints for every drone. It enforces the necessary capacity limitations to keep the drone from overloading beyond the capacity that it is expected to carry. Constraint (6) prevents sub-tours. It was added to prevent the drone from going on a wasteful tour by creating ridiculous loops.

II

Constraints Relating to the Order Picking Process

Constraint (7) ensures that all orders are assigned to a picking group (batch). This way, all orders are collected in a specific sequence and can be tracked. Constraint (8) guarantees that all items belonging to an order are collected within the same batch. It forces the order picker to process items within the same group, hence preventing the order from being disjointed. Constraint (9) represents that the drone is not allowed to split orders. As with the order picker, the drone must not deliver orders in pieces.

III

Constraints Related to the Order Picker’s Distance

Constraint (10) places the capacity constraints of the order picker. The amount of product that may be carried by the order picker is finite and this must not be exceeded. Constraint (11) allows entry into the aisle containing at least one product in an order. That is, the order picker can enter aisles containing products for an order. Constraint (12) computes horizontal distance of the order picker. It calculates the total distance the order picker travels on the horizontal axis. Constraint (13) computes the order picker vertical movement distance. Increases operational efficiency by calculating the maximum vertical movement distance to pick items.

IV

Constraints Related to the Distance of the Drone

Constraint (14) calculates the distance traveled by the drone. It computes how far orders carried by the drone travel, etc.

V

Constraints that Ensure the Math Model’s Integrity

Constraints (15)–(20) display the types of the variables. They restrict the model’s numeric variables to hold only certain integral values and render the model physically viable.

4. Adaptive Genetic Algorithm

In this research, AGA, as an improved version of the classic GA, is proposed to tackle the problem. The GA is a population-based metaheuristic search algorithm within metaheuristic algorithms and was developed in [44] by imitating the process of biological evaluation in a computer environment. The GA is an efficient and prominent solution method for optimization problems [45]. However, the algorithm has some difficulties such as the standard parameters including mutation and crossover rates that are certain and scalar parameters within the algorithm. These parameters are very important because being low means reducing the diversity of the algorithm while being high means not being able to find the global optimum point. Therefore, these parameters must be determined correctly to quickly find the global optimum point. In addition, since these rates are fixed, the GA quickly becomes stuck in the local optimum [46]. To solve this problem, an AGA is utilized wherein the crossover and mutation rates are calculated in the algorithm dynamically with the help of Equations (21) and (22) [46]:

$$P_c=P_{c0}-\alpha {\displaystyle \frac{gen}{maxgen}} {\displaystyle \frac{f\left(i\right)}{maxf\left(j\right)}} gen\le maxgen,$$

(21)

$$P_m=P_{m0}-\beta {\displaystyle \frac{gen}{maxgen}} {\displaystyle \frac{f\left(i\right)}{maxf\left(j\right)}} gen\le maxgen,$$

(22)

where $P_c$ denotes the probability of crossover, $P_m$ represents the probability of mutation, $P_{c0}$, and $P_{m0}$ are the initial rates of crossover and mutation, respectively, and $\alpha$ and $\beta$ denote stable values for updating the crossover and mutation rates in each iteration. Moreover, $f_i$ represents the objective function value and ${maxf}_j$ denotes the objective function value in the population.

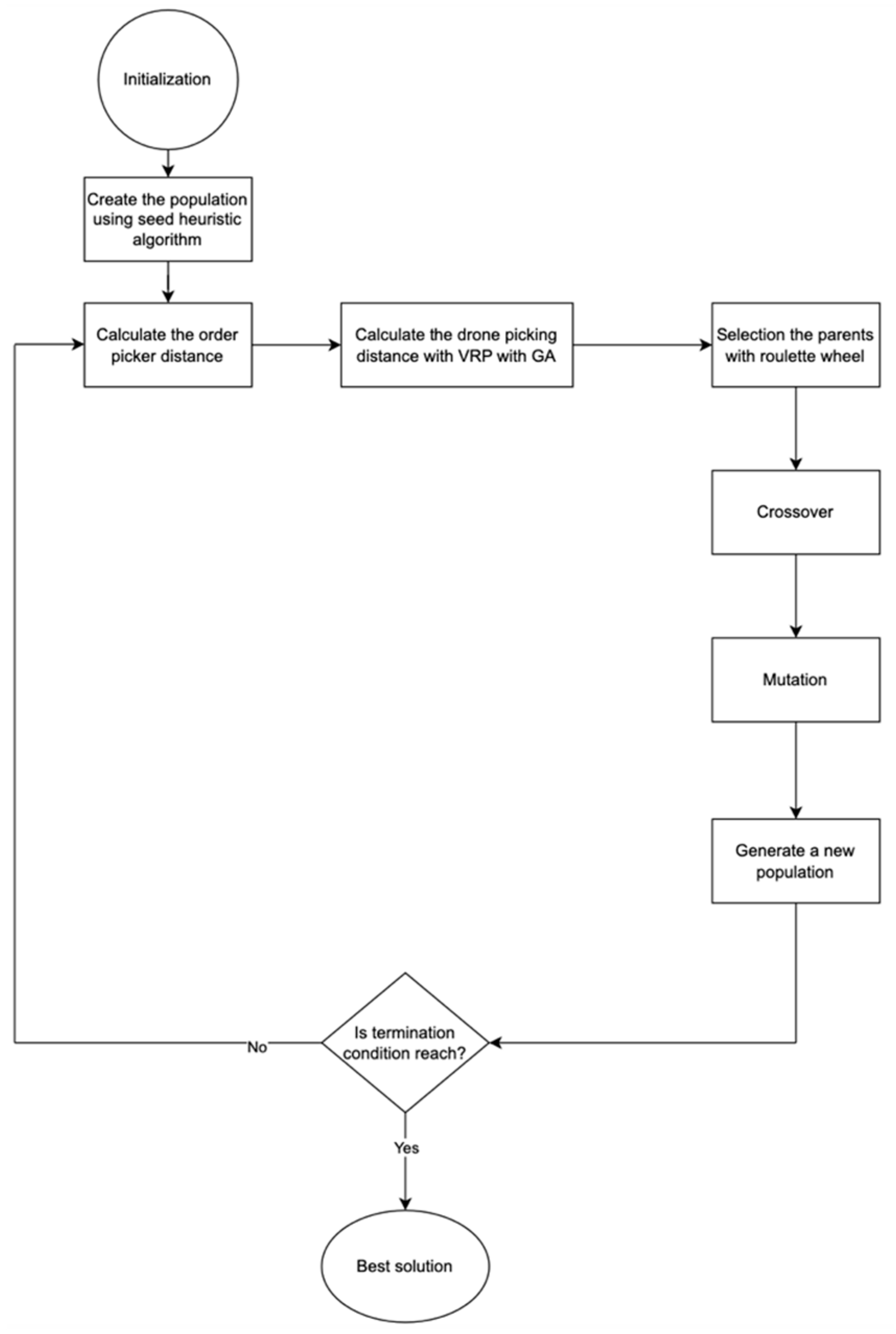
The flowchart of the suggested AGA is outlined in Figure 6. As per the flowchart, the algorithm initiates by generating the initial population using the seed algorithm. This seed algorithm, as described in the literature, is tailored to solve the order batching problem [47,48]. Within this algorithm, a seed order is chosen based on specific criteria, and subsequent orders are added to the batch according to predefined rules [47]. Here, the seed algorithm employs random selection criteria, and the addition rule is based on the number of common locations between two orders. Consequently, the initial population is established using the seed algorithm. Subsequently, the fitness function, representing the objective function value, is computed for each chromosome. Following this, parents are selected for reproduction using the roulette wheel method, with the aim of generating new individuals through crossover and mutation operations. Once the selection process is complete, the reproduction operations—crossover and mutation—are applied to the selected parents, resulting in the creation of a new population. The algorithm then evaluates whether the termination condition has been met; if so, the algorithm terminates; otherwise, it proceeds with a new generation.

The proposed solution comprises two stages. The objective function in the mathematical model includes two components: the distance covered by the order picker and the distance traveled by the drone. Therefore, it is necessary to calculate both the drone and order picker distances separately for each group. To achieve this, a GA is applied to the overarching problem outlined in this study. The chromosome representation of the AGA is depicted in Figure 7. In accordance with the GA, the orders from the first, third, and ninth customers are categorized into the first group; the orders from the fourth and seventh customers form the second group; the orders from the second, sixth, and eighth customers constitute the third group, while the orders from the fifth and tenth customers make up the fourth group. This process forms the chromosome structure for the GA.

The seed algorithm was utilized to establish the initial population. Within this seed algorithm, a random seed order is initially selected. Subsequently, a second order that closely resembles the products in the selected order is chosen. This process continues iteratively, with orders being added to the batches and chromosomes, ultimately leading to the creation of the initial population.

Furthermore, to determine the visit sequence of products to be picked by the drone within a batch, a VRP was formulated. The AGA chromosome representation for this VRP is displayed in Figure 8. For example, in the first group, the first product is not visited (the value is zero), the fourth product is visited in the first row, the seventh product in the second row, the second product in the third row, the third product in the fourth row, and the sixth product in the fifth row. In other words, the order specified in the cells represents the visit order.

Subsequently, the classical GA operations proceed. The initial population is randomly generated, and the roulette wheel method is employed for the selection process within the mating pool. Among the reproduction operators, both crossover and mutation operators are applied to the selected individuals. The termination criterion is determined based on the number of generations.

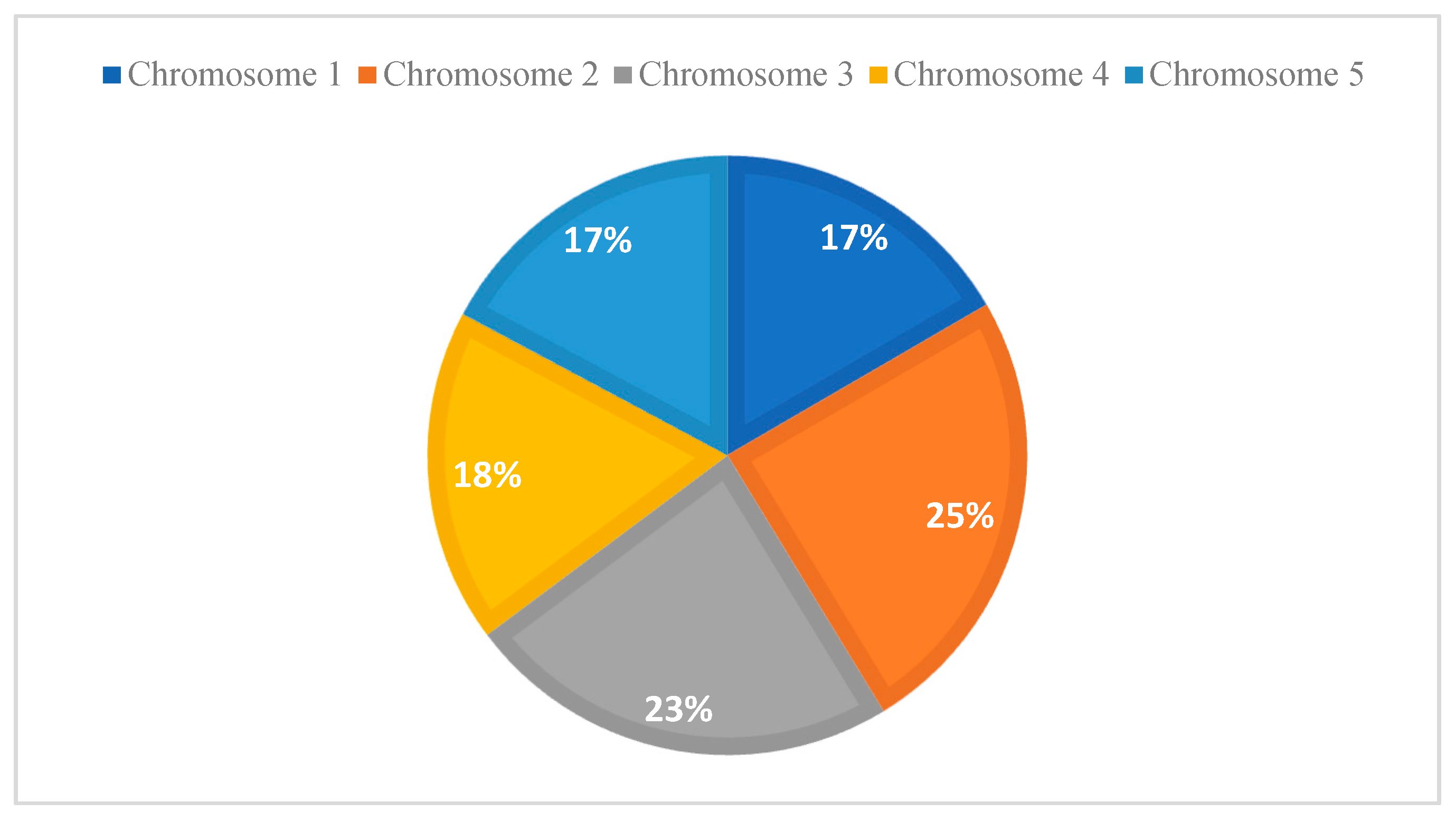
In both algorithms, namely the classic GA utilized for determining the minimum distance of the drone, and the AGA, the roulette wheel method is employed due to its ability to introduce a stochastic search procedure. The roulette wheel method involves several steps:

• Initially, chromosomes are arranged based on their objective functions.
• Subsequently, the selection probability of each chromosome is computed.
• Next, the cumulative probability is calculated.
• Following this, random numbers are generated, and based on these numbers, the corresponding chromosome is determined as given in

  Table 5. Example for the roulette wheel method.

  Chromosome	Fitness Function	Selection Probability	Cumulative Probability
  1	0.00552	0.17	0.17
  2	0.00822	0.25	0.42
  3	0.00781	0.23	0.65
  4	0.00599	0.18	0.83
  5	0.00571	0.17	1

  .
• Finally, a schema resembling Figure 9 is generated.

This approach facilitates the selection of individuals based on their fitness values, enabling the algorithm to efficiently explore the search space and converge towards optimal solutions.

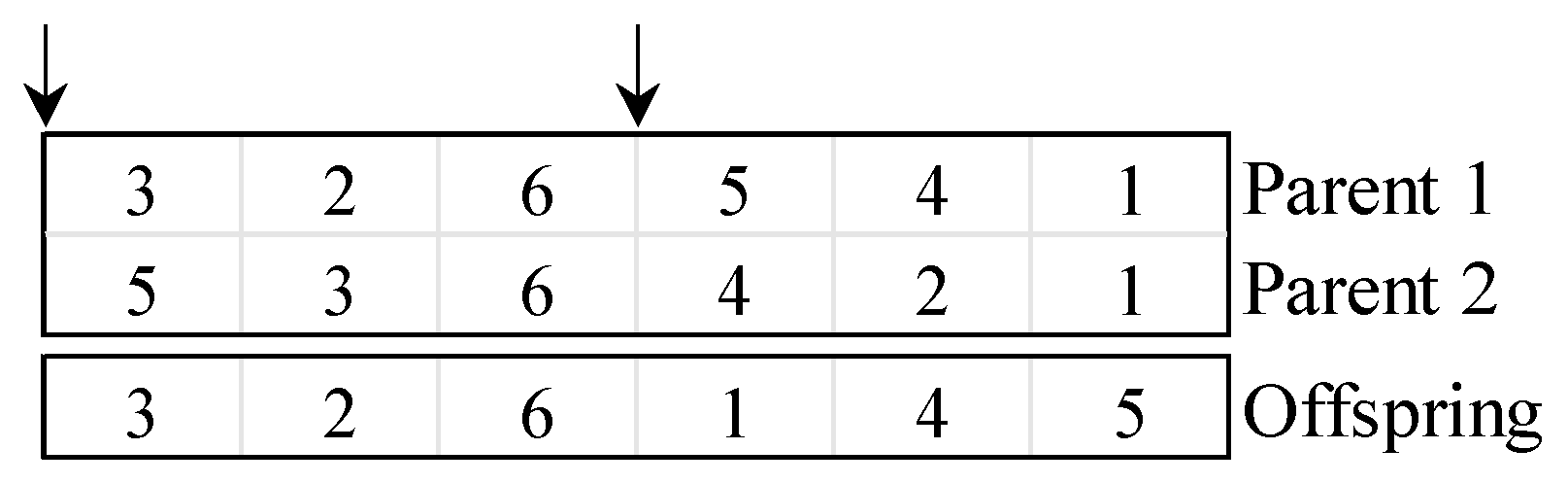
In both algorithms, crossover and mutation operations are used to reproduce the population. In the crossover operation, one pair of chromosomes from the matching pool is randomly chosen for crossover, and the crossover operator is used to create two new chromosomes from these two chromosomes. Of the methods of crossover, the two-point crossover method is used as given in Figure 10. It is determined randomly and the parent chromosomes split there. The mutation is used to replace certain genes in the offspring individuals that result from the crossover. Mutation is a significant factor because it leads the GA to solutions that are not possible to obtain by crossover.

5. Numerical Experiment

In this section, the data structure and performance of the algorithms are clarified to understand the solution example and to demonstrate that the algorithm produced the optimal solution value. The data structure is sufficiently explained here to serve as an example for future research.

5.1. Data Structure

In the example discussed in the study, the warehouse layout was established as depicted in Figure 1. As a result, the starting point for both the order picker and the drone is situated at the leftmost, while the location where they deposit the collected products is at the rightmost. The first aisle is positioned on the leftmost, and the ninth aisle is situated on the rightmost. The warehouse layout was based on general real-world fulfillment center layouts. The left-to-right sequence was chosen in order to follow a logical picking sequence common with modern warehouse operations. Aisle and starting point spatial distribution was determined based on existing warehouse best practices to render realistic distance values.

The warehouse mentioned in the study was identified as the same one discussed in [49]. Consequently, it comprises 900 storage locations, organized into 10 collection aisles. Each aisle contains 90 storage locations, with 45 located on the right side and 45 on the left side. The order picker can efficiently pick items from both sides of the aisle without any additional travel distance.

These data were hypothetically produced with a uniform distribution. The relevant data were obtained from a company operating in Turkey, and since the company did not want to provide all the data, it offered the min and max values, so the relevant data were produced hypothetically. To solve the problem effectively, some essential parameters need to be defined. Some of them are given in

Table 6. Model parameters.

Parameters	Values
Distances between the aisles	0.011 km
Capacity of drone	20 kg
Capacity of order picker	45 kg
Weight of products	0.1–5 kg
Coordinates of the products	0–10
Located aisle	1–8 (for medium-scale datasets), 1–10 (for large-scale datasets)
Horizontal distance	45 m

. Uniform distributions were applied to generate unbiased and even-spaced data points for order picking operations. In addition, the hypothetical data generation process was tested against warehouse layouts reported in the industry to ensure that the process stayed current. The minimum and maximum values generated allowed for realistic variance, incorporating different warehouse scenarios that may occur in the real world.

In the application part of the study, the solved examples are divided into three classes (i.e., small, medium and large-scale datasets) as given in

Table 7. Problem instance scales.

Problem Instances	No. of Customers	No. of Products	No. of Aisles
Small	5	10	4
Medium	35	50	8
Large	70	100	10

. Note that each dataset represents a different problem complexity level given by the example scales (small, medium, and large). This structure is actually created according to the problem size. Accordingly, when the parameters in the algorithms are kept the same and the CPU times are analyzed, it is demonstrated that there is a significant difference between medium and large datasets. This structure allows us to analyze the performance of the solution method at various sizes and complexities.

In addition to the warehouse and instance parameters, algorithm parameters are also significant for the solution of the problem. According to this, the parameters of the algorithm are the same as the parameters of the GA except for the crossover rate, mutation rate, and the creation of the initial solution. Because of this, we classify the AGA parameters and GA parameters as given in

Table 8. Parameters of the algorithms.

Parameters	Small-Size	Medium–Size	Large–Size
Crossover ratio	0.4	0.6	0.8
Mutation ratio	0.2	0.3	0.4

. Accordingly, the parameter set of the GA and AGA varies according to the instance structure. Crossover ratio and mutation ratio are used in the algorithm in a way so as not to force it into the small size instance. These parameters are enhanced for the medium-size instance and the large-size instance. The crossover and mutation rates were dynamically tuned to yield the optimum performance for different problem sizes. Higher crossover and mutation rates were necessary for larger datasets in order to maintain solution diversity and prevent premature convergence. These settings for parameters were established through empirical tuning and experience in using similar metaheuristics when solving logistics problems.

5.2. Performance of the Algorithm

This section outlines the computational experiments and analyzes the results generated by the algorithms for the given problem. It is logical to not expect commercial resolution programs to provide solutions on time. However, to establish a benchmark for comparison, we employed version 24.2 of the IBM ILOG CPLEX Optimization Studio (CPLEX) solver as the MILP Solver. Specifically, we set a maximum time limit of 3 h for GA, AGA, and the CPLEX solver to obtain the optimal solution. The algorithms were implemented in MATLAB 2015B and run on a computer equipped with an Intel Core i5 processor running at 2 GHz and 16 GB of RAM. Results and computation times were recorded after running the algorithms 10 times. The performance of the algorithm for the executions conducted was assessed based on the average Central Processing Unit (CPU) time obtained.

The OPP has been proven to be an NP-Hard problem [50] as well as VRP [51]. Therefore, our proposed problem is also classified as NP-Hard, which can be also confirmed based on the number of variables and constraints given in

Table 9. Number of variables and constraints in different scales.

Scale	#Binary Decision Variables	#Continuous Decision Variables	Total Number of Decision Variables	#Constraints
Small	372	45	417	872
Medium	98,050	905	98,955	88,530
Large	3,297,000	9350	3,306,350	3,154,580

for different problem scales.

Therefore, finding a solution is quite difficult, and the likelihood of obtaining a fast response is low. According to the information about the datasets used in this study, the small-scale dataset consists of five customer orders, and the solution was initially attempted using this dataset. Accordingly, GA, AGA, and CPLEX reached the optimum point for small-scale datasets, and GA, which has the fastest solution time, is the most efficient. Information regarding these is provided in

Table 10. Experimentation results for small instance problems.

Solution Method	Objective Function	CPU Time
CPLEX	182	4
GA	182	1
AGA	182	2

.

After solving the small-scale problems, the transition to medium-scale datasets was made, wherein the CPLEX did not render a solution within the specified time. Therefore, in the subsequent experiments, we just implemented and compared the suggested GA and AGA. Since the problem addressed in this work concurrently involves OPP and VRP, the algorithms require more time compared to solving other similar problems in the literature. Therefore, the problem could not be solved with the considered dataset due to exceeding the specified time limit (3 h). Accordingly, separate values were provided for both OPP and VRP using medium and large-scale datasets, and the objective function and CPU time values were obtained as outlined in

Table 11. Experimentation results for the large- and medium-scale datasets.

Experiment No.		AGA			GA			Algorithm used (GA or AGA)		GA for VRP
		OF		CPU Time	OF		CPU Time	Population	Iteration	Population	Iteration
		Average	Min		Average	Min
Medium	1	2511.5	2417.5	5.3	2584.6	2536	6.4	1	1	1	1
	2	2459.9	2352.8	7	2512.9	2459	7.4	1	1	10	10
	3	2393.2	2320.9	18.5	2494.2	2434.3	17.1	10	10	1	1
	4	2364.6	2293	29.1	2431.8	2403.2	26.4	10	10	10	10
	5	2293.6	2231.3	101.4	2385.4	2332.6	81.7	50	50	1	1
	6	2483.6	2391.4	11.8	2552.7	2486.3	10.5	1	1	50	50
	7	2292.9	2186.4	176.3	2330	2305.7	145.4	50	50	50	50
Large	1	3216.9	3124.9	11.6	3327.4	3282.6	10	1	1	1	1
	2	3204.2	3102.8	16.7	3295	3258.6	15.8	1	1	10	10
	3	3128.3	3043.3	39.2	3219.1	3192.7	32.2	10	10	1	1
	4	3105.2	3017.6	41.1	3207.5	3134.3	33.6	10	10	10	10
	5	3044.3	2961.7	108.1	3160.5	3101	95.1	50	50	1	1
	6	3178.6	3098.5	16.5	3288.7	3238.1	15.2	1	1	50	50
	7	3006.1	2900.8	233.7	6107.3	3068.4	189.5	50	50	50	50

OF: Objective function; AGA: Adaptive Genetic Algorithm; GA: Genetic Algorithm.

.

In Table 11, the “algorithm used” column in the table refers to the parameters of the AGA or GA considered to solve the basic problem. Moreover, the last column in the table represents the parameters of the GA used to solve the order picking process involving a drone in the problem. As mentioned before, the basic problem is created as OPP, but since the drone is also involved, a VRP must also be solved within the OPP to find the optimal route of the drone. Therefore, two separate algorithms were employed together in the corresponding solution. Since the VRP treated within the OPP is also of great importance, the GA parameters affect the OPP solution quality. In order to emphasize this impact, several experiments were conducted by assigning various values to the parameters.

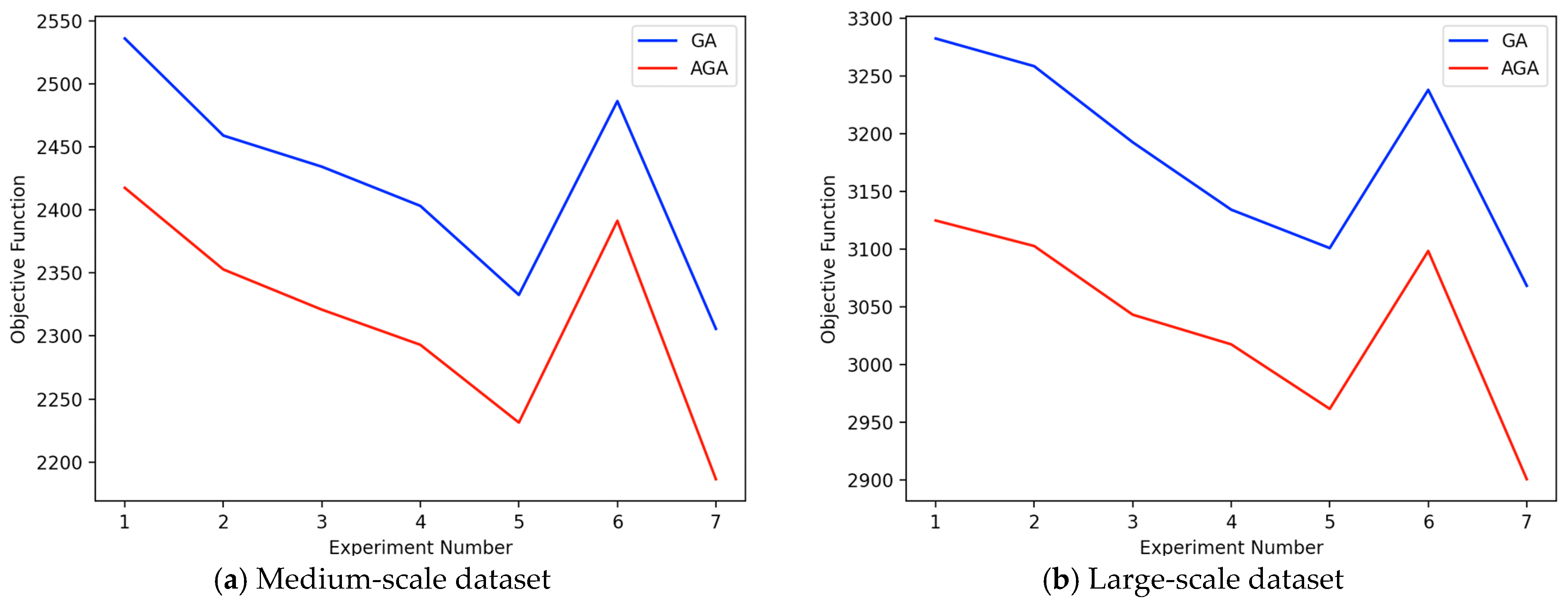
For the medium- and large-scale datasets, the detailed results are given in the Appendix A section. It is clear that the AGA outperforms the GA, which is also depicted in Figure 11. It is revealed that making the seed algorithm and regeneration operators adaptive within the GA is the cause for this superiority.

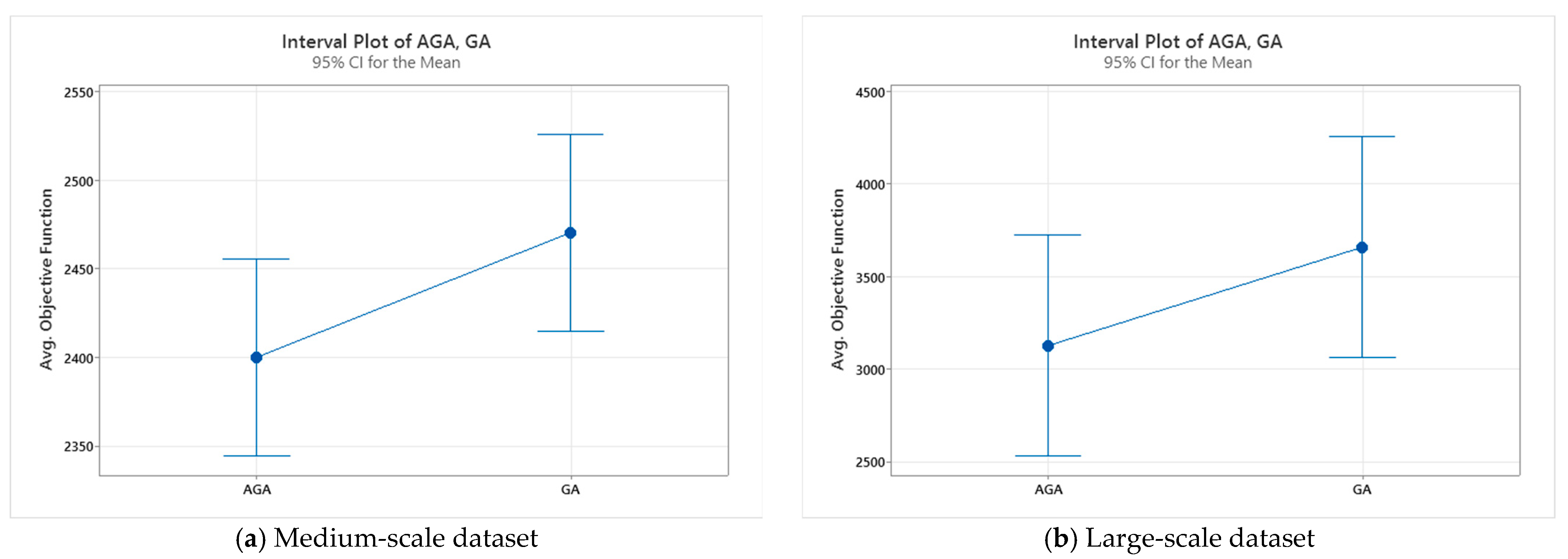
For a more detailed validation, a one-way Analysis of Variance (ANOVA) test was conducted with a confidence level of 0.95, considering 70 and 140 tests corresponding to medium- and large-scale datasets, respectively. The obtained results are displayed in Figure 12. It is clear that the suggested AGA made a visible superiority against the GA in both medium- and large-scale datasets.

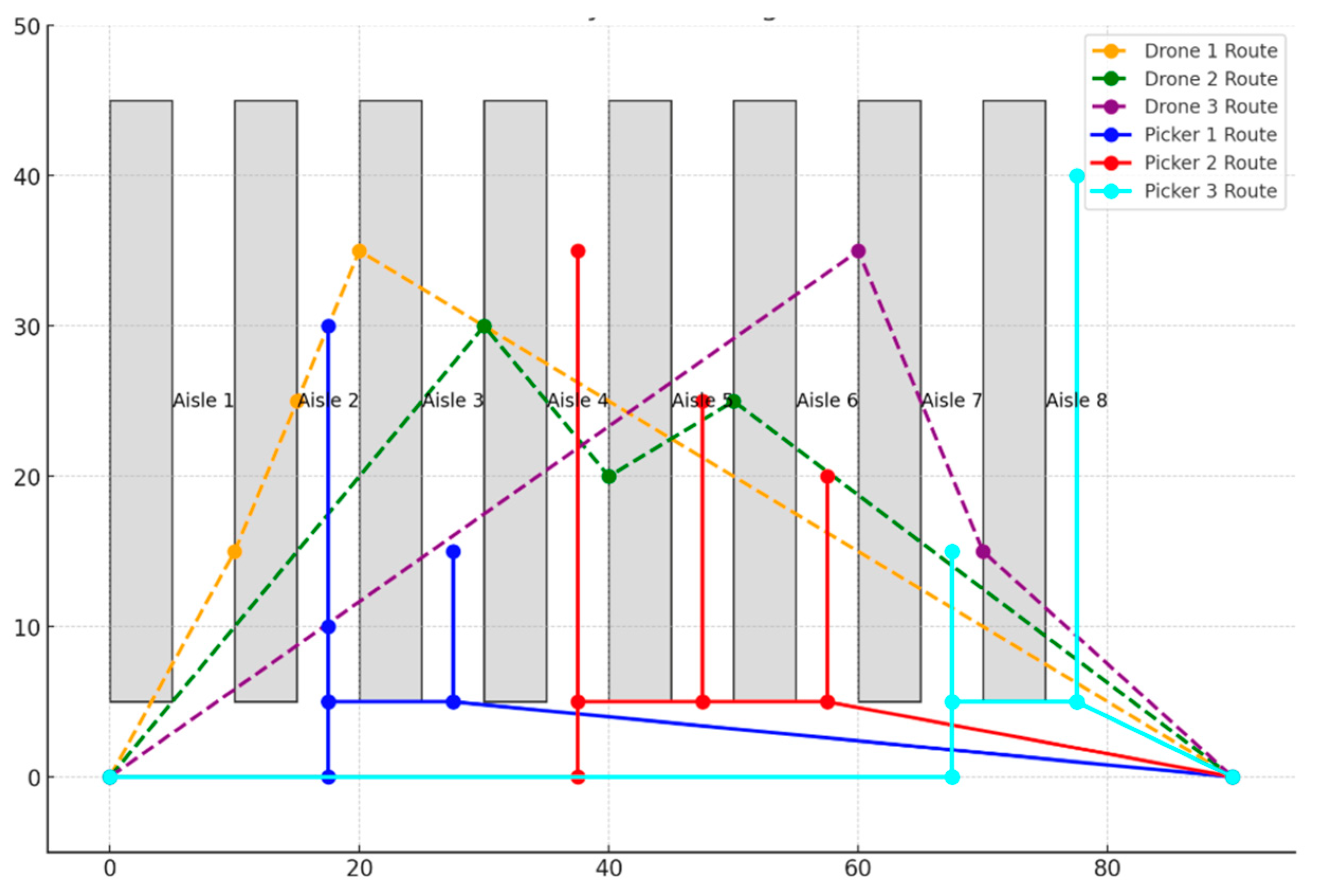
On the other hand, an example solution is shown in Figure 13 on the warehouse layout organized in the coordinate system. In this figure, drone routes are shown with dashed lines, while order picker routes are expressed with solid lines. The drone and order picker collect the products together and ensure the preparation of the products in the order list/batch.

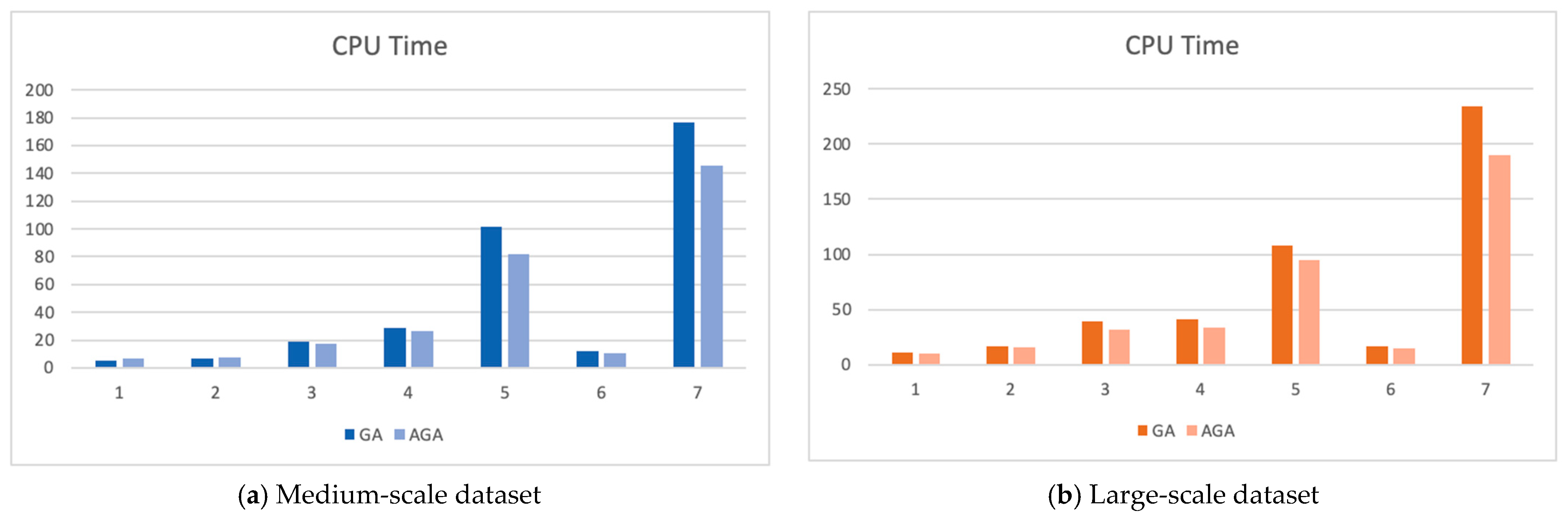
Moreover, when comparing the CPU times, GA yields better results due to its less complicated structure compared to AGA. Figure 14 displays the differences between the CPU times of both algorithms.

The computational results show that AGA maintains high performance for medium-sized problems and still keeps its advantage for large-sized problems. In medium-sized problems, adaptive crossover and mutation strategies are thought to prevent premature convergence through balancing exploration and exploitation. For large-sized problems, the adaptive feature of AGA makes it search a large solution space better than GA. However, the increased computational cost is still a major issue. Future work can be directed towards making AGA more efficient and scalable by adjusting parameters and using hybrid approaches.

5.3. Solutions of the Order Picking with and Without Drone Assistance

In order to investigate the impact of drone assistance on the order picking process, the solutions obtained with and without drone assistance are compared using the same problem and dataset. To achieve this, a large-scale dataset is taken into account where the experiment number and results are given in

Table 12. Comparison of the solutions.

Experiment No.	OF (with Drone Assistance)	OF (Without Drone Assistance)	Improvement Rate
1	24,738	34,180	27.62
2	25,701	36,440	29.47
3	25,708	36,432	29.43
4	25,703	36,418	29.42
5	24,574	36,394	32.47

OF: Objective function.

. According to these results, the order picking process with drone assistance yields superior results on average by 29.68%.

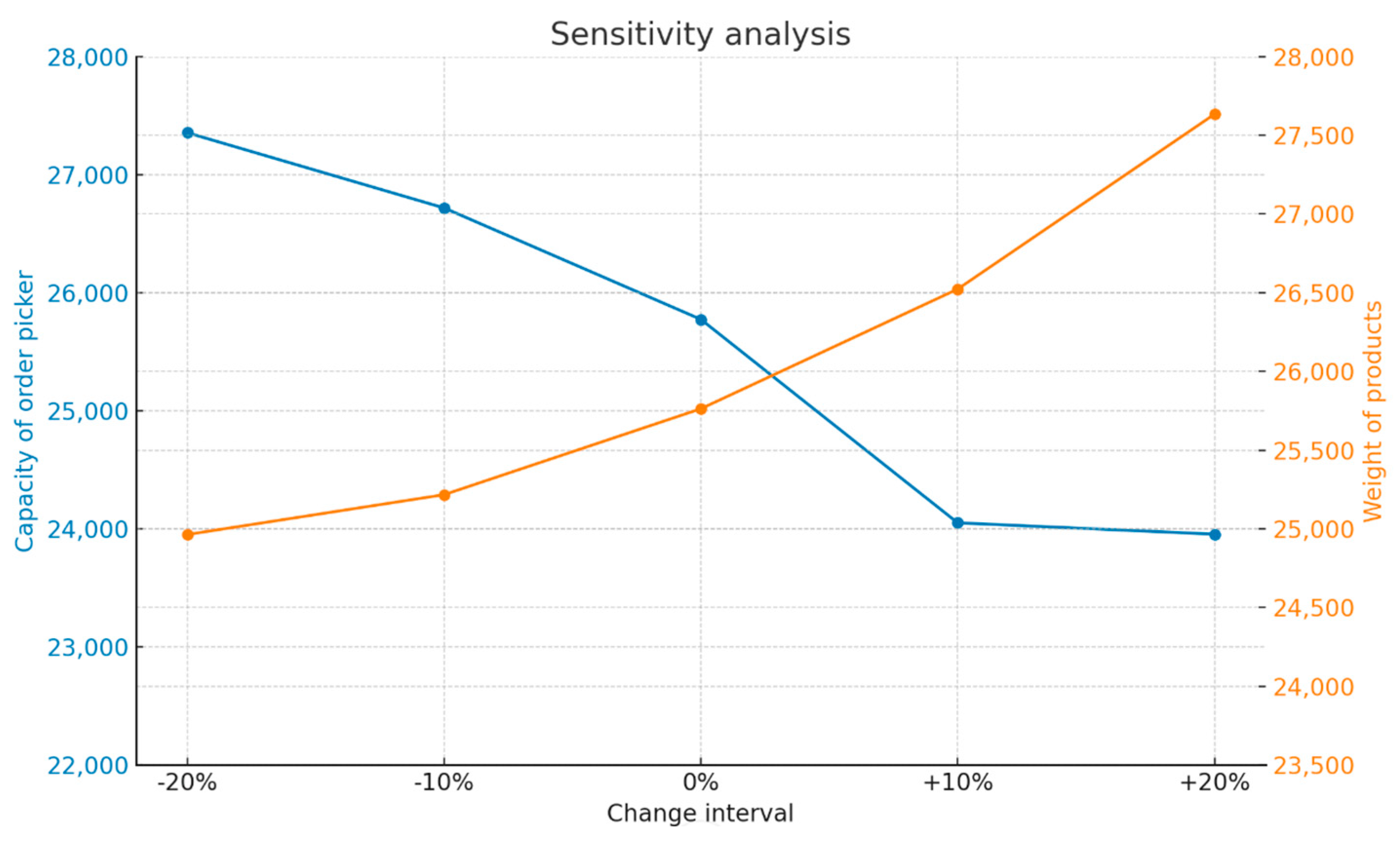
5.4. Sensitivity Analysis

To further examine the model, especially against real-world fluctuations, it is necessary to conduct a sensitivity analysis to determine the extent to which the outcome changes when the parameters within the mathematical model are altered. Hence, the capacity of order pickers and the weight of products are taken into account as two important parameters to be modified by certain percentages, and the impacts of these changes on the model performance are analyzed. The capacity of the order picker is a single parameter, because the capacity of all order pickers is the same. However, the weight of products parameter includes all products, and the weights of all products are changed. The sensitivity analysis is conducted in large part with the help of AGA. The results are represented in

Table 13. Results of the sensitivity analysis.

Parameters	Change Intervals
	−%20	−%10	0	+%10	+%20
Capacity of the order picker	27,355	26,718	25,774	24,051	23,955
Weight of the products	24,964	25,217	25,763	26,523	27,634

and Figure 15.

As can be observed, the objective function varies according to these two parameters. The greater the capacity of the order picker, the lower the value of the objective function in the problem. Thus, the capacity of the order picker is quite important for order picking efficiency. Changing the capacity of the order picker by 10% results in an average change of 3% in the objective function. Additionally, the greater the weight of the orders, the more distance and time are required for order picking, leading to an increase in the objective function of the problem. Changing the weight of the orders by 10% results in an average change of 2.5% in the objective function. Therefore, if the aim is to reduce the objective function, necessary adjustments can be made based on these two parameters.

6. Discussion and Managerial Implications

Nowadays, with the increasing importance of e-commerce, supply chain management and especially warehouse management issues are becoming more and more important. Therefore, it has become a necessity for companies to perform the functions performed in warehouses faster and with less cost in order to compete with their competitors. Thus, due to these requirements, the order picking process attracts attention. In this study, an OPP is considered where the drone is employed as an assistant to the order picker due to these requirements. By picking the products located at high altitudes by the drone, both the capacity of the order picker and the picking time of the order picker are gained.

The general outline of this research was created within the scope of the research questions stated in the introduction section. To answer RQ1, a mathematical model was developed wherein the drone is used as an assistant to the order picker (Section 3). In this model, while the order pickers collect the orders on the lower shelves, the drone collects the products on the upper shelves, which would take time for the order pickers to reach. Thus, the orders that need to be collected can be collected in a shorter time and the capacity of the order picker can be used more efficiently. To demonstrate the advantages of drones assisting in picking operations, product clusters are separated since some of the products that the order picker needs to pick are picked by the drone, and the necessary queues are created since the drone and the order pickers work simultaneously. In this way, the orders that need to be picked can be picked in a shorter time and the capacity of the order picker can be used more efficiently. By solving the relevant model, the answer to RQ2 is given. The problem is then solved with the help of the suggested algorithms as well as the relevant OPP encountered when the drone is used as an assistant to the order pickers in the order picking process (Section 4). To achieve this, the classical GA was applied and then AGA was adapted to the problem to possibly improve the results with various datasets and parameters. Accordingly, AGA was able to provide superior results against GA in all problem instances. Thus, RQ3 is answered as one of the research questions that led to the formation of the study. Then, in order to answer RQ4, sensitivity analysis was performed in Section 5.3. As a consequence, the capacity of the order picker and the weight of the products were taken into account as two main parameters and their impacts on the objective function were examined.

There are some risks and difficulties that may arise in the example discussed in this research and real-life applications for the use of drones as an assistant in the order picking process. Some examples of these are given below.

• Drones have limited battery capacity and may need to be charged frequently, which may cause difficulties in long-term operations.
• In order for drones to be used as assistants, they must be used in integration with WMS. This may require additional software and cost.
• Drones carry the risk of collision or falling while flying over employees in the warehouse.
• Air currents, temperature changes, or narrow spaces in closed areas may affect drone flight.
• Drones, sensors, and automation systems require a serious investment.
• There may be insurance requirements regarding how damages resulting from drone accidents are covered.

These and similar situations can be encountered during application. In addition, the categories and weights of the products kept in these real-life warehouses may be quite different from each other. In such cases, the method specified in this study may be quite difficult to implement, but it may be more efficient if the products in the warehouse can be divided into categories or in a way that is compatible with drones.

All in all, this work is based on the drone-assisted OPP that occurs when drones are used to facilitate order picking processes. The proposed methodology and findings can be utilized by researchers and practitioners who need to determine optimal policies considering real-life and technical limitations.

7. Conclusions and Outlook

This work addressed the use of drones to assist order pickers in the order picking process in warehouses. In this problem scenario, multiple order pickers concurrently collect grouped orders. This problem illustrated the process that would occur if robots collaborate with humans to assist them in warehouse processes, fulfilling the requirements of Industry 4.0. The aim was to guide decision-making processes for domain experts in the event such a process occurs. Additionally, it contributed to optimization solution techniques in the literature.

The order picking process is the most cost-intensive function in warehouses, making it both costly and time-consuming. During order picking, the picker retrieves products from the upper levels of the vehicle and places them onto the vehicle with the help of a device. However, this process consumes additional energy and time. Therefore, the use of drones was investigated as a solution to eliminate this movement of the order picker to reduce order picking time. Drones are now extensively used and have begun to be involved in many processes to assist humans in making their tasks easier. Therefore, using drones in processes suitable for drone constraints is highly suitable, particularly in operations that are challenging, unwanted, or risky for humans.

The suggestion of “using drones to assist humans in the order picking process” was treated as a problem. An MILP model was developed to formulate the problem, followed by an efficient AGA to tackle the problem’s complexity. In the development of the AGA, a core algorithm was employed in the initialization phase of the population, thereby ensuring better results. The results obtained from the proposed algorithm and the solution times were compared with a classical GA, which revealed the appropriate performance of the AGA. Eventually, a sensitivity analysis was conducted on the two key parameters of the capacity of order pickers and the weight of products. Based on the findings, the model represents almost identical sensitivity against the fluctuations of these parameters but the maximum change was made by raising the capacity parameter by 20%.

This research made significant theoretical contributions by addressing the OPP with order pickers and drones for the first time in the literature. A drone-supported model was first proposed within the classical OPP framework and formulated mathematically by using the MILP approach. Additionally, the AGA was proposed to overcome the deficiencies of GA and the seed algorithm was integrated into this algorithm for the first time. In this way, a new meta-heuristic algorithm hybrid was introduced to the literature and a contribution was made to the improvement of the problem-solving capacity of AGA. Finally, sensitivity analysis was performed to check the model behavior against real-world uncertainties and the quantitative potential of drones in order picking was unveiled. In these aspects, the study contributes significantly to the literature as one of the first detailed investigations laying the theoretical groundwork of drone-based order picking in warehouse logistics operations.

The solution proposed in this study may be suitable for e-commerce distribution centers, high-bay retail warehouses, and logistics facilities with robotic automation. Since small and light products need to be picked quickly in such centers, drones can speed up the order picking process. Cold storages, centers with heavy or bulky products, and narrow-aisle, dense warehouses may have difficulty adopting the model. Factors such as battery life, carrying capacity, and flight safety of drones may limit their effective use in such facilities.

On the other hand, this study also has limitations which can be addressed in future work. The type of warehouse used in the study is single. In addition, the order picker routing within the OPP was created based solely on one order picker routing heuristic. Further, zone picking was not included in this process. Future research can explore zoning scenarios, evaluate different warehouse layouts, consider alternative heuristics, and incorporate sustainability and environmental factors into the analysis. Additionally, some restrictions may be added to the drone (e.g., battery life, drone dimensions), and this problem and solution method may be complicated to solve with different product categories in different warehouse types.