An Improved Case-Based Reasoning Method Based on Dynamic Entropy Weighting: A Case Study of Scenario Prediction for Major Maritime Emergencies
Abstract
1. Introduction
- Proposed a case-based reasoning method with a cascaded retrieval mechanism to improve traditional CBR’s application to complex multi-layer objects, enhancing its applicability to such problems.
- Proposed a dynamic entropy weight method with secondary weight allocation to solve the weight assignment difficulty caused by CRCBR’s non-fixed model structure, enhancing CRCBR’s performance.
- Verified the effectiveness and superiority of the proposed method using real-world maritime emergency accident data.
2. Related Works
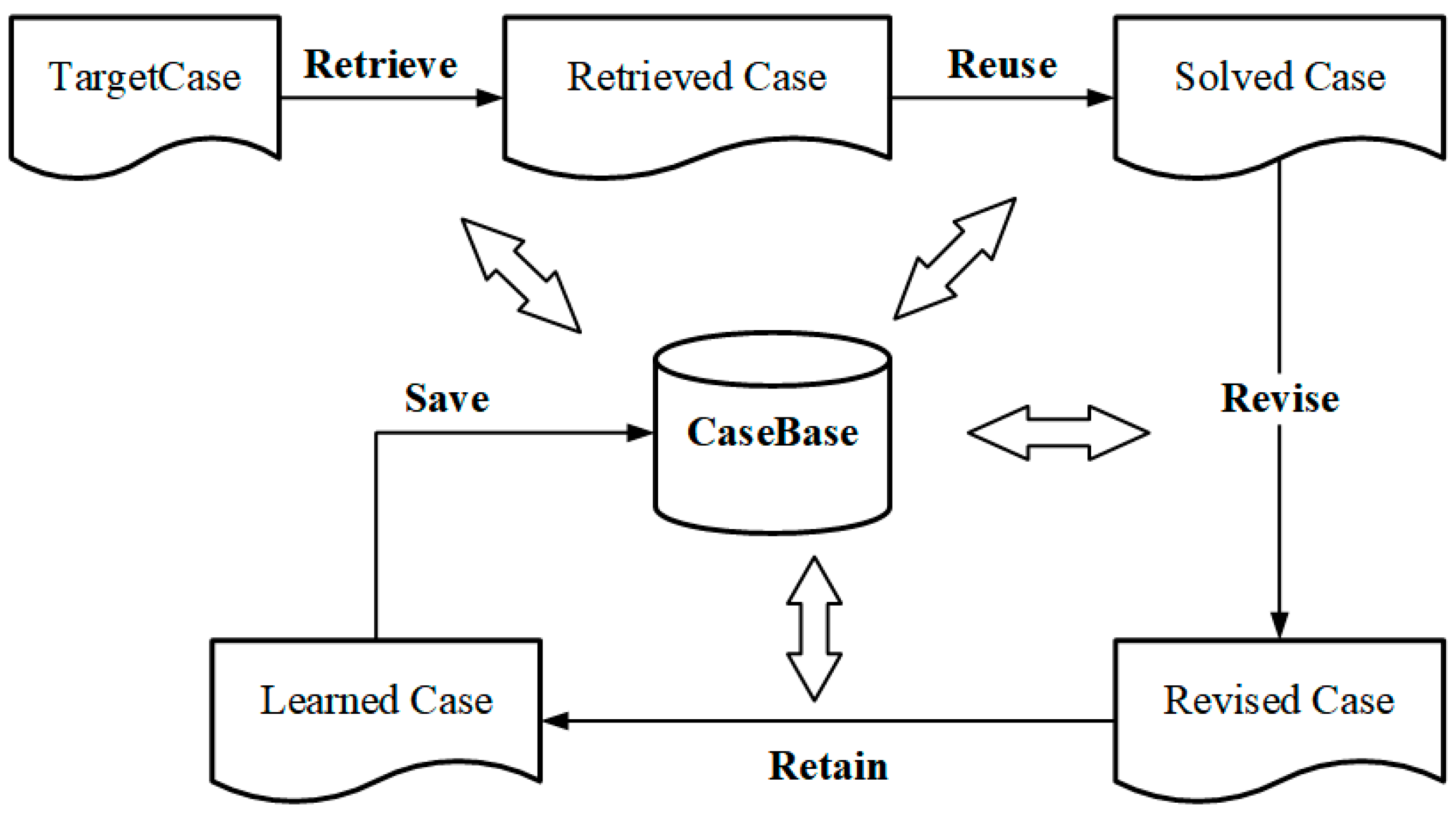
2.1. The Foundation of CBR
2.2. Application Research of CBR
2.3. Research on Improvements of CBR Retrieval Mechanism
2.4. Research on CBR Weight Calculation
3. Methodology
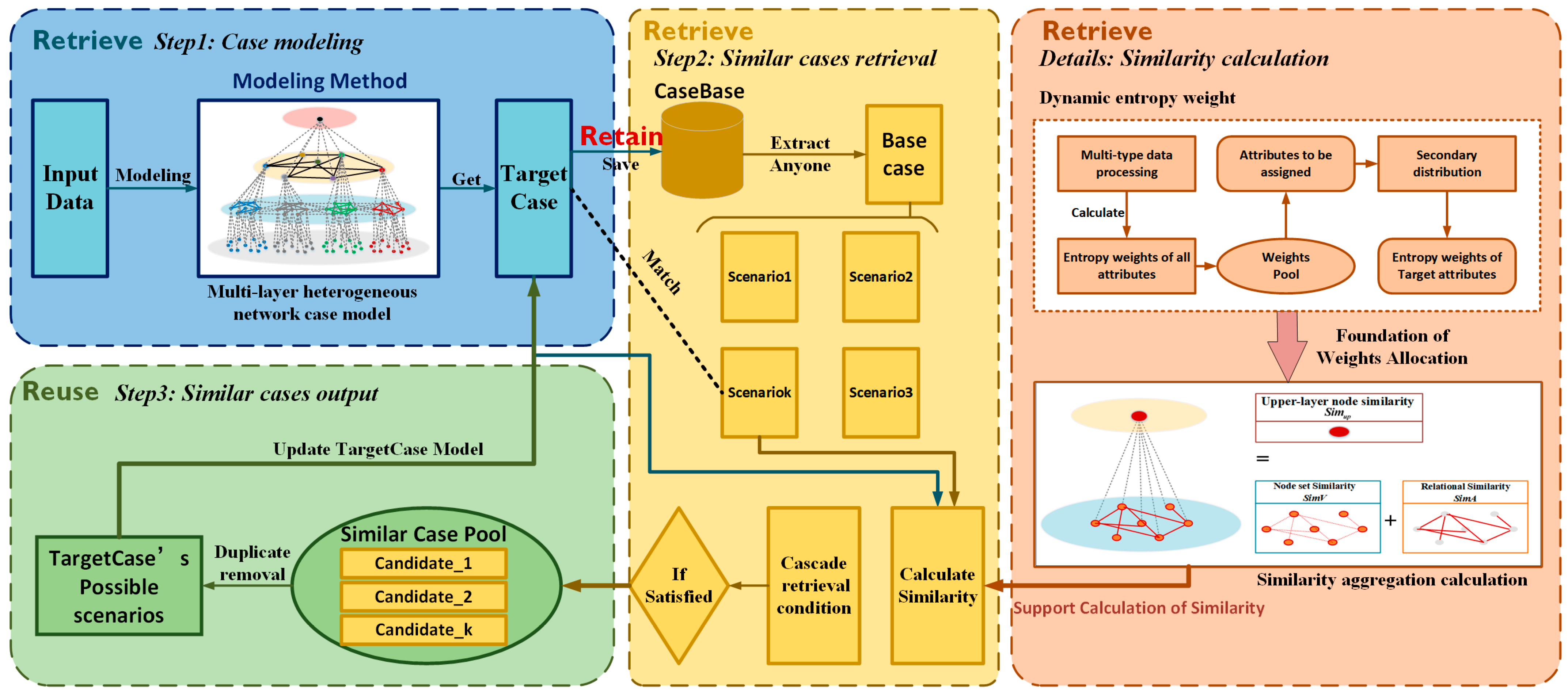
3.1. Cascade Retrieval-Based Case-Based Reasoning
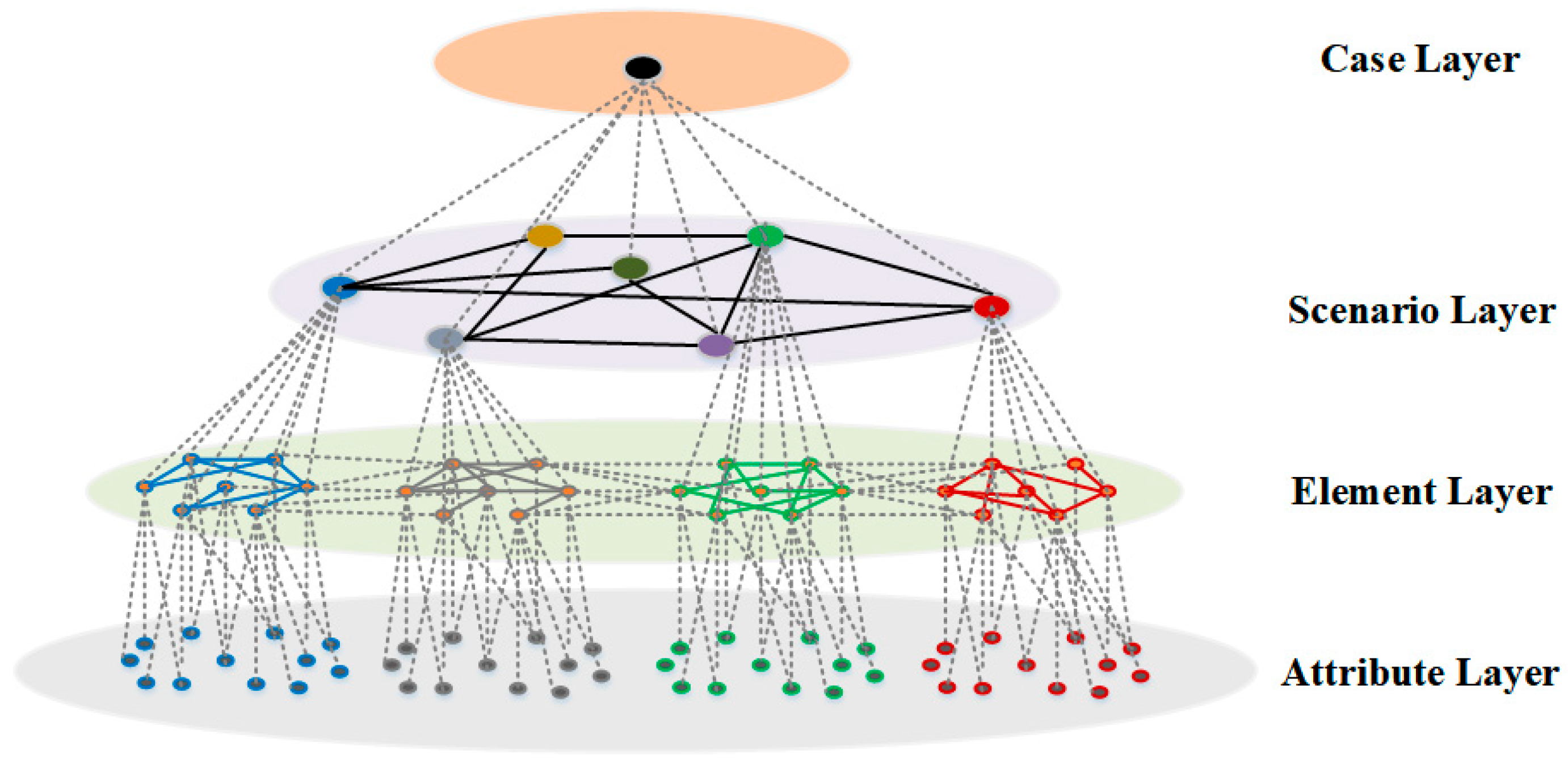
3.1.1. Case Modeling
3.1.2. Similarity Computation Model
3.1.3. Cascade Retrieval Mechanism
3.2. Dynamic Entropy Weight
3.2.1. Entropy Weight
3.2.2. Multi-Type Data Processing
3.2.3. Dynamic Assignment
4. Case Study
4.1. Data Introduction and Processing
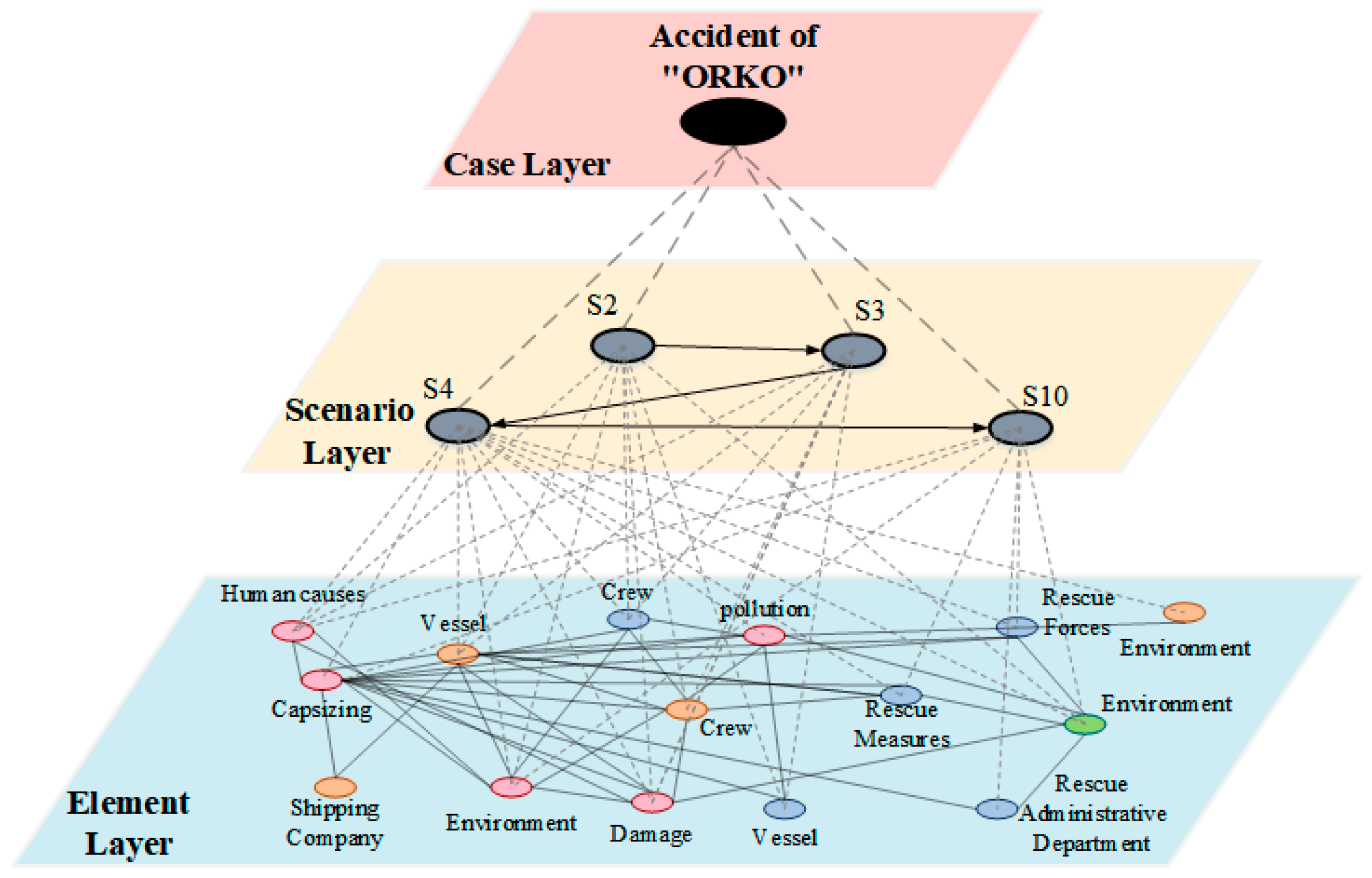
4.2. Major Maritime Emergency Case Modeling (Retrieve)
4.3. Case Base Construction and Basecase Model Examples (Retrieve)
4.4. TargetCase Modeling (Retrieve)
4.5. Construction of Similarity Computation Model (Retrieve)
4.6. Weight Allocation (Retrieve)
4.7. Retrieval Mechanism Setting (Retrieve)
4.8. Output of Prediction Results (Reuse and Retain)
5. Method Evaluation
5.1. Evaluation Metrics and Perspectives
5.2. Method Performance Analysis
5.2.1. Optimality
5.2.2. Satisfactoriness
5.2.3. Sensitivity
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CBR | Case-based reasoning |
| CRCBR | Cascade retrieval-based case-based reasoning |
| CMO | Complex multi-layer object |
| IMO | International Maritime Organization |
| China MSA | Maritime Safety Administration of the People’s Republic of China |
Appendix A
Appendix A.1
| Entity Category | Entity Name | Entity Attribute | |||
|---|---|---|---|---|---|
| Hazard Sources | Attribute Name | Attribute Value | Data Type | Value Range | |
| Human factors | Improper operation | Improper navigation | 42 | - | |
| Improper operation | Improper management | 42 | |||
| Damage | Cause of damage | Collision | 42 | - | |
| Extent of damage | 3 | 51 | 5 | ||
| Cause of damage | Rupture | 42 | |||
| Environment | Water level | Medium water level | 42 | ||
| Wave height | 2 | 1 | |||
| Tide | Ebb tide | 42 | |||
| Vulnerable Entities | Vessel | Quantity | 1 | 1 | - |
| Type of loss | Hull damage | 42 | - | ||
| Type of loss | Cargo loss | 42 | |||
| Extent of loss | 5 | 51 | 5 | ||
| Cause of loss | Collision | 42 | - | ||
| Crew | Number of injuries | 0 | 1 | - | |
| Number of deaths | 0 | 1 | |||
| Number of affected | 12 | 1 | - | ||
| Shipping company | Quantity | 1 | 1 | - | |
| Type of loss | Economic loss | 42 | - | ||
| Type of loss | Safety loss | 42 | - | ||
| Extent of loss | 4 | 51 | 5 | ||
| Mitigation Agents | Vessel | Quantity | 1 | 1 | - |
| Action | Emergency evasion | 42 | |||
| Action | Ship self-rescue | 42 | - | ||
| Crew | Action | Emergency evasion | 42 | - | |
| Action | Life-saving refuge | 42 | - | ||
| Rescue measures | Rescue measures | Personnel search and rescue | 42 | - | |
| Rescue measures | Pollution cleanup | 42 | - | ||
| Rescue resources | Rescue personnel | 8 | 1 | - | |
| Rescue ship | 1 | 1 | - | ||
| Rescue Administrative Department | Quantity | 2 | 1 | - | |
| Response level | 2 | 52 | 3 | ||
| Emergency measures | Pollution cleanup | 42 | |||
| Emergency measures | Personnel search and rescue | 42 | - | ||
| Environment | Environment | Weather | Clear | 42 | - |
| Wind strength | 3 | 1 | 1–10 | ||
| Wave height | 2 | 1 | - | ||
| Wind direction | North to northeast wind | 42 | - | ||
| Visibility | 4 | 52 | 6 | ||
Appendix A.2
| Entity Category | Entity Name | Entity Attribute | |||
|---|---|---|---|---|---|
| Hazard Sources | Attribute Name | Attribute Value | Data Type | Value Range | |
| Explosion | Explosion range | 20 | 1 | - | |
| Severity of explosion | 4 | 51 | 5 | ||
| Cause of explosion | Operational error | 42 | - | ||
| Open flame | Cause of fire | Welding | 42 | - | |
| Area of fire | 20 | 1 | - | ||
| Severity of fire | 3 | 51 | 5 | ||
| Damage | Type of damage | Hull damage | 42 | - | |
| Extent of damage | 3 | 51 | 5 | ||
| Cause of damage | Explosion | 42 | - | ||
| Explosive materials | Type | Unknown | 42 | - | |
| Quantity | 100 | 1 | - | ||
| Flammable materials | Type | Unknown | 42 | - | |
| Quantity | 150 | 1 | - | ||
| Environment | Wave height | 1 | 1 | - | |
| Wind strength | 3 | 1 | 1–10 | ||
Appendix A.3
| Entity Category | Entity Name | Entity Attribute | |||
|---|---|---|---|---|---|
| Vulnerable Entities | Attribute Name | Attribute Value | Data Type | Value Range | |
| Vessel | Quantity | 1 | 1 | - | |
| Type of loss | Hull damage | 42 | - | ||
| Extent of loss | 5 | 51 | 5 | ||
| Cause of loss | Explosion | 42 | - | ||
| Crew | Number of injuries | 1 | 1 | - | |
| Number of deaths | 1 | 1 | |||
| Shipping Company | Quantity | 1 | 1 | - | |
| Type of loss | Economic loss | 42 | - | ||
| Type of loss | Safety loss | 42 | - | ||
| Extent of loss | 5 | 51 | 5 | ||
Appendix A.4
| Entity Category | Entity Name | Entity Attribute | |||
|---|---|---|---|---|---|
| Mitigation Agents | Attribute Name | Attribute Value | Data Type | Value Range | |
| Vessel | Quantity | 1 | 1 | ||
| Action | Assistance alarm | 42 | |||
| Crew | Action | Emergency avoidance | 42 | - | |
| Action | Alarm | 42 | |||
| Action | Repair the hull | 42 | |||
| Action | Life-saving refuge | 42 | - | ||
| Rescue measures | Rescue measures | Fire extinguishing | 42 | - | |
| Rescue measures | Medical assistance | 42 | |||
| Rescue resources | Professional rescue vessel | 1 | 1 | - | |
| Rescue Administrative Department | Quantity | 2 | 1 | - | |
| Response level | 3 | 52 | 3 | ||
| Emergency measures | Personnel search and rescue | 42 | - | ||
Appendix A.5
| Entity Category | Entity Name | Entity Attribute | |||
|---|---|---|---|---|---|
| Environment | Attribute Name | Attribute Value | Data Type | Value Range | |
| Environment | Weather | Clear | 42 | - | |
| Air temperature | 35 | 1 | - | ||
| Wind strength | 3 | 1 | 1–10 | ||
| Wave height | 1 | 1 | - | ||
Appendix A.6
| Label | Implication |
|---|---|
| 1 | Precise Type |
| 2 | Interval Type |
| 3 | Discrete Type |
| 41 | Boolean Type (Numerical) |
| 42 | Enumerated Type (Textual) |
| 51 | Scale Type (Numerical) |
| 52 | Evaluative Type (Textual) |
Appendix A.7
| Attribute Name | Mapping Relationship |
|---|---|
| Fire cause | Flammable material leakage: 1, welding: 3, flammable material explosion: 5 |
| Collision cause | Improper operation: 1, navigation violation: 3, management failure: 5 |
| Tide | Ebb tide: 1, low tide: 3, flood tide: 5 |
| Weather | Clear: 1, cloudy: 2, cloudy with local fog: 3, gale with rough seas: 4 |
| Damage cause | Collision: 1, improper sealing: 1, fire: 1, engine room flooding: 1, hull breach: 1, vessel capsizing: 2, explosion: 2 |
| Rescue measures | Firefighting: 2, distress alert: 1, SAR operations: 2, MEDEVAC: 2, pollution containment: 1, damage control: 1 |
References
- Graessler, I.; Grewe, B. Stages of Systems Engineering: An Analysis and Characterization of Systems Engineering Approaches. Systems 2025, 13, 53. [Google Scholar] [CrossRef]
- De Domenico, M. More is different in real-world multilayer networks. Nat. Phys. 2023, 19, 1247–1262. [Google Scholar] [CrossRef]
- Mülâyim, M.O.; Arcos, J.L. Fast anytime retrieval with confidence in large-scale temporal case bases. Knowl.-Based Syst. 2020, 206, 106374. [Google Scholar] [CrossRef]
- Pascual-Pañach, J.; Sànchez-Marrè, M.; Cugueró-Escofet, M.À. A temporal case-based reasoning approach for performance improvement in intelligent environmental decision support systems. Eng. Appl. Artif. Intell. 2024, 136, 108833. [Google Scholar] [CrossRef]
- Pérez-Pons, M.E.; Parra-Dominguez, J.; Hernández, G.; Bichindaritz, I.; Corchado, J.M. OCI-CBR: A hybrid model for decision support in preference-aware investment scenarios. Expert Syst. Appl. 2023, 211, 118568. [Google Scholar] [CrossRef]
- Shen, L.; Li, J.; Suo, W. Risk response for critical infrastructures with multiple interdependent risks: A scenario-based extended CBR approach. Comput. Ind. Eng. 2022, 174, 108766. [Google Scholar] [CrossRef]
- Nakhjiri, N.; Salamó, M.; Sànchez-marrè, M. Reputation-Based Maintenance in Case-Based Reasoning. Knowl.-Based Syst. 2020, 193, 105283. [Google Scholar] [CrossRef]
- Cunningham, P.; Smyth, B.; Bonzano, A. An incremental retrieval mechanism for case-based electronic fault diagnosis. Knowl.-Based Syst. 1998, 11, 10. [Google Scholar] [CrossRef]
- Low, N.; Hesser, J.; Blessing, M. Multiple retrieval case-based reasoning for incomplete datasets. J. Biomed. Inform. 2019, 92, 103127. [Google Scholar] [CrossRef]
- Bouzar-Benlabiod, L.; Harrar, K.; Yamoun, L.; Khodja, M.Y.; Akhloufi, M.A. A novel breast cancer detection architecture based on a CNN-CBR system for mammogram classification. Comput. Biol. Med. 2023, 163, 107133. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Chen, W.; Zhu, Y.X.; Guo, Y.Q. Research on the integrated system of case-based reasoning and Bayesian network. ISA Trans. 2019, 90, 213–225. [Google Scholar] [CrossRef]
- Shao, J.; Liang, C.; Liu, Y.; Xu, J.; Zhao, S. Relief demand forecasting based on intuitionistic fuzzy case-based reasoning. Socio-Econ. Plan. Sci. 2021, 74, 100932. [Google Scholar] [CrossRef]
- Wang, D.; Liu, J.; Lin, Q.; Yu, H. A decision-making system based on case-based reasoning for predicting stroke rehabilitation demands in heterogeneous information environment. Appl. Soft Comput. 2024, 154, 111358. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Y.; Ni, J.; Wu, X.; Zheng, H. An improved case-based reasoning approach for mechanical design by enhancing the retrieval accuracy and leveraging the implicit knowledge. Adv. Eng. Inform. 2024, 60, 102374. [Google Scholar] [CrossRef]
- Yiyang, Z.; Zhang, Y.; Lang, K.; Wang, X. Case-based reasoning for shipwreck emergency salvage scheme assisted decision. Ocean. Eng. 2023, 278, 114332. [Google Scholar] [CrossRef]
- Lei, L.; Yu, S.; Ke, Y.; Deng, L.; Kang, Q. Evaluation Model for Emergency Material Suppliers in Emergency Logistics Systems Based on Game Theory–TOPSIS Method. Systems 2025, 13, 493. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, X.; Mao, H.; Yao, H.; Li, P. Evaluating Expressway Safety Based on Fuzzy Comprehensive Evaluation with AHP–Entropy Method: A Case Study of Jinliwen Expressway in Zhejiang Province, China. Systems 2023, 11, 496. [Google Scholar] [CrossRef]
- Duan, Y.; Cao, X.; Zhao, J.; Yang, X.; Zhao, F.; Guo, X. Research on health state evaluation method for shearer based on dynamic weight and fuzzy comprehensive evaluation. In Proceedings of the 2023 CAA Symposium on Fault Detection, Supervision and Safety for Technical Processes (SAFEPROCESS), Yibin, China, 22–24 September 2023; pp. 1–6. [Google Scholar]
- Zhang, Q.; Feng, J.; Ma, Z.; Chen, G. Threat assessment of air target based on dynamic relative entropy ranking method. In Proceedings of the 31st China Conference on Decision and Control, Nanchang, China, 3–5 June 2019; pp. 3750–3754. [Google Scholar]
- Seiger, R.; Schultheis, A.; Bergmann, R. Case-Based Activity Detection from Segmented Internet of Things Data. In Proceedings of the ICCBR 2025, Biarritz, France, 30 June–3 July 2025; Springer: Berlin/Heidelberg, Germany, 2025; p. 16. [Google Scholar]
- Armengol, E.; Esteva, F.; Godo, L.; Torra, V. On Learning Similarity Relations in Fuzzy Case-Based Reasoning. Trans. Rough Sets II 2004, 3135, 14–32. [Google Scholar]
- Corbat, L.; Nauval, M.; Henriet, J.; Lapayre, J.-C. A fusion method based on Deep Learning and Case-Based Reasoning which improves the resulting medical image segmentations. Expert Syst. Appl. 2020, 147, 113200. [Google Scholar] [CrossRef]
- Shen, Y.; Colloc, J.; Jacquet-Andrieu, A.; Lei, K. Emerging medical informatics with case-based reasoning for aiding clinical decision in multi-agent system. J. Biomed. Inform. 2015, 56, 307–317. [Google Scholar] [CrossRef]
- Bentaiba-Lagrid, M.B.; Bouzar-Benlabiod, L.; Rubin, S.H.; Bouabana-Tebibel, T.; Hanini, M.R. A case-based reasoning system for supervised classification problems in the medical field. Expert Syst. Appl. 2020, 150, 113335. [Google Scholar] [CrossRef]
- Guerrero, J.I.; Miró-Amarante, G.; Martín, A. Decision support system in health care building design based on case-based reasoning and reinforcement learning. Expert Syst. Appl. 2022, 187, 116037. [Google Scholar] [CrossRef]
- Lu, Y.; Yin, L.; Deng, Y.; Wu, G.; Li, C. Using cased based reasoning for automated safety risk management in construction industry. Saf. Sci. 2023, 163, 106113. [Google Scholar] [CrossRef]
- Xie, L.; Wu, S.; Chen, Y.; Chang, R.; Chen, X. A case-based reasoning approach for solving schedule delay problems in prefabricated construction projects. Autom. Constr. 2023, 154, 105028. [Google Scholar] [CrossRef]
- Gao, Y.; Bao, R.; Pan, Z.; Ma, G.; Li, J.; Cai, X.; Peng, Q. Mechanical equipment health management method based on improved intuitionistic fuzzy entropy and case reasoning technology. Eng. Appl. Artif. Intell. 2022, 116, 105372. [Google Scholar] [CrossRef]
- Liu, Z.-G.; Li, X.-Y.; Durrani, D.K.; Zhang, R.-J. Case-driven assessment of power grid emergency response capability considering typhoon disaster scenario diversity. J. Clean. Prod. 2023, 386, 135813. [Google Scholar] [CrossRef]
- Hadj-Mabrouk, H. Application of Case-Based Reasoning to the safety assessment of critical software used in rail transport. Saf. Sci. 2020, 131, 104928. [Google Scholar] [CrossRef]
- Luo, L.; Zhou, Y.; Zhou, Z.; Zhou, C.; Ji, X.; Liu, B.; He, G. Online optimization of petrochemical process via case-based reasoning and conditional mutual information. Chem. Eng. Res. Des. 2024, 207, 380–391. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Feng, Y.; Liu, L. Strategic response for ease of doing business using case-based reasoning. Expert Syst. Appl. 2022, 210, 118514. [Google Scholar] [CrossRef]
- Carmona, M.A.; Barbancho, J.; Larios, D.F.; León, C. Applying case based reasoning for prioritizing areas of business management. Expert Syst. Appl. 2013, 40, 3450–3458. [Google Scholar] [CrossRef]
- Wang, K.; Yang, Y.; Reniers, G.; Li, J.; Huang, Q. Predicting the spatial distribution of direct economic losses from typhoon storm surge disasters using case-based reasoning. Int. J. Disaster Risk Reduct. 2022, 68, 102704. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, J.; Xu, K.; Xie, H.; Gan, X.; Xu, H. A spatial case-based reasoning method for regional landslide risk assessment. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102381. [Google Scholar] [CrossRef]
- Duan, J.; Lin, Z.; Jiao, F.; Jiang, Y.; Chen, K. A dynamic case-based reasoning system for responding to infectious disease outbreaks. Expert Syst. Appl. 2022, 204, 117628. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, L.; Hu, J.; Chen, C.; Fan, X.; Li, X. An emergency task recommendation model of long-distance oil and gas pipeline based on knowledge graph convolution network. Process Saf. Environ. Prot. 2022, 167, 651–661. [Google Scholar] [CrossRef]
- Feng, Y.; Xiang-Yang, L. Improving emergency response to cascading disasters: Applying case-based reasoning towards urban critical infrastructure. Int. J. Disaster Risk Reduct. 2018, 30, 244–256. [Google Scholar] [CrossRef]
- An, X.; Meng, H.; Yin, Z.; Wen, J.; Liu, X. A knowledge transfer-based method for risk analysis and procedure optimization of emergency schemes. Process Saf. Environ. Prot. 2024, 182, 652–677. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, X.; Mao, J.; Ke, F.; Liang, H. How to select plan in emergency decision-making? A two-stage method with case-based reasoning and prospect theory. Appl. Soft Comput. 2024, 155, 111473. [Google Scholar] [CrossRef]
- Wang, D.; Wan, K.; Ma, W. Emergency decision-making model of environmental emergencies based on case-based reasoning method. J. Environ. Manag. 2020, 262, 110382. [Google Scholar] [CrossRef]
- Yu, X.; Li, C.; Zhao, W.-X.; Chen, H. A novel case adaptation method based on differential evolution algorithm for disaster emergency. Appl. Soft Comput. 2020, 92, 106306. [Google Scholar] [CrossRef]
- Chen, M.; Qu, R.; Fang, W. Case-based reasoning system for fault diagnosis of aero-engines. Expert Syst. Appl. 2022, 202, 117350. [Google Scholar] [CrossRef]
- Smyth, B.; Keane, M. Remembering to Forget-A Competence-Preserving Case Deletion Policy for Case-Based Reasoning System. In Proceedings of the 14th International Joint Conference on Artificial Intelligence (IJCAI-95), Montreal, QC, Canada, 20–25 August 1995. [Google Scholar]
- Zhao, Y.; Zhang, M.; Guo, X.; Zhou, Z.; Zhang, J. Research on Matching Method for Case Retrieval Process in CBR Based on FCM. Procedia Eng. 2017, 174, 267–274. [Google Scholar] [CrossRef]
- Hoffmann, M.; Bergmann, R. Using Graph Embedding Techniques in Process-Oriented Case-Based Reasoning. Algorithms 2022, 15, 27. [Google Scholar] [CrossRef]
- Plaza, E.; McGinty, L. Distributed case-based reasoning. Knowl. Eng. Rev. 2005, 20, 4. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, Y.; Fan, Z.-P.; Han, L.; Shen, Z.-X. Patient privacy protection: Generating available medical treatment plans based on federated learning and CBR. Inf. Manag. 2024, 61, 103908. [Google Scholar] [CrossRef]
- Yu, L.; Li, M. A case-based reasoning driven ensemble learning paradigm for financial distress prediction with missing data. Appl. Soft Comput. 2023, 137, 110163. [Google Scholar] [CrossRef]
- Forbus, K.D.; Gentner, D.; Law, K. MAC/FAC: A Model of Similarity-Based Retrieval. Cogn. Sci. 1995, 19, 64. [Google Scholar]
- Liao, W.; Wang, S.; Liu, Q.; Shu, X. Reactive Power Optimization of Distribution Network Based on Case-Based Reasoning. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 978–982. [Google Scholar]
- Ke, Y.; Yao, C.; Song, E.; Yang, L.; Dong, Q. Fault Diagnosis Method of Diesel Engine Injector Based on Hierarchical Weighted Permutation Entropy. In Proceedings of the 2021 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 17–20 May 2021; pp. 1–6. [Google Scholar]
- Chen, W.; Wang, X.; Wang, W.; Zhu, Y.; Cai, Z.; Yang, S. A heterogeneous GRA-CBR-based multi-attribute emergency decision-making model considering weight optimization with dual information correlation. Expert Syst. Appl. 2021, 182, 115208. [Google Scholar] [CrossRef]
- Park, S.; Park, S.; Jang, H.; Ahn, Y.; Kwon, N. Computing green remodeling construction cost for public buildings based on genetic algorithm and case-based reasoning. Dev. Built Environ. 2025, 22, 100655. [Google Scholar] [CrossRef]
- Begum, S.; Barua, S.; Filla, R.; Ahmed, M.U. Classification of physiological signals for wheel loader operators using Multi-scale Entropy analysis and case-based reasoning. Expert Syst. Appl. 2014, 41, 295–305. [Google Scholar] [CrossRef]
- Bergmann, R. Experience Management-Foundations, Development Methodology, and Internet-Based Applications; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Zhang, Y.; Zhong, Q.; Ye, X.; Qu, X. Research on method of emergency aid decision making based on CBR. Appl. Res. Comput. 2009, 26, 4. [Google Scholar]
- Malizia, F.; Corso, A.; Gambuzza, L.V.; Russo, G.; Latora, V.; Frasca, M. Reconstructing higher-order interactions in coupled dynamical systems. Nat. Commun. 2024, 15, 5184. [Google Scholar] [CrossRef]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.H.; Deyle, E.; Fogarty, M.; Munch, S. Detecting causality in complex ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef]
- Yuan, B.; Zhang, J.; Lyu, A.; Wu, J.; Wang, Z.; Yang, M.; Liu, K.; Mou, M.; Cui, P. Emergence and Causality in Complex Systems: A Survey of Causal Emergence and Related Quantitative Studies. Entropy 2024, 26, 108. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Liu, W.; Luan, Y.; Liu, Y. Construction of Scenario Graph for a Major Emergency. J. China Soc. Sci. Tech. Inf. 2021, 40, 10. [Google Scholar]
- Guo, Y.; Jin, Y.; Hu, S.; Yang, Z.; Xi, Y.; Han, B. Risk evolution analysis of ship pilotage operation by an integrated model of FRAM and DBN. Reliab. Eng. Syst. Saf. 2023, 229, 108850. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, Y.-M.; Zhang, K.; Gao, J.-Q.; Yang, L.-H. A heterogeneous multi-attribute case retrieval method for emergency decision making based on bidirectional projection and TODIM. Expert Syst. Appl. 2022, 203, 117382. [Google Scholar] [CrossRef]






| Scenario Category | Scenario Number | Scenario Name |
|---|---|---|
| Vessel | S1 | Vessel Collision |
| S2 | Hull Rupture | |
| S3 | Hull Flooding | |
| S4 | Vessel Capsizing | |
| S5 | Vessel Fire | |
| S6 | Vessel Explosion | |
| Personnel | S7 | Personnel Missing |
| S8 | General Personnel Casualties | |
| S9 | Major Personnel Casualties | |
| Environmental | S10 | General Pollutant Leakage |
| S11 | Major Pollutant Leakage |
| Symbol | Meaning | Symbol | Meaning |
|---|---|---|---|
| C | Major maritime emergency case | HZ | Hazard source set |
| S | Scenario set of a case | VL | vulnerable entities set |
| Sk | A scenario | MI | mitigation agents set |
| ES | Inter-scenario relationship set | ENV | environmental factors set |
| Ek | An inter-scenario relationship | H | Attribute set of an object |
| O | Object set of a scenario | hi | An attribute |
| Oi | An object | Na | Name of an attribute |
| EI | Inter-object relationship set | Sa | Value of an attribute |
| Case Number | Accident Name | Occurrence Time | Occurrence Place | Accident Level | Accident Scenarios |
|---|---|---|---|---|---|
| C1 | Shanghai “8.20” collision accident between “Longqing 1” and “Ning Gaopeng 688” | 20 August 2020 | China | Especially Major | S2, S5, S6, S7, S9, S11 |
| C2 | Qingdao “4.27” ship pollution accident | 27 April 2021 | China | Especially Major | S2, S11 |
| C3 | The “ORKO” grounding and overturning accident | 2 December 2024 | Portugal | Major | S2, S3, S4, S10 |
| C4 | “Don Tomasso” overturning accident | 11 December 2021 | Argentina | Major | S3, S4, S8, S10 |
| C5 | Shanghai “4.5” collision accident between “XIANGZHOU” and “VAN MANILA” | 5 April 2017 | China | Major | S2, S3, S4, S9, S11 |
| C6 | “Pescargen IV” overturning accident | 5 August 2022 | Argentina | Major | S2, S3, S4 |
| C7 | The “i-Catcher” capsizing accident | 10 September 2022 | New Zealand | Major | S4, S9, S10 |
| C8 | The overturning accident of “SAINT BERNARD” | 17 April 2023 | France | General | S4, S8 |
| C9 | “MARIA REINA MADRE” overturning accident | 9 February 2024 | Spain | General | S3, S4 |
| C10 | The fire and explosion accident of the “CD Manzanillo” | 10 October 2023 | Singapore | Major | S5, S6, S8 |
| Symbol | Meaning | Symbol | Meaning |
|---|---|---|---|
| Case similarity | Attribute set structure similarity | ||
| Scenario set similarity | Scenario set similarity weight | ||
| Scenario-level relation similarity | Scenario-level relation similarity weight | ||
| Specific scenario similarity | Element set similarity weight | ||
| Object set similarity | Element-level relation similarity weight | ||
| Object-level relation similarity | Specific-type element similarity weight | ||
| Specific-type object similarity | Specific element similarity weight | ||
| Specific-type object structure similarity | Attribute set similarity weight | ||
| Specific object similarity | Attribute-level relation similarity weight | ||
| Attribute set similarity | Specific attribute similarity weight | ||
| Specific attribute similarity |
| Data Type | Subtype | Variable Data Format | Examples | Similarity Calculation Method |
|---|---|---|---|---|
| Numerical Type | Precise Type | Specific Values | Cargo Capacity (10,000 tons), Draft (10 m), Temperature (30 °C) | Refer to Table 6 |
| Interval Type | Specific Intervals | Oil Spill Volume (10–20 tons), Explosion Range (30–50 m2) | Refer to Table 6 | |
| Discrete Type | Numerical Lists | Number of Injuries (20, 30 people), Number of Rescue Ships (10, 15 vessels) | Refer to Table 6 | |
| Boolean Type | 0–1 Variables | Ship Specifications (1,803,020 m) | ||
| Scale Type | Increasing Positive Integer Sequence | Wind Strength ([1, 2, …, 10] levels), Emergency Response Level ([1, 2, 3] levels) | ||
| Text Type | Enumeration Type | Data Descriptions | Ship Types (Cargo ships, Fishing vessels, Tankers, etc.) | |
| Evaluation Type | Series of Words with Comparative Value | Damage Condition (Slight, Moderate, Severe, Extremely Severe) |
| Targetcase Variable Type | Basecase Variable Type | Is the Value Range Determined | Calculation Formula |
|---|---|---|---|
| Precise Type | Precise Type | yes | |
| Precise Type | Precise Type | no | |
| Interval Type | Interval Type | yes | |
| Interval Type | Interval Type | no | |
| Discrete Type | Discrete Type | yes | |
| Discrete Type | Discrete Type | no |
| Indicator Name | Definition | Calculation Method |
|---|---|---|
| Number of Retrieved Scenarios (NRS) | Number of Output Similar Scenarios | Derived from Statistical Analysis of Method Output Results |
| Number of Retrieved True Scenarios (NRTS) | Number of Output Similar Scenarios Conforming to Facts | Number of Scenarios Conforming to Facts Among Retrieved Scenarios |
| Number of Retrieved Scenarios Obtained (NRSO) | Number of Similar Scenarios Retrieved from Case Base | Statistical Number of Similar Scenarios Retrieved by CBR Method from Case Base |
| Recall Ratio | Comprehensiveness of CBR Method in Retrieving Targetcase Fact Scenarios | |
| Accuracy | Accuracy of CBR Method in Retrieving Targetcase Fact Scenarios | |
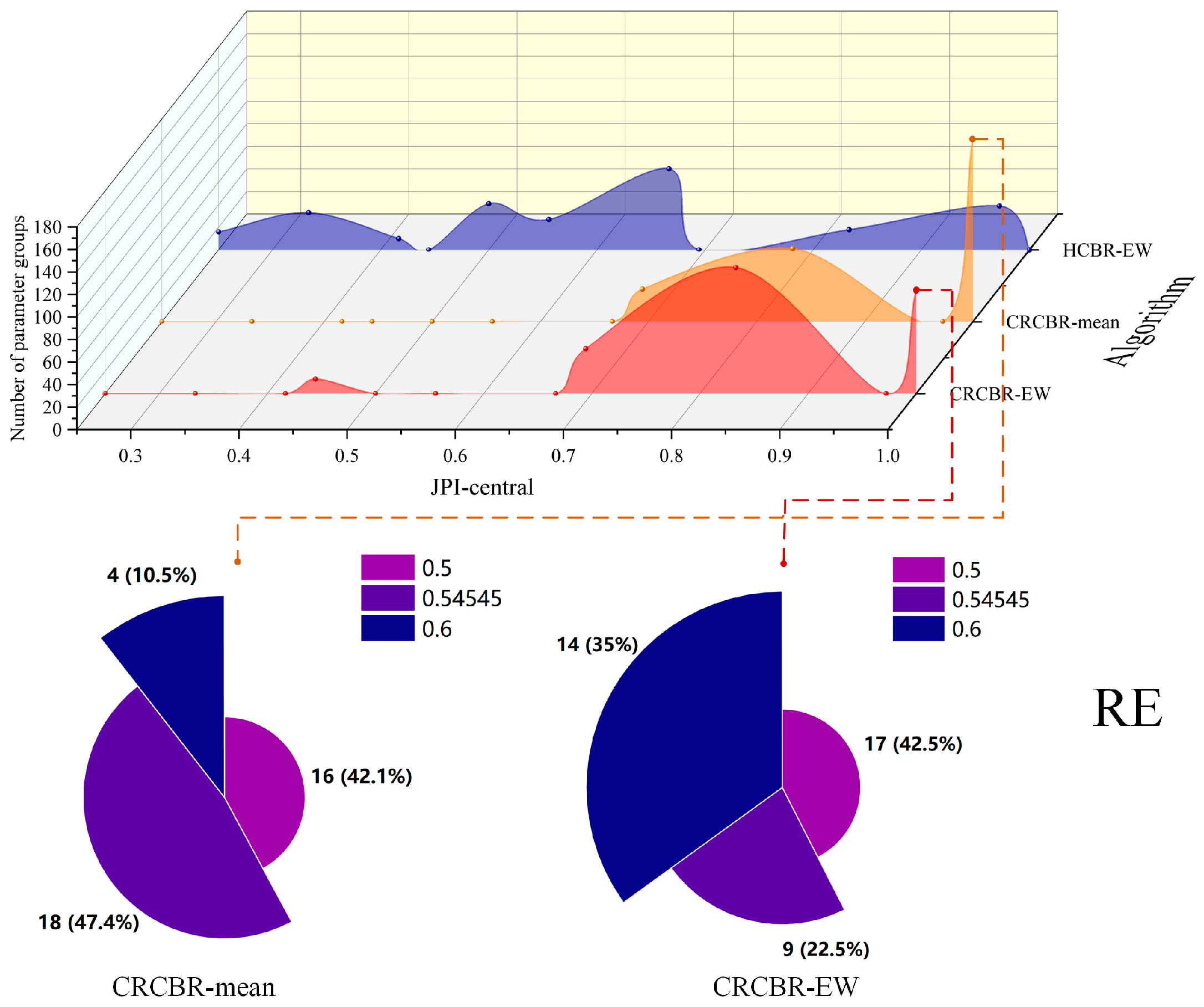
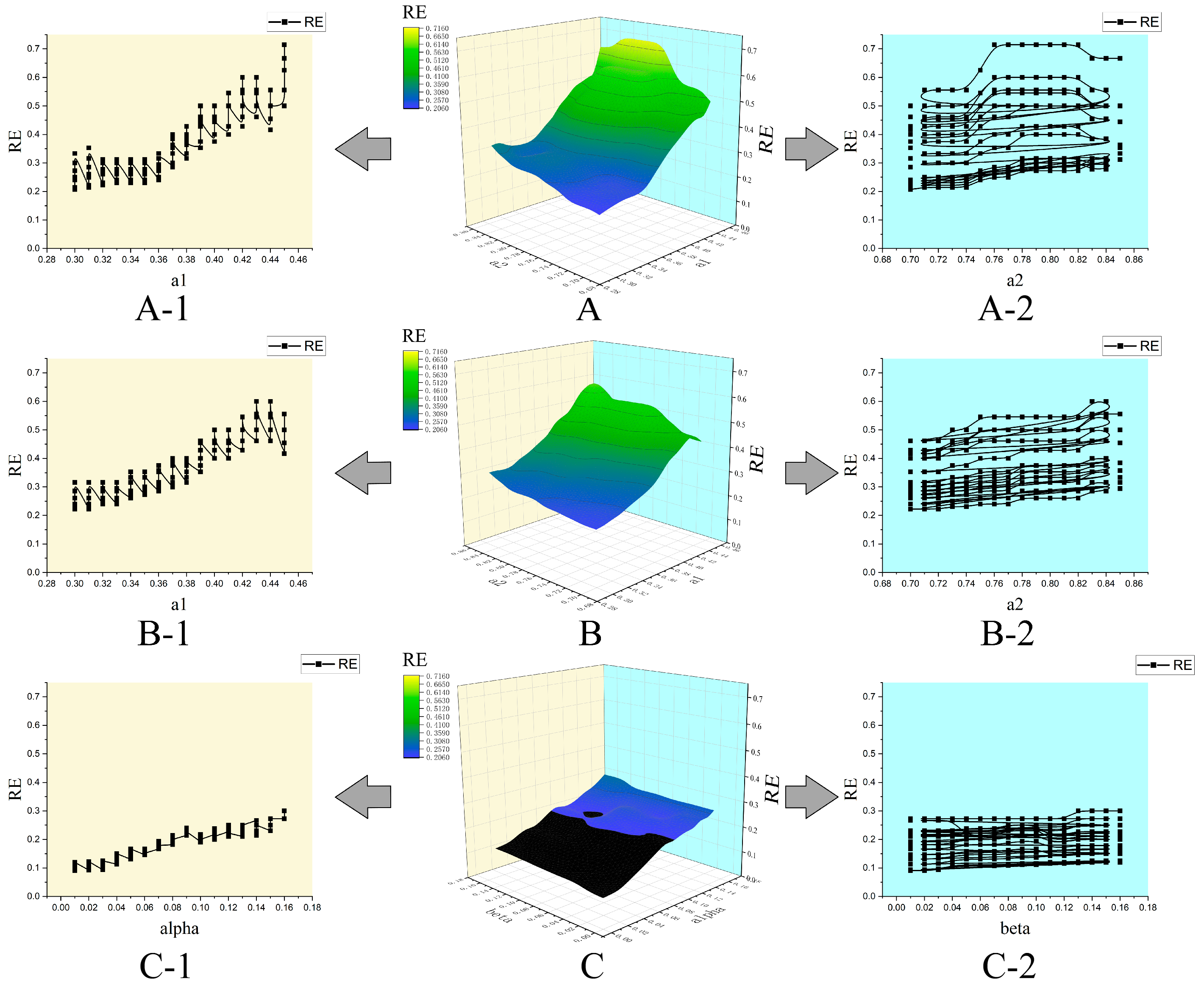
| Retrieval Efficiency (RE) | Ratio of Retrieval Effectiveness to Retrieval Cost for CBR Method in Retrieving Targetcase Fact Scenarios | |
| Joint Performance Indicator (JPI) | Comprehensive Performance of CBR Method in Retrieving Targetcase Fact Scenarios in Terms of Comprehensiveness and Accuracy |
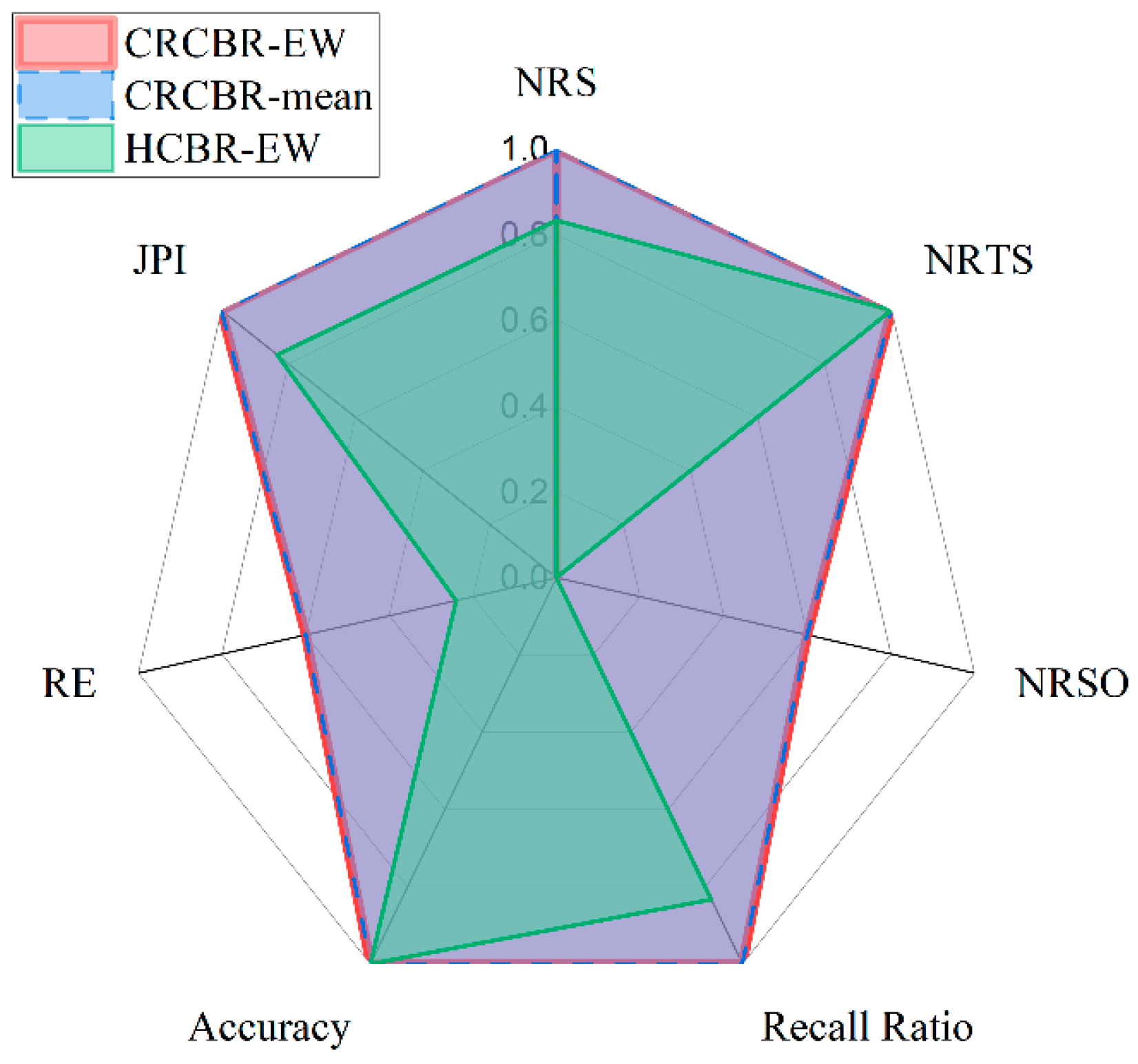
| Method Name | NRS | NRTS | NRSO | Recall Ratio | Accuracy | RE | JPI |
|---|---|---|---|---|---|---|---|
| CRCBR-EW | 6 | 6 | 10 | 1 | 1 | 0.6 | 1 |
| CRCBR-mean | 6 | 6 | 10 | 1 | 1 | 0.6 | 1 |
| HCBR-EW | 7 | 6 | 25 | 1.167 | 1 | 0.24 | 1.167 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Dou, Y.; Han, S.; Wang, J.; Yuan, R. An Improved Case-Based Reasoning Method Based on Dynamic Entropy Weighting: A Case Study of Scenario Prediction for Major Maritime Emergencies. Systems 2025, 13, 766. https://doi.org/10.3390/systems13090766
Li J, Dou Y, Han S, Wang J, Yuan R. An Improved Case-Based Reasoning Method Based on Dynamic Entropy Weighting: A Case Study of Scenario Prediction for Major Maritime Emergencies. Systems. 2025; 13(9):766. https://doi.org/10.3390/systems13090766
Chicago/Turabian StyleLi, Jinjie, Yajie Dou, Sining Han, Jikai Wang, and Renpeng Yuan. 2025. "An Improved Case-Based Reasoning Method Based on Dynamic Entropy Weighting: A Case Study of Scenario Prediction for Major Maritime Emergencies" Systems 13, no. 9: 766. https://doi.org/10.3390/systems13090766
APA StyleLi, J., Dou, Y., Han, S., Wang, J., & Yuan, R. (2025). An Improved Case-Based Reasoning Method Based on Dynamic Entropy Weighting: A Case Study of Scenario Prediction for Major Maritime Emergencies. Systems, 13(9), 766. https://doi.org/10.3390/systems13090766






