Understanding Congestion Evolution in Urban Traffic Systems Across Multiple Spatiotemporal Scales: A Causal Emergence Perspective

Abstract

Understanding how congestion forms and propagates over space and time is essential for improving the operational efficiency of urban traffic systems. Recent developments in causal emergence theory indicate that the causal structures underlying dynamic models are scale-dependent. Most existing studies on traffic congestion evolution focus on a single, fixed scale, which risks overlooking clearer causal patterns at other scales and thus limiting predictive power and practical applicability. To address this, we develop a multiscale congestion evolution modeling framework grounded in causal emergence theory. Within this framework we build dynamical models at multiple spatiotemporal scales using dynamic Bayesian networks (DBNs) and quantify the causal strength of these models using effective information (EI) and singular value decomposition (SVD)-based diagnostics. Using road networks from three central Kunshan regions, we validate the proposed framework across 24 spatiotemporal scales and five demand scenarios. Across all three regions and the tested scales, we observe evidence of causal emergence in congestion evolution dynamics. When results are pooled across regions and scenarios, models built at the 10 min/150 m scale exhibit stronger and more coherent causal structure than models at other scales. These findings demonstrate that the proposed framework can identify and help build dynamical models of congestion evolution at appropriate spatiotemporal scales, thereby supporting the development of proactive traffic management and effective resilience enhancement strategies for urban transport systems.

1. Introduction

As urbanization accelerates, the pressure on transportation systems continues to grow. Traffic congestion in cities has become increasingly severe, particularly during peak hours or under sudden disruptions such as accidents. This problem not only undermines travel efficiency and user experience but also exacerbates environmental pollution, energy waste, and significant socioeconomic losses [1]. While congestion has traditionally been treated as an engineering problem solvable through infrastructure expansion or optimization measures, it is increasingly recognized as the outcome of a complex interplay among human behavior, infrastructural constraints, and institutional responses [2].

Given the complex, nonlinear, and self-organizing nature of urban traffic systems [3], local congestion, if not effectively controlled, can gradually expand in both space and time. As traffic demand continues to rise, congestion may intensify and spread, ultimately leading to the collapse of large areas of the transportation network. This propagation process does not occur randomly. Instead, it tends to follow certain patterns shaped by travelers’ habitual behaviors and the structural constraints of the road network. Gaining insight into the propagation patterns is crucial for developing effective congestion mitigation strategies. In recent years, an increasing number of studies have sought to investigate the spatiotemporal dynamics of traffic congestion in complex road networks. These approaches generally fall into three categories: analytical methods, simulation-based methods, and data-driven methods.

Analytical methods abstract real-world road networks and traffic dynamics to develop mathematical models characterizing congestion propagation. Grounded in theoretical foundations, these models can be broadly categorized into six classical categories: traffic flow models, epidemic models, percolation models, cascading failure models, reaction-diffusion models, and cellular network models. Traffic flow models simulate the dynamic relationships among traffic parameters using continuous or discrete formulations [4,5,6]. They are effective for modeling link- and route-level propagation but become computationally intensive when applied to large-scale networks due to complex structures and control interactions. Epidemic models treat congestion propagation analogously to disease transmission, employing SIS or SIR frameworks to simulate the temporal evolution of congested nodes [7,8]. While effective in capturing the time-varying dynamics of congestion spread, these models offer limited insight into the spatial distribution of congested nodes across the network. Percolation models, inspired by fluid flow in porous media, are used to identify critical transitions in network connectivity and assess system vulnerability [9,10,11]. They effectively capture the spatial characteristics of congestion propagation through dynamic spatial clustering but often overlook key temporal features such as the speed of spread and dissipation, as well as the timing of congestion migration. Cascading failure models describe how localized disruptions can lead to network-wide breakdowns through flow redistribution [12,13]. These models were originally developed for power grids and communication networks. Similar to traditional traffic flow methods, they rely on manually defined assumptions to simplify system dynamics and parameter calibration, which constrains their flexibility and predictive accuracy. Reaction-diffusion models describe congestion as a local reaction diffusing across space under nonlinear dynamics [14]. Nevertheless, these models have limitations in representing long-distance influences and the spatial heterogeneity inherent in real-world traffic congestion. The cellular network model simulates congestion propagation by dividing the road network into cells and representing traffic dynamics through intra-cellular reactions and inter-cellular interactions [15]. However, this abstraction may oversimplify complex traffic behaviors by ignoring detailed vehicle-level interactions. Overall, analytical methods offer valuable theoretical insights into congestion mechanisms [16], yet their prior assumptions and computational burden in large-scale scenarios often lead to deviations from real-world observations.

Simulation-based methods are widely used and effective for modeling the spatiotemporal dynamics of traffic flow and travelers’ route choice behaviors, making them one of the mainstream approaches for studying congestion propagation dynamics. These methods rely on simulation tools to replicate traffic evolution under various conditions, offering strong scalability and intuitive visualization capabilities [17,18]. However, their effectiveness largely depends on the validity of the underlying traffic flow models and the accuracy of parameter calibration. Most of these models are built upon simplified assumptions and require extensive tuning effort to produce satisfactory results. As the road network and its complexity increase, the difficulty of simulation calibration and model construction rises substantially, resulting in increased output deviation and reduced reliability in practical applications.

With the rapid advancement of artificial intelligence and computing power, data-driven methods have gained widespread popularity across various domains [19,20,21]. Data-driven methods primarily employ modern statistical or artificial intelligence algorithms to model the spatiotemporal dynamics of congestion propagation. When sufficient data are available, these methods show stronger predictive accuracy and model adaptability. In recent years, spatiotemporal graph mining methods based on deep learning have been proposed to extract congestion propagation patterns, offering intuitive and structured representations of congestion dynamics [22]. Building on this, the CPM-ConvLSTM model [23], which integrates convolutional and long short-term memory networks, enhances the ability to capture spatial correlations and temporal dependencies, thereby precisely modeling the dynamic evolution of congestion across road networks. To further capture high-dimensional interactions in multi-source data, tensor-based representation learning has been introduced to model complex relationships among traffic states in higher-order feature spaces [24]. In addition, the Dynamic Bayesian Graph Convolutional Network, which treats congestion propagation as a graph message passing process, is capable of autonomously learning latent propagation structures from observational data. The model demonstrates strong dynamic adaptability and structural learning capabilities, showing notable advantages in handling non-stationary and nonlinear traffic evolution patterns [25]. The existing studies mentioned above are systematically categorized in

Table 1. Representative studies on traffic congestion evolution in road networks.

Method Category	Dynamics Models	Representative Studies
Analytical Methods	Traffic Flow Models	Wu et al. (2009) [4], Wright and Roberg (1998) [5], Bassolas et al. (2022) [6]
	Epidemic Models	Wu et al. (2004) [7], Saberi et al. (2020) [8]
	Percolation Models	Li et al. (2015) [9], Zeng et al. (2019) [10], Hamedmoghadam et al. (2021) [11]
	Cascading Failure Models	Zhao et al. (2016) [12], Duan et al. (2023) [13]
	Reaction-Diffusion Models	Bellocchi and Geroliminis (2020) [14]
	Network-Cell Models	Zhang et al. (2022) [15]
Simulation Methods	Traffic Simulation Models	Roberg and Abbess (1998) [17], Long et al. (2008) [18]
Data-Driven Methods	Deep Learning-based Models	Chen et al. (2018) [22], Di et al. (2019) [23], Yang et al. (2020) [24], Luan et al. (2022) [25]

.

Although a variety of models have been developed to capture congestion evolution dynamics, most of these studies focus on a single, fixed spatial or temporal modeling scale [26]. This single-scale paradigm often fails to fully capture the structural heterogeneity and dynamic complexity of urban traffic systems. In practical scenarios, traffic congestion evolution phenomena that seem stochastic and unpredictable at one modeling scale may become more regular and interpretable at another scale. Currently, congestion evolution modeling methods that explicitly integrate multiscale perspectives remain limited. It is therefore imperative to develop dimensionless metrics to support the comparative analysis and selection of congestion dynamics models across different scales.

In recent years, causal emergence has gained increasing attention as a core concept in complexity science [27]. Hoel et al. [28] demonstrated that the macro-level representation of a system, compared to its underlying micro-level description, can exhibit stronger and more effective causal influence. Essentially, it challenges the long-standing assumption that “more fine-grained models always yield more accurate or useful predictions” and has been widely applied in studies such as biology [29], artificial intelligence [30], brain networks [31], and complex systems science [32,33]. These studies have shown that when micro-level dynamics involve redundancy, noise, or high-dimensional entanglement, aggregated macro-level representations may reveal clearer and more interpretable causal structures. Recently, Zhang et al. [34] further extended this analytical framework by proposing a singular value decomposition (SVD)-based metric for measuring causal emergence without the need for predefined coarse-graining processes, enhancing the applicability of the method.

Based on the above discussion, this study adopts the perspective of causal emergence to compare traffic dynamics representations across different analytical scales. Following Hoel’s framework, “micro” and “macro” are understood here as relative notions defined by the level of aggregation: each scale corresponds to a projection that maps vehicle-level observations within a spatiotemporal cell to a cell state. For example, compared with a 5 min–100 m unit, a 1 min–50 m unit can be regarded as a micro-scale, since the former entails a greater degree of aggregation in both time and space. In this sense, causal emergence in traffic systems refers to the phenomenon that, relative to finer scales, certain coarser-scale representations provide a clearer and more consistent characterization of the causal structure underlying congestion evolution.

In this study, we develop a systematic, data-driven modeling framework to measure the causal emergence strength of congestion evolution dynamics across different spatiotemporal scales. First, a traffic state identification method, along with a multiscale road network partitioning strategy, is developed to construct traffic state vectors that represent the system’s traffic conditions over time. Next, dynamic models across multiple spatiotemporal scales are developed based on dynamic Bayesian networks (DBNs) to estimate transition probabilities of network traffic states. Finally, effective information (EI) and singular value decomposition (SVD) are employed to quantify the causal emergence strength of the proposed dynamic models.

This work makes the following three key contributions:

• We investigate causal emergence in road network congestion dynamics, providing a novel perspective on understanding the multiscale congestion evolution of traffic systems.
• We develop a quantitative framework that integrates machine learning techniques with causal emergence theory to measure the strength of causal emergence in traffic systems.
• We conduct extensive experiments grounded in a realistic road network to offer deeper insights into the multiscale structure of congestion evolution.

The remainder of this paper is organized as follows: Section 2 introduces the proposed methodology. Section 3 presents the experimental setup and results. Section 4 provides the theoretical implications and practical applications. Section 5 concludes the study and outlines future research directions.

2. Methodology

To investigate the dynamics of network congestion evolution and its causal emergence across multiple spatiotemporal scales, we developed a data-driven framework composed of three core components, as shown in Figure 1. The first component proposes a multiscale traffic state identification method to capture the characteristics of network traffic states. The second component constructs a spatiotemporal dynamic model of urban traffic congestion to characterize the structural evolution patterns of congestion states. Leveraging causal emergence theory, the third component quantifies the clarity of causal structures associated with congestion evolution models across different scales. By integrating machine learning techniques with causal emergence theory, the proposed framework effectively captures and quantifies the phenomenon of causal emergence in congestion dynamics under road network conditions.

2.1. Multiscale Network Traffic State Identification

2.1.1. Spatiotemporal Scale Partitioning

For the spatial division, each complete road segment r is divided into multiple smaller units $n_r$ based on a predefined minimum division length $l_{\min }$. For each segment, the start and end coordinates, denoted as $(x_r^{\mathrm{s}},y_r^{\mathrm{s}})$ and $(x_r^{\mathrm{e}},y_r^{\mathrm{e}})$, are first determined, along with the road direction ${\beta }_r$ and the total segment length $L_r$. The number of resulting segment units is calculated as:

$$n_r=⌈{\displaystyle \frac{L_r}{l_{\min }}}⌉.$$

(1)

For each unit $u\in \{1,\dots ,n_r\}$, its relative position along the road is expressed as $(l_u^{\mathrm{s}},l_u^{\mathrm{e}})$, indicating the start and end distances from the origin of segment r. These are then converted into spatial coordinates $(x_u^{\mathrm{s}},y_u^{\mathrm{s}})$ and $(x_u^{\mathrm{e}},y_u^{\mathrm{e}})$ using the road orientation ${\beta }_r$. If a residual segment remains outside the regular division scheme, it is treated as an independent unit to maintain spatial continuity. This process is repeated for all road segments in the study area. All resulting segment units, whose total number is N, are stored in the segment set $U=\{1,\dots ,N\}$. A binary connectivity matrix $A\in {\{0,1\}}^{N\times N}$ is constructed to describe the topological relationships among these units, defined as:

$$A_{uv}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathrm{road}\mathrm{segment}\mathrm{units}u\mathrm{and}v\mathrm{are}\mathrm{connected},\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(2)

Spatial scales are chosen to match the road network structure and modeling complexity of the study region, ensuring feasibility and generalizability [35].

In terms of temporal division, the selection of appropriate time intervals needs to balance representation accuracy with computational efficiency. The following principles guide this selection:

(a)

The selected scales should align with real-world traffic management needs to ensure practical relevance [36].

(b)

The selection of temporal scale needs to strike a balance between model fidelity and computational efficiency [37].

An excessively coarse spatiotemporal scale may span the entire duration of a congestion episode, masking intermediate transitions and limiting the ability to capture the underlying dynamics of congestion evolution. Conversely, an overly fine scale may introduce redundant state information and increase computational burden without improving predictive performance. To balance the accuracy and interpretability of the model while considering the actual conditions of the selected study area, we adopted four spatial scales: 50 m, 100 m, 150 m, and 200 m. These scales cover distances from short links near intersections to longer segments, enabling analyses from localized bottlenecks to broader spillover patterns. Similarly, six temporal scales were considered: 2, 5, 10, 15, 20, and 30 min. The shorter intervals capture rapid fluctuations, while the longer intervals reflect aggregated congestion trends. These candidate scales ensure that both short-term dynamics and long-term trends. In practice, the division of temporal and spatial scales can be customized.

2.1.2. Network Traffic State Identification

After the spatiotemporal scale partitioning, the traffic state of each road segment is determined by integrating vehicle trajectory data with road speed limit. In this study, traffic states are divided into two categories: “congested” and “uncongested”. At each time slice t, the traffic state of the road network is identified as follows.

Each road segment unit u is selected from the spatial partition set U, and its spatial location is determined. Then, vehicle trajectory points within time slice t that fall inside u are identified. For these points, the average speed ${\overline{v}}_{u,t}$ is calculated as the mean of their speed values:

$${\overline{v}}_{u,t}={\displaystyle \frac{{\sum }_{p\in P_{u,t}}{v}_p}{|P_{u,t}|}},$$

(3)

where $P_{u,t}$ denotes the set of trajectory points in unit u during interval t, and $v_p$ is the speed of point p. Based on the computed average speed ${\overline{v}}_{u,t}$ and speed limits, congestion classification criteria are applied to determine the traffic state $s_{u,t}$ for road segment u, where 0 indicates “uncongested” and 1 indicates “congested”.

The above process is repeated for all segment units in U, and the estimated traffic states are aggregated into the state vector $S_t={[s_{1,t},s_{2,t},\dots ,s_{N,t}]}^{\mathrm{T}}\in {\{0,1\}}^N$. By iterating this process across all time slices, a complete spatiotemporal series of congestion states $\{S_1,S_2,\dots ,S_T\}$ for the entire road network is obtained. In this study, the traffic state of each segment is identified as “congested” when the average speed drops below 60% of the free-flow speed; otherwise, it is classified as “uncongested” [38]. In practice, the speed threshold can be customized according to different scenarios [39].

2.2. Dynamic Modeling of Congestion Evolution

To gain deeper insights into the formation mechanisms and spatiotemporal propagation of traffic congestion, it is essential to capture both temporal dynamics and topological causal dependencies. In view of this, we developed a spatiotemporal dynamic model based on dynamic Bayesian networks (DBNs). Specifically, the causal graph encodes the spatial dependencies between road segments based on the road network connectivity matrix $A_{uv}$, providing the structural prior for causal interactions. Based on this structure, the DBN model is trained using the traffic state vector $S_t$ to model the temporal evolution and predict future states. This integrated approach enables the modeling of causal diffusion and interactive evolution of congestion across the network, providing methodological support for exploring causal emergence in traffic systems. Figure 2 illustrates an example of the structural representation of a dynamic Bayesian network for characterizing the spatiotemporal evolution of traffic congestion.

A causal graph is constructed to represent the causal relationships among traffic variables. This graph is defined as a directed acyclic graph, where nodes correspond to traffic state variables, and edges indicate the direction of causal influence. The urban arterial road network is abstracted as a directed graph $G=(V,E)$, where V represents the set of road segment nodes, and E denotes the set of directed edges established based on physical connections and the prevailing direction of traffic flow. Note that, although traffic flows from upstream to downstream, the causal dependencies for congestion are defined from downstream to upstream. This is based on the empirical observation that downstream congestion can propagate backward, influencing upstream traffic states [40].

Building on this causal structure, a DBN was developed to model the temporal evolution of road segment congestion. The DBN framework integrates the principles of Bayesian networks and Markov chains, enabling the characterization of probabilistic state transitions across time slices. Within this framework, it is assumed that the evolution of traffic states adheres to the first-order Markov property, meaning that the state of the system at time t depends only on its state at time $t-1$. Guided by the causal graph, the traffic state of spatial unit $u\in U$ at time t, denoted by $s_{u,t}\in \{0,1\}$, depends on the traffic state of its downstream parent units $\mathrm{Pa}\left(u\right)\subseteq U$ at the previous time step $t-1$. The global traffic state vector at time t is expressed as:

$$S_t={[s_{1,t},s_{2,t},\dots ,s_{N,t}]}^{\mathrm{T}},$$

(4)

where each $s_{u,t}$ indicates the traffic state of unit u at time t. The dependency structure can thus be written as:

$$s_{u,t}\sim P(s_{u,t}\mid S_{t-1}^{\mathrm{Pa}\left(u\right)}).$$

(5)

To estimate the local state transition probabilities for each node, this study adopted a frequency-based approach that directly uses observed data without any prior assumptions. The conditional probability is computed as:

$$P\left(s_{u,t}=k\mid S_{t-1}^{\mathrm{Pa}\left(u\right)}=m\right)={\displaystyle \frac{n_u(m,k)}{n_u\left(m\right)}},$$

(6)

where u denotes the node under consideration, and $\mathrm{Pa}\left(u\right)$ represents its downstream node set. Here, m is a possible combination of parent states. $n_u\left(m\right)$ is the number of occurrences of $S_{t-1}^{\mathrm{Pa}\left(u\right)}=m$, and $n_u(m,k)$ counts the observations where node u is in state k at time t given parent states m at time $t-1$. This estimation is conducted across all nodes to obtain the local transition probability distributions. Building on the local models, a global state transition probability for the entire road network is constructed. For each transition from a global state $S_t$ to a new state $S_{t+1}$, the transition probability is approximated by aggregating the local probabilities:

$$P(S_{t+1}\mid S_t)=\prod _{u\in U}P(s_{u,t+1}\mid S_t^{\mathrm{Pa}\left(u\right)}),$$

(7)

where $s_{u,t+1}$ is the state of unit u at time $t+1$, and $S_t^{\mathrm{Pa}\left(u\right)}$ is the state combination of its downstream nodes in $S_t$ at time t.

To mitigate the computational complexity of the high-dimensional global state space, we restricted the transition probability matrix to the set of global states observed in the data, denoted as $\Omega =\{S_t\mid t=1,\dots ,T\}$. For any two states $S,S^{\prime }\in \Omega$, the probability is normalized over this historical state set:

$$P_{\mathrm{hist}}(S^{\prime }\mid S)={\displaystyle \frac{P(S^{\prime }\mid S)}{{\sum }_{\tilde{S}\in \Omega }P(\tilde{S}\mid S)}},$$

(8)

where $\tilde{S}$ denotes any state in the historical set $\Omega$. This approach reduces the matrix size and improves computational efficiency while preserving the essential dynamic characteristics observed in the historical data.

2.3. Measuring Causal Emergence of Congestion Evolution

Modeling congestion evolution dynamics is inherently sensitive to spatiotemporal scale. As spatial and temporal scales change, the causal structures exhibited by congestion evolution models also vary. Considering these scale-dependent variations, identifying causal emergence across different spatiotemporal scales is both crucial and challenging for understanding the underlying mechanisms of congestion evolution. To this end, this section measures the strength of causal emergence in congestion evolution dynamics using two complementary methods grounded in information theory: effective information (EI) [30] and singular value decomposition (SVD) [34]. These two methods differ fundamentally in how they characterize system dynamics. EI measures the amount of information the current state provides about the next state, directly quantifying the strength of causal dependencies across state transitions. In contrast, SVD decomposes the transition matrix to reveal its spectral properties, capturing the intrinsic dimensionality and structural regularities of the dynamic process through the distribution of singular values. By leveraging both EI and SVD, this study constructs a more comprehensive and robust framework for measuring the strength of causal emergence in congestion evolution.

2.3.1. Measuring Causal Emergence Based on EI

The effective information (EI) is a quantitative measure used to assess how deterministically a system’s current state constrains its future state. Specifically, it captures the amount of information the current state provides about the next state, based on the entropy of the state transition probabilities $P_{\mathrm{hist}}$. For each global traffic state $S^{\left(\omega \right)}\in \Omega$, the outgoing transition probability vector is denoted by:

$$W^{\left(\omega \right)}=\left\{P(S_{t+1}\mid S_t=S^{\left(\omega \right)})\right\}.$$

(9)

The entropy of this distribution is given by:

$$H\left(W^{\left(\omega \right)}\right)=-\sum _{{\omega }^{\prime }=1}^{|\Omega |}{p}_{{\omega }^{\prime }}{log}_2{p}_{{\omega }^{\prime }},$$

(10)

where $p_{{\omega }^{\prime }}$ denotes the probability of the transition $S_{t+1}=S^{\left({\omega }^{\prime }\right)}$ (i.e., $p_{{\omega }^{\prime }}=P(S_{t+1}=S^{\left({\omega }^{\prime }\right)}\mid S_t=S^{\left(\omega \right)})$) and $|\Omega |$ denotes the total number of states in $\Omega$. Entropy reflects the uncertainty of future congestion states. The average entropy across all states is then calculated as:

$$\overline{H}={\displaystyle \frac{1}{|\Omega |}}\sum _{\omega =1}^{|\Omega |}H\left(W^{\left(\omega \right)}\right).$$

(11)

The effective information $EI$ of the network is defined as the difference between the entropy of the aggregated system-wide transition distribution $H\left(\overline{W}\right)$ and the average entropy $\overline{H}$:

$$EI=H\left(\overline{W}\right)-\overline{H}.$$

(12)

Specifically, the entropy of the aggregated transition distribution $H\left(\overline{W}\right)$ is computed as:

$$H\left(\overline{W}\right)=-\sum _{{\omega }^{\prime }=1}^{|\Omega |}{\overline{p}}_{{\omega }^{\prime }}{log}_2{\overline{p}}_{{\omega }^{\prime }},$$

(13)

where the aggregated probability ${\overline{p}}_{{\omega }^{\prime }}$ is given by:

$${\overline{p}}_{{\omega }^{\prime }}={\displaystyle \frac{1}{|\Omega |}}\sum _{\omega =1}^{|\Omega |}{p}_{{\omega }^{\prime }}.$$

(14)

A higher $EI$ indicates that the traffic system possesses stronger internal regularity, meaning that the evolution of congestion states is more structured and less random.

To explore causal emergence at a higher level of abstraction, we applied a greedy coarse-graining algorithm. Each global state block $B^{\left(\omega \right)}$, representing a group of similar micro-level state vectors $S_t={[s_{1,t},s_{2,t},\dots ,s_{N,t}]}^{\mathrm{T}}$, serves as the unit of coarse-graining. For a selected block $B^{\left(\omega \right)}$, its candidate merging set ${\mathcal{C}}^{\left(\omega \right)}$ is identified based on the Markov neighborhood defined by incoming and outgoing transitions. For each state block $B^{\left({\omega }^{\prime }\right)}\in {\mathcal{C}}^{\left(\omega \right)}$, the method evaluates whether merging blocks $B^{\left(\omega \right)}$ and $B^{\left({\omega }^{\prime }\right)}$ increases $EI$. If the effective information increases, the merge operation is retained. If it does not increase, the operation is discarded. This process continues until no further improvement is achieved, and the final maximum effective information $E{I}_{\max }$ is obtained. The emergence strength is then computed as:

$$CE=E{I}_{\max }-E{I}_{\mathrm{init}},$$

(15)

where $E{I}_{\mathrm{init}}$ is the $EI$ of the original network. A positive $CE$ confirms that macro-scale representations provide clearer and more deterministic causal structures than the micro-scale ones, indicating the presence of causal emergence.

2.3.2. Measuring Causal Emergence Based on SVD

The SVD-based method draws on singular value decomposition to reveal the latent structural patterns within the state transition matrix $P_{\mathrm{hist}}$. By decomposing the matrix into independent components, it captures the dominant modes of variation in traffic state dynamics, allowing the identification of low-dimensional structures that govern the evolution of congestion under different spatiotemporal scales. Mathematically, the decomposition is expressed as:

$$P_{\mathrm{hist}}=U\Sigma V^T,$$

(16)

where $\Sigma$ contains the singular values ${\sigma }_1,{\sigma }_2,\dots ,{\sigma }_{|\Omega |}$, reflecting the intrinsic degrees of freedom in congestion evolution at that scale. U and $V^T$ are the left and right singular vector matrices, respectively. The magnitude and decay of these singular values offer insight into the redundancy and structure in congestion transition pathways, particularly in relation to how spatial disturbances propagate or dissipate over time.

To further characterize the system’s dynamic reversibility and the concentration of information into dominant modes, we define the $\alpha$-order generalized norm as:

$${\Gamma }_{\alpha }=\sum _{\omega =1}^{|\Omega |}{\sigma }_{\omega }^{\alpha },\alpha \in (0,2),$$

(17)

where ${\sigma }_{\omega }$ denotes the $\omega$-th singular value of the state transition matrix, and $|\Omega |$ is the total number of singular values. The parameter $\alpha$ controls the sensitivity of the metric to dominant versus tail singular values, with smaller $\alpha$ emphasizing contributions from larger singular values. Thus, ${\Gamma }_{\alpha }$ captures the overall concentration of reversible dynamics into dominant modes.

To facilitate comparison across systems or parameter settings, we further normalize this metric as:

$${\gamma }_{\alpha }={\displaystyle \frac{{\Gamma }_{\alpha }}{|\Omega |}},0<{\gamma }_{\alpha }\le 1,$$

(18)

where ${\gamma }_{\alpha }$ represents the average reversibility per mode, reflecting the information transmission efficiency of the system. A higher value of ${\gamma }_{\alpha }$ indicates that a greater proportion of system dynamics is captured by a few dominant reversible modes, implying stronger information compactness and higher macroscopic predictability.

To measure causal emergence strength, a threshold $\epsilon$ is set to filter out low-significance singular values. The number of effective singular values retained is:

$$r_{\epsilon }=max\left\{\omega \mid {\sigma }_{\omega }>\epsilon \right\}.$$

(19)

If $r_{\epsilon }<|\Omega |$, it implies the existence of fuzzy causal emergence, where $\epsilon$ represents the degree of causal granularity. This allows identifying coarse-grained traffic dynamics that dominate network evolution. The causal emergence strength is then computed as:

$$\Delta {\Gamma }_{\alpha }\left(\epsilon \right)={\displaystyle \frac{{\sum }_{\omega =1}^{r_{\epsilon }}{\sigma }_{\omega }^{\alpha }}{r_{\epsilon }}}-{\displaystyle \frac{{\sum }_{\omega =1}^{|\Omega |}{\sigma }_{\omega }^{\alpha }}{|\Omega |}}.$$

(20)

A positive $\Delta {\Gamma }_{\alpha }\left(\epsilon \right)$ indicates that macro-level transition dynamics exhibit greater causal information than their micro-level counterparts, thereby revealing scale-induced simplification in traffic state predictability.

Together, these two methods enable a robust, data-driven measurement of causal emergence in congestion evolution dynamics. By measuring the strength of causal emergence, the framework supports the design of hierarchical traffic control strategies and informs scale-sensitive modeling decisions. This multiscale causal analysis offers a novel perspective on congestion propagation in complex urban road networks.

3. Experiments and Results

3.1. Data Source

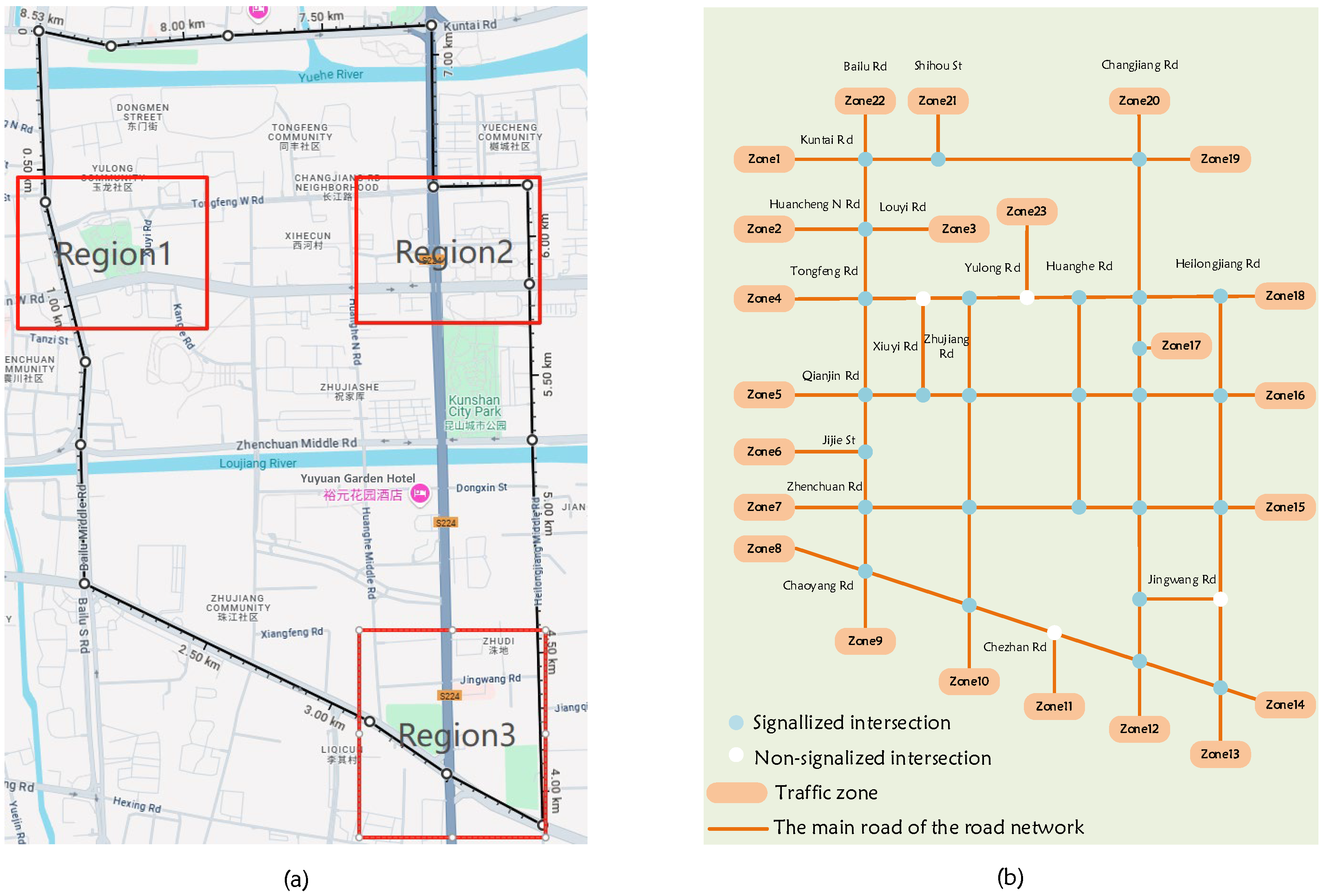
To investigate the evolution of road network congestion across multiple spatiotemporal scales, the proposed framework integrated road network topology with OD flow data. This study systematically varied traffic demand through simulation to generate a dataset of congestion patterns across multiple scales and demand scenarios, enabling the creation of more comprehensive and realistic traffic scenarios. Three representative regions within Kunshan’s urban network were selected to capture diverse congestion dynamics and structural heterogeneity. Each region comprised arterial and secondary roads with mixed signalized/unsignalized intersections, spanning distinct spatial extents. Congestion was analyzed at four spatial scales (i.e., 50 m, 100 m, 150 m, 200 m) and six temporal scales (2, 5, 10, 15, 20, and 30 min), yielding 24 spatiotemporal scales per demand scenario. Provided by the local traffic authority, the signal timing plans were dynamically adjusted to reflect real-time flow fluctuations. To simulate network traffic conditions under varying demand, OD demand matrices associated with 23 traffic zones were obtained. The spatial scope and zone division are illustrated in Figure 3.

The baseline OD matrix was derived from the vehicle license plate recognition system, from which vehicle trajectories within the region were extracted. By aggregating these trajectories, flow information between traffic zones was constructed at 15 min intervals, covering the period from 6:00 AM to 9:00 PM. To simulate a variety of congestion evolutions, we generated five demand scenarios by scaling the baseline matrix, denoted $O{D}_{\mathrm{base}}$. Two scaling strategies were employed: (1) uniformly scaling all OD pairs, and (2) selective scaling applied to both inflows to and outflows from high-attraction zones (e.g., commercial centers and hospitals). The corresponding scaling coefficients and descriptive labels are listed in

Table 2. OD settings for demand scenario generation.

Demand Scenario	OD Setting	Description
1	$O{D}_{\mathrm{base}}$	Baseline OD flow from license plate data
2	$1.2\times O{D}_{\mathrm{base}}$	All OD flows increased by 20%
3	$0.8\times O{D}_{\mathrm{base}}$	All OD flows decreased by 20%
4	$1.2\times Z_5$	Flows related to Traffic Zone 5 increased by 20%
5	$1.2\times Z_7$	Flows related to Traffic Zone 7 increased by 20%

.

The simulation duration was set to 57,600 s (16 h), from 6:00 AM to 10:00 PM, which is slightly longer than the original observation window, allowing congestion to dissipate completely. Floating Car Data (FCD) devices were configured with a sampling interval of 2 s and a reporting probability of 0.25. This high sampling frequency and relatively long observation window ensured that the resulting trajectory dataset was dense enough to capture fine-grained temporal variations in congestion without introducing significant data sparsity.

3.2. Traffic State Identification Results

Figure 4 presents the 5 min congestion evolution within every 50 m segment under Scenario 2. A greener color indicates smoother traffic flow, while a redder color signifies more severe congestion. The process of congestion propagation and dissipation is clearly illustrated. Focusing on the north–south corridor along Bailu Middle Road between its intersections with Tongfeng West Road and Kuntai Road, congestion emerges at 7:30 AM, extends to Kuntai Road by 8:30 AM, and then gradually subsides. It reoccurs in the evening, retreating to the Bailu Middle Road–Louyi Road intersection by 8:30 PM and clearing by 9:30 PM. In particular, morning and evening peaks exhibit different congestion patterns across different links.

3.3. Congestion Evolution Dynamics Modeling Results

Figure 5 presents heat maps of state transition probability matrices estimated from historical data. Each row represents the probability distribution of transitions from the current state to all other possible states. For instance, if the transition probability from S9 to S2 is one, it indicates that the system will inevitably evolve from S9 to S2, with no chance of transitioning to any other state. Since the number of roads and nodes varies across different regions, the dimensions of the transition matrices can differ even under the same spatiotemporal scale. Based on these matrices, the strength of causal emergence in congestion evolution was measured using both SVD and EI.

3.4. Causal Emergence Measurement Based on EI

By computing the effective information of the state transition matrices at each scale, we obtained the causal emergence strength across several spatiotemporal scales. Figure 6 presents the temporal evolution of this strength for several fixed spatial scales (50 m, 100 m, 150 m, and 200 m), with each subplot corresponding to one specific spatial scale under five traffic demand scenarios. At a spatial scale of 50 m, the causal emergence strength remains low across all time intervals and scenarios, indicating that overly fine spatial granularity may obscure macro-level causal patterns. As spatial scale increases to 100 m, some scenarios (e.g., Scenarios 1 and 2) begin to show moderate emergence peaks at 10, 15, and 20 min, reflecting improved structural clarity. At a 150 m spatial scale, the causal emergence strength exhibits significant peaks in most scenarios, particularly Scenarios 2 and 4, at 15 min. This spatiotemporal scale effectively captures the underlying causal transitions of congestion evolution. At a 200 m spatial scale, Scenarios 1 and 5 maintain high causal emergence strength, but some scenarios exhibit a declining trend. This suggests that excessive aggregation may weaken key causal signals of congestion dynamics. In summary, among the 24 scales, the scale of 150 m with 15 min exhibits higher causal emergence strength in most demand scenarios. This confirms the scale-dependent nature of causal structures in traffic systems.

Figure 7 complements this analysis by illustrating how causal emergence strength varies with spatial scale for several fixed temporal scales, with each subplot corresponding to one specific temporal scale. This arrangement highlights the spatial sensitivity of each demand scenario. Under short temporal scales (i.e., 2 and 5 min), the emergence strength is generally low across all spatial scales, with limited variation among scenarios. However, as the temporal scale increases, the emergence strength rises and exhibits more significant spatial divergence, suggesting that sufficient temporal depth is required for macro-level causal structures to emerge. At 10, 15, and 20 min, most scenarios achieve their peak emergence at the 150 m spatial scale, supporting the idea that this is a critical scale for capturing system-wide causal dynamics. At 30 min, the emergence patterns become more fragmented, indicating increased heterogeneity in the system response under longer temporal aggregation.

Table 3. Causal emergence strength for five demand scenarios across different scales based on EI.

Scale	Causal Emergence Strength
	Scenario 1	Scenario 2	Scenario 3	Scenario 4	Scenario 5
50_2	0.000	0.000	0.000	0.000	0.000
50_5	0.004	0.001	0.000	0.000	0.002
50_10	0.034	0.000	0.000	0.000	0.000
50_15	0.029	0.000	0.000	0.000	0.000
50_20	0.000	0.003	0.000	0.000	0.009
50_30	0.012	0.018	0.000	0.000	0.029
100_2	0.005	0.000	0.003	0.001	0.005
100_5	0.067	0.039	0.012	0.001	0.018
100_10	0.148	0.051	0.004	0.001	0.034
100_15	0.085	0.054	0.013	0.000	0.026
100_20	0.061	0.149	0.000	0.023	0.041
100_30	0.050	0.140	0.000	0.004	0.039
150_2	0.004	0.006	0.045	0.013	0.005
150_5	0.054	0.025	0.040	0.029	0.048
150_10	0.118	0.073	0.028	0.062	0.086
150_15	0.072	0.131	0.055	0.168	0.143
150_20	0.000	0.078	0.042	0.040	0.130
150_30	0.094	0.051	0.005	0.000	0.095
200_2	0.004	0.008	0.030	0.013	0.004
200_5	0.078	0.039	0.035	0.025	0.052
200_10	0.177	0.063	0.008	0.036	0.056
200_15	0.098	0.137	0.003	0.100	0.091
200_20	0.046	0.116	0.056	0.010	0.113
200_30	0.039	0.081	0.000	0.000	0.190

Each scale is denoted as “spatial scale_temporal scale”, e.g., “50_2” = 50 m and 2 min.

summarizes the causal emergence strength calculated by the EI-based method across 24 spatiotemporal scales and five demand scenarios. Several key patterns can be observed. First, finer scales (e.g., 50_2, 50_5) consistently yield near-zero emergence strength across all scenarios, indicating that traffic dynamics at micro-scales are mainly determined by stochastic fluctuations and lack identifiable causal structure. Second, the emergence strength generally increases with broader spatial and temporal scales but not in a strictly monotonic manner. Instead of improving continuously with scale, the values tend to fluctuate, with several intermediate scales showing more prominent peaks. For instance, 200_10, 200_15, and 150_15 exhibit relatively high emergence strength, particularly under high-demand conditions (e.g., Scenario 5), where enhanced interaction effects and persistent congestion propagation promote the formation of macro-level causal regularities. Third, the emergence patterns vary significantly across scenarios, reflecting their distinct network responses. Scenario 2 and Scenario 5 both exhibit strong emergence at mid-to-long temporal scales across multiple spatial scales (e.g., 100_20, 150_15, 200_15), suggesting enhanced causal coupling under heavier traffic loads or localized flow surges. In contrast, Scenario 3 shows consistently low emergence strength across all scales, likely due to reduced interaction intensity and the absence of sustained congestion propagation that would otherwise give rise to consistent macroscopic patterns. Scenario 4 exhibits strong causal emergence primarily at the 150_15 scale, indicating localized yet distinct propagation effects.

The better performance of the model at 150_15 scale can be explained by its alignment with characteristic features of congestion propagation on urban roads. Spatially, 150 m approximately corresponds to the typical propagation distance between traffic bottlenecks in urban road networks. This scale effectively captures localized congestion patterns while avoiding excessive noise introduced by overly fine-grained detail. Temporally, the 15 min window covers several traffic signal cycles, allowing the model to incorporate congestion evolution information across multiple signal phases. From the perspective of congestion evolution, this spatiotemporal scale smooths out short-term fluctuations caused by individual vehicle behavior and transient disturbances, while preserving meaningful dynamic changes relevant to how congestion forms, spreads, and dissipates. As a result, it facilitates clearer and more stable causal relationships, as reflected by the increased causal emergence strength. The similarly robust performance observed at the 200_15 scale further supports the idea that spatial scales on the order of typical bottleneck propagation distances combined with temporal scales covering multiple signal cycles provide an effective balance between noise reduction and dynamic fidelity in modeling urban traffic congestion evolution.

3.5. Causal Emergence Measurement Based on SVD

The causal emergence measurement based on SVD proposed in Section 2.3.2 enables in-depth analysis of state transition structures at multiple spatiotemporal scales. Taking demand Scenario 3 as an example, where the OD flow was increased to 1.2 times the baseline, congestion evolution in the road network became more pronounced. Using the SVD method, the singular values were obtained. Figure 8 shows the singular values ranked from largest to smallest, with labels below the graph indicating the corresponding spatiotemporal scales. For instance, “50_2” denotes the singular value at a spatial scale of 50 m and a temporal scale of 2 min. Although the singular value curves differ in magnitude across scales, their overall shapes are similar. The pattern observed in the singular value curves involves an initial steep decrease from high values to one, followed by a subsequent drop from one to zero. This second drop is indicative of causal emergence phenomena. Based on these singular value decompositions, causal emergence strength was measured by setting thresholds on valid singular values. However, due to the presence of two clear breakpoints, it was challenging to define a single reasonable threshold to determine valid singular values. Therefore, this paper adopted multiple thresholds for a comparative analysis.

Figure 9 shows the variation in $\Delta {\Gamma }_{\alpha }$ obtained based on SVD decomposition with respect to the temporal scale under different spatial scales. Different colored curves represent results obtained under different threshold values of $ϵ$. From the perspective of spatial scales, larger spatial scales (e.g., 200 m) lead to greater causal emergence strength, and the fluctuation range of the emergence strength increases. In contrast, smaller spatial scales (e.g., 50 m) exhibit weaker emergence strength. In terms of $ϵ$ values, higher $ϵ$ values enhance the causal emergence effect, specifically revealed as higher emergence strength and more drastic changes, while lower $ϵ$ values keep the emergence strength at a lower level with gentler changes. Regarding the temporal scale, the causal emergence values generally rise first, then tend to stabilize or continue to fluctuate, and the time points of peak values vary with different scales and $ϵ$ values.

A vertical comparison of different subgraphs (i.e., under different demand scenarios) reveals significant variations in causal emergence. Specifically, when the overall system demand increases (e.g., Scenario 2), the interactions and dependencies among internal components intensify, leading to higher complexity. This results in higher causal emergence strength, as well as larger fluctuations and peaks. When local demand increases (e.g., Scenarios 4 and 5), regional traffic pressure rises. Such local changes propagate through the system, affecting global causal relationships and strengthening causal emergence. Conversely, when overall demand decreases (e.g., Scenario 3), system load alleviates, internal interactions and dependencies simplify, and complexity decreases. Consequently, causal emergence strength and fluctuations both diminish. These results indicate that demand levels and their spatiotemporal distributions significantly influence causal emergence.

Figure 10 shows the variation in $\Delta {\Gamma }_{\alpha }$ with spatial scale under three demand scenarios at different temporal scales. Different colored curves represent results obtained under different threshold values of $ϵ$. Each subgraph in the figure represents a different temporal scale, and each curve indicates the variation trend of causal emergence strength with the spatial scale under specific threshold conditions. From an overall perspective, the causal emergence strength generally exhibits a fluctuating upward trend with increasing spatial scale, although in certain conditions (e.g., Scenario 2 with 20 and 30 min temporal scales), it first increases and then decreases at larger scales. Specifically, under the two shorter temporal scales of 2 and 5 min, although the overall causal emergence strength is low, it still shows an increase across the discrete spatial scales of 50, 100, and 150 m. This indicates that even in a short period, an appropriate spatial aggregation scale helps reveal the macroscopic causal structure within the system. However, when the spatial scale further increases to 200 m, some curves exhibit a slowdown or even a slight decline in causal emergence strength. This suggests that excessive spatial aggregation over short time intervals may introduce too much heterogeneous information, thereby weakening the clarity of the macroscopic causal structure. With the extension of the temporal scale, the figure presents more abundant characteristics. Especially at the scales of 15 min and 20 min, most curves reach their peaks near the spatial scale of 150 m, followed by a slight decline or stabilization. This indicates that under this spatiotemporal scale, the state transitions within the system have accumulated a strong macroscopic causal mechanism, while excessive spatial aggregation may weaken this mechanism. It can be found that 150 m may be a key spatial scale for revealing causal emergence under most temporal scales.

Table 4. Causal emergence strength for demand Scenario 1 across different scales and thresholds based on SVD.

Scale	Threshold $\mathit{\epsilon }$
	0.1	0.15	0.2	0.25	0.3	0.35	0.4	0.45	0.5	0.55	0.6	0.65	0.7	0.75	0.8	0.85	0.9
50_2	0.064	0.064	0.064	0.064	0.064	0.068	0.071	0.085	0.091	0.091	0.092	0.092	0.093	0.108	0.108	0.109	0.109
50_5	0.071	0.071	0.071	0.071	0.071	0.075	0.075	0.101	0.101	0.101	0.104	0.104	0.104	0.111	0.111	0.111	0.111
50_10	0.131	0.131	0.131	0.142	0.153	0.153	0.153	0.173	0.181	0.190	0.198	0.198	0.198	0.211	0.211	0.211	0.211
50_15	0.155	0.155	0.155	0.155	0.155	0.155	0.155	0.182	0.210	0.224	0.224	0.224	0.224	0.234	0.234	0.234	0.234
100_2	0.117	0.117	0.122	0.134	0.139	0.147	0.152	0.175	0.192	0.198	0.205	0.206	0.206	0.225	0.225	0.225	0.227
100_5	0.166	0.166	0.173	0.180	0.186	0.199	0.199	0.204	0.225	0.225	0.225	0.225	0.225	0.253	0.253	0.256	0.256
100_10	0.228	0.228	0.246	0.264	0.299	0.316	0.316	0.332	0.347	0.347	0.347	0.347	0.347	0.379	0.379	0.379	0.379
100_15	0.235	0.269	0.304	0.304	0.339	0.339	0.373	0.373	0.404	0.404	0.404	0.404	0.430	0.455	0.455	0.455	0.455
150_2	0.151	0.158	0.170	0.182	0.193	0.222	0.238	0.269	0.285	0.293	0.298	0.305	0.307	0.340	0.344	0.344	0.347
150_5	0.228	0.237	0.237	0.264	0.282	0.291	0.308	0.340	0.348	0.348	0.370	0.370	0.370	0.406	0.418	0.418	0.418
150_10	0.170	0.213	0.234	0.255	0.255	0.275	0.294	0.294	0.311	0.347	0.347	0.347	0.347	0.361	0.361	0.361	0.361
150_15	0.166	0.202	0.202	0.276	0.276	0.314	0.314	0.350	0.350	0.384	0.384	0.384	0.384	0.409	0.409	0.409	0.428
200_2	0.134	0.143	0.152	0.166	0.174	0.204	0.217	0.256	0.269	0.276	0.279	0.281	0.283	0.311	0.316	0.318	0.320
200_5	0.220	0.229	0.229	0.246	0.263	0.271	0.278	0.293	0.306	0.306	0.319	0.319	0.319	0.348	0.353	0.353	0.353
200_10	0.194	0.233	0.254	0.254	0.272	0.290	0.290	0.306	0.358	0.358	0.358	0.358	0.358	0.370	0.370	0.370	0.370
200_15	0.233	0.233	0.271	0.312	0.312	0.351	0.351	0.351	0.351	0.383	0.451	0.451	0.451	0.451	0.451	0.451	0.471

Each scale is denoted as “spatial scale_temporal scale”, e.g., “50_2” = 50 m and 2 min.

presents the causal emergence strength under demand Scenario 1 across a range of spatiotemporal scales and singular value thresholds ($\epsilon$). Several key patterns emerge. First, causal emergence strength generally increases with coarser spatial and temporal aggregation, especially for scales such as 150_15 and 200_15, which achieve relatively high values when $\epsilon$ is above 0.6. However, this trend is not strictly consistent. In several scales (e.g., 150_10, 100_15), the emergence strength stabilizes or exhibits slight fluctuations with increasing thresholds, indicating that the gain in structural clarity diminishes beyond a certain level of aggregation. Second, scales with finer spatial and temporal scales, such as 50_2 and 50_5, consistently show low emergence strength across all thresholds. This suggests that localized and short-duration observations tend to reflect more stochastic variability and lack identifiable causal structures at the macroscopic level, as individual vehicle behaviors and transient disturbances dominate at such scales.

These findings collectively highlight that while increased aggregation tends to enhance the detection of causal regularities by smoothing out noise and transient fluctuations, overly coarse scales or excessively strict thresholds may suppress finer but still meaningful structures inherent in congestion evolution dynamics. Thus, selecting appropriate spatiotemporal scales and thresholds is essential for effectively revealing causal emergence structures in traffic systems, especially considering the typical distances and temporal patterns characteristic of congestion evolution on urban roads.

3.6. Comprehensive Evaluation of Causal Emergence Results

In each process of measuring causal emergence in congestion evolution, the top five spatiotemporal scales with the highest causal emergence strength were selected. Based on this, the occurrence frequency of each spatiotemporal scale was statistically analyzed. The spatiotemporal scales with the highest rankings were those that exhibited the greatest causal emergence strength.

Figure 11 shows the ranking of each spatiotemporal scale obtained from two causal emergence quantification methods for Region 1 under Scenario 1. The EI-based method identifies the top-performing scales as “200_10”, “100_10”, “150_10”, “150_30”, and “200_15”. Among the top ten scales, seven involve spatial scales of 150 m or greater, and five correspond to temporal scales of 15 min or longer. This indicates that while EI also tends to favor larger spatial scales, it is more sensitive to moderate temporal scales, particularly around the 10 min level. In contrast, the SVD-based method ranks “200_30”, “200_20”, “200_10”, “100_15”, and “150_20” as the top five scales, with most falling within spatial scales of at least 150 m and temporal scales of at least 15 min. Overall, eight of the top ten scales involve spatial scales above 150 m, and seven feature temporal scales of 15 min or more, suggesting a clear preference of the SVD method for coarser spatiotemporal scales.

Table 5. The five scales with the highest causal emergence strength based on EI.

Study Region	Scenario	The Top Five Effective Scales
		1st	2nd	3rd	4th	5th
Region1	1	200_30	200_20	100_15	150_30	150_5
	2	100_30	150_30	200_30	200_20	100_20
	3	150_30	150_10	150_15	200_30	150_20
	4	150_15	150_20	200_15	150_10	100_20
	5	150_10	200_10	100_15	150_20	200_30
Region2	1	200_20	200_30	150_30	200_15	150_20
	2	200_20	200_30	200_15	200_10	150_10
	3	200_10	200_20	200_15	150_30	150_15
	4	200_30	200_20	200_10	200_15	150_15
	5	200_30	150_10	200_10	200_15	150_15
Region3	1	200_10	150_10	200_15	150_20	200_5
	2	150_10	200_10	200_5	200_20	200_15
	3	200_5	150_5	200_10	150_10	200_2
	4	200_5	150_30	200_2	200_10	150_5
	5	200_15	150_10	200_5	150_15	150_2

Each scale is denoted as “spatial scale_temporal scale”, e.g., “150_10” = 150 m and 10 min.

presents the top five spatiotemporal scales with the highest causal emergence strength based on EI across multiple study regions and demand scenarios. The results show a consistent and significant preference for medium-to-large spatial scales (i.e., 150 m and 200 m) combined with moderate temporal scales (i.e., 10, 15, 20, and 30 min). Scales such as 200_10, 200_15, 150_10, 150_15, 200_30, and 150_30 frequently appear among the top-ranked scales, indicating their robustness in capturing meaningful transition regularities in traffic dynamics. These spatial scales enable models to effectively represent congestion propagation and spill-back phenomena while avoiding excessive noise from overly fine-grained detail. The selected temporal scales capture important dynamic patterns in congestion evolution.

Notably, Regions 1 and 2 consistently prefer coarser spatiotemporal scales (e.g., 200_30, 150_30) across multiple scenarios, suggesting that macro-level abstraction in these areas better highlights stable and strong causal structures, possibly due to more homogeneous traffic patterns and longer congestion durations. In contrast, Region 3 exhibits greater variability in scale preference, occasionally favoring finer temporal scales (e.g., 200_5, 150_5, 200_2). This suggests that the traffic environment in this region is more unstable, with more frequent local fluctuations and shorter congestion cycles. This may be due to the region being relatively remote, having fewer secondary roads and intersections, and higher vehicle speeds. Therefore, it is necessary to retain finer-grained temporal details to achieve accurate modeling.

Table 6. The five scales with the highest causal emergence strength based on SVD.

Study Region	Scenario	The Top Five Effective Scales
		1st	2nd	3rd	4th	5th
Region1	1	200_10	100_10	150_10	150_30	200_15
	2	100_20	100_30	150_15	200_15	200_30
	3	200_20	150_15	150_2	150_20	150_5
	4	150_15	200_15	150_10	150_20	100_20
	5	150_15	150_20	200_30	200_20	150_30
Region2	1	200_15	200_20	150_30	150_15	50_30
	2	200_15	150_10	200_20	100_30	150_20
	3	200_15	150_15	200_10	150_30	150_20
	4	200_15	150_15	150_20	100_15	100_20
	5	200_15	150_15	100_30	200_10	200_30
Region3	1	200_5	100_5	50_10	150_10	200_10
	2	150_10	200_5	200_2	150_2	150_5
	3	200_5	150_10	200_10	150_20	100_30
	4	150_30	200_30	150_20	200_20	150_15
	5	200_10	150_15	150_10	150_2	200_5

Each scale is denoted as “spatial_temporal”, e.g., “150_10” = 150 m and 10 min.

lists the top five spatiotemporal scales with the highest causal emergence strength based on the SVD method across three regions and five demand scenarios. The results show a notable preference for medium-to-large spatial scales, particularly 150 and 200 m, combined with moderate-to-long temporal scales (i.e., 10, 15, 20, and 30 min). For example, scales such as 200_15, 150_15, 150_20, and 200_20 frequently appear among the top rankings across regions and scenarios, highlighting their robustness in capturing macro-level causal dynamics. These spatial scales closely correspond to typical distances between intersections on urban roads, enabling the models to effectively represent congestion propagation and queue spill-back phenomena without excessive noise. The temporal scales can capture key patterns in the formation, propagation, and dissipation of congestion waves.

Region 1 exhibits a relatively consistent pattern, with most of the scales showing the highest causal emergence strength having spatial ranges of 100, 150, and 200 m, and temporal ranges of 10, 15, 20, and 30 min. Region 2 shows a strong preference for coarser scales, especially 200_15, which ranks first or second in most scenarios. In contrast, Region 3 demonstrates greater variability in scale preference, occasionally favoring finer spatial and temporal scales such as 50_10, 100_5, 200_5, and 200_2. From the perspective of network topology, Region 3 has fewer and more sparsely distributed lower-class roads compared with Regions 1 and 2 and is located slightly away from the main corridor. These characteristics, together with more fragmented and short-lived congestion, may make it more sensitive to micro-scale variations, thus benefiting from smaller spatiotemporal scales to capture its congestion dynamics more accurately.

Figure 12 presents the top 19 spatiotemporal scales identified across three representative regions, five demand scenarios, and two causal emergence measurement methods, ranked by their selection frequency. The distribution of frequencies reveals four clear levels, with the scales of 200_15, 150_15, 150_10, and 200_10 emerging as the most consistently dominant across diverse conditions. These results highlight a clear preference for larger spatial scales and medium-to-long temporal scales in capturing strong causal emergence. The repeated prominence of these scales suggests that such scales are more effective in revealing stable macro-level causal patterns, likely due to their ability to smooth out local noise while preserving essential spatiotemporal dynamics. This layered frequency structure also indicates that causal emergence is not uniformly distributed across scales but exhibits strong selectivity toward specific spatiotemporal scales.

4. Discussion

4.1. Theoretical Implications

This study systematically modeled the multiscale dynamics of congestion evolution in urban traffic systems from the perspective of causal emergence, providing a novel theoretical framework for understanding complex traffic congestion evolution dynamics. Experimental results revealed that causal emergence strength exhibit a nonlinear coupling among spatial scale, temporal scale, and traffic load, rather than increasing linearly with scale. The existence of causal emergence in congestion evolution was quantitatively confirmed through two independent measurements, demonstrating that urban traffic dynamics are governed by multiscale causal structures. Although the strength of causal emergence varied across different regions and demand scenarios, strong causal emergence consistently tended to manifest at relatively macroscopic spatiotemporal scales. These findings offer a new theoretical lens for analyzing and predicting congestion evolution, highlighting the importance of multiscale causal interactions in urban traffic systems.

4.2. Practical Applications

Recent research [41] has shown that incorporating congestion evolution patterns into road network control strategies can significantly enhance operational efficiency. Our findings further confirm that urban traffic systems indeed exhibit pronounced multiscale causal structures in congestion evolution and can quantitatively capture the strength of causal emergence in congestion dynamics across different spatiotemporal scales. This study highlights the practical value of causal emergence theory in real-world traffic contexts, providing a quantitative foundation for hierarchical modeling and targeted interventions. These insights offer clear guidance on the effective implementation scope of traffic control policies, facilitating more refined management and proactive congestion mitigation. In the future, such multiscale causal analysis can be integrated into the multi-level response framework of urban governance, providing scientific support and operational coordination for regional control, network optimization, and emergency response strategies. This integration enhances the recovery capacity and adaptive resilience of urban traffic systems in the face of disruptions, strengthens the overall resilience of cities, and ultimately bridges the gap between theoretical insights and practical applications.

5. Conclusions and Future Work

This study presented a systematic framework from a causal emergence perspective to characterize the multiscale evolution dynamics of urban traffic congestion. Multiple dynamic models were developed using dynamic Bayesian networks, with intra-slice structures informed by causal graphs to capture spatial dependencies, and inter-slice connections modeling temporal evolution, enabling a comprehensive representation of congestion dynamics across multiple spatiotemporal scales. On this basis, two measurement methods based on EI and SVD were employed to quantify the strength of causal emergence across varying spatial and temporal scales. Experimental results demonstrated that the phenomenon of causal emergence existed in the evolution of traffic congestion. Stronger and clearer causal structures emerged at specific macro-level spatiotemporal scales, rather than continuously increasing with coarser aggregation.

The proposed framework advances the concept of causal emergence into the domain of transportation and provides an interpretable and scalable approach that enables the comparison of congestion evolution models across different scales, thereby supporting the design of hierarchical and adaptive traffic management strategies. Despite this, our study focused on three localized road networks. In the real world, many road networks are more complex and extensive. As the network scale increases, the computational complexity of dynamic modeling and causal emergence measurement grows significantly. Therefore, future research could focus on developing more efficient network partitioning strategies and adopting optimization techniques such as distributed computing or dimensionality reduction to improve the scalability of the framework for large-scale road networks.