Cascading Failure Modeling and Resilience Analysis of Coupled Centralized Supply Chain Networks Under Hybrid Loads
Abstract
1. Introduction
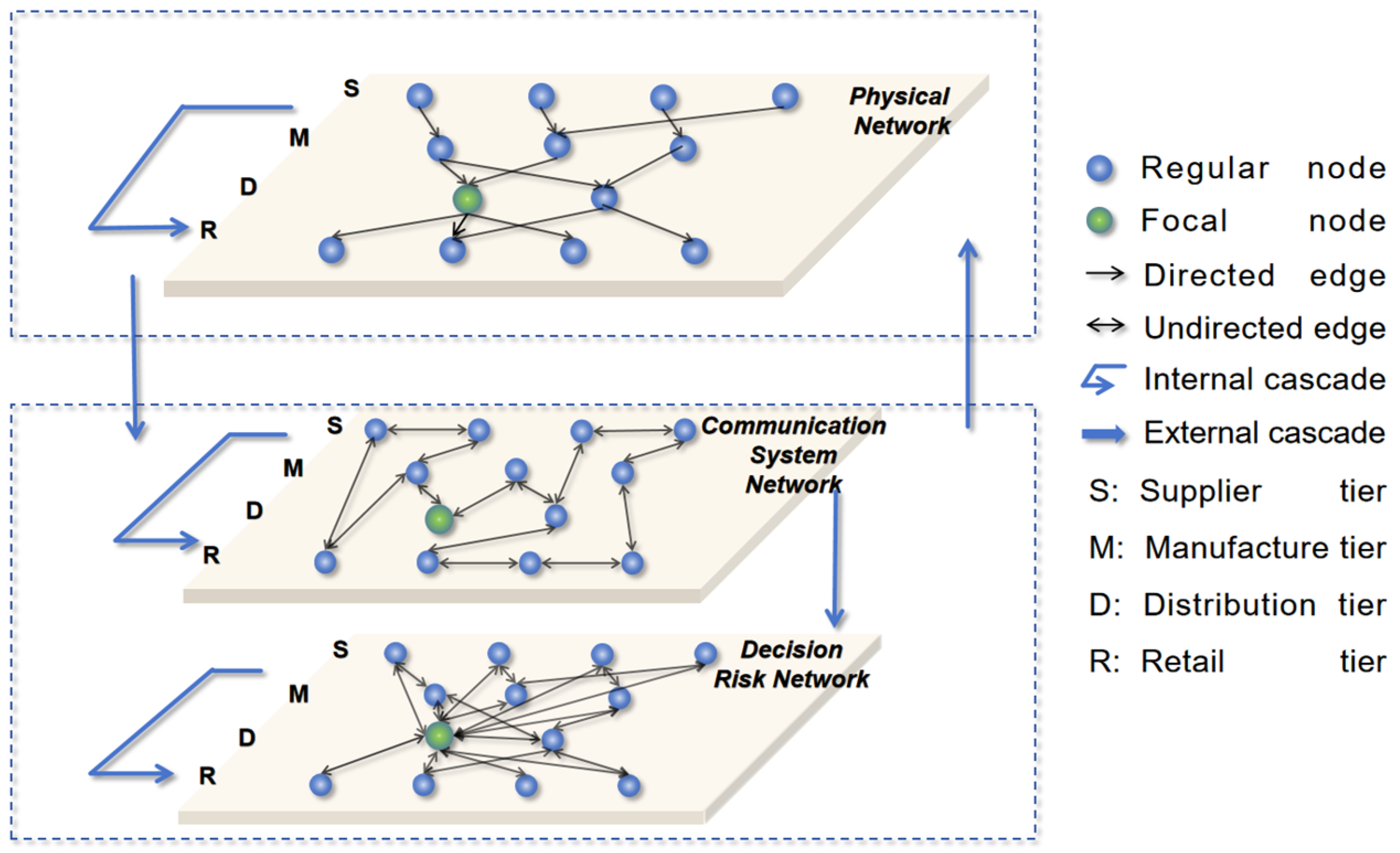
2. Coupled Model Construction
2.1. Physical Network Model
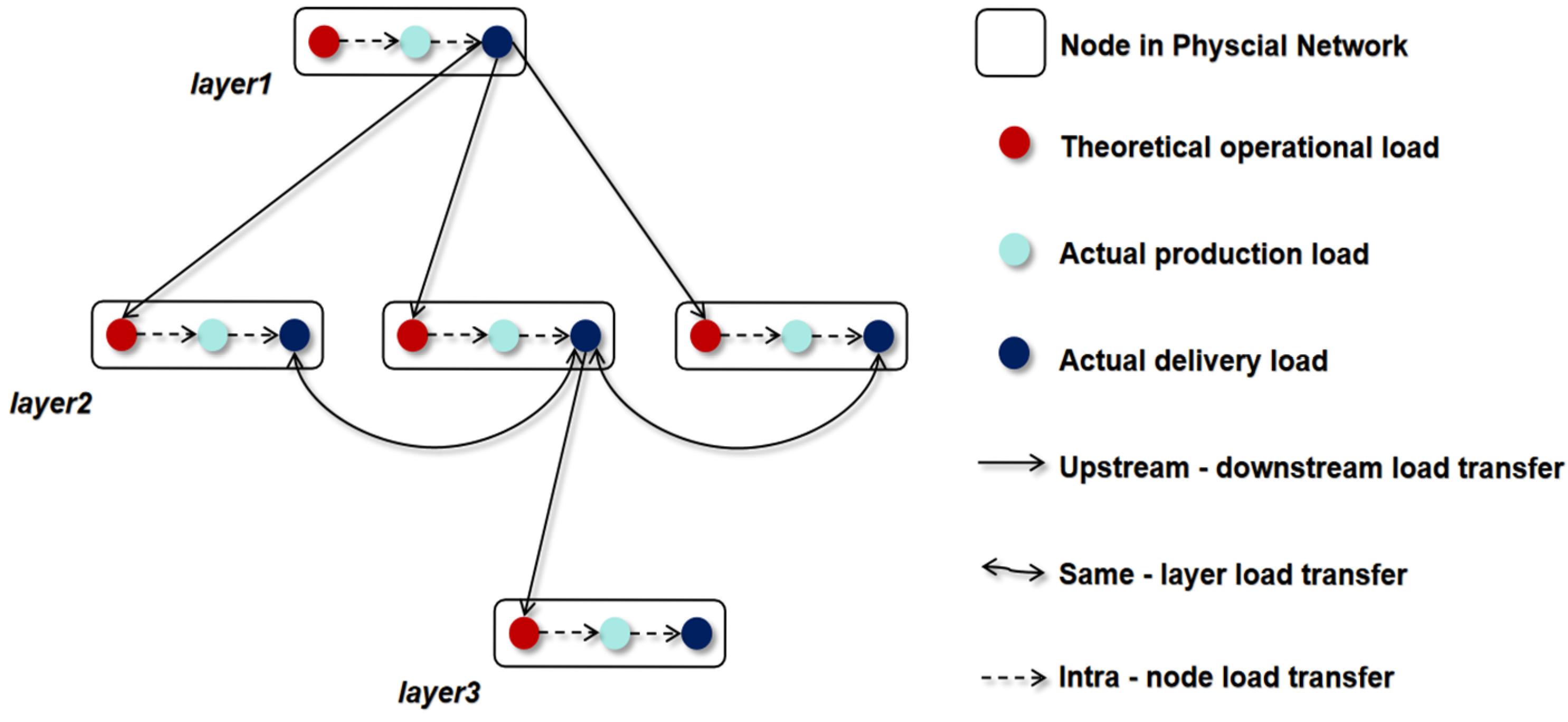
2.1.1. Load and Constraint Model
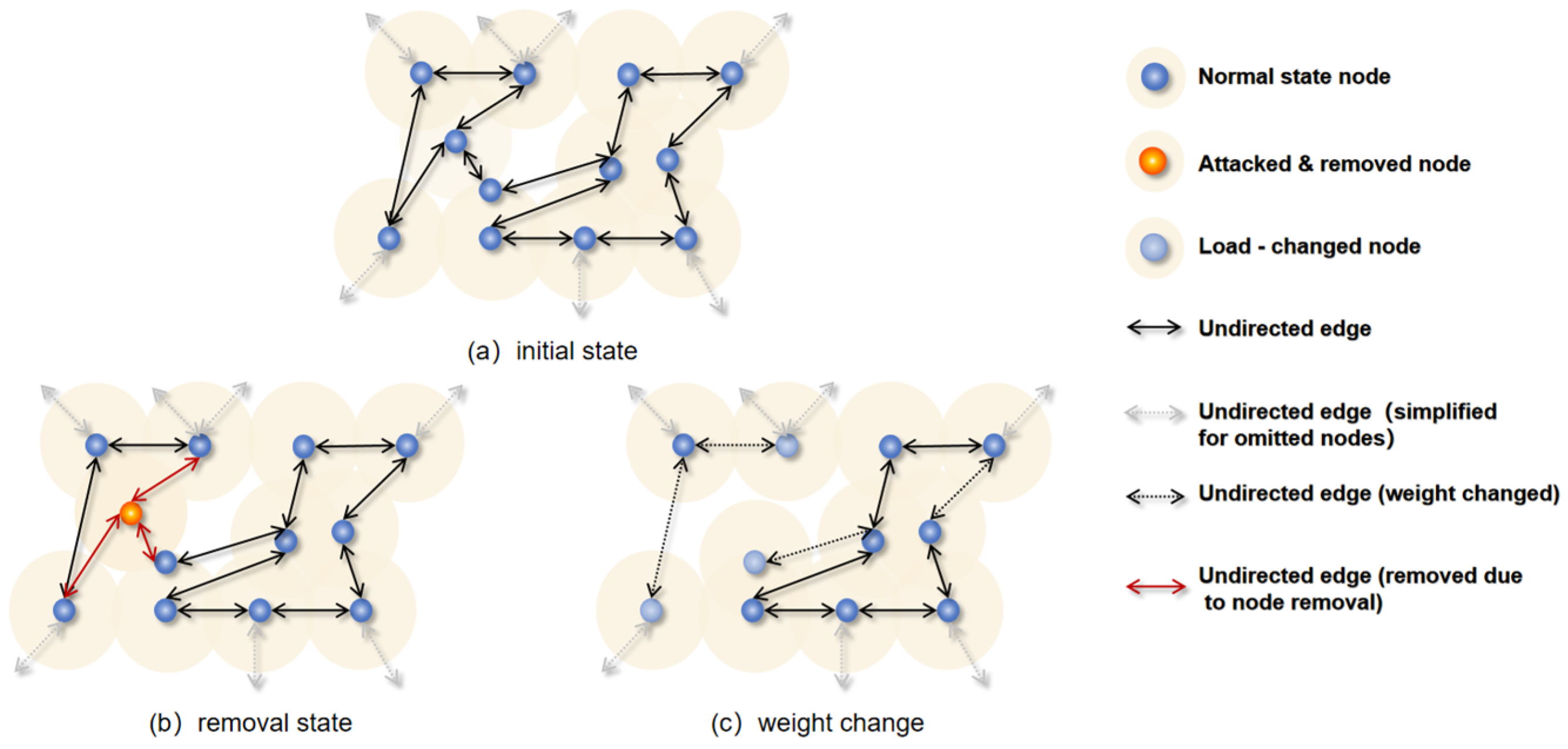
2.1.2. Physical Network Cascading Failure Process
2.1.3. Overload Reallocation Mechanism for Nodes in Centralized Supply Chain Physical Networks
2.2. Information and Decision Risk Network
2.2.1. Communication System Network Load and Constraint Model
2.2.2. Communication System Network Cascading Failure Process
2.2.3. Decision Risk Network Load and Constraint Model
2.2.4. Decision Risk Network Cascading Failure Process
2.3. Asymmetrically Coupled Centralized Supply Chain Network Model
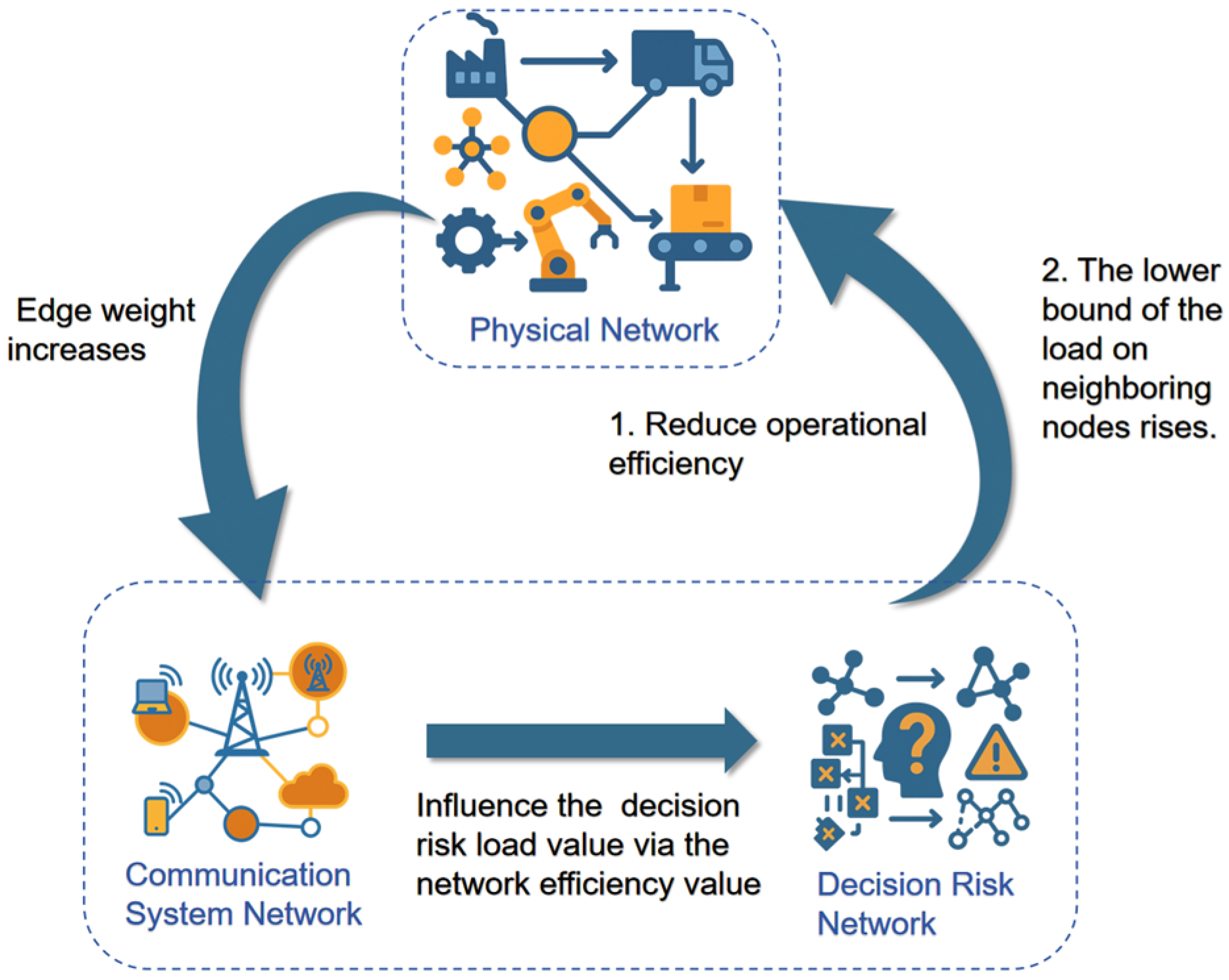
2.3.1. Coupling Mechanism of Physical Network with Information and Decision Risk Network
2.3.2. Intrinsic Coupling Dynamics of Information and Decision Risk Network
3. Numerical Simulation
3.1. Experimental Conditions
3.2. Synthetic Networks
3.3. Defining Focal Node in a Centralized Multi-Layer Network
3.4. Attack Mechanisms and Perturbation Scenarios
3.5. Resilience Evaluation Index for Supply Chain Networks
4. Numerical Simulation Results
4.1. The Cascading Process of One Node Failure
4.1.1. Node Failure in the Physical Network
4.1.2. Node Failure in the Communication System Network
4.1.3. Node Failure in the Decision Risk Network
4.1.4. Node Failures in the Communication System and Decision Risk Networks (Under Physical Network Load Boundary Fluctuation)
4.2. The Cascading Process of Several Node Failures
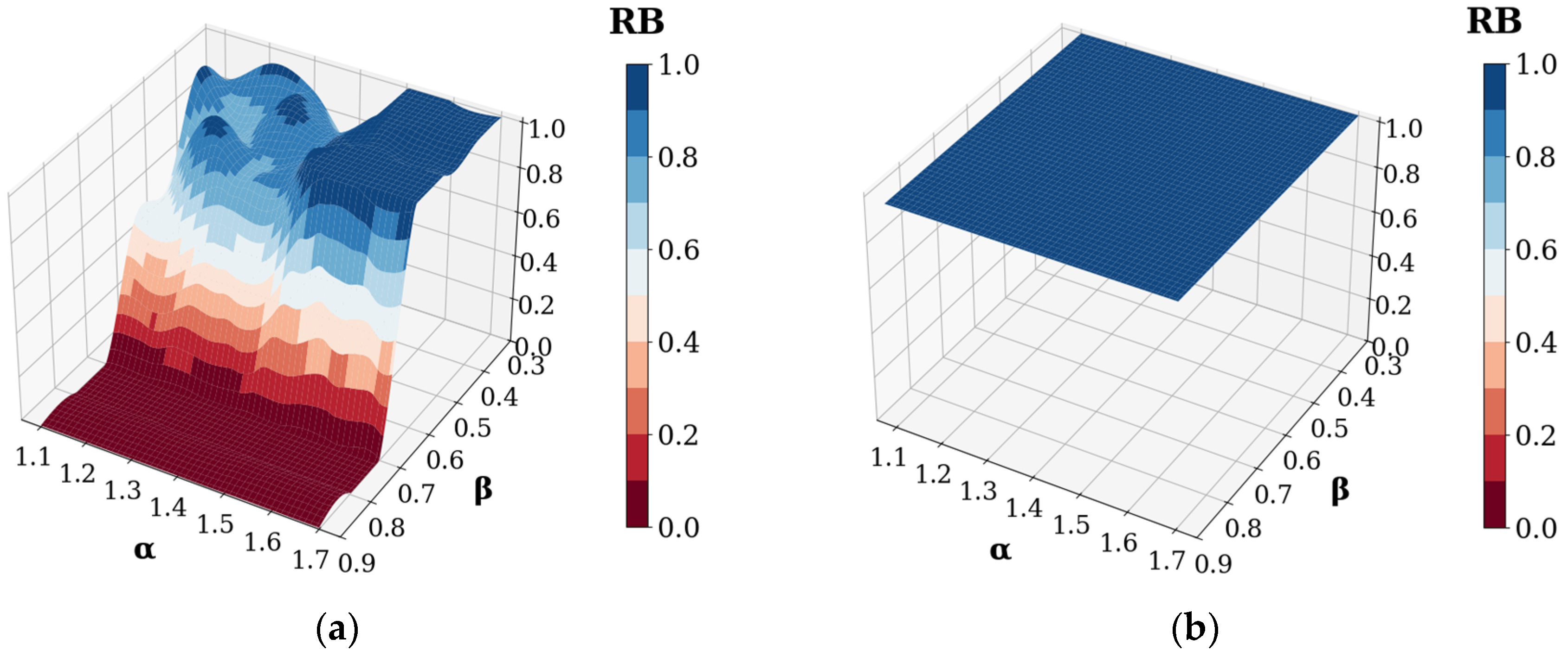
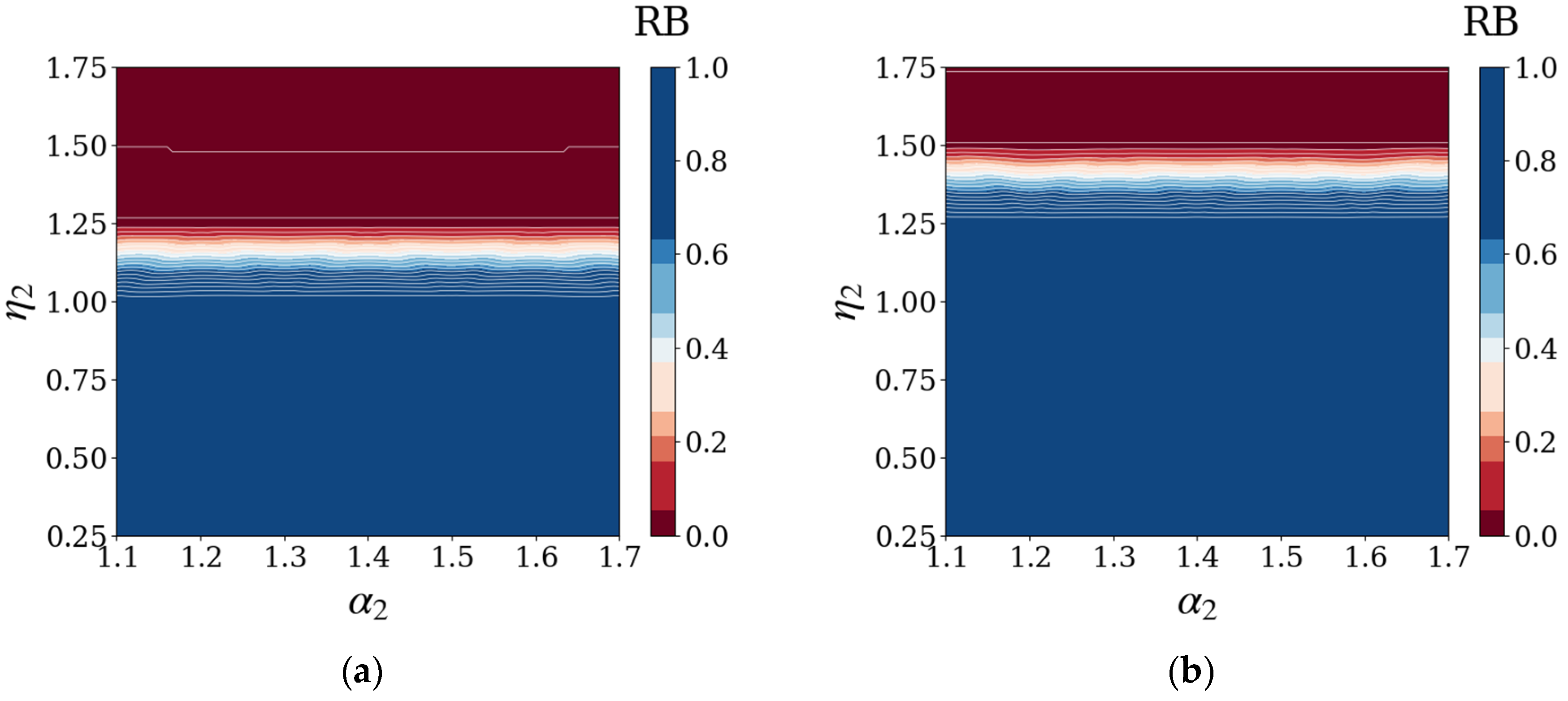
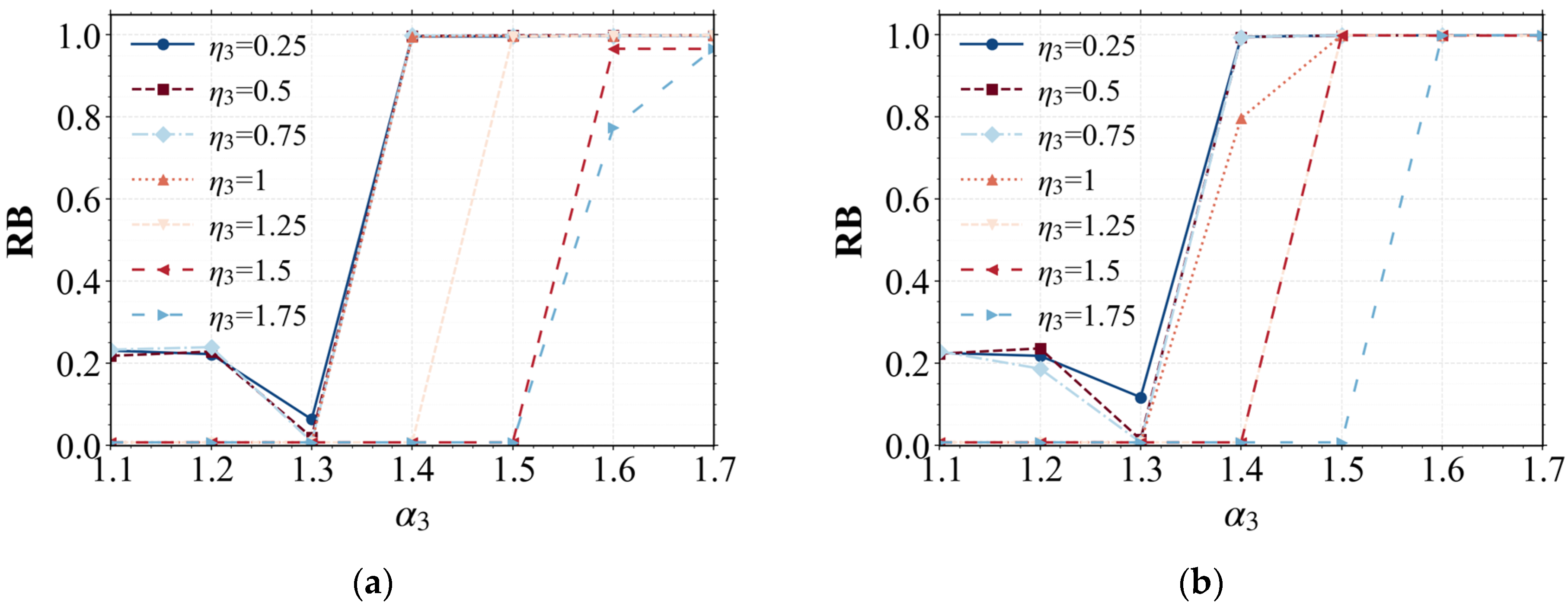
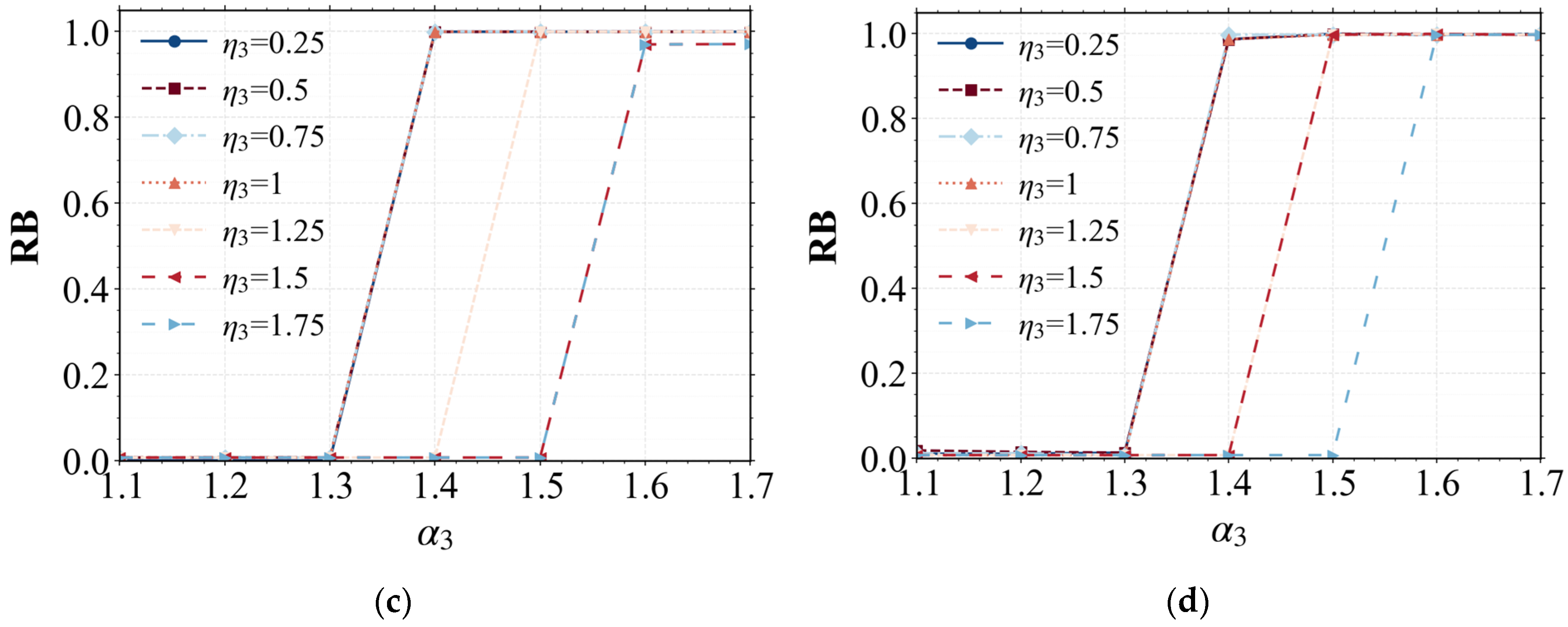
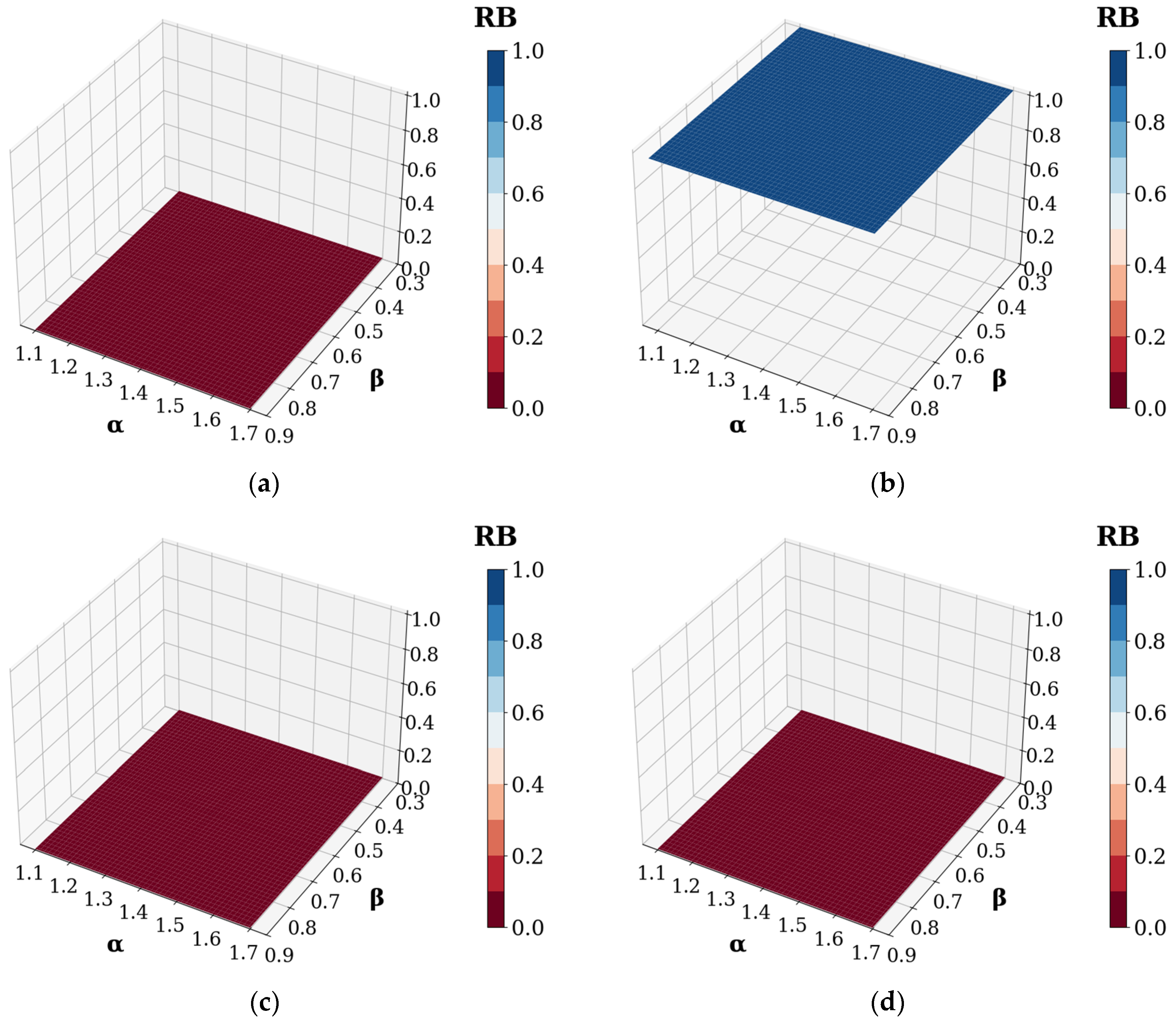
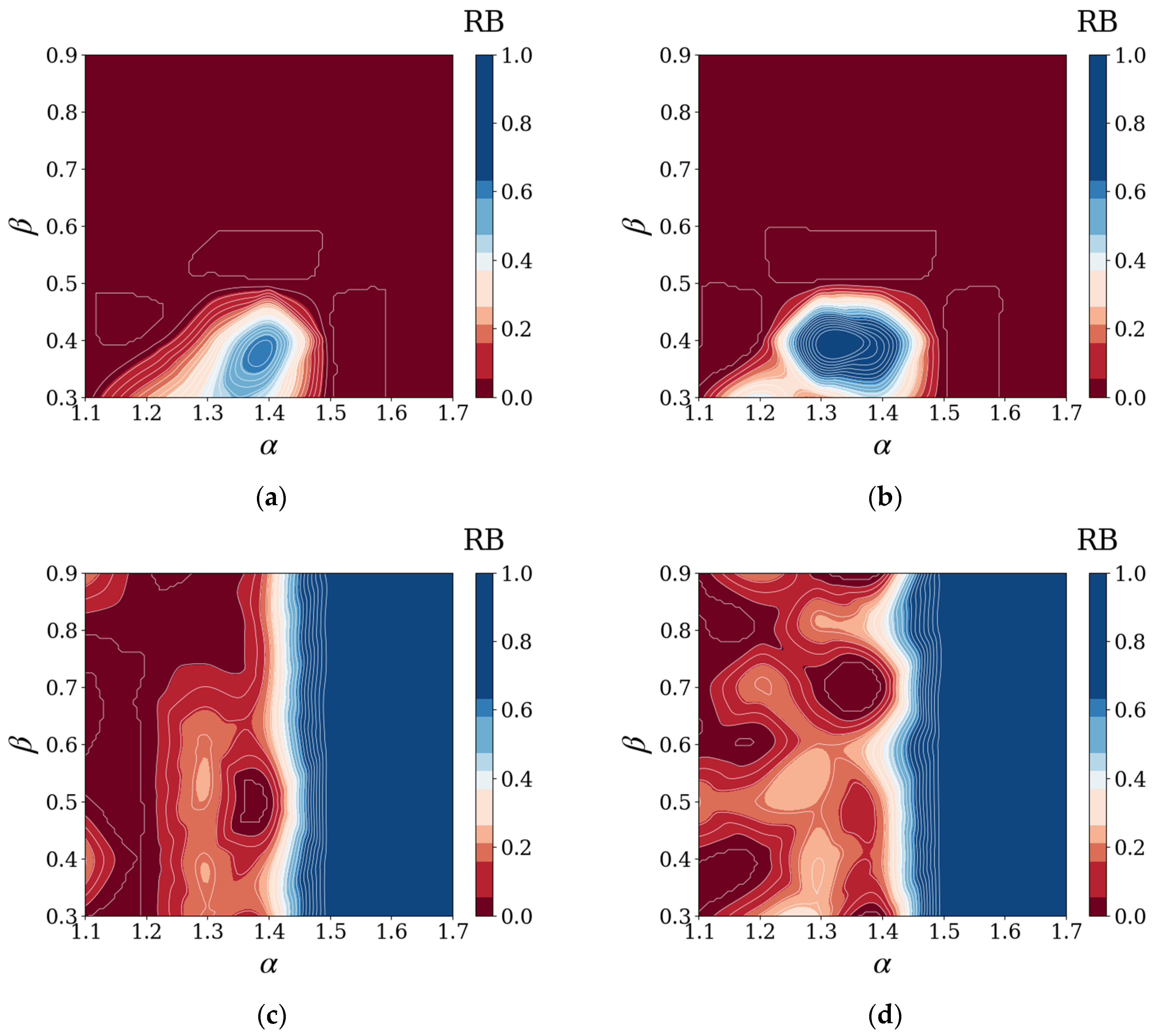
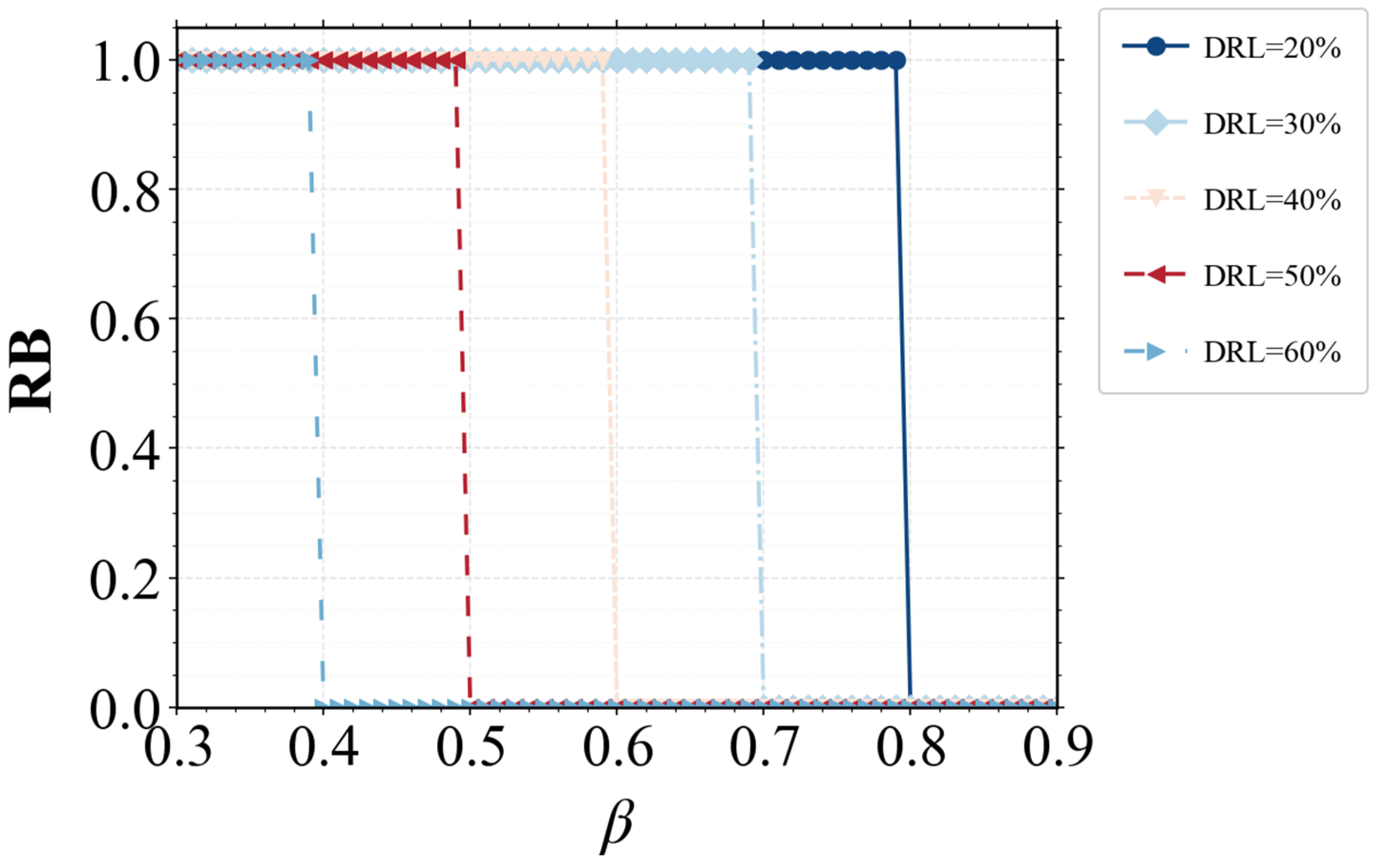
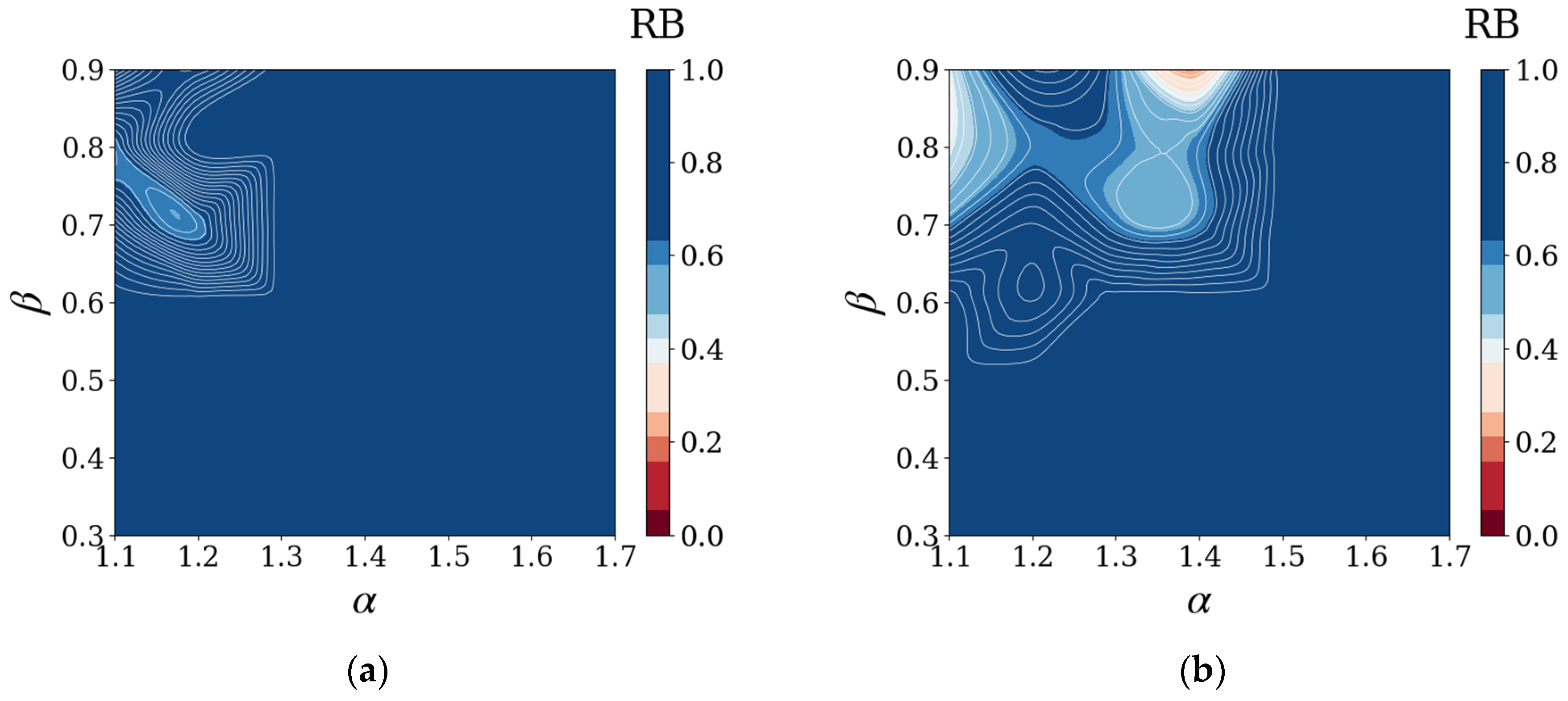
4.2.1. Node Failure and Operational Efficiency Reduction in the Physical Network
4.2.2. Load Decrease at Retail Tier Nodes in the Physical Network
4.2.3. Load Increase at Retail Tier Nodes in the Physical Network
4.3. Results and Discussion
5. Conclusions and Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1
| Concept | Symbol * | Description |
|---|---|---|
| Physical Network | ||
| Set | Physical Network graph | |
| Set | ) | Set of nodes |
| Set | Set of focal nodes | |
| Set | Set of regular nodes | |
| Set | Set of directed edges | |
| Variable | The connection relationship between node and node | |
| Set | Set of edge weights | |
| Variable | The weight of the link | |
| Variable | In-degree value of node | |
| Variable | Out-degree value of node | |
| Parameter | Tunable parameter used to adjust the weight | |
| Variable | Attribute vector of node | |
| Variable | The initial production capacity of node | |
| Variable | Nodes feature matrix | |
| Variable | Normalized nodes feature matrix | |
| Variable | Original attribute value in the matrix | |
| Variable | Min value of a column in the matrix | |
| Variable | Max value of a column in the matrix | |
| Variable | Normalized value of | |
| Parameter | Latent feature dimension | |
| Variable | Basis matrix from NMF of | |
| Variable | Coefficient matrix from NMF of | |
| Variable | Latent load feature of node | |
| Variable | Initial comprehensive load of node | |
| Variable | Internal operational efficiency of node | |
| Variable | Theoretical operational load of node | |
| Variable | Actual production load of node | |
| Variable | Actual delivery load of node | |
| Variable | Transferred load of node | |
| Variable | Load mapping term from node to node | |
| Set | Sets of upstream nodes of node | |
| Set | Sets of downstream nodes of node | |
| Variable | The resistance capacity of node against load fluctuation from node | |
| Variable | Upper bounds of node load | |
| Variable | Lower bounds of node load | |
| Parameter | The upper bound coefficient of node load | |
| Parameter | The lower bound coefficient of node load | |
| Variable | Change in theoretical operational load of node | |
| Variable | Actual load variation received by node from node | |
| Variable | Virtual load variation of caused by fluctuations of theoretical operational load ( can be replaced by and ; refer to previous definitions for load types) | |
| Variable | Virtual load variation of caused by fluctuations of theoretical operational load from upstream can be replaced by and ; refer to previous definitions for load types) | |
| Variable | Cumulative virtual load variation of theoretical opera-tional load aggregated on can be replaced by and ; refer to previous definitions for load types) | |
| Parameter | Probability that the node collapses completely | |
| Parameter | Probability that the node remains functional but operates at reduced efficiency | |
| Parameter | Efficiency loss coefficient | |
| Set | Set of overloaded nodes within the same tier | |
| Set | Set of redundant nodes capable of absorbing excess load within the same tier | |
| Variable | The actual delivery load required by node | |
| Variable | The actual delivery load output by redundant node | |
| Parameter | Resource redundancy safety threshold | |
| Communication System Network | ||
| Set | Communication System Network graph | |
| Set | Set of nodes | |
| Set | Set of focal nodes | |
| Set | Set of regular nodes | |
| Set | Set of directed edges | |
| Variable | The connection relationship between node and node | |
| Set | Set of edge weights | |
| Variable | The weight of the link | |
| Variable | The shortest path length from node to node at time | |
| Variable | Load of node | |
| Variable | Dynamic betweenness centrality of node | |
| Variable | The total number of shortest paths from node to node | |
| Variable | The number of shortest paths from node to node that pass through node | |
| Parameter | Information buffering capacity coefficient | |
| Variable | Upper bounds of node load | |
| Decision Risk Network | ||
| Set | Decision Risk Network graph | |
| Set | Set of nodes | |
| Set | Set of focal nodes | |
| Set | Set of regular nodes | |
| Set | Set of directed edges | |
| Variable | The connection relationship between node and node | |
| Set | Set of edge weights | |
| Variable | The weight of the link | |
| Variable | Normalized nodes feature matrix | |
| Variable | Basis matrix from NMF of | |
| Variable | Coefficient matrix from NMF of | |
| Set | Set of all nodes in the Decision Risk Network that are connected to node | |
| Variable | The degree value of decision processing node | |
| Variable | Latent load feature of node | |
| Variable | The self-imposed load of a node | |
| Variable | The node receives additional load | |
| Variable | Total load of each node | |
| Variable | Upper bounds of node load | |
| Parameter | The risk tolerance coefficient | |
| Variable | The function used to model the risk transmission between nodes | |
| Parameter | Parameter of | |
| Variable | Degree function of node | |
| Parameter | Constant of | |
| Parameter | Constant of | |
| Parameter | Intensity of risk amplification | |
| Variable | Risk random variable | |
| Variable | Variable defining the upper bound of the uniform distri-bution for | |
| Coupled Network | ||
| Parameter | The coupling coefficient between the Physical Network and the Communication System Network | |
| Parameter | The coupling coefficient between the Physical Network and the Decision Risk Network | |
| Parameter | The focal node impact multiplier | |
| Parameter | The coupling coefficient between the Communication System Network and the Decision Risk Network | |
| Variable | The decision risk panic coefficient of the removed node | |
| Variable | Represents the communication efficiency of node | |
| Variable | Robustness metric of the coupled network system | |
| Parameter | The initial number of nodes in the Physical Network | |
| Parameter | The initial number of nodes in the Decision Risk Network | |
| Variable | The number of nodes that remain after stabilization | |
| Variable | The number of nodes that remain after stabilization | |
| Parameter | The initial efficiency of the Communication System Network | |
| Parameter | The efficiency of the Communication System Network after stabilization | |
| Variable | Demand reduction level | |
Appendix A.2
References
- Klibi, W.; Martel, A.; Guitouni, A. The design of robust value-creating supply chain networks: A critical review. Eur. J. Oper. Res. 2010, 203, 283–293. [Google Scholar] [CrossRef]
- Levalle, R.R.; Nof, S.Y. Resilience in supply networks: Definition, dimensions, and levels. Annu. Rev. Control 2017, 43, 224–236. [Google Scholar] [CrossRef]
- Valdez, L.D.; Shekhtman, L.; La Rocca, C.E.; Zhang, X.; Buldyrev, S.V.; Trunfio, P.A.; Braunstein, L.A.; Havlin, S.; Estrada, E. Cascading failures in complex networks. J. Complex Networks 2020, 8, cnaa013. [Google Scholar] [CrossRef]
- Chowdhury, P.; Paul, S.K.; Kaisar, S.; Moktadir, M.A. COVID-19 pandemic related supply chain studies: A systematic review. Transp. Res. Part E Logist. Transp. Rev. 2021, 148, 102271. [Google Scholar] [CrossRef]
- Fortune. 94% of the Fortune 1000 Are Seeing Coronavirus Supply Chain Disruptions: Report. Fortune. 21 February 2020. Available online: https://fortune.com/2020/02/21/fortune-1000-coronavirus-china-supply-chain-impact/ (accessed on 20 June 2025).
- Resilinc. Top 5 Manufacturing Supply Chain Disruptions in 2024. Resilinc. 2024. Available online: https://resilinc.ai/blog/top-manufacturing-supply-chain-disruptions-h1-2024/ (accessed on 20 June 2025).
- Liu, H.; Han, Y.; Ni, J.; Zhu, A.; Pereira, A.M.B. Modelling Underload Cascading Failure and Mitigation Strategy of Supply Chain Complex Network in COVID-19. Math. Probl. Eng. 2022, 2022, 3965720. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, F. Modeling and analysis of under-load-based cascading failures in supply chain networks. Nonlinear Dyn. 2018, 92, 1403–1417. [Google Scholar] [CrossRef]
- Yang, Q.; Scoglio, C.M.; Gruenbacher, D.M. Robustness of supply chain networks against underload cascading failures. Phys. A Stat. Mech. Appl. 2021, 563, 125466. [Google Scholar] [CrossRef]
- Chen, L.; Dui, H.; Zhang, C. A resilience measure for supply chain systems considering the interruption with the cyber-physical systems. Reliab. Eng. Syst. Saf. 2020, 199, 106869. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, C.; Stojmenovic, M.; Nayak, A. Characterization of cascading failures in interdependent cyber-physical systems. IEEE Trans. Comput. 2014, 64, 2158–2168. [Google Scholar] [CrossRef]
- Mu, D.; Yue, X.; Ren, H. Robustness of cyber-physical supply networks in cascading failures. Entropy 2021, 23, 769. [Google Scholar] [CrossRef]
- Lin, K.Y.; Lin, Y.K. An algorithm for assessing a multistate resilience supply chain network in terms of system reliability. Ann Oper Res. 2025. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Bai, X. Designing a new robust resilience supply chain network under partial distribution information. Comput. Ind. Eng. 2024, 190, 110028. [Google Scholar] [CrossRef]
- Cinti, C.; Golini, R.; Moretto, A. Enhancing supply chain resilience through the supply network approach. J. Bus. Ind. Mark. 2025, 40, 858–876. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Mohanty, B.K.; Singh, K.N. Supply chain risk assessment during new product development: A group decision making approach using numeric and linguistic data. Int. J. Prod. Res. 2013, 51, 2790–2804. [Google Scholar] [CrossRef]
- Tang, L.; Jing, K.; He, J.; Stanley, H.E. Robustness of assembly supply chain networks by considering risk propagation and cascading failure. Phys. A Stat. Mech. Appl. 2016, 459, 129–139. [Google Scholar] [CrossRef]
- Li, Y.; Du, Z.; Zhang, L. Agri-Food supply chain network risk propagation research based on complex network. In Proceedings of the 6th International Asia Conference on Industrial Engineering and Management Innovation: Core Theory and Applications of Industrial Engineering, Munich, Germany, 7–9 January 2025; Atlantis Press: Dordrecht, The Netherlands, 2016; Volume 1, pp. 985–994. [Google Scholar] [CrossRef]
- Huo, L.; Guo, H.; Cheng, Y. Supply chain risk propagation model considering the herd mentality mechanism and risk preference. Phys. A Stat. Mech. Appl. 2019, 529, 121400. [Google Scholar] [CrossRef]
- Davis-Sramek, B.; Germain, R.; Krotov, K. Examining the process R&D investment–performance chain in supply chain operations: The effect of centralization. Int. J. Prod. Econ. 2015, 167, 246–256. [Google Scholar] [CrossRef]
- Pertusa-Ortega, E.M.; Zaragoza-Sáez, P.; Claver-Cortés, E. Can formalization, complexity, and centralization influence knowledge performance? J. Bus. Res. 2010, 63, 310–320. [Google Scholar] [CrossRef]
- Giannoccaro, I. Assessing the influence of the organization in the supply chain management using NK simulation. Int. J. Prod. Econ. 2011, 131, 263–272. [Google Scholar] [CrossRef]
- Duan, Q.; Liao, T.W. Optimization of replenishment policies for decentralized and centralized capacitated supply chains under various demands. Int. J. Prod. Econ. 2013, 142, 194–204. [Google Scholar] [CrossRef]
- Katsikopoulos, K.V.; Gigerenzer, G. Behavioral operations management: A blind spot and a research program. J. Supply Chain. Manag. 2013, 49, 3–7. [Google Scholar] [CrossRef]
- Ye, Y.; Suleiman, M.A.; Huo, B. Impact of just-in-time (JIT) on supply chain disruption risk: The moderating role of supply chain centralization. Ind. Manag. Data Syst. 2022, 122, 1665–1685. [Google Scholar] [CrossRef]
- Giannoccaro, I. Centralized vs. decentralized supply chains: The importance of decision maker’s cognitive ability and resistance to change. Ind. Mark. Manag. 2018, 73, 59–69. [Google Scholar] [CrossRef]
- Ellis, S.C.; Shockley, J.; Henry, R.M. Making sense of supply disruption risk research: A conceptual framework grounded in enactment theory. J. Supply Chain. Manag. 2011, 47, 65–96. [Google Scholar] [CrossRef]
- Duan, D.-L.; Wu, X.-Y. Cascading failure of scale-free networks based on a tunable load redistribution model. Acta Phys. Sin. 2014, 63, 030501. [Google Scholar] [CrossRef]
- Wang, J.W.; Rong, L.L. A model for cascading failures in scale-free networks with a breakdown probability. Phys. A Stat. Mech. Appl. 2009, 388, 1289–1298. [Google Scholar] [CrossRef]
- Motter, A.E. Cascade control and defense in complex networks. Phys. Rev. Lett. 2004, 93, 098701. [Google Scholar] [CrossRef]
- Barrat, A.; Barthelemy, M.; Pastor-Satorras, R.; Vespignani, A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. USA 2004, 101, 3747–3752. [Google Scholar] [CrossRef]
- Kong, Q.; Sun, J.; Xu, Z. Joint orthogonal symmetric non-negative matrix factorization for community detection in attribute network. Knowl.-Based Syst. 2024, 283, 111192. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, S.; Wang, L.; Guo, W.; Leung, M.-F. Constrained symmetric non-negative matrix factorization with deep autoencoders for community detection. Mathematics 2024, 12, 1554. [Google Scholar] [CrossRef]
- Afrin, T.; Yodo, N. A concise survey of advancements in recovery strategies for resilient complex networks. J. Complex Netw. 2019, 7, 393–420. [Google Scholar] [CrossRef]
- Galar, D.; Goebel, K.; Sandborn, P.; Kumar, U. Prognostics and Remaining Useful Life (rul) Estimation: Predicting with Confidence; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar] [CrossRef]
- Simchi-Levi, D.; Kaminsky, P.; Simchi-Levi, E. Designing and Managing the Supply Chain: Concepts, Strategies, and Cases; McGraw-hill: New York, NY, USA, 1999. [Google Scholar]
- Guo, H.; Yu, S.S.; Iu, H.H.C.; Fernando, T.; Zheng, C. A complex network theory analytical approach to power system cascading failure—From a cyber-physical perspective. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 053111. [Google Scholar] [CrossRef]
- Rong, Z.; Pan, L. Load analysis in correlated scale-free networked systems. In Proceedings of the 2010 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010; IEEE: New York, NY, USA, 2010; pp. 1986–1990. [Google Scholar] [CrossRef]
- Yang, C.; Lee, Y.; Lee, C. Data-Driven Order Consolidation with Vehicle Routing Optimization. Sustainability 2025, 17, 848. [Google Scholar] [CrossRef]
- Foumani, M. Adaptation of a Collaborative Truck and Robotic Vehicle for Sustainable Supply Chain Operations. In Proceedings of the International Conference on Robot Intelligence Technology and Applications, Taicang, China, 6–8 December 2023; Springer Nature: Cham, Switzerland, 2023; pp. 289–301. [Google Scholar] [CrossRef]
- Letsholo, R.G.; Pretorius, M.P. Investigating managerial practices for data and information overload in decision making. J. Contemp. Manag. 2016, 13, 767–792. Available online: https://hdl.handle.net/10520/EJC195601 (accessed on 20 June 2025).
- Huo, L.; Guo, H.; Cheng, Y.; Xie, X. A new model for supply chain risk propagation considering herd mentality and risk preference under warning information on multiplex networks. Phys. A Stat. Mech. Appl. 2020, 545, 123506. [Google Scholar] [CrossRef]
- Albert, R.; Jeong, H.; Barabási, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Buzna, L.; Peters, K.; Helbing, D. Modelling the dynamics of disaster spreading in networks. Phys. A Stat. Mech. Appl. 2006, 363, 132–140. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef]
- Artime, O.; Grassia, M.; De Domenico, M.; Gleeson, J.P.; Makse, H.A.; Mangioni, G.; Perc, M.; Radicchi, F. Robustness and resilience of complex networks. Nat. Rev. Phys. 2024, 6, 114–131. [Google Scholar] [CrossRef]
- Hernández, J.M.; Pedroza-Gutiérrez, C. Estimating the influence of the network topology on the agility of food supply chains. PLoS ONE 2019, 14, e0218958. [Google Scholar] [CrossRef]
- Cui, P.; Zhu, P.; Wang, K.; Xun, P.; Xia, Z. Enhancing robustness of interdependent network by adding connectivity and dependence links. Phys. A Stat. Mech. Appl. 2018, 497, 185–197. [Google Scholar] [CrossRef]
- Sun, J.; Tang, J.; Fu, W.; Chen, Z.; Niu, Y. Construction of a multi-echelon supply chain complex network evolution model and robustness analysis of cascading failure. Comput. Ind. Eng. 2020, 144, 106457. [Google Scholar] [CrossRef]
- Bar-Yam, Y. Making Things Work: Solving Complex Problems in a Complex World; New England Complex Systems Institute: Cambridge, MA, USA, 2004; Available online: https://www.necsi.edu/making-things-work (accessed on 20 June 2025).
- Ozel, O.; Sinopoli, B.; Yağan, O. Uniform redundancy allocation maximizes the robustness of flow networks against cascading failures. Phys. Rev. E 2018, 98, 042306. [Google Scholar] [CrossRef]

| Related Study | Multi-layer Coupled Network | Load Recovery Strategy | Multi-Load Failure Mode | Multi-Attack Scenario | Centralized Supply Chain Research Focus |
|---|---|---|---|---|---|
| Liu [7] | × | √ | × | × | / |
| Wang [8] | × | √ | × | × | / |
| Huang [11] | √ | × | √ | × | / |
| Mu [12] | √ | √ | √ | × | / |
| Ye [25] | × | × | × | × | Relationship with JIT |
| Giannoccaro [26] | × | × | × | × | The importance of decision-maker |
| This study | √ | √ | √ | √ | Cascading failure |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Z.; Wang, N.; Xu, D.; Chen, R. Cascading Failure Modeling and Resilience Analysis of Coupled Centralized Supply Chain Networks Under Hybrid Loads. Systems 2025, 13, 729. https://doi.org/10.3390/systems13090729
Zeng Z, Wang N, Xu D, Chen R. Cascading Failure Modeling and Resilience Analysis of Coupled Centralized Supply Chain Networks Under Hybrid Loads. Systems. 2025; 13(9):729. https://doi.org/10.3390/systems13090729
Chicago/Turabian StyleZeng, Ziqiang, Ning Wang, Dongyu Xu, and Rui Chen. 2025. "Cascading Failure Modeling and Resilience Analysis of Coupled Centralized Supply Chain Networks Under Hybrid Loads" Systems 13, no. 9: 729. https://doi.org/10.3390/systems13090729
APA StyleZeng, Z., Wang, N., Xu, D., & Chen, R. (2025). Cascading Failure Modeling and Resilience Analysis of Coupled Centralized Supply Chain Networks Under Hybrid Loads. Systems, 13(9), 729. https://doi.org/10.3390/systems13090729







