Spatiotemporal Characteristics of Land Use Carbon Budget and Carbon Balance Capacity in Karst Mountainous Areas: A Case Study Using Social Network Analysis
Abstract
1. Introduction
2. Materials and Methods
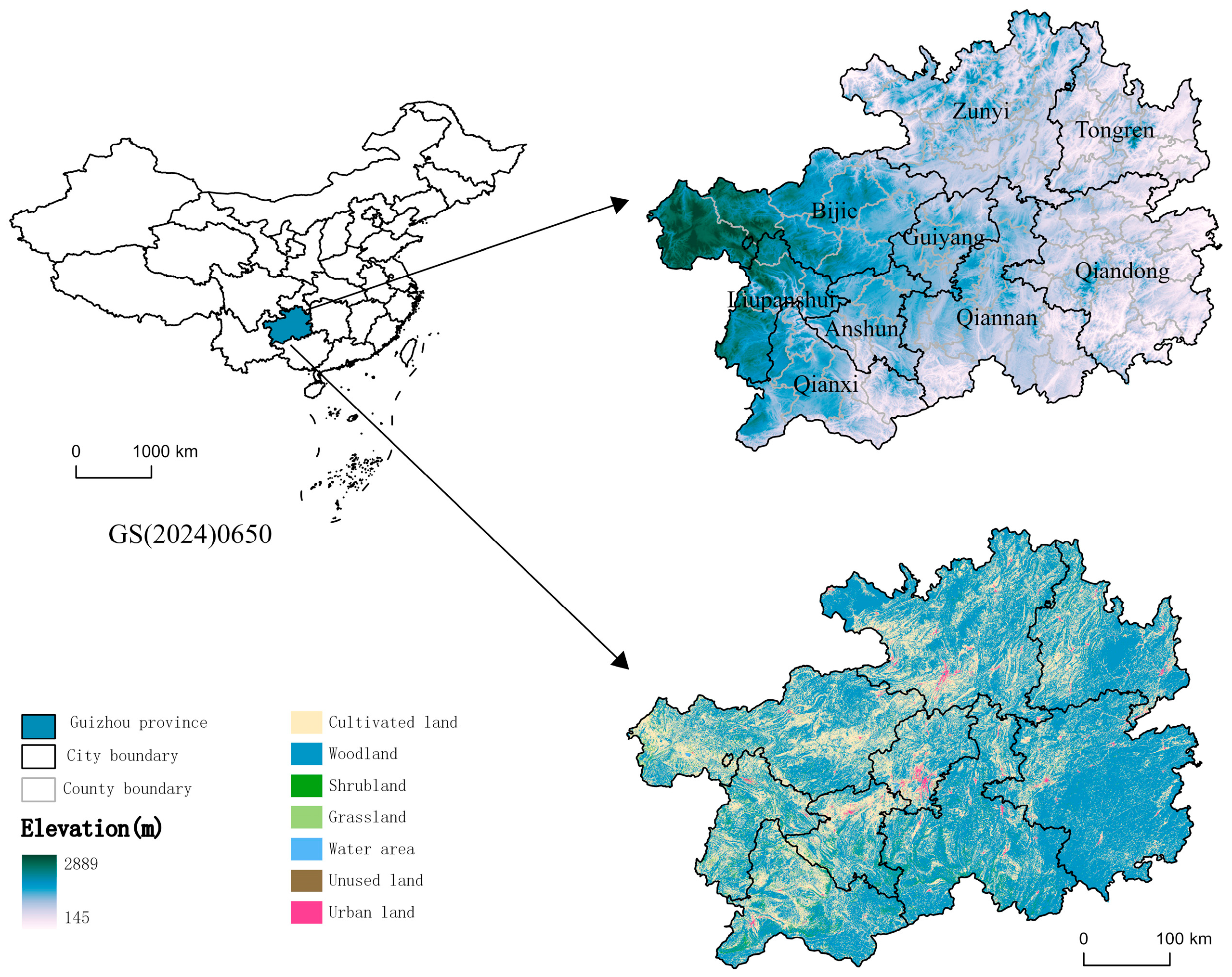
2.1. Study Area
2.2. Data Sources
2.3. Methods
3. Spatial Network Analysis of Carbon Budgets
3.1. Gravity Model
3.2. Social Network Analysis Method
3.3. Calculation of Carbon Balance Capacity
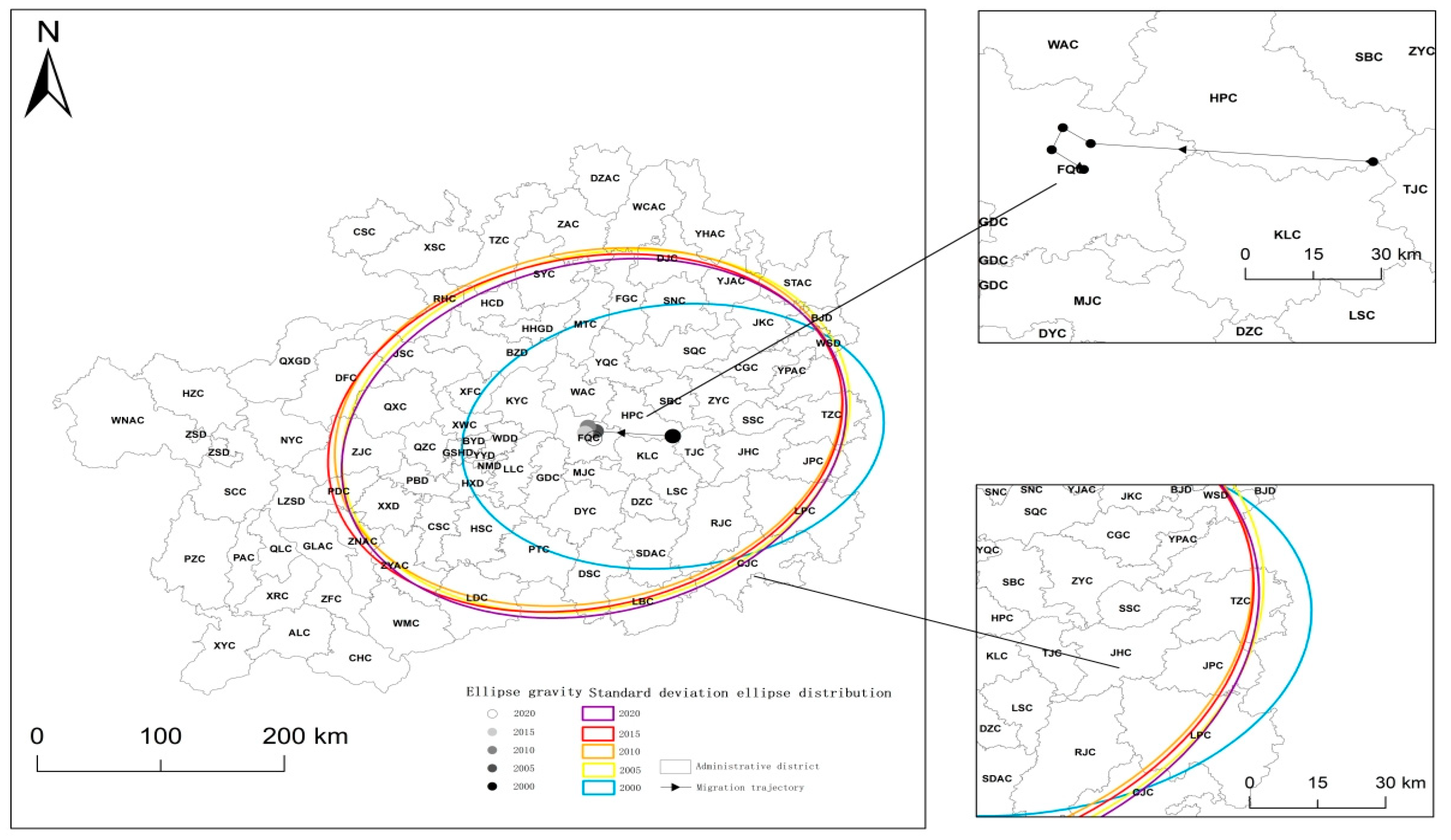
3.4. Standard Deviation Ellipse
3.5. Driving Factor Screening and Geo-Detector Model
| Dimension | Indicator | Indicator Connotation | Selection Rationale | Author |
|---|---|---|---|---|
| Natural Geography and Environment | Temperature (X1) | Annual average temperature | Optimum temperature promotes vegetation growth, while high temperature accelerates water evaporation [46]. | Zheng, J (2025) [46]. |
| Precipitation (X2) | Annual mean rainfall | Adequate rainfall facilitates vegetation growth and enhances carbon sink capacity [47]. | Tang, S. (2024) [47] | |
| NDVI (X3) | A higher NDVI indicates stronger vegetation photosynthesis and more carbon absorption capacity | NDVI reflects the carbon sequestration potential of ecosystems by quantifying vegetation coverage [48,49]. | Wang, T. (2025) [48] Fornaciari, M. (2024) [49] | |
| Economic and Social Development | Gross Regional Domestic Product (X4) | GDP (CNY) | Economic development features a dual mechanism: industrial expansion raises energy consumption, while factor prices and policies spur clean tech innovation [50] | Perissi, I. (2023) [50] |
| Industrial Structure (X5) | The proportion of the secondary industry in GDP(%) | The secondary industry has a relatively high degree of energy dependence, which significantly drives up carbon emissions. | ||
| County-level Electricity Consumption (X6) | Higher electricity consumption indicates greater embodied energy demand and more pronounced carbon balance pressure | High electricity consumption, when accompanied by a high share of fossil energy, indicates low potential for carbon emission reduction. | ||
| Nighttime Lights (X7) | Regions with high nighttime light intensity correspond to industrial clusters or urban core areas, serving as both carbon emission hotspots and key targets for emission reduction | Nighttime light intensity enables indirect quantification of the spatial heterogeneity in carbon emissions [51] | Rao, Y. (2024) [51] | |
| Environmental Pressure and Sustainability | PM2.5 (X8) | Annual concentration | PM2.5 and carbon emissions share common sources (coal combustion, vehicle exhaust). | |
| Population and Urbanization | Population Density (X9) | The number of permanent residents/the area of regional land(%) | The impact of population density on per capita carbon emissions exhibits nonlinear characteristics, with its inhibitory effect diminishing gradually as population density increases [52]. | Hong, S. [52] |
4. Results and Discussion
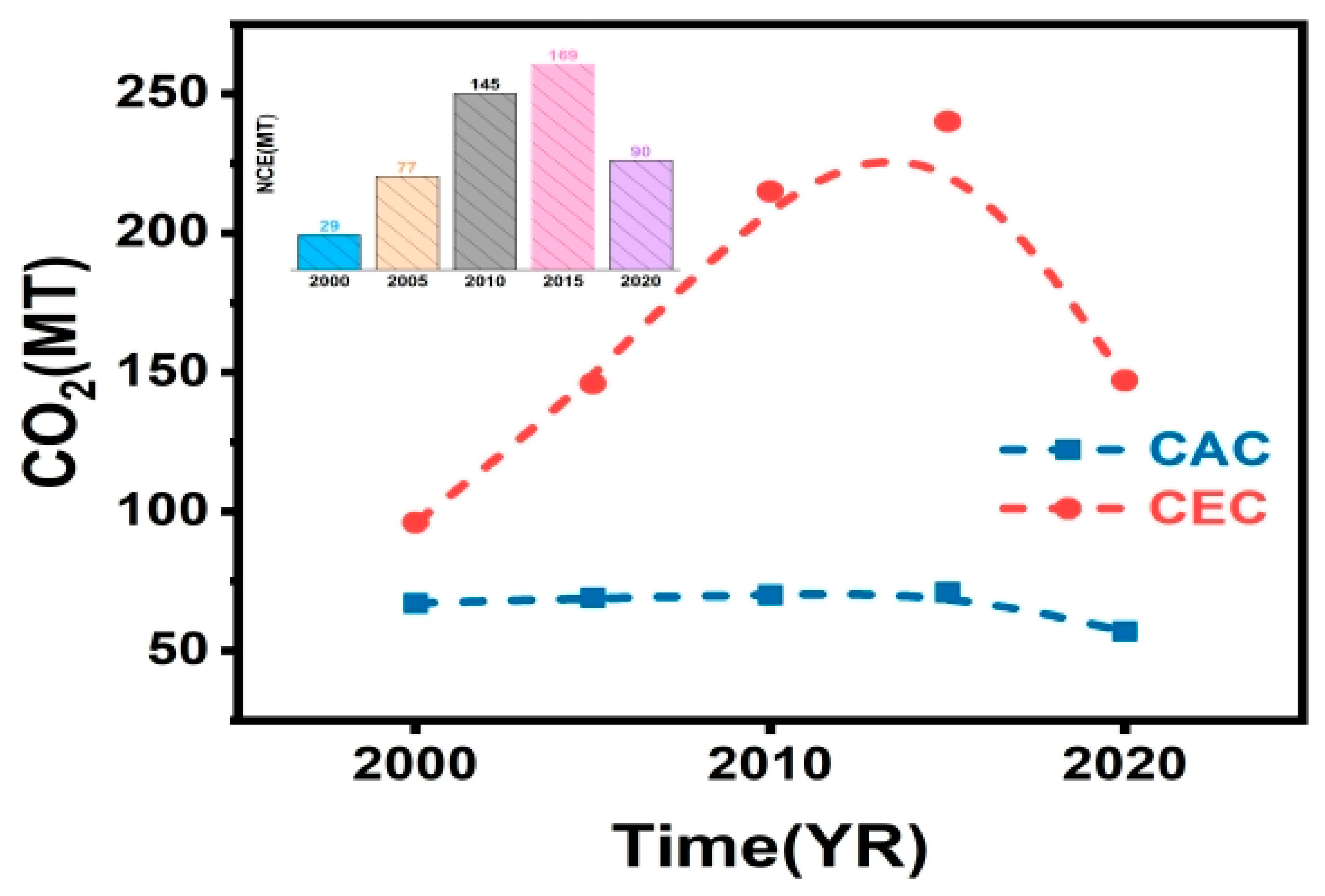
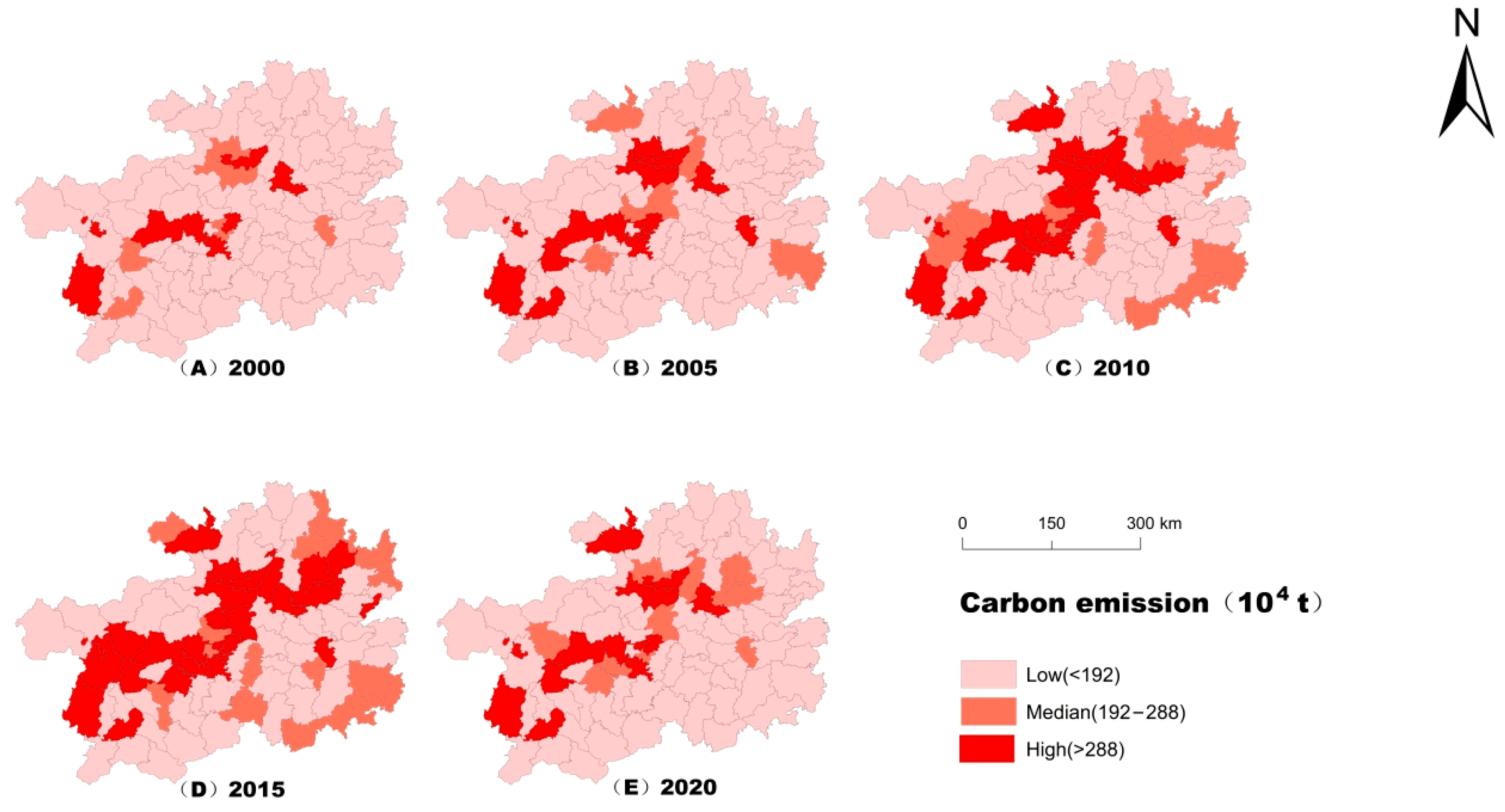
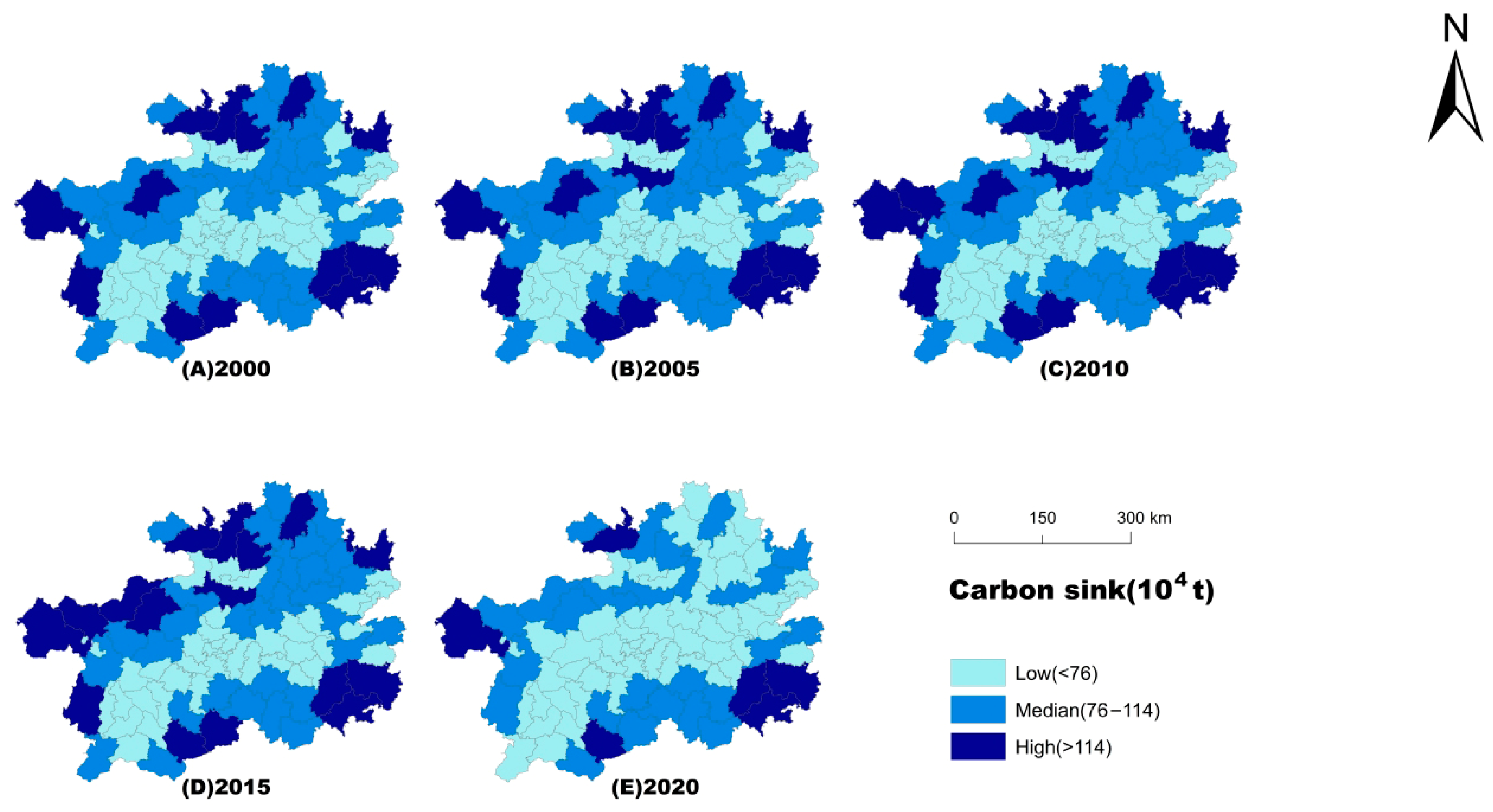
4.1. Analysis of Spatiotemporal Characteristics of Carbon Budget
4.2. Analysis of the Spatial Association Network for Carbon Budget Versus Land Use
4.2.1. Analysis of the Spatial Association Network for Carbon Emissions
4.2.2. Analysis of the Spatial Association Network for Carbon Absorption
4.3. Construction’s Spatiotemporal Evolution and Analysis of Driving Factors of the Carbon Balance Spectrum in County-Level Areas of Guizhou Province
4.3.1. Construction of the Carbon Balance Spectrum for County-Level Regions in Guizhou Province
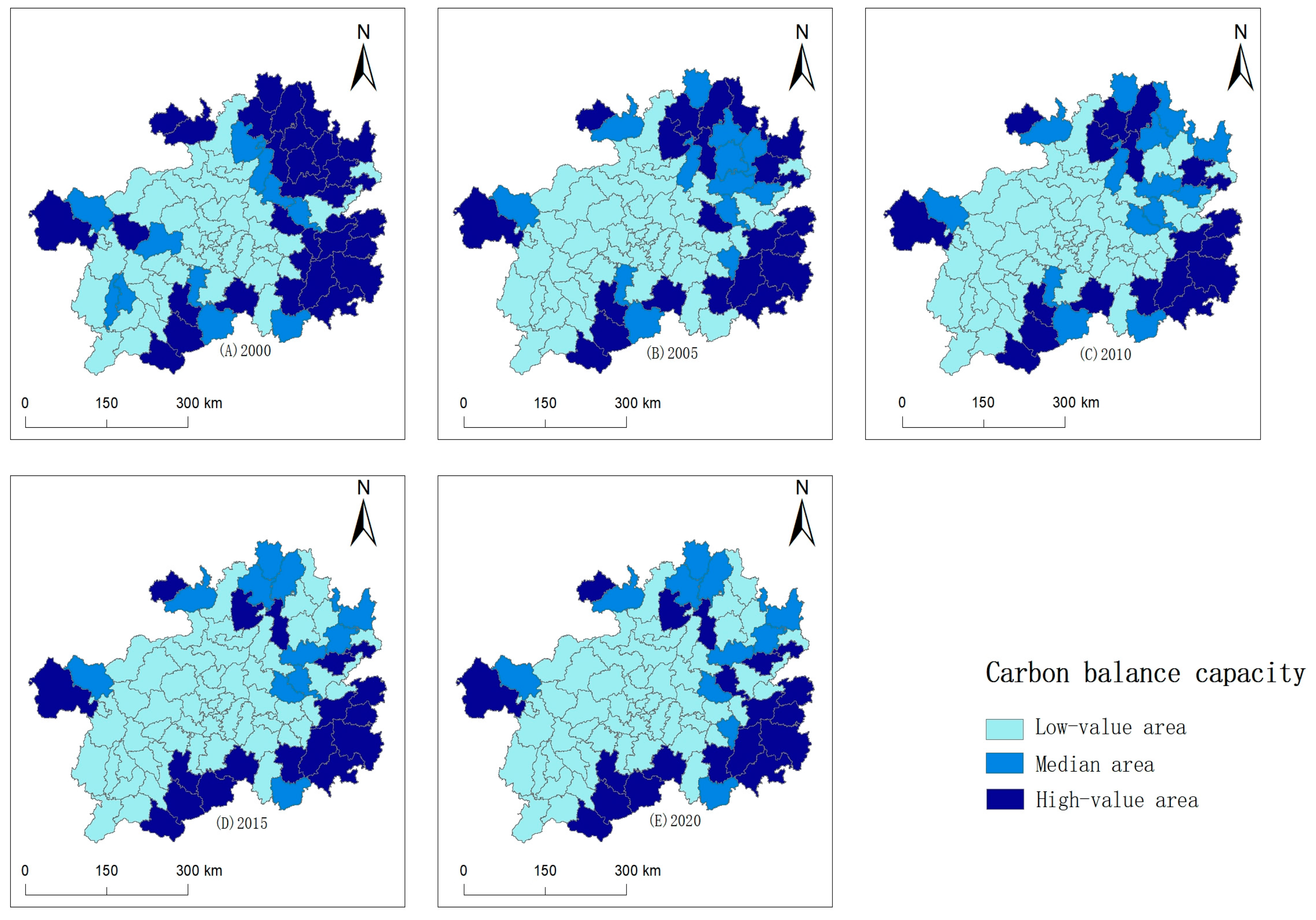
4.3.2. Spatiotemporal Differentiation of Carbon Balance in County-Level Regions of Guizhou Province
4.3.3. Dynamic Analysis of Spatial Evolution of Carbon Balance Capacity in County-Level Regions of Guizhou Province
4.3.4. Analysis of Driving Factors of Changes in the Carbon Balance Capacity of County-Level Regions in Guizhou Province
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| C/D | 2000 | 2005 | 2010 | 2015 | 2020 | C/D | 2000 | 2005 | 2010 | 2015 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NMD | 24.00 | 95.50 | 217.50 | 414.18 | 82.50 | MJC | 0.00 | 0.00 | 30.00 | 58.50 | 0.00 |
| WDD | 18.00 | 38.75 | 73.62 | 54.65 | 61.50 | MTC | 0.00 | 2.50 | 3.33 | 154.27 | 48.00 |
| ZJC | 8.00 | 16.00 | 44.25 | 978.90 | 17.00 | NYC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| PZC | 7.00 | 8.00 | 196.70 | 205.14 | 22.00 | PBD | 0.00 | 0.00 | 8.20 | 60.00 | 0.00 |
| HXD | 6.00 | 15.67 | 18.67 | 41.49 | 15.50 | PTC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| XFC | 2.00 | 6.14 | 10.94 | 7.79 | 14.00 | PAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| XWC | 2.00 | 5.00 | 56.45 | 0.73 | 2.00 | PDC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| YND | 1.50 | 0.00 | 0.00 | 0.00 | 0.00 | QXGD | 0.00 | 0.00 | 0.00 | 35.00 | 0.00 |
| KYC | 0.50 | 31.42 | 15.61 | 11.63 | 14.00 | QXC | 0.00 | 0.00 | 0.00 | 0.00 | 2.00 |
| ALC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | QZC | 0.00 | 0.00 | 172.83 | 1135.82 | 0.00 |
| BYD | 0.00 | 2.53 | 0.83 | 0.95 | 0.00 | QLC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| BJD | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | RHC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| BZD | 0.00 | 12.78 | 30.54 | 52.66 | 17.00 | RJC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| CHC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | SSC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| CGC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | SBC | 0.00 | 0.00 | 0.00 | 2.00 | 0.00 |
| CSC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | SQC | 0.00 | 0.00 | 2.00 | 10.00 | 45.00 |
| CJC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | SCD | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| DFC | 0.00 | 0.00 | 0.00 | 0.50 | 0.00 | SNC | 0.00 | 0.00 | 21.00 | 26.71 | 32.00 |
| DZC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | STAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| SYC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | DZAC | 0.00 | 0.00 | 0.00 | 3.00 | 0.00 |
| DJC | 0.00 | 0.00 | 24.00 | 6.45 | 0.00 | TJC | 0.00 | 17.00 | 4.50 | 7.00 | 16.00 |
| DYC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | TZC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| DSC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | TZC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| FGC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | WSD | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| FQC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | GLAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| WMC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | WNAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GSHD | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | WAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GDC | 0.00 | 0.00 | 2.50 | 10.50 | 0.00 | WCAC | 0.00 | 0.00 | 0.00 | 4.00 | 0.00 |
| HZC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | XXD | 0.00 | 3.83 | 12.45 | 43.85 | 11.50 |
| HHGD | 0.00 | 7.00 | 44.47 | 88.05 | 27.00 | XSC | 0.00 | 0.00 | 0.00 | 120.00 | 0.00 |
| HPC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | XRC | 0.00 | 0.00 | 26.00 | 1036.29 | 0.00 |
| HCD | 0.00 | 2.22 | 3.48 | 53.68 | 0.00 | XYC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| HSC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | YHAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| JHC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | YJAC | 0.00 | 0.00 | 21.00 | 22.26 | 0.00 |
| JKC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | YQC | 0.00 | 60.00 | 236.17 | 626.90 | 98.00 |
| JSC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | YPAC | 0.00 | 0.00 | 40.00 | 74.00 | 0.00 |
| JPC | 0.00 | 0.00 | 0.00 | 2.00 | 0.00 | CSC | 0.00 | 0.00 | 2.00 | 21.67 | 0.00 |
| KLC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ZFC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| LSC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ZNAC | 0.00 | 0.00 | 9.00 | 35.39 | 0.00 |
| LPC | 0.00 | 0.00 | 0.00 | 2.00 | 0.00 | ZYC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| LBC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ZAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| LZTD | 0.00 | 38.67 | 22.70 | 42.52 | 8.00 | ZSD | 0.00 | 0.00 | 43.25 | 108.50 | 0.00 |
| LLC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ZYAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| LDC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | SDAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| C/D | 2000 | 2005 | 2010 | 2015 | 2020 | C/D | 2000 | 2005 | 2010 | 2015 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| QZC | 228.82 | 1777.05 | 1822.38 | 1815.31 | 244.07 | ZAC | 45.51 | 49.99 | 44.97 | 45.00 | 10.21 |
| BZD | 151.16 | 1758.71 | 1711.05 | 1724.03 | 265.59 | QXC | 34.50 | 49.26 | 36.27 | 44.16 | 33.32 |
| PBD | 214.14 | 1470.64 | 1526.54 | 1468.63 | 53.79 | GLAC | 95.63 | 59.72 | 58.73 | 42.32 | 241.53 |
| SDAC | 160.50 | 213.91 | 891.09 | 891.46 | 659.21 | SNC | 19.21 | 41.78 | 36.97 | 37.12 | 23.32 |
| ZYAC | 237.83 | 842.77 | 810.39 | 797.58 | 68.37 | YJAC | 5.81 | 35.31 | 29.46 | 35.98 | 10.65 |
| RJC | 459.01 | 658.93 | 732.56 | 712.43 | 365.82 | DSC | 37.27 | 31.46 | 31.84 | 30.76 | 29.19 |
| ZNAC | 124.46 | 695.64 | 708.18 | 667.93 | 576.11 | WCAC | 11.17 | 34.58 | 30.23 | 30.55 | 40.17 |
| RHC | 861.30 | 632.65 | 628.00 | 652.79 | 851.00 | NMD | 127.62 | 31.41 | 33.32 | 30.00 | 86.00 |
| WNAC | 77.72 | 363.08 | 352.10 | 502.40 | 1.50 | CJC | 11.02 | 24.92 | 24.68 | 25.90 | 24.47 |
| JHC | 142.36 | 274.18 | 275.78 | 256.06 | 142.31 | XYC | 0.78 | 342.53 | 339.03 | 24.78 | 6.33 |
| YQC | 177.44 | 237.98 | 233.33 | 226.98 | 279.49 | GDC | 7.82 | 6.52 | 21.02 | 22.06 | 10.95 |
| ZYC | 219.35 | 223.98 | 218.49 | 208.93 | 169.40 | QLC | 31.53 | 20.14 | 17.35 | 21.08 | 0.00 |
| WDD | 278.20 | 186.02 | 138.87 | 206.47 | 288.25 | TJC | 27.05 | 20.10 | 18.76 | 19.36 | 39.06 |
| LPC | 150.70 | 195.04 | 197.63 | 178.87 | 127.94 | SSC | 31.14 | 20.69 | 20.06 | 18.79 | 27.22 |
| LDC | 47.24 | 72.08 | 173.55 | 174.27 | 64.82 | CGC | 19.16 | 18.61 | 18.56 | 17.60 | 13.52 |
| SYC | 190.09 | 173.67 | 159.50 | 162.26 | 335.15 | XFC | 27.44 | 8.46 | 8.14 | 10.20 | 0.00 |
| STAC | 156.59 | 177.33 | 176.85 | 160.55 | 131.02 | JPC | 16.47 | 10.49 | 10.34 | 8.94 | 11.87 |
| XSC | 278.06 | 168.66 | 165.21 | 156.94 | 626.31 | MJC | 4.73 | 10.57 | 16.71 | 8.25 | 3.56 |
| XWC | 130.88 | 114.23 | 149.97 | 156.13 | 147.75 | PAC | 0.20 | 6.80 | 6.97 | 7.35 | 4.87 |
| WMC | 130.02 | 158.48 | 156.09 | 154.07 | 58.34 | HCD | 10.35 | 5.30 | 5.15 | 5.84 | 15.80 |
| TZC | 141.32 | 108.86 | 108.70 | 142.54 | 324.53 | ZFC | 12.52 | 8.77 | 8.56 | 5.77 | 39.48 |
| PDC | 488.02 | 182.32 | 173.06 | 139.89 | 554.91 | NYC | 6.54 | 5.47 | 6.64 | 5.27 | 16.50 |
| JKC | 122.55 | 156.06 | 156.59 | 127.80 | 95.97 | ALC | 0.00 | 0.00 | 0.52 | 5.02 | 0.00 |
| MTC | 130.97 | 134.74 | 133.30 | 119.13 | 164.61 | DJC | 0.69 | 9.63 | 4.90 | 5.00 | 11.56 |
| WAC | 101.33 | 144.86 | 129.92 | 115.33 | 25.45 | YHAC | 0.29 | 0.28 | 4.70 | 4.80 | 1.13 |
| FGC | 102.49 | 104.13 | 104.04 | 112.07 | 62.80 | HHGD | 8.07 | 3.56 | 2.93 | 3.29 | 13.88 |
| QXGD | 49.56 | 97.39 | 69.85 | 106.69 | 62.42 | CSC | 4.76 | 2.87 | 4.01 | 2.86 | 13.60 |
| DYC | 90.19 | 112.75 | 107.94 | 97.60 | 170.85 | KLC | 2.28 | 2.57 | 2.25 | 2.20 | 21.51 |
| HSC | 136.84 | 142.75 | 112.50 | 97.07 | 243.98 | LBC | 1.93 | 3.52 | 1.96 | 1.95 | 7.02 |
| SBC | 68.27 | 109.86 | 106.26 | 96.09 | 117.01 | DZC | 0.00 | 1.35 | 1.38 | 1.37 | 9.41 |
| ZJC | 261.46 | 113.98 | 104.58 | 94.63 | 7.50 | LZSD | 1.00 | 1.31 | 1.31 | 1.14 | 17.50 |
| XXD | 60.26 | 88.04 | 88.58 | 91.33 | 15.62 | CHC | 1.88 | 1.78 | 0.73 | 0.81 | 6.17 |
| SQC | 76.77 | 111.44 | 103.08 | 90.88 | 147.31 | XRC | 1.48 | 1.03 | 1.03 | 0.70 | 6.33 |
| PZC | 11.35 | 27.80 | 83.99 | 84.90 | 172.00 | WSD | 3.70 | 2.29 | 2.26 | 0.25 | 4.70 |
| JSC | 73.75 | 59.00 | 57.97 | 64.48 | 0.00 | DZAC | 0.00 | 4.36 | 0.00 | 0.00 | 3.13 |
| TZC | 74.11 | 66.03 | 60.79 | 61.53 | 166.11 | BYD | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| PTC | 105.25 | 65.92 | 68.55 | 60.61 | 17.33 | BJD | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| HPC | 39.51 | 50.68 | 56.49 | 59.35 | 15.67 | CSC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| FQC | 63.35 | 67.79 | 57.58 | 53.74 | 56.41 | GSHD | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| SCD | 74.15 | 73.97 | 74.82 | 52.89 | 79.00 | HZC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| LSC | 54.69 | 52.51 | 18.76 | 50.68 | 93.36 | HXD | 0.00 | 0.00 | 33.81 | 0.00 | 0.00 |
| KYC | 261.89 | 78.95 | 82.50 | 48.76 | 260.08 | YPAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| LLC | 34.21 | 49.08 | 42.46 | 47.80 | 20.99 | YYD | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| DFC | 47.79 | 44.53 | 72.64 | 47.07 | 132.10 | ZSD | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Abbreviations | |
|---|---|
| SNA | Social network analysis |
| ESC | Carbon emission ecological carrying coefficient |
| CBC | Carbon balance capacity |
| Variables | |
| CO2 absorption quantity | |
| Area of various land types | |
| Carbon sequestration rate per unit area of various land types | |
| Total carbon uptake of crops | |
| Carbon uptake of the i-th crop | |
| Carbon uptake rate of the i-th crop | |
| Moisture content | |
| Yield | |
| Economic coefficient | |
| Intercity gravity value | |
| Distance between urban geometric centers | |
| Urban land use carbon budget | |
| Gravitational constant | |
| Threshold | |
| Number of node counties and districts | |
| Carbon budget spatial correlation quantity | |
| Direct association count of county i | |
| Total carbon sink amount | |
| Total carbon emissions | |
| Weight of each district/county | |
| Major axis | |
| Minor axis | |
| Azimuth angle of ellipse | |
| Explanatory power of influencing factors |
| Core Modules | Software |
|---|---|
| Spatiotemporal characteristics of carbon budget | Origin 2024 |
| Spatial association network for carbon budget in land use | Arcgis 10.8 |
| Gephi 0.10.0 | |
| UCINET 6 | |
| Carbon balance spectrum for county-level regions | Python 3.13 |
References
- IPPC. Asia. In Climate Change 2022–Impacts, Adaptation and Vulnerability: Working Group II Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2023; pp. 1457–1580. [Google Scholar]
- IPPC. Summary for Policymakers. In Climate Change 2022–Impacts, Adaptation and Vulnerability: Working Group II Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2023; pp. 3–34. [Google Scholar]
- Yang, Y.; Qu, S.; Cai, B.; Liang, S.; Wang, Z.; Wang, J.; Xu, M. Mapping global carbon footprint in China. Nat. Commun. 2020, 11, 2237. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yang, H.; Sun, R. Effectiveness of China’s provincial industrial carbon emission reduction and optimization of carbon emission reduction paths in “lagging regions”: Efficiency-cost analysis. J. Environ. Manag. 2020, 275, 111221. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.-Y.; Cai, B.F.; Wang, M.D.; Wang, J.X.; Xing, Y.K.; Dong, G.X.; Zhang, Z.; Mao, X.Q. City level CO2 and local air pollutants co-control performance evaluation: A case study of 113 key environmental protection cities in China. Adv. Clim. Change Res. 2022, 13, 118–130. [Google Scholar] [CrossRef]
- Ma, J.; Li, L.; Wang, H.; Du, Y.; Ma, J.; Zhang, X.; Wang, Z. Carbon Capture and Storage: History and the Road Ahead. Engineering 2022, 14, 33–43. [Google Scholar] [CrossRef]
- Chen, L.; Tan, L.; Zhao, M.; Sinha, A.; Wang, T.; Gao, Y. Karst carbon sink processes and effects: A review. Quat. Int. 2023, 652, 63–73. [Google Scholar] [CrossRef]
- Zhou, G.; Jia, B.; Tao, X.; Yan, H. Estimation of karst carbon sink and its contribution to CO2 emissions over a decade using remote sensing imagery. Appl. Geochem. 2020, 121, 104689. [Google Scholar] [CrossRef]
- Ao, Y.; Liu, X.; Zhou, X.; Ran, G.; Yang, S.; Yuan, W.; Hu, F. Differential thresholds of net ecosystem productivity in karst and non-karst regions for identifying their potential carbon sinks areas. J. Environ. Manag. 2025, 373, 123618. [Google Scholar] [CrossRef]
- Zhao, M.; Li, D.; Liu, Z.; Bao, Q.; Xia, F.; Yan, H.; Chen, B.; Hu, Y.; Cai, G.; Lang, R.; et al. Karst carbon sink mechanism and its contribution to carbon neutralization under land- use management. Sci. Total Environ. 2024, 937, 173381. [Google Scholar] [CrossRef]
- Cai, B.; Liang, S.; Zhou, J.; Wang, J.; Cao, L.; Qu, S.; Xu, M.; Yang, Z. China high resolution emission database (CHRED) with point emission sources, gridded emission data, and supplementary socioeconomic data. Resour. Conserv. Recycl. 2018, 129, 232–239. [Google Scholar] [CrossRef]
- Marchi, M.; Jørgensen, S.E.; Pulselli, F.M.; Marchettini, N.; Bastianoni, S. Modelling the carbon cycle of Siena Province (Tuscany, central Italy). Ecol. Model. 2012, 225, 40–60. [Google Scholar] [CrossRef]
- Wu, Y.; Tam, V.W.Y.; Shuai, C.; Shen, L.; Zhang, Y.; Liao, S. Decoupling China’s economic growth from carbon emissions: Empirical studies from 30 Chinese provinces (2001–2015). Sci. Total Environ. 2019, 656, 576–588. [Google Scholar] [CrossRef]
- Kumar, S.; Sen, R. Are larger or denser cities more emission efficient? Exploring the nexus between urban household carbon emission, population size and density. Appl. Energy 2025, 377, 124500. [Google Scholar] [CrossRef]
- Xu, L.; Du, H.; Zhang, X. Driving forces of carbon dioxide emissions in China’s cities: An empirical analysis based on the geodetector method. J. Clean. Prod. 2021, 287, 125169. [Google Scholar] [CrossRef]
- Liu, X.; Jin, X.; Luo, X.; Zhou, Y. Quantifying the spatiotemporal dynamics and impact factors of China’s county-level carbon emissions using ESTDA and spatial econometric models. J. Clean. Prod. 2023, 410, 137203. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, X.; Zhong, J.; Wang, D.; Miao, C.; Zhao, L.; Zhou, Z.; Liao, J.; Hu, B.; Zhu, L.; et al. Construction and Application of a Regional Kilometer-Scale Carbon Source and Sink Assimilation Inversion System (CCMVS-R). Engineering 2024, 33, 263–275. [Google Scholar] [CrossRef]
- Guo, M.; Chen, S.; Zhang, J.; Meng, J. Environment Kuznets Curve in transport sector’s carbon emission: Evidence from China. J. Clean. Prod. 2022, 371, 133504. [Google Scholar] [CrossRef]
- Zhao, Q.; Fan, L.; Chen, H.; Yang, Y.; Wang, Z. Green innovation and carbon emission reduction: Empirical insights from spatial durbin and dynamic threshold models. Int. Rev. Financ. Anal. 2025, 101, 103997. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Q.; Liu, N.; Sun, Y.; Guo, H.; Song, X. The impact of LUCC on the spatial pattern of ecological network during urbanization: A case study of Jinan City. Ecol. Indic. 2023, 155, 111004. [Google Scholar] [CrossRef]
- Fu, Z.; Li, R. The contributions of socioeconomic indicators to global PM2.5 based on the hybrid method of spatial econometric model and geographical and temporal weighted regression. Sci. Total Environ. 2020, 703, 135481. [Google Scholar] [CrossRef]
- Radmehr, R.; Henneberry, S.R.; Shayanmehr, S. Renewable Energy Consumption, CO2 Emissions, and Economic Growth Nexus: A Simultaneity Spatial Modeling Analysis of EU Countries. Struct. Change Econ. Dyn. 2021, 57, 13–27. [Google Scholar] [CrossRef]
- Perissi, I.; Jones, A. An Emissions Offset Strategy to Accomplish 2 °C Long-Term Mitigation Goals in the European Union. Sustainability 2024, 16, 4783. [Google Scholar] [CrossRef]
- Perissi, I.; Jones, A. Influence of economic decoupling in assessing carbon budget quotas for the European Union. Carbon Manag. 2023, 14, 2217423. [Google Scholar] [CrossRef]
- Yu, Z.; Chen, L.; Tong, H.; Chen, L.; Zhang, T.; Li, L.; Yuan, L.; Xiao, J.; Wu, R.; Bai, L.; et al. Spatial correlations of land-use carbon emissions in the Yangtze River Delta region: A perspective from social network analysis. Ecol. Indic. 2022, 142, 109147. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Z. Forecasting Chinese provincial carbon emissions using a novel grey prediction model considering spatial correlation. Expert Syst. Appl. 2022, 209, 118261. [Google Scholar] [CrossRef]
- Ye, X.; Chuai, X. Carbon sinks/sources’ spatiotemporal evolution in China and its response to built-up land expansion. J. Environ. Manag. 2022, 321, 115863. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Wu, T.; Pu, L.; Meadows, M.; Jiang, G.; Zhang, J.; Xie, X. Spatially heterogeneous relationships of PM2.5 concentrations with natural and land use factors in the Niger River Watershed, West Africa. J. Clean. Prod. 2023, 394, 136406. [Google Scholar] [CrossRef]
- Long, Z.; Zhang, Z.; Liang, S.; Chen, X.; Ding, B.; Wang, B.; Chen, Y.; Sun, Y.; Li, S.; Yang, T. Spatially explicit carbon emissions at the county scale. Resour. Conserv. Recycl. 2021, 173, 105706. [Google Scholar] [CrossRef]
- Yang, S.; Zhu, Z.; Fu, W.; Hu, S. Tele-connection of embodied carbon emissions from industries in China’s trade: A complex network analysis. J. Environ. Manag. 2024, 366, 121652. [Google Scholar] [CrossRef]
- Yang, S.; Li, Y.; Zhao, Y.; Lan, A.; Zhou, C.; Lu, H.; Zhou, L. Changes in vegetation ecosystem carbon sinks and their response to drought in the karst concentration distribution area of Asia. Ecol. Inform. 2024, 84, 102907. [Google Scholar] [CrossRef]
- You, J.; Dong, Z.; Jiang, H. Research on the spatiotemporal evolution and non-stationarity effect of urban carbon balance: Evidence from representative cities in China. Environ. Res. 2024, 252, 118802. [Google Scholar] [CrossRef]
- Wang, C.; Ibrahim, H.; Wu, F.; Chang, W. Spatial and temporal evolution patterns and spatial spillover effects of carbon emissions in China in the context of digital economy. J. Environ. Manag. 2025, 373, 123811. [Google Scholar] [CrossRef]
- Li, S.; Zhao, X.; Pu, J.; Miao, P.; Wang, Q.; Tan, K. Optimize and control territorial spatial functional areas to improve the ecological stability and total environment in karst areas of Southwest China. Land Use Policy 2021, 100, 104940. [Google Scholar] [CrossRef]
- Li, S. Liu, Y.; Kang, L. Spatial spillover effect of new-type urbanization on carbon emission intensity in counties around the Poyang Lake. Resour. Sci. 2022, 44, 1449–1462. [Google Scholar]
- Shen, X.; Yan, R.; Jiang, M. How does planting structure change affect the agricultural net carbon sink? Evidence from the Jiangsu coastal economic Belt. Ecol. Indic. 2025, 170, 112949. [Google Scholar] [CrossRef]
- Shen, W.; Liang, H.; Dong, L.; Ren, J.; Wang, G. Synergistic CO2 reduction effects in Chinese urban agglomerations: Perspectives from social network analysis. Sci. Total Environ. 2021, 798, 149352. [Google Scholar] [CrossRef]
- Huo, T.; Cao, R.; Xia, N.; Hu, X.; Cai, W.; Liu, B. Spatial correlation network structure of China’s building carbon emissions and its driving factors: A social network analysis method. J. Environ. Manag. 2022, 320, 115808. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Guo, B.; Liu, X.; Deng, C.; Zhao, Z.; Jiang, X.; Li, Y. Characteristics and formation mechanism of carbon emission efficiency spatial correlation network: Perspective from Shandong Province. Ecol. Indic. 2025, 170, 112996. [Google Scholar] [CrossRef]
- Borgatti, S.P.; Mehra, A.; Brass, D.J.; Labianca, G. Network analysis in the social sciences. Science 2009, 323, 892–895. [Google Scholar] [CrossRef]
- Liu, S.; Xiao, Q. An empirical analysis on spatial correlation investigation of industrial carbon emissions using SNA-ICE model. Energy 2021, 224, 120183. [Google Scholar] [CrossRef]
- Ghosh, S.; Dinda, S.; Chatterjee, N.D.; Dutta, S.; Bera, D. Spatial-explicit carbon emission-sequestration balance estimation and evaluation of emission susceptible zones in an Eastern Himalayan city using Pressure-Sensitivity-Resilience framework: An approach towards achieving low carbon cities. J. Clean. Prod. 2022, 336, 130417. [Google Scholar] [CrossRef]
- Rong, T.; Qin, M.; Zhang, P.; Chang, Y.; Liu, Z.; Zhang, Z. Spatiotemporal evolution of land use carbon emissions and multi scenario simulation in the future—Based on carbon emission fair model and PLUS model. Environ. Technol. Innov. 2025, 38, 104087. [Google Scholar] [CrossRef]
- Xiang, W.; Gan, L.; Cai, W. Spatiotemporal evolution characteristics and spillover effects of carbon emissions from public building in China: The tertiary industry perspective. Environ. Impact Assess. Rev. 2024, 106, 107545. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, X.; Yu, B.; Wang, Z.; Wang, L.; Lei, K.; Zuo, L.; Fan, P.; Liang, T. Exploring the environmental risks and seasonal variations of potentially toxic elements (PTEs) in fine road dust in resource-based cities based on Monte Carlo simulation, geo-detector and random forest model. J. Hazard. Mater. 2024, 473, 134708. [Google Scholar] [CrossRef]
- Zheng, J.; Groenigen, K.J.; Hartley, I.P.; Xue, R.; Wang, M.; Zhang, S.; Sun, T.; Yu, W.; Ma, B.; Luo, Y.; et al. Temperature sensitivity of bacterial species-level preferences of soil carbon pools. Geoderma 2025, 456, 117268. [Google Scholar] [CrossRef]
- Tang, S.; Tian, D.; Wang, J.; Zhang, R.; Wang, S.; Song, J.; Wan, S.; Zhang, J.; Zhang, S.; Li, Z.; et al. Synergistic effects of multiple global change drivers on terrestrial ecosystem carbon sink. Sci. Total Environ. 2024, 906, 167554. [Google Scholar] [CrossRef]
- Wang, T.; Mallick, K.; Verfaille, J.; Szutu, D.; Baldocchi, D. Water scarcity in semi-arid California compromises perennial alfalfa’s high yield and carbon sinking potentials. Agric. Water Manag. 2025, 308, 109284. [Google Scholar] [CrossRef]
- Fornaciari, M.; Muscas, D.; Rossi, F.; Filipponi, M.; Castellani, B.; Di Giuseppe, A.; Proietti, C.; Ruga, L.; Orlandi, F. CO2 Emission Compensation by Tree Species in Some Urban Green Areas. Sustainability 2024, 16, 3515. [Google Scholar] [CrossRef]
- Perissi, I.; Natalini, D.; Jones, A. Assessing the Emissions Related to European Households’ Expenditures and Their Impact on Achieving Carbon Neutrality. Climate 2023, 11, 203. [Google Scholar] [CrossRef]
- Rao, Y.; Wang, X.; Li, H. Forecasting electricity consumption in China’s Pearl River Delta urban agglomeration under the optimal economic growth path with low-carbon goals: Based on data of NPP-VIIRS-like nighttime light. Energy 2024, 294, 130970. [Google Scholar] [CrossRef]
- Hong, S.; Hui, E.C.; Lin, Y. Relationships between carbon emissions and urban population size and density, based on geo-urban scaling analysis: A multi-carbon source empirical study. Urban Clim. 2022, 46, 101337. [Google Scholar] [CrossRef]
- Jiao, L.; Yang, R.; Chen, B.; Zhang, Y. Variation, Variation, Determinants and prediction of carbon emissions in Guizhou, a new economic growth pole in southwest China. J. Clean. Prod. 2023, 417, 138049. [Google Scholar] [CrossRef]
- Li, Q.; Wu, S.; Lei, Y.; Li, S.; Li, L. China’s provincial CO2 emissions and interprovincial transfer caused by investment demand. Environ. Sci. Pollut. Res. 2019, 26, 312–325. [Google Scholar] [CrossRef]
- Wang, K.; Li, Z.; Xu, Z.; Wang, J.; Jia, M.; Wang, L.; Yue, X.; Duo, X. Evaluating and simulating the impacts of land use patterns on carbon emissions in coal resource-based regions: A case study of Shanxi province, China. J. Clean. Prod. 2024, 458, 142494. [Google Scholar] [CrossRef]
- Shi, N.; Xiao, N.; Wang, Q.; Han, Y.; Feng, J.; Quan, Z. Spatial Pattern of Ecosystems and the Driving Forces in the Yangtze River Economic Zone. Res. Environ. Sci. 2019, 32, 1779–1789. [Google Scholar]
- Xu, X.; Liu, J.; Jiao, F.; Zhang, K.; Ye, X.; Gong, H.; Lin, N.; Zou, C. Ecological engineering induced carbon sinks shifting from decreasing to increasing during 1981–2019 in China. Sci. Total Environ. 2023, 864, 161037. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Fei, X.; Zhu, J.; Chen, W.; Du, H.; Huang, Y.; Shen, Y.; Zhang, Y.; Niu, A.; Xu, P. Assessing carbon storage dynamics in an ecological civilization demonstration zone amid rapid urbanization: A multi-scenario study of Guizhou Province, China. Resour. Environ. Sustain. 2025, 21, 100223. [Google Scholar] [CrossRef]
- Qiu, S.; Peng, J.; Zheng, H.; Xu, Z.; Meersmans, J. How can massive ecological restoration programs interplay with social-ecological systems? A review of research in the South China karst region. Sci. Total Environ. 2022, 807, 150723. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, P.; Liu, Y.; Lu, S.; Wu, G. An analysis of the spatiotemporal evolution and driving force of cultivated land green utilization in karst region of southwest China. J. Clean. Prod. 2024, 434, 140002. [Google Scholar] [CrossRef]
- Zhang, Y.; Khan, S.U.; Wang, Y. The future is digital: Can the digital economy drive marine sustainability? Exploring regional impacts on fisheries’ carbon emissions in coastal China. J. Clean. Prod. 2025, 506, 145518. [Google Scholar] [CrossRef]
- Tong, X.; Wang, K.; Yue, Y.; Brandt, M.; Liu, B.; Zhang, C.; Liao, C.; Fensholt, R. Quantifying the effectiveness of ecological restoration projects on long-term vegetation dynamics in the karst regions of Southwest China. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 105–113. [Google Scholar] [CrossRef]
- Zhu, M.; Zhou, Z.; Wu, X.; Wan, J.; Wang, J.; Zheng, J.; Liu, R.; Li, F. Prediction and spillover effects of forest expansion and management to increase carbon sinks in karst mountainous areas: A case study in Guizhou, China. Land Use Policy 2025, 151, 107491. [Google Scholar] [CrossRef]
- Cheng, J.; Huang, C.; Gan, X.; Peng, C.; Deng, L. Can forest carbon sequestration offset industrial CO2 emissions? A case study of Hubei Province, China. J. Clean. Prod. 2023, 426, 139147. [Google Scholar] [CrossRef]
- Xia, S.; Yang, Y. Examining spatio-temporal variations in carbon budget and carbon compensation zoning in Beijing-Tianjin-Hebei urban agglomeration based on major functional zones. J. Geogr. Sci. 2022, 32, 1911–1934. [Google Scholar] [CrossRef]
- Abou Samra, R.M. How Urban Green Spaces Shape Unequal Cooling in Rapidly Urbanizing Egypt: Insights from Landsat and GEE Analysis. Earth Syst. Environ. 2025, 9, 605–624. [Google Scholar] [CrossRef]
- Rossi, F.; Di Giuseppe, A.; Soomro, A.R.; Nicolini, A.; Filipponi, M.; Castellani, B. Radiative cooling improvement by retro-reflective materials. Energy Build. 2025, 336, 115597. [Google Scholar] [CrossRef]
- Chen, J.; Gao, M.; Cheng, S.; Hou, W.; Song, M.; Liu, X.; Liu, Y.; Shan, Y. County-level CO2 emissions and sequestration in China during 1997–2017. Sci. Data 2020, 7, 391. [Google Scholar] [CrossRef]
- Wang, S.; Xie, Z.; Wang, Z. The spatiotemporal pattern evolution and influencing factors of CO2 emissions at the county level of China. Acta Geogr. Sin. 2021, 76, 3103–3118. [Google Scholar]
- Liu, H.; Shao, M.; Ji, Y. The Spatial Pattern and Distribution Dynamic Evolution of Carbon Emissions in China: Empirical Study Based on County Carbon Emission Data. Geogr. Sci. 2021, 41, 1917–1924. [Google Scholar]
- Zheng, Y.; Fan, M.; Cai, Y.; Fu, M.; Yang, K.; Wei, C. Spatio-temporal pattern evolution of carbon emissions at the city-county-town scale in Fujian Province based on DMSP/OLS and NPP/VIIRS nighttime light data. J. Clean. Prod. 2024, 442, 140958. [Google Scholar] [CrossRef]
- Tao, B.; Wu, F.; Wang, J.; Zhu, M.; Zhang, J.; Xing, Z. County-level source-sink balance and carbon allocation of regional peak emissions: Model construction and application. Ecol. Indic. 2025, 173, 113387. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Q.; Zhao, Y.; Zhai, J.; Zhang, J. Possible explanations for the “Matthew effect” of rainfall in the Beijing-Tianjin-Hebei metropolitan area. J. Hydrol. 2024, 642, 131880. [Google Scholar] [CrossRef]
- Wang, C.; Liu, P.; Ibrahim, H.; Yuan, R. The temporal and spatial evolution of green finance and carbon emissions in the Pearl River Delta region: An analysis of impact pathways. J. Clean. Prod. 2024, 446, 141428. [Google Scholar] [CrossRef]
- Shen, L.; Jiang, Y.; Zhai, D.; Wang, P. Teleconnections detection of land use carbon emissions beyond geographical proximity promotes the construction of cross-city networks. Ecol. Indic. 2025, 170, 113092. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Li, G.; Zhang, J. How to recognize and characterize land use-based carbon emissions within city networks in the Beijing-Tianjin-Hebei region of China. Urban Clim. 2024, 53, 101789. [Google Scholar] [CrossRef]
- Chen, H.; Liu, S.; Wang, J.; Wu, Z. The effect of geographic proximity on corporate tax avoidance: Evidence from China. J. Corp. Financ. 2022, 72, 102131. [Google Scholar] [CrossRef]
- Zhang, R.; Song, S.; Xiu, W. Does the efficiency of capital allocation have spatial carbon emission spillover effects? Int. Rev. Financ. Anal. 2025, 99, 103938. [Google Scholar] [CrossRef]
- Mallick, K.; Verfaillie, J.; Wang, T.; Ortiz, A.A.; Szutu, D.; Yi, K.; Kang, Y.; Shortt, R.; Hu, T.; Sulis, M.; et al. Net fluxes of broadband shortwave and photosynthetically active radiation complement NDVI and near infrared reflectance of vegetation to explain gross photosynthesis variability across ecosystems and climate. Remote Sens. Environ. 2024, 307, 114123. [Google Scholar] [CrossRef]
- Ren, X.; Xiong, R.; Ni, T. Spatial network characteristics of carbon balance in urban agglomerations– a case study in Beijing-Tianjin-Hebei city agglomeration. Appl. Geogr. 2024, 169, 103343. [Google Scholar] [CrossRef]
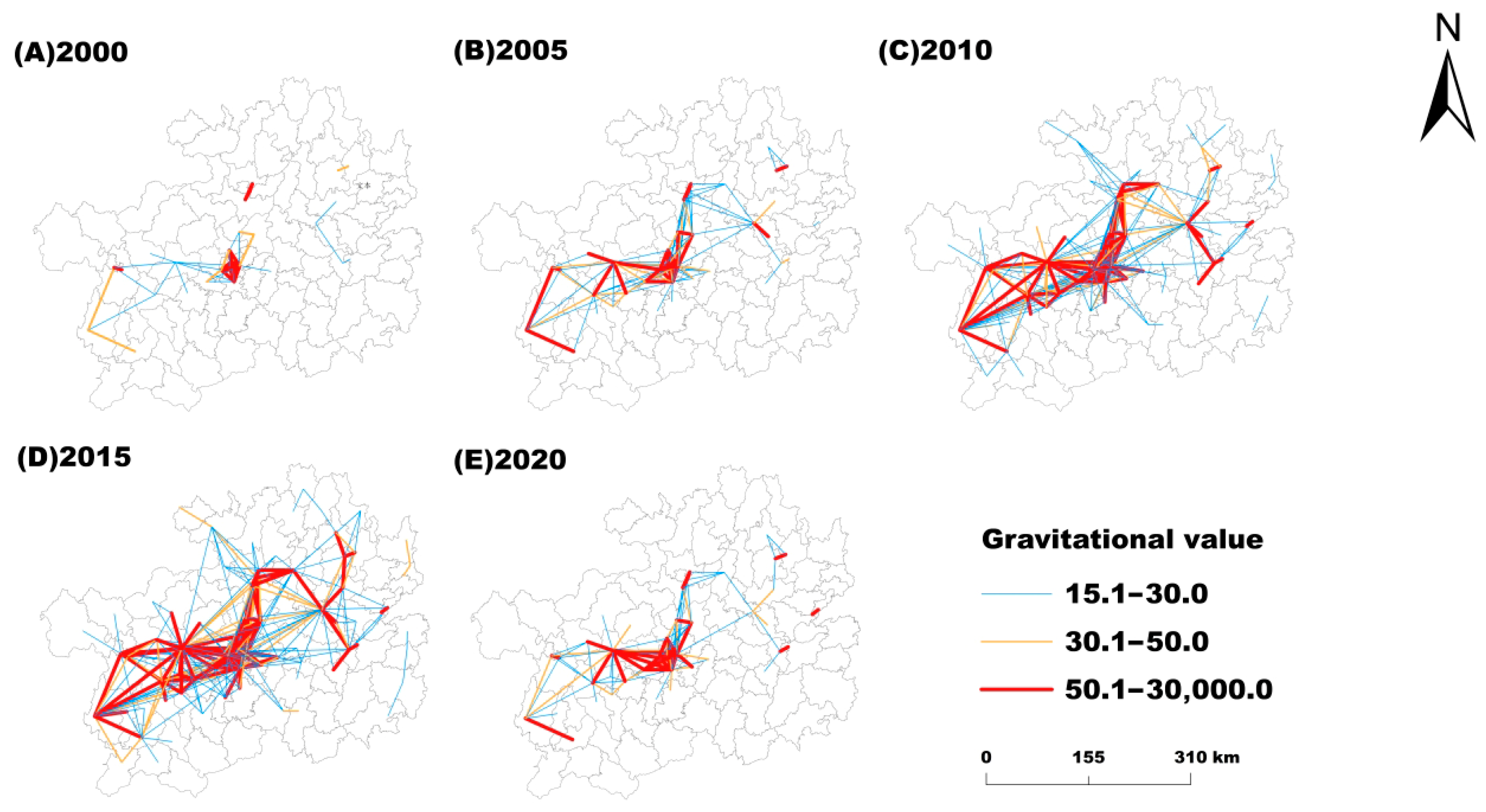
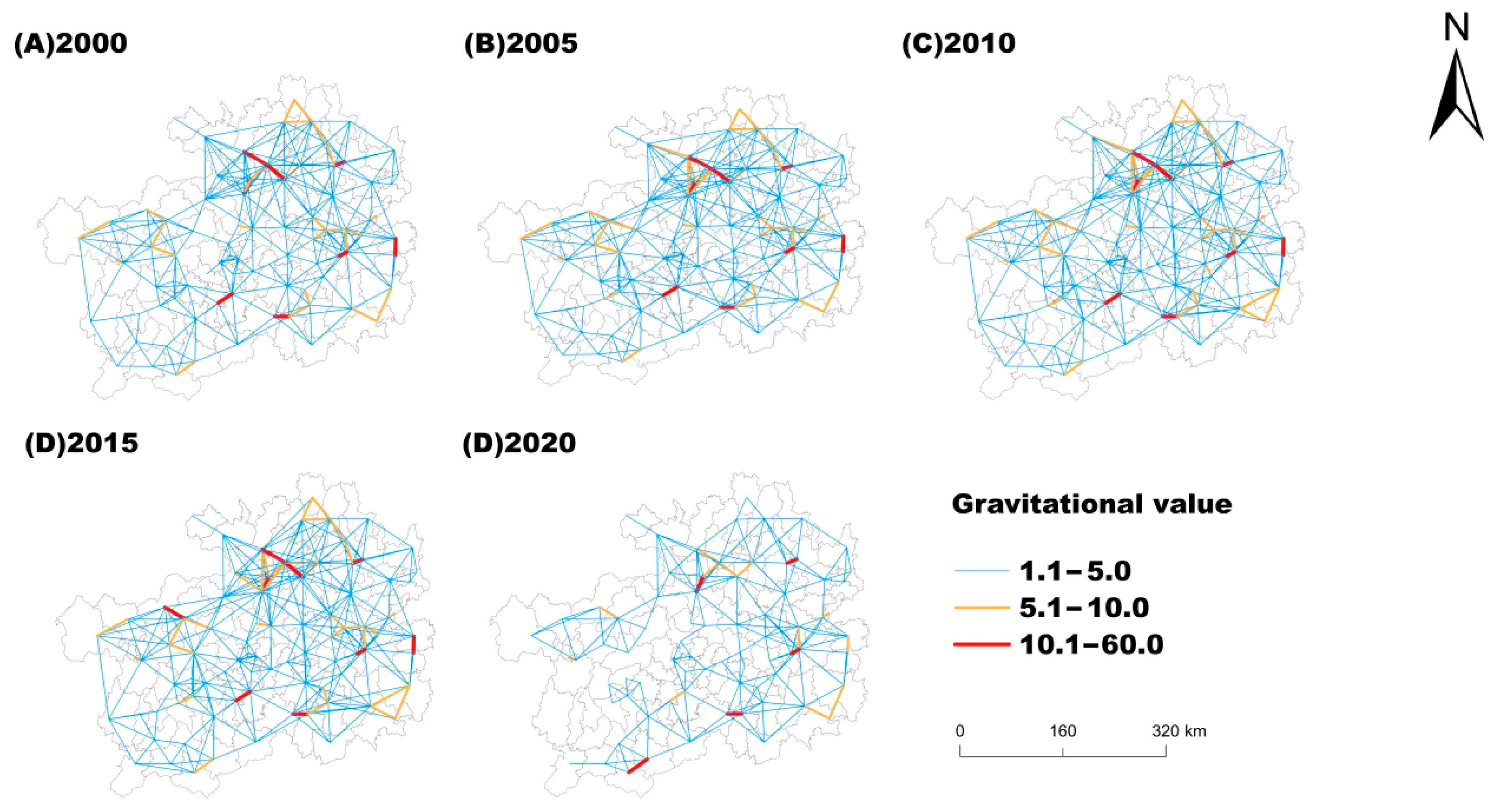

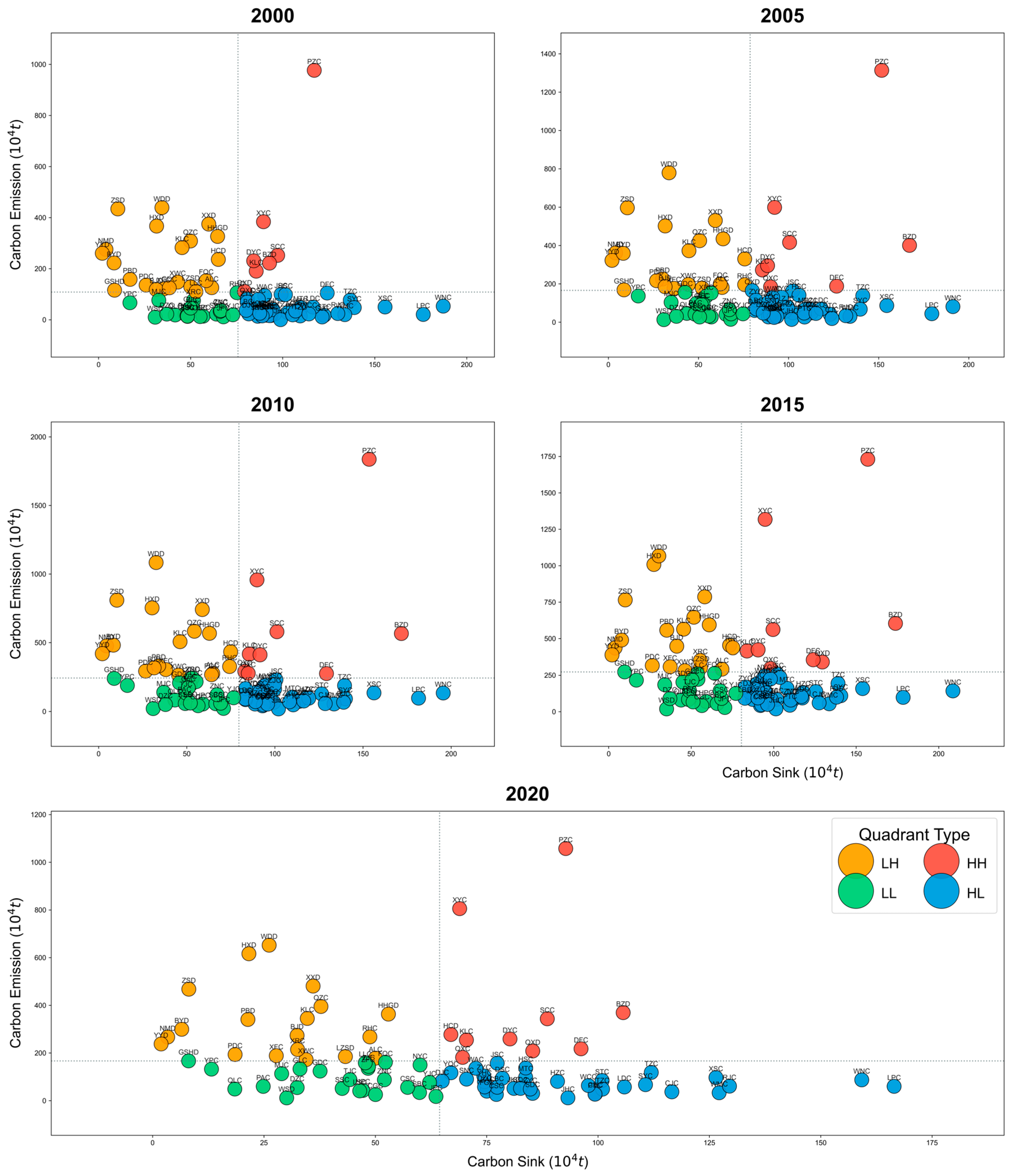


| Crop Type | Economic Coefficient | Moisture Content (%) | Carbon Absorption Rate |
|---|---|---|---|
| Cereal crops | 0.4 | 12 | 0.46 |
| Oilseed crops | 0.43 | 10 | 0.45 |
| Cotton | 0.1 | 8 | 0.45 |
| Flue-cured tobacco | 0.4 | 10 | 0.45 |
| Rapeseed | 0.25 | 10 | 0.45 |
| Beans | 0.34 | 13 | 0.45 |
| Year | Centroid Longitude | Centroid Dimension | Semi-major Axis/(km) | Semi-Minor Axis/(km) | Perimeter/(km) | Area/(km2) | Azimuth Angle/(°) |
|---|---|---|---|---|---|---|---|
| 2000 | 108°6′54″ | 26°46′46″ | 154.41 | 109.44 | 834.90 | 53,081.72 | 81.32 |
| 2005 | 107°33′15″ | 26°49′16″ | 189.01 | 145.93 | 1056.58 | 86,645.89 | 70.45 |
| 2010 | 107°29′56″ | 26°51′26″ | 188.19 | 144.83 | 1050.64 | 85,620.25 | 72.1 |
| 2015 | 107°28′36″ | 26°48′25″ | 191.03 | 144.51 | 1059.17 | 86,717.61 | 72.33 |
| 2020 | 107°32′26″ | 26°45′44″ | 188.02 | 144.49 | 1049.08 | 85,343.04 | 70.4 |
| Driving Factor | 2000 | 2005 | 2010 | 2015 | 2020 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| q | p | q | p | q | p | q | p | q | p | |
| Temperature (X1) | 0.123 | 0.08 | 0.126 | 0.071 | 0.091 | 0.197 | 0.102 | 0.147 | 0.113 | 0.108 |
| Precipitation (X2) | 0.079 | 0.27 | 0.18 | 0.0135 * | 0.096 | 0.172 | 0.2 | 0.006 * | 0.127 | 0.072 |
| NDVI (X3) | 0.269 | 0.000 * | 0.303 | 0.000 * | 0.36 | 0.000 * | 0.25 | 0.000 * | 0.262 | 0.000 * |
| GDP (X4) | 0.323 | 0.000 * | 0.354 | 0.000 * | 0.389 | 0.000 * | 0.35 | 0.000 * | 0.315 | 0.000 * |
| Industrial structure (X5) | 0.533 | 0.000 * | 0.437 | 0.000 * | 0.334 | 0.000 * | 0.254 | 0.000 * | 0.135 | 0.063 |
| County-level electricity consumption (X6) | 0.24 | 0.002 * | 0.282 | 0.000 * | 0.273 | 0.000 * | 0.234 | 0.003 * | 0.226 | 0.004 * |
| Nighttime lights (X7) | 0.776 | 0.000 * | 0.629 | 0.000 * | 0.695 | 0.000 * | 0.504 | 0.000 * | 0.591 | 0.000 * |
| PM2.5 (X8) | 0.099 | 0.166 | 0.092 | 0.199 | 0.06 | 0.436 | 0.025 | 0.845 | 0.021 | 0.886 |
| Population density (X9) | 0.304 | 0.000 * | 0.43 | 0.000 * | 0.385 | 0.000 * | 0.478 | 0.000 * | 0.512 | 0.000 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Zhao, J.; Yao, Y.; Chen, W. Spatiotemporal Characteristics of Land Use Carbon Budget and Carbon Balance Capacity in Karst Mountainous Areas: A Case Study Using Social Network Analysis. Systems 2025, 13, 686. https://doi.org/10.3390/systems13080686
Chen B, Zhao J, Yao Y, Chen W. Spatiotemporal Characteristics of Land Use Carbon Budget and Carbon Balance Capacity in Karst Mountainous Areas: A Case Study Using Social Network Analysis. Systems. 2025; 13(8):686. https://doi.org/10.3390/systems13080686
Chicago/Turabian StyleChen, Bo, Jiayi Zhao, Yongli Yao, and Wenjin Chen. 2025. "Spatiotemporal Characteristics of Land Use Carbon Budget and Carbon Balance Capacity in Karst Mountainous Areas: A Case Study Using Social Network Analysis" Systems 13, no. 8: 686. https://doi.org/10.3390/systems13080686
APA StyleChen, B., Zhao, J., Yao, Y., & Chen, W. (2025). Spatiotemporal Characteristics of Land Use Carbon Budget and Carbon Balance Capacity in Karst Mountainous Areas: A Case Study Using Social Network Analysis. Systems, 13(8), 686. https://doi.org/10.3390/systems13080686





