Standard Revision Project Scheduling Problem Considering Coordination Degree of Standards Systems
Abstract
1. Introduction
2. Literature Review
2.1. Research on Standard Revision and Standard Citation Network
2.2. Research on RCPSP
3. Problem Description and Mathematical Model
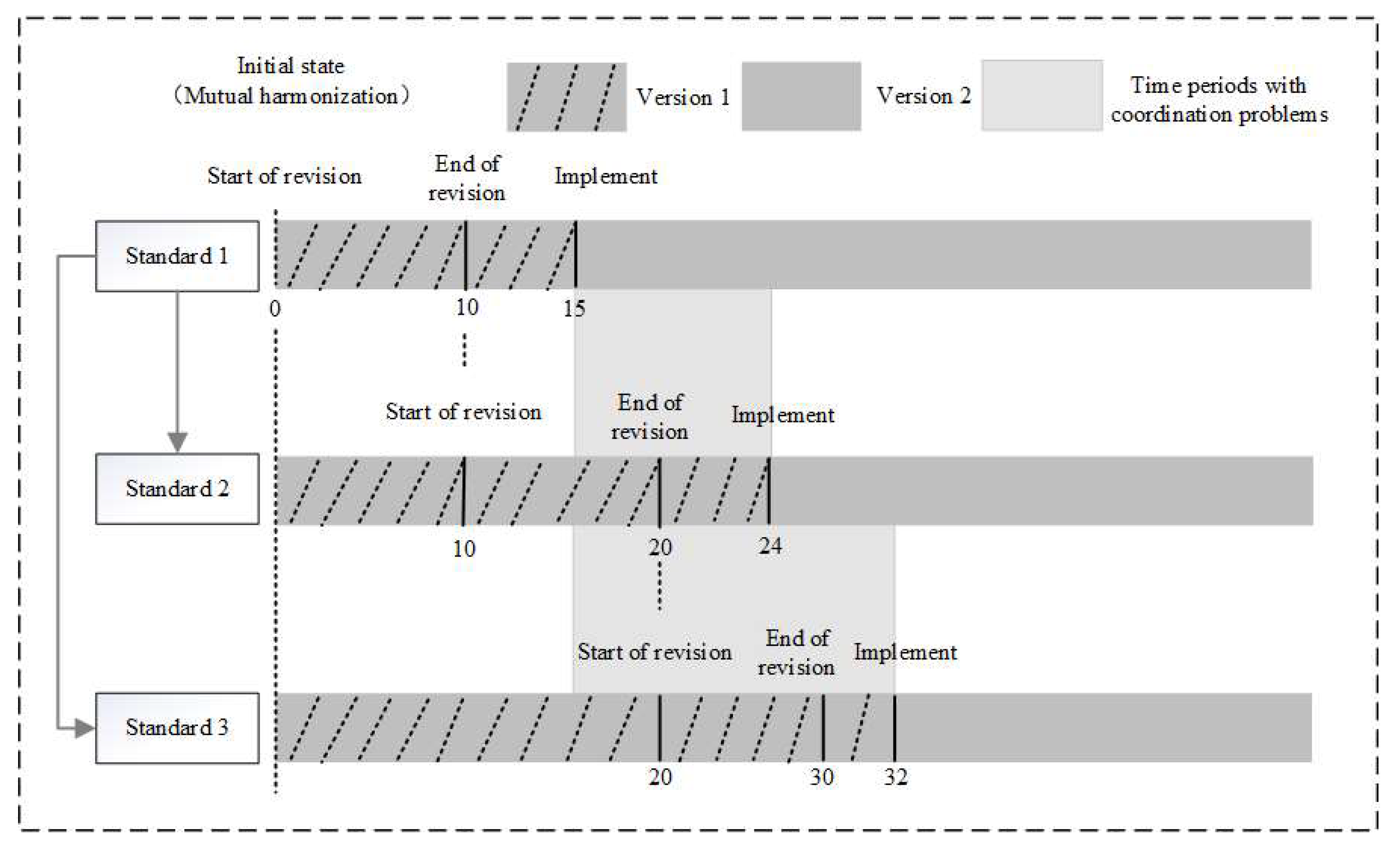
3.1. Problem Description
3.2. Parameters and Variables
3.3. Objective Function
3.4. Constraints
4. Solution Algorithm
4.1. Particle Swarm Algorithm Workflow
4.2. Algorithm Design
- 1.
- Firstly, according to the reference relationship between standards, input the standard relationship matrix (e.g., ), in this standard system, composed of four standards. According to the standard relationship matrix, there are four reference relationships in the system: standards 2, 3, and 4 refer to standard 1, and at the same time, standard 4 refers to standard 2. Input the number of standards , the maximum number of standards to be revised in a single TC revision , the revision duration , the standard implementation transition period , and a series of initial parameters for PSO.
- 2.
- Establish standard 1 as the first standard to be revised (a series of standard revision tasks caused by the revision of standard 1), i.e., . According to the revision period of standard 1, determine the next decision point as + = . is set to represent the set of standards eligible for revision at time . At time , the set of standards eligible for revision is determined, and the number of standards not exceeding the is randomly selected for revision.
- 3.
- According to the revision period of the standard being revised, select the earliest end of the revision of the standard for the next decision point time , and determine a new set of standards to be revised ; then, randomly select a number of standards to be revised and ensure that the standard revised at decision point time is not higher than the .
- 4.
- The decision-making process continues until the last standard revision is completed, resulting in a feasible standard revision program.
- 5.
- Calculate the fitness value of the scheme (i.e., the position of each particle) and record it, and iterate times to get the revised scheme with the highest fitness value.
5. Computational Experiments
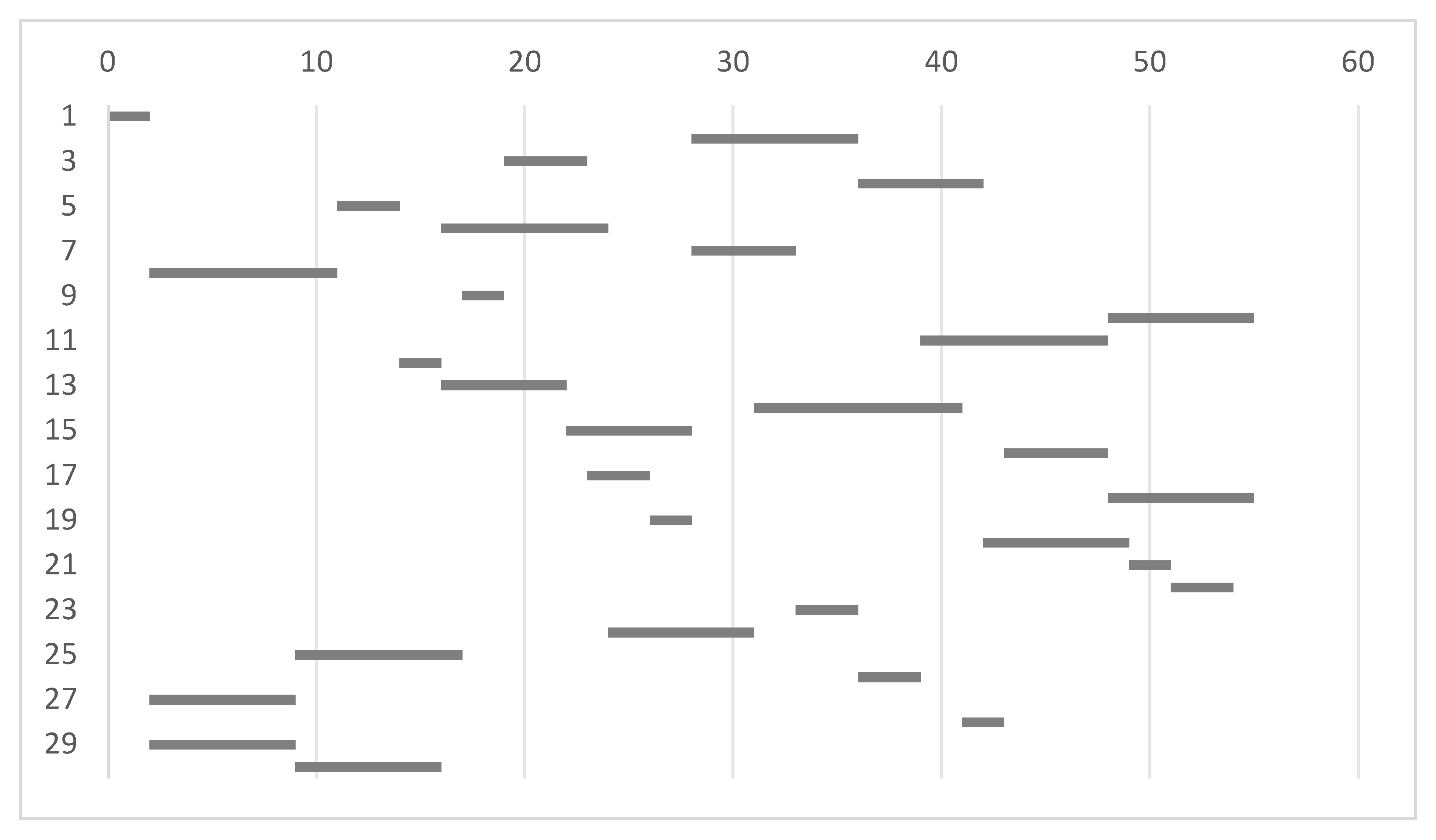
5.1. Experimental Design
5.2. Analysis of Experimental Results
5.2.1. Comparative Experimental Analysis of Objective Functions
5.2.2. Impact of Citation-Triggered Revision Ratio on
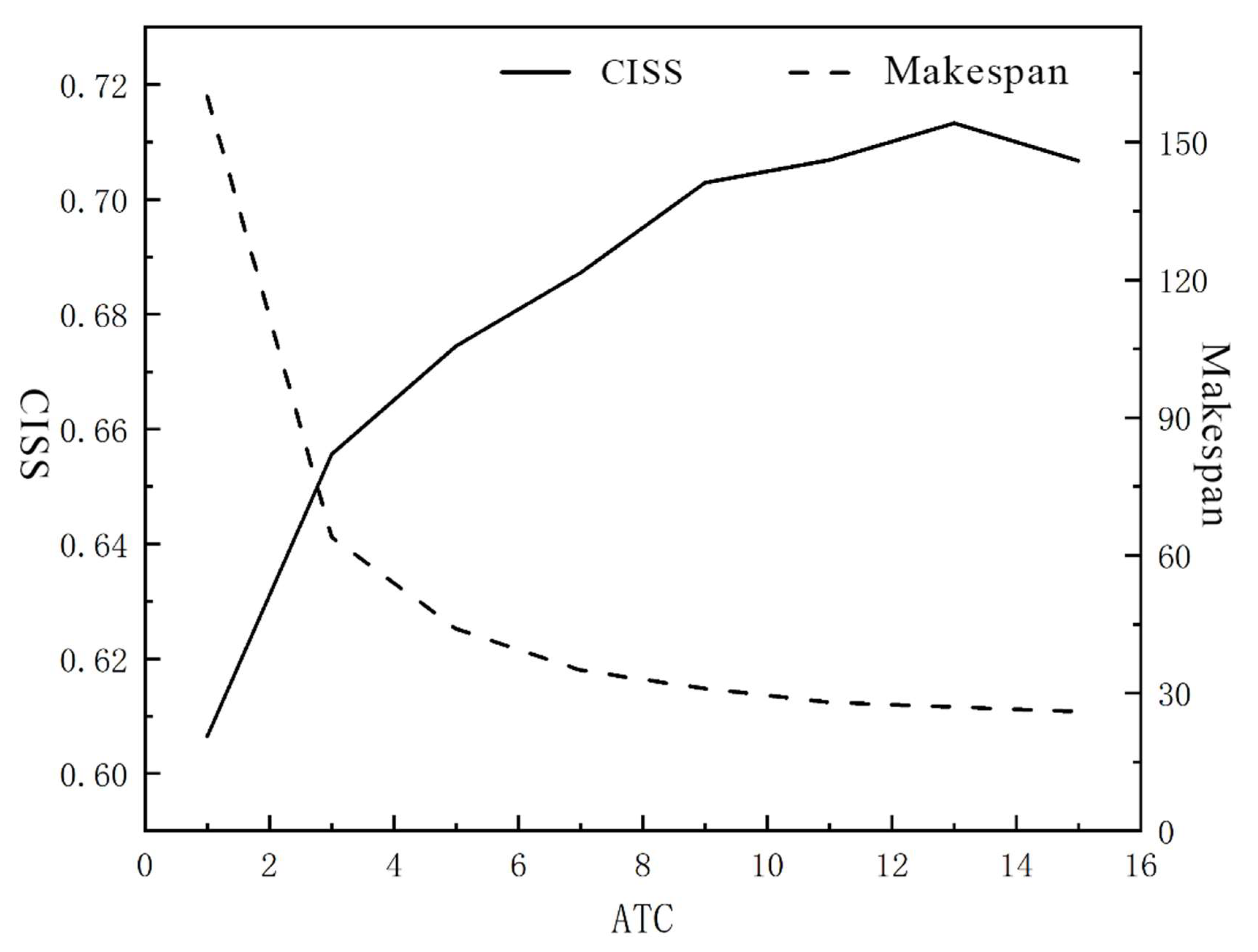
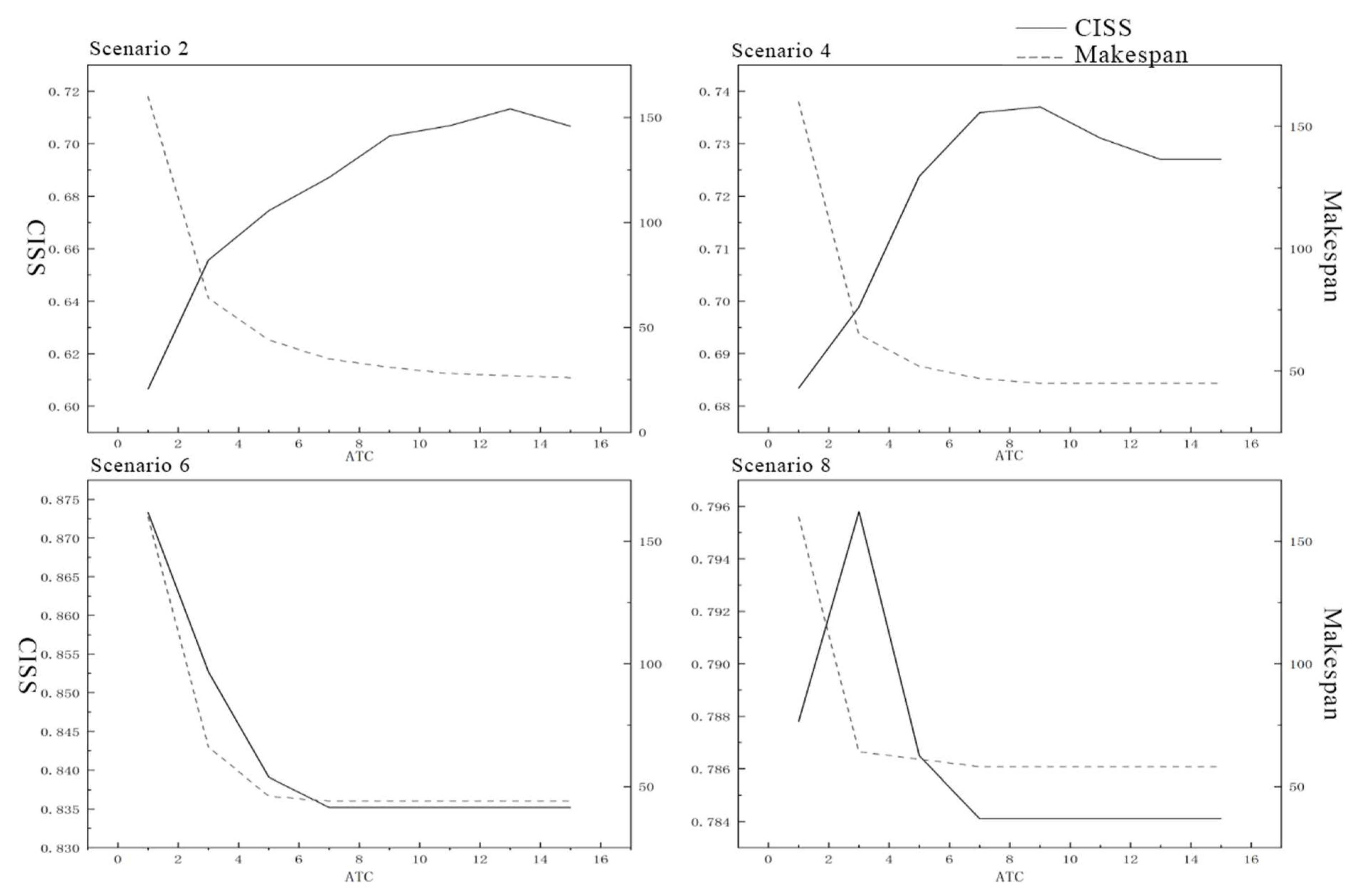
5.2.3. Analysis of TC Revision Capability
5.2.4. Analysis of Standard Citation Network Types
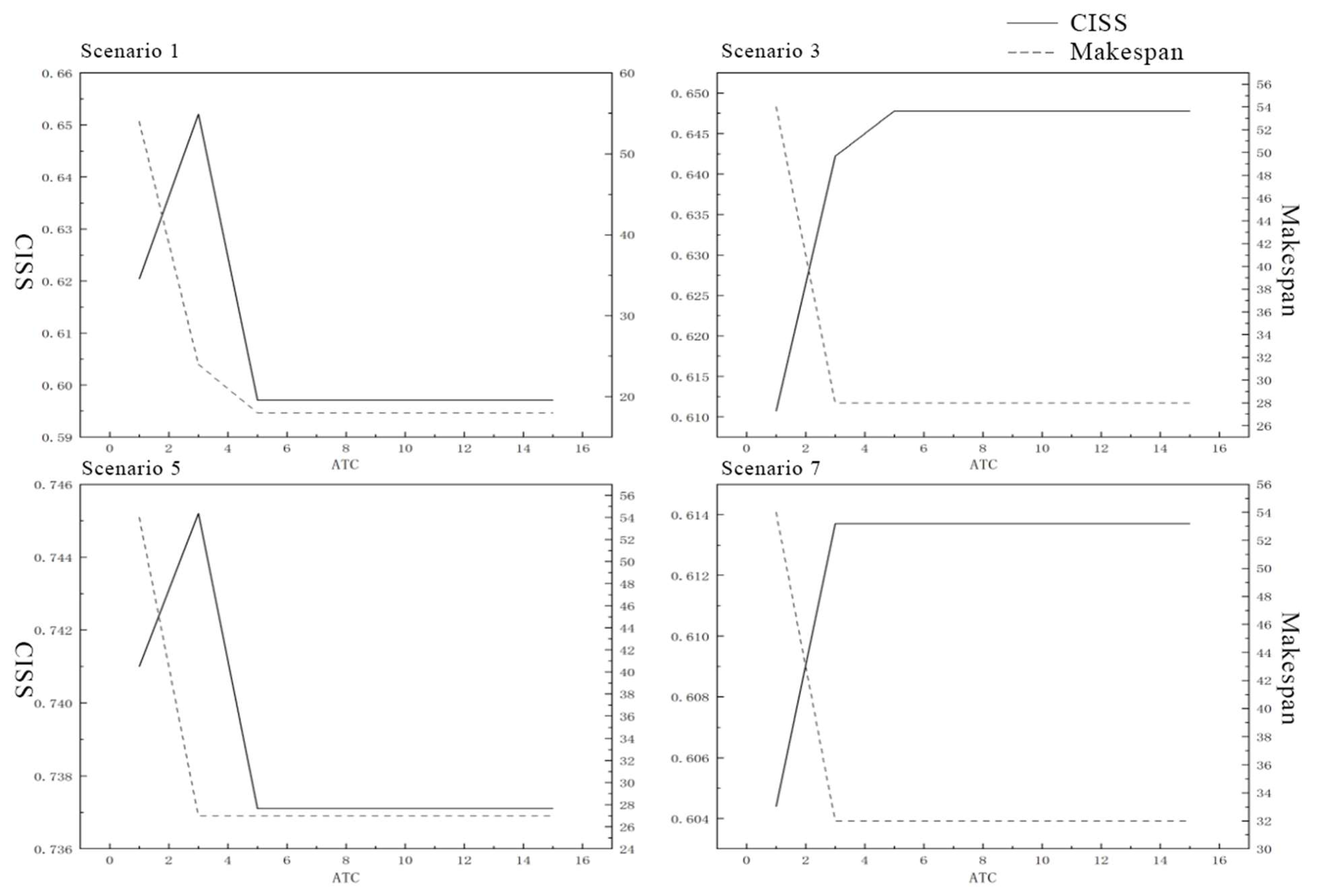
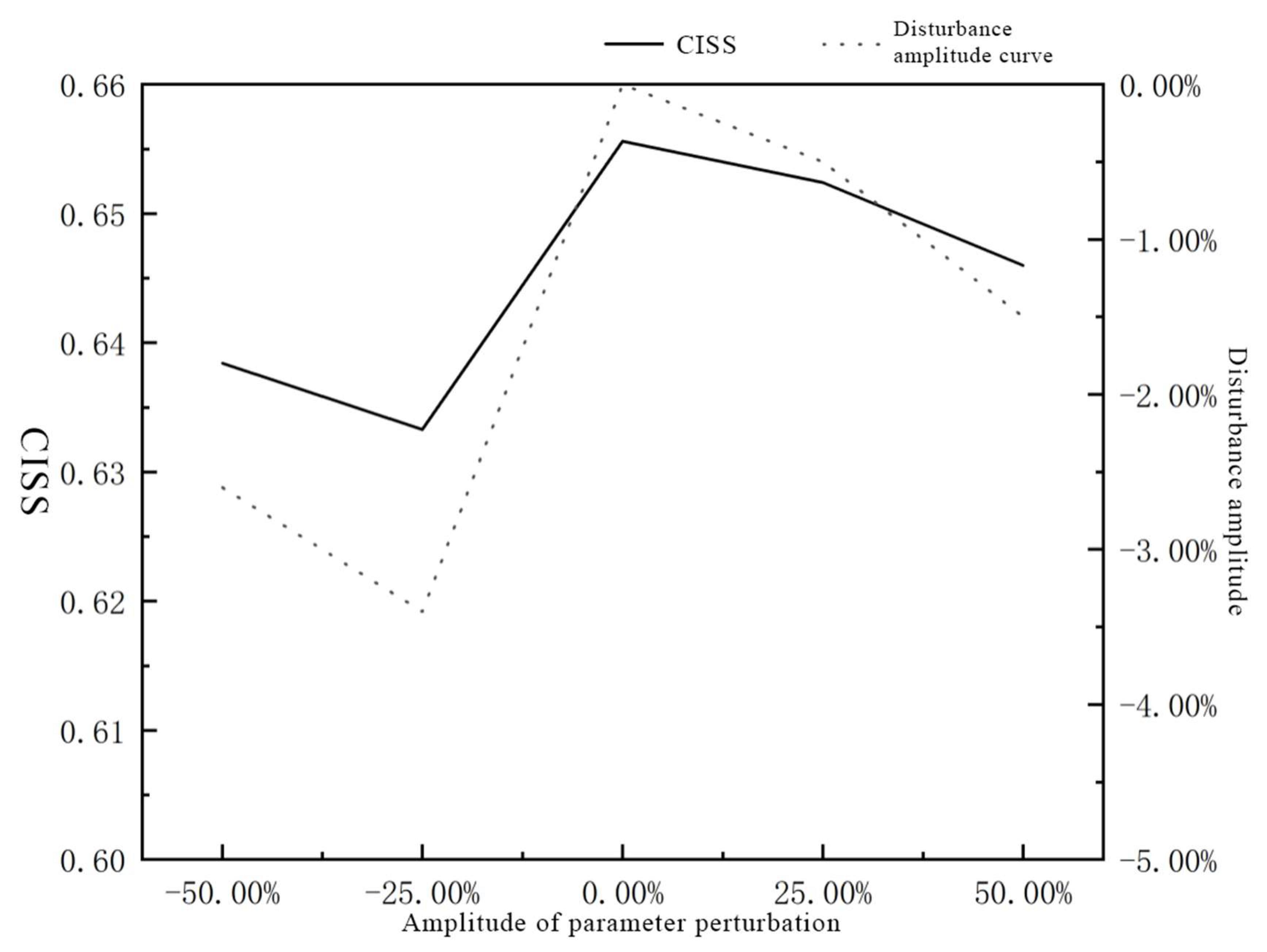
5.2.5. Parameter Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Grillo, F.; Wiegmann, P.M.; de Vries, H.J.; Bekkers, R.; Tasselli, S.; Yousefi, A.; Van De Kaa, G. Standardization: Research trends, current debates, and interdisciplinarity. Acad. Manag. Ann. 2024, 18, 788–830. [Google Scholar] [CrossRef]
- Moon, S.; Lee, H. Exploring Standard Dynamics in Electronics Industry: Focusing on Influencing Factors and Revision of IEC Standards. IEEE Trans. Eng. Manage. 2022, 69, 1365–1377. [Google Scholar] [CrossRef]
- ISO/IEC. Public Policy Use and Citation of ISO and IEC Standards; International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
- Wei, Y.; Chen, L.; Qi, Y.; Wang, C.; Li, F.; Wang, H.; Chen, F. A complex network method in criticality evaluation of air quality standards. Sustainability 2019, 11, 3920. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, F.; Xue, H.; Wang, L. Research on structural dynamics in Chinese automobile standard citation network. Neural Comput. Appl. 2020, 32, 31–39. [Google Scholar] [CrossRef]
- Blazewicz, J.; Lenstra, J.K.; Kan, A.H.G.R. Scheduling subject to resource constraints: Classification and complexity. Discret. Appl. Math. 1983, 5, 11–24. [Google Scholar] [CrossRef]
- Botzem, S.; Dobusch, L. Standardization cycles: A process perspective on the formation and diffusion of transnational standards. Organ. Stud. 2012, 33, 737–762. [Google Scholar] [CrossRef]
- Pritsker, A.A.B.; Waiters, L.J.; Wolfe, P.M. Multiproject scheduling with limited resources: A zero-one programming approach. Manag. Sci. 1969, 6, 93–127. [Google Scholar] [CrossRef]
- Bofill, M.; Coll, J.; Suy, J.; Villaret, M. SMT encodings for Resource-Constrained Project Scheduling Problems. Comput. Ind. Eng. 2020, 149, 106777. [Google Scholar] [CrossRef]
- Sadeghloo, M.; Emami, S.; Divsalar, A. A Benders decomposition algorithm for the multi-mode resource-constrained multi-project scheduling problem with uncertainty. Ann. Oper. Res. 2024, 339, 1637–1677. [Google Scholar] [CrossRef]
- Chen, H.J.; Li, X.Y.; Gao, L. A surrogate-assisted dual-tree genetic programming framework for dynamic resource constrained multi-project scheduling problem. Int. J. Prod. Res. 2024, 62, 5631–5653. [Google Scholar] [CrossRef]
- Mao, H.; Yuan, J.; Mao, Y.; Zhang, S. Efficient Priority Rules for Resource Allocation of Stochastic Decentralized Multi-Project Scheduling Problem. IEEE Access 2024, 12, 112729–112741. [Google Scholar] [CrossRef]
- Yu, Y.; Xu, Z.; Zhao, S. A Two-Stage Algorithm Based on 12 Priority Rules for the Stochastic Distributed Resource-Constrained Multi-Project Scheduling Problem With Multi-Skilled Staff. IEEE Access 2023, 11, 29554–29565. [Google Scholar] [CrossRef]
- Hu, X.; Li, J.; Li, F.; Wang, J.; Wang, Y. Priority Rule-Based Heuristics for Distributed Multi-Project Scheduling Considering Global Resource Failures. Oper. Res. Soc. 2025, 1–20. [Google Scholar] [CrossRef]
- Ellinas, C. The domino effect: An empirical exposition of systemic risk across project networks. Prod. Oper. Manag. 2019, 28, 63–81. [Google Scholar] [CrossRef]
- Shin, D.H.; Qian, D.; Zhang, J. Cascading effects in interdependent networks. IEEE Netw. 2014, 28, 82–87. [Google Scholar] [CrossRef]
- Klimek, M.; Lebkowski, P. Robustness of schedules for project scheduling problem with cash flow optimisation. Bull. Pol. Acad. Sci. Tech. Sci. 2013, 61, 1005–1015. [Google Scholar] [CrossRef][Green Version]
- Peng, W.; Yu, D.; Lin, J. Resource-Constrained Multi-Project Reactive Scheduling Problem With New Project Arrival. IEEE Access 2023, 11, 64370–64382. [Google Scholar] [CrossRef]
- Davari, M.; Demeulemeester, E. The Proactive and Reactive Resource-Constrained Project Scheduling Problem. J. Sched. 2019, 22, 211–237. [Google Scholar] [CrossRef]
- Wang, X.; Leus, R.; Creemers, S.; Chen, Q.; Mao, M. A CTMDP-based exact method for RCPSP with uncertain activity durations and rework. In Proceedings of the OR2017 Conference—The Annual International Conference of the Germ-An Operations Research Society (GOR), Berlin, Germany, 26 May 2018. [Google Scholar] [CrossRef]
- Zhu, H.; Lu, Z.; Lu, C.; Ren, Y. Modeling and algorithm for resource-constrained multi-project scheduling problem based on detection and rework. Assem. Autom. 2021, 41, 174–186. [Google Scholar] [CrossRef]
- Hazır, Ö.; Ulusoy, G. A classification and review of approaches and methods for modeling uncertainty in projects. Int. J. Prod. Econ. 2020, 223, 107522. [Google Scholar] [CrossRef]
- Akkan, C. Improving schedule stability in single-machine rescheduling for new operation insertion. Comput. Oper. Res. 2015, 64, 198–209. [Google Scholar] [CrossRef]
- Rahmani, D.; Ramezanian, R. A Stable Reactive Approach in Dynamic Flexible Flow Shop Scheduling With Unexpected Disruptions: A Case Study. Comput. Ind. Eng. 2016, 98, 360–372. [Google Scholar] [CrossRef]
- Roson, J.; Ksiek-Nowak, M.; Nowak, P. Schedules Optimization With the Use of Value Engineering and NPV Maximization. Sustainability 2020, 12, 7454. [Google Scholar] [CrossRef]
- Szwarcfiter, C.; Herer, Y.T.; Shtub, A. Project scheduling in a lean environment to maximize value and minimize overruns. J. Sched. 2022, 25, 177–190. [Google Scholar] [CrossRef]
- Szwarcfiter, C.; Herer, Y.T.; Shtub, A. Balancing project schedule, cost, and Value under Uncertainty: A reinforcement learning approach. Sustainability 2023, 16, 395. [Google Scholar] [CrossRef]
- Balouka, N.; Cohen, I.; Shtub, A. Extending the multimode resource-constrained project scheduling problem by including value considerations. IEEE Trans. Eng. Manag. 2016, 63, 4–15. [Google Scholar] [CrossRef]
- Prabakaran, K.; Ganesan, K. Fuzzy Hungarian Method for Solving Intuitionistic Fuzzy Travelling Salesman Problem. J. Phys. Conf. Ser. 2018, 1000, 012008. [Google Scholar] [CrossRef]
- Pongchairerks, P. A self-tuning PSO for job-shop scheduling problems. Int. J. Oper. Res. 2014, 19, 96–113. [Google Scholar] [CrossRef]
- Franco, E.G.; Zurita, F.L.T.; Delgadillo, G.M. A genetic algorithm for the resource constrained project scheduling problem (RCPSP). Rev. Investig. Desarro. 2007, 78, 1101–1114. [Google Scholar] [CrossRef][Green Version]
- Chen, W.N.; Tan, D.Z. Set-Based Discrete Particle Swarm Optimization and Its Applications: A Survey. Front. Comput. Sci. 2018, 12, 203–216. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Zhang, H.Y.; Liu, H.J.; Li, L.Y. Research on a kind of assembly sequence planning based on immune algorithm and particle swarm optimization algorithm. Int. J. Adv. Manuf. Technol. 2014, 71, 795–808. [Google Scholar] [CrossRef]
- Yousefzadeh, H.R.; Tirkolaee, E.B.; Kiani, F. A Novel Solution Approach Based on Dominance Evaluation Measure for Project Scheduling in Multi-Project Environments. Systems 2024, 12, 476. [Google Scholar] [CrossRef]
- Li, H.-R.; Gao, Y.-L. Particle Swarm Optimization Algorithm With Exponent Decreasing Inertia Weight and Stochastic Mutation. In Proceedings of the Second International Conference on Information and Computing Science, Manchester, UK, 21–22 May 2009; Volume 1, pp. 66–69. [Google Scholar] [CrossRef]
- Borowska, B. Nonlinear Inertia Weight in Particle Swarm Optimization. In Proceedings of the 12th International Scientific and Technical Conference on Computer Sciences and Information Technologies (CSIT), Lviv, Ukraine, 5–8 September 2017; pp. 296–299. [Google Scholar] [CrossRef]
- Nakamura, R.; Ohsaki, H. On the Effect of Scale-Free Structure of Network Topology on Performance of Content-Centric Networking. In Proceedings of the 2017 IEEE 41st Annual Computer Software and Applications Conference (COMPSAC), Turin, Italy, 4–8 July 2017; pp. 686–689. [Google Scholar] [CrossRef]
- Fujiwara, I.; Koibuchi, M.; Matsutani, H.; Casanova, H. Swap-And-Randomize: A Method for Building Low-Latency HPC Interconnects. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 2051–2060. [Google Scholar] [CrossRef]




| Index and sets | Index of standards, ; | |
| Index of time, ; | ||
| The set of normative references of standard ; | ||
| Parameters | Number of standards constituting the citation network; | |
| Standards citation relationship Matrix; | ||
| The upper bound on the duration of the entire revision process, spanning from the revision of the first standard to the implementation of the last revised standard; | ||
| Revision duration of standard ; | ||
| Implementation transition period of standard , which starts from the revision completion time point to the suggested implementation time point; | ||
| Upper capacity limit of TCs for concurrent standard revision; | ||
| Decision variables | Start time of standard revision; | |
| Other variables | Completion time of standard revision; | |
| Implementation time of the new version of standard ; | ||
| Version number of standard at time ; | ||
| 0/1 variable that equals 1 if standard is in a revision state at time , 0 otherwise; | ||
| 0/1 variable that equals 1 if standard and have identical version numbers at time t, 0 otherwise; | ||
| 0/1 variable that equals 1 if standard references standard , 0 otherwise; | ||
| 0/1 variable that equals 1 if standard requires revision after its normative reference standard is revised, 0 otherwise; | ||
| average Coordination Index of Standards System. |
| Standard Number | Number | Referenced Standard | Revised Duration | Implementation Transition Period |
|---|---|---|---|---|
| GB/T39267-2020 | 1 | None | 2 | 3 |
| GB/T39268-2020 | 2 | 1 | 8 | 5 |
| GB/T39396.1-2020 | 3 | 1 | 4 | 2 |
| GB/T39396.2-2020 | 4 | 1 | 6 | 4 |
| GB/T39397.1-2020 | 5 | 1 | 3 | 3 |
| GB/T39397.2-2020 | 6 | 1, 5 | 8 | 2 |
| GB/T39398-2020 | 7 | 1 | 5 | 6 |
| GB/T39399-2020 | 8 | 1 | 9 | 8 |
| GB/T39409-2020 | 9 | 1 | 2 | 6 |
| GB/T39410-2020 | 10 | 1, 2 | 7 | 2 |
| GB/T39411-2020 | 11 | 1 | 9 | 2 |
| GB/T39414.1-2020 | 12 | 1 | 2 | 3 |
| GB/T39414.2-2020 | 13 | 1 | 6 | 4 |
| GB/T39414.3-2020 | 14 | 1 | 10 | 3 |
| GB/T39414.4-2020 | 15 | 1 | 6 | 1 |
| GB/T39413-2020 | 16 | 1, 12, 13, 14, 15 | 5 | 2 |
| GB/T39472-2020 | 17 | 1 | 3 | 3 |
| GB/T39473-2020 | 18 | 1, 7, 12, 13, 14, 15 | 7 | 4 |
| GB/T39723-2020 | 19 | 1 | 2 | 3 |
| GB/T39772.1-2021 | 20 | 1, 19 | 7 | 2 |
| GB/T39772.2-2021 | 21 | 1, 19, 20 | 2 | 2 |
| GB/T39721-2021 | 22 | 1, 20, 21 | 3 | 3 |
| GB/T39783-2021 | 23 | 1 | 3 | 2 |
| GB/T39787-2021 | 24 | 1 | 7 | 3 |
| GB/T42575-2023 | 25 | 1 | 8 | 3 |
| GB/T42576-2023 | 26 | 1 | 3 | 3 |
| GB/T42577-2023 | 27 | 1, 6 | 7 | 2 |
| GB/T42579-2023 | 28 | 1, 12, 13, 14, 15 | 2 | 3 |
| GB/T42832.1-2023 | 29 | 1 | 7 | 4 |
| GB/T42833-2023 | 30 | 1, 29 | 7 | 2 |
| Model | Makespan | |
|---|---|---|
| Modeling with the goal of the shortest makespan | 55 | 0.5841 |
| Modeling with the goal of maximum | 64 | 0.6556 |
| Number of Reference Relationships That Need to Be Revised | Makespan | |
|---|---|---|
| 33% of citations | 50 | 0.8401 |
| 67% of citations | 42 | 0.7390 |
| 100% of citations | 64 | 0.6556 |
| Parameter | Parameter Value Setting | |
|---|---|---|
| Network scale | 10-Low scale | 30-Large scale |
| Network type | Scale-free network structure | Random network structure |
| Network average degree | 1.5-Low average degree | 1.5-High average degree |
| Scenario Setting | |
|---|---|
| Scenario 1 | Scale-free network-small—Low scale—Low average degree |
| Scenario 2 | Scale-free network-small—Large scale—Low average degree |
| Scenario 3 | Scale-free network-small—Low scale—High average degree |
| Scenario 4 | Scale-free network-small—Large scale—High average degree |
| Scenario 5 | Random network structure—Low scale—Low average degree |
| Scenario 6 | Random network structure—Large scale—Low average degree |
| Scenario 7 | Random network structure—Low scale—High average degree |
| Scenario 8 | Random network structure—Large scale—High average degree |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xu, D.; Zhou, L.; Li, Z. Standard Revision Project Scheduling Problem Considering Coordination Degree of Standards Systems. Systems 2025, 13, 685. https://doi.org/10.3390/systems13080685
Wang Y, Xu D, Zhou L, Li Z. Standard Revision Project Scheduling Problem Considering Coordination Degree of Standards Systems. Systems. 2025; 13(8):685. https://doi.org/10.3390/systems13080685
Chicago/Turabian StyleWang, Yunping, Dan Xu, Lijun Zhou, and Zhe Li. 2025. "Standard Revision Project Scheduling Problem Considering Coordination Degree of Standards Systems" Systems 13, no. 8: 685. https://doi.org/10.3390/systems13080685
APA StyleWang, Y., Xu, D., Zhou, L., & Li, Z. (2025). Standard Revision Project Scheduling Problem Considering Coordination Degree of Standards Systems. Systems, 13(8), 685. https://doi.org/10.3390/systems13080685






