A System Dynamics-Based Hybrid Digital Twin Model for Driving Green Manufacturing
Abstract
1. Introduction
2. Literature Review
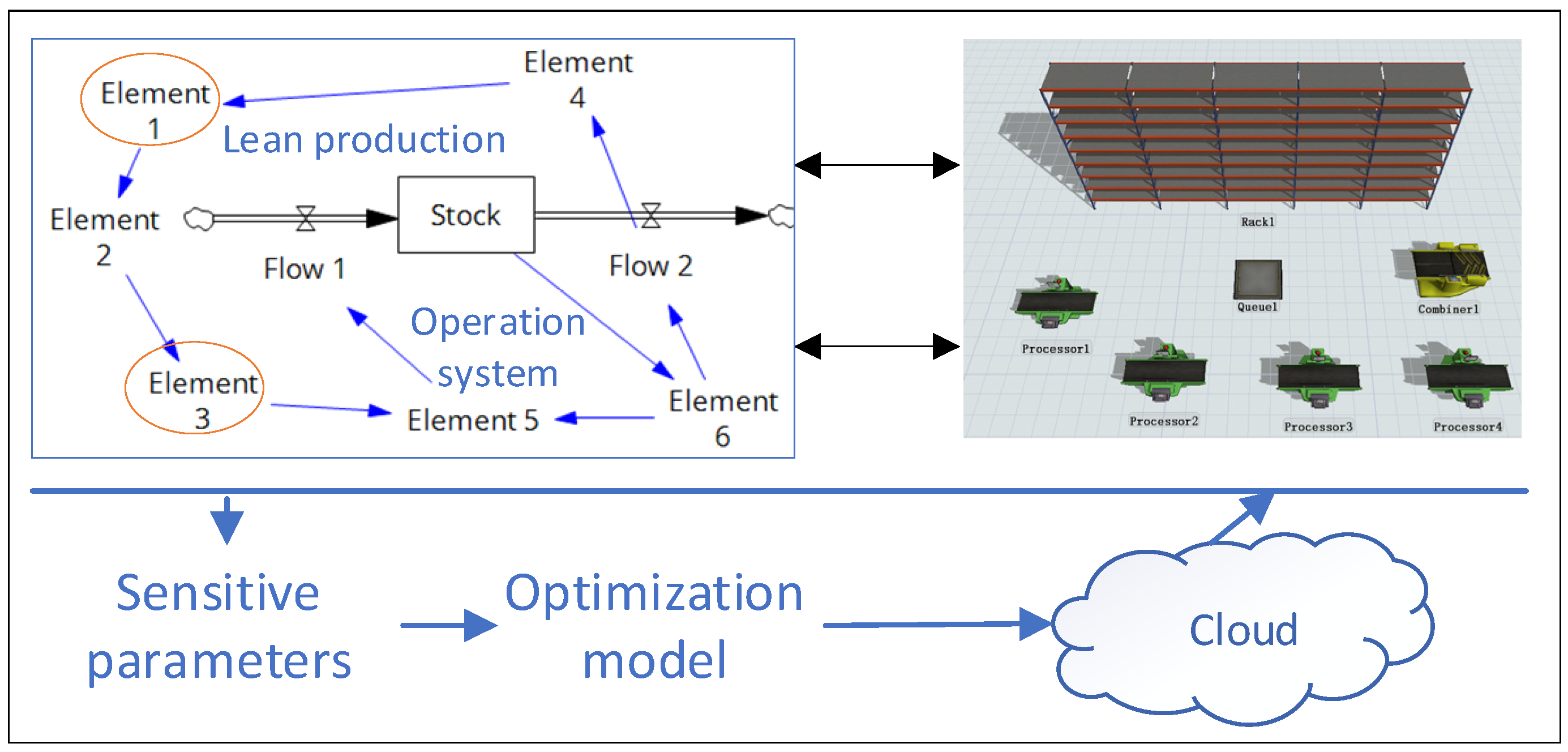
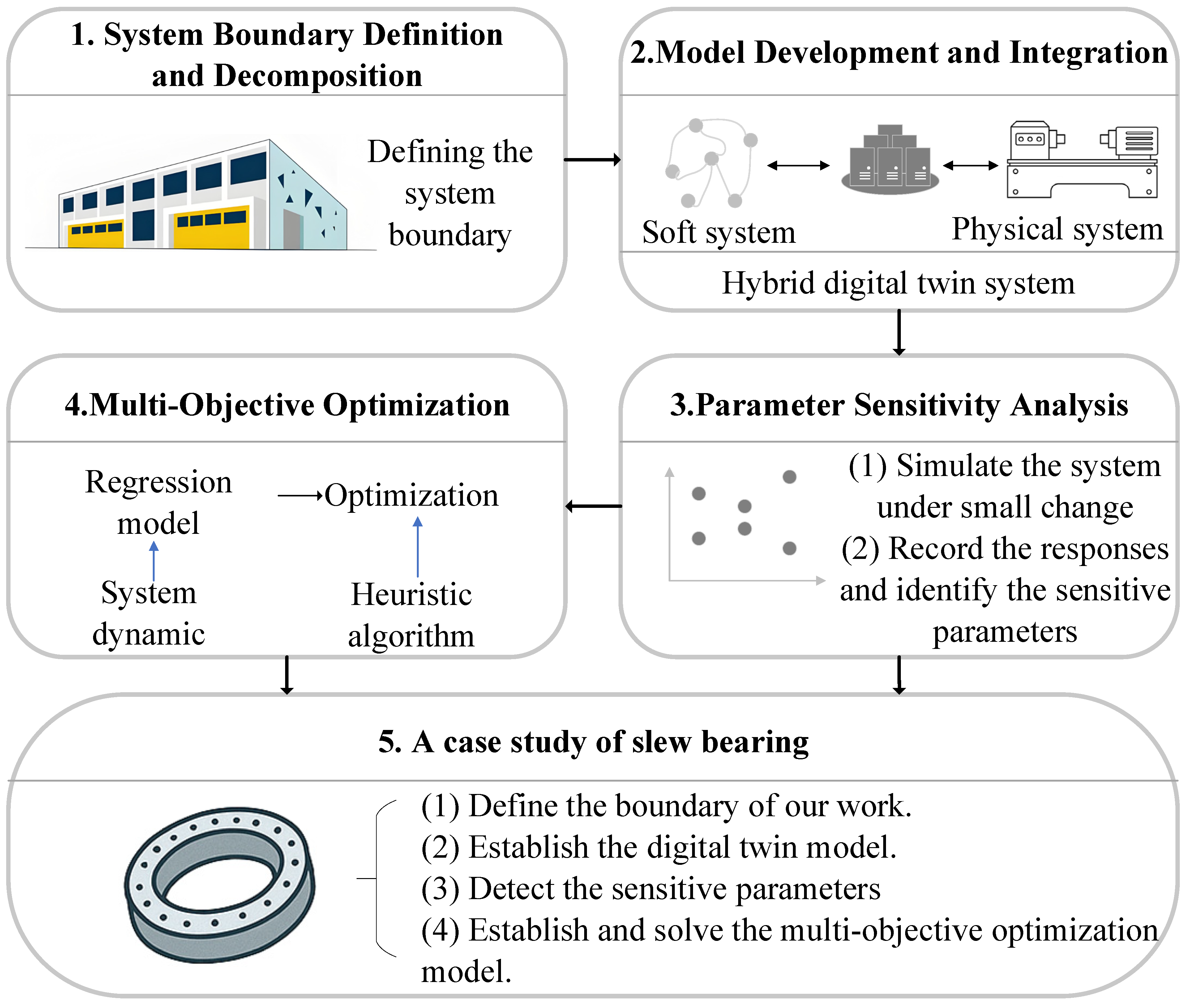
3. The Operation of the Hybrid Digital Twin Model
- (1)
- Physical System Layer: Captures real-time equipment states and material flows via IoT sensors;
- (2)
- Soft System Layer: Embeds system dynamics (SD) to model human/organizational factors (e.g., operator behavior, mutual influence) and lean principles (e.g., SMED, 5S);
- (3)
- Data Integration Layer: A centralized database synchronizes physical simulations (FlexSim 22) and SD-based soft system variables, allowing dynamic feedback between operational decisions and environmental outcomes.
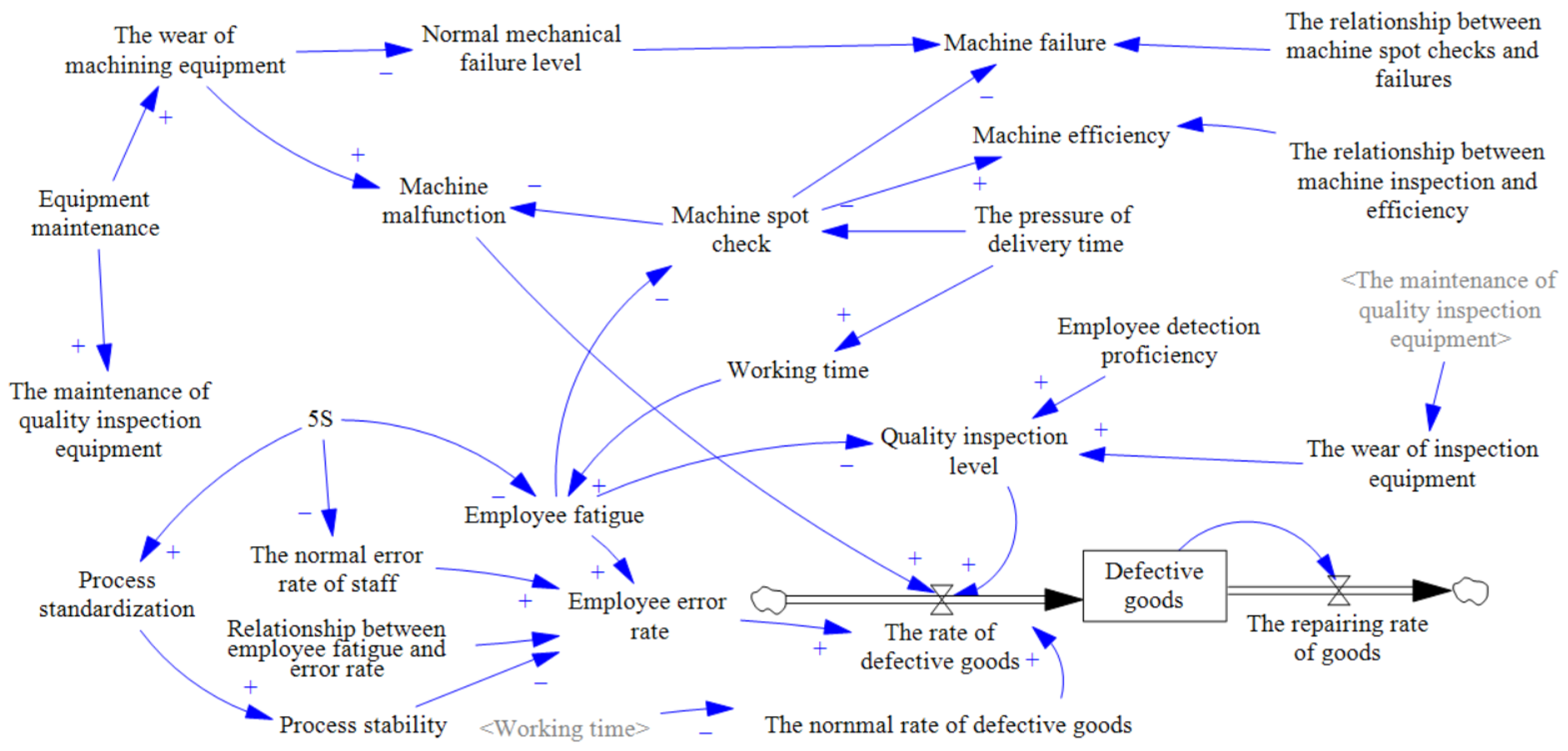
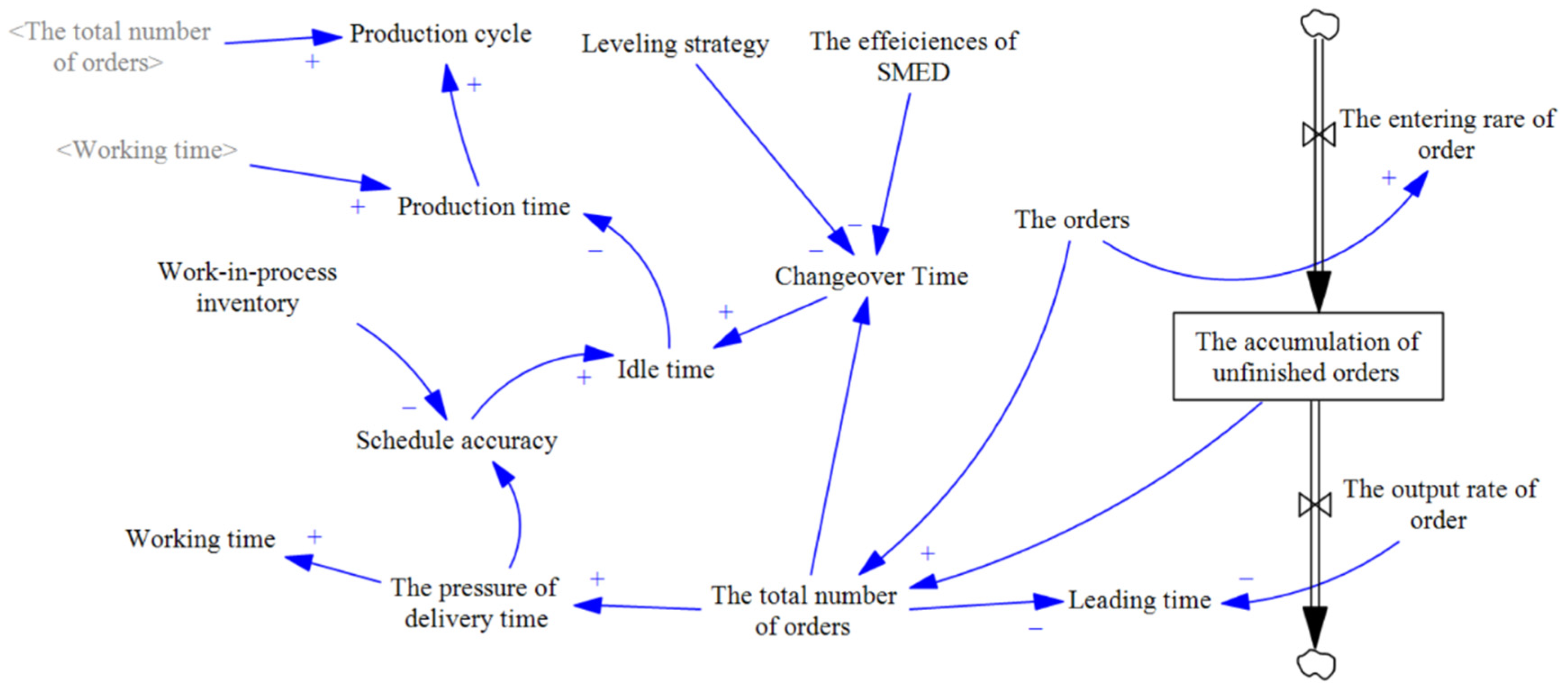
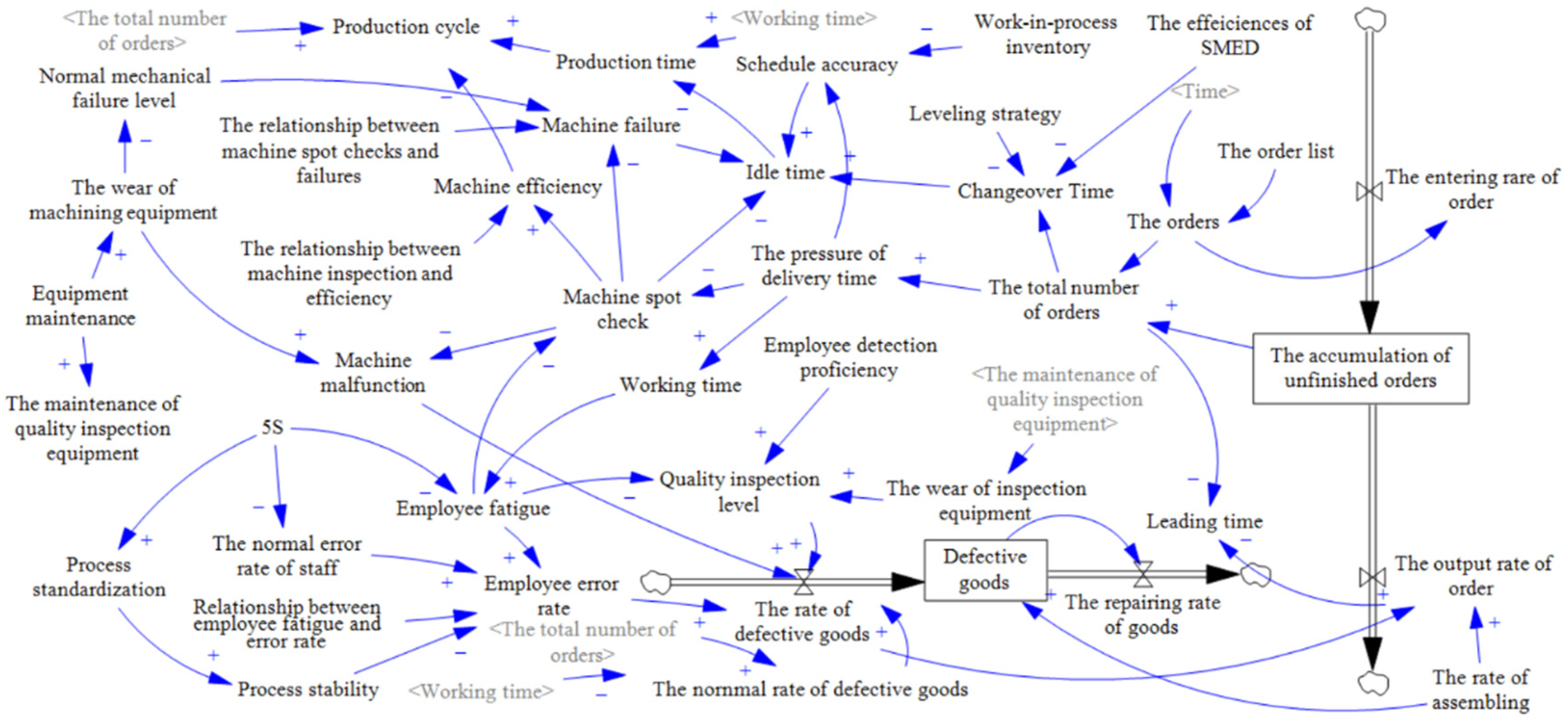
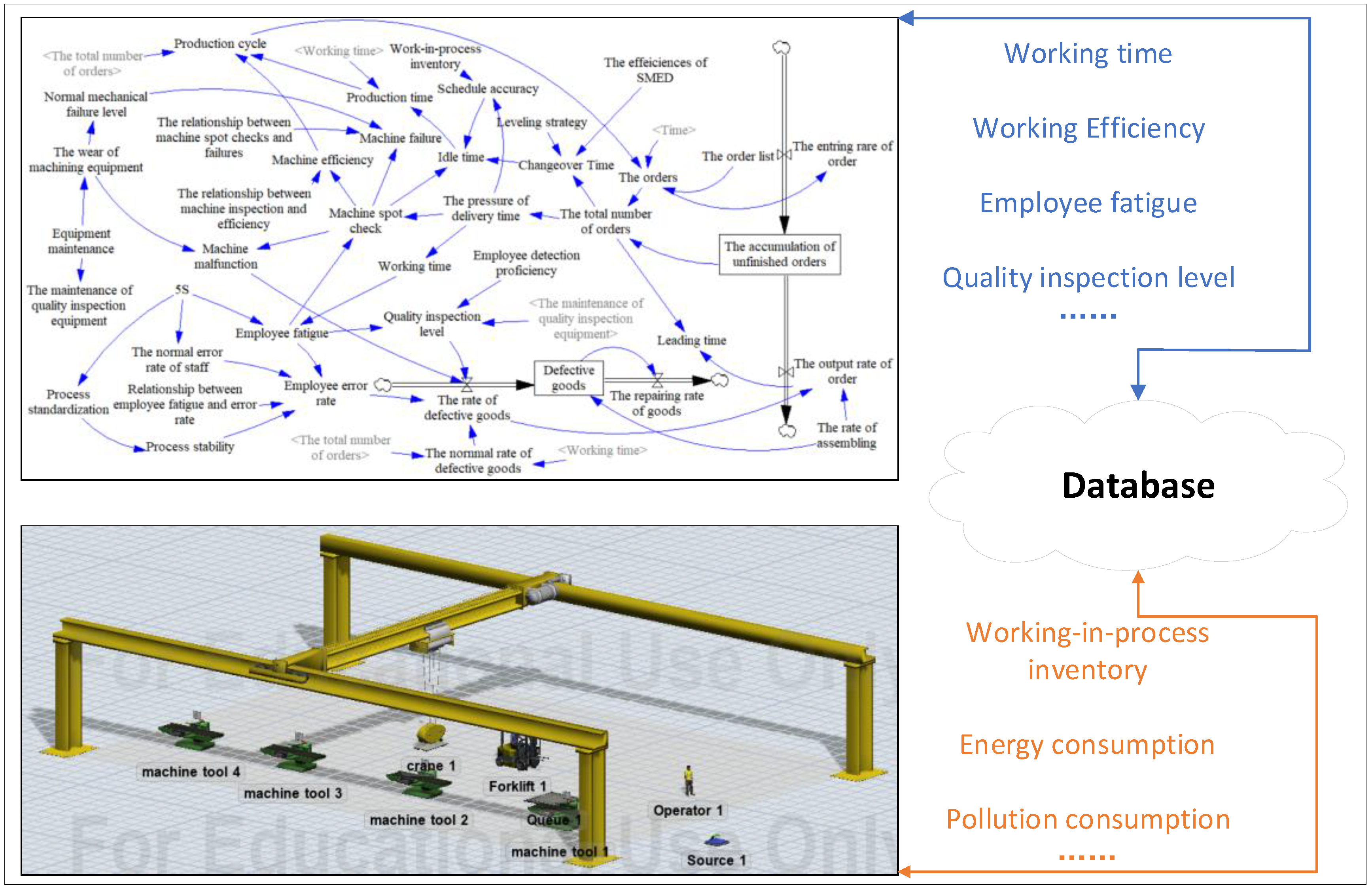
3.1. The Establishment of the Soft System
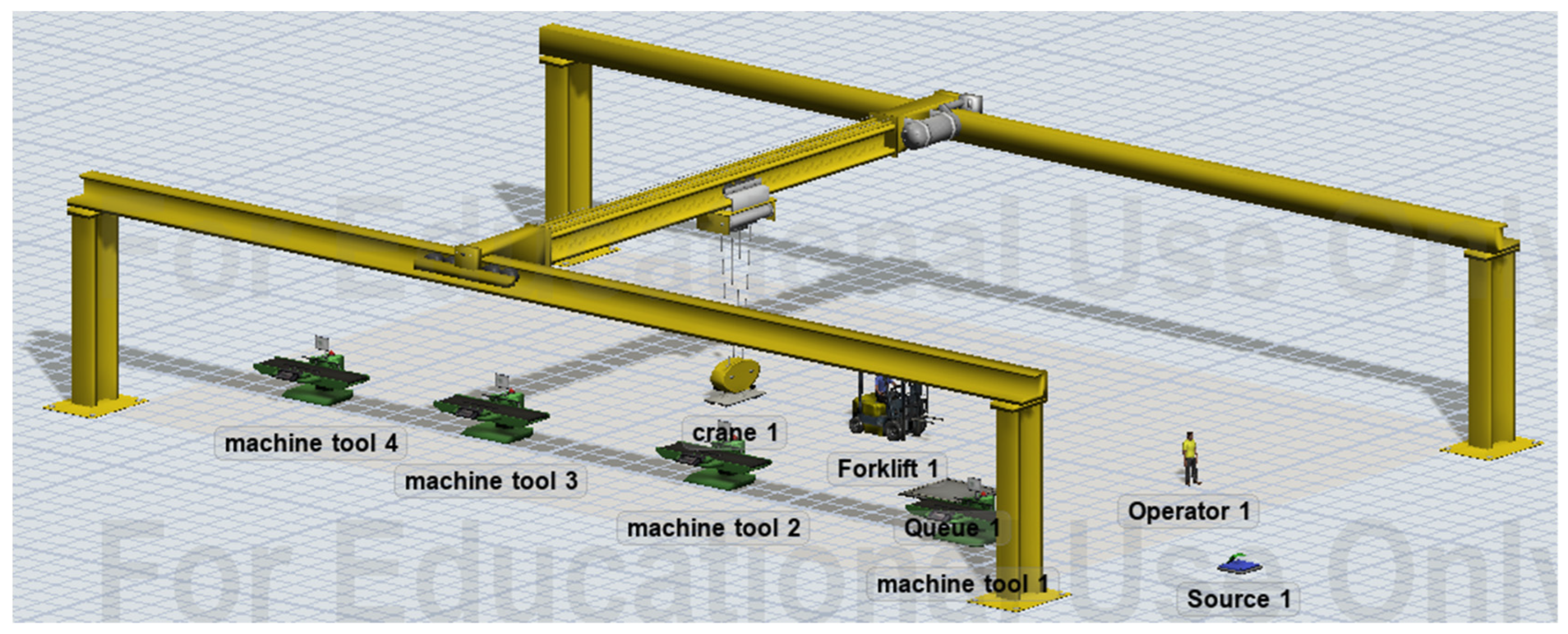
3.2. The Establishment of the Physical System
3.3. The Combinations of Soft Systems and Physical Systems
4. The Sensitive Parameters-Based Multi-Objective Scheduling Model
4.1. Establishing the Optimization Model Based on the Parameters
4.2. The Solution of the Optimization Model
5. Research Design
6. A Case Study About Slewing Bearings
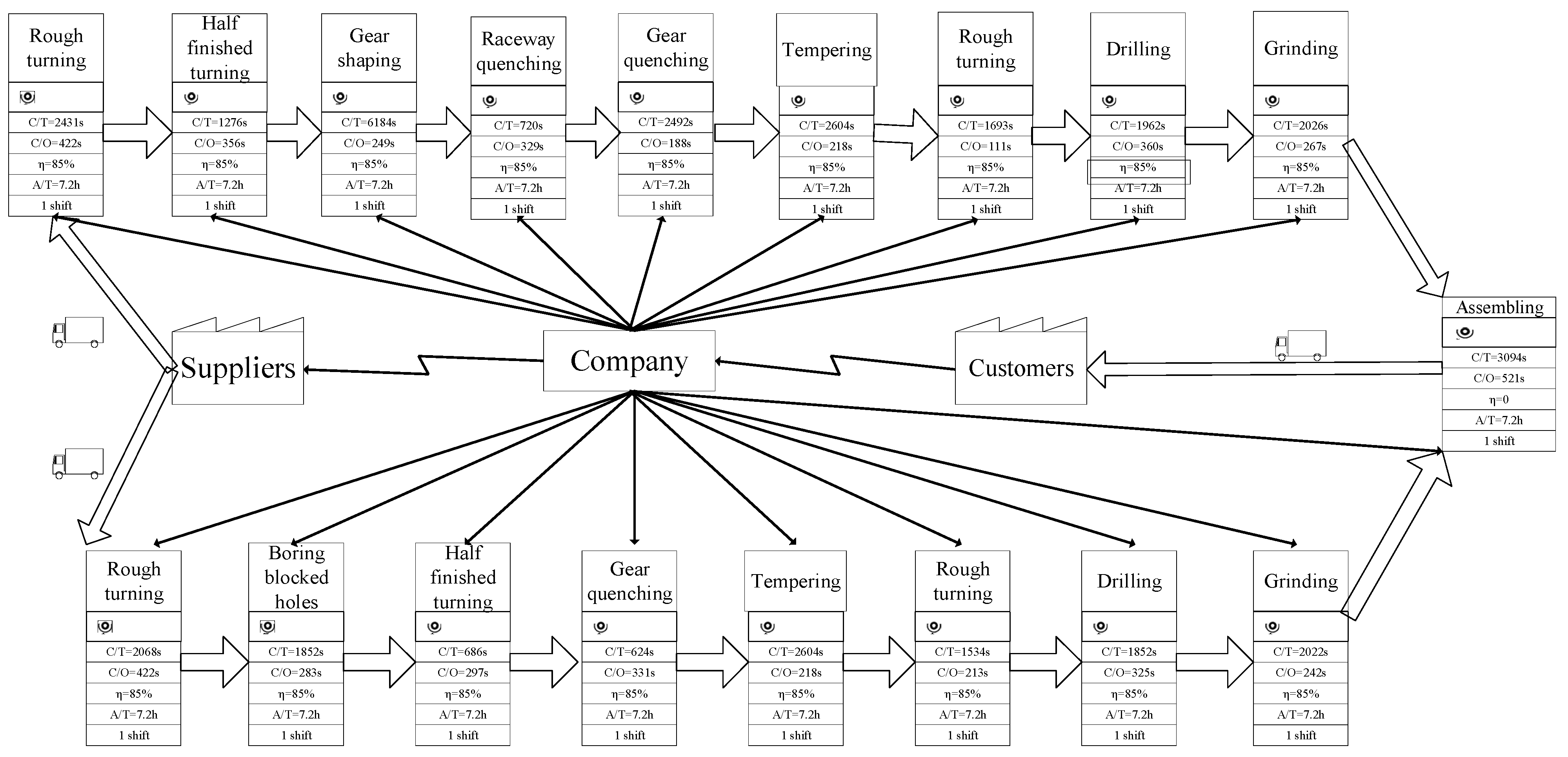
6.1. The Background of the Factory
6.2. The Hybrid Digital Twin Model of the Factory
6.3. The Verification of the Hybrid Digital Twin Model
6.4. The Scheduling Based on the Hybrid Digital Twin Model
6.4.1. The Scheduling Results of Our Study
6.4.2. The Advantages of Our Work
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duran, K.; Canberk, B. Digital Twin Enriched Green Topology Discovery for Next Generation Core Networks. IEEE Trans. Green Commun. Netw. 2023, 7, 1946–1956. [Google Scholar] [CrossRef]
- Ivanov, D. Conceptualisation of a 7-element digital twin framework in supply chain and operations management. Int. J. Prod. Res. 2024, 62, 2220–2232. [Google Scholar] [CrossRef]
- Kumbhar, M.; Ng, A.H.; Bandaru, S. A digital twin based framework for detection, diagnosis, and improvement of throughput bottlenecks. J. Manuf. Syst. 2023, 66, 92–106. [Google Scholar] [CrossRef]
- Jia, W.; Wang, W.; Zhang, Z. From simple digital twin to complex digital twin part II: Multi-scenario applications of digital twin shop floor. Adv. Eng. Inform. 2023, 56, 101915. [Google Scholar] [CrossRef]
- Kim, H.; Ben-Othman, J. Eco-Friendly Low Resource Security Surveillance Framework Toward Green AI Digital Twin. IEEE Commun. Lett. 2022, 27, 377–380. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.; Yang, W.; Shen, C.; Li, J. A digital-twin-based adaptive multi-objective Harris Hawks Optimizer for dynamic hybrid flow green scheduling problem with dynamic events. Appl. Soft Comput. 2023, 143, 110274. [Google Scholar] [CrossRef]
- van Eyk, L.; Heyns, P.S. A framework to define, design and construct digital twins in the mining industry. Comput. Ind. Eng. 2025, 200, 110805. [Google Scholar] [CrossRef]
- Li, D.; Li, J. Big data of enterprise supply chain under green financial system based on digital twin technology. Kybernetes 2024, 53, 543–556. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, H.; Zhang, C. Advancements and challenges of digital twins in industry. Nat. Comput. Sci. 2024, 4, 169–177. [Google Scholar] [CrossRef] [PubMed]
- Javaid, M.; Haleem, A.; Suman, R. Digital Twin applications toward Industry 4.0: A Review. Cogn. Robot. 2023, 3, 71–92. [Google Scholar] [CrossRef]
- Chen, Z.; Surendraarcharyagie, K.; Granland, K.; Chen, C.; Xu, X.; Xiong, Y.; Davies, C.; Tang, Y. Service oriented digital twin for additive manufacturing process. J. Manuf. Syst. 2024, 74, 762–776. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, F.; Wang, J.; Yang, Z.; Huang, Z.; Xue, R. Digital twin for smart manufacturing equipment: Modeling and applications. Int. J. Adv. Manuf. Technol. 2025, 137, 4929–4946. [Google Scholar] [CrossRef]
- Wright, L.; Davidson, S. Digital twins for metrology; metrology for digital twins. Meas. Sci. Technol. 2024, 35, 051001. [Google Scholar] [CrossRef]
- Xia, T.; Sun, H.; Ding, Y.; Han, D.; Qin, W.; Seidelmann, J.; Xi, L. Digital twin-based real-time energy optimization method for production line considering fault disturbances. J. Intell. Manuf. 2025, 36, 569–593. [Google Scholar] [CrossRef]
- Elemure, I.; Dhakal, H.N.; Leseure, M.; Radulovic, J. Integration of Lean Green and Sustainability in Manufacturing: A Review on Current State and Future Perspectives. Sustainability 2023, 15, 10261. [Google Scholar] [CrossRef]
- Porras, J.E.O.; Erquínigo, A.M.B.; Chávez, T.C.C.; Palma, L.M.H.; Torres, R.K.M.; Gomez, O.R.T. Green Lean Six Sigma model for waste reduction of raw material in a nectar manufacturing company of Lima, Peru. J. Ind. Eng. Manag. 2023, 16, 169–185. [Google Scholar] [CrossRef]
- Yadav, V.; Kaswan, M.S.; Gahlot, P.; Duhan, R.K.; Garza-Reyes, J.A.; Rathi, R.; Chaudhary, R.; Yadav, G. Green Lean Six Sigma for sustainability improvement: A systematic review and future research agenda. Int. J. Lean Six Sigma 2023, 14, 759–790. [Google Scholar] [CrossRef]
- Shao, G.; Helu, M. Framework for a digital twin in manufacturing: Scope and requirements. Manuf. Lett. 2020, 24, 105–107. [Google Scholar] [CrossRef] [PubMed]
- Melesse, T.Y.; Di Pasquale, V.; Riemma, S. Digital twin models in industrial operations: A systematic literature review. Procedia Manuf. 2020, 42, 267–272. [Google Scholar] [CrossRef]
- Negri, E.; Fumagalli, L.; Macchi, M. A Review of the Roles of Digital Twin in CPS-based Production Systems. Procedia Manuf. 2017, 11, 939–948. [Google Scholar] [CrossRef]
- Leng, J.; Zhang, H.; Yan, D.; Liu, Q.; Chen, X.; Zhang, D. Digital twin-driven manufacturing cyber-physical system for parallel controlling of smart workshop. J. Ambient. Intell. Humaniz. Comput. 2019, 10, 1155–1166. [Google Scholar] [CrossRef]
- Asad, U.; Khan, M.; Khalid, A.; Lughmani, W.A. Human-Centric Digital Twins in Industry: A Comprehensive Review of Enabling Technologies and Implementation Strategies. Sensors 2023, 23, 3938. [Google Scholar] [CrossRef]
- Ramasubramanian, A.K.; Mathew, R.; Kelly, M.; Hargaden, V.; Papakostas, N. Digital Twin for Human–Robot Collaboration in Manufacturing: Review and Outlook. Appl. Sci. 2022, 12, 4811. [Google Scholar] [CrossRef]
- Hananto, A.L.; Tirta, A.; Herawan, S.G.; Idris, M.; Soudagar, M.E.M.; Djamari, D.W.; Veza, I. Digital Twin and 3D Digital Twin: Concepts, Applications, and Challenges in Industry 4.0 for Digital Twin. Computers 2024, 13, 100. [Google Scholar] [CrossRef]
- Errandonea, I.; Beltrán, S.; Arrizabalaga, S. Digital Twin for maintenance: A literature review. Comput. Ind. 2020, 123, 103316. [Google Scholar] [CrossRef]
- Opoku, D.-G.J.; Perera, S.; Osei-Kyei, R.; Rashidi, M. Digital twin application in the construction industry: A literature review. J. Build. Eng. 2021, 40, 102726. [Google Scholar] [CrossRef]
- Lo, C.; Chen, C.; Zhong, R.Y. A review of digital twin in product design and development. Adv. Eng. Inform. 2021, 48. [Google Scholar] [CrossRef]
- Shahat, E.; Hyun, C.T.; Yeom, C. City digital twin potentials: A review and research agenda. Sustainability 2021, 13, 3386. [Google Scholar] [CrossRef]
- Botín-Sanabria, D.M.; Mihaita, A.-S.; Peimbert-García, R.E.; Ramírez-Moreno, M.A.; Ramírez-Mendoza, R.A.; Lozoya-Santos, J.d.J. Digital Twin Technology Challenges and Applications: A Comprehensive Review. Remote Sens. 2022, 14, 1335. [Google Scholar] [CrossRef]
- Ding, G.; Guo, S.; Wu, X. Dynamic Scheduling Optimization of Production Workshops Based on Digital Twin. Appl. Sci. 2022, 12, 10451. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y. Dynamic scheduling of multi-memory process flexible job shop problem based on digital twin. Comput. Ind. Eng. 2023, 183, 109498. [Google Scholar] [CrossRef]
- Gao, Q.; Liu, J.; Li, H.; Zhuang, C.; Liu, Z. Digital twin-driven dynamic scheduling for the assembly workshop of complex products with workers allocation. Robot. Comput. Manuf. 2024, 89, 102786. [Google Scholar] [CrossRef]
- Forrester, J.W. Industrial dynamics. J. Oper. Res. Soc. 1961, 48, 1037–1041. [Google Scholar] [CrossRef]
- Choi, J.; Moon, S.; Min, S. Digital twin simulation modeling process with system dynamics: An application to naval ship operation. Int. J. Robust Nonlinear Control 2023, 33, 10136–10150. [Google Scholar] [CrossRef]
- Tong, X.; Bao, J.; Tao, F. Co-evolutionary digital twins: A multidimensional dynamic approach to digital engineering. Adv. Eng. Inform. 2024, 61, 102554. [Google Scholar] [CrossRef]
- Wen, J.; Gabrys, B.; Musial, K. Toward Digital Twin Oriented Modeling of Complex Networked Systems and Their Dynamics: A Comprehensive Survey. IEEE Access 2022, 10, 66886–66923. [Google Scholar] [CrossRef]
- Yan, M.-R.; Hong, L.-Y.; Warren, K. Integrated knowledge visualization and the enterprise digital twin system for supporting strategic management decision. Manag. Decis. 2022, 60, 1095–1115. [Google Scholar] [CrossRef]
- Florescu, A.; Barabas, S. Development Trends of Production Systems Through the Integration of Lean Management and Industry 4.0. Appl. Sci. 2022, 12, 4885. [Google Scholar] [CrossRef]
- Buer, S.-V.; Semini, M.; Strandhagen, J.O.; Sgarbossa, F. The complementary effect of lean manufacturing and digitalisation on operational performance. Int. J. Prod. Res. 2021, 59, 1976–1992. [Google Scholar] [CrossRef]
- Bazaz, S.M.; Lohtander, M.; Varis, J. 5-dimensional definition for a manufacturing digital twin. Procedia Manuf. 2019, 38, 1705–1712. [Google Scholar] [CrossRef]

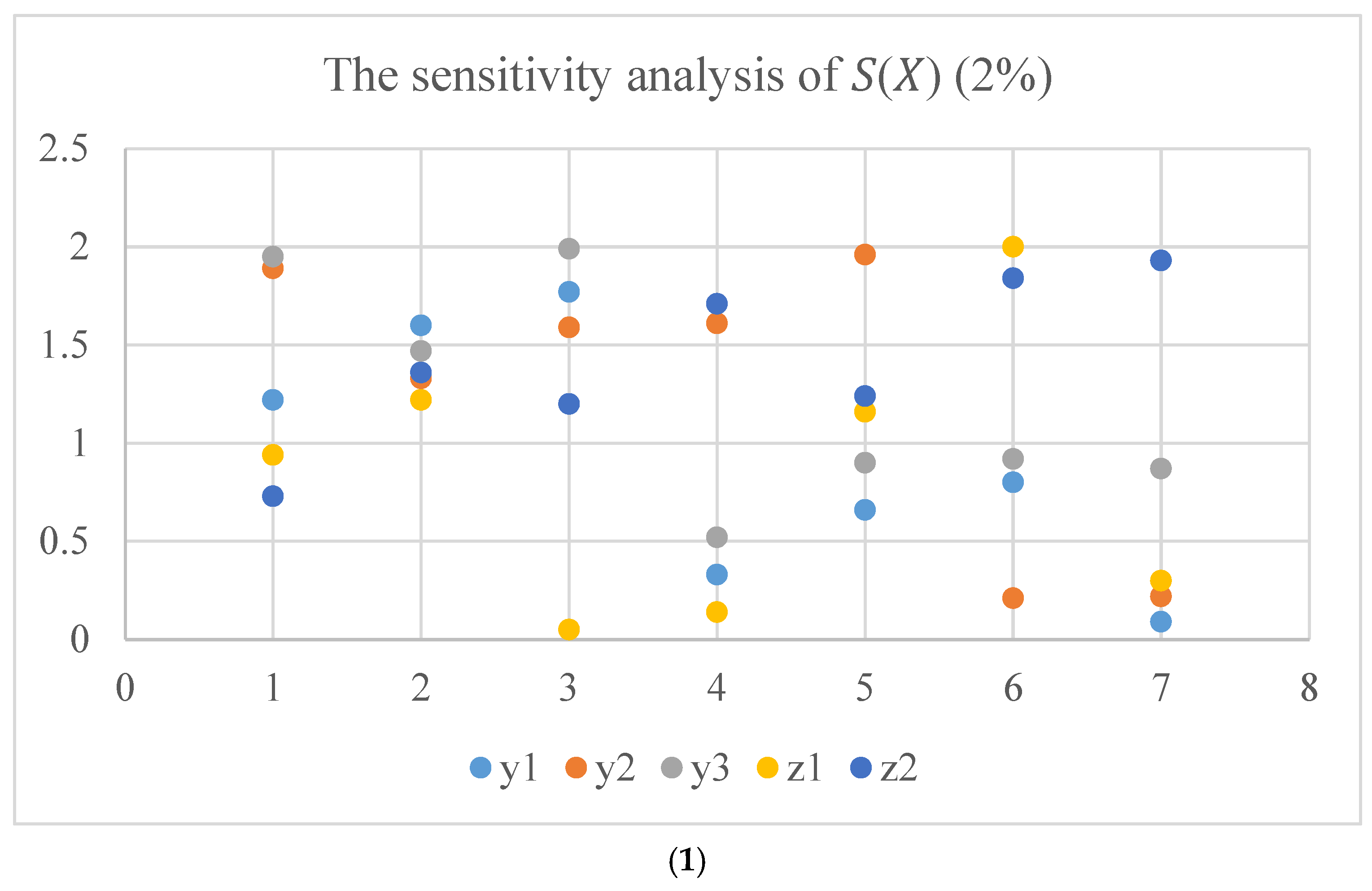

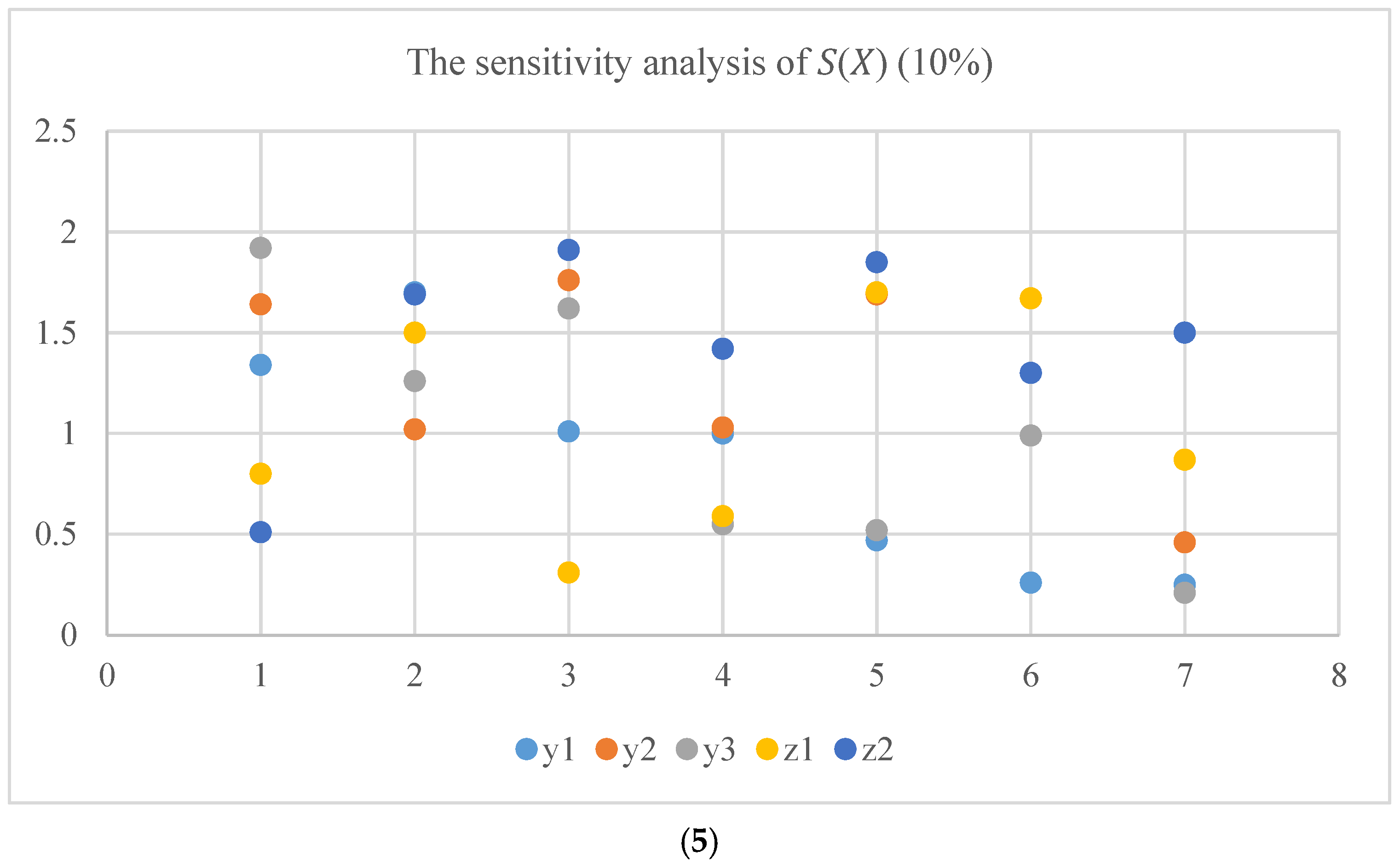
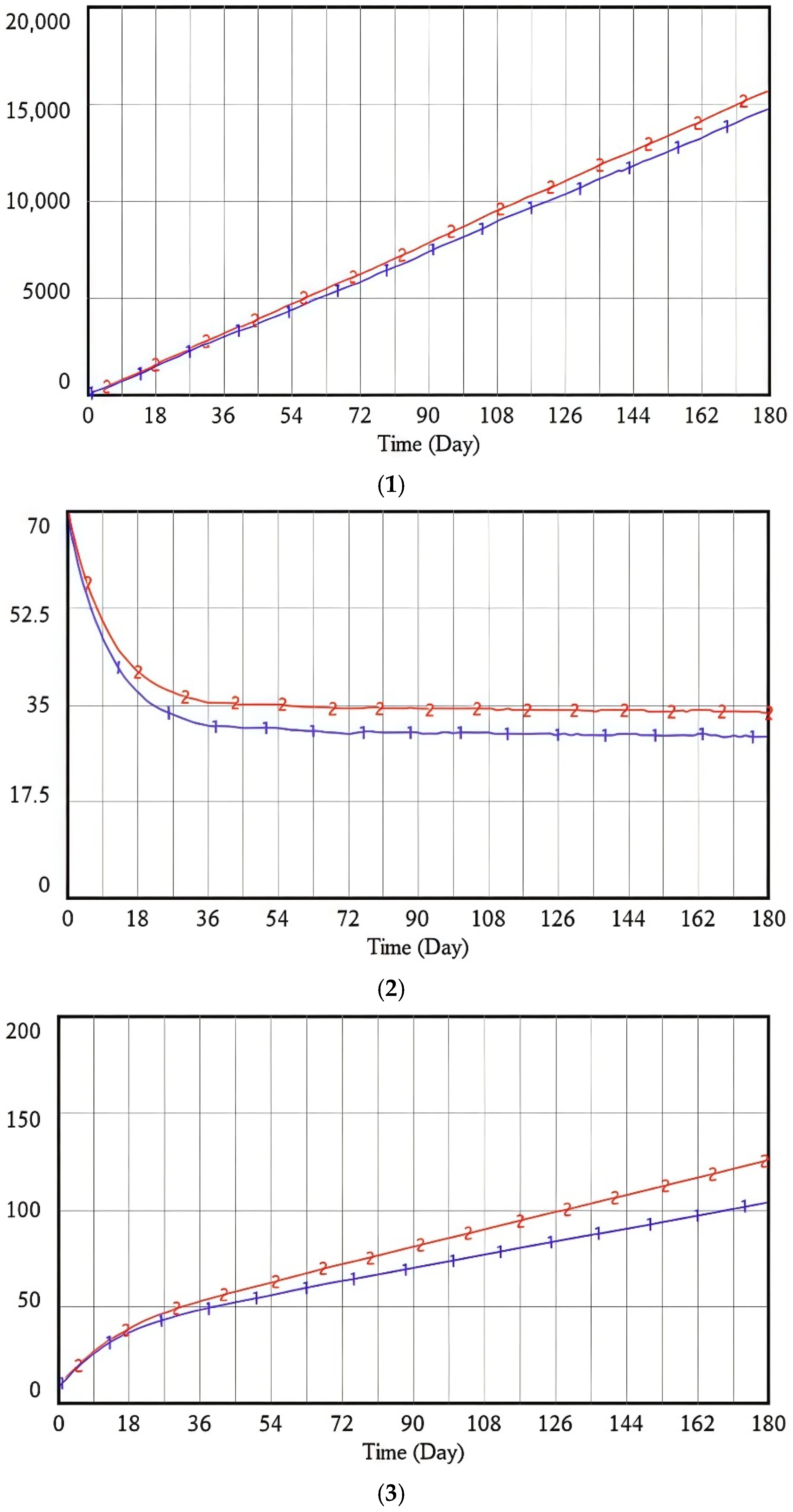

| Name | Meaning |
|---|---|
| The relationship between machine spot checks and failures | Indicating the relationship between the machine spot checks and failure |
| The relationship between machine inspection and efficiency | Indicating the relationship between machine inspection and efficiency |
| Relationship between employee fatigue and error rate | Indicating the relationship between employee fatigue and error rate |
| The Notation | The Formulas |
|---|---|
| The pressure of the delivery time | The total number of orders |
| Machine malfunction | The wear of machining equipment Machine spot check |
| Employee fatigue | Working time 5S |
| Quality inspection level | Employee detection proficiency/Employee fatigue The wear of inspection equipment |
| Employee error rate | The normal error rate of staff Relationship between employee fatigue and error rate-Process stability |
| The rate of defective goods | (Machine malfunction Quality inspection level Employee error rate)/3 The normal rate of defective goods |
| Production time | Working time-Idle time |
| Idle time | Schedule accuracy (Changeover Time Machine spot check Machine failure) |
| Schedule accuracy | The pressure of delivery time Work-in-process inventory |
| Normal mechanical failure level | The wear of machining equipment |
| The accumulation of unfinished orders | The entering rate of order The output rate of order |
| Defective goods | (The rate of defective goods The repairing rate of goods) The rate of assembling |
| Working time | The pressure of delivery time 8 |
| The relationship between machine spot checks and failures | Table function (machine spot checks, failures) |
| The relationship between machine inspection and efficiency | Table function (machine inspection, efficiency) |
| Relationship between employee fatigue and error rate | Table function (employee fatigue, error rate) |
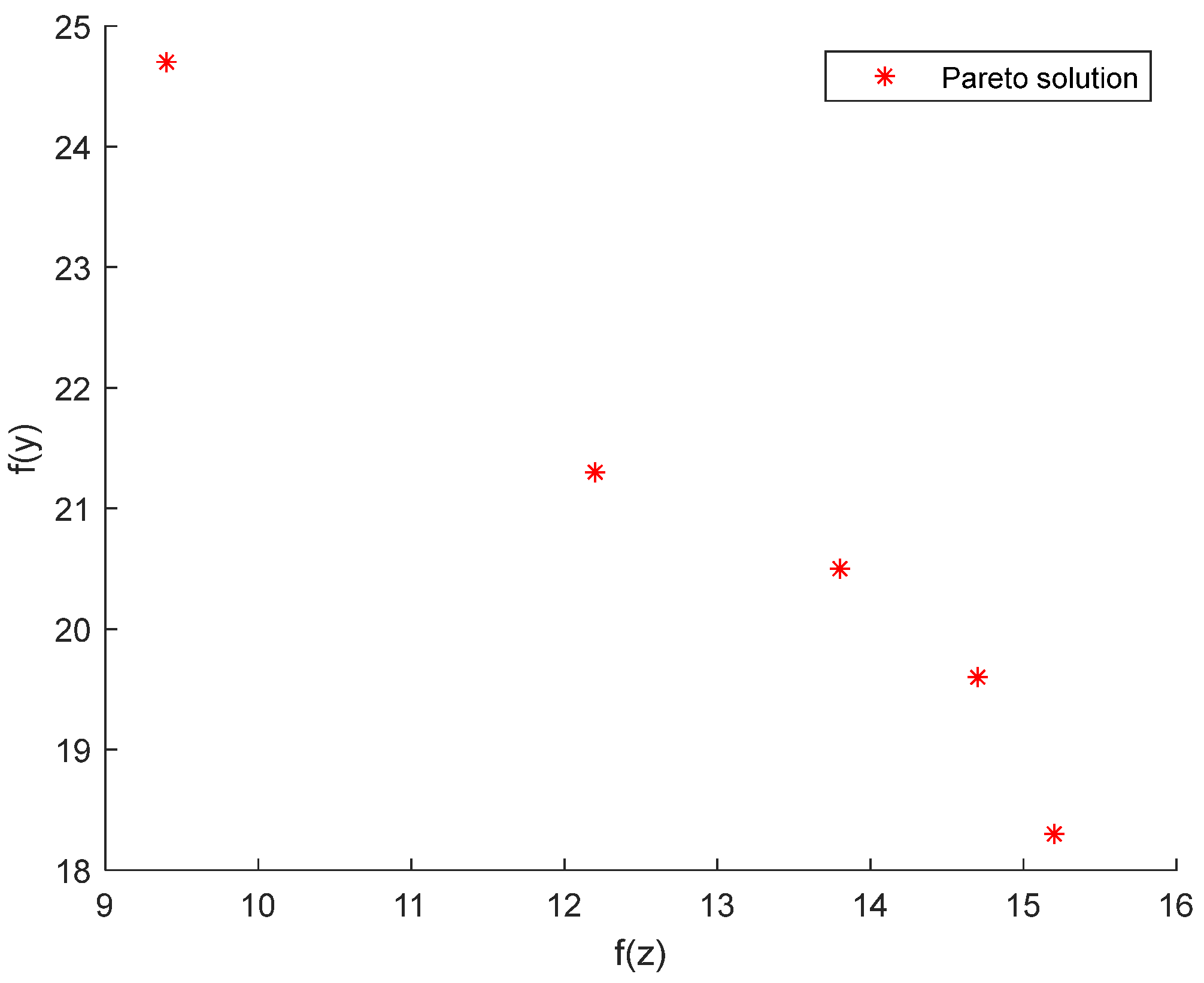
| Algorithm: NSGA-II (Real-Coded) |
|---|
| 1. Input: N (population size), G (generations), Pc, Pm, D (dimensions), LB, UB |
| 2. Initialize population |
| 3. Encode as real vector (random initialization) |
| 4. Set generation |
| 5. while |
| 6. Perform non-dominated sorting on |
| 7. Assign the crowding distance |
| 8. Select parents by binary tournament (rank + distance) |
| 9. Apply crossover () and mutation to generate offspring |
| 10. Decode and evaluate |
| 11. Combine and → |
| 12. Perform non-dominated sorting on |
| 14. End |
| 15. Return Pareto front |
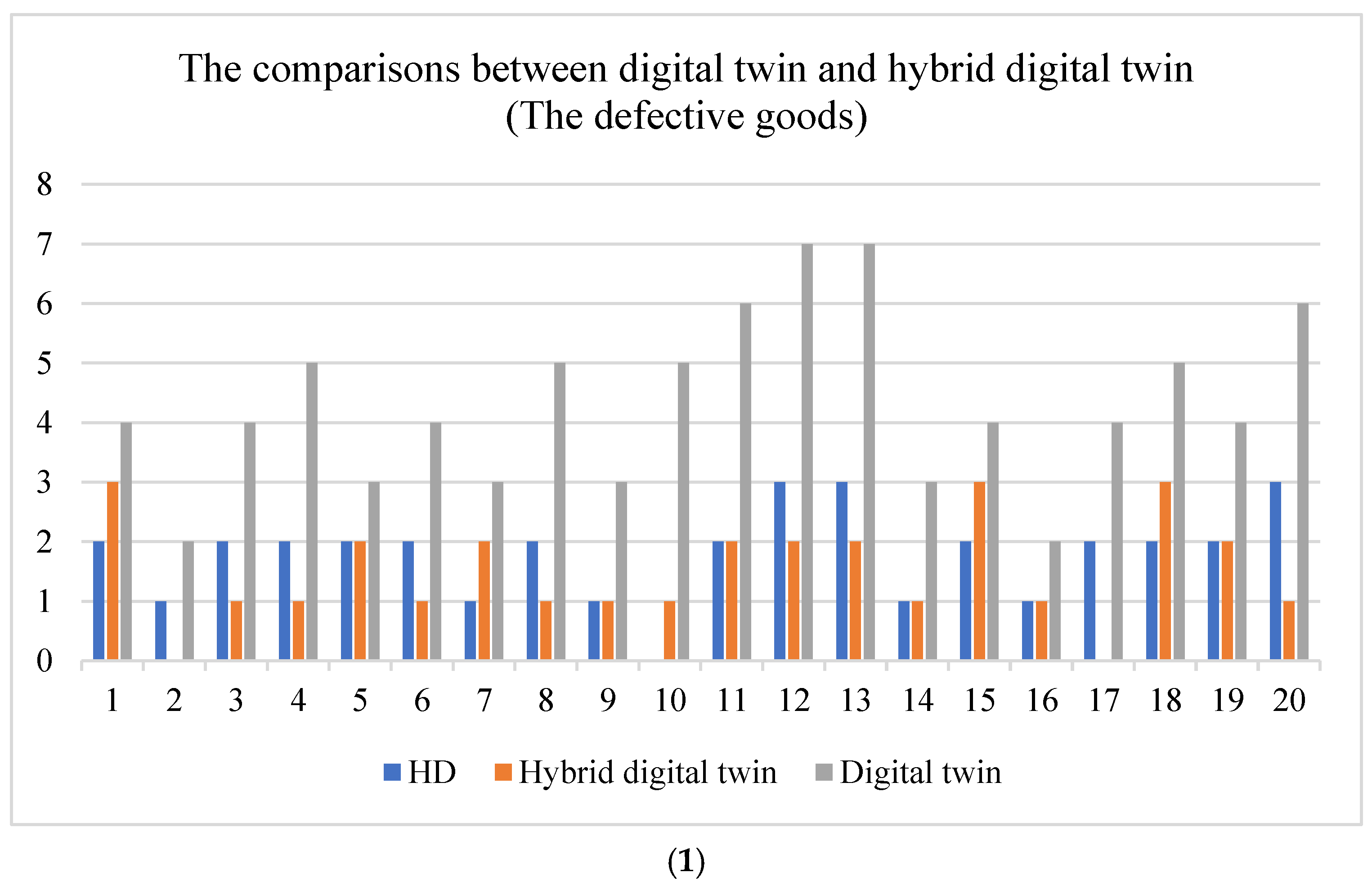
| Week | WIP | The Defective Goods | Outputting | ||||||
|---|---|---|---|---|---|---|---|---|---|
| HD | HDT | Differences | HD | HDT | Differences | HD | HDT | Differences | |
| 1 | 16 | 15 | 19 | 2 | 3 | 4 | 26 | 27 | 27 |
| 2 | 27 | 25 | 31 | 1 | 0 | 2 | 26 | 25 | 28 |
| 3 | 39 | 40 | 42 | 2 | 1 | 4 | 24 | 22 | 23 |
| 4 | 52 | 54 | 57 | 2 | 1 | 5 | 27 | 27 | 27 |
| 5 | 16 | 17 | 20 | 2 | 2 | 3 | 20 | 21 | 25 |
| 6 | 32 | 35 | 38 | 2 | 1 | 4 | 25 | 24 | 26 |
| 7 | 47 | 48 | 51 | 1 | 2 | 3 | 27 | 26 | 28 |
| 8 | 58 | 61 | 63 | 2 | 1 | 5 | 23 | 24 | 27 |
| 9 | 18 | 17 | 15 | 1 | 1 | 3 | 21 | 21 | 23 |
| 10 | 34 | 32 | 34 | 1 | 1 | 5 | 21 | 20 | 22 |
| 11 | 49 | 47 | 54 | 2 | 2 | 6 | 23 | 22 | 25 |
| 12 | 60 | 58 | 58 | 3 | 2 | 7 | 26 | 24 | 28 |
| 13 | 14 | 13 | 17 | 3 | 2 | 7 | 20 | 22 | 26 |
| 14 | 30 | 30 | 31 | 1 | 1 | 3 | 27 | 25 | 29 |
| 15 | 45 | 47 | 49 | 2 | 3 | 4 | 24 | 23 | 27 |
| 16 | 62 | 61 | 58 | 1 | 1 | 2 | 22 | 21 | 24 |
| 17 | 15 | 16 | 19 | 2 | 0 | 4 | 25 | 26 | 27 |
| 18 | 30 | 32 | 34 | 2 | 3 | 5 | 25 | 24 | 28 |
| 19 | 41 | 42 | 47 | 2 | 2 | 4 | 24 | 25 | 25 |
| 20 | 51 | 51 | 54 | 3 | 1 | 6 | 25 | 26 | 26 |
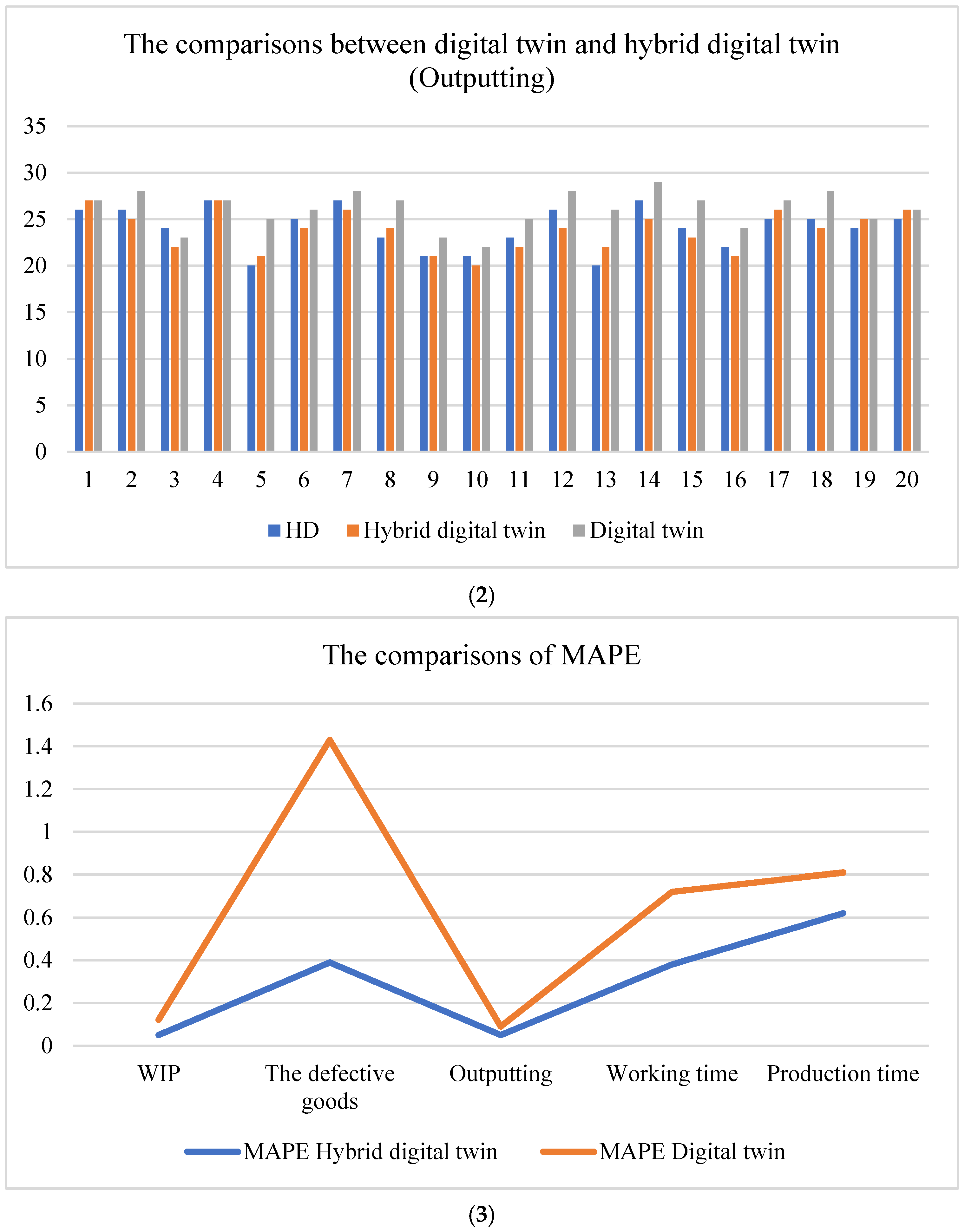
| WIP | The Defective Goods | Outputting | Working Time | Production Time | |
|---|---|---|---|---|---|
| MAPE | 0.05 | 0.39 | 0.05 | 0.38 | 0.62 |
| Notations | Explanations |
|---|---|
| Equipment maintenance | |
| 5S | |
| SMED efficiency | |
| Semi-finishing turning (external) cutting parameters | |
| Semi-finishing turning (internal) cutting parameters, | |
| Finishing turning (external) cutting parameters | |
| Finishing turning (internal) cutting parameters | |
| Inventory of work-in-progress | |
| Defective products | |
| The average production cycle | |
| Carbon dioxide | |
| Polluting emission |
| R2 | 0.82 | 0.84 | 0.79 | 0.88 | 0.85 |
| WIP | Defective Products | Lead Time | Carbon Emission | Pollution Emission | |
|---|---|---|---|---|---|
| RMSE | 2.06 | 2.13 | 0.16 | 3.76 | 7.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, S.; Tong, H.; Wang, S. A System Dynamics-Based Hybrid Digital Twin Model for Driving Green Manufacturing. Systems 2025, 13, 651. https://doi.org/10.3390/systems13080651
Fan S, Tong H, Wang S. A System Dynamics-Based Hybrid Digital Twin Model for Driving Green Manufacturing. Systems. 2025; 13(8):651. https://doi.org/10.3390/systems13080651
Chicago/Turabian StyleFan, Sucheng, Huagang Tong, and Song Wang. 2025. "A System Dynamics-Based Hybrid Digital Twin Model for Driving Green Manufacturing" Systems 13, no. 8: 651. https://doi.org/10.3390/systems13080651
APA StyleFan, S., Tong, H., & Wang, S. (2025). A System Dynamics-Based Hybrid Digital Twin Model for Driving Green Manufacturing. Systems, 13(8), 651. https://doi.org/10.3390/systems13080651






