Coupling Individual Psychological Security and Information for Modeling the Spread of Infectious Diseases

Abstract

Background: Faced with the profound impact of major infectious diseases on public life and economic development, humans have long sought to understand disease transmission and intervention strategies. To better explore the impact of individuals’ different coping behaviors—triggered by changes in their psychological security due to public information and external environmental changes—on the spread to infectious diseases, the model will place greater emphasis on quantifying psychological factors to make it more aligned with real-world situations. Methods: To better understand the interplay between information dissemination and disease transmission, we propose a two-layer network model that incorporates psychological safety factors. Results: Our model reveals key insights into disease transmission dynamics: (1) active defense behaviors help reduce both disease spread and information diffusion; (2) passive resistance behaviors expand disease transmission and may trigger recurrence but enhance information spread; (3) high-timeliness, low-fuzziness information reduces the peak of the initial infection but does not significantly curb overall disease spread, and the rapid dissemination of disease-related information is most effective in limiting the early stages of transmission; and (4) community structures in information networks can effectively curb the spread of infectious diseases. Conclusions: These findings offer valuable theoretical support for public health strategies and disease prevention after government information release.

1. Introduction

Curbing the spread of infectious diseases and safeguarding people’s physical and mental health has always been an eternal theme of human society. The rampant occurrence of infectious diseases exerts a significant impact on people’s lives and the economic development of all countries [1]. Hence, humans have been endeavoring to explore the transmission mechanisms of infectious diseases and the ways to intervene in their spread. Since Kermack et al. [2] established the renowned SIR Infectious disease model in 1927, various single network models such as SIS [3] and SEIR [4] have been constructed for different diseases. Wang et al. [5] developed a susceptible–infected–susceptible (SIS) transmission model involving both collective and individual contagion in a general hypernetwork. Ma et al. [6] proposed a networked SIRS epidemic model integrated with opinion dynamics to analyze the influence of community opinions on epidemic spread. However, a single network fails to fully demonstrate the dynamic role in disease transmission, which has led to multi-channel or multi-layer networks becoming an important research method for studying infectious disease transmission [7,8,9]. Zhou et al. [10] constructed a coupling mechanism of disease–information–disease transmission dynamics to investigate the interaction between information transmission and epidemic transmission, while also discussing the influencing factors. Along with the spread of diseases, disease-related information is also being disseminated in various forms such as verbal communication and online information. The dissemination of such information exerts new impacts on the spread of diseases. Therefore, the dynamic cascade transmission of information and diseases has emerged as a new research hotspot [11].

In recent years, researchers have investigated dynamic cascade transmission of information and diseases by incorporating various influencing factors and achieving certain progress, such as information transmission nodes [12], consciousness diffusion [13], consciousness diffusion. The transmission threshold of epidemics is affected by network topology [14,15]. Additionally, variations in information attributes within this dynamic cascade transmission process also exert an influence on the spread of infectious diseases, such as false information [16], negative information [17], and multi-source information [18]. Moreover, elements like information blocking [19] are also considered in the model construction.

When an infectious disease breaks out, an individual perceives risks according to the received information, which prompts the individuals to take risk-avoiding actions. Such individual behaviors, in turn, further alter the spread of the infectious disease. Protection Motivation Theory reveals that the likelihood of an individual adopting protective behaviors is influenced by the perception of danger [20]. The theory has been widely applied to study the effects of behaviors triggered by epidemic spread [21,22,23]. The interplay between infectious disease transmission and information dissemination and behavioral changes resulting from individuals’ perception of risk has attracted scholarly attention. Bedson et al. [24] emphasized the necessity of developing infectious disease models that better integrate social and behavioral dynamics. Existing studies have yielded certain findings on the impact of different behaviors on disease transmission. For instance, it has been proven that individual mobility affects the threshold and scope of disease transmission [10], self-protective behaviors triggered by information influence the actual transmission rate of diseases [25], and human factors impact the risk of epidemic transmission [26].

Behavioral studies in existing infectious disease models often adopt the setting of random occurrence. However, as activities generated by organisms under the influence of various internal and external stimuli, it is insufficient to consider only external stimuli; the state and process of individual mental activities should also be incorporated into the model. Psychological security [27] refers to the anticipation of potential physical or psychological dangers or risks. Therefore, in the face of the unknowns and uncertainties caused by the outbreak of infectious diseases, individuals’ psychological security tends to change, which drives them to adopt different risk-avoiding behaviors. After individuals obtain information of the occurrence of infectious diseases, they first exhibit the unconscious tendency of seeking benefits and avoiding harm. As a motivation to pursue safety and avoid insecurity, individuals are driven to take corresponding self-protective behaviors to evade the threat of infectious diseases, and the change in individual behaviors will further affect the transmission process of infectious diseases. However, in the process of public information dissemination, due to differences in information and heterogeneity of individual characteristics and attributes, individuals develop varying risk perceptions [28,29], which in turn lead to changes in their psychological security. Therefore, when facing disease outbreaks, the intensity or mode of protective behaviors adopted by individuals also differs. Some studies [11] have shown that individual behaviors based on local information about the number of infections of surrounding individuals or neighbors can effectively prevent disease transmission. Nevertheless, after individuals evaluate their environment following changes in personal psychological security, they may also engage in risky behaviors—such as fleeing the region or snapping up supplies—that promote disease spread. According to the study [30], behaviors that effectively prevent disease spread are defined as active defensive behaviors, while those that promote spread are defined as negative risk-taking behaviors. These differences tend to exert distinct impacts on infectious disease transmission, making it necessary to account for individual behaviors resulting from changes in psychological security triggered by public information.

Inspired by the above analysis, the dynamic coupling mechanism between information diffusion and infectious disease transmission deserves further investigation. Additionally, there are few models that integrate multiple influencing factors of infectious diseases, such as information diffusion, individual mobility, and so on. Therefore, incorporating factors like individual psychological security and individual behavior into the dynamic coupling propagation process is still an important research direction. When a disease outbreak occurs, the public disseminates information through word of mouth and mass media. Such disease-related information, along with the illness status of an individual’s neighbors, affects their sense of psychological security, which in turn triggers changes in psychological security and leads to different behaviors, ultimately altering the actual infection rate of the disease. Accordingly, in this study, we propose a dynamic coupling transmission model of information diffusion and infectious diseases spread considering behaviors triggered by changes in individual psychological security based on a two-layer network framework. Potential influencing factors, such as psychological security and individual behavior, are discussed in Markovian equations.

This study is structured as follows: To better explore the impact of individuals’ different coping behaviors—triggered by changes in their psychological security due to public information and external environmental changes—on the spread of infectious diseases, the model will place greater emphasis on quantifying psychological factors to make it more aligned with real-world situations. In Section 2, we construct a two-layer network framework that incorporates the “information diffusion—individual psychological security—disease transmission” mechanism. In Section 3, we propose a coupled transmission model of infectious diseases that accounts for individual psychological security, information diffusion, and diverse individual behaviors. The analysis of the Markov equation for this coupled transmission model provides a basis for theoretical analysis. In Section 4, we discuss, through simulations, the impacts of multiple influencing factors on infectious disease transmission, including the diffusion of public information, as well as individuals’ positive defensive behaviors and negative risk-taking behaviors triggered by changes in their psychological security. Finally, the discussion and conclusions are presented at the end of this study.

2. A Coupling Two-Layer Network Framework Considering Psychological Safety

With the spread of information following the outbreak of infectious diseases, the public obtains information related to infectious diseases through mass media, word of mouth, and other means. The further diffusion of information prompts people to adopt certain behaviors to cope with the impact of the spread of infectious diseases, and the spread of infectious diseases drives the spread of information. There is a significant correlation between diffusion of information and the adoption of preventive measures to curb the further spread of infectious diseases. To further reveal the coevolutionary and mutual coupling relationship between the two, this study adopts a two-layer network as the framework to explore the internal relationship between the coupled transmission of information and infectious diseases coupling transmission.

In the event of an infectious disease, an individual’s health behavior will influence the spread of the disease to some extent. Protection Motivation Theory (PMT), derived from expected value theory, reward theory, and self-efficacy theory, explores how individuals adopt health-protective behaviors. Under the influence of environmental factors and personal factors, people will go through one of the two intermediary processes of threat-assessment and coping assessment, which typically result in either adaptive coping or non-adaptive coping [31]. Therefore, considering that the threat individuals perceive and the response behaviors they adopt during the transmission of infectious, diseases will have an impact on the coupled transmission of information and infectious diseases situation; this study constructs a two-layer network of “information diffusion—disease transmission” based on a two-layer network framework to investigate the dynamic interaction in the coupled transmission of information and infectious diseases.

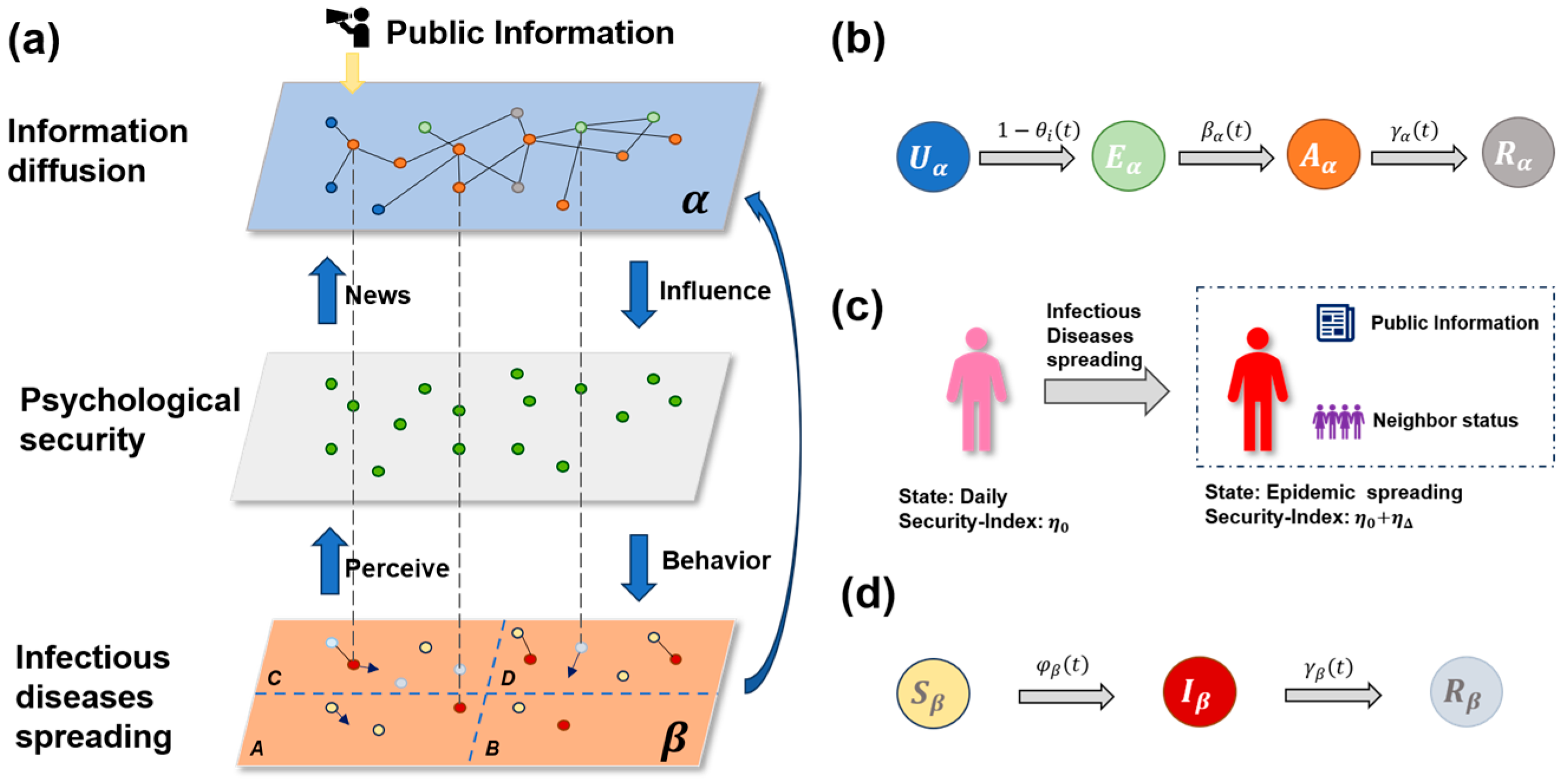
In the process of infectious disease transmission, there is often interactive transmission of information and disease. In order to better describe the two transmission processes, a multi-layer multiplex network is constructed. The top layer mainly simulates the transmission process of all kinds of publicly released disease information during the transmission of infectious diseases. The information transmission network at the top layer is an undirected graph, in which nodes represent individuals and the connections between nodes represent information interactions between individuals. According to the actual situation, the connections between individuals and others are often fixed in the short term, so the information transmission network is a static network in the short term. Moreover, considering that social networks in reality often have the characteristics of community structure, that is, the connections between nodes in the community are relatively close, while the connections between communities are relatively sparse, that is, the nodes in the same community communicate more closely. It is easier to exchange information. The bottom layer is to simulate the transmission of infectious diseases by individuals through contact with each other. The lowest level of the disease contact network is also an undirected graph, where nodes represent individuals and the connected edge between nodes indicates that the two interact within a certain range. Because infectious diseases are highly likely to be infected by contact and in real life, people’s positions are changing all the time, and their contact with others is also changing all the time. Therefore, the disease contact network is a dynamic network, whose node positions change at each time step.

2.1. Information and Disease Transmission Process

In the mobile Internet era, people’s communication efficiency has been improved. Individuals can exchange and publish their ideas and opinions on various software, while also receiving a great deal of information from other individuals. After receiving the information, individuals will digest and judge its content before choosing to forward it to others or stop sharing it. To better describe the hesitant moment when an individual receives a message but hesitates to forward or share it, we adopt the SEIR model to model propagation in the information transmission network. The latent state in the SEIR model is regarded as the hesitation period of the individual. Therefore, there are four different states of $N$ individuals in the information transmission network of the $\alpha$ layer: $U_{\alpha }$ (Unaware), $E_{\alpha }$ (Exposed), $A_{\alpha }$ (Aware), and $R_{\alpha }$ (Recover). The state transfer relationship of nodes in the information layer is shown in Figure 1b. The node in the $U_{\alpha }$ state at time $t$ has not received the disease information, has not yet understood the disease information, and is completely unknown but has the potential to understand the information. After contact with the node in $A_{\alpha }$ state, the disease information is obtained with the probability of ${\phi }_{\alpha }\left(t\right)$, but the content of the disease information is being digested, and the node is temporarily in a wait-and-see state, becoming an $E_{\alpha }$ state node with the potential to spread disease information but not spread in the network platform. There is a ${\beta }_{\alpha }\left(t\right)$ probability of becoming $A_{\alpha }$ status after thinking about it or changing from $U_{\alpha }$ status to $A_{\alpha }$ status through infection. The node in the $A_{\alpha }$ state chooses to spread the disease information to others on the social network platform, and finally, as time goes by, the individual is immune to the disease information with the probability of ${\gamma }_{\alpha }$, because he is not interested in it or forgets it, he will no longer spread the disease information and enter the $R_{\alpha }$ state. In the $\beta$ layer, diseases are transmitted through the contact between nodes in the contact network. In this study, the classical SIR Infectious disease model is used to simulate the process of disease transmission. In this model, $N$ individuals exist in three different states: $S_{\beta }$ (Susceptible), $I_{\beta }$ (Infected), and $R_{\beta }$ (Recover). After the disease occurs, individuals in the $S_{\beta }$ state have a certain probability of being infected by contact into the $I_{\beta }$ state, and after a period of time through treatment or self-rehabilitation and other ways, becomes an individual in the $R_{\beta }$ state. In this model, the cured individual is no longer infected and no longer has the ability to infect other individuals. $S_{\beta }$, $I_{\beta }$, and $R_{\beta }$ were used to represent the proportion of individuals in $S_{\beta }$, $I_{\beta }$, and $R_{\beta }$ states at time $t$, respectively, so $S_{\beta }\left(t\right)+I_{\beta }\left(t\right)+R_{\beta }\left(t\right)=1$. The node state transfer rule in the contact network is shown in Figure 1d. After contact between an individual in the $S_{\beta }$ state and an individual in the $I_{\beta }$ state, there is a probability of ${\phi }_{\beta }\left(t\right)$ being infected with the disease, so ${\phi }_{\beta }$ is called the disease transmission rate. At the next time step, an individual in the $I_{\beta }$ state has a probability of ${\gamma }_{\beta }\left(t\right)$ of becoming an individual in the $R_{\beta }$ state after recovery, so ${\gamma }_{\beta }$ is called the disease recovery rate. In simulating the disease transmission process, we randomly select some nodes to be in the $I_{\beta }$ state and others to be in the $S_{\beta }$ state, After that, with the progress of the time step, the nodes of the $I_{\beta }$ state began to move and infected the $S_{\beta }$ state individuals in contact with it with the probability of ${\phi }_{\beta }$, resulting in the gradual increase in the individuals of the $I_{\beta }$ state and the gradual emergence of the individuals of the $R_{\beta }$ state, in order to simulate the process of infectious disease transmission.

Reference defines the “reaction-diffusion” process as “reaction processes are understood as contagions within each subpopulation (patch), while diffusion represents the mobility of individuals between patches.” [32]. Based on this concept, we can elaborate as follows: In real-world scenarios, when no infectious diseases are spreading, people usually live in fixed regions (such as provinces and cities) with little cross-regional mobility. Therefore, the planar space $\mathsf{\Gamma }$ can be divided into four parts, corresponding to different regions where individuals initially carry out their activities. However, after the outbreak of an infectious disease, individuals may move to regions with lower infection density to avoid risks. This phenomenon corresponds to the diffusion process of infectious disease to other regions (such as other provinces or cities). Accordingly, in this study, the disease contact network is set to include $N$ individuals, which are distributed in the planar space $\mathsf{\Gamma }=\left\{\left(x,y\in {\mathbb{R}}^2:0\le x\le L,0\le y\le L\right)\right\}$, L is the side length of the plane space, as shown in Figure 1a. The position of $i$ at time $t$ is represented by $P_i\left(t\right)=\left(x_i\left(t\right),y_i\left(t\right)\right)$, moving at the speed $V_i\left(t\right)=\left(v_i\left(t\right)cos{\theta }_i\left(t\right), v_i\left(t\right)sin{\theta }_i\left(t\right)\right), i=1,2,\cdots ,N$. Assuming that at each time step, the individual moves at the same speed and only changes the direction of movement angle ${\theta }_i\left(t\right)$. The position and direction of node $i$ at time $t+1$ are

$$x_i\left(t+1\right)=x_i\left(t\right)+v_i\left(t\right)cos{\theta }_i\left(t\right)$$

$$y_i\left(t+1\right)=y_i\left(t\right)+v_i\left(t\right)sin{\theta }_i\left(t\right)$$

$${\theta }_i\left(t+1\right)={\xi }_i\left(t+1\right)$$

where ${\xi }_i\left(t+1\right)$ represents the random variable and is the uniform distribution of $[-\pi ,\pi ]$. According to the disease characteristics that a diseased individual may infect other individuals within a certain range, we assume that an individual has an interaction radius $r_i$, and the distance between two nodes $i$ and $j$ in the disease contact layer at time $t$ is measured by Euclidean distance, which is defined as

$$d_{ij}\left(t\right)=\sqrt{{\left(x_i\left(t\right)-x_j\left(t\right)\right)}^2+{\left(y_i\left(t\right)-y_j\left(t\right)\right)}^2}, i,j=1,2\cdots N.$$

According to the size relationship between $d_{ij}\left(t\right)$ and $r_i$, and the distance between node $i$ and node $j$ at any time $t$, it can be determined whether there is a disease infection and establish a link in the disease contact network according to the above rules, that is, for any two nodes $i$ and $j$ in the contact network; when $d_{ij}\left(t\right)\le r_i$, a link between node $i$ and $j$ is established. In addition, although the scope of People’s Daily life is relatively stable, there are still cases of long-distance crossing such as travel and business trips. Therefore, we allow some nodes in the disease contact layer to jump to other areas with a certain probability of $P_{jump}$ ($P_{jump}\in \left[0,1\right]$), that is, each node can jump to any location in other areas with a probability of $P_{jump}$ at each time step. Otherwise, it updates its position according to the rule (1) in this region with the probability of $1-P_{jump}$. In the next time step, the distance between nodes and other nodes and the interaction radius of nodes are compared again, a new connection edge is constructed, and a new disease contact network is updated.

2.2. The Interactive Effects of Psychological Safety on Information and Disease Transmission

The spread of infectious diseases drives the diffusion of related information, and the changes in individual psychological security and coping behaviors triggered by this process also impact the spread of infectious diseases. Therefore, we modeled the dynamic interaction of the two-layer network as follows.

Assumptions: Individuals infected with infectious diseases will be immediately aware of information related to infectious diseases. Thus, infected individuals in the $\beta$-layer will spontaneously transition to an $A_{\alpha }$ (Aware) post-transmission state in the $\alpha$-layer and will not return to an $R_{\alpha }$ (Recover) immune state until they are cured. The scale of infectious disease transmission in the $\beta$-layer also affects the spread of information in the $\alpha$-layer, so that individuals who are not infected with the disease can also obtain information about the infection. However, it is in the hesitant state of $E_{\alpha }$ (Exposed), where the information is known but not transmitted, and changes to the state of $A_{\alpha }$ (Aware) after being transmitted under certain probability. In the state of $A_{\alpha }$ (Aware), informed transmission, individuals will conduct risk assessment according to the global information, such as the official announcement of infectious disease hazards and local information about other individuals around them, and take different coping behaviors according to the assessment results. Finally, this interaction will continue to develop with the evolution of information transmission and infectious diseases transmission.

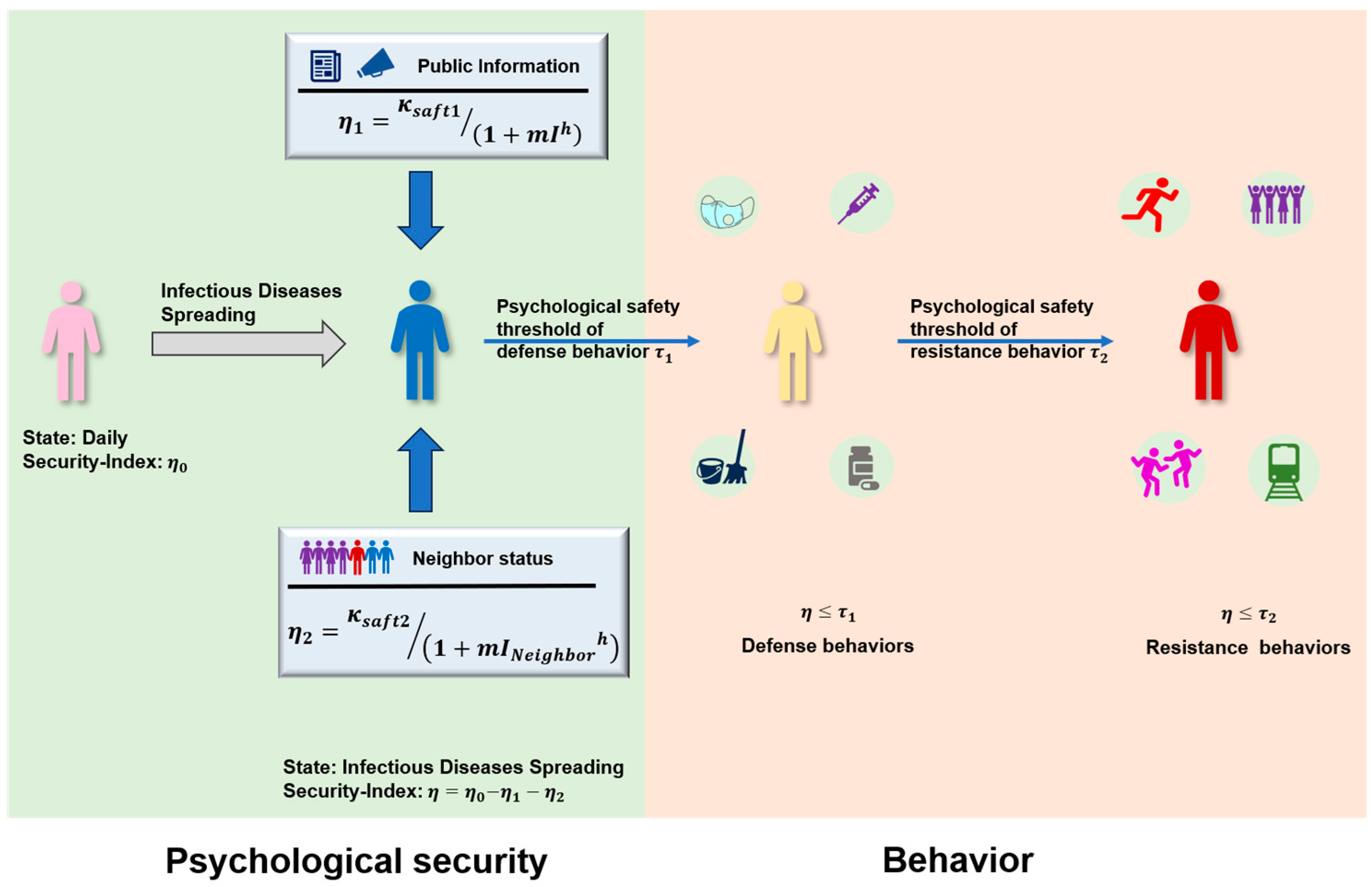
After receiving disease information and undergoing risk assessment, individuals will often take certain measures to prevent their own diseases, but they may take different protective measures according to their different psychological effects from the information received. In order to consider this psychological effect, some scholars have improved the SIRS model [33]. Therefore, in this study, we draw on this idea and take $1/(1+m{I}^h)$ as the psychological effect of the increase in infected individuals who have learned about the information related to the disease but have not been infected with the disease, as shown in Figure 1c. Parameters m and h are both non-negative constants, $I$ represents the number of individuals in the $I_{\beta }$ state. Since different individuals have different degrees of psychological security and different degrees of perception of diseases, we introduce coefficient k here to represent the degree of psychological security. When the degree of psychological safety is higher, the coefficient is larger, and the perception of disease risk is weaker, so the larger ${\kappa }_{saft}/(1+m{I}^h)$ is, the weaker the inhibitory effect will be. Conversely, the stronger the risk perception of disease, the lower the degree of psychological safety, the smaller the coefficient, the smaller ${\kappa }_{saft}/(1+m{I}^h)$ is, the inhibition effect will be enhanced accordingly.

Based on the above settings, we incorporate the psychological security effect of individuals into the model. For individuals who have received disease-related information, psychological effects will be generated according to their own conditions, and such effects will influence disease infection. Information from different sources also brings about distinct changes in individuals’ psychological sense of security, thereby leading to different behaviors. In this study, it is assumed that the infection status of neighboring individuals will make it easier for individuals to flee the current area, i.e., local information is more likely to trigger passive resistance behaviors. However, official public information often prompts individuals to pay more attention to self-protection and preventive behaviors, i.e., global information affects active defensive behaviors.

Therefore, as shown in Figure 2, the psychological security of an individual in daily situations is ${\eta }_0$. The psychological security of individuals with global disease information changes to ${\eta }_1=\raisebox{1ex}{${\kappa }_{saft1}$}\!\left/ \!\raisebox{-1ex}{$\left(1+m{I}^h\right)$}\right.$. The psychological security of individuals who feel the formation of local information changes to ${\eta }_2=\raisebox{1ex}{${\kappa }_{saft2}$}\!\left/ \!\raisebox{-1ex}{$\left(1+m{I_{Neighbor}}^h\right)$}\right.$.

${\kappa }_{saft1}$ and ${\kappa }_{saft2}$ represent the parameters of global information and local information affecting the individual’s psychological safety. When individual psychological security $\eta ={\eta }_0-{\eta }_1-{\eta }_2$ is lower than the psychological safety threshold of defensive behavior ${\tau }_1$, there is the probability of $P_{prevent}$. Under the psychological safety effect, preventive measures are taken to change the disease transmission rate from ${\gamma }_{\beta }$ to $q{\gamma }_{\beta }$, where $q$ is a constant between $(0,1)$. When the individual psychological security $\eta ={\eta }_0-{\eta }_1-{\eta }_2$ is lower than the psychological security threshold of their own resistance behavior ${\tau }_2$, there is the probability of $P_{jump}$ to escape from the current area to jump long distance. The parameters $m$ and $h$ are non-negative constants. Compared with nodes in $E_{\alpha }$ state, although nodes in $I_{\alpha }$ state have received disease information, they have different degrees of recognition of the information, so the probability of taking preventive measures is different. Therefore, $P_{E-prevent}$ and $P_{I-prevent}$, respectively, represent the difference in preventive measures taken by nodes in $E_{\alpha }$ state and nodes in $I_{\beta }$ state against disease risk perception.

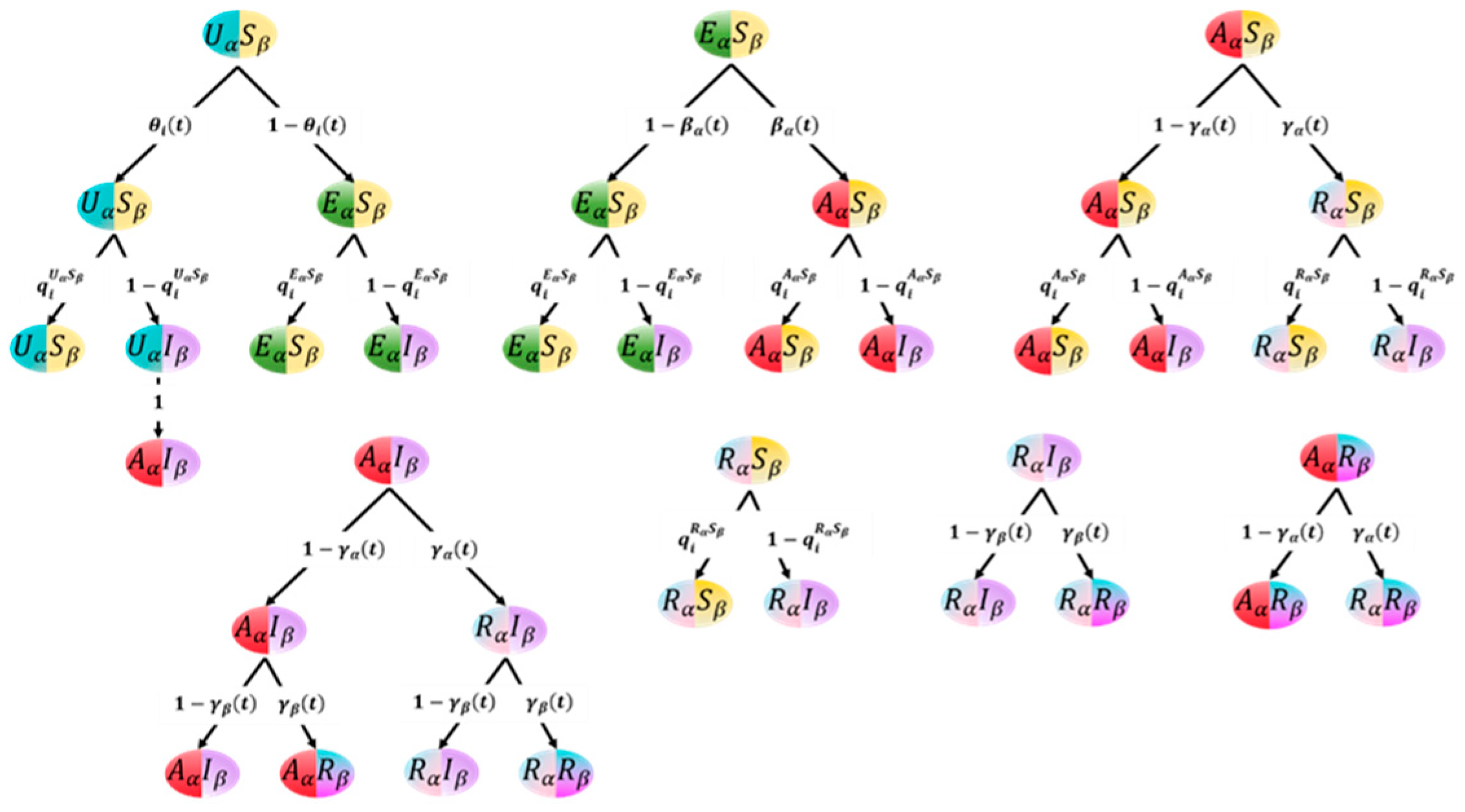
To sum up, in the multi-layer network framework of this study, there are eight possible states of individuals at time $t$:

$$Z=\left\{\begin{array}{c}Unaware and Susceptible\left(U_{\alpha }{S}_{\beta }\right),Exposed and Susceptible\left(E_{\alpha }{S}_{\beta }\right),\\ Aware and Susceptible\left(A_{\alpha }{S}_{\beta }\right),\\ Recover and Susceptible\left(R_{\alpha }{S}_{\beta }\right),Aware and Infected\left(A_{\alpha }{I}_{\beta }\right),\\ Recover and Infected\left(R_{\alpha }{I}_{\beta }\right),\\ Aware and Recover\left(A_{\alpha }{R}_{\beta }\right),Recover and Recover\left(R_{\alpha }{R}_{\beta }\right)\end{array}\right\}$$

The state transition tree is shown in Figure 3, where the node is the state, the branch is the transition process, and the weight on the branch is the probability of one state to another.

3. Theoretical Analysis

In this chapter, Markov equation is used to describe the dynamic evolution of information diffusion, individual psychological security and coping behavior, and infectious diseases transmission.

Information transmission network and disease contact network are represented by adjacency matrices ${\left(a_{ij}\right)}_{N\times N}$ and ${\left(b_{ij}\right)}_{N\times N}$, respectively. If node $i$ and node $j$ are connected in the information transmission network, $a_{ij}=1$; if they are not connected, $a_{ij}=0$; similarly, if node $i$ and node $j$ are connected in the disease contact network, $b_{ij}=1$; otherwise, $b_{ij}=0$. Because the disease exposure network is a dynamic network, the exposure network changes at each time step. We describe the interaction between information transmission and disease infection using the microscopic Markov chain method (MMCA). In this process, as described in the previous section, there are eight possible states of the individual at time t: $U_{\alpha }{S}_{\beta }$, $E_{\alpha }{S}_{\beta }$, $A_{\alpha }{S}_{\beta }$, $R_{\alpha }{S}_{\beta }$, $A_{\alpha }{I}_{\beta }$, $R_{\alpha }{I}_{\beta }$, $A_{\alpha }{R}_{\beta }$, and $R_{\alpha }{R}_{\beta }$. The probability that node $i$ is in one of the above states at time $t$ is expressed as $P_i^{U_{\alpha }{S}_{\beta }}\left(t\right)$, $P_i^{E_{\alpha }{S}_{\beta }}\left(t\right)$, $P_i^{A_{\alpha }{S}_{\beta }}\left(t\right)$, $P_i^{R_{\alpha }{S}_{\beta }}\left(t\right)$, $P_i^{A_{\alpha }{I}_{\beta }}\left(t\right)$, $P_i^{R_{\alpha }{I}_{\beta }}\left(t\right)$, $P_i^{A_{\alpha }{R}_{\beta }}\left(t\right)$, and $P_i^{R_{\alpha }{R}_{\beta }}\left(t\right)$. We assume that the probability that an individual in state $U_{\alpha }$ is not informed about the disease information by other individuals around him is ${\theta }_i\left(t\right)$, and the probability that node $i$ is in $A_{\alpha }$ hesitant state ($E_{\alpha }$) and turns into an informed state ($A_{\alpha }$) after analytical consideration is ${\beta }_{\alpha }\left(t\right)$. $A_{\alpha }\left(t\right)={\sum }_{j=1}^N{a}_{ij}$ is the sum of the number of neighbor nodes $j$ that are in the propagating state ($I_I$) around node $i$ at time $t$. The above probability is specifically expressed as

$${\theta }_i\left(t\right)=\prod _j\left[1-a_{ji}{P}_j^{A_{\alpha }}\left(t\right){\phi }_{\alpha }\left(t\right)\right]$$

Among, $P_j^{A_{\alpha }}\left(t\right)=P_i^{A_{\alpha }{S}_{\beta }}\left(t\right)+P_i^{A_{\alpha }{I}_{\beta }}\left(t\right)+P_i^{A_{\alpha }{R}_{\beta }}\left(t\right)$.

${\phi }_{\alpha }\left(t\right)$ represents the spread rate of disease information, which is affected by the information’s own propagation capacity ${\phi }_1\left(t\right)$ and the node’s individual characteristics ${\phi }_2\left(t\right)$.

$${\phi }_1\left(t\right)={\displaystyle \frac{1}{2}}\left(1-{\left(1-\xi \right)}^{A_{\alpha }\left(t\right)}\right)$$

$${\phi }_2\left(t\right)={\displaystyle \frac{1}{2}}·A·(1-B)·C$$

$${\phi }_{\alpha }\left(t\right)={\phi }_1\left(t\right)+{\phi }_2\left(t\right)$$

In the part of information communication ability ${\phi }_1\left(t\right)$, $\xi$ indicates the communication probability of information itself, and $\xi \in \left[0,1\right]$. Information communication ability ${\phi }_1\left(t\right)$ in information communication network is determined jointly by information value $V_1$, ambiguity of information $V_2$ and timeliness $V_3$. The higher $\xi$ is, the stronger the communication ability of information, and the more widely the information can be spread in the network.

$$\xi =V_1\times V_2\times V_3$$

$V_1$ represents the impact of information value on information dissemination ability and the importance of information to individuals, $V_1\in [0,1]$. The larger $V_1$ is, the higher the information value is.

$V_2$ represents the influence of ambiguity degree on information dissemination ability. The ambiguity degree of information is defined as $\epsilon$, where $\epsilon \in [0,1]$. $V_2=1$ represents the very low ambiguity degree of information so that the content of information, such as statistics and contact information, can be clearly understood. $V_2=0$ indicates that the ambiguity of the information is very high, and there are unclear meanings, ambiguities, or lack of key information, such as abbreviations, terms, or polysemous words. The influence of ambiguity on information dissemination ability is as follows:

$$V_2=1+{\displaystyle \frac{1}{e}}-{\displaystyle \frac{1}{e^{1-\epsilon }}}, where e is the natural base$$

$V_3$ represents the impact of the timeliness of information on its ability to spread information, and $V_3=e^{-1}$ is used to indicate that individuals’ attention to information decreases as time goes by.

The impact of node individual characteristics ${\phi }_2\left(t\right)$ on public opinion dissemination is specifically expressed as follows:

$\mathrm{A}$ stands for node authority: It is usually used to express authority, and nodes with greater authority tend to be paid more attention by more people and have greater influence on others. Authority is generally expressed by the ratio of the node’s degree $k$ to the degree $k_{max}$ of the node with the maximum degree:

$$\mathrm{A}={\displaystyle \frac{k}{k_{max}+\mathrm{C}}}, \mathrm{C} \mathrm{i}\mathrm{s} \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}$$

(1)

$\mathrm{B}$ is the cognitive ability of an individual, and the cognitive ability of nodes follows a normal distribution. Cognitive ability is related to knowledge level and cultural literacy. Therefore, the value $\mathrm{B}\in \left[0,1\right]$ is defined as the cognitive ability of an individual. A cognitive ability of $0$ indicates the lowest level of the individual’s ability to recognize, understand, learn, and process information, and a cognitive ability of 1 indicates the highest level of the individual’s ability to recognize, understand, learn, and process information.

$\mathrm{C}$ represents the influence of individual conformity effect on information dissemination. Under the influence of the conformity effect, when an individual disagrees with the majority of his friends or neighbors, he will be pressured by the group to change his mind and agree with everyone else. Therefore, the state proportion of neighbor nodes is taken as the quantitative measurement factor of group consistency. When the adjacent nodes of an individual are in the state of communication or the proportion of disseminators is high, the individual will be affected by the conformity effect and choose to disseminate the information, thus becoming the state of communication. When the adjacent nodes of an individual are immune to a certain information, the individual will not transmit it out of recognition of the “group rule”.

Based on this, we choose to use the proportion of neighbor state nodes to quantify the influence of herd effect on individual state transition. The higher the proportion of transmitters $A_{\alpha }\left(t\right)$, the more likely individuals are to change to the informed state of communication ($A_{\alpha }$), while the higher the proportion of forgetting $R_{\alpha }\left(t\right)$, the less likely individuals are to change to the informed state of communication ($A_{\alpha }$). The influence of individual conformity effect on individual state transfer is as follows:

$$C={\displaystyle \frac{e^{\frac{A_{\alpha }\left(t\right)-R_{\alpha }\left(t\right)}{k}}}{1-\frac{1}{e}}}$$

Suppose that the probability that node $i$ is not informed by any neighbor when it is in the state $U_{\alpha }$ is $q_i^{U_{\alpha }}\left(t\right)$, the probability that node $i$ is in the state of $E_{\alpha }{S}_{\beta }$ when hesitancy but not infected is $q_i^{E_{\alpha }{S}_{\beta }}\left(t\right)$, the probability that node $i$ is in the state of $A_{\alpha }{S}_{\beta }$ when it is aware of the disease information but not infected is $q_i^{A_{\alpha }{S}_{\beta }}\left(t\right)$, and the probability that node $i$ is in $R_{\alpha }{S}_{\beta }$ state when ignoring disease information but not infected with disease is $q_i^{R_{\alpha }{S}_{\beta }}\left(t\right)$, the above probability is specifically expressed as

$$q_i^{U_{\alpha }}\left(t\right)=\prod _j\left[1-b_{ji}{P}_j^{A_{\alpha }}\left(t\right)\left(1-{\theta }_i\left(t\right)\right)\right]$$

$$q_i^{E_{\alpha }{S}_{\beta }}\left(t\right)=P_{E-prevent}\prod _j\left[1-{k_{1}b}_{ji}{P}_j^{I_{\beta }}{\phi }_{\beta }\left(t\right)\right]+\left(1-P_{E-prevent}\right)\prod _j\left[1-b_{ji}{P}_j^{I_{\beta }}\left(t\right){\phi }_{\beta }\left(t\right)\right]$$

$$q_i^{A_{\alpha }{S}_{\beta }}\left(t\right)=P_{I-prevent}\prod _j\left[1-k_2{b}_{ji}{P}_j^{I_{\beta }}\left(t\right){\phi }_{\beta }\left(t\right)\right]+\left(1-P_{I-prevent}\right)\prod _j\left[1-b_{ji}{P}_j^{I_{\beta }}\left(t\right){\phi }_{\beta }\left(t\right)\right]$$

$$q_i^{R_{\alpha }{S}_{\beta }}\left(t\right)=\prod _j\left[1-b_{ji}{P}_j^{I_{\beta }}\left(t\right){\phi }_{\beta }\left(t\right)\right]$$

Among, $P_j^{I_{\beta }}\left(t\right)=P_i^{A_{\alpha }{I}_{\beta }}\left(t\right)+P_i^{R_{\alpha }{I}_{\beta }}\left(t\right)$, $P_{E-prevent}$ and $P_{I-prevent}$ represent the probability that an individual in a hesitating state and a spreading state will take effective measures to prevent the spread of the disease, respectively. According to the transition probability tree shown in Figure 3, the dynamic Markov equation of coevolution for each node i is obtained as follows:

$$P_i^{U_{\alpha }{S}_{\beta }}\left(t+1\right)=P_i^{U_{\alpha }{S}_{\beta }}\left(t\right){\theta }_i\left(t\right)q_i^{U_{\alpha }{S}_{\beta }}\left(t\right)$$

$$P_i^{E_{\alpha }{S}_{\beta }}\left(t+1\right)=P_i^{U_{\alpha }{S}_{\beta }}\left(t\right)\left[1-{\theta }_i\left(t\right)\right]q_i^{E_{\alpha }{S}_{\beta }}\left(t\right)+P_i^{E_{\alpha }{S}_{\beta }}\left(t\right)\left[1-{\beta }_{\alpha }\left(t\right)\right]q_i^{E_{\alpha }{S}_{\beta }}\left(t\right)$$

$$P_i^{A_{\alpha }{S}_{\beta }}\left(t+1\right)=P_i^{A_{\alpha }{S}_{\beta }}\left(t\right)\left(1-{\gamma }_{\alpha }\right)q_i^{A_{\alpha }{S}_{\beta }}\left(t\right)+P_i^{E_{\alpha }{S}_{\beta }}\left(t\right){\beta }_{\alpha }\left(t\right)q_i^{A_{\alpha }{S}_{\beta }}\left(t\right)$$

$$P_i^{R_{\alpha }{S}_{\beta }}\left(t+1\right)=P_i^{A_{\alpha }{S}_{\beta }}\left(t\right){{\gamma }_{\alpha }q}_i^{A_{\alpha }{S}_{\beta }}\left(t\right)+P_i^{R_{\alpha }{S}_{\beta }}\left(t\right)q_i^{R_{\alpha }{S}_{\beta }}\left(t\right)$$

$$\begin{array}{ll}{P}_i^{A_{\alpha }{I}_{\beta }}\left(t+1\right)=& P_i^{U_{\alpha }{S}_{\beta }}\left(t\right){\theta }_i\left(t\right)\left[1-q_i^{U_{\alpha }{S}_{\beta }}\left(t\right)\right]+P_i^{U_{\alpha }{S}_{\beta }}\left(t\right)\left[1-{\theta }_i\left(t\right)\right]\left[1-q_i^{E_{\alpha }{S}_{\beta }}\left(t\right)\right]\\ & \hspace{1em}+P_i^{A_{\alpha }{S}_{\beta }}\left(t\right)\left(1-{\gamma }_{\alpha }\right)\left[{1-q}_i^{A_{\alpha }{S}_{\beta }}\left(t\right)\right]+P_i^{A_{\alpha }{I}_{\beta }}\left(t\right)\left(1-{\gamma }_{\alpha }\right)\left(1-{\gamma }_{\beta }\right)\\ & \hspace{1em}+P_i^{E_{\alpha }{S}_{\beta }}\left(t\right){\beta }_{\alpha }\left(t\right)\left[1-q_i^{A_{\alpha }{S}_{\beta }}\left(t\right)\right]+P_i^{E_{\alpha }{S}_{\beta }}\left(t\right)\left[{1-\beta }_{\alpha }\left(t\right)\right]\left[1-q_i^{E_{\alpha }{S}_{\beta }}\left(t\right)\right]\end{array}$$

$$\begin{array}{ll}{P}_i^{R_{\alpha }{I}_{\beta }}\left(t+1\right)=& p_i^{A_{\alpha }{S}_{\beta }}\left(t\right){\gamma }_{\alpha }\left[1-q_i^{A_{\alpha }{S}_{\beta }}\left(t\right)\right]+P_i^{A_{\alpha }{I}_{\beta }}\left(t\right){\gamma }_{\alpha }\left(1-{\gamma }_{\beta }\right)\\ & \hspace{1em}+P_i^{R_{\alpha }{S}_{\beta }}\left(t\right)\left[{1-q}_i^{R_{\alpha }{S}_{\beta }}\left(t\right)\right]+P_i^{R_{\alpha }{I}_{\beta }}\left(t\right)\left(1-{\gamma }_{\beta }\right)\end{array}$$

$$P_i^{A_{\alpha }{R}_{\beta }}\left(t+1\right)=P_i^{A_{\alpha }{I}_{\beta }}\left(t\right)\left(1-{\gamma }_{\alpha }\right){\gamma }_{\beta }+P_i^{A_{\alpha }{R}_{\beta }}\left(t\right)\left(1-{\gamma }_{\alpha }\right)$$

$$P_i^{R_{\alpha }{R}_{\beta }}\left(t+1\right)=P_i^{A_{\alpha }{I}_{\beta }}\left(t\right){\gamma }_{\alpha }{\gamma }_{\beta }+P_i^{A_{\alpha }{R}_{\beta }}\left(t\right){\gamma }_{\alpha }+P_i^{R_{\alpha }{I}_{\beta }}\left(t\right){\gamma }_{\beta }+P_i^{R_{\alpha }{R}_{\beta }}\left(t\right)$$

When the coevolutionary dynamics reach a steady state, $P_i^{U_{\alpha }{S}_{\beta }}\left(t+1\right)=P_i^{U_{\alpha }{S}_{\beta }}\left(t\right)=P_i^{U_{\alpha }{S}_{\beta }}$ and the other states are the same.

This following section provides a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

4. Simulation Results and Discussion

We hope to conduct numerical simulation to verify the theoretical analysis of the coupling evolution mechanism between information diffusion, individual psychological security changes, and infectious diseases transmission. Therefore, we use Monte Carlo (MC) method to explore the feasibility and scientificity of Markov equation in Section 3.

Before simulating the coevolutionary transmission of disease and information, we first constructed a two-layer information–disease network. Because of the community structure in the information dissemination network, we choose a random network with 1000 nodes generated by LFR algorithm [34] and BA network [35] to simulate the information transmission of infectious diseases. These nodes form multiple communities, and the number of nodes contained in each community is different. The nodes in the information transmission network correspond to those in the disease transmission network one by one. To construct the disease contact network, we simulated the movement of nodes in a plane space. First, A square area with side length $L=\sqrt{1000}$ is generated, and it is equally divided into four small square areas A, B, C, and D to simulate different areas in real life, as shown in Figure 1a. We use a random function to generate 1000 points that meet the coordinate interval of the corresponding region. As time goes on, the nodes update their positions according to the rule (1). Meanwhile, when the distance between the nodes is within the interaction radius, it indicates that there is infection. Therefore, the disease exposure network is a dynamic network. The individual psychological security network corresponds to the nodes in the information transmission network and the disease contact network one by one and has the individual psychological security η_0 randomly in the initial state and updates the node state according to the rules shown in Figure 2. After the information–psychological security–disease exposure network is established, we simulate the transmission process of information, individual psychological security, and disease on this multi-layer network and analyze the factors affecting the transmission process. After constructing the above network structure, we will study the influence of different individual characteristics and psychological characteristics, individual psychological safety and coping behaviors, and network structure on the coupling transmission of information–disease. The following simulation results are based on the assumption of the initial moment. We set 70, 130, 250, and 550 nodes in the four regions of A, B, C, and D, respectively, and the initial number of diseased nodes in each region is five. The results obtained are an average of 20 experiments.

4.1. Models of Information and Disease Transmission Without Considering Psychological Safety

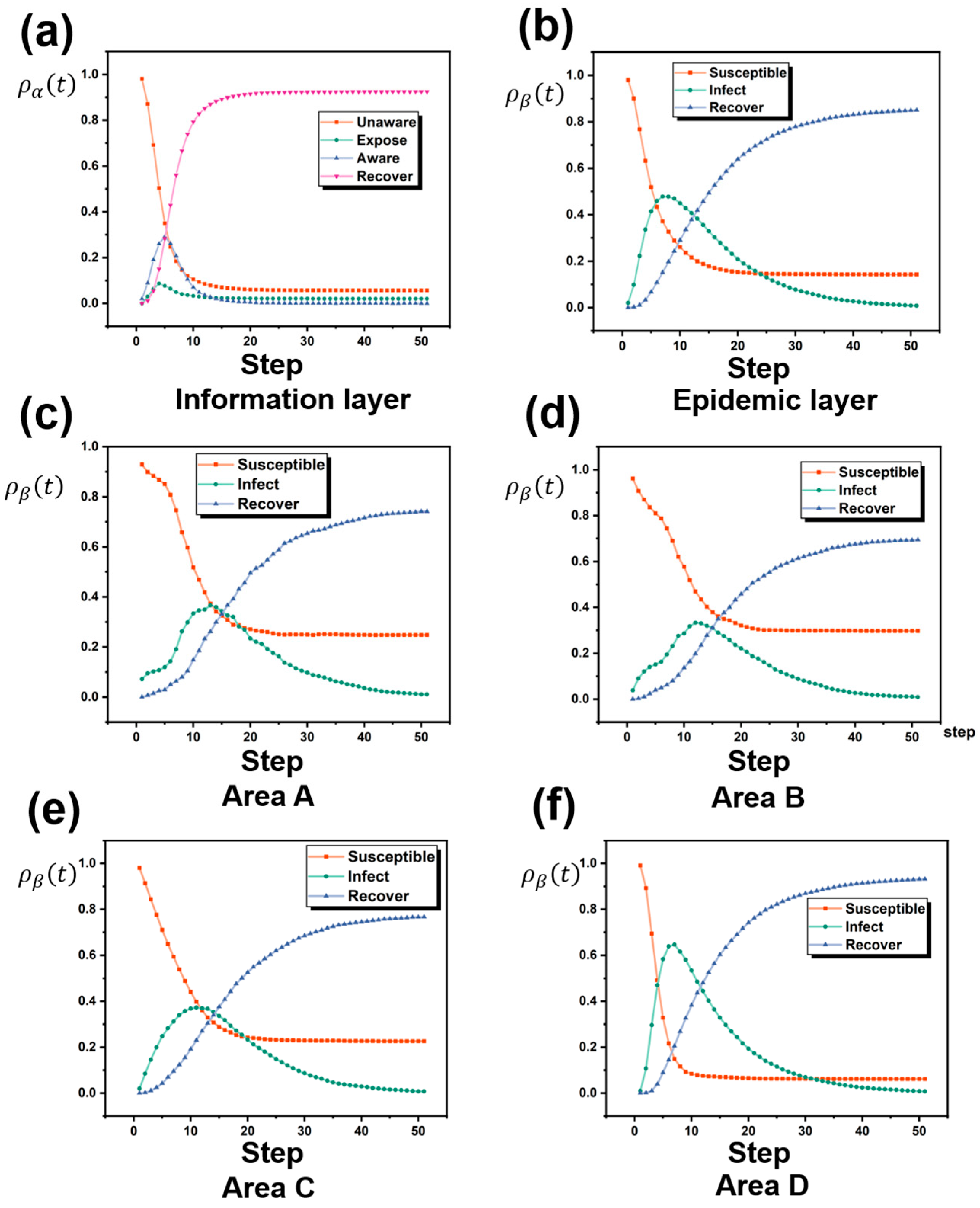
We first constructed a two-layer network to describe the coupling process of information diffusion and disease propagation, where the relevant parameters are set as ${\phi }_{\alpha }=0.1, {\gamma }_{\alpha }=0.5,{ \phi }_{\beta }=0.6,{ \gamma }_{\beta }=0.1, v=0.03,{ P}_{jump}=0.4,{ E}_{protect}=0.1, I_{protect}=0.4$. Figure 4a,b show the changes in node density at different states of the information layer and the disease layer, respectively. According to Figure 4a, during the information propagation process, the susceptible nodes (U) decrease over time, the nodes in the hesitant state (E) and the infected state (A) increase to a peak over time, and then begin to decrease, while the nodes in the recovery state (R) gradually increase until they stabilize. In this process, the system reaches a stable state after about 15 time steps, and most of the nodes are in the recovery state. According to Figure 4b, during the disease transmission process, the susceptible nodes (S) gradually decrease over time, the infectious disease begins to spread rapidly, and the number of nodes in the infected state (I) increases and then begins to decrease after reaching the peak until it drops to 0. At the same time, the number of nodes in the recovery state (R) continues to increase, and finally the system reaches a stable state at 35 time steps and the number of nodes in the recovery state in the system is the largest. In the process of disease transmission, information spreads more widely and rapidly and enters a stable state faster than the disease spreads. This result is consistent with the traditional infectious disease transmission model, proving that the model is feasible.

4.2. Considering the Factors That Affect the Spread of Infectious Diseases Under the Individual Psychological Safety and Emotional State

4.2.1. Psychological Safety and Coping Behaviors

Individuals who are aware of disease-related information will have a perception of disease risk. Such individuals will evaluate the risk of their environment, change their psychological security, and tend to take certain coping behaviors to avoid infection. This is the psychological security effect of individuals on diseases. Even if they know the same information, different individuals can perceive different risks. Different information will have an impact on individual psychological security, and the research results show that different information has different effects on disease transmission [29]. In this section, we categorize the psychological effects of different information on individuals. In the process of disease transmission, government departments, authoritative media, and other platforms will publish the current situation of the disease in the whole group, so that everyone receives the same information and the probability is equal [36]; such information is global information. Correspondingly, the individual infection situation around each individual is different, so the local information that the individual understands is also different [37,38]. Therefore, we hope to conduct a simulation study on the different psychological effects of individuals’ perceived risks and thus produce different behaviors.

In the above model, we assume that individuals who are not infected with the disease but receive information about the disease will act with a certain probability. Since individuals who know information related to the disease will perceive the risk of the disease, different individuals will have different risk perceptions, and the degree of protection measures will be different due to different changes in psychological security. Therefore, we hope to better consider the heterogeneity of changes in individual psychological security and the adoption of coping behavior measures. Individual behavior based on local information about the number of infections in the surrounding individuals or neighbors can effectively prevent the spread of disease [11]. However, at the same time, if individuals evaluate their own environment after the change in personal psychological security, they may also take risky behaviors, such as fleeing the region, buying, and other behaviors to promote the spread of diseases. Therefore, according to the research, we divided the coping behavior into positive defense behavior and negative resistance behavior and simulated the influence of these two behaviors caused by psychological effects [30].

The Effect of Active Defense on the Spread of Infectious Diseases

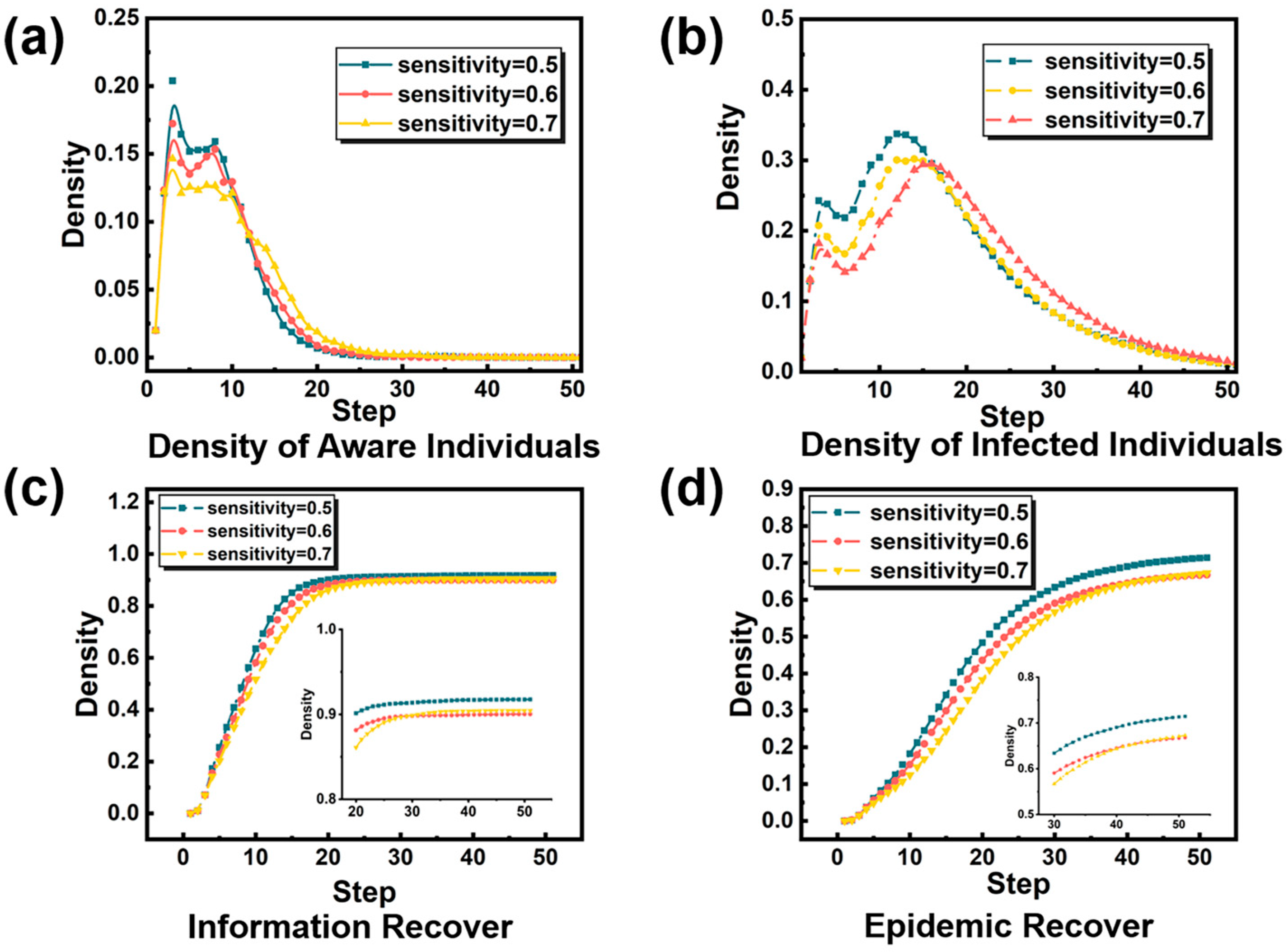
Active defensive behaviors, including protective, defensive (avoidance), and alternative behaviors, such as frequent hand washing, wearing masks, increasing cleanliness, and maintaining social distancing, can effectively prevent the further spread of infectious diseases. In this study, we will use $1/(1+\alpha I^h)$ to represent the changes in individual psychological effects caused by the increase in the number of infected individuals, and set the psychological safety threshold of defensive behavior ${\tau }_1$, that is, when the psychological safety level felt by individual $i$ is ${\phi }_1={\displaystyle \frac{1}{1+\alpha I^h}}<{\tau }_1$, he will take active defensive behavior to protect himself from infection by others, in which $\alpha$ and $h$ are fixed parameters. $I$ is the number of infected people around individual $i$.

Our parameters for this psychological effect simulation are set to ${\phi }_{\alpha }=0.1, {\gamma }_{\alpha }=0.5,{ \phi }_{\beta }=0.6,{ \gamma }_{\beta }=0.1, v=0.03,{ P}_{jump}=0.4,{ E}_{protect}=0.1,{ I}_{protect}=0.4, \alpha =0.02, h=2$.

The results are shown in Figure 5. We can see that the psychological effect of individuals will have an inhibitory effect on the spread of diseases. As shown in Figure 5b, with the increase in psychological safety threshold of an individual’s defensive behavior, the peak value of infection will gradually decrease. In other words, an individual who is aware of the infection situation of people around him and takes effective defensive measures earlier can inhibit the spread of infectious diseases. However, by observing the total number of recovered infected persons in Figure 5d, we find that the increase in the psychological safety threshold of defensive behavior can indeed make fewer people suffer from infection, but this effect is limited. In Figure 5a, we found that the psychological safety threshold of defensive behavior had an inhibitory effect on the transmission rate of disease information, and that more people could not receive the relevant information of infectious diseases in a relatively short time. However, the change in the total number of persons who forget the information, as seen in Figure 5c, showed that the psychological safety threshold of defensive behavior had no impact on the scope and breadth of information transmission. Information still spreads to a high level. To sum up, to enable individuals to effectively assess the level of disease around them, individuals can feel a moderate threat and take active and effective defense behaviors earlier, which can curb the spread of infectious diseases to a certain extent, but also have a certain inhibition effect on the spread of information, but the information will still spread in the end.

The Impact of Passive Resistance on the Spread of Infectious Diseases

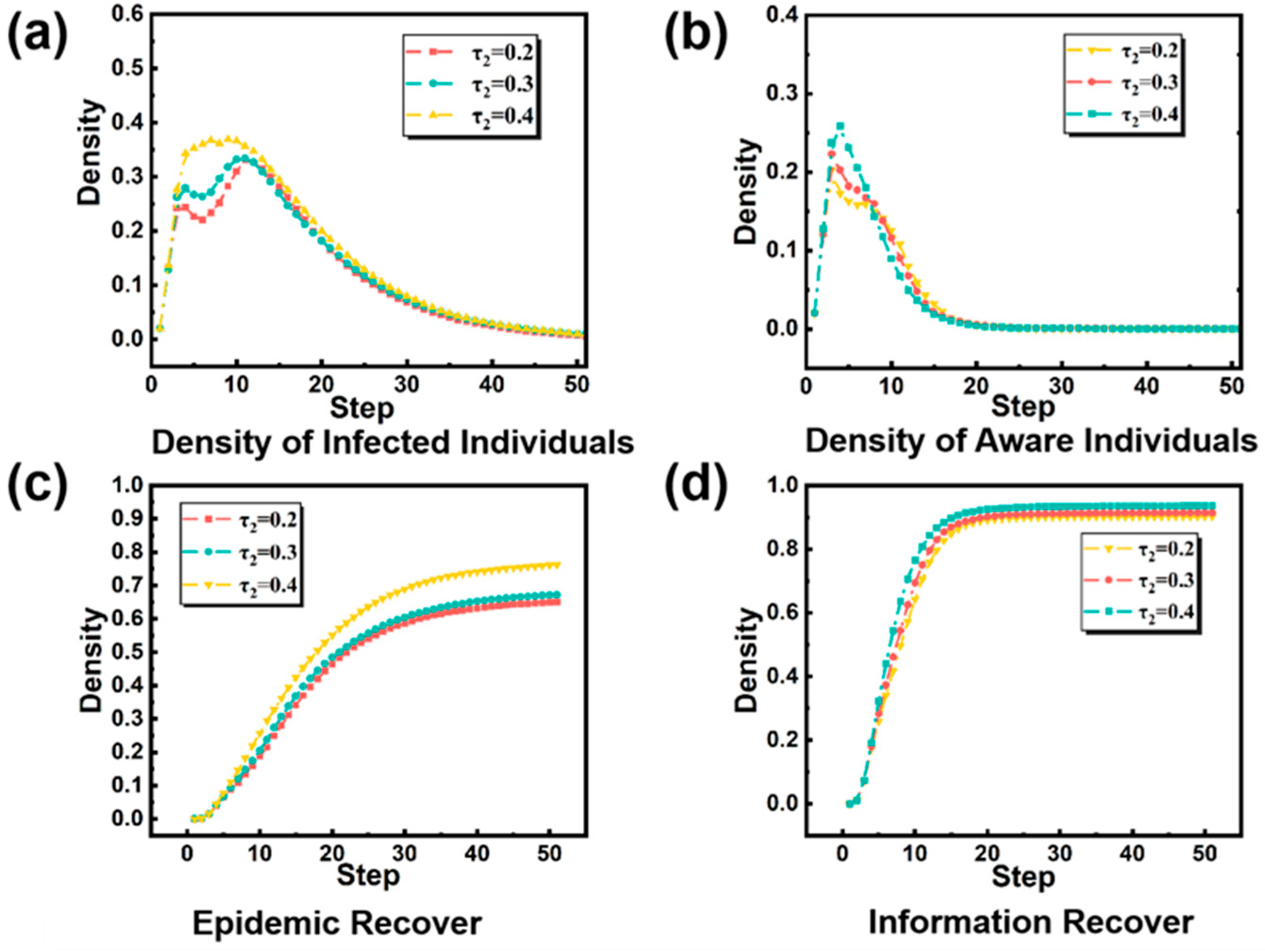
Due to the spread of infectious diseases, the panic caused by individuals’ unknown infectious diseases often leads to various resistance or destructive behaviors, such as refusing to vaccinate, hoarding daily necessities, buying medicines, and fleeing the area due to panic, which often deal a blow to the prevention and control of infectious diseases. In this study, we wanted to model these negative coping behaviors and explore their impact on the spread of infectious diseases. Therefore, we will use $1/(1+m{I_{Neighbor}}^h)$ to represent the changes in individual psychological effects caused by the increase in the number of infected individuals around individual $i$, and set the psychological safety threshold of resistance behavior ${\tau }_2$, that is, when the psychological safety level felt by individual $i$ is ${\phi }_1={\displaystyle \frac{1}{1+m{I_{Neighbor}}^h}}<{\tau }_2$, the resistance behavior mainly refers to the escape behavior from this region to other regions, where $m$ and $h$ are fixed parameters, and $I_{Neighbor}$ is the number of infected people around individual $i$.

We chose to fix the psychological safety threshold of individual defense behavior ${\phi }_1$ and adjust the psychological safety threshold of resistance behavior ${\tau }_2$, and obtained the infectious diseases transmission situation under different psychological safety threshold of resistance behavior ${\tau }_2$, as shown in Figure 6. Figure 6 shows the influence of psychological safety threshold ${\tau }_2$ of resistance behavior on disease transmission and information transmission when 0.2, 0.3, and 0.4 are taken. As shown in Figure 6a, the decrease in the psychological safety threshold of resistance behavior ${\tau }_2$ reduces the peak value of disease transmission, and when ${\tau }_2=0.4$, the spread to infectious diseases will not appear in multiple stages, which may be due to the high psychological safety threshold of individual resistance behavior, resulting in the spread to infectious diseases in multiple regions caused by individual resistance behavior, that is, jumping to other regions to escape. In addition, as shown in Figure 6c, it can be seen that better control of the psychological safety threshold of individual resistance behavior can greatly reduce the overall number of patients. As shown in Figure 6b, we found that the increase in the psychological safety threshold of individuals’ resistance behavior led to a gradual increase in the peak value of information transmission. This kind of flight behavior to other areas not only brought the risk of triggering infectious diseases in other areas, but also caused more people to know the relevant information of infectious diseases. The increase in the psychological safety threshold of individual resistance behavior makes the range of information dissemination wider and causes more individuals to understand the information of infectious diseases.

4.2.2. Information Diffusion

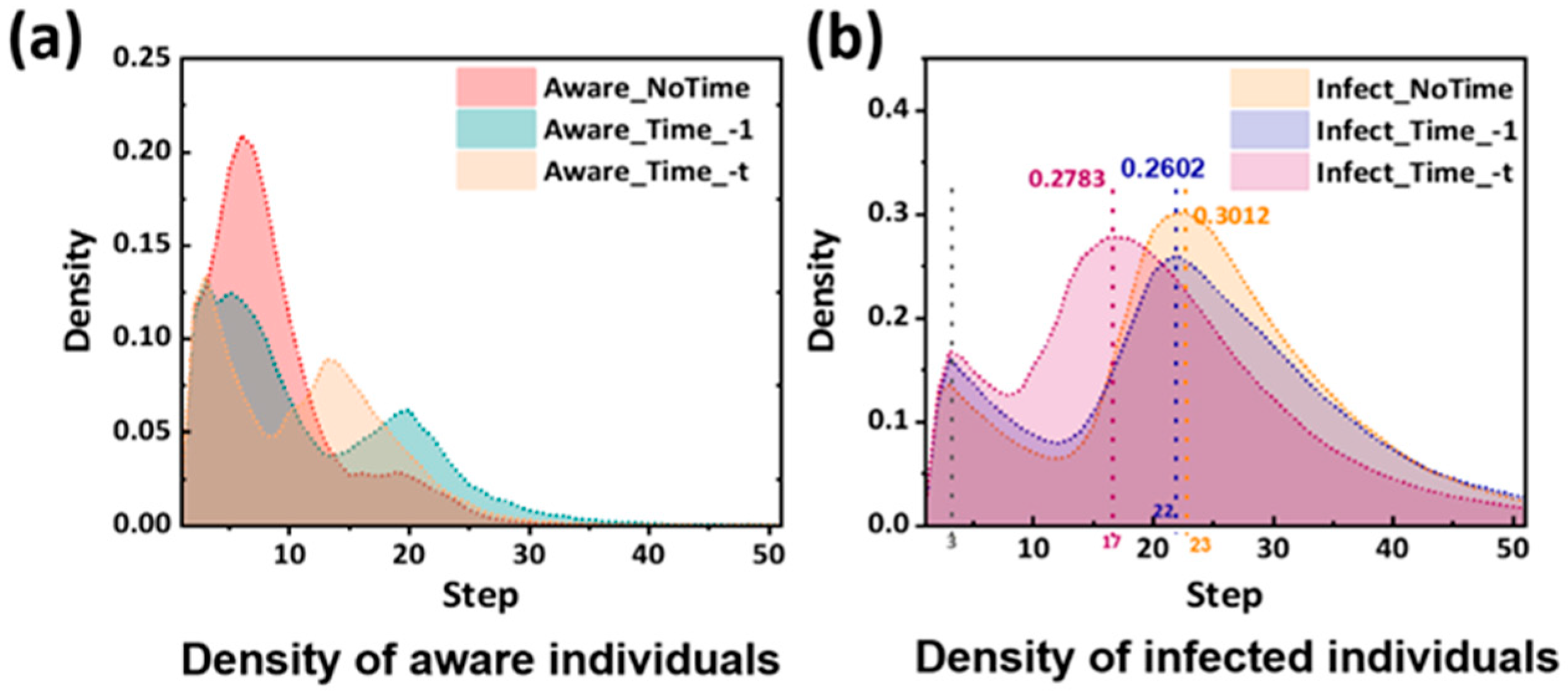
In reality, when an infectious disease breaks out, disease information often has the properties of multiple sources and rapid updates. Therefore, we hope to incorporate the impact of different characteristics of information on the spread of infectious diseases into the model, such as the timeliness and ambiguity of information.

Timeliness of Information

Since the content of information response has a certain lag, the use value of information will gradually decrease with the passage of time. We hope to explore the influence of the timeliness of information on the spread of infectious diseases, and the results are shown in Figure 7. Figure 7 shows the variation in individual density over time in the $\alpha$ layer in the state of informed transmission ($A_{\alpha }$) and in the $\beta$ layer in the state of infection transmission ($I_{\beta }$) when $V_3=1$, $V_3=e^{-1}$, and $V_3=e^{-t}$.

As shown in Figure 7a, considering the timeliness of information to decay with time ($V_3=e^{-t}$), compared with considering the timeliness of information to remain fixed ($V_1=1$, $V_2=e^{-1}$), the rate maintained a similar increase in the early stage of the experiment, but considering the constant timeliness, group ($V_1=1$) reached a higher peak in a short term (within 10 time steps). That information tends to reach more people more quickly and turn them into communicators. The peak value of the group with constant timeliness ($V_2=e^{-1}$) in the short term is basically the same as that of the group considering timeliness attenuation with time ($V_3=e^{-t}$), but the group considering timeliness attenuation with time ($V_3=e^{-t}$) enters the decline after the first peak faster and enters the peak of the second propagation. The peak value of the second propagation was higher than that of the time-invariant group ($V_2=e^{-1}$). At the same time, compared with Figure 7b, considering the constant timeliness of information ($V_1=1$), it was lower than the other two groups at the peak of the first infection, that is, at the early stage of the infectious diseases, strong timeliness of information would inhibit the spread of the disease. In addition, in Figure 7b, we found that in the process of considering the timeliness of information decreasing with time, within 1–10 steps, when $V_3=e^{-t}$, the first infection peak value was the highest, and the second infection wind value came faster, but the second infection peak value was lower than $V_1=1$ and slightly higher than $V_2=e^{-1}$. When $V_1=1$, the first infection peak value was the lowest, but the second infection peak value was the highest. When $V_2=e^{-1}$, the peak value of the first infection was higher than that of $V_1=1$, but slightly lower than that of $V_3=e^{-t}$. This may be due to the fact that the timeliness of information decreases with time, so individuals do not pay much attention to the information and so they ignore the information, resulting in the rapid arrival of the second infection peak. However, the timeliness of information has an effective but limited effect on the suppression of the spread of infectious diseases, and once it exceeds a certain threshold, it cannot have an obvious effect.

Vagueness of Information

When information is released, it cannot be accurately and clearly understood by everyone due to the wording, source, and other reasons. Therefore, we take the ambiguity of information into account in the model, hoping to explore how the diffusion of information affects the spread of infectious diseases under different information ambiguity. The results are shown in Figure 8, which shows the situation of information diffusion and infectious disease spread under the three conditions of high, medium, and low ambiguity $V_2$ by adjusting $\epsilon =1$, $\epsilon =0.5$, and $\epsilon =0$. As shown in Figure 8a, with the decrease in ambiguity, it can obviously be observed that in the first infection, the peak value of infection with high ambiguity is higher, and the peak value of infection with low ambiguity is lowest. In the second infection, the peak value of infection with high ambiguity is faster, while the peak value of infection with low ambiguity is slowest. This may be due to the limited inhibitory effect of information ambiguity on the spread of infectious diseases after the first infection. In Figure 8b, it can be observed that the decrease in information ambiguity increases the number of people in the information informed and spreading state $A_{\alpha }$ at the time of the first infection. This may be because the decrease in ambiguity increases the chance of individuals getting infected with the disease $A_{\alpha }$. When the second infection peak comes, because the number of infected people is basically the same, the increase in information ambiguity limits the transmission of information and thus leads to the faster arrival of the peak number of infected people. In Figure 8c, we conducted a simulation study on the density of people in the recovery state of $R_{\beta }$ in the transmission layer during the outbreak of infectious diseases and found that the ambiguity of information had a certain effect on inhibiting the spread of the disease at the beginning of the infectious diseases. In the situation of low ambiguity of information, fewer individuals became ill and fewer people recovered. However, at the end of the infectious diseases, the total number of patients recovered from the disease was lower in the scenario with high information ambiguity. This may be due to the fact that the information transmission failed to effectively inhibit the disease transmission in the early stage due to low information ambiguity, resulting in more individuals falling ill and making individuals choose more effective defensive measures after risk assessment. The influence of information ambiguity on information transmission has a certain inhibitory effect in the early stage of disease occurrence but does not play a major role in the middle and late stage of infectious diseases development. In Figure 8d, the change in the number of people in $R_{\alpha }$ (Recover) immune state in the information dissemination layer over time is analyzed. We find that in the early stage of infectious diseases and with high information ambiguity, more individuals learn the information and then forget it after a certain period of time. This may be due to the rapid spread of the disease and the transformation of the individual into A state of informed transmission $A_{\alpha }$ depends not only on the transmission of information but also on the spread of the disease. By observing the curve development in the middle and later stages of Figure 8d, it can be observed that the increase in information ambiguity eventually has a certain impact on the scale of information diffusion. When the information ambiguity is moderate and low, more and more individuals can understand the information related to disease transmission. In summary, the ambiguity of information has an impact on the final range of information transmission and can effectively inhibit the level of the peak of the first infection and the speed of the peak of the second infection, but it fails to significantly inhibit the overall final scale of the disease.

4.2.3. Network Structure

In order to explore the influence of different network structures on disease transmission on social media, we set the information layer as LFR artificial network and BA scale-free network, respectively, to explore the influence of network structure and community structure on the infectious diseases transmission scale and other factors, and the parameters are set as above.

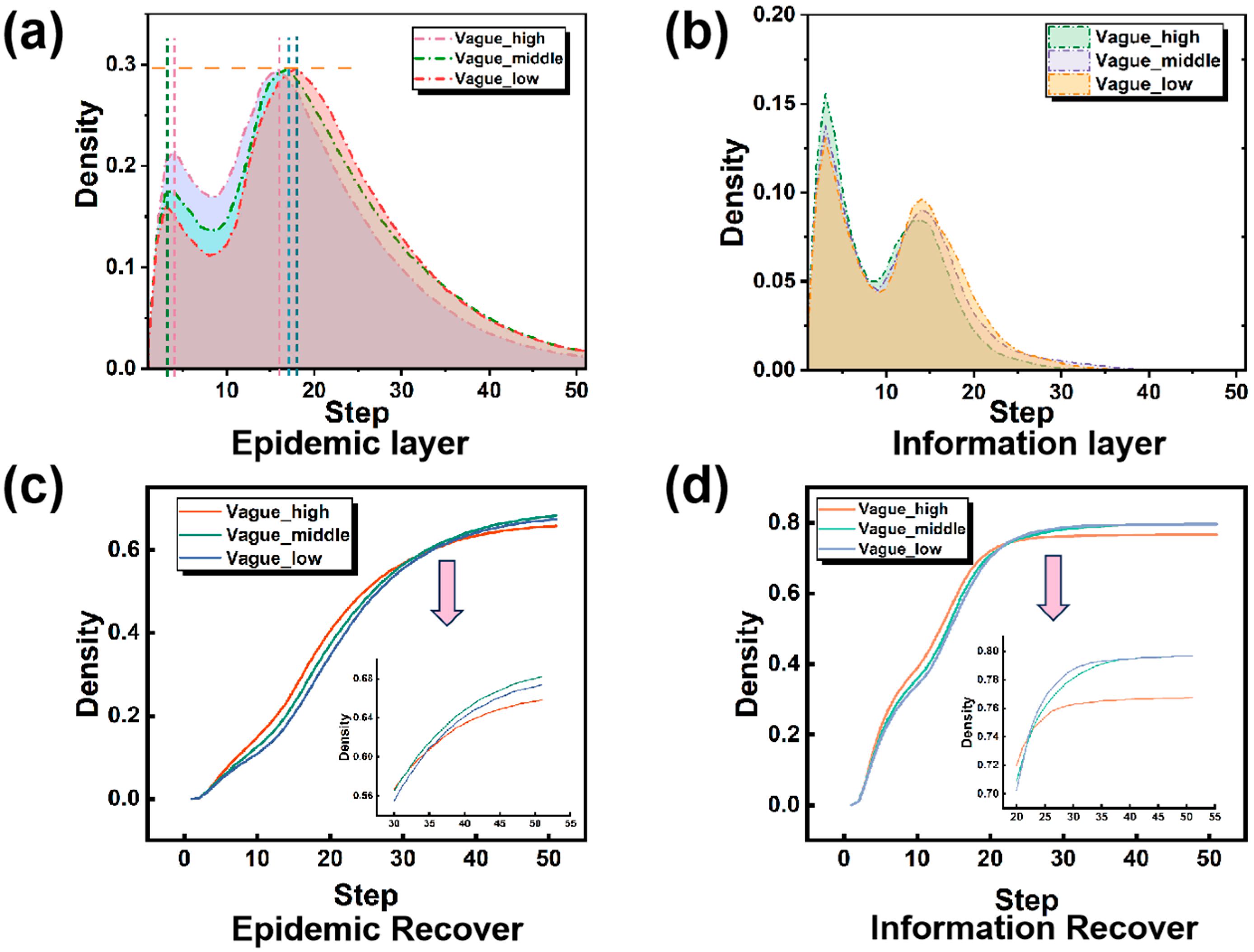
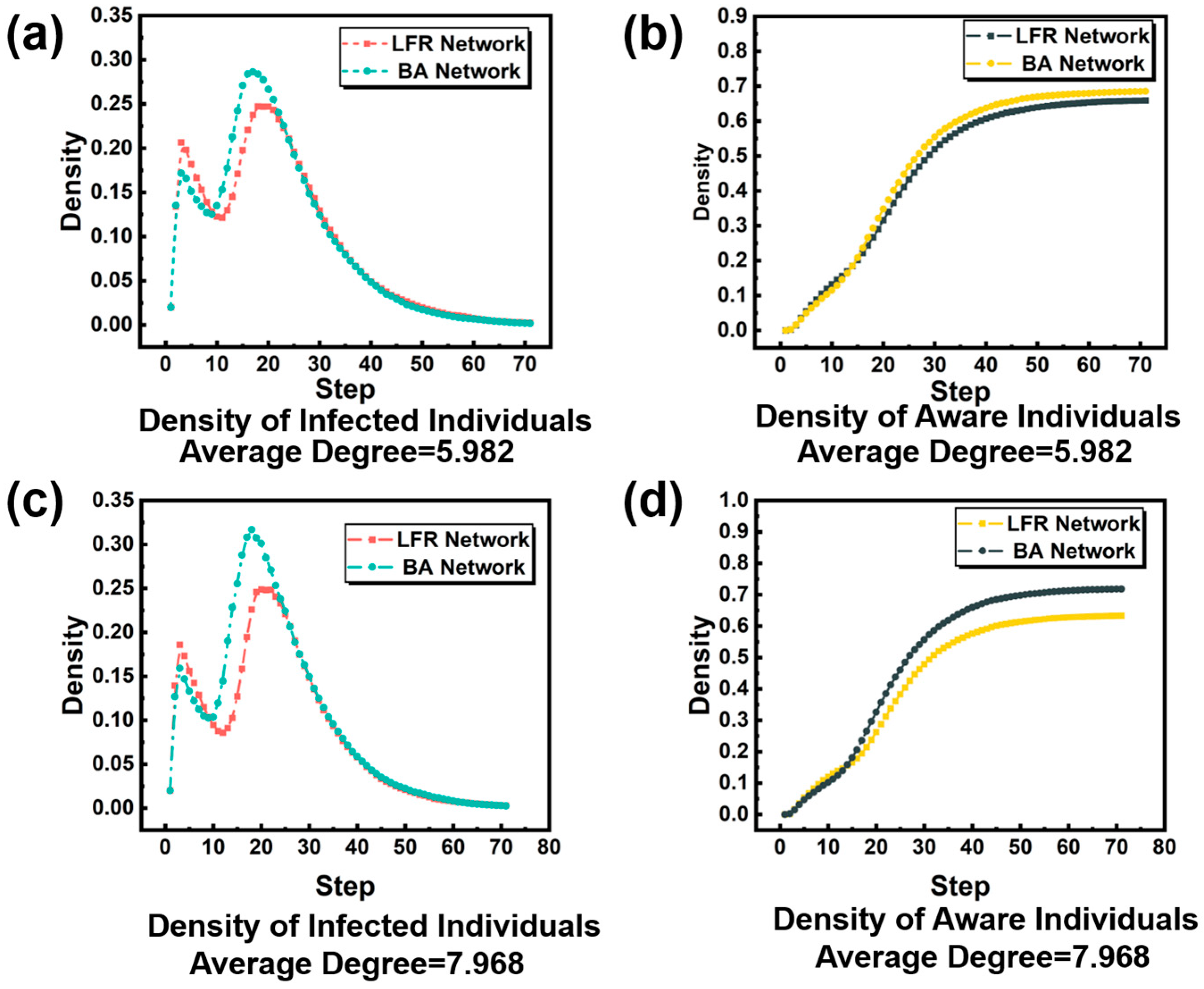
As shown in Figure 9, the density of diseased individuals varies with different network structures under the same average degree. We found that in Figure 9a,c, when the first infection peak came, the infection peak was higher when the structure of the social network was an LFR network. However, when the peak of the recurrent infectious disease infection came, we observed that the situation was the opposite of the first infection. That is, when the recurrent infectious disease was infected, the structure of the social network was the LFR network, which was significantly lower than the peak of the infection when the social network structure was the BA network. Comparing Figure 9a with Figure 9c shows that the differences between the two networks become more pronounced as the network average increases. Comparing Figure 9b,d, it can be seen that under the same average degree, there is a significant difference in the final number of infected people between the two networks. BA network has more individuals infected and sick than LFR network, which may be due to the more obvious community structure in LFR network, and the closer the contact between individuals in the community, the faster the individuals will obtain information and take effective preventive measures, and finally control the infection scale.

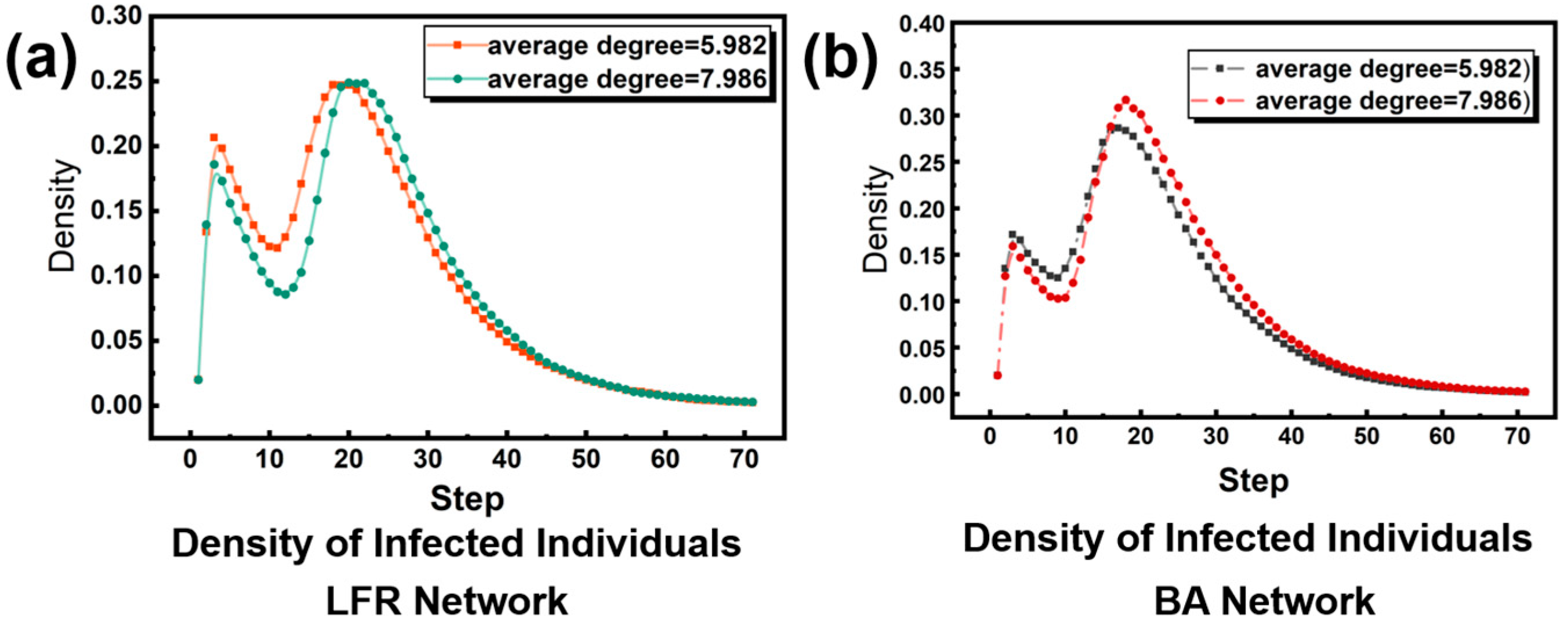
We want to explore how different network structures are affected by network averages, as shown in Figure 10. Figure 10a shows the influence of the average degree change in LFR artificial network on the individual density of disease infection. It can be seen that the increase in network average degree in LFR artificial network makes the peak density of individuals infected with the first disease decrease and delays the arrival time of the peak density of individuals infected with the second disease, but the peak density of individuals infected with the second disease is almost unchanged. This may be due to the fact that in the early stage of infectious diseases, individuals who are closer together in the community are more likely to spread information, so that individuals can take effective preventive measures to control the spread to infectious diseases. However, as time goes on, more and more individuals have obtained disease information, and the influence of community structure is no longer obvious, such as the arrival of the second wave of infection. Figure 10b shows the influence of BA network mean degree change on individual density of disease infection. It can be seen that the increase in BA network mean degree makes the peak density of individuals infected with the first disease decrease and delays the arrival time of the second infection peak, but the peak density of individuals infected with the second disease increases. We guess that this may be due to the characteristics of BA network. When the first infection comes, the increase in average degree makes it easier for individuals to obtain information and take effective measures, which is consistent with the structure of LFR network. However, in the second infection, the nodes that may obtain information are not relatively large nodes in the BA network. Therefore, the influence of information on the disease layer cannot be exerted in the second infection, which is what we need to further study.

Therefore, we find that different network structures in the information layer have influence on the peak value and the final scale of infectious disease transmission through simulation of network structure and network average degree, and the community structure in the early stage of infectious disease has influence on information transmission and disease control, but in the subsequent multi-wave infection, different measures should be taken for different network structures to control disease transmission.

5. Conclusions

In the previous chapter, we explored the various factors that influence the spread of infectious diseases. It includes diverse coping behaviors arising from changes in individual psychological security and information characteristics in the communication of public information. To summarize, this paper proposes a two-layer network model based on individual psychological security. The upper layer is the information diffusion process in the transmission of infectious diseases and the lower layer is the process of disease prevalence in the transmission of infectious diseases. Compared with the traditional two-layer network of disease information, this model can better demonstrate the multi-wave spread of infectious disease transmission. The transmission dynamics of the two-layer network interact with each other. On the one hand, individuals who receive disease information will alter their sense of security and then adopt different behaviors to cope with the spread of infectious diseases; on the other hand, individuals infected with diseases can immediately become aware of information related to infectious diseases and change their level of psychological security. The spread of infectious diseases in the lower disease layer will promote the spread of information in the upper information layer. Finally, the dynamic equation of the system can be obtained by constructing the probability transfer tree among various states. Through numerical simulations, a large number of experimental results were obtained to discuss the influence of some important parameters in the model, that is, different factors on the transmission scale and transmission peak. The experimental results show that in terms of individual psychological security and coping behavior, active defensive behavior can curb the spread of infectious diseases to a certain extent but also inhibit the rate of information diffusion. Passive resistance behavior may lead to the recurrence of multiple infectious diseases, while promoting information diffusion. In addition, we also conducted a certain study on the impact of information characteristics on information diffusion, and the results showed that maintaining high timeliness and low fuzziness of information can effectively reduce the peak value of the first infection, but it cannot significantly inhibit the overall final scale of the disease. Therefore, information diffusion plays a significant role in the early stage of infectious disease transmission. Additionally, we investigated the influence of community structure of information networks on disease transmission. The results showed that disease transmission varies under different network structures. The community structure and closeness of network individuals exert a certain effect in the early stage of infectious diseases, but the exploration of subsequent multi-wave disease transmission remains unclear.

The research results of this paper can provide a theoretical basis for the prevention and control of infectious disease transmission after the government publicly releases information, from the perspective of individual psychological security. In addition, our study offers an effective reference for infectious disease prevention and control, which can further assist relevant departments in formulating effective and reasonable response measures. For instance, timely and accurate updating of information enables individuals to maintain a certain sense of risk and adopt active defensive behaviors, thereby effectively controlling the spread of infectious diseases in the initial stage of transmission. However, individuals’ psychological security should not be excessively low, otherwise it will trigger passive resistance behaviors and expand the transmission scale of infectious diseases. Therefore, effective geographical isolation is necessary. However, there are still some shortcomings in this study that warrant further discussion. On the one hand, individual behaviors are not limited to active defense behaviors and passive resistance behaviors in real situations, and the model should take into account the impact of more diverse behaviors on the spread of infectious diseases. On the other hand, the limited system and stability analysis of the model are also issues worthy of further consideration.