An Evolutionary Game Analysis of AI Health Assistant Adoption in Smart Elderly Care
Abstract
1. Introduction
2. Literature Review and Theoretical Background
2.1. Adoption of AI Health Assistants Among Older Adults
2.2. Platform Responsibility and Service Optimization Strategies
2.3. Government Incentive Mechanisms for Digital Health Promotion
2.4. Evolutionary Game Theory and Digital Health Behavior
3. Model Construction
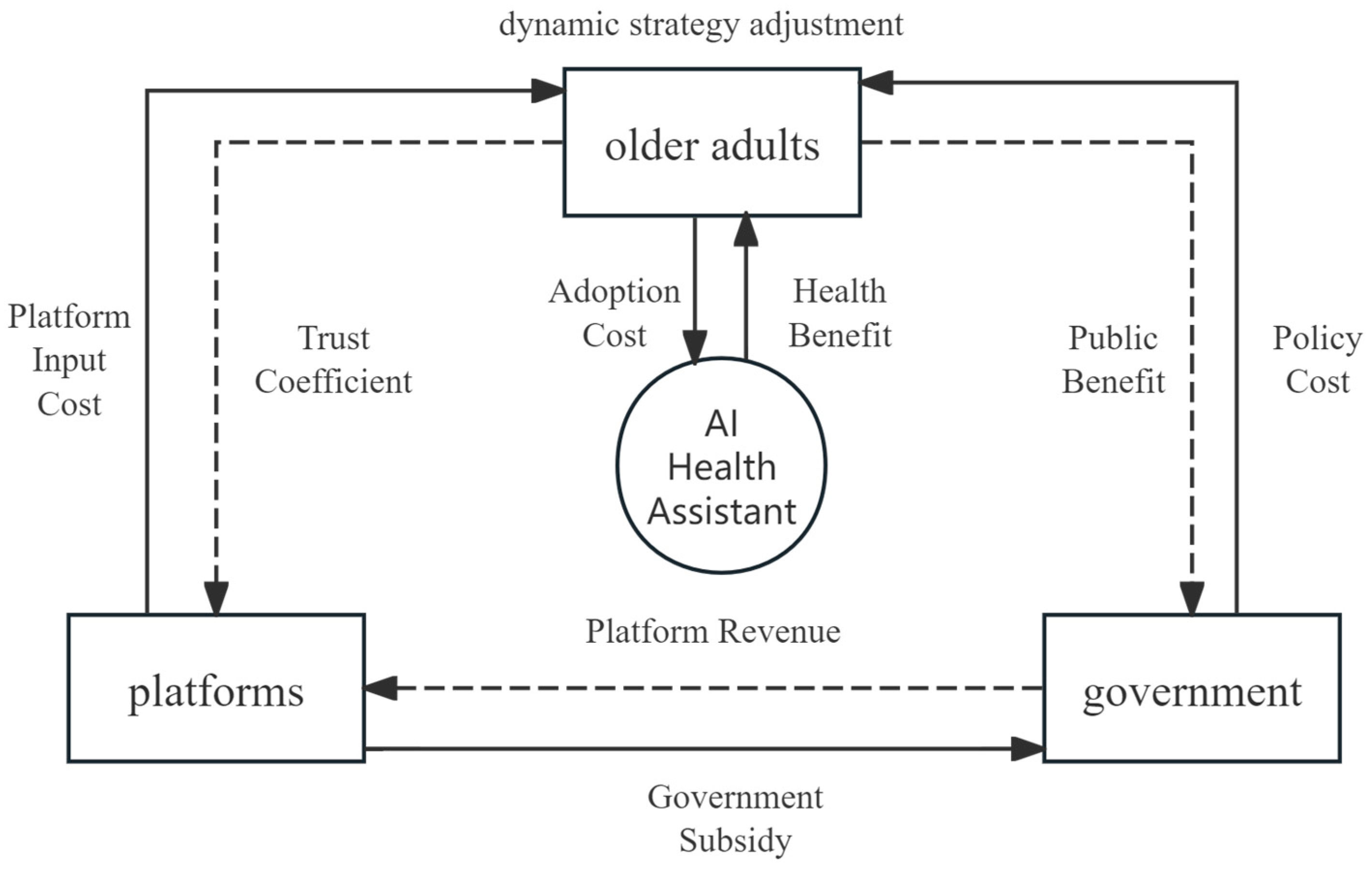
3.1. Definition of Participants and Strategies
3.2. Modeling Assumptions
- Bounded Rationality: All three actors—older adults (users), platforms (service providers), and the government (policy makers)—are assumed to exhibit bounded rationality. Instead of seeking globally optimal strategies, they adjust their behaviors based on observed payoff differences over time. This aligns with the foundational principle of evolutionary game theory and reflects real-world decision-making constraints such as incomplete information and cognitive limitations.
- Replicator Dynamics and Continuous Time: Strategy evolution follows continuous-time replicator dynamics. Agents are more likely to adopt strategies with above-average payoffs. This mechanism applies to platforms optimizing services based on feedback, older adults following peer behavior, and governments adjusting subsidies based on system performance.
- Sequential Decision Structure: The model assumes a three-stage sequential decision structure reflecting real-world decision-making: (1) The government first determines whether to implement subsidies. (2) The platform observes policy and decides its service investment level. (3) The user decides whether to adopt, based on perceived service quality and trust.
- Trust and Reputation Mechanism: Platform service quality influences user trust through a reputation mechanism represented by coefficient . High-quality service leads to increased trust (→1), while poor service reduces trust (→0).
- Market Competition: Multiple platforms compete in the market. Competition intensity is captured by , with larger indicating fiercer competition.
- Network Externalities: Older adult adoption exhibits network effects. The adoption rate influences perceived value through externality coefficient .
- Policy Spillover Effects: Government subsidies not only reduce platform costs directly, but also enhance user confidence indirectly via signaling. This is captured by spillover coefficient .
- Parameter Stability and Population Homogeneity: Key parameters such as service cost, user benefit, and incentive coefficients are held constant in the baseline model for clarity. All actor groups are assumed to be homogeneous within, meaning individuals in the same group respond similarly to payoffs.
3.3. Evolutionary Game Payoff Matrix Constructing
- Stage 1: Government Decision-Making Stage. The government acts first, evaluating whether to implement subsidy incentives based on the anticipated public health returns and fiscal constraints .
- Stage 2: Platform Response Stage. Platforms make strategic decisions in response to observed government policies, considering factors such as incentive strength, market competition, and expected user demand. This determines their level of investment in service quality .
- Stage 3: User Adaptation Stage. Older adults respond lastly by observing actual platform service performance and policy support. Their adoption decisions are shaped primarily by trust levels, which are influenced by the preceding stages .
3.3.1. Definition of Core Variables
- Health Benefit (): The health management benefits gained by older adults from using AI health assistants, such as early disease detection and personalized health recommendations. The values are normalized within the range , reflecting the potential value of the technology.
- Adoption Cost (): The cost incurred by older adults when adopting AI health assistants, including learning costs, privacy risk, and psychological barriers. The values are normalized in the range , estimated based on the technology adoption literature.
- Trust Coefficient (): Represents the level of trust older adults place in the service quality of the platform, with . When the platform adopts a high-quality optimization (HQ) strategy, approaches 1; when it opts for low-cost operation (LC), tends toward 0.
- Platform Input Cost (): The resource cost borne by the platform under a high-quality optimization strategy, including R&D and system maintenance. The values are normalized within the range , reflecting the realistic cost spectrum of technology development.
- Government Subsidy (): The financial support provided by the government to incentivize service optimization by the platform, such as direct subsidies or tax relief. This is normalized to the range , with references to digital health policy literature.
- Public Benefit (): The public health benefits obtained by the government as a result of older adults adopting AI health assistants, such as reduced medical resource consumption and enhanced social welfare. Values are normalized within the range .
- Policy Cost (): The fiscal cost incurred by the government when implementing subsidy incentives. This is normalized to the range .
- Platform Revenue (): The benefits earned by the platform from older adult adoption, such as subscription fees, data value, or other commercial returns. This is normalized within ; is assumed to be a constant for model simplification.
- Reputation Influence Coefficient (): , portraying the strength of reputation’s influence on users’ adoption decisions.
- Market Competition Intensity (): , reflecting the impact of market competition on platforms’ strategy choices.
- Network Externality Coefficient (): , capturing the network effect of user adoption.
- Policy Spillover Coefficient (): , measuring the signaling effect of government subsidies.
3.3.2. Three-Party Game Payoff Matrix
- Based on the defined variables above, the benefit functions under the eight possible combinations of strategies are derived as follows:
- Strategy combination (A, HQ, S): The older adult adopts the AI assistant under high trust (i.e., high-quality service), the platform invests in service optimization and receives government subsidy, and the government bears policy costs but gains public benefit. The older adult’s utility is the trust-weighted health benefit minus the adoption cost: . The platform’s utility is the user-derived revenue minus optimization cost plus subsidy: . The government’s utility is public benefit minus policy cost: .
- Strategy combination (A, HQ, NI): The older adult adopts under high trust, the platform invests in high-quality optimization without subsidy, and the government incurs no cost but still gains public benefit,. The platform’s utility decreases due to no subsidy: . The government’s utility is , as no expenditure is involved.
- Strategy combination (A, LC, S): The older adult adopts under low trust (i.e., low-quality service), the platform opts for low-cost operation and receives a subsidy, and the government pays the policy cost. Due to lower trust, the older adult’s utility is . The platform incurs no optimization cost and gains: . Government utility: .
- Strategy combination (A, LC, NI): The older adult adopts under low trust, the platform chooses a low-cost operation without subsidy, and the government does not intervene. Older adult utility: . Platform utility:. Government utility: .
- Strategy combination (NA, HQ, S): The older adult does not adopt; the platform invests in high-quality service and receives a subsidy; the government pays the policy cost but gains no public benefit. Older adult utility: . Platform utility (no user gain but incurs cost): . Government utility: .
- Strategy combination (NA, HQ, NI): The older adult does not adopt, the platform optimizes without subsidy, and the government does not intervene. Older adult utility:. Platform utility: . Government utility: .
- Strategy combination (NA, LC, S): The older adult does not adopt, the platform operates at low cost and receives a subsidy, the government pays policy cost. Older adult utility: . Platform utility: . Government utility: .
- Strategy combination (NA, LC, NI): The older adult does not adopt, the platform operates at low cost without subsidy, and the government does not intervene. All parties receive zero utility: , , .
4. Dynamics and Analytical Derivations
4.1. Derivation of Tripartite Evolutionary Equations
4.1.1. Replicator Dynamics of Older Adults
4.1.2. Replicator Dynamics of Platforms
4.1.3. Replicator Dynamics of Government
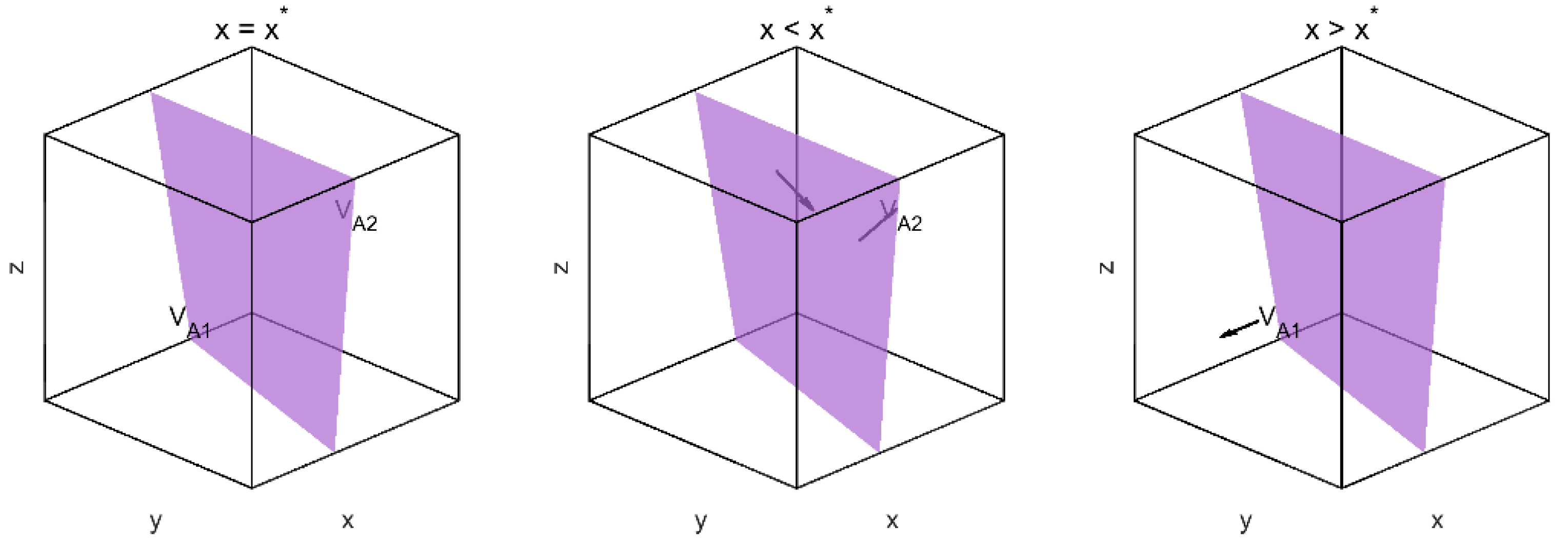
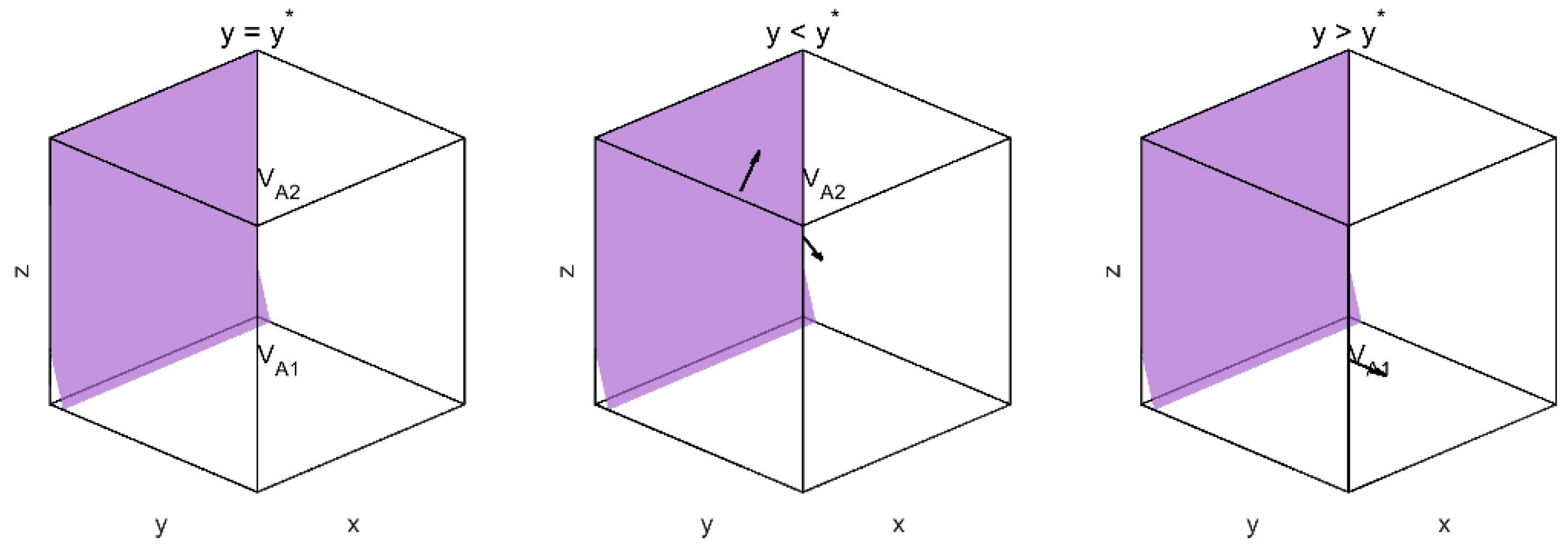
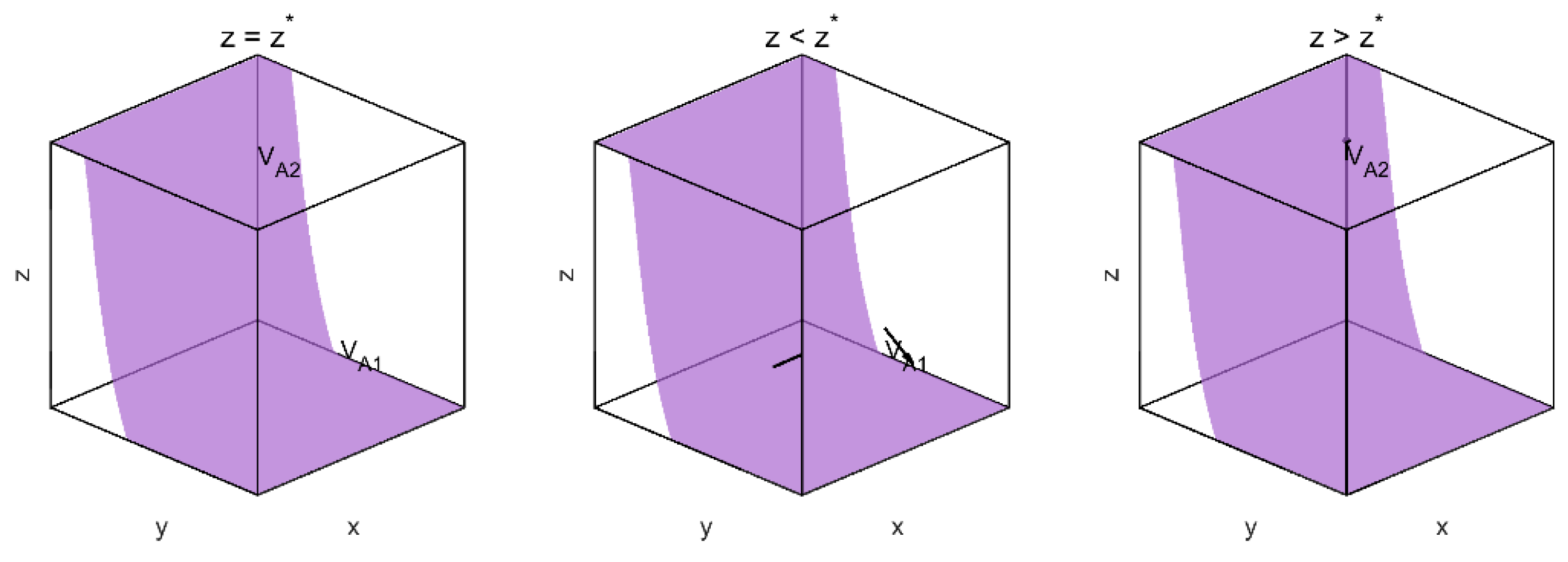
4.1.4. Evolutionary Direction and Equilibrium Conditions
4.2. ESS Analysis and Stability Conditions
4.2.1. Conditions for Evolutionary Stability
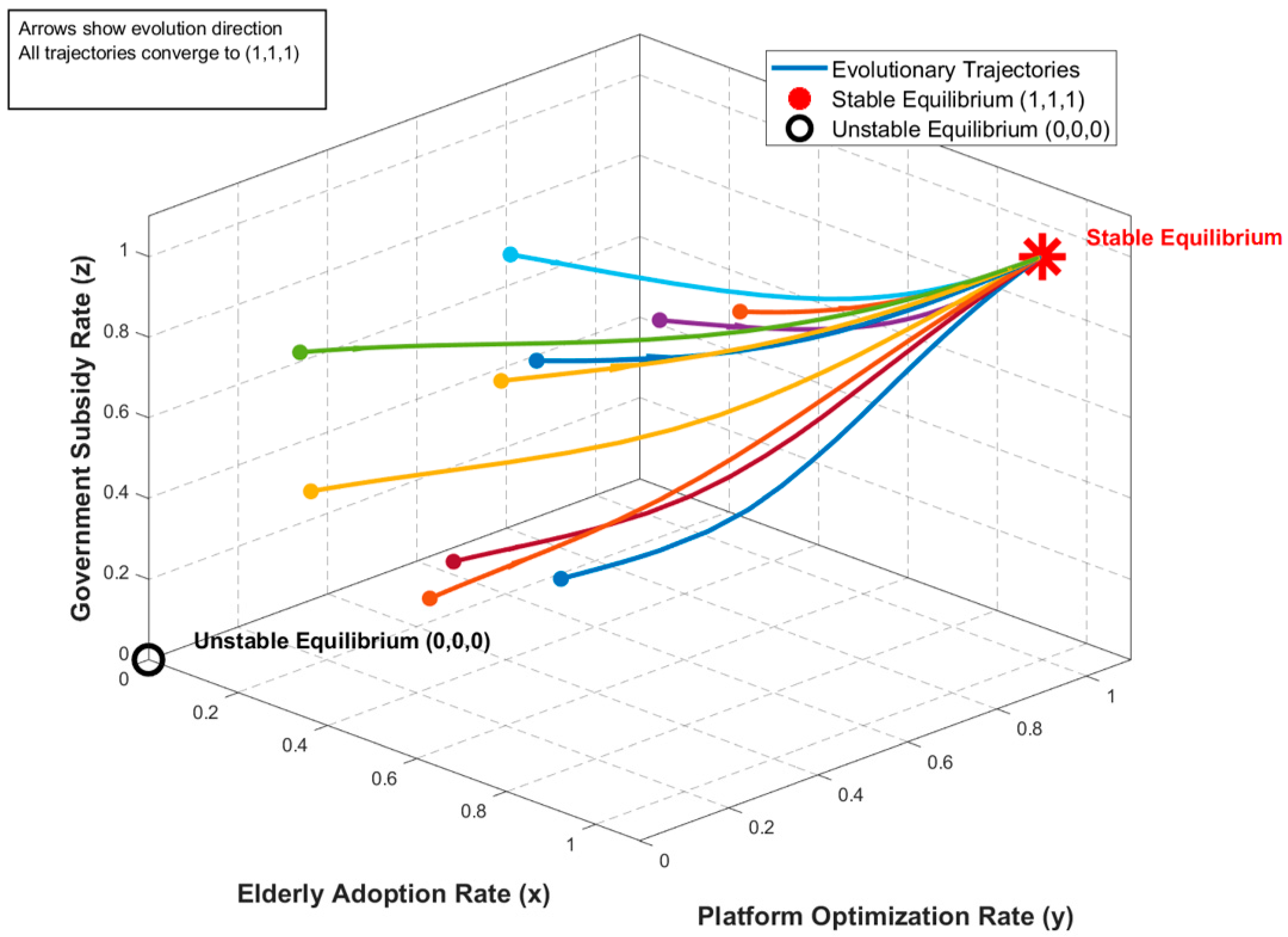
- (0,0,0): Non-adoption by older adults, low-cost operation by platforms, and no intervention by government, indicating a degenerative cycle;
- (1,1,1): Full adoption by older adults, high-quality optimization by platforms, and subsidization by the government, indicating a desirable high-performance state.
- Although (0,0,0) is a steady state, its local stability must be verified using the Jacobian matrix. The Jacobian matrix is defined as follows:
4.2.2. Parameter Conditions Leading to Degenerative Cycles
- High adoption costs: , older adults are reluctant to adopt due to high costs;
- Low trust level: , the low-cost operation of the platform erodes user trust;
- High optimization cost: is too high, platforms lack incentive to optimize;
- High policy cost: , the government is unwilling to bear subsidies.
- Conditions for adoption by older adults: ;
- Conditions for platform optimization: ;
- Conditions for government incentives: .
5. Numerical Simulation and Results
5.1. The Simulation Settings
5.2. Results and Path Analysis
6. Sensitivity Analysis
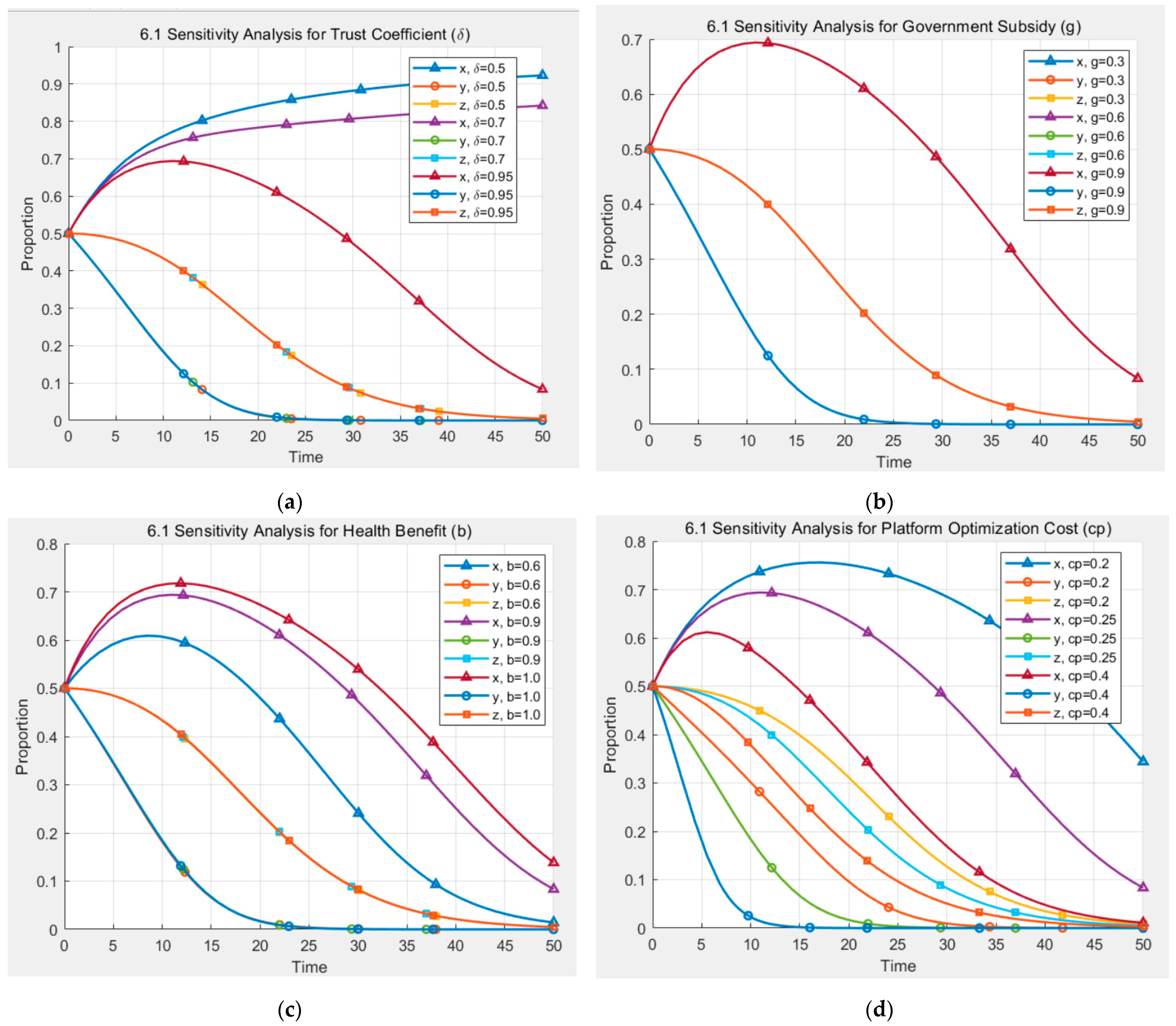
6.1. Sensitivity Analysis of Parameters
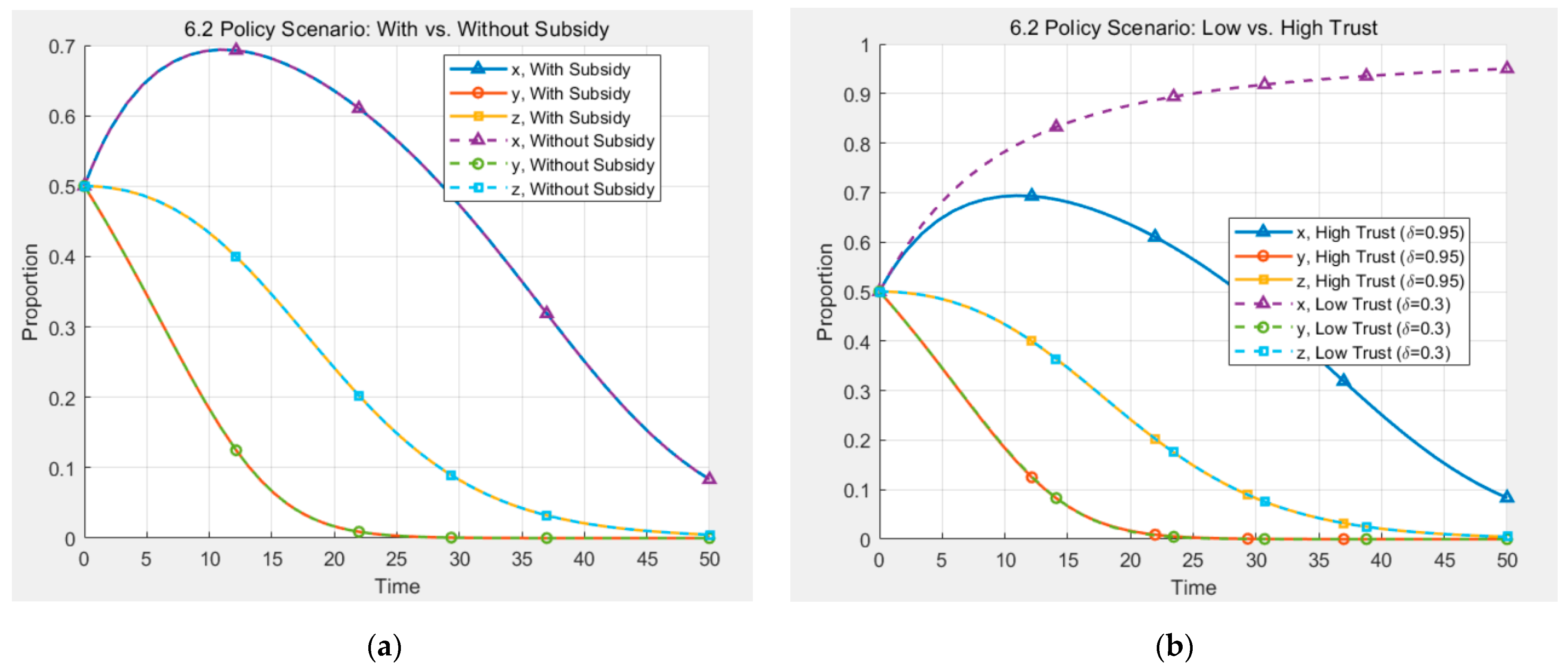
6.2. Policy Simulation and Scenario Comparison
7. Discussion
7.1. Theoretical Contributions and Model Significance
7.2. Practical Implications
7.3. Research Limitations and Future Directions
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Value | Meaning |
|---|---|---|
| 0.9 | Health benefit | |
| 0.2 | Adoption cost | |
| 0.95 | Trust coefficient | |
| 0.25 | Platform optimization cost | |
| 0.7 | Government subsidy | |
| 0.8 | Public welfare gain | |
| 0.15 | Policy cost | |
| 0.5 | Platform revenue | |
| 0.5 | Trust spillover effect | |
| 0.6 | Subsidy amplification effect | |
| 0.1 | Convergence constant (for phase diagram only) | |
| [0, 50] | Time span | |
| 0.1 | Time step |
References
- United Nations Department of Economic and Social Affairs. World Population Prospects. 2024. Available online: https://www.un.org/zh/node/219470 (accessed on 10 April 2025).
- Liu, Y.; Tamura, R.; Xiao, L. Barriers to Older Adults Adapting Smart Homes: Perceived Risk Scale Development. Buildings 2024, 14, 1226. [Google Scholar] [CrossRef]
- Ramirez, D.E.A.; Grasse, L.; Stone, S.; Tata, M.; Gonzalez, C.L. AI-powered speech device as a tool for neuropsychological assessment of an older adult population: A preliminary study. Acta Psychol. 2025, 257, 105084. [Google Scholar] [CrossRef] [PubMed]
- Imkome, E.U.; Soonthornchaiya, R.; Lakanavisid, P.; Deepaisarn, S.; Wongpatikasereeb, K.; Suebnukarn, S.; Matthews, A.K. Ai-Aun Chatbot: A Pilot Study on the Effectiveness of an Artificial Intelligence Intervention for Mental Health Among Thai Older Adults. Nurs. Health Sci. 2025, 27, e70093. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.F.; Summers, C.; Panesar, A.; Kaura, A.; Zhang, L. AI Hesitancy and Acceptability—Perceptions of AI Chatbots for Chronic Health Management and Long COVID Support: Survey Study. JMIR Hum. Factors 2024, 11, e51086. [Google Scholar] [CrossRef]
- Wang, A.; Zhou, Y.; Ma, H.; Tang, X.; Li, S.; Pei, R.; Piao, M. Preparing for aging: Understanding middle-aged user acceptance of AI chatbots through the technology acceptance model. Digit. Health 2024, 10, 20552076241284903. [Google Scholar] [CrossRef]
- Al-Somali, S.A. Integrating artificial intelligence (AI) in healthcare: Advancing older adults’ health management in Saudi Arabia through AI-powered chatbots. PeerJ Comput. Sci. 2025, 11, e2773. [Google Scholar] [CrossRef]
- Schoenborn, N.L.; Chae, K.; Massare, J.; Ashida, S.; Abadir, P.; Arbaje, A.I.; Unberath, M.; Phan, P.; Cudjoe, T.K.M. Perspectives on AI and Novel Technologies Among Older Adults, Clinicians, Payers, Investors, and Developers. JAMA Netw. Open 2025, 8, e253316. [Google Scholar] [CrossRef]
- Luo, C.; Yang, C.; Yuan, R.; Liu, Q.; Li, P.; He, Y. Barriers and facilitators to technology acceptance of socially assistive robots in older adults-A qualitative study based on the capability, opportunity, and motivation behavior model (COM-B) and stakeholder perspectives. Geriatr. Nurs. 2024, 58, 162–170. [Google Scholar] [CrossRef]
- Kim, K.M.; Kim, S.H. Experience of the Use of AI Conversational Agents Among Low-Income Older Adults Living Alone. SAGE Open 2024, 14, 21582440241301022. [Google Scholar] [CrossRef]
- Wu, Y.H.; Damnée, S.; Kerhervé, H.; Ware, C.; Rigaud, A.S. Bridging the digital divide in older adults: A study from an initiative to inform older adults about new technologies. Clin. Interv. Aging 2015, 10, 193–201. [Google Scholar] [CrossRef]
- Jiang, T.; Huang, C.; Xu, Y.; Zheng, H. Cognitive vs. emotional empathy: Exploring their impact on user outcomes in health-assistant chatbots. Behav. Inf. Technol. 2025, 1–16. [Google Scholar] [CrossRef]
- Dino, M.J.S.; Dion, K.W.; Abadir, P.M.; Budhathoki, C.; Huang, C.-M.; Padula, W.V.; Ong, I.; Himmelfarb, C.R.D.; Davidson, P.M.; Thiamwong, L. What drives older adults’ acceptance of virtual humans? A conjoint and latent class analysis on virtual exercise coach attributes for a community-based exercise program. Comput. Hum. Behav. 2025, 164, 108507. [Google Scholar] [CrossRef]
- Wolfe, B.H.; Oh, Y.J.; Choung, H.; Cui, X.; Weinzapfel, J.; Cooper, R.A.; Lee, H.-N.; Lehto, R. Caregiving artificial intelligence chatbot for older adults and their preferences, well-being, and social connectivity: Mixed-method study. J. Med. Internet Res. 2025, 27, e65776. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.J.; Lee, J.H.; Lee, W. Factors Influencing Health Care Technology Acceptance in Older Adults Based on the Technology Acceptance Model and the Unified Theory of Acceptance and Use of Technology: Meta-Analysis. J. Med. Internet Res. 2025, 27, e65269. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ma, Y.; Liang, C. Understanding older adults’ continuance intention toward wearable health technologies: An empowerment perspective. Behav. Inf. Technol. 2025, 44, 1277–1294. [Google Scholar] [CrossRef]
- Davis, F.D. Perceived Usefulness, Perceived Ease of Use, and User Acceptance. MIS Q. 1989, 13, 319–340. [Google Scholar] [CrossRef]
- Venkatesh, V.; Morris, M.G.; Davis, G.B.; Davis, F.D. User Acceptance of Information Technology. MIS Q. 2003, 27, 425–478. [Google Scholar] [CrossRef]
- Li, Z.; Duan, J.A.; Ransbotham, S. Coordination and dynamic promotion strategies in crowdfunding with network externalities. Prod. Oper. Manag. 2020, 29, 1032–1049. [Google Scholar] [CrossRef]
- Jin, J.; Ryu, M.H. Sustainable Healthcare in China: Analysis of User Satisfaction, Reuse Intention, and Electronic Word-of-Mouth for Online Health Service Platforms. Sustainability 2024, 16, 7584. [Google Scholar] [CrossRef]
- Yu, S.; Chen, T. Understanding older adults’ acceptance of Chatbots in healthcare delivery: An extended UTAUT model. Front. Public Health 2024, 12, 1435329. [Google Scholar] [CrossRef]
- Fan, M.; Ukaegbu, O.C. Information literacy and intention to adopt e-pharmacy: A study based on trust and the theory of reasoned action. BMC Health Serv. Res. 2024, 24, 912. [Google Scholar] [CrossRef]
- Ho, M.T.; Le, N.T.B.; Mantello, P.; Ghotbi, N. Understanding the acceptance of emotional artificial intelligence in Japanese healthcare system: A cross-sectional survey of clinic visitors’ attitude. Technol. Soc. 2024, 72, 102166. [Google Scholar] [CrossRef]
- Kane, G.C.; Palmer, D.; Phillips, A.N.; Kiron, D.; Buckley, N. Strategy, not technology, drives digital transformation. MIT Sloan Manag. Rev. 2015, 14, 1–25. [Google Scholar]
- Guo, P.; Feng, G.; Wang, K.; Hua, J. Analysis of financing strategies for digital technology investment under privacy concerns and competition. Int. J. Prod. Econ. 2024, 274, 109294. [Google Scholar] [CrossRef]
- Sazvar, Z.; Zokaee, M.; Tavakkoli-Moghaddam, R.; Salari, S.A.S.; Nayeri, S. Designing a sustainable closed-loop pharmaceutical supply chain in a competitive market considering demand uncertainty, manufacturer’s brand and waste management. Ann. Oper. Res. 2022, 315, 2057–2088. [Google Scholar] [CrossRef]
- Zhang, M.; Wei, X.; Zeng, D.D. A matter of reevaluation: Incentivizing users to contribute reviews in online platforms. Decis. Support Syst. 2020, 128, 113158. [Google Scholar] [CrossRef]
- Wong, A.K.C.; Lee, J.H.T.; Zhao, Y.; Lu, Q.; Yang, S.; Hui, V.C.C. Exploring Older Adults’ Perspectives and Acceptance of AI-Driven Health Technologies: Qualitative Study. JMIR Aging 2025, 8, e66778. [Google Scholar] [CrossRef]
- Campmas, A.; Iacob, N.; Simonelli, F. How can interoperability stimulate the use of digital public services? An analysis of national interoperability frameworks and e-Government in the European Union. Data Policy 2022, 4, e19. [Google Scholar] [CrossRef]
- Lindgren, I.; Madsen, C.Ø.; Hofmann, S.; Melin, U. Close encounters of the digital kind: A research agenda for the digitalization of public services. Gov. Inf. Q. 2019, 36, 427–436. [Google Scholar] [CrossRef]
- Municipal Civil Affairs Bureau. Online and Offline Linkage to Meet Diversified Elderly Service Needs (2024 Edition). Available online: https://www.mca.gov.cn/n2623/n2684/n2703/c1662004999979998399/content.html (accessed on 10 April 2025).
- Shanghai Smart City Development Institute. “Healthy Cloud” Ageing Adaptation Transforms Across the Digital Divide, Creating a New Ecology of Intelligent Services for the Elderly (2022 Edition). Available online: https://www.sscdi.cn/index.php?id=552 (accessed on 10 April 2025).
- Wen, H.; Sun, S.; Huang, T.; Xiao, D. An intrinsic integrity-driven rating model for a sustainable reputation system. Expert Syst. Appl. 2024, 249, 123804. [Google Scholar] [CrossRef]
- Lin, T.K.; Werner, K.; Witter, S.; Alluhidan, M.; Alghaith, T.; Hamza, M.M.; Herbst, C.H.; Alazemi, N. Individual performance-based incentives for health care workers in Organisation for Economic Co-operation and Development member countries: A systematic literature review. Health Policy 2022, 126, 512–552. [Google Scholar] [CrossRef]
- Connelly, B.L.; Certo, S.T.; Reutzel, C.R.; DesJardine, M.R.; Zhou, Y.S. Signaling theory: State of the theory and its future. J. Manag. 2025, 51, 24–61. [Google Scholar] [CrossRef]
- Weibull, J.W. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef]
- Shi, T.; Xiao, H.; Han, F.; Chen, L.; Shi, J. A regulatory game analysis of smart aging platforms considering privacy protection. Int. J. Environ. Res. Public Health 2022, 19, 5778. [Google Scholar] [CrossRef]
- Yang, S.; Wang, H. Evolutionary Game Analysis of Medical System Information Collaboration under Government Incentives. Int. J. Innov. Comput. Inf. Control. 2024, 20, 1449–1461. [Google Scholar]
| (EE, PP, GG) | Older Adults Earnings (UEE) | Platform Earnings (UPP) | Government Earnings (UGG) |
|---|---|---|---|
| (A, HQ, S) | |||
| (A, HQ, NI) | |||
| (A, LC, S) | |||
| (A, LC, NI) | |||
| (NA, HQ, S) | 0 | ||
| (NA, HQ, NI) | 0 | 0 | |
| (NA, LC, S) | 0 | ||
| (NA, LC, NI) | 0 | 0 | 0 |
| Equilibrium Point | Stability Conditions | Eigenvalues | Meaning |
|---|---|---|---|
| (0,0,0) | Stable: Low adoption, low optimization, no incentive; the system falls into a degenerative cycle. | ||
| (1,0,0) | Unstable: Adoption without optimization; low trust undermines sustainability. | ||
| (0,1,0) | Unstable: Optimization without adoption; high cost drives platform to cut quality. | ||
| (0,0,1) | Unstable: Subsidy without adoption; high cost leads to withdrawal of support. | ||
| (1,1,0) | Unstable: Adoption and optimization without subsidy; high platform cost weakens sustainability. | ||
| (1,0,1) | Unstable: Adoption and subsidy without optimization; trust deficit undermines uptake. | ||
| (0,1,1) | Unstable: Optimization and subsidy without adoption; high cost destabilizes system. | ||
| (1,1,1) | Stable: High adoption, high optimization, continuous subsidy; the system reaches a virtuous cycle. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, R.; Mi, J. An Evolutionary Game Analysis of AI Health Assistant Adoption in Smart Elderly Care. Systems 2025, 13, 610. https://doi.org/10.3390/systems13070610
Shang R, Mi J. An Evolutionary Game Analysis of AI Health Assistant Adoption in Smart Elderly Care. Systems. 2025; 13(7):610. https://doi.org/10.3390/systems13070610
Chicago/Turabian StyleShang, Rongxuan, and Jianing Mi. 2025. "An Evolutionary Game Analysis of AI Health Assistant Adoption in Smart Elderly Care" Systems 13, no. 7: 610. https://doi.org/10.3390/systems13070610
APA StyleShang, R., & Mi, J. (2025). An Evolutionary Game Analysis of AI Health Assistant Adoption in Smart Elderly Care. Systems, 13(7), 610. https://doi.org/10.3390/systems13070610






