A Study on the Impact of Industrial Robot Applications on Labor Resource Allocation

Abstract

With the rapid advancement of artificial intelligence and smart manufacturing technologies, the penetration of industrial robots into Chinese markets has profoundly reshaped the structure of the labor market. However, existing studies have largely concentrated on the employment substitution effect and the diffusion path of these technologies, while systematic analyses of how industrial robots affect labor resource allocation efficiency across different regional and industrial contexts in China remain scarce. In particular, research on the mechanisms and heterogeneity of these effects is still underdeveloped, calling for deeper investigation into their transmission channels and policy implications. Drawing on panel data from 280 prefecture-level cities in China from 2006 to 2023, this paper employs a Bartik-style instrumental variable approach to measure the level of industrial robot penetration and constructs a two-way fixed effects model to assess its impact on urban labor misallocation. Furthermore, the analysis introduces two mediating variables, industrial upgrading and urban innovation capacity, and applies a mediation effect model combined with Bootstrap methods to empirically test the underlying transmission mechanisms. The results reveal that a higher level of industrial robot adoption is significantly associated with a lower degree of labor misallocation, indicating a notable improvement in labor resource allocation efficiency. Heterogeneity analysis shows that this effect is more pronounced in cities outside the Yangtze River Economic Belt, in those experiencing severe population aging, and in areas with a relatively weak manufacturing base. Mechanism tests further indicate that industrial robots indirectly promote labor allocation efficiency by facilitating industrial upgrades and enhancing innovation capacity. However, in the short term, improvements in innovation capacity may temporarily intensify labor mismatch due to structural frictions. Overall, industrial robots not only exert a direct positive impact on the efficiency of urban labor allocation but also indirectly contribute to resource optimization through structural transformation and innovation system development. These findings underscore the need to account for regional disparities and demographic structures when advancing intelligent manufacturing strategies. Policymakers should coordinate the development of vocational training systems and innovation ecosystems to strengthen the dynamic alignment between technological adoption and labor market restructuring, thereby fostering more inclusive and high-quality economic growth.

1. Research Background and Objectives

With the rapid development of intelligent manufacturing technologies, industrial robots have been widely adopted across the globe [1]. According to the 2024 report by the International Federation of Robotics [2], China has become the world leader in industrial robot installations, with a total stock reaching 500,000 units, followed by the United States with 300,000 units, and Germany, Japan, and India trailing closely behind. The accelerated investment and deployment of intelligent manufacturing in various countries are laying the technological foundation for the future upgrading of industrial systems. Existing studies have shown [3] that the widespread application of industrial robots significantly enhances production efficiency and product quality, while also expediting the transformation and upgrading of the manufacturing sector. For China—a major manufacturing powerhouse—the development of this technology holds strategic significance in strengthening international competitiveness and optimizing industrial structure.

China is currently undergoing a critical phase of economic restructuring, as the traditional growth model driven by low-cost labor and resource-intensive production has become increasingly unsustainable. High-quality development now urgently requires a shift toward innovation-driven growth, with technological advancement at its core [4]. In 2017, the State Council of China released the New Generation Artificial Intelligence Development Plan [5], which explicitly called for the deep integration of artificial intelligence (AI) with the real economy. As a key component of AI, industrial robots play a central role in enhancing productivity, reducing production costs, and improving product quality.

Meanwhile, China’s labor market faces two pressing structural challenges. First, there is a severe shortage of high-skill labor. According to the Labor Market and Salary Report published by the German Chamber of Commerce in China [6], both the manufacturing and service sectors are experiencing the widespread undersupply of skilled workers. The Future Employment Report 2023 predicts that China will face an average annual labor shortage of approximately 11.8 million over the next decade [7]. Second, population aging is accelerating. Data from the Seventh National Population Census show that the average age of the labor force rose from 37.1 in 2017 to 38.4 in 2022, with theupward trend expected to continue [8]. A report by the MI Institute notes that younger workers are increasingly reluctant to engage in traditional manufacturing jobs, further exacerbating structural mismatches in the labor market [9].

Against this backdrop, optimizing labor resource allocation has become an urgent and complex challenge. The application of industrial robots has not only reshaped traditional production processes but has also exerted profound effects on the structure of the labor market. According to the International Federation of Robotics (IFR) [10], automation and intelligent technologies have partially displaced low-skill jobs, raising concerns over unemployment risks. However, the International Labour Organization (ILO) argues that robot adoption also creates numerous new types of employment, placing greater demands on workers’ skill sets. Positions in robot operation and maintenance, systems integration, and data analytics have witnessed significant growth in demand for high-skill labor [11].

Furthermore, given the stark regional disparities in economic development across China, the adoption of industrial robots varies considerably by region [12]. The economically advanced eastern coastal areas, with strong technological foundations, have higher robot penetration rates, which support the development of high-end manufacturing and more efficient labor allocation. In contrast, the central and western regions—characterized by weaker capital and technology accumulation—have lower levels of robot adoption and face more pressing challenges in improving labor allocation efficiency. Thus, a systematic investigation into the regional application of industrial robots and their impacts on labor resource allocation is essential for uncovering the underlying causes of regional disparities and informing strategies for balanced regional development.

In light of these considerations, this paper utilizes prefecture-level data from China to systematically evaluate the overall impact of industrial robot adoption on labor resource allocation. It further explores regional heterogeneity in this relationship under varying levels of economic development and industrial structure. In addition, the study investigates the mediating roles of industrial restructuring and urban innovation capacity in the robot–labor allocation nexus, aiming to uncover the underlying mechanisms through which robots affect allocation efficiency. Based on the empirical findings, the paper provides targeted policy recommendations to enhance labor resource allocation efficiency and promote coordinated regional development and high-quality economic growth.

2. Literature Review

2.1. The Economic Impacts of Industrial Intelligence and Industrial Robots

Industrial intelligence is a defining feature of the Fourth Industrial Revolution, referring to the integration of emerging technologies such as robotics, artificial intelligence (AI), and the Internet of Things (IoT) into production processes. It aims to digitalize, automate, and optimize manufacturing activities. At its core, industrial intelligence involves replacing traditional manual labor with intelligent machinery, thereby reshaping production workflows, enhancing efficiency, and altering labor force structures [13].

A growing body of research suggests that industrial intelligence significantly improves productivity, optimizes resource allocation, and accelerates industrial upgrading [14,15]. According to endogenous growth models [16], the introduction of intelligent machinery enhances output per worker and serves as a critical driver of long-term economic growth. Aghion et al. [13] further developed a production function incorporating differentiated task structures, highlighting the crucial role of technological innovation in driving economic efficiency. They also emphasized that complementary policy design is essential for promoting technology diffusion and optimizing employment structures.

With industrial robots emerging as a representative technology of industrial intelligence, scholars have increasingly examined their empirical effects on macroeconomic indicators. Based on data from 17 developed economies, Graetz and Michaels [17] found that the application of industrial robots in manufacturing significantly increased labor productivity and GDP growth. Kromann [18] confirmed, using panel data from nine countries, that robot density is positively associated with total factor productivity (TFP). From a global value chain perspective, Zhang [19] incorporated the embedding of industrial robots into the study of China’s manufacturing sector, revealing that robot adoption enhances product technological content, strengthens firms’ positions in global value chains, and ultimately raises the value added of manufacturing.

However, not all studies present an optimistic view of the economic implications of industrial intelligence. Some researchers warn of potential long-term structural risks associated with technological advancement. Guerreiro [20] developed a model that incorporates automation and endogenous skill selection, demonstrating that although automation can raise output in the steady state, its suppressive effect on wage growth may reduce consumption and investment willingness in the long run, thus hindering sustainable economic development. Gasteiger and Prettner [21] also cautioned that excessive reliance on capital-labor substitution may undermine the inherent vitality of the economy. On the societal level, Wang and Siau [22] approached the issue from a governance perspective, noting that while intelligent technologies improve efficiency, they also intensify income inequality and social stratification, potentially leading to deeper social instability risks [23].

2.2. Labor Resource Allocation: Economic Drivers and Structural Evolution

Labor resource allocation refers to the movement and redistribution of labor across regions, industries, and occupations. It serves as a key indicator of allocative efficiency and economic dynamism. The determinants of labor allocation are generally categorized into economic and non-economic factors [24].

Among economic factors, the most critical are income differentials and the distribution of employment opportunities. In his seminal work, Hicks [25] argued that the core driver of labor migration lies in disparities in economic opportunities across regions. Falaris [26] found in a study on Peru that long-term migration is significantly constrained by regional income levels and employment environments. Using historical labor data from the United States, Greenwood [27] provided quantitative evidence that local job creation exerts a direct effect in attracting labor. More recent research by Bönisch et al. [28] reaffirmed that regional wage gaps and employment inequalities remain the primary forces driving intra-European Union labor mobility. In addition, individuals’ perceptions of expected income and employment probabilities also critically influence their migration decisions. Haapanen [29] demonstrated that an increase in expected disposable income significantly boosts migration intentions. Cattaneo [30] and Arntz et al. [31] further confirmed, from a micro-level perspective, the decisive roles of employment uncertainty and income expectations in shaping labor mobility.

Market potential and industrial agglomeration effects also function as important mechanisms influencing labor allocation. Within the framework of the new economic geography, Crozet [32] and Kancs [33] found that larger market size positively correlates with labor inflows, and central cities tend to attract more high-skill workers due to agglomeration economies.

On the non-economic side, urban public services and residential quality are becoming increasingly influential. Tiebout’s “voting with their feet” theory [34] suggests that individuals choose locations based on their preferences for bundles of urban services. Matallah [35] argued that a sound governance system and high-quality public services can significantly reduce labor outflows. Moreover, studies have shown that climate comfort and overall quality of life exert long-term influence on labor location choices, especially among highly educated and skilled populations [36,37].

Recent research has also emphasized inter-industry labor reallocation mechanisms. On one hand, globalization has facilitated labor flows toward industries with higher productivity [38,39,40]. On the other hand, institutional changes—such as environmental regulations and techno-nationalist policies—have reshaped the industrial and spatial distribution of labor [41,42,43,44,45,46].

2.3. The Impact of Industrial Robots on Labor Resource Allocation

As the new wave of technological revolution deepens, industrial robots are increasingly becoming a key force, reshaping the landscape of labor resource allocation. Compared with previous waves of technological change, robots which integrate perception, execution, and learning exert a more profound impact on employment structures. Existing studies generally agree that industrial robots influence the spatial, sectoral, and skill-level distribution of labor through a threefold mechanism of substitution–creation–structural reconfiguration, producing a dynamic and evolving process of labor reallocation.

Substitution Effect: The Compression of Low-Skill Jobs. Industrial robots exhibit a distinct advantage in terms of replacing highly repetitive and routine-based tasks, posing a direct threat to low-skill workers. Frey and Osborne [47], based on data from 702 occupations in the U.S., estimated that approximately 47% of jobs face a high risk of automation, particularly in manufacturing, logistics, and basic services. David [15], in a study of the Japanese labor market, similarly found that the widespread deployment of industrial robots significantly reduces the demand for low- and medium-skill labor. However, task-level heterogeneity within occupations implies that evaluating automation risk purely at the occupational level may lead to systematic overestimation. Arntz et al. [48] argue for a task-based perspective, noting that most occupations consist of diverse tasks, many of which remain difficult to fully automate. This has spurred theoretical extensions toward a “task–skill–substitution adaptability” framework.

In the Chinese context, substitution effects demonstrate distinct regional disparities. In the eastern coastal regions, where automation is more advanced, low-skill job substitution mainly manifests as occupational restructuring and upgrading. In contrast, the central and western regions characterized by a more homogeneous industrial structure and weaker skill-matching mechanisms have experienced a trend of “low-skill job hollowing” [49], exacerbating labor resource misallocation risks.

Creation Effect: The Expansion of High-Skill Jobs. Coexisting with the substitution effect is the job-creating potential brought about by robotics. Technological advances not only improve productivity but also generate new occupations through industrial upgrading and the emergence of new markets. Autor [50] proposed the “automation–consumption–reproduction” chain, suggesting that automation fosters product diversification and consumption expansion, thereby stimulating labor demand. Acemoglu and Restrepo [51] found that around half of all new jobs created in the U.S. between 1980 and 2007 stemmed from the introduction of new technology-related tasks, including robot maintenance, data analytics, and software development areas that generate substantial demand for skilled labor.

Similar trends are emerging in China. In the eastern region, supported by a robust technological base and integrated industrial chains, the advancement of intelligent manufacturing has catalyzed the rise of new occupations in algorithm engineering, system integration, and equipment maintenance, forming a virtuous cycle of “robot adoption–high-skill absorption–structural upgrading” [52].

Structural Reconfiguration: Gains in Efficiency and Risks of Mismatch. Beyond substitution and creation, robotics also drives structural reconfiguration by altering the skill composition and marginal returns to production factors. First, heterogeneity in technology types leads to varied effects on employment structures. Arenas Díaz et al. [53], through a meta-regression analysis, found that product innovation generally promotes employment via market expansion and demand creation, whereas process innovation though improving efficiency can reduce net employment, particularly in manufacturing. Hou et al. [54], using micro-level data from China and Europe, further validated the structural logic of “process innovation–non-growth innovation–job risk”. Second, technological change has markedly asymmetric effects across different labor groups. Mondolo [55] pointed out that high-skill workers, due to greater adaptability and lower retraining costs, tend to be the primary beneficiaries of technological dividends. In contrast, low-skill workers often face a dual dilemma of being replaced and struggling with occupational transition, resulting in skill stratification and structural unemployment. Pellegrino et al. [56] found that intangible technologies such as R&D tend to concentrate in large firms and promote job creation, whereas tangible technologies (e.g., robotic equipment investments) in small and medium enterprises are more likely to reduce employment.

In the Chinese structural context, this reconfiguration effect exhibits a dual pattern of firm size divergence and skill polarization [57]. Capital- and technology-intensive enterprises tend to attract high-skill workers and optimize job structures. In contrast, labor-intensive SMEs, under the pressure of robot penetration, face risks of “traditional labor–technology mismatch–structural redundancy”.

In sum, the impact of industrial robots on labor resource allocation is not a linear process, but rather a dynamic evolution shaped by the interplay of substitution, creation, and structural reconfiguration mechanisms. The final outcome largely depends on the type of technology, application scenarios, workforce structure, and the effectiveness of policy responses. Policymakers should respond systemically by strengthening regional innovation systems, reforming vocational training programs, and improving social protection mechanisms to achieve optimal labor resource allocation and dynamic adaptability.

2.4. Research Assessment

The above literature review indicates that existing studies have made considerable progress in examining the economic and social implications of industrial robots and, more broadly, artificial intelligence technologies. These studies have explored diverse dimensions, including the economic impacts of technology adoption, industrial upgrading, job displacement risks, and policy responses. They provide valuable theoretical and empirical foundations for understanding changes in labor resource dynamics under the broader trend of industrial intelligence. They also serve as important starting points for analyzing how industrial robot applications affect labor resource allocation.

Nevertheless, several research gaps and limitations remain, warranting further investigation and empirical validation:

First, there is still a relative scarcity of systematic studies on the relationship between industrial robot adoption and labor resource allocation efficiency. While numerous works have examined the link between technological progress and labor substitution, most of them focus on issues such as employment quantity, structural unemployment, or skill-biased technological change. Far fewer studies delve into how this key technology industrial robotics affects the efficiency with which labor as a production factor is allocated within the economic system. In particular, empirical evidence on how the degree of labor misallocation evolves alongside the growing adoption of industrial robots remains limited. This research gap constrains our understanding of the mechanisms through which AI technologies contribute to improving resource allocation and marginal productivity of inputs.

Second, the analytical frameworks used to examine the mechanisms of AI technologies, especially industrial robots, remain overly simplistic. Some studies continue to treat robotics merely as an extension of traditional technological advancement, often adopting a binary perspective of either “capital substituting labor” or “technology creating jobs”. In reality, AI technologies, particularly industrial robots, induce complex transformations in both industrial structure and employment composition. Their impacts are not limited to capital-labor substitution, but also extend to reshaping value chains, reorganizing task structures, and altering corporate organization. Therefore, a more comprehensive analytical framework is needed one that integrates multiple transmission channels including industrial upgrading, urban innovation capacity, human capital accumulation, and regional heterogeneity in order to unpack how technology affects labor resource allocation in a nuanced manner.

Third, empirical research in this domain remains heavily concentrated on developed economies, with limited studies situated in the Chinese context. Most quantitative studies on the impact of industrial robots rely on data from the U.S. and Europe, where the maturity of technology, labor market structure, and institutional environment differ markedly from those in China. As a result, the external validity and policy relevance of such findings for China are questionable. Additionally, existing studies often rely on outdated data or use inconsistent measurement frameworks for robot adoption and labor allocation efficiency. There is thus an urgent need for systematic empirical research based on updated and fine-grained data in China to fill the contextual gap.

In summary, while prior research has provided useful insights into the relationship between technological change and labor allocation, the specific question of how industrial robots influence labor resource allocation efficiency, particularly in the Chinese context, remains insufficiently addressed. This study focuses on the multi-dimensional impacts of industrial robot application on labor allocation, taking allocation efficiency as the core research objective. It further explores how such effects vary by regional development level, demographic aging, and the size and structure of the manufacturing sector. In addition, the study incorporates industrial restructuring and urban innovation capacity as potential mediating variables, constructing a comprehensive theoretical framework and empirical identification strategy. Through this approach, the paper aims to systematically reveal how industrial robots affect labor optimization across different regional and structural contexts, thereby providing policy-relevant insights for enhancing the resource allocation effects of technological progress.

3. Theoretical Framework and Research Hypotheses

To systematically identify the impact pathways through which industrial robot adoption affects labor resource allocation efficiency at the urban level, this study adopts a logical framework of “technological shock—structural reallocation—efficiency variation”. Drawing upon task-based technological shock theory, skill-biased technological change theory, and resource allocation efficiency theory, a theoretical framework is constructed to guide the empirical analysis. Based on this framework (as shown in Figure 1), both baseline hypotheses and mechanism-based hypotheses are proposed.

3.1. Industrial Robot Adoption and Labor Resource Allocation

Technological progress, as a fundamental driver of economic growth and social transformation, continuously reshapes production processes and patterns of labor allocation through evolving mechanisms. Each major wave of technological change particularly the widespread diffusion of general—purpose technologies such as industrial robots and artificial intelligence—has led to systematic adjustments in production modes, organizational structures, and occupational systems. These shifts not only alter how firms organize production but also trigger deep restructuring within labor markets. Driven by the dynamic interplay of skill adaptation, task transformation, and factor reallocation, labor resource distribution both spatially and structurally undergoes significant changes.

Existing studies have shown that technological advancement often results in a reconfiguration of task structures, thereby altering labor demand. Katz et al. [58] argue that technological progress is inherently skill-biased: high-skill workers, with stronger learning and adaptation capacities, are more capable of taking on complex, non-routine tasks and thus benefit disproportionately from innovation. In contrast, low-skill workers face a higher risk of marginalization. This bias manifests not only within specific industries but also more broadly in the context of large-scale AI diffusion. Zhu et al. [59], using a human capital index Q to measure labor quality from 1978 to 2015 in China, found that although workforce quality has improved over time, technological progress has advanced even more rapidly, resulting in a significant “matching lag”. Under the current widespread adoption of intelligent production systems, this mismatch further exacerbates the structural imbalance between labor supply and demand, becoming a key constraint on improving resource allocation efficiency.

It is worth noting that the impact of industrial robots on the labor market is not limited to the substitution effect but also involves significant “creation effects”. Autor et al. [60] distinguish between routine and non-routine tasks: the former, characterized by repetitive and standardized processes, are more susceptible to automation, while the latter, requiring judgment, creativity, and interpersonal coordination, remain relatively resilient to AI replacement. Based on this classification, technological progress not only displaces obsolete jobs but also gives rise to new occupations, tasks, and skill requirements, thereby expanding the division of labor and enabling the dynamic reallocation of labor across old and emerging structures.

Following the theoretical logics of “employment compensation effects” and the “Ricardo paradox”, scholars further argue that technological advancement, while enhancing productivity, also promotes the emergence of new industries and job categories. Acemoglu and Restrepo [14] emphasize that new technologies restructure labor not only through task substitution but also by creating novel employment opportunities, facilitating the reallocation of labor from inefficient sectors toward higher-value-added activities. In China, as the demographic dividend gradually wanes and structural fragmentation emerges in the labor market, the traditional growth model reliant on quantitative labor expansion is increasingly unsustainable. In this context, improving labor allocation efficiency through the application of industrial robots and other AI technologies optimizing labor distribution across cities and industries has become a strategic breakthrough for achieving high-quality growth.

At the city level, industrial robots are profoundly altering the organization of production and the structure of input factors in the manufacturing sector. On one hand, intelligent systems are accelerating the substitution of middle- and low-skill routine jobs, thereby releasing surplus labor. On the other hand, newly created positions require advanced digital literacy, technical operation, and systems management skills, which in turn attract and concentrate high-skill talent. This has resulted in a pronounced trend of labor reallocation across different skill levels. If such adjustments lead to better alignment between job requirements and labor supply, the marginal productivity of factor inputs can be significantly enhanced, promoting the dynamic optimization of resource distribution.

In summary, as a representative force of current technological progress, industrial robots exert transformative effects on labor resource allocation—transcending the traditional binary of “substitution versus creation”. It is driving a deeper restructuring of spatial distributions, skill hierarchies, and factor compatibility mechanisms. The key to improving allocation efficiency lies in understanding how industrial robots alter task content, job attributes, and factor demand structures, thereby facilitating the reallocation of labor toward higher-productivity employment.

Against this backdrop, this study centers on industrial robots’ application and investigates its impact on labor resource allocation efficiency at the urban level. Accordingly, the following hypothesis is proposed:

H1: 

The widespread application of industrial robots significantly improves the efficiency of labor resource allocation in cities.

3.2. Industrial Structural Transformation

With the rapid iteration and deep integration of new-generation information technologies including artificial intelligence, big data, cloud computing, and the Internet of Things intelligent manufacturing has emerged as a major engine driving global industrial transformation. As a key pillar of this system, the widespread deployment of industrial robots in industrial settings has not only reshaped production processes and organizational structures but has also exerted far-reaching impacts on labor composition and the allocation of production factors [61]. The concept of labor resource allocation efficiency examined in this study refers specifically to the efficiency loss arising from the deviation of urban-level marginal labor productivity from its optimal state, as captured by the labor resource misallocation index. This index reflects the extent to which labor achieves an equilibrium distribution of marginal returns across different cities and industries.

In the context of China’s vast manufacturing base and rapid technological advancement, the increasing penetration of industrial robots has significantly accelerated the substitution of labor by technological capital. This shift has in turn triggered systemic changes in factor allocation patterns, fundamentally altering the spatial and industrial distribution of marginal productivity across cities.

Against this backdrop, industrial structural transformation by influencing the spatial and intra-industry distribution of labor’s marginal productivity [62] serves as a critical structural mechanism through which industrial robots affect labor resource misallocation. First, the rise of high-tech industries and intelligent services, propelled by robotics, tends to be concentrated in cities with abundant innovation resources and institutional advantages. This leads to the formation of technology–industry–talent agglomeration systems. In this process, the concentration of high-skill labor in high-value-added cities and sectors drives up marginal productivity in these regions. Conversely, regions dominated by traditional manufacturing or lower-skilled occupations may face both talent outflows and technological substitution pressures, leading to surplus labor shifting toward low-productivity sectors or becoming unemployed.

Second, within industries, industrial robots are reshaping job structures. The deployment of new technologies accelerates the replacement of low-skill jobs and generates substantial demand for newly emerging, skill-intensive positions. However, if reskilling mechanisms are inadequate and there is a mismatch between talent supply and the skill demands of new positions, the existing labor force may struggle to adapt. This widens the disparity in marginal productivity across different skill groups an important source of intra-industry misallocation at the urban level.

In summary, by inducing both spatial industrial reconfiguration and task-skill structural transformation, industrial robots systematically affect the geographic and demographic distribution of labor’s marginal productivity. The key transmission mechanisms are twofold: (1) The spatial agglomeration of technology-intensive industries reinforces the siphoning effect for high-skill labor, thereby widening intercity disparities in marginal labor productivity. (2) Intra-industry upgrading, if not accompanied by effective reskilling support, may intensify the productivity gap between different labor groups. This dual structural effect, spatial divergence and intra-industry heterogeneity, ultimately leads to suboptimal labor allocation efficiency at the city level, reflected in a rising misallocation index. Accordingly, this study proposes the following hypothesis:

H2: 

Industrial structural transformation serves as a critical structural transmission mechanism through which industrial robot adoption influences the degree of labor resource misallocation across cities.

3.3. Urban Innovation and Allocation Efficiency

In the transformation of labor resource allocation driven by industrial robots, urban innovation capacity plays an increasingly critical role as a key transmission mechanism linking technological deployment and improvements in allocation efficiency [61]. As a general-purpose technology, the effective application of industrial robots does not solely depend on the technology itself, but is heavily influenced by the technological environment and institutional foundations at the urban level. Urban innovation capacity, in this context, refers to a comprehensive set of capabilities that facilitate technology adoption, task restructuring, and human capital reconfiguration ultimately shaping the path of technology diffusion and the outcomes of resource allocation [63].

First, urban innovation capacity determines both the absorptive efficiency and the depth of application of industrial robotics [64]. Cities with strong innovation capacity typically possess a high density of research institutions, robust institutional environments, and well-developed technological infrastructure, enabling them to more rapidly and systematically achieve technology introduction, process reengineering, and organizational restructuring. This process of technological deepening enhances productivity and optimizes job structures, thereby improving the matching efficiency between labor and job requirements, and ultimately advancing labor resource allocation efficiency. Conversely, cities with weaker innovation capacity may fail to realize the potential of industrial robots due to limited absorptive capability and institutional constraints, even after the initial deployment of robotic equipment thus leaving resource misallocation unresolved.

Second, a city’s innovation ecosystem plays an essential role in task restructuring and skill adaptation [65]. The integration of robotics into industrial systems gives rise to a wide range of new tasks and occupations. Cities with strong innovation capacity supported by higher education institutions, research centers, and comprehensive talent development systems are better positioned to respond to the labor market transformations induced by technology. These cities can establish responsive systems centered on task redefinition and reskilling initiatives, thereby increasing the elasticity of human capital supply and improving the alignment between skill structures and job requirements. This adaptive capacity helps alleviate structural imbalances caused by technological shocks and enhances resource allocation efficiency.

Moreover, urban innovation capacity amplifies its effects through both infrastructural support and regional diffusion mechanisms [66]. The development of digital infrastructure improves data transmission and feedback efficiency for robotic systems, enabling better human–machine coordination and higher marginal productivity. At the regional level, cities with strong innovation capacity can drive surrounding areas to optimize resource allocation through mechanisms such as knowledge spillovers, institutional imitation, and labor mobility. These effects jointly constitute the channels through which innovation capacity shapes the outcomes of technology deployment and labor allocation.

In sum, urban innovation capacity establishes a critical transmission chain between industrial robot application and labor resource allocation efficiency through multiple pathways, namely, technology absorption, task restructuring, and capability adaptation. This mechanism not only determines the depth and breadth of robot adoption but also affects labor structure flexibility and market responsiveness, making it an indispensable factor in understanding the broader impacts of robotics. Accordingly, this study proposes the following hypothesis:

H3: 

Urban innovation capacity serves as a transmission mechanism through which industrial robot adoption influences labor resource allocation efficiency at the city level.

Figure 1. Mechanism diagram.

Figure 1. Mechanism diagram.

4. Research Design

4.1. Model Specification

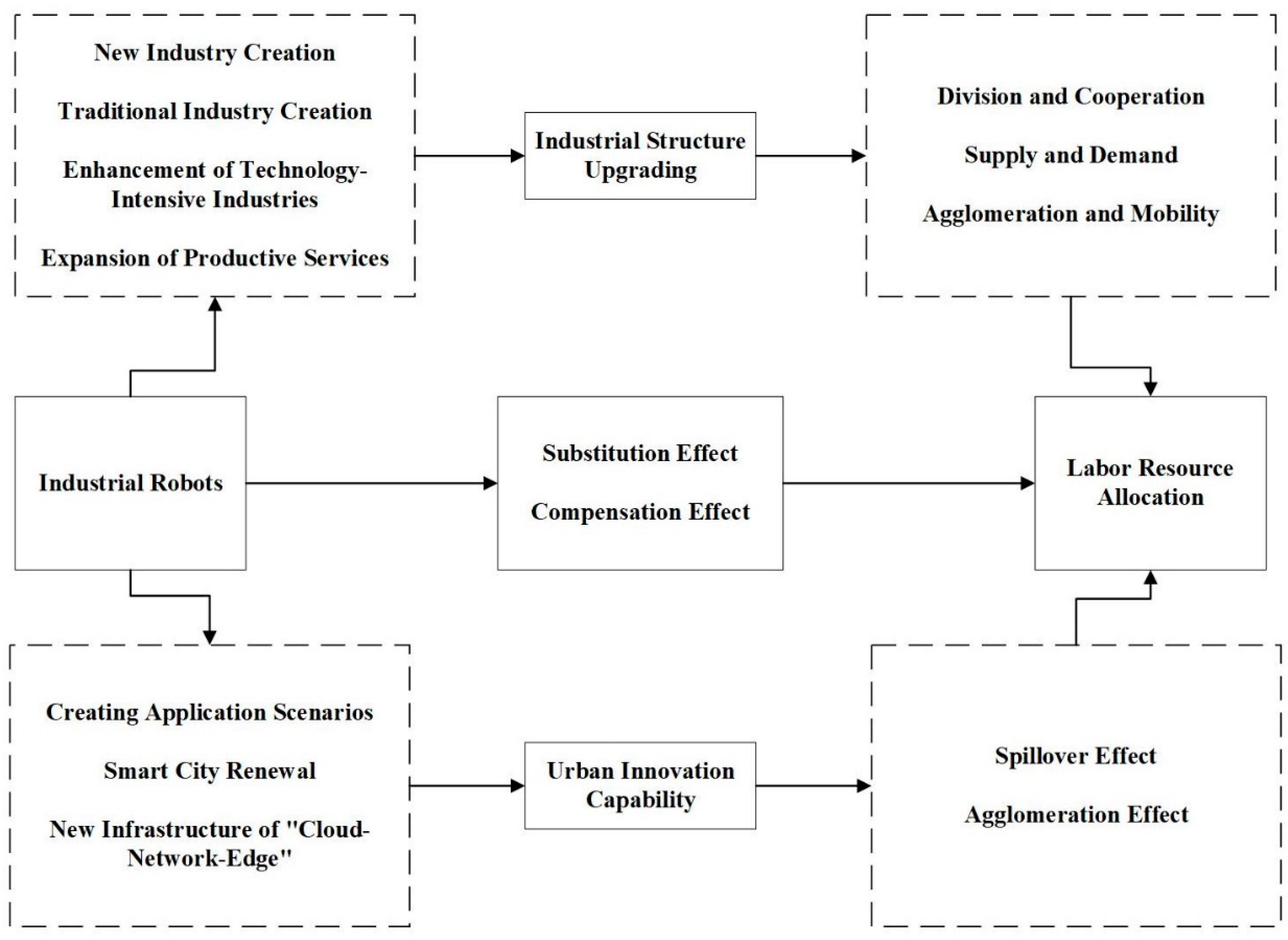
To systematically evaluate the impact pathways through which industrial robot adoption affects labor resource allocation efficiency at the city level, this study first establishes a baseline two-way fixed effects regression model that incorporates both city fixed effects and year fixed effects. The model is then extended to a mediation analysis framework by introducing two key intermediary variables, industrial upgrading and urban innovation capacity. This modeling strategy not only facilitates the estimation of the direct effect of industrial robot adoption on labor resource allocation but, more importantly, helps to uncover the underlying transmission mechanisms. Specifically, it allows us to examine how industrial robots indirectly reshape intra-city and interregional labor allocation patterns through intermediary channels such as industrial restructuring and urban innovation systems, thereby enhancing the overall efficiency of factor markets.

For empirical testing, this study selects the industrial robot penetration index and the labor resource mismatch index as core variables based on panel data at the prefecture-level city level in China to identify the impact of industrial robot application on the efficiency of labor resource allocation in prefecture-level cities. Accordingly, the following baseline regression model is constructed:

$${Lab}_{ct}={\alpha }_0+{\alpha }_1{Robots}_{ct}+\gamma {CTR}_{ct}+{\theta }_c+{\phi }_t+{\epsilon }_{ct}$$

(1)

In this model, $c$ and $t$ denote the city and year dimensions, respectively. ${Lab}_{ct}$ represents the labor misallocation index of city $c$ in $t$ year reflecting the efficiency of labor resource allocation—where lower values indicate higher allocation efficiency. ${Robots}_{ct}$ measures the penetration of industrial robots and is the core variable for measuring the level of industrial robot application in prefecture-level cities in China.

${CTR}_{ct}$ is a vector of control variables, including indicators such as city economic size, demographic structure, educational attainment, and industrial base. ${\theta }_c$ denotes city fixed effects, which control for unobservable regional heterogeneity, while ${\phi }_t$ represents year fixed effects, accounting for temporal shocks and national trends. ${\epsilon }_{ct}$ is the idiosyncratic error term.

The coefficient ${\alpha }_1$ is the core parameter of this paper. If its estimated value is significantly negative, it means that the penetration of industrial robots helps to reduce the level of mismatch, that is, the application of industrial robots significantly improves the efficiency of urban labor resource allocation.

To further identify the mechanisms through which industrial robot adoption influences labor resource allocation efficiency, this study extends the baseline model by incorporating a mediation analysis framework. The goal is to examine how robot adoption may indirectly affect allocation efficiency through specific structural variables.

Mediation analysis, first systematically proposed by Baron and Kenny [67], is one of the most widely used approaches for mechanism identification. It investigates whether the effect of an independent variable (X) on a dependent variable (Y) is transmitted through a mediating variable (M). The model follows a stepwise regression-based path analysis framework, decomposing the total effect into direct and indirect effects, and determines the presence of mediation by testing the statistical significance of each path coefficient.

In recent years, as mediation analysis has gained traction in econometrics and the social sciences, it has been extensively applied to research in labor economics, urban economics, and technology diffusion. The method is particularly well-suited to uncovering the structural mechanisms underlying complex economic phenomena. Compared with traditional regression models, mediation analysis emphasizes hierarchical causal structures, transmission logic among variables, and explanatory power with respect to mechanisms—making it especially appropriate for the “technology–structure–allocation” transmission chain that this study seeks to investigate.

In the specific empirical design, this study selects two mediating variables: urban industrial structure upgrading (${ISU}_{ct}$) and urban innovation capacity (${Inno}_{ct}$). The three-step estimation procedure for mediation analysis is as follows:

Step 1: Test whether the application of industrial robots significantly affect allocation efficiency by estimating the total effect of the application of industrial robots on ${Lab}_{ct}$.

$${Lab}_{ct}={\alpha }_0+{\alpha }_1{Robots}_{ct}+{\alpha }_2{CTR}_{ct}+{\theta }_c+{\phi }_t+{\epsilon }_{ct}$$

(2)

Step 2: Test whether the application of industrial robots significantly affect the mediating variable (${Mediator}_{ct}$).

$${Mediator}_{ct}={\beta }_0+{\beta }_1{Robots}_{ct}+{\beta }_2{CTR}_{ct}+{\theta }_c+{\phi }_t+{\epsilon }_{ct}$$

(3)

Step 3: Incorporate the mediating variable into the baseline regression model to examine whether it serves as a transmission channel between the application of industrial robots and labor allocation efficiency.

$${Lab}_{ct}={\lambda }_0+{\lambda }_1{Robots}_{ct}+{\lambda }_2{Mediator}_{ct}+{\lambda }_3{CTR}_{ct}+{\theta }_c+{\phi }_t+{\epsilon }_{ct}$$

(4)

According to the stepwise regression logic, if coefficient ${\alpha }_1$ in Model (2), ${\beta }_1$ in Model (3), and ${\lambda }_2$ in Model (4) are all statistically significant, this indicates that the mediation pathway is valid, and that the impact of industrial robot adoption on allocation efficiency operates at least in part through an indirect mechanism.

Furthermore, if ${\lambda }_1$ becomes statistically insignificant after including the mediating variable, this suggests a case of full mediation. If ${\lambda }_1$ remains significant but its absolute value decreases, the result is interpreted as partial mediation.

To enhance the statistical significance and robustness of the mediation effect identification, this study employs the Bootstrap nonparametric resampling method to test the significance of the mediation pathway. Originally proposed by Efron [68], the Bootstrap method generates an empirical distribution of parameter estimates by repeatedly resampling with replacement from the original sample. Without requiring assumptions of normality or independence of the error terms, it enables robust estimation of indirect effects. The Bootstrap method is particularly effective when dealing with non-symmetric mediation paths, skewed distributions of estimators, or limited sample sizes, and has become a mainstream approach in mediation analysis.

In summary, this study adopts a three-pronged modeling strategy baseline regression, mediation analysis, and Bootstrap testing to systematically identify both the direct effects and indirect mechanisms through which industrial robot adoption influences labor resource allocation efficiency at the urban level. This integrated econometric framework provides a comprehensive approach to understanding the interaction between technological advancement and factor allocation, and offers empirical support for designing efficient labor allocation systems that are adaptive to ongoing technological transformation.

4.2. Variable Description and Data Sources

To empirically examine the effects and underlying mechanisms of industrial robot adoption applications on labor resource allocation efficiency at the urban level, this study constructs a multidimensional variable system that includes the dependent variable, core explanatory variable, mediating variables, and a set of control variables. These variables collectively reflect the dynamic characteristics of urban systems in terms of technological shocks, structural evolution, and allocative performance. The definitions and measurement methods for each type of variable are as follows:

4.2.1. Dependent Variable: Labor Resource Allocation Efficiency (Lab)

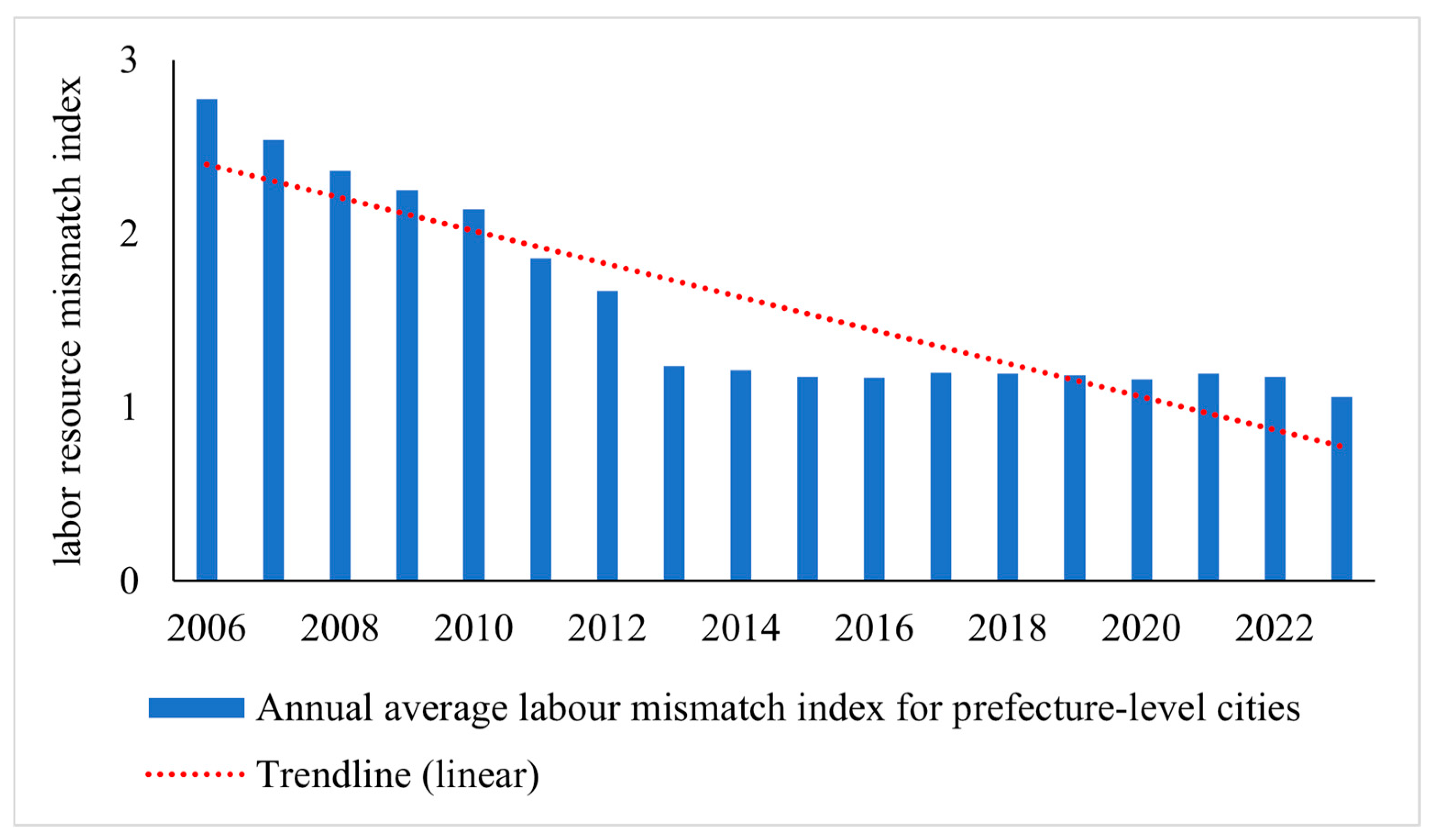
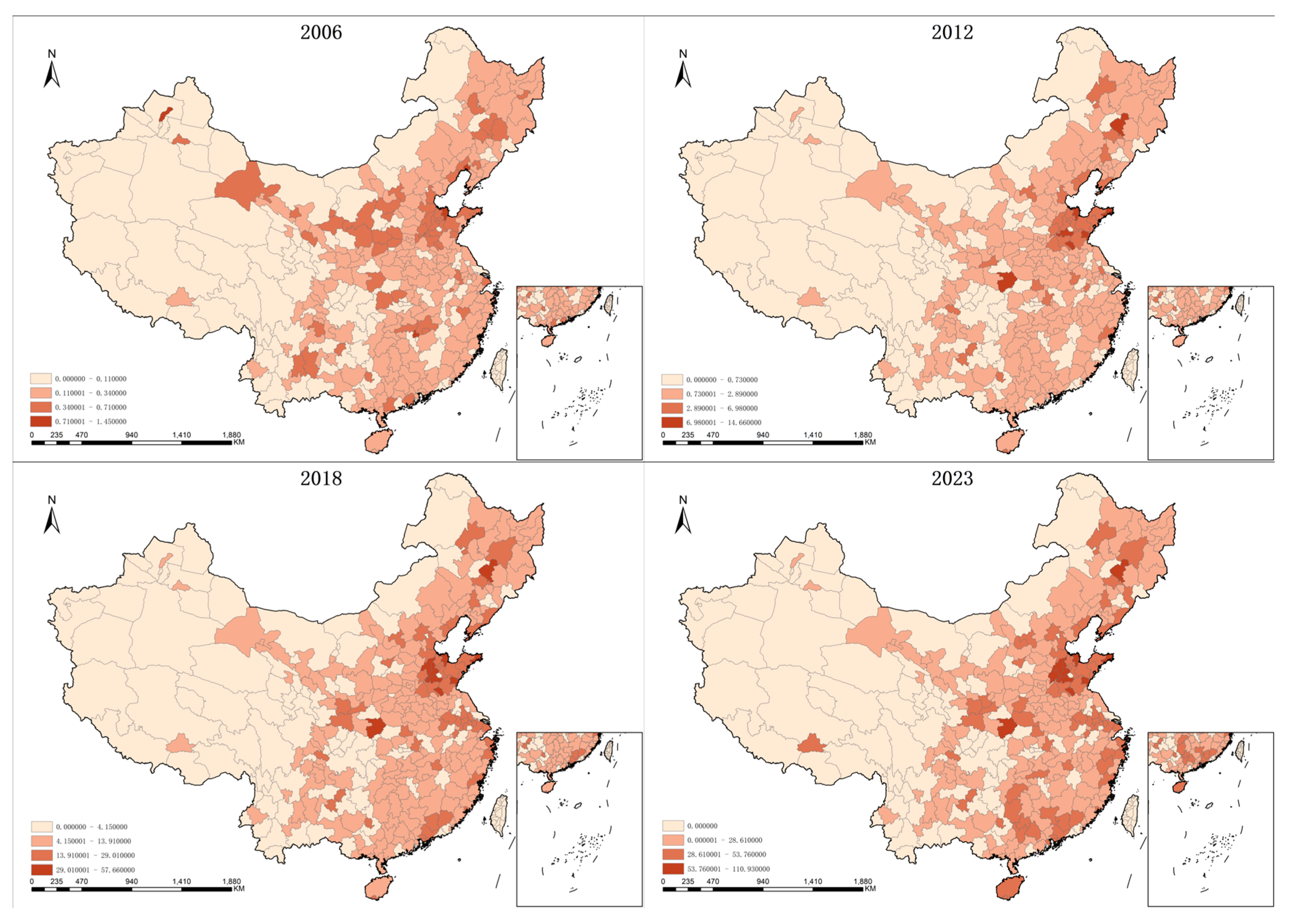
This study uses a labor misallocation index as the core indicator to measure labor resource allocation efficiency at the city level. This selection is based on both solid theoretical foundations and practical advantages. According to resource misallocation theory, in a perfectly competitive market without institutional distortions, the marginal productivity of production factors across regions and sectors should converge. Any divergence signals resource misallocation, which leads to a total factor productivity (TFP) level below its potential optimum. As a fundamental production input, labor plays a critical role in determining the operational efficiency and growth potential of both urban and national economies. Therefore, measuring the degree of labor misallocation helps uncover distortions arising from variations in market structure, policy environments, or technological shocks across cities, offering both theoretical and practical significance.

From an empirical perspective, the labor misallocation index can be constructed using standardized, publicly available data with a transparent and replicable calculation path. This reduces reliance on subjective assumptions and enhances comparability across studies. Compared to surface-level indicators such as employment or unemployment rates, the misallocation index provides a more intrinsic measure of disparities in marginal labor productivity, thereby capturing structural adjustments in the labor market. This makes it particularly suitable for analyzing reallocation dynamics under the influence of technological change.

This study focuses on how labor resource allocation efficiency evolves during the diffusion of industrial robot technologies. Existing literature shows that industrial robots reshape labor markets through two main channels: (1) directly substituting for low-skill, repetitive jobs, and (2) creating new tasks and skill demands, thereby transforming the structure of labor demand and inducing dynamic changes in marginal productivity. Accordingly, the labor misallocation index serves as an ideal dependent variable to capture the reallocation effects triggered by robot adoption, aligning closely with the theoretical logic and core research objectives of this paper.

From a dynamic analysis perspective, the index is also highly sensitive to temporal changes and structural shifts. Utilizing a panel data framework allows for the tracking of allocation efficiency trajectories across cities and over time, thereby enabling the identification of temporal effects associated with technology diffusion, policy interventions, and market adjustments—further enhancing the explanatory power of the empirical analysis.

Capital Stock Estimation for Misallocation Calculation

To compute the labor misallocation index, it is necessary to estimate city-level capital stock data. Since fixed asset capital stock is not directly observable and national statistics do not provide city-level capital stock figures, this study employs the Perpetual Inventory Method (PIM) as proposed by Goldsmith [69]. PIM estimates capital stock by accumulating investment flows over time and adjusting for depreciation. Specifically, starting from an initial capital stock, each year’s new investment is added and depreciation is subtracted to dynamically update capital stock. Given its conceptual clarity, moderate data requirements, and wide international acceptance, PIM has become a standard method in macroeconomic and regional economic research when direct capital stock data are unavailable.

In implementing this method, the study uses each prefecture-level city’s annual completed fixed asset investment as the base indicator. This measure reliably reflects the flow of new capital formation and is consistent across cities and years, making it suitable for constructing comparable intertemporal capital stock series. To adjust for inflation and ensure that real capital dynamics are captured, nominal investment figures are deflated using the fixed asset investment price index, with 2006 set as the base year.

Depreciation Rates

Following the methodology of Wu [70], fixed asset investment is divided into three categories: (1) construction and installation, (2) equipment and tools purchases, and (3) other costs. Each category is assigned a separate depreciation rate: 8.12%, 17.08%, and 12.1%, respectively. These values are based on empirical estimates of asset lifespan and economic depreciation derived from large-scale micro-level firm data in China. Compared to a uniform depreciation rate, this category-specific approach captures internal differences in investment composition and reduces systematic bias in capital stock estimation.

Given regional and temporal heterogeneity in investment structures, the study uses data from the China Fixed Asset Investment Yearbook and the Statistical Yearbook of China’s Investment Fields to compute the annual proportion of each investment category in provincial-level total investment. These proportions are used to calculate a weighted average economic depreciation rate for each province, which is then assigned to cities within the corresponding province. This approach balances data availability with regional accuracy, enhancing both the granularity and validity of the capital stock estimates.

Based on the settings described above, capital stock for each city and year is calculated using the standard PIM formula:

In summary, this paper adopts a three-pronged modeling strategy comprising baseline regression, mediation analysis, and Bootstrap testing to systematically identify the impact of AI applications on labor resource allocation efficiency in cities. By capturing both direct effects and structural transmission mechanisms, the proposed framework offers a comprehensive econometric approach for analyzing the interaction between technological progress and factor allocation. It also provides a solid empirical basis for designing adaptive and efficient labor allocation systems in the era of rapid technological transformation.

$$K_t=I_t/P_t\ast 100+\left(1-{\delta }_t\right)K_{t-1}$$

In the formula, $K_t$ represents the capital stock in year $t,$ $I_t$ is the nominal fixed asset investment in year $t$, $P_t$ is the fixed asset investment price index (base year: 2006), and ${\delta }_t$ denotes the weighted economic depreciation rate in year $t$. The initial capital stock is set as twice the completed fixed asset investment in 2006. Prior studies have shown that setting the base-year capital stock at 1.5 to 2 times the investment value can effectively mitigate early-stage estimation errors and ensure the stability and plausibility of the long-term capital stock series.

After estimating the capital stock, this study incorporates city-level GDP and employment data to construct a Cobb–Douglas production function and estimate factor output elasticities. The general form of the production function is defined as follows:

$$Y_{it}=A{K}_{it}^{{\alpha }_{Ki}}{L}_{it}^{{\alpha }_{Li}}$$

where $Y_{it}$ is the real GDP of city $i$ in year $t$ (measured in 2006 constant prices), $K_{it}$ and $L_{it}$ represent capital and labor inputs, respectively; $A$ is a constant denoting technology level; and ${\alpha }_{Ki}$, ${\alpha }_{Li}$ are the output elasticities of capital and labor. It is assumed that returns to scale are constant, i.e., $\alpha \_Ki+\alpha \_Li=1$. Taking natural logarithms on both sides yields a linearized regression equation:

$$ln\left(Y_{it}/L_{it}\right)=lnA+{\alpha }_{K}ln\left(K_{it}^{{\alpha }_{Ki}}/L_{it}^{{\alpha }_{Li}}\right)+{\mu }_i+{\lambda }_t+{\epsilon }_{it}$$

A two-way fixed effects panel regression is employed to estimate the equation, controlling for unobserved city-specific and time-fixed effects, thereby ensuring the robustness of the elasticity estimates.

Based on the estimated elasticities, the relative distortion coefficients for capital and labor in each city are calculated as follows:

$${\gamma }_{Ki}=\left({\displaystyle \frac{K_i}{K}}\right)/\left({\displaystyle \frac{s_i{\alpha }_{Ki}}{{\alpha }_K}}\right),{\gamma }_{Li}=\left({\displaystyle \frac{L_i}{L}}\right)/\left({\displaystyle \frac{s_i{\alpha }_{Li}}{{\alpha }_L}}\right)$$

where $K_{it}$ and $L_{it}$ are the capital and labor inputs of city $i$, $K$ and $L$ denote the national total capital and labor, $s_i$ is the share of city $i$ in total national output, and ${\alpha }_K$ and ${\alpha }_L$ represent the national average output elasticities of capital and labor, respectively. A distortion coefficient closer to 1 indicates a more optimal allocation of factors; greater deviation implies more severe resource misallocation.

Subsequently, the capital and labor misallocation indices ${\tau }_{Ki}$ and ${\tau }_{Li}$ are calculated based on the relative distortion coefficients:

$${\tau }_{Ki}=1/{\gamma }_{Ki}-1, {\tau }_{Li}=1/{\gamma }_{Li}-1$$

These indices measure the absolute deviation of unit input efficiency from the optimal configuration. Following the method of Xie et al. [71], the absolute value is taken to ensure the indices are always positive and exhibit monotonicity for ease of interpretation.

In summary, through investment deflation, region-specific depreciation rate estimation, capital stock computation via the perpetual inventory method, output elasticity estimation, and misallocation index calculation, this study constructs a rigorous and comprehensive measure of labor resource allocation efficiency at the city level. This provides a solid empirical foundation for investigating how the impact of industrial robot application influences factor allocation efficiency.

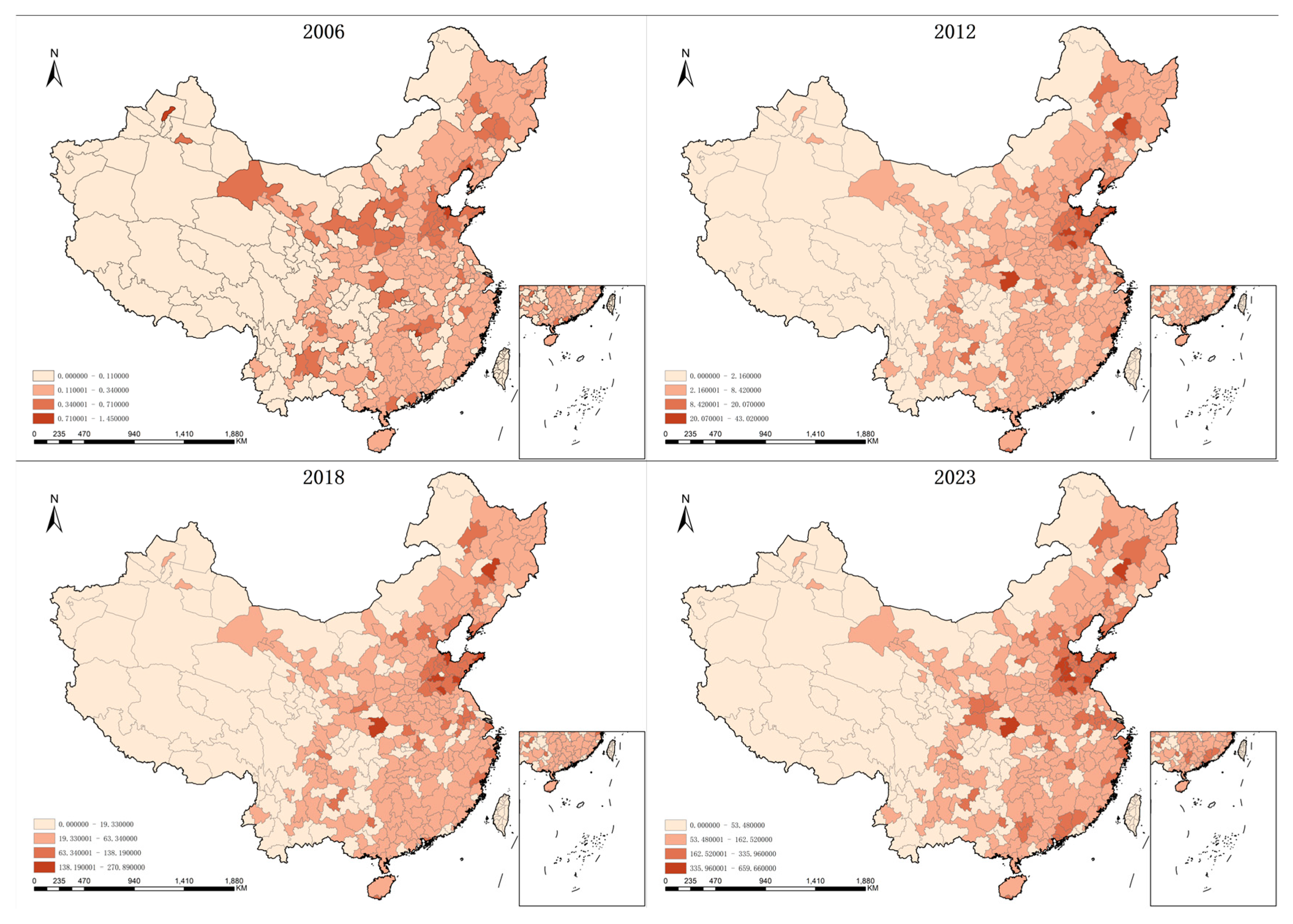
4.2.2. Core Explanatory Variable: Industrial Robot Adoption at the Prefecture Level (Robots)

Regarding efforts to measure the regional application level of industrial robot technologies, constructing an indicator that is exogenous, representative, and operationalizable has long been a critical challenge in empirical research. Given that China’s statistical system has not yet established a standardized official index for robot adoption intensity at the city level, this study, drawing on international research paradigms and data availability, selects the penetration rate of industrial robots at the prefecture level as the core explanatory variable. This measure not only aligns closely with theoretical expectations and methodological rigor but also provides a solid foundation for subsequent causal identification and mechanism analysis.

From an econometric perspective, the measure of “robot adoption intensity” at the city level in this study is not simply based on the number of robots installed locally. Instead, it follows the Bartik instrumental variable approach proposed by Acemoglu and Restrepo [51], combining national-level changes in robot penetration across industries with city-level baseline employment structures to construct each city’s exposure to technological shocks. The underlying logic is that cities whose baseline employment is more concentrated in industries experiencing rapid national-level robot adoption are more likely to face stronger technological substitution or restructuring in the future.

Essentially, this variable captures the degree to which a city is exposed to exogenous technological trends due to its historically determined industrial and employment structure. It helps to mitigate endogeneity concerns arising from local policy choices, economic adjustments, or firm-level behaviors. From a data feasibility standpoint, the International Federation of Robotics (IFR) provides authoritative and continuous data on robot deployment across industries in major countries and regions since 1993. Meanwhile, China’s national statistical system provides industry-level employment data from economic censuses and annual labor statistics, which can be used to construct the baseline employment structure at the city level.

By linking these two datasets, this study builds an industrial robot adoption index at the city level that is both exogenous and comparative across time and space. This design ensures data quality and enhances the external validity and generalizability of the findings.

In summary, the selection of the industrial robot stock penetration rate at the prefecture-level as the core explanatory variable for measuring the level of industrial robot application represents a synthesis of theoretical perspective and practical trajectory, as well as a methodological innovation aligned with empirical constraints. This indicator not only closely captures the logic of industrial robot adoption in practice but also provides a solid foundation for identifying the causal effects of technological progress on labor resource allocation efficiency. By employing a Bartik-style instrumental variable design, it further enhances the robustness of causal inference, offering more scientifically grounded and policy-relevant empirical evidence.

The robot exposure index for city $c$ in year $t$ is calculated as follows:

$${Robots}_{c,t}^{China}={\sum }_{i\in l}\left({\displaystyle \frac{{Robots}_{i,t}^{China}}{l_{i,t=2010}^{China}}}\right)\times l_{c,t}^{t=2010}$$

where

• ${Robots}_{i,t}^{China}$ denotes the total number of industrial robots deployed in industry i nationwide in year t, sourced from the International Federation of Robotics (IFR);
• $l_{i,t=2010}^{China}$ is the number of employees in industry i nationwide in 2010, serving as a normalization base;
• $l_{c,i,t=2010}$ represents the number of workers employed in industry i in city c in the base year 2010, capturing the city’s initial industrial structure.

This formula can be interpreted as a weighted average of national robot adoption intensity across industries, with the weights reflecting each city’s baseline exposure to robot-intensive sectors. The specific weight is defined as follows:

$$l_{c,t}^{t=2010}={\displaystyle \frac{l_{c,i,t=2010}}{l_{c,t=2010}}}$$

where $l_{c,t=2010}$ is the total number of employees in city $c$ in 2010, ensuring that the weighting captures the relative employment share of each industry in the city’s baseline structure.

The industrial robot usage data employed in this study are sourced from the International Federation of Robotics (IFR) Global Robot Database, which provides detailed records of industrial robot deployments disaggregated by country and industry. Although IFR does not directly report city-level robot usage, we estimate each city’s robot exposure intensity by combining national-level industry-specific robot penetration rates with the industrial composition of each prefecture-level city.

Data on city-level industrial structures and the working-age population (ages 16–64) are primarily drawn from China’s Sixth National Population Census, which is highly authoritative and offers comprehensive coverage.

The year 2010 is selected as the baseline year for two main reasons. First, from the perspective of data completeness and comparability, 2010 is the only year in recent history when both a nationwide economic census and population census were conducted simultaneously. This provides detailed and consistent data on industry employment structures and demographic composition at the city level. The spatial coverage, industry classification, and statistical standards in this year are highly consistent across sources, offering a solid empirical foundation for constructing a comparable and accurate city-level robot exposure index.

Second, the choice of 2010 ensures both temporal relevance and reasonable lag structure. Around this time, China entered a phase of rapid industrial robot adoption. Using 2010 as the baseline year captures the initial responsiveness of urban industrial structures to the emerging technology diffusion, while allowing sufficient time lags to analyze the subsequent impacts on labor resource allocation efficiency. Fixing the baseline year also helps mitigate the potential endogeneity arising from contemporaneous changes in industry structure, thereby enhancing the exogeneity of the constructed instrument.

Moreover, using national-level robot penetration by industry as the exogenous source of variation ensures horizontal comparability and consistency over time. National robot diffusion trends can be regarded as exogenous technological shocks, largely unaffected by individual city-level policies or market dynamics, which strengthens the instrument’s validity [72].

In conclusion, this study constructs a city-level measure of industrial robot adoption by combining national industry-level robot penetration rates with city-specific baseline employment structures using a Bartik-type instrument. This variable exhibit strong theoretical grounding, practical feasibility, and robust identification strategy, thereby providing a critical foundation for analyzing the causal impact of industrial robots on labor resource allocation efficiency in subsequent empirical analyses.

4.2.3. Control Variables (CV)

In econometric modeling, the omission of key explanatory variables may lead to biased estimates, thereby compromising causal identification between the core explanatory and dependent variables. To address this concern and enhance the robustness and validity of the empirical analysis, this study incorporates a series of control variables that capture macroeconomic conditions and institutional factors that may systematically affect labor resource allocation efficiency. The selection of these variables is grounded in theoretical insights and empirical findings from prior literature [14,40,50,51,59], covering key dimensions such as urban economic development level, urban financial development, local government behavior, infrastructure construction, local science and technology investment, and opening up to the outside world.

① Level of Economic Development (GDP)

This study uses the logarithm of per capita GDP at the prefecture level as a core indicator of regional economic development. This variable reflects not only the overall economic output capacity of a city but also its ability to absorb, allocate, and redistribute labor resources. It serves as a fundamental condition for evaluating labor allocation efficiency.

② Financial Development (FIN)

The level of financial development is a key institutional foundation for technology diffusion and industrial upgrading. Higher financial efficiency enhances firms’ access to credit and financing, thereby improving their ability to invest in high-tech equipment such as industrial robots and implement job restructuring. To capture this effect, the study uses the ratio of year-end loan balances of financial institutions to regional GDP as an indicator of financial development, reflecting the influence of regional capital markets on technology investment and employment structure.

③ Government Intervention (GOV)

In the context of China’s institutional framework, local governments play a central role in shaping economic development. Their policy preferences, fiscal expenditure structures, and administrative behavior exert both direct and indirect influences on factor market allocation. To measure the degree of government intervention, this study uses the ratio of local general public budget expenditure to regional GDP. This proxy reflects the extent to which government resources are involved in economic activities and partially captures their impact on industrial restructuring and employment orientation.

④ Infrastructure Level (BASE)

Infrastructure represents the foundational conditions for regional economic operations. High-quality infrastructure such as transportation, water supply, and energy can reduce production costs, improve inter-regional connectivity, and enhance the capacity to attract labor and capital, thereby improving labor resource allocation. This study measures infrastructure development using the ratio of total fixed asset investment to GDP, capturing the supportive role of infrastructure in facilitating factor agglomeration and urban functionality.

⑤ Government Science and Technology Expenditure (SCI)

Public expenditure on science and technology is a critical enabler of technological innovation and the development of high-end manufacturing, and serves as an institutional basis for AI deployment. Government spending in this area accelerates R&D and the diffusion of technologies such as robotics, and indirectly influences structural labor reallocation by promoting industrial upgrading. Accordingly, this study measures technological support intensity by the ratio of local government science and technology expenditure to GDP.

⑥ Openness to the Outside World (OPEN)

In recent years, regional openness has been widely recognized as a major source of economic dynamism. Highly open regions tend to possess stronger resource integration capacity, higher technological absorptive capacity, and more active industrial linkages. These features promote regional technological progress and industrial restructuring, thereby altering labor demand structures. This study uses the ratio of total imports and exports to city-level GDP as a proxy for openness, capturing the influence of outward-oriented economic activity on labor allocation.

4.2.4. Mechanism Variables

① Industrial Structure Upgrading (ISU): As one of the key mediating variables in this study, the level of industrial structure upgrading reflects the degree and trajectory of a region’s economic transition from low-end to high-end sectors. It serves as a core indicator for evaluating industrial optimization and structural advancement. In the existing literature, industrial upgrading is widely regarded as a hallmark of high-quality economic development and is frequently employed to analyze structural transformation driven by technological progress, changes in factor allocation efficiency, and industrial transition dynamics. Incorporating this variable into the mediation analysis framework enables a deeper understanding of how industrial robot adoption may influence labor allocation efficiency through structural evolution pathways.

Current approaches to quantifying industrial upgrading fall into four main categories: the industrial output ratio method [69], the industrial hierarchy index method [59], the Moore structural change index [73], and the cosine similarity (angle) method [74]. Each method has its own strengths and limitations and is suited to different research objectives and analytical contexts.

The first is the industrial output ratio method, a more traditional approach that typically uses the share of tertiary industry value added in regional GDP as the core indicator. It reflects the rising prominence of the service sector within the overall economy. This metric is straightforward and data-accessible, making it widely used in studies of China’s industrial evolution, particularly the growing dominance of services. However, the main limitation of this method lies in its simplicity: it captures only the quantity of the tertiary sector share without addressing inter-sectoral relationships, value-added capabilities, or the quality of structural transformation. It also fails to reflect the full upgrading trajectory from primary to tertiary industries, thus producing a somewhat “flattened” index.

The second is the industrial hierarchy index method, which assigns different weights to the three major sectors (typically 1 for primary, 2 for secondary, and 3 for tertiary industries) to construct an index that reflects the direction of structural change. Compared to the output ratio method, this approach better captures the “directionality” of transformation from traditional to modern sectors. However, its subjective weighting system may undermine accuracy, and its performance is limited in contexts with strong structural heterogeneity or complex internal industrial dynamics. Furthermore, its comparability over time is often weak, limiting its usefulness in longitudinal panel studies.

The third method is the Moore structural change index, which quantifies the absolute magnitude of changes in sectoral shares over time to reflect the intensity of structural evolution. This index is particularly suitable for dynamic trajectory analysis, as it captures how quickly structural change is occurring. Nevertheless, it suffers from a critical limitation: it does not distinguish between the direction or quality of change. For example, a shift from primary to tertiary industries and a regression from tertiary back to primary may yield the same index value, thereby weakening the index’s explanatory power as a proxy for upgrading.

The fourth method, which is also adopted in this paper, is the Cosine Angle Method, which has been optimized on the basis of inheriting the advantages of Moore’s change index method, with special emphasis on the directionality and quality level of structural change. The basic principle is that the proportion of value added of primary, secondary and tertiary industries in a certain region constitutes a vector, and the three-unit vectors representing the ideal state of industrial structure are calculated to calculate the cosine angle value, and accordingly weighted to synthesize the index of structural sophistication. Specifically, firstly, let the industrial structure vector of a certain region be $X_0=(x_{\mathrm{1,0}}, x_{\mathrm{2,0}}, x_{\mathrm{3,0}})$, which represents the proportion of the primary, secondary and tertiary industries in the GDP of the place. Then set three ideal unit vectors, $X_1=\left(1, 0, 0\right), X_2=\left(0, 1, 0\right), { X}_3=\left(0, 0, 1\right)$, which represent the ideal structural state dominated by primary, secondary and tertiary industries, respectively. By calculating the angle cosine value ${\theta }_j$ between $X_0$ and $X_1, X_2, X_3$ respectively, the similarity of its structure near the three ideal states is obtained, and then according to the level of industrial development, the weight (3, 2, 1) is given to form the final structural index of advanced structure, and the calculation formula is as follows:

$$ISU=3\times \mathit{arcos}\left({\displaystyle \frac{x_{1,0}}{\sqrt{x_{\mathrm{1,0}}^2+x_{\mathrm{2,0}}^2+x_{\mathrm{3,0}}^2}}}\right)+2\times \mathit{arcos}\left({\displaystyle \frac{x_{\mathrm{2,0}}}{\sqrt{x_{\mathrm{1,0}}^2+x_{\mathrm{2,0}}^2+x_{\mathrm{3,0}}^2}}}\right)+\mathit{arcos}\left({\displaystyle \frac{x_{\mathrm{3,0}}}{\sqrt{x_{1,0}^2+x_{\mathrm{2,0}}^2+x_{\mathrm{3,0}}^2}}}\right)$$

The key advantages of this method are twofold. First, it captures the evolutionary direction of industrial transformation from low-end to high-end sectors. Second, it reflects the degree of deviation from the ideal high-end structure by measuring the angular distance from the tertiary-industry-dominated vector. A larger ISU value indicates a stronger orientation toward a service-led, advanced industrial structure. This method addresses the limitations of traditional structural metrics in directional interpretation and explanatory power, and has been increasingly adopted in recent studies on regional industrial upgrading and urban development quality.

② Urban Innovation Capacity (Inno): Within the analytical framework that investigates how technological progress affects labor resource allocation efficiency through structural mechanisms, urban innovation capacity emerges as a critical, multidimensional construct. It encompasses a region’s capacity for technology absorption, knowledge generation, and institutional support, serving as a composite indicator of a city’s technological supply capabilities, factor allocation efficiency, and policy effectiveness. Urban innovation capacity reflects not only a region’s current level of technological advancement but also its resilience and adaptability in response to science-driven economic transformation.

From the perspective of resource allocation, regions with higher levels of innovation capacity tend to possess more agile and efficient mechanisms for integrating production factors. These regions are better positioned to anticipate and adapt to structural adjustments triggered by technological change, enabling more accurate and efficient matches within the labor market. Therefore, incorporating innovation capacity as a mediating variable in this study not only enriches the understanding of potential causal mechanisms, but also provides a pivotal analytical lens for identifying structural transformation pathways across macro, meso, and micro levels.

In the earlier literature, urban innovation capacity was typically proxied by patent data. For instance, Guan and Liu [75] employed the share of invention patents in total granted patents at the prefecture-level as a representative metric. This approach has gained wide application in early studies of regional innovation due to the transparency and availability of patent statistics, as well as the ease of operationalization. However, as innovation activities have become increasingly diverse and systemically embedded in urban economies, the limitations of patent-counting metrics have become more pronounced.

First, patent counts primarily capture the output side of innovation processes, without adequately reflecting the practical utility, commercial value, or real-world application of technological outcomes. Second, due to significant cross-industry variation in reliance on patenting practices, such indicators may produce misleading comparisons across regions. High-tech industries typically exhibit a high density of patent output, whereas traditional manufacturing or resource-intensive sectors may contribute fewer patents, leading to potential biases in inter-city assessments. Finally, patent data may also be distorted by local government incentives, corporate patenting strategies, and inconsistencies in R&D reporting, all of which undermine their reliability as comprehensive indicators of a region’s true innovation capacity.

To overcome these limitations, this study adopts the Urban and Industrial Innovation Index published in the China Urban and Industrial Innovation Report by Kou and Liu. [76] This index offers a multidimensional and comprehensive evaluation framework covering four dimensions: “innovation environment, innovation input, innovation output, and innovation performance”. It integrates key indicators such as the density of R&D personnel, the number of high-tech enterprises, patent applications, and the value of technology market transactions. This framework captures the full process of innovation activity ranging from resource input to institutional responsiveness and economic outcomes thus providing a more robust and theoretically grounded measure compared to single-dimension proxies.

Due to the latest publicly available version of the report being limited to 2021, this study extends the dataset to 2023 following the methodology outlined in the original report. During the extension process, all city-level innovation indices were harmonized to the 2020 administrative division standard, and industrial innovation components were aligned with the Industrial Classification for National Economic Activities of China (GB/T 4754–2017) [77]. Due to space constraints, the calculation method and technical details of the indicators can be found in the public information description of the “China City and Industry Innovation Report (2017)”, which will not be repeated here.

4.3. Data Sources and Descriptive Statistics

This study is based on a panel dataset covering 280 prefecture-level cities in China from 2006 to 2023. The primary data sources include the China Statistical Yearbook, China City Statistical Yearbook, China Labor Statistical Yearbook, and other relevant statistical yearbooks and sector-specific statistical reports.

The core explanatory variable prefecture-level industrial robot application intensity is constructed using sector-level robot installation data published by the International Federation of Robotics (IFR). Following the Bartik instrument design proposed by Acemoglu and Restrepo [14], the measure captures city-level exposure to national trends in industrial automation across sectors.

The dependent variable, labor resource allocation efficiency, is constructed based on misallocation theory, with foundational data drawn from various statistical yearbooks. Two mechanism variables are included: (1) industrial upgrading—measured by the relative value-added shares of different industries, and (2) urban innovation capacity—quantified using the China Urban and Industrial Innovation Report compiled by Kou and Liu [76].

The model further incorporates a set of control variables to account for macroeconomic and institutional influences on labor allocation efficiency. These controls include government intervention, infrastructure development, science and technology expenditure, and financial development, with data derived from the same official statistical sources.

To address potential issues related to missing values or outliers, supplementary information from other statistical bulletins and the National Economic and Social Development Statistical Communiqués was utilized to ensure the accuracy and objectivity of the dataset.

Summary statistics for all key variables are presented in

Table 1. Descriptive analysis.

Variables	Sample Size	Mean	p50	sd	Min	Max
Lab	5040	1.589	1.419	1.123	0.001	12.862
Robots	5040	37.420	13.421	56.023	0.064	659.661
ISU	5021	6.512	6.500	0.367	5.518	7.722
Inno	5040	22.278	2.033	110.780	0.000	2907.851
GDP	5040	10.594	10.625	0.761	4.595	13.056
FIN	5040	0.981	0.804	0.606	0.075	7.450
GOV	5040	0.191	0.164	0.105	0.043	1.485
BASE	5040	0.818	0.759	0.397	0.000	3.003
SCI	5040	0.016	0.011	0.017	0.000	0.207
OPEN	5040	0.186	0.077	0.321	−0.001	3.499

Drawing by the author.

.

5. Characterization of Facts

5.1. Evolutionary Characteristics of Labor Resource Allocation Efficiency in Chinese Prefecture-Level Cities

To capture the long-term evolution of labor resource allocation efficiency across Chinese prefecture-level cities, this study constructs and computes the annual average index of labor misallocation for the period 2006–2023 based on the measured degree of misallocation in each city. This index serves as a reliable indicator of the deviation from optimal factor allocation, with higher values indicating more severe mismatches in labor distribution across regions or industries. Overall, the trend reveals a steady improvement in labor resource allocation efficiency since 2006, with the misallocation index showing a marked downward trajectory. This suggests that the spatial and structural reallocation of labor resources have been progressively optimized.

Specifically, the average misallocation index stood at a historically high level of 2.77 in 2006, reflecting widespread inefficiencies in labor allocation amidst rapid industrialization. Labor mobility across regions and industries was substantially constrained, leading to significant resource misallocation. In subsequent years, the index declined steadily, reaching 1.86 by 2011 and falling further to 1.24 by 2013. This significant improvement is largely attributable to post-2008 structural adjustments and increased openness in labor markets. Between 2014 and 2016, the index remained relatively stable at a lower level, fluctuating between 1.17 and 1.21, indicating notable progress in factor coordination and the establishment of more market-oriented labor mobility mechanisms at the local level.

However, beginning in 2017, the index entered a period of relative stagnation, fluctuating within the range of 1.18 to 1.20 in most years. A mild rebound to 1.19 was observed in 2021, suggesting that transitional frictions and mismatches in skill requirements emerged during the shift from traditional growth engines to new drivers of development. Nevertheless, the overall trend remained positive. By 2023, the misallocation index had further declined to a historical low of 1.06, signaling substantial improvements in labor allocation efficiency driven by industrial upgrading, deepened regional coordination policies, and enhanced information symmetry in labor markets.

As illustrated in Figure 2, the misallocation index over this period exhibits a near-linear downward trend with gradually decreasing volatility. This trend not only confirms the sustained improvement in resource allocation efficiency but also reflects enhanced labor mobility across regions and improved alignment between urban industrial structures and labor market demand. Moreover, the observed evolution provides a solid empirical and theoretical foundation for the subsequent analysis on whether the application of industrial robotics has contributed to the improvement in resource allocation efficiency.

5.2. Spatial Distribution Characteristics of Artificial Intelligence Application in Prefecture-Level Cities

To further examine the spatial diffusion patterns of industrial robot technology in China, this study analyzes the evolution of the top ten prefecture-level cities across different years based on two key indicators: the stock-based and delivery-based penetration rates of industrial robots. As shown in

Table 2. Top 10 cities in China by industrial robot stock penetration (units/10,000 people).

	2006				2015
No.	City	Stock Penetration	City	Stock Penetration	City	Stock Penetration
1	Karamay	1.45	Dongying	120.98	Dongying	659.66
2	Wuhai	1.19	Rizhao	110.82	Rizhao	593.90
3	Dongying	1.18	Zaozhuang	96.68	Zaozhuang	533.54
4	Panjin	0.91	Shiyan	87.26	Weihai	465.35
5	Pingxiang	0.84	Changchun	79.09	Shiyan	455.52
6	Daqing	0.71	Zhoushan	78.20	Changchun	420.07
7	Fushun	0.69	Weihai	76.06	Tai’an	413.85
8	Huludao	0.65	Tai’an	72.09	Zhoushan	401.44
9	Jilin	0.64	Jinan	59.28	Jinan	357.08
10	Shizuishan	0.64	Dezhou	59.24	Dezhou	352.26

Drawing by the author.

and

Table 3. Top 10 cities in China by industrial robot delivery penetration (units/10,000 people).

	2006				2015
No.	City	Delivery Penetration	City	Delivery Penetration	City	Delivery Penetration
1	Karamay	1.45	Dongying	32.19	Dongying	110.93
2	Alashan	1.32	Rizhao	29.60	Rizhao	97.39
3	Wuhai	1.19	Zaozhuang	25.99	Zaozhuang	88.71
4	Dongying	1.18	Shiyan	23.29	Weihai	79.98
5	Panjin	0.91	Changchun	21.18	Shiyan	71.89
6	Pingxiang	0.84	Zhoushan	20.97	Tai’an	69.07
7	Daqing	0.71	Weihai	20.89	Changchun	67.38
8	Fushun	0.69	Tai’an	19.84	Ngari	64.93
9	Huludao	0.65	Ngari	19.63	Zhoushan	63.09
10	Jilin	0.64	Jinan	16.60	Jinan	61.38

Drawing by the author.

, the application of industrial robots in China exhibits a distinct spatial evolution pattern characterized by a transition from “resource-based city leadership” to “manufacturing hub dominance”, followed by “regional gradient diffusion”.

In 2006, the overall penetration of industrial robots remained low, with the top-ranking cities primarily consisting of resource-oriented cities such as Karamay, Wuhai, Panjin, and Daqing. These cities, dominated by energy and petrochemical industries, had relatively strong capital accumulation capacities and specific automation substitution demands, which led to higher robot density per capita in the early stage. Nonetheless, the overall penetration remained limited, with no top-ten city exceeding 1.5 robots per 10,000 people.

By 2015, the leading city profile had undergone a significant shift. Manufacturing-oriented cities such as Dongying, Rizhao, Zaozhuang, Shiyan, and Weihai rapidly emerged, accompanied by a marked increase in penetration rates. Dongying ranked first nationwide with 120.98 robots per 10,000 people nearly a hundredfold increase from 2006. This surge reflects the strong demand for robotics driven by industrial systems centered on equipment manufacturing, automotive production, and component supply chains, particularly in provinces like Shandong and Hubei. The expansion was further facilitated by local government policies promoting technological upgrading and investment in intelligent equipment.

By 2023, the agglomeration effect of the manufacturing sector had become even more pronounced, with the top ten cities all located in eastern and parts of central China. Dongying, Rizhao, and Zaozhuang reported penetration rates of 659.66, 593.90, and 533.54 robots per 10,000 people, respectively, indicating a substantial expansion of their leading positions. Meanwhile, cities such as Weihai, Tai’an, Zhoushan, and Jinan surpassed 350 robots per 10,000 people, signifying that small- and medium-sized coastal manufacturing cities have entered a high-density phase of intelligent equipment adoption. A similar ranking pattern is observed for delivery-based penetration rates, suggesting that these cities not only maintain high stock levels of industrial robots but also demonstrate strong and sustained purchasing capacity.

Overall, the spatial diffusion of industrial robots in China follows an evolutionary path from resource-based to manufacturing-based and ultimately to technology-intensive cities. The deployment of intelligent equipment has evolved from concentrated points to corridor-like expansion patterns, closely aligned with local industrial structures and policy environments. Cities with high penetration rates typically share two characteristics: (1) comprehensive industrial chains in key sectors such as automotive, electronics, and equipment manufacturing; and (2) consistent fiscal and policy support from local governments for intelligent manufacturing. Looking ahead, as the share of manufacturing rises in inland provinces and regional policy coordination improves, the penetration gap across regions is expected to narrow. However, in the short term, leading cities are likely to retain their competitive edge.

By further incorporating GIS-based distribution maps of the stock and delivery penetration rates of industrial robots across prefecture-level cities (see Figure 3 and Figure 4), the spatial diffusion path of industrial robot technology in China can be visualized more intuitively. From a temporal perspective, penetration rates were generally low nationwide in 2006, with only a few early clusters forming primarily located in the eastern coastal region and the traditional industrial bases of Northeast China. By 2012, prominent “high-penetration belts” began to emerge in manufacturing-strong provinces such as Shandong, Liaoning, and Jiangsu, with the Shandong Peninsula developing into an initial industrial robotics cluster.

After 2018, the trend of regional diffusion accelerated further. An increasing number of prefecture-level cities in Shandong, Jiangsu, Anhui, and Hubei entered the darkest shaded zones on the map, indicating that central manufacturing cities had begun large-scale adoption of robotic equipment. By 2023, the national distribution pattern had evolved into a multi-core agglomeration structure characterized by “Shandong as the core, the Bohai Rim and Yangtze River Delta as the wings, and several breakthrough points in Central China”.

In terms of stock penetration, growth in density reflects a stable accumulation effect, with spatial patterns transitioning from isolated bright spots to multiple belt-like concentrations. In contrast, the delivery penetration map reveals recent investment dynamics. Notably, in 2023, in addition to traditional strongholds such as Shandong and Jiangsu, regions like Sichuan-Chongqing, northern Jiangxi, and central Anhui also emerged as local high-penetration zones, indicating that policy incentives and industrial relocation have significantly driven the local intelligent manufacturing process.

It is important to note that a few cities in central and western China, due to their small population bases and high firm concentration, show “high-delivery, high-penetration” outlier peaks under statistical measures, which should be interpreted in the context of their specific industrial structures.

Overall, the spatial pattern of industrial robot penetration at the prefecture level in China follows a trajectory of “eastern leadership—central catch-up—sporadic breakthroughs in the west”. The joint evolution of both stock and delivery penetration indicators suggests that China’s manufacturing sector has entered a stage characterized by simultaneous regional differentiation and deepening industrial clustering in intelligent transformation.

(The Chinese cities are based on the standard map No. GS (2020)4619 of the standard map website of the Ministry of Natural Resources of China, and the base map boundaries are not modified, the same below).

6. Empirical Results and Analysis

6.1. Baseline Regression Results

This study employs a two-way fixed effects model to systematically examine the impact of industrial robot adoption on labor resource allocation efficiency at the prefecture-city level. The model controls for both city-specific fixed effects and year fixed effects, thereby effectively accounting for time-invariant regional heterogeneity and cyclical macroeconomic fluctuations. To enhance the interpretability and robustness of the regression results, the analysis follows a “general to specific” modeling strategy—initially estimating the basic relationship between the dependent and key explanatory variables, and subsequently incorporating a full set of control variables to construct the complete regression framework.

Table 4. Summary of benchmark returns.

	Lab	Lab	Lab	Lab	Lab	Lab	Lab
	(1)	(2)	(3)	(4)	(5)	(6)	(7)
Robots	−0.003 ***	−0.003 ***	−0.003 ***	−0.003 ***	−0.003 ***	−0.002 ***	−0.002 ***
	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)
GDP		−0.158	−0.133	−0.044	−0.046	−0.040	−0.074
		(0.112)	(0.123)	(0.135)	(0.133)	(0.129)	(0.113)
FIN			0.065	−0.010	−0.011	−0.006	−0.001
			(0.063)	(0.060)	(0.059)	(0.058)	(0.060)
GOV				1.702 ***	1.584 ***	1.411 ***	1.353 ***
				(0.518)	(0.486)	(0.466)	(0.435)
BASE					0.122	0.106	0.090
					(0.099)	(0.098)	(0.086)
SCI						−4.534 **	−3.629
						(2.139)	(2.459)
OPEN							0.272
							(0.350)
cons	2.774 ***	4.289 ***	4.003 ***	3.002 **	2.978 **	2.956 **	3.225 ***
	(0.045)	(1.060)	(1.183)	(1.330)	(1.330)	(1.288)	(1.142)
N	5040	5040	5040	5040	5040	5040	5040
R2	0.507	0.508	0.509	0.515	0.517	0.519	0.521
Year	Control	Control	Control	Control	Control	Control	Control
City	Control	Control	Control	Control	Control	Control	Control

Note: ** and *** represent 5% and 1% significance levels, respectively, and values in parentheses are robust standard errors.

presents the baseline regression results regarding the relationship between industrial robot application and labor resource misallocation. The core explanatory variable is the intensity of robot adoption, while the dependent variable is the labor misallocation index at the city level. The models sequentially control for economic development, financial development, government intervention, industrial base, technological capacity, and openness to trade. All specifications include city and year fixed effects.

The results consistently show that the coefficient of the robot variable is negative and highly significant across all model specifications. This suggests that the diffusion of industrial robots contributes to reducing labor misallocation and improving the efficiency of factor allocation at the urban level. The negative effect remains robust even after the inclusion of extensive control variables, thereby lending strong support to Hypothesis H1. These findings indicate that the application of industrial robots, as a form of technological investment, has effectively alleviated factor misallocation during the study period.

With respect to the control variables, the effects of economic development and financial development on the labor misallocation index are mixed and generally statistically insignificant. The coefficient on government intervention becomes positive after controlling for other factors, suggesting that administrative involvement may, under certain circumstances, introduce distortions to resource allocation. The effects of industrial base and technological capacity appear somewhat unstable, indicating that their moderating roles on labor misallocation are context-dependent and not robust across specifications. The degree of openness to trade shows a relatively limited impact on allocation efficiency.

Overall, industrial robot adoption as an emerging technological factor demonstrates a consistently significant and positive effect in promoting labor resource allocation efficiency. The regression models exhibit good overall fit, with explanatory power improving progressively as additional variables are included. These results align well with the theoretical expectations underlying the research hypothesis, further validating the role of advanced technology in addressing factor misallocation.

6.2. Robustness Checks

To address potential concerns regarding omitted variable bias, endogeneity, or model misspecification that may compromise the validity and explanatory power of the baseline estimation, this study conducts a series of robustness checks. These tests aim to evaluate the reliability and consistency of the core findings through multiple methodological approaches.

6.2.1. Excluding Outliers

As shown in the descriptive statistics in

Table 5. Robustness test results.

	Shrinking 1%	Cutting 1%	Replace Explanatory Variables	Time Trend Test
	(1)	(2)	(3)	(4)
Robot_w	−0.003 ***
	(0.001)
Robot_tr		−0.021 ***
		0.005
Robot_install			−0.017 ***
			(0.004)
Robot_lead1				0.001
				(0.001)
CV	Yes	Yes	Yes	Yes
City	Yes	Yes	Yes	Yes
Year	Yes	Yes	Yes	Yes
R2	0.594	0.599	0.587	0.482
N	5040	4377	5040	4760

Note: *** represent 1% significance levels, respectively, and values in parentheses are robust standard errors.

, both the explanatory and dependent variables exhibit some distributional heterogeneity across cities and years. To eliminate the potential bias introduced by a small number of extreme observations, this study adopts two common techniques winsorization and truncation at the 1st and 99th percentiles for both the core explanatory and dependent variables. Specifically, bilateral winsorization and truncation are applied to reduce the influence of outliers. Columns (1) and (2) of Table 5 demonstrate that the coefficient of the core variable remains negative and statistically significant at the 1% level after excluding extreme values. These estimates are highly consistent with the baseline results, indicating that the main conclusions are not driven by outliers and exhibit strong robustness.

6.2.2. Alternative Explanatory Variable Specification

To examine the sensitivity of the results to alternative measures of the explanatory variable, the analysis replaces the stock-based penetration rate of industrial robots with the delivery-based penetration rate (i.e., the number of newly installed robots per 10,000 people at the city level). As shown in Column (3) of Table 5, the alternative variable also yields a significantly negative coefficient at the 1% level, with the same direction and magnitude as in the baseline model. This consistency across alternative specifications suggests that the relationship between robot adoption and labor resource allocation efficiency holds regardless of whether robot penetration is measured using stock or flow indicators, thereby enhancing the robustness and external validity of the study’s findings.

6.2.3. Time Trend Placebo Test

The observed relationship between industrial robot adoption and labor misallocation may be confounded by common macro-level trends rather than reflecting a direct causal mechanism. To rule out this possibility, a placebo test is conducted by replacing the core explanatory variable with its one-period-ahead value, following standard practice in related literature [14,78]. If the future value of robot penetration is found to significantly affect the current level of labor misallocation, this would suggest the presence of spurious correlation due to shared trends, model misspecification, or reverse causality. As shown in Column (4) of Table 5, the future robot penetration variable has no statistically significant effect on current labor misallocation, supporting the temporal validity of the baseline model and indicating that the original findings are not merely driven by underlying time trends. This lends further credibility to the causal interpretation of the estimated relationship.

6.3. Endogeneity Treatment

6.3.1. Instrumental Variable Approach

To further verify the causal relationship between industrial robot adoption and labor misallocation, and to address potential endogeneity bias, this study employs an instrumental variable (IV) strategy. Given the possible reverse causality wherein higher labor misallocation may induce firms to adopt intelligent equipment more actively such endogeneity may bias the estimation results. Drawing on the approach proposed by Jung and Lim [79], this study constructs an instrumental variable based on the number of industrial robots installed in the United States and applies a two-stage least squares (2SLS) estimation.

The theoretical rationale for this instrument is twofold. First, as the global technological frontier, the U.S. exhibits sector-specific trends in industrial robot deployment that are often emulated by Chinese industries, generating technological spillovers and trend synchronization thereby satisfying the relevance condition. Second, due to structural and geographic differences between the two economies, U.S. robot installations are unlikely to directly affect labor market conditions in Chinese prefecture-level cities, thus fulfilling the exclusion restriction.

Specifically, in the first stage, the U.S. robot variable is used to predict the robot penetration rate in Chinese cities. As shown in Column (1) of

Table 6. Endogeneity treatment results.

	American Industrial Robots		Lab
	(1)	(2)	(3)
Phase 1	−0.006 ***
	(−4.384)
Phase 2		−0.002 ***
		(−4.466)
L.Lab			3.132 ***
			(0.801)
Robot			−0.022 ***
			(0.007)
Kleibergen–Paap rk LM statistic		141.621 ***
Kleibergen–Paap rk Wald F statistic	984.082 [16.38]
CV	Yes	Yes	Yes
City	Yes	Yes	Yes
Year	Yes	Yes	Yes
R2	0.763	0.044
N	5040	5040	4760
AR(1)			0.042
AR(2)			0.422
Hansen			0.344

Note: *** represent 1% significance levels, respectively. The values in brackets are robust t statistics and coefficient errors, respectively.

, the coefficient is significantly negative. The Kleibergen–Paap rk LM statistic and F-statistic are 141.621 and 984.082, respectively, well above the conventional threshold of 16.38 indicating no weak instrument problem. In the second stage (Table 6, Column 2), the coefficient of the core explanatory variable Robots remains significantly negative at the 1% level, confirming that the mitigating effect of robot adoption on labor misallocation remains robust even after addressing endogeneity.

6.3.2. System GMM Estimation

To further test the robustness of the causal relationship from a dynamic perspective, this study also employs the System Generalized Method of Moments (System GMM) estimator. Developed by Arellano and Bover and Blundell and Bond [80,81], the System GMM estimator combines the level equation and first-differenced equation, using lagged values of the variables as instruments. This approach allows for efficient estimation while controlling for fixed effects and heteroskedasticity and is particularly well-suited for panel datasets with a large cross-sectional dimension and relatively short time span.

In this specification, the lagged dependent variable is included to capture the path dependence and adjustment inertia inherent in labor misallocation, resulting in a dynamic panel regression framework. The results are presented in Column (3) of Table 6. The coefficient of the lagged dependent variable (L.Lab) is 3.132 and significantly positive, indicating strong dynamic persistence in labor misallocation. The coefficient of the core explanatory variable Robots is −0.022 and significant at the 1% level, further confirming that robot penetration continues to exert a significant suppressing effect on labor misallocation even within a dynamic setting.

The AR (1) test yields a p-value of 0.042, indicating expected first-order autocorrelation in the differenced residuals. The AR (2) test yields a p-value of 0.422, suggesting no second-order serial correlation, thus supporting the validity of the model specification. The Hansen test produces a p-value of 0.344, failing to reject the null hypothesis of instrument validity, thereby confirming the overall exogeneity of the instruments and satisfying the identification requirements.

In summary, by introducing an external instrumental variable and employing the System GMM estimation approach, this study effectively addresses potential endogeneity concerns from both cross-sectional and dynamic perspectives. The consistency and robustness of the estimation results across these two distinct identification strategies further reinforce the causal validity and theoretical soundness of the core findings. These efforts provide a solid econometric foundation for the subsequent mechanism analysis and the development of policy recommendations.

6.4. Heterogeneity Analysis

The baseline regression results reveal the overall impact of industrial robot adoption on labor resource allocation efficiency at the national level. However, significant disparities exist across regions in terms of resource endowments, economic foundations, technological capabilities, and industrial structures, which may lead to differential impacts of robot adoption on local labor markets. To more comprehensively identify the heterogeneous effects of this technological shock, this study conducts subgroup regressions from three perspectives-regional economic development level, population aging, and manufacturing scale-to examine the marginal differences and underlying mechanisms of robot adoption across different contexts.

6.4.1. Regional Dimension

In analyzing the impact of industrial robot adoption on labor resource allocation efficiency, it is crucial to incorporate regional heterogeneity into the empirical framework. On one hand, China’s vast geographical expanse and pronounced regional disparities manifest in uneven levels of economic development, industrial composition, technological infrastructure, and factor endowments. Accordingly, labor markets vary significantly in their adjustment mechanisms and responsiveness to technological shocks. Relying solely on national-level estimates may mask important within-region heterogeneity and reduce the explanatory power and policy relevance of the findings. On the other hand, industrial robots as capital-intensive technologies reshape labor allocation through substitution, restructuring, and reconfiguration processes. Their effects are jointly conditioned by local innovation capacity, institutional environment, and industrial absorptive capacity. Therefore, investigating the regional variation in marginal effects is key to understanding the spatial dynamics of robot diffusion and its reallocation mechanisms, as well as to reinforcing the study’s policy implications.

For regional grouping, this study adopts the distinction between the Yangtze River Economic Belt (YREB) and non-YREB regions [82] based on the following rationale. First, the YREB spans eastern, central, and western China, encompassing 11 provinces and municipalities. It represents a key national economic corridor with a complete industrial chain, strong technological innovation capacity, and a concentrated labor market—serving as a frontier region for China’s manufacturing transformation and intelligent upgrading. Second, the YREB has laid a solid foundation for robot deployment, with numerous pilot projects and high absorption capacity, making it an ideal setting to examine marginal technology effects in “high baseline” regions. In contrast, non-YREB regions covering northeastern, northern, northwestern, and parts of central inland cities often suffer from weaker technological capacity, limited industrial bases, and severe factor mismatches, offering a useful counterfactual for identifying adjustment space in “low baseline” regions. Third, this classification has been widely adopted in urban grouping and regional policy evaluation studies and is theoretically and practically well-supported [83].

The empirical results (

Table 7. Heterogeneity analysis.

	(1)	(2)	(3)	(4)	(5)	(6)
	YREB	Non-YREB	Mild PA	Heavy PA	Low MSS	High MSS
	Lab	Lab	Lab	Lab	Lab	Lab
Robots	−0.001	−0.003 ***	−0.001	−0.003 ***	−0.001 *	−0.003 ***
	(0.002)	(0.001)	−0.001	−0.003 ***	(0.001)	(0.001)
CV	Control	Control	Control	Control	Control	Control
Year	Control	Control	Control	Control	Control	Control
City	Control	Control	Control	Control	Control	Control
N	1890	3150	2376	2268	2520	2286
R2	0.612	0.479	0.471	0.631	0.587	0.531

Note: * and *** represent 10% and 1% significance levels, respectively, and values in parentheses are robust standard errors.

, Columns 1 and 2) reveal notable regional differences in the effects of robot adoption. In non-YREB cities, the diffusion of industrial robots significantly reduces labor misallocation. This can be interpreted as a “low-baseline–high-elasticity” effect of technological improvement: these cities typically exhibit outdated occupational structures and low skill–demand alignment, allowing automation technologies to rapidly replace inefficient positions and restructure skill requirements ultimately enhancing allocation efficiency. Moreover, robot diffusion in these regions demonstrates a “corrective effect” by accelerating the elimination of obsolete production factors and restructuring employment systems, thereby unlocking structural adjustment potential.

By contrast, in YREB cities, although industrial robot adoption is also widespread, its impact on labor allocation efficiency is not statistically significant. This may indicate that in high-capacity regions, labor markets have matured and the marginal contribution of additional technology adoption is limited. Here, robotics primarily serve to optimize and reinforce existing systems, rather than drive fundamental restructuring.

From an institutional perspective, the regional heterogeneity observed reflects differences in the alignment among technological absorption capacity, institutional adaptability, and labor market flexibility. Non-YREB regions, despite weaker economic foundations, offer greater technological catch-up potential and institutional flexibility, creating a “low-pressure zone” conducive to robotic reconfiguration. In contrast, YREB regions, with already high robot densities and well-developed structures, integrate automation more into precision management and industrial coordination, yielding diminishing marginal effects on resource misallocation.

Based on this analysis, policy implications should emphasize “structural matching” and “factor adaptability” in region-specific technology promotion strategies. In non-YREB cities, efforts should focus on aligning robot adoption with skill system restructuring through reforms in vocational education, support for skill transfer, and job retraining systems to fully realize the structural gains from automation. In YREB cities, emphasis should shift to deep integration of intelligent systems and upstream–downstream industrial coordination. The goal is to achieve incremental efficiency gains in factor allocation through refined smart manufacturing and human–machine collaboration. Ultimately, a place-based, multi-tiered pathway toward intelligent transformation should be fostered ensuring a virtuous interaction between technological advancement and structural optimization.

6.4.2. Population Aging (PA)

As China rapidly enters an era of demographic aging, the diminishing demographic dividend and the significant regional variations in labor supply structure and age composition are likely to exert substantive influences on the marginal effects of industrial robot adoption. In regions with relatively younger populations, labor markets tend to exhibit greater fluidity and skill adaptability, making it easier for robotic technologies to integrate into industrial systems and enhance allocation efficiency. Conversely, in areas experiencing pronounced population aging, labor supply constraints and the aging of human capital may introduce friction and resistance in the technological substitution process, thereby weakening the potential of automation to improve resource allocation. Therefore, examining the heterogeneity of industrial robot impact from the perspective of population aging is not only theoretically compelling but also enhances the policy relevance of the empirical findings.

To categorize cities by their degree of aging in a scientifically rigorous manner, this study draws on authoritative criteria issued by the National Bureau of Statistics of China (May 2021) [84] and the Price Monitoring Center of the National Development and Reform Commission (June 2022) [85]. Using data from the Seventh National Population Census (2020), we define the proportion of residents aged 65 and above in the total population as the core indicator. Cities with a share of 14% or higher are classified as “severely aged”, while those below this threshold are categorized as “mildly aged”. This classification aligns with official national standards and accurately captures intercity differences in labor force pressures and technological absorptive capacity, thereby providing a solid empirical basis for subsequent regression analysis.

The results, as shown in Columns 3 and 4 of Table 7, reveal a clear moderating effect of aging on the impact of industrial robots. In severely aging cities, the coefficient of the Robots variable is −0.003 and statistically significant at the 1% level, indicating that increased robot penetration significantly reduces the labor misallocation index. Even under structural rigidity in the labor force, technological substitution remains strong, highlighting the capacity of industrial robots to reshape resource allocation. By contrast, in mildly aging cities, although the coefficient shares the same sign, it is not statistically significant. This suggests that younger cities may have already achieved relatively high levels of allocation efficiency, leaving limited room for further improvement through marginal technological inputs. In contrast, in high-aging cities, where initial misallocation is more severe and job updating is delayed, robot adoption appears more effective in restructuring employment and reallocating production factors, thus significantly improving allocation outcomes.

Mechanistically, this heterogeneity may stem from three interrelated factors:

First, labor supply constraints are more acute in aging cities, making technological substitution a crucial means of addressing labor shortages and maintaining production continuity thereby enhancing allocation efficiency.

Second, skill mismatch gaps are more pronounced in these cities, which means the reallocation effects induced by technology-driven job restructuring are more likely to materialize.

Third, differences in technology readiness lead to a paradox: mildly aging cities, despite having stronger adaptive capacities, may have already undergone structural upgrades, reducing the marginal room for improvement and thus resulting in statistically insignificant outcomes.

In sum, while industrial robot technology generally holds the potential to improve allocation efficiency across different demographic contexts, its marginal effectiveness is conditioned by the foundational structure of the labor force and the adaptability of skill systems. These findings carry important policy implications. In severely aging cities, policy efforts should accelerate the integration of intelligent technologies and human–machine collaboration systems, promote job standardization and automation transformation, and use technology to alleviate demographic pressures on resource allocation. At the same time, greater emphasis should be placed on reskilling the existing workforce, enhancing their ability to absorb and apply new technologies. In mildly aging cities, the policy focus should shift toward promoting the deep synergy between high-skill labor and intelligent technologies, improving the alignment between high-end positions and innovative talent. By boosting the efficiency of human–machine complementarity, the structural dividends of intelligent technology can be more fully realized. Ultimately, a differentiated, demography-aware, and inclusive transformation pathway should be developed to achieve effective technology empowerment across diverse population structures.

6.4.3. Manufacturing Sector Size (MSS)

When examining the impact of industrial robot adoption on the efficiency of labor resource allocation, heterogeneity in the size of the manufacturing sector provides a critical structural context for identifying technological effects. As the key sector for absorbing employment, integrating industrial chains, and facilitating technological implementation, manufacturing not only determines the depth of technology adoption but also significantly influences the reach and effectiveness of industrial robot in restructuring human resources and enhancing allocation efficiency [86]. The marginal contribution of technology rarely occurs in isolation; rather, it operates within the embedded structures of industrial organization. Accordingly, cities with larger manufacturing sectors offer more extensive and diversified pathways for industrial robot applications, potentially yielding stronger impacts on the labor market.

Accordingly, this study classifies cities into two groups based on whether the share of manufacturing value added in GDP is above or below the sample median, resulting in “high-manufacturing cities” and “low-manufacturing cities”. Separate regressions are then conducted for each subsample. As shown in Columns (5) and (6) of Table 7, the coefficient of the Robots variable in high-manufacturing cities is −0.003 and statistically significant at the 1% level, indicating that increased robot penetration significantly reduces labor misallocation and enhances resource allocation efficiency. This may be attributed to the presence of more complete industrial chains, stronger technological absorption and transformation capabilities, and relatively mature labor market mechanisms in these cities facilitating a virtuous cycle of “technology adoption—job optimization—skill matching”.

By contrast, in low-manufacturing cities, although the coefficient of Robots remains negative and statistically significant at the 10% level, the marginal effect is weaker. This suggests that the capacity of robot adoption to improve allocation efficiency is considerably constrained in such contexts. Several factors may contribute to this outcome:

First, weak industrial foundations and a scarcity of core manufacturing segments limit the practical scenarios for technology application.

Second, the skill structure of the labor force is relatively outdated, meaning the substitution effect of automation often outweighs its creative potential leading to structural mismatches through “job restructuring—skill disconnection”.

Third, technological deployment may precede institutional adjustments and training mechanisms, resulting in a misaligned diffusion path characterized by “technology-first, human capital lagging”.

These results highlight the structural modulation role of manufacturing capacity in the localization and transformation of industrial robot technologies. Manufacturing is not only the physical carrier of technological applications but also a decisive factor in determining the marginal productivity of such technologies. Therefore, in promoting intelligent manufacturing and technology-driven transformation policies, it is crucial to recognize the constraints posed by local industrial absorption capacity.

For cities with strong manufacturing bases, efforts should focus on deepening the integration of robotics into upstream and downstream segments of the industrial chain, amplifying spillover effects and facilitating horizontal diffusion. For cities with weaker manufacturing foundations, simultaneous progress is needed in strengthening industrial chain infrastructure, building reskilling systems, and optimizing the human capital structure. These measures can help avoid a scenario in which technology introduction inadvertently exacerbates structural mismatches in the labor market.

7. Mechanism Analysis

7.1. Industrial Upgrading

In assessing the impact of industrial robot on the efficiency of labor resource allocation, it is insufficient to focus solely on the direct effects of industrial robot applications; instead, it is essential to uncover the underlying transmission mechanisms. To this end, this study incorporates the level of industrial upgrading (ISU) as a mediating variable and employs the stepwise regression method proposed by Baron and Kenny [60] to construct a mechanism testing framework. This approach aims to empirically identify how industrial robot applications indirectly influence labor allocation efficiency by promoting structural shifts in the industrial sector.

Table 8. Mechanism tests for advanced industrial structure.

	(1)	(2)
	ISU	Lab
Robots	0.001 ***	−0.002 ***
	(0.000)	(0.000)
ISU		−0.393 ***
		(0.088)
CV	Yes	Yes
Year	Yes	Yes
City	Yes	Yes
N	5021	5021
R2	0.684	0.523

Note: *** represent and 1% significance levels, respectively, and values in parentheses are robust standard errors.

reports the regression results for the effects of robot adoption on industrial upgrading, as well as the effects of industrial upgrading on labor misallocation. In Column (1), the coefficient of the Robots variable on ISU is significantly positive at the 1% level, suggesting that industrial robot diffusion has a strong positive effect on the upgrading of urban industrial structures. This finding indicates that robot technology not only enhances automation in manufacturing processes, but also plays a critical role in steering the overall industrial system toward higher-value-added, technology-intensive sectors. This structural shift provides both the institutional foundation and sectoral support necessary for reallocating labor resources more efficiently.

Column (2) incorporates ISU into the labor misallocation model (Lab), in order to examine the mediating role of industrial upgrading in the relationship between robot adoption and allocation efficiency. The results show that the negative effect of Robots remains statistically significant, although its absolute magnitude slightly declines compared to the baseline model. This suggests that part of the effect of robot adoption on labor misallocation is mediated through industrial upgrading. Moreover, the coefficient of ISU is significantly negative, indicating that the more advanced the industrial structure, the lower the degree of labor misallocation and the higher the efficiency of labor allocation. This result aligns with the core tenets of structuralist economics, which emphasize that structural transformation enables a more efficient distribution of job opportunities and skill requirements, facilitating both spatial and occupational matching of the labor force. Hypothesis H2 is thus empirically supported.

In summary, the mechanism analysis clearly reveals that industrial upgrading plays a key mediating role in the process by which industrial robot adoption improves labor resource allocation. Robots not only directly accelerate the upgrading of production systems, but also indirectly shape job structures and industrial hierarchies guiding labor to shift from low- to high-value-added sectors. This, in turn, helps correct structural mismatches in labor markets. These findings underscore the importance of promoting synergy between technological advancement and industrial transformation. Policy efforts should focus on fostering a “technology–industry–labor” triadic coordination mechanism to fully leverage the allocative potential and structural dividends of industrial robots.

To further verify the robustness of the mediating role of industrial upgrading in the relationship between industrial robot adoption and labor resource allocation efficiency, this study employs a non-parametric Bootstrap resampling method to test the mediation effect. This approach does not rely on strong assumptions regarding the distribution of error terms and is particularly suitable for accurately estimating the statistical distribution of indirect effects in samples of limited size. It has become a widely accepted and reliable tool in recent years for mechanism analysis.

As shown in

Table 9. Full-sample Bootstrap test results for advanced industrial structure.

Mediating Variables		Observed Coef.	Std.Err.	z	p > |z|
ISU	Indirect effect	−0.000	0.000	−4.050	0.000
	Direct effect	−0.002	0.000	−13.790	0.000
	Total effect	−0.002	0.000	−15.140	0.000

, overall the results obtained through the Bootstrap method are consistent with those from the stepwise regression approach in terms of direction and significance, thereby reinforcing the statistical robustness of the mechanism identification. In particular, the statistical significance of the indirect effect provides strong empirical support for the conclusion that industrial upgrading serves as a key transmission channel through which industrial robot adoption influences labor allocation efficiency. This mechanism exhibits both structural and institutional characteristics, offering a deeper understanding of how technological change reshapes factor allocation.

These findings provide solid econometric evidence for the optimization path of production factors in the context of technological transformation. Moreover, they offer a practical foundation for designing more integrated industrial and human capital policies, aimed at enhancing the synergy between technological progress and labor market development.

7.2. Urban Innovation Capacity

To further investigate the mechanisms through which industrial robot adoption influences labor resource allocation efficiency, this study introduces urban innovation capacity (Inno) as a mediating variable. A mediation model is constructed to identify potential transmission channels. As a general-purpose technology, industrial robots not only enhance firm-level productivity but also reshape the urban innovation ecosystem. Through this process, technological diffusion may stimulate local innovation activities, foster knowledge spillovers, and improve institutional environments, thereby indirectly affecting labor market restructuring and job–skill matching efficiency.

Table 10. Mechanistic tests of urban innovative capacity.

	(1)	(2)
	Inno	Lab
Robots	0.259 *	−0.003 ***
	(0.112)	(0.001)
Inno		0.001 *
		(0.000)
CV	Yes	Yes
Year	Yes	Yes
City	Yes	Yes
N	5040	5040
R2	0.240	0.523

Note: * and *** represent 10% and 1% significance levels, respectively, and values in parentheses are robust standard errors.

presents the regression results examining the mediating role of urban innovation capacity. In Column (1), the adoption of industrial robots shows a significantly positive effect on Inno, suggesting that the widespread deployment of robots across manufacturing, services, and management has effectively stimulated innovation activity at the city level. This process may manifest through increased corporate R&D investment, rising demand for innovative talent, and accelerated concentration of upstream technological resources thereby enhancing a city’s innovation output and knowledge diffusion. In this sense, industrial robots serve not only as technical endpoints improving operational efficiency but also as triggers for institutional and environmental upgrading, indirectly promoting the development of regional innovation systems.

Column (2) incorporates Inno into the labor misallocation model to test the mediation mechanism. The results indicate that the Robots variable remains significantly negative, implying a persistent direct effect of robot adoption on reducing labor misallocation. However, the Inno variable itself exhibits a significantly positive coefficient, suggesting that enhanced urban innovation capacity is associated with a temporary increase in labor misallocation. This result reflects what may be termed a “structure-friction effect” under innovation-driven transformation: improvements in the innovation environment often trigger rapid changes in job structures and upskilling of labor demand, while the existing labor force may lag behind in terms of skills and adaptability. This mismatch can temporarily widen the imbalance between available jobs and workforce qualifications, thereby increasing labor misallocation in the short run.

This mechanism identification result suggests that while industrial robot adoption boosts urban innovation capacity, it may also indirectly influence labor allocation through a “structural leap” pathway. Although greater innovation capacity lays the foundation for high-quality employment and long-term labor market optimization, it can, in the short term, intensify the contradiction between job upgrading and skill shortages especially in the absence of effective retraining programs and certification systems. This finding aligns with existing literature that posits a coexistence of short-term mismatches and long-term improvements induced by technological change. It also reinforces the view that structural frictions are inherent intermediaries in the “technology–innovation–allocation” chain during periods of transformation.

In summary, urban innovation capacity plays a significant mediating role in the relationship between industrial robot adoption and labor resource optimization, thereby supporting Hypothesis H3. However, this transmission mechanism exhibits distinct temporal characteristics: it may intensify labor misallocation in the short term, while in the medium to long term, it facilitates structural upgrading and efficient allocation. Accordingly, policy should emphasize not only the promotion of robot technology diffusion, but also the development of innovation-supportive urban environments and human capital adaptation mechanisms. Enhancing workforce adaptability and job mobility under innovation-driven conditions will be essential for achieving dynamic equilibrium and inclusive transformation in the course of structural change.

The Bootstrap results reported in

Table 11. Full-sample Bootstrap test results for urban innovation capacity.

Mediating Variables		Observed Coef.	Std.Err.	z	p > |z|
Inno	Indirect effect	0.000	0.000	2.430	0.015
	Direct effect	−0.003	0.001	−4.920	0.000
	Total effect	−0.003	0.001	−4.430	0.000

provide further statistical validation for the above mechanism analysis. Specifically, the indirect effect coefficient of urban innovation capacity (Inno) is significantly positive, confirming the presence of a meaningful mediating channel through which innovation capacity transmits the impact of industrial robot adoption onto labor resource allocation efficiency.

At the same time, both the direct effect and total effect coefficients of robot adoption on labor misallocation remain significantly negative. This indicates that industrial robots, on the whole, continue to play a positive role in improving allocation efficiency. Although the short-term effect of enhanced innovation capacity may temporarily increase labor mismatches reflected in the positive indirect effect the overall effect remains negative, suggesting that the joint advancement of robot adoption and innovation environments ultimately contributes to mitigating labor misallocation in the long run.

In summary, the above mechanism analysis reveals that urban innovation capacity plays a pivotal role in the pathway through which industrial robot adoption influences labor resource allocation efficiency. In the short term, this influence is manifested through structural frictions arising from improvements in the innovation environment. However, from a longer-term perspective, a more advanced urban innovation ecosystem facilitates the upskilling of the labor force and the optimization of job structures, thereby gradually mitigating temporary structural imbalances.

Accordingly, policymakers should recognize the dual dynamics of this relationship. While promoting the diffusion of industrial robot technologies, equal emphasis should be placed on improving vocational training systems and enhancing the adaptive capacity of human capital. Accelerating the alignment between labor force structures and innovation-driven demand is essential for achieving strategic synergy between robot adoption and innovation capacity enhancement ultimately contributing to the long-term optimization of labor markets.

8. Conclusions

With the continuous advancement of artificial intelligence and smart manufacturing technologies, industrial robots have emerged as a key driver of the new wave of industrial transformation and labor market restructuring. This study, based on panel data from 280 prefecture-level cities in China between 2006 and 2023, estimates city-level robot penetration using a Bartik instrumental variable approach and constructs a two-way fixed effects model to systematically assess the impact of industrial robot adoption on labor resource allocation efficiency. Building on this foundation, the study incorporates two mechanism variables industrial upgrading (ISU) and urban innovation capacity (Inno) into a mediation analysis framework, using both stepwise regression and the Bootstrap method to identify transmission pathways. Additionally, heterogeneity analyses are conducted along regional and structural dimensions.

The empirical results show that the application of industrial robots significantly improved the efficiency of urban labor resource allocation, and hypothesis H1 was verified. Specifically, higher robot penetration is associated with lower labor misallocation indices, suggesting that technological diffusion helps alleviate structural distortions in resource allocation. This finding supports the view that industrial robots not only replace inefficient labor, but also improve factor allocation through task restructuring, job transformation, and marginal productivity optimization.

Further analysis reveals pronounced heterogeneity in the effect of robots across contexts. The positive impact is more pronounced in non-Yangtze River Economic Belt cities, severely aging regions, and cities with weaker manufacturing bases. This suggests that in less-developed areas, robots exhibit stronger marginal incentives and play a more transformative role in restructuring labor markets. Conversely, in cities with high manufacturing intensity and advanced technological foundations, the room for marginal improvement is limited, given that existing allocation structures are already relatively efficient.

Regarding the mechanism analysis, the study incorporates both industrial upgrading and urban innovation capacity to examine how industrial robots indirectly affect labor allocation efficiency. The results of mechanism regression show that the application of industrial robots can indirectly improve the efficiency of labor resource allocation by promoting the evolution of industries from low-value-added to high-tech and knowledge-intensive industries, and hypothesis H2 is verified. Through this process, smart technologies automate traditional manufacturing tasks, reshape the industrial division of labor, and alter occupational demand, fostering the agglomeration of high-skill labor and forming a technology-led upgrading chain.

Meanwhile, enhanced urban innovation capacity also emerges as a critical mechanism through which industrial robots improve allocation outcomes. Robot adoption stimulates the reconfiguration and coordination of innovation-related factors at the regional level, increasing the efficiency of job–skill matching and strengthening the responsiveness of the talent supply. Although the surge in innovation activities may be accompanied by some skill mismatch problems in the short term, from a long-term perspective, the improvement of the regional innovation system significantly enhanced the ability to reconfigure the labor force and improved the overall quality of human resource allocation, and hypothesis H3 was verified.

This study provides several policy implications for developing countries. First, the diffusion of industrial robots should be pursued in a regionally adaptive manner to reduce spatial disparities. Rather than concentrating smart manufacturing policies in already advanced regions, countries should prioritize the deployment of robotics in structurally weaker areas. This can be achieved through regional manufacturing funds, tax incentives, and coordinated infrastructure investment, thereby unlocking productivity potential and enabling factor reconfiguration in lagging regions, achieving the dual goals of efficiency gains and regional balance.

Second, the improvement in allocation efficiency brought by robotics relies on the synergy between technology diffusion, industrial upgrading, and innovation capacity. Governments should strengthen the technology–structure coupling mechanism, simultaneously promoting industrial upgrading alongside robot deployment by building localized technical standards, data platforms, and institutional frameworks. It is also crucial to prevent transitional mismatches caused by faster structural transformation than labor adjustment, ensuring that the pace of technological diffusion is socially absorbable and translates into real allocation benefits.

Moreover, under the dual pressures of population aging and skill imbalances, robot adoption may amplify short-term mismatch risks. Countries should establish labor adaptability-oriented institutional arrangements, including job retraining programs, support for low- and medium-skill transitions, and the expansion of foundational digital education. Through proactive intervention and flexible adjustment, workers’ capacity to adapt to new technologies can be enhanced, avoiding a vicious cycle of “technological advance—structural imbalance—social exclusion” and realizing an inclusive and intelligent transformation.

As artificial intelligence and automation technologies continue to spread globally, research on the “technology–structure–allocation efficiency” nexus will remain an important scholarly and policy frontier. Future studies could explore cross-country comparisons, task-level mismatches, or green intelligent manufacturing, providing more actionable micro-level evidence and theoretical support for technology policy and structural reform.