Research on the Spatial Correlation Pattern of Sustainable Development of Cities in the Yangtze River Delta Region of China, Based on the Dynamic Coupling Perspective of “Ecology-Economy”
Abstract
1. Introduction and Literature Review
- (1)
- At a time when multiple systemic crises continue to impact the sustainable development of cities, it is of great practical significance to explore, for the first time, urban sustainable development and its spatial correlation for sustainable development from the perspective of the dynamic coupling of ecology and economy.
- (2)
- This paper evaluates the sustainable development level of cities in the Yangtze River Delta city cluster from the aspects of spatial differentiation and evolution, focusing on the stability of sustainable development and the influence of neighboring regions on the region.
- (3)
- Based on unique relational data and novel network perspectives, this paper adopts a modified gravity model to construct a spatial correlation network for sustainable development of cities in the Yangtze River Delta region, by depicting the structural characteristics of the network as a whole, portraying the status and roles of the cities in the network, and revealing the way of spatial clustering in the network and the roles played by various segments.
- (4)
- This paper innovates the concept of subordination to measure the characteristics of node connections and derives the subordination network on the basis of the spatial association network, which is an effective supplement to the existing social network analysis methods.
2. Materials and Methods
2.1. Study Area
2.2. Evaluation Indicators
2.3. Entropy Method
2.4. Coupling Coordination Model
2.5. Spatial Markov Chain
2.6. Indicators of the Spatial Correlation Network
2.6.1. Modified Gravity Model
2.6.2. Spatial Affiliation Degree
2.6.3. Indicators of Overall Network Characteristics
2.6.4. Indicators of Individual Network Characteristics
2.7. Data Source
3. Results and Discussion
3.1. Analysis of Spatial Discrepancy and Evolution of Sustainable Development
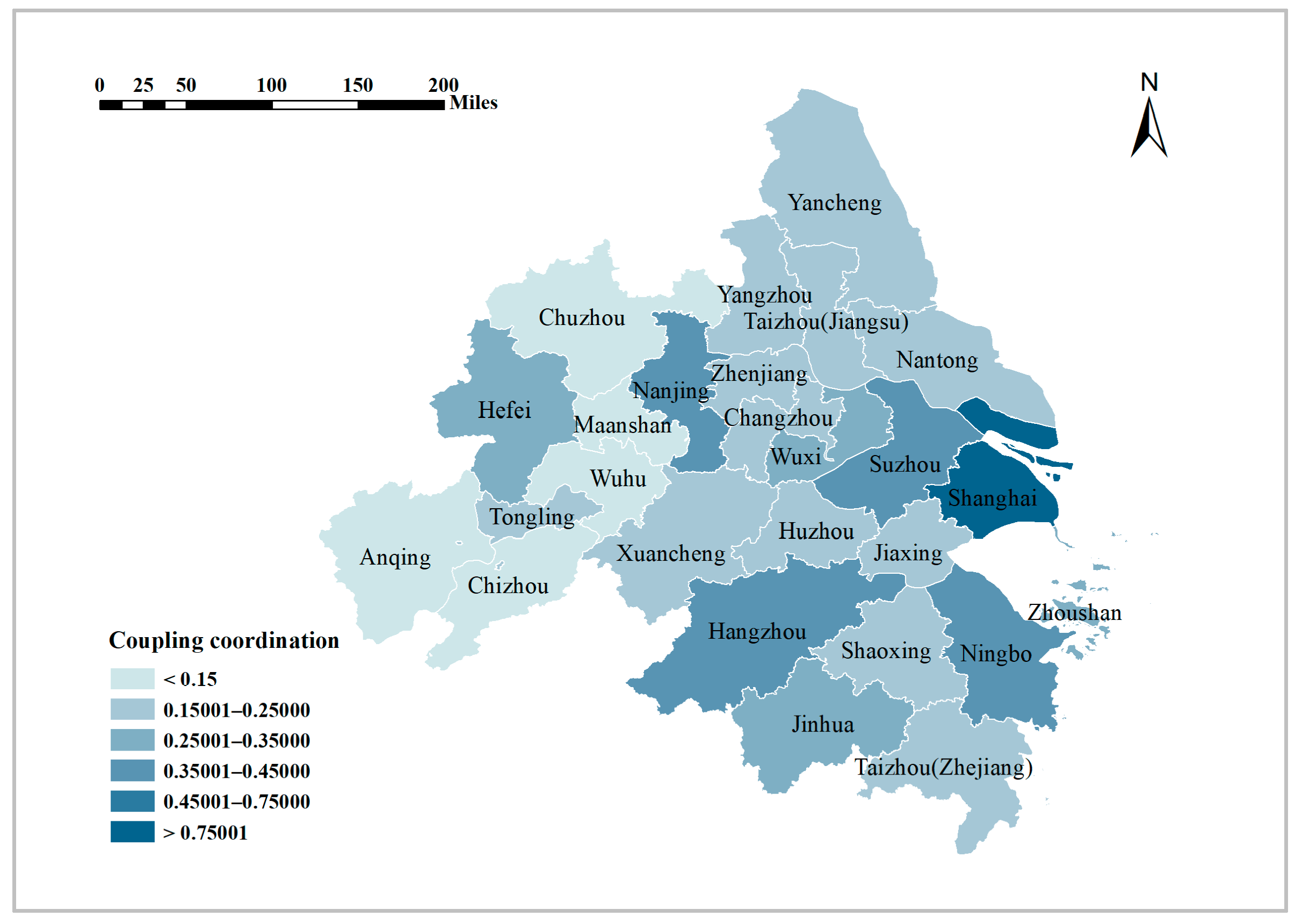
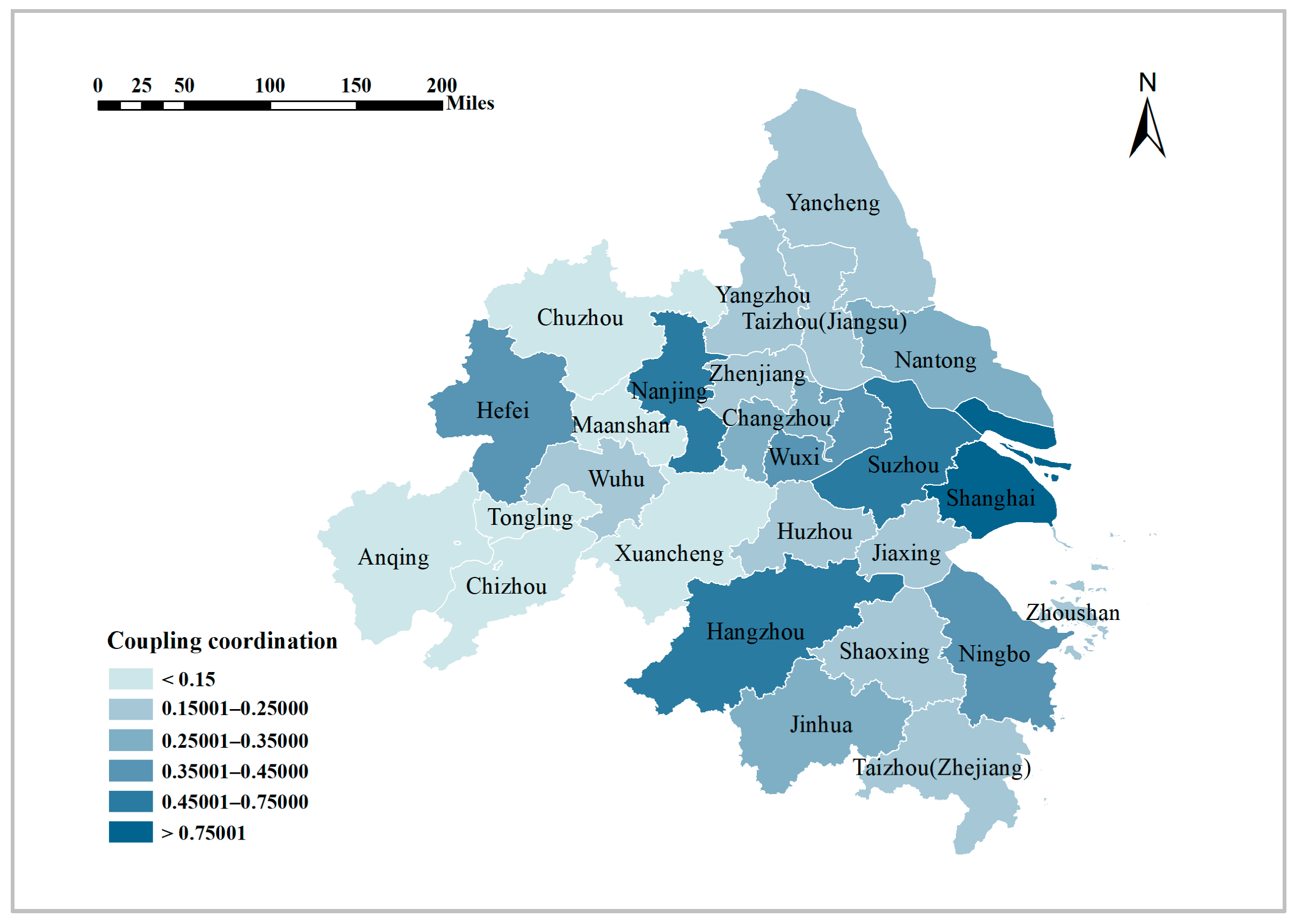
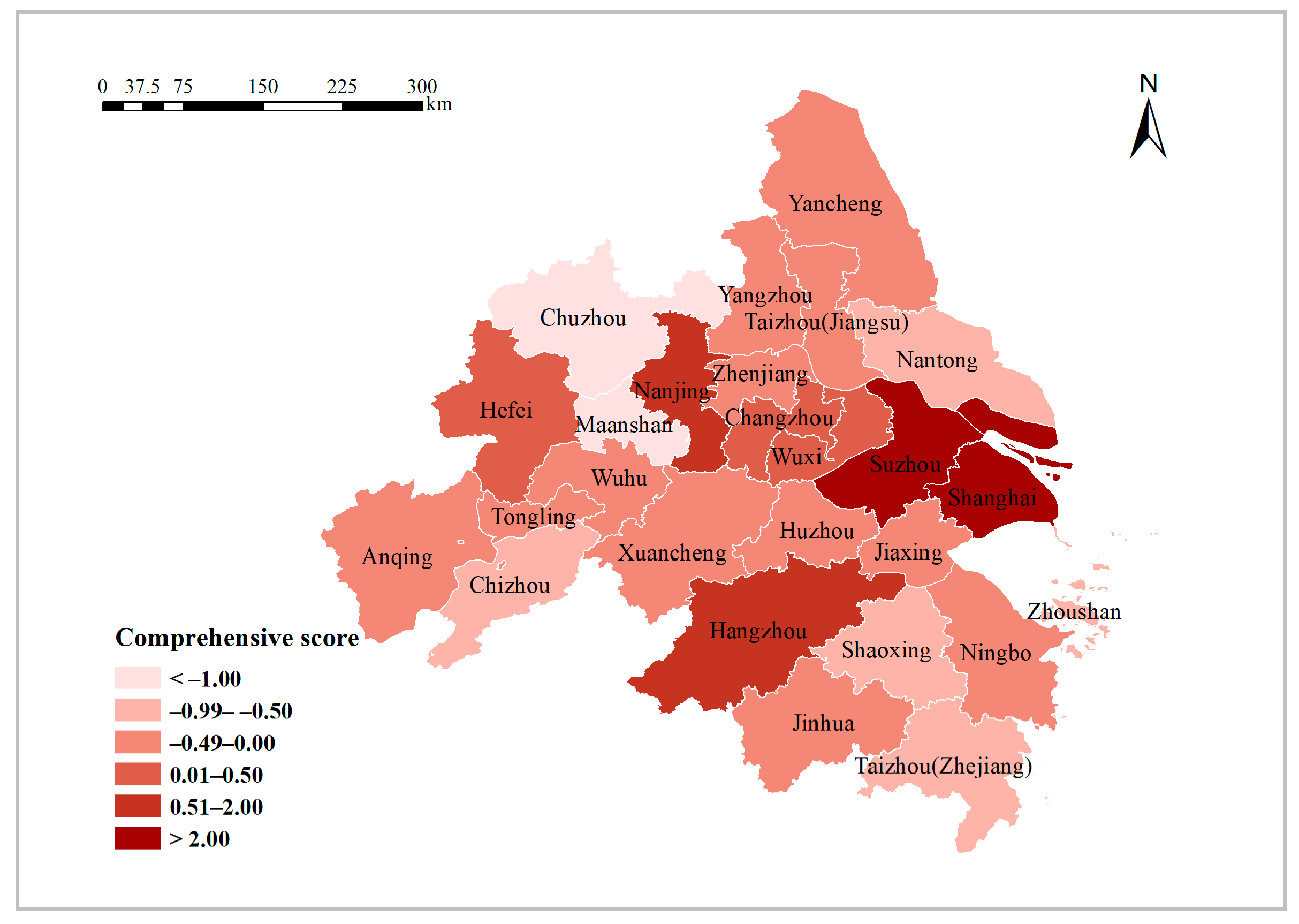
3.1.1. Spatial Discrepancy of the Sustainable Development
3.1.2. Spatial Evolution of Sustainable Development
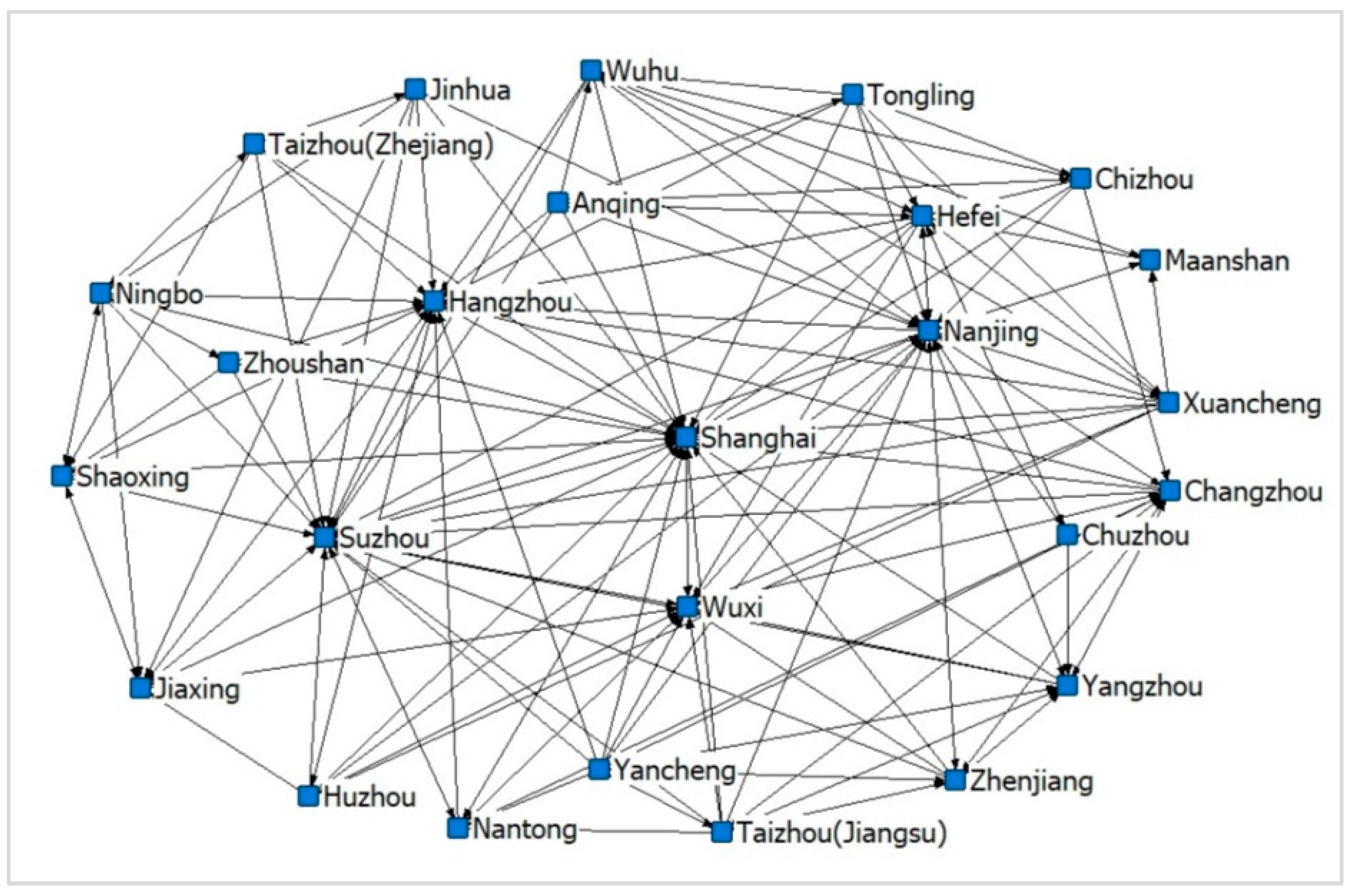
3.2. Analysis of the Spatial Correlation Network
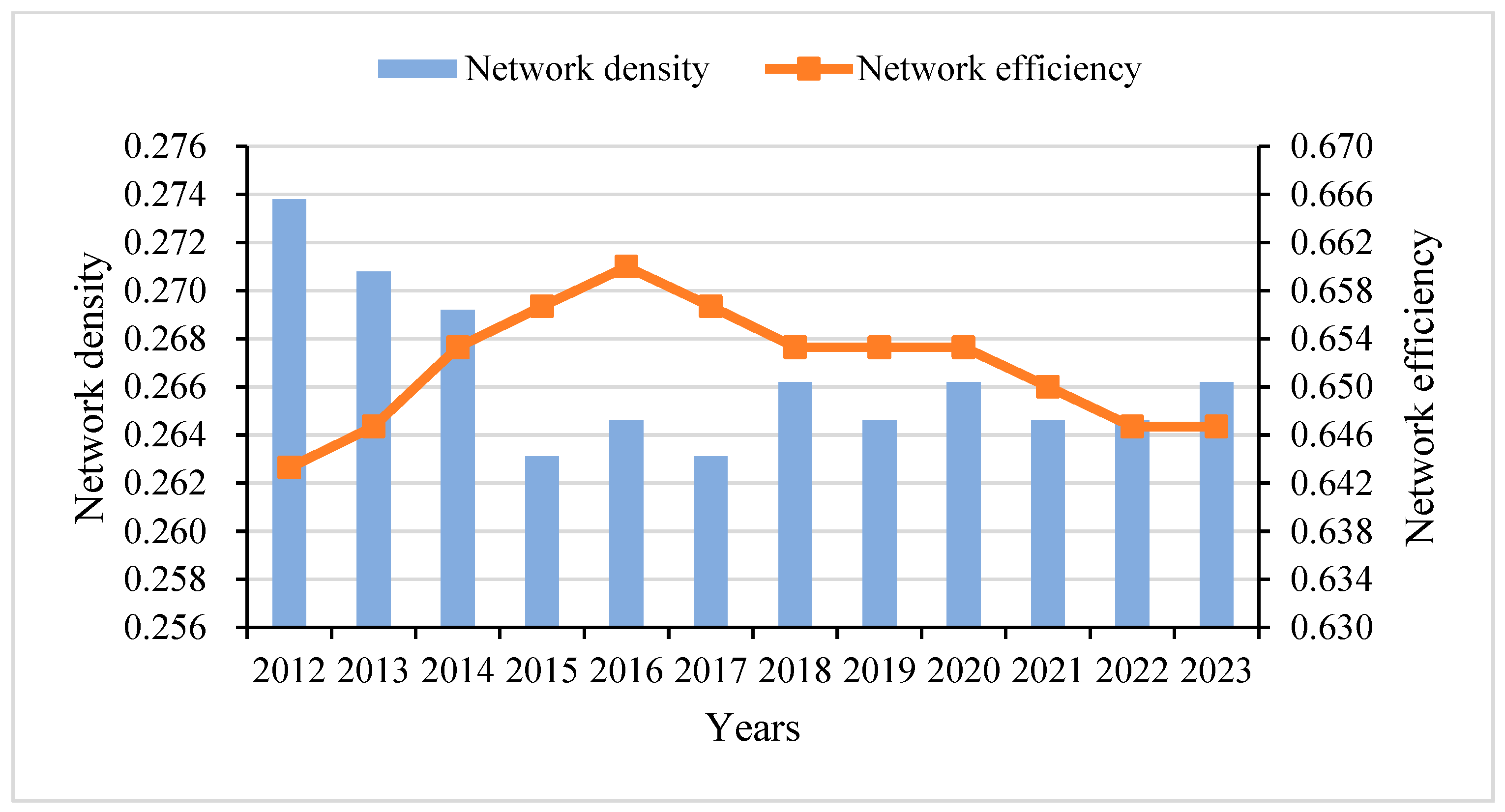
3.2.1. Overall Network Structure Characteristics
3.2.2. Right Characteristics of Nodes
3.2.3. Spatial Subordination Degree
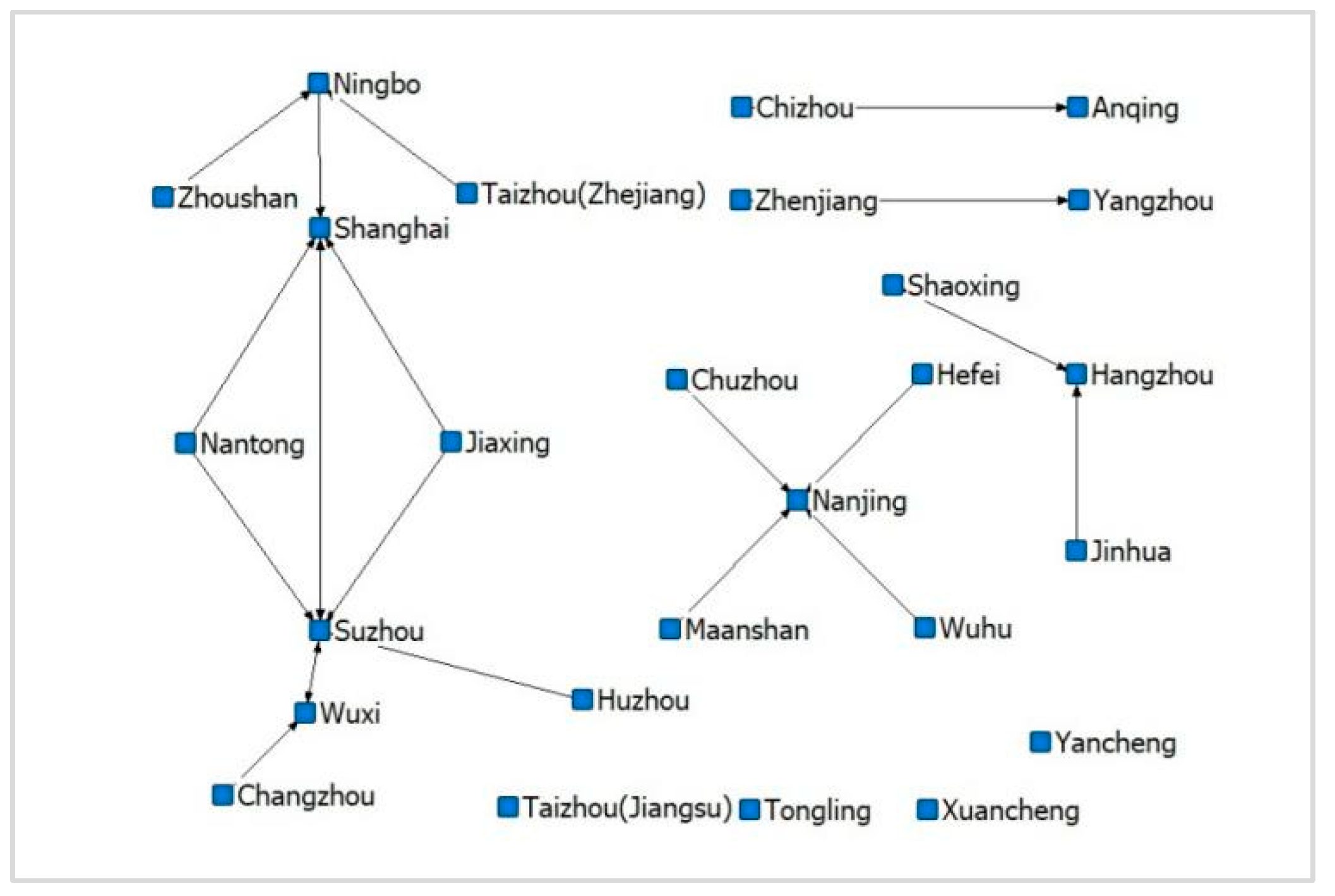
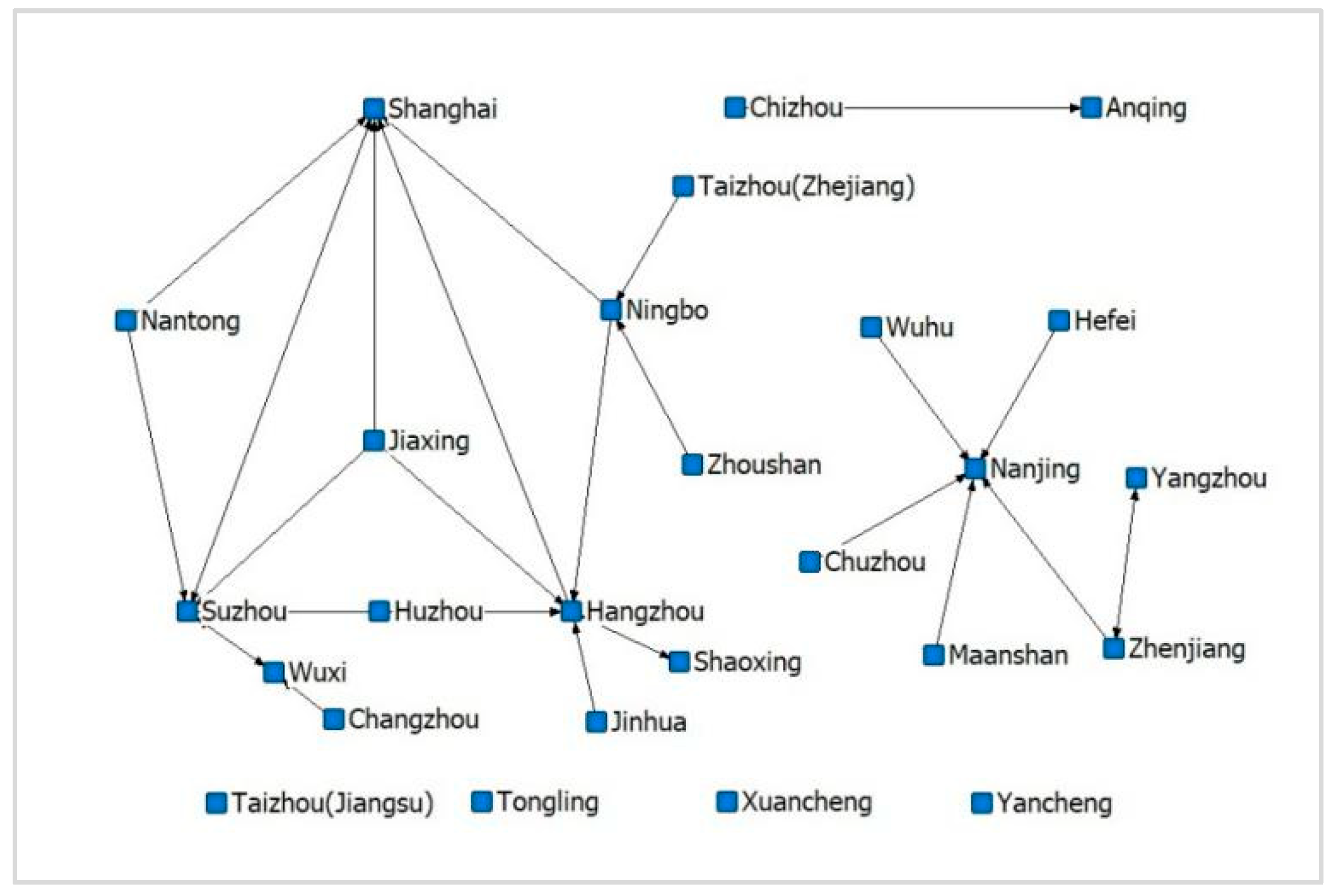
3.2.4. Spatial Clustering Analysis
4. Conclusions and Discussion
- (1)
- Optimize regional spatial layout
- (2)
- Strengthen regional cooperation and collaborative governance
- (3)
- Constructing a Smart City Cluster and Innovation Ecology
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thanigaivel, S.; Vickram, S.; Dey, N.; Jeyanthi, P.; Subbaiya, R.; Kim, W.; Govarthanan, M.; Karmegam, N. Ecological disturbances and abundance of anthropogenic pollutants in the aquatic ecosystem: Critical review of impact assessment on the aquatic animals. Chemosphere 2023, 313, 137475. [Google Scholar] [CrossRef]
- Liu, S.; Junaid, M.; Sadaf, M.; Ai, W.; Lan, X.; Wang, J. A novel framework-based meta-analysis for in-depth characterization of microplastic pollution and associated ecological risks in Chinese Bays. J. Hazard. Mater. 2023, 444, 130423. [Google Scholar] [CrossRef]
- Zhang, T.; Sun, Y.; Zhang, X.; Yin, L.; Zhang, B. Potential heterogeneity of urban ecological resilience and urbanization in multiple urban agglomerations from a landscape perspective. J. Environ. Manag. 2023, 342, 118129. [Google Scholar] [CrossRef] [PubMed]
- Pile, S. What is a city. In City Worlds; Routledge: London, UK, 1999; pp. 3–52. [Google Scholar]
- Abu-Rayash, A.; Dincer, I. Development of an integrated sustainability model for resilient cities featuring energy, environmental, social, governance and pandemic domains. Sustain. Cities Soc. 2023, 92, 104439. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H.; You, C.; Yang, Z.; Yao, J. The impact of sustainable development policy for resource-based cities on green technology innovation: Firm-level evidence from China. J. Clean. Prod. 2024, 469, 143246. [Google Scholar] [CrossRef]
- Fu, B.; Liu, Y.; Meadows, M.E. Ecological restoration for sustainable development in China. Natl. Sci. Rev. 2023, 10, nwad033. [Google Scholar] [CrossRef]
- Fan, S.; Huang, H.; Mbanyele, W.; Guo, Z.; Zhang, C. Inclusive green growth for sustainable development of cities in China: Spatiotemporal differences and influencing factors. Environ. Sci. Pollut. Res. 2023, 30, 11025–11045. [Google Scholar] [CrossRef]
- Hariram, N.P.; Mekha, K.B.; Suganthan, V.; Sudhakar, K. Sustainalism: An integrated socio-economic-environmental model to address sustainable development and sustainability. Sustainability 2023, 15, 10682. [Google Scholar] [CrossRef]
- Liu, J.; Tian, Y.; Huang, K.; Yi, T. Spatial-temporal differentiation of the coupling coordinated development of regional energy-economy-ecology system: A case study of the Yangtze River Economic Belt. Ecol. Indic. 2021, 124, 107394. [Google Scholar] [CrossRef]
- Saqib, N.; Ozturk, I.; Usman, M. Investigating the implications of technological innovations, financial inclusion, and renewable energy in diminishing ecological footprints levels in emerging economies. Geosci. Front. 2023, 14, 101667. [Google Scholar] [CrossRef]
- Liu, R.; Dong, X.; Wang, X.; Zhang, P.; Liu, M.; Zhang, Y. Relationship and driving factors between urbanization and natural ecosystem health in China. Ecol. Indic. 2023, 147, 109972. [Google Scholar] [CrossRef]
- Wan, J.; Li, Y.; Ma, C.; Jiang, T.; Su, Y.; Zhang, L.; Song, X.; Sun, H.; Wang, Z.; Zhao, Y.; et al. Measurement of coupling coordination degree and spatio-temporal characteristics of the social economy and ecological environment in the Chengdu–Chongqing urban agglomeration under high-quality development. Int. J. Environ. Res. Public Health 2021, 18, 11629. [Google Scholar] [CrossRef]
- Caviglia-Harris, J.L.; Chambers, D.; Kahn, J.R. Taking the “U” out of Kuznets: A comprehensive analysis of the EKC and environmental degradation. Ecol. Econ. 2009, 68, 1149–1159. [Google Scholar] [CrossRef]
- Zhou, R.; Jin, J.; Wu, C.; Zhou, L.; Zhang, L.; Cui, Y.; Zhang, Y.; Zhou, Y. Connection number based model for coordination development evaluation of regional water resources, social economy and ecological environment complex system. J. Environ. Manag. 2023, 339, 117913. [Google Scholar] [CrossRef]
- Zhu, C.; Fang, C.; Zhang, L. Analysis of the coupling coordinated development of the Population–Water–Ecology–Economy system in urban agglomerations and obstacle factors discrimination: A case study of the Tianshan North Slope Urban Agglomeration, China. Sustain. Cities Soc. 2023, 90, 104359. [Google Scholar] [CrossRef]
- Fan, Y.; Fang, C.; Zhang, Q. Coupling coordinated development between social economy and ecological environment in Chinese provincial capital cities-assessment and policy implications. J. Clean. Prod. 2019, 229, 289–298. [Google Scholar] [CrossRef]
- Li, W.; Yi, P.; Zhang, D.; Zhou, Y. Assessment of coordinated development between social economy and ecological environment: Case study of resource-based cities in Northeastern China. Sustain. Cities Soc. 2020, 59, 102208. [Google Scholar] [CrossRef]
- Ji, J.; Wang, L.; Xie, M.; Lv, W.; Yu, C.; Liu, W.; Shifaw, E. Evaluation of Coupling Coordination Degree between Economy and Eco-Environment Systems in the Yangtze River Delta from 2000 to 2020. Systems 2023, 11, 500. [Google Scholar] [CrossRef]
- Reyers, B.; Moore, M.L.; Haider, L.J.; Schlüter, M. The contributions of resilience to reshaping sustainable development. Nat. Sustain. 2022, 5, 657–664. [Google Scholar] [CrossRef]
- Das, S.; Pradhan, B.; Shit, P.K.; Alamri, A.M. Assessment of wetland ecosystem health using the pressure–state–response (PSR) model: A case study of mursidabad district of West Bengal (India). Sustainability 2020, 12, 5932. [Google Scholar] [CrossRef]
- Yu, Y.; Bao, Y.; Zhang, Q.; Shen, P.; Yang, H.; Xu, Z. Evaluation of marine resources environmental responsibility audit based on PSR framework. Ocean Coast. Manag. 2023, 245, 106742. [Google Scholar] [CrossRef]
- Costanza, R. Toward an operational definition of ecosystem health. In Ecosystem Health: New Goals for Environmental Management; Island Press: Washington, DC, USA, 1992. [Google Scholar]
- Costanza, R. Ecosystem health and ecological engineering. Ecol. Eng. 2012, 45, 24–29. [Google Scholar] [CrossRef]
- Holt, A.R.; Mears, M.; Maltby, L.; Warren, P. Understanding spatial patterns in the production of multiple urban ecosystem services. Ecosyst. Serv. 2015, 16, 33–46. [Google Scholar] [CrossRef]
- Martin, R. Regional economic resilience, hysteresis and recessionary shocks. J. Econ. Geogr. 2012, 12, 1–32. [Google Scholar] [CrossRef]
- Boschma, R. Towards an evolutionary perspective on regional resilience. Reg. Stud. 2015, 49, 733–751. [Google Scholar] [CrossRef]
- Martin, R.; Sunley, P. On the notion of regional economic resilience: Conceptualization and explanation. J. Econ. Geogr. 2015, 15, 1–42. [Google Scholar] [CrossRef]
- Zhang, P.; Zhao, Y.; Zhu, X.; Cai, Z.; Xu, J.; Shi, S. Spatial structure of urban agglomeration under the impact of high-speed railway construction: Based on the social network analysis. Sustain. Cities Soc. 2020, 62, 10240. [Google Scholar] [CrossRef]
- Ouyang, F. Using three social network analysis approaches to understand computer-supported collaborative learning. J. Educ. Comput. Res. 2021, 59, 1401–1424. [Google Scholar] [CrossRef]
- Wang, H.; Ge, Q. Spatial association network of PM2. 5 and its influencing factors in the Beijing–Tianjin–Hebei urban agglomeration. Environ. Sci. Pollut. Res. 2023, 30, 70541–70557. [Google Scholar] [CrossRef]
- Su, Y.; Yu, Y. Spatial association effect of regional pollution control. J. Clean. Prod. 2019, 213, 540–552. [Google Scholar] [CrossRef]
- Shen, W.; Liang, H.; Dong, L.; Ren, J.; Wang, G. Synergistic CO2 reduction effects in Chinese urban agglomerations: Perspectives from social network analysis. Sci. Total Environ. 2021, 798, 149352. [Google Scholar] [CrossRef] [PubMed]
| Dimensions | Indicators | How Indicators Are Measured | Efficacy |
|---|---|---|---|
| Ecological health | Pressure | Population density | + |
| Ecological carrying capacity per capita | + | ||
| State | Ecological services | + | |
| Landscape fragmentation index | + | ||
| Ecosystem recovery force | + | ||
| Response | Centralized treatment rate of sewage treatment plant | + | |
| Harmless treatment rate of domestic waste | + | ||
| Comprehensive utilization rate of general industrial solid waste | + | ||
| Proportion of environmental protection expenditure to financial expenditure | + | ||
| Percentage of green invention patent applications | + | ||
| Economic resilience | Resistance | GDP growth rate | + |
| GDP per capita | + | ||
| Diversification of industrial structure | + | ||
| FDI | − | ||
| Urbanization rate | + | ||
| Adaptation | Rationalization of industrial structure | + | |
| Total retail sales of consumer goods | + | ||
| Investment rate | + | ||
| Deposit-to-loan ratio | + | ||
| Proportion of fiscal expenditure to GDP | + | ||
| Transformation | Advancement of industrial structure | + | |
| R&D expenditure | + | ||
| Technology transaction turnover | + | ||
| Per capita patent authorizations | + |
| Types of Coupling Coordination | Extreme Uncoordination | Lower Coordination | Low Coordination | High Coordination | Higher Coordination | Extreme Coordination |
|---|---|---|---|---|---|---|
| interval | [0, 0.15] | (0.15, 0.25] | (0.25, 0.35] | (0.35, 0.45] | (0.45, 0.75] | (0.75, 1] |
| ti/ti + 1 | n | Lower-Level Sustainable Development | Low-Level Sustainable Development | High-Level Sustainable Development | Higher-Level Sustainable Development |
|---|---|---|---|---|---|
| lower-level sustainable development | 126 | 1.000 | 0.000 | 0.000 | 0.000 |
| low-level sustainable development | 43 | 0.047 | 0.860 | 0.093 | 0.000 |
| high-level sustainable development | 12 | 0.000 | 0.417 | 0.333 | 0.250 |
| higher-level sustainable development | 27 | 0.000 | 0.000 | 0.037 | 0.963 |
| Spatial Lag | ti/ti + 1 | n | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|
| 1 | 1 | 56 | 1.000 | 0.000 | 0.000 | 0.000 |
| 2 | 14 | 0.000 | 0.786 | 0.214 | 0.000 | |
| 3 | 9 | 0.000 | 0.333 | 0.444 | 0.222 | |
| 4 | 12 | 0.000 | 0.000 | 0.083 | 0.917 | |
| 2 | 1 | 59 | 1.000 | 0.000 | 0.000 | 0.000 |
| 2 | 19 | 0.053 | 0.895 | 0.053 | 0.000 | |
| 3 | 3 | 0.000 | 0.667 | 0.000 | 0.333 | |
| 4 | 15 | 0.000 | 0.000 | 0.000 | 1.000 | |
| 3 | 1 | 11 | 1.000 | 0.000 | 0.000 | 0.000 |
| 2 | 10 | 0.100 | 0.900 | 0.000 | 0.000 | |
| 3 | 0 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 4 | 0 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 4 | 1 | 0 | 0.000 | 0.000 | 0.000 | 0.000 |
| 2 | 0 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 3 | 0 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 4 | 0 | 0.000 | 0.000 | 0.000 | 0.000 |
| City | Degree | Betweenness | Closeness | Eigenvector |
|---|---|---|---|---|
| Shanghai | 92 | 18.291 | 92.53 | 50.609 |
| Nanjing | 76 | 12.865 | 80.645 | 43.435 |
| Wuxi | 52 | 2.622 | 67.568 | 33.472 |
| Changzhou | 44 | 1.236 | 64.103 | 30.284 |
| Suzhou | 84 | 13.406 | 86.207 | 47.416 |
| Nantong | 28 | 0.089 | 55.556 | 21.654 |
| Yancheng | 40 | 0.439 | 62.500 | 28.803 |
| Yangzhou | 36 | 1.509 | 60.976 | 24.592 |
| Zhenjiang | 32 | 0.000 | 59.524 | 23.952 |
| Taizhou (Jiangsu) | 36 | 0.216 | 60.976 | 25.635 |
| Hangzhou | 72 | 9.451 | 78.125 | 40.761 |
| Ningbo | 32 | 0.328 | 56.818 | 19.318 |
| Jiaxing | 32 | 0.628 | 56.818 | 21.216 |
| Huzhou | 28 | 0.218 | 58.140 | 22.285 |
| Shaoxing | 28 | 0.189 | 55.556 | 17.751 |
| Jinhua | 28 | 0.447 | 58.140 | 20.162 |
| Zhoushan | 20 | 0.000 | 53,191 | 14.818 |
| Taizhou (Zhejiang) | 24 | 0.056 | 54.348 | 16.517 |
| Hefei | 48 | 3.904 | 65.789 | 29.779 |
| Wuhu | 40 | 1.252 | 62.500 | 26.538 |
| Maanshan | 16 | 0.000 | 48.077 | 10.728 |
| Tongling | 32 | 0.162 | 59.524 | 22.019 |
| Anqing | 32 | 0.151 | 59.524 | 23.562 |
| Chuzhou | 12 | 0.067 | 47.170 | 8.242 |
| Chizhou | 28 | 0.272 | 58.140 | 19.063 |
| Xuancheng | 40 | 1.535 | 62.500 | 27.558 |
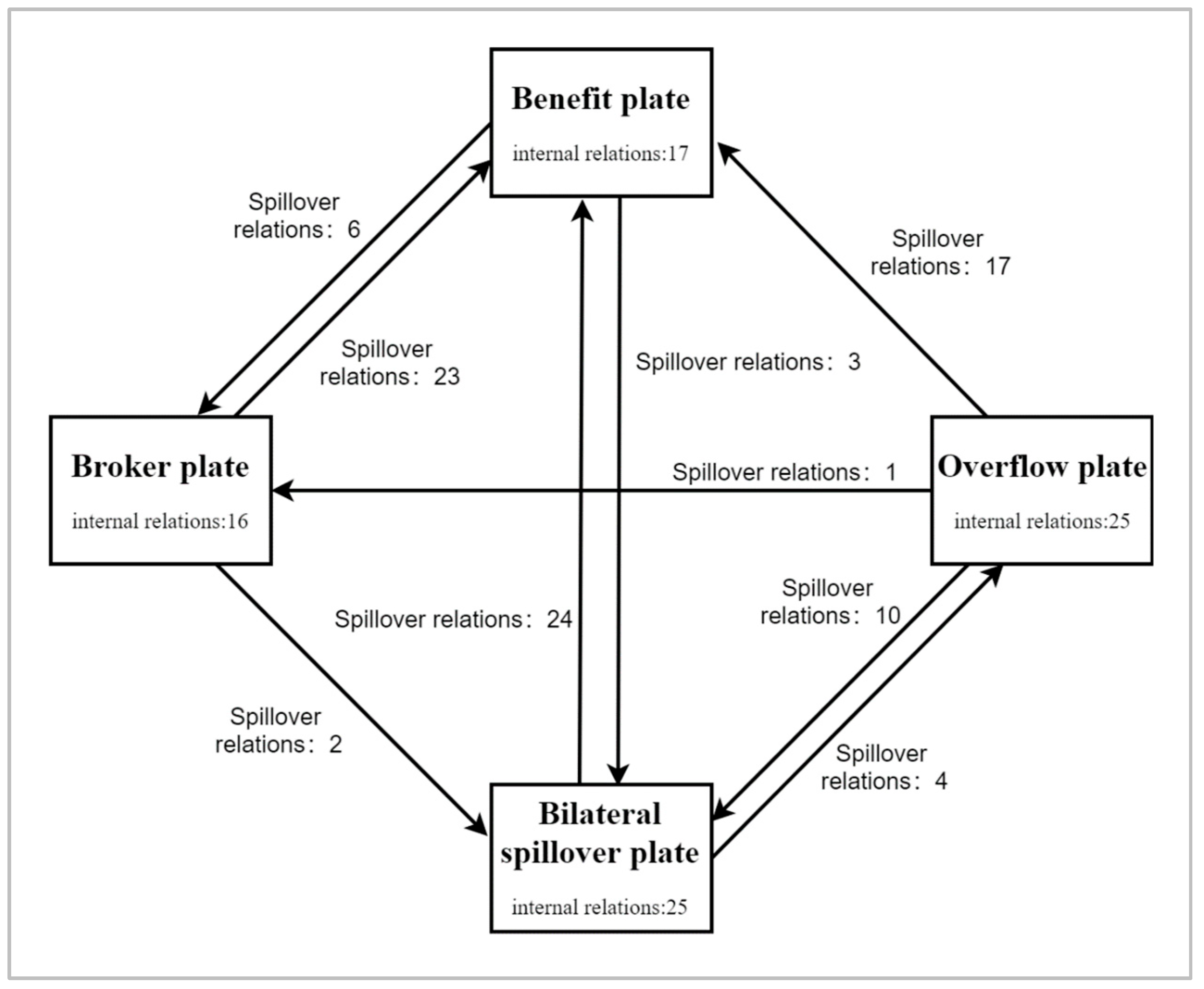
| Block | Receive Relationship | Overflow Relationship | Expected Internal Relationship Ratio | Actual Internal Relationship Ratio | ||
|---|---|---|---|---|---|---|
| Inside | Outside | Inside | Outside | |||
| I | 17 | 64 | 17 | 9 | 16 | 65 |
| II | 16 | 7 | 16 | 25 | 24 | 39 |
| III | 25 | 15 | 25 | 28 | 20 | 47 |
| IV | 25 | 4 | 25 | 28 | 28 | 47 |
| Block | I | II | III | IV |
|---|---|---|---|---|
| I | 0.850 | 0.171 | 0.100 | 0.000 |
| II | 0.657 | 0.381 | 0.048 | 0.000 |
| III | 0.800 | 0.000 | 0.833 | 0.083 |
| IV | 0.425 | 0.018 | 0.208 | 0.446 |
| Block | I | II | III | IV |
|---|---|---|---|---|
| I | 1 | 0 | 0 | 0 |
| II | 1 | 1 | 0 | 0 |
| III | 1 | 0 | 1 | 0 |
| IV | 1 | 0 | 0 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, Z.; Ge, Q.; Zhang, L. Research on the Spatial Correlation Pattern of Sustainable Development of Cities in the Yangtze River Delta Region of China, Based on the Dynamic Coupling Perspective of “Ecology-Economy”. Systems 2025, 13, 533. https://doi.org/10.3390/systems13070533
Chu Z, Ge Q, Zhang L. Research on the Spatial Correlation Pattern of Sustainable Development of Cities in the Yangtze River Delta Region of China, Based on the Dynamic Coupling Perspective of “Ecology-Economy”. Systems. 2025; 13(7):533. https://doi.org/10.3390/systems13070533
Chicago/Turabian StyleChu, Zhujie, Qi Ge, and Lufa Zhang. 2025. "Research on the Spatial Correlation Pattern of Sustainable Development of Cities in the Yangtze River Delta Region of China, Based on the Dynamic Coupling Perspective of “Ecology-Economy”" Systems 13, no. 7: 533. https://doi.org/10.3390/systems13070533
APA StyleChu, Z., Ge, Q., & Zhang, L. (2025). Research on the Spatial Correlation Pattern of Sustainable Development of Cities in the Yangtze River Delta Region of China, Based on the Dynamic Coupling Perspective of “Ecology-Economy”. Systems, 13(7), 533. https://doi.org/10.3390/systems13070533





