Mathematical Modeling Approach to Assessing Math Education Levels in Secondary and High Schools: Pandemic Impact and Post-Pandemic Projections
Abstract
1. Introduction
2. Research Questions and Hypotheses
- (1)
- What were the differences between public and private schools in terms of resources and quality of instruction when they switched to online learning?
- (2)
- What problems did students and teachers have, and how were these problems different in different types of schools?
- (3)
- What good things happened because of online math classes during the pandemic?
- (4)
- How can mathematical modeling be used to improve online math teaching for a lot of people?
- (5)
- How much worse did the differences in education between public and private schools become, and what can be done to fix them?
- Public school kids had a harder time learning math online since they did not have as many tools.
- The change helped private schools more, giving them more freedom and access to technology.
- Mathematical modeling can assist in making online education better and more effective.
- The epidemic made the gap between public and private schooling bigger, and this tendency is likely to continue without specific actions.
3. Materials and Methods
3.1. Research Method
3.2. Population and Sample
3.3. Data Collection Tools
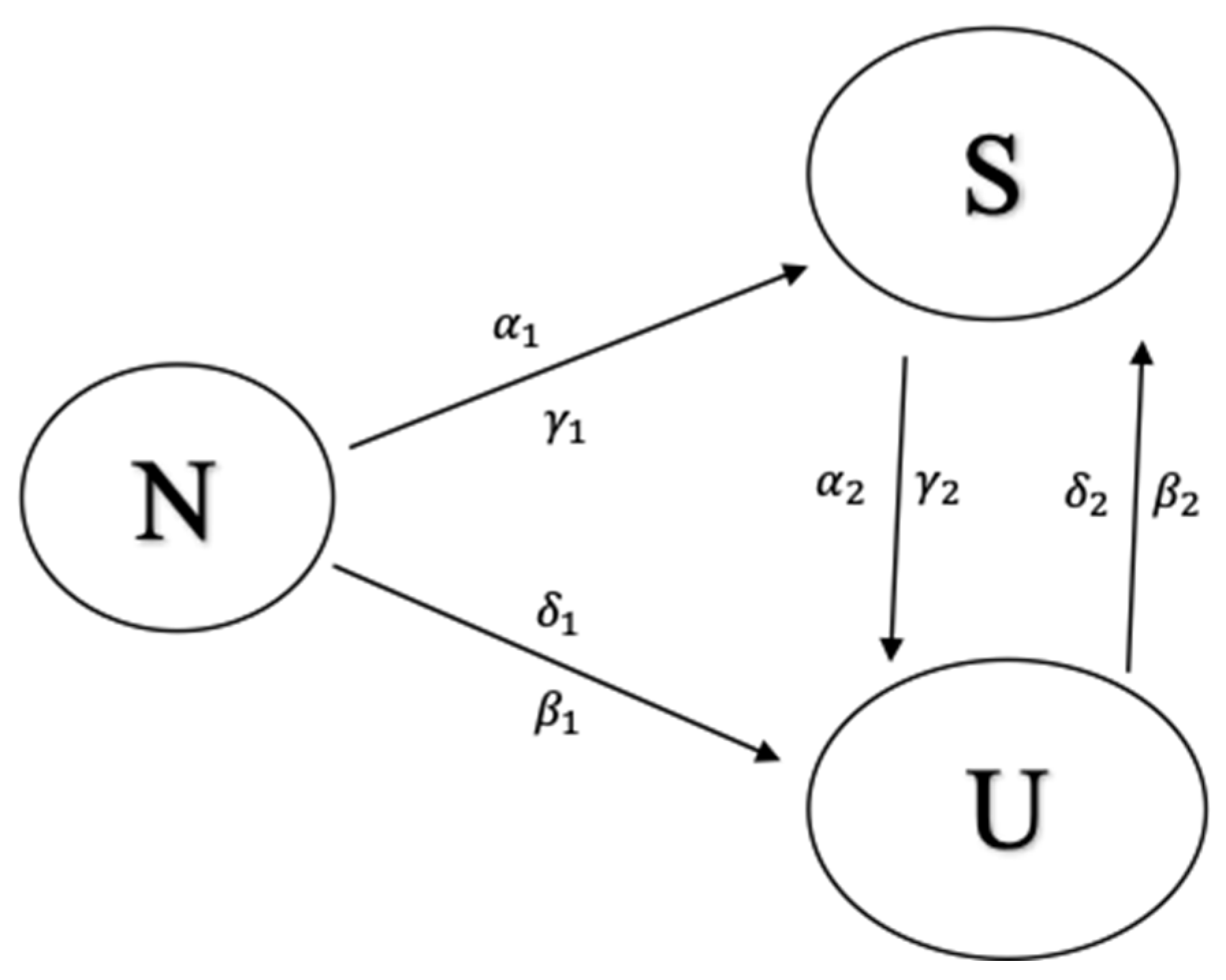
3.4. Construction of the Model
3.5. Mathematical Adaptation of the Collected Data to a Model
3.5.1. Free Equilibrium Points and Threshold Parameters
3.5.2. Numerical Simulation
3.5.3. Sensitivity Analysis
4. Results
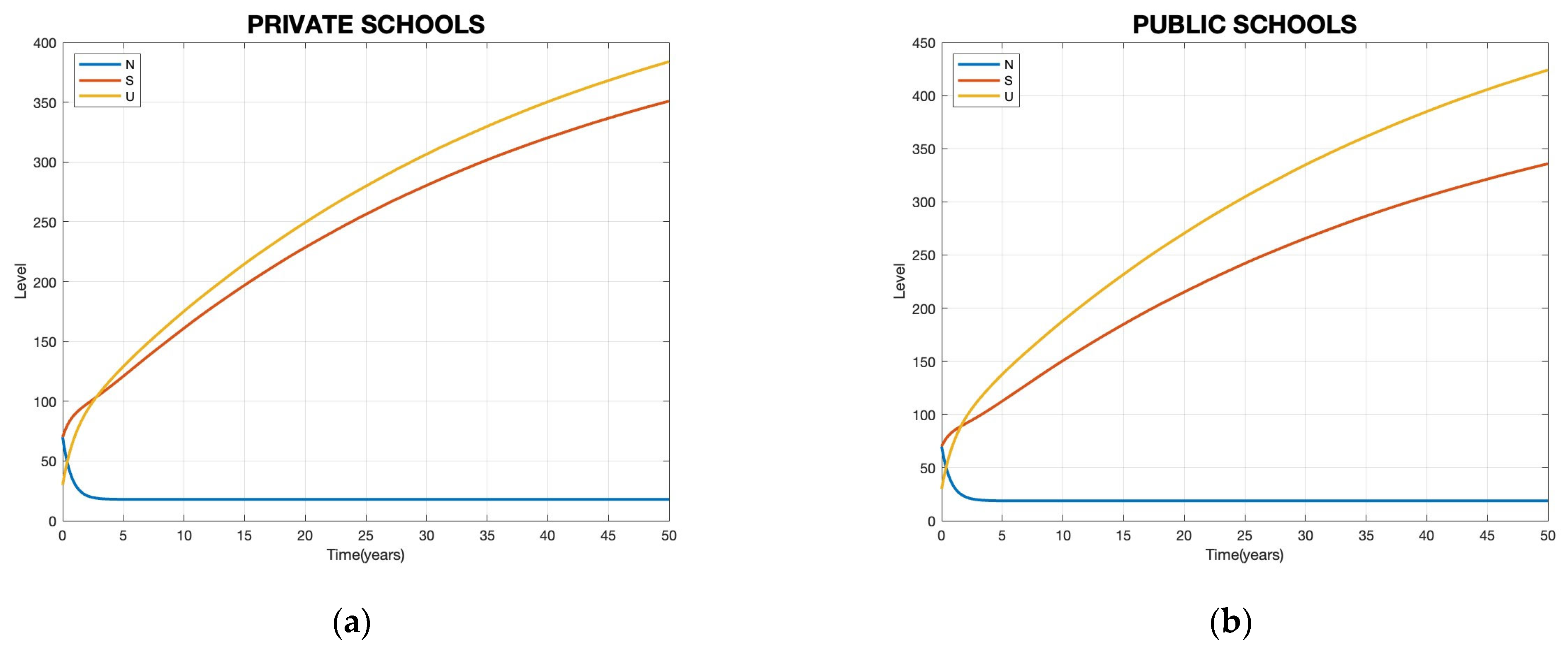
4.1. Numerical Simulation and Threshold Parameter
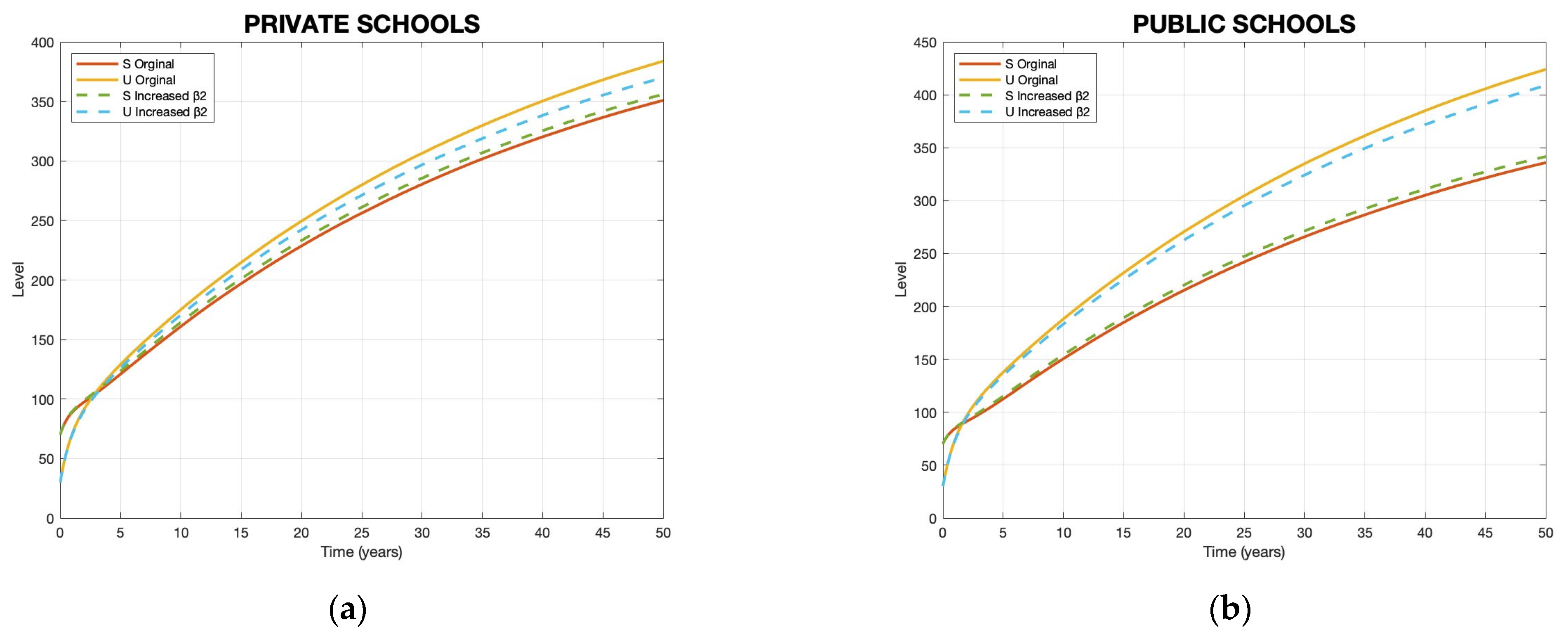
4.2. Sensitivity Analysis of R0
4.3. A Statistical Look at How Engaged Students Are in Different Types of Schools
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alper, A. Pandemī Sürecīnde K-12 Düzeyīnde Uzaktan Eğītīm: Durum Çalişmasi. Milli Eğitim Derg. 2020, 49, 45–67. [Google Scholar] [CrossRef]
- Middleton, K.V. The longer-term impact of COVID-19 on K–12 student learning and assessment. Educ. Meas. Issues Pract. 2020, 39, 41–44. [Google Scholar] [CrossRef]
- Özdoğan, A.Ç.; Berkant, H.G. Covid-19 pandemi dönemindeki uzaktan eğitime ilişkin paydaş görüşlerinin incelenmesi. Milli Eğitim Derg. 2020, 49, 13–43. [Google Scholar] [CrossRef]
- Andrew, A.; Cattan, S.; Costa Dias, M.; Farquharson, C.; Kraftman, L.; Krutikova, S.; Phimister, A.; Sevilla, A. Inequalities in children’s experiences of home learning during the COVID-19 lockdown in England. Fisc. Stud. 2020, 41, 653–683. [Google Scholar] [CrossRef]
- eLearning Inside. How Does Online Learning Affect Educational Inequality? eLearning Inside. Available online: https://news.elearninginside.com/how-does-online-learning-affect-educational-inequality/#google_vignette (accessed on 3 June 2021).
- Harlen, W.; Qualter, A. The Teaching of Science in Primary Schools; David Fulton Publishers: London, UK, 2004. [Google Scholar]
- Chetty, R.; Friedman, J.; Rockoff, J. Measuring the impacts of teachers II: Teacher value-added and student outcomes in adulthood. Am. Econ. Rev. 2014, 104, 2633–2679. [Google Scholar] [CrossRef]
- Hamre, B.; Pianta, R. Can instructional and emotional support in the first-grade classroom make a difference for children at risk of school failure? Child Dev. 2005, 76, 949–967. [Google Scholar] [CrossRef]
- Slater, H.; Davies, N.; Burgess, S. Do teachers matter? Measuring the variation in teacher effectiveness in England. Oxf. Bull. Econ. Stat. 2012, 74, 629–645. [Google Scholar] [CrossRef]
- Ermeling, B.A.; Gallimore, R. Close-to-practice learning. Educ. Leadersh. 2014, 72, 4. [Google Scholar]
- Sacré, M.; Ries, N.; Wolf, K.; Kunter, M. Teachers’ well-being and their teaching quality during the COVID-19 pandemic: A retrospective study. Front. Educ. 2023, 8, 1136940. [Google Scholar] [CrossRef]
- Lee, J.; Kwon, K.H. Promoting Sustainable Learning inthe Post-Pandemic Era: Focused onthe Role of Motivation, GrowthMindset, Self-Regulated Learning, Well-Being, and Smart DeviceUtilization. Sustainability 2023, 15, 13247. [Google Scholar] [CrossRef]
- Darling-Hammond, L. Strengthening Clinical Preparation: The Holy Grail of Teacher Education. Peabody J. Educ. 2014, 89, 547–561. [Google Scholar] [CrossRef]
- Kaymakamzade, B.; Cumhur, M. The effects of maths anxiety on mathematical modelling. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2021; Volume 2325. [Google Scholar]
- Gokbulut, N.; Hincal, E.; Besim, H.; Kaymakamzade, B. Reducing the Range of Cancer Risk on BI-RADS 4 Subcategories via Mathematical Modelling. CMES-Comput. Model. Eng. Sci. 2022, 133. [Google Scholar] [CrossRef]
- Bagkur, C.; Guler, E.; Kaymakamzade, B.; Hincal, E.; Suer, K. Near future perspective of ESBL-Producing Klebsiella pneumoniae strains using mathematical modeling. CMES 2022, 130, 111–132. [Google Scholar] [CrossRef]
- Hincal, E.; Alzadjali, A.H. Dynamical Model to Optimize Student’s Academic Performance. CMES-Comput. Model. Eng. Sci. 2022, 132, 393–411. [Google Scholar] [CrossRef]
- Abrahamson, D.; Sánchez-García, R. Learning Is Moving in New Ways: The Ecological Dynamics of Mathematics Education. J. Learn. Sci. 2016, 25, 203–239. [Google Scholar] [CrossRef]
- Büyüköztürk, Ş.; Kılıç-Çakmak, E.; Akgün, Ö.; Karadeniz, Ş.; Demirel, F. Bilimsel Araştırma Yöntemleri, 31st ed.; Pegem Akademi Yayınları: Ankara, Türkiye, 2018. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. A Math. Phys. Eng. Sci. 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Başaran, Y.K. Sosyal Bilimlerde Örnekleme Kurami. J. Acad. Soc. Sci. 2024, 47, 480–495. [Google Scholar]
- Miller, R.L.; Butler, J.M. Outcomes associated with student engagement. Promot. Stud. Engagem. 2011, 1, 18–19. [Google Scholar]
- Dinham, S. Principal leadership for outstanding educational outcomes. J. Educ. Adm. 2005, 43, 338–356. [Google Scholar] [CrossRef]
- Trust, T.; Whalen, J. Emergency remote teaching with technology during the COVID-19 pandemic: Using the whole teacher lens to examine educator’s experiences and insights. Educ. Media Int. 2021, 58, 145–160. [Google Scholar] [CrossRef]
- Ingersoll, R.M.; Strong, M. The impact of induction and mentoring programs for beginning teachers: A critical review of the research. Rev. Educ. Res. 2011, 81, 201–233. [Google Scholar] [CrossRef]
- Kember, D.; Leung, D.Y.P. Development of a questionnaire for assessing students’ perceptions of the teaching and learning environment and its use in quality assurance. Learn. Environ. Res. 2009, 12, 15–29. [Google Scholar] [CrossRef]
- Kahn, J.H. Factor analysis in counseling psychology research, training, and practice: Principles, advances, and applications. Couns. Psychol. 2006, 34, 684–718. [Google Scholar] [CrossRef]
- Büyüköztürk, Ş. Sosyal bilimler için veri analizi el kitabı: İstatistik, araştırma deseni, SPSS uygulamaları ve yorum, 24th ed.; Pegem Akademi: Ankara, Turkey, 2018; pp. 18–19. [Google Scholar] [CrossRef]
- Hutcheson, G.D.; Sofroniou, N. The Multivariate Social Scientist: Introductory Statistics Using Generalized Linear Models; Sage: Thousand Oaks, CA, USA, 1999. [Google Scholar]
- Kaiser, H.F. The application of electronic computers to factor analysis. Educ. Psychol. Meas. 1960, 20, 141–151. [Google Scholar] [CrossRef]
- Kim, J.O.; Mueller, C.W. Factor Analysis: Statistical Methods and Practical Issues; Sage: Beverly Hills, CA, USA, 1978. [Google Scholar]
- Özdamlı, F.; Aydoğan, Ş.K. Validity and reliability of the “Gamification Applications in Education” scale. Folklor/edebiyat 2019, 25, 64–76. [Google Scholar]
- Schreiber, J.B. Issues and recommendations for exploratory factor analysis and principal component analysis. Res. Soc. Adm. Pharm. 2021, 17, 1004–1011. [Google Scholar] [CrossRef]
- Çokluk, Ö.; Şekercioğlu, G.; Büyüköztürk, Ş. Sosyal Bilimler Için Çok Değişkenli Istatistik: SPSS ve LISREL Uygulamaları; Pegem akademi: Ankara, Türkiye, 2012; Volume 2. [Google Scholar]
- Pieters, Z.; Strong, M.; Pitzer, V.E.; Beutels, P.; Bilcke, J. A computationally efficient method for probabilistic parameter threshold analysis for health economic evaluations. Med. Decis. Mak. 2020, 40, 669–679. [Google Scholar] [CrossRef]
- Viamonte, A.J.; Sousa, A.; Roque, L.; Ferreira, M. The Impact of the COVID-19 Pandemic in a Mathematics Subject. In Proceedings of the 2021 4th International Conference of the Portuguese Society for Engineering Education (CISPEE), Lisboa, Portugal, 21–23 June 2021; pp. 1–6. [Google Scholar]
- Wang, M.T.; Holcombe, R. Adolescents’ perceptions of school environment, engagement, and academic achievement in middle school. Am. Educ. Res. J. 2010, 47, 633–662. [Google Scholar] [CrossRef]
- Department for Education. Remote Education Research. Available online: https://www.gov.uk/government/publications/remote-education-research/remote-education-research (accessed on 18 February 2021).
- Mutch-Jones, K.; Hicks, J.; Sorge, B. Elementary science professional development to impact learning across the curriculum. Teach. Teach. Educ. 2022, 112, 103625. [Google Scholar] [CrossRef]
- Scherzinger, M.; Wettstein, A. Classroom disruptions, the teacher–student relationship and classroom management from the perspective of teachers, students and external observers: A multimethod approach. Learn. Environ. Res. 2019, 22, 101–116. [Google Scholar] [CrossRef]
- Thompson, H.W. An Analysis of Teacher Years of Inexperience and Student Discipline Placements in Grades 9–12 at Texas High School Campuses by Student Enrollment Size. Ph.D. Thesis, Sam Houston State University, Huntsville, TX, USA, 2024. [Google Scholar]




| Kaiser–Meyer–Olkin Measure of Sampling Adequacy | 0.825 | |
|---|---|---|
| Bartlett’s Test of Sphericity | Approx. Chi-Square | 1162.013 |
| Df | 78 | |
| Sig. | 0.001 | |
| Component | Initial Eigenvalues | Extraction Sums of Squared Loadings | Rotation Sums of Squared Loadings | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Total | % of Variance | Cumulative% | Total | % of Variance | Cumulative% | Total | % of Variance | Cumulative% | |
| 1 | 2.941 | 22.622 | 22.622 | 2.941 | 22.622 | 22.622 | 1.993 | 15.330 | 15.330 |
| 2 | 1.750 | 13.465 | 36.087 | 1.750 | 13.465 | 36.087 | 1.772 | 13.635 | 28.965 |
| 3 | 1.125 | 8.654 | 44.741 | 1.125 | 8.654 | 44.741 | 1.579 | 12.146 | 41.111 |
| 4 | 1.026 | 7.893 | 52.635 | 1.026 | 7.893 | 52.635 | 1.498 | 11.523 | 52.635 |
| 5 | 0.906 | 6.967 | 59.601 | ||||||
| 6 | 0.892 | 6.861 | 66.463 | ||||||
| 7 | 0.810 | 6.229 | 72.692 | ||||||
| 8 | 0.773 | 5.949 | 78.641 | ||||||
| 9 | 0.705 | 5.421 | 84.062 | ||||||
| 10 | 0.644 | 4.954 | 89.016 | ||||||
| 11 | 0.556 | 4.273 | 93.289 | ||||||
| 12 | 0.498 | 3.834 | 97.123 | ||||||
| 13 | 0.374 | 2.877 | 100.000 | ||||||
| Parameter | Description |
|---|---|
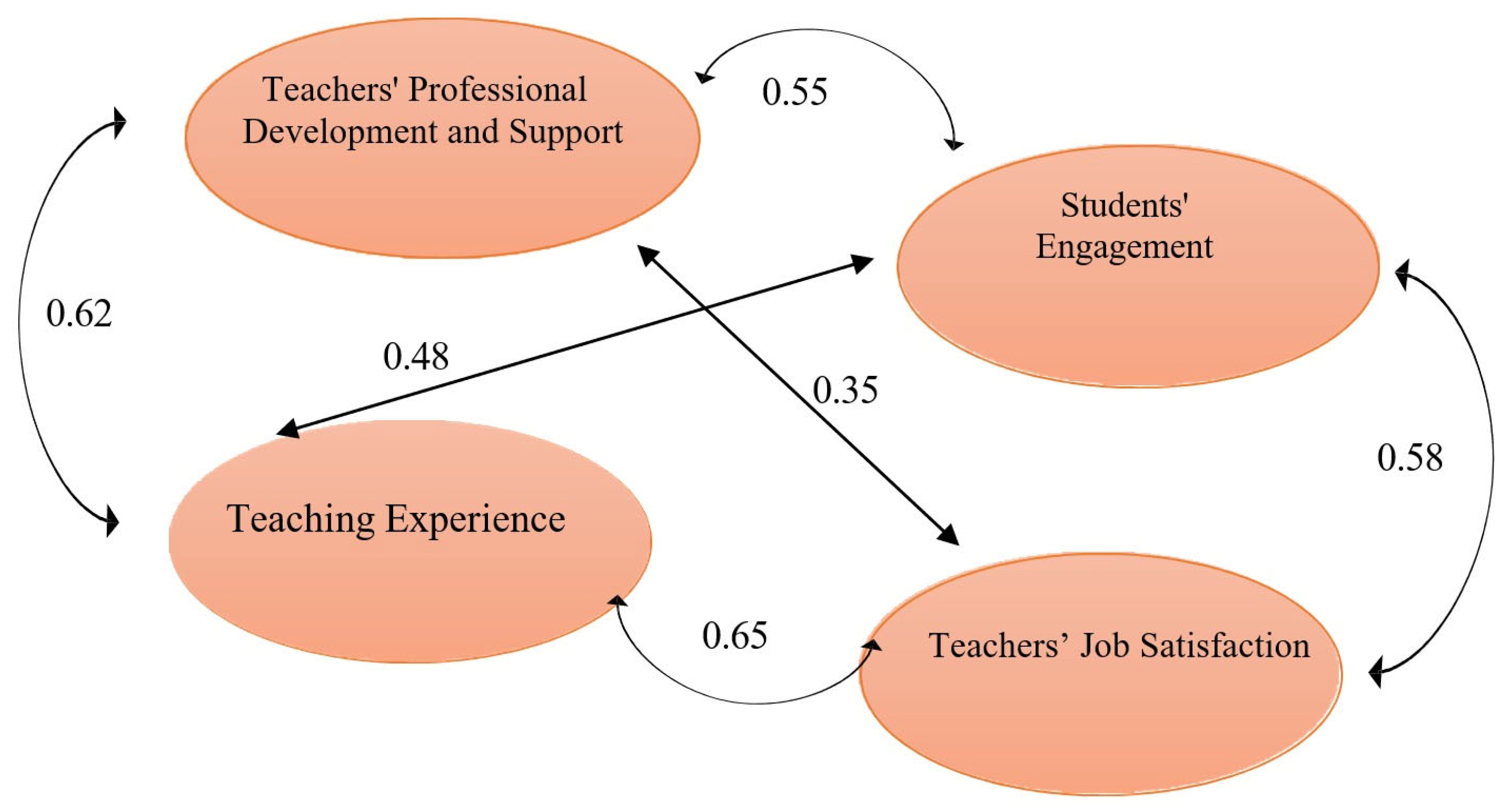
| δ1 | Rates of scale’s factor in relation to “Job dissatisfaction.” |
| δ2 | Rates of scale’s factor in relation to “Job satisfaction.” |
| α1 | Rates of scale’s factor in relation to “Teachers’ professional development and support.” |
| α2 | Rates of scale’s factor in relation to “Lack of teachers’ professional development and support.” |
| β1 | Rates of scale’s factor in relation to “Students’ disengagement.” |
| β2 | Rates of scale’s factor in relation to “Students’ engagement.” |
| γ1 | Rates of scale’s factor in relation to “Teaching experience.” |
| γ2 | Rates of scale’s factor in relation to “Lack of teaching experience.” |
| Secondary and high school teachers in the sample |
| Private Schools | Public Schools | |
|---|---|---|
| β1 | 0.335 | 0.318 |
| β2 | 0.165 | 0.172 |
| ⍺1 | 0.371 | 0.3 |
| ⍺2 | 0.129 | 0.2 |
| γ1 | 0.325 | 0.342 |
| γ2 | 0.175 | 0.158 |
| δ1 | 0.367 | 0.371 |
| δ2 | 0.133 | 0.129 |
| θ | 0.05 | 0.05 |
| λ | 25.069 | 25.069 |
| Private | Public | |
|---|---|---|
| 0.87226 | 0.90118 | |
| 0.67397 | 0.64708 | |
| −0.19425 | −0.24536 | |
| −0.26352 | −0.19384 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gharib, S.I.; Kaymakamzade, B.; Karahan, A.; Tezer, M. Mathematical Modeling Approach to Assessing Math Education Levels in Secondary and High Schools: Pandemic Impact and Post-Pandemic Projections. Systems 2025, 13, 532. https://doi.org/10.3390/systems13070532
Gharib SI, Kaymakamzade B, Karahan A, Tezer M. Mathematical Modeling Approach to Assessing Math Education Levels in Secondary and High Schools: Pandemic Impact and Post-Pandemic Projections. Systems. 2025; 13(7):532. https://doi.org/10.3390/systems13070532
Chicago/Turabian StyleGharib, Sakar Ismael, Bilgen Kaymakamzade, Ahmet Karahan, and Murat Tezer. 2025. "Mathematical Modeling Approach to Assessing Math Education Levels in Secondary and High Schools: Pandemic Impact and Post-Pandemic Projections" Systems 13, no. 7: 532. https://doi.org/10.3390/systems13070532
APA StyleGharib, S. I., Kaymakamzade, B., Karahan, A., & Tezer, M. (2025). Mathematical Modeling Approach to Assessing Math Education Levels in Secondary and High Schools: Pandemic Impact and Post-Pandemic Projections. Systems, 13(7), 532. https://doi.org/10.3390/systems13070532






