Novel Conformable Fractional Order Unbiased Kernel Regularized Nonhomogeneous Grey Model and Its Applications in Energy Prediction
Abstract
1. Introduction
2. Kernel-Regularized Nonhomogeneous Grey Model
2.1. Mathematical Basis of GM(1,1)
2.2. Kernel-Regularized Nonhomogeneous Grey Model
2.3. Time-Response Series of the KRNGM
3. Proposed Conformable Fractional Unbiased Kernel Regularized Nonhomogeneous Grey Model
3.1. The Definition of Conformable Fractional Accumulation and Difference
3.2. The Conformable Fractional Unbiased Kernel Regularized Nonhomogeneous Grey Model
3.3. Parameter Estimation for the CFUKRNGM Model
3.4. The Time Response Series of the CFUKRNGM
4. Parameters Optimization of CFUKRNGM Model
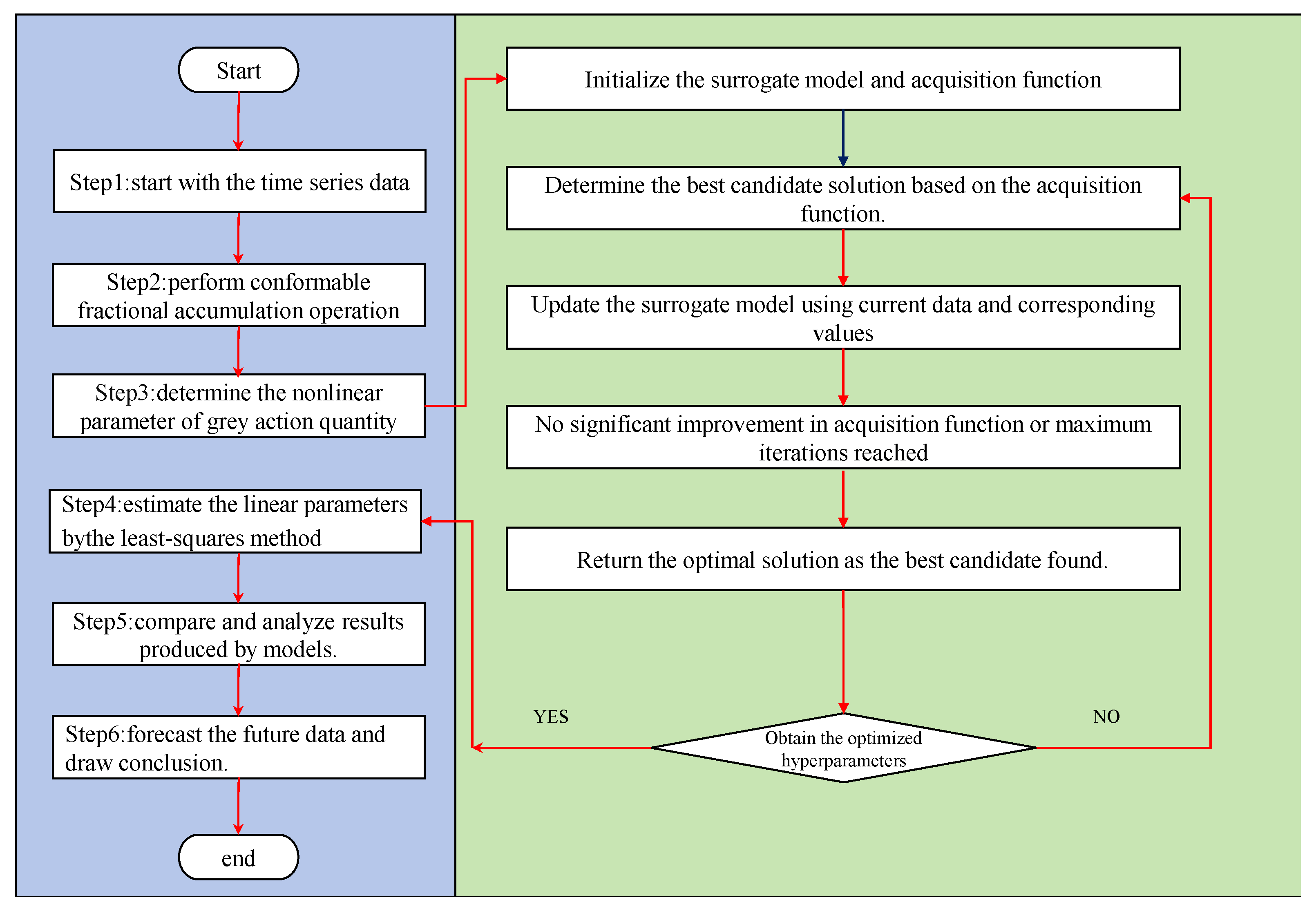
4.1. Optimization Strategies for Hyperparameters
4.2. Bayesian Optimization Algorithm
4.3. Optimization Steps of Parameters
| Algorithm 1: Bayesian Optimization for Hyperparameter Tuning |
| Input: Dataset , initial parameter . 1: while k < IterMax do 2: Step 1: Surrogate Model Update 3: Train the surrogate model using the current dataset = {, }. 4: Step 2: Acquisition Function Maximization 5: Find the by maximizing the acquisition function A(): = arg max A() 6: Use the predictive value update acquisition function of the surrogate model. 7: Step 3: Evaluate Objective Function f () 8: Step 4: Update Dataset 9: = ∪ {, f ()} 10: Step 5: Convergence Check 11: err = |f () − f ()| 12: if err ≤ then 13: Exit the loop. 14: end if 15: k ← k + 1 16: end while Output: The optimal hyperparameters |
5. Numerical Experiment
5.1. Evaluation Metrics
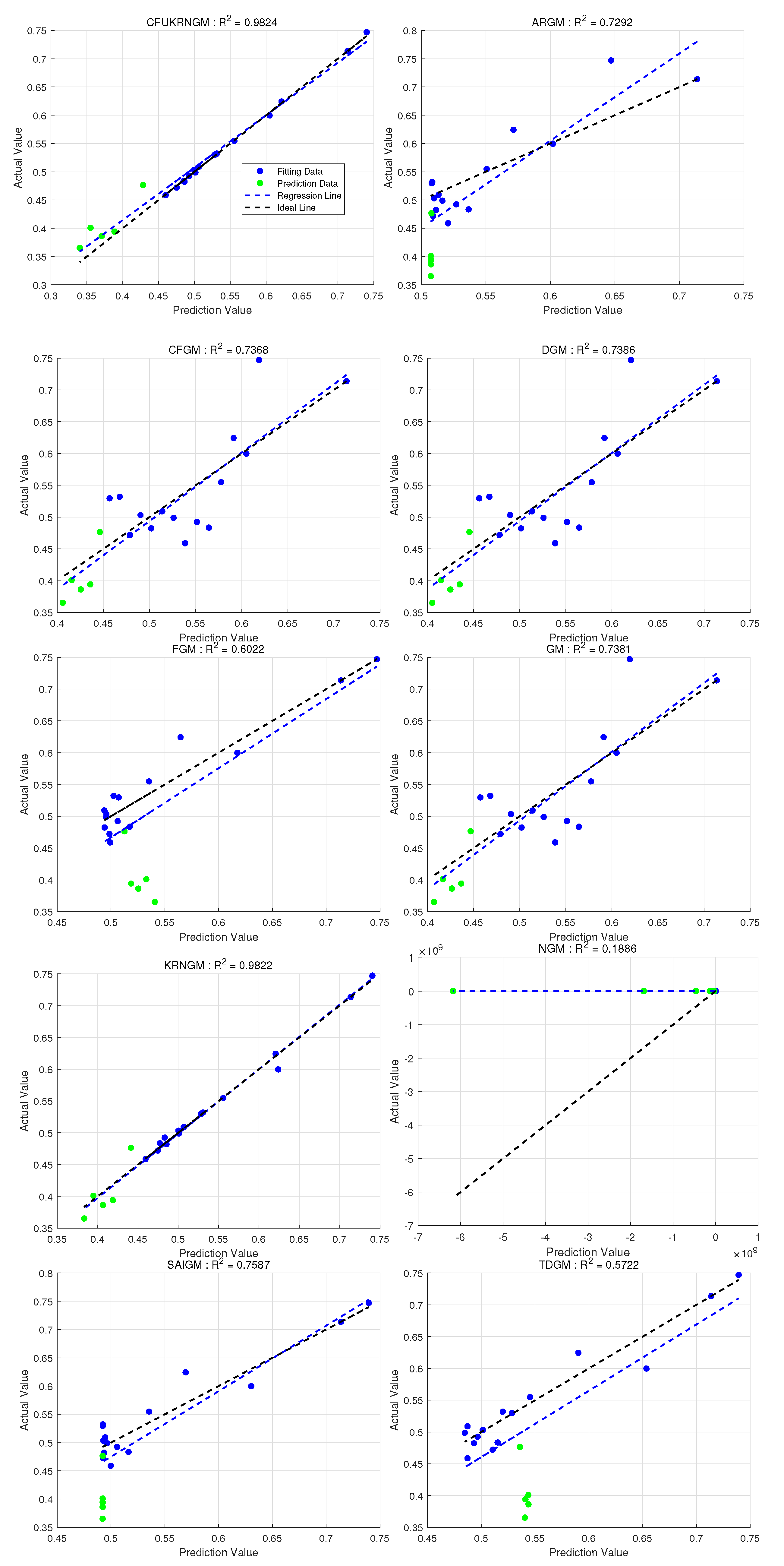
5.2. Case 1: Forecasting Oil Production in Block L
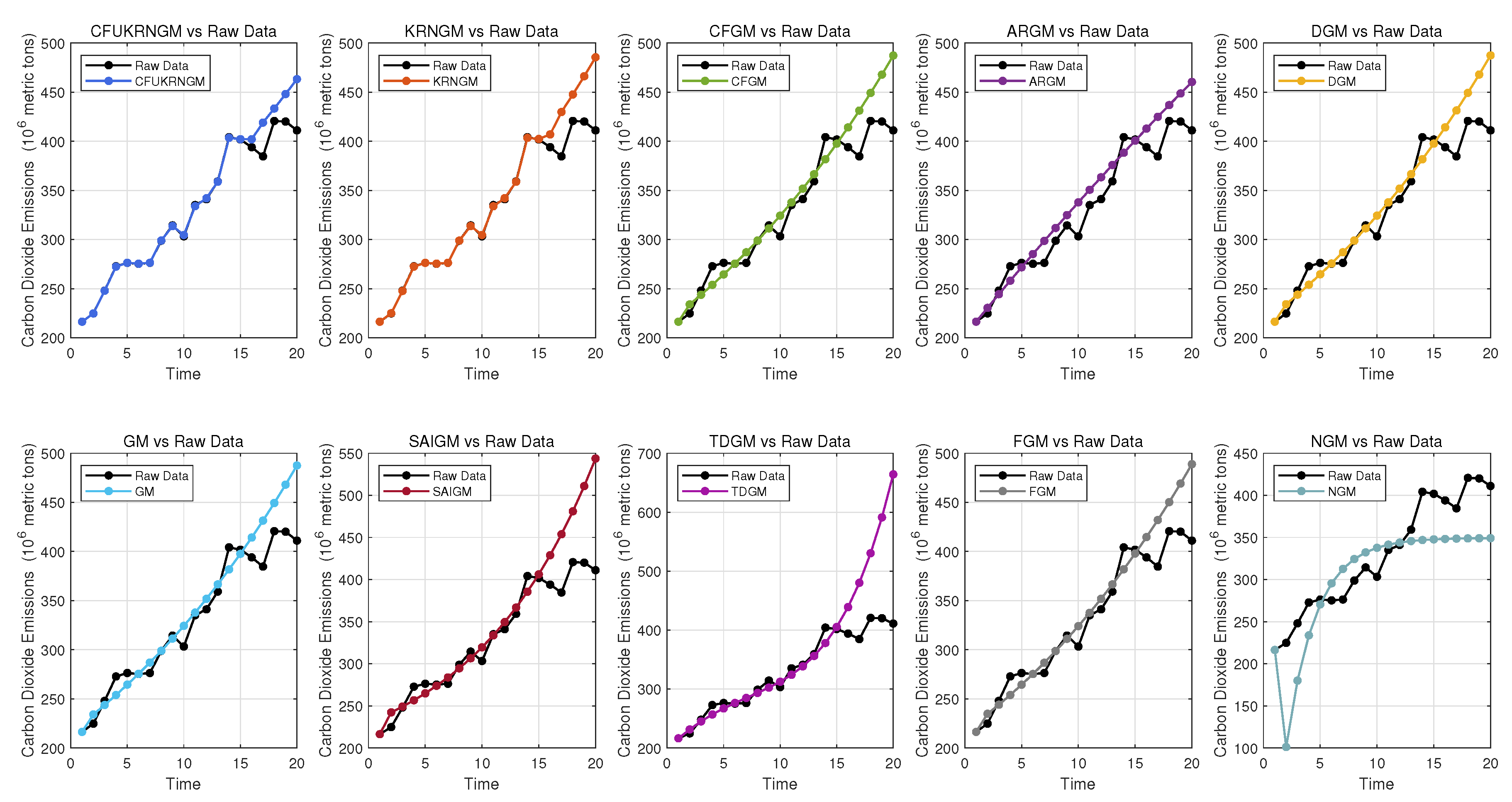
5.3. Case 2: Forecasting Carbon Dioxide Emissions in Turkey
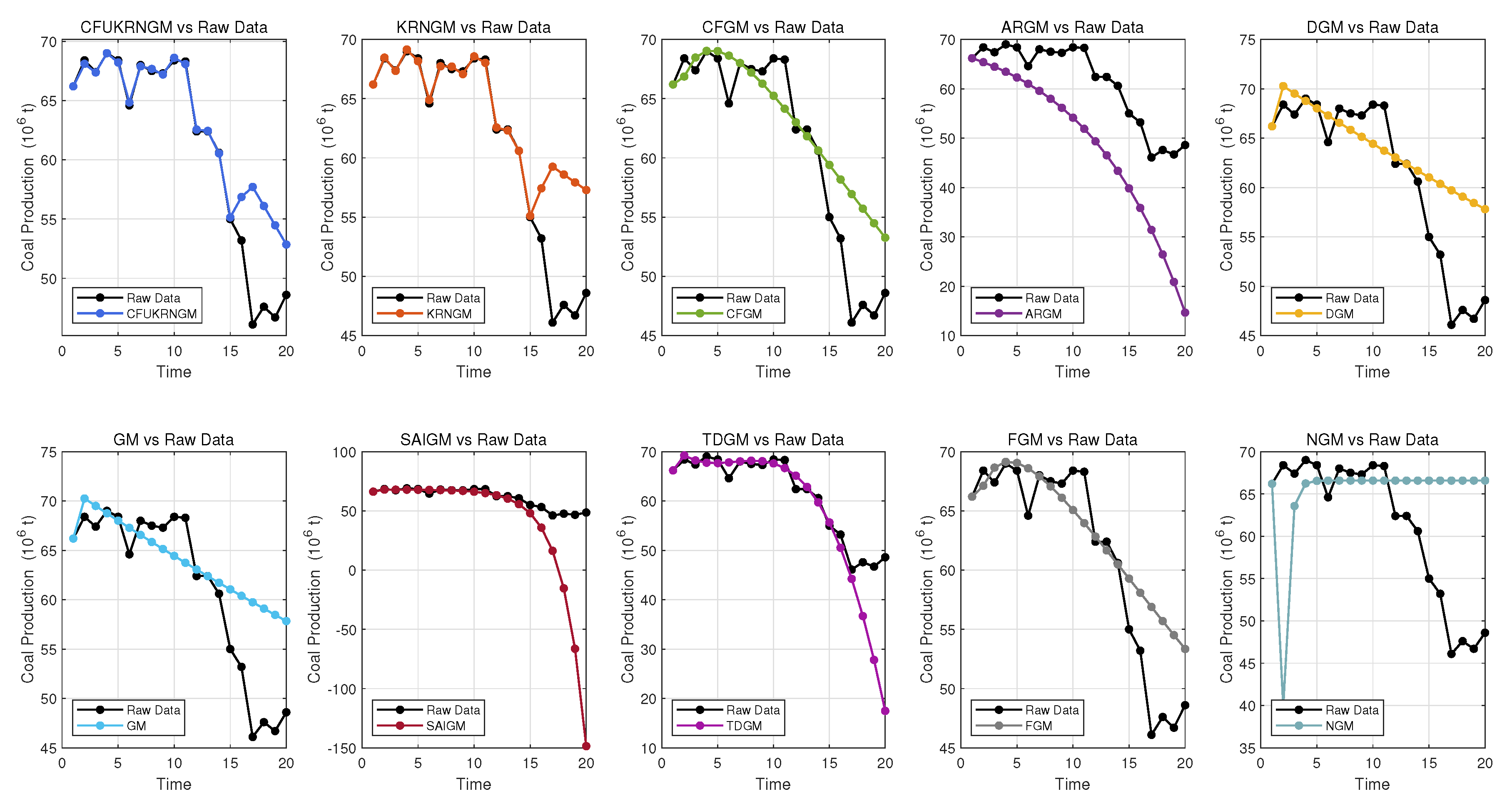
5.4. Case 3: Forecasting Coal Production of Canada
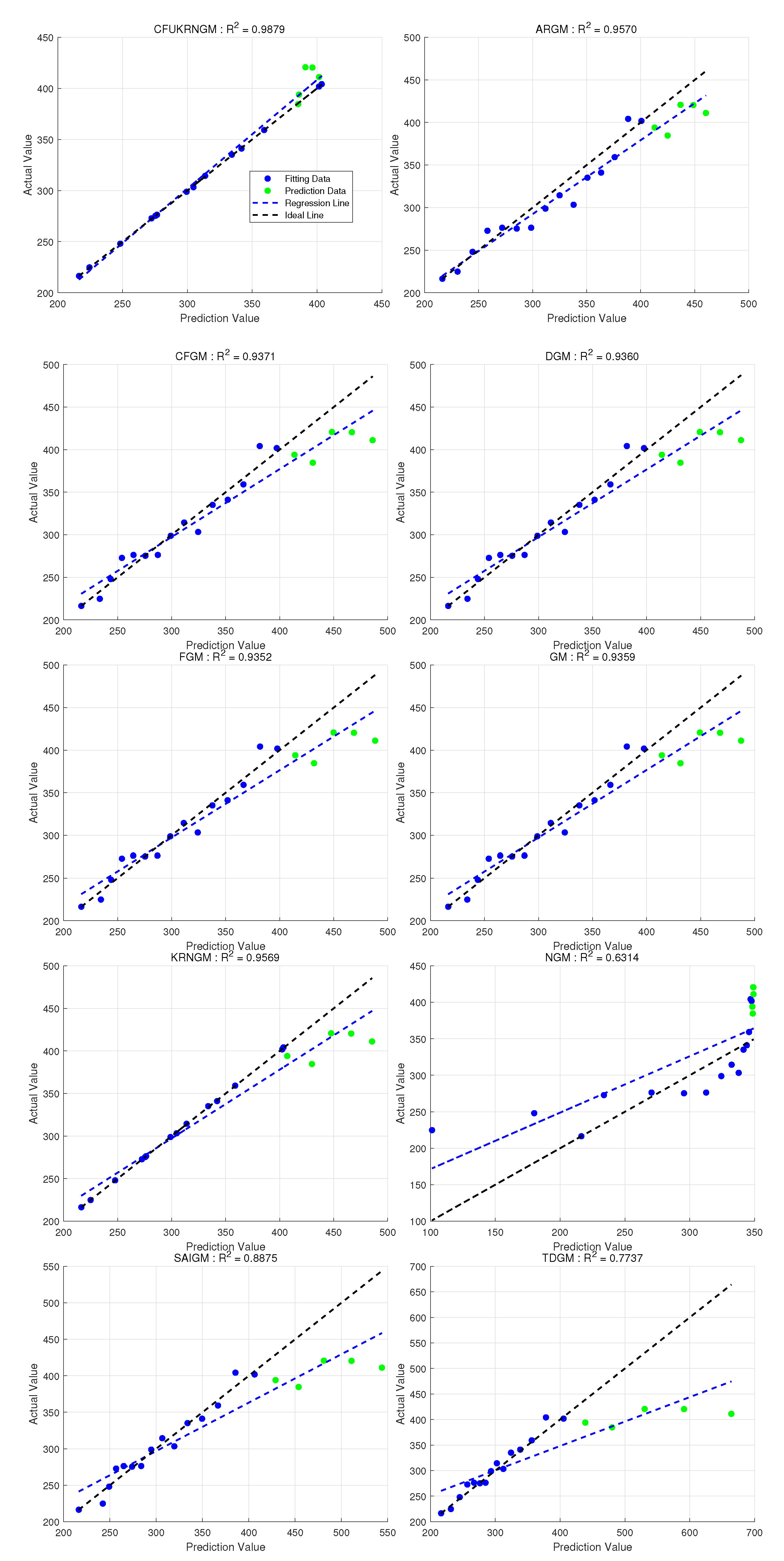
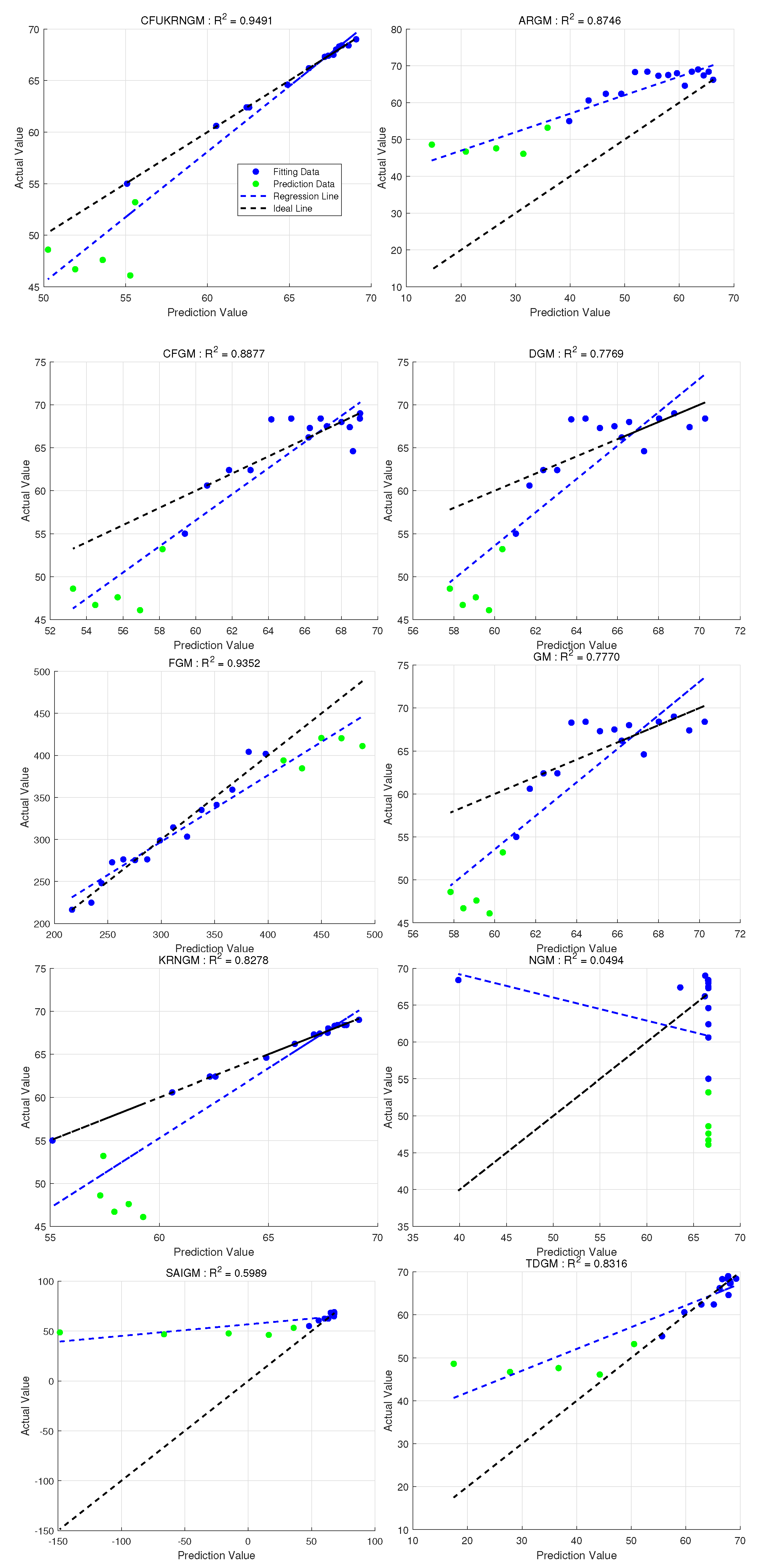
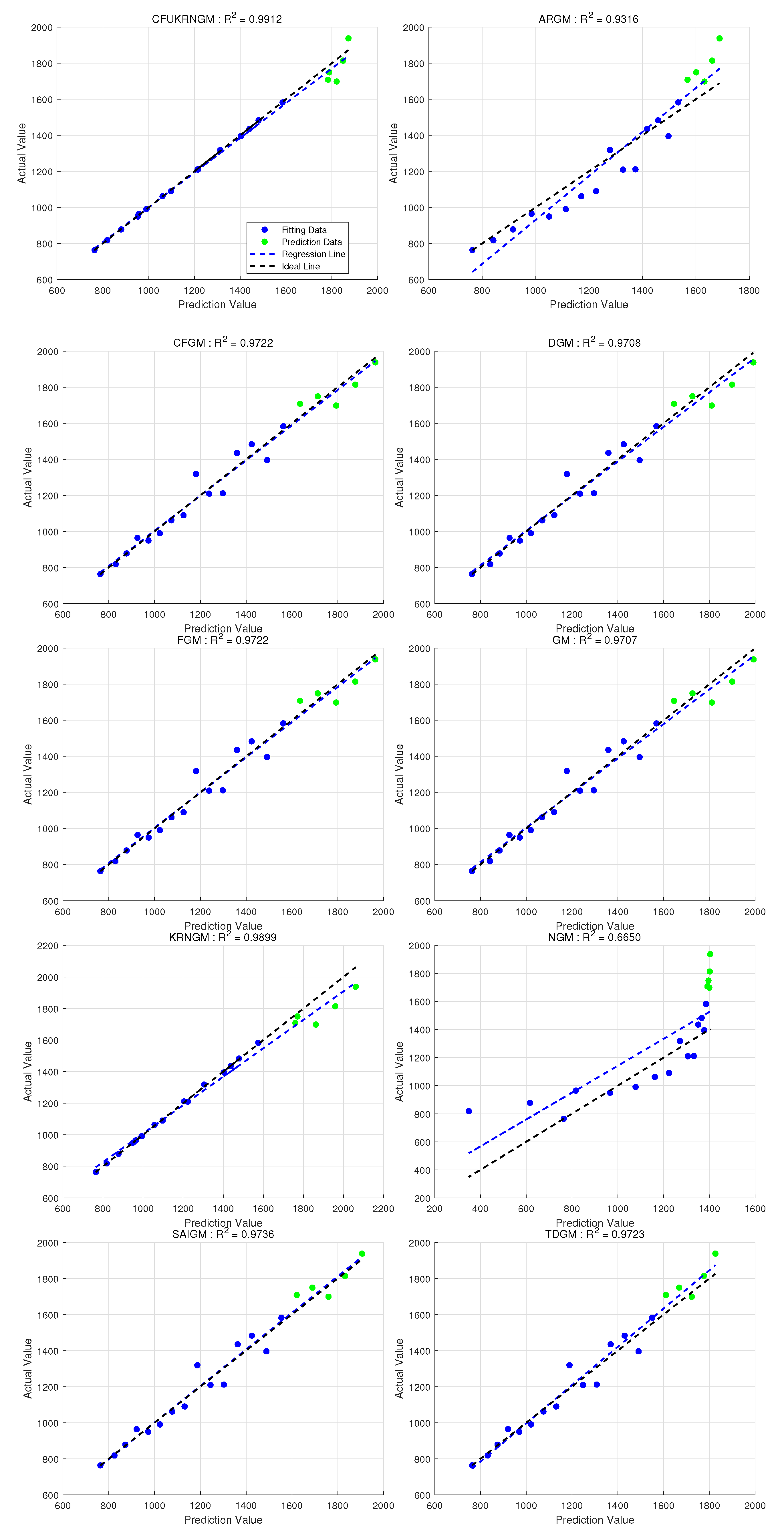
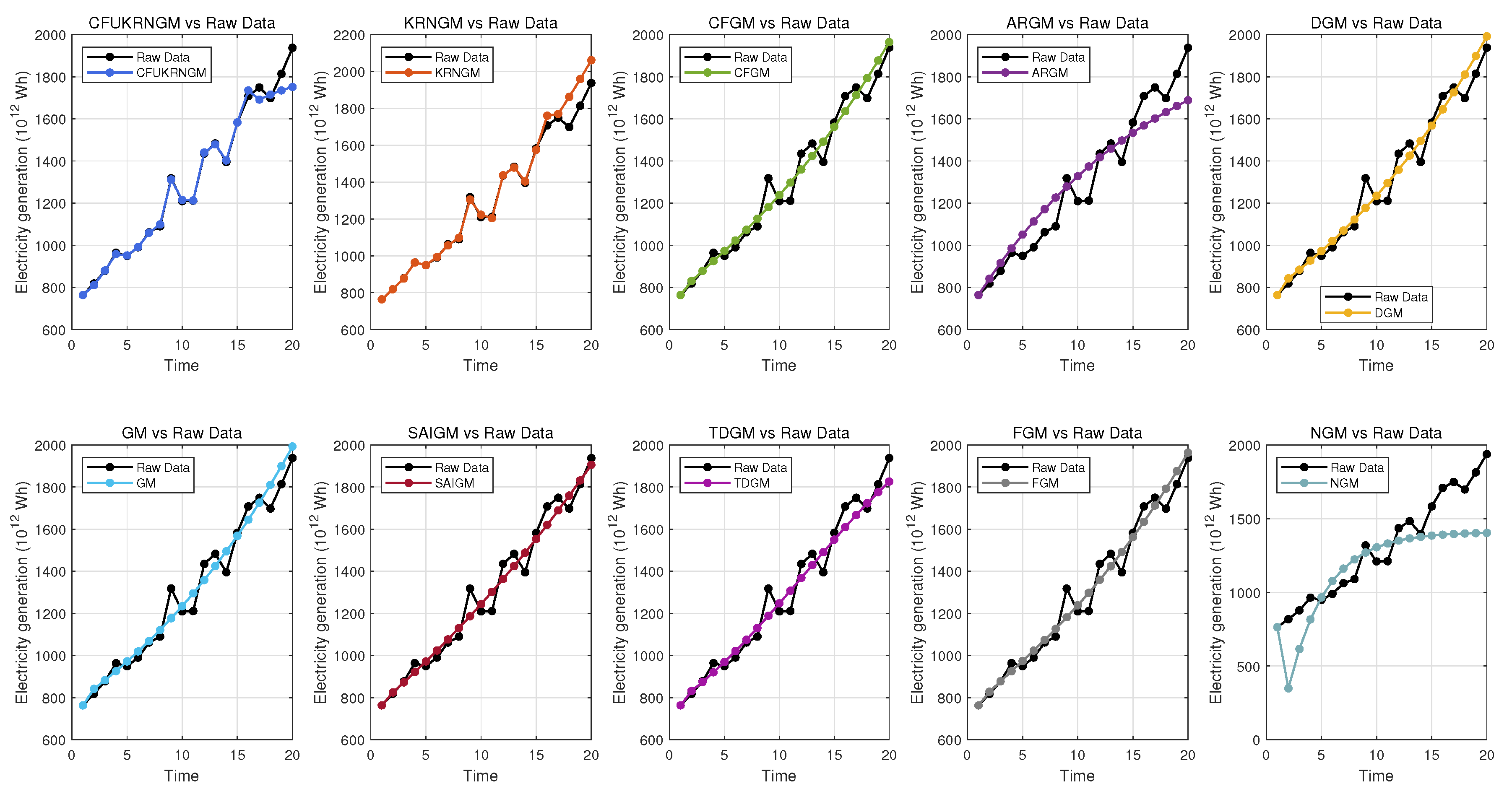
5.5. Case 4: Forecasting Natural Gas Electricity Generation in U.S.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | https://github.com/gongwenkang/CFUKRNGM (accessed on 25 June 2025). |
| 2 | https://www.energyinst.org/statistical-review(accessed on 25 June 2025). |
References
- Lu, C.; Li, S.; Lu, Z. Building energy prediction using artificial neural networks: A literature survey. Energy Build. 2022, 262, 111718. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Zeng, R.; Srinivasan, R.S.; Ahrentzen, S. Random Forest based hourly building energy prediction. Energy Build. 2018, 171, 11–25. [Google Scholar] [CrossRef]
- Fan, C.; Sun, Y.; Zhao, Y.; Song, M.; Wang, J. Deep learning-based feature engineering methods for improved building energy prediction. Appl. Energy 2019, 240, 35–45. [Google Scholar] [CrossRef]
- Cammarano, A.; Petrioli, C.; Spenza, D. Pro-Energy: A novel energy prediction model for solar and wind energy-harvesting wireless sensor networks. In Proceedings of the 2012 IEEE 9th International Conference on Mobile Ad-Hoc and Sensor Systems (MASS 2012), Las Vegas, NV, USA, 8–11 October 2012; pp. 75–83. [Google Scholar]
- He, X.; Wang, Y.; Zhang, Y.; Ma, X.; Wu, W.; Zhang, L. A novel structure adaptive new information priority discrete grey prediction model and its application in renewable energy generation forecasting. Appl. Energy 2022, 325, 119854. [Google Scholar] [CrossRef]
- Feng, S.; Ma, Y.; Song, Z.; Ying, J. Forecasting the energy consumption of China by the grey prediction model. Energy Sources Part Econ. Planning Policy 2012, 7, 376–389. [Google Scholar] [CrossRef]
- Tsai, S.B. Using grey models for forecasting China’s growth trends in renewable energy consumption. Clean Technol. Environ. Policy 2016, 18, 563–571. [Google Scholar] [CrossRef]
- Duan, H.; Pang, X. A multivariate grey prediction model based on energy logistic equation and its application in energy prediction in China. Energy 2021, 229, 120716. [Google Scholar] [CrossRef]
- Ju-Long, D. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar] [CrossRef]
- Julong, D. Essential Topics on Grey System: Theory and Application. In A Report on the Project of National Science Foundation of China; China Ocean Press: Beijing, China, 1988. [Google Scholar]
- Mao, M.; Chirwa, E.C. Application of grey model GM (1, 1) to vehicle fatality risk estimation. Technol. Forecast. Soc. Change 2006, 73, 588–605. [Google Scholar] [CrossRef]
- Wang, Y.; He, X.; Zhou, Y.; Luo, Y.; Tang, Y.; Narayanan, G. A novel structure adaptive grey seasonal model with data reorganization and its application in solar photovoltaic power generation prediction. Energy 2024, 302, 131833. [Google Scholar] [CrossRef]
- Li, X.; Li, N.; Ding, S.; Cao, Y.; Li, Y. A novel data-driven seasonal multivariable grey model for seasonal time series forecasting. Inf. Sci. 2023, 642, 119165. [Google Scholar] [CrossRef]
- Zhou, W.; Wu, X.; Ding, S.; Ji, X.; Pan, W. Predictions and mitigation strategies of PM2. 5 concentration in the Yangtze River Delta of China based on a novel nonlinear seasonal grey model. Environ. Pollut. 2021, 276, 116614. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Wu, X.; Ding, S.; Cheng, Y. Predictive analysis of the air quality indicators in the Yangtze River Delta in China: An application of a novel seasonal grey model. Sci. Total Environ. 2020, 748, 141428. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Liu, S.; Yao, L.; Yan, S.; Liu, D. Grey system model with the fractional order accumulation. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1775–1785. [Google Scholar] [CrossRef]
- Wu, L.; Liu, S.; Chen, D.; Yao, L.; Cui, W. Using gray model with fractional order accumulation to predict gas emission. Nat. Hazards 2014, 71, 2231–2236. [Google Scholar] [CrossRef]
- Wang, Y.; Chi, P.; Nie, R.; Ma, X.; Wu, W.; Guo, B. Self-adaptive discrete grey model based on a novel fractional order reverse accumulation sequence and its application in forecasting clean energy power generation in China. Energy 2022, 253, 124093. [Google Scholar] [CrossRef]
- Wensong, J.; Zhongyu, W.; Mourelatos, Z.P. Application of Nonequidistant Fractional-Order Accumulation Model on Trajectory Prediction of Space Manipulator. IEEE/ASME Trans. Mechatronics 2016, 21, 1420–1427. [Google Scholar] [CrossRef]
- Zhang, J.; Qin, Y.; Zhang, X.; Che, G.; Sun, X.; Duo, H. Application of non-equidistant GM (1, 1) model based on the fractional-order accumulation in building settlement monitoring. J. Intell. Fuzzy Syst. 2022, 42, 1559–1573. [Google Scholar] [CrossRef]
- Gao, M.; Mao, S.; Yan, X.; Wen, J. Estimation of Chinese CO2 Emission Based on A Discrete Fractional Accumulation Grey Model. J. Grey Syst. 2015, 27, 114–130. [Google Scholar]
- Ma, X.; Wu, W.; Zeng, B.; Wang, Y.; Wu, X. The conformable fractional grey system model. ISA transactions 2020, 96, 255–271. [Google Scholar] [CrossRef]
- Duan, H.; Lei, G.R.; Shao, K. Forecasting Crude Oil Consumption in China Using a Grey Prediction Model with an Optimal Fractional-Order Accumulating Operator. Complexity 2018, 2018, 3869619. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Z.; Ma, N. Time-Delayed Polynomial Grey System Model with the Fractional Order Accumulation. Math. Probl. Eng. 2018, 2018, 3640625. [Google Scholar] [CrossRef]
- Wu, L.; Gao, X.; Xiao, Y.; Yang, Y.; Chen, X. Using a novel multi-variable grey model to forecast the electricity consumption of Shandong Province in China. Energy 2018, 157, 327–335. [Google Scholar] [CrossRef]
- Cai, M. Non-homogeneous Grey Model NGM (1, 1) with initial value modification and its application. In Proceedings of the 2010 2nd International Conference on Industrial and Information Systems, Dalian, China, 10–11 July 2010; Volume 1, pp. 102–104. [Google Scholar]
- Jiang, J.; Zhang, Y.; Liu, C.; Xie, W. An improved nonhomogeneous discrete grey model and its application. Math. Probl. Eng. 2020, 2020, 4638296. [Google Scholar] [CrossRef]
- Wu, W.; Ma, X.; Zeng, B.; Zhang, P. A Conformable Fractional Non-homogeneous Grey Forecasting Model with Adjustable Parameters CFNGMA (1, 1, k, c) and its Application. J. Grey Syst. 2024, 36, 1–12. [Google Scholar]
- Ma, X.; Hu, Y.s.; Liu, Z.b. A novel kernel regularized nonhomogeneous grey model and its applications. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 51–62. [Google Scholar] [CrossRef]
- Vapnik, V. Statistical Learning Theory; John Wiley & Sons Google Schola: Hoboken, NJ, USA, 1998; Volume 2, pp. 831–842. [Google Scholar]
- Hofmann, T.; Schölkopf, B.; Smola, A.J. Kernel methods in machine learning. Ann. Stat. 2008, 36, 1171–1220. [Google Scholar] [CrossRef]
- Camastra, F.; Verri, A. A novel kernel method for clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 801–805. [Google Scholar] [CrossRef]
- Blanchard, G.; Bousquet, O.; Zwald, L. Statistical properties of kernel principal component analysis. Mach. Learn. 2007, 66, 259–294. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Chaos control using least-squares support vector machines. Int. J. Circuit Theory Appl. 1999, 27, 605–615. [Google Scholar] [CrossRef]
- Wang, H.; Fu, G.; Cai, Y.; Wang, S. Multiple feature fusion based image classification using a non-biased multi-scale kernel machine. In Proceedings of the 2015 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Zhangjiajie, China, 15–17 August 2015; pp. 700–704. [Google Scholar]
- Wang, S.; Tang, L.; Yu, L. SD-LSSVR-based decomposition-and-ensemble methodology with application to hydropower consumption forecasting. In Proceedings of the 2011 Fourth International Joint Conference on Computational Sciences and Optimization, Kunming and Lijiang City, China, 15–19 April 2011; pp. 603–607. [Google Scholar]
- Juyal, A.; Sharma, S. A Study of landslide susceptibility mapping using machine learning approach. In Proceedings of the 2021 Third International Conference on Intelligent Communication Technologies and Virtual Mobile Networks (ICICV), Tirunelveli, India, 4–6 February 2021; pp. 1523–1528. [Google Scholar]
- Wang, H.Q.; Sun, F.C.; Cai, Y.N.; Ding, L.G.; Chen, N. An unbiased LSSVM model for classification and regression. Soft Comput. 2010, 14, 171–180. [Google Scholar] [CrossRef]
- Jeon, M.; Kim, D.; Lee, W.; Kang, M.; Lee, J. A conservative approach for unbiased learning on unknown biases. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16752–16760. [Google Scholar]
- de Mello, C.E.R. Active Learning: An Unbiased Approach. Ph.D. Thesis, Ecole Centrale Paris. Universidade federal do Rio de Janeiro, Paris, France, 2013. [Google Scholar]
- Syarif, I.; Prugel-Bennett, A.; Wills, G. SVM parameter optimization using grid search and genetic algorithm to improve classification performance. TELKOMNIKA Telecommun. Comput. Electron. Control 2016, 14, 1502–1509. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Bertsimas, D.; Tsitsiklis, J. Simulated annealing. Stat. Sci. 1993, 8, 10–15. [Google Scholar] [CrossRef]
- Brochu, E.; Cora, V.M.; De Freitas, N. A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning. arXiv 2010, arXiv:1012.2599. [Google Scholar]
- Mao, S.; Gao, M.; Xiao, X.; Zhu, M. A novel fractional grey system model and its application. Appl. Math. Model. 2016, 40, 5063–5076. [Google Scholar] [CrossRef]
- Xie, N.m.; Liu, S.f. Discrete grey forecasting model and its optimization. Appl. Math. Model. 2009, 33, 1173–1186. [Google Scholar] [CrossRef]
- Zeng, B.; Meng, W.; Tong, M. A self-adaptive intelligence grey predictive model with alterable structure and its application. Eng. Appl. Artif. Intell. 2016, 50, 236–244. [Google Scholar] [CrossRef]
- Ma, X.; Mei, X.; Wu, W.; Wu, X.; Zeng, B. A novel fractional time delayed grey model with Grey Wolf Optimizer and its applications in forecasting the natural gas and coal consumption in Chongqing China. Energy 2019, 178, 487–507. [Google Scholar] [CrossRef]
- Shaikh, F.; Ji, Q.; Shaikh, P.H.; Mirjat, N.H.; Uqaili, M.A. Forecasting China’s natural gas demand based on optimised nonlinear grey models. Energy 2017, 140, 941–951. [Google Scholar] [CrossRef]
- Wu, L.; Liu, S.; Chen, H.; Zhang, N. Using a novel grey system model to forecast natural gas consumption in China. Math. Probl. Eng. 2015, 2015, 686501. [Google Scholar] [CrossRef]
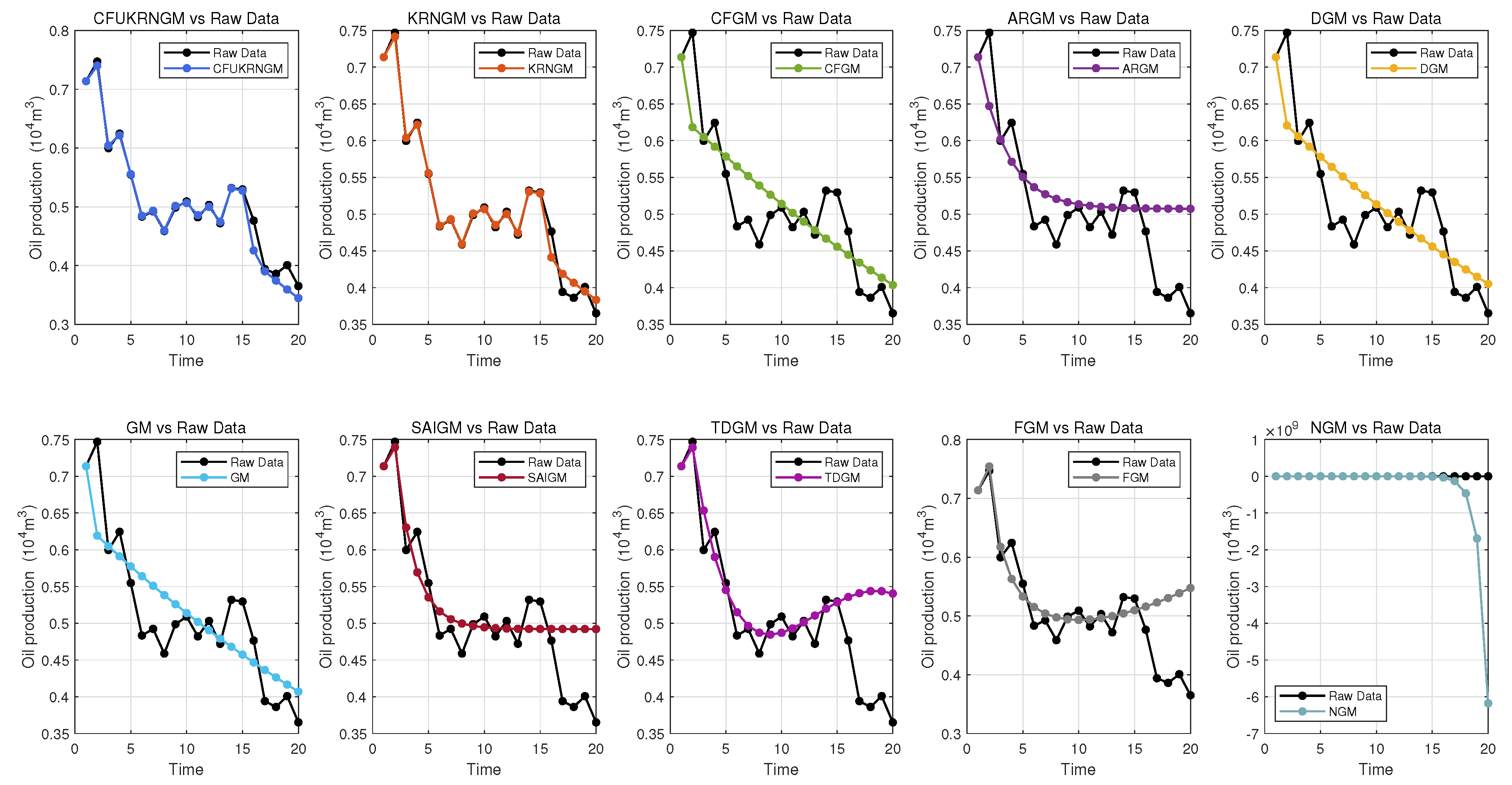
| NO. | Name | Total | Modeling | Prediction |
|---|---|---|---|---|
| Case 1 | China’s Oil Production | 20 Months | From 1 to 15 | From 16 to 20 |
| Case 2 | Carbon Dioxide Emissions from Energy | From 2004 to 2023 | From 2004 to 2018 | From 2019 to 2023 |
| Case 3 | Coal Production | From 2004 to 2023 | From 2004 to 2018 | From 2019 to 2023 |
| Case 4 | Electricity Generation from Gas | From 2004 to 2023 | From 2004 to 2018 | From 2019 to 2023 |
| Evaluation Metrics | Mathematical Formula |
|---|---|
| RMSE | |
| MAE | |
| NRMSE | |
| MAPE | |
| RMSPE | |
| MSE | |
| IA | |
| U1 | |
| U2 |
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Oil production | 0.7137 | 0.747 | 0.5997 | 0.6244 | 0.5548 | 0.4834 | 0.4924 | 0.4588 | 0.4988 | 0.5091 |
| Month | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Oil production | 0.4822 | 0.5032 | 0.4721 | 0.532 | 0.5296 | 0.4765 | 0.3941 | 0.3862 | 0.4009 | 0.3652 |
| Month | Oil Production | CFUKRNGM (, , , ) | ARGM | CFGM () | DGM | FGM () | GM | KRNGM (, ) | NGM | SAIGM | TDGM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.7137 | 0.7137 | 0.7137 | 0.7137 | 0.7137 | 0.7137 | 0.7137 | 0.7137 | 0.7137 | 0.7137 | |
| 2 | 0.7470 | 0.7412 | 0.6471 | 0.6173 | 0.6206 | 0.7471 | 0.6192 | 0.7415 | 0.7395 | 0.7392 | |
| 3 | 0.5997 | 0.6040 | 0.6019 | 0.6056 | 0.6061 | 0.6175 | 0.6050 | 0.6038 | 0.6303 | 0.6534 | |
| 4 | 0.6244 | 0.6217 | 0.5714 | 0.5928 | 0.5919 | 0.5646 | 0.5910 | 0.6217 | 0.5693 | 0.5902 | |
| 5 | 0.5548 | 0.5558 | 0.5507 | 0.5797 | 0.5780 | 0.5353 | 0.5774 | 0.5558 | 0.5353 | 0.5453 | |
| 6 | 0.4834 | 0.4844 | 0.5367 | 0.5664 | 0.5645 | 0.5173 | 0.5641 | 0.4843 | 0.5162 | 0.5151 | |
| 7 | 0.4924 | 0.4932 | 0.5272 | 0.5531 | 0.5513 | 0.5061 | 0.5511 | 0.4931 | 0.5056 | 0.4966 | |
| 8 | 0.4588 | 0.4596 | 0.5207 | 0.5400 | 0.5383 | 0.4992 | 0.5384 | 0.4595 | 0.4997 | 0.4871 | |
| 9 | 0.4988 | 0.5010 | 0.5164 | 0.5270 | 0.5257 | 0.4954 | 0.5260 | 0.5008 | 0.4964 | 0.4846 | |
| 10 | 0.5091 | 0.5068 | 0.5134 | 0.5142 | 0.5134 | 0.4938 | 0.5138 | 0.5069 | 0.4945 | 0.4871 | |
| 11 | 0.4822 | 0.4855 | 0.5114 | 0.5016 | 0.5014 | 0.4941 | 0.5020 | 0.4854 | 0.4935 | 0.4931 | |
| 12 | 0.5032 | 0.5002 | 0.5101 | 0.4892 | 0.4897 | 0.4957 | 0.4904 | 0.5002 | 0.4929 | 0.5013 | |
| 13 | 0.4721 | 0.4747 | 0.5091 | 0.4771 | 0.4782 | 0.4985 | 0.4791 | 0.4747 | 0.4926 | 0.5106 | |
| 14 | 0.5320 | 0.5307 | 0.5085 | 0.4653 | 0.4670 | 0.5024 | 0.4681 | 0.5306 | 0.4924 | 0.5199 | |
| 15 | 0.5296 | 0.5281 | 0.5081 | 0.4537 | 0.4561 | 0.5071 | 0.4573 | 0.5283 | 0.4923 | 0.5285 | |
| 16 | 0.4765 | 0.4383 | 0.5078 | 0.4423 | 0.4454 | 0.5125 | 0.4467 | 0.4413 | 0.4923 | 0.5358 | |
| 17 | 0.3941 | 0.4131 | 0.5076 | 0.4312 | 0.4350 | 0.5187 | 0.4364 | 0.4188 | 0.4922 | 0.5410 | |
| 18 | 0.3862 | 0.4001 | 0.5075 | 0.4204 | 0.4248 | 0.5254 | 0.4264 | 0.4067 | 0.4922 | 0.5438 | |
| 19 | 0.4009 | 0.3876 | 0.5074 | 0.4098 | 0.4148 | 0.5328 | 0.4166 | 0.3949 | 0.4922 | 0.5437 | |
| 20 | 0.3652 | 0.3754 | 0.5073 | 0.3994 | 0.4051 | 0.5407 | 0.4070 | 0.3834 | 0.4922 | 0.5404 |
| Metrics | CFUKRNGM | ARGM | CFGM | DGM | FGM | GM | KRNGM | NGM | SAIGM | TDGM |
|---|---|---|---|---|---|---|---|---|---|---|
| Fitting RMSE (↓) | 0.0026 | 0.0403 | 0.0561 | 0.0547 | 0.0255 | 0.0547 | 0.0547 | 2.5592 | 0.0273 | 0.0238 |
| MAE (↓) | 0.0022 | 0.0299 | 0.0421 | 0.0411 | 0.0201 | 0.0410 | 0.0410 | 8.7529 | 0.0224 | 0.0180 |
| NRMSE (↓) | 0.4796 | 7.3630 | 10.2683 | 10.0119 | 4.6681 | 10.0114 | 10.0114 | 4.6808 | 4.9895 | 4.3456 |
| MAPE (↓) | 0.3922 | 5.5111 | 7.7636 | 7.5837 | 3.8495 | 7.5684 | 7.5684 | 1.6643 | 4.2266 | 3.4135 |
| RMSPE (↓) | 0.4536 | 7.0912 | 10.0954 | 9.8440 | 4.8004 | 9.8207 | 9.8207 | 4.8342 | 5.1117 | 4.4707 |
| MSE (↓) | 0.0000 | 0.0016 | 0.0032 | 0.0030 | 0.0007 | 0.0030 | 0.0030 | 6.5495 | 0.0007 | 0.0006 |
| IA (↑) | 0.9990 | 0.7737 | 0.5599 | 0.5816 | 0.9090 | 0.5817 | 0.5817 | −9.1441 | 0.8961 | 0.9212 |
| U1 (↓) | 0.0024 | 0.0364 | 0.0509 | 0.0496 | 0.0231 | 0.0496 | 0.0496 | 1.0000 | 0.0247 | 0.0214 |
| U2 (↓) | 0.0047 | 0.0728 | 0.1015 | 0.0989 | 0.0461 | 0.0989 | 0.0989 | 4.6257 | 0.0493 | 0.0429 |
| Prediction RMSE (↓) | 0.0214 | 0.1097 | 0.0315 | 0.0344 | 0.1299 | 0.0354 | 0.0230 | 2.8724 | 0.0955 | 0.1422 |
| MAE (↓) | 0.0189 | 0.1030 | 0.0297 | 0.0329 | 0.1214 | 0.0339 | 0.0209 | 1.6989 | 0.0876 | 0.1364 |
| NRMSE (↓) | 5.2983 | 27.1047 | 7.7872 | 8.4996 | 32.1106 | 8.7605 | 5.6785 | 7.0998 | 23.5976 | 35.1374 |
| MAPE (↓) | 4.5128 | 26.4543 | 7.4040 | 8.2577 | 31.2333 | 8.5461 | 5.0912 | 4.5463 | 22.6392 | 34.8273 |
| RMSPE (↓) | 4.8874 | 28.5656 | 7.8880 | 8.7339 | 33.9029 | 9.0402 | 5.4627 | 7.8163 | 24.9476 | 36.8284 |
| MSE (↓) | 0.0005 | 0.0120 | 0.0010 | 0.0012 | 0.0169 | 0.0013 | 0.0005 | 8.2508 | 0.0091 | 0.0202 |
| IA (↑) | 0.6802 | −7.3690 | 0.3092 | 0.1770 | −10.7458 | 0.1257 | 0.6327 | −5.7421 | −5.3434 | −13.0645 |
| U1 (↓) | 0.0265 | 0.1200 | 0.0381 | 0.0414 | 0.1393 | 0.0425 | 0.0282 | 1.0000 | 0.1063 | 0.1501 |
| U2 (↓) | 0.0528 | 0.2699 | 0.0775 | 0.0846 | 0.3197 | 0.0872 | 0.0565 | 7.0688 | 0.2349 | 0.3498 |
| Year | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| Emission | 216.4 | 224.8 | 248.0 | 272.8 | 276.3 | 275.3 | 276.3 | 298.8 | 314.4 | 303.3 |
| Year | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
| Emission | 335.1 | 341.1 | 359.2 | 404.2 | 401.8 | 394.0 | 384.6 | 420.7 | 420.4 | 411.1 |
| Year | Carbon Dioxide Emissions | CFUKRNGM (, , , ) | ARGM | CFGM () | DGM | FGM () | GM | KRNGM (, ) | NGM | SAIGM | TDGM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2004 | 216.4 | 216.4000 | 216.4000 | 216.4000 | 216.4000 | 216.4000 | 216.4000 | 216.4000 | 216.4000 | 216.4000 | 216.4000 |
| 2005 | 224.8 | 224.9704 | 230.4513 | 233.9799 | 234.1835 | 234.5877 | 234.0667 | 224.9704 | 101.2048 | 242.3103 | 231.4886 |
| 2006 | 248 | 247.6885 | 244.3601 | 243.7709 | 243.9169 | 244.0031 | 243.8046 | 247.6885 | 179.9963 | 249.1465 | 245.0977 |
| 2007 | 272.8 | 272.4826 | 258.1279 | 253.9461 | 254.0547 | 253.9683 | 253.9477 | 272.4826 | 233.7770 | 256.6431 | 256.8477 |
| 2008 | 276.3 | 276.2969 | 271.7562 | 264.5313 | 264.6139 | 264.4261 | 264.5127 | 276.2969 | 270.4861 | 264.8639 | 267.1155 |
| 2009 | 275.3 | 275.4745 | 285.2463 | 275.5482 | 275.6120 | 275.3669 | 275.5173 | 275.4745 | 295.5425 | 273.8790 | 276.3172 |
| 2010 | 276.3 | 276.3359 | 298.5996 | 287.0170 | 287.0672 | 286.7962 | 286.9797 | 276.3359 | 312.6453 | 283.7650 | 284.9122 |
| 2011 | 298.8 | 298.8901 | 311.8176 | 298.9578 | 298.9985 | 298.7263 | 298.9189 | 298.8901 | 324.3191 | 294.6061 | 293.4076 |
| 2012 | 314.4 | 313.8068 | 324.9015 | 311.3912 | 311.4257 | 311.1730 | 311.3549 | 313.8068 | 332.2873 | 306.4946 | 302.3634 |
| 2013 | 303.3 | 304.6087 | 337.8528 | 324.3383 | 324.3694 | 324.1547 | 324.3082 | 304.6087 | 337.7262 | 319.5316 | 312.3980 |
| 2014 | 335.1 | 333.8528 | 350.6728 | 337.8208 | 337.8511 | 337.6913 | 337.8005 | 333.8528 | 341.4386 | 333.8282 | 324.1941 |
| 2015 | 341.1 | 342.0929 | 363.3629 | 351.8612 | 351.8931 | 351.8044 | 351.8541 | 342.0929 | 343.9726 | 349.5059 | 338.5053 |
| 2016 | 359.2 | 358.7860 | 375.9242 | 366.4830 | 366.5188 | 366.5171 | 366.4923 | 358.7860 | 345.7022 | 366.6983 | 356.1640 |
| 2017 | 404.2 | 403.4932 | 388.3583 | 381.7105 | 381.7523 | 381.8534 | 381.7396 | 403.4932 | 346.8828 | 385.5516 | 378.0889 |
| 2018 | 401.8 | 402.3295 | 400.6663 | 397.5689 | 397.6190 | 397.8388 | 397.6211 | 402.3295 | 347.6886 | 406.2263 | 405.2947 |
| 2019 | 394 | 406.9946 | 412.8495 | 414.0846 | 414.1452 | 414.5000 | 414.1634 | 406.9946 | 348.2386 | 428.8985 | 438.9014 |
| 2020 | 384.6 | 429.8464 | 424.9092 | 431.2850 | 431.3582 | 431.8648 | 431.3939 | 429.8464 | 348.6140 | 453.7610 | 480.1458 |
| 2021 | 420.7 | 447.6455 | 436.8466 | 449.9624 | 449.2866 | 449.9624 | 449.3413 | 447.6455 | 348.8703 | 481.0254 | 530.3934 |
| 2022 | 420.4 | 466.1816 | 448.6630 | 467.8548 | 467.9602 | 468.8233 | 468.0353 | 466.1816 | 349.0452 | 510.9239 | 591.1520 |
| 2023 | 411.1 | 485.4853 | 460.3596 | 487.2848 | 487.4099 | 488.4791 | 487.5071 | 485.4853 | 349.1646 | 543.7110 | 664.0860 |
| Metrics | CFUKRNGM | ARGM | CFGM | DGM | FGM | GM | KRNGM | NGM | SAIGM | TDGM |
|---|---|---|---|---|---|---|---|---|---|---|
| Fitting RMSE (↓) | 0.5915 | 15.5371 | 11.1719 | 11.1371 | 11.1191 | 11.1374 | 0.6231 | 46.0347 | 10.3180 | 10.1745 |
| MAE (↓) | 0.4266 | 12.6907 | 8.4843 | 8.4474 | 8.4115 | 8.4371 | 0.4597 | 33.6663 | 8.2478 | 7.8018 |
| NRMSE (↓) | 0.1951 | 5.1246 | 3.6848 | 3.6733 | 3.6674 | 3.6734 | 0.2055 | 15.1836 | 3.4032 | 3.3559 |
| MAPE (↓) | 0.1345 | 4.1206 | 2.7748 | 2.7672 | 2.7585 | 2.7637 | 0.1421 | 11.9358 | 2.7632 | 2.5084 |
| RMSPE (↓) | 0.1851 | 5.0301 | 3.6197 | 3.6181 | 3.6194 | 3.6180 | 0.1909 | 17.9738 | 3.5653 | 3.1263 |
| MSE (↓) | 0.3499 | 241.4020 | 124.8118 | 124.0343 | 123.6341 | 124.0410 | 0.3883 | 2119.1920 | 106.4605 | 103.5211 |
| IA(↑) | 0.9999 | 0.9205 | 0.9589 | 0.9591 | 0.9593 | 0.9591 | 0.9999 | 0.3019 | 0.9649 | 0.9659 |
| U1(↓) | 0.0010 | 0.0249 | 0.0181 | 0.0181 | 0.0181 | 0.0181 | 0.0010 | 0.0760 | 0.0167 | 0.0166 |
| U2(↓) | 0.0019 | 0.0504 | 0.0363 | 0.0361 | 0.0361 | 0.0361 | 0.0020 | 0.1494 | 0.0335 | 0.0330 |
| Prediction RMSE (↓) | 9.4834 | 19.0895 | 19.0895 | 27.6822 | 28.0097 | 27.7173 | 26.5472 | 34.1332 | 48.5939 | 88.0666 |
| MAE (↓) | 4.2268 | 10.1885 | 10.1885 | 14.6240 | 14.8058 | 14.6427 | 13.6902 | 19.1245 | 25.8347 | 44.9252 |
| NRMSE (↓) | 2.3349 | 4.7000 | 4.7000 | 6.8156 | 6.8962 | 6.8242 | 6.5361 | 8.4039 | 11.9642 | 21.6827 |
| MAPE (↓) | 1.0500 | 2.5205 | 2.5205 | 3.5961 | 3.6405 | 3.6006 | 3.3635 | 4.6723 | 6.3313 | 10.9646 |
| RMSPE (↓) | 2.3620 | 4.7346 | 4.7346 | 6.7954 | 6.8750 | 6.8039 | 6.5131 | 8.2826 | 11.8650 | 21.3910 |
| MSE (↓) | 89.9352 | 364.4101 | 364.4101 | 766.3015 | 784.5446 | 768.2483 | 704.7523 | 1165.0730 | 2361.3699 | 7755.7298 |
| IA(↑) | -0.2832 | −4.1995 | −4.1995 | −9.9337 | −10.1940 | −9.9615 | −9.0555 | −15.6234 | −32.6924 | −109.6600 |
| U1(↓) | 0.0199 | 0.0392 | 0.0392 | 0.0559 | 0.0566 | 0.0560 | 0.0538 | 0.0783 | 0.0944 | 0.1600 |
| U2(↓) | 0.0404 | 0.0814 | 0.0814 | 0.1180 | 0.1194 | 0.1181 | 0.1131 | 0.1455 | 0.2071 | 0.3753 |
| Year | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| Production | 66.2 | 68.4 | 67.4 | 69.0 | 68.4 | 64.6 | 68.0 | 67.5 | 67.3 | 68.4 |
| Year | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
| Production | 68.3 | 62.4 | 62.4 | 60.6 | 55.0 | 53.2 | 46.1 | 47.6 | 46.7 | 48.6 |
| Year | Coal Production | CFUKRNGM (, , , ) | ARGM | CFGM () | DGM | FGM () | GM | KRNGM (, ) | NGM | SAIGM | TDGM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2004 | 66.2 | 66.2000 | 66.2000 | 66.2000 | 66.2000 | 66.2000 | 66.2000 | 66.2000 | 66.2000 | 66.2000 | 66.2000 |
| 2005 | 68.4 | 68.2216 | 65.3821 | 66.8776 | 70.2773 | 67.0168 | 70.2553 | 68.4647 | 39.8600 | 67.9255 | 69.2202 |
| 2006 | 67.4 | 67.3750 | 64.4665 | 68.4679 | 69.5186 | 68.6201 | 69.5003 | 67.3433 | 63.5703 | 67.9008 | 68.2143 |
| 2007 | 69 | 69.1399 | 63.4417 | 69.0294 | 68.7681 | 69.1478 | 68.7534 | 69.1417 | 66.2411 | 67.8611 | 67.7561 |
| 2008 | 68.4 | 68.1894 | 62.2945 | 69.0133 | 68.0257 | 69.0778 | 68.0145 | 68.1654 | 66.5420 | 67.7971 | 67.6783 |
| 2009 | 64.6 | 64.9392 | 61.0104 | 68.6314 | 67.2914 | 68.6395 | 67.2836 | 64.8975 | 66.5759 | 67.6940 | 67.8204 |
| 2010 | 68 | 67.8849 | 59.5729 | 68.0019 | 66.5649 | 67.9578 | 66.5605 | 67.7324 | 66.5797 | 67.5278 | 68.0290 |
| 2011 | 67.5 | 67.7206 | 57.9639 | 67.1974 | 65.8463 | 67.1086 | 65.8452 | 67.7056 | 66.5802 | 67.2599 | 68.1567 |
| 2012 | 67.3 | 67.1785 | 56.1628 | 66.2665 | 65.1355 | 66.1412 | 65.1376 | 67.0754 | 66.5802 | 66.8283 | 68.0625 |
| 2013 | 68.4 | 68.6506 | 54.1467 | 65.2429 | 64.4323 | 65.0893 | 64.4375 | 68.5674 | 66.5802 | 66.1327 | 67.6114 |
| 2014 | 68.3 | 68.0281 | 51.8898 | 64.1512 | 63.7367 | 63.9773 | 63.7450 | 68.0254 | 66.5802 | 65.0118 | 66.6737 |
| 2015 | 62.4 | 62.5462 | 49.3636 | 63.0096 | 63.0486 | 62.8229 | 63.0600 | 62.5710 | 66.5802 | 63.2054 | 65.1253 |
| 2016 | 62.4 | 62.3902 | 46.5358 | 61.8321 | 62.3680 | 61.6398 | 62.3823 | 62.3121 | 66.5802 | 60.2944 | 62.8475 |
| 2017 | 60.6 | 60.5245 | 43.3704 | 60.6299 | 61.6947 | 60.4382 | 61.7119 | 60.5895 | 66.5802 | 55.6033 | 59.7262 |
| 2018 | 55 | 55.0397 | 39.8272 | 59.4114 | 61.0286 | 59.2263 | 61.0487 | 55.1032 | 66.5802 | 48.0435 | 55.6522 |
| 2019 | 53.2 | 53.4582 | 35.8609 | 58.1837 | 60.3698 | 58.0107 | 60.3926 | 57.4318 | 66.5802 | 35.8609 | 50.5211 |
| 2020 | 46.1 | 51.1536 | 31.4212 | 56.9523 | 59.7181 | 56.7963 | 59.7436 | 59.2572 | 66.5802 | 16.2286 | 44.2325 |
| 2021 | 47.6 | 49.0311 | 26.4514 | 55.7218 | 59.0734 | 55.5873 | 59.1015 | 58.5940 | 66.5802 | −15.4090 | 36.6903 |
| 2022 | 46.7 | 46.9494 | 20.8884 | 54.4960 | 58.4356 | 54.3870 | 58.4664 | 57.9383 | 66.5802 | −66.3933 | 27.8027 |
| 2023 | 48.6 | 44.9155 | 14.6613 | 53.2779 | 57.8048 | 53.1982 | 57.8381 | 57.2900 | 66.5802 | −148.5548 | 17.4813 |
| Metrics | CFUKRNGM | ARGM | CFGM | DGM | FGM | GM | KRNGM | NGM | SAIGM | TDGM |
|---|---|---|---|---|---|---|---|---|---|---|
| Fitting RMSE (↓) | 0.1887 | 10.9724 | 2.1378 | 2.5750 | 2.1580 | 2.5750 | 0.1801 | 8.4009 | 2.6659 | 1.3385 |
| MAE (↓) | 0.1505 | 9.4848 | 1.4354 | 1.9254 | 1.4844 | 1.9256 | 0.1539 | 4.7655 | 1.8277 | 1.0255 |
| NRMSE (↓) | 0.2876 | 16.7279 | 3.2591 | 3.9257 | 3.2900 | 3.9257 | 0.2746 | 12.8076 | 4.0643 | 2.0405 |
| MAPE (↓) | 0.2256 | 14.7713 | 2.2416 | 3.0036 | 2.3109 | 3.0044 | 0.2324 | 7.4134 | 2.9465 | 1.5764 |
| RMSPE (↓) | 0.2825 | 17.3293 | 3.4052 | 4.1534 | 3.4125 | 4.1558 | 0.2707 | 12.7990 | 4.5000 | 2.0723 |
| MSE (↓) | 0.0356 | 120.3936 | 4.5701 | 6.6307 | 4.6571 | 6.6306 | 0.0324 | 70.5751 | 7.1072 | 1.7915 |
| IA (↑) | 0.9975 | −7.3195 | 0.6842 | 0.5418 | 0.6782 | 0.5418 | 0.9978 | −3.8769 | 0.5089 | 0.8762 |
| U1 (↓) | 0.0014 | 0.0897 | 0.0163 | 0.0196 | 0.0164 | 0.0196 | 0.0014 | 0.0643 | 0.0205 | 0.0102 |
| U2 (↓) | 0.0029 | 0.1670 | 0.0325 | 0.0392 | 0.0328 | 0.0392 | 0.0027 | 0.1279 | 0.0406 | 0.0204 |
| Prediction RMSE (↓) | 3.3936 | 23.5858 | 7.6118 | 10.8715 | 7.4209 | 10.8991 | 10.1361 | 18.3152 | 106.6051 | 17.0597 |
| Prediction MAE (↓) | 2.7258 | 22.5834 | 7.2649 | 10.6403 | 7.0669 | 10.6684 | 9.6623 | 18.1402 | 84.0935 | 13.0944 |
| Prediction NRMSE (↓) | 7.0057 | 48.6907 | 15.7139 | 22.4432 | 15.3197 | 22.5003 | 20.9251 | 37.8100 | 220.0765 | 35.2183 |
| Prediction MAPE (↓) | 5.6870 | 46.7934 | 15.2135 | 22.2381 | 14.8042 | 22.2965 | 20.3074 | 37.8034 | 175.5199 | 27.3004 |
| Prediction RMSPE (↓) | 7.0590 | 48.9523 | 16.1097 | 22.9149 | 15.7136 | 22.9725 | 21.4948 | 38.4112 | 221.8091 | 35.5089 |
| Prediction MSE (↓) | 11.5163 | 556.2899 | 57.9397 | 118.1896 | 55.0691 | 118.7912 | 102.7406 | 335.4455 | 11364.6431 | 291.0341 |
| Prediction IA (↑) | −0.8055 | −86.2146 | −8.0837 | −17.5297 | −7.6337 | −17.6240 | −15.1076 | −51.5909 | −1780.7389 | −44.6281 |
| Prediction U1 (↓) | 0.0355 | 0.3127 | 0.0730 | 0.1010 | 0.0713 | 0.1013 | 0.0951 | 0.1591 | 0.8619 | 0.1990 |
| Prediction U2 (↓) | 0.0700 | 0.4863 | 0.1569 | 0.2241 | 0.1530 | 0.2247 | 0.2090 | 0.3776 | 2.1978 | 0.3517 |
| Year | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| Generation | 763.5 | 818.2 | 877.9 | 964.1 | 949.4 | 990.3 | 1062.0 | 1090.0 | 1318.2 | 1209.5 |
| Year | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
| Generation | 1211.4 | 1435.1 | 1483.1 | 1395.4 | 1582.6 | 1708.1 | 1749.2 | 1698.1 | 1814.1 | 1937.7 |
| Year | Electricity Generation | CFUKRNGM (, ) (, ) | ARGM | CFGM () | DGM | FGM () | GM | KRNGM (, ) | NGM | SAIGM | TDGM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2004 | 763.5 | 763.5000 | 763.5000 | 763.5000 | 763.5000 | 763.5000 | 763.5000 | 763.5000 | 763.5000 | 763.5000 | 763.5000 |
| 2005 | 818.2 | 817.7287 | 841.7479 | 830.5556 | 842.6334 | 829.8193 | 841.8743 | 818.2038 | 349.0039 | 824.7984 | 831.7717 |
| 2006 | 877.9 | 877.7716 | 915.5636 | 878.0895 | 883.8792 | 878.3379 | 883.1496 | 877.1191 | 616.2725 | 872.6037 | 874.5524 |
| 2007 | 964.1 | 963.6613 | 985.1980 | 925.2792 | 927.1440 | 925.7748 | 926.4486 | 963.7392 | 816.1849 | 921.6595 | 920.5546 |
| 2008 | 949.4 | 949.3191 | 1050.8881 | 973.2401 | 972.5265 | 973.7472 | 971.8704 | 949.2829 | 965.7162 | 971.9986 | 969.5025 |
| 2009 | 990.3 | 993.4805 | 1112.8573 | 1022.5145 | 1020.1304 | 1022.9408 | 1019.5191 | 992.9757 | 1077.5631 | 1023.6545 | 1021.1078 |
| 2010 | 1062 | 1056.9566 | 1171.3163 | 1073.4344 | 1070.0645 | 1073.7430 | 1069.5039 | 1056.9827 | 1161.2228 | 1076.6616 | 1075.0693 |
| 2011 | 1090 | 1098.1911 | 1226.4639 | 1126.2379 | 1122.4428 | 1126.4179 | 1121.9394 | 1097.5235 | 1223.7988 | 1131.0554 | 1131.0718 |
| 2012 | 1318.2 | 1305.7601 | 1278.4878 | 1181.1166 | 1177.3849 | 1181.1711 | 1176.9457 | 1305.0361 | 1270.6047 | 1186.8720 | 1188.7860 |
| 2013 | 1209.5 | 1221.6999 | 1327.5648 | 1238.2375 | 1235.4689 | 1238.1781 | 1295.1811 | 1222.7420 | 1305.6147 | 1244.1488 | 1247.8675 |
| 2014 | 1211.4 | 1204.9476 | 1373.8620 | 1297.7546 | 1295.4689 | 1297.5990 | 1295.1811 | 1204.0768 | 1331.8016 | 1302.9238 | 1307.9563 |
| 2015 | 1435.1 | 1438.0868 | 1417.5367 | 1359.8157 | 1358.8804 | 1359.5862 | 1358.6811 | 1437.4796 | 1351.3890 | 1363.2364 | 1368.6760 |
| 2016 | 1483.1 | 1478.2894 | 1458.7374 | 1424.5659 | 1425.3958 | 1424.2892 | 1425.2943 | 1478.9293 | 1366.0400 | 1425.1267 | 1429.6330 |
| 2017 | 1395.4 | 1403.5242 | 1497.6044 | 1492.1507 | 1495.1671 | 1491.8571 | 1495.1734 | 1403.8016 | 1376.9987 | 1488.6359 | 1490.4160 |
| 2018 | 1582.6 | 1575.7005 | 1534.2699 | 1562.7174 | 1568.3537 | 1562.4413 | 1568.4786 | 1574.9704 | 1385.1957 | 1553.8065 | 1550.5948 |
| 2019 | 1708.1 | 1738.6849 | 1568.8584 | 1636.4168 | 1645.1226 | 1636.1961 | 1645.3778 | 1759.9234 | 1391.3269 | 1620.6819 | 1609.7199 |
| 2020 | 1749.2 | 1720.6003 | 1601.4878 | 1713.4036 | 1725.6492 | 1713.2805 | 1726.0471 | 1770.3782 | 1395.9129 | 1689.3067 | 1667.3209 |
| 2021 | 1698.1 | 1796.0167 | 1632.2688 | 1793.8378 | 1810.1175 | 1793.8587 | 1810.6715 | 1862.4934 | 1399.3432 | 1759.7266 | 1722.9065 |
| 2022 | 1814.1 | 1874.1510 | 1661.3064 | 1877.8849 | 1898.7205 | 1878.1007 | 1899.4449 | 1959.4017 | 1401.9090 | 1831.9886 | 1775.9628 |
| 2023 | 1937.7 | 1955.1344 | 1688.6991 | 1965.7168 | 1991.6604 | 1966.1832 | 1992.5706 | 2061.3523 | 1403.8281 | 1906.1410 | 1825.9526 |
| Metrics | CFUKRNGM | ARGM | CFGM | DGM | FGM | GM | KRNGM | NGM | SAIGM | TDGM |
|---|---|---|---|---|---|---|---|---|---|---|
| Fitting RMSE (↓) | 5.8836 | 87.1415 | 58.0112 | 58.5286 | 58.0764 | 58.5268 | 6.6559 | 169.7289 | 57.8895 | 57.8325 |
| MAE (↓) | 4.7493 | 70.9890 | 44.2124 | 43.9447 | 43.9046 | 43.7341 | 4.9861 | 126.4018 | 45.0248 | 45.1177 |
| NRMSE (↓) | 0.5146 | 7.6214 | 5.0737 | 5.1189 | 5.0794 | 5.1188 | 0.5821 | 14.8445 | 5.0630 | 5.0580 |
| MAPE (↓) | 0.3895 | 6.3110 | 3.5592 | 3.5779 | 3.5350 | 3.5551 | 0.3957 | 12.2434 | 3.6338 | 3.6539 |
| RMSPE (↓) | 0.4744 | 7.8017 | 4.5080 | 4.5499 | 4.5069 | 4.5448 | 0.5253 | 18.5457 | 4.5192 | 4.5315 |
| MSE (↓) | 34.6167 | 7593.6389 | 3365.2959 | 3425.5957 | 3372.8670 | 3425.3854 | 44.3007 | 28807.9108 | 3351.1989 | 3344.5959 |
| IA (↑) | 0.9994 | 0.8762 | 0.9451 | 0.9441 | 0.9450 | 0.9441 | 0.9993 | 0.5302 | 0.9453 | 0.9455 |
| U1 (↓) | 0.0025 | 0.0365 | 0.0248 | 0.0250 | 0.0248 | 0.0250 | 0.0028 | 0.0737 | 0.0248 | 0.0247 |
| U2 (↓) | 0.0050 | 0.0745 | 0.0496 | 0.0500 | 0.0496 | 0.0500 | 0.0057 | 0.1451 | 0.0495 | 0.0494 |
| Prediction RMSE (↓) | 43.9885 | 161.7951 | 60.5482 | 60.5482 | 63.4389 | 74.0770 | 115.3784 | 392.2584 | 57.1716 | 78.6640 |
| MAE (↓) | 39.0028 | 150.9159 | 54.9020 | 54.9020 | 58.5168 | 67.7324 | 101.2688 | 382.9760 | 51.6771 | 70.9901 |
| NRMSE (↓) | 14.4429 | 45.9183 | 41.5274 | 42.1727 | 41.6295 | 42.2044 | 39.3578 | 59.1307 | 34.3863 | 19.1493 |
| MAPE (↓) | 12.9037 | 46.3896 | 41.8662 | 42.5365 | 41.9723 | 42.5695 | 39.5093 | 59.9959 | 34.2980 | 16.2495 |
| RMSPE (↓) | 15.5456 | 48.9127 | 44.2576 | 44.9317 | 44.3648 | 44.9644 | 42.2001 | 62.4097 | 36.6595 | 19.9406 |
| MSE (↓) | 298.4790 | 3017.0218 | 2467.6132 | 2544.8987 | 2479.7622 | 2548.7300 | 2216.5021 | 5003.0382 | 1691.9107 | 524.7003 |
| IA (↑) | −0.9758 | −18.9711 | −15.3343 | −15.8459 | −15.4147 | −15.8712 | −13.6721 | −32.1174 | −10.1995 | −2.4732 |
| U1 (↓) | 0.0685 | 0.1872 | 0.1724 | 0.1746 | 0.1727 | 0.1747 | 0.1650 | 0.2285 | 0.1471 | 0.0910 |
| U2 (↓) | 0.1437 | 0.4568 | 0.4131 | 0.4195 | 0.4141 | 0.4198 | 0.3915 | 0.5882 | 0.3421 | 0.1905 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, W.; An, Q. Novel Conformable Fractional Order Unbiased Kernel Regularized Nonhomogeneous Grey Model and Its Applications in Energy Prediction. Systems 2025, 13, 527. https://doi.org/10.3390/systems13070527
Gong W, An Q. Novel Conformable Fractional Order Unbiased Kernel Regularized Nonhomogeneous Grey Model and Its Applications in Energy Prediction. Systems. 2025; 13(7):527. https://doi.org/10.3390/systems13070527
Chicago/Turabian StyleGong, Wenkang, and Qiguang An. 2025. "Novel Conformable Fractional Order Unbiased Kernel Regularized Nonhomogeneous Grey Model and Its Applications in Energy Prediction" Systems 13, no. 7: 527. https://doi.org/10.3390/systems13070527
APA StyleGong, W., & An, Q. (2025). Novel Conformable Fractional Order Unbiased Kernel Regularized Nonhomogeneous Grey Model and Its Applications in Energy Prediction. Systems, 13(7), 527. https://doi.org/10.3390/systems13070527





