Optimal Pricing Strategies for Trade-In Programs: A Comparative Theoretical Analysis of No-Price-Commitment and Price-Commitment Models for Remanufacturing
Abstract
1. Introduction
2. Literature Review
2.1. Trade-In
2.2. Remanufacturing
2.3. Price Commitment
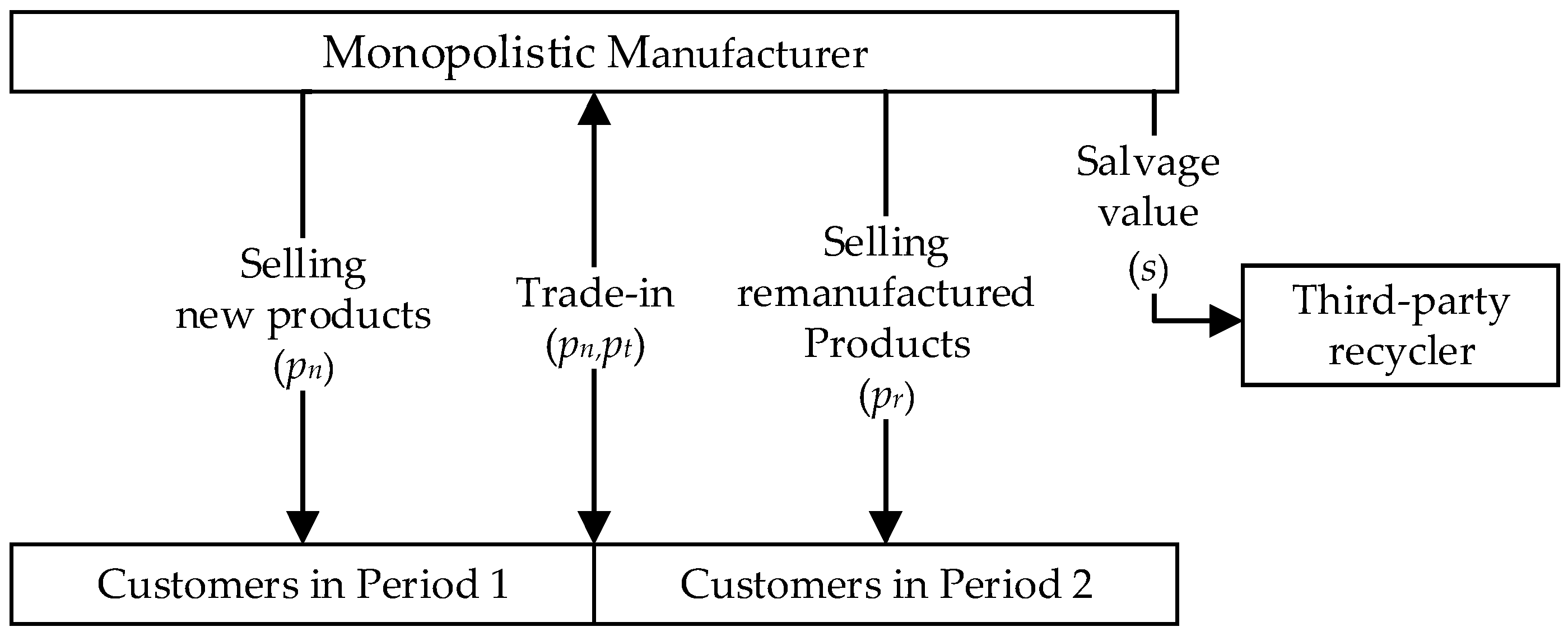
3. Model Description and Assumptions
3.1. Model Description
3.2. Model Assumptions
4. Model Analysis
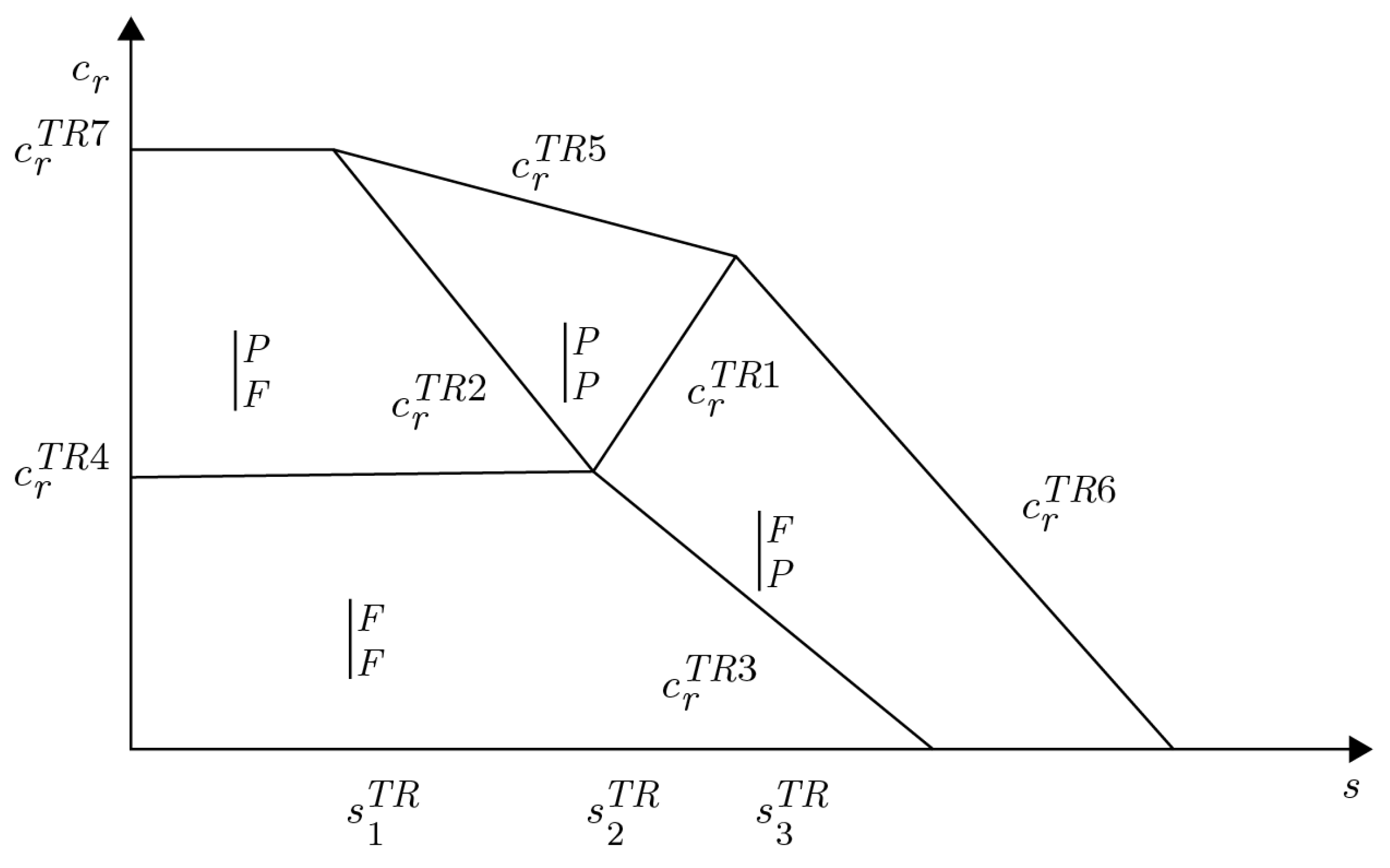
4.1. Trade-In Without Remanufactured-Product Price Commitment (TR Model)
- (1)
- When , the manufacturer adopts a strategy of full recycling and full remanufacturing ();
- (2)
- When , the manufacturer adopts a strategy of partial recycling and full remanufacturing ();
- (3)
- When , the manufacturer adopts a strategy of partial recycling and partial remanufacturing ();
- (4)
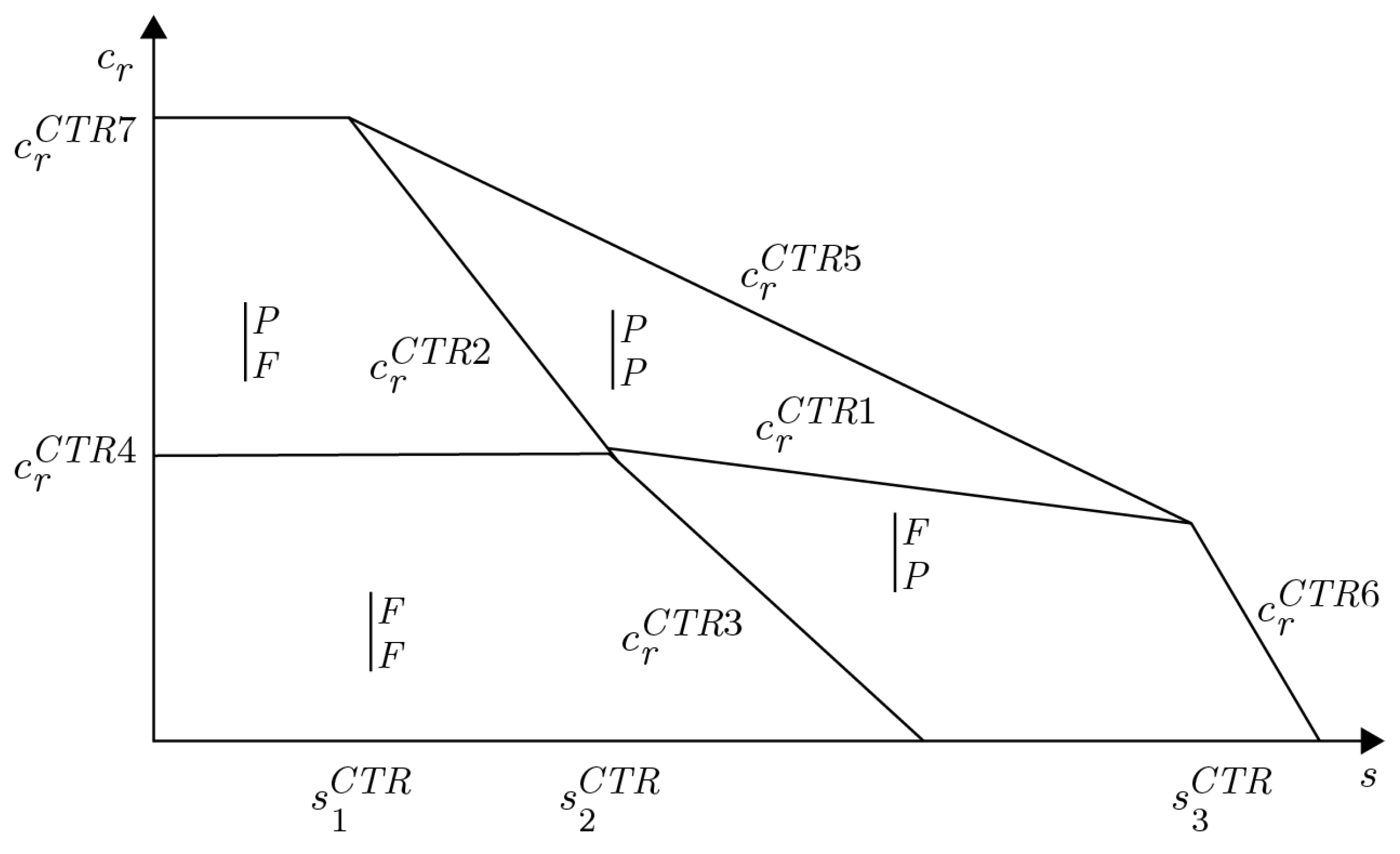
4.2. Trade-In with Remanufactured-Product Price Commitment (CTR Model)
- (1)
- When , the manufacturer adopts a full-recycling and full-remanufacturing strategy ();
- (2)
- When , the manufacturer enacts a partial-recycling and full-remanufacturing strategy ();
- (3)
- When , the manufacturer implements a partial-recycling and partial-remanufacturing strategy ();
- (4)
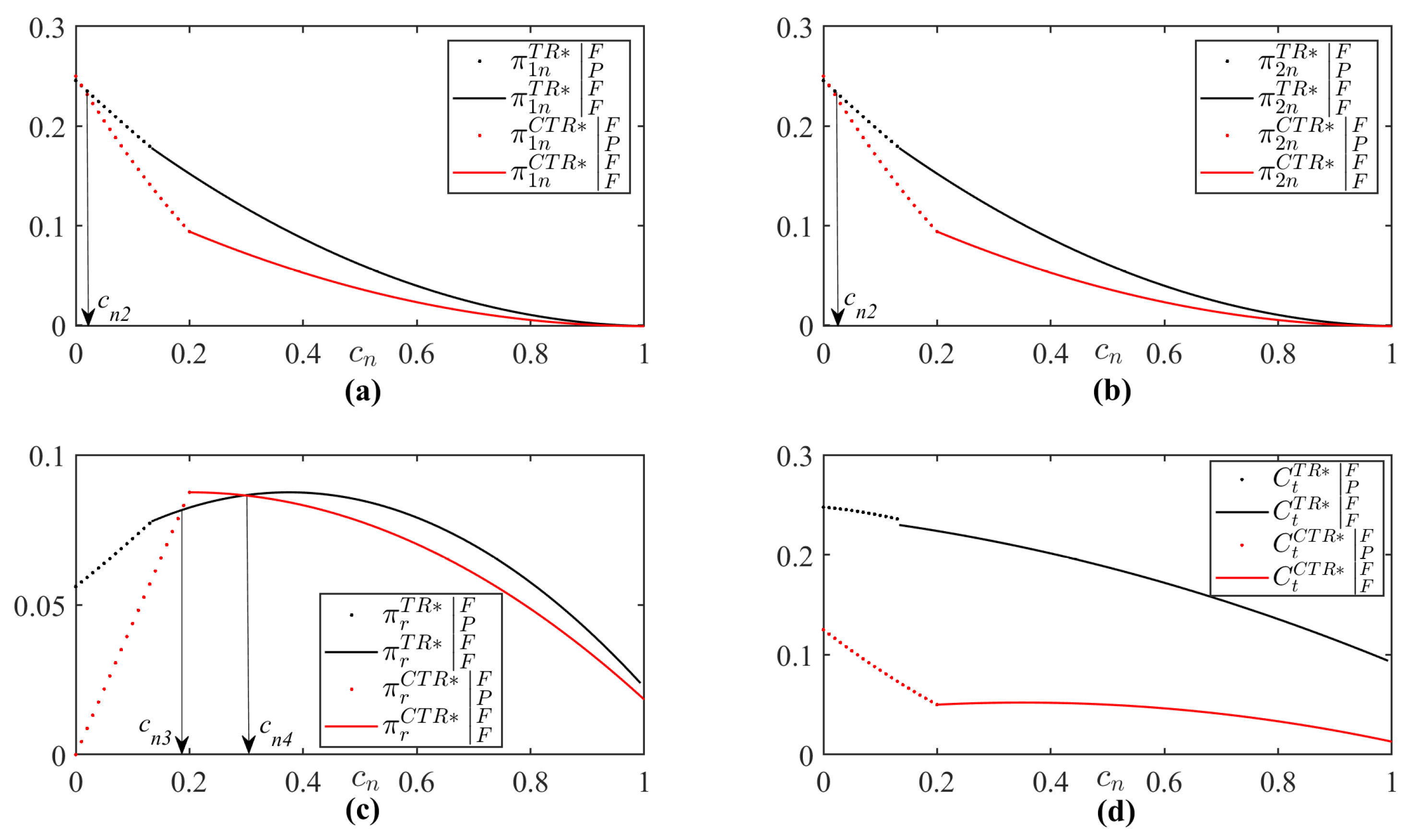
5. Model Comparison
5.1. Optimal Prices
5.2. Optimal Quantities
5.3. Profits
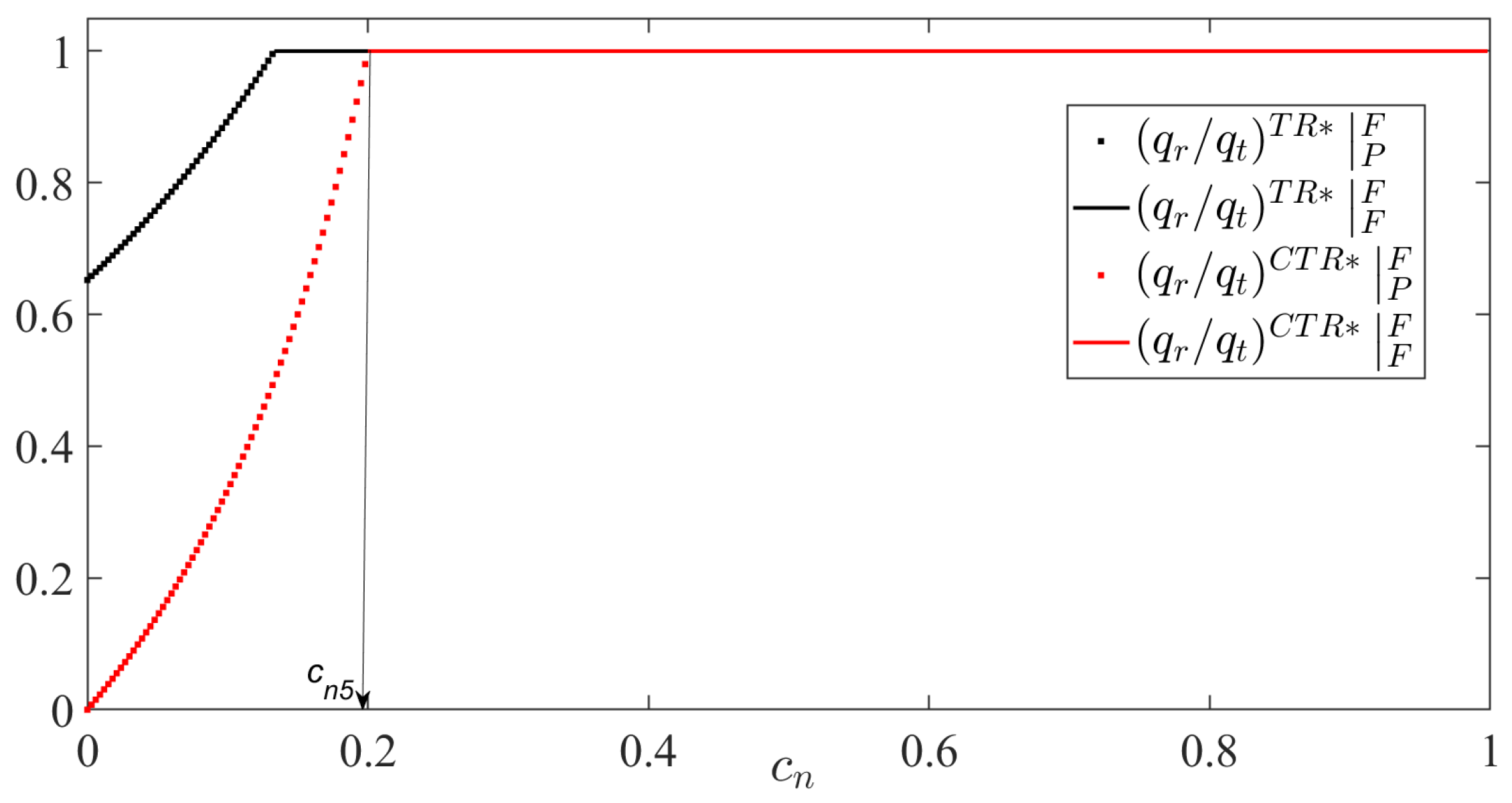
5.4. Remanufacturing Rate
6. Conclusions and Management Insights
6.1. Conclusions
6.2. Management Insights
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- (1)
- , .
- (2)
- , .
- (3)
- , .
- (4)
- , .
- (1)
- , .
- (2)
- , .
- (3)
- , .
- (4)
- , .
- (1)
- When , , , .
- (2)
- When ,,,.
- (3)
- When , , , .
- (1)
- When ,,;.
- (2)
- When ,,;.
- (3)
- When ,;.
- (1)
- When ,.
- (2)
- When ,.
- (3)
- When ,.
- (1)
- When ,.
- (2)
- When ,.
- (3)
- When , .
Appendix B
| Strategy | ||||
|---|---|---|---|---|
| Strategy | ||||
|---|---|---|---|---|
Appendix C
| Enterprise | Website |
|---|---|
| Samsung | https://www.samsung.com/uk/certified-re-newed-phones/ (accessed on 16 May 2025) |
| Surface | https://www.microsoftstore.com.cn/hardware/surface/refurbishedsurface (accessed on 16 May 2025) |
| Huawei | https://m.vmall.com/portal/activity/index.html?pageId=401054582 (accessed on 16 May 2025) |
| Dell | https://www.dell.com/zh-cn/outlet?gacd=9749712-2444702-0-8nyns-10080026&dgc=st&cid=2444702&lid=8nyns (accessed on 16 May 2025) |
| Lenovo | https://s7d1.scene7.com/is/content/Lenovoassetsprod/Lenovo-certified-refurbsihed_brochure_ww_enpdf-1?refId=70e46d2b-afa0-4d84-955e-5af45f3ab012 (accessed on 16 May 2025) |
| Cannon | https://shop.canon.com.cn/prolist?category_id=166 (accessed on 16 May 2025) |
| Xiaomi | http://item.mi.com/re (accessed on 16 May 2025) |
| Dji | https://store.dji.com/cn/pages/refurbished (accessed on 16 May 2025) |
| EPSON | https://www.epson.com.cn/campaign/refurbish/index.html (accessed on 16 May 2025) |
| Apple | https://www.apple.com.cn/shop/refurbished (accessed on 16 May 2025) |
| 1 | https://www.vmall.com/help/faq-7923.html (accessed on 16 May 2025) |
| 2 | https://www.mi.com/a/h/16769.html (accessed on 16 May 2025) |
| 3 | https://m.lenovo.com.cn/page/oldfornew/oldfornew.html (accessed on 16 May 2025) |
| 4 | https://www.vmall.com/product/10086291594649.html (accessed on 16 May 2025) |
| 5 | https://www.samsung.com/uk/certified-re-newed-phones/ (accessed on 16 May 2025) |
| 6 | https://www.microsoftstore.com.cn/hardware/surface/refurbishedsurface (accessed on 16 May 2025) |
| 7 | https://www.cat.com/zh_CN/products/new/parts/reman/the-remanufacturing-process.html (accessed on 16 May 2025) |
| 8 | https://www.apple.com.cn/shop/refurbished (accessed on 16 May 2025) |
| 9 | https://www.apple.com/shop/refurbished/iphone/iphone-15-plus (accessed on 16 May 2025) |
| 10 | , , , , , , . |
| 11 | By solving , ; by solving , . |
| 12 | , , , , , , . |
| 13 | By solving , ; by solving , . |
| 14 | http://item.mi.com/re (accessed on 16 May 2025) |
References
- Guide, V.D.R.; Wassenhove, L.N. Managing product returns for remanufacturing. Prod. Oper. Manag. 2001, 10, 142–155. [Google Scholar] [CrossRef]
- Östlin, J.; Sundin, E.; Björkman, M. Importance of closed-loop supply chain relationships for product remanufacturing. Int. J. Prod. Econ. 2008, 115, 336–348. [Google Scholar] [CrossRef]
- Yin, R.; Li, H.; Tang, C.S. Optimal pricing of two successive-generation products with trade-in options under uncertainty. Decis. Sci. 2015, 46, 565–595. [Google Scholar] [CrossRef]
- Cao, K.; Xu, X.; Bian, Y.; Sun, Y. Optimal trade-in strategy of business-to-consumer platform with dual-format retailing model. Omega 2019, 82, 181–192. [Google Scholar] [CrossRef]
- Hu, S.; Zhu, S.X.; Fu, K. Optimal trade-in and refurbishment strategies for durable goods. Eur. J. Oper. Res. 2023, 309, 133–151. [Google Scholar] [CrossRef]
- Tang, F.; Dai, Y.; Ma, Z.J.; Choi, T.M. Trade-in operations under retail competition: Effects of brand loyalty. Eur. J. Oper. Res. 2023, 310, 397–414. [Google Scholar] [CrossRef]
- Dong, R.; Wang, N.; Jiang, B.; He, Q. Within-brand or cross-brand: The trade-in option under consumer switching costs. Int. J. Prod. Econ. 2023, 255, 108676. [Google Scholar] [CrossRef]
- Dou, G.; Choi, T.M. Does implementing trade-in and green technology together benefit the environment? Eur. J. Oper. Res. 2021, 295, 517–533. [Google Scholar] [CrossRef]
- Cao, K.; Choi, T. Optimal Trade-in Return Policies: Is it Wise to be Generous? Prod. Oper. Manag. 2022, 31, 1309–1331. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, R. Trade-in Remaufacturing, Customer Purchasing Behavior, and Government Policy. Manuf. Serv. Oper. Manag. 2018, 20, 601–616. [Google Scholar] [CrossRef]
- Zhao, S.; You, Z.; Zhu, Q. Quality choice for product recovery considering a trade-in program and third-party remanufacturing competition. Int. J. Prod. Econ. 2021, 240, 108239. [Google Scholar] [CrossRef]
- Feng, L.; Li, Y.; Fan, C. Optimization of pricing and quality choice with the coexistence of secondary market and trade-in program. Ann. Oper. Res. 2020, 1–18. [Google Scholar] [CrossRef]
- Ferrer, G.; Swaminathan, J.M. Managing New and Remanufactured Products. Manag. Sci. 2006, 52, 15–26. [Google Scholar] [CrossRef]
- Ferguson, M.E.; Toktay, L.B. The Effect of Competition on Recovery Strategies. Prod. Oper. Manag. 2006, 15, 351–368. [Google Scholar] [CrossRef]
- Ovchinnikov, A. Revenue and Cost Management for Remanufactured Products. Prod. Oper. Manag. 2011, 20, 824–840. [Google Scholar] [CrossRef]
- Agrawal, V.V.; Atasu, A.; Van Ittersum, K. Remanufacturing, Third-Party Competition, and Consumers’ Perceived Value of New Products. Manag. Sci. 2015, 61, 60–72. [Google Scholar] [CrossRef]
- Yan, W.; Xiong, Y.; Xiong, Z.; Guo, N. Bricks vs. clicks: Which is better for marketing remanufactured products? Eur. J. Oper. Res. 2015, 242, 434–444. [Google Scholar] [CrossRef]
- Yan, X.; Chao, X.; Lu, Y.; Zhou, S.X. Optimal Policies for Selling New and Remanufactured Products. Prod. Oper. Manag. 2017, 26, 1746–1759. [Google Scholar] [CrossRef]
- Zhou, Q.; Meng, C.; Yuen, K.F. Remanufacturing authorization strategy for competition among OEM, authorized remanufacturer, and unauthorized remanufacturer. Int. J. Prod. Econ. 2021, 242, 108295. [Google Scholar] [CrossRef]
- Aviv, Y.; Pazgal, A. Optimal pricing of seasonal products in the presence of forward-looking consumers. Manuf. Serv. Oper. Manag. 2008, 10, 339–359. [Google Scholar] [CrossRef]
- Cachon, G.P.; Feldman, P. Price commitments with strategic consumers: Why it can be optimal to discount more frequently … than optimal. Manuf. Serv. Oper. Manag. 2015, 17, 399–410. [Google Scholar] [CrossRef]
- Correa, J.; Montoya, R.; Thraves, C. Contingent preannounced pricing policies with strategic consumers. Oper. Res. 2016, 64, 251–272. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, B. Dynamic pricing and price commitment of new experience goods. Oper. Res. 2021, 30, 2752–2764. [Google Scholar] [CrossRef]
- Dasu, S.; Tong, C. Dynamic pricing when consumers are strategic: Analysis of posted and contingent pricing schemes. Eur. J. Oper. Res. 2010, 204, 662–671. [Google Scholar] [CrossRef]
- Papanastasiou, Y.; Savva, N. Dynamic pricing in the presence of social learning and strategic consumers. Mark. Sci. 2017, 63, 919–939. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J. Strategic customer behavior with disappointment aversion customers and two alleviation policies. Int. J. Prod. Econ. 2017, 191, 170–177. [Google Scholar] [CrossRef]
- Wang, H.; Guan, Z.; Dong, D.; Zhao, N. Optimal pricing strategy with disappointment-aversion and elation-seeking consumers: Compared to price commitment. Int. Trans. Oper. Res. 2019, 28, 2810–2840. [Google Scholar] [CrossRef]
- Sheng, J.; Du, S.; Nie, T.; Zhu, Y. Dynamic pricing vs. pre-announced pricing in supply chain with consumer heterogeneity. Electron. Commer. Res. Appl. 2023, 62, 101311. [Google Scholar] [CrossRef]
- Liu, J.; Zhai, X.; Chen, L. Optimal pricing strategy under trade-in program in the presence of strategic consumers. Omega 2019, 84, 1–17. [Google Scholar] [CrossRef]
- Esenduran, G.; Lu, L.X.; Swaminathan, J.M. Buyback pricing of durable goods in dual distribution channels. Manuf. Serv. Oper. Manag. 2020, 22, 412–428. [Google Scholar] [CrossRef]
- De Giovanni, P.; Zaccour, G. Optimal quality improvements and pricing strategies with active and passive product returns. Omega. 2018, 88, 248–262. [Google Scholar] [CrossRef]
- Genc, T.S.; Giovanni, P.D. Optimal return and rebate mechanism in a closed-loop supply chain game. Eur. J. Oper. Res. 2018, 269, 661–681. [Google Scholar] [CrossRef]
- Fan, X.; Guo, X.; Wang, S. Optimal collection delegation strategies in a retail-/dual-channel supply chain with trade-in programs. Eur. J. Oper. Res. 2022, 303, 633–649. [Google Scholar] [CrossRef]
- Bai, X.; Choi, T.; Li, Y.; Sun, X. Implementing trade-in programs in the presence of resale platforms: Mode selection and pricing. Prod. Oper. Manag. 2023, 32, 3193–3208. [Google Scholar] [CrossRef]
- Li, Y.; Feng, L.; Govindan, K.; Xu, F. Effects of a secondary market on original equipment manufactures’ pricing, trade-in remanufacturing, and entry decisions. Eur. J. Oper. Res. 2019, 279, 751–766. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiong, Y.; Jin, M. Less is more: Consumer education in a closed-loop supply chain with remanufacturing. Omega 2021, 101, 102259. [Google Scholar] [CrossRef]
- Xiong, Y.; Li, G.; Zhou, Y.; Fernandes, K.; Harrison, R.; Xiong, Z. Dynamic pricing models for used products in remanufacturing with lost-sales and uncertain quality. Int. J. Prod. Econ. 2014, 147, 678–688. [Google Scholar] [CrossRef]
- Atasu, A.; Sarvary, M.; Van Wassenhove, L.N. Remanufacturing as a marketing strategy. Manag. Sci. 2008, 10, 1731–1746. [Google Scholar] [CrossRef]
- Li, W.; Wang, P.; Nie, K. Transnational remanufacturing decisions under carbon taxes and tariffs. Eur. J. Oper. Res. 2024, 312, 150–163. [Google Scholar] [CrossRef]
- Huang, X.; Atasu, A.; Tereyagoglu, N.; Toktay, L.B. Lemons, trade-ins, and certified pre-owned programs. Manuf. Serv. Oper. Manag. 2023, 25, 737–755. [Google Scholar] [CrossRef]



| Research Focus | Research Content or Findings | Authors |
|---|---|---|
| Trade-ins as a recycling incentive policy | Economic incentives boost reverse-logistics efficiency. | Guide and VanWassenhove [1] |
| Trade-ins are an effective recycling incentive. | Östlin et al. [2] | |
| Trade-in industry practices | High product durability/uncertainty increases trade-in benefits. | Yin et al. [3] |
| Gift card redemption rates do not necessarily increase platform profit. | Cao et al. [4] | |
| Conditions for adopting trade-ins/refurbishment. | Hu et al. [5] | |
| Brand loyalty affects trade-in policy choice. | Tang et al. [6] | |
| Fixed cost threshold determines cross-brand adoption. | Dong et al. [7] | |
| Manufacturer vs. retailer recycling impacts profit/emissions. | Dou and Choi [8] | |
| Optimal refund strategy selection. | Cao and Choi [9] | |
| Remanufacturing used products recycled through trade-ins | Trade-ins and remanufacturing boost profit, but may harm environment/social welfare. | Zhang and Zhang [10] |
| Trade-ins are effective for coping with competition from third-party remanufacturers. | Zhao et al. [11] | |
| Trade-in context influences manufacturers’ strategies for selling remanufactured products to independent secondary markets. | Feng et al. [12] |
| Scenario | Price Announcement in Each Period | |
|---|---|---|
| First Period | Second Period | |
| TR | , | |
| CTR | , | |
| Parameters | |||
|---|---|---|---|
| Symbol | Definition | Symbol | Definition |
| unit production cost (new product) | customer valuation coefficient for remanufactured product | ||
| unit remanufacturing cost (remanufactured product) | customer valuation discount coefficient for used product | ||
| residual value per unit of used product | |||
| Variables | |||
| Symbol | Definition | Symbol | Definition |
| unit price of new product in Period | demand for remanufactured products in Period 2 | ||
| trade-in subsidy per unit of used product | profit from new products in Period i | ||
| unit price of remanufactured product | profit from remanufactured products in Period 2 | ||
| demand for new products in Period | recycling cost | ||
| quantity of used products collected via trade-in | total profit across both periods | ||
| Optimal Solutions | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ↑ | ↑ | ↑ | ↓ | ↓ | ↑ | |||||||
| ↓ | ||||||||||||
| ↓ | ↓ | ↑ | ↑ | → | ↓ | |||||||
| ↑ | ||||||||||||
| ↑ | ↑ | ↓ | ↓ | |||||||||
| ↓ | ↑ | ↑ | ↑ | ↑ | ↓ | |||||||
| ↓ | ||||||||||||
| → | → | → | → | → | → | |||||||
| Optimal Solution | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ↑ | → | → | ↓ | ↓ | ↑ | |||||||
| ↓ | ↓ | |||||||||||
| ↑ | ↑ | |||||||||||
| → | → | ↑ | ↑ | → | ↓ | |||||||
| ↑ | ↑ | |||||||||||
| ↑ | ↓ | ↓ | ↓ | |||||||||
| ↑ | ↑ | ↑ | ↑ | ↑ | ↓ | |||||||
| → | → | → | → | → | → | |||||||
| Enterprise | Price Commitment | Enterprise | Price Commitment |
|---|---|---|---|
| Samsung | No | Cannon | No |
| Surface | No | Xiaomi | No |
| Huawei | No | Dji | Yes |
| Dell | No | EPSON | Yes |
| Lenovo | No | Apple | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Lin, J.; Wang, Y.; Peng, J. Optimal Pricing Strategies for Trade-In Programs: A Comparative Theoretical Analysis of No-Price-Commitment and Price-Commitment Models for Remanufacturing. Systems 2025, 13, 472. https://doi.org/10.3390/systems13060472
Xu S, Lin J, Wang Y, Peng J. Optimal Pricing Strategies for Trade-In Programs: A Comparative Theoretical Analysis of No-Price-Commitment and Price-Commitment Models for Remanufacturing. Systems. 2025; 13(6):472. https://doi.org/10.3390/systems13060472
Chicago/Turabian StyleXu, Shuting, Juanling Lin, Yu Wang, and Jing Peng. 2025. "Optimal Pricing Strategies for Trade-In Programs: A Comparative Theoretical Analysis of No-Price-Commitment and Price-Commitment Models for Remanufacturing" Systems 13, no. 6: 472. https://doi.org/10.3390/systems13060472
APA StyleXu, S., Lin, J., Wang, Y., & Peng, J. (2025). Optimal Pricing Strategies for Trade-In Programs: A Comparative Theoretical Analysis of No-Price-Commitment and Price-Commitment Models for Remanufacturing. Systems, 13(6), 472. https://doi.org/10.3390/systems13060472






