Quantitative Evaluation of Value for Money in Sponge City Construction Public–Private Partnership Projects Through a System Dynamics Model
Abstract
1. Introduction
2. Literature Review
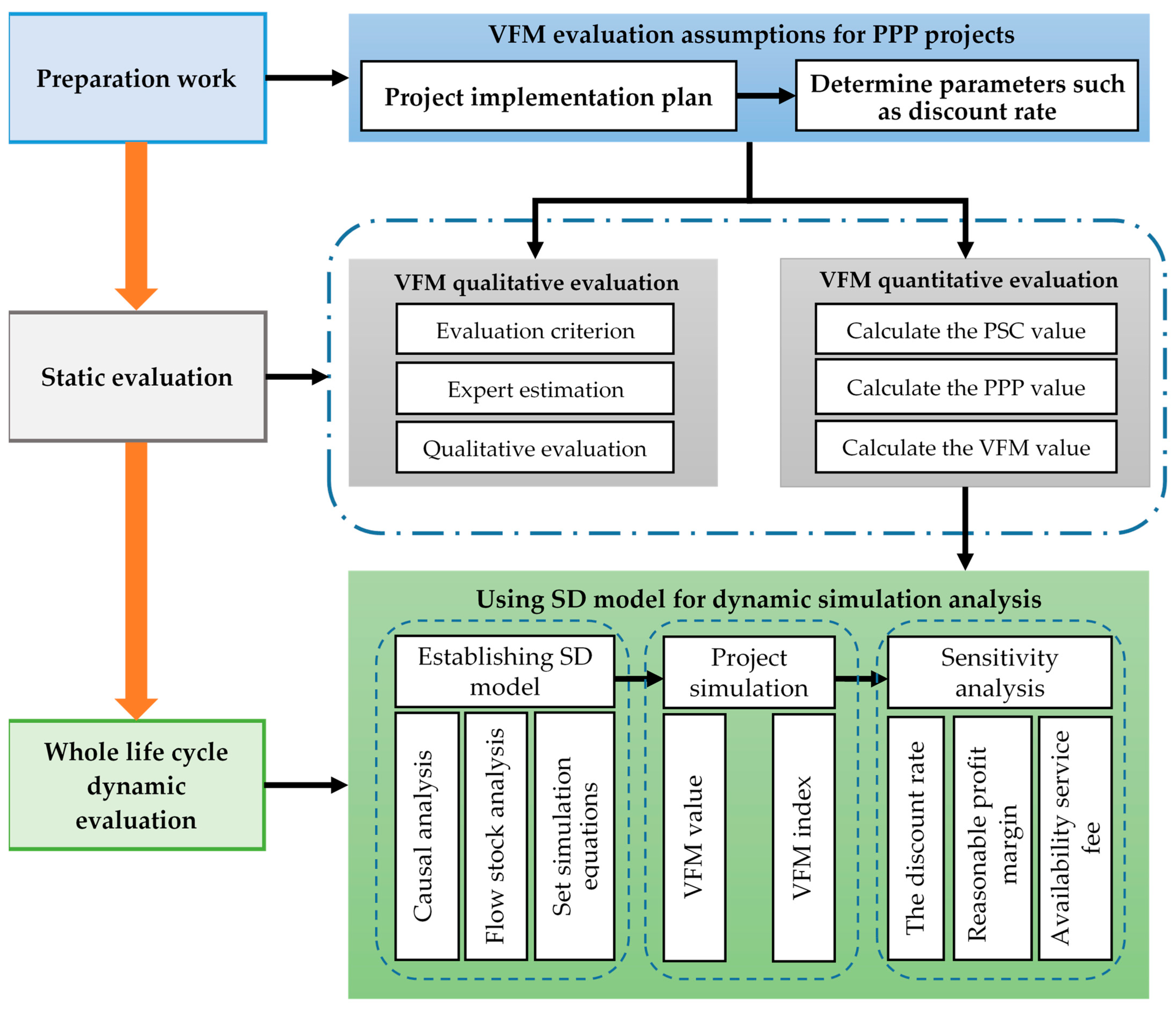
3. Methodology
3.1. Calculation of VFM
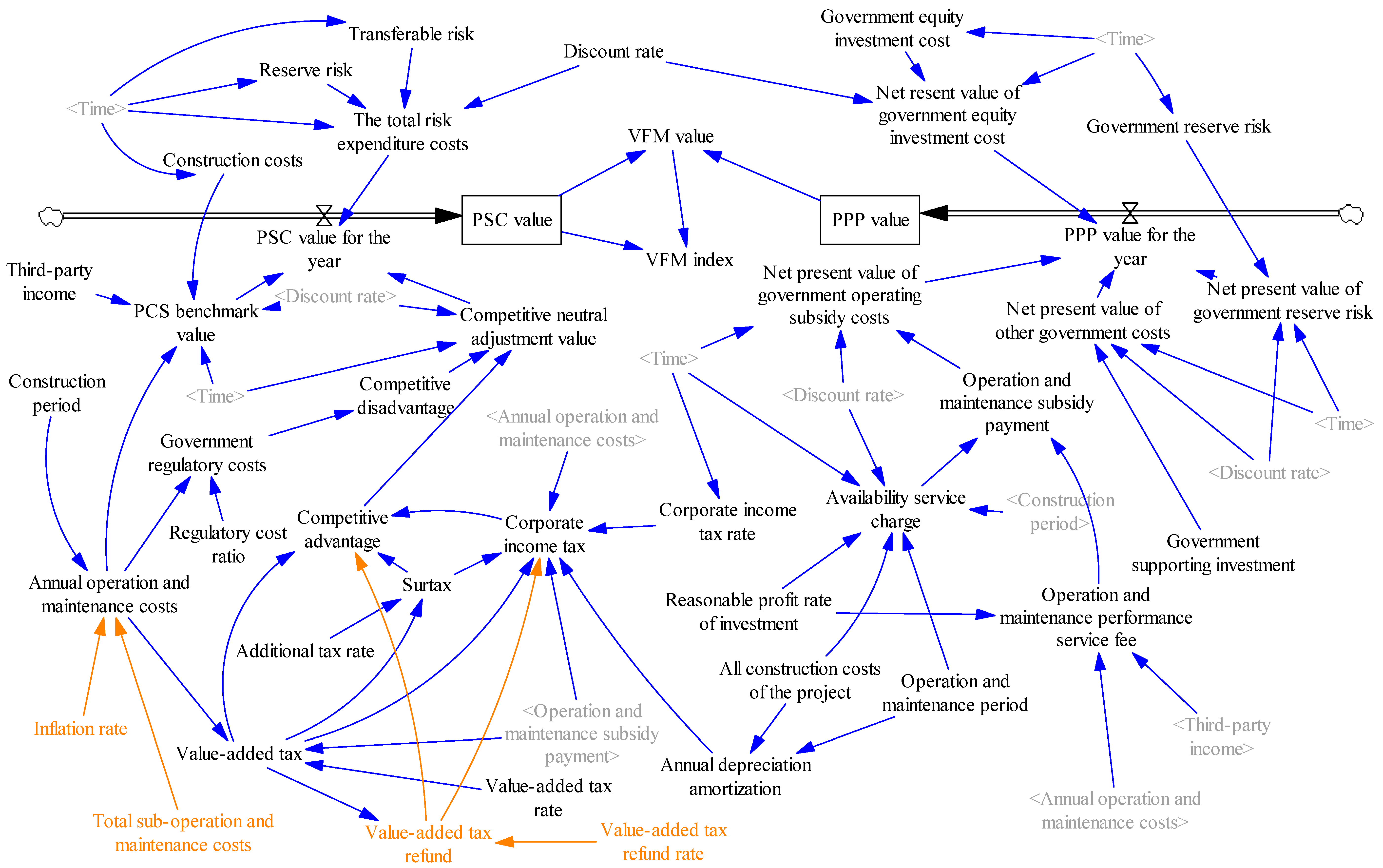
3.2. Simulation Method of VFM
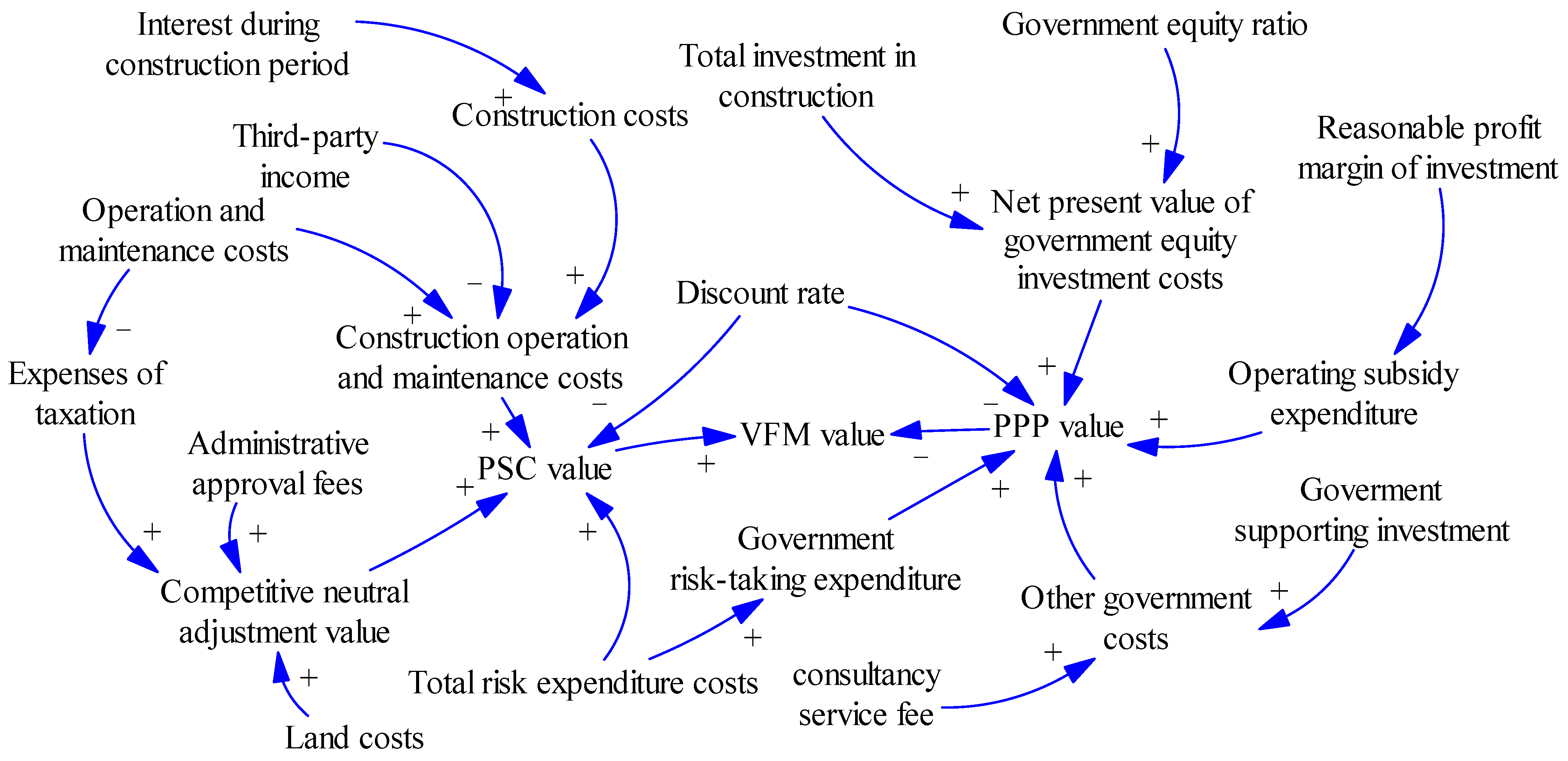
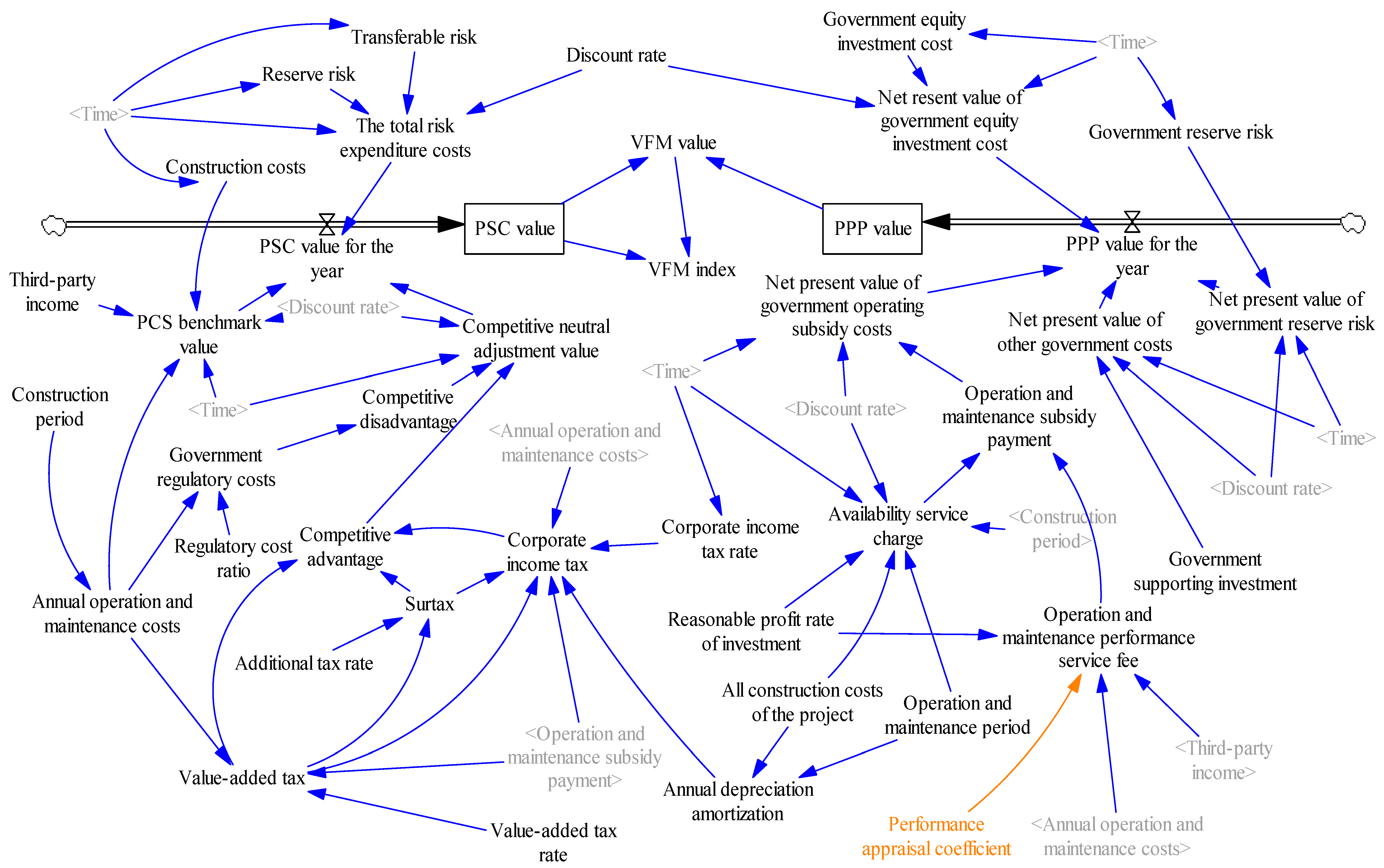
3.3. Construction System Causality of VFM
3.4. Analysis of the Key Influencing Factors
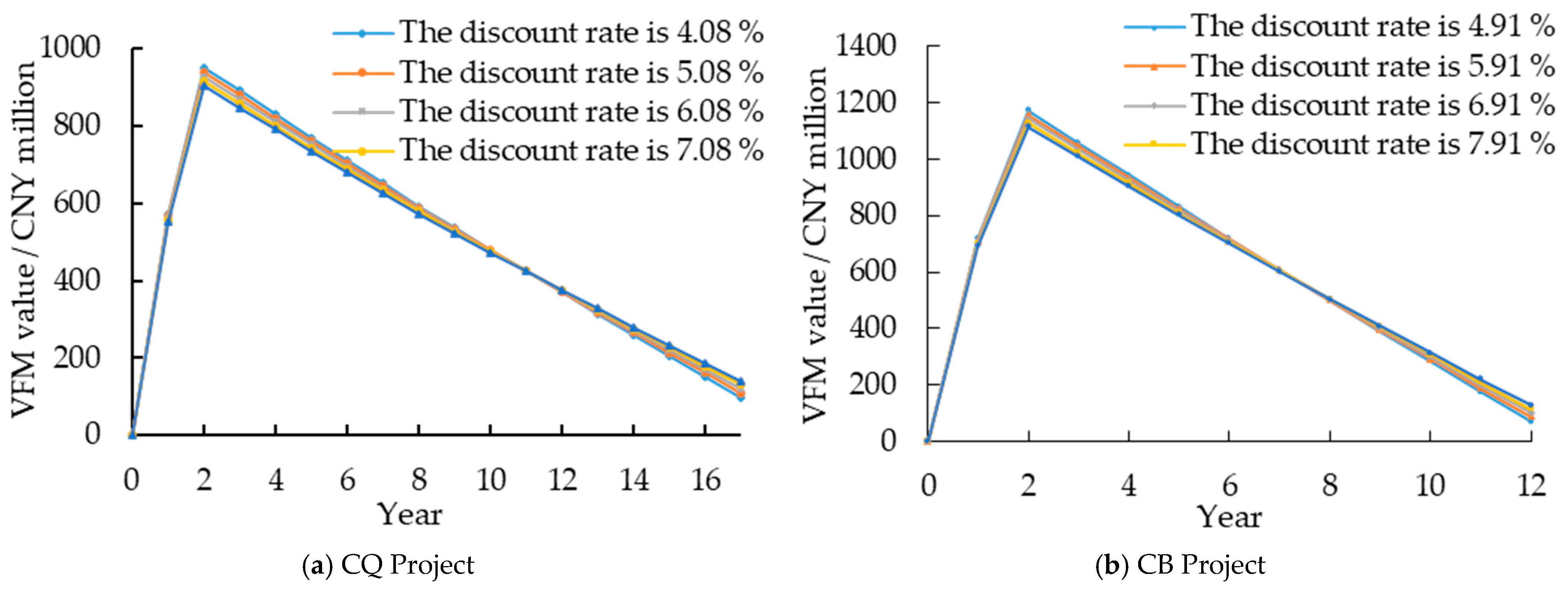
3.4.1. Discount Rate
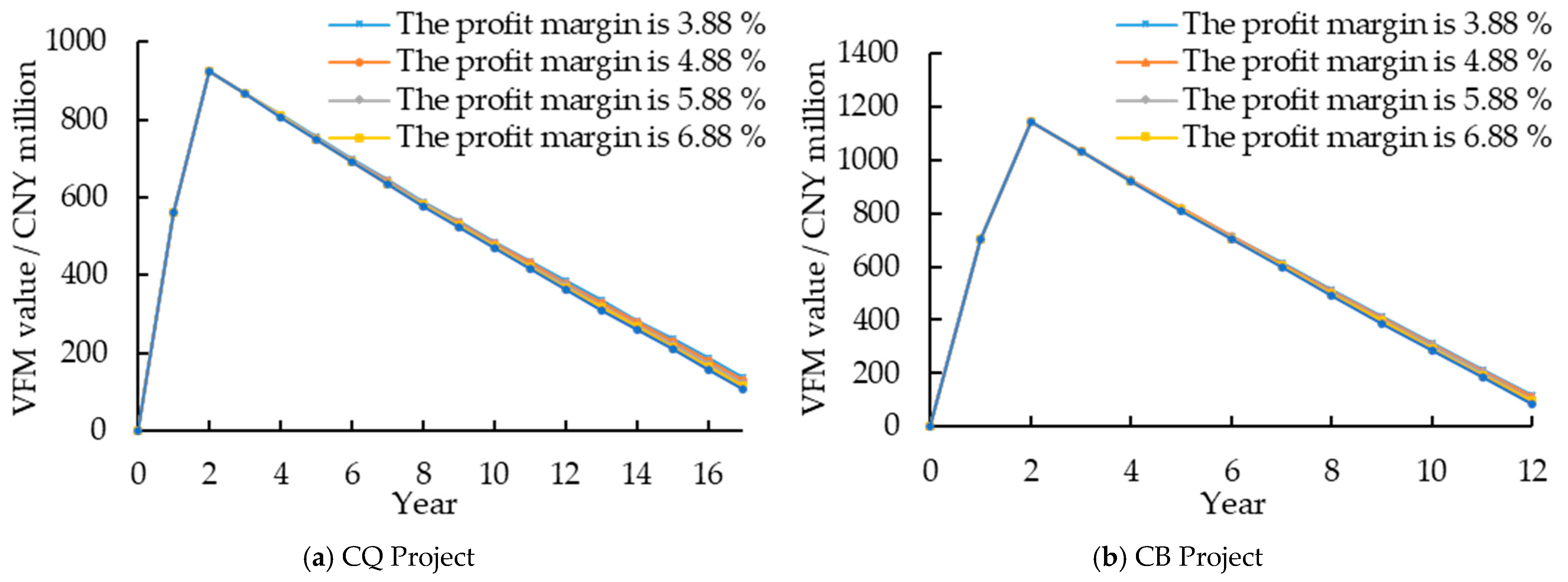
3.4.2. Reasonable Profit Margin of Investment
3.4.3. Availability Service Fee
4. Case Study
4.1. Case Overview
4.2. Data Collection
4.3. Case Simulation
- PSC value in the current year = PSC benchmark value + total risk expenditure + competitive neutral adjustment value;
- PSC benchmark value = (construction cost + annual operation and maintenance cost − third-party income)/POWER (discount rate + 1, Time + 1);
- Annual operation and maintenance cost = STEP ((PPP projects) × POWER (1 + inflation rate, Time construction period), construction period);
- Competitive neutral adjustment value = (competitive advantage competitive disadvantage)/POWER (1 + discount rate, Time + 1);
- Corporate income tax = IF THEN ELSE (operating subsidy payment + VAT refund − VAT − annual depreciation and amortization – annual operation and maintenance cost – surtax > 0, (operating subsidy payment + VAT refund – VAT – annual depreciation and amortization – annual operation and maintenance cost – surtax) × corporate income tax rate, 0);
- Total risk expenditure = (reserved risk + transferable risk)/POWER (1 + discount rate, Time + 1);
- PPP value in the current year = government retained risk present value + government other cost present value + government equity investment present value + operation subsidy present value;
- Present value of government equity investment = government equity investment/POWER (1 + discount rate, Time + 1);
- Availability service fee = STEP (total construction cost of the project × (1 + reasonable profit rate of investment) × POWER (1 + discount rate, Time – 1)/transportation and nutrition protection period, construction period). (The calculation of availability service fee refers to the calculation method in the Guidelines for Demonstration of Financial Affordability of Government and Social Capital Cooperation Projects ([2015] No. 21) issued by the Ministry of Finance.);
- Operation and maintenance performance service fee = annual operation and maintenance cost × (1 + reasonable profit margin of investment) × performance appraisal coefficient – third-party income;
- Present value of government retained risk = government retained risk cost/POWER (1 + discount rate, Time + 1);
- Present value of other government costs = government supporting investment/POWER (1 + discount rate, Time).
5. Results
5.1. General Findings
5.2. Sensitivity Effects
5.2.1. Sensitivity Effects of Discount Rate
5.2.2. Sensitivity Effects of Reasonable Profit Margin of Investment
5.2.3. Sensitivity Effects of Availability Service Fee
6. Discussions
7. Conclusions and Recommendations
7.1. Conclusions
7.2. Recommendations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chan, F.K.S.; Griffiths, J.A.; Higgitt, D.; Xu, S.; Zhu, F.; Tang, Y.-T.; Xu, Y.; Thorne, C.R. “Sponge City” in China—A breakthrough of planning and flood risk management in the urban context. Land Use Policy 2018, 76, 772–778. [Google Scholar] [CrossRef]
- Li, Q.; Wang, F.; Yu, Y.; Huang, Z.; Li, M.; Guan, Y. Comprehensive performance evaluation of LID practices for the sponge city construction: A case study in Guangxi, China. J. Environ. Manag. 2019, 231, 10–20. [Google Scholar] [CrossRef] [PubMed]
- Yu, K.; Li, D.; Yuan, H.; Fu, W.; Qiao, Q.; Wang, S. “Sponge City”: Theory and Practice. City Plan. Rev. 2015, 39, 26–36. [Google Scholar] [CrossRef]
- Zhao, H.; Ma, S.; Bu, Z.; Zhang, Y. Constructing a Risk-Sharing Framework for Sponge City PPP Projects from the Perspective of the Individual Participant. Adv. Civ. Eng. 2020, 2020, 8832664. [Google Scholar] [CrossRef]
- Li, W.; Guo, J.; Yuan, J.; Liu, H.J.; Edwards, D.J. Exploring the Key Indicators of Social Impact Assessment for Sponge City PPPs: A Sustainable Development Perspective. Buildings 2022, 12, 1329. [Google Scholar] [CrossRef]
- Yuan, J.; Zhang, L.; Tan, Y.; Skibniewski, M.J. Evaluating the regional social sustainability contribution of public-private partnerships in China: The development of an indicator system. Sustain. Dev. 2019, 28, 259–278. [Google Scholar] [CrossRef]
- Liu, B.; Li, J.; Wang, D.; Liu, H.; Wu, G.; Yuan, J. Public–private partnerships: A collaborative framework for ensuring project sustainable operations. Eng. Constr. Archit. Manag. 2022, 31, 264–289. [Google Scholar] [CrossRef]
- Cao, X.; Yu, L. Thoughts and Suggestions on the Application of Public-Private Partnership in Sponge City Project Construction: A Case Study of Sponge City Project in Cuwen Scenic District, Taian, Shandong. Urban Dev. Stud. 2018, 25, 29–36. [Google Scholar]
- Liu, B.; Ji, J.; Chen, J.; Qi, M.; Li, S.; Tang, L.; Zhang, K. Quantitative VfM evaluation of urban rail transit PPP projects considering social benefit. Res. Transp. Bus. Manag. 2023, 49, 101015. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, H.J.; Love, P.E.D.; Greenwood, D.; Sing, M.C.P. Value for Money assessments for Public-Private Partnerships: Characteristics, research directions, and policy implications. Dev. Built Environ. 2023, 16, 100246. [Google Scholar] [CrossRef]
- Zhao, J. Addressing the elephant in the room: How do we understand value for money in transport Public Private Partnerships? Cities 2024, 154, 105401. [Google Scholar] [CrossRef]
- Chen, S.; Wang, M. Research on VFM Evaluation System of PPP Projects. Fisc. Sci. 2016, 8, 65–71. [Google Scholar] [CrossRef]
- Jia, H.; Zhang, S. Research on the Application of VFM Evaluation Method in PPP Model: From the Perspective of Literature Review. Constr. Econ. 2019, 40, 46–50. [Google Scholar] [CrossRef]
- Yu, S.; Dai, T.; Yu, Y.; Zhang, J. Investment decision model of wastewater treatment public–private partnership projects based on value for money. Water Environ. J. 2020, 35, 322–334. [Google Scholar] [CrossRef]
- Boardman, A.; Hellowell, M. A Comparative Analysis and Evaluation of Specialist PPP Units’ Methodologies for Conducting Value for Money Appraisals. J. Comp. Policy Anal. Res. Pract. 2016, 19, 191–206. [Google Scholar] [CrossRef]
- McKevitt, D.; Davis, P. Value for money: A broken piñata? Public Money Manag. 2016, 36, 257–264. [Google Scholar] [CrossRef]
- Christina, P.; Gary, S. Value for money: A utilization-focused approach to extending the foundation and contribution of economic evaluation. Eval. Program Plan. 2020, 80, 101799. [Google Scholar] [CrossRef]
- Grimsey, D.; Lewis, M.K. Are Public Private Partnerships value for money? Account. Forum 2019, 29, 345–378. [Google Scholar] [CrossRef]
- Zhang, Z. The Process and Program of the VFM Evaluating and the Method of Dynamic Regulation for PPP Project. Manag. Rev. 2018, 30, 270–278. [Google Scholar] [CrossRef]
- Almarri, K.; Boussabaine, H. The Influence of Critical Success Factors on Value for Money Viability Analysis in Public–Private Partnership Projects. Proj. Manag. J. 2017, 48, 93–106. [Google Scholar] [CrossRef]
- Cui, C.; Wang, J.; Liu, Y.; Coffey, V. Relationships among Value-for-Money Drivers of Public–Private Partnership Infrastructure Projects. J. Infrastruct. Syst. 2019, 25, 04019007. [Google Scholar] [CrossRef]
- Cui, C.; Wang, J.; Liu, Y.; Li, H. Importance of VFM drivers in PPP projects using AHP-DEMATEL. J. Huaqiao Univ. (Nat. Sci.) 2018, 39, 682–688. [Google Scholar]
- Lin, X.; Wang, M. The Improvement and Application of PPP Performance Evaluation in China. J. Beijing Jiaotong Univ. (Soc. Sci. Ed.) 2019, 18, 19–29. [Google Scholar] [CrossRef]
- Malek, M.; Gundaliya, P. Value for money factors in Indian public-private partnership road projects: An exploratory approach. J. Proj. Manag. 2021, 6, 23–32. [Google Scholar] [CrossRef]
- Magalhães, L.; Figueiredo, L.B.; Jesus, L.T.D. Project management in public-private partnerships: A conceptual framework based on a systematic literature review. Gestão Produção 2020, 27, e3772. [Google Scholar] [CrossRef]
- Opara, M. Value for Money and Risk Relationships in Public-Private Partnerships: Evaluating Program-based Evidence. Aust. Account. Rev. 2018, 28, 391–404. [Google Scholar] [CrossRef]
- Jílek, P.; Černá Silovská, H.; Kolařík, P.; Lukavec, M. Selection of Quantitative and Qualitative Methods for Comprehensive Evaluation of PPP Projects Focusing on the Czech Republic. Transylv. Rev. Adm. Sci. 2018, 14, 38–54. [Google Scholar] [CrossRef]
- Wibowo, A.; Sundermeier, M. Developing a Fuzzy Value-for-Money Analysis Model for Annuity-Based Public-Private Partnership Infrastructure Projects under Consideration of Risk Mitigation Capability. J. Constr. Eng. Manag. 2020, 146, 04020081. [Google Scholar] [CrossRef]
- Soomro, M.A.; Zhang, X. Roles of Private-Sector Partners in Transportation Public-Private Partnership Failures. J. Manag. Eng. 2015, 31, 04014056. [Google Scholar] [CrossRef]
- Moro Visconti, R. Multidimensional principal–agent value for money in healthcare project financing. Public Money Manag. 2014, 34, 259–264. [Google Scholar] [CrossRef]
- Moro Visconti, R.; Monda, B.; Giorgino, M. Improving Value for Money in Italian Project Finance. Manag. Financ. 2014, 40, 1058–1077. [Google Scholar] [CrossRef]
- Zhao, Z.; Yuan, S.; Dai, T.; Bao, G. Application of System Dynamics Model for VFM Evaluation of PPP Project. J. Huaqiao Univ. (Nat. Sci.) 2020, 41, 765–771. [Google Scholar]
- Bi, W.; Du, J.; Li, Q. Research on VFM Evaluation of PPP Model: Taking A Cultural and Creative Industrial Park as an Example. J. Eng. Manag. 2019, 33, 51–56. [Google Scholar] [CrossRef]
- Sang, P.; Zhang, P. An Evaluation of PPP Model in Sponge City Project Based on VFM. J. Eng. Manag. 2017, 31, 61–65. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, T.; Zheng, B.; Tang, G. Study on System Dynamics Model of VFM Quantitative Evaluation of Sponge City PPP Project —Taking S Sponge City Project in Tianjin as an Example. J. Tianjin Univ. (Soc. Sci.) 2022, 24, 212–222. [Google Scholar]
- Li, J.; Zhao, J. Quantitative Evaluation of Value for Money of PPP Project in Sponge City. Financ. Account. Mon. 2019, 7, 101–108. [Google Scholar]
- Liu, H.J.; Love, P.E.D.; Smith, J.; Sing, M.C.P.; Matthews, J. Evaluation of public–private partnerships: A life-cycle Performance Prism for ensuring value for money. Environ. Plan. C Politics Space 2018, 36, 1133–1153. [Google Scholar] [CrossRef]
- Luo, L.; Zou, Z.; Chen, S. Discounting for public-private partnership projects in China. Econ. Model. 2021, 98, 218–226. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, H.J.; Love, P.E.D.; Greenwood, D.J.; Sing, M.C.P. Public-private partnerships: A dynamic discrete choice model for road projects. Socio-Econ. Plan. Sci. 2022, 82, 101227. [Google Scholar] [CrossRef]
- Wang, S.; Yu, L.; Qiu, R. Evolutionary Game Analysis of Participations in Museum Public–Private Partnership Projects Based on System Dynamics. Systems 2022, 11, 7. [Google Scholar] [CrossRef]
- Lai, R.; Liu, S.; Wang, Y. Sustainable Operations: Risk Evolution and Diversification Strategies Throughout the Lifecycle of Wind Energy Public–Private Partnership Projects. Systems 2025, 13, 237. [Google Scholar] [CrossRef]
- Park, H.; Lee, S.; Kim, J. Do public private partnership projects deliver value for money? An ex post Value for Money (VfM) Test on three road projects in Korea. Int. J. Urban Sci. 2018, 22, 579–591. [Google Scholar] [CrossRef]
- Ren, G.; Li, H.; Zhang, J. A BIM-Based Value for Money Assessment in Public-Private Partnership: An Overall Review. Appl. Sci. 2020, 10, 6483. [Google Scholar] [CrossRef]
- Liu, H.; Sun, J.; Li, F. Evaluation of PPP Model in Utility Tunnel Project Based on VFM. J. Civ. Eng. Manag. 2016, 33, 122–126. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, A.; Bao, X. A Study on the Qualitative VFM-Evaluation of Rail Transit PPP Projects Based on Matter Element Analysis. J. Eng. Manag. 2018, 32, 69–74. [Google Scholar] [CrossRef]
- Liu, F.; Liu, J.; Yan, X. Quantifying the Decision-Making of PPPs in China by the Entropy-Weighted Pareto Front: A URT Case from Guizhou. Sustainability 2018, 10, 1753. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H. Research on Method Improvement of Value for Money Evaluation of PPP Mode. Eng. Econ. 2020, 30, 9–13. [Google Scholar] [CrossRef]
- Kweun, J.Y.; Wheeler, P.K.; Gifford, J.L. Evaluating highway public-private partnerships: Evidence from U.S. value for money studies. Transp. Policy 2018, 62, 12–20. [Google Scholar] [CrossRef]
- Cui, C.; Liu, Y.; Hope, A.; Wang, J. Review of studies on the public–private partnerships (PPP) for infrastructure projects. Int. J. Proj. Manag. 2018, 36, 773–794. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, F.; Li, Q.; Deng, X. Research and Application of VFM Evaluation Method for the PPP Projects in Infrastructure. Mod. Manag. Sci. 2012, 1, 27–30. [Google Scholar]
- Carpintero, S.; Siemiatycki, M. PPP projects in local infrastructure: Evidence from schools in the Madrid region, Spain. Public Money Manag. 2015, 35, 439–446. [Google Scholar] [CrossRef]
- Liang, L.; Han, F.; Zhou, F.; Jing, Z. Comparison at Home and Abroad on Value for Money Assessment of PPP Projects. J. Civ. Eng. Manag. 2018, 35, 182–188. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, K.; Chen, J.; Wang, Z.; Li, G.; Yang, Y. System dynamics model of taxi management in metropolises: Economic and environmental implications for Beijing. J. Environ. Manag. 2018, 213, 555–565. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Nie, Q.; Chen, B.; Chai, J.; Zhao, Z. Multi-scale evaluation and multi-scenario simulation analysis of regional energy carrying capacity-Case study: China. Sci. Total Environ. 2020, 734, 139440. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Dong, J.; Yan, C.; Dong, H.; Liu, P. What Causes Waterlogging?—Explore the Urban Waterlogging Control Scheme through System Dynamics Simulation. Sustainability 2021, 13, 8546. [Google Scholar] [CrossRef]
- Pluchinotta, I.; Pagano, A.; Vilcan, T.; Ahilan, S.; Kapetas, L.; Maskrey, S.; Krivtsov, V.; Thorne, C.; O’Donnell, E. A participatory system dynamics model to investigate sustainable urban water management in Ebbsfleet Garden City. Sustain. Cities Soc. 2021, 67, 102709. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, Z.; Xin, H.; Chai, J.; Wang, G. Charge pricing model for electric vehicle charging infrastructure public-private partnership projects in China: A system dynamics analysis. J. Clean. Prod. 2018, 199, 321–333. [Google Scholar] [CrossRef]
- Wang, S.; Hao, S. A Risk Dynamic Evaluation of PPP Projects in Sponge City Based on System Dynamics. J. Eng. Manag. 2019, 33, 63–68. [Google Scholar] [CrossRef]
- Zwalf, S.; Hodge, G.; Alam, Q. Choose Your Own Adventure: Finding a Suitable Discount Rate for Evaluating Value for Money in Public-Private Partnership Proposals*. Aust. J. Public Adm. 2017, 76, 301–315. [Google Scholar] [CrossRef]
- Cruz, C.O.; Marques, R.C. Theoretical Considerations on Quantitative PPP Viability Analysis. J. Manag. Eng. 2014, 30, 122–126. [Google Scholar] [CrossRef]
- Visconti, R.M. Evaluating a Project Finance SPV: Combining Operating Leverage with Debt Service, Shadow Dividends and Discounted Cash Flows. Int. J. Econ. Financ. Manag. Sci. 2013, 1, 9–20. [Google Scholar] [CrossRef]
- Qiu, P.; Sorourkhah, A.; Kausar, N.; Cagin, T.; Edalatpanah, S.A. Simplifying the Complexity in the Problem of Choosing the Best Private-Sector Partner. Systems 2023, 11, 80. [Google Scholar] [CrossRef]
- Lu, X. Calculation of Operating Subsidy Expenditure under the Government Payment Model. Financ. Account. Mon. 2018, 22, 102–110. [Google Scholar]
- Siemiatycki, M.; Farooqi, N. Value for Money and Risk in Public–Private Partnerships. J. Am. Plan. Assoc. 2012, 78, 286–299. [Google Scholar] [CrossRef]
- Zhao, J.Z.; Su, G.; Li, D. Financing China’s unprecedented infrastructure boom: The evolution of capital structure from 1978 to 2015. Public Money Manag. 2019, 39, 581–589. [Google Scholar] [CrossRef]
- Liang, Q.; Hu, H. Challenges and Countermeasures for the Application of Value for Money Appraisal in Infrastructure PPP Projects. Contemp. Econ. Manag. 2018, 40, 54–59. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, X.; Xue, H. Identifying critical risks in Sponge City PPP projects using DEMATEL method: A case study of China. J. Clean. Prod. 2019, 226, 949–958. [Google Scholar] [CrossRef]
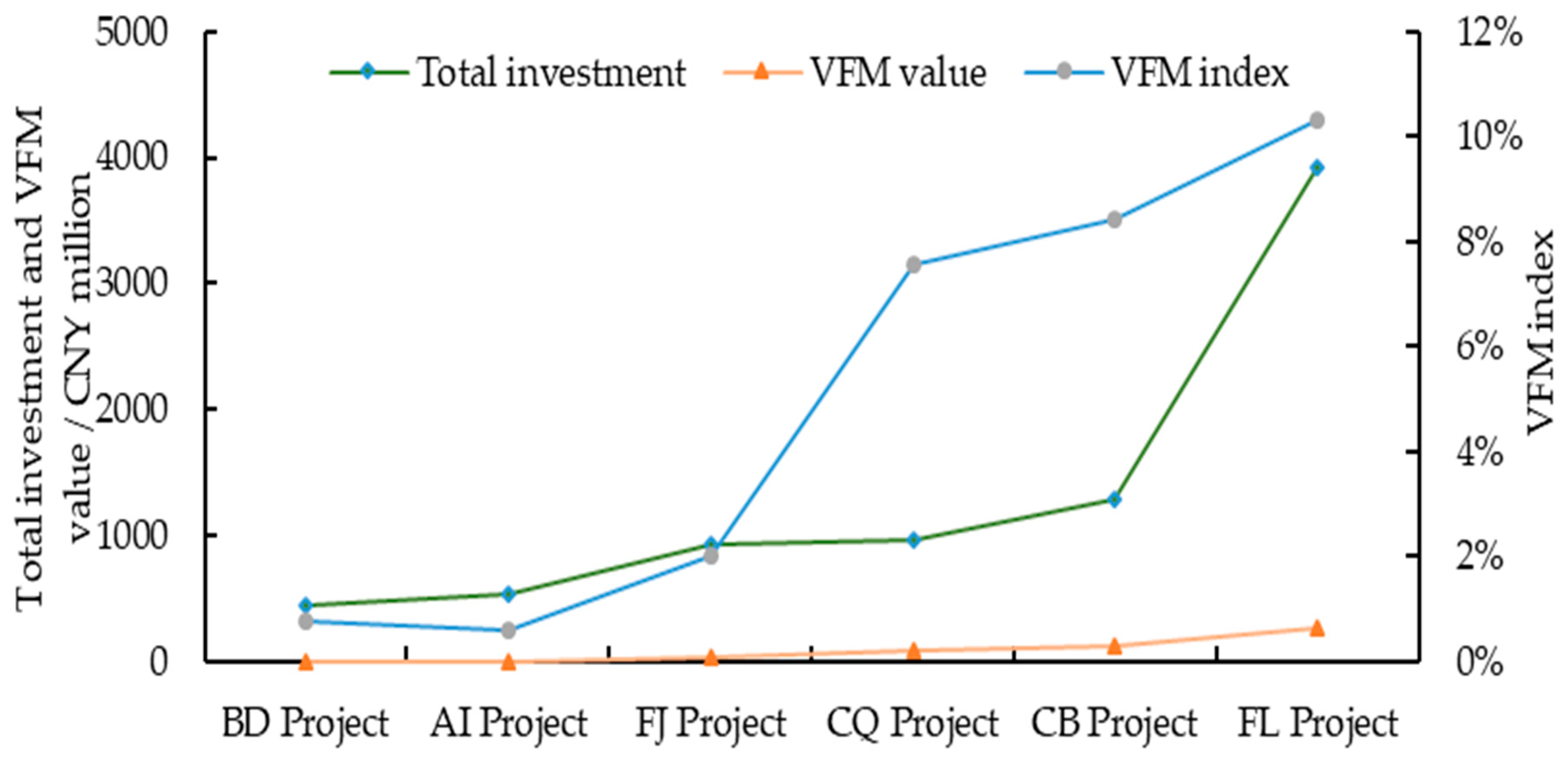
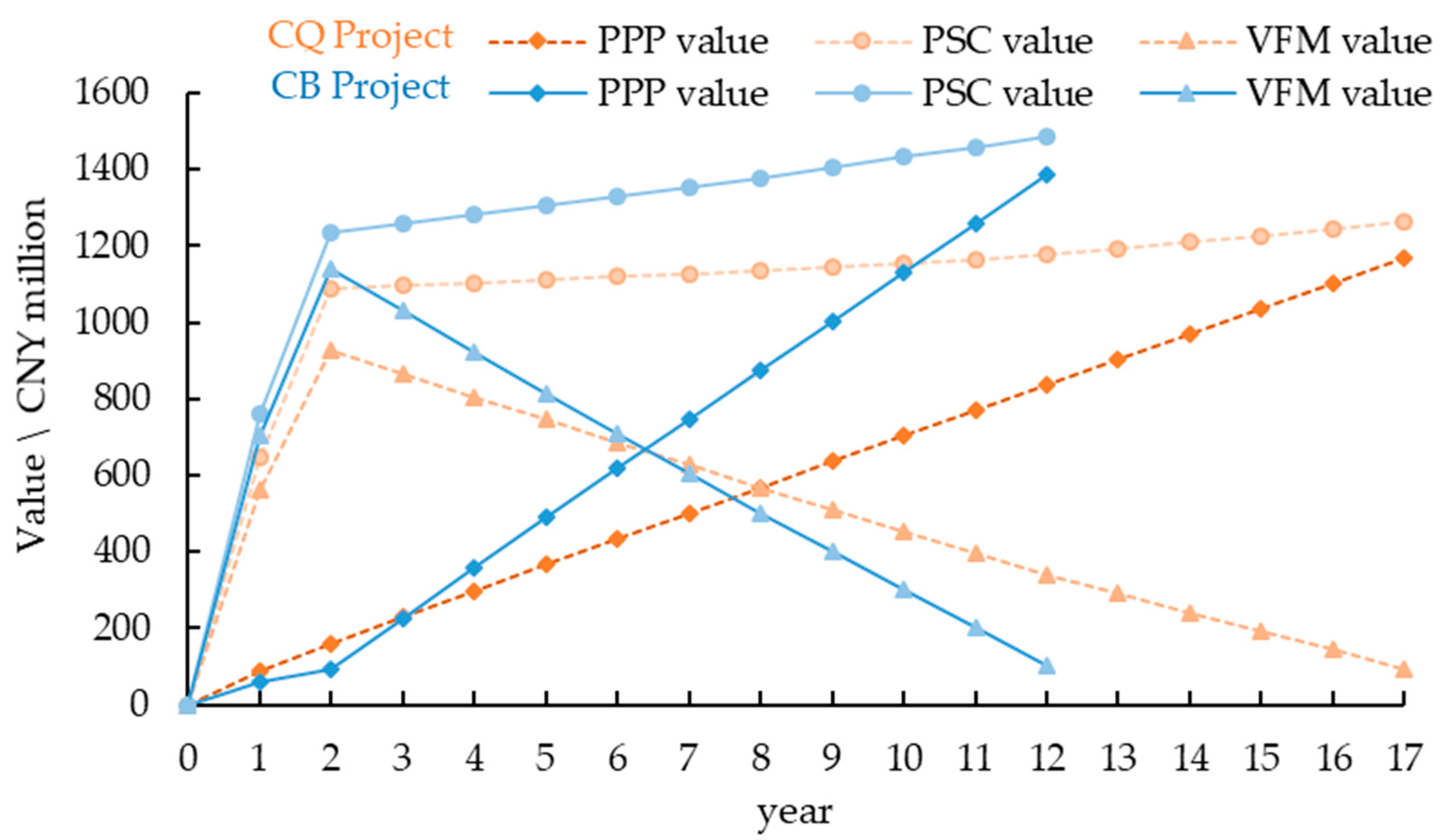
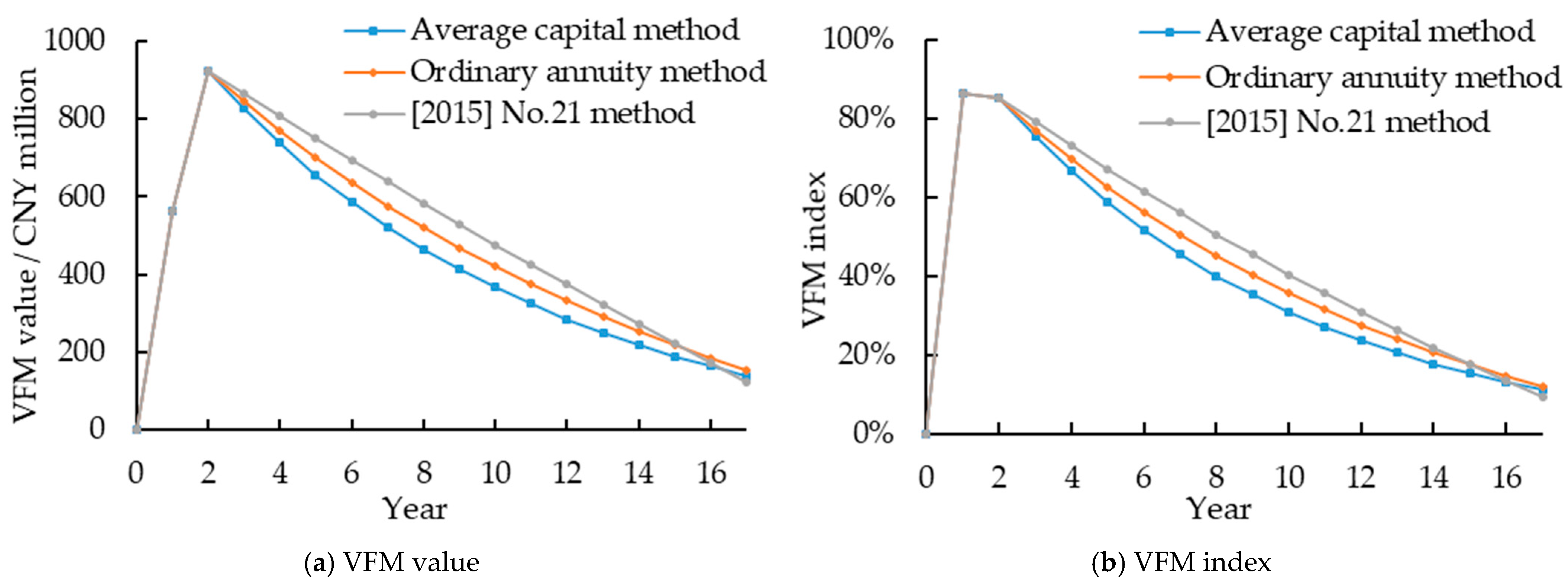
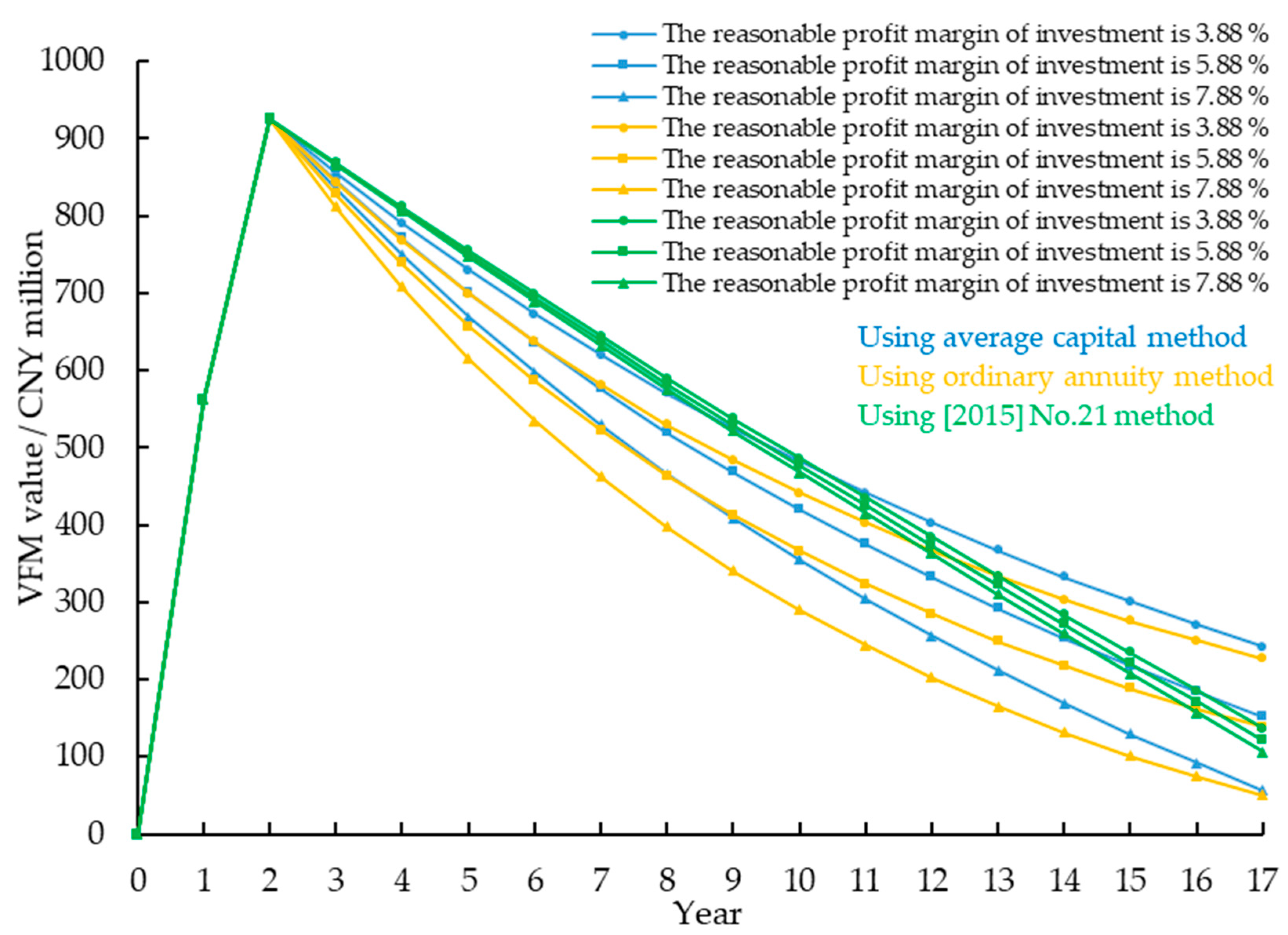
| Project | Total Investment (CNY Million) | Years of Cooperation (Construction) | Operation Mode | Discount Rate | Risk Quantification Method | Reasonable Profit Rate | PSC Value (CNY Million) | PPP Value (CNY Million) | VFM Value (CNY Million) | VFM Index |
|---|---|---|---|---|---|---|---|---|---|---|
| CQ | 959.76 | 17 (2) | BOT | 6.08% | Probability method | 5.88% | 1262.4558 | 1167.1159 | 95.3389 | 7.55% |
| FJ | 928 | 12 (2) | BOT | 4.90% | Scenario analysis | 7% | 1245.9753 | 1220.7641 | 25.2112 | 2.02% |
| CB | 1 280 | 12 (2) | BOT | 6.91% | Probability method | - | 1502.6148 | 1376.0797 | 126.5352 | 8.42% |
| AI | 530 | 12 (2) | BOT TOT | 4.90% | Scenario analysis | 8% | 637.6038 | 633.8124 | 3.7914 | 0.59% |
| BD | 454.73 | 15 (3) | BOT | 5.88% | Scenario analysis | 8% | 537.0029 | 532.8659 | 4.137 | 0.77% |
| FL | 3930.72 | 18 (3) | BOT TOT | 6.37% | Scenario analysis | 8% | 2530.14 | 2269.11 | 261.03 | 10.32% |
| Index | CQ Project | CB Project |
|---|---|---|
| First year construction cost/CNY million | 575.856 | 770.7047 |
| Second year construction cost/CNY million | 383.904 | 513.8031 |
| First year government equity investment/CNY million | 23.034 | 30.8282 |
| Second year government equity investment/CNY million | 15.356 | 20.5521 |
| Inflation rate/% | 3% | - |
| Total sub-operation and maintenance costs/CNY million | 921.54 | - |
| Corporate income tax rate/% | 25% | 25% |
| Value-added tax rate/% | 6% | 6% |
| Additional tax rate/% | 12% | 12% |
| Performance appraisal coefficient/% | - | 118.53 |
| Proportion of capital to total investment/% | 20% | 20% |
| Proportion of government equity investment/% | 20% | 20% |
| Discount rate | 6.08% | 6.91% |
| Reasonable profit margin of investment | 5.88% | 5.88% |
| Model | Calculation Procedure |
|---|---|
| [2015] No. 21 method | STEP (all costs of project construction × (1 + reasonable profit margin of investment) × POWER (1 + discount rate, Time − 1)/operation and maintenance period, construction period) |
| Ordinary annuity method | STEP (all costs of project construction × reasonable profit margin of investment × POWER (1 + reasonable profit margin of investment, operation and maintenance period)/(POWER (1 + reasonable profit margin of investment, operation and maintenance period) − 1), construction period) |
| Average capital method | STEP (all costs of project construction/operation and maintenance period + (all costs of project construction − (cost of full construction of the project/operation and maintenance period) × (Time − 2)) × reasonable profit margin of investment, construction period) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Chang, J.; Lin, T. Quantitative Evaluation of Value for Money in Sponge City Construction Public–Private Partnership Projects Through a System Dynamics Model. Systems 2025, 13, 471. https://doi.org/10.3390/systems13060471
Zhang H, Chang J, Lin T. Quantitative Evaluation of Value for Money in Sponge City Construction Public–Private Partnership Projects Through a System Dynamics Model. Systems. 2025; 13(6):471. https://doi.org/10.3390/systems13060471
Chicago/Turabian StyleZhang, Heng, Jiang Chang, and Tianci Lin. 2025. "Quantitative Evaluation of Value for Money in Sponge City Construction Public–Private Partnership Projects Through a System Dynamics Model" Systems 13, no. 6: 471. https://doi.org/10.3390/systems13060471
APA StyleZhang, H., Chang, J., & Lin, T. (2025). Quantitative Evaluation of Value for Money in Sponge City Construction Public–Private Partnership Projects Through a System Dynamics Model. Systems, 13(6), 471. https://doi.org/10.3390/systems13060471






