Multi-Skilled Project Scheduling for High-End Equipment Development Considering Newcomer Cultivation and Duration Uncertainty
Abstract
1. Introduction
2. Literature Review
2.1. Multi-Skilled Resource-Constrained Project Scheduling Considering the Skill Development
2.2. Project Scheduling Under Uncertain Duration
2.3. Literature Gaps
3. Problem Statement
3.1. Problem Description
3.2. Problem Formulation
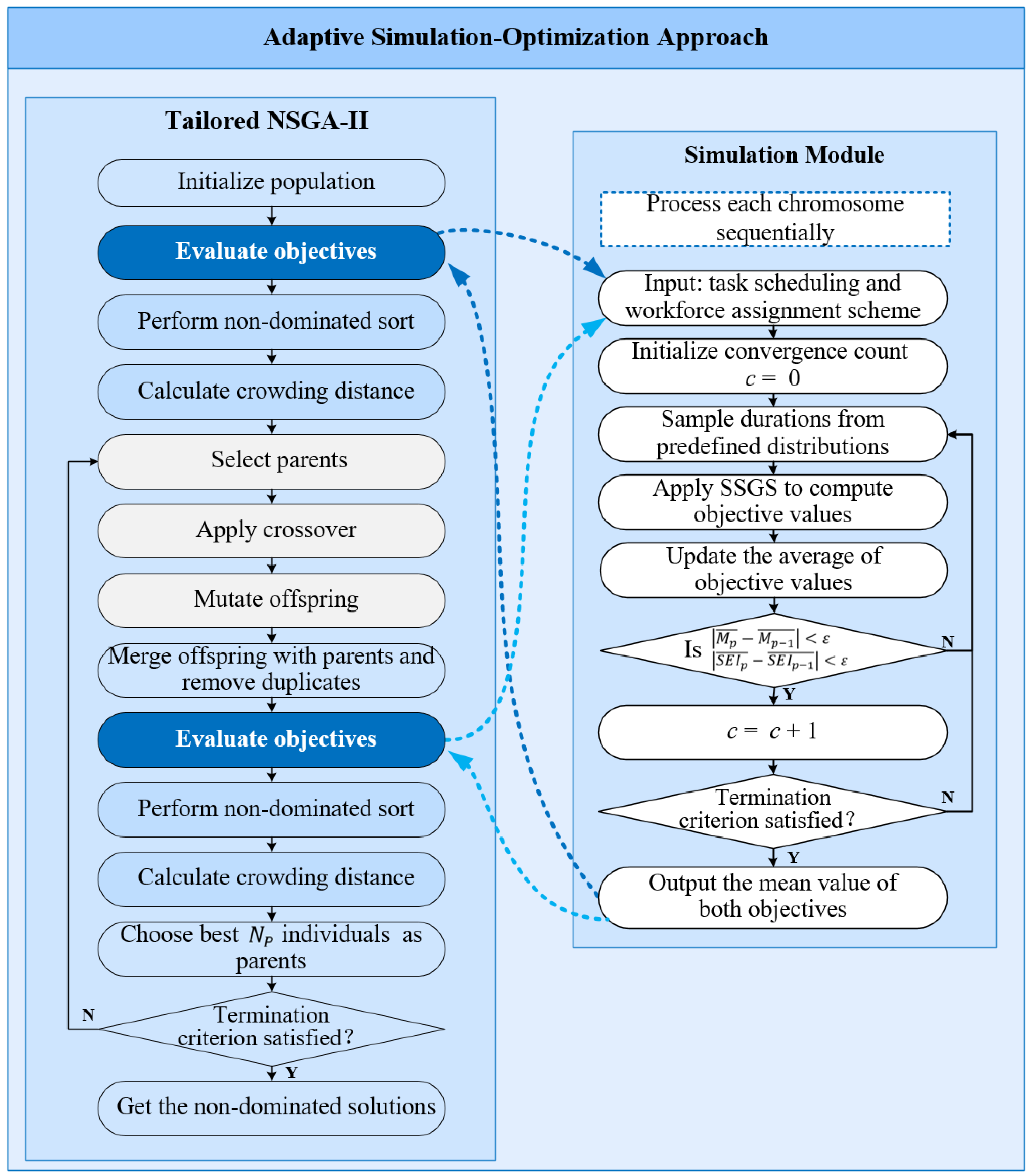
4. Proposed Approach
4.1. Tailored Non-Dominated Sorting Genetic Algorithm II
| Algorithm 1: Tailored NSGA-II |
| Data: |
| Result: |
| 1 Generate initial population ; |
| 2 using Algorithm 2; |
| 3 ; |
| 4 based on crowding distance; |
| 5 ; |
| 6 for |
| 7 via binary tournament selection; |
| 8 based on front size and crowding distance; |
| 9 ; |
| 10 ; |
| 11 ; |
| 12 ; |
| 13 using Algorithm 2; |
| 14 ; |
| 15 based on crowding distance; |
| 16 ; |
| 17 end |
| 18 . |
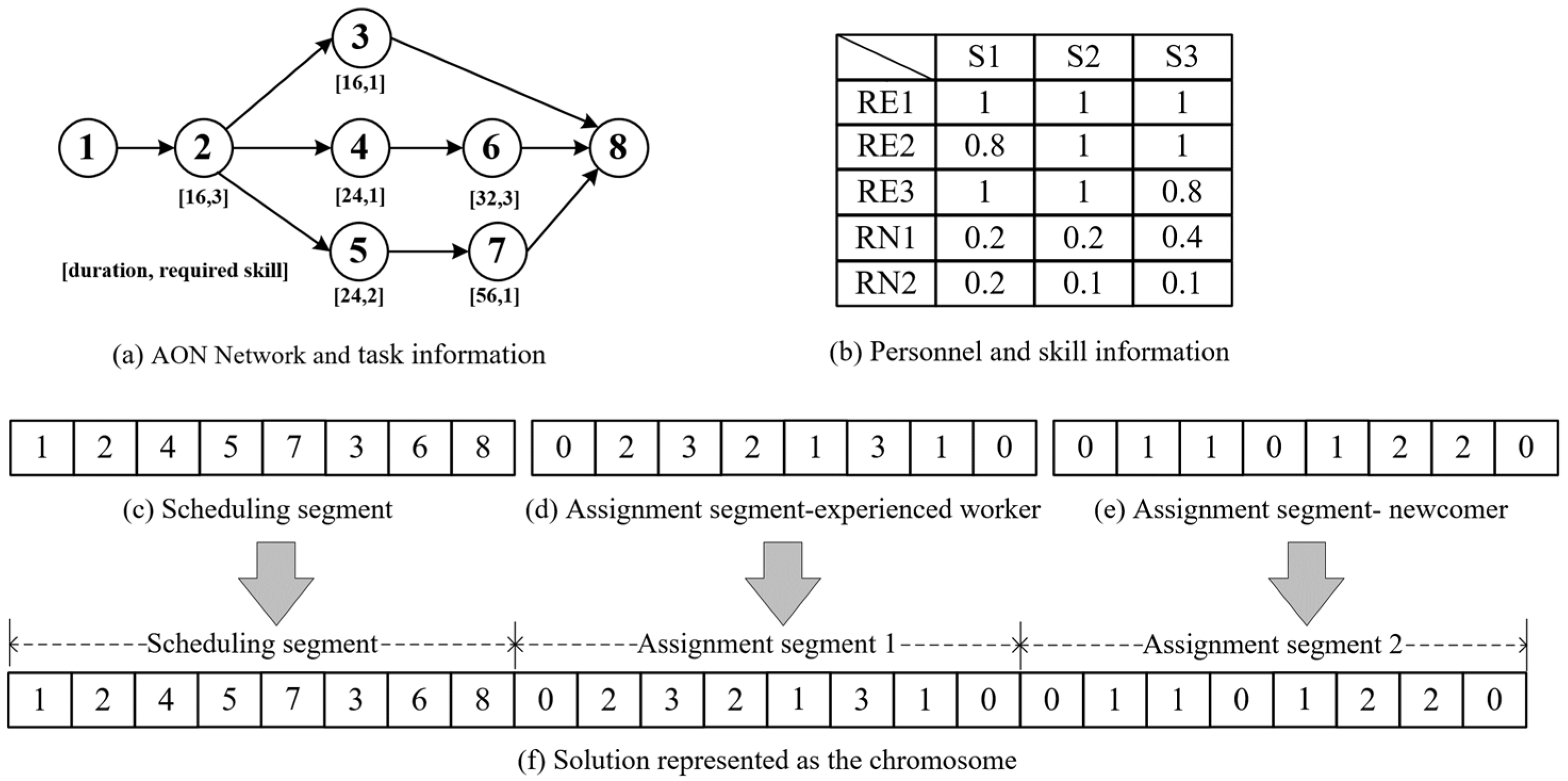
4.1.1. Solution Coding
4.1.2. Initial Population and Evaluation
4.1.3. Genetic Operator
4.1.4. Adaptive Mechanism
4.2. Simulation Module
| Algorithm 2: Simulation Module |
| Data: |
| Result: |
| 1 ; |
| 2 while true do |
| 3 ; |
| 4 for do |
| 5 |
| 6 end |
| 7 ; |
| 8 |
| 9 Schedule via SSGS while enforcing precedence and resource constraints; |
| 10 when task is scheduled; |
| 11 ; |
| 12 if then |
| 13 |
| 14 end |
| 15 if then |
| 16 break; |
| 17 end |
| 18 end |
| 19 |
5. Case Study
5.1. Case Description
5.2. Environment and Parameter
5.3. Results and Discussion
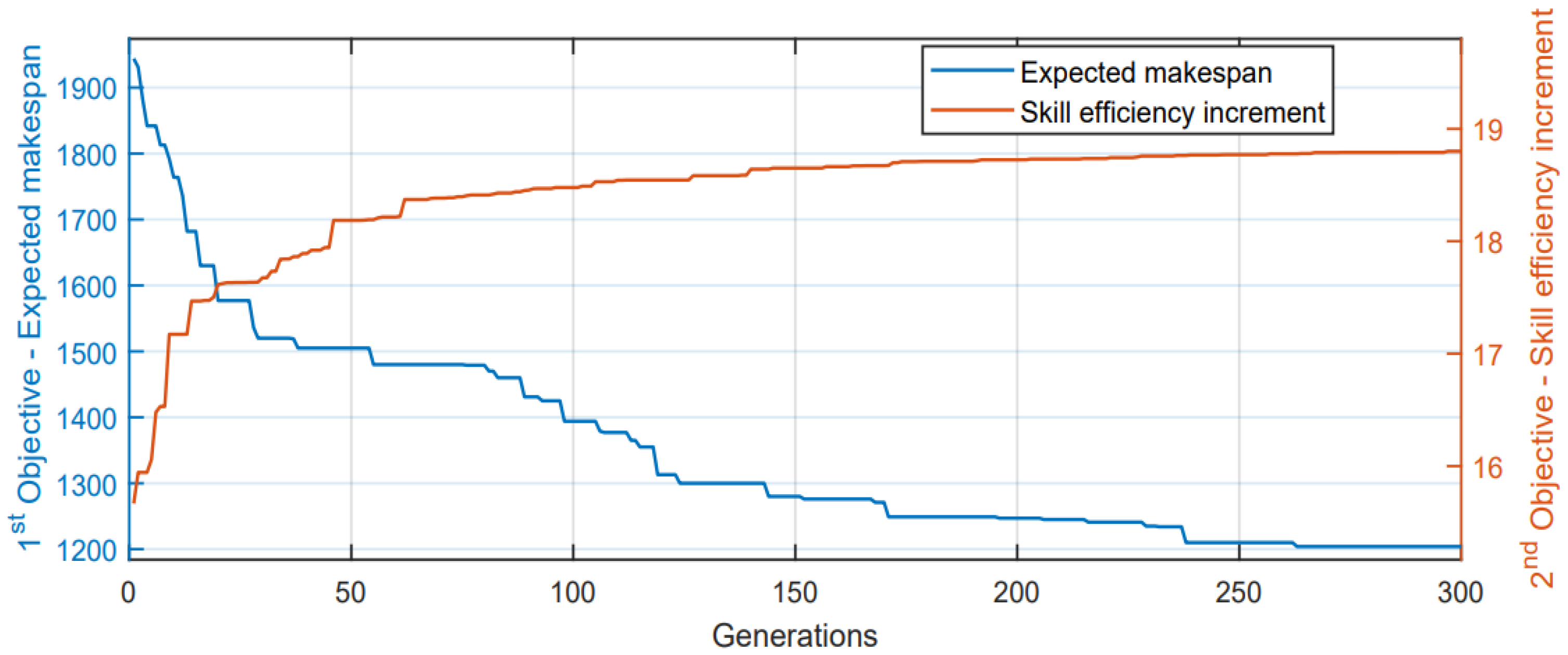
5.3.1. Pareto Solution and Front
5.3.2. Analysis and Validation
- (1)
- Effectiveness of the adaptive simulation–optimization approach
- (2)
- Stability of the adaptive simulation–optimization approach
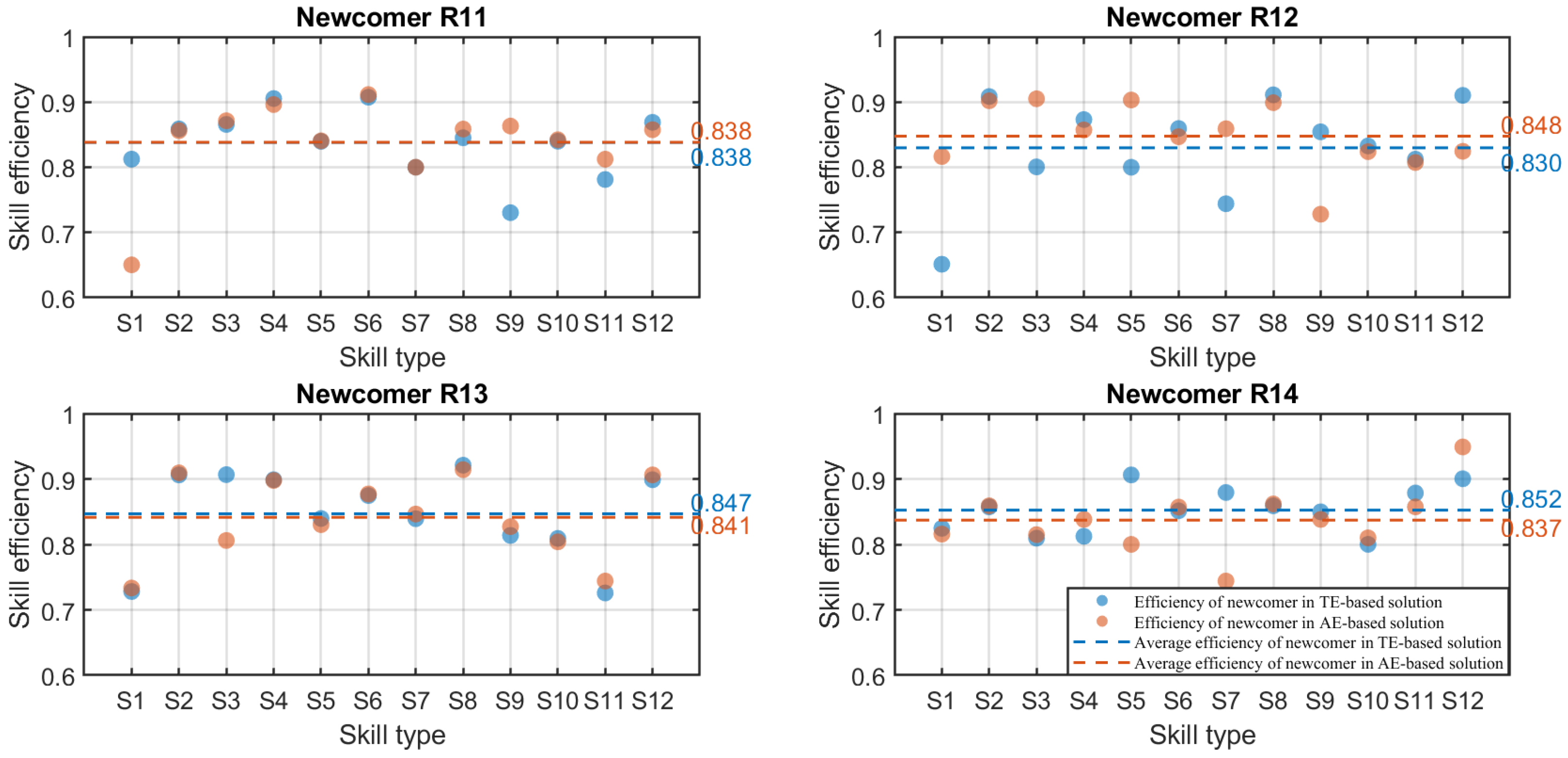
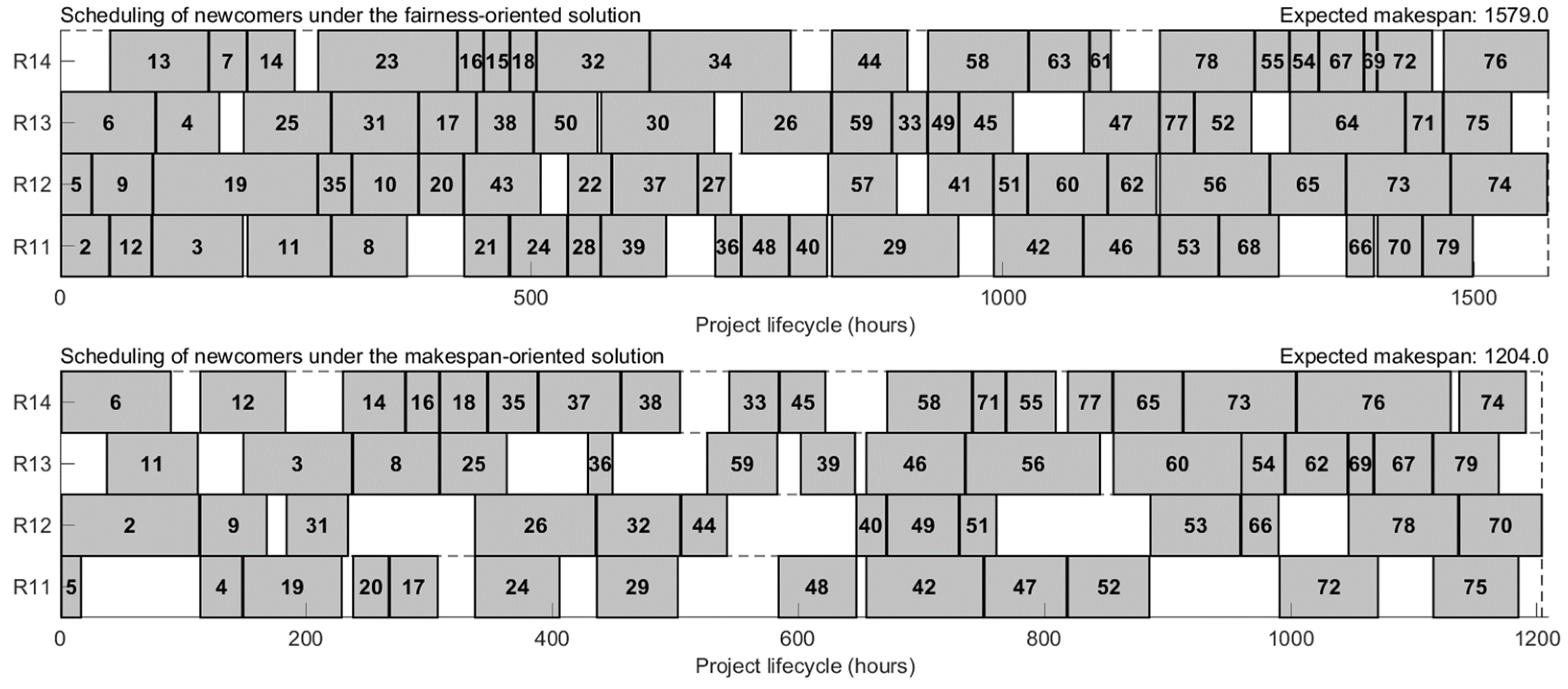
5.3.3. Personalized Solution Selection
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, N.; Zhang, R.; Liu, B. Impact of Government Subsidy on Diagnostic Tests Decisions of Core Products in High-End Equipment Manufacturing. Comput. Ind. Eng. 2023, 177, 109042. [Google Scholar] [CrossRef]
- Cui, L.; Liu, X.; Lu, S.; Jia, Z. A Variable Neighborhood Search Approach for the Resource-Constrained Multi-Project Collaborative Scheduling Problem. Appl. Soft Comput. 2021, 107, 107480. [Google Scholar] [CrossRef]
- Chen, R.; Liang, C.; Gu, D.; Zhao, H. A Competence-Time-Quality Scheduling Model of Multi-Skilled Staff for IT Project Portfolio. Comput. Ind. Eng. 2020, 139, 106183. [Google Scholar] [CrossRef]
- Chen, Y.C. Enhancing Teaching Competence through Bidirectional Mentoring and Structured On-the-Job Training Model. Mentor. Tutoring Partnersh. Learn. 2018, 26, 267–288. [Google Scholar] [CrossRef]
- Van Peteghem, V.; Vanhoucke, M. Influence of Learning in Resource-Constrained Project Scheduling. Comput. Ind. Eng. 2015, 87, 569–579. [Google Scholar] [CrossRef]
- Bianco, L.; Caramia, M. An Exact Algorithm to Minimize the Makespan in Project Scheduling with Scarce Resources and Generalized Precedence Relations. Eur. J. Oper. Res. 2012, 219, 73–85. [Google Scholar] [CrossRef]
- Néron, E. Lower Bounds for a Multi-Skill Project Scheduling Problem. In Proceeding of the Eighth International Workshop on Project Management and Scheduling, Valencia, Spain, 3–5 April 2002; pp. 274–277. [Google Scholar]
- Bellenguez, O.; Néron, E. Lower Bounds for the Multi-Skill Project Scheduling Problem with Hierarchical Levels of Skills. In Proceedings of the International Conference on the Practice and Theory of Automated Timetabling, Pittsburgh, PA, USA, 18–20 August 2004; Burke, E., Trick, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 229–243. [Google Scholar]
- Bahroun, Z.; As’Ad, R.; Tanash, M.; Athamneh, R. The Multi-Skilled Resource-Constrained Project Scheduling Problem: A Systematic Review and an Exploration of Future Landscapes. Manag. Syst. Prod. Eng. 2024, 32, 108–132. [Google Scholar] [CrossRef]
- Mozhdehi, S.; Baradaran, V.; Hosseinian, A.H. Multi-Skilled Resource-Constrained Multi-Project Scheduling Problem with Dexterity Improvement of Workforce. Autom. Constr. 2024, 162, 105360. [Google Scholar] [CrossRef]
- Yu, Y.; Xu, Z.; Liu, D.; Zhao, S. A Two-Stage Approach with Softmax Scoring Mechanism for a Multi-Project Scheduling Problem Sharing Multi-Skilled Staff. Expert Syst. Appl. 2022, 203, 117385. [Google Scholar] [CrossRef]
- Gutjahr, W.J.; Katzensteiner, S.; Reiter, P.; Stummer, C.; Denk, M. Competence-Driven Project Portfolio Selection, Scheduling and Staff Assignment. Cent. Eur. J. Oper. Res. 2008, 16, 281–306. [Google Scholar] [CrossRef]
- Wright, T.P. Factors Affecting the Cost of Engineering. J. Aeronaut. Sci. 1936, 3, 122–128. [Google Scholar] [CrossRef]
- Wu, M.C.; Sun, S.H. A Project Scheduling and Staff Assignment Model Considering Learning Effect. Int. J. Adv. Manuf. Technol. 2006, 28, 1190–1195. [Google Scholar] [CrossRef]
- Guo, Y.; Ji, J.; Ji, J.; Gong, D.; Cheng, J.; Shen, X. Firework-Based Software Project Scheduling Method Considering the Learning and Forgetting Effect. Soft Comput. 2019, 23, 5019–5034. [Google Scholar] [CrossRef]
- Hosseinian, A.H.; Baradaran, V. Modified Pareto Archived Evolution Strategy for the Multi-Skill Project Scheduling Problem with Generalized Precedence Relations. JIEMS J. Ind. Eng. Manag. Stud. 2020, 7, 59–86. [Google Scholar]
- Ammar, M.A.; Abdel-Maged, A.F. Modeling of LOB Scheduling with Learning Development Effect. Int. J. Constr. Manag. 2018, 18, 517–526. [Google Scholar] [CrossRef]
- Gutjahr, W.J.; Katzensteiner, S.; Reiter, P.; Stummer, C.; Denk, M. Multi-Objective Decision Analysis for Competence-Oriented Project Portfolio Selection. Eur. J. Oper. Res. 2010, 205, 670–679. [Google Scholar] [CrossRef]
- Chen, R.; Liang, C.; Gu, D.; Leung, J.Y.T. A Multi-Objective Model for Multi-Project Scheduling and Multi-Skilled Staff Assignment for IT Product Development Considering Competency Evolution. Int. J. Prod. Res. 2017, 55, 6207–6234. [Google Scholar] [CrossRef]
- Aghileh, M.; Tereso, A.; Alvelos, F.; Monteiro Lopes, M.O. Multi-Project Scheduling under Uncertainty and Resource Flexibility: A Systematic Literature Review. Prod. Manuf. Res. 2024, 12, 2319574. [Google Scholar] [CrossRef]
- Herroelen, W.; Leus, R. Project Scheduling under Uncertainty: Survey and Research Potentials. Eur. J. Oper. Res. 2005, 165, 289–306. [Google Scholar] [CrossRef]
- Hazır, Ö.; Ulusoy, G. A Classification and Review of Approaches and Methods for Modeling Uncertainty in Projects. Int. J. Prod. Econ. 2020, 223, 107522. [Google Scholar] [CrossRef]
- Slany, W. Fuzzy Scheduling; Christian Doppler Laboratory for Expert Systems: Wien, Austria, 1994. [Google Scholar]
- Van de Vonder, S.; Demeulemeester, E.; Herroelen, W. Proactive Heuristic Procedures for Robust Project Scheduling: An Experimental Analysis. Eur. J. Oper. Res. 2008, 189, 723–733. [Google Scholar] [CrossRef]
- Deblaere, F.; Demeulemeester, E.; Herroelen, W. Reactive Scheduling in the Multi-Mode RCPSP. Comput. Oper. Res. 2011, 38, 63–74. [Google Scholar] [CrossRef]
- Peng, W.; Lin, X.; Li, H. Critical Chain Based Proactive-Reactive Scheduling for Resource-Constrained Project Scheduling under Uncertainty. Expert Syst. Appl. 2023, 214, 119188. [Google Scholar] [CrossRef]
- Sobel, M.J.; Szmerekovsky, J.G.; Tilson, V. Scheduling Projects with Stochastic Activity Duration to Maximize Expected Net Present Value. Eur. J. Oper. Res. 2009, 198, 697–705. [Google Scholar] [CrossRef]
- Creemers, S. Minimizing the Expected Makespan of a Project with Stochastic Activity Durations under Resource Constraints. J. Sched. 2015, 18, 263–273. [Google Scholar] [CrossRef]
- Zhou, Y.; Miao, J.; Yan, B.; Zhang, Z. Stochastic Resource-Constrained Project Scheduling Problem with Time Varying Weather Conditions and an Improved Estimation of Distribution Algorithm. Comput. Ind. Eng. 2021, 157, 107322. [Google Scholar] [CrossRef]
- Chen, H.J.; Ding, G.; Zhang, J.; Li, R.; Jiang, L.; Qin, S. A Filtering Genetic Programming Framework for Stochastic Resource Constrained Multi-Project Scheduling Problem under New Project Insertions. Expert Syst. Appl. 2022, 198, 116911. [Google Scholar] [CrossRef]
- De Reyck, B.; Herroelen, W. A Branch-and-Bound Procedure for the Resource-Constrained Project Scheduling Problem with Generalized Precedence Relations. Eur. J. Oper. Res. 1998, 111, 152–174. [Google Scholar] [CrossRef]
- Alba, E.; Francisco Chicano, J. Software Project Management with GAs. Inf. Sci. 2007, 177, 2380–2401. [Google Scholar] [CrossRef]
- Snauwaert, J.; Vanhoucke, M. A New Algorithm for Resource-Constrained Project Scheduling with Breadth and Depth of Skills. Eur. J. Oper. Res. 2021, 292, 43–59. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A Fast Elitist Non-Dominated Sorting Genetic Algorithm for Multi-Objective Optimization: NSGA-II. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Paris, France, 18–20 September 2000; Volume 1917, pp. 849–858. [Google Scholar]
- Liu, J.; Chen, X. An Improved NSGA-II Algorithm Based on Crowding Distance Elimination Strategy. Int. J. Comput. Intell. Syst. 2019, 12, 513–518. [Google Scholar] [CrossRef]
- Miller, B.L.; Goldberg, D.E. Genetic Algorithms, Tournament Selection, and the Effects of Noise. Complex Syst. 1995, 9, 193–212. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Alhijawi, B.; Awajan, A. Genetic Algorithms: Theory, Genetic Operators, Solutions, and Applications. Evol. Intell. 2024, 17, 1245–1256. [Google Scholar] [CrossRef]
- Kolisch, R. Serial and Parallel Resource-Constrained Project Scheduling Methods Revisited: Theory and Computation. Eur. J. Oper. Res. 1996, 90, 320–333. [Google Scholar] [CrossRef]
- Mashwani, W.; Salhi, A.; Jan, M.; Khanum, R.; Sulaiman, M. Impact Analysis of Crossovers in a Multi-Objective Evolutionary Algorithm. Sci. Int. 2015, 27, 4943–4956. [Google Scholar]
- Audet, C.; Bigeon, J.; Cartier, D.; Le Digabel, S.; Salomon, L. Performance Indicators in Multiobjective Optimization. Eur. J. Oper. Res. 2021, 292, 397–422. [Google Scholar] [CrossRef]





| References | Scheduling Content 1 | Resource Attribute 2 | Learning Effect | Uncertain Duration | Objective 3 | Method 4 | Dataset | ||
|---|---|---|---|---|---|---|---|---|---|
| TS | WA | MST | HSE | ||||||
| [14] | √ | √ | √ | OC | GA | Real case | |||
| [5] | √ | √ | √ | M | BGA | Using [31] | |||
| [17] | √ | √ | √ | M | LOB | Real case | |||
| [15] | √ | √ | √ | √ | √ | M, C | MOFA | Using the generator of [32] and PSPLIB | |
| [16] | √ | √ | √ | √ | √ | M, R, C | MV-PAES | PSPLIB | |
| [10] | √ | √ | √ | √ | √ | M | MBBOA | iMOPSE | |
| [12] | √ | √ | √ | √ | √ | WAEG, SEI | MIP-HT | Real case | |
| [18] | √ | √ | √ | √ | √ | EG, SEI | NSGA-II, P-ACO | Real case | |
| [19] | √ | √ | √ | √ | √ | DT, DC, SEI | NSGA-II | Real case | |
| [28] | √ | √ | EM | BSDPR | PSPLIB | ||||
| [29] | √ | √ | EM, ENPV | EDA | PSPLIB and Real case | ||||
| Our paper | √ | √ | √ | √ | √ | √ | EM, SEI | ASOA | Real case |
| Category | Symbol | Description |
|---|---|---|
| Indices and Sets | Set of tasks | |
| Set of non-dummy tasks | ||
| Set of edges | ||
| Set of precedence relations for task , where is a predecessor of | ||
| Directed graph representing the project network | ||
| Set of available workers, | ||
| Set of newcomers (to be trained) | ||
| Set of experienced workers | ||
| Set of skills | ||
| Index of task, | ||
| Index of worker, | ||
| Index of skill, | ||
| Index of time, | ||
| Parameters | Binary parameter to indicate if task i requires skill , | |
| Initial efficiency of worker in skill , | ||
| Upper bound of skill efficiency | ||
| Learning percentage, | ||
| Forgetting percentage, f | ||
| Learning factor calculated as | ||
| Forgetting factor calculated as | ||
| Auxiliary variables | Start time of task | |
| End time of task , | ||
| A random variable representing the uncertain duration of task , modeled as | ||
| A random variable obtained by scaling with the average efficiency of the assigned workers, | ||
| Average efficiency of workers assigned to task , | ||
| Idle time since worker last used skill | ||
| Efficiency increment factor based on the time worker spent using skill and idle time since last use. | ||
| Updated efficiency of worker in skill at time | ||
| Efficiency increment of worker in skill at time , | ||
| Position of task in the sequence, | ||
| Decision variables | Binary variable to indicate if worker works on the task | |
| An ordered list of tasks, |
| Category | Variables/Parameters | Description |
|---|---|---|
| NSGA-II | Initial population | |
| Generation index, | ||
| Parents at generation | ||
| Offspring at generation | ||
| Combined population at generation (merged parent and offspring) | ||
| Population size | ||
| Maximum number of generations | ||
| Baseline crossover probability | ||
| Baseline mutation probability | ||
| Exploration reinforcement factor ( | ||
| Diversity preservation factor | ||
| Simulation Module | Sampling index, | |
| Count of consecutive samplings where the difference in means between the first and samplings is below the threshold | ||
| Convergence threshold | ||
| Maximum number of simulations allowed | ||
| Minimum number of simulations is required before checking the convergence | ||
| The predefined number of consecutive samplings required for the mean difference to be below the threshold | ||
| Makespan of the schedule at the -th sampling | ||
| Set of historical makespans recorded across all samplings | ||
| Mean makespan across the first samplings | ||
| Skill efficiency increment at the -th sampling | ||
| Set of historical skill efficiency increments recorded across all samplings | ||
| Mean skill efficiency increment across the first samplings |
| Task Index | Expected Duration | Task Index | Expected Duration | Task Index | Expected Duration | Task Index | Expected Duration |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 21 | 64 | 41 | 96 | 61 | 16 |
| 2 | 56 | 22 | 32 | 42 | 104 | 62 | 64 |
| 3 | 96 | 23 | 88 | 43 | 64 | 63 | 64 |
| 4 | 40 | 24 | 48 | 44 | 40 | 64 | 104 |
| 5 | 16 | 25 | 64 | 45 | 40 | 65 | 56 |
| 6 | 80 | 26 | 104 | 46 | 48 | 66 | 24 |
| 7 | 24 | 27 | 24 | 47 | 88 | 67 | 56 |
| 8 | 56 | 28 | 40 | 48 | 56 | 68 | 48 |
| 9 | 32 | 29 | 80 | 49 | 40 | 69 | 16 |
| 10 | 56 | 30 | 96 | 50 | 80 | 70 | 56 |
| 11 | 88 | 31 | 64 | 51 | 24 | 71 | 32 |
| 12 | 48 | 32 | 88 | 52 | 72 | 72 | 40 |
| 13 | 104 | 33 | 48 | 53 | 80 | 73 | 104 |
| 14 | 64 | 34 | 104 | 54 | 24 | 74 | 72 |
| 15 | 16 | 35 | 24 | 55 | 40 | 75 | 72 |
| 16 | 16 | 36 | 16 | 56 | 104 | 76 | 88 |
| 17 | 48 | 37 | 72 | 57 | 80 | 77 | 32 |
| 18 | 32 | 38 | 24 | 58 | 96 | 78 | 80 |
| 19 | 104 | 39 | 48 | 59 | 56 | 79 | 40 |
| 20 | 32 | 40 | 32 | 60 | 104 | 80 | 0 |
| Skill Index | Skill Types | Index of Tasks Requiring Such Skill Primarily |
|---|---|---|
| S1 | Engineering design | |
| S2 | Certification and compliance | |
| S3 | Simulation and modeling | |
| S4 | Control systems | |
| S5 | Fuel and combustion systems | |
| S6 | System integration | |
| S7 | Requirements analysis | |
| S8 | Aerodynamic analysis | |
| S9 | Performance testing | |
| S10 | Material science | |
| S11 | Manufacturing processes | |
| S12 | Thermodynamic analysis |
| Skill Index | Experienced Workers | Newcomers | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | R10 | R11 | R12 | R13 | R14 | |
| S1 | 0.8 | 1.0 | 0.8 | 2.0 | 1.8 | 1.4 | 1.0 | 0.8 | 1.0 | 1.0 | 0.2 | 0.2 | 0.4 | 0.2 |
| S2 | 0.8 | 2.0 | 1.4 | 1.0 | 0.8 | 1.0 | 0.8 | 0.8 | 1.4 | 1.6 | 0.4 | 0.6 | 0.8 | 0.4 |
| S3 | 1.8 | 1.6 | 0.8 | 1.0 | 0.8 | 1.0 | 2.0 | 1.4 | 0.8 | 1.6 | 0.4 | 0.6 | 0.2 | 0.6 |
| S4 | 1.0 | 0.8 | 1.8 | 0.8 | 1.0 | 2.0 | 1.0 | 0.8 | 0.8 | 1.2 | 0.6 | 0.4 | 0.8 | 0.2 |
| S5 | 1.6 | 0.8 | 1.4 | 1.4 | 1.6 | 1.2 | 0.6 | 0.8 | 0.8 | 2.0 | 0.2 | 0.8 | 0.2 | 0.8 |
| S6 | 1.2 | 0.8 | 1.2 | 0.8 | 1.0 | 1.0 | 1.0 | 1.6 | 2.0 | 0.8 | 0.8 | 0.4 | 0.4 | 0.4 |
| S7 | 0.6 | 1.2 | 1.0 | 0.8 | 2.0 | 1.4 | 1.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.4 | 0.2 | 0.4 |
| S8 | 0.8 | 0.8 | 2.0 | 0.8 | 0.8 | 1.6 | 0.8 | 1.8 | 0.8 | 0.8 | 0.4 | 0.6 | 0.4 | 0.4 |
| S9 | 1.8 | 1.0 | 0.6 | 1.2 | 0.8 | 0.8 | 1.0 | 1.8 | 0.8 | 2.0 | 0.4 | 0.4 | 0.2 | 0.2 |
| S10 | 2.0 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 1.2 | 1.0 | 1.2 | 1.8 | 0.2 | 0.2 | 0.6 | 0.6 |
| S11 | 1.0 | 1.2 | 0.8 | 1.8 | 1.2 | 0.8 | 1.6 | 1.4 | 1.2 | 1.2 | 0.6 | 0.6 | 0.4 | 0.4 |
| S12 | 0.8 | 1.6 | 0.8 | 0.8 | 0.8 | 0.8 | 1.2 | 0.8 | 1.6 | 2.0 | 0.4 | 0.2 | 0.8 | 0.8 |
| Parameters * | Parameter Levels | ||||
|---|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | Level 4 | Level 5 | |
| 25 | 50 | 100 | 200 | 300 * | |
| 20 | 40 | 60 | 80 | 100 * | |
| 0.3 | 0.4 | 0.5 | 0.6 * | 0.7 | |
| 0.05 | 0.10 | 0.15 * | 0.20 | 0.25 | |
| Level | ||||
|---|---|---|---|---|
| 1 | 8.149 | 9.727 | 13.231 | 14.465 |
| 2 | 10.518 | 12.827 | 14.211 | 13.774 |
| 3 | 14.119 | 14.471 | 14.554 | 14.745 |
| 4 | 17.716 | 16.005 | 14.73 | 13.989 |
| 5 | 20.08 | 17.551 | 13.855 | 13.609 |
| Delta | 11.931 | 7.824 | 1.499 | 1.136 |
| Rank | 1 | 2 | 3 | 4 |
| Project Scale | Task Count | Network Seriality * | Skill Count | Worker Count | |
|---|---|---|---|---|---|
| Experienced Workers | Newcomers | ||||
| Small case | 40 | 0.4 | 12 | 5 | 2 |
| Base case | 80 | 0.2 | 12 | 10 | 4 |
| Big case | 120 | 0.2 | 12 | 12 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Ding, R.; Liu, S.; Wang, L. Multi-Skilled Project Scheduling for High-End Equipment Development Considering Newcomer Cultivation and Duration Uncertainty. Systems 2025, 13, 448. https://doi.org/10.3390/systems13060448
Liu Y, Ding R, Liu S, Wang L. Multi-Skilled Project Scheduling for High-End Equipment Development Considering Newcomer Cultivation and Duration Uncertainty. Systems. 2025; 13(6):448. https://doi.org/10.3390/systems13060448
Chicago/Turabian StyleLiu, Yaohui, Ronggui Ding, Shanshan Liu, and Lei Wang. 2025. "Multi-Skilled Project Scheduling for High-End Equipment Development Considering Newcomer Cultivation and Duration Uncertainty" Systems 13, no. 6: 448. https://doi.org/10.3390/systems13060448
APA StyleLiu, Y., Ding, R., Liu, S., & Wang, L. (2025). Multi-Skilled Project Scheduling for High-End Equipment Development Considering Newcomer Cultivation and Duration Uncertainty. Systems, 13(6), 448. https://doi.org/10.3390/systems13060448






