Decision-Making in Complementary Products Supply Chain: Game Theory and Sensitivity Analysis

Abstract

This paper explores how to reduce supply-demand conflicts in supply chains by utilizing complementary products’ unique relationships and shared objectives. Also, it considers the service level concerns of consumers. Primarily employing game theory, this paper analyzes the pricing strategies of complementary products within a three-tier dual-channel supply chain, the relationship between pricing and service levels, and the performance optimization across channels. Numerical results demonstrate that elevated values of α₁ indicate heightened consumer sensitivity to manufacturer price fluctuations. To sustain sales volume, manufacturers are compelled to reduce prices, consequently leading to a decline in equilibrium prices within the market. A rise in β₁ induces an across-the-board increase in all price tiers, albeit with differential magnitudes. The intensification of channel competition α₂ exerts downward pressure on all pricing components. The retailer’s price demonstrates maximal responsiveness to β₂ fluctuations, as retailers directly absorb cost variances.

1. Introduction

With the continuous development and deepening of economic globalization, new drivers represented by the Internet are deeply integrating with various industries. The combination of “Internet + online payment + logistics” has significantly accelerated the development of global online marketing. In the context of economic slowdown and intensifying market competition, product manufacturers in the supply chain establish online direct sales channels to maintain competitive advantages and expand market shares [1]. However, manufacturers’ establishment of online direct sales channels has led to price conflicts with retailers due to the sale of identical products through both traditional retail and online direct sales channels. For instance, when a certain enterprise sells products at promotional prices on online platforms, its offline distributors are often forced to lower the prices together. This will lead to a two-way squeeze on channel profits.

Consumers in the new era demand lower prices for goods within the supply chain and require improved service levels for these goods. Similarly, there exists a positive spillover effect of service on complementary products, where an increase in one party’s service level, while raising its costs, also leads to an increase in the profits of its competitors. For instance, when smart door lock manufacturers invest more resources in improving their cloud customer service systems, the suppliers of their supporting smart home systems will also simultaneously gain an increase in users. However, the service costs incurred are borne independently by the door lock manufacturers. In a highly competitive market, rational decision-makers will not increase their own costs to boost the profits of their rivals. Therefore, service conflicts also arise in dual-channel supply chains. Deciding pricing and service levels is an issue of great concern and urgency for enterprises. Modern supply chains increasingly leverage real-time data from online platforms and offline stores to optimize pricing and inventory decisions simultaneously. This trend toward digital transformation introduces both new opportunities for efficiency gains and additional risks of channel conflicts, requiring more sophisticated coordination mechanisms [2].

Regarding the supply chain demand function, the linear demand function can intuitively reflect the cross-price effects in a dual-channel supply chain. Additionally, previous research has shown that there are corresponding products whose demand exhibits a linear relationship with price. The linear demand function is also flexible and concise, making it easy to establish models and incorporate other factors influencing demand beyond price. For instance, the impact of service quality on demand has been studied by numerous scholars using the linear demand model in the context of dual-channel supply chains. Dual-channel supply chains primarily adopt centralized and decentralized strategies, and this paper employs these two strategies to study the game behavior between manufacturers and retailers. However, regardless of the approach, the focus on commodity pricing and corporate profits remains the primary concern of both businesses and scholars within the supply chain system. By reviewing and analyzing relevant literature on dual-channel supply chains, complementary products, and service quality levels, it is found that studies combining any two of these aspects have yielded abundant results. However, joint research considering the pricing of complementary products and investment in service costs within dual-channel supply chain systems is relatively scarce.

Manufacturers in the supply chain produce two complementary products, one sold through direct online sales channels, and the other wholesaled to retailers for distribution through traditional retail channels. Since both parties in the supply chain aim to maximize their profits, a decrease in the sales price of one product will lead to an increase in demand across both channels. This may result in reduced profits for the party that lowered prices, while the other party, benefiting from the positive spillover effect of complementary products, experiences increased demand and profit without changing its price. Therefore, price conflicts also arise in dual-channel supply chains involving complementary products. The innovations and contributions of this paper are mainly reflected in:

(1)

This paper, from the perspectives of manufacturers and retailers as sellers in the supply chain for the first time, introduces complementary products to mitigate the conflicts arising from manufacturers establishing direct online sales channels between both parties and reducing vicious competition. It constructs a dual-channel, three-tier supply chain system comprising one manufacturer, retailer, and consumers to alleviate such conflicts.

(2)

This paper introduces complementary products within the supply chain to alleviate conflicts between dual channels. The special relationship between complementary products brings about positive spillovers in demand while also leading to service-free-riding behavior. Pricing and service investment decisions for complementary products are made within the dual-channel supply chain of complementary products.

(3)

Systematic exploration of the pricing and service coordination of complementary products under different decision-making power structures is still relatively lacking, especially considering price elasticity, cross-price elasticity, and service spillover simultaneously. This paper fills this research gap.

2. Literature Review

With the development of society, the market gradually changes from seller to buyer. The closer the supply chain members are to consumers, the more pricing power they have. Therefore, the market power of manufacturers and retailers has also changed. Manufacturers have greater market power in a seller’s market; retailers have more market power in a buyer’s market. In the process of market power change, the market power of manufacturers and retailers will also appear equal.

With the development of e-commerce and logistics, consumers believe that the differences between channels are gradually becoming smaller. Researchers introduce new impact factors into the dual-channel supply chain system to analyze price decisions and the impact on profits.

Wang Jian et al. (2022) [1] introduced the concept of fraudulent returns into the dual-channel supply chain system, analyzing four common strategies employed by manufacturers to establish direct online sales channels while also selling products through traditional retail stores. Liu Mengqi et al. (2016) [3] examined the impact of the risk attitudes of both channel parties, concluding that optimal prices under risk aversion are lower than those under risk neutrality. Fang Fei et al. (2021) [4] considered pricing and ordering decisions for products in a dual-channel supply chain with product substitutability, where profits are comprised of sales revenue and inventory costs. The research results indicate that, regardless of the substitution level, the vertical Nash equilibrium scheme yields higher profits than the Stackelberg scheme. Wang Yuyan et al. (2020) [5] introduced the concept of fairness concerns into the dual-channel supply chain, analyzing manufacturers’ wholesale prices and direct online sales prices, as well as retailers’ retail prices, under scenarios where only the manufacturer is fairness-conscious, only the retailer is fairness-conscious, and both parties are fairness-conscious. Liu Jian et al. (2022) [6] incorporated consumers’ low-carbon preferences as an influencing factor in modeling a dual-channel supply chain. Their analysis revealed that differences in consumers’ low-carbon preferences intensify channel conflicts. Zhou Jianheng et al. (2020) [7] considered the impact of differentiated products on a dual-channel supply chain, analyzing from a game theory perspective how the quality level of products influences optimal pricing to the same extent as consumers’ preferences for different channels. Shang et al. (2024) [8] studied the impact of potential entrants entering the complementary goods market on the technological innovation of basic products. Sha et al. (2024) [9] based on wholesale price discrimination and sales effort, established a revenue matrix for whether retailers pay sales effort when manufacturers charge different wholesale prices to different retailers, and used Nash equilibrium game theory to solve the conditions under which each decision combination in a dual-channel supply chain becomes a Nash equilibrium.

Coordination, as a focal issue in dual-channel supply chain optimization, has been extensively and deeply researched. Hamzaoui et al. (2024) [10], in response to the dual-channel pharmaceutical supply chain under the impact of e-commerce, adopted the Stackelberg game to construct a multi-cycle pricing and remanufacturing model. They innovatively introduced a sales commission mechanism paid by online channels to pharmacies and analyzed the impact of consumer preferences, recovery costs, and commission ratios on channel profits through numerical simulation. Boyaci Tamer et al. (2005) [11] considered the impact of inventory on the profits of both parties in a dual-channel supply chain and found that common cooperation methods cannot achieve supply chain coordination, but a two-step compensation delegation contract can. Crettez B et al. (2025) [12] considered the linear quadratic differential game setting of supply chain competition and vertical coordination and found that the competition between supply chains may be unsustainable when they sell complementary products and rely on revenue-sharing agreements. Sarkar S. et al. (2021) [13], through research on dual-channel supply chains, analyzed that wholesale price contracts cannot achieve supply chain coordination, but price increases can lead to Pareto improvement. Song C.J. et al. (2023) [14] examined pricing and coordination issues in dual-channel supply chains under carbon emissions and achieved supply chain coordination through dual-channel price discounts. Modak N.M. et al. (2024) [15] studied dual-channel supply chains with stochastic customer demand dependent on price and delivery time, using a combination of all-units quantity discounts and franchise fee contracts to achieve supply chain coordination. Bart N. et al. (2021) [16] found through analysis that revenue-sharing contracts can achieve supply chain coordination in the absence of disruptions, and modifying revenue-sharing contracts can help improve dual-channel supply chains with disruptions. Avinadav T. et al. (2022) [17], in a dual-channel supply chain system with one manufacturer and two retailers, considered the impact of price and service on the supply chain. When the revenue-sharing coefficient is within a certain range, revenue sharing and cost-sharing can achieve supply chain coordination. Pu X. et al. (2018) [18] analyzed that reasonable dual-channel service cost sharing can fully achieve supply chain coordination. From the above, to ensure the smooth implementation of coordination contracts from the perspective of both channel parties, Pareto optimization must be achieved. Therefore, a well-designed coordination contract must enable Pareto improvement in the performance of both channel parties. However, coordination is typically based on a comparison of profits between centralized and decentralized decision-making. In practice, centralized decision-making is difficult to achieve, and profit comparisons based on decentralized decision-making are more common in enterprise operations. Thus, how to achieve Pareto optimization before and after decentralized decision-making is also an important issue facing dual-channel supply chains.

Ariu A (2020) et al. (2020) [19] studied pricing decisions between unilaterally complementary products. Zennyo Y et al. (2020) [20] analyzed the pricing decisions for dual-channel products from the perspective of product relatedness, where a manufacturer produces two goods that are either substitutes or complements and wholesales them to retailers for traditional channel sales. Hemmati, M et al. (2025) [21] investigated complementary products of a retailer using a dual purchasing strategy. The results indicated that simple bundled sales were more sensitive to supply disruptions than mixed bundled sales and individual sales. Sun F et al. (2023) [22] explored the quality and pricing decisions between a manufacturer of perfectly complementary products and retailers. Soltani R et al. (2024) [23] studied the competitive relationship between consumer utility and the quality of complementary goods, taking into account the external characteristics of the online channel. Hosseini-Motlagh S.M. et al. (2014) [24] investigated Stackelberg game problems in the context of dual-channel supply chains, revealing the impact of the degree of complementarity between goods, consumer brand loyalty, and channel loyalty on selling prices. Previous research has primarily focused on pricing [25], channel preference, brand loyalty, and product quality among complementary goods. With the progression of research, complementary products have been elevated to a strategic level to mitigate channel conflicts, and studying how to leverage the unique relationships between complementary products has become a hot research topic.

Despite the fact that the spillover effects between complementary products can effectively mitigate channel conflicts, there are not many related extension studies. Hemmati M et al. (2023) [26] analyzed the issue of advertising decisions and bundled sales of complementary products among enterprises, deriving the optimal advertising strategy. Zhang Y et al. (2021) [27] studied how to make advertising and pricing decisions in a dual-channel supply chain system consisting only of manufacturers and retailers. Sana S.S. et al. (2022) [28] investigated a supply chain system composed of two manufacturers and one retailer in the context of green supply chains, where the two manufacturers produce complementary products, and analyzed the impact of different game models on pricing. Ren M et al. (2020) [29] considered bundled sales of complementary products in a dual-channel supply chain consisting of one manufacturer and one retailer.

He et al. (2024) [30] referred to the mass effect as having a cross-positive impact on the equilibrium price and profit of the dual-channel supply chain. Hu et al. (2024) [31] found through research that consumers’ perception of high quality is beneficial to all supply chain members. The coordination contract can achieve coordination and enable supply chain members to obtain relatively fair profits. Nematollahi, M et al. (2024) [32] studied the coordination and competition in the dual-channel supply chain by starting from factors such as pricing strategies, home delivery services, sales services, and warranty decisions. Li P et al. (2021) [33] analyzed the optimal pricing strategies and maximum profits obtained by manufacturers and retailers when both parties in the channel provide services. Linde L et al. (2021) [34] considered scenarios where no service is provided, where services are provided but independent of products, and where services and products are bundled for sale. Lu J.C. et al. (2011) [35] analyzed and concluded that when consumers are susceptible to both product prices and service levels, manufacturers improving service levels will significantly enhance their market competitiveness. Choi T.M. et al. (2019) [36] constructed a dual competition model based on price and service levels, analyzing the optimal decisions for manufacturers and retailers when market demand is stochastic. Gu S.Q. et al. (2018) [37] found that a reasonable service cost-sharing contract can fully coordinate dual-channel supply chains. Tallon P.P. et al. (2011) [38] found that the service spillover effect coefficient can increase the demand for both parties in the supply chain within a specific range, having a positive impact on profits and service levels. Zhang Z. et al. (2021) [39] studied the fact that both manufacturers and retailers should provide differentiated services, and whether they adopt decentralized or centralized decision-making will be influenced by the acceptance of online direct sales channels.

3. Problem Description and Model Assumptions

3.1. Problem Description

Considering a dual-channel, three-tier supply chain system comprising manufacturers, retailers, and consumers, where manufacturers not only supply goods to retailers but also establish online direct sales channels to market complementary products of those goods. The supply chain structure, consisting of manufacturers, retailers, and consumers, is illustrated in Figure 1.

3.2. Basic Assumptions

The symbol setting of this paper is shown in

Table 1. Symbol settings.

Symbol	Explain
$c$	The manufacturing cost of Commodity B
$w$	The wholesale price of commodity B
$p_a$	The direct selling price of commodity A by the manufacturer
$p_b$	The retail price of commodity B by the retailer
${\alpha }_1$	The elasticity coefficient of the influence of the price of commodity A itself on demand
${\beta }_1$	The elasticity coefficient of the cross-price influence of commodity B on commodity A
${\alpha }_2$	The elasticity coefficient of the influence of the price of commodity B itself on demand
${\beta }_2$	The elasticity coefficient of the cross-price influence of commodity A on commodity B
$D_m$	The demand for online direct sales channels
$D_r$	The demand of traditional retail channels
$a$	The potential market size of Commodity A
$b$	The potential market size of Commodity B
${\pi }_m$	The profit of the manufacturer
${\pi }_r$	The profits of retailers

.

Assuming that the manufacturer produces two products, A and B, which are complementary, similar to the assumptions made in reference. The manufacturer supplies product B to the retailer for sale through traditional retail channels, while simultaneously selling product A through online direct sales channels.

In many dual-channel cases, especially for digital goods or low marginal cost products, the production cost is negligible compared to distribution and pricing effects [17]. Thus, this passage assumes the manufacturing cost of product A is negligible to highlight the impact of pricing strategies and elasticity effects without losing generality.

Without considering the manufacturing cost of Product A and solely focusing on the manufacturing cost of Product B, denoted as $c$, the wholesale price of Product B is represented by $w$, where $w>c$ is a given condition.

The retail price for Product B set by the retailer is ${\mathrm{p}}_{\mathrm{b}}$, while the direct sales price for Product A set by the manufacturer is $p_a$, where $p_a$ is greater than the production cost of Product A.

Similar to the findings in References [1,4], the demand for the online direct sales channel can be expressed as:

$$D_m=a-{\alpha }_1{p}_a-{\beta }_1{p}_b$$

The demand for the traditional retail channel is:

$$D_r=b-{\alpha }_2{p}_b-{\beta }_2{p}_a$$

where $a$ and $b$ represent the potential market sizes for the products, respectively. Given that the cross-price elasticity coefficients are smaller than the own-price elasticity coefficients for the products, it is stipulated that: ${\alpha }_1>{\beta }_1>0$, ${\alpha }_2>{\beta }_2>0$.

The manufacturer’s profit:

$${\pi }_m=\left(a-{\alpha }_1{p}_a-{\beta }_1{p}_b\right)p_a+\left(w-c\right)(b-{\alpha }_2{p}_b-{\beta }_2{p}_a)$$

The retailer’s profit:

$${\pi }_r=\left(p_b-w\right)(b-{\alpha }_2{p}_b-{\beta }_2{p}_a)$$

4. Model Solution and Equilibrium Result Analysis

4.1. Pricing Strategy in a Centralized Scenario

In a centralized decision-making scenario, the manufacturer and the retailer are treated as a single entity. With the premise of maximizing the supply chain profit, the manufacturer and the retailer make pricing decisions. The profit of the supply chain is: ${\pi }_{sc}={\pi }_m+{\pi }_r$

Namely,

$${\pi }_{sc}=\left(a-{\alpha }_1{p}_a-{\beta }_1{p}_b\right)p_a+\left(p_b-c\right)(b-{\alpha }_2{p}_b-{\beta }_2{p}_a)$$

(1)

To ensure that the profit ${\pi }_{sc}$ of the supply chain has a maximum value, it is necessary to prove that ${\pi }_{sc}$ is a joint concave function of $p_a$ and $p_b$. By taking the derivatives of $p_a$ and $p_b$ according to Equation (1), we obtain:

$${\displaystyle \frac{\partial {\pi }_{sc}}{\partial p_a}}=a-{2\alpha }_1{p}_a-\left({\beta }_1+{\beta }_2\right)p_b+c{\beta }_2$$

(2)

$${\displaystyle \frac{\partial {\pi }_{sc}}{\partial p_b}}=b-{2\alpha }_2{p}_b-\left({\beta }_1+{\beta }_2\right)p_a+c{\alpha }_2$$

(3)

By taking the derivatives of $p_a$ and $p_b$ according to Equation (1), and of $p_a$ and $p_b$ according to Equation (3), we obtain:

$${\displaystyle \frac{{\partial }^2{\pi }_{sc}}{\partial {p_a}^2}}=-{2\alpha }_1, {\displaystyle \frac{{\partial }^2{\pi }_{sc}}{\partial p_a\partial p_b}}=-\left({\beta }_1+{\beta }_2\right), {\displaystyle \frac{{\partial }^2{\pi }_{sc}}{\partial {p_b}^2}}=-{2\alpha }_2, {\displaystyle \frac{{\partial }^2{\pi }_{sc}}{\partial p_b\partial p_a}}=-\left({\beta }_1+{\beta }_2\right)$$

Then, the Hessian matrix of profit ${\pi }_{sc}$ of the dual-channel supply chain for complementary products under centralized control, with respect to $p_a$ and $p_b$, is:

$$H=\left[\begin{array}{cc}-2{\alpha }_1& -({\beta }_1+{\beta }_2)\\ -({\beta }_1+{\beta }_2)& -2{\alpha }_2\end{array}\right]$$

Based on the assumed conditions, the first-order principal minors of the matrix are: $-2{\alpha }_1<0$. The second-order principal minors of the matrix are: $4{\alpha }_1{\alpha }_2-{({\beta }_1+{\beta }_2)}^2$. Combining the known conditions: ${\alpha }_1>{\beta }_1>0$, ${\alpha }_2>{\beta }_2>0$, and utilizing the properties of inequalities, we can deduce that: ${({\beta }_1+{\beta }_2)}^2$=${{\beta }_1}^2+{{\beta }_2}^2+2{\beta }_1{\beta }_2$ ≥ 4${\beta }_1{\beta }_2$. Therefore, there exists a positive real number $\mathsf{\sigma }$ such that $4{\alpha }_1{\alpha }_2-{({\beta }_1+{\beta }_2)}^2\le 4{\alpha }_1{\alpha }_2-4{\beta }_1{\beta }_2=\sigma$. By setting $0<4{\alpha }_1{\alpha }_2-{\left({\beta }_1+{\beta }_2\right)}^2<\sigma$ appropriately, the Hessian matrix becomes a negative definite matrix. Consequently, the profit ${\pi }_{sc}$ of the dual-channel supply chain for complementary products has a joint maximum value with respect to $p_a$ and $p_b$.

Under the premise of satisfying the aforementioned conditions, by setting Equations (2) and (3) equal to zero simultaneously, we can solve for the optimal prices under centralized decision-making.

$$p_a^{*}={\displaystyle \frac{\left(b+c{\alpha }_2\right)\left({\beta }_1+{\beta }_2\right)-2{\alpha }_2\left(a+c{\beta }_2\right)}{{\left({\beta }_1+{\beta }_2\right)}^2-4{\alpha }_1{\alpha }_2}}$$

$$p_b^{*}={\displaystyle \frac{\left(a+c{\beta }_2\right)\left({\beta }_1+{\beta }_2\right)-2{\alpha }_1\left(b+c{\alpha }_2\right)}{{\left({\beta }_1+{\beta }_2\right)}^2-4{\alpha }_1{\alpha }_2}}$$

Theorem 1.

When $0<4{\alpha }_1{\alpha }_2-{\left({\beta }_1+{\beta }_2\right)}^2<\sigma$ (where σ is a positive real number), the centralized decision-making supply chain profit ${\pi }_{sc}$, defined by Equation (1), has a maximum value, with the maximum point being ($p_a^{*},p_b^{*}$).

4.2. Pricing Strategy in a Manufacturer-Dominant Stackelberg Game

In this scenario, we consider a Stackelberg game decision-making process where the manufacturer acts as the leader of the channel and the retailer as the follower. Under this game-based decision-making framework, the manufacturer sets wholesale and online direct sales prices for complementary products based on the retailer’s pricing response, aiming to maximize its own interests. Firstly, the manufacturer sets wholesale and online prices based on the retailer’s optimal pricing response. The retailer then sets its price based on the manufacturer’s wholesale and online prices to maximize profit. The decision-making model is as follows:

$$Max{\pi }_m{(p}_a,w)=p_a\left(a-{\alpha }_1{p}_a-{\beta }_1{p}_b\right)+\left(w-c\right)(b-{\alpha }_2{p}_b-{\beta }_2{p}_a)$$

(4)

$$s.t.Max{\pi }_r{(p}_b)=\left(p_b-w\right)(b-{\alpha }_2{p}_b-{\beta }_2{p}_a)$$

(5)

By taking the first-order derivative of the retailer’s traditional retail price $p_b$ according to Equation (5), we can obtain:

$${\displaystyle \frac{\partial {\mathsf{\pi }}_{\mathrm{r}}}{\partial {\mathrm{p}}_{\mathrm{b}}}}=\mathrm{b}-2{\mathsf{\alpha }}_2{\mathrm{p}}_{\mathrm{b}}-{\mathsf{\beta }}_2{\mathrm{p}}_{\mathrm{a}}+\mathrm{w}{\mathsf{\alpha }}_2$$

By setting ${\displaystyle \frac{\partial {\mathsf{\pi }}_{\mathrm{r}}}{\partial {\mathrm{p}}_{\mathrm{b}}}}=0$, we can obtain the retailer’s reaction function for the traditional retail price.

$$p_b={\displaystyle \frac{1}{2{\alpha }_2}}(b-{\beta }_2{p}_a+w{\alpha }_2)$$

(6)

Using its reaction function, we can derive the manufacturer’s pricing for the online direct sales channel and the wholesale price for the complementary product. By substituting Equation (6) into Equation (4) and taking the first-order derivatives of $p_a$ and $w$, then setting them equal to zero simultaneously, we can obtain:

$${\displaystyle \frac{\partial {\pi }_m}{\partial p_a}}={\displaystyle \frac{1}{2{\alpha }_2}}\left[\left(2{{\beta }_1\beta }_2-4{\alpha }_1{\alpha }_2\right)p_a-w{\alpha }_2\left({\beta }_1+{\beta }_2\right)+2a{\alpha }_2+c{\alpha }_2{\beta }_2-{\beta }_1\right]=0$$

(7)

$${\displaystyle \frac{\partial {\pi }_m}{\partial w}}={\displaystyle \frac{b-p_a\left({\beta }_1+{\beta }_2\right)-2w{\alpha }_2+c{\alpha }_2}{2}}=0$$

(8)

By combining Equations (7) and (8), we can obtain the manufacturer’s pricing for the online direct sales channel and the wholesale price for the complementary product.

$${\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}\mathrm{*}}={\displaystyle \frac{\mathrm{c}{\mathsf{\alpha }}_2{{\mathsf{\beta }}_2}^2-{{\mathsf{\beta }}_1}^2-{\mathsf{\beta }}_1{\mathsf{\beta }}_2+2\mathrm{a}{\mathsf{\beta }}_1{\mathsf{\alpha }}_2-4\mathrm{b}{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2+2\mathrm{b}{\mathsf{\beta }}_1{\mathsf{\beta }}_2+2\mathrm{a}{\mathsf{\alpha }}_2{\mathsf{\beta }}_2-4\mathrm{c}{\mathsf{\alpha }}_1{{\mathsf{\alpha }}_2}^2+3\mathrm{c}{\mathsf{\alpha }}_2{\mathsf{\beta }}_1{\mathsf{\beta }}_2}{{\mathsf{\alpha }}_2[{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2+4{\mathsf{\beta }}_1{\mathsf{\beta }}_2-8{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2]}}$$

$${\mathrm{w}}^{\mathrm{*}\mathrm{*}}={\displaystyle \frac{2{\mathsf{\beta }}_1+\mathrm{b}{\mathsf{\beta }}_1-4\mathrm{a}{\mathsf{\alpha }}_2+\mathrm{b}{\mathsf{\beta }}_2+\mathrm{c}{\mathsf{\beta }}_1{\mathsf{\alpha }}_2-\mathrm{c}{\mathsf{\alpha }}_2{\mathsf{\beta }}_2}{{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2+4{\mathsf{\beta }}_1{\mathsf{\beta }}_2-8{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2}}$$

Substituting ${\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}\mathrm{*}}$ and ${\mathrm{w}}^{\mathrm{*}\mathrm{*}}$ into Equation (6), we can obtain the retailer’s retail price ${\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}\mathrm{*}}$ in the traditional channel. Due to the lengthy expression, it is not provided here. The relationship between ${\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}\mathrm{*}}$ and various factors is mainly presented through numerical simulations.

Theorem 2.

In the manufacturer-dominant Stackelberg game process, the manufacturer’s profit defined by Equation (4) attains its maximum value at ($p_a^{**}$, $w^{**}$), and the retailer’s profit defined by Equation (5) attains its maximum value at $p_b^{**}$.

There is a simple example that can verify the above inference result. For example, smartphone and accessories strategy often faces tension between online flagship stores and offline resellers. The manufacturer sets a wholesale price and online price, while retailers adjust prices based on local demand. This sometimes leads to offline retailers being undercut, demonstrating the coordination challenge analyzed in this model.

4.3. Analysis of Equilibrium Results

Corollary 1.

There is a positive correlation between the wholesale price and the manufacturer’s potential market demand. As the manufacturer’s potential market demand expands, the wholesale price of its complementary products will gradually increase. Conversely, a negative correlation exists between wholesale price and the retailer’s potential market demand. As the retailer’s potential market demand increases, the manufacturer’s wholesale price for the product will gradually decrease.

Proof. 

According to condition ${\mathsf{\alpha }}_1>{\mathsf{\beta }}_1>0$, ${\mathsf{\alpha }}_2>{\mathsf{\beta }}_2>0$, 4${\mathsf{\alpha }}_1{\mathsf{\alpha }}_2-{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2>0$, it follows that

$${\displaystyle \frac{\partial {\mathrm{w}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{a}}}={\displaystyle \frac{-4{\mathsf{\alpha }}_2}{{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2+4{\mathsf{\beta }}_1{\mathsf{\beta }}_2-8{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2}}={\displaystyle \frac{-4{\mathsf{\alpha }}_2}{{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2-4{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2+4({\mathsf{\beta }}_1{\mathsf{\beta }}_2-{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2)}}>0$$

$${\displaystyle \frac{\partial {\mathrm{w}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{b}}}={\displaystyle \frac{{\mathsf{\beta }}_1+{\mathsf{\beta }}_2}{{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2+4{\mathsf{\beta }}_1{\mathsf{\beta }}_2-8{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2}}={\displaystyle \frac{{\mathsf{\beta }}_1+{\mathsf{\beta }}_2}{{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2-4{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2+4({\mathsf{\beta }}_1{\mathsf{\beta }}_2-{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2)}}<0$$

From ${\displaystyle \frac{\partial {\mathrm{w}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{a}}}>0$, we can infer that there is a positive correlation between wholesale price and the manufacturer’s potential market demand. From ${\displaystyle \frac{\partial {\mathrm{w}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{b}}}<0$, we can deduce that there is a negative correlation between wholesale price and the retailer’s potential market demand. Therefore, Corollary 1 is proven. □

Corollary 2.

In the centralized scenario, both parties’ prices increase with their own market demand but decrease with the other’s. That is, as the manufacturer’s (retailer’s) potential market demand increases, the manufacturer’s (retailer’s) selling price also increases. In contrast, in the decentralized decision-making scenario, both parties’ prices decrease with their own demand but increase with the other’s.

Proof. 

By taking the derivatives of $\mathrm{a}$ and $\mathrm{b}$ with respect to ${\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}}$ and ${\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}},$ respectively, based on condition ${\mathsf{\alpha }}_1>{\mathsf{\beta }}_1>0$, ${\mathsf{\alpha }}_2>{\mathsf{\beta }}_2>0$, 4${\mathsf{\alpha }}_1{\mathsf{\alpha }}_2-{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2>0$, we obtain:

$${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}}}{\partial \mathrm{a}}}={\displaystyle \frac{-2{\mathsf{\alpha }}_2}{{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2-4{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2}}>0, {\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}}}{\partial \mathrm{b}}}={\displaystyle \frac{{\mathsf{\beta }}_1+{\mathsf{\beta }}_2}{{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2-4{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2}}<0$$

$${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}}}{\partial \mathrm{b}}}={\displaystyle \frac{-2{\mathsf{\alpha }}_1}{{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2-4{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2}}>0, {\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}}}{\partial \mathrm{a}}}={\displaystyle \frac{{\mathsf{\beta }}_1+{\mathsf{\beta }}_2}{{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2-4{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2}}<0$$

From ${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}}}{\partial \mathrm{a}}}>0, {\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}}}{\partial \mathrm{b}}}<0, {\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}}}{\partial \mathrm{b}}}>0, {\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}}}{\partial \mathrm{a}}}<0$, it can be deduced that in the centralized scenario, both parties’ prices positively relate to own demand and inversely to the other’s. Similarly, by taking the first-order derivatives of ${\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}\mathrm{*}}$ with respect to $\mathrm{a}$ and $\mathrm{b}$, we find:

$${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{a}}}={\displaystyle \frac{2{\mathsf{\beta }}_1{\mathsf{\alpha }}_2+2{\mathsf{\alpha }}_2{\mathsf{\beta }}_2}{{\mathsf{\alpha }}_2[{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2-4{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2+4\left({\mathsf{\beta }}_1{\mathsf{\beta }}_2-{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2\right)]}}<0$$

$${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{b}}}={\displaystyle \frac{-4{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2+2{\mathsf{\beta }}_1{\mathsf{\beta }}_2}{{\mathsf{\alpha }}_2[{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2-4{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2+4\left({\mathsf{\beta }}_1{\mathsf{\beta }}_2-{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2\right)]}}>0$$

when taking the first-order derivatives of $\mathrm{a}$ and $\mathrm{b}$ based on ${\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}\mathrm{*}}$, the result (${\displaystyle \frac{\partial {\mathrm{w}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{b}}}<0, {\displaystyle \frac{\partial {\mathrm{w}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{a}}}>0$) from Corollary 1 needs to be utilized.

$${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{b}}}={\displaystyle \frac{1}{2{\mathsf{\alpha }}_2}}(-{\mathsf{\beta }}_2{\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{b}}}+{\mathsf{\alpha }}_2{\displaystyle \frac{\partial {\mathrm{w}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{b}}})<0$$

$${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{a}}}={\displaystyle \frac{1}{2{\mathsf{\alpha }}_2}}(-{\mathsf{\beta }}_2{\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{a}}}+{\mathsf{\alpha }}_2{\displaystyle \frac{\partial {\mathrm{w}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{a}}})>0$$

From ${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{a}}}<0,{\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{b}}}>0,{\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{b}}}<0,{\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}\mathrm{*}}}{\partial \mathrm{a}}}>0$, it can be deduced that in the decentralized decision-making scenario, both parties’ prices inversely relate to own demand and positively to the other’s. Therefore, Corollary 2 is proven. □

Corollary 3.

In the centralized scenario, the manufacturer’s direct online sales price negatively correlates with the product’s price elasticity coefficient. As the price elasticity coefficient of the direct sales product increases, the manufacturer tends to reduce its selling price. Conversely, the retailer’s retail price for complementary products positively correlates with the price elasticity coefficient of the manufacturer’s product. This implies that using direct sales products with high price elasticity as a loss leader can be a bait to gain an overall competitive advantage.

Proof. 

Due to ${\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2-4{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2<0$, in order to ensure that ${\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}} \mathrm{a}\mathrm{n}\mathrm{d} {\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}}$ is non-negative, there exists $\left(\mathrm{b}+\mathrm{c}·{\mathsf{\alpha }}_2\right)\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)<2{\mathsf{\alpha }}_2\left(\mathrm{a}+\mathrm{c}·{\mathsf{\beta }}_2\right)$. Consequently, we derive $\left(\mathrm{b}+\mathrm{c}·{\mathsf{\alpha }}_2\right){\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2<2{\mathsf{\alpha }}_2\left(\mathrm{a}+\mathrm{c}·{\mathsf{\beta }}_2\right)\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)$, and further obtain $2\left(\mathrm{b}+\mathrm{c}·{\mathsf{\alpha }}_2\right){\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2<4{\mathsf{\alpha }}_2\left(\mathrm{a}+\mathrm{c}·{\mathsf{\beta }}_2\right)\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)$. Therefore, it follows that:

$${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}}}{\partial {\mathsf{\alpha }}_1}}={\displaystyle \frac{4{\mathsf{\alpha }}_2\left[\left(\mathrm{b}+\mathrm{c}·{\mathsf{\alpha }}_2\right)\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)-2{\mathsf{\alpha }}_2\left(\mathrm{a}+\mathrm{c}·{\mathsf{\beta }}_2\right)\right]}{{\left[{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2-4{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2\right]}^2}}<0$$

$${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}}}{\partial {\mathsf{\alpha }}_1}}={\displaystyle \frac{4{\mathsf{\alpha }}_2\left(\mathrm{a}+\mathrm{c}·{\mathsf{\beta }}_2\right)\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)-2\left(\mathrm{b}+\mathrm{c}·{\mathsf{\alpha }}_2\right){\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2}{{\left[{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2-4{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2\right]}^2}}>0$$

Based on ${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}}}{\partial {\mathsf{\alpha }}_1}}<0, {\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}}}{\partial {\mathsf{\alpha }}_1}}>0$, it can be deduced that the manufacturer’s direct online sales price has a negative correlation with the price elasticity coefficient of the product, while the retailer’s retail price for complementary products has a positive correlation with the price elasticity coefficient of the manufacturer’s product. Therefore, Corollary 3 is proven. □

Corollary 4.

In the centralized scenario, when ${\mathsf{\beta }}_1-{\mathsf{\beta }}_2<{\displaystyle \frac{2\mathrm{a}}{\mathrm{c}}}$ and ${\mathsf{\beta }}_1+{\mathsf{\beta }}_2<{\displaystyle \frac{4\mathrm{b}{\mathsf{\alpha }}_1}{\mathrm{c}\left({\mathsf{\beta }}_2-{\mathsf{\beta }}_1\right)+2\mathrm{b}}}$ hold, as the price elasticity of the complementary goods the retailer sells increases, the retailer will lower the sales price. For instance, in the case of daily necessities, when the product’s price elasticity increases, the retailer will consider the risk of consumers switching to other brands and generally reduce the selling price appropriately. Conversely, when ${\mathsf{\beta }}_1-{\mathsf{\beta }}_2<{\displaystyle \frac{2\mathrm{a}}{\mathrm{c}}}$ and ${\mathsf{\beta }}_1+{\mathsf{\beta }}_2>{\displaystyle \frac{4\mathrm{b}{\mathsf{\alpha }}_1}{\mathrm{c}\left({\mathsf{\beta }}_2-{\mathsf{\beta }}_1\right)+2\mathrm{a}}}$ hold, as the price elasticity of the complementary goods the retailer sells increases, the retailer will increase the sales price. For example, in the case of luxury goods, when the price elasticity of the product increases, the retailer will consider the purchasing preferences of luxury goods buyers and raise prices to cater to consumers’ buying psychology. In both scenarios, the manufacturer’s direct sales price exhibits opposite pricing behavior compared to the retailer’s, satisfying the loss leader effect.

Proof. 

By taking the first-order derivatives of the optimal prices ${\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}}$ and ${\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}}$ in the centralized scenario with respect to ${\mathsf{\alpha }}_2$, we obtain:

$${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}}}{\partial {\mathsf{\alpha }}_2}}={\displaystyle \frac{[\mathrm{c}\left({\mathsf{\beta }}_1-{\mathsf{\beta }}_2\right)-2\mathrm{a}]{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2+4{\mathsf{\alpha }}_1\mathrm{b}\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}{{\left[{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2-4{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2\right]}^2}}$$

$${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}}}{\partial {\mathsf{\alpha }}_2}}={\displaystyle \frac{2{\mathsf{\alpha }}_1\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)(2\mathrm{a}-\mathrm{c}{\mathsf{\beta }}_1)-8\mathrm{b}{{\mathsf{\alpha }}_1}^2}{{\left[{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2-4{\mathsf{\alpha }}_1{\mathsf{\alpha }}_2\right]}^2}}$$

when ${\mathsf{\beta }}_1-{\mathsf{\beta }}_2<{\displaystyle \frac{2\mathrm{a}}{\mathrm{c}}}$ and ${\mathsf{\beta }}_1+{\mathsf{\beta }}_2<{\displaystyle \frac{4\mathrm{b}{\mathsf{\alpha }}_1}{\mathrm{c}\left({\mathsf{\beta }}_2-{\mathsf{\beta }}_1\right)+2\mathrm{a}}}$ hold, $\mathrm{c}\left({\mathsf{\beta }}_1-{\mathsf{\beta }}_2\right)-2\mathrm{a}]{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2$ is negative. At the same time, $\left[\mathrm{c}\left({\mathsf{\beta }}_2-{\mathsf{\beta }}_1\right)+2\mathrm{a}\right]\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)<4\mathrm{b}{\mathsf{\alpha }}_1$ is true. By multiplying both sides of this inequality by $-\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)$, we can obtain $\left[\mathrm{c}\left({\mathsf{\beta }}_1-{\mathsf{\beta }}_2\right)-2\mathrm{a}\right]{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2>-4\mathrm{b}{\mathsf{\alpha }}_1\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)$. Therefore, ${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}}}{\partial {\mathsf{\alpha }}_2}}>0$.

Based on the condition $\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)\left[\mathrm{c}\left({\mathsf{\beta }}_2-{\mathsf{\beta }}_1\right)+2\mathrm{a}\right]<4\mathrm{b}{\mathsf{\alpha }}_1$, by multiplying both sides of the inequality by $2{\mathsf{\alpha }}_1$, we can obtain $2{\mathsf{\alpha }}_1\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)\left[\mathrm{c}\left({\mathsf{\beta }}_2-{\mathsf{\beta }}_1\right)+2\mathrm{a}\right]<8\mathrm{b}{{\mathsf{\alpha }}_1}^2$. Therefore, $2{\mathsf{\alpha }}_1\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)\left(2\mathrm{a}-\mathrm{c}{\mathsf{\beta }}_1\right)<8\mathrm{b}{{\mathsf{\alpha }}_1}^2$, and consequently ${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}}}{\partial {\mathsf{\alpha }}_2}}<0$. Hence, under this condition, the manufacturer’s direct online sales price has a positive correlation with the price sensitivity coefficient of the retailer’s complementary goods, while the retailer’s retail price has a negative correlation with its own price sensitivity.

Similarly, it can be proven that when ${\mathsf{\beta }}_1-{\mathsf{\beta }}_2<{\displaystyle \frac{2\mathrm{a}}{\mathrm{c}}}$ and ${\mathsf{\beta }}_1+{\mathsf{\beta }}_2>{\displaystyle \frac{4\mathrm{b}{\mathsf{\alpha }}_1}{\mathrm{c}\left({\mathsf{\beta }}_2-{\mathsf{\beta }}_1\right)+2\mathrm{a}}}$ hold, ${\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{a}}^{\mathrm{*}}}{\partial {\mathsf{\alpha }}_2}}<0,{\displaystyle \frac{\partial {\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}}}{\partial {\mathsf{\alpha }}_2}}>0$ is true. Under this premise, the manufacturer’s direct online sales price has a negative correlation with the price sensitivity coefficient of the retailer’s complementary goods, while the retailer’s retail price has a positive correlation with its own price sensitivity. Therefore, Corollary 4 is proven. □

As a major home appliance brand, Midea adopts differentiated but coordinated pricing across JD.com, Tmall, and offline distributors, particularly during major sales events like “Double Eleven”.

By controlling discounts on complementary appliances (e.g., air conditioners and purifiers), Midea ensures that both online and offline channels benefit, aligning with the centralized coordination advantage illustrated by our model.

5. Example Analysis

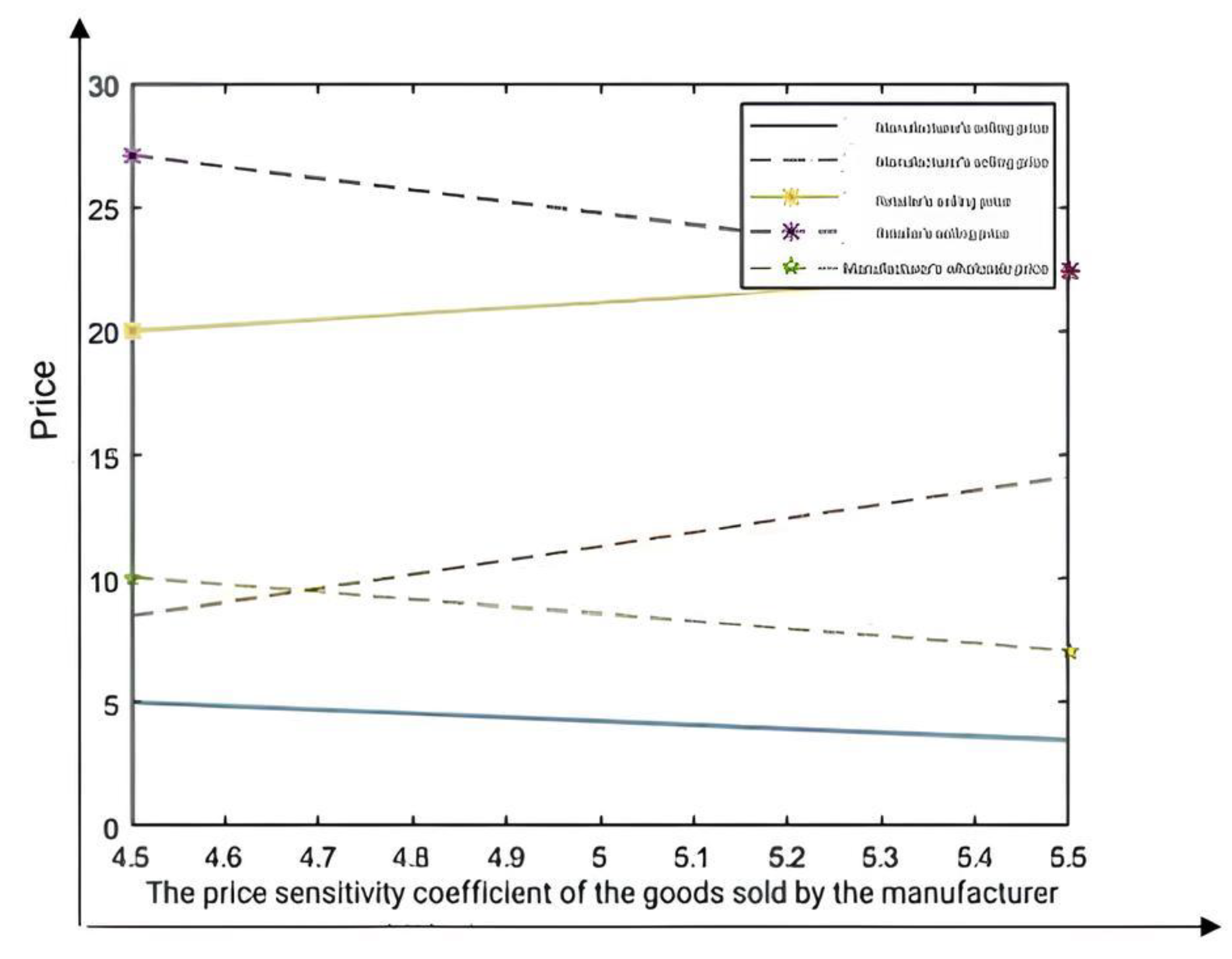
Due to the difficulty in deriving the optimal prices concerning various parameters under the decentralized decision-making scenario, a numerical simulation approach is employed to analyze the impact of price sensitivity and cross-sensitivity coefficients on various optimal solutions in centralized and decentralized situations. This approach serves two purposes: to verify the previous inferences and to analyze the relationship between ${\mathrm{p}}_{\mathrm{b}}^{\mathrm{*}\mathrm{*}}$ and various parameters under the decentralized scenario. The following analysis utilizes numerical simulations, assigning values to parameters that satisfy the conditions outlined in the previous inferences. In the following figures, “1” represents the equilibrium solution under the centralized scenario, while “2” represents the equilibrium solution under the decentralized scenario. Wholesale prices only exist in the decentralized scenario.

5.1. The Impact of ${\alpha }_1$ on Equilibrium Prices

When analyzing the impact of the manufacturer’s own price sensitivity coefficient (${\mathsf{\alpha }}_1$) on equilibrium prices under both centralized and decentralized scenarios, by assigning values that satisfy the conditions $\mathrm{a}=100,\mathrm{b}=50,{\alpha }_1\in \left[4.5,5.5\right],{\mathsf{\alpha }}_2=1,{\mathsf{\beta }}_1=2,{\mathsf{\beta }}_2=1,\mathrm{c}=5$, satisfy ${\mathsf{\alpha }}_1>{\mathsf{\beta }}_1>0$, ${\mathsf{\alpha }}_2>{\mathsf{\beta }}_2>0$, 4${\mathsf{\alpha }}_1{\mathsf{\alpha }}_2-{\left({\mathsf{\beta }}_1+{\mathsf{\beta }}_2\right)}^2>0$, ${\mathsf{\beta }}_1-{\mathsf{\beta }}_2<{\displaystyle \frac{2\mathrm{a}}{\mathrm{c}}}$, ${\mathsf{\beta }}_1+{\mathsf{\beta }}_2<{\displaystyle \frac{4\mathrm{b}{\mathsf{\alpha }}_1}{\mathrm{c}\left({\mathsf{\beta }}_2-{\mathsf{\beta }}_1\right)+2\mathrm{a}}}$, we can obtain the influence of ${\mathsf{\alpha }}_1$ on equilibrium prices as illustrated in Figure 2.

The analysis highlights that when products exhibit high price elasticity, manufacturers should strategically reduce direct sales prices to attract consumers, while allowing complementary products to support profitability.

In a centralized setting—such as vertically integrated firms or platforms with unified pricing—cross-product coordination can be leveraged: using elastic products as traffic generators while adjusting prices of complementary goods to maintain margin. This is particularly applicable to firms like Suning or Guomei, which manage both online and offline channels.

In contrast, under decentralized structures, manufacturers and retailers must anticipate each other’s pricing responses, as manufacturers may reduce wholesale prices to induce favorable retail actions.

To avoid inefficiencies, firms should consider establishing strategic pricing alliances, shared data platforms, or transfer pricing mechanisms to mimic centralized benefits.

Overall, exploiting complementary product spillover effects via coordinated pricing is a practical pathway to enhance channel synergy and profitability.

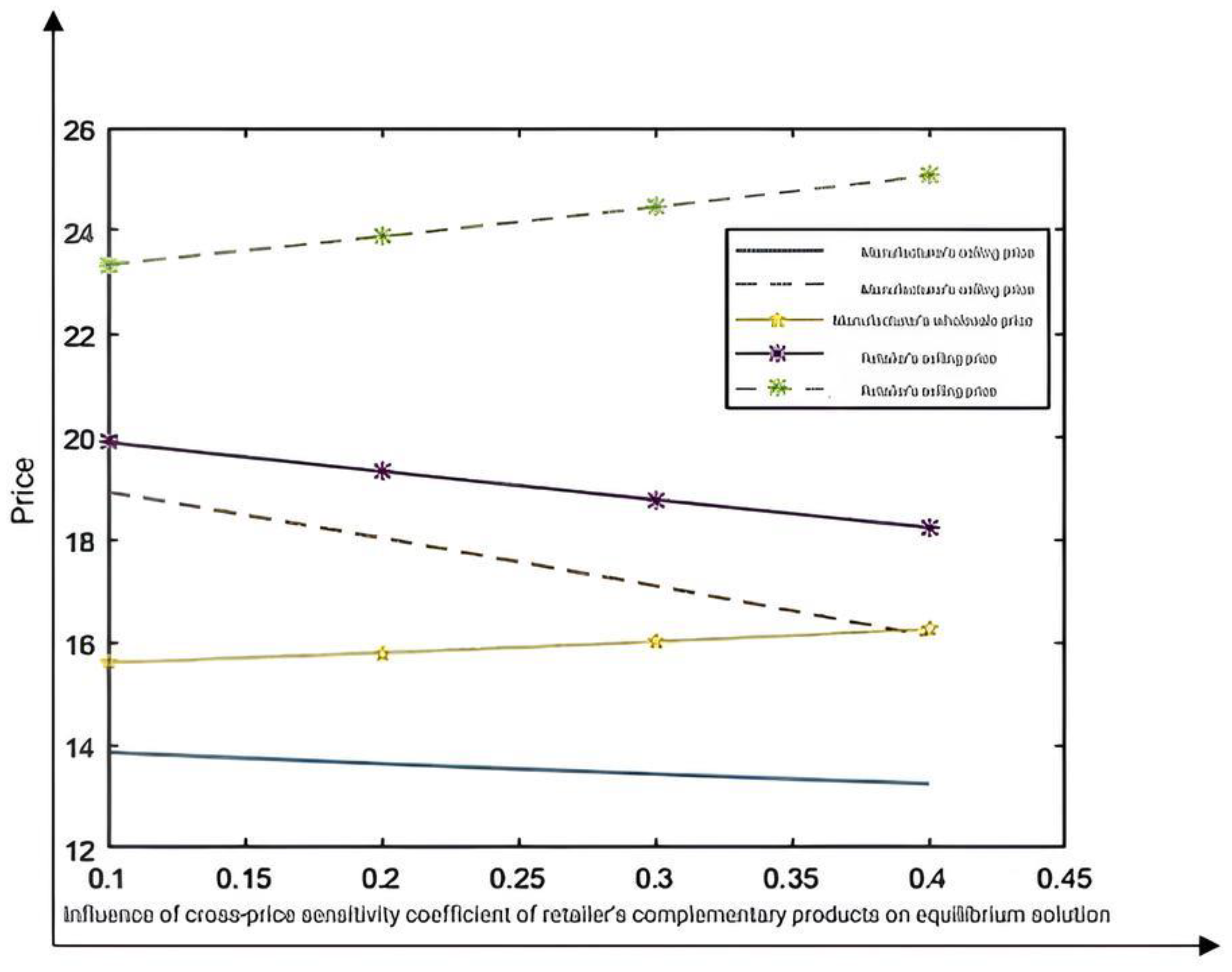
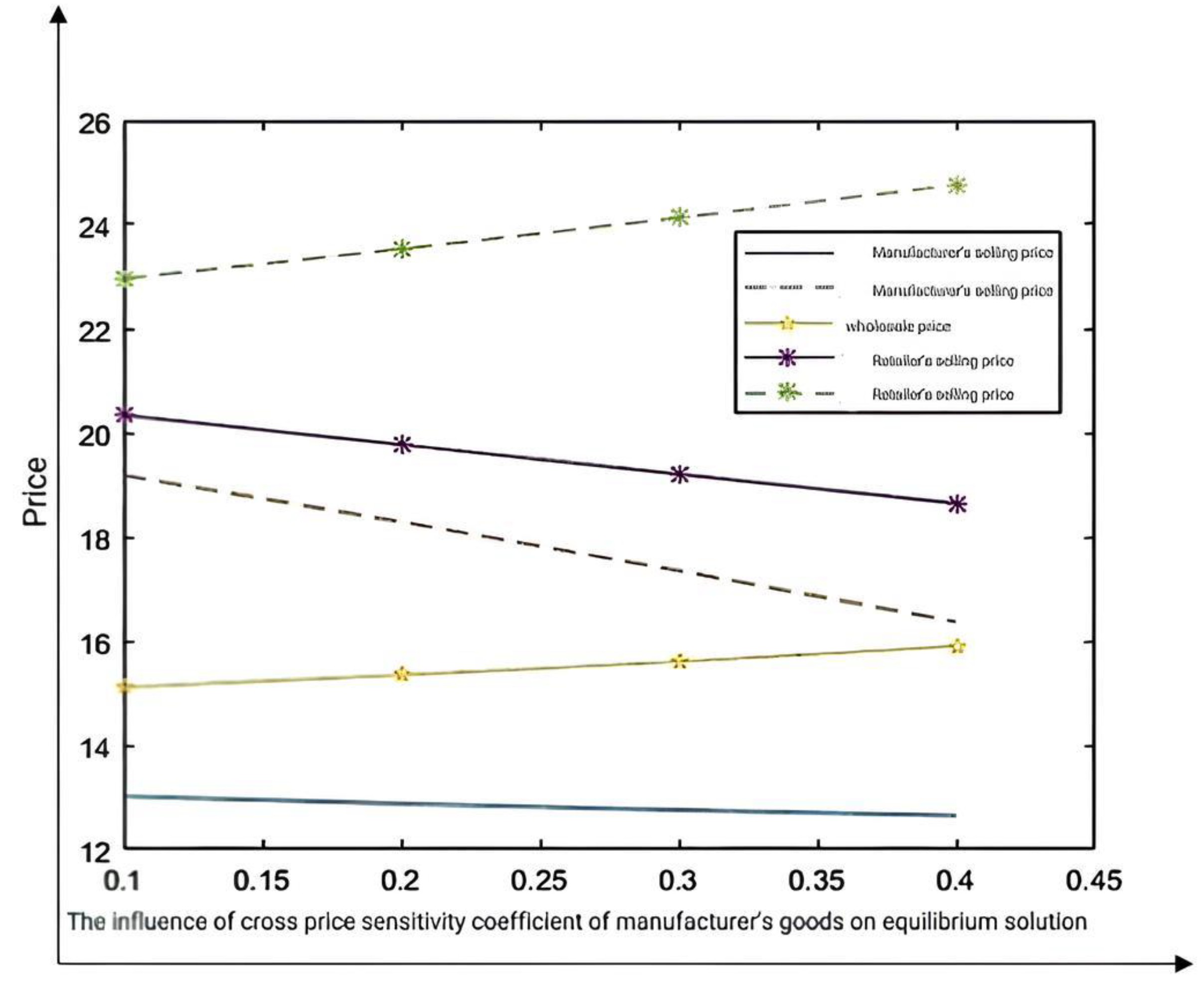
5.2. The Impact of ${\beta }_1$ on Equilibrium Prices

When analyzing the impact of ${\mathsf{\beta }}_1$ on equilibrium prices, let us assign the values as $\mathrm{a}=100$, $\mathrm{b}=50$, ${\mathsf{\alpha }}_1=3$, ${\mathsf{\alpha }}_2=1$, ${\mathsf{\beta }}_2=1$, ${\mathsf{\beta }}_1\in [0.1,0.4]$, $\mathrm{c}=5$, which satisfy all the aforementioned prerequisites. Based on these values, the influence of ${\mathsf{\beta }}_1$ on equilibrium prices can be illustrated as shown in Figure 3.

The findings underscore the strategic value of leveraging high cross-price elasticity in dual-channel environments. When CPEC is high, coordinated price reductions across complementary products can drive mutual demand growth and accelerate inventory turnover.

In centralized structures, firms should actively adopt bidirectional promotional strategies, using real-time sales data to dynamically adjust prices across channels. This helps minimize inventory holding costs and improves system responsiveness.

For decentralized supply chains, asymmetric information and misaligned incentives may lead to pricing inefficiencies. Manufacturers may increase wholesale prices in response to growing retailer orders, potentially undermining retailer margins.

To mitigate this, firms can establish data-sharing platforms or long-term contract mechanisms to enable better coordination. Pricing strategies should be aligned not only with own-channel objectives but also with cross-channel externalities, especially when products exhibit strong complementarity.

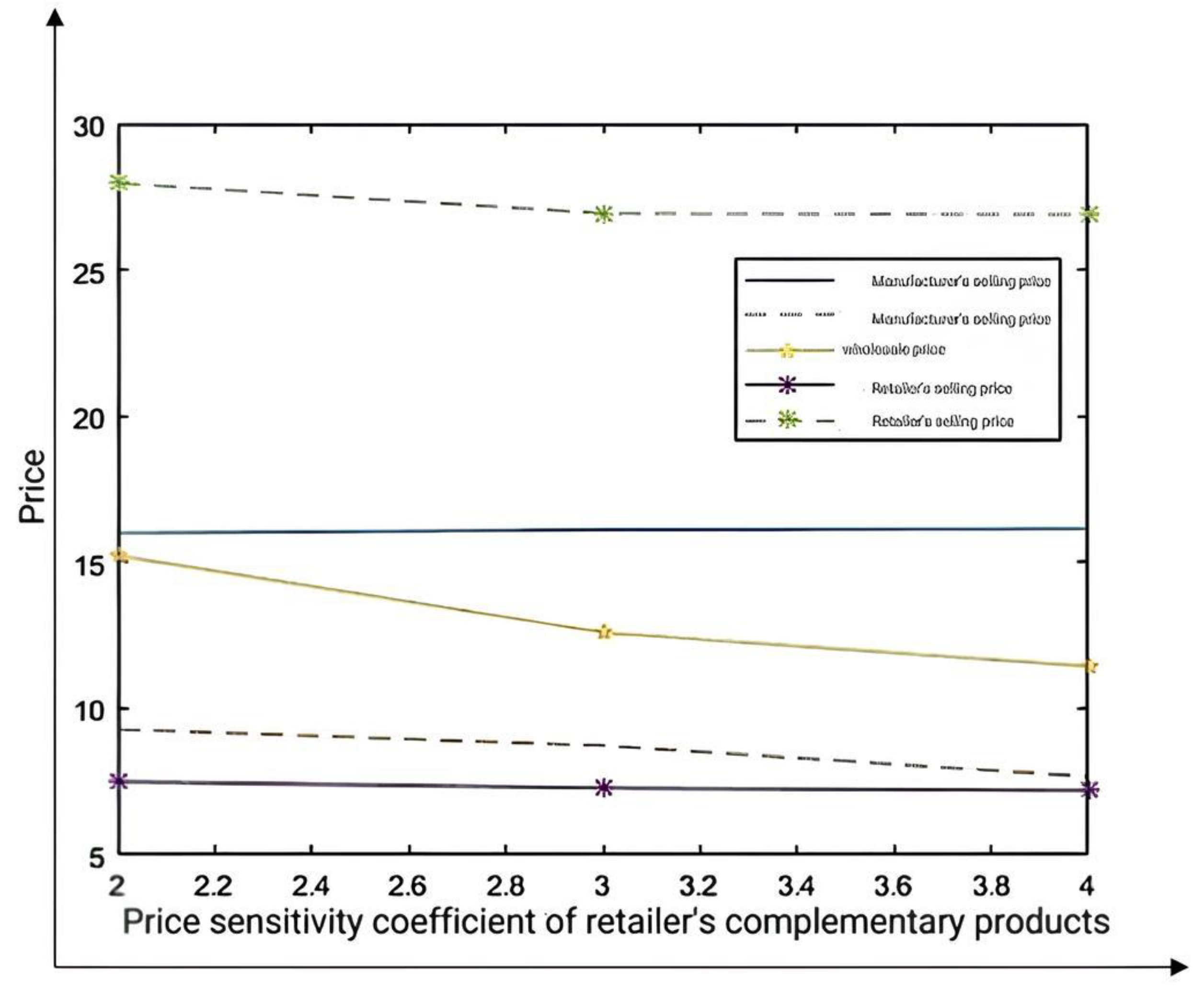
5.3. The Impact of ${\alpha }_2$ on Equilibrium Prices

To analyze the impact of ${\mathsf{\alpha }}_1$ on equilibrium prices, let us assign the values as $\mathrm{a}=100,\mathrm{b}=50,{\mathsf{\alpha }}_1=3,{\mathsf{\alpha }}_2\in [2,4],{\mathsf{\beta }}_1=2,{\mathsf{\beta }}_2=1,\mathrm{c}=5$, which satisfy all the aforementioned prerequisites. Based on these values, the influence of ${\mathsf{\alpha }}_2$ on equilibrium prices can be illustrated as shown in Figure 4.

When retailers face high price elasticity on complementary products, firms can strategically use loss-leader pricing to stimulate cross-channel demand. In centralized systems, this allows the retailer to attract foot traffic and offload inventory, while the manufacturer benefits from increased demand in the direct sales channel—achieving channel synergy.

For decentralized systems, the presence of a dominant manufacturer with greater information access leads to coordinated but self-interested price adjustments, such as lowering both the direct-sale product price and the wholesale price offered to retailers.

This dynamic highlights the importance of transparent information sharing and aligned incentives in decentralized systems to avoid unilateral profit-seeking that could destabilize channel collaboration.

Managers should therefore consider designing pricing contracts or profit-sharing schemes that encourage both parties to leverage high-elasticity products collaboratively, improving overall performance while reducing channel conflict.

5.4. The Impact of ${\beta }_2$ on Equilibrium Price

To analyze the impact of ${\mathsf{\beta }}_2$ on equilibrium prices, let us define variables as follows: $\mathrm{a}=100,\mathrm{b}=50,{\mathsf{\alpha }}_1=3,{\mathsf{\alpha }}_2=1,{\mathsf{\beta }}_1=1,\mathrm{c}=5$. Under these conditions $,{\mathsf{\beta }}_2\in [0.1,0.4]$, the influence of ${\mathsf{\beta }}_2$ on the equilibrium price can be illustrated as shown in Figure 5.

The above analysis reveals several key managerial implications. First, coordination among supply chain members significantly improves overall performance. In a centralized decision-making scenario, both the manufacturer and retailer adopt mutually supportive pricing strategies, leveraging cross-price elasticity to stimulate demand across channels and enhance total supply chain profit. This highlights the value of integrated supply chain management and strategic collaboration.

Second, in decentralized scenarios, individual profit maximization leads to pricing conflicts and potential inefficiencies. The manufacturer lowers prices to stimulate complementary demand, but the retailer responds with a price increase to protect its margins, leading to a mismatch in pricing strategies and suboptimal outcomes for the supply chain as a whole.

Therefore, establishing coordination mechanisms—such as revenue-sharing contracts, two-part tariffs, or joint pricing strategies—can mitigate the negative impact of decentralized decisions and align incentives across partners. Moreover, supply chain leaders should pay attention to cross-price elasticity dynamics when designing channel strategies, as coordinated pricing adjustments can be used as a tool for market expansion and profit optimization.

This paper, for the first time, integrates the positive spillover effects of demand for complementary products with the price conflict arising from dual-channel strategies, and develops a collaborative model for a three-tier supply chain (manufacturer–retailer–consumer). It demonstrates how high-elasticity products can be employed as loss leaders to align the interests of various channels.

Based on an analysis of price sensitivity coefficients and cross-price elasticity, the study highlights the positive externalities associated with service inputs (e.g., smart door lock services boosting the demand for smart home products), thus establishing a foundation for future research on service cost-sharing mechanisms.

Furthermore, by comparing centralized decision-making with a Stackelberg game framework dominated by manufacturers, the paper proves that centralized decision-making results in lower prices and higher overall profits. It also quantifies the dynamic relationship between wholesale prices and market demand under manufacturer-dominant scenarios. Numerical simulations further validate the differentiated impacts of elasticity coefficient variations on equilibrium prices.

6. Conclusions and Outlook

6.1. Conclusions

With the establishment of manufacturers’ online direct sales channels, conflicts have gradually arisen with traditional manufacturer–retailer channel models. Complementary products have been introduced as a channel mitigation factor to alleviate these conflicts. Enterprises aim to maximize their interests by leveraging the free-riding effect among complementary products and engaging in price competition with each other to achieve their goals. This paper considers the establishment of centralized decision-making and manufacturer-led Stackelberg game decision-making in the context of dual-channel sales of complementary products, focusing on analyzing the relationship between prices and various factors. It concludes that, in general, centralized decision-making results in lower sales prices than decentralized decision-making, and consumers obtain more excellent utility under centralized decision-making. In centralized decision-making, when the manufacturer or the retailer has a higher price sensitivity coefficient, they will reduce the sales price of their products. At the same time, the other party will increase the sales price of their complementary products, fully utilizing the positive spillover effect between complementary products. However, in decentralized decision-making, retailers, as weaker enterprises, will always adopt a price reduction strategy.

In contrast, retailers will adjust the prices of direct sales products and the wholesale prices of complementary products sold to retailers based on the situation. In centralized decision-making, both parties will adopt price reduction strategies as cross-price elasticity increases. In decentralized decision-making, as cross-price elasticity increases, manufacturers will adopt price reduction strategies while increasing the wholesale prices of complementary products, increasing retailers’ retail prices. With society’s rapid development, constantly changing consumer preferences, and increasing demands for services, simply considering price factors can no longer meet consumer needs. Introducing service levels into dual-channel supply chains for complementary products represents the next research direction.

In real-world settings, managers often face challenges such as incomplete market information, consumer preference uncertainty, and brand positioning constraints. To effectively apply the pricing strategy proposed in this article, managers can start from the following aspects:

Data-Driven Demand Estimation: Managers should invest in advanced analytics to estimate real-time demand elasticity and cross-price effects, even with incomplete information.

Dynamic Pricing Mechanisms: Implement dynamic pricing models that can adapt quickly to market feedback, using machine learning techniques where possible.

Brand-Consistent Strategy Design: Pricing adjustments for complementary products must align with the brand image. For example, luxury brands may selectively lower complementary product prices without devaluing the core product.

Multi-Channel Communication Coordination: Ensure that promotional activities across online direct channels and traditional retail channels are harmonized to prevent consumer confusion and brand dilution.

These practical guidelines help translate theoretical insights into actionable strategies, enabling firms to better manage dual-channel conflicts under real-world constraints.

This article proposes a strategic loss-leader pricing approach (Corollary 3) and a dynamic pricing mechanism (Section 6.1), demonstrating their practical efficacy in dual-channel coordination. For instance, home appliance manufacturers (e.g., Midea) can leverage online price reductions for complementary products (e.g., air purifiers) to stimulate demand for core products (e.g., air conditioners) in offline retail channels, thereby optimizing cross-channel profitability.

Furthermore, the proposed model facilitates data-driven elasticity estimation (Section 5), enabling firms to quantify demand sensitivity and adjust pricing strategies in real time. Additionally, it provides a theoretical foundation for designing cross-channel coordination contracts, such as wholesale price adjustments or revenue-sharing agreements, to mitigate channel conflicts and enhance supply chain efficiency.

6.2. Outlooks

This paper considers the relationship between price and service levels in dual-channel supply chains for complementary products under ideal conditions. It does not consider the impact of inventory and stockouts on prices during production and operation. Therefore, the following research direction is to incorporate inventory as an important influencing factor in dual-channel supply chains for complementary products and to adopt stochastic demand functions in the selection of demand functions to better reflect the relationships between service levels and complementary product inventory, service levels, complementary product pricing, and profits. Corresponding contracts will also be designed to improve the performance of dual-channel sales of complementary products.

While this study adopts a static game-theoretic framework, future research could benefit from more dynamic and adaptive approaches. For instance, evolutionary game theory can model how supply chain members adjust their strategies over time through repeated interactions and bounded rational learning. This would be particularly useful in capturing real-world behavior where information is incomplete or participants are heterogeneous.

In addition, dynamic optimal control methods can be employed to analyze multi-period pricing and coordination strategies under environmental constraints, demand volatility, and investment decisions—similar to their recent applications in carbon capture and sustainable technology innovation [40].

These methodologies offer promising directions for enhancing the realism and robustness of supply chain conflict resolution models.

Meanwhile, the combination of the latest artificial intelligence can bring new thoughts to future research directions.

Inventory decisions under random demand can be expanded by incorporating AI-driven inventory forecasting tools, which can achieve timely coordination and minimize holding costs to the greatest extent.

AI-driven pricing algorithms can adjust pricing strategies dynamically. Consumer personalization technologies can modify prices based on customer behavior, purchasing patterns, and real-time feedback from both online and offline channels.

Applying evolutionary game theory and dynamic optimal control can capture adaptive strategy learning among channel participants, especially under information asymmetry or bounded rationality. Future research may also explore how reinforcement learning techniques can help enterprises optimize pricing and service strategies in complex and constantly changing markets.