Empirical Insights into Economic Viability: Integrating Bitcoin Mining with Biorefineries Using a Stochastic Model
Abstract
1. Introduction
2. Bitcoin Mining: Technical Background and Economic Rationale
3. Methodology
3.1. Minimum Profitable Mining Price and Profitability Criterion
3.2. Model Assumptions and Key Details
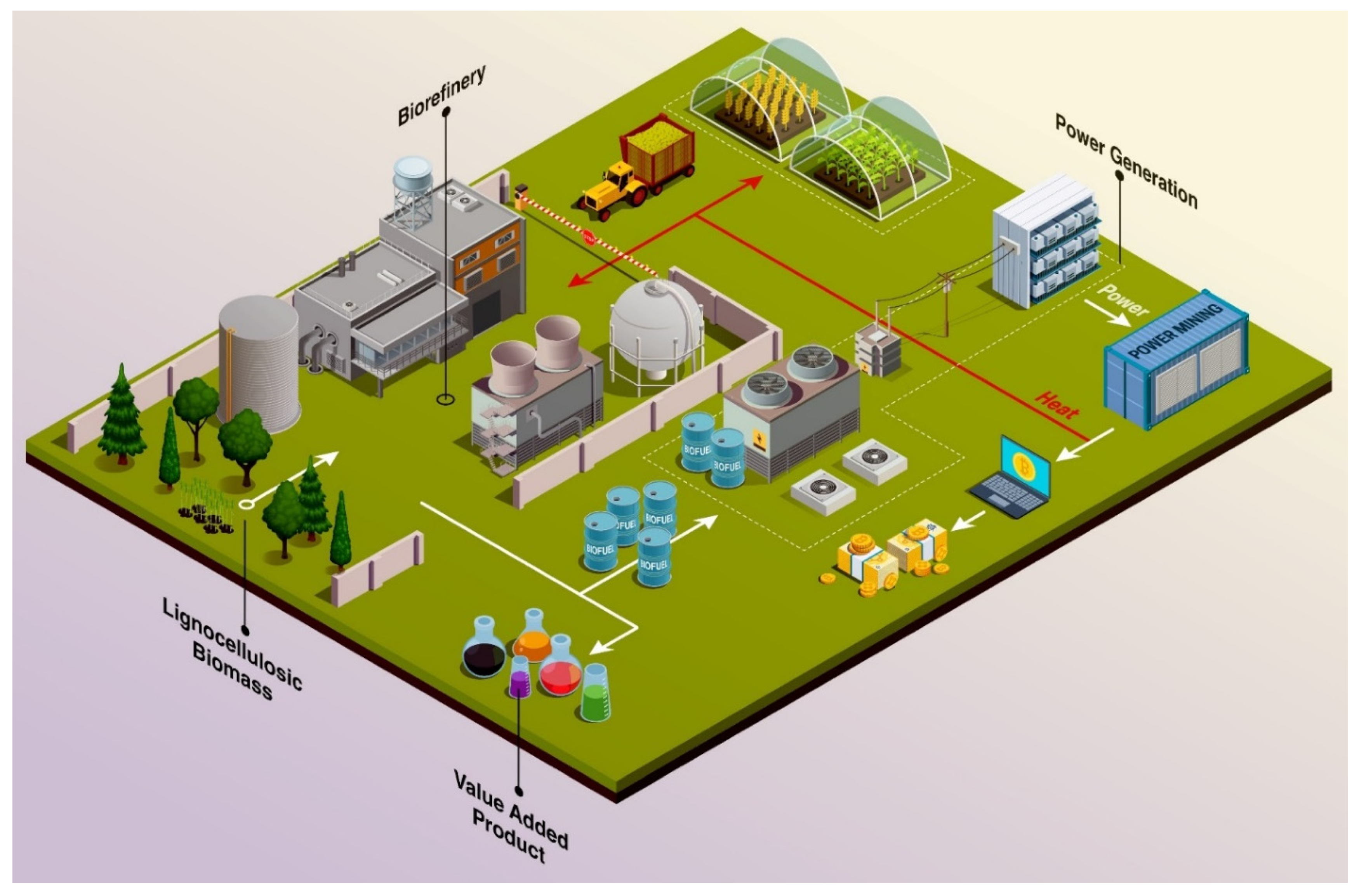
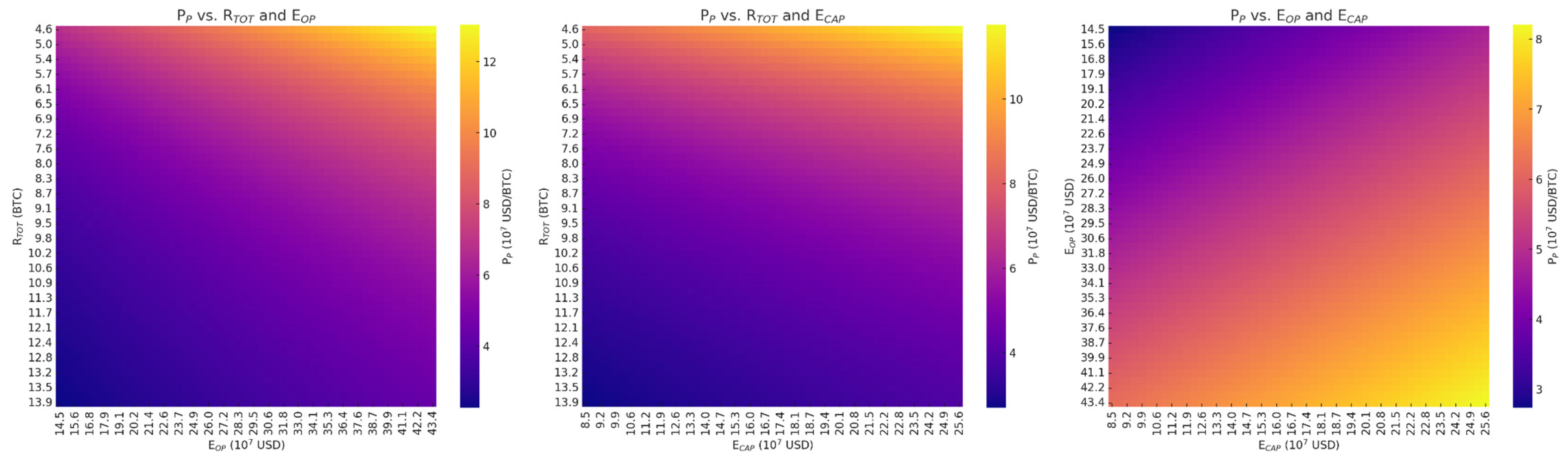
4. Results and Discussion
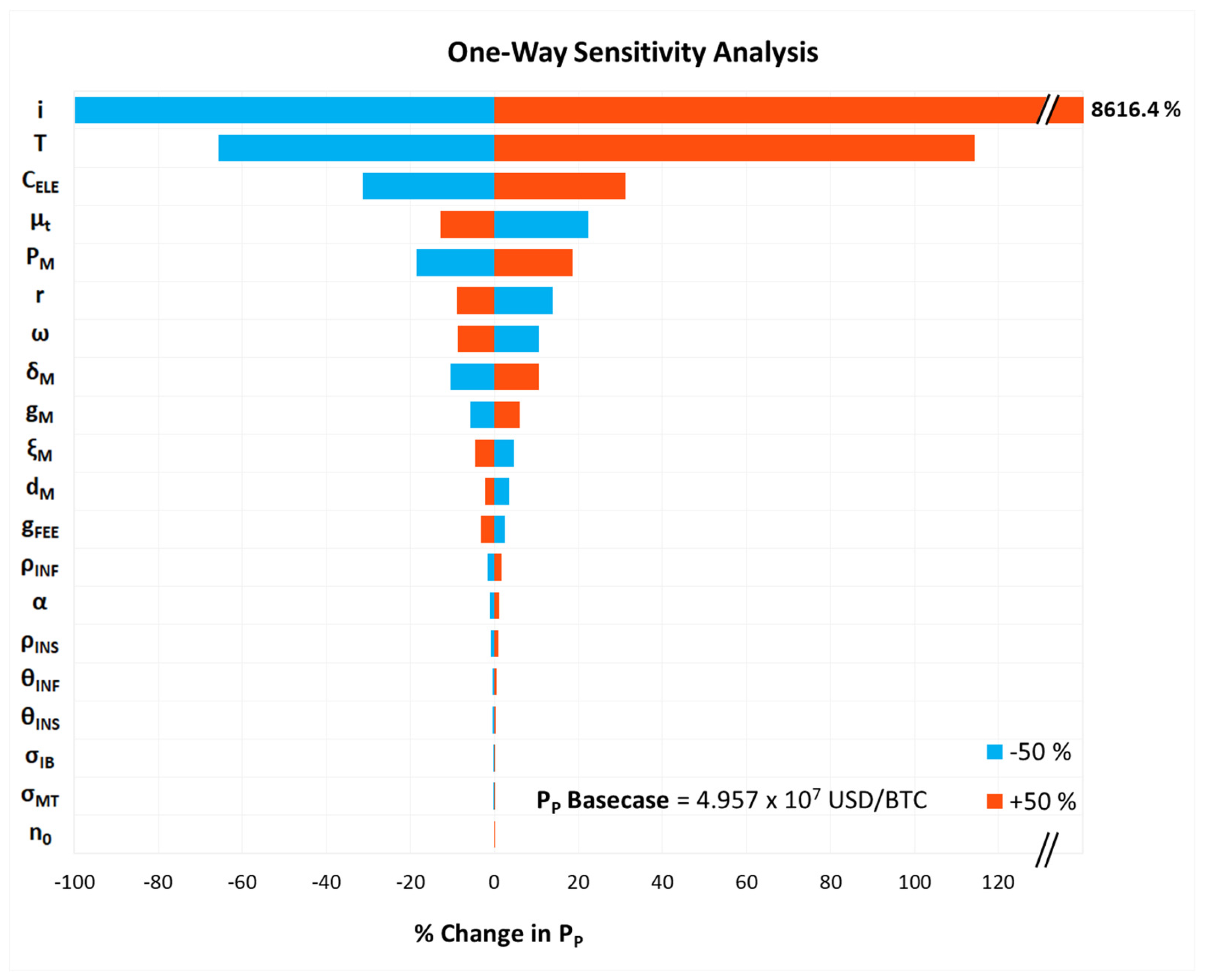
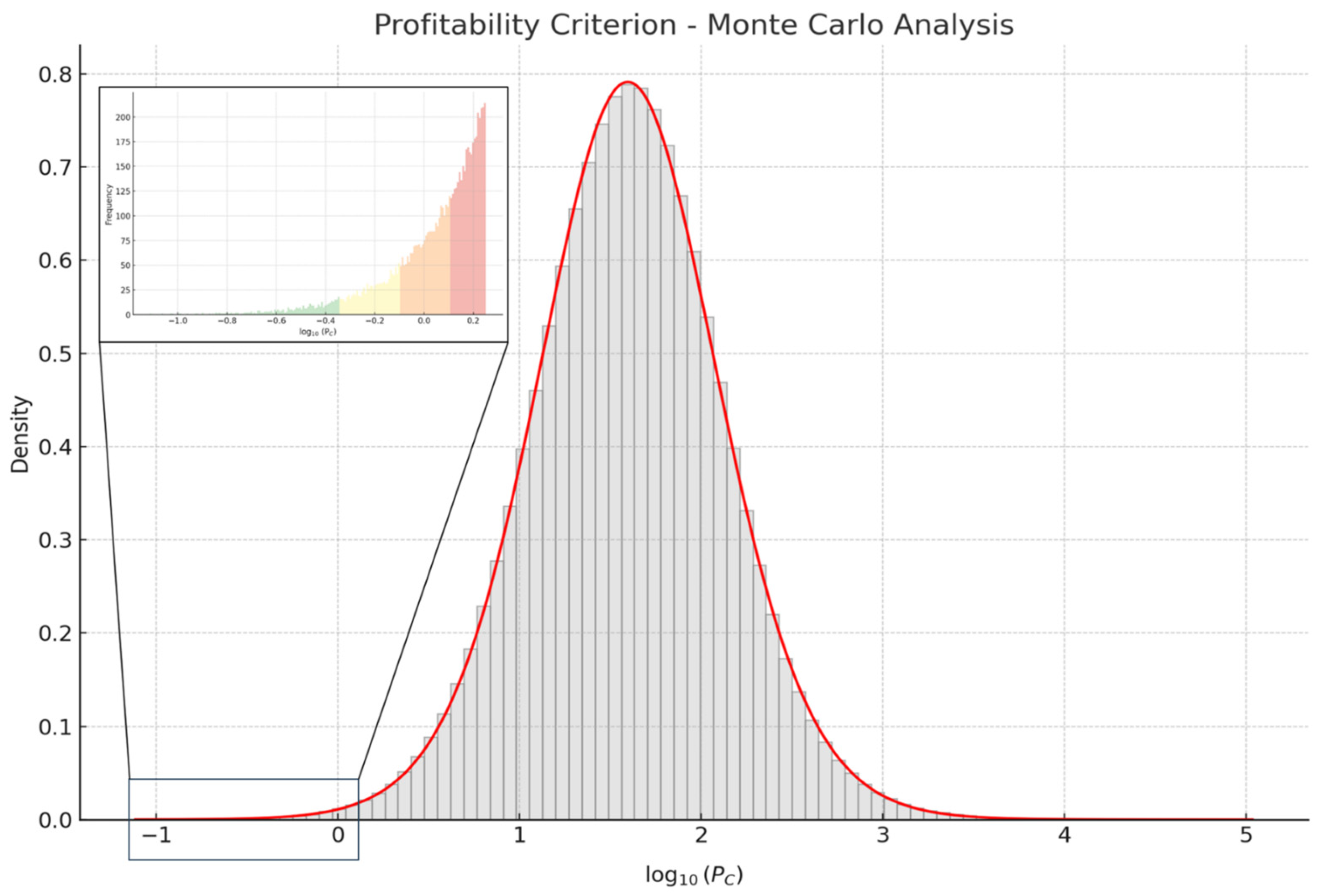
Sensitivity Analysis and Monte Carlo Simulations
5. Model Limitations and Other Considerations
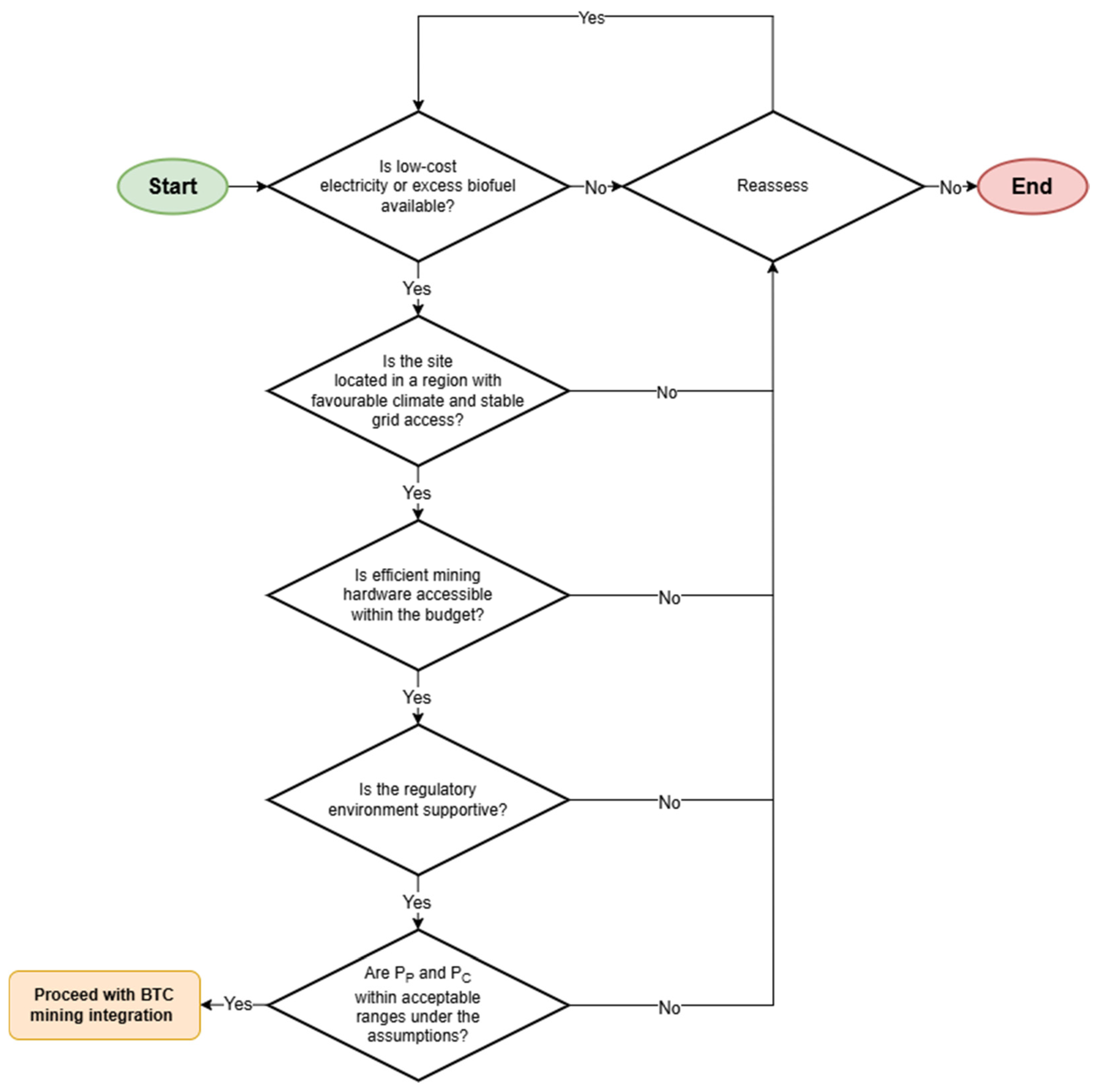
6. Environmental Concerns, Regulations, Risks, Opportunities, and Other Issues
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Minimum profitable mining price. | |
| Total cost over mining operational time. | |
| Capital expenditure over mining operational time. | |
| Operational expenditure over mining operational time. | |
| Total Bitcoin revenue over mining operational time. | |
| Profitability criterion. | |
| Bitcoin spot price. | |
| Number of ASICs. | |
| Number of Bitcoin mined during year t. | |
| Growth rate in number of ASICs over epoch. | |
| Decay rate in number of ASICs over epoch. | |
| Cost of computation per ASIC. | |
| Year-over-year decrease in the cost of computation. | |
| IB-specific costs related to mining. | |
| Total ASIC cost. | |
| Bulk discount for large ASIC purchases. | |
| Annual percentage ASIC depreciation. | |
| Discount rate. | |
| Cost fraction assigned to infrastructure at t = i. | |
| Cost fraction assigned to installation at t = i. | |
| Cost fraction assigned to infrastructure at τ. | |
| Cost fraction assigned to installation at τ. | |
| Maintenance-related costs. | |
| Cost of electricity. | |
| ASIC hashrate. | |
| ASIC efficiency. | |
| Total network hashrate. | |
| Bitcoin block subsidy. | |
| Bitcoin fees per block. | |
| Fee growth rate. | |
| Mining pool fees. | |
| Number of blocks generated per year. | |
| Current year. | |
| Initial year of operation. | |
| Total operational time. | |
| Epoch (210,000 blocks ≈ 4 years). |
References
- Ning, P.; Yang, G.; Hu, L.; Sun, J.; Shi, L.; Zhou, Y.; Wang, Z.; Yang, J. Recent advances in the valorization of plant biomass. Biotechnol. Biofuels 2021, 14, 102. [Google Scholar] [CrossRef] [PubMed]
- González-González, R.B.; Iqbal, H.M.N.; Bilal, M.; Parra-Saldívar, R. (Re)-thinking the bio-prospect of lignin biomass recycling to meet Sustainable Development Goals and circular economy aspects. Curr. Opin. Green Sustain. Chem. 2022, 38, 100699. [Google Scholar] [CrossRef]
- Dahmen, N.; Lewandowski, I.; Zibek, S.; Weidtmann, A. Integrated lignocellulosic value chains in a growing bioeconomy: Status quo and perspectives. GCB Bioenergy 2019, 11, 107–117. [Google Scholar] [CrossRef]
- Macias Aragonés, M.; de la Viña Nieto, G.; Nieto Fajardo, M.; Páez Rodríguez, D.; Gaffey, J.; Attard, J.; McMahon, H.; Doody, P.; Anda Ugarte, J.; Pérez-Camacho, M.N.; et al. Digital Innovation Hubs as a Tool for Boosting Biomass Valorisation in Regional Bioeconomies: Andalusian and South-East Irish Case Studies. J. Open Innov. Technol. Mark. Complex. 2020, 6, 115. [Google Scholar] [CrossRef]
- Bhatia, S.K.; Jagtap, S.S.; Bedekar, A.A.; Bhatia, R.K.; Patel, A.K.; Pant, D.; Rajesh Banu, J.; Rao, C.V.; Kim, Y.-G.; Yang, Y.-H. Recent developments in pretreatment technologies on lignocellulosic biomass: Effect of key parameters, technological improvements, and challenges. Bioresour. Technol. 2020, 300, 122724. [Google Scholar] [CrossRef]
- Patel, A.; Shah, A.R. Integrated lignocellulosic biorefinery: Gateway for production of second generation ethanol and value added products. J. Bioresour. Bioprod. 2021, 6, 108–128. [Google Scholar] [CrossRef]
- Clauser, N.M.; Felissia, F.E.; Area, M.C.; Vallejos, M.E. A framework for the design and analysis of integrated multi-product biorefineries from agricultural and forestry wastes. Renew. Sustain. Energy Rev. 2021, 139, 110687. [Google Scholar] [CrossRef]
- Vu, H.P.; Nguyen, L.N.; Vu, M.T.; Johir, M.A.H.; McLaughlan, R.; Nghiem, L.D. A comprehensive review on the framework to valorise lignocellulosic biomass as biorefinery feedstocks. Sci. Total Environ. 2020, 743, 140630. [Google Scholar] [CrossRef]
- Ioannidou, S.M.; Galanopoulos, C.; Ladakis, D.; Koutinas, A. Chapter 21—Techno-economic evaluation and life-cycle assessment of integrated biorefineries within a circular bioeconomy concept. In Biomass, Biofuels, Biochemicals; Varjani, S., Pandey, A., Bhaskar, T., Mohan, S.V., Tsang, D.C.W., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 541–556. [Google Scholar] [CrossRef]
- Sharma, V.; Tsai, M.-L.; Nargotra, P.; Chen, C.-W.; Sun, P.-P.; Singhania, R.R.; Patel, A.K.; Dong, C.-D. Journey of lignin from a roadblock to bridge for lignocellulose biorefineries: A comprehensive review. Sci. Total Environ. 2023, 861, 160560. [Google Scholar] [CrossRef]
- Yuan, Z.; Bals, B.D.; Hegg, E.L.; Hodge, D.B. Technoeconomic evaluation of recent process improvements in production of sugar and high-value lignin co-products via two-stage Cu-catalyzed alkaline-oxidative pretreatment. Biotechnol. Biofuels Bioprod. 2022, 15, 45. [Google Scholar] [CrossRef]
- Martinez-Hernandez, E.; Cui, X.; Scown, C.D.; Amezcua-Allieri, M.A.; Aburto, J.; Simmons, B.A. Techno-economic and greenhouse gas analyses of lignin valorization to eugenol and phenolic products in integrated ethanol biorefineries. Biofuels Bioprod. Biorefin. 2019, 13, 978–993. [Google Scholar] [CrossRef]
- Halder, P.; Shah, K. Techno-economic analysis of ionic liquid pre-treatment integrated pyrolysis of biomass for co-production of furfural and levoglucosenone. Bioresour. Technol. 2023, 371, 128587. [Google Scholar] [CrossRef] [PubMed]
- Seufitelli, G.V.S.; El-Husseini, H.; Pascoli, D.U.; Bura, R.; Gustafson, R. Techno-economic analysis of an integrated biorefinery to convert poplar into jet fuel, xylitol, and formic acid. Biotechnol. Biofuels Bioprod. 2022, 15, 143. [Google Scholar] [CrossRef]
- Morakile, T.; Mandegari, M.; Farzad, S.; Görgens, J.F. Comparative techno-economic assessment of sugarcane biorefineries producing glutamic acid, levulinic acid and xylitol from sugarcane. Ind. Crops Prod. 2022, 184, 115053. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System; 2008; p. 9. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 5 March 2023).
- Wang, G.; Hausken, K. Unravelling the global landscape of Bitcoin research: Insights from bibliometric analysis. Technol. Anal. Strateg. Manag. 2024, 1–18. [Google Scholar] [CrossRef]
- Sánchez Bayón, A.; García Ramos, M.Á. A win-win case of CSR 3.0 for wellbeing economics: Digital currencies as a tool to improve the personnel income, the environmental respect & the general wellness. REVESCO. Rev. Estud. Coop. 2021, 138, e75564. [Google Scholar] [CrossRef]
- Velický, M. Renewable Energy Transition Facilitated by Bitcoin. ACS Sustain. Chem. Eng. 2023, 11, 3160–3169. [Google Scholar] [CrossRef]
- Rudd, M.A.; Jones, M.; Sechrest, D.; Batten, D.; Porter, D. An integrated landfill gas-to-energy and Bitcoin mining framework. J. Clean. Prod. 2024, 472, 143516. [Google Scholar] [CrossRef]
- Ehyaei, M.A.; Esmaeilion, F.; Shamoushaki, M.; Afshari, H.; Das, B. The feasibility study of the production of Bitcoin with geothermal energy: Case study. Energy Sci. Eng. 2024, 12, 755–770. [Google Scholar] [CrossRef]
- Moreno, D.; Antoli, M.; Quintana, D. Benefits of investing in cryptocurrencies when liquidity is a factor. Res. Int. Bus. Financ. 2022, 63, 101751. [Google Scholar] [CrossRef]
- Velvizhi, G.; Balakumar, K.; Shetti, N.P.; Ahmad, E.; Kishore Pant, K.; Aminabhavi, T.M. Integrated biorefinery processes for conversion of lignocellulosic biomass to value added materials: Paving a path towards circular economy. Bioresour. Technol. 2022, 343, 126151. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, Y. Micro gas turbine: Developments, applications, and key technologies on components. Propuls. Power Res. 2023, 12, 1–43. [Google Scholar] [CrossRef]
- Semaan, G.; Wang, G.; Vo, Q.S.; Kumar, G. The Potential Relationship between Biomass, Biorefineries, and Bitcoin. Sustainability 2024, 16, 7919. [Google Scholar] [CrossRef]
- Semret, N. Dynamics of Bitcoin mining. arXiv 2022, arXiv:2201.06072. [Google Scholar] [CrossRef]
- Rudd, M.A.; Bratcher, L.; Collins, S.; Branscum, D.; Carson, M.; Connell, S.; David, E.; Gronowska, M.; Hess, S.; Mitchell, A.; et al. Bitcoin and Its Energy, Environmental, and Social Impacts: An Assessment of Key Research Needs in the Mining Sector. Challenges 2023, 14, 47. [Google Scholar] [CrossRef]
- Rudd, M.A. Bitcoin Is Full of Surprises. Challenges 2023, 14, 27. [Google Scholar] [CrossRef]
- Lal, A.; Niaz, H.; Liu, J.J.; You, F. Can bitcoin mining empower energy transition and fuel sustainable development goals in the US? J. Clean. Prod. 2024, 439, 140799. [Google Scholar] [CrossRef]
- Lal, A.; You, F. Climate sustainability through a dynamic duo: Green hydrogen and crypto driving energy transition and decarbonization. Proc. Natl. Acad. Sci. USA 2024, 121, e2313911121. [Google Scholar] [CrossRef]
- Lal, A.; Zhu, J.; You, F. From Mining to Mitigation: How Bitcoin Can Support Renewable Energy Development and Climate Action. ACS Sustain. Chem. Eng. 2023, 11, 16330–16340. [Google Scholar] [CrossRef]
- KPMG. Bitcoin’s Role in the ESG Imperative: An Overview of the Opportunities and Creative Approaches That Deliver Value and Drive Trust with Key Stakeholders; KPMG LLP.: London, UK, 2023; Available online: https://kpmg.com/kpmg-us/content/dam/kpmg/pdf/2023/bitcoins-role-esg-imperative.pdf (accessed on 29 May 2024).
- Malfuzi, A.; Mehr, A.S.; Rosen, M.A.; Alharthi, M.; Kurilova, A.A. Economic viability of bitcoin mining using a renewable-based SOFC power system to supply the electrical power demand. Energy 2020, 203, 117843. [Google Scholar] [CrossRef]
- Niaz, H.; Liu, J.J.; You, F. Can Texas mitigate wind and solar curtailments by leveraging bitcoin mining? J. Clean. Prod. 2022, 364, 132700. [Google Scholar] [CrossRef]
- Ghaebi Panah, P.; Bornapour, M.; Cui, X.; Guerrero, J.M. Investment opportunities: Hydrogen production or BTC mining? Int. J. Hydrogen Energy 2022, 47, 5733–5744. [Google Scholar] [CrossRef]
- Bastian-Pinto, C.L.; Araujo, F.V.d.S.; Brandão, L.E.; Gomes, L.L. Hedging renewable energy investments with Bitcoin mining. Renew. Sustain. Energy Rev. 2021, 138, 110520. [Google Scholar] [CrossRef]
- Snytnikov, P.; Potemkin, D. Flare gas monetization and greener hydrogen production via combination with cryptocurrency mining and carbon dioxide capture. iScience 2022, 25, 103769. [Google Scholar] [CrossRef]
- Treiblmaier, H. A comprehensive research framework for Bitcoin’s energy use: Fundamentals, economic rationale, and a pinch of thermodynamics. Blockchain Res. Appl. 2023, 4, 100149. [Google Scholar] [CrossRef]
- Andoni, M.; Robu, V.; Flynn, D.; Abram, S.; Geach, D.; Jenkins, D.; McCallum, P.; Peacock, A. Blockchain technology in the energy sector: A systematic review of challenges and opportunities. Renew. Sustain. Energy Rev. 2019, 100, 143–174. [Google Scholar] [CrossRef]
- Podhorsky, A. Bursting the bitcoin bubble: Do market prices reflect fundamental bitcoin value? Int. Rev. Financ. Anal. 2024, 93, 103158. [Google Scholar] [CrossRef]
- Ammous, S.; D’Andrea, F.A.M.C. Hard Money and Time Preference: A Bitcoin perspective. MISES Interdiscip. J. Philos. Law Econ. 2022, 10, 1–17. [Google Scholar] [CrossRef]
- Borodin, A.; Mityushina, I.; Streltsova, E.; Kulikov, A.; Yakovenko, I.; Namitulina, A. Mathematical Modeling for Financial Analysis of an Enterprise: Motivating of Not Open Innovation. J. Open Innov. Technol. Mark. Complex. 2021, 7, 79. [Google Scholar] [CrossRef]
- Power, A.J. Bitcoin Mining Industry Report. Available online: https://education.compassmining.io/education/bitcoin-mining-industry-report/ (accessed on 2 May 2025).
- Santostasi, G. The Bitcoin Power Law Theory. Available online: https://giovannisantostasi.medium.com/the-bitcoin-power-law-theory-962dfaf99ee9 (accessed on 24 April 2024).
- Santostasi, G. The Physics of Bitcoin. Available online: https://giovannisantostasi.medium.com/btc-is-a-power-law-because-it-is-an-infinite-recursive-feedback-loop-5f54de5e501b (accessed on 24 April 2024).
- Luxor. Bitcoin ASIC Price Index. Luxor Technology Corp. Available online: https://data.hashrateindex.com/chart/asic-price-index (accessed on 30 April 2024).
- Hayes, A.S. Cryptocurrency value formation: An empirical study leading to a cost of production model for valuing bitcoin. Telemat. Inform. 2017, 34, 1308–1321. [Google Scholar] [CrossRef]
- Murthy, G.S. Chapter TWO—Techno-economic assessment. In Biomass, Biofuels, Biochemicals; Murthy, G.S., Gnansounou, E., Khanal, S.K., Pandey, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 17–32. [Google Scholar] [CrossRef]
- Kristoufek, L. Bitcoin and its mining on the equilibrium path. Energy Econ. 2020, 85, 104588. [Google Scholar] [CrossRef]
- Asgari, N.; McDonald, M.T.; Pearce, J.M. Energy Modeling and Techno-Economic Feasibility Analysis of Greenhouses for Tomato Cultivation Utilizing the Waste Heat of Cryptocurrency Miners. Energies 2023, 16, 1331. [Google Scholar] [CrossRef]
- Niaz, H.; Shams, M.H.; Liu, J.J.; You, F. Mining bitcoins with carbon capture and renewable energy for carbon neutrality across states in the USA. Energy Environ. Sci. 2022, 15, 3551–3570. [Google Scholar] [CrossRef]
- CCAF. Cambridge Bitcoin Electricity Consumption Index (CBECI). Cambridge Centre for Alternative Finance (CCAF). Available online: https://ccaf.io/cbnsi/cbeci (accessed on 29 May 2024).
- Tomatsu, Y.; Han, W. Bitcoin and Renewable Energy Mining: A Survey. Blockchains 2023, 1, 90–110. [Google Scholar] [CrossRef]
- Blandin, A.; Pieters, G.; Wu, Y.; Eisermann, T.; Dek, A.; Taylor, S.; Njoki, D. 3rd Global Cryptoasset Benchmarking Study; Cambridge Centre for Alternative Finance: Cambridge, UK, 2020; Available online: https://www.jbs.cam.ac.uk/faculty-research/centres/alternative-finance/publications/3rd-global-cryptoasset-benchmarking-study/ (accessed on 29 May 2024).
- Miśkiewicz, R.; Matan, K.; Karnowski, J. The Role of Crypto Trading in the Economy, Renewable Energy Consumption and Ecological Degradation. Energies 2022, 15, 3805. [Google Scholar] [CrossRef]
- Butler, S. Criminal use of cryptocurrencies: A great new threat or is cash still king? J. Cyber Policy 2019, 4, 326–345. [Google Scholar] [CrossRef]
- Mikhaylov, A. Cryptocurrency Market Analysis from the Open Innovation Perspective. J. Open Innov. Technol. Mark. Complex. 2020, 6, 197. [Google Scholar] [CrossRef]
- Griffith, T.; Clancey-Shang, D. Cryptocurrency regulation and market quality. J. Int. Financ. Mark. Inst. Money 2023, 84, 101744. [Google Scholar] [CrossRef]

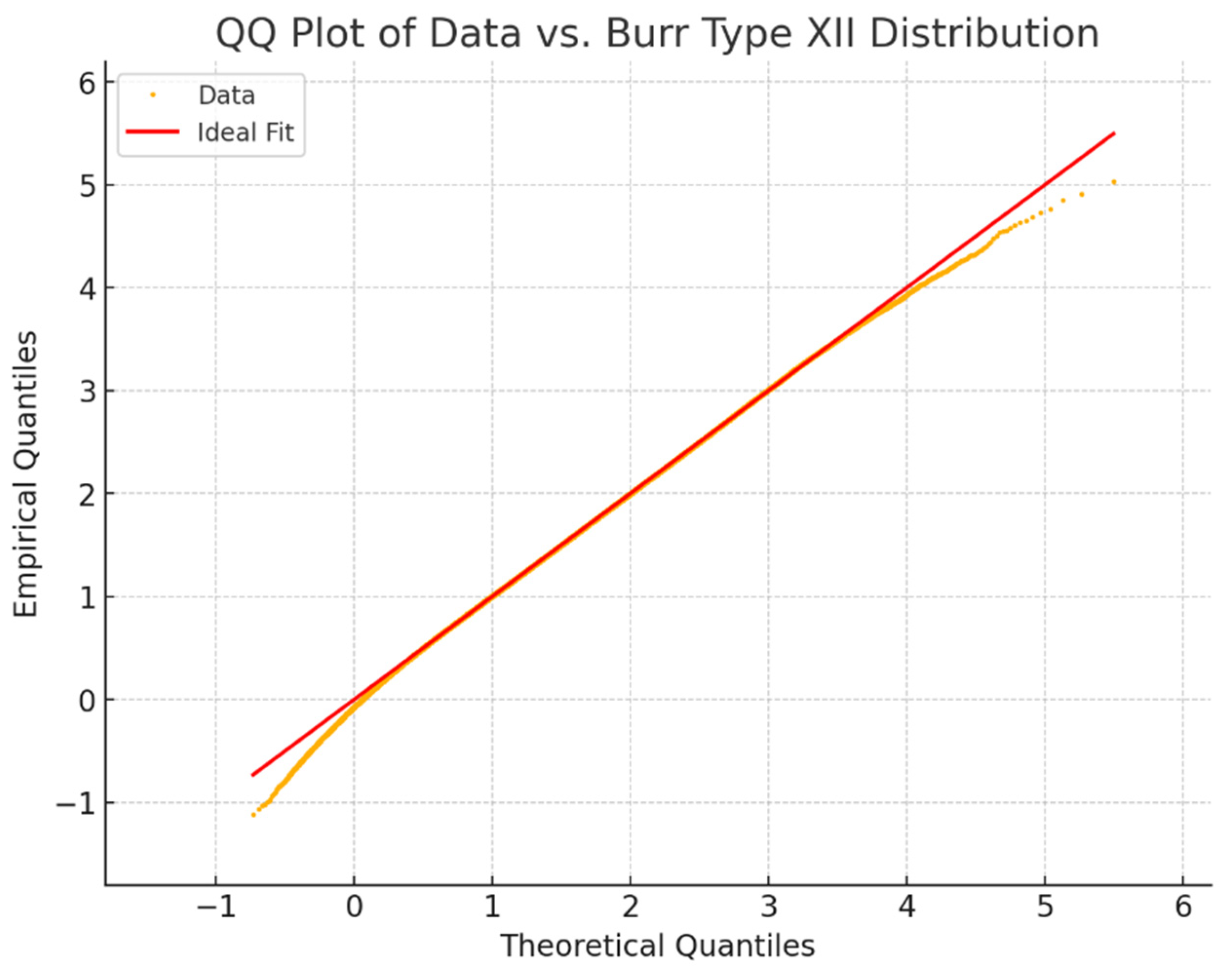
| Parameter Information | Statistics | |||||
|---|---|---|---|---|---|---|
| Parameter | Units | Distribution | Mean | Standard Deviation | 5th Percentile | 95th Percentile |
| T | Years | Discrete Uniform Distribution (min = 6; max = 34) a | 20 | 8.08 | 7.4 | 32.6 |
| σIB | USD/ASIC/year | Log-Normal Distribution (μ = 4.771; σ = 0.339) a | 125 | 43.6 | 67.6 | 206.2 |
| n0 | - | Discrete Negative Binomial Distribution (n = 3; p = 0.004) a | 747 | 432.1 | 202 | 1569 |
| r | %/year | Gamma Distribution (k = 3.274; θ = 0.0226) a | 0.074 | 0.041 | 0.022 | 0.151 |
| δM | %/year | Beta Distribution (α = 13.4; β = 4.7; min = 0; max = 0.25) a | 0.185 | 0.025 | 0.14 | 0.222 |
| θINS | % | Beta Distribution (α = 19.8; β = 79.2) a | 0.2 | 0.04 | 0.138 | 0.269 |
| θINF | % | Beta Distribution (α = 16.4; β = 49.3) a | 0.25 | 0.053 | 0.167 | 0.341 |
| ρINS | % | Beta Distribution (α = 10.8; β = 205.2) a | 0.05 | 0.015 | 0.028 | 0.076 |
| ρINF | % | Beta Distribution (α = 15.6; β = 139.7) a | 0.10 | 0.024 | 0.064 | 0.142 |
| σMT | USD/ASIC/year | Log-Normal Distribution (μ = 4.272; σ = 0.301) a | 75 | 23.1 | 43.7 | 117.6 |
| gFEE | %/year | Weibull Distribution (k = 3.434; λ = 0.0834) a | 0.075 | 0.024 | 0.035 | 0.115 |
| α | % | Gamma Distribution (k = 11; θ = 0.002) a | 0.022 | 0.0066 | 0.0123 | 0.0339 |
| β | Blocks/year | Discrete Binomial Distribution (n = 525000; p = 0.1) a | 52,500 | 217.4 | 52,143 | 52,858 |
| i | Year | Shifted Geometric Distribution (p = 0.3333) for x ≥ 16 a, b | 18 | 2.448 | 16 | 23 |
| CELE | USD/kWyear | Log-Normal Distribution (μ = 6.594; σ = 0.389) a | 788.1 | 318.6 | 385.3 | 1385.5 |
| gM | %/year | Gamma Distribution (k = 3.333; θ = 0.03) a | 0.1 | 0.055 | 0.029 | 0.204 |
| dM | %/year | Gamma Distribution (k = 8.333; θ = 0.03) a | 0.25 | 0.087 | 0.127 | 0.407 |
| ξM | % | Beta Distribution (α = 15.3; β = 61.2) a | 0.2 | 0.045 | 0.129 | 0.279 |
| μt | % | Gamma Distribution (k = 6.245; θ = 0.0142) a | 0.088 | 0.035 | 0.039 | 0.154 |
| PM | USD/TH/s | Inverse Gaussian Distribution (μ = 44.115; λ = 40.168) c | 44.115 | 46.232 | 7.586 | 132.531 |
| ω | Bitcoin/Block | Log-Normal Distribution (σ = 1.1336; loc = 0.0157; scale = 0.2054) c | 0.4062 | 0.6315 | 0.0475 | 1.3412 |
| HN,t e | TH/s | Triangular Distribution (c = 0.689; loc = −1.409; scale = 2.531) c | 0.016 | 0.529 | −0.939 | 0.807 |
| HM,t e | TH/s | Skew-Normal Distribution (a = −3.392; loc = 0.205; scale = 0.266) c | 0.0014 | 0.1712 | −0.3163 | 0.238 |
| εM,t e | kW/TH/s | Normal Distribution (μ = 0; σ = 0.075) c | 0 | 0.075 | −0.123 | 0.123 |
| PBTC,t e | USD/Bitcoin | Exponentially Modified Gaussian Distribution (k = 4.0165; loc = −0.3529; scale = 0.0877) c | −0.0005 | 0.3631 | −0.3884 | 0.7136 |
| ϕ0 | Bitcoin/Block | Discrete Uniform Distribution (min = 50; max = 50) d | 50 | 0 | 50 | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Semaan, G.; Wang, G.; Durmaz, T.; Kumar, G. Empirical Insights into Economic Viability: Integrating Bitcoin Mining with Biorefineries Using a Stochastic Model. Systems 2025, 13, 359. https://doi.org/10.3390/systems13050359
Semaan G, Wang G, Durmaz T, Kumar G. Empirical Insights into Economic Viability: Integrating Bitcoin Mining with Biorefineries Using a Stochastic Model. Systems. 2025; 13(5):359. https://doi.org/10.3390/systems13050359
Chicago/Turabian StyleSemaan, Georgeio, Guizhou Wang, Tunç Durmaz, and Gopalakrishnan Kumar. 2025. "Empirical Insights into Economic Viability: Integrating Bitcoin Mining with Biorefineries Using a Stochastic Model" Systems 13, no. 5: 359. https://doi.org/10.3390/systems13050359
APA StyleSemaan, G., Wang, G., Durmaz, T., & Kumar, G. (2025). Empirical Insights into Economic Viability: Integrating Bitcoin Mining with Biorefineries Using a Stochastic Model. Systems, 13(5), 359. https://doi.org/10.3390/systems13050359







