Abstract
Autonomous ride-hailing services, as an innovative solution in the shared mobility sector, have sparked intense competition with traditional ride-hailing platforms. This study examines a traditional large-scale ride-hailing platform and an autonomous ride-hailing platform, constructing profit models for both platforms under competitive and cooperative scenarios. The impact of these scenarios on the platforms’ optimal profits is analyzed using a game-theoretic framework. The study identifies passenger trust in the autonomous platform and the commission rate as critical factors influencing the strategic choices of the two platforms. Surprisingly, irrespective of variations in passenger valuation coefficients and commission rates, there is no scenario where both platforms simultaneously prefer cooperation, which contradicts intuitive expectations. Furthermore, the findings suggest that when passenger trust and valuation differences are relatively low, the autonomous platform can maximize profits by adopting a high-pricing strategy. However, as passenger trust and valuation differences increase, the autonomous platform must adjust its strategy, shifting toward cost optimization and price competition. The study also explores the role of transfer payments as an incentive mechanism for traditional platforms to encourage cooperation from autonomous platforms, providing a robust theoretical foundation for fostering collaboration between traditional and autonomous ride-hailing platforms.
1. Introduction
The ride-hailing industry is undergoing a transformative shift with the rapid emergence of autonomous vehicle (AV) technologies [1]. Leading autonomous ride-hailing platforms such as Baidu’s Apollo Go and Pony.ai are challenging traditional giants like Didi Chu Xing and Uber by offering services with lower operating costs, higher vehicle utilization rates, and improved supply–demand matching efficiency [2]. Despite these advantages, the transition to fully autonomous fleets remains gradual, and traditional ride-hailing platforms—still reliant on human drivers—are expected to coexist with AV platforms for the foreseeable future [3]. This coexistence creates a complex interplay of competition and cooperation. For instance, Waymo and Uber have partnered to integrate Waymo’s autonomous vehicles into Uber’s app, yet simultaneously compete through their standalone platforms [4]. Such strategic ambiguity underscores the need to understand how traditional and autonomous platforms can navigate this duality to optimize their market positions [5].
The adoption of an open-platform strategy by traditional ride-hailing platforms exemplifies this complexity. While integrating autonomous services could alleviate supply-demand imbalances and generate commission revenue—as seen in Didi’s pilot program with autonomous fleets in Guangzhou, which reduced wait times by 15% (https://www.globaltimes.cn/content/1192752.shtml URL (accessed on 27 June 2020))—it also risks eroding user loyalty. A 2023 McKinsey report projects the global autonomous vehicle market to reach USD 800 billion by 2030, with ride-hailing services driving nearly 40% of this growth (https://www.mckinsey.com/~/media/mckinsey/industries/automotive%20and%20assembly/our%20insights/the%20future%20of%20mobility/the-future-of-mobility.pdf?trk=public_post-text (accessed on 10 January 2025)). This rapid expansion intensifies pressure on traditional platforms to innovate, yet empirical studies on their strategic responses remain scarce. Existing research has largely focused on competition among traditional platforms or the technical challenges of AV deployment, neglecting the nuanced dynamics of hybrid market structures where cooperation and competition intersect [6].
This study addresses this critical gap by constructing a game-theoretic model to analyze the strategic interactions between a traditional ride-hailing platform (e.g., Didi) and an autonomous platform (e.g., Apollo Go) under competitive and cooperative scenarios. Three key innovations distinguish our work. First, we introduce platform openness as a strategic lever for traditional platforms, enabling them to host AV services while balancing revenue-sharing trade-offs. Second, we incorporate passenger trust and valuation heterogeneity—factors empirically validated by a 2022 survey showing that 62% of urban commuters still prefer human-driven services due to safety concerns (https://www.globaltimes.cn/content/1192752.shtml (accessed on 10 January 2025))—to model demand dynamics. Third, we explore the role of transfer payments as a novel incentive mechanism to resolve cooperation barriers, a dimension overlooked in prior studies.
The practical implications of this research are significant. For traditional platforms, our findings provide actionable insights into when to adopt openness strategies: for example, when passenger trust in AVs is moderate (e.g., θ = 0.6–0.8) and commission rates exceed 15%, cooperation yields 20–30% higher profits than pure competition. For policymakers, the model highlights regulatory levers to mitigate spatial inequalities exacerbated by AV prioritization in high-demand areas. Theoretically, this work advances the literature on platform economics by bridging the gap between competition and cooperation in hybrid markets, offering a framework applicable to other sectors facing disruptive technological transitions, such as logistics and retail.
2. Literature Review
In the field of operations management, only a few studies have addressed the interaction between autonomous ride-hailing platforms and traditional ride-hailing services. Castro and Frazelle [7] analyzed the dual sourcing of supply in ride-hailing platforms and identified an inherent resource competition between autonomous vehicles (AVs) and human drivers. They emphasized that traditional platforms introducing AVs must balance fleet size and driver compensation; failure to do so could result in reduced profitability due to elevated costs. This study highlights a critical management challenge in the interaction between autonomous and traditional ride-hailing services—namely, achieving a balance between costs and benefits. Furthermore, Baron et al. [8] noted that the societal welfare impact of introducing AVs depends on network efficiency and sharing scenarios. In partially automated environments, maximizing social welfare benefits from enhanced traffic flow efficiency though challenges such as deadheading trips must be mitigated. Lian and Van Ryzin [9] further examined the impact of market structure on service pricing in autonomous ride-hailing platforms. Their findings suggest that competitive AV supply on a unified platform can effectively lower prices, whereas independent platforms may drive up costs due to monopolistic behavior, adversely affecting consumer welfare. From a market evolution perspective, Noh et al. [10] pointed out that AV companies often adopt fixed-capacity strategies to compete with traditional platforms. However, traditional ride-hailing platforms, benefiting from flexible supply management, maintain a competitive advantage, particularly in high-demand markets. Regarding spatial distribution, Castro and Gao [11] revealed that AV prioritization strategies could exacerbate spatial inequalities. Platforms tend to concentrate AV deployment in high-demand areas, which diminishes service quality in low-demand regions and intensifies disparities in service allocation. Additionally, Siddiq and Taylor [3] investigated the impact of AV ownership structures on market competition. Their study found that platform-owned AVs could restrict market competition and reduce social welfare, whereas individually owned AVs could optimize overall resource allocation through enhanced market supply.
Since multiple platforms are considered, this discussion is related to the literature on platform competition and cooperation. Nagarajan et al. [12] proposed a model for alliance formation between competitors and described the equilibrium behaviors of strategic alliances that arise as a result. Yuan et al. [13] demonstrated that, with intensified price competition, service providers may unexpectedly charge higher prices under cooperation. Niu et al. [14] showed that cooperative outcomes of open platforms may occur in markets characterized by intermediate network effects. Fan et al. [15] explored the cooperation between competitive retailers and retail platforms and found that cooperation only occurs when the market size of the retail platform is sufficiently large. Chen et al. [16] revealed that competition and cooperation between platform enterprises depend on the intensity of competition in the market. Li et al. [17] investigated the question of whether manufacturers should collaborate with P2P platforms or B2C platforms. Cohen and Zhang [18] investigated competition and cooperation between ride-hailing platforms in two-sided markets and analyzed the effects of introducing joint services between competing platforms through profit-sharing contracts. They concluded that when platforms face intense competition on the demand side, well-designed contracts can benefit platforms, passengers, and drivers alike.
Finally, this article is also related to pricing of ride-hailing platforms (see, for example, Wu et al. [19] and Kostas et al. [20]), considering the spatial differences between the supply and demand sides in the ride-hailing market. Within the framework of two-sided market theory, they developed spatial pricing models for ride-hailing platforms and studied the issue of spatial price discrimination. Harish and Upender [21] examined how surge pricing and demand forecasting influence the relocation of ride-hailing drivers to areas with higher demand. Cachon et al. [22] found that passengers, drivers, and ride-hailing platforms can all benefit from surge pricing models. Lin and Zhou [23] considered three pricing strategies for ride-hailing platforms: dynamic pricing, surge pricing, and static pricing, and discussed the profitability of the platform under each strategy. Sun et al. [24], by taking ride details and driver locations into account, determined the optimal pricing strategy for ride-hailing platforms and found that the platform’s service price increases as customers’ waiting costs rise. For other recent studies involving ride-hailing platforms, we refer the reader to [25,26,27].
The research mentioned above regarding the interaction between autonomous ride-hailing platforms and traditional ride-hailing services, as well as the competitive and cooperative dynamics between platforms, provides an important theoretical foundation [28]. However, most scholars have focused on the competition between traditional ride-hailing platforms, neglecting the market structure changes brought about by autonomous driving technology. The pricing and market entry strategies of autonomous ride-hailing platforms, as emerging market players, remain underexplored. Additionally, existing studies provide limited game-theoretical analyses of the competition and cooperation between traditional and autonomous ride-hailing platforms, making it challenging to systematically uncover their potential interaction mechanisms. To address this gap, this paper incorporates the real-world context of autonomous ride-hailing platforms entering the market and proposes research questions focusing on the competitive dynamics between traditional and autonomous ride-hailing platforms. We consider a ride-hailing market composed of one traditional platform and one autonomous ride-hailing platform, and construct profit models under both competitive and cooperative scenarios to analyze price competition between the two platforms. Compared with autonomous platforms, traditional platforms have valuation and brand recognition advantages for consumers. Valuation advantages stem from the traditional platforms’ reputation and service quality, while brand recognition advantages arise from their established market presence. The traditional platform strategically decides whether to adopt an openness strategy, allowing the autonomous platform to offer ride-hailing services on its platform in exchange for commissions, while the autonomous platform decides whether to join. This creates two scenarios: competition and cooperation. By comparing the optimal service prices and profits in these two scenarios, the study examines how each scenario impacts the platforms’ pricing strategies and profitability. Furthermore, the analysis explores how consumer preferences influence the traditional platform’s motivation to open its platform and the autonomous platform’s decision to join. The findings of this study provide theoretical support for ride-hailing platforms in different cities and regions and offer insights for local governments and relevant authorities to regulate ride-hailing platforms. Compared with existing studies, this research makes three key contributions. First, a focus on platform openness and franchise strategies: this paper investigates the strategic choice of platform openness by traditional ride-hailing platforms and franchise strategies by autonomous platforms, a topic not previously addressed in the literature. Second, profit modeling under competition and cooperation: we construct profit models for traditional and autonomous ride-hailing platforms under competitive and cooperative scenarios and determine the optimal service prices and profits for each platform, filling a gap in the existing research. Third, new findings and practical implications: we reveal new insights, such as the conditions under which traditional platforms adopt openness strategies, the conditions for autonomous platform franchising, and how consumer heterogeneity influences platform profitability. These findings provide practical management implications for ride-hailing platforms’ openness strategies and enrich the understanding of the societal implications of cooperation strategies between different platforms. This research contributes to the theoretical foundation for platform strategy in the ride-hailing market and offers valuable guidance for both platform operators and policymakers.
3. Model
This study examines a ride-hailing market consisting of a well-established traditional platform with high brand recognition (e.g., Didi Chuxing, Meituan Ride-Hailing) and a relatively less recognized emerging autonomous ride-hailing platform (e.g., Baidu Apollo Go, Pony.ai), both of which provide ride-hailing services. The traditional platform may consider opening its platform to the autonomous ride-hailing platform, while the autonomous platform may choose to join the traditional platform, resulting in a cooperative scenario. Considering the different strategic choices of the two platforms, we define two distinct scenarios: (I) this occurs when the traditional platform is unwilling to adopt an open-platform strategy, or the autonomous ride-hailing platform declines to join the traditional platform (Competitive Scenario); (II) this occurs when the traditional platform adopts an open-platform strategy and the autonomous ride-hailing platform agrees to join the traditional platform (Cooperative Scenario). To facilitate analysis and align with real-world market conditions, the following assumptions are made.
Referring to the studies of Adhikari et al. [29], this paper assumes that the total market capacity is normalized to 1, consisting of a unit mass of continuous passengers. Each passenger with a travel demand places an order with one of the ride-hailing platforms, and each passenger has a unit demand for ride-hailing services. Platforms match passengers to drivers based on their destinations, and once passengers are delivered to their destinations, the order is completed. Passengers then pay the ride fare to the platform via mobile applications. There exists price competition between the two ride-hailing platforms, which directly affects the market demand for each platform. This competitive dynamic plays a critical role in shaping platform strategies and market outcomes.
This study assumes that the value brought by ride-hailing services to consumers is denoted as v, which follows a uniform distribution over [0,1] [30,31]. Compared to autonomous ride-hailing platforms, traditional ride-hailing platforms possess trust and valuation advantages. The trust advantage means that, under otherwise identical conditions, passengers tend to have greater trust in traditional ride-hailing platforms compared to autonomous platforms. This is primarily because autonomous driving technology is not yet fully mature, and passengers often experience unfamiliarity or resistance toward autonomous ride-hailing services. As a result, passengers are more inclined to choose traditional platforms for their ride-hailing needs. The valuation advantage means that, in the absence of the autonomous ride-hailing platform joining the traditional platform, traditional platforms have already established a strong user base and reputation. This reputation is built on factors such as efficient order processing and reliable ride safety, as well as overall high-quality customer service. In contrast, autonomous platforms are at a disadvantage in these aspects. As a result, passengers assign a relatively lower valuation to the services provided by autonomous platforms compared to those offered by traditional platforms.
Therefore, this study assumes that passengers’ valuations of the ride-hailing services provided by the two platforms are heterogeneous, with passengers having a higher level of recognition for traditional ride-hailing platforms compared to autonomous platforms. Reflecting real-world conditions, the recognition level for traditional platforms is set to 1, while the recognition level for autonomous ride-hailing platforms is denoted as θk. Accordingly, the value of the ride-hailing service provided by the traditional platform to consumers is represented by v, while the value of the service provided by the autonomous platform to consumers is θkv. To ensure the existence of an optimal solution for the model and to make the equilibrium outcomes practically meaningful, this study assumes that the ranges of θ and k are within [0,1].
We assume that the ride-hailing platform incurs zero marginal costs and zero fixed costs for providing platform services to passengers and drivers. This implies that the platform does not incur additional costs when adding a new passenger or driver, nor does it have any initial setup expenses.
The sequence of the game analyzed in this study is as follows [32]: in the first stage, the traditional platform decides whether to implement an open-platform strategy. If the platform chooses to open, it announces a commission rate λ. If the traditional platform adopts the open-platform strategy, the autonomous platform then considers whether to join the traditional platform. In the second stage, both platforms independently set their ride-hailing service prices, aiming to maximize their respective profits. Finally, in the third stage, consumers make their ride-hailing decisions based on the prices and services offered by the two platforms. Figure 1 shows the game sequence diagram of this article.
Figure 1.
The sequence of the game.
There are some notations that this study uses in addressing the problem above. Such notations are detailed in Table 1.

Table 1.
Symbols and interpretation table.
3.1. Competitive Scenario (N)
This section first examines the scenario in which the traditional platform is unwilling to adopt an open-platform strategy or the autonomous ride-hailing platform is unwilling to join the traditional platform. Under this scenario, the two platforms compete to provide ride-hailing services. For the purpose of analysis, the traditional ride-hailing platform and the autonomous ride-hailing platform are denoted as A and B. The utility of passengers choosing Platform A (the traditional platform) is defined as , while the utility of passengers choosing Platform B (the autonomous platform) is . Based on the utility-maximizing behavior of passengers, the following conditions determine their platform choice: passengers choose platform A if the utility obtained from A is positive, and greater than the utility from B, i.e., and ; passengers choose Platform B if the utility obtained from B is positive, and greater than the utility from A, i.e., and . Passengers are indifferent between Platforms A and B if = . Therefore, we obtain . When , passengers choose the traditional platform. When , passengers choose the autonomous platform.
When Platform B does not join A’s platform, a portion of consumers are exclusively aware of Platform A’s ride-hailing services, while the remaining proportion (1 − α) are aware of both platforms [33]. Thus, α represents the exclusive demand for platform A, reflecting its awareness advantage over platform B. Passengers familiar with both platforms will choose the ride-hailing service that offers them higher utility. We can formulate the demand functions for both platforms as:
θ represents passengers’ trust in Platform B, reflecting the degree of differentiation in consumer valuations between Platform B and Platform A. Specifically, 0 < θ < 1 indicates the disadvantage of Platform B in terms of consumer valuation relative to Platform A. This suggests that, when the autonomous ride-hailing Platform B does not join the traditional ride-hailing Platform A, it suffers from disadvantages in aspects such as user base and reputation compared to Platform A. Consequently, passengers exhibit lower trust and service valuation for Platform B. However, in the model discussed in Section 3.2, where the two platforms cooperate, platform B joins Platform A, thereby eliminating this valuation disadvantage. As a result, we set θ = 1 in the cooperative scenario. The parameter k denotes the valuation coefficient of passengers, representing the relative valuation difference between autonomous ride-hailing services and traditional ride-hailing services. Given that autonomous driving technology is not yet fully mature and passengers may harbor resistance toward autonomous ride-hailing services, this study assumes that passengers value autonomous ride-hailing services less than traditional services, i.e., 0 < k < 1. Furthermore, the larger the valuation coefficient k, the smaller the perceived service differences between the two platforms by passengers. The two platforms’ profits can thus be written as:
Both platforms maximize their profits by choosing optimal prices. Based on the best response functions, we can derive the equilibrium prices. Furthermore, by substituting the equilibrium prices into the profit functions in Equations (2) and (3), we can obtain the equilibrium profits. The following lemma summarizes the equilibrium outcome.
Lemma 1.
If the traditional platform does not adopt an open-platform strategy or the autonomous ride-hailing platform chooses not to join, the equilibrium prices are
and the equilibrium profits are
Proof.
All proofs are in the Appendix A. □
In the competitive scenario, the optimal prices, demands, and profits of Platform A and Platform B are influenced by passengers’ valuation coefficient k and trust level θ toward Platform B. Propositions 1–3 analyse the impact of these factors on the optimal prices, demands, and profits of Platform A and Platform B, respectively.
Proposition 1.
① ; ②③; ④ ⑤ .
Proposition 2.
① , ; ② , ; ③ , .
Proposition 3.
① ; ② If , ; , ; ③ ; ④ If , ; , ; ⑤ ; ⑥ If , ; , .
We concisely synthesize the critical relationships between key parameters (, , ) and equilibrium outcomes (prices, demands, profits) in the competitive scenario, as shown in Table 2.

Table 2.
Key findings.
Proposition 1 states that in the competitive scenario, the pricing strategies of Platform A (traditional) and Platform B (autonomous) are dynamically shaped by passengers’ valuation of autonomous services and their trust in Platform B. As k increases, reflecting stronger passenger preference for autonomous technology, Platform A reduces its optimal price to retain market share, signaling a defensive strategy against demand erosion. Meanwhile, Platform B’s pricing behavior bifurcates based on trust levels: under low (), rises with k, capitalizing on early adopters willing to pay premium prices for innovation. However, as θ grows and the market homogenizes, Platform B faces intensified competition, forcing a strategic shift from price premiums to competitive reductions. Concurrently, rising θ weakens Platform A’s pricing power, compelling further price cuts to counterbalance trust-driven demand shifts toward Platform B. Notably, Platform B’s response to θ is non-linear: at low k, higher trust linearly boosts , but under high k, saturation triggers an inverted U-shaped relationship, where initial trust gains enable price hikes before competition-driven declines. Finally, an increase in Platform A’s exclusive demand share (α) elevates prices for both platforms. Platform A leverages its monopolized user base to target high-valuation segments, while Platform B adopts niche pricing, focusing on tech-savvy passengers willing to pay premiums despite limited market reach. This interplay of k, θ, and α underscores the tension between innovation-driven demand growth and competitive saturation, defining equilibrium outcomes where Platform A’s dominance wanes as autonomous services gain acceptance, while Platform B navigates diminishing returns under heightened rivalry.
Proposition 2 shows that in the competitive scenario, shifts in passenger preferences and trust levels critically reshape demand dynamics between Platform A and Platform B. As passengers’ valuation of autonomous services increases, Platform B’s demand grows, reflecting its technological appeal, while Platform A’s demand declines due to eroding competitiveness. Similarly, heightened trust in Platform B accelerates demand migration, as passengers increasingly perceive traditional services as suboptimal. This zero-sum reallocation—under a fixed total market demand—amplifies Platform B’s gains at the direct expense of Platform A’s market share. However, Platform A’s resilience is partially sustained through its exclusive demand share, which represents passengers solely aware of its services. A higher α strengthens Platform A’s demand while suppressing Platform B’s penetration, illustrating how market fragmentation and asymmetric awareness can counterbalance technological disruption. Thus, while rising k and θ favor Platform B’s expansion, Platform A retains strategic leverage through its entrenched user base, underscoring the dual forces of innovation adoption and market inertia in shaping competitive outcomes.
Proposition 3 indicates that under the competitive scenario, Platform A’s profitability declines as passengers’ valuation of autonomous services and trust in Platform B increase, signaling the erosion of its brand advantage as autonomous technology gains acceptance. Conversely, Platform B’s profit responds nonlinearly to these parameters. When , rising boosts B’s profit through increased demand and cost efficiencies from autonomous operations (e.g., reduced labor costs). However, beyond this threshold, market saturation triggers intensified price competition and margin compression. Platform B is forced to lower prices and invest heavily in technology to retain market share, leading to diminishing marginal returns and declining profits. Similarly, higher trust initially enhances profit by attracting passengers, but excessive trust under high accelerates market saturation, shifting competition from innovation-driven differentiation to cost-driven rivalry. Thus, while Platform B benefits from early-stage adoption, its profit trajectory ultimately hinges on balancing technological appeal with sustainable market positioning—a tension exacerbated by Platform A’s resilience through exclusive demand, which partially offsets its competitive losses. This duality underscores the fragile equilibrium between disruptive innovation and incumbent advantage in evolving markets.
3.2. Cooperative Scenario (C)
This section examines the cooperative scenario in which A adopts an open-platform strategy, and B agrees to join A. When the autonomous Platform B chooses to join A and provide ride-hailing services through A’s platform, B is required to pay a commission rate λ per order to A. This commission is considered the cost of B’s participation and reflects the revenue share A earns from B’s sales. Joining A offers several advantages for B. First, it increases B’s brand awareness and trust. All passengers become aware of B, and since A typically has a large user base and high brand trust, B can leverage A’s platform to rapidly enhance its visibility and attract more passengers to its services. This also eliminates the valuation disadvantage associated with B, and therefore, θ = 1. Second, it significantly enhances B’s competitiveness. In the cooperative scenario, the market dynamics between the two platforms become more intricate. By adopting the open-platform strategy, A shares its well-established user base and brand trust with B, enabling B to showcase its technological advantages and create differentiated services, thereby competing with A in terms of service quality. Additionally, through its partnership with A, B can reduce substantial costs related to market promotion, user education, and other early-stage operational burdens. This cooperation not only lessens B’s initial competitive challenges but also expands its user base, significantly enhancing its market competitiveness and appeal.
The utility of passengers choosing Platform A (the traditional platform) is defined as , while the utility of passengers choosing Platform B (the autonomous platform) is . Based on the utility-maximizing behavior of passengers, the following conditions determine their platform choice: passengers choose Platform A if the utility obtained from A is positive, and greater than the utility from B, i.e., and . Passengers choose Platform B if the utility obtained from B is positive, and greater than the utility from A, i.e., and . Passengers are indifferent between Platforms A and B if = . Therefore, we obtain , . When , passengers choose the traditional platform. When , passengers choose the autonomous platform.
We can formulate the demand functions for both platforms as:
The two platforms’ profits can thus be written as:
Similar to the case where B does not join A’s platform, both platforms optimize their profits by determining the optimal prices. Based on the best response functions, we can derive the equilibrium prices. Furthermore, we can obtain the equilibrium profits by substituting the equilibrium prices into the profit functions. The following lemma summarizes the equilibrium outcome.
Lemma 2.
When the traditional platform adopts an open-platform strategy and the autonomous ride-hailing platform agrees to join the traditional platform, the equilibrium prices are
and the equilibrium profits are
Profit Allocation in the Cooperative Scenario
Proposition 4.
① ;
②
Proposition 5.
① ; ② .
Proposition 6.
① ; ② If , ; otherwise, .
Proposition 7.
① , ; ② ; .
Proposition 4 examines pricing strategies under cooperation. Platform A’s optimal price decreases as passengers’ valuation of autonomous services rises, reflecting its effort to retain demand amid competition. For Platform B, the relationship between and k is nonlinear, shaped by commission rates and market saturation. When k is low, Platform B raises prices, leveraging Platform A’s user base and trust to expand demand. However, as k approaches saturation, differentiation between platforms diminishes, and Platform B must lower prices to counter Platform A’s competitive pricing. The critical threshold highlights how higher commissions accelerate price competition, necessitating strategic balance: Platform A must avoid overburdening Platform B with commissions, while Platform B must optimize pricing to delay profit erosion.
Proposition 5 reveals demand reallocation under cooperation. As k increases, Platform A’s demand declines, while Platform B’s demand grows. This asymmetry stems from Platform B’s enhanced attractiveness, which diverts passengers from Platform A despite shared market access. The fixed total demand amplifies this zero-sum dynamic, where Platform B’s gains directly erode Platform A’s market presence, underscoring the tension between collaboration and competition.
Proposition 6 analyzes profit dynamics. Platform A’s profit declines with k, as commission income fails to offset demand and price losses. Platform B’s profit initially rises with k but declines after surpassing the breakpoint. Early cooperation boosts profits through demand expansion and cost efficiencies, but saturation triggers price wars and margin compression. Platform A can modulate this threshold, while Platform B must pivot from demand growth to cost optimization post-breakpoint to avoid premature profit decline.
Proposition 7 evaluates commission rate effects. Higher λ increases Platform A’s prices and profits, as it leverages Platform B’s integration to enhance service value and justify premium pricing. Conversely, Platform B’s prices rise with λ to offset commission costs, but its profits decline due to unsustainable cost pressures. This paradox underscores the trade-off between short-term revenue sharing and long-term profitability, necessitating careful calibration of λ to align incentives without destabilizing cooperation.
Cooperation introduces complex interdependencies—Platform A balances commission gains against demand erosion, while Platform B navigates growth saturation and cost trade-offs. The interplay of k, λ, and market thresholds define a fragile equilibrium where strategic missteps in pricing or commission settings risk triggering destructive competition.
4. Comparative Analysis of the Two Scenarios
Based on Section 3.1 and Section 3.2, this study has derived the optimal equilibrium solutions under different scenarios. The following analysis will compare the equilibrium solutions of the competitive and cooperative scenarios to further examine how these scenarios influence the pricing strategies and revenues of Platforms A and B.
4.1. Comparison of Price in Different Scenarios
Proposition 8.
- (1)
- There exists a unique critical value such that: ① If , then ; ② If , then .
- (2)
- There exists a unique critical value such that: ① If , then ; ② If , then .
Proposition 8(1) indicates that when a traditional ride-hailing platform adopts an open platform strategy and collaborates with autonomous ride-hailing services, its pricing strategy is influenced by two key factors. On one hand, Platform A and the onboarded Platform B still compete for passenger demand and pricing, requiring Platform A to adjust its prices to balance its own demand with the revenue generated from the collaboration. On the other hand, Platform B, by providing services through Platform A, is required to pay a certain percentage of its revenue as a commission. In the cooperative scenario, Platform A not only relies on fares paid by passengers but also gains additional revenue from commissions, leading to adjustments in its pricing strategy. When passengers have low trust in Platform B, platform A’s strong brand recognition and reputation dominate, and B’s influence is limited. Under such circumstances, Platform A is motivated to lower its prices to attract more passengers, increase order volume, and expand revenue, compensating for the price reduction through commission income. Therefore, prices in the cooperative scenario are lower than in the competitive scenario. Conversely, when passengers have high trust in Platform B, their willingness to choose Platform B increases. In this case, Platform A, while sharing revenue through the collaboration, can set higher prices to maximize profits. As a result, prices in the cooperative scenario are higher than those in the competitive scenario.
Proposition 8(2) indicates that when Platform B chooses to collaborate with Platform A by joining its ecosystem, B’s pricing strategy is driven by two main factors. On one hand, Platform B still needs to compete with Platform A for passenger demand and pricing, requiring B to adjust its prices to balance its own demand with the costs associated with the collaboration. On the other hand, by joining Platform A, B gains access to A’s passenger base, which increases its demand. This gives B the incentive to raise service prices to achieve higher profits. When the commission rate is low, Platform B can collaborate with Platform A at a low cost while leveraging A’s resources (e.g., traffic and brand recognition). This motivates B to increase its prices, transferring part of the costs to passengers, thereby maintaining its profit levels and expanding its market share. As a result, prices in the cooperative scenario are higher than in the competitive scenario. However, when the commission rate is high, the collaboration increases B’s cost pressures. To address this, Platform B needs to lower its prices to compensate for its relatively low brand recognition, enhance market competitiveness, and attract more users. In this case, B’s overall revenue increases, as it can benefit from economies of scale even if its profit per transaction is lower. Thus, in this situation, prices in the cooperative scenario are lower than in the competitive scenario.
4.2. Comparison of Profit in Different Scenarios
Proposition 9.
- (1)
- There exists a unique critical value such that: ① If , then ; ② If , then .
- (2)
- There exists a unique critical value such that: ① If , then ; ② If , then .
Proposition 9(1) indicates that in markets with low trust, the competitive scenario allows Platform A to achieve higher profits compared to the cooperative scenario. According to Proposition 8, prices are set higher in the competitive scenario, which directly contributes to increased profits. In environments where passenger trust in autonomous driving technology remains low, traditional ride-hailing platforms can leverage passengers’ familiarity and trust in their services to maintain market dominance without prematurely relying on a cooperative strategy. In the competitive scenario, traditional ride-hailing platforms can fully capitalize on their market position and resource advantages to effectively compete with Platform B, thereby securing higher profits. In contrast, the cooperative scenario may lead to reduced profit margins and bargaining power, limiting the profitability of traditional ride-hailing platforms in low-trust markets. However, in highly competitive environments, introducing Platform B as a partner can help Platform A achieve mutual benefits, enhance market attractiveness, share risks and costs, and meet passengers’ demands for efficient services. This strategy not only avoids the high costs of direct competition but also creates new profit growth opportunities through technological innovation, making it an optimal response to intense market competition.
Proposition 9(2) indicates that in the early stages of market entry, when the trust in autonomous driving Platform B is relatively low, the cooperative scenario allows B to leverage the market foundation and resources of the traditional ride-hailing Platform A. For instance, B can utilize A’s brand effect to attract more passengers, thereby reducing the costs of independent promotion. In low-trust markets, price sensitivity is also relatively low, enabling Platform B to maintain its independence through flexible pricing strategies and technological innovation, even while paying a certain commission (cooperation cost). This allows Platform B to achieve higher net profits through cooperation. However, as autonomous driving technology becomes more widely adopted and market competition intensifies, choosing cooperation would require Platform B to pay high commissions while also facing competitive pressures, such as price reductions by Platform A. This would further compress profit margins, limit the potential for market expansion, and render the marginal benefits of cooperation insufficient to offset its costs.
Authors should discuss the results and how they can be interpreted from the perspective of previous studies and of the working hypotheses. The findings and their implications should be discussed in the broadest context possible. Future research directions may also be highlighted.
4.3. The Impact of k on the Equilibrium Results
In this section, we verify the above propositions using numerical studies. We refer to the relevant literature [8,34] to set the values of the following parameters in a specific range of values: .
As illustrated in Figure 2, the influence of passengers’ valuation coefficient on platform profits aligns with the theoretical propositions derived in Section 3.
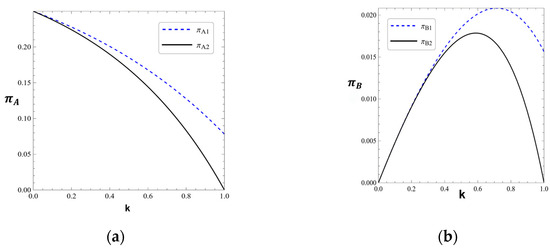
Figure 2.
(a) The impact of k on A’s profits. (b) The impact of k on B’s profits.
Figure 2a validates Proposition 1 and Proposition 3, which posit that Platform A’s profits decline monotonically as k increases. This trend holds across both competitive and cooperative scenarios, reflecting Platform A’s strategic dilemma: rising k strengthens Platform B’s appeal, forcing Platform A to either lower prices or cede market share—both eroding profitability. The fixed total market demand exacerbates this zero-sum dynamic, as Platform B’s gains directly reduce Platform A’s revenue, consistent with Proposition 2’s demand reallocation mechanism.
Figure 2b corroborates the nonlinear profit dynamics for Platform B outlined in Proposition 3 and Proposition 6. In competitive scenarios, Platform B’s profits initially rise with k due to demand growth and cost efficiencies, but eventually decline as market saturation triggers price competition. In cooperative scenarios, this profit peak occurs earlier, as commission costs amplify margin pressures. This aligns with Proposition 4’s threshold analysis, where higher λ accelerates the transition from profit growth to decline. The delayed turning point in competitive scenarios (vs. cooperative) underscores Proposition 7’s insight: cooperation introduces cost trade-offs that constrain Platform B’s profitability despite shared demand. In practice, Platform B needs to closely monitor the dynamic balance between diminishing marginal returns and cost changes during demand expansion to optimize its profit structure.
The contrast between competitive and cooperative curves highlights the dual role of cooperation: while expanding demand, it hastens profit decline due to structural asymmetries (Propositions 4–7).
5. Numerical Studies
The coexistence of trustworthiness and commission rates complicates the expression of platform profits. Therefore, in this section, we compare the magnitude of platform profits under the two scenarios based on numerical analysis. Meanwhile, to reflect its dynamic changes in reality, we expand the range of values for (i.e., = 0.4, 0.6, 0.9) and analyze its three-dimensional interaction effects with θ and λ.
5.1. Interaction Analysis of θ and λ
5.1.1. Effect of θ and λ on A’s Optimal Outcomes
Figure 3 illustrates the impact of trust level and commission rate on Platform A’s profits under different valuation coefficients. When (Figure 3a), Platform A achieves higher profits under competition (blue regions) when θ < 0.6 and λ < 0.2. In this range, low trust in Platform B and minimal commission income make cooperation unviable, as the demand loss outweighs revenue-sharing benefits. However, as increases to 0.6 (Figure 3b), cooperation becomes advantageous for Platform A in regions where θ > 0.7 and λ > 0.25 (pink regions). Here, higher trust ensures Platform B’s demand contribution compensates for Platform A’s market share erosion, while elevated commissions provide additional revenue. At (Figure 3c), Platform A’s profit under competition collapses due to Platform B’s dominance, and cooperation offers only marginal benefits when θ > 0.8 and λ > 0.35. This highlights the critical role of trust and commissions in shaping Platform A’s strategic choices, particularly as autonomous services gain market acceptance.
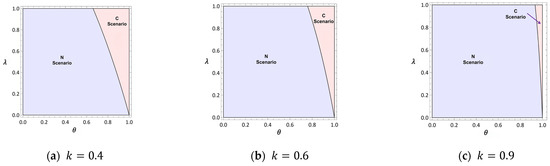
Figure 3.
Effect of and on A’s optimal outcomes.
In summary, the figure clearly illustrates the profit dynamics of traditional ride-hailing platforms under cooperative and competitive scenarios. Trust level (θ) and commission rate (λ) are the two key variables influencing the profitability of cooperation. Platform A can only maximize its profits through cooperation when both trust and commission rates are high. Under other conditions, competition remains the more advantageous choice. This provides clear guidance for Platform A in formulating cooperation or competition strategies during market transitions.
5.1.2. Effect of and on B’s Optimal Outcomes
Figure 4 examines Platform B’s profit dynamics under varying θ and λ. For (Figure 4a), Platform B benefits from cooperation (yellow regions) when θ is moderate (0.5 < θ < 0.7) and λ is low (λ < 0.15). In this range, Platform B leverages Platform A’s user base without incurring excessive commission costs. At (Figure 4b), the cooperative region expands slightly, but Platform B faces a trade-off: cooperation remains profitable only if θ > 0.6 and λ < 0.3. Beyond λ = 0.3, commission costs erode profits despite higher demand. For (Figure 4c), Platform B’s profit under cooperation declines universally (green regions), as market saturation triggers price wars and diminishes returns. Independent competition becomes the preferred strategy, reflecting the diminishing marginal benefits of cooperation in highly competitive markets.
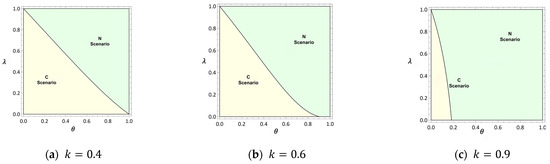
Figure 4.
Effect of and on B’s optimal outcomes.
5.2. Total Profit and Market Efficiency
5.2.1. Total Profit
Figure 5 compares total market profits under competitive and cooperative scenarios. At (Figure 5a), competition maximizes total profit (blue regions) by enabling platforms to attract more passengers and achieve economies of scale. Cooperation, in contrast, limits pricing flexibility and leaves certain demand unmet, reducing overall efficiency. At (Figure 5b), cooperation becomes viable in regions where θ > 0.7 and λ < 0.25 (pink regions), as it reduces internal friction and improves resource allocation. However, at (Figure 5c), competition again dominates, as cooperation fails to mitigate the inefficiencies of market saturation. These findings underscore the importance of aligning cooperation strategies with market conditions to maximize total welfare.
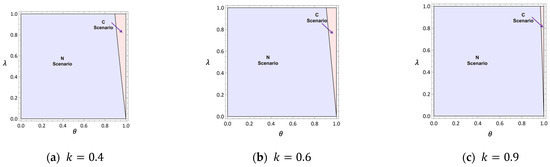
Figure 5.
Total profit.
5.2.2. Market Efficiency
Figure 6 analyzes the optimal strategy choices for Platforms A and B under varying θ and λ. At (Figure 6a), conflicts of interest prevent cooperation (blue regions), as neither platform is sufficiently motivated to collaborate. At (Figure 6b), cooperation becomes feasible in regions where θ > 0.7 and λ < 0.25 (pink regions), but Platform B’s profit expectations often remain unmet, leading to independent competition. At (Figure 6c), cooperation is universally unattainable (gray/pink regions), as extreme valuation shifts destabilize collaboration. This reflects a classic Prisoner’s Dilemma, where strategic competition and unequal benefit distribution hinder mutually beneficial outcomes. This section analyses the optimal strategy choices for the two platforms under varying parameter conditions, assuming k = 0.6. As shown in Figure 6, in the blue region, conflicts of interest between Platform A and Platform B prevent cooperation from being achieved. In this scenario, Platform A ultimately opts for competition, and Platform B’s willingness to cooperate cannot be realized. In the gray region, the equilibrium of the game results in a state of complete competition, where both platforms reject cooperation and compete independently in the market. In the pink region, the conditions for cooperation fail to meet Platform B’s profit expectations, prompting it to choose independent competition. As a result, Platform A’s intention to open cooperation cannot materialize.
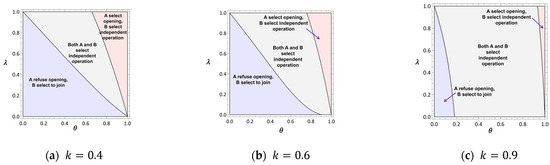
Figure 6.
Overall strategy selection.
Regardless of changes in commission rates or passenger trust levels, there is no scenario in which Platform A is willing to open cooperation and Platform B is simultaneously willing to join, meaning that neither platform is sufficiently motivated to pursue cooperation. Although both platforms could theoretically benefit from collaboration, factors such as information asymmetry, unequal risk allocation, and short-term profit considerations prevent both parties from simultaneously maximizing their respective gains, making cooperation unattainable. This situation reflects a classic Prisoner’s Dilemma in game theory, where strategic interactions and conflicts of interest impede mutually beneficial outcomes. Even if market conditions change, the unequal distribution of benefits and the strategic competition between platforms render long-term cooperation difficult to achieve, highlighting the absence of a stable incentive mechanism for cooperation within the market.
5.3. Transfer Payment Mechanism Design
Based on the analysis above, the market exhibits characteristics of a Prisoner’s Dilemma. One potential solution to this problem is the implementation of a transfer payment strategy. Transfer payment involves providing additional benefits to the other party, thereby breaking the “rational choice” equilibrium that characterizes the Prisoner’s Dilemma. In a competitive market, both Platform A and Platform B may recognize that cooperation could generate greater overall profits for both parties. However, due to concerns over the possibility that the other party might fail to uphold their commitment, both platforms ultimately choose not to cooperate. Transfer payments serve as an incentive mechanism that can increase the returns for Platform B from participating in cooperation. By doing so, Platform B gains sufficient motivation to join the cooperative arrangement, thereby leading to a Pareto-optimal solution, where both platforms derive greater benefits from cooperation than they would from independent competition. This strategy not only facilitates the establishment of mutual trust but also addresses the imbalance in perceived benefits, ensuring that cooperation becomes a rational and rewarding choice for both parties. A can allocate a certain proportion of its revenue as a transfer payment to B to ensure that B gains higher returns from the cooperation. The transfer payment can take various forms, such as reducing commission rates, increasing revenue shares, or providing other financial incentives. In this arrangement, although A needs to relinquish part of its profits, the expansion of market share and the reduction in costs may result in higher overall earnings compared to operating under pure competition. By implementing the transfer payment, B’s profits can surpass those of operating independently, significantly enhancing its willingness to cooperate. At the same time, the transfer payment reduces the risks associated with market entry for B and increases its returns after cooperation. This mechanism shifts B’s position from rejecting collaboration to actively engaging in it. In conclusion, the transfer payment design not only balances the distribution of benefits but also effectively promotes cooperation. By reducing risks and increasing returns, this approach resolves barriers to collaboration and lays the foundation for more stable and sustainable profitability for both sides.
As shown in Figure 7, when a certain critical value of transfer payment is reached, both platforms are willing to cooperate. Figure 7 evaluates the effectiveness of transfer payments in resolving cooperation barriers. At (Figure 7a), transfer payments expand the cooperative region (yellow) by aligning incentives between Platforms A and B. For (Figure 7b), a 10–15% revenue transfer from Platform A to Platform B significantly enhances cooperation viability, particularly when θ > 0.7 and λ < 0.25. However, at (Figure 7c), even 20% transfer payments fail to incentivize cooperation, as Platform B’s profit potential is irreversibly constrained by market saturation. These results highlight the dual role of transfer payments: while they can facilitate cooperation in moderate markets, their efficacy diminishes under extreme competitive pressures.
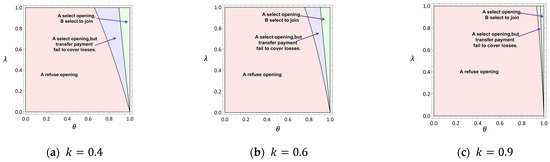
Figure 7.
Transfer payment strategy.
6. Conclusions and Future Directions
This study constructs a game-theoretic model to analyze the strategic interactions between traditional and autonomous ride-hailing platforms under competitive and cooperative scenarios. By integrating numerical simulations with theoretical analysis, we systematically examine the impact of passenger valuation differences, trust levels, commission rates, and incentive mechanisms on platform pricing, profit distribution, and collaboration dynamics. The findings provide critical insights into the evolving ride-hailing market and offer actionable implications for platform operators, policymakers, and researchers. The main conclusions and managerial implications are as follows:
(1) Impact of passenger valuation coefficients and preferences on both platforms: The analysis reveals that passenger valuation coefficients and trust levels asymmetrically influence platform strategies. While traditional platforms experience declining profits as k and θ increase due to demand erosion, autonomous platforms initially benefit from market expansion but face profit stagnation or decline under intense price competition and diminishing marginal returns. Pricing strategies diverge significantly across scenarios: in low-trust and low-commission markets, cooperative pricing exceeds competitive pricing, as traditional platforms leverage commission revenue to mitigate price pressures. Conversely, high trust and commission rates amplify autonomous platforms’ bargaining power, leading to higher competitive prices. Platform openness emerges as a pivotal strategic lever for traditional platforms. While cooperation is advantageous in early-stage markets to harness autonomous technology’s potential, high commission pressures often undermine collaboration viability. Transfer payments, as an incentive mechanism, effectively resolve the Prisoner’s Dilemma by redistributing profits, yet their efficacy diminishes in saturated markets due to irreversible competitive pressures.
(2) Managerial and policy implications: For traditional platforms, maintaining competitive pricing is critical in low-trust markets, while adopting dynamic commission structures becomes optimal as trust and autonomous adoption grow. Autonomous platforms should prioritize cost optimization and service differentiation to counteract price wars in mature markets. Policymakers must address spatial inequalities arising from autonomous vehicle prioritization in high-demand areas and encourage transfer payment mechanisms to enhance social welfare. Regulatory frameworks should balance innovation incentives with equitable service distribution, particularly in underserved regions.
(3) Theoretical contributions: This research advances platform economics by introducing openness strategy as a core strategic variable for traditional platforms, bridging the gap between competition and cooperation in hybrid markets. By incorporating heterogeneous passenger trust and valuation dynamics, the model captures real-world complexities often overlooked in prior studies. Furthermore, the conceptualization of transfer payments as a coordination mechanism provides a novel framework for resolving collaboration barriers in two-sided markets.
(4) Limitations and future research: The study assumes a duopolistic market structure, limiting its applicability to multi-platform ecosystems. Future work could extend the model to explore coalition formation, driver multi-homing, and cross-platform mobility. Additionally, the uniform distribution of passenger valuations simplifies preference heterogeneity; integrating risk aversion or environmental consciousness could yield richer insights. Empirical validation of commission rate thresholds and transfer payment effectiveness in real-world settings remains a critical next step. Lastly, dynamic analyses of autonomous technology maturation and its long-term market impacts warrant further exploration.
This study establishes a foundational framework for understanding platform strategies in the autonomous ride-hailing era, offering theoretical and practical guidance for navigating technological disruption. Future research should integrate behavioral economics and network theory to unravel the evolving dynamics of platform ecosystems.
Author Contributions
Writing—original draft, investigation, formal analysis, data curation, conceptualization. L.F.; investigation, reviewing and editing, M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. Proof of Lemma 1
Proof.
The optimal prices of A and B are characterized by the first-order conditions of and in Equations (3) and (4), respectively:
Solving this system of equations, we can derive the equilibrium prices as in Equation (5). Substituting these optimal prices into Equations (3) and (4), we derive the equilibrium profits as in Equation (6). □
Appendix A.2. Proof of Proposition 8
Comparing scenario II (“competition”) with scenario I (“cooperation”), we derive the equilibrium A’s price difference as
Because the above-profit difference decreases indifference decreases in , we have if and only if , where is the solution to and can be derived as .
Appendix A.3. Proof of Proposition 9
Let , We can further derive that .
Appendix A.4. Proof of Proposition 10
Comparing scenario II (“competition”) with scenario I (“cooperation”), we derive the equilibrium A’s profit difference as
Because the above-profit difference decreases indifference decreases in , we have if and only if , where is the solution to and can be derived as , where
Appendix A.5. Proof of Proposition 11
Let , We can further derive that , where
References
- Xu, Y.; Ling, L.; Wu, J.; Xu, S. On-demand ride-hailing platforms under green mobility: Pricing strategies and government regulation. Transp. Res. Part E Logist. Transp. Rev. 2024, 189, 103650. [Google Scholar] [CrossRef]
- Benjaafar, S.; Hu, M. Operations management in the age of the sharing economy: What is old and what is new? Manuf. Serv. Oper. Manag. 2020, 22, 93–101. [Google Scholar] [CrossRef]
- Siddiq, A.; Taylor, T.A. Ride-hailing platforms: Competition and autonomous vehicles. Manuf. Serv. Oper. Manag. 2022, 24, 1511–1528. [Google Scholar] [CrossRef]
- Wang, Z.; Li, S. Competition between autonomous and traditional ride-hailing platforms: Market equilibrium and technology transfer. Transp. Res. Part C Emerg. Technol. 2024, 165, 104728. [Google Scholar] [CrossRef]
- Assegaff, S.B.; Pranoto, S.O. Price determines customer loyalty in ride-hailing services. Am. J. Humanit. Soc. Sci. Res. 2020, 3, 453–463. [Google Scholar]
- Naumov, S.; Keith, D. Optimizing the economic and environmental benefits of ride-hailing and pooling. Prod. Oper. Manag. 2023, 32, 904–929. [Google Scholar] [CrossRef]
- Castro, F.; Frazelle, A. Getting out of your own way: Introducing autonomous vehicles on a ride-hailing platform. Prod. Oper. Manag. 2024, 33, 2014–2030. [Google Scholar] [CrossRef]
- Niu, B.; Deng, X.; Xie, F.; Shen, Z. Dual sourcing hurts supply chain viability? The value of brand-owners’ cooperation under single sourcing. Omega 2025, 133, 103250. [Google Scholar] [CrossRef]
- Lian, Z.; van Ryzin, G. Capturing the Benefits of Autonomous Vehicles in Ride Hailing: The Role of Market Configuration. Manag. Sci. 2024. [Google Scholar] [CrossRef]
- Noh, D.; Tunca, T.I.; Xu, Y. Evolution of Ride Services: From Ride Hailing to Autonomous Vehicles. SSRN 2023, 3903493. [Google Scholar]
- Castro, F.; Gao, J.; Martin, S. Autonomous vehicles in ride-hailing and the threat of spatial inequalities. SSRN 2024, 4332493. [Google Scholar] [CrossRef]
- Nagarajan, M.; Sošić, G. Stable farsighted coalitions in competitive markets. Manag. Sci. 2007, 53, 29–45. [Google Scholar] [CrossRef]
- Yuan, X.; Dai, T.; Chen, L.G.; Gavirneni, S. Co-opetition in service clusters with waiting-area entertainment. Manuf. Serv. Oper. Manag. 2021, 23, 106–122. [Google Scholar] [CrossRef]
- Niu, B.; Xie, F.; Chen, L.; Xu, X. Join logistics sharing alliance or not? Incentive analysis of competing E-commerce firms with promised-delivery-time. Int. J. Prod. Econ. 2020, 224, 107553. [Google Scholar] [CrossRef]
- Fan, X.; Yin, Z.; Liu, Y. The value of horizontal cooperation in online retail channels. Electron. Commer. Res. Appl. 2020, 39, 100897. [Google Scholar] [CrossRef]
- Chen, X.; Luo, Z.; Wang, X. Compete or cooperate: Intensity, dynamics, and optimal strategies. Omega 2019, 86, 76–86. [Google Scholar] [CrossRef]
- Li, Y.J.; Bai, X.M.; Xue, K.L. Business modes in the sharing economy: How does the OEM cooperate with third-party sharing platforms? Int. J. Prod. Econ. 2020, 221, 107467. [Google Scholar] [CrossRef]
- Cohen, M.C.; Zhang, R. Competition and coopetition for two-sided platforms. Prod. Oper. Manag. 2022, 31, 1997–2014. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, M.; Tian, X.; Wang, S.; Hua, G. Spatial differentiation and network externality in pricing mechanism of online car hailing platform. Int. J. Prod. Econ. 2020, 219, 275–283. [Google Scholar] [CrossRef]
- Bimpikis, K.; Candogan, O.; Saban, D. Spatial pricing in ride-sharing networks. Oper. Res. 2019, 67, 744–769. [Google Scholar] [CrossRef]
- Guda, H.; Subramanian, U. Your uber is arriving: Managing on-demand workers through surge pricing, forecast communication, and worker incentives. Manag. Sci. 2019, 65, 1995–2014. [Google Scholar] [CrossRef]
- Cachon, G.P.; Daniels, K.M.; Lobel, R. The role of surge pricing on a service platform with self-scheduling capacity. Manuf. Serv. Oper. Manag. 2017, 19, 368–384. [Google Scholar] [CrossRef]
- Lin, X.; Zhou, Y.-W. Pricing policy selection for a platform providing vertically differentiated services with self-scheduling capacity. J. Oper. Res. Soc. 2019, 70, 1203–1218. [Google Scholar] [CrossRef]
- Sun, L.; Teunter, R.H.; Babai, M.Z.; Hua, G. Optimal pricing for ride-sourcing platforms. Eur. J. Oper. Res. 2019, 278, 783–795. [Google Scholar] [CrossRef]
- Wang, S.; Chen, H.; Wu, D. Regulating platform competition in two-sided markets under the O2O era. Int. J. Prod. Econ. 2019, 215, 131–143. [Google Scholar] [CrossRef]
- Li, M.; Jiang, G.; Lo, H.K. Pricing strategy of ride-sourcing services under travel time variability. Transp. Res. Part E Logist. Transp. Rev. 2022, 159, 102631. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, M. Pricing and matching with forward-looking buyers and sellers. Manuf. Serv. Oper. Manag. 2020, 22, 717–734. [Google Scholar] [CrossRef]
- Hu, B.; Hu, M.; Zhu, H. Surge pricing and two-sided temporal responses in ride hailing. Manuf. Serv. Oper. Manag. 2022, 24, 91–109. [Google Scholar] [CrossRef]
- Adhikari, A.; Basu, A.; Raj, S.P. Pricing of experience products under consumer heterogeneity. Int. J. Hosp. Manag. 2013, 33, 6–18. [Google Scholar] [CrossRef]
- Chiang, W.-Y.K.; Chhajed, D.; Hess, J.D. Direct marketing, indirect profits: A strategic analysis of dual-channel supply-chain design. Manag. Sci. 2003, 49, 1–20. [Google Scholar] [CrossRef]
- Hong, J.H.; Kim, B.C.; Park, K.S. Optimal risk management for the sharing economy with stranger danger and service quality. Eur. J. Oper. Res. 2019, 279, 1024–1035. [Google Scholar] [CrossRef]
- Chen, J.; Guo, Z. New-Media Advertising and Retail Platform Openness. MIS Q. 2022, 46, 431–456. [Google Scholar] [CrossRef]
- Song, W.; Chen, J.; Li, W. Spillover Effect of Consumer Awareness on Third Parties’ Selling Strategies and Retailers’ Platform Openness. Inf. Syst. Res. 2021, 32, 172–193. [Google Scholar] [CrossRef]
- Lai, G.; Liu, H.; Xiao, W.; Zhao, X. “Fulfilled by Amazon”: A Strategic Perspective of Competition at the e-Commerce Platform. Manuf. Serv. Oper. Manag. 2022, 24, 1406–1420. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).