A Hybrid AI Framework for Enhanced Stock Movement Prediction: Integrating ARIMA, RNN, and LightGBM Models
Abstract
1. Introduction
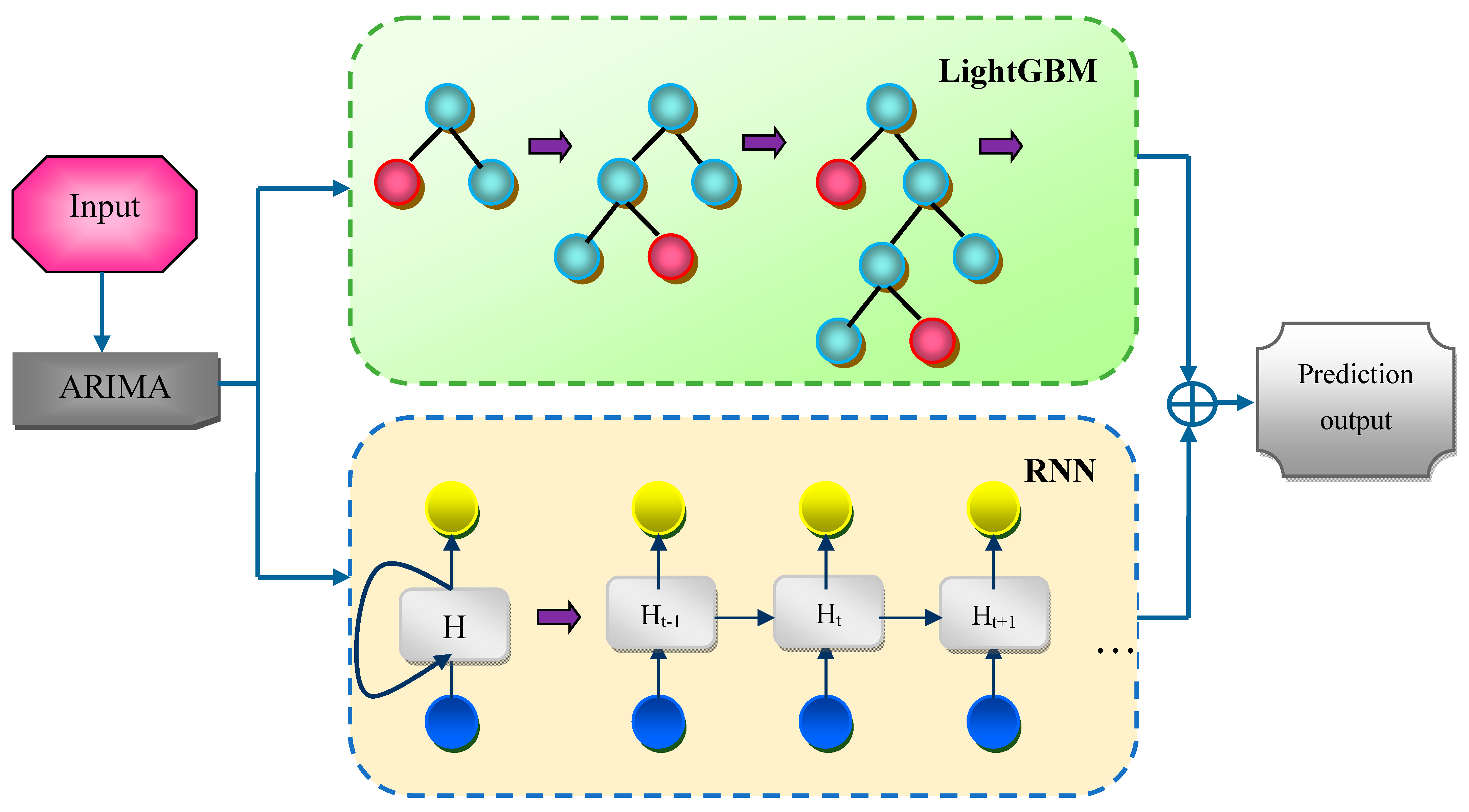
- Autoregressive integrated moving average ensemble recurrent light gradient boosting machine (AR-ERLM): The ensemble AR-ERLM model combines the strengths of decision trees and gradient boosting, resulting in accurate predictions. Furthermore, the RNN can learn long-term dependencies, allowing them to capture patterns over extended periods and automatically extract relevant features, which reduces the need for manual feature extraction.
2. Literature Review
- (i)
- Statistical models
- (ii)
- Machine Learning models
- (iii)
- Deep Learning models
- (iv)
- Transformer Models
2.1. Challenges
- In the process of predicting financial variables, the existing large number of high correlation features contains a minimal amount of information, which increases the time complexity [14];
- The SVM approach proved to be computationally expensive for voluminous datasets and unsuitable for forecasting extensive stock data [5];
- The development of incorporating the market stock prices introduced obstacles such as misspellings, information duplication in text data, and shortcuts, causing low efficiency in output results [9];
- The DPSA model has limited ability to predict the daily downward and upward stock trends [15];
- The layered architecture in the ConvLSTM model increases the computational expenses and requires careful tuning [8];
- However, the proposed approach addressed the aforementioned challenges in the existing techniques via the application of the AR-ERLM model. Specifically, the AR-ERLM hybridizes the synergic strength of individual models, such as the potential of ARIMA for determining the linear dependencies, the ability of RNN to capture temporal dynamics, and LightGBM’s capability in handling the large-scale datasets and their non-linear relationships for achieving the effective stock price prediction. Consequently, the proposed approach improves the predictive accuracy, eliminates overfitting, and minimizes the computational overhead.
2.2. Problem Statement
3. Proposed AR-ERLM Model for Stock Movement Prediction
3.1. Input for Stock Movement Prediction
3.1.1. Stock Market Data
3.1.2. Google Trends Data
3.2. Daily and Weekly Rolling Binary Calculation
3.3. Data Preprocessing
3.4. Technical Indicators
3.4.1. Moving Average
3.4.2. Bollinger Bands (BB)
3.4.3. Relative Strength Index (RSI)
3.4.4. Money Flow Index (MFI)
3.4.5. Average True Range (ATR)
3.4.6. Force Index
3.4.7. Ease of Movement Value (EMV)
3.4.8. Aroon Indicator
3.4.9. Aroon up Channel
3.4.10. Aroon Down Channel
3.4.11. MA Convergence Divergence (MACD)
3.4.12. MACD Histogram
3.4.13. MACD Signal Line
3.4.14. Exponential Moving Average (EMA)
3.4.15. Simple Moving Average (SMA-50)
3.4.16. SMA-200
3.4.17. Weighted Moving Average (WMA)
3.4.18. Triple Exponential Average (TRIX)
3.4.19. Mass Index
3.4.20. Ichimoku Kinko Hyo Span A
3.4.21. Ichimoku Kinko Hyo Span B
3.4.22. Know Sure Thing (KST)
3.4.23. Detrended Price Oscillator (DPO)
3.4.24. Commodity Channel Index (CCI)
3.4.25. Average Directional Index (ADX)
3.4.26. Minus Directional Indicator (–DI)
3.4.27. Plus Directional Indicator (+DI)
3.4.28. Schaff Trend Cycle (STC)
3.5. Autoregressive Integrated Moving Average Ensemble Recurrent Light Gradient Boosting Machine for Stock Movement Prediction
4. Results and Discussion
4.1. Experimental Setup
4.2. Performance Metrics
4.3. Dataset Description
4.4. Comparative Methods
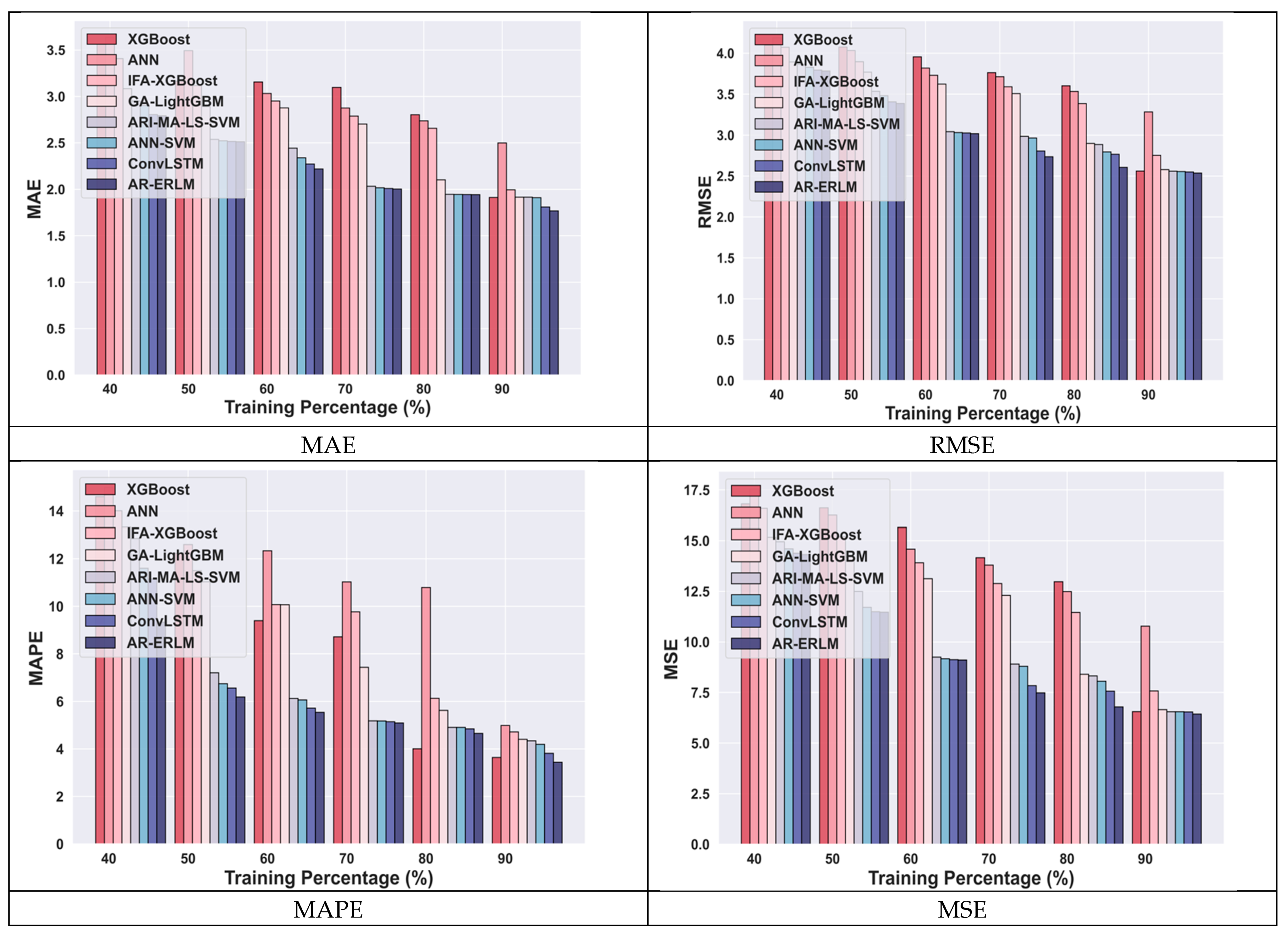
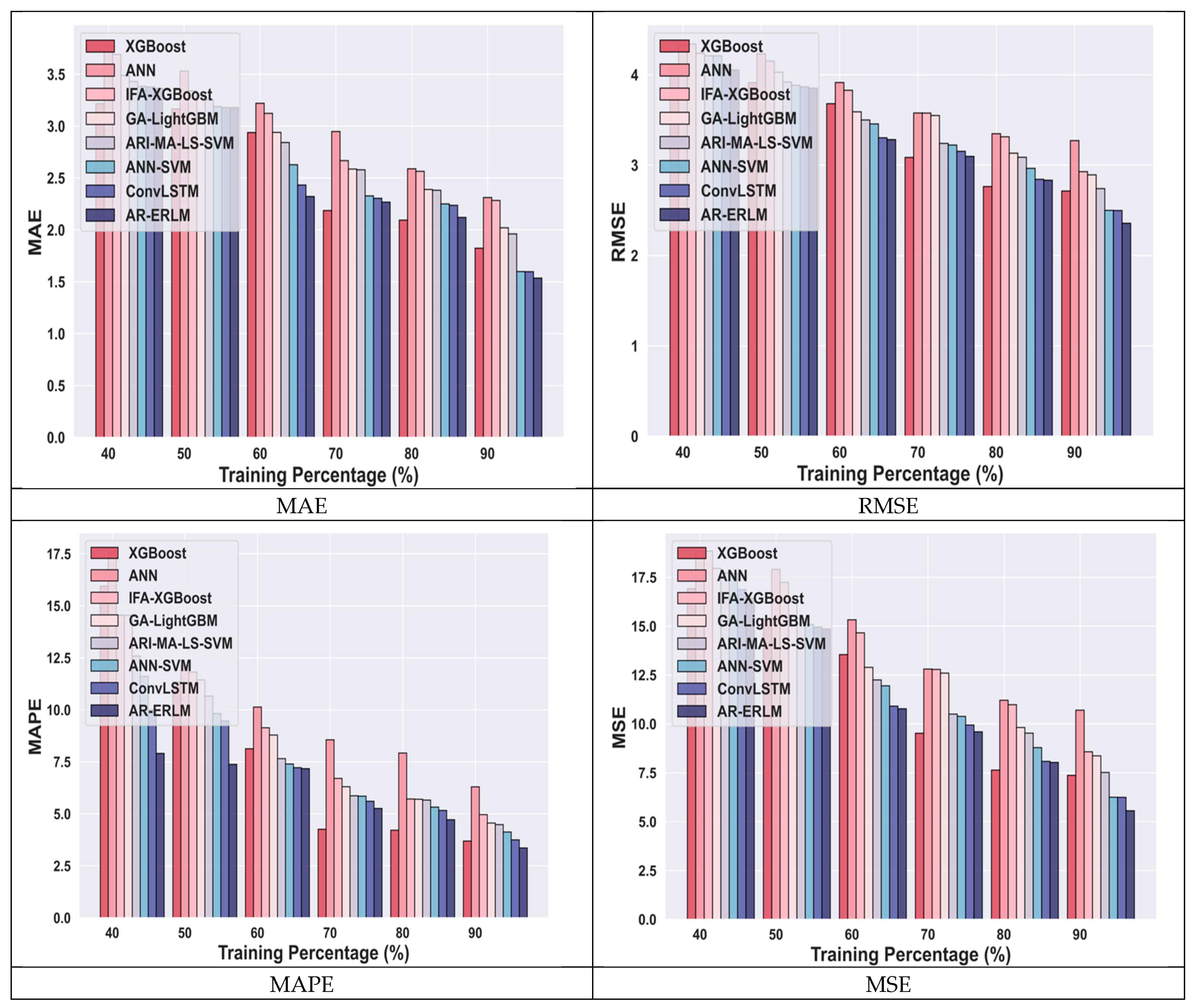
4.4.1. Comparative Analysis for Meta Data Using Training Percentage
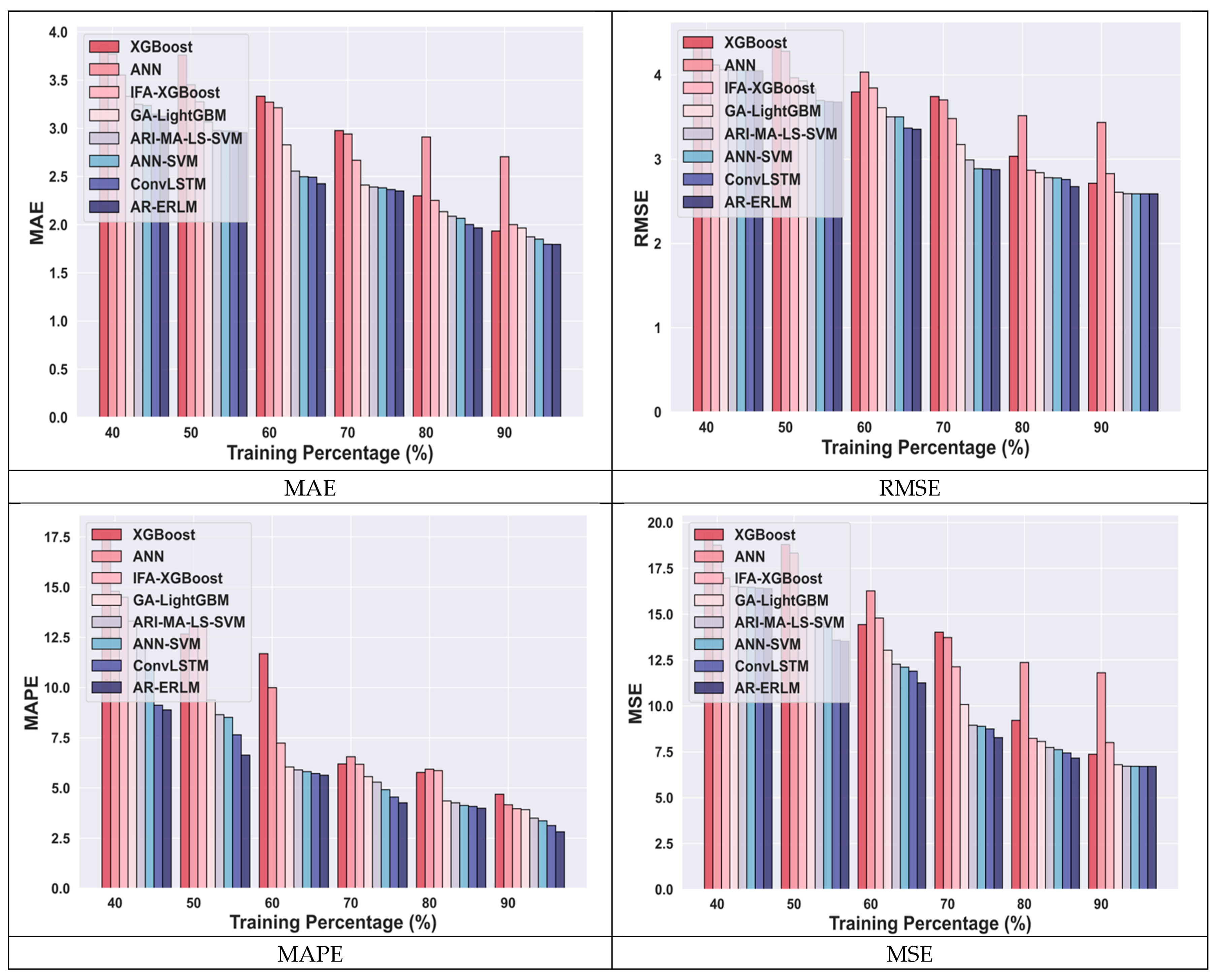
4.4.2. Comparative Analysis for Amazon Data Using TP
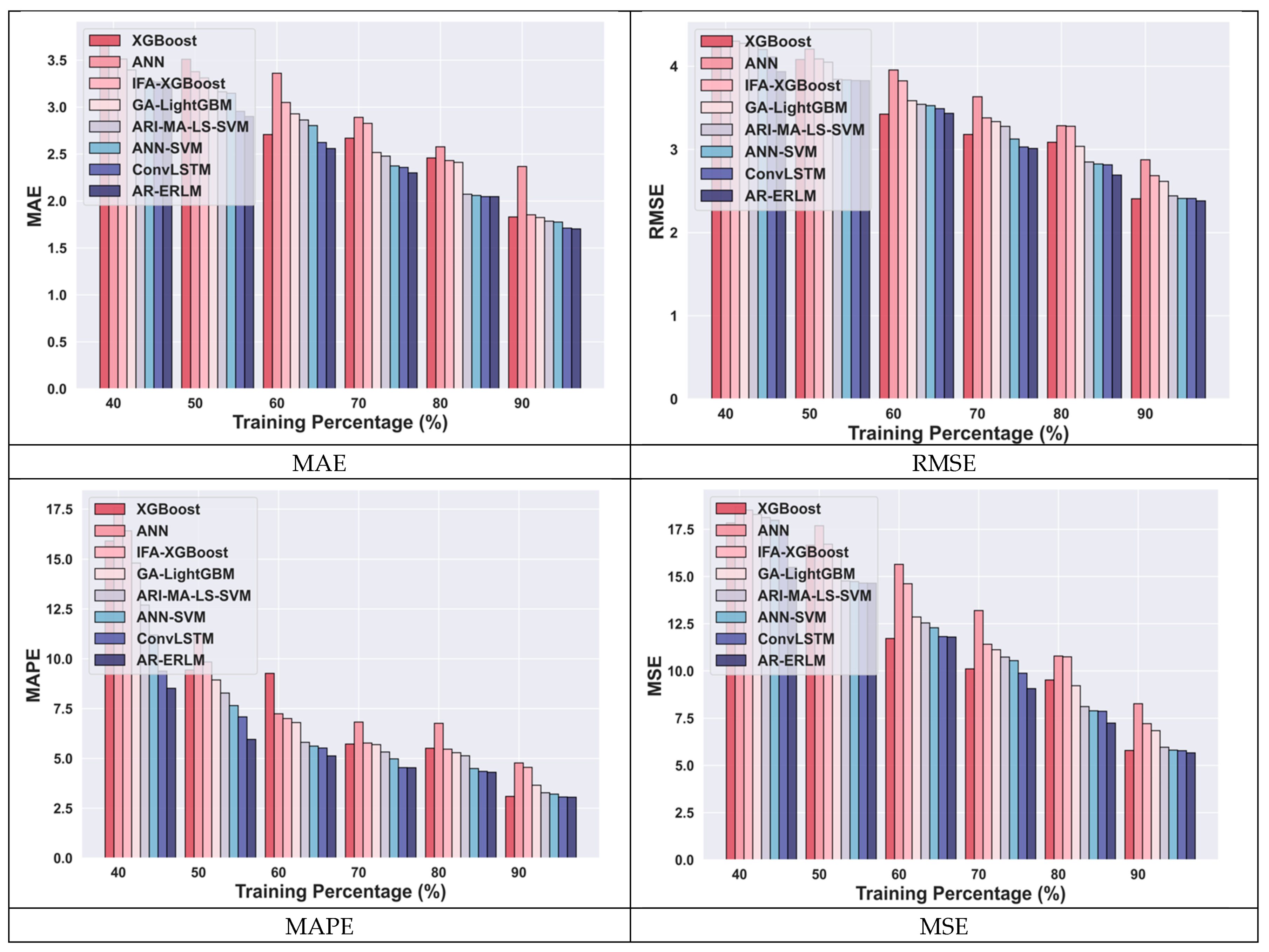
4.4.3. Comparative Analysis for Netflix Data
4.4.4. Comparative Analysis for Nifty50 Using Training Percentage
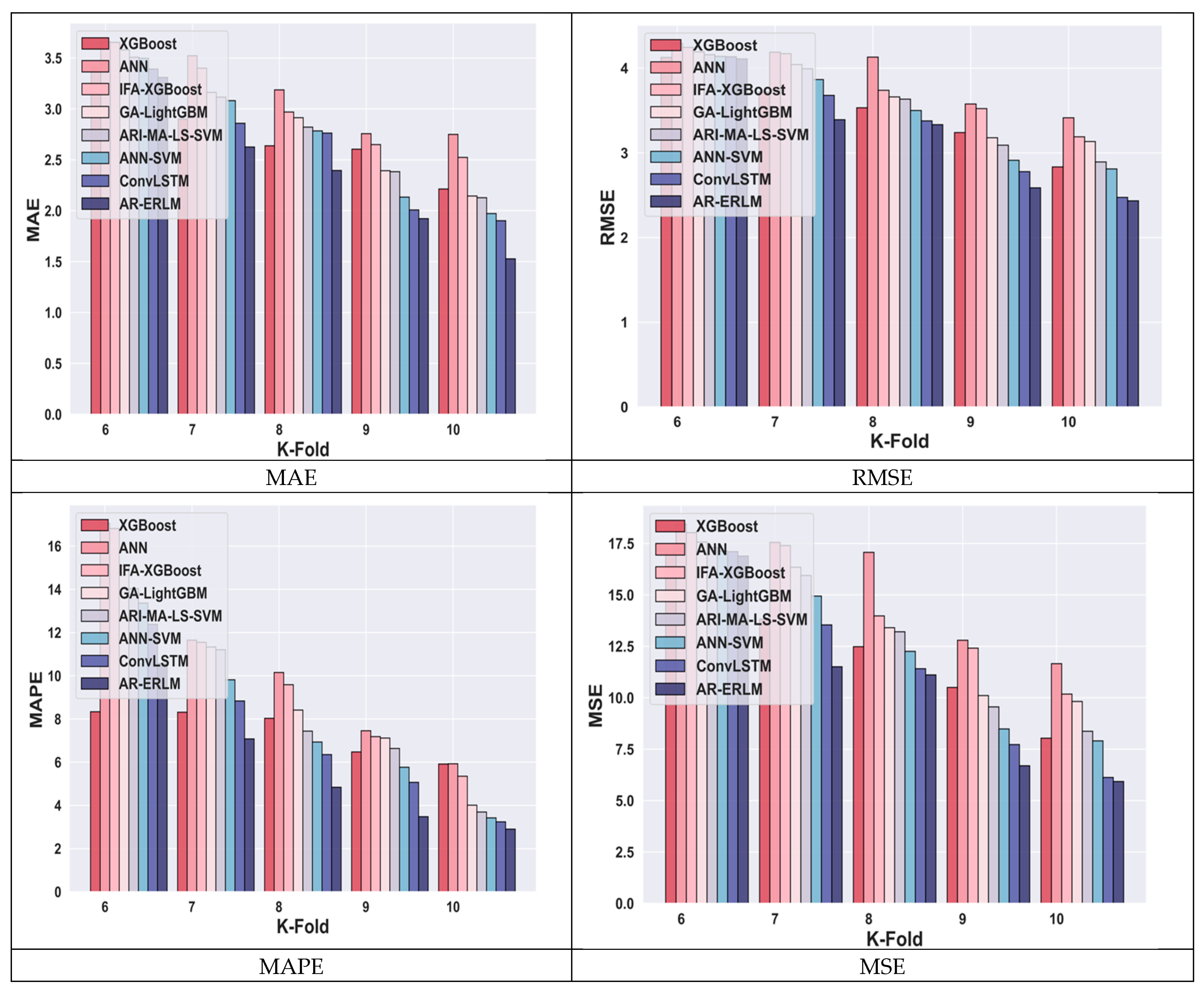
4.4.5. Comparative Analysis for Meta Data Using k-Fold
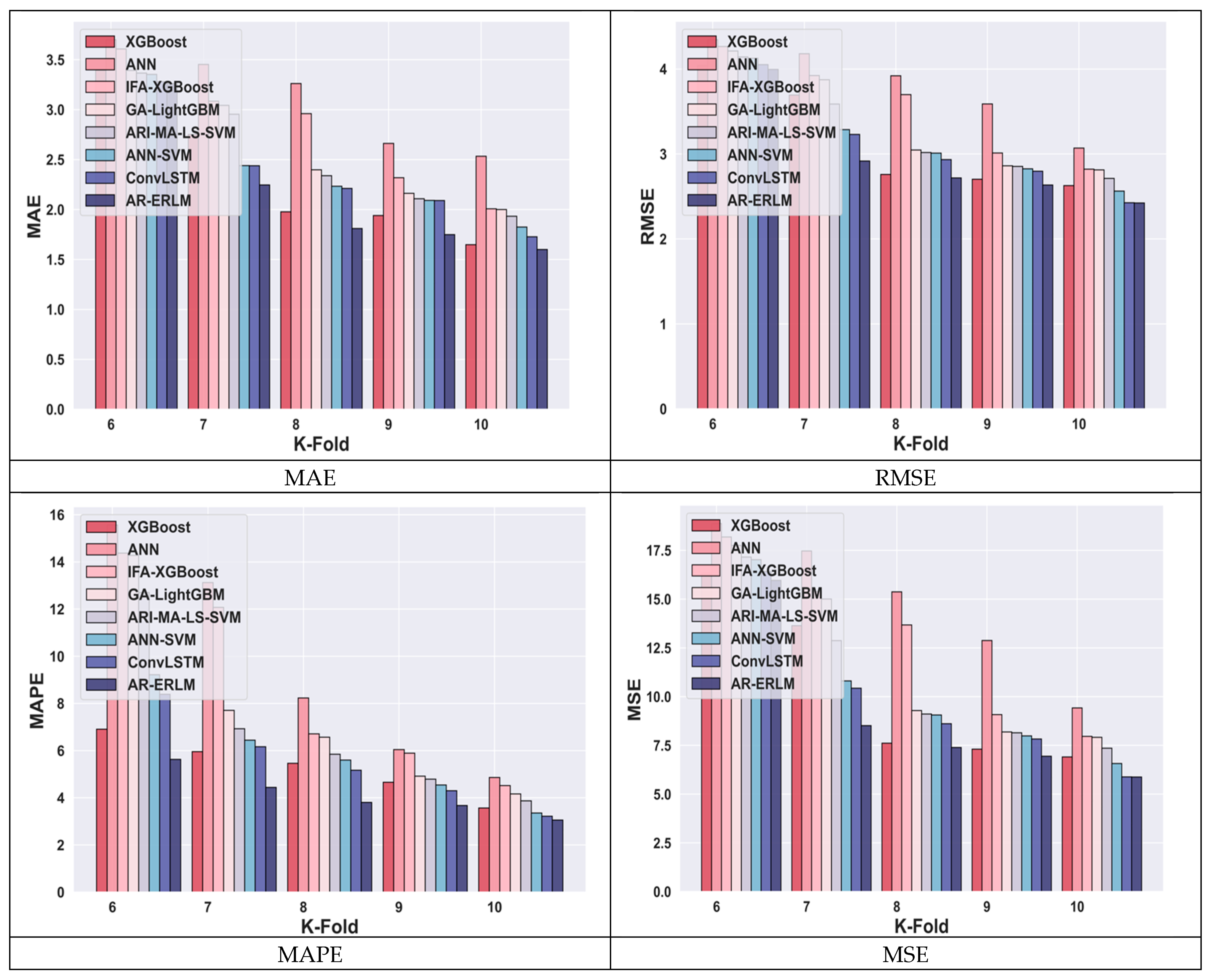
4.4.6. Comparative Analysis for Amazon Data Using k-Fold
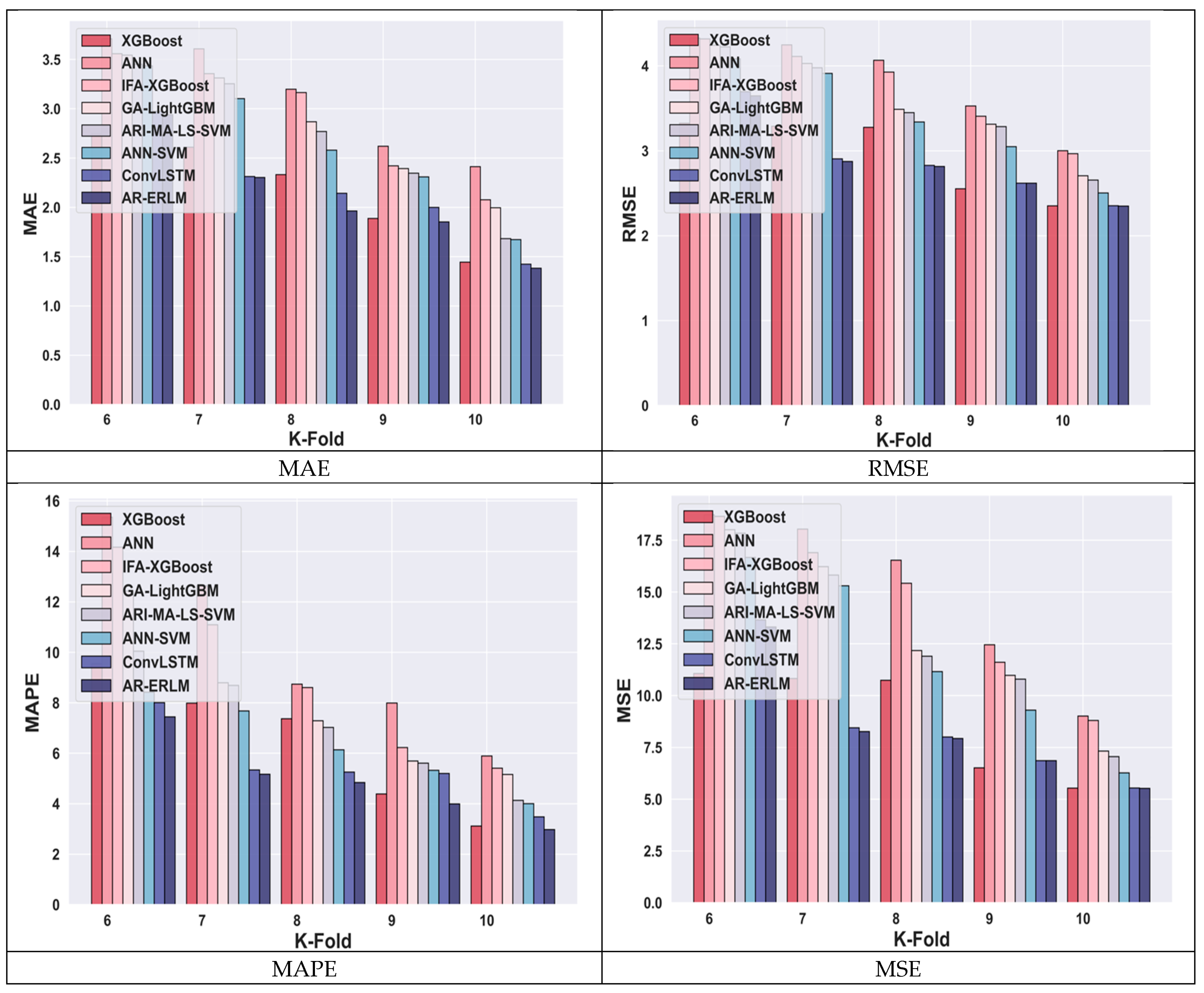
4.4.7. Comparative Analysis for Netflix Data Using k-Fold
4.4.8. Comparative Analysis for Nifty50 Using k-Fold
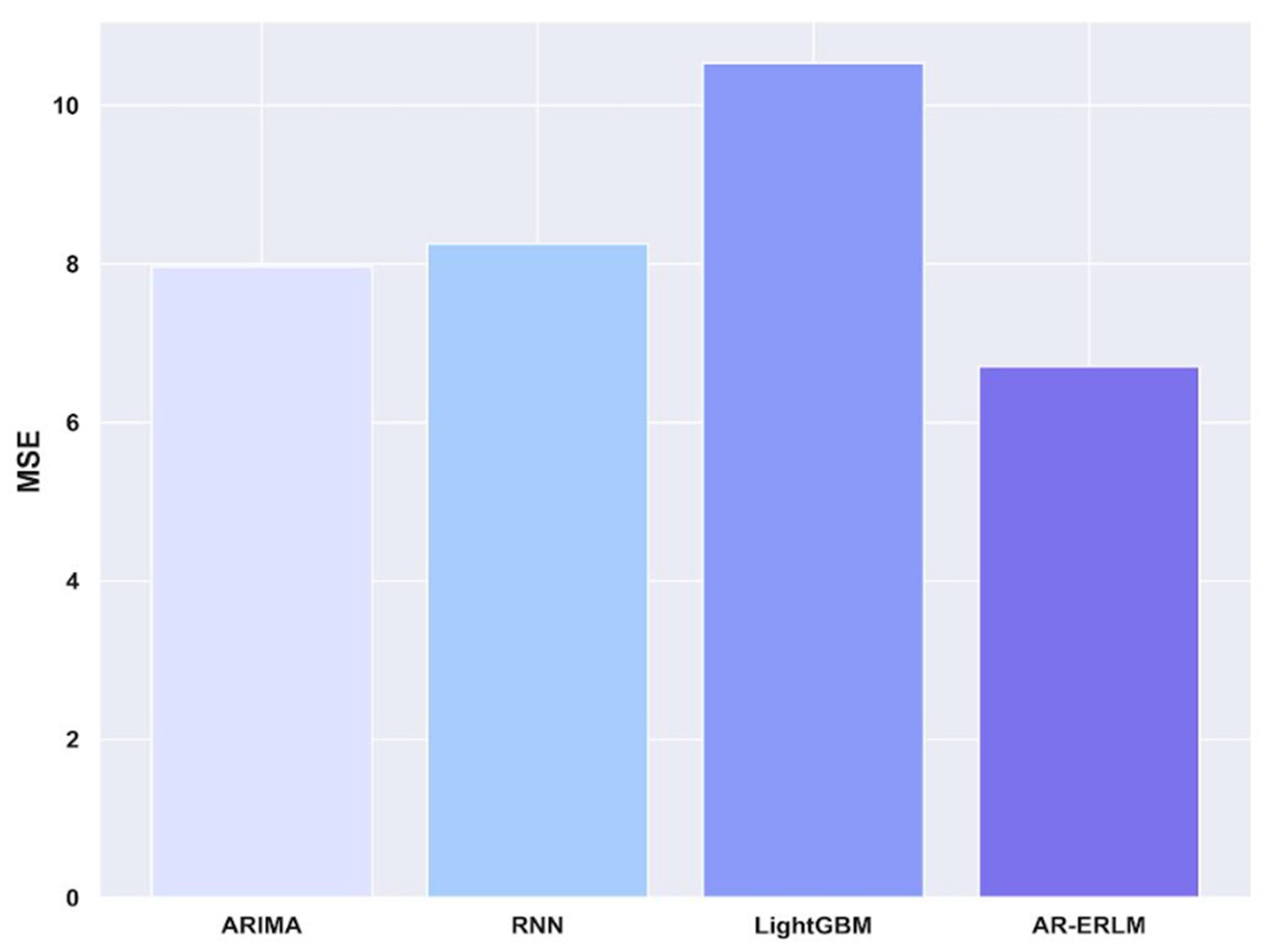
4.5. Comparative Discussion
4.6. Ablation Study
4.7. Diebold–Mariano Test
4.8. Statistical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Patel, M.; Jariwala, K.; Chattopadhyay, C. A Hybrid Relational Approach Towards Stock Price Prediction and Profitability. IEEE Trans. Artif. Intell. 2024, 5, 5844–5854. [Google Scholar] [CrossRef]
- Bezerra, P.C.S.; Albuquerque, P.H.M. Volatility forecasting via SVR–GARCH with mixture of Gaussian kernels. Comput. Manag. Sci. 2017, 14, 179–196. [Google Scholar] [CrossRef]
- Nti, I.K.; Adekoya, A.F.; Weyori, B.A. A systematic review of fundamental and technical analysis of stock market predictions. Artif. Intell. Rev. 2020, 53, 3007–3057. [Google Scholar] [CrossRef]
- Ahmadi, E.; Jasemi, M.; Monplaisir, L.; Nabavi, M.A.; Mahmoodi, A.; Jam, P.A. New efficient hybrid candlestick technical analysis model for stock market timing on the basis of the Support Vector Machine and Heuristic Algorithms of Imperialist Competition and Genetic. Expert Syst. Appl. 2018, 94, 21–31. [Google Scholar] [CrossRef]
- Lin, Y.; Liu, S.; Yang, H.; Wu, H. Stock trend prediction using candlestick charting and ensemble machine learning techniques with a novelty feature engineering scheme. IEEE Access 2021, 9, 101433–101446. [Google Scholar] [CrossRef]
- Saetia, K.; Yokrattanasak, J. Stock movement prediction using machine learning based on technical indicators and Google trend searches in Thailand. Int. J. Financ. Stud. 2022, 11, 5. [Google Scholar] [CrossRef]
- Khan, W.; Ghazanfar, M.A.; Azam, M.A.; Karami, A.; Alyoubi, K.H.; Alfakeeh, A.S. Stock market prediction using machine learning classifiers and social media, news. J. Ambient. Intell. Humaniz. Comput. 2022, 13, 3433–3456. [Google Scholar] [CrossRef]
- Peng, Y.; Albuquerque, P.H.M.; Kimura, H.; Saavedra, C.A.P.B. Feature selection and deep neural networks for stock price direction forecasting using technical analysis indicators. Mach. Learn. Appl. 2021, 5, 100060. [Google Scholar] [CrossRef]
- Ayala, J.; García-Torres, M.; Noguera, J.L.V.; Gómez-Vela, F.; Divina, F. Technical analysis strategy optimization using a machine learning approach in stock market indices. Knowl.-Based Syst. 2021, 225, 107119. [Google Scholar] [CrossRef]
- Jiang, J.; Wu, L.; Zhao, H.; Zhu, H.; Zhang, W. Forecasting movements of stock time series based on hidden state guided deep learning approach. Inf. Process. Manag. 2023, 60, 103328. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, H.; Mehlawat, M.K.; Jia, L. Mean–variance portfolio optimization using machine learning-based stock price prediction. Appl. Soft Comput. 2021, 100, 106943. [Google Scholar] [CrossRef]
- Fabozzi, F.J.; Markowitz, H.M.; Gupta, F. Portfolio selection. Handb. Financ. 2008, 2, 3–13. [Google Scholar]
- Yun, K.K.; Yoon, S.W.; Won, D. Prediction of stock price direction using a hybrid GA-XGBoost algorithm with a three-stage feature engineering process. Expert Syst. Appl. 2021, 186, 115716. [Google Scholar] [CrossRef]
- Jiang, L.C.; Subramanian, P. Forecasting of stock price using autoregressive integrated moving average model. J. Comput. Theor. Nanosci. 2019, 16, 3519–3524. [Google Scholar] [CrossRef]
- Koki, C.; Leonardos, S.; Piliouras, G. Exploring the predictability of cryptocurrencies via Bayesian hidden Markov models. Res. Int. Bus. Financ. 2022, 59, 101554. [Google Scholar] [CrossRef]
- Dong, S.; Wang, J.; Luo, H.; Wang, H.; Wu, F.X. A dynamic predictor selection algorithm for predicting stock market movement. Expert Syst. Appl. 2021, 186, 115836. [Google Scholar] [CrossRef]
- Wang, C.; Chen, Y.; Zhang, S.; Zhang, Q. Stock market index prediction using deep Transformer model. Expert Syst. Appl. 2022, 208, 118128. [Google Scholar] [CrossRef]
- Tao, Z.; Wu, W.; Wang, J. Series decomposition Transformer with period-correlation for stock market index prediction. Expert Syst. Appl. 2024, 237, 121424. [Google Scholar] [CrossRef]
- Ronaghi, F.; Salimibeni, M.; Naderkhani, F.; Mohammadi, A. COVID19-HPSMP: COVID-19 adopted Hybrid and Parallel deep information fusion framework for stock price movement prediction. Expert Syst. Appl. 2022, 187, 115879. [Google Scholar] [CrossRef]
- Amazon Dataset. Available online: https://finance.yahoo.com/quote/AMZN (accessed on 2 May 2024).
- Meta Dataset. Available online: https://finance.yahoo.com/quote/META (accessed on 2 May 2024).
- Netflix Dataset. Available online: https://finance.yahoo.com/quote/NFLX (accessed on 2 May 2024).
- Ouyang, Y.; Li, S.; Yao, K.; Wang, J. Analysis of Investment Indicators for the Electronic Components Sector of the A-Share Market. In Proceedings of the 2022 International Conference on Bigdata Blockchain and Economy Management (ICBBEM 2022), Guangzhou, China, 26–28 August 2022; Atlantis Press: Paris, France, 2022; pp. 180–186. [Google Scholar]
- Joshi, D.L. Use of Moving Average Convergence Divergence for Predicting Price Movements. Int. Res. J. MMC (IRJMMC) 2022, 3, 21–25. [Google Scholar] [CrossRef]
- Chandrika, P.V.; Srinivasan, K.S.; Taylor, G. Predicting stock market movements using artificial neural networks. Univers. J. Account. Financ. 2021, 9, 405–410. [Google Scholar] [CrossRef]
- Wahyudi, S.T. The ARIMA Model for the Indonesia Stock Price. Int. J. Econ. Manag. 2017, 11, 223–236. [Google Scholar]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Gan, M.; Pan, S.; Chen, Y.; Cheng, C.; Pan, H.; Zhu, X. Application of the machine learning lightgbm model to the prediction of the water levels of the lower columbia river. J. Mar. Sci. Eng. 2021, 9, 496. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Zhao, X.; Liu, Y.; Zhao, Q. Cost Harmonization LightGBM-Based Stock Market Prediction. IEEE Access 2023, 11, 105009–105026. [Google Scholar] [CrossRef]
- Selvin, S.; Vinayakumar, R.; Gopalakrishnan, E.A.; Menon, V.K.; Soman, K.P. Stock price prediction using LSTM, RNN and CNN-sliding window model. In Proceedings of the 2017 international conference on advances in computing, communications and informatics (ICACCI), Udupi, India, 13–16 September 2017; pp. 1643–1647. [Google Scholar]
- Nifty50 Dataset. Available online: https://finance.yahoo.com/quote/%5ENSEI/history/?fr=sycsrp_catchall (accessed on 22 February 2025).
- Huang, C.; Cai, Y.; Cao, J.; Deng, Y. Stock complex networks based on the GA-LightGBM model: The prediction of firm performance. Inf. Sci. 2024, 700, 121824. [Google Scholar] [CrossRef]
- Xiao, C.; Xia, W.; Jiang, J. Stock price forecast based on combined model of ARI-MA-LS-SVM. Neural Comput. Appl. 2020, 32, 5379–5388. [Google Scholar] [CrossRef]
- Ali, M.; Khan, D.M.; Aamir, M.; Ali, A.; Ahmad, Z. Predicting the direction movement of financial time series using artificial neural network and support vector machine. Complexity 2021, 2021, 2906463. [Google Scholar] [CrossRef]


| TP 90 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Dataset/Methods | Metrics | XGBoost | ANN | IFA-XGBoost | GA-Light GBM | ARI-MA-LS-SVM | ANN-SVM | ConvLSTM | AR-ERLM |
| Meta Data | MAE | 1.91 | 2.49 | 1.99 | 1.91 | 1.91 | 1.9 | 1.8 | 1.76 |
| RMSE | 2.56 | 3.28 | 2.75 | 2.57 | 2.55 | 2.55 | 2.54 | 2.53 | |
| MAPE | 3.64 | 4.98 | 4.71 | 4.4 | 4.34 | 4.19 | 3.81 | 3.43 | |
| MSE | 6.55 | 10.78 | 7.57 | 6.65 | 6.55 | 6.55 | 6.53 | 6.43 | |
| Amazon Data | MAE | 1.93 | 2.7 | 1.99 | 1.96 | 1.87 | 1.84 | 1.8 | 1.79 |
| RMSE | 2.71 | 3.43 | 2.82 | 2.607 | 2.59 | 2.589 | 2.589 | 2.588 | |
| MAPE | 4.68 | 4.16 | 3.96 | 3.91 | 3.49 | 3.36 | 3.13 | 2.81 | |
| MSE | 7.36 | 11.8 | 8 | 6.79 | 6.71 | 6.72 | 6.71 | 6.70 | |
| Netflix Data | MAE | 1.83 | 2.36 | 1.85 | 1.82 | 1.78 | 1.77 | 1.71 | 1.70 |
| RMSE | 2.4 | 2.87 | 2.68 | 2.61 | 2.44 | 2.41 | 2.41 | 2.38 | |
| MAPE | 3.09 | 4.77 | 4.55 | 3.65 | 3.27 | 3.21 | 3.06 | 3.05 | |
| MSE | 5.79 | 8.26 | 7.20 | 6.84 | 5.96 | 5.81 | 5.78 | 5.66 | |
| Nifty50 Data | MAE | 2.27 | 2.53 | 2.30 | 2.18 | 2.05 | 1.90 | 1.87 | 1.82 |
| RMSE | 3.05 | 3.06 | 2.98 | 2.89 | 2.88 | 2.69 | 2.52 | 2.39 | |
| MAPE | 4.41 | 7.49 | 6.31 | 4.76 | 4.36 | 4.31 | 3.42 | 2.55 | |
| MSE | 9.30 | 9.36 | 8.86 | 8.37 | 8.28 | 7.22 | 6.37 | 5.72 | |
| k-Fold 10 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Dataset/Methods | Metrics | XGBoost | ANN | IFA-XGBoost | GA-Light GBM | ARI-MA-LS-SVM | ANN-SVM | ConvLSTM | AR-ERLM |
| Meta Data | MAE | 2.21 | 2.75 | 2.52 | 2.14 | 2.13 | 1.97 | 1.90 | 1.53 |
| RMSE | 2.83 | 3.41 | 3.19 | 3.13 | 2.89 | 2.81 | 2.47 | 2.43 | |
| MAPE | 5.91 | 5.92 | 5.35 | 4.01 | 3.69 | 3.42 | 3.24 | 2.90 | |
| MSE | 8.04 | 11.65 | 10.18 | 9.82 | 8.37 | 7.90 | 6.12 | 5.93 | |
| Amazon Data | MAE | 1.65 | 2.53 | 2.01 | 2.00 | 1.93 | 1.82 | 1.73 | 1.60 |
| RMSE | 2.63 | 3.07 | 2.82 | 2.81 | 2.71 | 2.56 | 2.43 | 2.42 | |
| MAPE | 3.57 | 4.86 | 4.52 | 4.17 | 3.87 | 3.36 | 3.22 | 3.06 | |
| MSE | 6.91 | 9.42 | 7.96 | 7.91 | 7.36 | 6.57 | 5.88 | 5.88 | |
| Netflix Data | MAE | 1.44 | 2.41 | 2.08 | 2.00 | 1.68 | 1.67 | 1.42 | 1.38 |
| RMSE | 2.4 | 2.87 | 2.68 | 2.61 | 2.44 | 2.41 | 2.41 | 2.38 | |
| MAPE | 3.11 | 5.89 | 5.41 | 5.16 | 4.13 | 4.00 | 3.48 | 2.98 | |
| MSE | 2.36 | 3.00 | 2.97 | 2.71 | 2.66 | 2.50 | 2.35 | 2.34 | |
| Nifty50 Data | MAE | 1.87 | 2.19 | 2.19 | 2.03 | 2.00 | 1.91 | 1.87 | 1.80 |
| RMSE | 2.47 | 2.85 | 2.84 | 2.71 | 2.70 | 2.58 | 2.52 | 2.45 | |
| MAPE | 3.60 | 7.36 | 6.42 | 5.41 | 4.45 | 4.37 | 3.84 | 3.17 | |
| MSE | 6.09 | 8.13 | 8.07 | 7.34 | 7.30 | 6.66 | 6.35 | 6.01 | |
| Model | ARIMA | RNN | LightGBM |
|---|---|---|---|
| ARIMA | - | −0.854 | −7.346 |
| RNN | 0.000 | - | −8.976 |
| LightGBM | 0.000 | −0.275 | - |
| S. No | Stock Data | Technical Indicators | ||||
|---|---|---|---|---|---|---|
| Best | Mean | Variance | Best | Mean | Variance | |
| 1 | 82,100 | 16,436.41 | 7.32 × 108 | 82,100 | 5292.3 | 2.05 × 108 |
| 2 | 77,700 | 15,813.91 | 6.51 × 108 | 77,700 | 5155.382 | 1.84 × 108 |
| 3 | 84,500 | 16,794.48 | 7.77 × 108 | 84,500 | 5377.683 | 2.16 × 108 |
| 4 | 101,900 | 19,326.21 | 1.15 × 109 | 101,900 | 5937.903 | 3.12 × 108 |
| 5 | 118,200 | 21,685.12 | 1.57 × 109 | 118,200 | 6455.745 | 4.18 × 108 |
| 6 | 172,800 | 29,384.55 | 3.44 × 109 | 172,800 | 8134.185 | 8.89 × 108 |
| 7 | 164,100 | 28,076.77 | 3.1 × 109 | 164,100 | 7843.107 | 8.02 × 108 |
| 8 | 143,800 | 25,233.83 | 2.36 × 109 | 143,800 | 7223.883 | 6.16 × 108 |
| 9 | 148,000 | 25,866.29 | 2.5 × 109 | 148,000 | 7621.368 | 6.51 × 108 |
| 10 | 103,200 | 19,484.65 | 1.18 × 109 | 103,200 | 6227.626 | 3.18 × 108 |
| 11 | 129,600 | 23,267.16 | 1.9 × 109 | 129,600 | 7055.614 | 5 × 108 |
| 12 | 146,100 | 25,606.84 | 2.43 × 109 | 146,100 | 7402.419 | 6.36 × 108 |
| 13 | 232,100 | 37,989.47 | 6.29 × 109 | 232,100 | 10,115.53 | 1.61 × 109 |
| 14 | 176,000 | 30,000.12 | 3.57 × 109 | 176,000 | 8373.068 | 9.22 × 108 |
| 15 | 125,400 | 22,800.46 | 1.77 × 109 | 125,400 | 6807.859 | 4.69 × 108 |
| 16 | 158,700 | 27,607.59 | 2.88 × 109 | 158,700 | 7873.989 | 7.5 × 108 |
| 17 | 185,900 | 31,540.09 | 3.99 × 109 | 185,900 | 8734.912 | 1.03 × 109 |
| 18 | 175,500 | 30,072.63 | 3.54 × 109 | 175,500 | 8421.444 | 9.17 × 108 |
| 19 | 191,200 | 32,360.76 | 4.22 × 109 | 191,200 | 8940.341 | 1.09 × 109 |
| 20 | 192,000 | 32,504.62 | 4.25 × 109 | 192,000 | 8983.887 | 1.1 × 109 |
| 21 | 185,100 | 31,539.45 | 3.95 × 109 | 185,100 | 8784.664 | 1.02 × 109 |
| 22 | 256,300 | 41,711.68 | 7.69 × 109 | 256,300 | 11,016.64 | 1.96 × 109 |
| 23 | 267,300 | 43,268.17 | 8.38 × 109 | 267,300 | 11,360.65 | 2.13 × 109 |
| 24 | 210,100 | 35,041.69 | 5.12 × 109 | 210,100 | 9570.6 | 1.31 × 109 |
| 25 | 208,700 | 34,834.81 | 5.05 × 109 | 208,700 | 9535.426 | 1.3 × 109 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alarbi, A.; Khalifa, W.; Alzubi, A. A Hybrid AI Framework for Enhanced Stock Movement Prediction: Integrating ARIMA, RNN, and LightGBM Models. Systems 2025, 13, 162. https://doi.org/10.3390/systems13030162
Alarbi A, Khalifa W, Alzubi A. A Hybrid AI Framework for Enhanced Stock Movement Prediction: Integrating ARIMA, RNN, and LightGBM Models. Systems. 2025; 13(3):162. https://doi.org/10.3390/systems13030162
Chicago/Turabian StyleAlarbi, Adel, Wagdi Khalifa, and Ahmad Alzubi. 2025. "A Hybrid AI Framework for Enhanced Stock Movement Prediction: Integrating ARIMA, RNN, and LightGBM Models" Systems 13, no. 3: 162. https://doi.org/10.3390/systems13030162
APA StyleAlarbi, A., Khalifa, W., & Alzubi, A. (2025). A Hybrid AI Framework for Enhanced Stock Movement Prediction: Integrating ARIMA, RNN, and LightGBM Models. Systems, 13(3), 162. https://doi.org/10.3390/systems13030162







