Optimal Delay Product Differentiation System Under the Cap-and-Trade Environment
Abstract
1. Introduction
2. Literature Review
- (i)
- Unit emissions allowances sell price equals the purchase price
- (ii)
- Unit emissions allowances purchase and sell prices are unequal
- (iii)
- Unit emissions allowances trade price is stochastic
3. Model
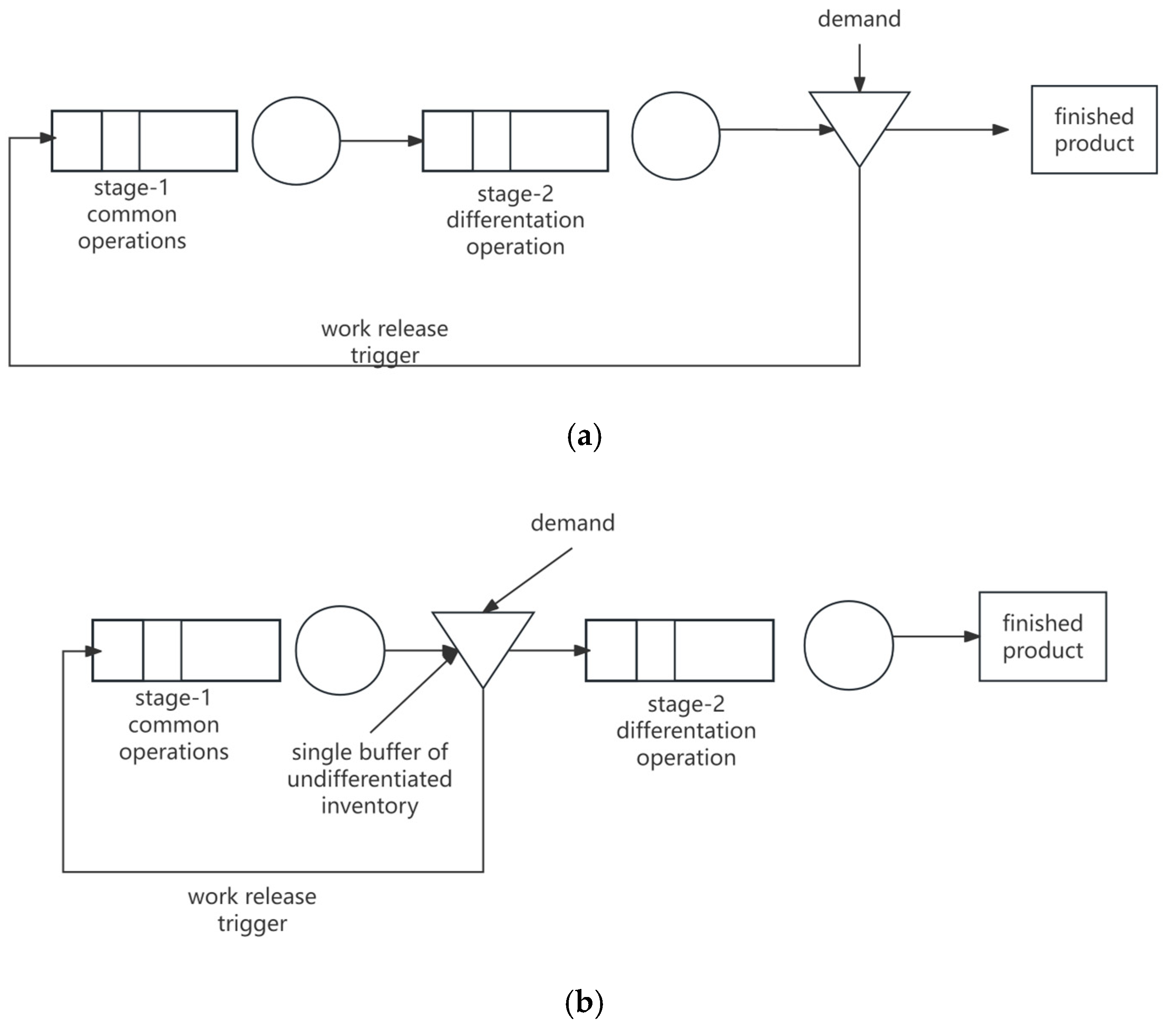
3.1. Model Description
- maximum demand for product-j in a single production period
- the summary cost in the MTS system.
- the summary cost in the DD system.
- the total emissions in the MTS system.
- the total emissions in the DD system.
- the base stock level for the semi-finished product in the DD system (decision variable).
- the base stock level for the finished product (decision variable).
- the initial emission allowances in the system.
- Emissions allowances after trading decisions in pure MTS (decision variable).
- Emissions allowances after trading decisions in DD (decision variable).
- Emissions allowances purchase price.
- Emissions allowances sale price.
- the unit finished product storage cost.
- semi-finished product storage cost per unit.
- penalty cost for excess emissions per unit.
- the processing rate at stage-i.
- the stage-i loading, .
- the rate of total demand.
- the expected inventory of finished product in the pure MTS system.
- the expected inventory of semi-finished product in the DD system.
- the expected backorders of semi-finished product in the DD system.
- the expected backorders of finished product in the pure MTS system.
- the order-fulfillment time in the DD system.
- the order-fulfillment time in the pure MTS system.
- the rate of a Poisson process that demand for product-j occurs.
- the emissions of producing unit product in stage-1.
- the emissions of producing unit product in stage-2.
- the emissions of storing unit finished product.
- the emissions of storing unit semi-finished product.
- the lead time of unit customer order.
3.2. Pure Make-to-Stock System
3.2.1. Emissions Trading Cost
3.2.2. Inventory Cost
3.2.3. Penalty Cost for Backorders
3.2.4. Penalty Cost for the Excess Emissions
- MTS stage-1 emissions:
- MTS stage-2 emissions:
- Inventory emissions:
3.2.5. MTS Summary
3.3. Delayed Differentiation System
3.3.1. Emissions Trading Cost
3.3.2. Inventory Cost
3.3.3. Penalty Cost for Backorders
3.3.4. Penalty Cost for the Excess Emissions
- Stage-1 manufacturing emissions:
- Stage-2 manufacturing emissions:
- Inventory emissions:
- Total emissions:
- The penalty cost for the excess emissions is
3.3.5. DD Summary
4. Optimal Policies
4.1. Production Decisions and Emissions Decisions in the Pure MTS System
- (1)
- If , is obtained from the following equation:
- (2)
- If , is obtained from the following equation:
- (1)
- If , means that the manufacturer needs to purchase emissions allowances; the minimum cost for the manufacturer is:
- (2)
- If , means the manufacturer needs to sell emissions allowances; the minimum cost for the manufacturer is:
4.2. Production Decisions and Emissions Decisions in the DD System
- (1)
- If
- (2)
- If
- (1)
- if , means that the manufacturer needs to purchase emissions allowances; the minimum cost for the manufacturer is:
- (2)
- if , means that the manufacturer needs to purchase emissions allowances; the minimum cost for the manufacturer is:
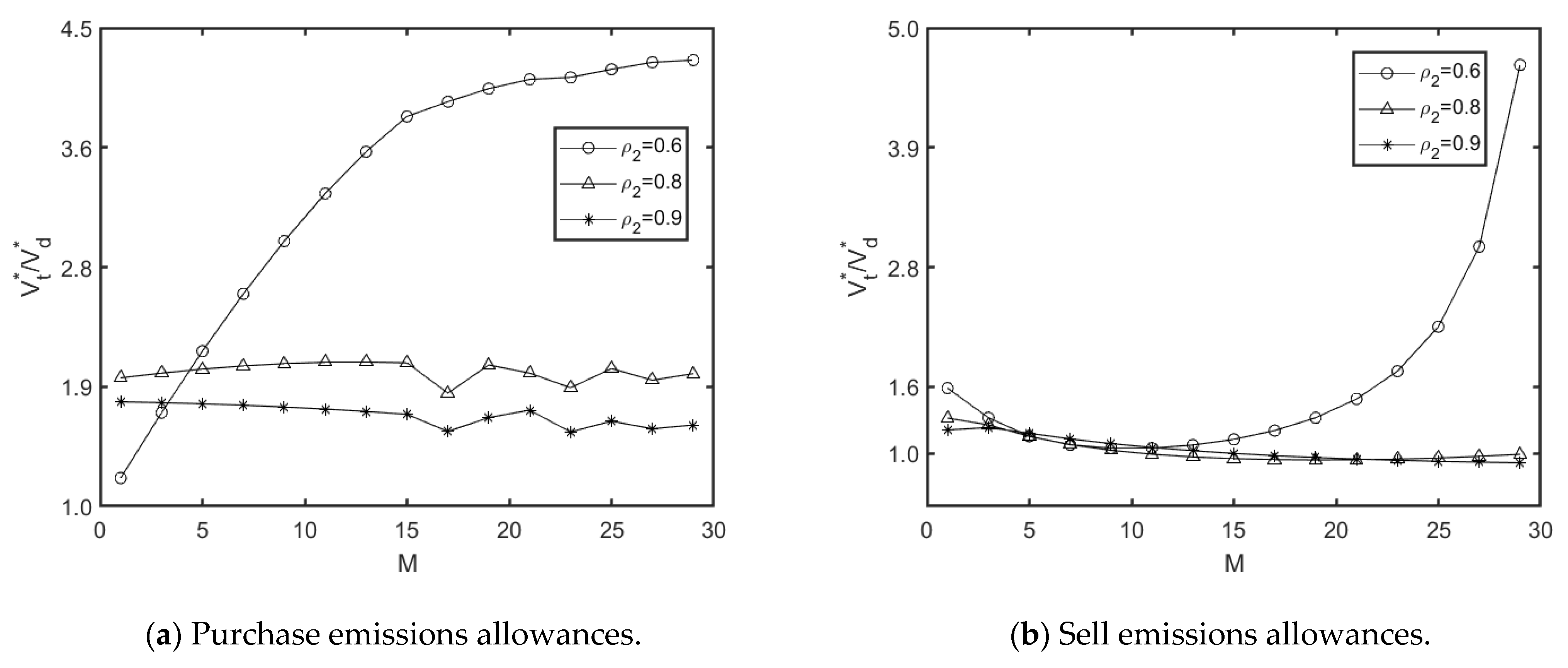
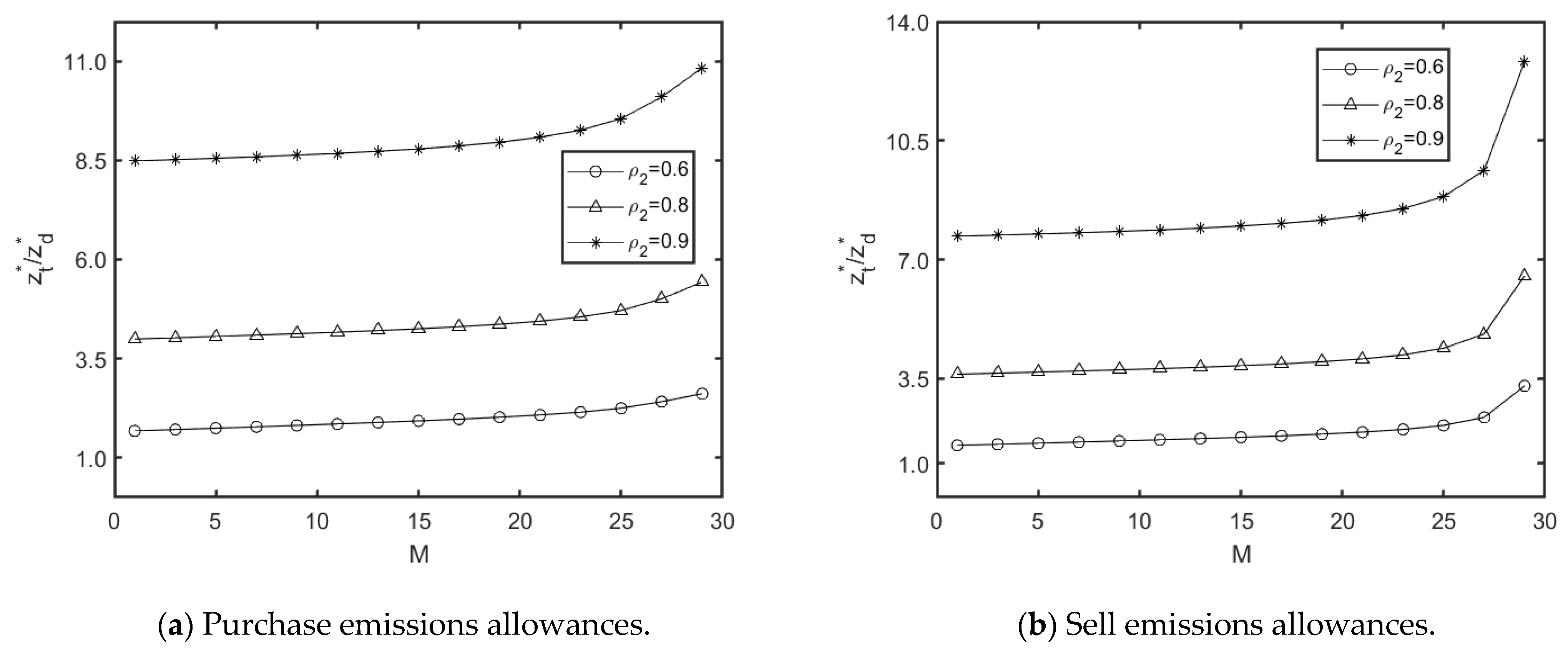
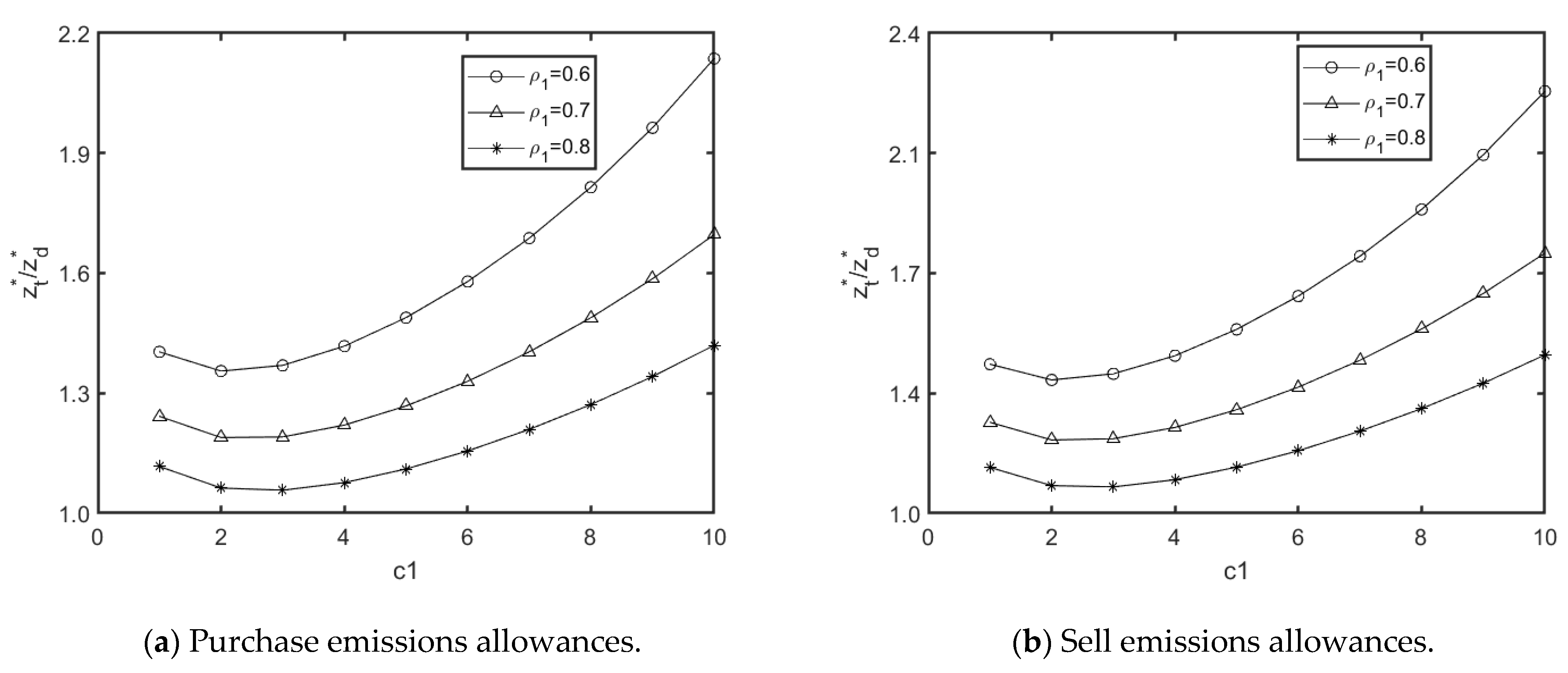
5. Numerical Analysis and Comparisons
5.1. DD with Emissions Trade vs. DD Without Emissions Trade
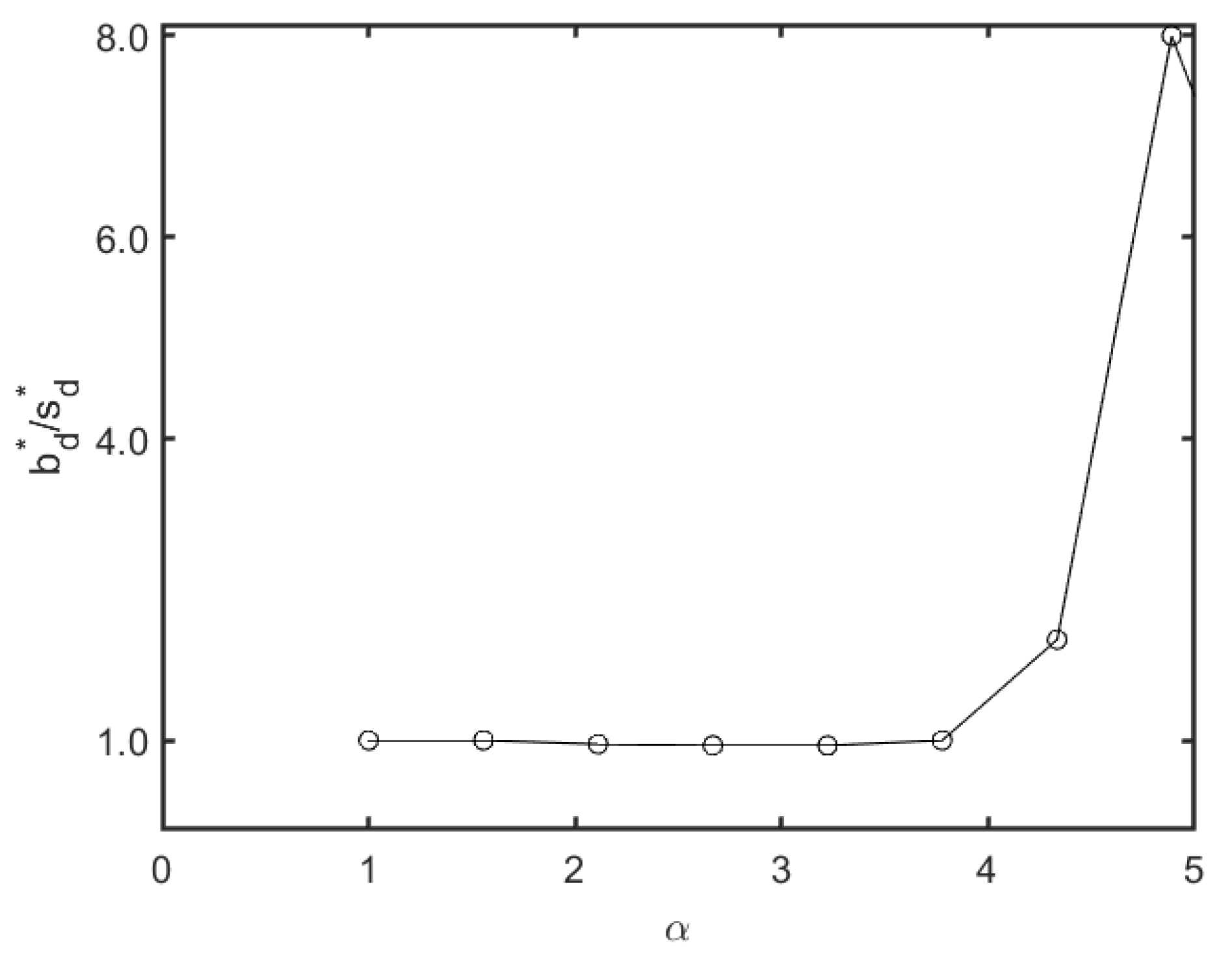
5.2. Impacts of Loading
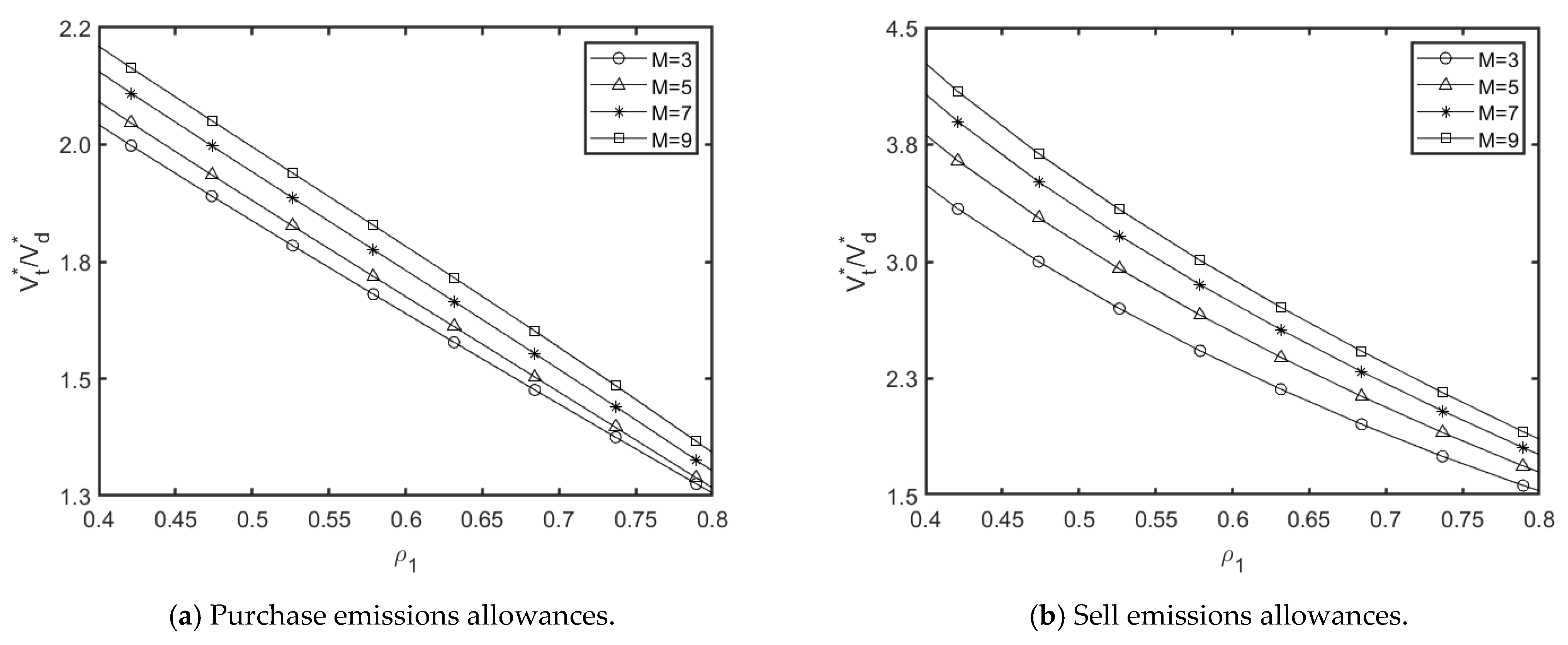
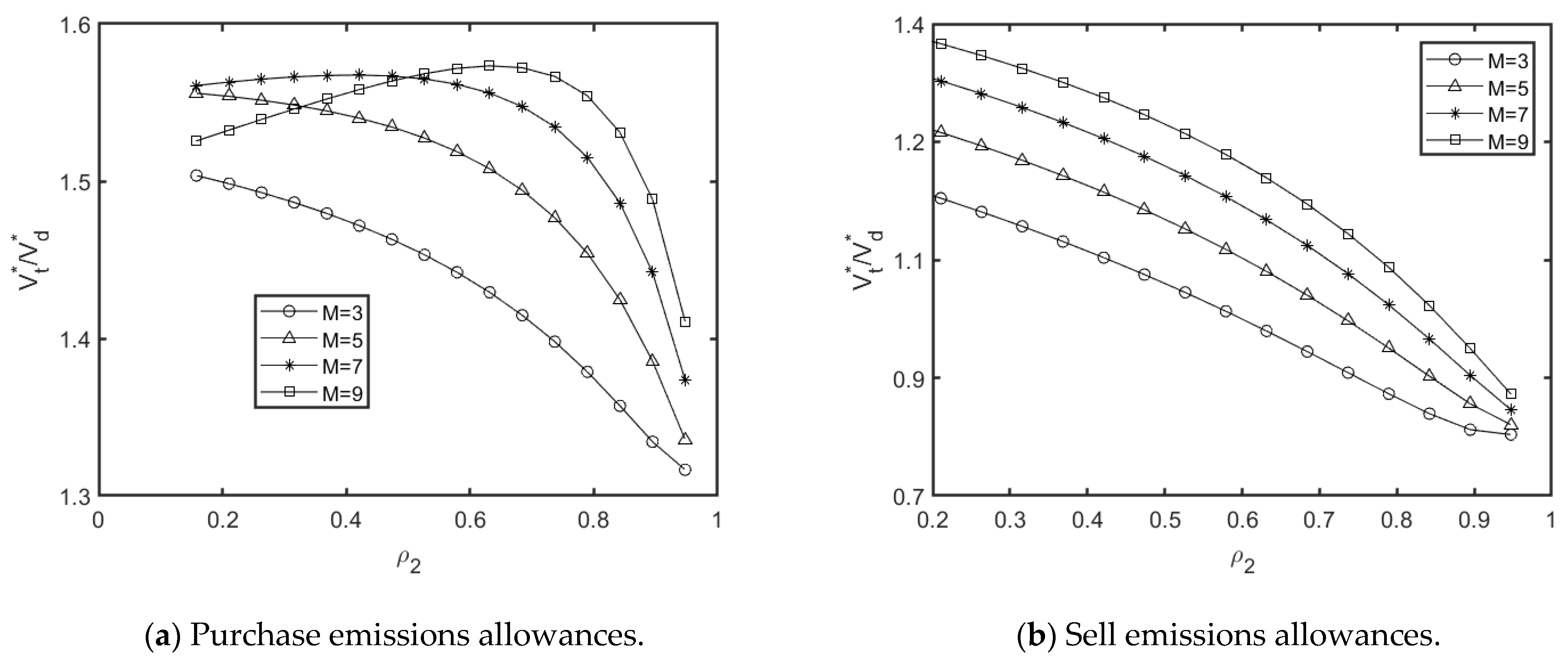
5.3. Sensitivity Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- (1)
- if ,
- ,
- ,
- ,
- (2)
- if ,
- ,
- ,
Appendix B
Appendix C
- (1)
- if ,
- (2)
- if ,
Appendix D
References
- European Environment Agency. EU Emissions Trading System (ETS) Data Viewer. Available online: https://www.eea.europa.eu/data-and-maps/dashboards/emissions-trading-viewer-1/ (accessed on 10 May 2024).
- Shao, X.F.; Dong, M. Comparison of order-fulfilment performance in MTO and MTS systems with an inventory cost budget constraint. Int. J. Prod. Res. 2012, 50, 1917–1931. [Google Scholar] [CrossRef]
- Rafiei, H.; Rabbani, M.; Alimardani, M. Novel bi-level hierarchical production planning in hybrid MTS/MTO production contexts. Int. J. Prod. Res. 2013, 51, 1331–1346. [Google Scholar] [CrossRef]
- Ebadian, M.; Rabbani, M.; Jolai, F.; Torabi, S.; Tavakkoli-Moghaddam, R. A new decision-making structure for the order entry stage in make-to-order environments. Int. J. Prod. Econ. 2008, 111, 351–367. [Google Scholar] [CrossRef]
- Van Donk, D.P. Make to stock or make to order: The decoupling point in the food processing industries. Int. J. Prod. Econ. 2001, 69, 297–306. [Google Scholar] [CrossRef]
- Olhager, J. Strategic positioning of the order penetration point. Int. J. Prod. Econ. 2003, 319–329. [Google Scholar] [CrossRef]
- Adan, I.J.B.F.; van der Wal, J. Combining make to order and make to stock. OR Spectr. 1998, 20, 73–81. [Google Scholar] [CrossRef]
- Eivazy, H.; Rabbani, M.; Ebadian, M. A developed production control and scheduling model in the semiconductor manufacturing systems with hybrid make-to-stock/make-to-order products. Int. J. Adv. Manuf. Technol. 2009, 45, 968–986. [Google Scholar] [CrossRef]
- Sun, X.; Ji, P.; Sun, L.; Wang, Y. Positioning multiple decoupling points in a supply network. Int. J. Prod. Econ. 2008, 113, 943–956. [Google Scholar] [CrossRef]
- Lee, H.L.; Billington, C. Designing products and processes for postponement. In Management of Design: Engineering and Management Perspectives; Springer: Berlin/Heidelberg, Germany, 1994; pp. 105–122. [Google Scholar]
- Lee, H.L.; Tang, C.S. Modeling the costs and benefits of delayed product differentiation. Manag. Sci. 1997, 43, 40–53. [Google Scholar] [CrossRef]
- Swaminathan, J.M.; Tayur, S.R. Managing broader product lines through delayed differentiation using vanilla boxes. Manag. Sci. 1998, 44, 161–172. [Google Scholar] [CrossRef]
- Gupta, D.; Benjaafar, S. Make-to-order, make-to-stock, or delay product differentiation? A common framework for modeling and analysis. IIE Trans. 2004, 36, 529–546. [Google Scholar] [CrossRef]
- Jewkes, E.M.; Alfa, A.S. A queueing model of delayed product differentiation. Eur. J. Oper. Res. 2009, 199, 734–743. [Google Scholar] [CrossRef]
- Almehdawe, E.; Jewkes, E. Performance analysis and optimization of hybrid manufacturing systems under a batch ordering policy. Int. J. Prod. Econ. 2013, 144, 200–208. [Google Scholar] [CrossRef]
- Su, J.C.P.; Chang, Y.-L.; Ferguson, M.; Ho, J.C. The impact of delayed differentiation in make-to-order environments. Int. J. Prod. Res. 2010, 48, 5809–5829. [Google Scholar] [CrossRef]
- Zhou, W.H.; Huang, W.X.; Zhang, R.Q. A two-stage queueing network on form postponement supply chain with correlated demands. Appl. Math. Model. 2014, 38, 2734–2743. [Google Scholar] [CrossRef]
- Fei, Q.; Kong, N.; Zhao, L. Investment decision optimization for delayed product differentiation based on queuing theory. J. Southeast Univ. (Engl. Ed.) 2018, 34, 532–539. [Google Scholar]
- Bandaly, D.C.; Hassan, H.F. Postponement implementation in integrated production and inventory plan under deterioration effects: A case study of a juice producer with limited storage capacity. Prod. Plan. Control. 2019, 31, 322–337. [Google Scholar] [CrossRef]
- Zhang, B.; Xu, L. Multi-item production planning with carbon cap and trade mechanism. Int. J. Prod. Econ. 2013, 144, 118–127. [Google Scholar] [CrossRef]
- Cao, K.Y.; Xu, X.P.; Wu, Q.; Zhang, Q.P. Optimal production and carbon emission reduction level under cap-and-trade and low carbon subsidy policies. J. Clean. Prod. 2017, 167, 505–513. [Google Scholar]
- Hu, B.Y.; Feng, Y. Emission reduction decision and coordination of a make-to-order supply chain with two products under cap-and-trade regulation. Comput. Ind. Eng. 2018, 119, 131–145. [Google Scholar]
- Ping, H.; Zhang, W.; Xu, X.; Bian, Y. Production lot-sizing and carbon emissions under cap-and-trade and carbon tax regulations. J. Clean. Prod. 2015, 103, 241–248. [Google Scholar]
- Xu, X.; Zhang, W.; He, P.; Xu, X. Production and pricing problems in make-to-order supply chain with cap-and-trade regulation. Omega Int. J. Manag. Sci. 2017, 66, 248–257. [Google Scholar] [CrossRef]
- Xiong, S.Y.; Feng, Y.Y.; Huang, K. Optimal MTS and MTO Hybrid Production System for a Single Product Under the Cap-And-Trade Environment. Sustainability 2020, 12, 24–26. [Google Scholar] [CrossRef]
- Gong, X.; Zhou, S.X. Optimal production planning with emissions trading. Oper. Res. 2013, 61, 908–924. [Google Scholar] [CrossRef]
- Yuan, B.Y.; Gu, B.M.; Xu, C.M. The Multi-Period Dynamic Optimization with Carbon Emissions Reduction under Cap-and-Trade. Discret. Dyn. Nat. Soc. 2019, 1, 1–12. [Google Scholar] [CrossRef]
- Williams, T.M. Special products and uncertainty in production/inventory systems. Eur. J. Oper. Res. 1984, 15, 46–54. [Google Scholar] [CrossRef]
- Carr, S.; Duenyas, I. Optimal Admission Control and Sequencing in a Make-To-Stock/Make-To-Order Production System. Oper. Res. 2000, 48, 709–720. [Google Scholar] [CrossRef]
- Gupta, D.; Weerawat, W. Supplier–manufacturer coordination in capacitated two-stage supply chains. Eur. J. Oper. Res. 2006, 175, 67–89. [Google Scholar] [CrossRef]

| Paper | Subjects Addressed | Demand Product Process Structure | Performance Criteria | Solution Approach |
|---|---|---|---|---|
| Willams (1984) [28] | MTO/MTS partitioning | Stochastic demand, multi-product, multi-machines | Minimizing sum of inventory holding costs, stock-out, and set-up costs | Approximations of M/G/m queues |
| Carr (2000) [29] | Joint admission control and sequencing problem | Single machine and two types of product No backordering, no set-up times, | Profit maximization | Markov decision process for two-class M/M/1 queue |
| Gupta and Benjaafar (2004) [13] | inventory management for the semi-finished goods between the two stages | multi-product, No set-up cost | Minimizing sum of inventory holding costs, backorder costs | Approximations of M/M/1 queues |
| Jewkes and Alfa (2009) [14] | the optimal point of differentiation | a-product, multi-periods | Minimizing sum of costs of order fulfillment delay, costs of holding semi-finished goods in inventory, cost of salvaging. | Markov decision process for queue theory |
| Swaminathan and Tayur (1998) [12] | the optimal configuration for semi-finished products from the point of view of commonality among different final products | single-periods and multi-periods | Minimizing sum of stock-out cost, holding cost | gradient derivative methods for two-stage integer program with recourse |
| Gupta and Weerawat (2006) [30] | looks into coordination between the two stages | decentralized model: the fixed-markup contract, the simple revenue-sharing contract | Profit maximization | Approximations of M/M/1 queues |
| 0.42 | 10.54 | 9.96 | 9.62 | 9.40 |
| 0.47 | 8.24 | 7.77 | 7.51 | 7.33 |
| 0.53 | 6.65 | 6.27 | 6.05 | 5.91 |
| 0.58 | 5.49 | 5.16 | 4.99 | 4.87 |
| 0.63 | 4.59 | 4.31 | 4.17 | 4.07 |
| 0.68 | 3.88 | 3.64 | 3.51 | 3.43 |
| 0.74 | 3.30 | 3.09 | 2.98 | 2.92 |
| 0.79 | 2.81 | 2.63 | 2.54 | 2.48 |
| 0.42 | 12.78 | 11.70 | 11.18 | 10.86 |
| 0.47 | 9.73 | 8.90 | 8.51 | 8.26 |
| 0.53 | 7.73 | 7.07 | 6.75 | 6.56 |
| 0.58 | 6.31 | 5.77 | 5.51 | 5.35 |
| 0.63 | 5.25 | 4.79 | 4.58 | 4.45 |
| 0.68 | 4.42 | 4.03 | 3.85 | 3.74 |
| 0.74 | 3.75 | 3.42 | 3.27 | 3.17 |
| 0.79 | 3.20 | 2.92 | 2.79 | 2.71 |
| 0.16 | 0.99 | 0.93 | 0.89 | 0.87 |
| 0.21 | 1.02 | 0.96 | 0.92 | 0.90 |
| 0.26 | 1.06 | 0.99 | 0.95 | 0.93 |
| 0.32 | 1.10 | 1.03 | 0.99 | 0.97 |
| 0.37 | 1.15 | 1.08 | 1.04 | 1.02 |
| 0.42 | 1.22 | 1.14 | 1.10 | 1.08 |
| 0.47 | 1.30 | 1.22 | 1.18 | 1.15 |
| 0.53 | 1.41 | 1.32 | 1.28 | 1.25 |
| 0.58 | 1.56 | 1.46 | 1.42 | 1.39 |
| 0.63 | 1.79 | 1.68 | 1.63 | 1.60 |
| 0.68 | 2.17 | 2.03 | 1.97 | 1.94 |
| 0.74 | 2.91 | 2.73 | 2.66 | 2.62 |
| 0.79 | 5.10 | 4.81 | 4.70 | 4.64 |
| 0.84 | 0.99 | 0.93 | 0.89 | 0.87 |
| 0.89 | 1.02 | 0.96 | 0.92 | 0.90 |
| 0.95 | 1.06 | 0.99 | 0.95 | 0.93 |
| 0.16 | 0.96 | 0.88 | 0.84 | 0.82 |
| 0.21 | 0.99 | 0.90 | 0.86 | 0.84 |
| 0.26 | 1.01 | 0.92 | 0.88 | 0.86 |
| 0.32 | 1.04 | 0.95 | 0.91 | 0.88 |
| 0.37 | 1.07 | 0.98 | 0.93 | 0.91 |
| 0.42 | 1.11 | 1.01 | 0.97 | 0.94 |
| 0.47 | 1.15 | 1.05 | 1.01 | 0.98 |
| 0.53 | 1.21 | 1.10 | 1.05 | 1.02 |
| 0.58 | 1.28 | 1.16 | 1.11 | 1.08 |
| 0.63 | 1.36 | 1.24 | 1.19 | 1.15 |
| 0.68 | 1.48 | 1.35 | 1.29 | 1.25 |
| 0.74 | 1.63 | 1.49 | 1.42 | 1.38 |
| 0.79 | 1.87 | 1.70 | 1.63 | 1.58 |
| 0.84 | 2.25 | 2.06 | 1.97 | 1.92 |
| 0.89 | 3.01 | 2.75 | 2.64 | 2.57 |
| 0.95 | 5.26 | 4.83 | 4.63 | 4.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, S.; Yang, L. Optimal Delay Product Differentiation System Under the Cap-and-Trade Environment. Systems 2025, 13, 161. https://doi.org/10.3390/systems13030161
Xiong S, Yang L. Optimal Delay Product Differentiation System Under the Cap-and-Trade Environment. Systems. 2025; 13(3):161. https://doi.org/10.3390/systems13030161
Chicago/Turabian StyleXiong, Shouyao, and Liu Yang. 2025. "Optimal Delay Product Differentiation System Under the Cap-and-Trade Environment" Systems 13, no. 3: 161. https://doi.org/10.3390/systems13030161
APA StyleXiong, S., & Yang, L. (2025). Optimal Delay Product Differentiation System Under the Cap-and-Trade Environment. Systems, 13(3), 161. https://doi.org/10.3390/systems13030161






