The Dynamic Interplay of Consumption and Wealth: A Systems Analysis of Horizon-Specific Effects on Chinese Stock Returns
Abstract
1. Introduction
Background
2. Literature Review and Hypothesis Analysis
2.1. Consumption-Based CAPM
- Many adequate investors are price-takers;
- The investment period is the same for all investors;
- Taxes and transaction costs are ignorable;
- The risk-free rate is a real reference rate for borrowing and lending;
- Expected return and variance have the most attention from the perspective of investors;
- (a)
- A high mean and low variance are preferable;
- (b)
- The market included all generally exchanged assets.
2.2. Chinese Stock Market
2.3. Hypothesis Development
3. Data and Models
3.1. Data
3.2. Variable Selection and Measurements Ratio
- Dependent variable: excess return (rt);
- Independent variables: scrt and cayt;
- Control variables: dividend yield (dpt), dividend payout coefficient (det) and government bond term spread (TRMt).
3.2.1. Dependent Variable
3.2.2. Independent Variables
3.2.3. Control Variables
3.3. Descriptive Statistical Analysis
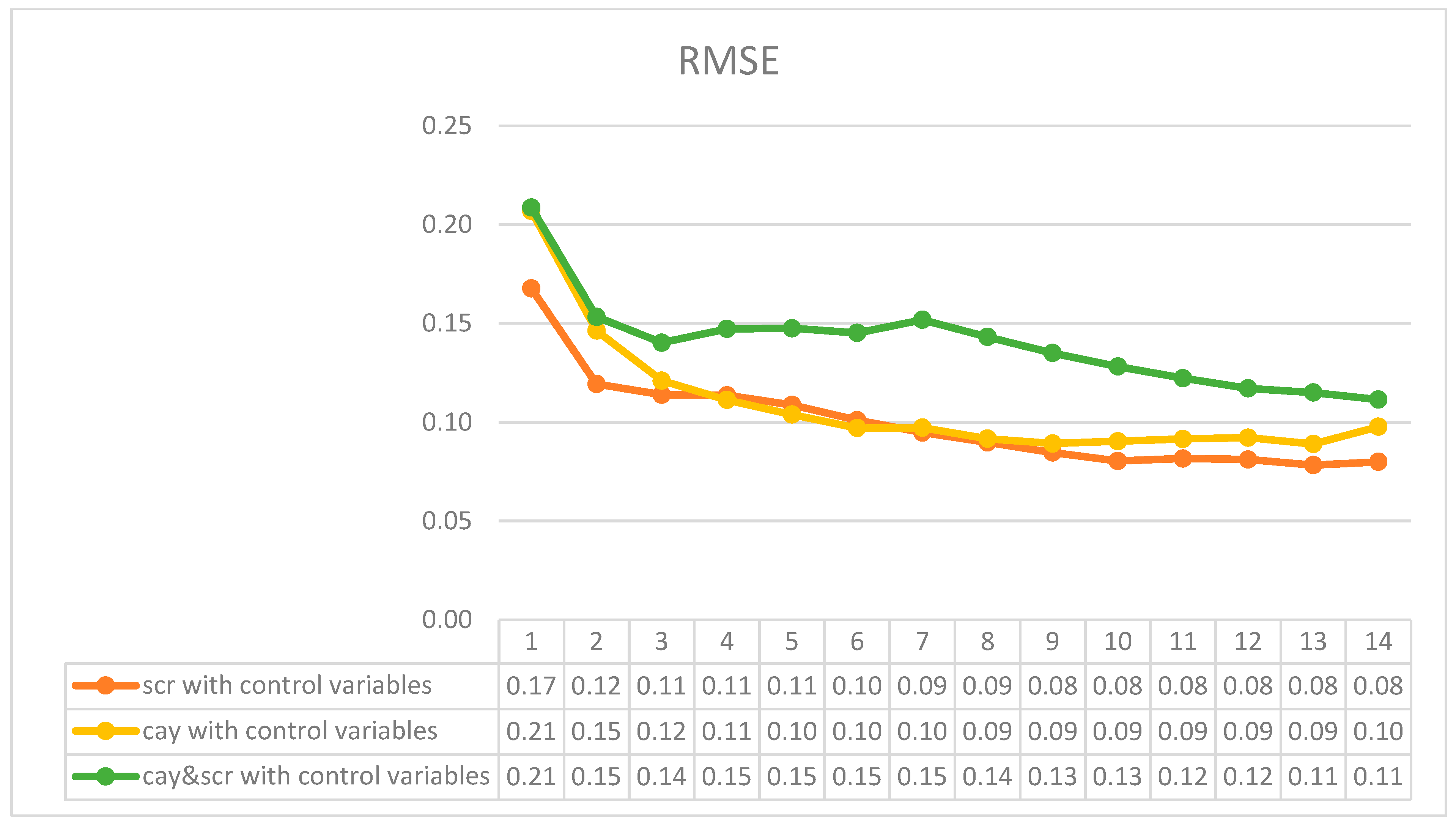
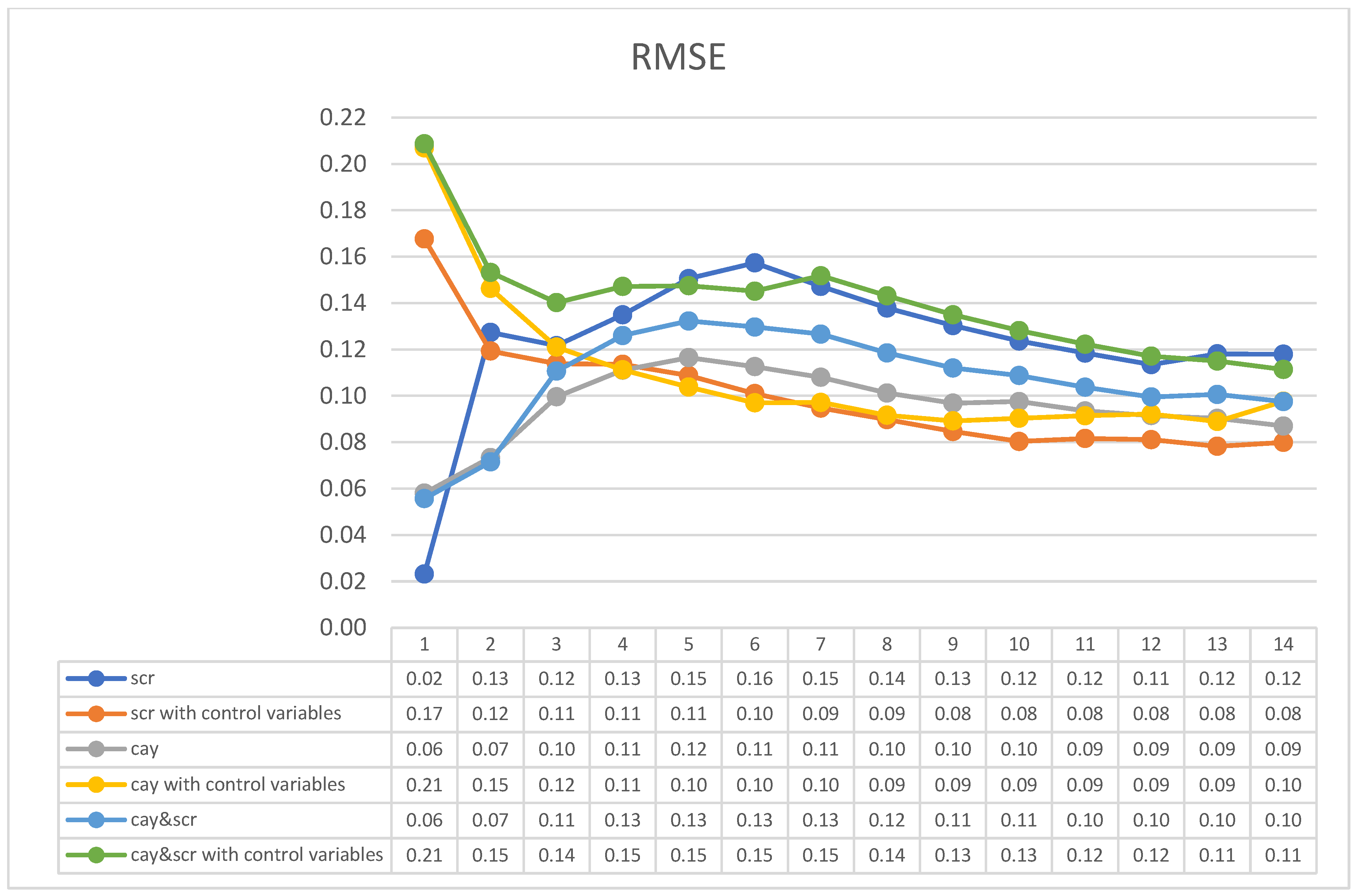
4. Results
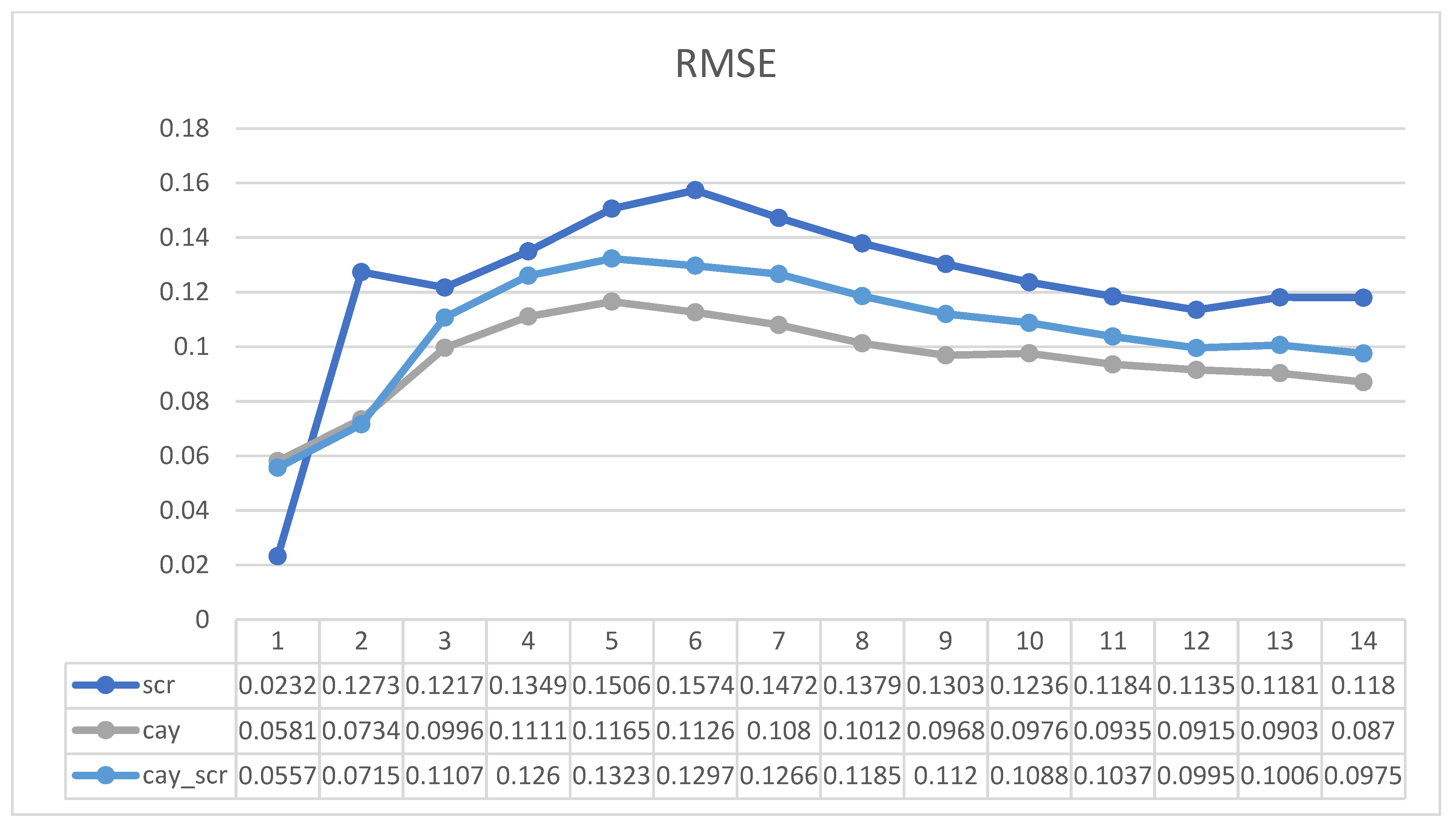
4.1. Surplus Consumption Ratio
4.2. Consumption Wealth Ratio
4.3. Two-State Variable
4.4. Further Diagnostic Test: The Jarque–Bera Statitics
4.5. Regression Test Based on Nonlinear TSLS Estimation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, G.; Li, Y. Intraday and Post-Market Investor Sentiment for Stock Price Prediction: A Deep Learning Framework with Explainability and Quantitative Trading Strategy. Systems 2025, 13, 390. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, X.; He, Q. Multi-Scale Systemic Risk and Spillover Networks of Commodity Markets in the Bullish and Bearish Regimes. N. Am. J. Econ. Financ. 2022, 62, 101766. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, W.; Ma, B.; Sun, G.; Kang, X. Does the opening of the China’s stock market improve market liquidity? Financ. Res. Lett. 2025, 85, 108273. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.; Failler, P.; Wang, Z. The Dynamic Evolution of Agricultural Trade Network Structures and Its Influencing Factors: Evidence from Global Soybean Trade. Systems 2025, 13, 279. [Google Scholar] [CrossRef]
- Lyu, J.; Li, Z. Time-Varying Spillover Effects of Carbon Prices on China’s Financial Risks. Systems 2024, 12, 534. [Google Scholar] [CrossRef]
- Fehrle, D.; Heiberger, C. The return on everything and the business cycle in production economies. Econ. Model. 2024, 136, 106742. [Google Scholar] [CrossRef]
- Kwan, Y.K.; Leung, C.K.Y.; Dong, J. Comparing Consumption-Based Asset Pricing Models: The Case of an Asian City. J. Hous. Econ. 2015, 28, 18–41. [Google Scholar] [CrossRef]
- Polimenis, V. The historical lepto-variance of the US stock returns. Data Sci. Financ. Econ. 2024, 4, 270–284. [Google Scholar] [CrossRef]
- French, J. A Practitioner’s Guide to the CAPM: An Empirical Study. In Global Tensions in Financial Markets; Research in Finance; Emerald Publishing Limited: Leeds, UK, 2018; Volume 34, p. 1. [Google Scholar]
- Vendrame, V.; Guermat, C.; Tucker, J. A Conditional Regime Switching CAPM. Int. Rev. Financ. Anal. 2018, 56, 1–11. [Google Scholar] [CrossRef]
- Engsted, T.; Hyde, S.; Møller, S. V Habit Formation, Surplus Consumption and Return Predictability: International Evidence. J. Int. Money Financ. 2010, 29, 1237–1255. [Google Scholar] [CrossRef]
- Boudoukh, J.; Michaely, R.; Richardson, M.; Roberts, M.R. On the Importance of Measuring Payout Yield: Implications for Empirical Asset Pricing. J. Financ. 2007, 62, 877–915. [Google Scholar] [CrossRef]
- McMillan, D.G. Consumption and Stock Prices: Evidence from a Small International Panel. J. Macroecon. 2013, 36, 76–88. [Google Scholar] [CrossRef]
- John, Y.C.; Shiller, R.J. Valuation Ratios and the Long-Run Stock Market Outlook. J. Portf. Manag. 1998, 24, 11–26. [Google Scholar] [CrossRef]
- Xiao, Y.; Faff, R.; Gharghori, P.; Min, B.K. Pricing Innovations in Consumption Growth: A Re-Evaluation of the Recursive Utility Model. J. Bank. Financ. 2013, 37, 4465–4475. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Z. A Note on an Interpretation to Consumption-Based CAPM. Econ. Lett. 2008, 99, 443–445. [Google Scholar] [CrossRef]
- Chang, T.; Gupta, R.; Majumdar, A.; Pierdzioch, C. Predicting Stock Market Movements with a Time-Varying Consumption-Aggregate Wealth Ratio. Int. Rev. Econ. Financ. 2019, 59, 458–467. [Google Scholar] [CrossRef]
- Lettau, M.; Ludvigson, S. Resurrecting the (C)CAPM: A Cross-Sectional Test When Risk Premia Are Time-Varying. J. Polit. Econ. 2001, 109, 1238–1287. [Google Scholar] [CrossRef]
- Balcilar, M.; Bekiros, S.; Gupta, R. The Role of News-Based Uncertainty Indices in Predicting Oil Markets: A Hybrid Nonparametric Quantile Causality Method. Empir. Econ. 2017, 53, 879–889. [Google Scholar] [CrossRef]
- Fung, K.W.T.; Lau, C.K.M.; Chan, K.H. The Conditional Equity Premium, Cross-Sectional Returns and Stochastic Volatility. Econ. Model. 2014, 38, 316–327. [Google Scholar] [CrossRef]
- Márquez, E.; Nieto, B.; Rubio, G. Stock Returns with Consumption and Illiquidity Risks. Int. Rev. Econ. Financ. 2014, 29, 57–74. [Google Scholar] [CrossRef]
- Li, B.; Zhong, M. Predictability of Stock Returns and Consumption-Based CAPM: Evidence from a Small Open Market. Eur. J. Econ. Financ. Adm. Sci. 2010, 22, 148–173. [Google Scholar]
- Farag, H.; Meng, Q.; Mallin, C. The Social, Environmental and Ethical Performance of Chinese Companies: Evidence from the Shanghai Stock Exchange. Int. Rev. Financ. Anal. 2015, 42, 53–63. [Google Scholar] [CrossRef]
- Chen, C.; Hu, C.; Yao, H. Behavioral Framework of Asset Price Bubbles: Theoretical and Empirical Analyses. Systems 2022, 10, 251. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, W.; Zhang, Y.; Zhang, H. The Five-Factor Asset Pricing Model Tests for the Chinese Stock Market. Pac.-Basin Financ. J. 2017, 43, 84–106. [Google Scholar] [CrossRef]
- Meng, Q.; Qi, J.; Wang, S.; Zhao, X. Disciplining the Factor Zoo: Identifying Pricing Factors in the Chinese Stock Market. Econ. Model. 2025, 155, 107370. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, Q.; Chen, C. Risk Attitude, Financial Literacy and Household Consumption: Evidence from Stock Market Crash in China. Econ. Model. 2021, 94, 995–1006. [Google Scholar] [CrossRef]
- Huang, T.-L. Is the Fama and French Five-Factor Model Robust in the Chinese Stock Market? Asia Pac. Manag. Rev. 2019, 24, 278–289. [Google Scholar] [CrossRef]
- Chen, C.-D.; Demirer, R.; Jategaonkar, S.P. Risk and Return in the Chinese Stock Market: Does Equity Return Dispersion Proxy Risk? Pac.-Basin Financ. J. 2015, 33, 23–37. [Google Scholar] [CrossRef]
- Le, A.T.; Nguyen, H.; Nguyen, C. Regret to reward: Investor regret and the cross-sectional stock returns in the Chinese market. Glob. Financ. J. 2025, 68, 101205. [Google Scholar] [CrossRef]
- Kang, J.; Kim, T.S.; Lee, C.; Min, B.-K. Macroeconomic Risk and the Cross-Section of Stock Returns. J. Bank. Financ. 2011, 35, 3158–3173. [Google Scholar] [CrossRef]
- Itoy, M.; Noda, A. CCAPM with Time-Varying Parameters: Some Evidence from Japan; Keio Economic Society, Keio University: Tokyo, Japan, 2011. [Google Scholar]
- Liu, L.; Wan, J. The Relationships between Shanghai Stock Market and CNY/USD Exchange Rate: New Evidence Based on Cross-Correlation Analysis, Structural Cointegration and Nonlinear Causality Test. Phys. A Stat. Mech. Its Appl. 2012, 391, 6051–6059. [Google Scholar] [CrossRef]
- Koutmos, D.; Song, W. Speculative Dynamics and Price Behavior in the Shanghai Stock Exchange. Res. Int. Bus. Financ. 2014, 31, 74–86. [Google Scholar] [CrossRef]
- Auer, B.R. Can Habit Formation under Complete Market Integration Explain the Cross-Section of International Equity Risk Premia? Rev. Financ. Econ. 2013, 22, 61–67. [Google Scholar] [CrossRef]
- Li, Y. The Wealth-Consumption Ratio and the Consumption-Habit Ratio. J. Bus. Econ. Stat. 2014, 23, 226–241. [Google Scholar] [CrossRef]
- Møller, S.V. Habit Persistence: Explaining Cross-Sectional Variation in Returns and Time-Varying Expected Returns. J. Empir. Financ. 2009, 16, 525–536. [Google Scholar] [CrossRef]
- Bianchi, F.; Lettau, M.; Ludvigson, S.C. Monetary Policy and Asset Valuation; No. 22572; National Bureau of Economic Research: Cambridge, MA, USA, 2016. [Google Scholar]
- Caporale, G.M.; Sousa, R.M. Consumption, Wealth, Stock and Housing Returns: Evidence from Emerging Markets. Res. Int. Bus. Financ. 2016, 36, 562–578. [Google Scholar] [CrossRef]
- Gardberg, M.; Pozzi, L. Aggregate consumption and wealth in the long run: The impact of financial liberalization. J. Appl. Econom. 2022, 37, 161–186. [Google Scholar] [CrossRef]
- Xie, H. Nonlinear and nonseparable structural functions in regression discontinuity designs with a continuous treatment. J. Econom. 2024, 242, 105784. [Google Scholar] [CrossRef]
- Jarque, C.M.; Bera, A.K. Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Econ. Lett. 1980, 6, 255–259. [Google Scholar] [CrossRef]
| Author(s) | Method(s) | Feature(s) and Results | Case Study | Source |
|---|---|---|---|---|
| Kang et al., (2011) | Conditional CAPM using macroeconomic indices. | - The conditioning variable had a durable power to predict market excess returns. - The suggested variable strongly forecasts excess stock returns. | Korea | [31] |
| Itoy and Noda (2011) | Standard CCAPM | - Using the Hansen method for generalized empirical likelihood (GEL) estimation. - That both factors predicted the CCAPM, the degree of risk aversion, and the rate of time discount change over time. | Japan | [32] |
| Liu and Wan (2012) | Linear and nonlinear Granger causality tests | - Examined the co-movement of the Shanghai stock market and exchange rates of Chinese currency (CNY). - The stock price and exchange rate are significantly cross-correlated. | Shanghai Stock Exchange | [33] |
| Koutmosa and Songb (2014) | A range-based autoregressive volatility framework. | - Examined the degree to which changes in asset portfolio stock prices reflect the trading patterns of diverse individuals. - Information-driven investors believe that periods of declining stock prices are entirely tied to low-volume trading time, whereas rising stock prices are often associated with a significant quantity of trading time. | Shanghai Stock Exchange | [34] |
| Vendrame, Guermat, and Tucker (2018) | Conditional CAPM | - There are severe time deviations in betas across their approaches and frameworks. - The regime-switching framework deducts the proper prediction of one-day-ahead value-at-risk. | USA, Germany, England, France, China, and Malaysia | [10] |
| Name | Symbol | Calculation | Description |
|---|---|---|---|
| Dividend yield | dpt | This is the coefficient of a corporation’s yearly dividend compared to its share price. | A stock investment’s dividend-only return is predicted by the dividend yield. The yield will increase when the stock price declines and fall when the stock price rises, assuming that the dividend is neither increased nor decreased. |
| Dividend payout ratio | det | This is the overall volume ratio of dividends distributed to investors as a percentage of the firm’s net income. | An innovative, growing company with ambitious intentions to expand into new markets and provide innovative results might be excused for its low payout ratio as it is anticipated to reinvest most or all of its profits. |
| Government bond term spread | TRMt | The China Bond Pricing Center provides this information as the difference between the China Bond Long Term Index and the China Bond Short-Middle Term Index. | It is a crucial factor that bond funders calculate when gauging the level of const for single or plural bonds. |
| Indicators | Mean | Median | Maximum | Minimum | Standard Error | Autocorrelation |
|---|---|---|---|---|---|---|
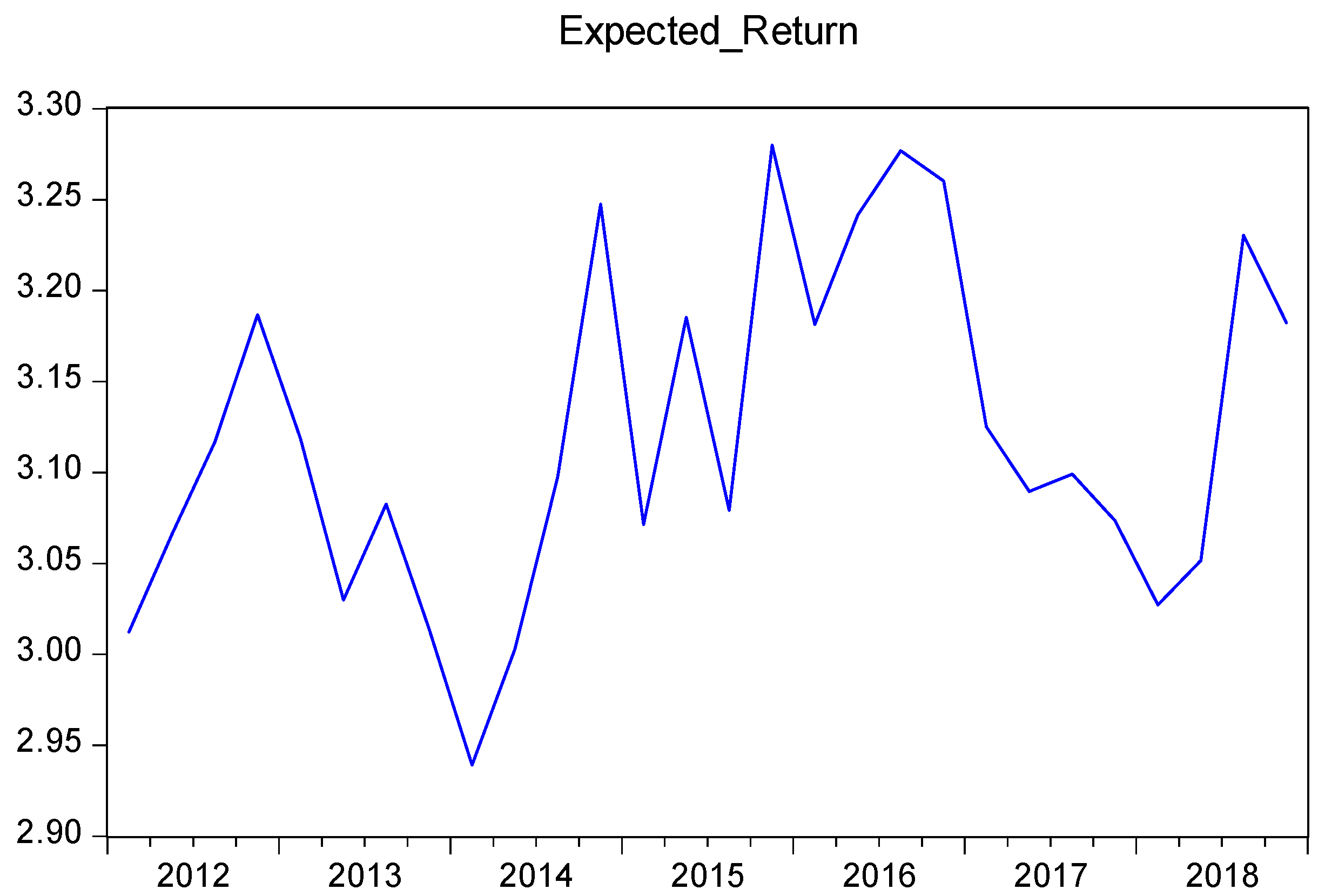
| r | 3.12027 | 3.09823 | 3.27979 | 2.93912 | 0.01753 | 0.452 |
| scrt | −0.58781 | −0.59034 | −0.50139 | −0.69505 | 0.01039 | 0.871 |
| cayt | 14.86361 | 15.04799 | 16.56272 | 12.86988 | 0.210268 | −0.025 |
| dpt | 6.63106 | 6.56013 | 7.46083 | 6.23385 | 0.05642 | 0.797 |
| det | 6.009458 | 5.97481 | 7.03574 | 5.53335 | 0.06795 | 0.790 |
| TRMt | 6.09590 | 5.80564 | 22.38690 | −10.66830 | 1.67778 | 0.848 |
| R | scrt | cayt | dpt | det | TRMt | |
|---|---|---|---|---|---|---|
| r | 1 | |||||
| scrt | −0.25758 | 1 | ||||
| cayt | 0.50318 | 0.21855 | 1 | |||
| dpt | 0.28746 | 0.22822 | 0.12673 | 1 | ||
| det | 0.29778 | 0.24236 | 0.10829 | 0.99497 | 1 | |
| TRMt | 0.73501 | 0.65481 | 0.26817 | 0.38058 | 0.39779 | 1 |
| Variable | (1) | (2) |
|---|---|---|
| C | 2.991591 *** (3.983746) | 2.443527 (1.166974) |
| scrt | −0.146233 * (−0.120682) | −0.728282 ** (−0.988364) |
| det | −0.162131 (−0.173376) | |
| dpt | 0.175458 (0.157883) | |
| TRMt | 0.014413 *** (3.432777) | |
| MA(1) | 0.385215 (1.011465) | −0.596789 (−3.58 × 105) |
| MA(2) | 0.230451 (0.417315) | −0.403211 (−2.31 × 105) |
| Observation | 14 | 14 |
| R-squared | 0.120446 | 0.725737 |
| Adjusted R-squared | −0.270466 | 0.405764 |
| F-statistic | 0.308115 | 2.268120 |
| Horizon | 1 | 2 | ||
|---|---|---|---|---|
| RMSE | TIC | RMSE | TIC | |
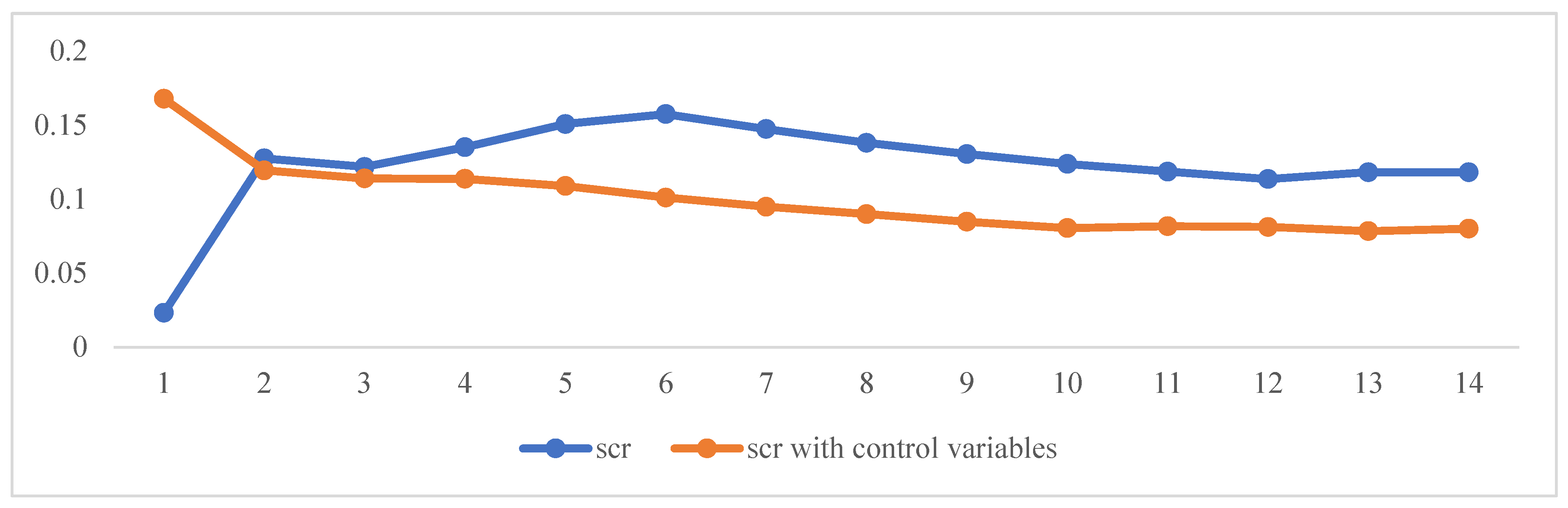
| Q1 | 0.023192 | - | 0.167689 | - |
| Q2 | 0.127344 | 0.020269 | 0.119303 | 0.018486 |
| Q3 | 0.121666 | 0.019395 | 0.113867 | 0.017633 |
| Q4 | 0.134936 | 0.021474 | 0.113568 | 0.017493 |
| Q5 | 0.150575 | 0.02391 | 0.108731 | 0.016671 |
| Q6 | 0.15735 | 0.02496 | 0.10098 | 0.0155 |
| Q7 | 0.14721 | 0.02341 | 0.09474 | 0.01461 |
| Q8 | 0.13788 | 0.021983 | 0.089768 | 0.013916 |
| Q9 | 0.130308 | 0.020812 | 0.084634 | 0.013176 |
| Q10 | 0.123625 | 0.019782 | 0.080349 | 0.01256 |
| Q11 | 0.118442 | 0.018995 | 0.0816 | 0.0128 |
| Q12 | 0.113465 | 0.018225 | 0.081116 | 0.012757 |
| Q13 | 0.11808 | 0.01895 | 0.07827 | 0.0123 |
| Q14 | 0.11796 | 0.01893 | 0.07992 | 0.01254 |
| Variable | (3) | (4) |
|---|---|---|
| C | 2.435656 *** (11.66133) | −0.079700 (−0.071793) |
| cayt | 0.045176 ** (3.211853) | 0.042841 *** (4.550892) |
| dpt | 1.270126 * (2.191582) | |
| det | −0.977815 * (−2.055565) | |
| TRMt | 0.005716 (0.654912) | |
| MA (1) | 0.591084 (1.578985) | 0.391322 (0.000243) |
| MA (2) | 0.694545 (1.664657) | 0.999991 (0.000121) |
| Observations | 14 | 14 |
| R-squared | 0.600520 | 0.878058 |
| Adjusted R-squared | 0.422973 | 0.735793 |
| F-statistic | 3.382316 | 6.171977 |
| Horizon | 3 | 4 | ||
|---|---|---|---|---|
| RMSE | TIC | RMSE | TIC | |
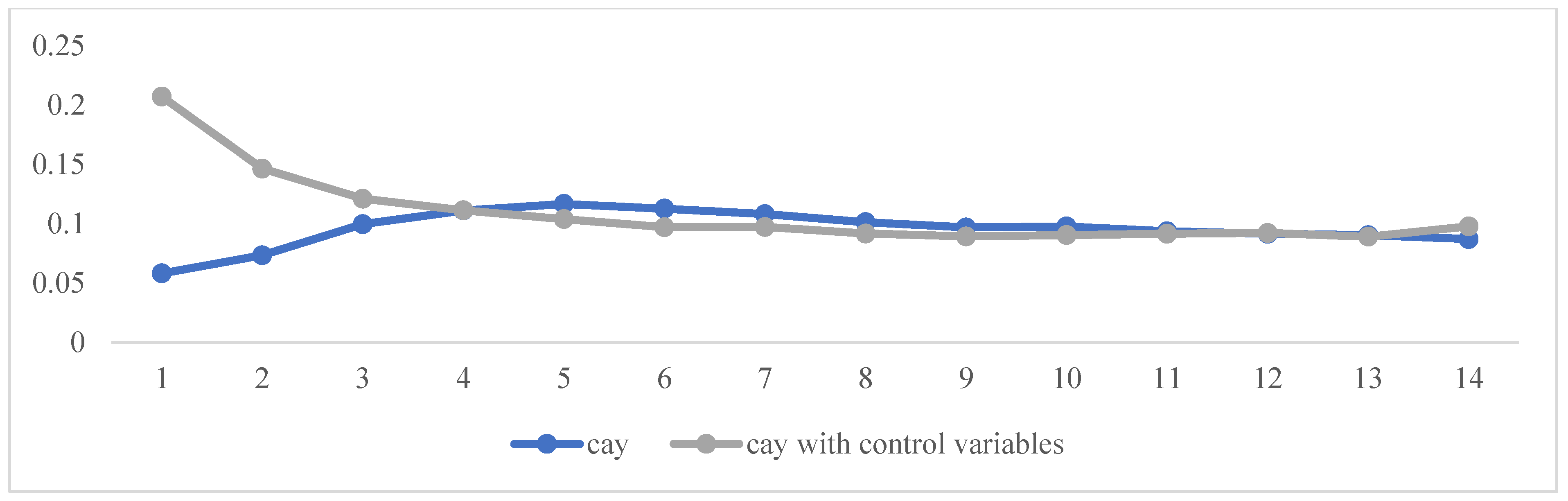
| Q1 | 0.058083 | - | 0.206886 | - |
| Q2 | 0.073398 | 0.011565 | 0.146329 | 0.022646 |
| Q3 | 0.099579 | 0.015789 | 0.12099 | 0.018851 |
| Q4 | 0.111052 | 0.017583 | 0.11122 | 0.017335 |
| Q5 | 0.11651 | 0.018387 | 0.103809 | 0.016143 |
| Q6 | 0.11261 | 0.01773 | 0.097 | 0.01507 |
| Q7 | 0.10799 | 0.01707 | 0.09718 | 0.01519 |
| Q8 | 0.101233 | 0.01604 | 0.091631 | 0.014375 |
| Q9 | 0.096831 | 0.01536 | 0.089194 | 0.014019 |
| Q10 | 0.09756 | 0.015488 | 0.090327 | 0.014223 |
| Q11 | 0.09351 | 0.01489 | 0.091458 | 0.01444 |
| Q12 | 0.091498 | 0.014591 | 0.092158 | 0.014576 |
| Q13 | 0.0903 | 0.01438 | 0.08895 | 0.01404 |
| Q14 | 0.08702 | 0.01384 | 0.09766 | 0.01538 |
| Variable | (5) | (6) |
|---|---|---|
| C | 2.237905 *** (3.298284) | −0.755299 (−0.606806) |
| Scrt | −0.329407 * (−0.359154) | −0.740563 * −(0.708127) |
| Cayt | 0.044544 ** (2.789661) | 0.036815 ** (3.026916) |
| det | −0.981177 (−1.620132) | |
| dpt | 1.317897 (1.844020) | |
| TRMt | 0.004287 * (0.606492) | |
| MA(1) | 0.826218 (0.026679) | 0.813163 (0.000236) |
| MA(2) | 0.997404 (0.013390) | 1.000000 (0.000118) |
| Observation | 14 | 14 |
| R-squared | 0.677445 | 0.897542 |
| Adjusted R-squared | 0.475847 | 0.733610 |
| F-statistic | 3.360388 | 5.475089 |
| Horizon | 5 | 6 | ||
|---|---|---|---|---|
| RMSE | TIC | RMSE | TIC | |
| Q1 | 0.05567 | - | 0.208636 | - |
| Q2 | 0.071538 | 0.011272 | 0.153257 | 0.023814 |
| Q3 | 0.110682 | 0.017573 | 0.140203 | 0.021989 |
| Q4 | 0.126013 | 0.01999 | 0.147173 | 0.023134 |
| Q5 | 0.132302 | 0.020924 | 0.147483 | 0.023151 |
| Q6 | 0.129688 | 0.020466 | 0.14514 | 0.022772 |
| Q7 | 0.12664 | 0.020072 | 0.151785 | 0.023977 |
| Q8 | 0.118537 | 0.01884 | 0.14314 | 0.022701 |
| Q9 | 0.112 | 0.017823 | 0.134958 | 0.021445 |
| Q10 | 0.108754 | 0.017323 | 0.128163 | 0.020406 |
| Q11 | 0.10372 | 0.016576 | 0.12225 | 0.019524 |
| Q12 | 0.099531 | 0.015934 | 0.117102 | 0.018744 |
| Q13 | 0.100626 | 0.016089 | 0.114983 | 0.018376 |
| Q14 | 0.097531 | 0.015582 | 0.111398 | 0.017772 |
| Variable(s) | Observations | R-Squared | Adjusted R-Squared | F-Statistic | Jarque–Bera Test (p-Value) | Output |
|---|---|---|---|---|---|---|
| cay | 28 | 0.6078 | 0.5396 | 8.91 | 0.3237 | Normality not rejected |
| scr | 28 | 0.6079 | 0.5397 | 8.92 | 0.3043 | Normality not rejected |
| scr-cay | 28 | 0.6082 | 0.5192 | 6.83 | 0.3231 | Normality not rejected |
| Horizon | 7 | 8 | ||
|---|---|---|---|---|
| RMSE | TIC | RMSE | TIC | |
| Q1 | 0.006022 | - | 0.007581 | - |
| Q2 | 0.01996 | 0.024254 | 0.012914 | 0.022591 |
| Q3 | 0.017761 | 0.022696 | 0.013628 | 0.025247 |
| Q4 | 0.016289 | 0.021291 | 0.011897 | 0.02218 |
| Q5 | 0.014901 | 0.01956 | 0.010943 | 0.020166 |
| Q6 | 0.014335 | 0.01904 | 0.012388 | 0.022193 |
| Q7 | 0.014696 | 0.01989 | 0.01759 | 0.03198 |
| Q8 | 0.014789 | 0.020267 | 0.021422 | 0.038759 |
| Q9 | 0.014548 | 0.020049 | 0.022592 | 0.040363 |
| Q10 | 0.014553 | 0.020204 | 0.023935 | 0.041983 |
| Q11 | 0.015292 | 0.02153 | 0.025849 | 0.045739 |
| Q12 | 0.016008 | 0.022835 | 0.028846 | 0.050818 |
| Q13 | 0.015185 | 0.761689 | 0.02087 | 0.041536 |
| Q14 | 0.016723 | 0.024281 | 0.01439 | 0.032061 |
| Moment Conditions | Orthogonal to | |||
| 1 | ||||
| 1 | ||||
| Horizon | cay | scr | ||
|---|---|---|---|---|
| N-TSLS | OLS | N-TSLS | OLS | |
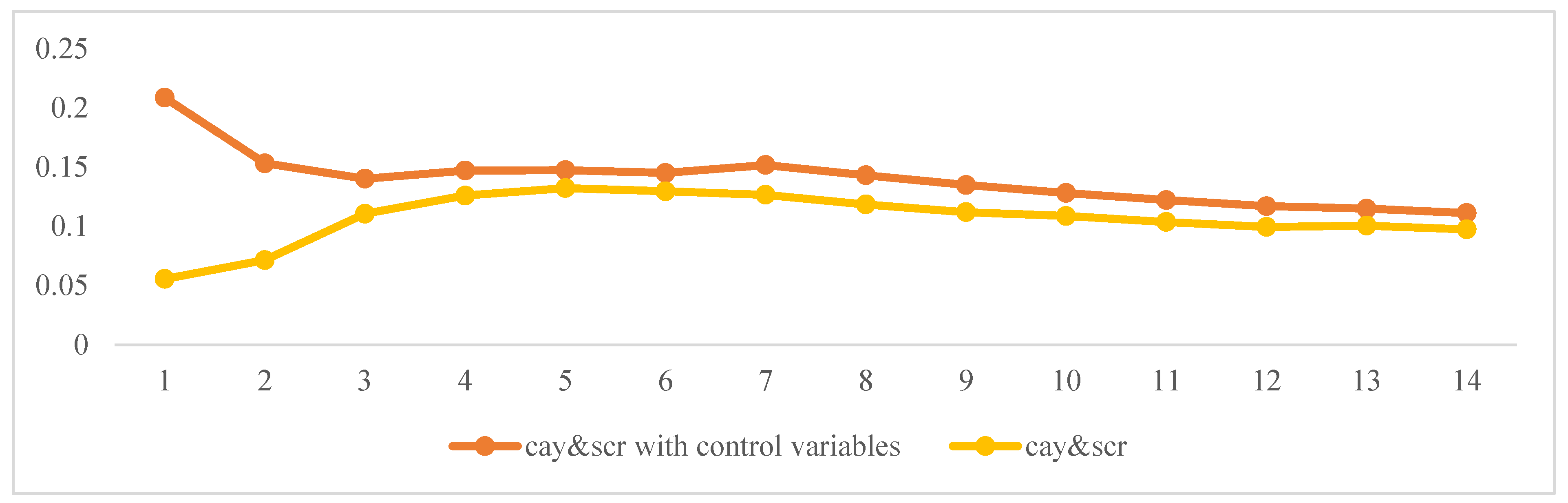
| Q1 | 0.0076 | 0.0581 | 0.0060 | 0.0232 |
| Q2 | 0.0129 | 0.0734 | 0.0200 | 0.1273 |
| Q3 | 0.0136 | 0.0996 | 0.0178 | 0.1217 |
| Q4 | 0.0119 | 0.1111 | 0.0163 | 0.1349 |
| Q5 | 0.0109 | 0.1165 | 0.0149 | 0.1506 |
| Q6 | 0.0124 | 0.1126 | 0.0143 | 0.1574 |
| Q7 | 0.0176 | 0.1080 | 0.0147 | 0.1472 |
| Q8 | 0.0214 | 0.1012 | 0.0148 | 0.1379 |
| Q9 | 0.0226 | 0.0968 | 0.0145 | 0.1303 |
| Q10 | 0.0239 | 0.0976 | 0.0146 | 0.1236 |
| Q11 | 0.0258 | 0.0935 | 0.0153 | 0.1184 |
| Q12 | 0.0288 | 0.0915 | 0.0160 | 0.1135 |
| Q13 | 0.0209 | 0.0903 | 0.0152 | 0.1181 |
| Q14 | 0.0144 | 0.0799 | 0.0167 | 0.0870 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zareian Baghdad Abadi, F.; Hashemizadeh, A.; Liu, W. The Dynamic Interplay of Consumption and Wealth: A Systems Analysis of Horizon-Specific Effects on Chinese Stock Returns. Systems 2025, 13, 1066. https://doi.org/10.3390/systems13121066
Zareian Baghdad Abadi F, Hashemizadeh A, Liu W. The Dynamic Interplay of Consumption and Wealth: A Systems Analysis of Horizon-Specific Effects on Chinese Stock Returns. Systems. 2025; 13(12):1066. https://doi.org/10.3390/systems13121066
Chicago/Turabian StyleZareian Baghdad Abadi, Faezeh, Ali Hashemizadeh, and Weili Liu. 2025. "The Dynamic Interplay of Consumption and Wealth: A Systems Analysis of Horizon-Specific Effects on Chinese Stock Returns" Systems 13, no. 12: 1066. https://doi.org/10.3390/systems13121066
APA StyleZareian Baghdad Abadi, F., Hashemizadeh, A., & Liu, W. (2025). The Dynamic Interplay of Consumption and Wealth: A Systems Analysis of Horizon-Specific Effects on Chinese Stock Returns. Systems, 13(12), 1066. https://doi.org/10.3390/systems13121066









