Abstract
The dual-channel structure resulted from manufacturer encroachment could alter the incentives of downstream retailer to ex ante communicate demand forecast. And different types of channel competition need to be investigated in this dual-channel information sharing scenario. This paper aims to investigate retailer’s ex ante imperfect demand information sharing strategy given that upstream manufacturer has set up direct sales channel (manufacturer encroachment). The imperfect information sharing means the demand information shared is uncertain and has some error relative to the real-world demand condition. It examines two types of channel competition: quantity competition and price competition. Additionally, this study discusses the encroaching manufacturer’s incentives for adjusting channel substitution. The paper adopts a stylized game theoretic model to describe interactions between retailer and the encroaching manufacturer. Contrary to conventional wisdom, the paper shows that under manufacturer encroachment, it is always possible for ex ante demand information sharing. Specifically, in the Cournot competition scenario where retailer channel and the encroaching manufacturer direct channel compete in quantity, the encroaching manufacturer could encourage demand information communication through side payment. Furthermore, in the Bertrand competition scenario, retailer may voluntarily share demand information. In addition, in either quantity or price competition, the encroaching manufacturer has incentives to adjust channel substitution for profit maximization.
1. Introduction
In recent decades, when online selling has become popular and cost-effective, the traditional manufacturer–retailer channel structure has also changed correspondingly. For example, besides the incumbent retailer’s selling channel, many manufacturers have established their own direct channel. This dual-channel structure is usually defined as manufacturer encroachment [1,2,3,4,5]. Manufacturer encroachment has become widespread in many industries such as electronic products, hotels, and airlines [3]. About half of the top manufacturers (e.g., IBM, Pioneer Electronics, Cisco System, Estee Lauder, and Nike) have adopted the direct sales channel [6]. In addition, many small and local firms have also started to sell through their own direct marketing channels besides the traditional (incumbent) retailer channel [5]. In apparel sector, Nike’s Consumer Direct Acceleration Offense emphasizing direct selling to consumers, is a key strategy to allow the brand to continue to grow even during pandemic. With revenues up 16% in 2021 compared to 2020, Nike direct sales were up 28% in 2021 compared to the first quarter in 2020 [7].
We study imperfect information sharing decisions of retailer under manufacturer encroachment. There are two main reasons. First, the co-existence of both the retailer channel and manufacturer direct channel is pervasive nowadays. Second, various information sharing programs between downstream retailer and upstream manufacturer is common. Therefore, it is important to understand the obstacles and incentives of information sharing under encroachment. In our study, we use the term “imperfect information sharing”, because the demand forecast shared by retailer is not extremely precise. This shared demand forecast is still uncertain and has some error relative to the real-world demand condition.
Many retailers share credible market demand information with upstream suppliers. The Electronic Data Interchange (EDI) technology has made it easier for retailers to communicate with suppliers. Surveys by BearingPoint Management and Technology Consultants indicated that the frequency and scope of information communicated from the retailer to their vendors have been accelerated in these years [8]. The Grocery Manufacturers Association (GMA), which is named the Consumer Brands Association, pointed out that in US grocery industry, most retailers and mass merchandisers communicate weekly and even daily with their vendors, sharing a variety of information types, including store sales, directly and at no cost [9]. It should be emphasized that the emerging trend of large language models (LLMs) facilitated market research could not eliminate but may strengthen the need for retailer to communicate retail demand information with upstream manufacturer. This is because, in perceptual analysis of market research, the validity of LLMs should be compared with human-generated data [10]. Also, when previous survey data from similar contexts is incorporated, marketers could enhance the responses of LLMs such as GPT [11]. As retailer has real sales data and is more specialized in sales process, they can better pre-train and fine-tune the LLMs such as GPT they use and obtain more accurate demand forecast than upstream manufacturer [12].
It has been shown that demand communication from retailer to manufacturer could benefit both partners and even coordinate the supply chain [13]. However, there exist obstacles for demand information sharing. First, it may put the retailer in a disadvantage position if he communicates demand information. Only when his loss could be compensated by some means does he has an incentive to share. Therefore, incentive mechanism such as side payment is needed to incentivize the retailer to share his privately demand information. Second, if the retailer shares his privately demand information with upstream firm and the upstream firm such as manufacturer strategically utilizes this information to adjust the wholesale price and marketing activities, it will put the retailer at a disadvantage market position. The extant literature has investigated incentives of demand information sharing in various supply chain contexts, such as “one supplier-multiple retailers” [14], “two manufacturers-one common retailer” [15], and “competing supply chains” [16,17,18]. These studies show that the retailer should be wary of sharing demand information.
Motivated by the co-opetitive relationship in the dual-channel structure where the encroaching manufacturer competes with her wholesale customer (i.e., the retailer), we investigate whether the downstream retailer would like to share demand information in uncertain market on the condition that manufacturer has encroached on the retail channel. Using a general demand forecast model, we show that both in quantity and price competition scenarios, downstream retailer can be encouraged to share privately demand forecast information with upstream encroaching manufacturer. Specifically, when retailer and the encroaching manufacturer compete in price, then the retailer voluntarily shares demand forecast information on the condition that the channel competition (substitution) is relatively intensified. In this price competition scenario, the reason underlying this result is encroachment by manufacturer: encroachment would alter manufacturer’s own strategic utilization of the received demand information. When manufacturer has encroached on the retail market, the manufacturer has to take a trade off between the retailer’s indirect channel and her own direct channel. Although the double marginalization is enhanced, encroachment by the manufacturer indeed enables demand information sharing to improve the performance of the supply chain. The benefit of the encroaching manufacturer from the shared demand information is larger than the loss of the retailer; therefore, both of them may benefit from demand information sharing.
We first investigate quantity (Cournot) competition with information asymmetry when the manufacturer has encroached on retail channel. Then we examine a price (Bertrand) competition scenario and explore whether the demand information sharing decision of retailer is different than the counterpart in quantity competition scenario. Quantity competition with encroachment is widely studied in the literature [1,3,4,5,19,20]. The price competition scenario is studied in ex ante information sharing with competing supply chains [18] and is also studied briefly under encroachment both with symmetric [1,19] and asymmetric demand information [3,4,5].
We focus on retailer’s demand information sharing when manufacturer has encroached on retail channel. At the beginning, in either quantity or price competition, retailer pre-commits to the sharing arrangements which prescribe whether retailer shares demand information. Then, before selling season, retailer obtains demand forecast signal and shares (or does not share) this demand signal according to the pre-commitment arrangements. Third, based on this demand information sharing arrangements, manufacturer decides wholesale price. Fourth, retailer sets order quantity (sales price) and after observing retailer’s decision, manufacturer decides her own direct sales quantity (sales price). Finally, demand is realized and both obtain their respective profits. Note that we employ the sequential decision which the encroaching manufacturer decides after the retailer’s decision. This is because the extant literature has shown the superiority of sequential decisions relative to simultaneous decisions under encroachment setting [1,20]. The encroaching manufacturer is the Stackelberg leader. Backward induction is used to obtain the optimal solutions.
We investigate three scenarios under manufacturer encroachment. The first scenario is homogeneous quantity competition in which the retailer channel and the encroaching manufacturer channel compete perfectly in quantity. This simplified scenario would guide us to obtain some insights and prepare us to analyze the subsequent scenarios. The second scenario is the differentiated quantity competition in which the product of the retailer channel and the product of the encroaching manufacturer channel are perceived by the consumer as imperfect substitutes. The third scenario is the differentiated price competition in which both compete in price. We show that the mechanisms are consistent in all of these three scenarios. That is, if we do not consider horizontal competition or other operational decisions (e.g., quality), manufacturer encroachment makes information sharing an equilibrium even if information sharing intensifies double marginalization. This result contrasts with the no encroachment setting where information sharing is not an equilibrium because it intensifies double marginalization. Therefore, we show that channel structure change driven by manufacturer encroachment from single channel to dual-channel can facilitate truthfully imperfect demand forecast information communication from downstream retailer to upstream encroaching manufacturer.
The findings of our study are presented in detail as follows. First, in homogeneous quantity competition scenario, retailer sharing imperfect demand information would make double marginalization more pronounced under manufacturer encroachment. This is due to the fact that although sales quantity in the encroaching manufacturer’s direct channel is positive, order quantity in the retailer’s channel is reduced more aggressively. The overall of the sales quantity decreases more compared with the traditional single channel. Fortunately, the reduction of the overall sales quantity improves the market clearing price. This improved market clearing price, while benefiting the encroaching manufacturer, does not hurt the retailer. Moreover, with cost disadvantage in the direct channel, the encroaching manufacturer would not set the wholesale price so aggressively to squeeze the retailer out of the market.
Second, in the differentiated quantity competition scenario, the retailer is always worse off if he shares imperfect demand information and the encroaching manufacturer is always better off. The imperfect demand information sharing of retailer still enhances double marginalization, but the channel competition intensity between the retailer channel and the encroaching manufacturer channel plays an important role in determining the value of imperfect demand information sharing. Contrary to conventional wisdom, with the channel competition becoming more intensive, the profit decrement of the retailer from imperfect demand information sharing is reduced and the profit increment of the encroaching manufacturer from shared demand information is also reduced. This is because when the channel competition is very intensive, the encroaching manufacturer has to consider more the retailer’s channel.
In this differentiated quantity competition scenario, there exists a threshold regarding channel competition intensity. Below this channel competition intensity threshold, although double marginalization is enhanced by shared imperfect demand information, the increment of the whole supply chain tends to decrease with channel competition becoming more intensive. An interesting result is that the retailer’s order quantity is reduced more. This means the sales quantity in the encroaching manufacturer’s direct channel is increased more quickly, hurting the retailer and benefiting the encroaching manufacturer herself. Above this channel competition intensity threshold, the increment of the whole supply chain tends to increase with channel competition becoming more intensive. In addition, imperfect demand information sharing improves the performance of the supply chain, which means Pareto gain can be achieved and the retailer can be incentivized through side payment to share his imperfect demand information.
To mirror the above outcomes, we show that the performance of the whole supply chain with shared imperfect demand information represents an inverted U-shaped relationship with respect to channel competition intensity. When the channel competition intensity is intermediate (neither very small nor very large) between retailer channel and encroaching manufacturer direct channel, the profit increment from imperfect demand information sharing of the supply chain is the largest. And when the degree of channel competition is intermediate, the profit increment of the supply chain is smallest but still larger than zero. This is because, when the channel competition intensity is very small, the encroaching manufacturer would be very aggressive in the direct channel. And when the channel competition intensity is very large, the manufacturer would consider more the retailer’s channel. Therefore, the supply chain benefits most from information sharing if the channel competition intensity is very small or very large. However, when the channel competition is intermediate, both the retailer and the encroaching manufacturer combat aggressively, thus the benefit of the supply chain from shared imperfect demand information is compromised.
Third, in the differentiated price competition scenario, retailer sharing imperfect demand information also enhances double marginalization and this enhancement is reinforced with the price competition becoming more intensive. Specifically, the encroaching manufacturer’s equilibrium wholesale price increases with the retailer sharing demand information. With price competition becoming more intensive, the increment of wholesale price increases, the sales prices of both the retailer and the encroaching manufacturer also increase.
In this price competition scenario, the shared imperfect demand information is reflected in the encroaching manufacturer’s demand function. This is very different from the quantity competition scenario. Because in this price competition scenario, the shared imperfect demand information concerning uncertain part of market demand would be incorporated into the encroaching manufacturer’s demand function, which would increase the expected sales quantity in the encroaching manufacturer’s direct channel. We define this effect as demand-enhancing effect of information sharing. This demand-enhancing effect is important, because the demand in the encroaching manufacturer’s channel or even of the whole supply chain would be perceived increased with the demand-enhancing effect of information sharing and would be perceived decreased without it.
Another interesting finding is that when price competition intensity between retailer channel and encroaching manufacturer direct channel is very large, then voluntary sharing of imperfect demand information from downstream retailer to upstream encroaching manufacturer is possible in this price competition scenario. This is because, although the increment of the wholesale price from information sharing increases as channel price competition becomes more intensive, the increment of the retailer’s sales price increases more, thus improving the retailer’s profit margin. Again, due to this intensive channel price competition, the sales prices of both the retailer and the encroaching manufacturer are confined and could not be set too high. Therefore, with demand forecast communication from downstream retailer to upstream encroaching manufacturer, the demand increment in retailer channel increases as channel price competition becomes more intensive. Therefore, with the price competition sufficiently intensive, the increased profit margin plus the improved demand makes the retailer himself better off if he shares imperfect demand information. In other price competition intensity cases where competition is not sufficiently intensive, the encroaching manufacturer would encourage the retailer to share demand forecast information through side payment.
The remainder of this paper is organized as follows. Section 2 presents the literature related to this study and positions our contribution. Section 3 presents basic model. Section 4 investigates quantity competition scenario. Section 5 investigates price competition scenario. In Section 6, the main findings are summarized and future research directions are illustrated. All proofs and supplemental materials are detailed in “Proofs and Statements” Section in e-companion of this study.
2. Literature Review
Our study belongs to the research on ex ante demand information sharing in different supply chain structures [14,15,16,18,21,22,23,24]. Although the retailer is unwilling to share ex ante demand information in “one supplier-one retailer” supply chain structure, these studies show that other industrial structures may induce voluntary ex ante demand forecast communication from downstream retailer to upstream manufacturer or supplier: for example, the downstream retailer competition [14,23,24], upstream manufacturer competition [15] or competing supply chains [16,18]. Consistent with and complementary to these studies, our research finds another supply chain structure, that is the dual-channel structure resulted from manufacturer encroachment, would facilitate ex ante demand information sharing in “one supplier-one retailer” channel structure.
Our study is also closely linked with the research that examines impact of supplier encroachment on retailer’s profit. As the channel conflict resulted from supplier encroachment may intensify competition, leading to dissent and outrage from incumbent retailers [25,26,27], the retailer could deter supplier from setting up direct channel by investing in retail service [28]. Contrary to the conventional wisdom, many studies show that supplier encroachment could benefit retailer and achieve a win–win outcome [1,6,29,30,31,32,33,34,35,36,37,38,39,40,41]. For example, Ref. [1] investigate supplier encroachment in quantity competition and show that encroachment by supplier could indeed achieve Pareto improvement in many cases. Ref. [6] has ascertained similar results in price competition scenario. Ref. [40] show that encroachment could enhance consumer demand. Additionally, Ref. [29] prove that the advantages of retailer’s channel in convenience and cost guarantee the retailer’s benefit from encroachment. Ref. [42] show that retailer fairness concern may be detrimental to supplier if supplier encroaches and fairness concern could improve system profit. Ref. [43] investigate impact of manufacturer encroachment with endogenous quality decisions in manufacturer-led or retailer-led supply chain. Ref. [44] investigate the manufacturer’s encroachment decisions taking into consideration channels’ misplacement rates with RFID deployment. For different channel power structures and pricing sequences, Ref. [45] examine the online–offline channel pricing game in which a manufacturer has an online direct channel and also resells through the retailer’s brick-and-mortar store channel. In a Hotelling model, Ref. [37] investigate the contract manufacturer’s encroachment strategy by launching a customized product, in addition to producing standard product for the original equipment manufacturer. They also design a revenue-sharing contract to collaborate the supply chain under encroachment by contract manufacturer. In a little bit different problem from supplier encroachment where the retail platform such as Amazon enters into the third-party seller’s sales market, Ref. [46] captures two horizontal effects: the competition effect between retail platform and third-party seller on it, and the product-value-enhancement spillover effect of this retail platform. Their results characterize the horizontal aspect of supplier encroachment and prove the potential “win-win” outcomes of supplier encroachment. Ref. [47] investigate how consumer digital privacy preferences (privacy-protecting vs. privacy-disclosing) influence manufacturer encroachment strategy. These studies have shown the benefits of encroachment, which lay a solid foundation for investigating demand information sharing under encroachment in our paper. As encroachment is pervasive in a variety of industries, we do not discuss the encroachment decisions, but focus on retailer ex ante truthful imperfect demand information communication, in either quantity or price competition scenario, given that encroachment has occurred.
Our study belongs to the signaling or screening literature considering supplier encroachment. For example, in a signaling game under asymmetric information considering supplier encroachment, retailer may distort order quantity downward, amplifying double marginalization, and encroachment by supplier could make retailer as well as encroaching supplier herself worse off or better off [4]. Furthermore, Ref. [5] study a screening game in which the encroaching supplier could screen the true market demand through nonlinear pricing. In their screening game, encroachment by supplier could also make retailer as well encroaching supplier herself worse off or better off. Ref. [48] study endogenous quality decisions of the manufacturer and the demand information sharing decisions of the retailer in a signaling game when the manufacturer has the potential to encroach into retailer sales channel. Ref. [49] show that direct selling by suppliers facilitates bilateral information flow between retailer and supplier. Ref. [50] study ex post demand information sharing under potential supplier encroachment. Refs. [51,52] investigate the interactions between supplier encroachment and cost reduction using signaling paradigm. Our paper is different from these studies. The main difference is that the retailer in our study ex ante commits to the demand sharing arrangements and the manufacturer sets the wholesale price based on this commitment. As pointed out by [4], when the supplier has developed the encroachment capability, the retailer may tend to credibly share his demand information rather than signal this demand through order quantity. In our study, the retailer truthfully shares imperfect demand information. Therefore, there is no efficiency loss caused by signaling. We focus on the strategic decisions regarding ex ante imperfect demand information sharing under manufacturer encroachment and therefore complements the signaling or screening paradigm with encroachment.
Our study belongs to ex ante demand information sharing literature considering supplier encroachment [3,20,53,54]. Specifically, Ref. [3] investigate the role of retailer ex ante demand information sharing in deterring supplier encroachment. Ref. [20] study how nonlinear production cost of upstream encroaching manufacturer impacts retailer’s ex ante demand information sharing strategy under manufacturer encroachment. Ref. [54] examine the information leakage problem considering both one-sided and two-sided sharing in dual channel supply chain. Ref. [55] investigate an bilateral demand forecast information sharing problem considering manufacturer encroachment, but not deal with information leakage problem. Ref. [53] study the scenario in which manufacturer encroachment decisions are contingent upon retailer’s ex ante demand sharing strategy when manufacturer demand-enhancing investment spillovers exist. Ref. [56] show that supplier encroachment or supplier quality decision may motivate retailer information sharing. Ref. [57] investigate the interplay of manufacturer encroachment and extended warranty provision and show that encroachment and extended warranty provision may be substitutes or complements. These research study ex ante demand information problem in an embedded scenario, considering operations decisions such as deterring encroachment, nonlinear production cost or information leakage, or quality decision. The ex ante demand information alone is not sufficient to support their mechanisms. Recently, some researchers investigate ex ante information sharing with encroachment in online marketplace or online retail platform scenarios [58,59]. Ref. [60] investigate the direct channel cost uncertainty scenario and study the disincentive and incentive of the encroaching manufacturer’s information acquisition for this cost. Ref. [61] investigate the impact of production cost reduction of manufacturer on retailer ex ante demand information sharing under manufacturer encroachment. Similarly, Ref. [62] study how manufacturer encroachment and production learning effect motivate retailer information sharing. Of these studies on information sharing with encroachment, Ref. [3] is most related to our study. But our study is different from [3]. First, Ref. [3] focus on the role of ex ante demand information communication on deterring encroachment, while our study concentrate on whether retailer is willing to ex ante share imperfect demand under encroachment. Second, Ref. [3] delineate demand uncertainty using a uniform distribution while our study adopts a general distribution. Third, Ref. [3] employ a simultaneous move in which retailer channel and supplier direct channel make quantity decisions simultaneously while our study employs a sequential move in either quantity or price competition under manufacturer encroachment.
3. Model
We consider a supply chain consisting of a manufacturer and an incumbent retailer. For simplicity of exposition, we call the manufacturer as she and the retailer as he. The dual-channel structure is as follows. First, the retailer selling channel: product is manufactured and delivered to retailer and then is sold to end consumers. They adopt a wholesale price contract. Second, the manufacturer direct channel: as it has become convenient for the manufacturer to sell directly to consumers through opening up online sales channels, the manufacturer also delivers her product directly to end consumers. This phenomenon is usually considered “encroachment”. The manufacturer organizes her production according to the retailer’s order (i.e., the make-to-order strategy). And both of them maximize their objective function based on the expected profit (risk neutrality). In addition, the manufacturer’s marginal production cost is constant. For simplicity of analysis and without loss of generality, the production cost of the manufacturer is normalized to zero.
Under encroachment, the transaction characteristics are as follows. Firstly, there exist manufacturer–retailer transactions through a wholesale price contract. Secondly, there exist channel competition between encroaching manufacturer and retailer: quantity competition or price competition.
Different from the extant literature that assumes homogeneous quantity competition (i.e., [1,20,23]), we assume two types of differentiated competition: the differentiated quantity competition (Cournot competition) and the differentiated price competition (Bertrand competition). Consumer market demand consists of two parts: the certain part a and the uncertain part . Here, a is a positive constant representing the demand base and is a random variable representing market uncertainty and volatility. For simplicity and consistent with the literature, the expectation of is normalized zero and the variance is represented by . Although the market demand fluctuates, the range of fluctuation lies in an interval. Therefore, through our paper, we assume that is relatively small. The demand base a is common knowledge, but the forecast for conditional on a signal Y is only privately known to the retailer.
For differentiated quantity competition scenario, the (inverse) demand functions for both the encroaching manufacturer and the retailer are, respectively, given by
For differentiated price competition scenario, demand functions are
where , represents retailer or manufacturer, and characterize channel substitution rate or channel competition intensity between encroaching manufacturer direct selling channel and retailer selling channel. A higher or reflects a more intense channel competition. The above demand functions characterizing differentiated competition are widely used in the literature on encroachment and information sharing [3,16,19,24,63].
Though the encroaching manufacturer’s direct channel brings about pressure on retailer’s channel, the incumbent retailer indeed embraces two advantages in the competition with the encroaching manufacturer.
The first advantage of the retailer is the lower sales cost in the sales processes. This is because the (incumbent) retailer has been operating sales activities for many years and has mastered abundant knowledge such as consumer preferences, the principle of consumer behavior, skills in communicating with and collecting feedbacks from the consumers, etc. While the manufacturer is an entrant to the consumer sales industry and needs more cost and effort to attract consumers. Based on these facts, to emphasize sales cost advantage in a retailer channel, the unit selling cost of encroaching manufacturer is denoted by and unit selling cost of the retailer is normalized as zero.
The second advantage of the retailer is the privately demand forecast mined from sales data. Obviously, the retailer has accumulated a large amount of historical consumer sales data. In addition, these accumulated sales data could be best utilized by retailer, either through advanced data mining and machine learning techniques or outsourcing forecast work to a third party forecasting company. Although the encroaching manufacturer may collect sales data from the direct channel, the accumulated sales data is much less than the retailer’s sales data. And it is reasonable to assume that the retailer’s demand forecast is much more precise than that of the encroaching manufacturer. Therefore, the demand forecast information is still asymmetric between the retailer and the encroaching manufacturer. To model this demand information asymmetry setting, we give two assumptions. First, the encroaching manufacturer just predicts market condition based on prior distribution of , and has no further information before demand is realized. Second, retailer has access to a demand signal Y before uncertain demand is realized. The demand signal Y is an unbiased estimator of (). Consistent with [64], the signal accuracy t is defined as . From [65] we have
and the information structure is common knowledge between the retailer and the encroaching manufacturer.
We investigate the retailer’s ex ante demand information sharing decisions under manufacturer encroachment.
The chronology of moves is as follows. First, under encroachment and given the encroaching manufacturer’s transfer payment, the retailer decides whether to sign an arrangement with the manufacturer. If the information sharing arrangement has been signed, then the retailer should share the imperfect demand signal (Y) truthfully with the manufacturer. Otherwise, the demand signal is private to the retailer himself. For simplicity of exposition, this dual-channel is communicative when the retailer shares demand signal Y truthfully with the encroaching manufacturer or noncommunicative otherwise. Second, before the uncertain demand is realized, the retailer observes his privately imperfect demand signal, and if the information sharing arrangement has been reached, he then transmits this demand signal truthfully to the encroaching manufacturer. Third, in the quantity (price) competition scenario, the encroaching manufacturer decides her wholesale price and the retailer determines his order quantity (sales price); then, the encroaching manufacturer determines the direct sales quantity (direct sales price). Finally, profits are realized for both the retailer and the encroaching manufacturer. We solve this Stackelberg game using backward induction.
The three scenarios studied in our paper are detailed in Table 1.

Table 1.
The scenarios.
The notations are illustrated in Table 2.

Table 2.
Notations.
4. Cournot Competition Under Manufacturer Encroachment
In this Cournot competition scenario, we first examine the perfect substitute case (Section 4.1); then, we investigate the differentiated substitute case (Section 4.2).
4.1. Cournot Competition: Perfect Quantity Competition
This section aims to detail the algebraic process and laid a solid foundation for further investigations in the subsequent sections. In this section, we consider the () scenario where the products in retailer channel and manufacturer direct channel are perceived as perfect substitutes by consumers. Their respective (inverse) demand function is given by
where . Based on the information sharing agreement, the encroaching manufacturer decides her direct sales quantity after wholesaling the order quantity to the retailer.
4.1.1. Noncommunicative
When the encroaching manufacturer receives no knowledge about demand forecast, she maximizes the profit function below to solve her optimal direct sales quantity:
where . The encroaching manufacturer only has the information about prior distribution of . From Equation (3), the encroaching manufacturer’s sales quantity contingent upon can be obtained, which is illustrated as
Using backward induction, the retailer embeds Equation (4) into his profit function to obtain his order quantity
The retailer’s optimal order quantity given wholesale price w is
Because the encroaching manufacturer only owns the prior distribution about market condition, in her eyes, both the quantity in Equation (4) and the quantity in Equation (6) are evaluated based on prior distribution about . Thus, we have
Then profit function of the encroaching manufacturer is given by
For some algebraic processes, the above equation can be translated into the following expression:
Based on this expression regarding wholesale price w, we solve the optimal wholesale price . Then, we solve for the optimal quantity in the retailer’s channel and the optimal quantity in the manufacturer direct channel. These expressions are given below
Note that in our study, we do not consider information leakage or signaling effect problem resulted from the term in the expression of in Equation (7). The reasons are presented in detail in the e-companion to this study (Section 7.2). The optimal decisions in Equation (7) have determined their optimal payoffs:
4.1.2. Communicative
The most prominent difference in this communicative scenario is that the encroaching manufacturer now forecasts the market condition uncertain part conditional on the demand signal Y; that is, . Therefore, the encroaching manufacturer’s objective function is now illustrated as
where . Optimizing Equation (9), we can obtain the encroaching manufacturer’s sales quantity contingent upon , when demand information is communicative:
Similar to Equation (5), the retailer’s objective function in the communicative scenario is given by
Then, in this communicative scenario, we obtain the retailer’s order quantity conditional on wholesale price w:
Now that the encroaching manufacturer knows the demand signal Y, the two quantities in Equations (10) and (12) are evaluated by her using the following expressions
Then the informed encroaching manufacturer’s expected profit function is now given by
Once again, we obtain the profit expression only regarding wholesale price w:
By solving the optimal wholesale price , we obtain the optimal order quantity of the retailer and the optimal sales quantity of the encroaching manufacturer in the direct channel . All of these are characterized as follows
With , we have the optimal payoff in the communicative scenario
4.1.3. Comparisons: Noncommunicative vs. Communicative
Based on the results in Section 4.1.1 and Section 4.1.2, we present the following results when the encroaching manufacturer direct channel and the retailer channel compete perfectly in quantity. These findings are presented as follows and the proofs are detailed in the e-companion to this study.
Proposition 1.
With perfect quantity competition between the encroaching manufacturer direct channel and the retailer channel, the retailer is indifferent with ex ante demand information sharing, while the encroaching manufacturer indeed benefits from this shared demand forecast signal.
Proposition 2.
In this perfect quantity competition scenario, the encroaching manufacturer could benefit more from ex ante demand information sharing when there is a more uncertain demand (larger ) or a more accurate demand forecast signal (larger t).
4.2. Cournot Competition: Differentiated Quantity Competition
In this () setting where the product of the encroaching manufacturer and the product of the retailer are perceived by consumers as differentiated substitutes, the (inverse) demand function is
where , indicates competition intensity or the degree of product substitution.
As the sequence of events and the calculation process are similar to that of Section 4.1, we directly give the optimal decisions and the corresponding payoffs in both the noncommunicative and communicative scenarios.
4.2.1. Noncommunicative
The optimal decisions in the () setting with no information sharing is given by
The corresponding payoffs are characterized as
4.2.2. Communicative
In this communicative scenario, the retailer shares demand signal Y with the manufacturer. The optimal decisions in the setting with information sharing is given by
The corresponding payoffs are characterized as
4.2.3. Comparisons: Noncommunicative vs. Communicative
In this differentiated quantity competition scenario, the retailer sharing demand information with the encroaching manufacturer will lead to the subsequent results: increasing the retailer’s market clearing price but decreasing the profit margin; increasing the encroaching manufacturer’s market clearing price. The overall effect is that information sharing benefits the encroaching manufacturer but hurts the retailer himself. The following proposition explains this finding.
Proposition 3.
With differentiated quantity competition between encroaching manufacturer direct channel and retailer channel, then retailer’s ex ante demand information sharing can only be achieved when the encroaching manufacturer provides transfer payment to the retailer.
Under encroachment, if the encroaching manufacturer direct channel competes in differentiated quantity with retailer channel in consumer market, then information sharing will increase both the wholesale price and the direct sales quantity for the encroaching manufacturer, and decrease the retailer’s order quantity. The overall effect reveals that truthful demand communication reduces the retailer’s profit but increases the manufacturer’s profit more. Therefore, the encroaching manufacturer may be willing to encourage truthful demand communication through transfer payment. The “transfer payment” means the encroaching manufacturer needs to pay the retailer some money to compensate retailer for profit losses caused by sharing demand information. As a result, supply chain performance could be improved through truthful demand communication.
Overall, demand communication makes the double marginalization more pronounced (, ), and it also increases sales quantity of the encroaching manufacturer’s direct channel ().
For the retailer, sharing demand information increases his market clearing price . But it reduces his profit margin . In addition, sharing demand information decreases the retailer’s order quantity (). As a result, the implementation of demand communication negatively impacts the retailer’s profitability.
Now we consider the encroaching manufacturer. For the manufacturer, on one hand, demand information sharing increases her market clearing price () as well as direct sales quantity (), thus increasing the direct sales profit (). On the other hand, demand information sharing reduces order quantity of retailer channel (), which may negatively influence the profit extracted from retailer channel. In addition, the profit increase in the encroaching manufacturer’s direct channel dominates the profit decrease extracted from retailer channel. Altogether, the encroaching manufacturer benefits from demand information sharing.
Next, we examine how the channel substitution between the manufacturer and the retailer influences the manufacturer’s profit increment from information sharing. Let , then , where and . As always hold, let , where . The first derivative with respect to is given by , where holds if and only if and . Therefore, for , it always hold that , but decreases with respect to .
Figure 1 illustrates that changes with .
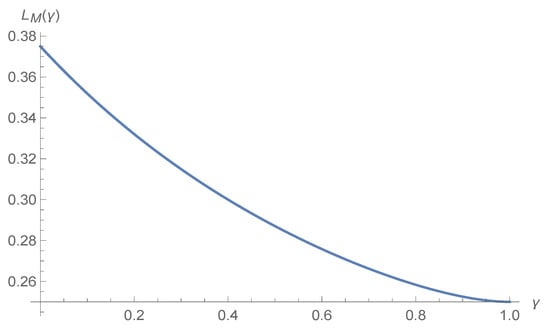
Figure 1.
Quantity competition intensity impacts value of demand for manufacturer given encroachment.
Under encroachment, retailer demand communication benefits the encroaching manufacturer. As , we can show that the term decreases when channel substitution increases. This means if the consumers no longer view the products in the two channels as the same, the encroaching manufacturer’s profit increment from demand communication will decrease when the degree of channel substitution increases.
Next, we will examine the impact of information sharing on the whole supply chain. Define
Because always holds, let , where . The first derivative with respect to is given by . Therefore, as , then has a unique solution. Denote the unique solution as , then . When , , is a decreasing function of ; when , , is an increasing function of . As , , , thus .
From the above analysis, we can show that retailer demand communication benefits the whole supply chain. But the increment (that is ) is decreasing when channel substitution locates in interval and increasing in , where . In summary, the total profit of the dual-channel supply chain is U-shaped with channel substitution .
Figure 2 illustrates how changes with .
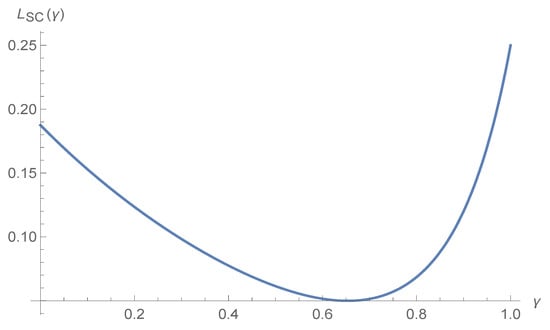
Figure 2.
Quantity competition intensity mediates value of demand for supply chain given encroachment.
The information structure assumed in our study gives the expression below for :
In the above equation, measures accuracy of demand signal Y. It is obvious that is an increasing function with respect to both the demand signal accuracy t and market uncertainty .
Proposition 4.
With differentiated quantity competition between the encroaching manufacturer direct channel and the retailer channel, the encroaching manufacturer with shared demand information prefers a more accurate demand signal from the retailer or a more uncertain market condition.
The logic behind Proposition 4 is that, with shared demand information, the encroaching manufacturer benefits more from a more accurate demand signal (larger t) and a more uncertain market condition (larger ).
When comparing Proposition 1 with Proposition 3, and taking into consideration the delineation of Figure 1 and Figure 2, we find that the channel substitution degree between retailer channel and manufacturer direct channel mediates the value of information. Although Figure 1 shows the value of imperfect demand sharing for encroaching manufacturer decreases with channel substitution degree (), the value of information sharing for the whole supply chain is U-shaped with channel substitution degree. In equilibrium, the value of information sharing for the whole supply (the total payoff increment for the whole supply chain) determines how much indeed the encroaching manufacturer benefits from information sharing. As is discussed above, when channel substitution degree , the value for supply chain is the lowest (still positive). Therefore, the encroaching manufacturer has incentives to takes measures to adjust the channel substitution degree , to either mitigate or intensify channel competition, depending on the current channel competition intensity (). These measures, for example, may include direct channel logistics in-time quality, online purchase experience, product returns availability and convenience, etc. The following proposition summarizes this finding.
Proposition 5.
With differentiated quantity competition between the encroaching manufacturer direct channel and the retailer channel, the encroaching manufacturer has incentives to adjust channel substitution degree for improving the benefit from retailer’s shared demand information.
5. Bertrand Competition Under Manufacturer Encroachment
Now, we examine the differentiated price competition scenario in which the direct channel of manufacturer and the retailer channel compete in price given encroachment. The demand function is expressed as
where , indicates competition intensity or the degree of channel substitution.
In the price competition scenario, we assume that the retailer first moves (first decides the sales price ), the encroaching manufacturer second moves (sets the sales price in the direct channel after observing ). The reasons for subsequent moves in price competition are explained in Section 7.3.
5.1. Noncommunicative
In this differentiated price competition scenario, the optimal pricing decisions with no information sharing is given by
The corresponding payoffs are represented below
5.2. Communicative
With shared demand information, the optimal pricing decisions are given by
The corresponding payoffs are characterized as
5.3. Comparisons: Noncommunicative vs. Communicative
Given encroachment and the encroaching manufacturer direct channel competes in price with the retailer channel, the retailer sharing demand information with the encroaching manufacturer will lead to the subsequent results: (i) increasing the retailer’s market clearing price but decreasing the profit margin; (ii) making the demand of the retailer first decrease and then increase with the channel competition intensity ; (iii) increasing the manufacturer’s direct market sales price. The overall effects are as follows: (i) when the channel competition intensity is relatively small, sharing demand information makes the retailer himself worse off but benefits the encroaching manufacturer (and the supply chain); (ii) as the channel competition intensity increases to a relatively large value, sharing demand information also makes the retailer himself better off. These findings are summarized in Proposition 6.
Proposition 6.
With differentiated price competition between direct channel and retailer channel, retailer’s information sharing is reached with transfer payment when channel competition intensity is small and is voluntary when channel competition intensity is large. Here “voluntary” means that the retailer’s information sharing is reached without need of transfer payment.
Information sharing makes the double marginalization more pronounced (, ), it also increases the manufacturer’s direct sales price ().
The change in the retailer’s profit can be attributed to the following reasons: sharing demand information reduces the retailer’s profit margin (); the demand of the retailer first decreases and then increases with the channel competition intensity . We have
In the above equation, define the coefficient of as , where . Then .
Figure 3 illustrates how changes with .
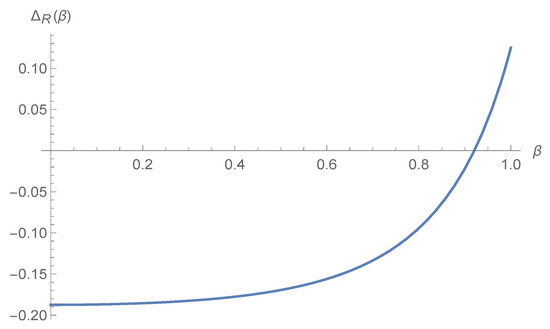
Figure 3.
Price competition intensity impacts value of demand for retailer given encroachment.
From the observation of Figure 3, we show that is increasing when . Moreover, and . Therefore, has a unique real solution, which is denoted by . From Figure 3, we can show that lies in the interval . Through numerical analysis, we can obtain an approximate value .
We can see that when , , thus . That is, if the price competition intensity between the encroaching manufacturer direct channel and the retailer channel is relatively small, sharing demand information hurts the retailer himself. When , , thus . That is, if the price competition intensity between the encroaching manufacturer direct channel and the retailer channel is relatively large, sharing demand information benefits the retailer himself.
Now we consider the manufacturer. For the manufacturer, information sharing adds increment to the sales quantity through the retailer channel (), it also increases the manufacturer’s wholesale price (). Therefore, the manufacturer’s sales profit through the retailer channel is improved if the supply chain is communicative. Furthermore, sharing demand information increases the manufacturer’s profit margin of the direct selling channel (). The two effects taken into consideration, it is straightforward that retailer demand communication always benefits the encroaching manufacturer.
Next, we examine how the price competition intensity between the two channels influences the encroaching manufacturer’s profit increment from information sharing. We have
Define the coefficient of as .
Figure 4 illustrates how changes with .
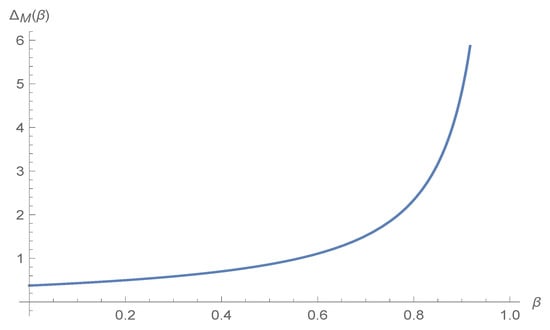
Figure 4.
Price competition intensity impacts value of demand for manufacturer given encroachment.
From Figure 4, we can see that in the price competition scenario, information sharing always benefits the encroaching manufacturer. And the more intensified the price competition, the more benefit information sharing will bring about to the encroaching manufacturer.
Next, we will examine the impact of information sharing on the whole supply chain in the price competition scenario. When noncommunicative, supply chain profit is given by . When communicative, supply chain profit is given by . The difference in the profit is illustrated as
Define the coefficient of in the above equation as . The illustration of is given in Figure 5.
Figure 5.
Impact of competition intensity on the value of information sharing for the supply chain.
From Figure 5, holds for any . The more fierce the price competition is or the larger the value of is, the more the supply chain benefits from retailer demand communication.
In our paper, we have where measures the accuracy of demand signal Y. Note that a more accurate signal (larger t) or a more uncertain demand (larger ) would lead to a larger , we have the following finding.
Proposition 7.
In the price competition scenario, either a more uncertain demand (larger ) or a more accurate demand forecast signal (larger t), would make the encroaching manufacturer and the supply chain benefit more from retailer demand communication. Therefore, the encroaching manufacturer may tend to encourage the retailer to improve demand forecast accuracy through transfer payment.
In the above analysis and from the illustration of Figure 5 under price competition, we can show that, performance improvement of whole supply chain from demand communication always increases when channel substitution degree () increases. Therefore, we have the following result under price competition.
Proposition 8.
With differentiated price competition between the encroaching manufacturer direct channel and the retailer channel, the encroaching manufacturer has incentives to increase channel substitution degree for improving the benefit from retailer’s shared demand information.
In this differentiated price competition scenario where the retailer channel and the encroaching manufacturer’s direct channel compete in price, the larger the channel substitution degree, the larger benefit for the encroaching manufacturer from demand forecast information sharing. And when the channel substitution degree is relatively large, sharing demand forecast is consistent with retailer’s payoff, thus, is voluntary. Specifically, from Figure 3, the retailer can benefit from his own ex ante demand forecast sharing when channel substitution degree is very large. From Figure 4, the encroaching manufacturer’s benefit from demand forecast sharing increases when channel substitution degree increases. Therefore, the encroaching manufacturer has incentives to make channel substitution degree larger. Proposition 8 summarizes this logic for the encroaching manufacturer.
The proof of Proposition 8 is similar to that of Proposition 1 and, thus, is omitted.
6. Conclusions
This paper studies the retailer’s ex ante demand communication strategy when the manufacturer encroaches on the retailer channel. Therefore, channel conflict and cooperation coexist. This paper considers two types of competition: quantity competition and price competition. Under either type of competition, the information sharing decision of the retailer and the impact of this decision on the manufacturer and the whole supply chain are obtained respectively. The results show that without encroachment, ex ante retailer demand sharing is not possible; given encroachment, the manufacturer is able to “buy” demand forecast information from retailer to achieve a win–win situation. In addition, when the encroaching manufacturer competes with the retailer in price and the competition intensity is relatively high, information sharing also benefits the retailer himself and the retailer voluntarily shares demand forecast information. In sum, given encroachment, it is possible for the retailer to ex ante share imperfect demand information in equilibrium despite the enhanced double marginalization resulted from this ex ante shared demand forecast.
Based on the results of our paper. The managerial implications are as follows.
First, dual-channel structure would facilitate information flow along the supply chain. Supply chain members should consider the channel structure and change this structure if possible to achieve information sharing. The dual-channel structure resulted from manufacturer encroachment should be taken into consideration for demand forecast communication programs by both the upstream encroaching manufacturer and the downstream retailer. Second, it should be noted how consumers perceive the products in retailer channel or the encroaching manufacturer direct channel. By providing additional service or bundling sales with lower price, some e-commerce retailers such Amazon, Walmart, and JD.com can influence how consumers perceive the two channels. This helps us to distinguish Cournot (quantity) competition or Bertrand (price) competition between the two channels. Third, the value of ex ante imperfect demand forecast information is also determined by channel substitution degree. The encroaching manufacturer or the retailer could improve profit by changing the channel substitution degree through price, service, or other sales and operational techniques.
There are several future research directions. First, further research may investigate the ex ante demand information sharing strategy under encroachment when the manufacturer adopts a make-to-stock production strategy. Second, this paper assumes wholesale price contracts are adopted, future research may examine other forms of contracts in ex ante demand information sharing, such as revenue-sharing contracts. Third, taking into considerations production technology improvements and firm-consumer interactions would help to understand channel issues. Fourth, it would be very important to investigate how interactions between channel structure and basic marketing activities or operations decisions change information sharing in supply chains, where basic marketing activities may include pricing, promotion or price guarantees, operations decisions may include capacity flexibility or production technology improvement. Fifth, our model assumes that the manufacturer is a Stackelberg leader. In real industry background, there exist other power distribution dual-channels. For example, the wholesale price may be negotiated between encroaching manufacturer and retailer or the retailer is dominant and has the most bargaining power. It will be interesting to investigate information sharing in dual-channel supply chains in other power distribution between firms in this supply chain. Sixth, the encroaching manufacturer may also have some demand forecast information about consumer demand, though this information may not be as precise as the information retailer owns. And in contemporary minichain, the manufacturer may have more accurate demand forecast information than retailer. It is also worthwhile to study bilateral information sharing in quantity or price competition scenario in this dual-channel supply chain. And it will be fascinating to explore the encroaching manufacturer’s incentives to improve accuracy of demand forecast she has. Seventh, in our model we assume both encroaching manufacturer and retailer have perfect rationality and risk neutrality, further study may explore the bounded rationality and risk aversion/seeking assumption and explain how rationality and risk attitudes influence the equilibrium results.
7. Proofs and Statements
We first give the algebraic processes for the solutions and the proofs in Section 4.1 (the same goes for Section 4.2 and Section 5). Then, we give the reasons why we do not consider signaling effect if the retailer does not share demand forecast signal in our main text.
7.1. Algebraic Process and Proofs
We give the algebraic processes in Section 4.1 in detail. And based on these results, we prove the propositions. The processes and proofs in Section 4.2 and Section 5 are similar and, thus, omitted here.
7.1.1. Algebraic Process in Section 4.1
If the retailer does not share demand forecast signal. Then in Equation (3), first derivative respect to direct selling quantity gives the expression in Equation (4). Substituting the expression into Equation (5) and first derivative respect to retailer’s sales quantity give the expression in Equation (6). To solve the manufacturer’s profit, we need to substitute the expressions of in Equation (4) and in Equation (6) back into Equation (3). But one point must be noted. As the retailer does not share demand signal, the manufacturer has no knowledge of the demand signal Y, besides the prior distribution on (). Therefore, in solving the manufacturer’s profit, we should substitute the expectation and into Equation (3). This procedure in algebraic process represents information asymmetry between the encroaching manufacturer and the retailer, with the retailer knowing the demand signal Y and with the manufacturer only knowing the prior distribution on .
Based on the above procedure, we obtain the optimal wholesale price , retailer’s sales quantity and manufacturer’s direct sales quantity , all of which are characterized in Equation (7). Then, we calculate the optimal profits and conditional on the demand signal Y for the retailer and the manufacturer, respectively. The retailer’s optimal profit conditional on the demand signal Y is
Therefore, the retailer’s optimal profit is
Likewise, the encroaching manufacturer’s optimal profit conditional on the demand signal Y is
Therefore, the encroaching manufacturer’s optimal profit is
Here, and .
The expressions of and are characterized in Equation (8).
If the retailer shares demand forecast signal. The procedures are similar to the situation where the retailer does not share demand signal. But there are two points that are different. First, as the retailer shares demand forecast signal, the manufacturer has the knowledge of demand signal Y. Therefore, demand forecast information is symmetric between the retailer and the encroaching manufacturer. Second, in computing the optimal profits, we would use the equation , where and increases when t or increases.
The algebraic processes in solving the optimal decisions and profits in Section 4.2 and Section 5 are similar to the above procedures and, thus, omitted here.
7.1.2. Proof of the Propositions
Proof of Proposition 1.
Define the supply chain profit as the sum of the retailer’s profit and the encroaching manufacturer’s profit. If the supply chain profit when retailer shares demand signal is larger than that when the retailer does not share demand signal, then it is possible to incentivize the retailer to share demand forecast information through transfer payment. Specifically, if the retailer’s profit remains the same or improves with demand signal sharing and, meanwhile, the encroaching manufacturer benefits from demand signal sharing, then voluntary information sharing can be achieved. Comparing the profits in Equations (8) and (14) instantly obtains the results in Proposition 1. □
The principle in the proofs of propositions in Section 4.2 and Section 5 are the same as that in the proof of Proposition 1, though may be a bit different in specific processes. Therefore, the proofs in Section 4.2 and Section 5 are omitted here and are available upon request from the authors.
7.2. The Reasons for Not Considering Signaling Effects
In this section, we explain the reasons why we do not consider signaling effect if the retailer does not share demand signal in the main text. We reexamine the perfect Cournot competition in Section 4.1. Similar logic goes with Section 4.2 and Section 5 and, thus, are omitted here.
Some readers may have doubts about the results when the retailer does not share demand signal. This is because in Section 4.1, if the demand forecast signal is not shared, then the current result concerning the retailer’s optimal sales quantity is . We can see that is an increasing function of the demand signal . And you may say that the encroaching manufacturer can perfectly infer the demand signal through the value of , as the encroaching manufacturer decides her direct sales quantity after observing the retailer’s order quantity .
There are several reasons for not considering signaling effect when the retailer does not share demand forecast signal. First, our study focuses on double marginalization under encroachment and the subsequent imperfect demand information sharing decisions of the retailer. Our results would be sharper and more meaningful if we do not consider signaling effect. Second, the retailer could deter the demand forecast inference behavior of the manufacturer by making the demand signal noisy in purpose or delay the order quantity decision such that the manufacturer could not adjust in time her direct sales quantity even after observing the retailer’s order quantity (thus the demand signal). Third, if the retailer employs a quantity flexible contract to order part of the quantity, and orders the residual quantity, then the manufacturer also could not effectively inter the demand signal just from the retailer’s order quantity. Fourth, the retailer could deter demand information inference by deciding the order quantity at the same time when the encroaching manufacturer reveals her direct sales quantity (the simultaneous encroachment). However, as proved in [20], in most cases, the retailer and the manufacturer are better off under sequential encroachment (in our main text) than under the simultaneous encroachment if we consider imperfect demand forecast signal sharing of the retailer. Last, the problem would be the horizontal quantity competition with information inference between the retailer and the encroaching manufacturer if we consider signaling effect in the main text. This is because, if the retailer does not share demand signal, the manufacturer has no knowledge of the demand signal and has no chance to infer this demand signal when deciding her wholesale price, as the wholesale price precedes the retailer’s order quantity. Then the problem would be the first mover disadvantages studied in [66].
Anyway, in the following content, we consider the information inference behavior of the encroaching manufacturer and show that our main results are robust. Therefore, it is trivial to consider the signaling effect or demand forecast inference of the encroaching manufacturer.
Even if the encroaching manufacturer can perfectly infer the demand signal after observing the retailer’s order quantity, the wholesale price is unchanged. What changed is the information structure between the encroaching manufacturer and the retailer when they compete in quantity in end user market. For the demand forecast inference, we following the spirit in [4,14]. That is, can represent the demand signal , where , and is a linear and increasing function of . Here, the wholesale price in Equation (7) is unchanged. In deciding the direct sales quantity, the encroaching manufacturer chooses to maximize her expected profit:
First derivative gives the encroaching manufacturer’s direct sales quantity given the retailer’s sales quantity :
Then the Equation (5) in the main text is changed into the following expression:
As , then first derivative gives the retailer’s optimal order quantity , where . Therefore, the expression of is characterized as follows:
And the optimal direct selling quantity of the encroaching manufacturer is represented as
Based on the above optimal decisions, we can compute the optimal profits of the retailer and the encroaching manufacturer:
In the main text, the retailer voluntarily shares demand forecast signal (Proposition 1). While information sharing is incentivized through transfer payment from the encroaching manufacturer to the retailer if we consider the information inference behavior (signaling effect). Though the result is a bit different, our results in the main text is robust.
In sum, just because of the reasons presented above, we do not consider the information inference or signaling effect in our main text.
7.3. The Reasons for Sequential Pricing in Section 5
In the main content in Section 5, we assume the retailer decides the price in his retail channel before the encroaching manufacturer decides her direct sales price. The reasons for subsequent moves in price competition are explained as follows.
First of all, the retailer is usually dominant in the marketing channel. For example, large retailers such as Walmart and Amazon are advanced in marketing and pricing. These retailers have relatively advanced marketing plans, giving priority to the introduction of their own product prices. Moreover, sales are more important to these retailers than to encroaching manufacturers, so retailers do not wait for manufacturers and do make price decisions in advance. In addition, retailers have more marketing activities, through which manufacturers can know or accurately infer the retailer’s sales price . After that, the encroaching manufacturer decides her direct selling price in response to . The second reason is that the retailer has many years of sales experience. Before the manufacturer formulate direct sales channel, the retailer’s sales prices have been well known. Moreover, the retailing activity can not easily change the selling price too much. We do not consider the case of price variability (dynamic pricing).
Therefore, the retailer first decides his sales price , and then the encroaching manufacturer determines her selling price in the direct channel.
Author Contributions
Conceptualization, Z.L.; Methodology, B.W. and Z.L.; Software, B.W. and Z.L.; Validation, B.W. and Z.L.; Formal analysis, B.W. and Z.L.; Investigation, B.W. and Z.L.; Resources, B.W.; Writing—original draft, B.W. and Z.L.; Writing—review & editing, B.W. and Z.L.; Visualization, Z.L.; Funding acquisition, B.W. and Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Shanghai Planning Office of Philosophy and Social Science, Grant Number: 2024BGL020.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest. The funder had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Arya, A.; Mittendorf, B.; Sappington, D.E.M. The bright side of supplier encroachment. Mark. Sci. 2007, 26, 651–659. [Google Scholar] [CrossRef]
- Emerson, R.W. Franchise encroachment. Am. Bus. Law J. 2010, 47, 191–290. [Google Scholar] [CrossRef]
- Huang, S.; Guan, X.; Chen, Y. Retailer information sharing with supplier encroachment. Prod. Oper. Manag. 2018, 27, 1133–1147. [Google Scholar] [CrossRef]
- Li, Z.; Gilbert, S.; Lai, G. Supplier encroachment under asymmetric information. Manag. Sci. 2014, 60, 449–462. [Google Scholar] [CrossRef]
- Li, Z.; Gilbert, S.M.; Lai, G. Supplier encroachment as an enhancement or a hindrance to nonlinear pricing. Prod. Oper. Manag. 2015, 24, 89–109. [Google Scholar] [CrossRef]
- Chiang, W.Y.K.; Chhajed, D.; Hess, J.D. Direct marketing, indirect profits: A strategic analysis of dual-channel supply-chain design. Manag. Sci. 2003, 49, v-142. [Google Scholar] [CrossRef]
- Kohan, S.E. Nike prices to rise amid supply chain issues while profits increase 23%. Forbes 2021. Available online: https://www.forbes.com/sites/shelleykohan/2021/09/23/nike-prices-to-rise-amid-supply-chain-issues-while-profits-increase-23/?sh=5d3021df47fd (accessed on 30 October 2025).
- Guo, L. The benefits of downstream information acquisition. Mark. Sci. 2009, 28, 457–471. [Google Scholar] [CrossRef]
- Mittendorf, B.; Shin, J.; Yoon, D.H. Manufacturer marketing initiatives and retailer information sharing. Quant. Mark. Econ. 2013, 11, 263–287. [Google Scholar] [CrossRef]
- Li, P.; Castelo, N.; Katona, Z.; Sarvary, M. Frontiers: Determining the validity of large language models for automated perceptual analysis. Mark. Sci. 2024, 43, 254–266. [Google Scholar] [CrossRef]
- Brand, J.; Israeli, A.; Ngwe, D. Using LLMs for market research. Harvard Business School, 2023, Working Paper Number: 23-062. Available online: https://www.hbs.edu/ris/Publication%20Files/23-062_6bfe7a5b-3ed9-4afd-a4c1-c91b60dd82e5.pdf (accessed on 30 October 2025).
- Xu, F.; Wang, X.; Chen, W.; Xie, K. The Economics of AI Foundation Models: Openness, Competition, and Governance. 2024. SSRN:1–31. Available online: https://ssrn.com/abstract=4999355 (accessed on 30 October 2025).
- Lee, H.L.; Whang, S. Information sharing in a supply chain. Int. J. Technol. Manag. 2000, 20, 373–387. [Google Scholar] [CrossRef]
- Li, L.; Zhang, H. Confidentiality and information sharing in supply chain coordination. Manag. Sci. 2008, 54, 1467–1481. [Google Scholar] [CrossRef]
- Shang, W.; Ha, A.Y.; Tong, S. Information sharing in a supply chain with a common retailer. Manag. Sci. 2016, 62, 245–263. [Google Scholar] [CrossRef]
- Ha, A.Y.; Tian, Q.; Tong, S. Information sharing in competing supply chains with production cost reduction. Manuf. Serv. Oper. 2017, 19, 246–262. [Google Scholar] [CrossRef]
- Ha, A.Y.; Tong, S. Contracting and information sharing under supply chain competition. Manag. Sci. 2008, 54, 701–715. [Google Scholar] [CrossRef]
- Ha, A.Y.; Tong, S.; Zhang, H. Sharing demand information in competing supply chains with production diseconomies. Manag. Sci. 2011, 57, 566–581. [Google Scholar] [CrossRef]
- Yoon, D.H. Supplier encroachment and investment spillovers. Prod. Oper. Manag. 2016, 25, 1839–1854. [Google Scholar] [CrossRef]
- Zhao, D.; Li, Z. The impact of manufacturer’s encroachment and nonlinear production cost on retailer’s information sharing decisions. Ann. Oper. Res. 2018, 264, 499–539. [Google Scholar] [CrossRef]
- Cai, K.; He, S.; He, Z. Information sharing under different warranty policies with cost sharing in supply chains. Int. Trans. Oper. Res. 2020, 27, 1550–1572. [Google Scholar] [CrossRef]
- Jain, A.; Sohoni, M. Should firms conceal information when dealing with common suppliers? Nav. Res. Logist. (NRL) 2015, 62, 1–15. [Google Scholar] [CrossRef]
- Li, L. Information sharing in a supply chain with horizontal competition. Manag. Sci. 2002, 48, 1196–1212. [Google Scholar] [CrossRef]
- Zhang, H. Vertical information exchange in a supply chain with duopoly retailers. Prod. Oper. Manag. 2002, 11, 531–546. [Google Scholar] [CrossRef]
- Nair, G.; Pleasance, D. Mitigating channel conflict. McKinsey Q. 2005, 3, 16–17. [Google Scholar]
- Tannenbaum, J. Franchisees Resist Poaching via Software, Kiosks, Internet; Dow Jones Company: New York, NY, USA, 1995. [Google Scholar]
- Tedeschi, B. E-Commerce Report; Traditional Manufacturers Are Grappling with the Pros and Cons of Direct Sales on the Internet. The New York Times, 3 January 2000. [Google Scholar]
- Zhang, S.; Zhang, J.; Zhu, G. Retail service investing: An anti-encroachment strategy in a retailer-led supply chain. Omega 2019, 84, 212–231. [Google Scholar] [CrossRef]
- Cattani, K.; Gilland, W.; Heese, H.S.; Swaminathan, J. Boiling frogs: Pricing strategies for a manufacturer adding a direct channel that competes with the traditional channel. Prod. Oper. Manag. 2006, 15, 40–56. [Google Scholar] [CrossRef]
- Fu, F.; Chen, S.; Yan, W. The implications of supplier encroachment via an online platform. RAIRO-Oper. Res. 2022, 56, 529–564. [Google Scholar] [CrossRef]
- Guan, X.; Liu, B.; Chen, Y.J.; Wang, H. Inducing supply chain transparency through supplier encroachment. Prod. Oper. Manag. 2020, 29, 725–749. [Google Scholar] [CrossRef]
- Ha, A.Y.; Tong, S.; Wang, Y. Channel structures of online retail platforms. Manuf. Serv. Oper. Manag. 2022, 24, 1547–1561. [Google Scholar] [CrossRef]
- Hotkar, P.; Gilbert, S.M. Supplier encroachment in a nonexclusive reselling channel. Manag. Sci. 2021, 67, 5821–5837. [Google Scholar] [CrossRef]
- Hsieh, C.C.; Putera, R.R. Product rollover and direct sales decisions in dual-channel supply chains. RAIRO-Oper. Res. 2022, 56, 2203–2220. [Google Scholar] [CrossRef]
- Jiang, J.; He, C. Low-price guarantees in a dual channel of distribution. Mark. Sci. 2021, 40, 765–782. [Google Scholar] [CrossRef]
- Liu, B.; Guan, X.; Wang, Y. Supplier encroachment with multiple retailers. Prod. Oper. Manag. 2021, 30, 3523–3539. [Google Scholar] [CrossRef]
- Liu, J.; Wu, X.; Yang, B.; Yang, S. Suppliers’ online channel structure strategies under product innovation effect and spillover effect. RAIRO-Oper. Res. 2022, 56, 3341–3365. [Google Scholar] [CrossRef]
- Pei, Y.; Li, M. Manufacturer encroachment and promotional effort on a hybrid online retailing platform. RAIRO-Oper. Res. 2025, 59, 2003–2030. [Google Scholar] [CrossRef]
- Shi, S.; Wang, C.; Cheng, T.E.; Liu, S. Manufacturer encroachment with an e-commerce division. Prod. Oper. Manag. 2023, 32, 2002–2019. [Google Scholar] [CrossRef]
- Tsay, A.A.; Agrawal, N. Channel conflict and coordination in the e-commerce age. Prod. Oper. Manag. 2004, 13, 93–110. [Google Scholar] [CrossRef]
- Zheng, B.; Yu, N.; Jin, L.; Xia, H. Effects of power structure on manufacturer encroachment in a closed-loop supply chain. Comput. Ind. 2019, 137, 106062. [Google Scholar] [CrossRef]
- Li, T.; Xie, J.; Zhao, X.; Tang, J. On supplier encroachment with retailer’s fairness concerns. Comput. Ind. Eng. 2016, 98, 99–512. [Google Scholar] [CrossRef]
- Xue, M.; Zhang, J. Supply chain encroachment with quality decision and different power structures. RAIRO-Oper. Res. 2020, 54, 693–718. [Google Scholar] [CrossRef]
- Zhang, L.H.; Tian, L.; Chang, L.Y. Equilibrium strategies of channel structure and rfid technology deployment in a supply chain with manufacturer encroachment. Int. J. Prod. Res. 2021, 60, 1890–1912. [Google Scholar] [CrossRef]
- Li, Y.; Ma, J.; Liu, Y. Study on the complexity of channel pricing game in showrooming o2o supply chain. RAIRO-Oper. Res. 2022, 56, 3373–3392. [Google Scholar] [CrossRef]
- Qi, L.; Song, H.; Xiao, W. Coopetition in platform-based retailing: On the platform’s entry. Manag. Sci. 2024, 71, 3641–4531. [Google Scholar] [CrossRef]
- Li, H.; Lu, J.; Yan, N.; Lai, K.K. Manufacturer encroachment with consumer digital privacy in dual-channel supply chains. Int. J. Ind. Eng. Comput. 2025, 16, 825–846. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S.; Zhang, S.; Dai, R. Manufacturer encroachment with quality decision under asymmetric demand information. Eur. Oper. Res. 2019, 273, 217–236. [Google Scholar] [CrossRef]
- Hao, Z.; Jiang, L. Direct selling by suppliers improves system-wide information flow. Oper. Res. Lett. 2019, 47, 305–310. [Google Scholar] [CrossRef]
- Wang, J.; Zhuo, W. Strategic information sharing in a supply chain under potential supplier encroachment. Comput. Ind. Eng. 2020, 150, 106880. [Google Scholar] [CrossRef]
- Sun, X.; Tang, W.; Chen, J.; Li, S.; Zhang, J. Manufacturer encroachment with production cost reduction under asymmetric information. Transp. Part E Logist. Transp. Rev. 2019, 128, 191–211. [Google Scholar] [CrossRef]
- Sun, X.; Tang, W.; Zhang, J.; Chen, J. The impact of quantity-based cost decline on supplier encroachment. Transp. Res. Part E Logist. Transp. Rev. 2021, 147, 102245. [Google Scholar] [CrossRef]
- Huang, S.; Chen, S.; Guan, X. Retailer information sharing under endogenous channel structure with investment spillovers. Comput. Ind. 2020, 142, 106346.1–106346.16. [Google Scholar] [CrossRef]
- Zhang, Q.; Tang, W.; Zaccour, G.; Zhang, J. Should a manufacturer give up pricing power in a vertical information-sharing channel? Eur. J. Oper. Res. 2019, 276, 910–928. [Google Scholar] [CrossRef]
- Yan, Y.; Hou, F.; Zhang, H. Demand forecast information sharing with manufacturer encroachment. RAIRO-Oper. Res. 2024, 58, 2421–2443. [Google Scholar] [CrossRef]
- Hou, R.; Li, W.; Lin, X.; Zhao, Y. Impact of quality decisions on information sharing with supplier encroachment. RAIRO-Oper. Res. 2022, 56, 145–164. [Google Scholar] [CrossRef]
- Qi, Y.; Ye, T.; Zhang, G. Manufacturer encroachment and extended warranty provision. RAIRO-Oper. Res. 2024, 58, 4717–4740. [Google Scholar] [CrossRef]
- Ha, A.Y.; Luo, H.; Shang, W. Supplier encroachment, information sharing, and channel structure in online retail platforms. Prod. Oper. Manag. 2022, 31, 1235–1251. [Google Scholar] [CrossRef]
- Li, G.; Tian, L.; Zheng, H. Information sharing in an online marketplace with co-opetitive sellers. Prod. Oper. Manag. 2021, 30, 3713–3734. [Google Scholar] [CrossRef]
- Guan, H.; Yang, Z.; Gurnani, H. Value of information with manufacturer encroachment. Prod. Oper. Manag. 2023, 32, 780–793. [Google Scholar] [CrossRef]
- Li, Z.; Wang, B. Retailer information sharing under manufacturer encroachment and production cost reduction. Manag. Decis. 2025, 46, 602–626. [Google Scholar] [CrossRef]
- Hu, X.; Guan, Z.; Ren, J. The retailer’s information sharing decisions with manufacturer’s encroachment and production learning effects. RAIRO-Oper. Res. 2025, 59, 771–802. [Google Scholar] [CrossRef]
- Li, L.; Zhang, H. Supply chain information sharing in a competitive environment. In Supply Chain Structures: Coordination, Information and Optimization; Song, J.S., Yao, D.D., Eds.; Kluwer Academic Publishers: Norwell, MA, USA, 2002; pp. 161–206. [Google Scholar]
- Li, L. Cournot oligopoly with information sharing. Rand J. Econ. 1985, 16, 521–536. [Google Scholar] [CrossRef]
- Ericson, W.A. A note on the posterior mean of a population mean. J. R. Stat. Soc. Ser. B (Methodol.) 1969, 31, 332–334. [Google Scholar] [CrossRef]
- Gal-Or, E. First mover advantages with private information. Rev. Econ. Stud. 1987, 54, 279–292. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).