DSDEVS-Based Simulation Acceleration with Event Filtering: USV Naval Combat Case

Abstract

This study presents a DSDEVS-based method to accelerate simulation execution for AI training in USV (Unmanned Surface vehicle) naval combat scenarios. The proposed approach introduces an event filtering technique that selectively suppresses low-importance sensing events based on the distance to enemy targets. By dynamically adjusting structural couplings and modifying sensing frequency through domain-specific thresholds, the method reduces execution time while maintaining a balance between speed and fidelity. Two key parameters—Event Filtering Distance (EFD) and Sensor Acceleration Time Advance (SATA)—enable conditional event filtering and time advance adjustments within the sensor model. Experimental results demonstrate a 3.03 improvement in runtime, highlighting the effectiveness of the method and the trade-off between simulation speedup and fidelity.

1. Introduction

The Discrete Event System Specification (DEVS) formalism [1] provides a modular and hierarchical framework for modeling and simulating discrete event systems (DESs). As an event-driven formalism, it enables efficient execution by handling changes only at discrete event points making it particularly suitable for applications such as manufacturing systems, communication networks, logistics, and military simulations. DEVS promotes model reusability and composability, which enhances the scalability and maintainability of large-scale simulation models.

However, classical DEVS assumes a static structure throughout the simulation runtime. This limitation makes it challenging to model systems that inherently require dynamic structural changes, such as the creation or deletion of components, reconfiguration of subsystems, or changes in coupling relationships. As modern systems increasingly demand adaptive and reconfigurable behavior, this rigidity in structural modeling becomes a significant constraint on the applicability of conventional DEVS.

To overcome the rigidity of classical DEVS in dynamic environments, the Dynamic Structure Discrete Event System Specification (DSDEVS) [2] extends the DEVS formalism to support runtime structural reconfiguration. DSDEVS enables the dynamic addition or removal of model components and the changes of couplings, offering enhanced flexibility and adaptability. These features make it particularly suitable for modeling autonomous systems, intelligent manufacturing, and adaptive traffic control. Moreover, DSDEVS has emerged as a promising simulation framework for reinforcement learning (RL) applications, where adaptability and efficient data generation are critical.

As simulation is increasingly used as a data generation tool for AI training, execution efficiency has become a critical concern. Training AI agents, particularly in complex multi-agent environments like naval combat, requires a large number of simulation episodes to ensure sufficient exploration and convergence. However, the computational cost of running these simulations—especially when using detailed models with real-time interactions—can become a major bottleneck in the overall training process. This necessitates simulation acceleration methods that can reduce execution time without compromising fidelity, enabling faster iteration and more scalable learning frameworks.

While DSDEVS provides powerful mechanisms for structural adaptation, simulations based on this formalism often suffer from increased modeling complexity and frequent inter-model communication, which can lead to long execution times. While this poses a performance challenge, we exploit the structural flexibility of DSDEVS to address it directly. We introduce a selective event sampling mechanism, referred to as Event Filtering, which dynamically adjusts couplings and message propagation during simulation to reduce computational overhead while preserving essential system behavior.

In particular, when DSDEVS-based simulations are used for reinforcement learning, the proposed event filtering directly enhances sample efficiency by reducing the wall-clock time of each training episode. In reinforcement learning (RL) environments, the efficiency of data generation is a key factor that determines the overall learning speed. Since proposed method, event filtering can reduce unnecessary event exchanges without altering the underlying model logic, they allow faster generation of training data through accelerated simulation runs. This enables agents to collect a larger number of interaction samples within the same computational budget, thereby improving sample efficiency in AI training. Therefore, event filtering can provide sample efficiency for faster training data generation and may be more effective in online reinforcement learning than offline reinforcement learning.

This research focuses on a distributed naval combat simulation scenario, where multiple friendly unmanned surface vehicles (USVs) are deployed to detect, track, and engage enemy USVs approaching a protected zone. Each USV operates autonomously based on local sensing and decision-making, with constraints on communication and sensor range.

This scenario captures key challenges of autonomous naval combat scenario, including decentralized control, limited sensing, real-time coordination, and perceptual uncertainty. These factors lead to frequent and dense message transmissions between sensor and control entities, which significantly increase computational demands during simulation. To address this issue, we propose an adaptive message filtering and structural control mechanism based on the DSDEVS formalism, termed Event Filtering, which selectively reduces simulation workload while preserving critical engagement dynamics.

In this study, we introduce a novel method for execution acceleration in DSDEVS-based simulations by leveraging event importance. Traditional DEVS simulations treat all events equally, resulting in high communication overhead. However, not every event significantly influences the simulation outcome. By prioritizing critical events and reducing the frequency of less impactful ones, our approach significantly reduces computational overhead while maintaining a high level of simulation fidelity. This enables more scalable and efficient simulation environments, especially for AI learning-based applications.

2. Backgrounds

2.1. DEVS and DSDEVS Formalism

Discrete Event System Specification (DEVS) is a formal framework designed to model discrete event systems (DES) with hierarchical and modular structures [1,3]. It defines system behavior using two core abstractions: the atomic model and the coupled model. By combining these two components, DEVS enables structured modeling of complex systems in a scalable and organized manner. The atomic model specifies the behavior of basic components, while the coupled model represents the composition and interaction of multiple atomic or coupled submodels. The standard specifications of these models are described as follows.

The formal definition of an atomic model (AM) in the DEVS formalism is given as:

$$AM=\langle X,Y,S,{\delta }_{ext},{\delta }_{int},\lambda ,ta\rangle$$

where

• X: Set of input events;
• Y: Set of output events;
• S: Set of states;
• ${\delta }_{ext}:Q\times X\to S$: External transition function, with $Q=\left\{\right(s,e)\mid s\in S,0\le e\le ta(s\left)\right\}$;
• ${\delta }_{int}:S\to S$: Internal transition function;
• $\lambda :S\to Y$: Output function;
• $ta:S\to {\mathbb{R}}_0^{+}\cup \{\infty \}$: Time advance function.

The coupled model (CM), which organizes multiple atomic or coupled submodels into a single system, is formally defined as:

$$CM=\langle X,Y,M,EIC,EOC,IC,SELECT\rangle$$

where

• X: Set of external input events;
• Y: Set of output events;
• M: Set of component models;
• $EIC\subseteq X\times {\bigcup }_{m\in M}m.X$: External input coupling relations;
• $EOC\subseteq {\bigcup }_{m\in M}m.Y\times Y$: External output coupling relations;
• $IC\subseteq {\bigcup }_{m\in M}m.Y\times {\bigcup }_{n\in M}n.X$: Internal coupling relations;
• $SELECT:2^M-\mathrm{\varnothing }\to M$: Tie-breaking function for simultaneous events.

The Dynamic Structure DEVS (DSDEVS) formalism extends the classical DEVS framework to support structural change during simulation execution [2]. This allows models to dynamically add, remove, or reconfigure components and coupling relations within a DEVS coupled model. To enable this capability, DSDEVS introduces a new abstract entity called the network executive, which maintains the current structural configuration of the model network as part of its internal state.

A DSDEVS dynamic structure network, referred to as DSDEVN, is defined as follows:

$$DSDEVN=\langle \chi ,M_{\chi }\rangle$$

where

• $\chi$: The network executive;
• $M_{\chi }=\langle X_{\chi },Y_{\chi },S_{\chi },{\delta }_{ex{t}_{\chi }},{\delta }_{in{t}_{\chi }},{\lambda }_{\chi },t{a}_{\chi }\rangle$: The behavioral model of the executive $\chi$;
• $S_{\chi }=\langle X_{\Delta },Y_{\Delta },M_{\Delta },EI{C}_{\Delta },EO{C}_{\Delta },I{C}_{\Delta },Selec{t}_{\Delta }\rangle$: The structural state of the DSDEVS model network.

2.2. Related Works

DEVS (Discrete Event System Specification) provides a modular and hierarchical framework for system modeling, and has been widely used across various simulation domains [1]. However, as the complexity of DES-based models increases, the corresponding growth in execution time significantly limits their applicability to large-scale or real-time scenarios, making execution time a key bottleneck. To address this challenge, numerous approaches have been proposed to accelerate DES-based simulations.

Distributed execution environments such as DEVS/CORBA were introduced to support scalable supply chain simulations [4], and Amdahl’s law was revisited to analyze the theoretical performance limit of distributed simulation [5]. Several approaches have focused on leveraging parallel computing structures to accelerate simulation. Trabes and Wainer proposed a shared-memory parallel algorithm for DEVS simulations [6], while Liu and Wainer explored multi-grained parallelism in compute-intensive DEVS models [7]. Himmelspach et al. implemented a distributed architecture for Parallel DEVS models [8], and Cardenas et al. further enhanced performance using shared-memory-based DEVS execution algorithms [9].

Multi-resolution modeling (MRM) has also been introduced as a strategy to balance simulation accuracy and execution speed, by adjusting the level of model granularity [10,11]. These studies mainly focus on structural or platform-level enhancements to reduce the computational burden of large-scale DEVS models.

While the above studies focus on accelerating DEVS-based simulators, other approaches beyond the DEVS formalism have also been explored in the discrete-event simulation (DES) domain. For example, Wang and Tropper applied reinforcement learning to optimize time warp simulation [12], and NetSquid presented an efficient discrete-event simulation framework for quantum networks, demonstrating scalable and accurate event scheduling [13]. The DONS simulator was also introduced as a high-performance DES system using event coalescing and batching strategies [14]. While these approaches Ware not DEVS-specific, their principles inform the design of runtime event filtering and event suppression.

Surrogate-based optimization (SBO) has emerged as another class of techniques for improving simulation efficiency. Hong and Zhang [15] review the use of surrogate models to approximate expensive simulation outputs and guide optimization. Surrogate models have also been combined with evolutionary algorithms for high-dimensional, computation-intensive problems [16]. These methods reduce the number of expensive simulation evaluations by learning predictive models that estimate performance metrics.

More recent research explores the integration of DEVS and machine learning. Saadawi and Wainer [17] proposed a machine-learning-based regression model to approximate repeated DEVS components, thereby reducing computation, but did not engage in runtime event importance evaluation or suppression. Capocchi and Santucci [18] demonstrated the integration of DEVS-based simulation with reinforcement learning agents, showing that adaptive control can be embedded within DES environments.

While these prior studies have significantly advanced the performance and scalability of simulation systems, most of them focus on hardware-oriented parallelization strategies, static model abstraction, or simulation-level optimization. However, relatively little attention has been given to runtime event-level control based on contextual event importance—especially within scenarios requiring adaptive fidelity management such as real-time naval combat simulations. Furthermore, few approaches integrate dynamic structural adjustments at runtime based on learned or rule-based evaluation of message relevance.

To address these limitations, we propose an event filtering method (formerly referred to as event filtering) that suppresses low-importance events based on rule-based criteria. Unlike conventional static optimization techniques, this method leverages the capabilities of DSDEVS to dynamically control couplings and filter events during runtime, enabling a more adaptive trade-off between computational efficiency and simulation fidelity.

In distributed simulation, HLA Data Distribution Management (DDM) provides a mechanism for controlling inter-federate data exchange by defining routing spaces and subscription regions. According to the IEEE 1516.2 Standard [19], DDM configurations such as attributes and routing spaces are specified in the Federation Object Model (FOM) prior to execution and remain fixed during runtime, permitting only the modification of region boundaries. As a result, DDM improves network-level communication efficiency but cannot modify the internal structure of simulation models.

Several studies have attempted to enhance the filtering efficiency of HLA DDM. Tan et al. [20] proposed an agent-based DDM that employs intelligent agents to filter data at the publisher side, thereby reducing redundant inter-federate messages. Their results demonstrated a significant reduction in communicated messages compared with traditional region-based and grid-based DDM, but the overall simulation processing time increased due to agent-management overhead. This finding indicates that DDM-based approaches are effective for improving communication efficiency yet limited in terms of runtime performance.

By contrast, the proposed DSDEVS-based event-filtering method operates within a single simulator, where coupling relationships between models can be changed during simulation execution to control event propagation. This model-level structural control reduces unnecessary event generation before propagation occurs, directly improving computational efficiency and simulation runtime. Such execution efficiency is particularly advantageous in AI-training environments, where simulations must be executed repeatedly for policy learning and validation.

This study addresses the USV combat system. Recent studies have focused on improving the autonomy and coordination of unmanned maritime systems through advanced control strategies. For example, prescribed-performance and robust control schemes have been applied to USV and USV–UAV cooperation problems to guarantee bounded tracking errors and stable coordination under environmental disturbances [21,22,23]. These works highlight ongoing progress in ensuring stability and performance for autonomous vehicle operations in maritime environments. While such control-oriented research focuses on agent-level behavior design, the present study complements this direction by developing a scalable simulation framework that enables rapid experimentation and validation of these algorithms.

3. USV Naval Combat Model Development

In this study, we developed a DES based naval combat simulator with DEVS formalism to serve as a testbed for execution efficiency optimization. The simulator models combat scenarios involving friendly Unmanned Surface Vehicles (USVs) and enemy USVs. The core purpose of the simulation is to capture the operational dynamics of USVs as they detect, maneuver toward, and engage enemy USVs using onboard sensors and autonomous decision-making. The system is designed to support large-scale engagements involving numerous agents, enabling the study of distributed behavior in naval warfare contexts. The ultimate objective of the simulator is to support the development of optimal engagement strategies by training AI-based algorithms within the simulated environment. This goal necessitates a large number of simulation runs, making execution efficiency a critical requirement for the system.

3.1. USV Naval Combat Scenario

The simulation scenario employed in this study represents a distributed naval engagement environment. In this setup, 20 friendly unmanned surface vehicles (USVs) are deployed with the objective of intercepting 20 approaching enemy USVs before they reach designated target areas. Each USV autonomously detects, tracks, and engages enemy units using onboard sensors and control logic. Figure 1 shows the progress of the scenario.

At the beginning of the simulation, the enemy USVs depart from predefined locations and move toward their respective destinations. These adversarial units do not perform detection or counterattacks; rather, they follow static, predetermined trajectories. In Figure 1, the enemy USVs can be seen maneuvering along orange trajectories from their initial positions (red circles) toward their target positions (gray squares).

Meanwhile, the 20 friendly USVs are positioned across the sea and begin to operate as soon as the simulation starts, using their sensors to detect and pursue enemy USVs to eliminate the threat. In Figure 1, 20 friendly USVs, indicated by blue dots, are shown waiting at their initial positions. The pink line denotes the operational boundary that should not be crossed prior to mission commencement; after the operation begins, this boundary is redefined as the permissible area.

Each friendly USV determines its engagement target through a distance-based selection process. For every adversarial USV detected within the sensor range, the Euclidean distance is calculated. Among the detected set, the adversarial unit with the minimum distance is designated as the target. The movement objective of the friendly USV is updated toward the position of this target, and firing is initiated once the designated adversarial unit enters the engagement range. The USVs are initialized with 200 rounds of ammunition and fire one round per second at their selected target. The probability of a successful hit is determined by predefined firing parameters, which consider factors such as the distance and relative orientation to the target. When an enemy USV is hit, it is considered neutralized and remains stationary at its last known position. The simulation concludes when all 20 enemy USVs are either neutralized or have successfully reached their respective target positions (gray squares in Figure 1).

Each USV selects its target independently based on proximity. Consequently, multiple friendly USVs may engage the same adversarial unit simultaneously, resulting in many-to-one engagements. This behavior arises naturally from the independent decision-making process of each USV. Although mission assignment or conflict resolution algorithms could be introduced in future work to improve the scenario, the contribution of this study lies in improving the execution of a fixed scenario rather than modifying the scenario itself.

This scenario encapsulates the essential characteristics of decentralized, multi-agent maritime operations, where each USV makes decisions based solely on local sensing data and event-driven control logic. The simulation is implemented using a fully event-driven DSDEVS model, in which communication between system components—such as sensor and maneuver modules—occurs via frequent event messages.

While this modeling approach enables high-fidelity representation of engagement dynamics, it also introduces considerable execution overhead, particularly as the number of agents increases.

Therefore, the main challenge lies not only in accurately modeling the combat behavior, but also in efficiently managing the simulation execution under high message density. This makes the scenario a suitable testbed for evaluating event importance estimation and coupling regulation techniques.

3.2. USV Naval Combat System Modeling

The simulation adopts a hierarchical modeling framework built upon the DSDEVS formalism to realistically represent the complexity of maritime combat environments. As an extension of the traditional DEVS methodology, DSDEVS enables structural reconfiguration during simulation runtime, providing greater flexibility and scalability in dynamic operational settings.

The simulation model constructed in this work is composed primarily of friendly USV entities and enemy USV entities, organized in a hierarchical manner to represent their operational interactions. This layered architecture facilitates modular development and clear separation of functional components, allowing for seamless integration of sensing, decision-making, and engagement behaviors within the simulation environment.

3.2.1. Structural Modeling

The hierarchical modeling structure as depicted in Figure 2, supports multi-level abstraction, capturing both the behavior of individual units (USVs and enemy USVs) and the overall dynamics of the simulated battlespace. At the top-level root model, global environmental parameters and the general combat scenario are defined. The middle layer governs the strategic navigation and mission-level behavior of each platform. At the lowest level, fine-grained behaviors are implemented using atomic models, providing detailed control over individual entity actions.

Each USV and enemy USV in the simulation shares a common structural model, but they differ in the internal logic of their Command & Control (C2) atomic models. The USV model incorporates a more sophisticated decision-making system that allows it to detect enemy movements and respond accordingly. In contrast, the enemy USV model follows a predetermined path toward its objective, operating with a simplified control mechanism.

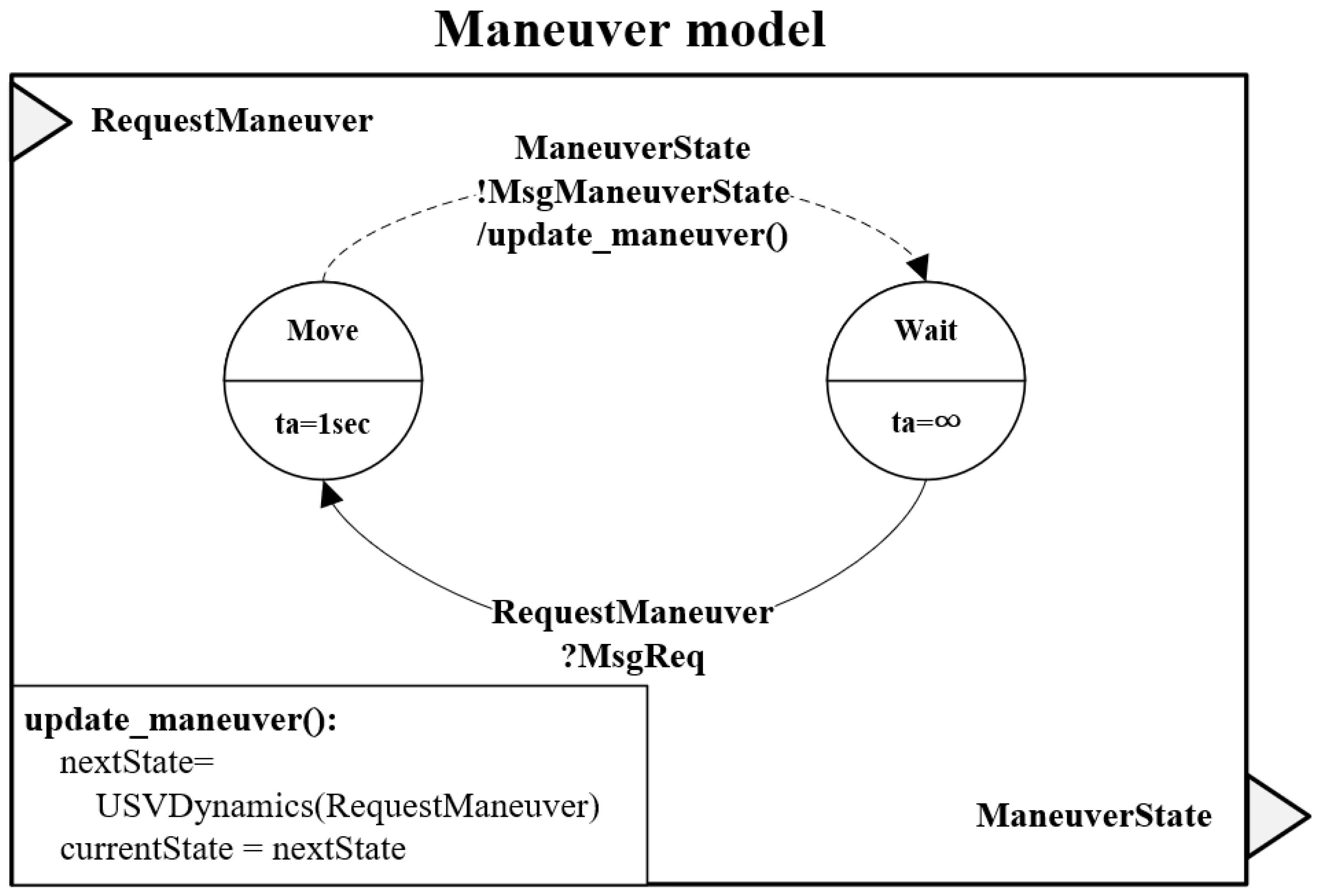
As illustrated in Figure 3, these entities interact through the exchange of ManeuverState and DamageState messages, enabling the simulation to reflect real-time engagement dynamics with high accuracy.

In the proposed model, each USV updates and transmits its position information at every internal transition, which occurs according to the model’s predefined time advance. At each such transition, a maneuver state event containing the current position of the USV is generated and broadcast to all adversarial units. This broadcasting is applied uniformly to all adversarial units, and the transmission interval remains constant throughout the simulation.

3.2.2. Behavior Modeling

As illustrated in Figure 4, the USV coupled model consists of four atomic models—Sensor, Gun, Maneuver, and C2 (Command & Control)—each responsible for a specific behavioral function. These atomic models represent the leaf nodes in the hierarchical structure (Figure 2) and operate via event-driven state transitions. The couplings among them collectively define the behavior of an individual USV, and the overall simulation progresses through the interaction of these components.

The Sensor model, shown in Figure 5, begins in the Wait state. Upon receiving a ManeuverState input event, it performs an external transition to the Sensing others state and stores the received data. The model also receives its own motion information through the MyManeuverState input port. Using this data, the model computes the distances to enemy USVs and determines whether they are within radar detection range, which reflects real-world sensing capabilities. Based on this assessment, it performs an internal transition and outputs the sensing result via the ManeuverState_OUT port as a MsgSensorState message, which contains the observed maneuver states of enemy units.

The Maneuver model receives target maneuver commands from the C2 model and updates the USV’s state accordingly. The RequestManeuver input port accepts a MsgReq message containing maneuver instructions. Based on this message, the model calculates and updates the next position and velocity of the USV. The updated state is sent through the ManeuverState output port as a MsgManeuverState, which is transmitted to the Sensor and C2 models as well as the external output port. The internal structure of the Maneuver model is illustrated in Figure A1. The dynamic behavior of the USV is modeled using a simplified kinematic formulation driven by thrust and bank commands. At each simulation step, the position is updated from the current velocity,

$$x_{t+1}=x_t+v_x\Delta t,y_{t+1}=y_t+v_y\Delta t,$$

where $(x,y)$ denote the position and $(v_x,v_y)$ the velocity components. The forward speed is updated as

$$v_{t+1}=v·f+T\Delta t,$$

where v is the current speed, f is the friction coefficient, and T is the thrust command. The velocity components are then determined from the updated speed and bank command,

$$v_x=v_{t+1}cos(\psi +\varphi ),v_y=v_{t+1}sin(\psi +\varphi ),$$

where $\psi$ is the yaw angle and $\varphi$ is the bank command. The yaw is recalculated from the velocity vector as

$$\psi =arctan\left({\displaystyle \frac{v_y}{v_x}}\right).$$

Through this formulation, the USV steers toward the commanded maneuver direction while accounting for thrust and frictional effects. This representation balances physical realism with computational efficiency, making it suitable for large-scale naval combat simulations.

The Gun model initiates its behavior when a firing command message (MsgGunFire) is received through the Gunfire port. The Decide_Fire() function evaluates whether to fire based on the command contents, triggering an external transition to the Fire state. After a predefined delay in the Fire state, the model returns to the Wait state via an internal transition. If the firing condition is satisfied, a MsgDamageAssess message is generated and sent to the corresponding enemy SV through the DamageAssess port. The internal structure of the Gun model is provided in Figure A2.

The C2 (Command and Control) model synthesizes situational awareness by combining enemy position data from the OtherManeuverState port and self-state data from the MyManeuverState port. This information is processed by the produce_behavior function, which generates maneuver and firing commands. Target maneuver commands are transmitted to the Maneuver model, while firing commands are sent to the Gun model. It also receives damage reports from the DamageState port and handles unit neutralization if necessary. A diagram of the C2 model is shown in Figure A3. In contrast, the enemy USV model uses a simplified C2 mechanism. It does not rely on any perception input; instead, it generates maneuver commands based solely on predefined trajectories and does not issue firing commands.

3.3. Event Filtering for Simulation Acceleration

In the proposed simulation, all USVs detect the positions of enemy USVs at fixed intervals, continuously updating sensing data. While this ensures responsiveness, it also increases message traffic and computational load, which may significantly degrade simulation performance—especially in scenarios requiring real-time operation or multiple simulation runs for AI training. In particular, detecting distant enemy USVs with a low probability of engagement may introduce unnecessary computational burden. To address this issue, this study applies the Event Filtering method, which dynamically adjusts the sensing frequency based on the relative importance of enemy targets. To address this issue, we apply an event filtering method, which dynamically regulates sensing frequency based on the relative importance of enemy targets. Specifically, event filtering refers to a mechanism that enables or disables couplings based on internal model states or scenario-specific conditions.

Figure 6 illustrates how DSDEVS enables dynamic structural modifications through the event filtering process. The operation can be understood as a sequence of steps ➀–➅ depicted in the figure. First, when a message arrives at the ManeuverState_IN port of the Sensor model ➀, its content is examined, and the EventFilteringFlag port sends a triggering message to the DSDEVS executive ➁. The executive then removes the coupling from ManeuverState_IN to Sensor.ManeuverState_IN ➂, suppressing unnecessary message traffic.

After the predefined time advance elapses, the EventFilteringFlag again signals the executive ➃, which restores the previously removed coupling ➄. Messages can then resume flowing into the Sensor model through the reconnected ManeuverState_IN port ➅.

This sequence of steps represents how event filtering is applied during simulation: the Sensor model monitors incoming messages and signals the executive, while the executive dynamically removes and restores couplings to regulate event propagation without altering the overall model definition.

The Event Filtering method modifies the sensing interval based on the distance between a USV and an enemy USV while dynamically regulating message transmission when necessary. To implement this, the conventional static sensor model was transformed into a DSDEVS-based model. By leveraging DSDEVS, the sensing mechanism and structure of the sensor model can be flexibly adjusted during simulation execution, thereby reducing unnecessary computations while minimizing the impact on simulation accuracy.

A specific threshold, referred to as the Event Filtering Distance (EFD), is defined, and the sensing frequency is adjusted accordingly. USVs normally detect enemy USVs at a standard rate, but when an enemy USV is located beyond the EFD, the sensing frequency is reduced, or message transmission is temporarily suspended. To reduce the sensing frequency, the time advance of the sensor model is increased during this process. This increased time advance is referred to as SATA (Sensing Acceleration Time Advance). Conversely, when an enemy USV enters the EFD, the detection interval returns to its normal state.

During the initial phase, when enemy USVs are still approaching from a long distance, most of them remain outside the EFD, leading to a reduction in detection events and message transmissions. However, as enemy USVs enter the engagement range, detection accuracy becomes critical, and the normal sensing cycle is applied to those within the EFD.

In the process of applying the event filtering method, DSDEVS-based structural change are performed. When an enemy USV is located outside the EFD, the simulator disables the coupling between USVmodel.ManeuverState_IN and Sensor.ManeuverState_IN, effectively suspending message transmission for the duration defined by SATA. This dynamically increases the sensing interval. Conversely, when the enemy enters the EFD, normal sensing resumes, and the coupling is reactivated.

The event filtering method aims to reduce simulation calculation load and improve execution speed by selectively suppressing low-importance events. In this simulator, EFD serves as the threshold for applying event filtering, determined based on the domain characteristics and modeling objectives. Since the simulator is designed to simulate the autonomous decision-making of friendly USVs, EFD is used to identify events unlikely to influence simulation outcomes. SATA complements this by adjusting the time advance of atomic models, reducing internal transitions triggered by those low-importance events.

The dynamic coupling process between the sensor atomic model and the DSDEVS executive is summarized in Algorithm 1. The algorithm operates in a unified event-driven loop where both external and internal events are sequentially processed. When the distance between a sensor $S_i$ and an adversarial unit exceeds the predefined Event Filtering Distance (EFD), the sensor triggers an EventFilteringFlag and holds its operation for the duration of $\mathsf{SATA}$. Upon receiving this signal, the executive temporarily removes all inbound couplings to S_i.ManeuverState_IN, thereby suspending unnecessary event propagation. Once the holding period expires, the couplings are restored, ensuring that the overall system behavior remains consistent while reducing computational overhead during inactive sensing periods.

Algorithm 1: Single-Loop Dynamic Event Filtering and Coupling Control for Sensor $S_i$.

Input: Event list (internal/external), simulation end time $T_{max}$ Data: Event Filtering Distance (EFD), Sensor Acceleration Time Advance ($\mathsf{SATA}$) ${\mathtt{flag}}_{S_i}\in \{\mathtt{TRUE},\mathtt{FALSE}\}\leftarrow \mathtt{FALSE}$; temporary removal list $\mathcal{R}\left(S_i\right)\leftarrow \mathrm{\varnothing }$; nominal time advance ${\tau }_{S_i}^{\mathrm{nom}}$; current time $t\leftarrow 0$

4. Case Study

In this chapter, we conduct a case study using the simulator defined in the previous section. Specifically, we investigate how the two features—EFD (Event Filtering Distance) and SATA (Sensing Acceleration Time Advance)—affect simulation outcomes and execution time when applying Event Filtering to the scenario. The objective is to analyze their influence and provide guidance on selecting appropriate EFD and SATA values to support decision-making within the given scenario.

4.1. Regression Analysis of Event Filtering

This section presents a case study designed to evaluate acceleration performance and fidelity degradation based on acceleration parameters. Specifically, we examine the impact of the Event Filtering method by testing a total of 48 cases, consisting of 8 EFD (Event Filtering Distance) settings and 6 SATA (Sensing Acceleration Time Advance) settings, each replicated 40 times. Experimental results are recorded as CSV logs, and performance measures are derived through log analysis.

Table 1. Experimental design of Case Study.

Variable Name (Unit)	Variation Cases	Implements
EFD (m)	1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000	Distance threshold of operation event filtering
SATA (-)	1, 20, 40, 60, 80, 100	The amount of accelerated time advance activated when event filtering is activated
Total cases	8 × 6 = 48 cases
Complete Experiment Design	48 cases × 40 replications = 1920 experiments

presents the experimental design, including variable names, variation cases, and the implementation details of each variable.

Additionally, this study proposes two performance measures to evaluate simulation speedup and fidelity: Simulation Execution Time (runtime) and Mean Trajectory Distance Discrepancy (MTDD).

Simulation execution time (runtime) is used as the primary performance metric for the proposed Event Filtering method. This measure assesses the efficiency of the simulation execution optimization approach. Under identical hardware conditions, a reduction in simulation execution time indicates that the simulation was executed with a lower computational load.

Additionally, the impact of the optimization method on simulation results is evaluated as a measure of fidelity degradation. Specifically, this study examines the difference in the trajectories of 20 friendly USV models before and after applying the proposed method. This difference is quantified using the Mean Trajectory Distance Discrepancy (MTDD), which serves as an indicator of fidelity loss. The Dynamic Time Warping (DTW) algorithm [24] is employed to compute MTDD. DTW is selected because it can robustly compare two trajectories even when they differ in length or temporal alignment. In naval combat simulations, the movement patterns of USVs may exhibit time shifts or speed variations due to stochastic sensing and decision-making processes. A direct point-to-point comparison at identical time steps could misrepresent the similarity between trajectories when the same maneuver occurs at slightly different times. DTW addresses this by performing a non-linear alignment that minimizes cumulative spatial distance while allowing flexible temporal matching, making it particularly suitable for fidelity assessment in such scenarios.

Although outcome-based indicators such as hit or survival rate also exhibited observable variations under event filtering, their changes were not always proportional to the degree of structural modification. In several cases, different filtering configurations produced nearly identical engagement results despite distinct maneuver patterns, indicating that such discrete outcomes are less effective for analyzing incremental fidelity degradation. In this study, our focus was on examining micro-level behavioral fidelity—that is, how the trajectories of individual agents evolve when event filtering alters their sensing and maneuvering behavior. For this purpose, the Mean Trajectory Distance Discrepancy (MTDD) was selected, as it provides a continuous and sensitive measure that correlates with the extent of message suppression and captures subtle kinematic deviations between baseline and filtered runs. Nevertheless, MTDD mainly reflects geometric and temporal consistency rather than overall mission success. A combined framework that integrates trajectory-based and outcome-based indicators will therefore be explored in future research to enable a more comprehensive multi-scale assessment of simulation fidelity.

The MTDD for a simulation case ‘c’, where an event filtering method is applied, is defined as follows:

$$\begin{array}{cc}\hfill P_{n,i}& =\left\{(x_{n,i}\left(t\right),y_{n,i}\left(t\right))\mid t=0,1,\dots ,T_n\right\}\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill P_{c,i}& =\left\{(x_{c,i}\left(t\right),y_{c,i}\left(t\right))\mid t=0,1,\dots ,T_c\right\}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill d_c\left(i\right)& =DTW(P_{n,i},P_{c,i})\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill MTD{D}_c& ={\displaystyle \frac{1}{B}}\sum _{i\in Blues}{d}_c\left(i\right)\hfill \end{array}$$

(4)

where

• $Blues$: A set of IDs of friendly USVs.
• i: Component of $Blues$, which is ID of USV.
• B: Number of $Blues$ components.
• n: Length of DTW matching path.
• c: Experiment case, n: Non-accelerated case.
• $x_{c,i}\left(t\right),y_{c,i}\left(t\right)$: Longitude, Latitude of USV whose ID is i, at time t and case c.

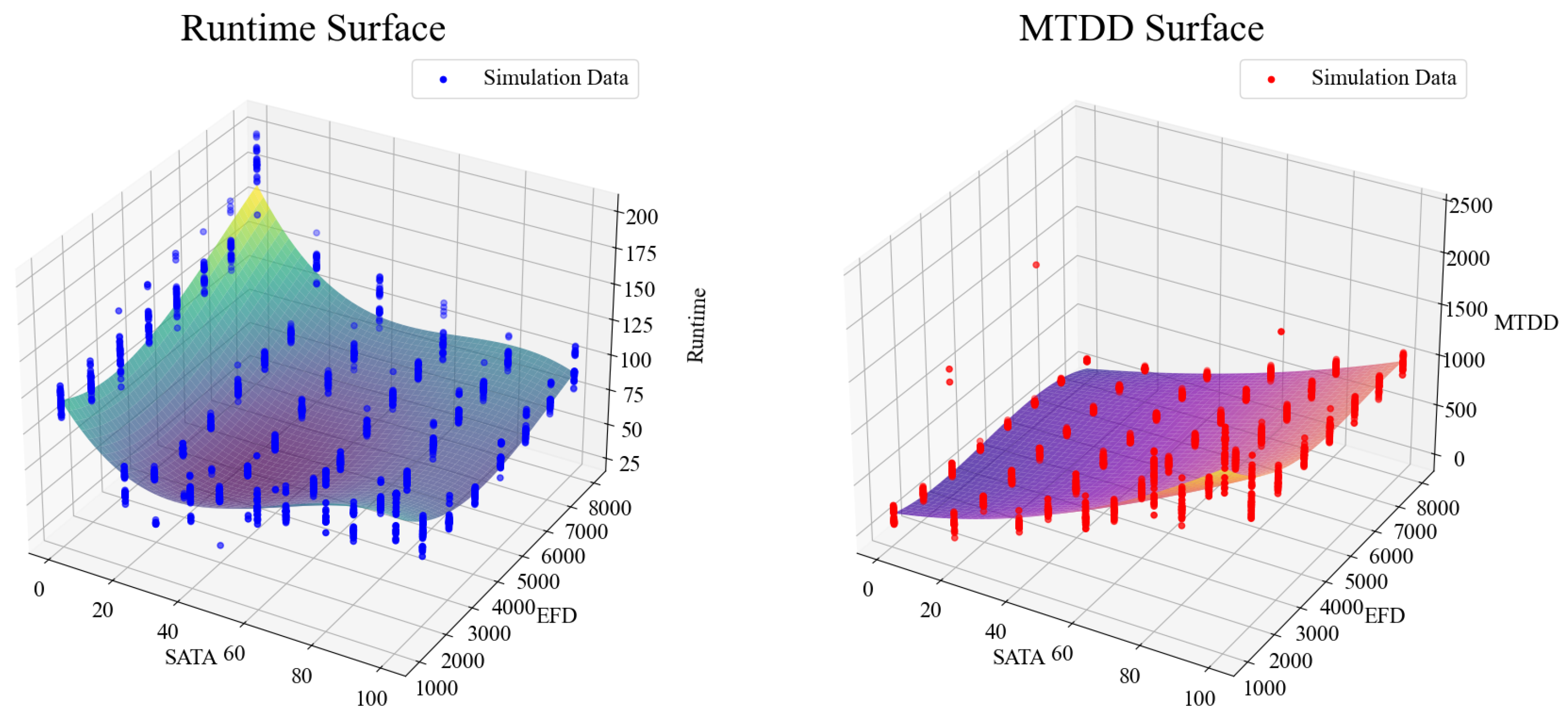
The data collected from the experiments were analyzed to evaluate the impact of acceleration parameters on simulation execution runtime and fidelity. A response surface was plotted in Figure 7 and Figure 8 to examine the trends in simulation runtime with respect to SATA and EFD. The results indicate that simulation runtime decreases as SATA increases and EFD decreases.

However, when SATA and EFD exceed a certain range, runtime begins to increase. This suggests that excessive adjustments to acceleration parameters can have negative effects. From the experimental data, it was observed that SATA values between 20–60 (s) and EFD values between 2000–5000 (m) demonstrated notable acceleration efficiency.

A response surface for the fidelity measure MTDD is presented in Figure 7. The results clearly show that as SATA increases and EFD decreases, MTDD increases significantly, indicating a trade-off between acceleration efficiency and fidelity. As shown in

Table 2. Result of Regression analysis for Runtime and MTDD.

Dependent Variable	Experimental	Coef.	p $>\left|\mathit{t}\right|$	R2 (Adj.R2)
(Model)	Variable
Runtime (linear)	SATA	−0.3825	0.000	0.198 (0.197)
	EFD	0.2264	0.000
Runtime (2nd polynomial)	SATA	−0.3866	0.000	0.397 (0.396)
	EFD	0.2264	0.000
	SATA2	0.2475	0.000
	SATA × EFD	−0.2683	0.000
	EFD2	0.0399	0.015
MTDD (linear)	SATA	0.8921	0.000	0.831 (0.831)
	EFD	−0.1872	0.000
MTDD (2nd polynomial)	SATA	0.8910	0.000	0.859 (0.859)
	EFD	−0.1872	0.000
	SATA2	0.0623	0.000
	SATA × EFD	−0.1270	0.000
	EFD2	0.0301	0.000

, when a second-order polynomial regression was applied, it was observed that SATA has a dominant influence on the increase in MTDD.

Table 2 presents the results of a regression analysis used to construct a meta-model that evaluates how well the acceleration parameters (EFD and SATA) explain the performance measures (runtime and MTDD). The regression coefficients for the runtime model confirm that runtime decreases as SATA increases and EFD decreases.

To examine the statistical significance of parameter effects, a two-way ANOVA was conducted with Event Filtering Distance (EFD) and Sensor Acceleration Time Advance (SATA) as factors. The results, summarized in

Table 3. Two-way ANOVA results showing the effects of Event Filtering Distance (EFD) and Sensor Acceleration Time Advance (SATA) on simulation runtime and fidelity (MTDD). All effects were statistically significant at $p<0.001$, based on 40 replications per configuration.

Dependent Variable	Source	Sum of Squares	df	Mean Square	F	p-Value
Runtime	EFD	$2.72\times {10}^5$	7	$3.89\times {10}^4$	662.079	<0.001
	SATA	$7.42\times {10}^5$	5	1.48$\times {10}^5$	2528.837	<0.001
	EFD×SATA	$1.45\times {10}^5$	35	$4.13\times {10}^3$	70.393	<0.001
	Residual	$1.10\times {10}^5$	1872	$5.87\times {10}^1$
MTDD	EFD	$1.92\times {10}^7$	7	$2.74\times {10}^6$	336.231	<0.001
	SATA	$2.26\times {10}^8$	5	$4.53\times {10}^7$	5552.476	<0.001
	EFD×SATA	$1.40\times {10}^7$	35	$4.01\times {10}^5$	49.163	<0.001
	Residual	$1.53\times {10}^7$	1872	$8.16\times {10}^3$

Note: Two-way ANOVA with 40 replications per configuration. p-values $<0.001$ are shown as “<0.001”.

, show that both main effects and their interaction significantly influenced simulation runtime and fidelity.

For runtime, both EFD and SATA exhibited strong effects ($F=662.079$ and $2528.837$, respectively, $p<0.001$), while their interaction was also significant ($F=70.393$, $p<0.001$).

Similarly, for the fidelity metric (MTDD), both EFD and SATA had statistically significant impacts ($F=336.231$ and $5552.476$, $p<0.001$), along with their interaction term ($F=49.163$, $p<0.001$).

These results confirm that variations in filtering distance and time advance parameters meaningfully affect both the execution performance and trajectory-level fidelity of the simulation. Overall, the ANOVA results quantitatively validate that the proposed event-filtering mechanism is sensitive to the parameter configuration, supporting the experimental trends observed in Figure 7 and Figure 8.

4.2. Detailed Analysis for Case Study

To further investigate the relationship between the previously analyzed acceleration parameters and performance measures, we categorize the acceleration parameters into three levels and examine their effects.

Table 4. Cases extracted based on the level of influence of parameters in the experimental results.

Level	EFD	SATA
Weak	8000	1
Normal	5000	40
Strong	1000	80
EFD 3 case × SATA 3 case = 9 case

presents the EFD and SATA values extracted from the experimental design, classified into three acceleration levels: weak, normal, and strong.

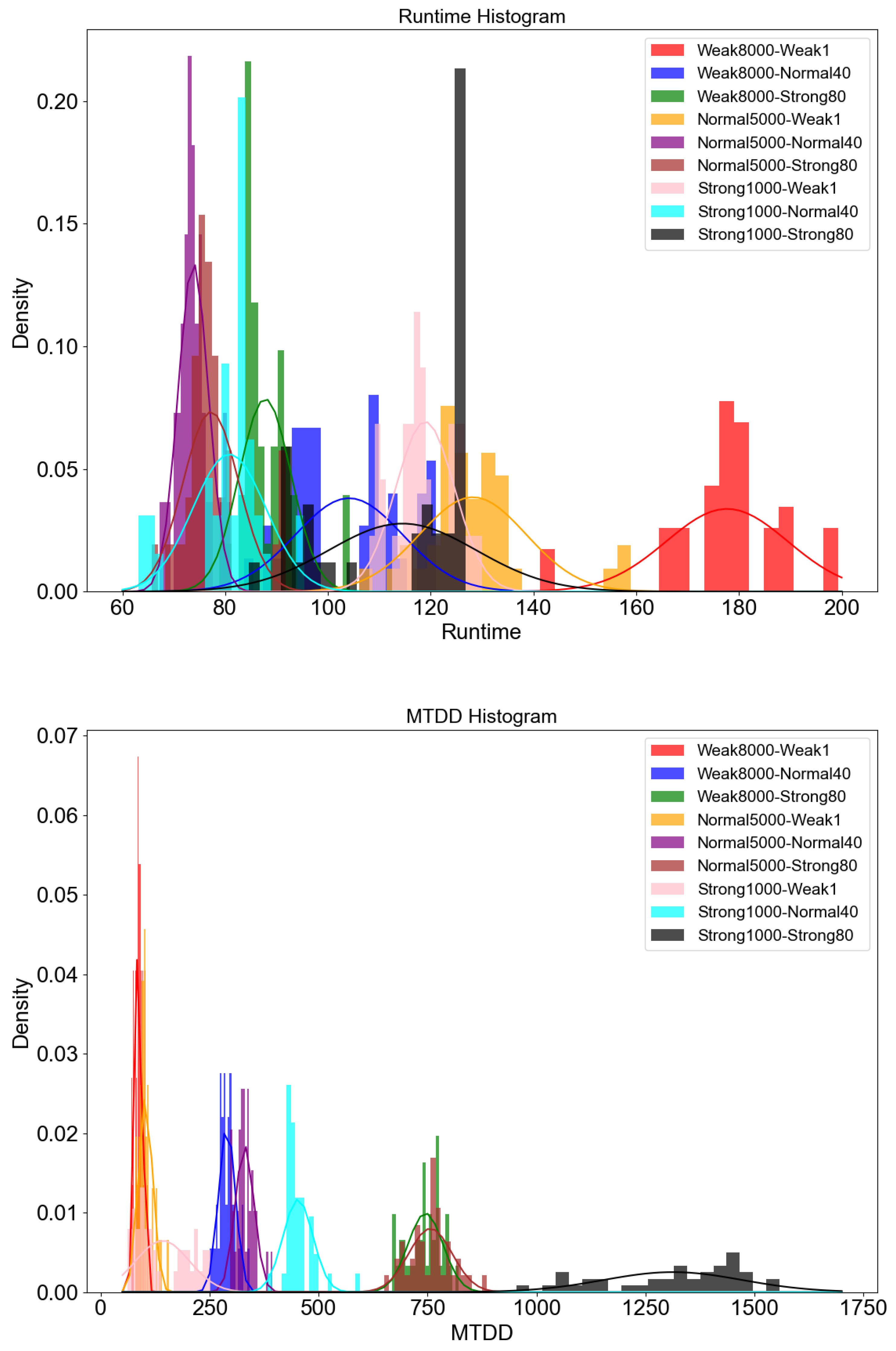
A scatter plot illustrating runtime and MTDD for the nine extracted cases is shown in Figure 9, with each case distinguished by color. Figure 10 presents density histograms for runtime and MTDD across these cases. In the ‘EFD weak-SATA weak’ case (red), MTDD remains around 100, but the runtime is relatively high. As the EFD acceleration level increases (i.e., EFD decreases) through ‘EFD normal-SATA weak’ (orange) and ‘EFD strong-SATA weak’ (pink), runtime improves by an average of 1.41 and 1.49 times, respectively. Conversely, as the SATA acceleration level increases (i.e., SATA increases) through ‘EFD weak-SATA normal’ (blue) and ‘EFD weak-SATA strong’ (green), runtime improves significantly by an average of 1.70 and 2.02 times. However, this improvement comes at the cost of fidelity, as MTDD increases substantially by an average of 3.31 and 8.54 times, respectively, indicating a notable fidelity loss.

Figure 11 depicts the simulation state at the moment when the trajectory error increases in the latter half of the simulation, transitioning from ‘EFD normal-SATA strong’ to ‘EFD strong-SATA strong’ (as shown in Figure 9). When both SATA and EFD acceleration levels are excessively high, it has a significant impact on sensing, which in turn affects both the tracking performance and firing performance of the USV model. As a result, enemy USVs fail to be neutralized, leading to substantial trajectory discrepancies compared to non-accelerated cases.

At higher EFD settings, some enemy USVs were not neutralized during the final stage of engagement. This is because as the filtering interval gets longer, the detection update frequency decreases too much, causing friendly USVs to lose target information when the target leaves the effective detection range. As a result, certain enemy USVs remained undetected or were re-acquired too late for successful interception. This behavioral outcome highlights the trade-off between acceleration and situational awareness in event-filtered simulations.

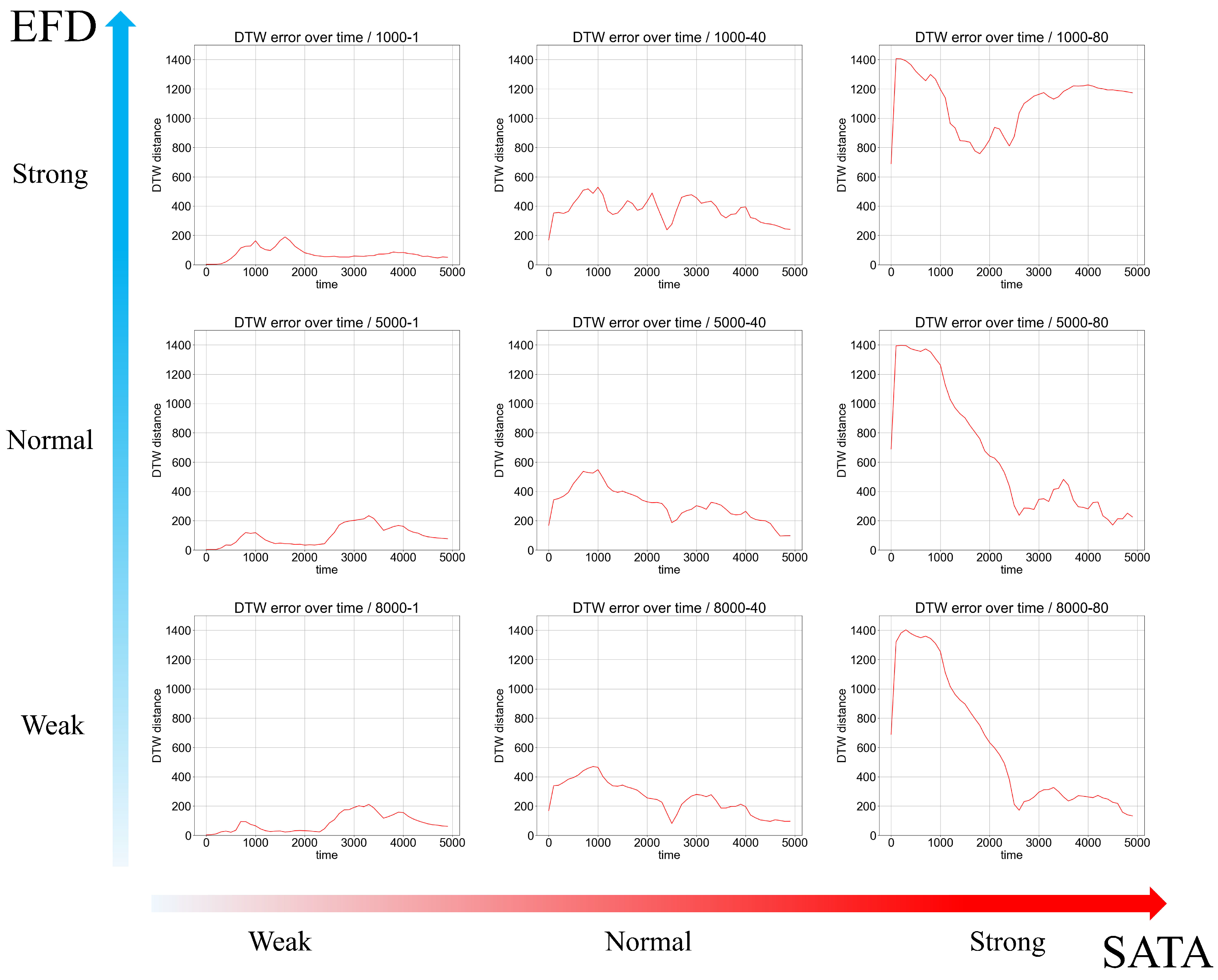
Figure 12 illustrates the trajectory error over time for each acceleration level. The trajectory error is computed by dividing the simulation time into 100-s intervals and calculating MTDD for each segment. The results show that an increase in SATA has a significant impact on trajectory error, which aligns with the analysis in Table 4, where the coefficient for SATA is much larger than that for EFD. In the ‘EFD strong-SATA strong’ case, trajectory error in the later stages of the simulation is noticeably higher compared to cases where EFD is at normal or weak levels. Notably, around the 2000-step mark, situations arise where a small EFD value significantly affects simulation fidelity. To further investigate this phenomenon, the simulator will be utilized for additional validation.

5. Discussion

Although the proposed event filtering method demonstrates notable effectiveness in accelerating DEVS-based simulations, several limitations remain. First, the performance gain is highly dependent on the structural characteristics of each model. Different model configurations or interaction patterns may lead to varying trade-offs between runtime reduction and fidelity loss. Second, the effectiveness of the event filtering mechanism is sensitive to parameter tuning. In this study, parameters such as the Event Filtering Distance (EFD) and Sensor Acceleration Time Advance (SATA) were empirically determined, which may not be optimal for all scenarios. Developing an automated or adaptive parameter tuning strategy would further improve the robustness of the method. One possible direction is to employ optimization or reinforcement learning-based techniques to dynamically identify suitable parameter values during simulation.

Beyond naval combat simulation, the proposed event-filtering approach can be extended to other domains that feature well-structured and human-engineered system architectures. Representative examples include manufacturing systems, smart factory operations, and industrial process simulations, where inter-model dependencies and data flows are explicitly defined. In such environments, dynamic coupling control can selectively reduce redundant communication events without compromising system functionality, thereby improving simulation efficiency. However, applying this method to black-box or purely data-driven systems would be challenging because their internal causal relationships are not directly observable. For these systems, additional interpretability or surrogate modeling mechanisms would be required to identify meaningful event dependencies before structural event filtering can be applied. This distinction highlights that the proposed approach is particularly suited to domains with transparent system logic and well-defined model interactions.

In addition, the proposed event filtering contributes to the stability and robustness of reinforcement learning by expanding the accessible learning domain. By accelerating data generation while maintaining consistent observation and reward semantics, the RL agent can explore a broader range of scenarios within limited computational resources. This improved diversity and density of experience enhances both sample efficiency and training stability, leading to faster and more reliable convergence of learning policies. Therefore, the proposed approach serves as an effective integration point between DSDEVS-based simulation acceleration and AI training pipelines.

The present study assessed simulation fidelity using the Mean Trajectory Distance Discrepancy (MTDD), which captures trajectory-level deviations between baseline and accelerated runs. This trajectory-based metric effectively quantifies micro-level behavioral consistency but does not fully represent higher-level outcomes such as engagement success or survival rate. Since the primary objective of this study was to examine how event filtering influences fine-grained motion behavior, MTDD was considered appropriate for this stage of analysis. Nevertheless, a more comprehensive evaluation of fidelity should account for both kinematic similarity and mission-level effectiveness. Future research will therefore extend the current framework by integrating trajectory-based and outcome-based indicators, enabling a multi-scale assessment that encompasses both continuous behavioral coherence and discrete engagement outcomes across various simulation domains.

6. Conclusions

This study proposed an event filtering method that improves the execution performance of a DEVS-based naval combat simulator by exploiting the structural flexibility of DSDEVSs. The method dynamically adjusts model couplings based on the importance of each event, reducing the computational load while maintaining simulation fidelity. In a USV naval combat scenario, where frequent sensing and communication causes long execution times, the proposed approach significantly shortened runtime without critical degradation of accuracy. The results confirm that DSDEVSs can be effectively used not only for structural modeling but also as a framework for performance optimization in complex event-driven simulations. By properly selecting parameters such as the Event Filtering Distance (EFD) and Sensor Acceleration Time Advance (SATA), the method provides a practical means to balance simulation speed and fidelity.