Abstract
The identification of anomalous data objects within massive datasets is a critical technique in financial auditing. Most existing methods, however, focus on global outlier anomalies detection with less effective in contexts such as Chinese financial budget auditing, where local outliers are often more prevalent and meaningful. To overcome this limitation, a unified outlier detection framework is proposed that integrates both global and local detection mechanisms using k-nearest neighbors (KNN) and kernel density estimation (KDE) methodologies. The global outlier score is redefined as the sum of the distances to the k-nearest neighbors, while the local outlier score is computed as the ratio of the average cluster density to the kernel density—replacing the cutoff distance employed in Density Peak Clustering (DPC). Furthermore, an adaptive adjustment coefficient is further incorporated to balance the contributions of global and local scores, and outliers are identified as the top-ranked objects based on the combined outlier scores. Extensive experiments on synthetic datasets and benchmarks from Python Outlier Detection (PyOD) demonstrate that the proposed method achieves superior detection accuracy for both global and local outliers compared to existing techniques. When applied to real-world Chinese financial budget data, the approach yields a substantial improvement in detection precision-with 38.6% enhancement over conventional methods in practical auditing scenarios.
1. Introduction
Outlier detection is a commonly used approach for the identification of data instances that exhibit significant deviation from the predominant patterns in a dataset [1]. These outliers often possess substantial analytical value, helping researchers discover potential anomalies or underlying issues within the data source [2]. In recent years, outlier detection has expanded significantly across diverse fields, such as financial fraud monitoring, intelligent medical systems, cyber intrusion identification, and industrial fault analysis [3,4]. In particular, clustering-based outlier detection methods exhibit satisfactory detection performance and efficiency compared with other approaches [5,6]. However, the rapid detection of anomalies (or outliers) in large-scale datasets is still challenging in auditing because the outlier definition is often subjective and context-dependent [7,8]. As an illustration, the H Provincial Department of Finance in China received close to forty-three million individual records every month in 2025, encompassing declarations, payments, medical treatments, and related documentation, and some of the data objects may not be outliers from a global perspective. Still, from a local analysis perspective, they are anomalies [9,10]. In this way, heterogeneous massive data poses a significant challenge for auditors to quickly identify suspicious clues in auditing. This is because most clustering-based outlier detection methods are designed from a global perspective, which limits their effectiveness in detecting local outliers [11]. Ramaswamy et al. proposed a distance-based outlier measure derived from the separation between a point and its kth nearest neighbor (KNN) [12]. Subsequently, Breunig developed the local outlier factor (LOF), a metric designed to quantify an object’s relative isolation within its local context [13]. Nonetheless, the precision of these approaches is highly sensitive to the parameter k, and their performance decreases significantly as the number of local outliers increases. As a result, they cannot be directly applied to Chinese finance budget auditing, and the reasons can be ascribed to different criteria for abnormal data in different contexts. For example, the proportion of individual’s payment often fluctuates in finance budget funds. Additionally, only a few studies have focused on local outlier detection in data auditing, yet these problems have not been comprehensively solved [14,15]. There is a pressing need to detect localized anomalies by leveraging the distinctive attributes of auditing datasets.
Based on the above analysis, this study intends to develop a combined outlier detection method from both global and local perspectives. The key idea of our approach is to first compute the local density of data objects using KNN and KDE methods, thereby replacing the local density measure used in the traditional DPC algorithm. Subsequently, the sum of the k-nearest neighbor distances for each data object is utilized as its global outlier factor. Then, a clustering algorithm is employed to determine the cluster densities and identify local outliers. Thereafter, the global and local outlier factors are integrated to generate a comprehensive anomaly score for each data object. Finally, the proposed framework is implemented on a Chinese financial auditing dataset, with its feasibility and effectiveness in identifying anomalous data verified through three metrics: false positive rate, false negative rate, and recommendation quality.
The main contributions of this paper can be summarized as follows:
- Two novel anomaly metrics for each data object are introduced: local exception score (Les) based on kernel density estimation and global exception score (Ges) based on k-nearest neighbor distances, which measure the deviation in a data object from local and global perspectives, respectively.
- A comprehensive anomaly score is defined by combining Ges and Les using an adjustment coefficient α, which adaptively balances the importance of local and global outliers for final detection.
- Extensive comparison with baseline outlier detectors using artificially generated and PyOD benchmark datasets are conducted, and the results demonstrate the effectiveness and feasibility of the proposed method.
- The proposed method is applied to Chinese financial budget auditing datasets, and the results exhibit a notable increase in detection auditing clues in large-scale databases.
The paper is structured as follows. Section 2 surveys existing outlier detection techniques in the literature. Section 3 introduces fundamental concepts and summarizes key prior findings. The core framework and methodology for detecting outliers from both local and global viewpoints are developed in Section 4. Section 5 demonstrates an application of the proposed approach to a Chinese auditing dataset. Finally, Section 6 offers concluding remarks and outlines promising avenues for further investigation.
2. Literature Review
As an entry point for further investigation in auditing, abnormal data (e.g., rare events, deviations from the majority, or exceptional cases) may be more interesting and valuable than the common cases for auditors. Consequently, outlier detection is designed to identify these anomalous instances based on their significant deviations in attributes. In recent years, significant research has been conducted on outlier detection, and great achievements have been made until now. In practical applications of knowledge discovery and data mining (KDD), the limited availability of annotated anomaly instances has led to the widespread adoption of unsupervised techniques as the primary methodology. As a result, existing outlier detection techniques can be broadly categorized into three types: distance-based, density-based, and clustering-based methods.
As a classical distance-based technique, KNN assesses outlier likelihood by measuring the separation between each point and its nearest neighbor. Points are subsequently ranked according to these distances, with the top n candidates identified as outliers [12]. Nevertheless, KNN’s performance tends to be limited when applied to heterogeneous real-world datasets, where implicit data structures and parameter sensitivity pose significant challenges. To address these limitations, Zhang et al. developed the local distance-based outlier factor (LDOF), which quantifies deviation in scattered datasets by evaluating each object’s positional relationship relative to its surrounding neighbors [15]. Separately, Jiawei et al. introduced a mean-shift-based outlier detector (MOD) that reduces outlier-induced bias through data modification [14]. This method substitutes each instance with the average of its k-nearest neighbors, effectively mitigating outlier influence during clustering without requiring prior anomaly knowledge. While the above methods demonstrate excellent performance in detecting global outliers, there are still some limitations, such as poor detection efficacy for local outliers, difficulty in adapting to data of different densities, and significant performance sensitivity to parameter k value.
Compared to distance-based outlier detection methods, density-based approaches exhibit superior performance in identifying local anomalies because neighborhood density can describe the data distribution characteristics. Tang et al. developed a connectivity-based outlier factor (COF) approach, which enhances the performance of conventional LOF method in scenarios where outlier regions exhibit density characteristics similar to those of normal patterns [16]. Nevertheless, neighbor-based outlier detection methods in handling low-density and local density-varying data exhibit poor accuracy and robustness and are overly dependent on parameter settings. Consequently, Zhongping et al. leveraged local density ratios to characterize regional density variations, establishing a novel outlier metric known as the Relative Density Ratio Outlier Factor [17]. Although it can enhance local outlier detection performance with low-density data, the performance will severely decrease when the number of local outliers increases.
Significant progress in cluster-based outlier detection has made it a vibrant and active research field. In reference [18], the cluster-based local outlier factor (CBLOF) was formulated to quantify the substantive significance of anomalies, with an accompanying algorithm designed to enhance the identification of meaningful outliers. Another approach leveraging fuzzy clustering techniques begins by applying the Fuzzy C-Means (FCM) algorithm, after which potential outliers are assessed by monitoring variations in the objective function upon temporary removal of individual data points [19]. A recognized limitation of this methodology, however, is its diminished capacity to detect local outliers within datasets featuring clusters of heterogeneous densities. To overcome this challenge, Zhou et al. introduced the FCM Objective Function-based LOF (FOLOF), which incorporates the elbow criterion to automatically identify the optimal cluster count prior to outlier analysis [20]. The dataset is pruned by the objective function of FCM to obtain the outlier candidate set, and the weighted local outlier factor detection algorithm is used to calculate the outlier degree of each point finally. Yet the above methods are limited by clustering algorithms and have low performance in detecting outliers in datasets of arbitrary shapes. Introduced by Rodriguez in 2014, Density Peaks Clustering (DPC) identifies cluster centers as local density peaks that maintain considerable separation from all data points possessing higher density [21]. Compared to traditional clustering algorithms, the DPC algorithm offers several advantages: it can rapidly identify cluster centers without iterative optimization, adapt to arbitrary cluster shapes, and handle large-scale datasets. Despite these strengths, however, the DPC algorithm still suffers from two main limitations: its dependence on manual parameter setting and its high computational complexity. To address this limitation, reference [22] presented an outlier detection method utilizing a density peak clustering-based outlier factor. This approach employs k-nearest neighbors for density estimation instead of conventional density peaks, incorporates a KD-Tree index for efficient neighbor search, and automatically identifies cluster centers through the product of density and distance metrics [23,24]. This method analyzes the features of each cluster through clustering and detects outliers based on the size of the outlier factors, while avoiding the impact of clustering with different densities on outlier detection. However, it is difficult to determine cluster centers with lower cluster densities using traditional DPC algorithms when data points form clusters with different densities.
Despite the significant achievements in unsupervised outlier detection, existing methods still exhibit several limitations when confronted with the complex demands of real-world applications such as financial auditing [25,26]. (1) There exists a notable disconnect between global and local outlier perspectives. Distance-based methods (e.g., KNN, LDOF) are generally effective at identifying global outliers but perform poorly in detecting local anomalies within scattered or multi-density datasets. While density-based methods (e.g., LOF, COF) excel at finding local outliers, their performance is highly sensitive to parameter settings and deteriorates significantly as the number of local outliers increases. (2) Secondly, the performance of many state-of-the-art detectors remains heavily dependent on and sensitive to specific parameters (particularly the neighborhood size k). This sensitivity poses a substantial challenge in practical scenarios like auditing, where data distribution is often heterogeneous and prior knowledge is scarce, making optimal parameter selection difficult. (3) Thirdly, although clustering-based approaches like DPC and its variants offer advantages in handling arbitrary cluster shapes, they struggle to effectively identify cluster centers and detect local outliers in datasets with complex, varying densities. The inherent limitations of the underlying clustering algorithms directly impact the accuracy of subsequent outlier detection, especially when local outliers reside in low-density regions adjacent to high-density clusters.
As a result, this study proposes a combined global and local outlier detection method based on an improved fast search and discovery density peak clustering algorithm, utilizing KNN and KDE methods, to evaluate the outliers from both global and local perspectives. After that, we apply the proposed method in Chinese audit dataset analysis, validating its effectiveness and feasibility.
3. Preliminaries
KNN is one of the most popular nonparametric clustering techniques using the k-nearest neighbor classification rule (k-NNR) [12]. Following this principle, an unclassified instance is categorized into the class most frequently represented among its k-nearest neighbors within the training dataset. Cover and Hart [27] demonstrated that as both the number of data objects N and the neighborhood size k approach infinity under the condition k/N→0, the classification error of the k-NNR method converges to the theoretically optimal Bayes error rate. And the pairwise Euclidean distances between points in the dataset can be described as in Equation (1).
where xi, xj∈N, xim is the mth attribute of data object xi; xjm is the mth attribute of data object xj; d is the number of data point’s attributes. Obviously, the smaller the distance between two data points, the closer they are. To describe the relationship between the sum of distances from a data point to all its k-nearest neighbors and their spatial distribution, two-dimensional data were randomly generated, as shown in Figure 1. Points xi (black) and xj (red) represent two selected data points, for which k-nearest neighbors were computed with k = 4 as an example. As observed in Figure 1, the data points around xi are more dispersed compared to those around xj, resulting in larger distances between xi and its k-nearest neighbors. The k-nearest neighbor distances can thus be regarded as an indicator of data point distribution and facilitate the analysis of local density characteristics.
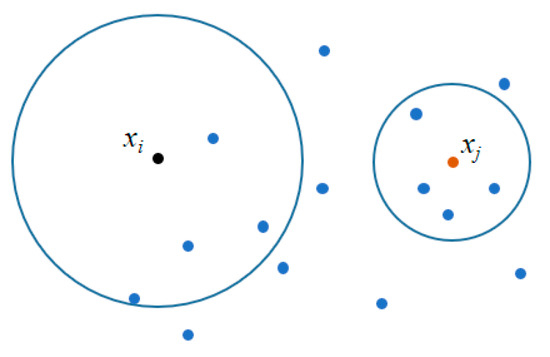
Figure 1.
Example of KNN neighborhood distribution (k = 4).
The DPC algorithm assumes that cluster centers are surrounded by neighbors with lower local density and that they are at a relatively large distance from any point with a higher local density. In this way, two attributes are defined for each data point xi: local density ρi and relative distance δi.
Definition 1 ([21]).
Local density ρi. The local density ρi of a data point xi is defined as follows:
where is the Euclidean distance between two data points xi and xj defined in Formula (1); the function (adopting the notation from [21]) is defined as χ(x) = 1 if x < 0 and χ(x) = 0 otherwise; and dc is a cutoff distance.
Basically, ρi is equal to the number of points that are closer than dc to data point xi. As a general guideline, the cutoff distance dc may be selected such that the mean number of neighbors falls within approximately 1–2% of the total dataset size.
Definition 2 ([21]).
Relative distance. The relative distance of data point xi is defined as the minimum distance between the point xi and any other point with higher density, described as
For the data point possessing the maximum density δᵢ, it is conventionally assigned the value of maxⱼ(d). It is noteworthy that δᵢ substantially exceeds typical nearest-neighbor distances only when the point corresponds to a local or global density peak. Consequently, cluster centers are identified as instances exhibiting anomalously high δᵢ values, this principle constitutes the foundational basis of the DPC methodology. Taking the values of ρi as the horizontal axis (X-axis) and values of δi as the vertical axis (Y-axis), the two-dimensional decision graph can be drawn, and those points with higher ρi and lower δi can be identified as cluster centers.
4. A Unified Outlier Detection Method from Global and Local Perspectives
In this part, we will present a unified outlier detection framework, which considers not only the local anomalous points but also global anomalous data objects.
4.1. Local Density with Gaussian Function
In the traditional DPC algorithm, the cutoff distance dc is set to 2% of the total number of points in the dataset. However, in datasets with significant differences in cluster density, cluster centers with low density are difficult to select. To solve this problem, the k-nearest neighbor distance of the data points is first calculated, then kernel density estimation on the local density of the data points is performed, so that each data point can have a relatively stable local density, thereby enabling more accurate clustering. In this way, the Gaussian Function is employed as the kernel function to estimate the local density of data points.
The procedure for estimating the local density of data point xi is as follows. First, the proximity distance between xi and a neighboring point xj is computed using Equation (1). This value is then used as input to the Gaussian kernel function in Equation (4) to compute a local density contribution. Finally, the overall local density for data point xi is defined as the mean of the density contributions from its k-nearest neighbors.
where d(xi, xj) is the Euclidean distance between data point xi and another data point xj; d is the number of dimensions.
According to Equations (1) and (4), the average distance of point xi can be described as shown in Equation (5).
where KNN(xi) refers to the set of k-nearest neighbors of a data point xi, which is obtained by calculating the Euclidean distances between xi and all other points in the dataset using Equation (1), sorting these distances in ascending order and selecting the k points with the smallest distances. As can be seen from Equations (4) and (5), the function e−x is a monotonic decreasing function, and local density will be smaller if the k-nearest distance of xi is larger, therefore the data points will be sparser.
4.2. Global Exception Score
In dense regions of a dataset, the distance to a point’s k-nearest neighbors is small, whereas it becomes large in sparse regions. Since outliers typically reside in sparse regions, they exhibit significantly larger k-NN distances than any normal point (a data object that is not an outlier). Consequently, the k-NN distance serves as an effective metric for global outlier detection.
Definition 3.
Global exception score (Ges). The global exception score of a data object xi is the sum of the distance between data object xi and its k-nearest neighbors, described as shown in Equation (6).
where Ges(xi) is the global exception score of data object xi, d(xi, xj) is the distance between data object xi and its k-nearest neighbor xj.
Essentially, the larger the value of Ges, the sparser the density between two data objects, indicating that the data object is more likely to be an outlier. When data objects form clusters with large density differences, this method can only detect outliers around clusters with low density, resulting in a decrease in local outlier detection performance in the overall dataset.
Intuitively, outliers are far away from the normal data points, with a small number and sparse distribution. In this way, the following inequality can be drawn, as can be seen in Theorem 1.
Theorem 1.
Let Xoutlier be a set of data outliers, Xnormal be a set of normal data, then for any data object xi ∈ Xoutlie, xj ∈ Xnormal, the distance between xi and its kth nearest neighbor is greater than that of the kth nearest neighbor of data object xj, that is,> 1.
Proof.
According to Definition 3, the k-nearest neighbor of xi Xoutlier is greater than the k-nearest neighbor of xj Xnormal, that is, d(xi, xk) > dk(xj, xk), xi Xoutlie, xj Xnormal. In this way, the following inequality can be concluded:
that is,
End.□
From Theorem 1, we can conclude that the global exception score of any outlier is greater than that of any normal data point. Therefore, outliers can be identified by the value of the global exception score.
4.3. Local Exception Score
The local outlier refers to an anomaly data object that is significantly different from its surrounding data points. The local outlier can help us identify anomaly data more accurately. To identify local outliers among data objects, cluster analysis is first performed to partition the data into several clusters. The average density of each cluster is then calculated. This approach allows clustering-based methods to efficiently detect local outliers for individual data points while significantly reducing computational complexity. In this way, the value of k is calculated using Equation (1), then the local density of xi can be obtained using Equations (4) and (5). After that, the relative distance can be obtained using Equation (2), and the DPC algorithm is conducted for data clustering. The average density of each cluster can be calculated with Equation (8).
where is the average density of the lth cluster, |N(l)| is the number of the lth cluster, and xi is the ith data object in the lth cluster. In this way, the local exception score can be defined as follows.
Definition 4.
Local exception score (Les). The local exception score of a data object xi is defined as the ratio of the average density of the cluster to which xi belongs and the kernel density of xi, described as
where Les(xi) is the local exception score of data point xi,
is the average density of the lth cluster.
Theorem 2.
Let Xoutlier be a set of data outliers and Xnormal be a set of normal data; then for any data object xi ∈ Xoutlie, xj ∈ Xnormal, the following inequality holds: > 1.
Proof.
It is obvious that for any xi Xoutlie, xj Xnormal, we can conclude that dk(xi, xm) > dk(xj, xm). Let dk(xi, xm) = αk × dk(xj, xm) where αk is a real number greater than 1. In this way, the following inequity can be drawn using Equation (4).
Since ak is greater than 1 and the function ex is a monotonically increasing function, then
As a result, we can conclude that the kernel density estimation of the kth nearest neighbor of a normal data point is greater than that of the kth nearest neighbor of an outlier, that is,
As can be seen, the local density of normal data points is greater than that of outliers. Also, the number of outliers is substantially smaller than the number of normal data points. After clustering is completed, the density of the lth cluster is approximately equal to the average density of normal data points, that is,
Combining Equations (12) and (15), the following equities can be drawn.
Then,
End.□
According to Equation (18), the local exception score of an outlier is greater than that of normal data points. As a result, the local outliers can be identified according to the value of the local exception score of data objects.
4.4. Comprehensive Exception Score
By combining the global and local exception evaluations, the comprehensive exception score of a data object can be defined as in Definition 5.
Definition 5.
Comprehensive exception score (CGLes). The comprehensive exception score CGLes of a data point xi is the sum of the global exception score Ges(xi) and local exception Les(xi) with a proportional parameter α, as described in Equation (19).
where α is a proportional parameter used to balance the importance of global exception degree Ges(xi) and Les(xi). If they are equally important, the value of α will be set to 0.5. Furthermore, to identify as many local outliers as possible, α should be set to a value close to 0; conversely, to detect as many global outliers as possible, α should be assigned a value close to 1. In extreme cases, when α equals 0, the result reflects the evaluation from a local outlier perspective; when α equals 1, it corresponds to the evaluation from a global outlier perspective.
CGLes(xi) = α × Ges(xi) + (1 − α) × Les(xi),
Using Equation (19), top-ranked data objects with the highest comprehensive exception scores can be identified as outliers in the dataset. Moreover, we will present the different detection results between the comprehensive exception score evaluation and the global exception score evaluation.
Suppose there are two clusters in the dataset, whose samples are evenly distributed. And the density of normal samples in cluster c1 is higher than that of samples in cluster c2, that is, dk(x1n) = βdk(x2n) where β > 1 and x1n and x2n are normal samples in cluster c1 and cluster c2, respectively. There is a local outlier x1o in cluster c1, whose kth nearest neighbor distance is δ times that of a normal data point x1n, that is, dk(x1o) = δ × dk(x1n), δ > 1. The global exception value of a normal data point x2n in cluster c2 can be described as
Similarly,
Ges(xo) = δ × Ges(x1n).
In this way, the following equation holds true according to Equations (20) and (21).
Corollary 1.
To detect local outliers in cluster c1 with a higher sample distribution density, then
< 1, δ > β.
Furthermore, the local exception value can be obtained according to Equation (18), and the inequity holds, > 1. Let Les(xo) = λLes(xn) and λ > 1. Also, the local density of normal data objects is approximately equal to that of outliers in an evenly distributed cluster, that is,
In this way, the following equation holds true using the above Equations (22) and (23).
Corollary 2.
To detect local outliers in a cluster with a higher density of data point distribution, then δ > β/λ.
As shown in Table 1, 1 >2, indicating that a greater is required to detect local outliers from the perspective of global exception detection. Obviously, it is necessary to lower the value of to improve the accuracy of outlier detection. In summary, the comprehensive exception evaluation method can detect both global outliers and local outliers.

Table 1.
Comparison of the outlier detection results with different cluster densities.
4.5. Algorithms for Outlier Detection from Global and Local Perspectives
Based on the analysis above, the core procedure of the proposed outlier detection algorithm, termed outlier detection based on global and local exception scores (GLES), can be summarized as follows. First, the k-nearest neighbor method is employed to analyze global data structures and compute global exception scores. Next, the Gaussian kernel function is applied to estimate the local density of each data point and derive its relative distance. These local density and relative distance measures are then used to perform clustering and assign local exception scores. Finally, the global and local scores are integrated to detect outliers, and a global–local outlier decision graph is constructed to visualize and interpret the results. The entire process for computing the combined exception scores is detailed in Algorithm 1.
| Algorithm 1: Comprehensive exception scores computation algorithm | |
| Input: | Dataset D, cutoff distance p; number of nearest neighbors k; |
| Output: | Comprehensive exception scores CGLes[N]. |
| (1) | Begin |
| (2) | #Distance matrix between two data points |
| (3) | Dist[N][N]←0; # initial value |
| (4) | For each data point xi in D do |
| (5) | For each data point xj in D do |
| (6) | #Compute the distance of each pair of data points using Equation (3); |
| (7) | Dist[i][j] = dk(xi,yj); |
| (8) | #Compute the global exception score Ges(xi) of xi |
| (9) | Ges(xi) ←0; # initial value |
| (10) | For each data point xi in D do |
| (11) | Sort(Dist[i][]); # sort in an ascending order |
| (12) | For s = 1 to k do |
| (13) | Ges[xi] ←Ges[xi]+ Dist[i][s]; |
| (14) | #Compute the local density of xi using Equation |
| (15) | rho[xi] ←0; |
| (16) | For each data point xi in D do |
| (17) | Sort(Dist[i][]); # sort in an ascending order |
| (18) | For s = 1 to k |
| (19) | rho[xi] ← rho[xi] + exp(-Dist[i][s]); |
| (20) | #Compute the relative distance of xi in D |
| (21) | delta[xi] ←0; |
| (22) | For each data point xi in D do |
| (23) | delta[xi] = min(Dist[i][]); |
| (24) | #Choose centers of clusters c_centers |
| (25) | c_centers[] = select_cluster_centers(rho, delta, threshold) |
| (26) | sub_clusters[]= Call k-NN(c_centers[], D); |
| (27) | #Compute the average density of each sub_cluster crho[] |
| (28) | srho[]←0; |
| (29) | For each sub_cluster sc do |
| (30) | For each data point xi∈sc do |
| (31) | For each point xi∈kNN(xi) do |
| (32) | srho[sc]= srho[sc]+ exp(-Dist[i][j]); |
| (33) | srho[sc]= crho[sc]/; |
| (34) | #Compute the local exception score Les(xi) |
| (35) | For each cluster sc do |
| (36) | For each data point xi in cluster sc do |
| (37) | Les(xi) ←srho[sc]/rho[xi]; |
| (38) | #Compute the comprehensive exception score using Equation (19) |
| (39) | For each data point xi in D do |
| (40) | CGLes(xi) ←α × Ges(xi) + (1 − α) × Les(xi); |
| (41) | Return CGLes[N]; |
| (42) | End. |
In Algorithm 1, Sort(x) is a sorting function; min(x) returns the minimum value of x. The time complexity of Algorithm 1 can be analyzed as follows:
- (1)
- The time complexity of k-nearest neighbors searching using KD tree is O(NlogN), where N is the number of data samples from line 4 to line 7.
- (2)
- The time complexity of the average density of each sub-cluster in local exception score computation is O(N3) from line 29 to line 33.
- (3)
- The time complexity of global exception scores computation and the local density is O(N2) from line 10 to 13.
- (4)
- The time complexity of Sort(x) function using Shell Sort Algorithm is O(NlogN) in line 11.
In this way, the total time complexity of Algorithm 1 is the sum of O(NlogN), O(N3), and O(N2). That is, O(NlogN) + O(N3) + O(N2) + O(NlogN) ≈ O(N3). Although this algorithm is not better than the KNN and LOF algorithm in average time complexity, the outliers are identified from the global and local perspectives simultaneously.
Using the algorithm of comprehensive exception score computation, the outlier detection result can be obtained as in Algorithm 2.
| Algorithm 2: Outlier detection based on global and local exceptions | |
| Input: | CGLes[N], top size n; |
| Output: | Set of outlier O[k] |
| (1) | Begin |
| (2) | Sort(CGLes[N]); //sorting the comprehensive exception scores |
| (3) | For i = 1 to n do |
| (4) | O[i] ←mark D[i] with outlie; |
| (5) | Return O[k]; |
| (6) | End. |
In Algorithm 2, the Sort() function sorts the comprehensive exception scores first. Then, the top-n data points will be marked as outliers. Moreover, the value of n is typically determined based on expert experience in practice. A larger value of n yields a greater number of suspicious outliers but results in a lower missed detection rate; conversely, a smaller value of n identifies fewer suspicious outliers but is associated with a higher missed detection rate. The primary time consumption is the sorting procedure, whose optimal time complexity is O(N3).
4.6. Performance Evaluation of Proposed Outlier Detection Algorithms
In this subsection, the performance evaluation of the proposed method is conducted and compared with other approaches. The simulation environment settings are as follows: Intel Core i7 CPU @1.6GHz, AMD HD8600, 16.0G RAM, Python 3.9. The outlier detection is typically regarded as a binary classification problem with four potential classification outcomes: true positive (TP), false negative (FN), true negative (TN), and false positive (FP). To thoroughly evaluate the performance of the proposed method, we compare it against several established algorithms using precision, recall, F-measure, and AUC as performance metrics.
4.6.1. Data Description
In this study, ten benchmark datasets were employed to assess the detection capability and computational efficiency of the proposed outlier identification algorithm, including four randomly generated datasets, and six existing datasets from the PyOD toolkit, which is an easy-to-use Python library for detecting anomalies in multivariate data. Moreover, it integrates many traditional anomaly detection algorithm models, making it easy to verify the performance superiority of existing algorithms.
In the multidimensional dataset, each column represents a feature (i.e., dimension) or a label (i.e., y-values) of the data objects. And the number of rows in the dataset represents the sample count. In outlier detection, the model takes X as the multidimensional data input, and the required labels (y-values) 1 represent outliers and 0 represent normal values. Table 2 provides specific distribution for each dataset, and Figure 2 describes the distribution of the two-dimensional artificial datasets.

Table 2.
Dataset description for simulation.
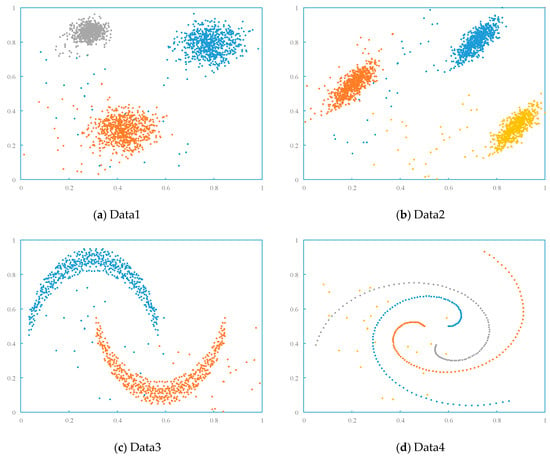
Figure 2.
Distribution of two-dimensional artificial datasets.
4.6.2. Results and Analysis
In the simulation, each dataset was partitioned according to an 80-20 ratio for testing the classification results, with the larger subset allocated for training and the remainder reserved for evaluating classification performance. Afterwards, these datasets are input into the models for classification and validation, respectively. After calculating the global and local outliers of datasets Data1 to Data4 separately, decision graphs can be drawn with each data object’s local exception score (Les) as the X-axis and global exception score (Ges) as the Y-axis, as shown in Figure 3. In Figure 3, the dense samples located in the lower left part of the decision graph can be considered as normal samples, while those samples in the middle are relatively scattered and can be considered as local outliers; and the samples in the upper right corner with the largest global and local exception scores, can be regarded as global outliers.
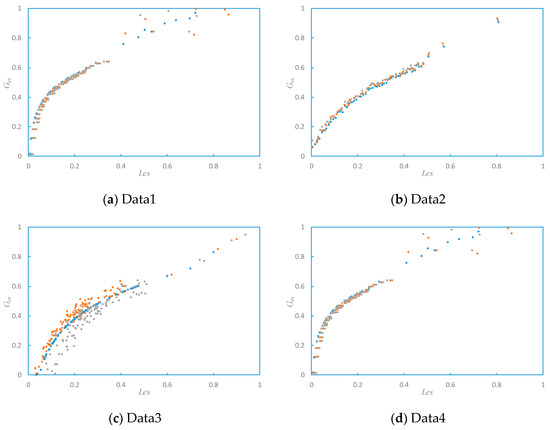
Figure 3.
Ges-Les relation graph of artificial data.
Table 3 presents the performance metrics of the outlier detection method proposed in this study on different datasets. From Table 3, it can be seen that the proposed GLES outlier detection algorithm has high detection performance in all datasets. At the same time, the AUC value also demonstrates good performance. And the average detection precision of GLES has improved by 70.1% on experimental datasets over conventional methods.

Table 3.
Performance indicators of the proposed outlier detection with different datasets.
Furthermore, comparative experiments were conducted using the proposed model and other outlier detection methods, including KDPC [28], KNN [12], DPC [29], LOF [13], MOD [14], LDF [30], and FCM [19]. The AUC of the GLES model was compared with other baseline methods, and the results are shown in Table 4.

Table 4.
Comparisons of AUC values of different outlier detection methods with different datasets.
According to Table 4, the GLES model proposed in this study achieves the optimal AUC values in five datasets, suboptimal AUC values in two datasets, and ranked third in the other three datasets, demonstrating good anomaly detection performance. On the other hand, among the seven unsupervised machine learning methods, the KNN method exhibits the best performance in the wbc dataset. Still, its ranking in other datasets is relatively poor.
In addition, the AUC value of FCM in the optdigits dataset (0.8722) was significantly lower than that of the GLES model (0.9369). In comparison, the AUC values of LOF in the optdigits and pendigits datasets (AUC values of 0.8586 and 0.8567) were significantly lower than those of the GLES model (0.9369 and 0.9781), indicating feature dependence on different datasets. Furthermore, although the KDPC method achieved the optimal AUC values in the data wbc and mush datasets, and the LDF method achieved optimal results in one dataset and suboptimal results in three datasets, their AUC values in other datasets were significantly lower than those of the GLES model. Additionally, semi-supervised learning requires training on normal data, which has certain limitations in actual data anomaly detection.
From the above comparative experimental results, it can be concluded that the seven baseline methods used in this experiment have significant dependence on the dataset and have poor stability and reliability in anomaly detection on different data. In contrast, the GLES model has stronger stability and reliability, making it more suitable for practical data anomaly detection. The improved model not only overcomes the limitations of traditional methods that require normal data for model training but also has higher AUC values and model stability in data anomaly detection compared to traditional machine learning models, demonstrating significant performance advantages.
In addition, Figure 4 shows the ROC curves of various methods with the Data1 dataset. The horizontal axis represents the pseudo-positive class FPR, and the vertical axis represents the true rate TPR. Different colored curves represent different methods, with the orange solid line representing the DPC method, the dashed line representing other baseline methods, and the AUC values of different methods in the lower right corner.
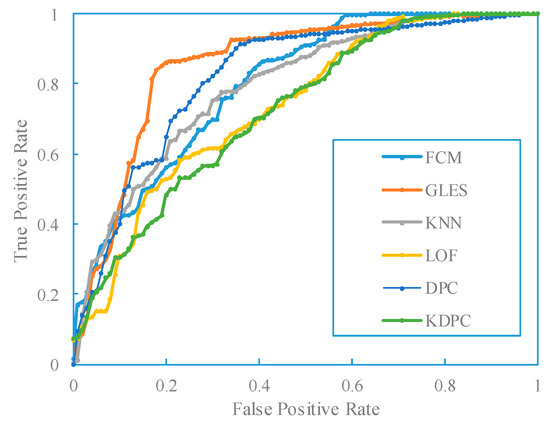
Figure 4.
ROC of Data1 with different outlier detection methods.
Based on the preceding analysis, the main findings can be summarized as follows: (1) From Data1 to Data4, it can be seen that the outlier detection methods all exhibit better performances. However, due to the strict requirements of clustering algorithms for dataset shape, datasets with irregular shapes (Data3, Data4) usually lead to a decrease in the performance of traditional outlier detection. (2) In cases where the dataset is significantly imbalanced and there are outlier clusters, the GLES method outperforms other outlier detection methods.
5. Application in Finance Budget Auditing Data Using the Proposed Outlier Detection Method
This section evaluates the proposed outlier detection method using financial budget auditing data derived from China’s Integrated Financial Budget Management System, a platform designed to facilitate budgetary reform and enable seamless fiscal data sharing.
5.1. Finance Budget Data
Financial budget data are typically organized into multiple standardized two-dimensional tables, such as budget indicator tables, non-tax revenue tables, treasury centralized payment records, and financial settlement reports. These tables collectively encompass key financial information, including budgetary allocations, revenue details, expenditure records, and accounting data. In practice, auditors extract relevant financial tables to analyze the data and identify any anomalies or suspicious patterns.
The auditing data mainly includes two tables: the centralized payment data table of the national treasury and the budget indicator data table. Among them, the centralized payment data table of the national treasury records the expenditure details of each budget unit in the execution of the finance budget in the year 2024, including 147,809 payment records of 180 budget units. There is a total of 36 attribute features, including 11 useful features for auditing, such as OrganizationID, OrganizationName, etc. Table 5 provides a detailed list of key field explanations for centralized payment data, with field examples extracted from real samples. The example indicates that the budget unit “Meteorological Bureau” was allocated RMB 8579.65 to “A Computer Company” on 18 June 2025, for the procurement of desktop computers. The funds were sourced from the budget project titled “Office Equipment Purchase”.

Table 5.
Fields of table state–centralized–payment.
In Table 5, “OrganizationID” and “ProjectID” correspond to budget organization and budget projects, respectively. This study uses the combination of “OrganizationID + ProjectID” as the primary key for data analysis. Additionally, the attributes “DepExpName” and “GovExpName” are not the same; these two classification systems are independent, and each attribute focuses on different aspects. The economic classification of government expenditure places greater emphasis on the key aspects of government budget management, including specific budgetary subjects such as wages of government agencies, expenditures on goods and services, capital expenditures, and other related categories. On the other hand, the economic classification of departmental expenditure reflects the requirements of departmental budget management and includes specific accounts that capture the characteristics of each department’s budget.
The budget indicator data table provides detailed information on the issuance of budget project indicators for the year 2024, covering 179 budget units and 3187 budget projects. It contains a total of 10,380 records related to the issuance, adjustment, and approval of budget project indicators, with 34 features in total. Among these, seven features are beneficial for auditing purposes: budget units, budget projects, project categories, available amounts, issued amounts, and issued dates, as shown in Table 6 below.

Table 6.
Fields of the budget allocation table.
Similarly, the combination of “OrganizationID + ProjectID” is regarded as the primary key for data analysis in the budget allocation table. Table 6 provides an example extracted from real samples, indicating that the budget unit “O010095” received approval from the higher-level department on 1 June 2024 and obtained the budget target amount of “623,500.00 yuan” for the project’s “public funds”.
In addition, the dataset primarily comprises continuous, discrete, and textual attributes. Among these, continuous attributes represent numerical quantities—such as payment amounts and budget indicator values—that can be measured on an uninterrupted scale. The value of the payment amount varies greatly, ranging from a few hundred yuan to tens of millions of yuan. Discrete attributes include unit code, unit name, project code, project name, government expenditure economic classification subject name, department expenditure economic classification name, collection name, and date, among other classified attributes. These textual attributes are primarily used to describe the purpose of payment.
5.2. Finance Budget Data Auditing with the Proposed Approach
Financial budget auditing refers to the process by which auditors at various levels conduct supervision and inspection of local government budget execution as well as examine the authenticity, compliance, and effectiveness of other fiscal revenue and expenditure activities. According to the Chinese Audit Law, government audit agencies are required to conduct budget execution audits every year. The main audit contents include budget preparation and adjustment additions, budget project income and expenditure, asset procurement management and utilization, etc. Auditors will conduct audits according to carefully designed audit procedures to obtain audit results and issue audit reports based on them, providing a basis for the adjustment and formulation of the following year’s finance budget. In the implementation stage of budget auditing, traditional audit methods are conducted through checking, interviews, and other means. We present an auditing clues identification-based anomaly data detection method. To evaluate the detection capability of the proposed method when applied to the financial budget auditing data, three performance metrics are adopted: the false positive rate, the false negative rate, and the recommendation quality of identified anomalies.
5.2.1. Performance Evaluation of the False Positive Rate with Auditing Data
It is necessary to evaluate the proposed model’s ability to reduce false positives, ensuring the detection of all suspicious points at the start. The false positive rate of outliers at different top-n values can be regarded as the percentage of data points with the top n% of outlier scores defined as outlier data, where non-outlier data accounts for the entire data. This indicator can reflect the proportion of outlier data that is not suspicious, and the value of the false positive rate is FP/(TP + FP). In the experiment, a total of 4301 data points were labeled as abnormal data points, with a total of 147,809 data objects. Table 7 summarizes the corresponding experimental outcomes.

Table 7.
Performance of the false positive rate with the proposed method on budget allocation table.
Based on the experimental outcomes presented in Table 7, it is evident that the GLES model exhibits certain advantages in evaluating the two leading performance indicators of precision and F1-score. Specifically, when considering different top-n as outlier abnormal data, the values of recall always remain high. At the same time, when n = 1%, the false positive rate is low, reporting three data outliers; when the value of n is set to 2%, the false positive rate is 2.6049%; when the value of n is set to 6%, the false positive rate is significantly improved. In order to detect all suspicious points, in the combination of GLES and standard deviation, only the top 2% of budget items contain nearly 97% of suspicious points. This result means that the GLES model has the ability to accurately identify suspicious points while maintaining a low false alarm rate. This result also indicates that GLES has better generalization ability in processing data from different scenarios.
5.2.2. Performance Evaluation of the False Negative Rate with Auditing Data
Subsequently, the model’s effectiveness in minimizing false negatives is assessed with actual auditing data. Ideally, all suspicious data points with high anomaly scores should be included in the top-n set. The simulation experiment was conducted using data from the budget allocation table, where a total of 321 data objects were labeled as suspicious data points. The experiment calculated the rate of missed suspicious data points at different n values. The simulation results are shown in Table 8.

Table 8.
Performance of the false negative rate with the proposed method on budget allocation table.
From Table 8, it can be seen that the false positive rate is at a high level when n is set to a small value, and the reason can be ascribed to an underrepresentation of anomalous instances in the dataset relative to the actual occurrence of abnormalities. Furthermore, the precision value is high at this time and there are more data points that are missed. Overall, when the parameter n was configured to represent 3% of the total dataset, the false positive rate of the model is only 4.3614%, which means that almost all suspicious points in the data have been detected. As the value of n increases, the false positive rate decreases to 0, indicating that all suspicious points in the data have been successfully detected.
The results demonstrate the potential of the proposed model in improving audit efficiency and reducing omission rates, which is particularly important for audit practice, as high omission rates may lead to significant financial anomalies being overlooked, thereby increasing the risk of inaccurate financial statements.
5.2.3. Performance Evaluation of the Ranking Quality with Auditing Data
In practice, auditors pay more attention to the ranking quality of top n suspicious data points, that is, whether suspicious data objects at most risk are ranked higher, meaning that those data points are evaluated with high exception scores. Based on this, to assess the ranking quality of the model’s detection outcomes, this study adopts the normalized discounted cumulative gain (NDCG) as an evaluation metric. NDCG is widely utilized in information retrieval and recommendation systems to quantify the effectiveness of ranked results.
NDCG can help us evaluate the relevance of the returned results, especially in evaluating whether the top-ranked results are more relevant to user interests. Its value is the discounted cumulative gain (DCG) divided by the ideal cumulative discount gain (IDCG), and the corresponding value needs to be determined based on the value of n; values approaching 1 indicate stronger recommendation performance. Specifically, cumulative gain (CG) is the sum of the gains of all results to obtain the overall ranking gain value. In other words, if the result is highly relevant, its gain is high; otherwise, its gain is very low if not relevant. DCG considers rank position, indicating that the gain brought by the result in a lower ranking position will decrease, as seen in Equation (25). That is, the lower the ranking of the results, the less gain value is considered because users usually focus more on the top-ranked results. Discount values are usually set with a decreasing function, such as applying a decay factor to results ranked lower. IDCG stands for ideal discounted cumulative gain (the expected results). The value of NDCG can be seen in Equation (26).
where reli is set to 1 if the recommended outlier is a suspicious point of interest to auditors, otherwise it is 0. Table 9 shows the values of NDCGs of the proposed method.

Table 9.
NDCGs of the proposed method.
The experimental results show that the GLES model has a good effect on ranking quality evaluation, which means that auditors are more interested in the detection results of this model. Furthermore, when the n value is set to 3%, NDCGs achieve higher values, indicating that the sorting results reflect the suspicious points of data that auditors are concerned about, thus verifying the effectiveness of outlier detection in audit suspicious point mining. Moreover, the detection precision has improved by 38.6% on real auditing data over conventional methods.
In summary, the outlier detection model designed in this article has a significant positive impact on the mining of audit clues, proving the effectiveness of outlier detection in the audit business. In addition, the proposed model is capable of handling large-scale and complex datasets and has demonstrated excellent performance in various dispersion metrics.
5.3. Results and Discussion
5.3.1. Practical Implementation of the Integrated Outlier Detection Framework in Financial Auditing Systems
The proposed outlier detection algorithm offers a systematic approach for enhancing auditing efficiency in financial systems through the following implementation framework:
- (1)
- Data preparation and parameter configuration. Auditors initially compile comprehensive financial datasets encompassing budget execution records, fund allocation flows, procurement transactions, and project expenditure details. Following data cleaning and normalization procedures, critical parameters including the number of nearest neighbors (k) and the adaptive coefficient (α) are calibrated based on historical audit findings and domain expertise to optimize detection performance.
- (2)
- Dual-mode anomaly detection. The algorithm operates through complementary detection mechanisms. The global outlier component identifies conspicuous anomalies through k-nearest neighbor distance summation, effectively flagging extreme budgetary deviations and substantial unauthorized transfers. Concurrently, the local outlier module employs kernel density estimation to detect subtle contextual anomalies, such as departmental expenditure patterns that deviate significantly from peer groups or temporal financial flows that contradict established operational norms. The adaptive coefficient dynamically balances these complementary perspectives, ensuring comprehensive coverage of diverse anomaly types.
- (3)
- Prioritized audit investigation. The system generates comprehensive exception scores that facilitate risk-based resource allocation. Auditors focus investigative efforts on the top-ranked outliers (typically the highest 5–10% scores), which represent the most promising candidates for fraudulent activities, compliance violations, or operational irregularities. This targeted approach demonstrably enhances detection precision by 38.6% compared to conventional methods, substantially reducing false positives and investigation latency.
This implementation transforms traditional auditing practices from labor-intensive comprehensive reviews to intelligent, risk-driven examination. By leveraging computational efficiency to identify critical audit targets within massive financial datasets, the framework significantly improves both audit quality and operational effectiveness while maintaining comprehensive regulatory oversight.
5.3.2. Discussion
Because the DPC algorithm has not involved the local scene of the data when calculating local density, it cannot identify the centers of sparse clusters when they have different densities between clusters. Therefore, we proposed an improved DPC algorithm for anomaly detection in the field of auditing, and the following aspects can be discussed.
- (1)
- k-nearest neighbor method and kernel density estimation methods are employed to calculate the local density of data points in this study, replacing the local density calculated based on truncation distance in the traditional DPC algorithm. The improved method can enhance the clustering performance of DPC algorithm in data objects with different density distributions and improve the accuracy of cluster center selection [31].
- (2)
- The combined global and local outliers of data objects can be obtained based on k-nearest neighbors and clustering methods, which improves the detection accuracy of outliers by combining global and local outliers [32,33]. Thus, global and local outliers can be effectively identified in big data auditing.
- (3)
- The common outlier detection methods are greatly affected by n, but the DPC-based outlier detection approach developed in this work is less affected by n and is convenient for auditors to apply [34,35].
6. Conclusions and Future Works
The detection of anomalous instances in large-scale datasets represents a crucial capability in financial auditing. Aiming to solve DPC algorithm’s limited attention to local data characteristics, particularly its difficulty in identifying cluster centers within sparsely distributed regions, this work introduces GLES, a hybrid outlier detection method that integrates global and local perspectives. The proposed approach proceeds through several computational stages: the k-nearest neighbor distances are computed for each point, with their summation defining a global outlier measure; local density is then estimated via kernel density estimation, enabling the derivation of relative distances used for clustering. Subsequently, the ratio of cluster density to local density yields a local outlier score. These global and local components are combined to generate a composite anomaly score, from which top-ranking instances are identified as outliers. Furthermore, the proposed methodology has been successfully implemented in the H Provincial Department of Finance in China, demonstrating significant practical utility. Its application has substantially reduced the time required for identifying audit clues, leading to marked gains in operational efficiency. More importantly, this systematic approach provides a reliable guarantee for enhancing the overall quality and effectiveness of audit processes. This real-world case underscores the method’s robust potential for practical deployment within governmental audit institutions, offering a tangible pathway for translating analytical advancements into improved supervisory outcomes. Future works can further improve the clustering performance of the DPC algorithm and provide an adaptive method for selecting the nearest neighbor parameter n. Also, we will apply it to the budget data of other economies to validate the reliability and effectiveness of the detection algorithm.
Funding
This research was funded by the Humanities and Social Sciences Foundation, Ministry of Education of China, grant number 22YJAZH113.
Data Availability Statement
The used dataset is available upon request from the authors.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Hodge, V.J.; Austin, J. A survey of outlier detection methodologies. Artif. Intell. Rev. 2004, 22, 85–126. [Google Scholar] [CrossRef]
- Cribeiro-Ramallo, J.; Arzamasov, V.; Bhm, K. Efficient generation of hidden outliers for improved outlier detection. ACM Trans. Knowl. Discov. Data 2024, 18, 234. [Google Scholar] [CrossRef]
- Zhang, Z.; Hou, Y.; Jia, Y.; Zhang, R. An outlier detection algorithm based on local density feedback. Knowl. Inf. Syst. 2025, 67, 3599–3629. [Google Scholar] [CrossRef]
- Savić, M.; Atanasijević, J.; Jakovetić, D.; Krejić, N. Tax evasion risk management using a hybrid unsupervised outlier detection method. Expert Syst. Appl. 2022, 193, 116409. [Google Scholar] [CrossRef]
- Papastefanopoulos, V.; Linardatos, P.; Kotsiantis, S. Combining normalizing flows with decision trees for interpretable unsupervised outlier detection. Eng. Appl. Artif. Intell. 2025, 141, 109770. [Google Scholar] [CrossRef]
- Dragomir, D.; Biljana, J.; Suncica, M. The scope and limitations of external audit in detecting frauds in company’s operations. J. Financ. Crime 2021, 28, 632–646. [Google Scholar] [CrossRef]
- Danyang, W.; Soohyun, C.; Miklos, A.V.; Liam, T. Outlier Detection in Auditing: Integrating Unsupervised Learning within a Multilevel Framework for General Ledger Analysis. J. Inf. Syst. 2024, 38, 123–142. [Google Scholar] [CrossRef]
- Gangopadhyay, A.K.; Sheth, T.; Chauhan, S. LAD in finance: Accounting analytics and fraud detection. Adv. Comput. Intell. 2023, 3, 4. [Google Scholar] [CrossRef]
- Nonnenmacher, J.; Gómez, J.M. Unsupervised anomaly detection for internal auditing: Literature review and research agenda. Int. J. Digit. Account. Res. 2021, 21, 1–22. [Google Scholar] [CrossRef]
- She-I, C.; Chih-Fong, T.; Dong-Her, S.; Chia-Ling, H. The development of audit detection risk assessment system: Using the fuzzy theory and audit risk model. Expert Syst. Appl. 2008, 35, 1053–1067. [Google Scholar] [CrossRef]
- Won, G.N.; Kyungha, L.; Feiqi, H.; Qiao, L. Multidimensional audit data selection (MADS): A framework for using data analytics in the audit data selection process. Account. Horiz. 2019, 33, 127–140. [Google Scholar] [CrossRef]
- Ramaswamy, S.; Rastogi, R.; Shim, K. Efficient algorithms for mining outliers from large data sets. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 427–438. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.-P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 93–104. [Google Scholar] [CrossRef]
- Yang, J.; Rahardja, S.; Fränti, P. Mean-shift outlier detection and filtering. Pattern Recognit. 2021, 115, 107874. [Google Scholar] [CrossRef]
- Zhang, K.; Hutter, M.; Huidong, J. A new local distance based outlier detection approach for scattered real-world data. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Bangkok, Thailand, 27–30 April 2009; pp. 813–822. [Google Scholar] [CrossRef]
- Tang, J.; Chen, Z.; Fu, A.W.C.; Cheung, D.W. Enhancing effectiveness of outlier detections for low density patterns. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Taipei, Taiwan, 6–8 May 2002; pp. 535–548. [Google Scholar] [CrossRef]
- Zhongping, Z.; Kuo, W.; Jinyu, D.; Sen, L. Outlier detection algorithm based on relative skewness density ratio outlier factor. Comput. Integr. Manuf. Syst. 2024, 7, 67. [Google Scholar] [CrossRef]
- Zengyou, H.; Xiaofei, X.; Shengchun, D. Discovering cluster based local outliers. Pattern Recognit. Lett. 2003, 24, 1641–1650. [Google Scholar] [CrossRef]
- Al-zoubi, M.B.; Al-dahoud, A.; Yahya, A.A. New outlier detection method based on fuzzy clustering. WSEAS Trans. Inf. Sci. Appl. 2010, 7, 681–690. [Google Scholar]
- Zhou, Y.; Zhu, W.; Sun, H. A local outlier detection method based on objective function. J. Northeast. Univ. (Nat. Sci.) 2022, 43, 1405–1412. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, S.; Liu, W.; Wang, Y.; Li, D.X. Outlier detection algorithm based on fast density peak clustering outlier factor. J. Commun. 2022, 43, 186–195. [Google Scholar] [CrossRef]
- Lei, B.; Jiasheng, W.; Yu, Z. Outlier detection and explanation method based on FOLOF algorithm. Entropy 2025, 27, 582. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, H.; Zhang, Y.; Zhang, Y. An outlier detection algorithm based on an integrated outlier factor. Intell. Data Anal. 2019, 23, 975–990. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, S.; Wu, Z.; Li, X. Outlier detection using local density and global structure. Pattern Recognit. 2025, 157, 110947. [Google Scholar] [CrossRef]
- Proshad, R.; Asha, S.A.A.; Tan, R.; Lu, Y.; Abedin, A.; Ding, Z.; Zhang, S.; Li, Z.; Chen, G.; Zhao, Z. Machine learning models with innovative outlier detection techniques for predicting heavy metal contamination in soils. J. Hazard. Mater. 2025, 481, 136536. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiahao, X.; Zexuan, P. Improved outlier detection and Interpretation method for DPC clustering algorithm. J. Harrbin Inst. Technol. 2024, 56, 68–85. [Google Scholar] [CrossRef]
- Ji, X.; Zhang, T.; Zhu, J.L.; Liu, S.C.; Li, X.J. Improved DPC Clustering Algorithm with Neighbor Density Distribution Optimized Sample Assignment. J. S. China Univ. Technol. (Nat. Sci. Ed.) 2019, 47, 98–105. [Google Scholar] [CrossRef]
- Latecki, L.J.; Lazarevic, A.; Pokrajac, D. Outlier detection with kernel density functions. In Proceedings of the Machine Learning and Data Mining in Pattern Recognition (MLDM 2007), Leipzig, Germany, 18–20 July 2007; pp. 61–75. [Google Scholar] [CrossRef]
- Azzedine, B.; Lining, Z.; Omar, A. Outlier detection: Methods, models, and classification. ACM Comput. Surv. (CSUR) 2020, 53, 55. [Google Scholar] [CrossRef]
- Smiti, A. A critical overview of outlier detection methods. Comput. Sci. Rev. 2020, 38, 100306. [Google Scholar] [CrossRef]
- Olteanu, M.; Rossi, F.; Yger, F. Meta-survey on outlier and anomaly detection. Neurocomputing 2023, 555, 126634. [Google Scholar] [CrossRef]
- Rathi, G.; Kamble, S.; Sharma, N. AI-driven road traffic management: A comprehensive review of outlier detection techniques and challenges. Knowl. Inf. Syst. 2025, 67, 8267–8309. [Google Scholar] [CrossRef]
- Ghadekar, P.; Manakshe, A.; Madhikar, S.; Patil, S.; Mukadam, M.; Gambhir, T. Predictive maintenance for industrial equipment: Using XGBoost and local outlier factor with explainable AI for analysis. In Proceedings of the 2024 14th International Conference on Cloud Computing, Noida, India, 18–19 January 2024; pp. 25–30. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).