AI-Assisted Regional Collaborative Game of an Emergency Supplies Reserve Supply Chain
Abstract
1. Introduction
2. Literature Review
2.1. Emergency Supply Reserve Mechanisms
2.2. Emergency Supply Chain Collaboration
2.3. AI’s Role in Supply Chain Management
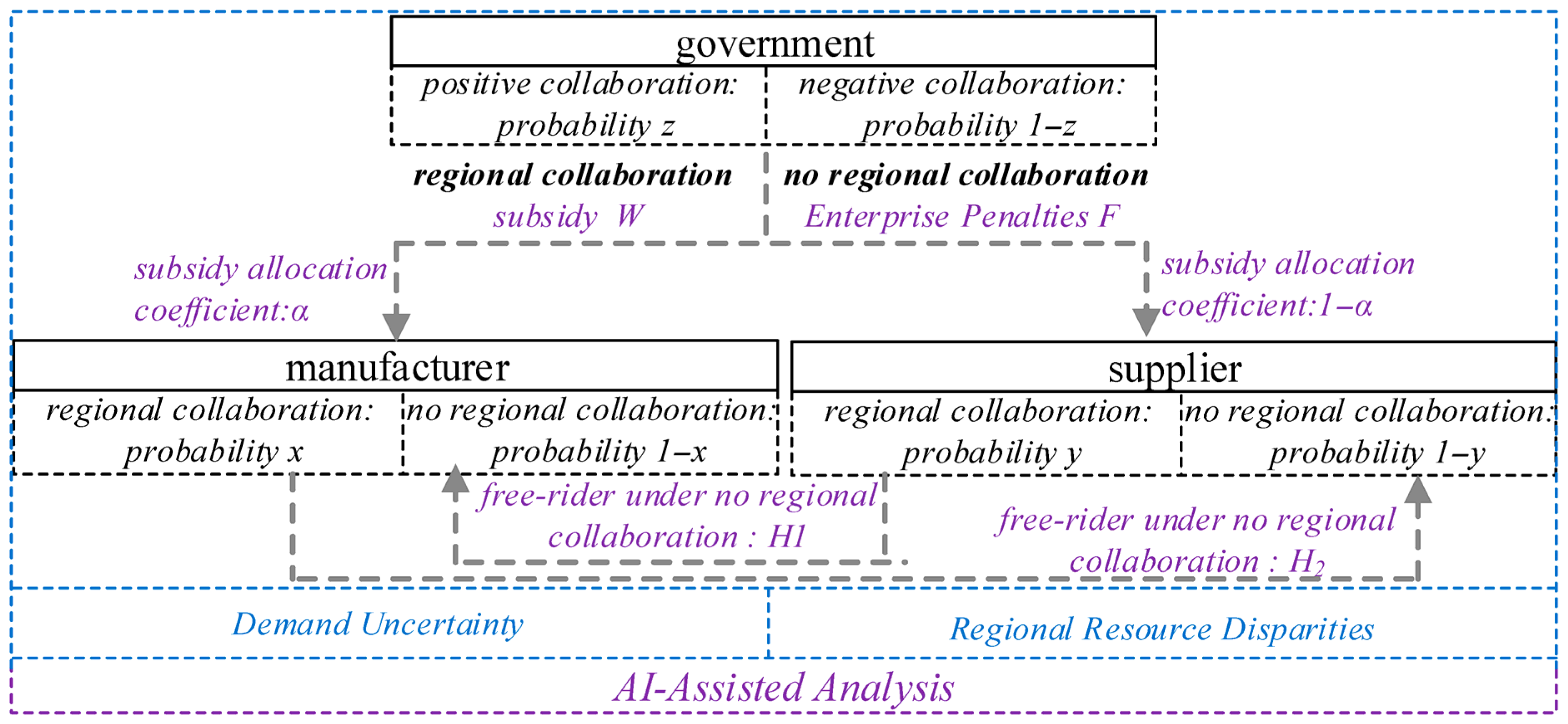
3. Game Model Construction
3.1. Problem Description
3.2. Research Hypothesis and Model Construction
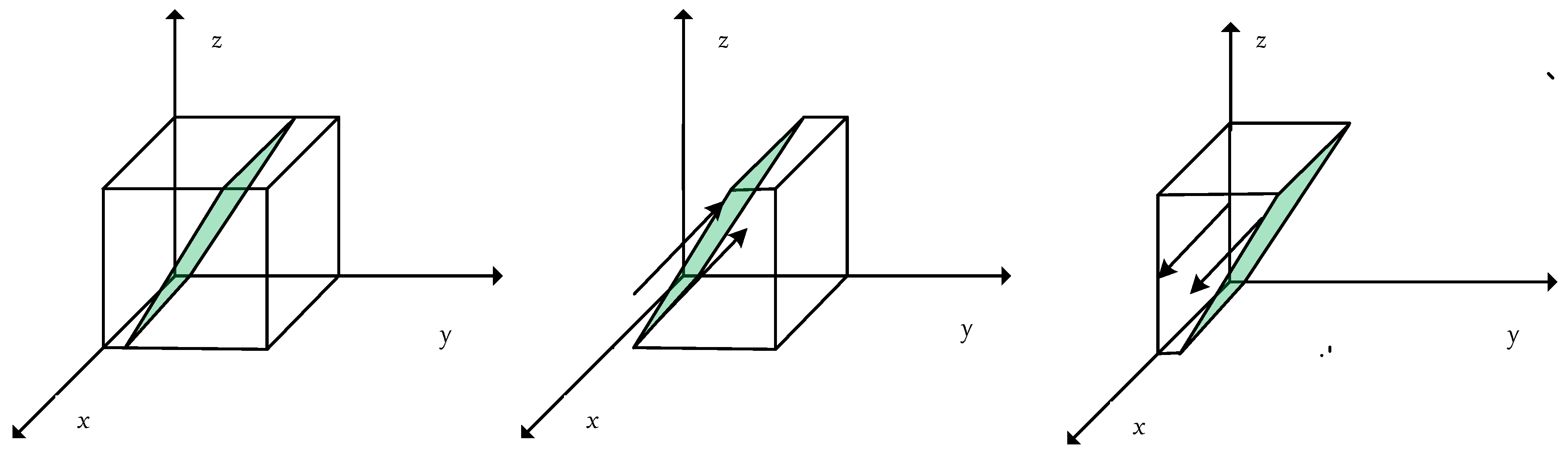
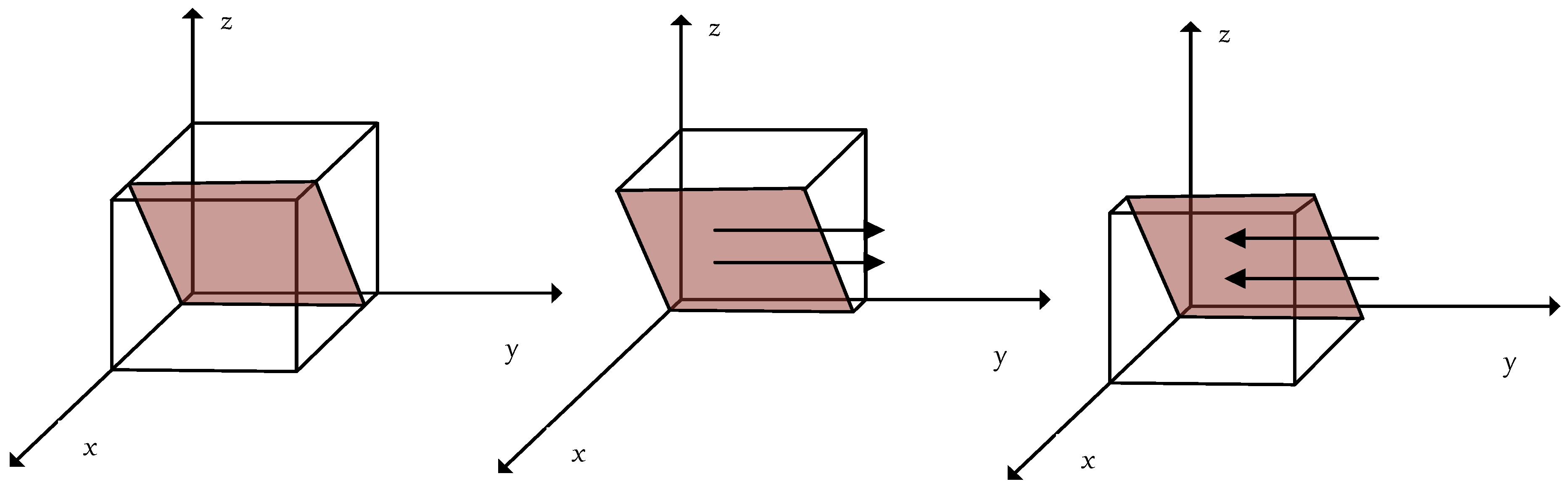
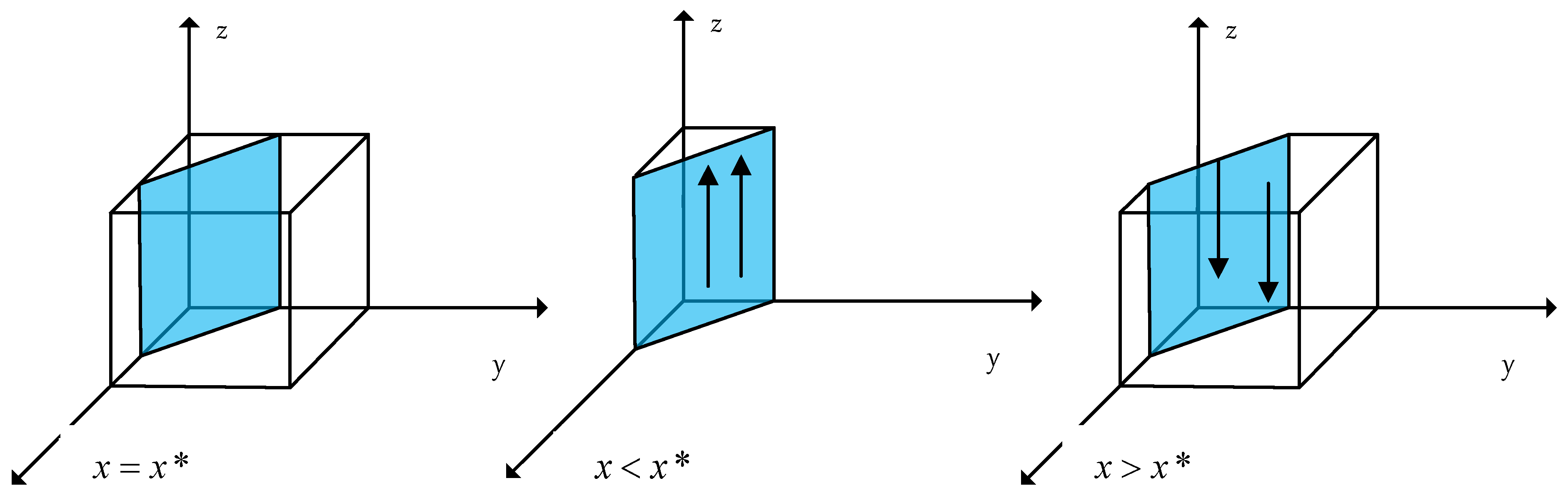
3.3. Strategic Evolution Stability Analysis of the Participating Subjects
3.4. Framework for Empirical Parameter Calibration
4. Calculated Case Analysis
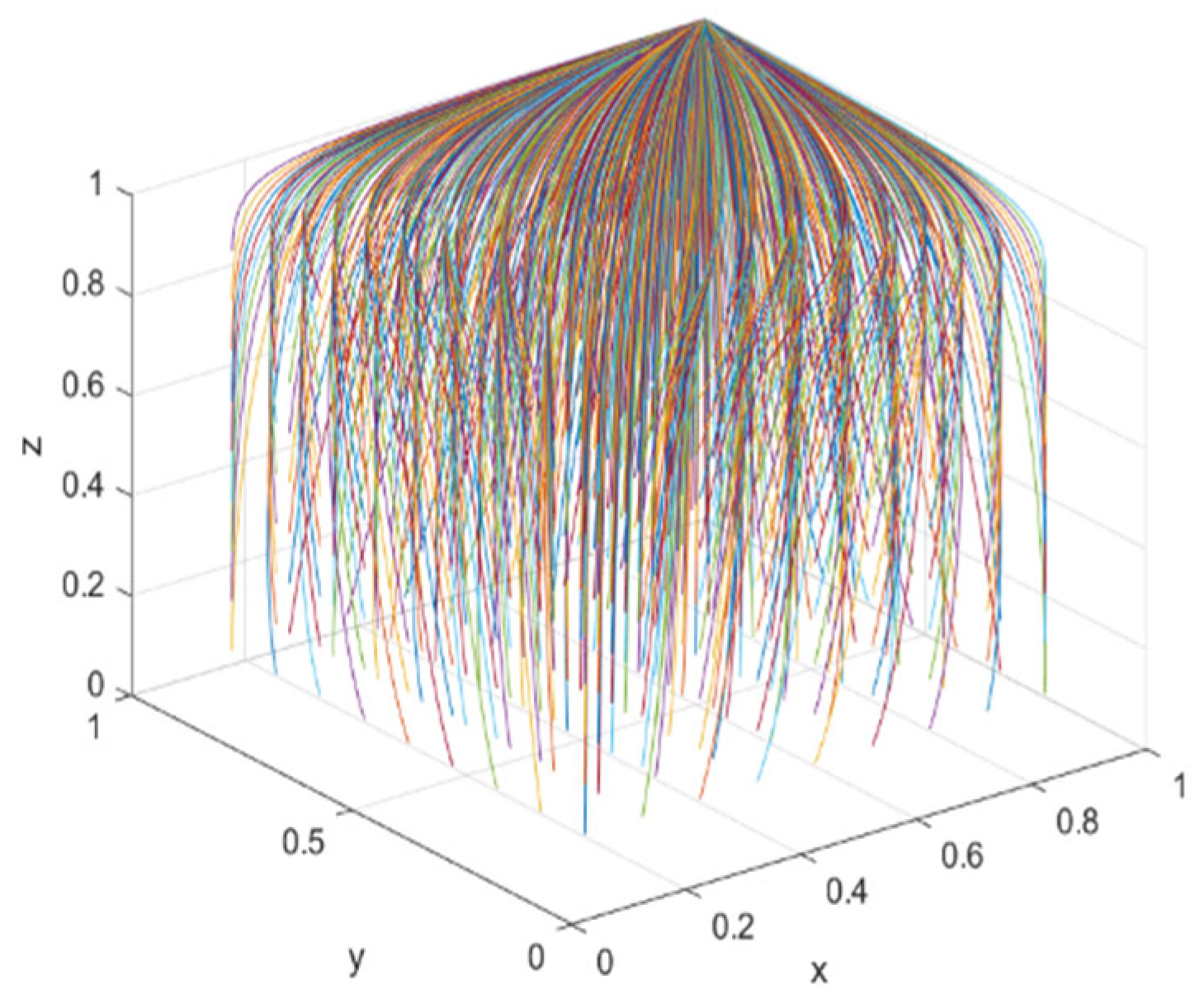
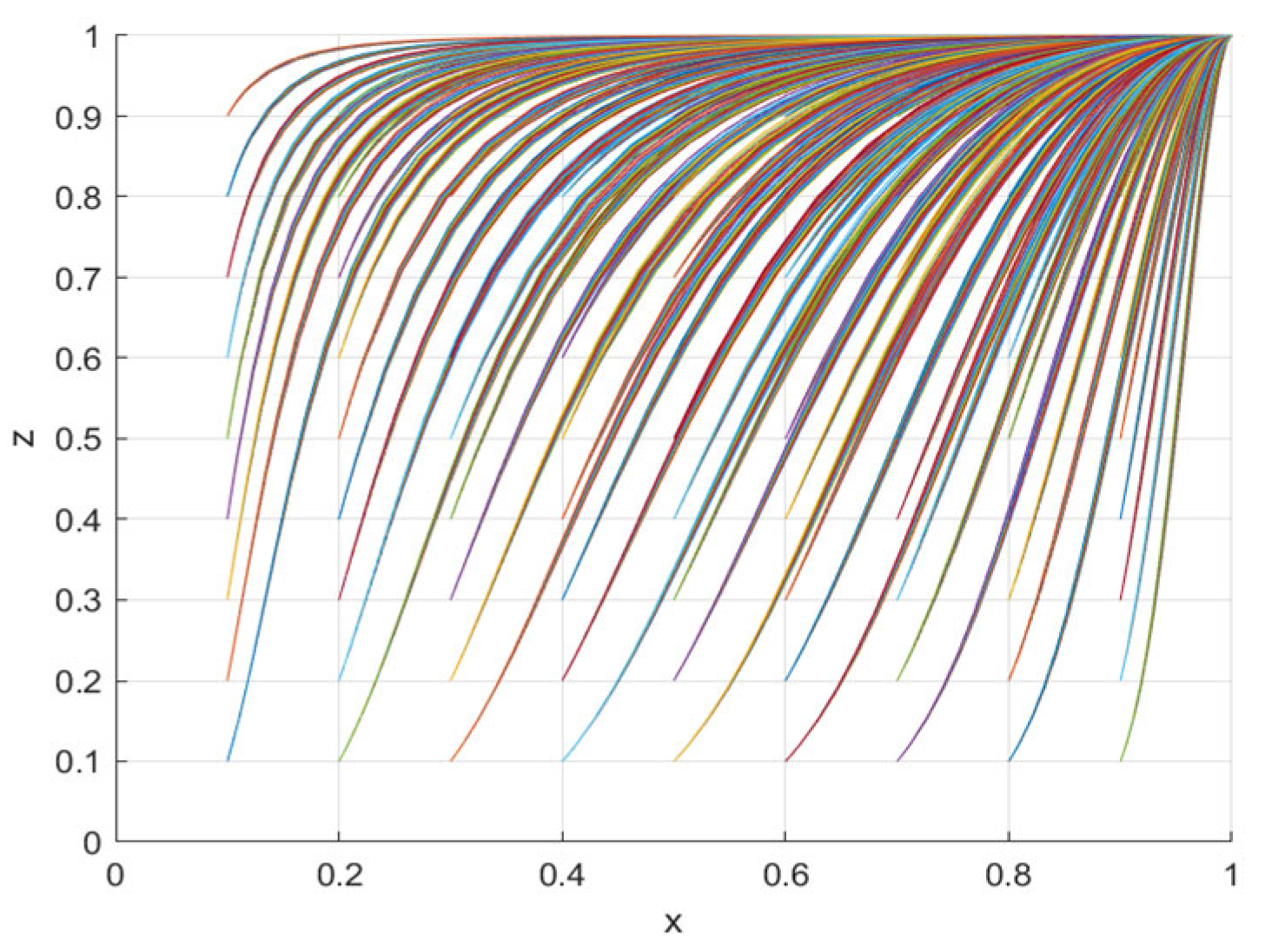
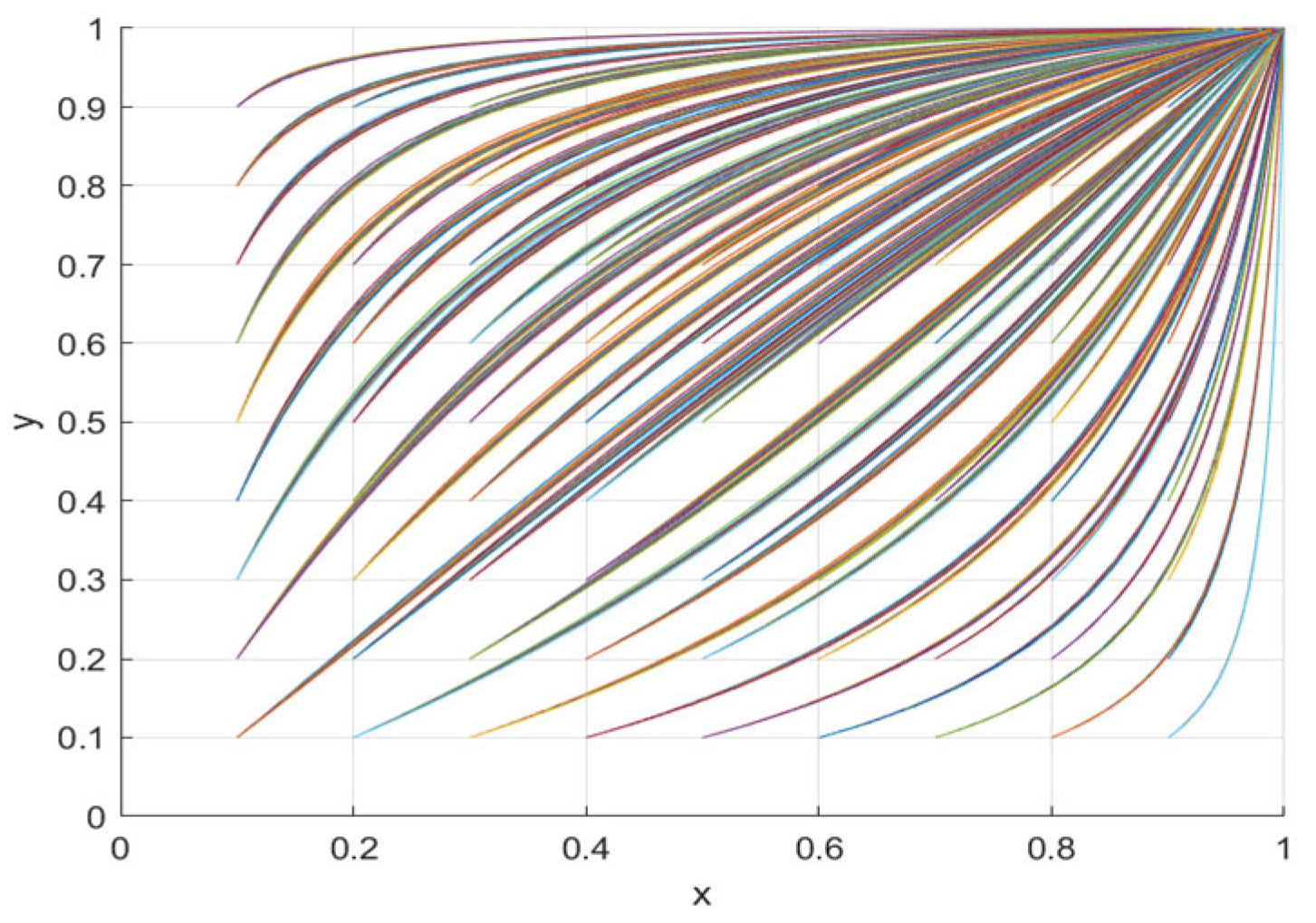
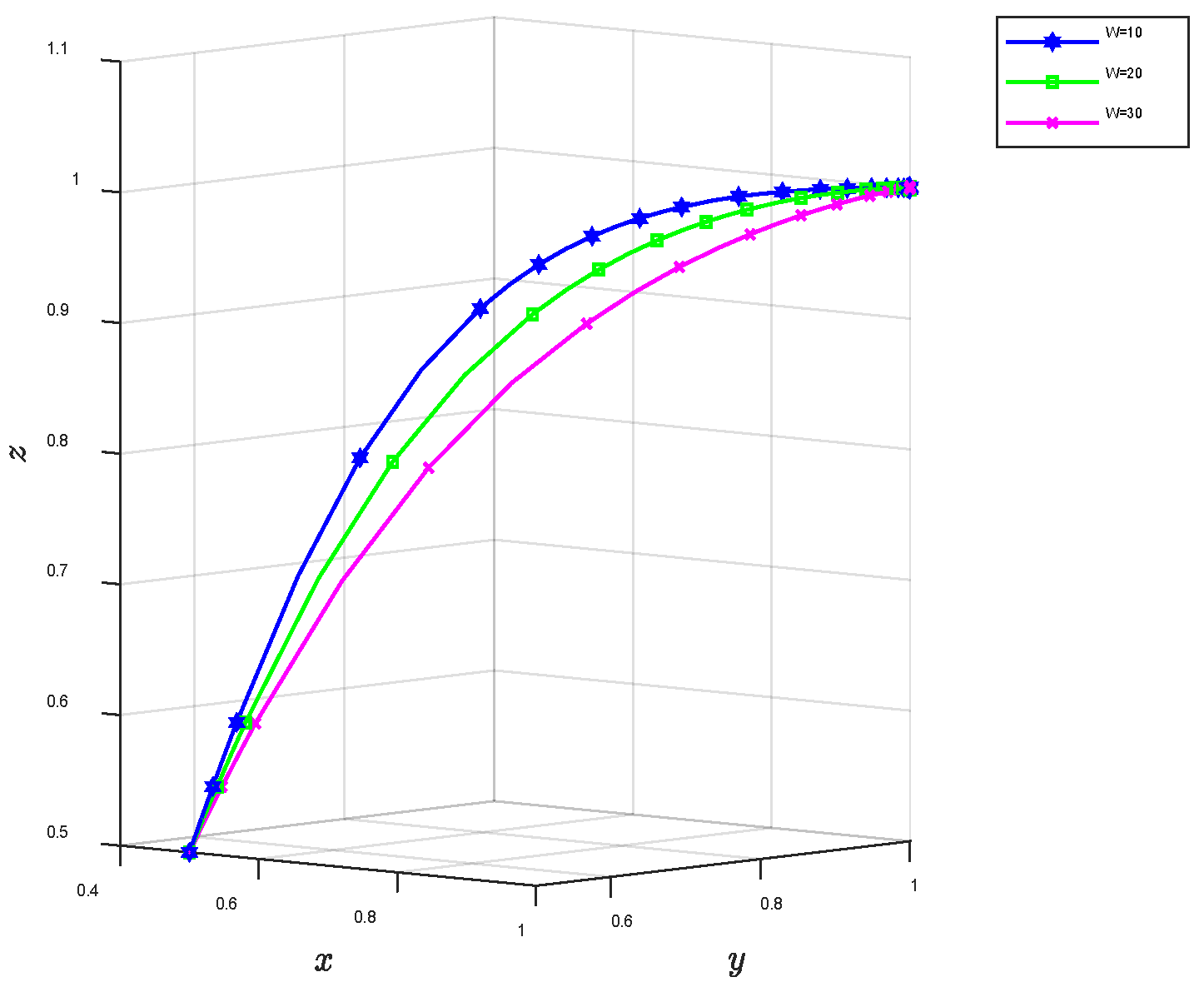
4.1. Numerical Simulation Analysis
4.2. Countermeasures and Suggestions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Xie, K. Emergency supplies requisition negotiation principle of government in disasters. Kybernetes 2016, 45, 1174–1193. [Google Scholar] [CrossRef]
- Zhou, Q.S.; Olsen, T.L. Inventory rotation of medical supplies for emergency response. Eur. J. Oper. Res. 2017, 257, 810–821. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, J.; Feng, G.Z.; Zhou, K. Research on Emergency Material Reserve Model under Option Contract Mechanism. Chin. J. Manag. Sci. 2022, 30, 338–351. [Google Scholar]
- Wang, Y.; Liu, M.; Viana, J.; Dube, N. How to improve the quality of emergency supplies? A tripartite evolutionary game model. Kybernetes 2025, 54, 5766–5787. [Google Scholar] [CrossRef]
- Huang, J.; Xie, D.; Qiu, Y.; Wang, J.; Song, J. Green supply chain management: A renewable energy planning and dynamic inventory operations for perishable products. Int. J. Prod. Res. 2024, 62, 8924–8951. [Google Scholar] [CrossRef]
- Wankmüller, C.; Reiner, G. Coordination, cooperation and collaboration in relief supply chain management. J. Bus. Econ. 2020, 90, 239–276. [Google Scholar] [CrossRef]
- Kadiyala, B.; Özer, Ö.; Bensoussan, A. A mechanism design approach to vendor managed inventory. Manag. Sci. 2020, 66, 2628–2652. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y.; Li, S.; Li, S.; Chen, W. Bi-objective robust optimisation on relief collaborative distribution considering secondary disasters. Int. J. Prod. Res. 2024, 62, 2435–2454. [Google Scholar] [CrossRef]
- Xia, H.; Sun, Z.; Wang, Y.; Zhang, J.Z.; Kamal, M.M.; Jasimuddin, S.M.; Islam, N. Emergency medical supplies scheduling during public health emergencies: Algorithm design based on AI techniques. Int. J. Prod. Res. 2025, 63, 628–650. [Google Scholar] [CrossRef]
- Adhikari, A.; Joshi, R.; Basu, S. Collaboration and coordination strategies for a multi-level AI-enabled healthcare supply chain under disaster. Int. J. Prod. Res. 2025, 63, 497–523. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Z.; Huang, M.; Wang, H.; Wang, X.; Fang, S.C. Collaborative supply chain network design under demand uncertainty: A robust optimization approach. Int. J. Prod. Econ. 2025, 279, 109465. [Google Scholar] [CrossRef]
- Bimpikis, K.; Ehsani, S.; Il Kilic, R. Cournot competition in networked markets. Manag. Sci. 2019, 65, 2467–2481. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, X.; Huang, A.; Hua, G.; Teunter, R.H. Optimal stock and capital reserve policies for emergency medical supplies against epidemic outbreaks. Eur. J. Oper. Res. 2023, 304, 183–191. [Google Scholar] [CrossRef]
- Katsaliaki, K.; Kumar, S.; Loulos, V. Supply chain coopetition: A review of structures, mechanisms and dynamics. Int. J. Prod. Econ. 2024, 267, 109057. [Google Scholar] [CrossRef]
- Charles, V.; Emrouznejad, A.; Gherman, T. A critical analysis of the integration of blockchain and artificial intelligence for supply chain. Ann. Oper. Res. 2023, 327, 7–47. [Google Scholar] [CrossRef]
- Jackson, I.; Ivanov, D.; Dolgui, A.; Namdar, J. Generative artificial intelligence in supply chain and operations management: A capability-based framework for analysis and implementation. Int. J. Prod. Res. 2024, 62, 6120–6145. [Google Scholar] [CrossRef]
- Belhadi, A.; Mani, V.; Kamble, S.S.; Khan, S.A.R.; Verma, S. Artificial intelligence-driven innovation for enhancing supply chain resilience and performance under the effect of supply chain dynamism. Ann. Oper. Res. 2024, 333, 627–652. [Google Scholar] [CrossRef]
- Ivanov, D. Intelligent digital twin (iDT) for supply chain stress-testing, resilience, and viability. Int. J. Prod. Econ. 2023, 263, 108938. [Google Scholar] [CrossRef]
- Grover, P.; Kar, A.K.; Dwivedi, Y.K. Understanding artificial intelligence adoption in operations management: Insights from the review of academic literature and social media discussions. Ann. Oper. Res. 2022, 308, 177–213. [Google Scholar] [CrossRef]
- Wamba, S.F.; Guthrie, C.; Queiroz, M.M.; Minner, S. ChatGPT and generative artificial intelligence: An exploratory study of key benefits and challenges in operations and supply chain management. Int. J. Prod. Res. 2024, 62, 5676–5696. [Google Scholar] [CrossRef]
- Meena, P.L.; Kumar, G.; Ramkumar, M. Supply chain sustainability in emerging economy: A negative relationship conditions’ perspective. Int. J. Prod. Econ. 2023, 261, 108865. [Google Scholar] [CrossRef]
- Han, Y.; Fang, X. Systematic review of adopting blockchain in supply chain management: Bibliometric analysis and theme discussion. Int. J. Prod. Res. 2024, 62, 991–1016. [Google Scholar] [CrossRef]
- Ivanov, D.; Guo, Z.; Shen, B.; Chang, Q.C. Analysis, optimization, and collaboration in digital manufacturing and supply chain systems. Int. J. Prod. Econ. 2024, 269, 109130. [Google Scholar] [CrossRef]
- Simon, H. A behavioral model of rational choice. Models of man, social and rational: Mathematical essays on rational human behavior in a social setting. J. Philos. 1957, 6, 241–260. [Google Scholar]


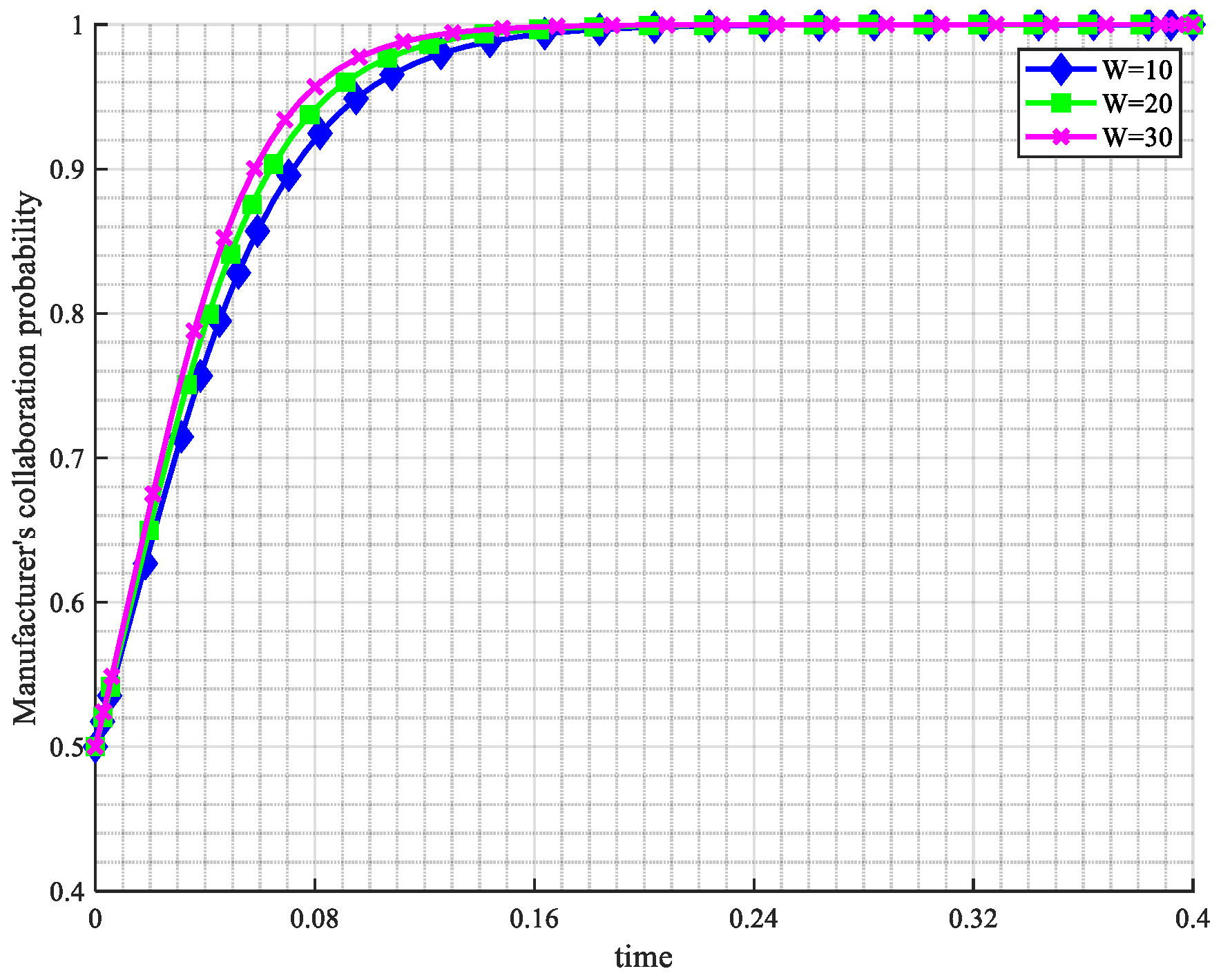



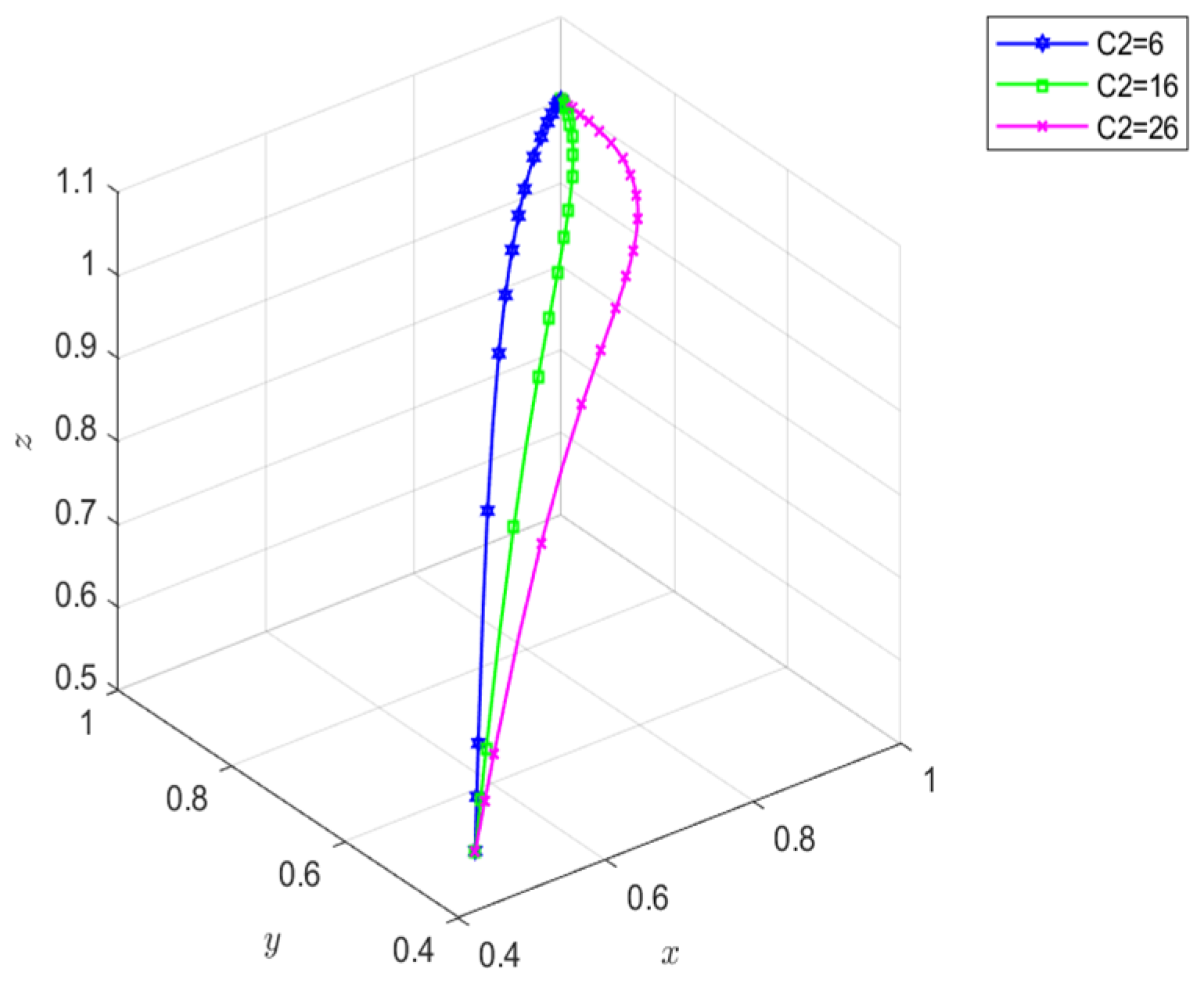


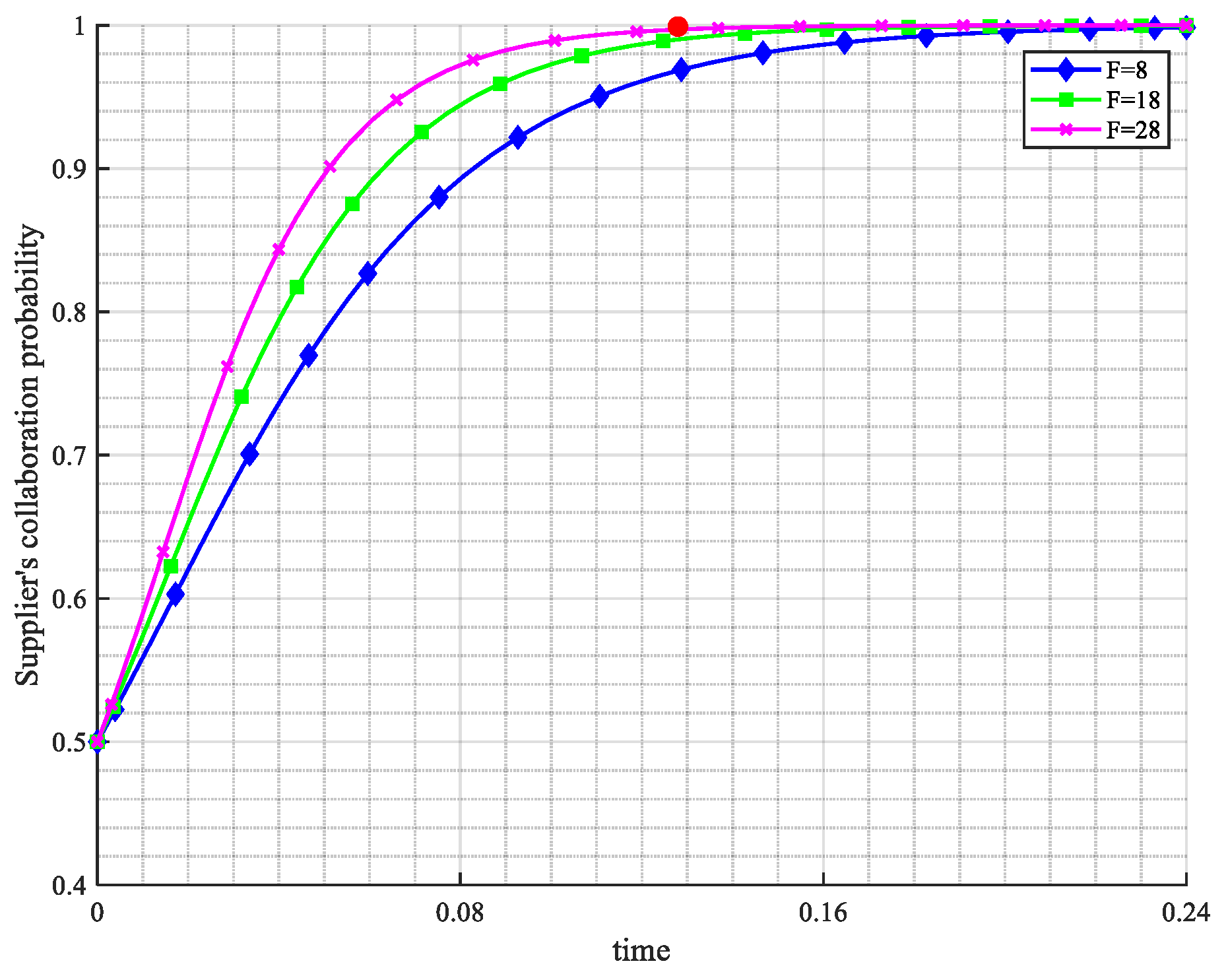
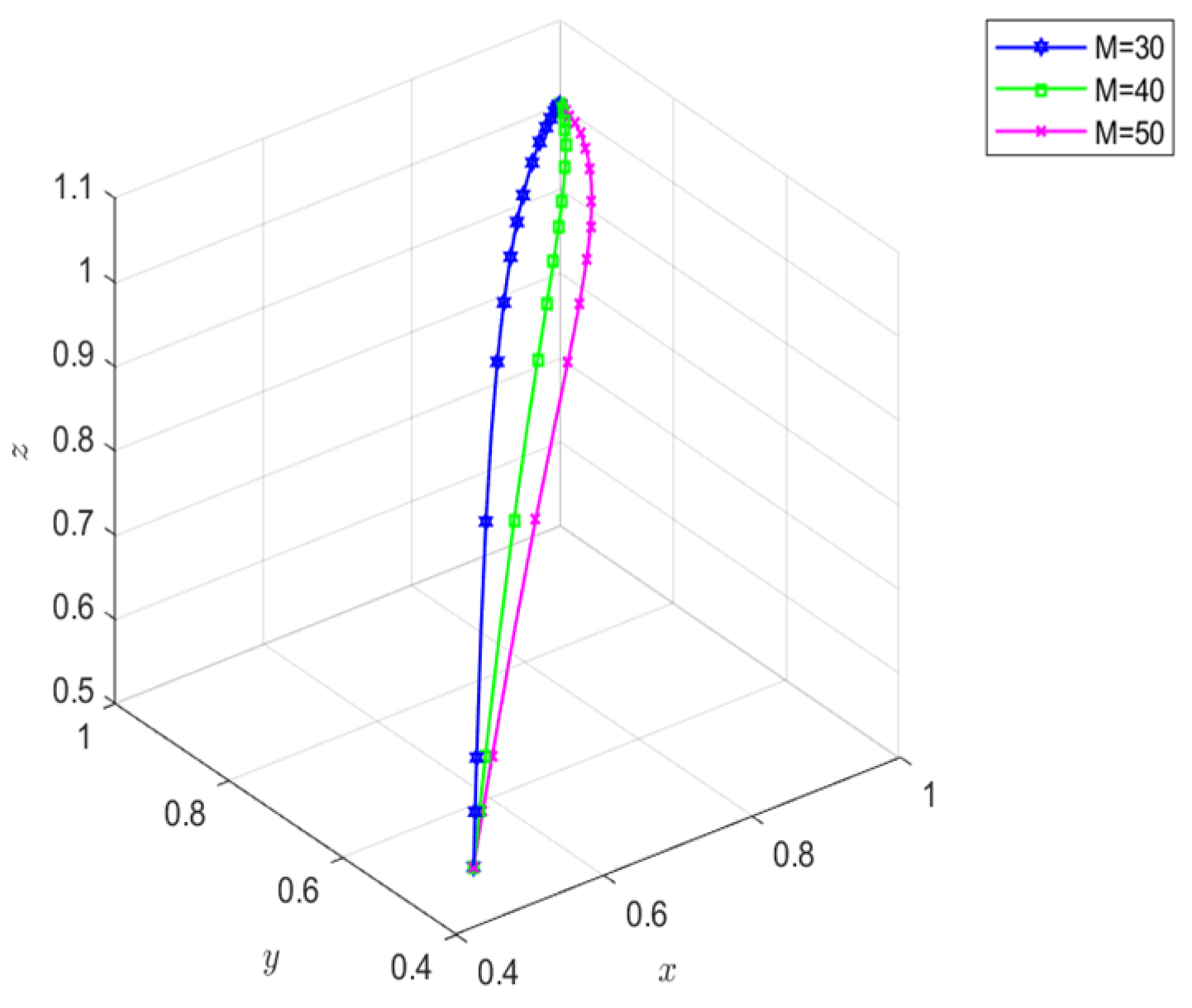
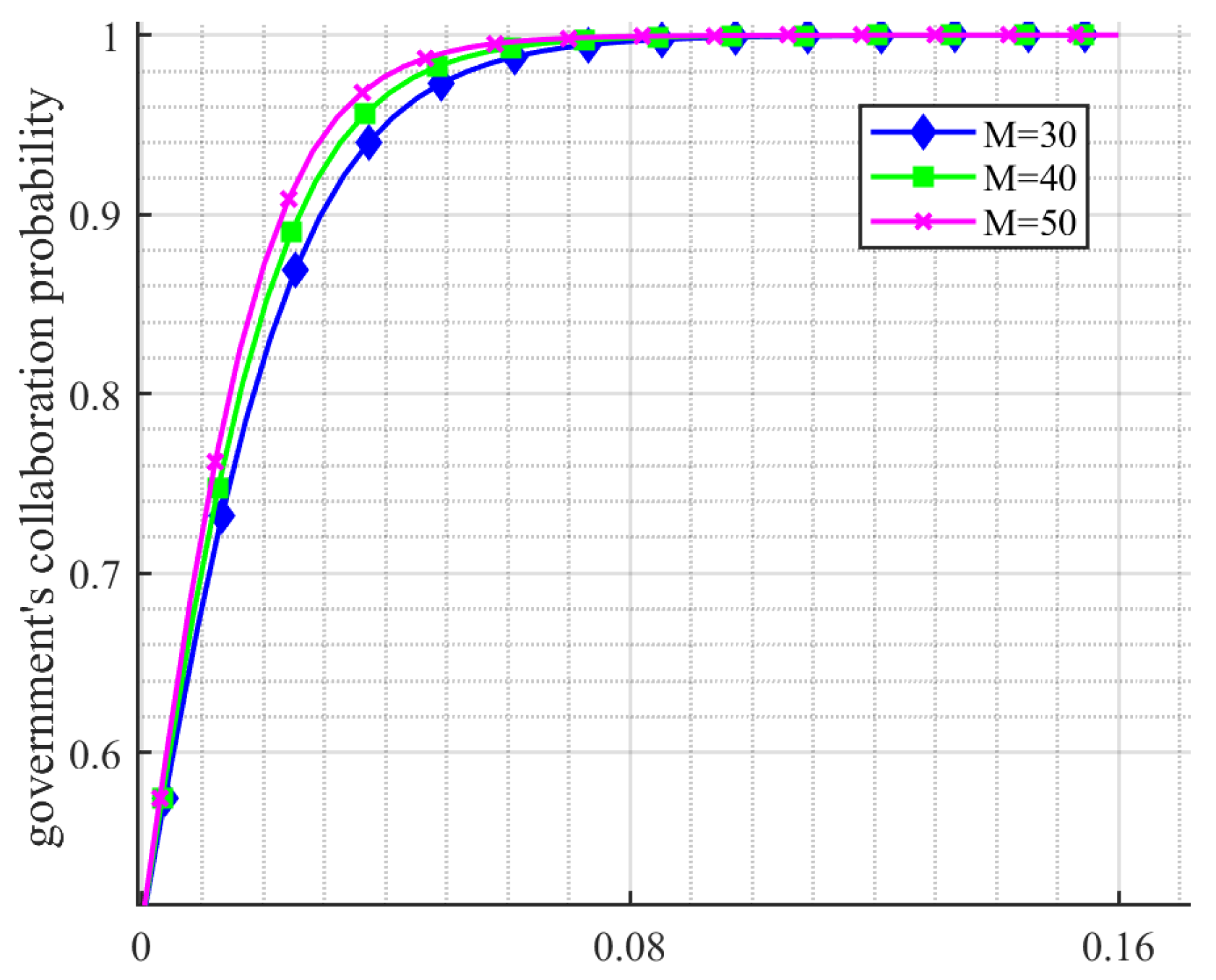
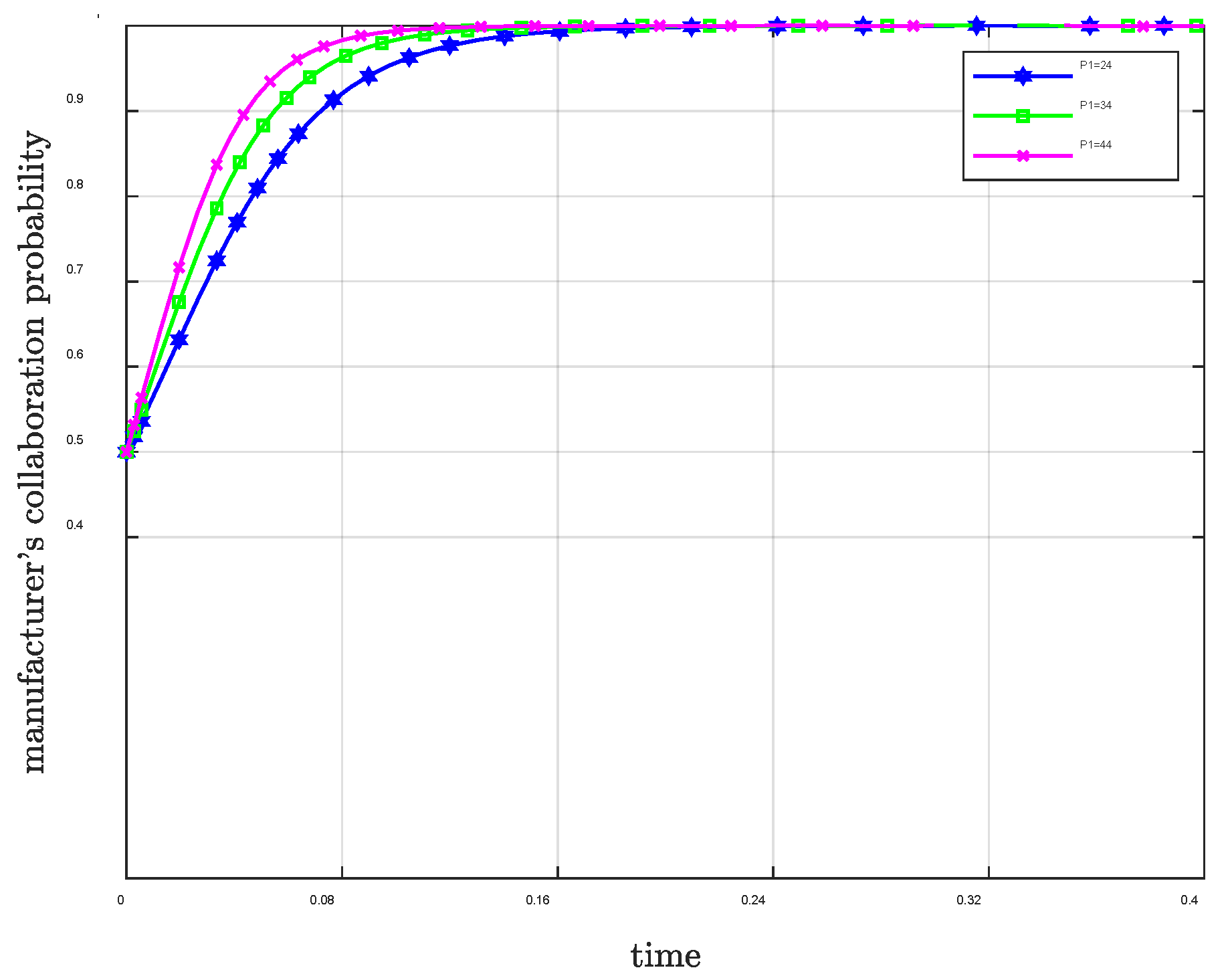
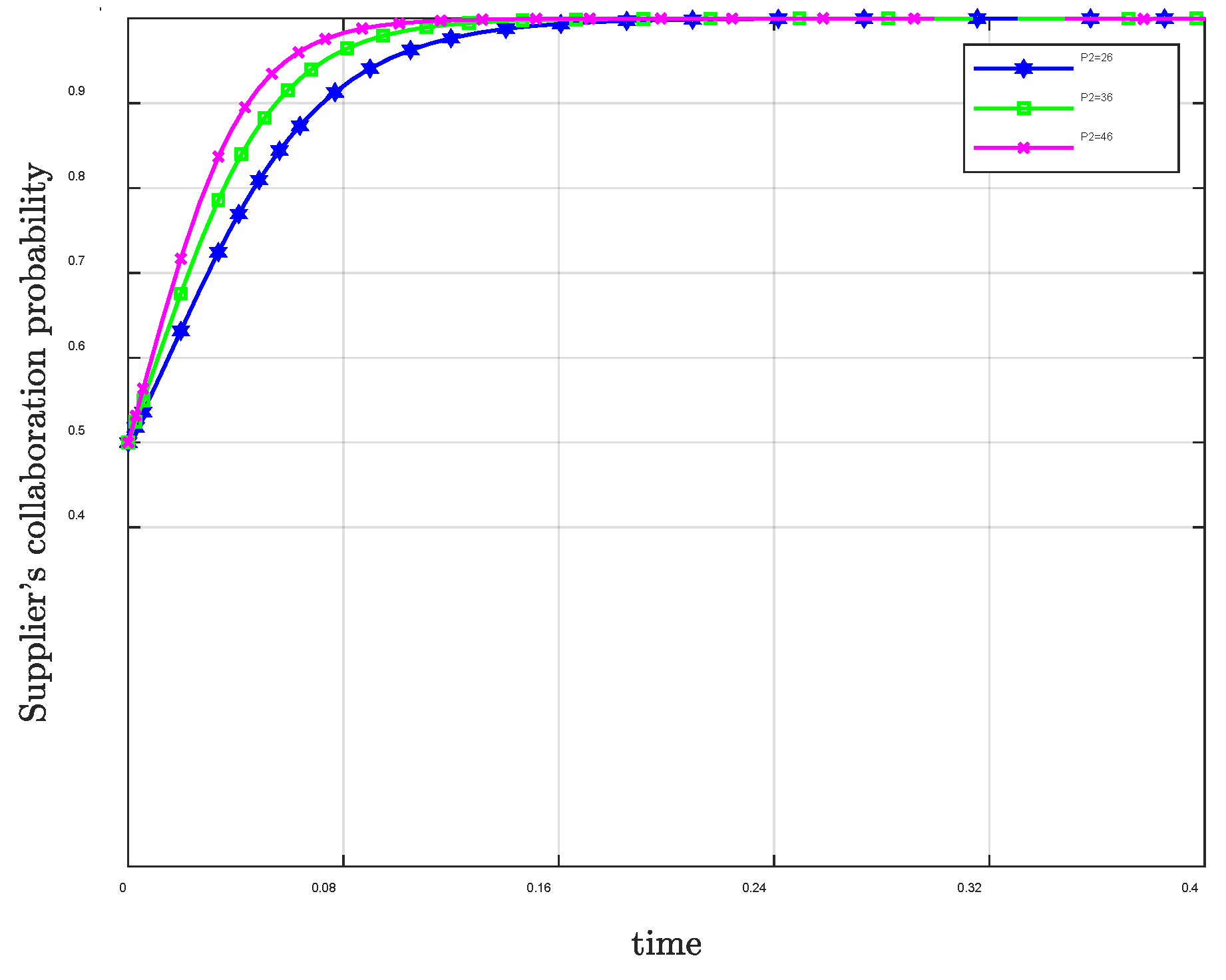
| Parameter Symbol | Definition |
|---|---|
| Government Subsidy Allocation Factor | |
| Government Collaboration Costs | |
| Manufacturer Collaboration Costs | |
| Supplier Collaboration Costs | |
| Government Basic Benefits | |
| Government Collaboration Benefits | |
| Return on Investment of Manufacturers’ Idle Resources | |
| Return on Investment of Supplier Idle Resources | |
| Manufacturer Collaboration Benefits | |
| Supplier Collaboration Benefits | |
| Hitchhiking by Manufacturer | |
| Hitchhiking by Supplier | |
| Losses from Negative Government Collaboration | |
| Losses from Manufacturer Non-collaboration | |
| Losses from Supplier Non-collaboration | |
| Government Subsidies | |
| Government Negative Collaboration Penalty | |
| Enterprise Penalties |
| Manufacturer | Supplier | Government | |
|---|---|---|---|
| Regional collaboration | Regional collaboration | ||
| No regional collaboration | |||
| No regional collaboration | Regional collaboration | ||
| No regional collaboration | |||
| Equilibrium Point | Eigenvalue | Stability |
|---|---|---|
| Instability point | ||
| Saddle point | ||
| Saddle point | ||
| Saddle point | ||
| Saddle point | ||
| Saddle point | ||
| Saddle point | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Feng, Y.; Cao, G. AI-Assisted Regional Collaborative Game of an Emergency Supplies Reserve Supply Chain. Systems 2025, 13, 977. https://doi.org/10.3390/systems13110977
Zhou J, Feng Y, Cao G. AI-Assisted Regional Collaborative Game of an Emergency Supplies Reserve Supply Chain. Systems. 2025; 13(11):977. https://doi.org/10.3390/systems13110977
Chicago/Turabian StyleZhou, Jinhua, Yanan Feng, and Guangxin Cao. 2025. "AI-Assisted Regional Collaborative Game of an Emergency Supplies Reserve Supply Chain" Systems 13, no. 11: 977. https://doi.org/10.3390/systems13110977
APA StyleZhou, J., Feng, Y., & Cao, G. (2025). AI-Assisted Regional Collaborative Game of an Emergency Supplies Reserve Supply Chain. Systems, 13(11), 977. https://doi.org/10.3390/systems13110977






