Dynamic Reward–Punishment Mechanisms Driving Agricultural Systems Toward Sustainability in China
Abstract
1. Introduction
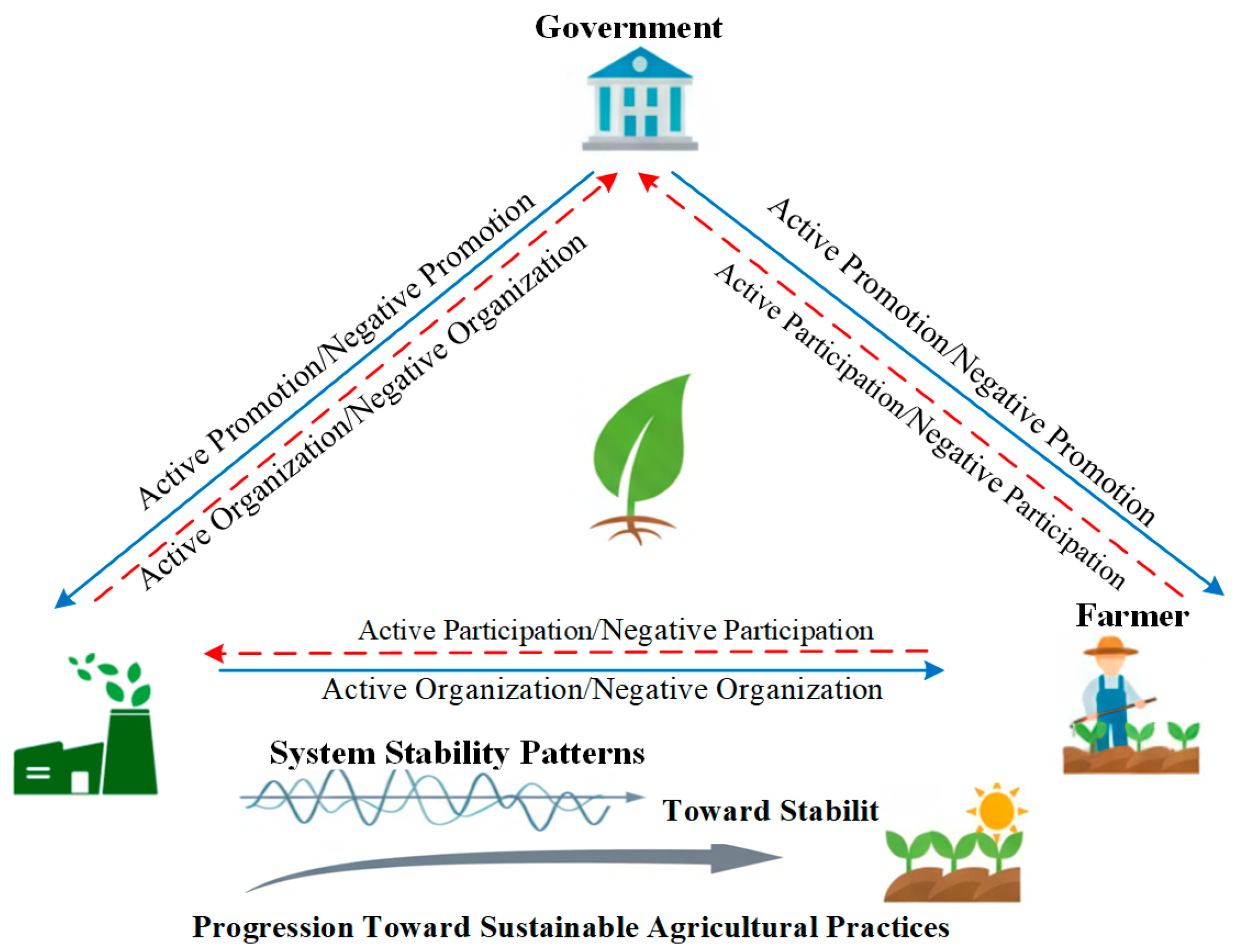
2. Model Assumptions and Construction
2.1. Model Assumptions
2.2. Model Construction
3. Evolutionary Game Analysis
3.1. Stability Analysis of Government
3.2. Stability Analysis of Corporate Strategy
3.3. Stability Analysis of Farmer Strategy
3.4. Solutions for System Stability
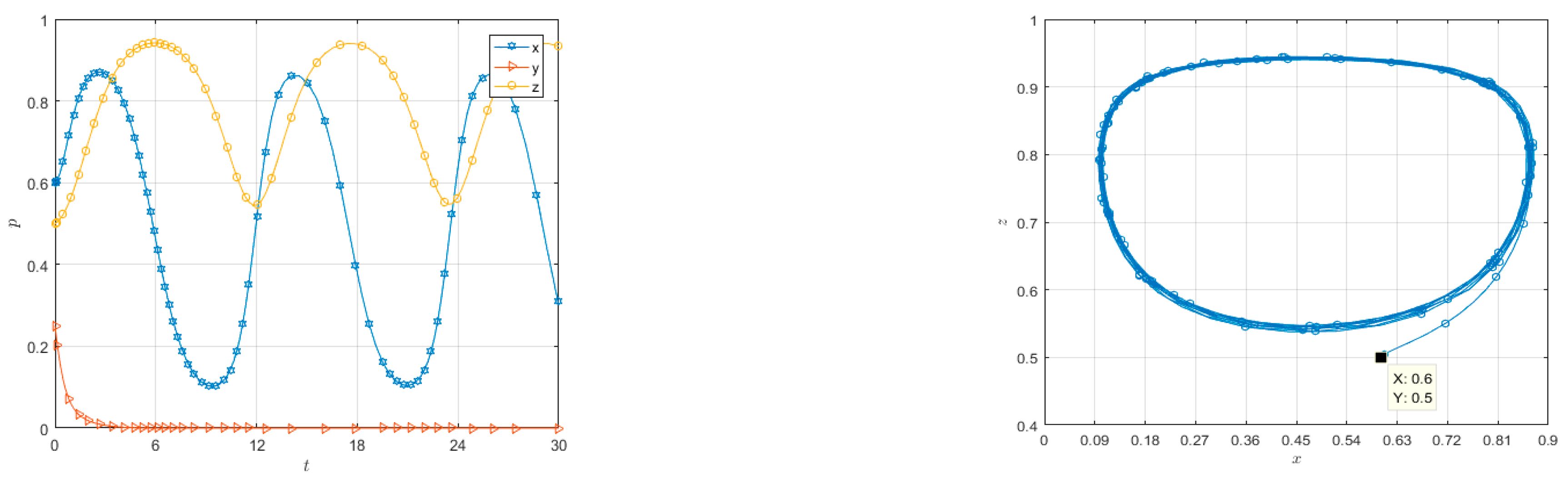
4. Numerical Analysis of Evolutionary Strategy
4.1. Simulation Data
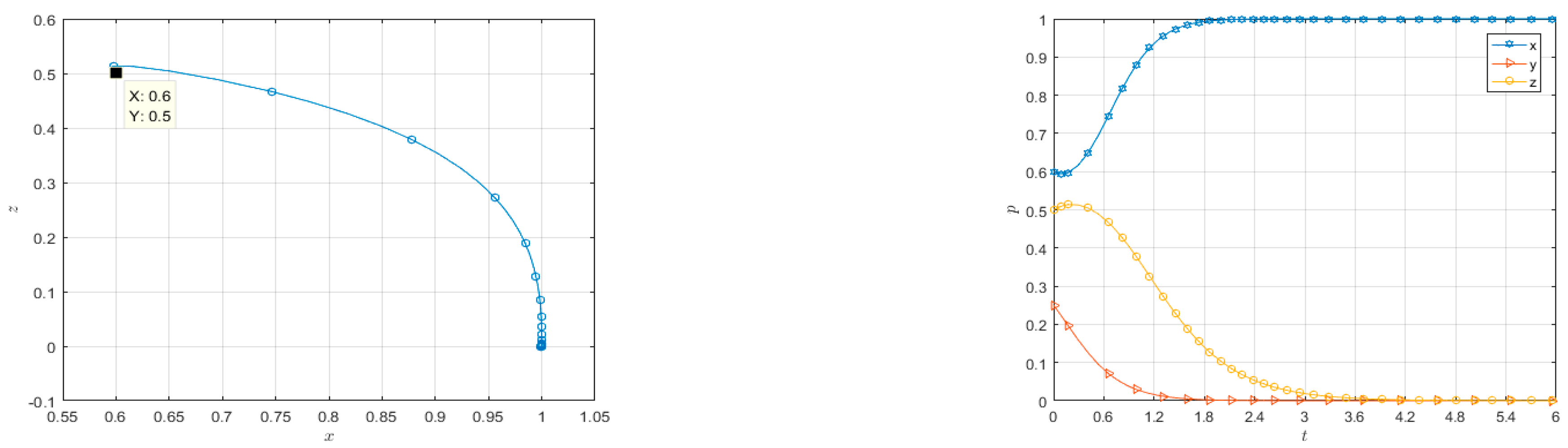
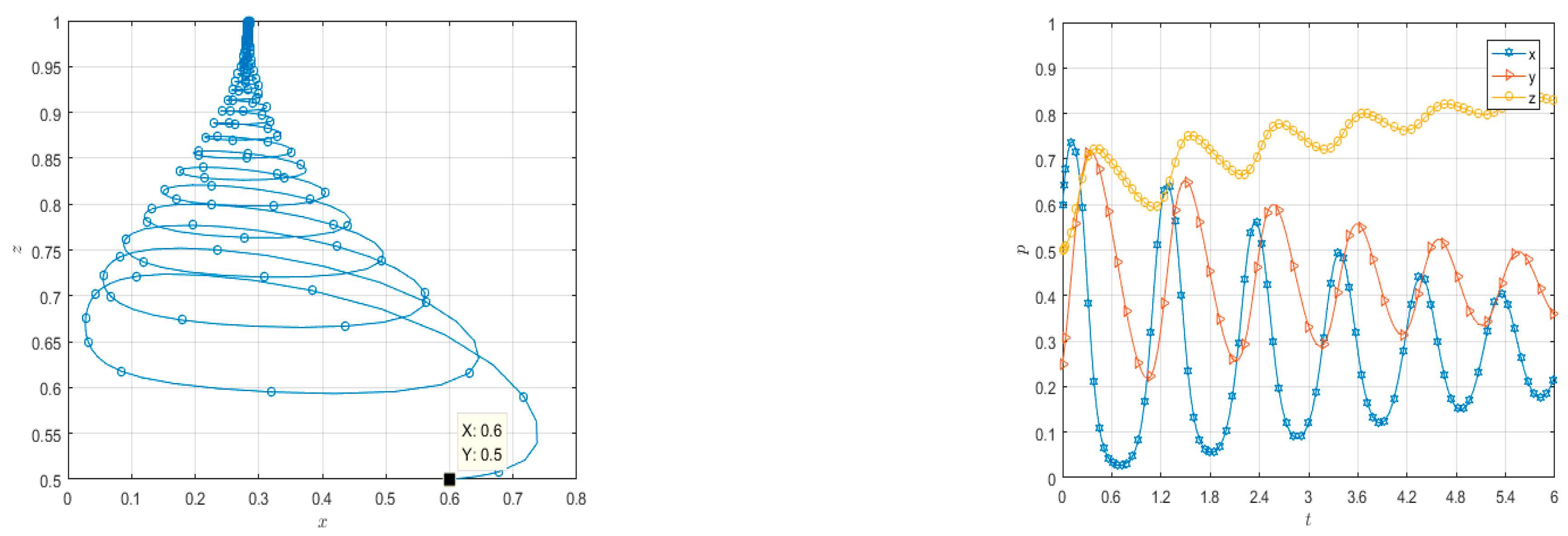
4.2. Numerical Simulation of Three-Party Evolutionary Game
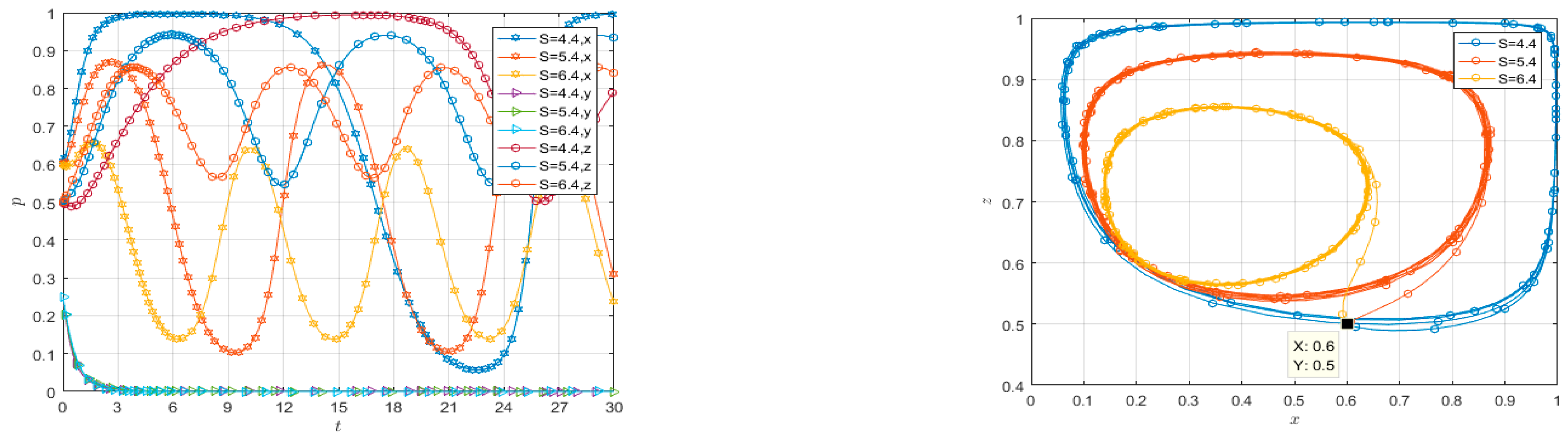
4.3. Linear Reward and Punishment Machine Mechanism
4.3.1. Linear Static Rewards
4.3.2. Linear Static Penalty
4.3.3. Linear Static Reward and Dynamic Punishment
4.3.4. Linear Dynamic Reward and Static Penalty
4.3.5. Linear Dynamic Reward and Dynamic Penalty
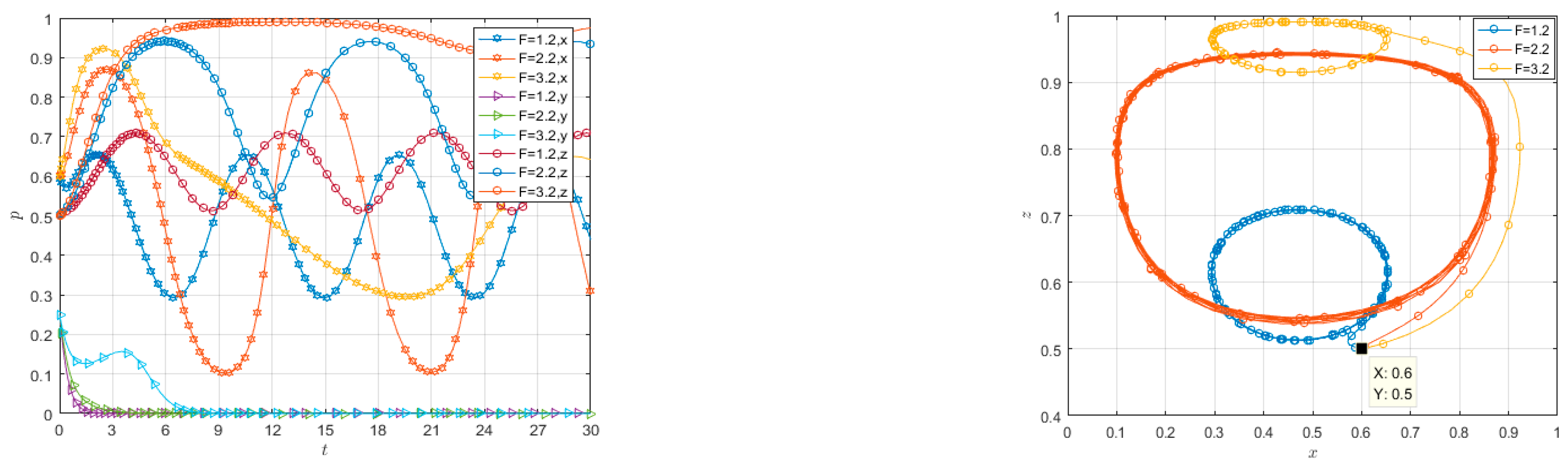
4.4. Nonlinear Dynamic Reward and Penalty
4.4.1. Nonlinear Dynamic Reward and Penalty Mechanism
4.4.2. Sensitivity Analysis of Incentive Allocation and Penalty Intensity
5. Discussion
6. Conclusions
- (i)
- Mechanism ranking. The analysis shows that nonlinear dynamic reward–punishment mechanisms outperform linear dynamic mechanisms, and linear dynamic mechanisms outperform purely static reward or static penalty schemes. Nonlinear dynamic mechanisms are therefore identified as the most effective approach for achieving a stable cooperative equilibrium among government, enterprises, and farmers.
- (ii)
- Policy relevance. The Conclusions emphasize that effective agricultural sustainability governance should not rely on uniform, one-size-fits-all subsidies or fixed penalties. Instead, the most robust outcomes emerge from calibrated, performance-contingent incentives that adapt to observed behavior. This reflects a shift from continuous maximal intervention by government to targeted, fiscally sustainable guidance that still maintains enterprise organization and farmer participation.
- (iii)
- Limitations and future work. The Conclusions explicitly acknowledge the current study’s scope and remaining gaps. First, although the model captures patterns observed in practice (e.g., unstable enterprise participation), full empirical validation using longitudinal policy and market data is identified as a priority for future research. Second, the present model focuses on three stakeholders—government, enterprises, and farmers—and does not yet incorporate other influential actors such as financial institutions, downstream retailers, or consumers. Third, region-specific heterogeneity in China is not yet parameterized. These issues are now clearly identified as directions for subsequent work.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNY | (Chinese Yuan) |
| USD | (United States Dollar) |
References
- Hmamou, M.; Chafiq, T.; Ouhammou, I.; Lmoudden, O.A.; Raji, M.; Ouaskit, S. Assessing Land Cover Change Detection in a Developing Country with Machine and Deep Learning Algorithms: A Case Study. Environ. Dev. Sustain. 2025. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, H.; Xia, X.; Yang, Z.; Zhu, S. Can a Crop Rotation and Fallow System Reduce the Carbon Emission intensity of Agriculture? Land 2024, 13, 293. [Google Scholar] [CrossRef]
- Abbasi, K.R.; Zhang, Q. Augmenting Agricultural Sustainability: Investigating the Role of Agricultural Land, Green innovation, and Food Production in Reducing Greenhouse Gas Emissions. Sustain. Dev. 2024, 32, 6918–6933. [Google Scholar] [CrossRef]
- Bathige, N.S.P.; Moseley, W.G. Snapshot of a Crisis: Food Security and Dietary Diversity Levels Among Disrupted Conventional and Long-Term Organic Tea-Smallholders in Sri Lanka. Singap. J. Trop. Geogr. 2024, 45, 18–38. [Google Scholar] [CrossRef]
- Mausch, K.; Hall, A.; Hambloch, C. Colliding Paradigms and Trade-offs: Agri-Food Systems and Value Chain interventions. Glob. Food Secur. 2020, 26, 100439. [Google Scholar] [CrossRef]
- Nicli, S.; Elsen, S.U.; Bernhard, A. Eco-Social Agriculture For Social Transformation and Environmental Sustainability: A Case Study of the UPAS-Project. Sustainability 2020, 12, 5510. [Google Scholar] [CrossRef]
- Pashkov, S.V.; Imashev, E.Z.; Baubekova, G.K.; Kaimuldinova, K.D.; Tokpanov, Y.A.; Nurgaliyeva, G.Z.; Baimukasheva, G.K.; Kenzhebay, R.N.; Kassenov, S.K.; Ukrainskiy, P.A. Ecological–Economical and Ethno-Cultural Determinants of the Develop-ment of Organic Farming in Kazakhstan. Sustainability 2024, 16, 4065. [Google Scholar] [CrossRef]
- Hong, T.; Yang, C. Temporal and Spatial Evolution of Ecosystem Service Supply and Demand in the Tibetan Plateau: Implications For Land Use Patterns and Relationships. Pol. J. Environ. Stud. 2024, 33, 2679–2691. [Google Scholar] [CrossRef]
- Shi, Y.; Wei, W. Terracing Drives Chinese Loess Plateau toward Carbon Neutrality: Spatiotemporal interaction Between Land Use Transitions and SOC Storage. J. Environ. Manag. 2025, 385, 125760. [Google Scholar] [CrossRef] [PubMed]
- Kozicka, M.; Gotor, E.; Ocimati, W.; de Jager, T.; Kikulwe, E.; Groot, J.C. Responding to Future Regime Shifts with Agrobiodi-versity: A Multi-Level Perspective on Small-Scale Farming in Uganda. Agric. Syst. 2020, 183, 102864. [Google Scholar] [CrossRef]
- Amoak, D.; Lupafya, E.; Dakishoni, L.; Luginaah, I. Towards Food Sovereignty: The Role of Smallholder Farmers’ Seed Security in Improving Climate Change Resilience in Northern Malawi. Geogr. Rev. 2025, 115, 243–268. [Google Scholar] [CrossRef]
- Jamal, R. Blue Grabbing of the Green Crop Fields: A Development Conundrum in Southwest Coastal Bangladesh. Land Use Policy 2024, 141, 107161. [Google Scholar] [CrossRef]
- Kasztelan, A.; Nowak, A. Green Growth in Agriculture―New Measurement Concept and Its Empirical Verification. Sustain. Dev. 2024, 32, 325–335. [Google Scholar] [CrossRef]
- Zhou, F.; Wen, C. Research on the Level of Agricultural Green Development, Regional Disparities, and Dynamic Distribution Evolution in China from the Perspective of Sustainable Development. Agriculture 2023, 13, 1441. [Google Scholar] [CrossRef]
- Yang, C.; Liang, X.; Xue, Y.; Zhang, Y.Y.; Xue, Y. Can Government Regulation Weak the Gap between Green Production Intention and Behavior? Based on the Perspective of Farmers’ Perceptions. J. Clean. Prod. 2024, 434, 139743. [Google Scholar] [CrossRef]
- Labianca, M. Proposal of a Method for Identifying Socio-Economic Spatial Concentrations for the Development of Rural Areas: An Application to the Apulia Region (Southern Italy). Sustainability 2023, 15, 3180. [Google Scholar] [CrossRef]
- Zhan, J.; Zhang, F.; Chu, X.; Liu, W.; Zhang, Y. Ecosystem Services Assessment Based on Emergy Accounting in Chongming Island, Eastern China. Ecol. Indic. 2019, 105, 464–473. [Google Scholar] [CrossRef]
- Zieliński, M.; Koza, P.; Łopatka, A. Agriculture from Areas Facing Natural or Other Specific Constraints (ANCs) in Poland, Its Characteristics, Directions of Changes and Challenges in the Context of the European Green Deal. Sustainability 2022, 14, 11828. [Google Scholar] [CrossRef]
- Zuberi, M.; Spies, M.; Nielsen, J.Ø. Is There a Future for Smallholder Farmers in Bioeconomy? The Case of ‘Improved’ Seeds in South Punjab, Pakistan. For. Policy Econ. 2024, 158, 103100. [Google Scholar] [CrossRef]
- Wang, Q.; Ni, M.; Wen, W.; Qi, R.; Zhang, Q. Study on Sustainable Operation Mechanism of Green Agricultural Supply Chain Based on Uncertainty of Output and Demand. Sustainability 2024, 16, 5460. [Google Scholar] [CrossRef]
- Varela-Candamio, L.; Calvo, N.; Novo-Corti, I. The Role of Public Subsidies For Efficiency and Environmental Adaptation of Farming: A Multi-Layered Business Model Based on Functional Foods and Rural Women. J. Clean. Prod. 2018, 183, 555–565. [Google Scholar] [CrossRef]
- Shackelford, G.E.; Kelsey, R.; Dicks, L.V. Effects of Cover Crops on Multiple Ecosystem Services: Ten Meta-Analyses of Data from Arable Farmland in California and the Mediterranean. Land Use Policy 2019, 88, 104204. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, H.; Ding, X.; Chen, Y. Does Digital Village Construction Empower the Green Allocation of Agricultural Water Resources? Systems 2024, 12, 214. [Google Scholar] [CrossRef]
- Liu, M.; Liu, H. influence of Climate Change on Carbon Emissions During Grain Production and Its Mechanism. Sustainability 2023, 15, 10237. [Google Scholar] [CrossRef]
- Ghazi, A.A.; El-Nahrawy, S.; El-Ramady, H.; Ling, W. Biosynthesis of Nano-Selenium and Its Impact on Germination of Wheat under Salt Stress for Sustainable Production. Sustainability 2022, 14, 1784. [Google Scholar] [CrossRef]
- Villamor, G.B.; Steer, B.S.C.; Baluyot, A.; Meason, D.F. Understanding Land-Use Transitions in Rural Areas of the North Island, New Zealand from 1996 to 2018: An Intensity Analysis Approach. GeoJournal 2025, 90, 76. [Google Scholar] [CrossRef]
- Yu, M.; Li, H.; Song, S.; Shan, X.; He, G.; Li, F.; Shi, Y.; Hirwa, H.; Chen, G. Addressing Ethiopia’s Grand Challenge of Achieving Food Security While Ensuring Land-Use Sustainability. Land Use Policy 2025, 157, 107664. [Google Scholar] [CrossRef]
- Pereira, P.; Pinto, L.V.; Gomes, E.; Inácio, M. Land Use Changes in Klaipeda, Kaunas and Vilnius (Lithuania) Functional Urban Areas. Geocarto Int. 2025, 40, 2511156. [Google Scholar] [CrossRef]
- Wang, M.; Lin, N.; Huang, X.; Tang, Y. Mitigating Farmland Use Carbon Emissions: The Dynamic Role of Farmland Use Transition. J. Clean. Prod. 2024, 450, 141866. [Google Scholar] [CrossRef]
- Gurgel, A.; Narayan, K.B.; Reilly, J.; Gao, X.; Vernon, C.; Morris, J.; Schlosser, A.; Paltsev, S. Future Spatially Explicit Patterns of Land Transitions in the United States with Multiple Stressors. Earth’s Futur. 2025, 13, e2024EF005016. [Google Scholar] [CrossRef]
- Chandel, P.; Muskan; Kumar, R. Assessment of Forest Fragmentation in the Sub-Himalayan Region in Haryana State and Ad-joining Area. Scott. Geogr. J. 2025, 1–20. [Google Scholar] [CrossRef]
- Shi, X.; Zhang, J.; Liu, S.; Ding, H.; Chen, X.; Wang, L.; Zhang, D. Impact of Land Use Change on Carbon Storage in the Middle Reaches of the Yellow River, China. J. Arid. Land 2025, 17, 167–181. [Google Scholar] [CrossRef]
- Hussain, M.; Khan, A.S.; Khaliq, I.; Maqsood, M. Correlation Studies of Some Qualitative and Quantitative Traits with Grain Yield in Spring Wheat across Two Environments. Pak. J. Agric. Sci. 2012, 49, 1–4. [Google Scholar]
- Li, J.; Wang, J.; Du, Y.; Hou, X.; Xi, R.; Yang, Y. Assessing Landscape Fragmentation and Its Driving Factors in Arid Regions: A Case Study of the Manas River, China. Ecol. Indic. 2025, 171, 113253. [Google Scholar] [CrossRef]
- Wang, Y.; Song, D.; Liu, C.; Li, S.; Yuan, M.; Gong, J.; Yang, J. Spatial Correlation of Non-Agriculturalization and Non-Grain Utilization Transformation of Cultivated Land in China and Its Implications. Land 2025, 14, 1031. [Google Scholar] [CrossRef]
- Selvi, B.V.; Raj, S.V.; Parthiban, K.T.; Ramesh, D. Land Use and Cropping Pattern Dynamics under the Climate Change Regime. Plant Sci. Today 2025, 12, 6614. [Google Scholar] [CrossRef]
- Ma, R.; Wang, M.; Wang, C.; Zhang, Y.; Zhou, X.; Jiang, L. Spatiotemporal Decoupling of Vegetation Productivity and Sustainable Carbon Sequestration in Karst Ecosystems: A Deep-Learning Synthesis of Climatic and Anthropogenic Drivers. Sustainability 2025, 17, 5840. [Google Scholar] [CrossRef]
- Cai, X.; Wang, Y.; Luo, W.; Wu, Y.; Cheng, A.; Chen, J.; Zhang, L.; Wang, S. Characteristics of Tree Growth at the Early Stage of Natural Succession on Abandoned Farmland in Southwest China’s Karst Region. Forests 2025, 16, 674. [Google Scholar] [CrossRef]
- Haque, R.; Moniruzzaman, M.; Arman; Hasan, R.; Lat, T.; Kabir, N.; Sarker, J.; Tijing, L.; Shon, H.K.; Ayejoto, D.A.; et al. Land Use Transition and Ecological Consequences: A Spatiotemporal Analysis in South-Eastern Bangladesh. Earth Syst. Environ. 2025, 9, 1135–1148. [Google Scholar] [CrossRef]
- Wang, M.; Huang, X.; Chen, Y.; Tang, Y. Multifunctional Farmland Use Transition and Its Impact on Synergistic Governance Efficiency for Pollution Reduction, Carbon Mitigation, and Production Increase: A Perspective of Major Function-Oriented Zoning. Habitat Int. 2024, 153, 103207. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, S.; Li, Y. the Hidden Costs of Land Use Transformation: Ecological Degradation in Arid and Semi-Arid Areas. J. Arid. Environ. 2025, 230, 105433. [Google Scholar] [CrossRef]
- Bates, J.; Morrison, K.D.; Madella, M.; Hill, A.C.; Whitehouse, N.J.; Abro, T.; Ajithprasad, P.; Anupama, K.; Casile, A.; Chandio, A.; et al. Early to Mid-Holocene Land Use Transitions in South Asia: A New Archaeological Synthesis of Potential Human Impacts. PLoS ONE 2025, 20, e0313409. [Google Scholar] [CrossRef] [PubMed]
- Moore, J.D.; Donaldson, J.A. Going Green in Thailand: Upgrading in Global Organic Value Chains. J. Agrar. Change 2023, 23, 844–867. [Google Scholar] [CrossRef]
- de Waroux, Y. Frontier Constellations: A History of Land-Use Regimes in Paraguay’s Pilcomayo River Basin. Geogr. Rev. 2024, 114, 489–519. [Google Scholar] [CrossRef]
- Fendel, V.; Maurer, C.; Kranert, M.; Huang, J.; Schäffner, B. The Potential of the Co-Recycling of Secondary Biodegradable Household Resources Including Wild Plants to Close Nutrient and Carbon Cycles in Agriculture in Germany. Sustainability 2022, 14, 5277. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, Z.; Zhang, L.; Chen, Q.; Luo, D.; Huang, D.; Feng, Q.; Zhu, C. Trade-Offs and Synergistic Evolution of Ecosystem Services and Land Use Driving Mechanisms in Karst Ecologically Vulnerable Areas of China. Geocarto Int. 2025, 40, 2509111. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, X.; Shu, Q.; Yao, Z.; Wu, H.; Gao, S. Effects of Urbanization-induced Land Use Changes on Ecosystem Services: A Case Study of the Anhui Province, China. Land 2025, 14, 1238. [Google Scholar] [CrossRef]
- McManamay, R.A.; Vernon, C.R.; Chen, M.; Thompson, I.; Khan, Z.; Narayan, K.B. Dynamic Urban Land Extensification Is Projected to Lead to Imbalances in the Global Land-Carbon Equilibrium. Commun. Earth Environ. 2024, 5, 70. [Google Scholar] [CrossRef]
- Wei, W.; Wang, N.; Yin, L.; Guo, S.; Bo, L. Spatio-Temporal Evolution Characteristics and Driving Mechanisms of Urban–Agricultural–Ecological Space in Ecologically Fragile Areas: A Case Study of the Upper Reaches of the Yangtze River Economic Belt, China. Land Use Policy 2024, 145, 107282. [Google Scholar] [CrossRef]
- Zysk, E.; Dawidowicz, A.; Nowak, M.; Figurska, M.; Źróbek, S.; Źróbek, R.; Burandt, J. Organizational Aspects of the Concept of a Green Cadastre for Rural Areas. Land Use Policy 2020, 91, 104373. [Google Scholar] [CrossRef]
- Cheng, L.; Huang, P.; Zhang, M.; Wang, K.; Zhang, K.; Zou, T.; Lu, W. Optimizing virtual power plants cooperation via evolutionary game theory: The role of reward–punishment mechanisms. Mathematics 2025, 13, 2428. [Google Scholar] [CrossRef]
- Li, K.; Wang, X.; Lu, F.; Zhang, Z.; Sun, X. Research on monitoring mechanism of autonomous taxi: An evolutionary game approach. Appl. Math. Comput. 2025, 507, 129596. [Google Scholar] [CrossRef]
- Guttman, D.; Young, O.; Jing, Y.; Bramble, B.; Bu, M.; Chen, C.; Furst, K.; Hu, T.; Li, Y.; Logan, K. Environmental governance in China: Interactions between the state and “Nonstate Actors”. J. Environ. Manag. 2018, 220, 126–135. [Google Scholar] [CrossRef] [PubMed]
- Lai, J.; Beethem, K.; Marquart-Pyatt, S.T. Farmers’ social capital in agricultural decision-making☆. Rural. Sociol. 2025. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Zhang, R.; Zhang, S. Sustainable promotion of farmers’ work performance: Servant leadership insights from Chinese agricultural entities. Front. Sustain. Food Syst. 2025, 9, 1474602. [Google Scholar] [CrossRef]
- Xu, Y.; Faraz, A.Z.; Sarfraz, M.; Arshad, S.; Sun, J.; Ahmad, A. Strategic capabilities for sustainability: An integrated model of digital inclusion and sustainable performance. Sustain. Dev. 2025. [Google Scholar] [CrossRef]
- Vermunt, D.; Negro, S.; Van Laerhoven, F.; Verweij, P.; Hekkert, M. Sustainability transitions in the agri-food sector: How ecology affects transition dynamics. Environ. Innov. Soc. Transit. 2020, 36, 236–249. [Google Scholar] [CrossRef]




| Symbol | Parameter | Description |
|---|---|---|
| G | Government | G > 0 |
| E | Agricultural enterprises | E > 0 |
| F | Farmers | F > 0 |
| Cg | Government actively promotes agricultural system sustainability transitions and pays the cost | Cg > 0 |
| Ec | Costs of government not promoting agricultural system sustainability practices | Ec > 0 |
| S | Costs of economic incentives to governments for firms and farmers to actively promote agricultural system sustainability transitions | S > 0 |
| Rg | Government policy incentives from the central government for proactive promotional behavior | Rg > 0 |
| Ce | Costs associated with the implementation of sustainable technologies | Ce > 0 |
| Cf | Search cost incurred by an enterprise in seeking new cooperative farmers | Cf > 0 |
| Re | Enterprise agricultural system sustainability market gains | Re > 0 |
| CI | Financial returns to firms undertaking agricultural system sustainability transitions | CI > 0 |
| Df | Additional costs for farmers to participate in agricultural system sustainability transitions | Df > 0 |
| Rf | Benefits derived from farmers’ participation in agricultural system sustainability transitions | Rf > 0 |
| Ck | Market finding costs incurred by farmers selling on their own | Ck > 0 |
| Tf | Farmers’ income when they do not participate in agricultural system sustainability transitions | Tf > 0 |
| δ | Additional social benefits from the participation of enterprises and farmers in agricultural system sustainability transitions | δ > 0 |
| γ | Enterprises and farmers actively participate in agricultural system sustainability transitions to obtain health benefits for the local ecosystem | γ > 0 |
| P | Social losses from the government not promoting agricultural system sustainability transitions | P |
| T | Social losses from enterprises not organizing agricultural system sustainability transitions | T |
| Q | Social losses from farmers’ non-participation in sustainable agricultural system development | Q |
| Game Subject | Enterprises | Farmers | ||
|---|---|---|---|---|
| Positive Participation z | Negative Participation 1 − z | |||
| Government | Promotion of sustainable agricultural production | Organizing sustainable agricultural production | ||
| Not organizing sustainable agricultural production | ||||
| Failure to promote sustainable agricultural production | Organizing sustainable agricultural production | |||
| Not organizing sustainable agricultural production | ||||
| Equilibrium Point | |||
|---|---|---|---|
| (0, 0, 0) | |||
| (0, 1, 0) | |||
| (0, 0, 1) | |||
| (0, 1, 1) | |||
| (1, 0, 0) | |||
| (1, 1, 0) | |||
| (1, 0, 1) | |||
| (1, 1, 1) |
| Parameter | Parameter Meaning | Assigned Value |
|---|---|---|
| Government actively promotes sustainable agricultural system use transition rewards provided by higher authorities | 5 | |
| Costs incurred by the government in actively promoting sustainable agricultural system use transition behaviors | 7.8 | |
| S | Amount of economic incentives provided by the government | 5.4 |
| Proportion of economic incentives obtained by enterprises | 0.5 | |
| Government constraints on enterprises not promoting sustainable agricultural system transition | 2.2 | |
| Market returns for enterprises | 8 | |
| Proportion of returns from enterprises organizing agricultural sustainable agricultural system transition | 0.5 | |
| Costs incurred by enterprises seeking farmer participation in agricultural sustainable agricultural system transition | 3.8 | |
| Financial returns on investments made by enterprises in sustainable technologies and practices | 2.8 | |
| Costs incurred by enterprises organizing sustainable agricultural system transition | 4.3 | |
| Returns for farmers participating in sustainable agricultural system transition | 1.5 | |
| Costs for farmers participating in sustainable agricultural system transition | 3.1 | |
| Returns for farmers not participating in sustainable agricultural system use transition | 3 | |
| Market seeking costs for farmers selling independently | 0.6 | |
| L | Agricultural sustainability transitions losses caused by farmers not participating in sustainable agricultural system transition | 2.2 |
| Costs of the government not promoting sustainable agricultural system transition behaviors | 1.1 | |
| Social losses of the government | 3 | |
| T | Social losses of enterprises | 2 |
| Social losses of farmers | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, R.; Zhang, T.; Wang, X. Dynamic Reward–Punishment Mechanisms Driving Agricultural Systems Toward Sustainability in China. Systems 2025, 13, 976. https://doi.org/10.3390/systems13110976
Cai R, Zhang T, Wang X. Dynamic Reward–Punishment Mechanisms Driving Agricultural Systems Toward Sustainability in China. Systems. 2025; 13(11):976. https://doi.org/10.3390/systems13110976
Chicago/Turabian StyleCai, Rongjiang, Tao Zhang, and Xi Wang. 2025. "Dynamic Reward–Punishment Mechanisms Driving Agricultural Systems Toward Sustainability in China" Systems 13, no. 11: 976. https://doi.org/10.3390/systems13110976
APA StyleCai, R., Zhang, T., & Wang, X. (2025). Dynamic Reward–Punishment Mechanisms Driving Agricultural Systems Toward Sustainability in China. Systems, 13(11), 976. https://doi.org/10.3390/systems13110976





