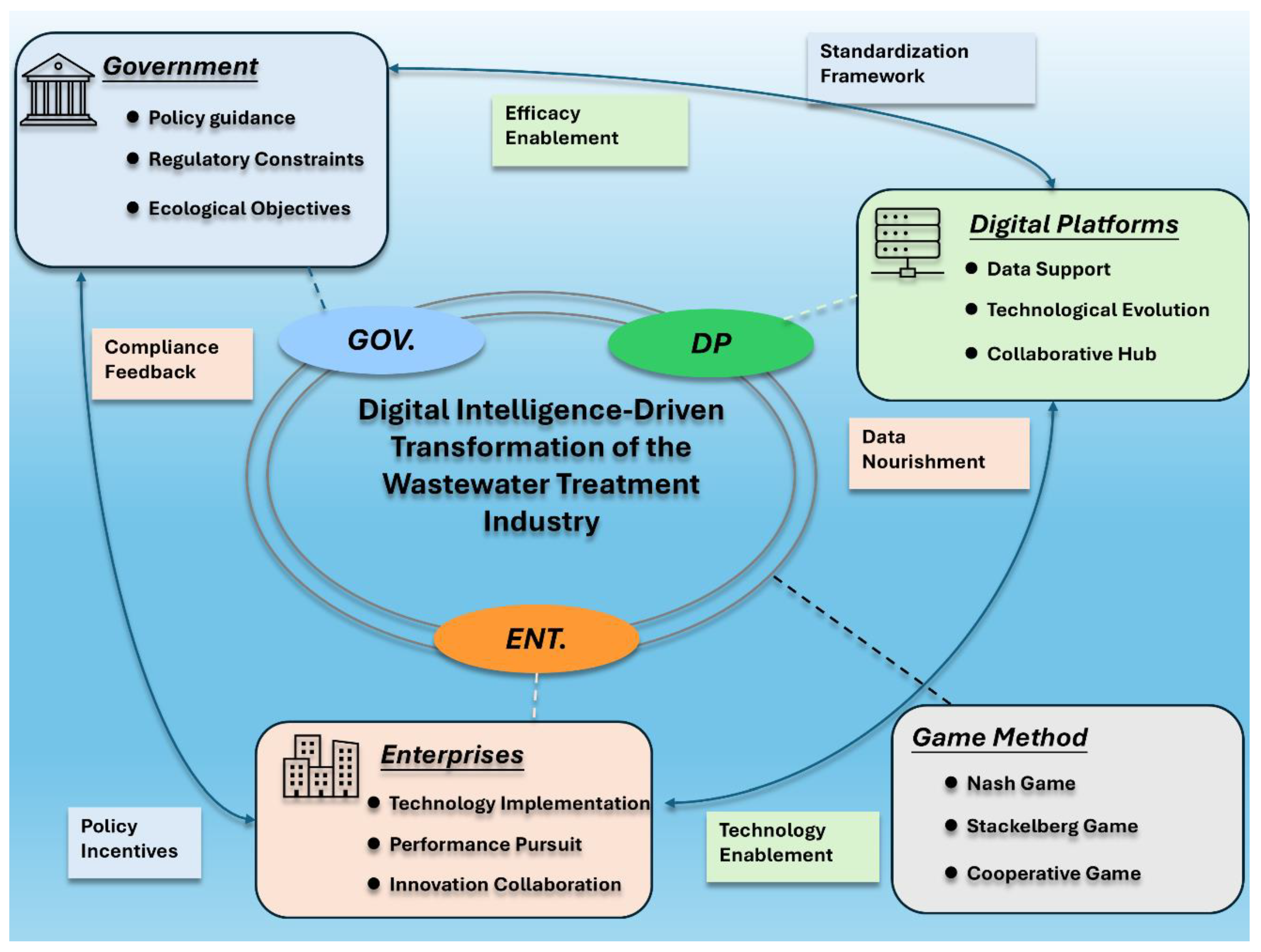
A Tripartite Differential Game Approach to Understanding Intelligent Transformation in the Wastewater Treatment Industry

Abstract

The intelligent transformation of the wastewater treatment industry, as a core component of the modern environmental governance system, is of decisive significance for achieving sustainable development goals. This study focuses on the issue of multi-stakeholder collaborative governance in the intelligent transformation of the wastewater treatment industry, with differential game theory as the core framework. A tripartite game model involving the government, wastewater treatment enterprises, and digital twin platforms is developed to depict the dynamic interrelations and mutual influences of strategy choices, thereby capturing the coordination mechanisms among government regulation, enterprise technology adoption, and platform support in the transformation process. Based on the dynamic optimization properties of differential games, the Hamilton–Jacobi–Bellman (HJB) equation is employed to derive the long-term equilibrium strategies of the three parties, presenting the evolutionary paths under Nash non-cooperative games, Stackelberg games, and tripartite cooperative games. Furthermore, the Sobol global sensitivity analysis is applied to identify key parameters influencing system performance, while the response surface method (RSM) with central composite design (CCD) is used to quantify parameter interaction effects. The findings are as follows: (1) compared with Nash non-cooperative and Stackelberg games, the tripartite cooperative strategy based on the differential game model achieves global optimization of system performance, demonstrating the efficiency-enhancing effect of dynamic collaboration; (2) the most sensitive parameters are β, α, μ₃, and η₃, with β having the highest sensitivity index (ST_i = 0.459), indicating its dominant role in system performance; (3) significant synergistic enhancement effects are observed among α–β, α–μ₃, and β–μ₃, corresponding, respectively, to the “technology stability–benefit conversion” gain effect, the “technology decay–platform compensation” dynamic balance mechanism, and the “benefit conversion–platform empowerment” performance threshold rule.

1. Introduction

Against the backdrop of global efforts to address climate change and promote green and low-carbon transition, the concept of sustainable development is profoundly reshaping traditional environmental governance paradigms. According to the UNEP Emissions Gap Report 2023, urban water systems account for 2–5% of global greenhouse gas emissions and improving their energy efficiency is critical to achieving the temperature control targets set by the Paris Agreement. From the perspective of a low-carbon economy, innovation in wastewater treatment requires breaking through the traditional linear treatment model characterized by high energy consumption and low efficiency and shifting towards an intelligent pathway that integrates resource recycling and digital empowerment. The World Bank’s Water in Circular Economy and Resilience (2022) report indicates that smart water technologies can reduce the carbon footprint of wastewater treatment facilities by 30–45% through mechanisms of energy efficiency optimization, resource recovery, and process decarbonization. This technological evolution not only responds to the synergetic requirements of the United Nations’ Sustainable Development Goal 6 (Clean Water and Sanitation) and Sustainable Development Goal 13 (Climate Action) but also establishes a micro-level practical foundation for the green transition of urban infrastructure.

The intelligent transformation of wastewater treatment systems has become an important development direction in modern urban environmental infrastructure construction, with its core objective being the comprehensive improvement of governance efficiency through next-generation information technologies [1,2,3]. In recent years, the rapid development of technologies such as the Internet of Things (IoT), big data analytics, and artificial intelligence (AI) has provided new technical support for this transformation [4]. Smart water governance systems, by constructing a “monitoring–prediction–decision” closed-loop management mechanism, have achieved significant improvements in wastewater treatment efficiency and resource utilization [5]. According to the Annual Sustainability Report 2020 published by Singapore’s Public Utilities Board (PUB), the Changi Water Reclamation Plant applied big data analytics and AI to accurately predict sludge dewatering equipment failures, reducing maintenance costs by 20% and increasing resource recovery rates to 75%. The 2022 Smart Water Pilot Report issued by the Shenzhen Water Affairs Bureau reported that the Buji Wastewater Treatment Plant, through the introduction of an intelligent dosing system, reduced overall chemical usage by approximately 30% and cut operational costs by 18%. In addition, the Rotterdam Sustainability White Paper 2023 disclosed that the Smart Urban Water data grid system deployed in Rotterdam, through real-time sensor monitoring and AI-based optimization scheduling, extended the service life of its drainage system by about 10 years and saved approximately 25% of the pipeline renewal costs.

Despite the broad prospects of intelligent transformation, its current development still faces many challenges. First, wastewater treatment enterprises, as the primary actors of transformation, are constrained by technological and financial limitations and remain cautious toward intelligent upgrading [6]. Second, intelligent technology providers tend to prioritize the maximization of commercial value, leading to a clear misalignment between their technological solutions and actual governance needs [7]. In addition, government departments, as regulators and policy-makers, have not yet formed effective synergies between policy instruments and market mechanisms, making it difficult to provide effective guidance [8]. This imbalance in collaboration among governments, enterprises, and technology providers manifests in problems such as fragmented technology applications, disputes over cost sharing, and the absence of long-term development mechanisms. In particular, issues such as unified data standards and benefit-sharing mechanisms highlight the urgent need for a scientific coordination framework to break existing bottlenecks [9,10].

Existing research has made progress in the field of intelligent wastewater treatment, yet there remains room for deepening the analysis of multi-agent interactions in dynamic contexts [11]. Specifically, most studies focus only on single-technology applications or static game models, without adequately addressing the impact of dynamic variables such as technological iteration and policy adjustment on the strategic evolution of multiple actors [12]. In this regard, differential game theory, by incorporating time into the strategy optimization framework, provides crucial support for dynamic interaction analysis. Theoretically, by solving the Hamilton–Jacobi–Bellman (HJB) equation for long-term dynamic equilibrium, it can effectively identify strategy adjustment thresholds across different stages, highly consistent with the long-term and gradual nature of intelligent wastewater transformation [13,14]. Practically, by relying on real-time data obtained through the Internet of Things (e.g., pollutant concentrations, energy consumption) and dynamic cross-agent information (e.g., regulatory efficiency, technology iteration), game variables can be updated at high frequency, making strategy optimization closer to real decision-making scenarios [15]. It is worth noting that the application of differential game models in intelligent wastewater transformation can be further improved in the following aspects: (1) incorporating the dynamic impacts of intelligent technologies on the game structure more comprehensively; (2) strengthening the coupling analysis of strategies among governments, wastewater treatment enterprises, and technology providers; and (3) advancing empirical studies beyond theoretical assumptions to validate model effectiveness with real-world cases.

This study aims to advance research in this field by constructing a tripartite differential game model involving governments, wastewater treatment enterprises, and intelligent technology providers, to systematically explore dynamic strategy interactions in the intelligent transformation of wastewater treatment. The main innovations and contributions of this study are threefold:

• It establishes a dynamic strategic framework by solving a tripartite differential game, which quantitatively demonstrates that cooperative governance dominates both non-cooperative and Stackelberg scenarios in maximizing long-term system benefits for intelligent wastewater transformation. This provides a rigorous analytical foundation for advocating cross-sector collaboration [16,17,18].
• Moving beyond conventional local sensitivity analysis [19], the study employs Sobol’s method to globally identify and rank the four most critical parameters within the cooperative regime. It precisely quantifies their first-order effects and the first time in this context, their non-negligible interactions effects on system performance, offering targeted guidance for parameter prioritization.
• By integrating central composite design (CCD) with the response surface method (RSM) [20,21], the study maps the complex, nonlinear relationships and trade-offs between key parameters and multi-objective system outcomes. This systematic approach uncovers optimal parameter combinations, thereby transitioning the decision-making process from heuristic adjustment to a scientifically guided optimization.

The remainder of the research in this paper was arranged as follows. Section 2 provides a literature review that synthesizes existing research in relevant fields to position our study and identify areas for further exploration. Section 3 develops a differential game model, specifying the payoff functions, cost functions, and the dynamic evolution of intelligent level for the government, wastewater treatment enterprises, and the digital twin platform. Section 4 presents a comparative analysis of system performance across different game modes, deriving equilibrium strategies under Nash non-cooperative, Stackelberg, and cooperative games by solving the Hamiliton-Jacobi–Bellman equations and evaluating disparities in system efficiency. Section 5 conducts simulations experiments, utilizing Sobol global sensitivity analysis to identify key parameters and leveraging response surface methodology to investigate their dynamic influence mechanisms. Finally, Section 6 summarizes the main contributions and findings of the study.

2. Literature Review

2.1. Research Evolution of Intelligent Technologies

Research on intelligent wastewater treatment has developed along three major technological pillars. First, in the domain of sensing technologies, Wei et al. [22] demonstrated through controlled experiments that an optimized IoT sensor network layout can enhance monitoring accuracy. However, the study did not account for sensor attenuation under different water quality conditions. Second, in data analysis technologies, Jia and Sun [23] developed a deep-learning-based water quality prediction model, which showed superior predictive performance compared to traditional methods when applied across multiple wastewater treatment plants. Third, in control technologies, Liu [24] designed an intelligent aeration system that achieved 15% energy savings by optimizing dissolved oxygen parameters in real time. Nevertheless, such technology-oriented studies still face theoretical limitations. On the one hand, their assumptions are often overly idealized, failing to consider organizational adaptation issues during technology diffusion [25]. On the other hand, the research paradigm largely relies on single-case validation, lacking systematic explanations of adoption differences under diverse institutional environments [26]. A cross-regional comparative study by Wang et al. [27] highlighted this shortcoming, revealing that the adoption rates of identical intelligent technologies vary significantly across regions with different degrees of marketisation. This suggests that pure technological performance optimization cannot fully explain actual adoption behavior—precisely for this reason, this paper couples technological characteristic with institutional environments and subject strategy interactions through a tripartite differential game model to address this research limitation.

2.2. Dynamic Evolution of Decision Analysis Methods

Decision analysis methods for intelligent wastewater treatment have undergone three stages of development, each with technical limitations while also providing methodological foundations for subsequent research. The early static analysis stage was characterized by single-factor linear assumptions [28]. For instance, Rui et al. [29] constructed a cost–benefit analysis model showing that the expected payback period was the most critical economic parameter. However, the use of local sensitivity analysis in this study only assessed marginal effects of single-parameter fluctuations and could not capture interactions between key factors such as technology adoption costs and policy subsidies, thereby limiting its explanatory power in multi-parameter dynamic contexts. The dynamic analysis stage achieved a breakthrough in quantifying parameter interaction effects but did not integrate deeply with game-theoretic policy frameworks [30]. Sirsant and Reddy [31] introduced the Sobol global sensitivity analysis method into the model and confirmed that nonlinear correlations among parameters significantly affect decision-making. Nevertheless, the study remained confined to parameter-level sensitivity rankings without extending to strategy interactions among game participants, making it difficult to translate sensitivity results into actionable equilibrium strategies [32]. The recent integration stage has begun exploring the combination of dynamic models and sensitivity methods but still requires further refinement. For example, Fortela et al. [33] combined differential games with the Morris screening method and demonstrated that, in dynamic environments, the optimal matching point between technological maturity and policy intensity exhibits stage-specific changes. However, the screening method used was limited to identifying parameters with significant main effects and failed to adequately capture low-sensitivity but highly interactive parameters [34].

2.3. Evolution of the Game Theory Framework

Research on wastewater treatment games has shown a gradual increase in modeling complexity. Each stage has promoted theoretical advancement while also exposing limitations in adapting to intelligent transformation. In the basic modeling stage, the binary static equilibrium was the main feature. For example, Tao et al. [35] constructed a “government–enterprise” game model and confirmed a significant substitution relationship between pollution discharge fees and regulatory intensity. However, the study did not include technological variables, resulting in a substantial gap between predicted results and actual policy effects, and making it difficult to explain policy adjustments following the adoption of intelligent monitoring technologies [36]. In the extended modeling stage, the actor dimension was expanded, but the dynamic interrelations among actors were insufficiently captured. De Frutos and Martín-Herrán [37] introduced technology providers as an independent actor, constructing a three-party static model. The results indicated a non-monotonic relationship between patent protection intensity and the speed of technology diffusion, rather than a simple linear one. However, the model assumed constant technological characteristics, failing to capture the dynamic reshaping of the payoff matrix caused by intelligent system iterations, thereby weakening explanatory power. In the dynamic modeling stage, time variables were incorporated, but adaptability to intelligent transformation still requires strengthening. For instance, Mu et al. [38] applied a differential game model and demonstrated that the time-varying nature of government subsidies could significantly accelerate technology diffusion. However, the model did not integrate the real-time feedback mechanisms unique to intelligent technologies, leading to insufficient depiction of the dynamic response between “improvement in monitoring accuracy” and “enterprise compliance behavior.”

The existing literature on technology application, decision analysis methods, and game modeling has laid a foundation for studying intelligent wastewater transformation, but three key theoretical gaps remain. First, the disconnection between technology application studies and game analysis makes it difficult to explain why technology can be feasible in theory yet difficult to implement in practice. Second, the mismatch between static decision-making methods and dynamic transformation processes limits the ability to support real-time optimization of multi-agent strategies. Third, current game models insufficiently characterize three-party actors and the features of intelligent technologies, restricting their explanatory capacity. Addressing these gaps requires constructing an integrated “technology–game–parameter” analytical framework. At the technological level, the real-time feedback characteristics of intelligent systems should be incorporated to align policy adjustments more closely with practice. At the actor level, the dynamic strategy sets of governments, enterprises, and technology providers need to be clarified. At the methodological level, differential games should be combined with global sensitivity analysis to quantify the impact of parameter interactions on game equilibria. Such a framework not only deepens the understanding of intelligent transformation dynamics but also provides theoretical support for differentiated policy design and the development of efficient collaborative mechanisms.

3. Differential Game Model Construction

3.1. Problem Description

To promote the intelligent transformation of the wastewater treatment industry, the government is implementing a tiered subsidy policy for enterprises deploying digital twin technologies. To enhance the stability of treatment performance, the digital twin platform applies real-time data fusion techniques and strategically allocates computing resources to optimize simulation accuracy [39]. To reduce operating costs, wastewater treatment enterprises strategically allocate funds for upgrading intelligent equipment to improve pollutant removal efficiency and energy control.

This study analyses a collaborative governance system comprising the government, wastewater treatment enterprises, and the digital twin platform. The digital twin platform provides dynamic simulation services to enterprises, while strategically determining service pricing and data update frequency. Enterprises adjust treatment process parameters based on simulation results and allocate funds for equipment maintenance. The government sets subsidy standards and regulatory intensity to guide the behavior of all actors [40]. If each party pursues only individual optimization, the system may fall into a Nash equilibrium trap characterized by “loose regulation–insufficient investment–inefficient service.” If the government dominates strategy formulation, a Stackelberg leader–follower structure may emerge. By contrast, trilateral cooperation through a cooperative game can maximize overall system benefits.

Accordingly, this paper applies differential game theory to construct a three-party dynamic game model. The government, wastewater treatment enterprises, and the digital twin platform may adopt three modes: a Nash non-cooperative game, characterized by simultaneous decision-making by all three actors aiming for individual optimization; a Stackelberg game, which features government leadership with enterprise and platform adjustments; and a cooperative game, involving joint strategy formulation and benefit sharing. By comparing the equilibrium outcomes of these game models, the optimal strategies of each actor under different governance modes can be derived, generating collaborative efficiency improvement guidelines for scenario adaptation. This approach provides theoretical support for regulating game relationships in the intelligent transformation of wastewater treatment. Figure 1 shows the operational framework of this model.

3.2. Model Construction

Assumption 1. 

The effort of the government towards intelligent wastewater treatment is denoted as E₁(t); the total effort of wastewater treatment enterprises is denoted as E₂(t); and the effort of the digital twin platform is denoted as E₃(t). Drawing on the research framework of Zhao et al. [41], the cost function is constructed such that cost input is a convex function of effort. Therefore, in the context of intelligent transformation, the cost functions for the government, wastewater treatment enterprises, and the digital twin platform can be expressed as

$$\left\{\begin{array}{l}{C}_1(t)={\displaystyle \frac{{\eta }_1{E}_1{(t)}^2}{2}}\hfill \\ C_2(t)={\displaystyle \frac{{\eta }_2{E}_2{(t)}^2}{2}}\hfill \\ C_3(t)={\displaystyle \frac{{\eta }_3{E}_3{(t)}^2}{2}}\hfill \end{array}\right.$$

(1)

where ${\eta }_1$, ${\eta }_2$, and ${\eta }_3$ represent the cost coefficients of the government, wastewater treatment enterprises, and the digital twin platform, respectively. C₁(t), C₂(t) and C₃(t) denote the effort costs for developing the intelligent economy over time t. These are convex functions with respect to the individual effort level  ${\mathit{E}}_{\mathit{i}} \in [0, +\infty ],$ $\mathit{i} \in \{1, 2, 3\}$, and the quadratic form is consistent with the law of increasing marginal cost.

Assumption 2. 

The intelligent level is represented by the variable x(t). Its derivative dx(t)/dt indicates the evolution of the intelligent level over time  $\mathit{t} \in [0, +\infty ]$, determined by the efforts of the government, wastewater treatment enterprises, and the digital twin platform. The intelligent level of the industry is a dynamic process with time sensitivity: as time progresses and digital twin technologies are upgraded, existing intelligent technologies become obsolete and eliminated. When the wastewater treatment industry approaches saturation in intelligent transformation, both government subsidies and enterprise attention decline, and the growth rate of intelligence gradually decreases. Building upon the concept of the dynamic data governance model proposed by Plambeck [42], it is assumed that the evolution of the industry’s intelligence level over time can be described by the following stochastic differential equation:

$$\begin{array}{l}\stackrel{·}{x}(t)=dx(t)/dx={\mu }_1{E}_1(t)+{\mu }_2{E}_2(t)+{\mu }_3{E}_3(t)-\alpha x(t)\\ x(0)=x_0\ge 0\end{array}$$

(2)

where the intelligent level x(t) is defined as a continuous, non-negative variable, representing the industry’s intelligent state measured against a benchmark unit.  ${\mathsf{{\rm M}}}_1$, ${\mu }_2,$ and ${\mu }_3$ represent the contribution coefficients of the government, wastewater treatment enterprises, and the digital twin platform, respectively, in promoting industry intelligence.$\alpha$ denotes the decay rate of the intelligent level, implying that as the effort level E_I increases, the growth of x(t) gradually slows down, reflecting the diminishing marginal effect. x₀ represents the initial state of industry intelligence.

Assumption 3. 

The intelligent transformation of the wastewater treatment industry relies on the collaborative participation of the government, enterprises, and digital twin platforms. The active input of all three parties is the key to the intelligent level of the industry, while the improvement of this level in turn affects system performance, forming an interrelated whole. In this process, the actions of each participant not only generate their own benefits, but also influence system performance through the intelligent level, thereby constituting the total revenue model of the industry:

$$\pi (t)={\theta }_1{E}_1(t)+{\theta }_2{E}_2(t)+{\theta }_3{E}_3(t)+\beta x(t)$$

(3)

where ${\mathsf{\theta }}_1,$${\mathsf{\theta }}_2,$and ${\mathsf{\theta }}_3$ denote the marginal revenue coefficients of the government, enterprises, and the digital twin platform, respectively, and $\beta > 0$ represents the effect of the intelligent level on system performance.

Assumption 4. 

The total revenue from industrial intelligent transformation is distributed among the participants according to a pre-agreed ratio. The share obtained by the government is ${\mathsf{\sigma }}_1$, by enterprises is ${\mathsf{\sigma }}_2$, and by the digital twin platform is ${\mathsf{\sigma }}_3$, where ${\mathsf{\sigma }}_{\mathit{i}} \in (0, 1)$ are distribution coefficients determined by the contributions of each participant in the transformation process. To promote the intelligence level of the industry, the government provides subsidies for technological innovation activities in traditional wastewater treatment (${\mathsf{\varpi }}_1$) and policy support for the promotion of digital twin platforms (${\mathsf{\varpi }}_2$). The government, enterprises, and the digital twin platform all adopt a positive discount rate$\rho$, and their ultimate objective is to maximize long-term payoffs through collaborative development over an infinite time horizon.

3.3. Nash Non-Cooperative Game

In this game model, participants make strategic decisions independently without cooperation, aiming to maximize their own payoffs. The objective functions of the government, enterprises, and the digital twin platform are given by

$$\left\{\begin{array}{l}\underset{E_1}{\max }{V}_1^N={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}[{\sigma }_1({\theta }_1{E}_1(t)+{\theta }_2{E}_2(t)+{\theta }_3{E}_3(t)+\beta x(t))-{\displaystyle \frac{{\eta }_1}{2}}{E}_1{\mathit{(t)}}^2]dt\\ \underset{E_2}{\max }{V}_2^N={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}[{\sigma }_2({\theta }_1{E}_1(t)+{\theta }_2{E}_2(t)+{\theta }_3{E}_3(t)+\beta x(t))-{\displaystyle \frac{{\eta }_2}{2}}{E}_2{\mathit{(t)}}^2]dt\\ \underset{E_3}{\max }{V}_3^N={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}[{\sigma }_3({\theta }_1{E}_1(t)+{\theta }_2{E}_2(t)+{\theta }_3{E}_3(t)+\beta x(t))-{\displaystyle \frac{{\eta }_3}{2}}{E}_3{\mathit{(t)}}^2]dt\end{array}\right.$$

(4)

Theorem 1. 

In the non-cooperative game among the government, enterprises, and the digital twin platform, the dynamic feedback Nash equilibrium strategies are

$$\left\{\begin{array}{l}{E}_1={\displaystyle \frac{{\sigma }_1[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}{{\eta }_1(\alpha +\rho )}}\\ E_2={\displaystyle \frac{{\sigma }_2[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}{{\eta }_2(\alpha +\rho )}}\\ E_3={\displaystyle \frac{{\sigma }_3[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}{{\eta }_3(\alpha +\rho )}}\end{array}\right.$$

(5)

Proof. 

In the non-cooperative game model, we assume that the differential payoff functions ${\mathit{V}}_{\mathit{i}}^{\mathit{N}}\left(\mathit{x}\right)$ of the government, enterprises, and the digital twin platform are continuous and bounded $(\mathit{i} \in \{1, 2, 3\left\}\right)$. For any $\mathit{x} \ge 0,$ the HJB equation is satisfied to obtain the Markov Perfect Equilibrium:

$$\left\{\begin{array}{l}\rho V_1^N(x)=\underset{E_1\ge 0}{\max }\{{\sigma }_1({\theta }_1{E}_1+{\theta }_2{E}_2+{\theta }_3{E}_3+\beta x)-{\displaystyle \frac{{\eta }_1}{2}}{E}_1{}^2\\ +k_1({\mu }_1{E}_1+{\mu }_2{E}_2+{\mu }_3{E}_3-\alpha x)\}\\ \rho V_2^N(x)=\underset{E_2\ge 0}{\max }\{{\sigma }_2({\theta }_1{E}_1+{\theta }_2{E}_2+{\theta }_3{E}_3+\beta x)-{\displaystyle \frac{{\eta }_2}{2}}{E}_2{}^2\\ +k_2({\mu }_1{E}_1+{\mu }_2{E}_2+{\mu }_3{E}_3-\alpha x)\}\\ \rho V_3^N(x)=\underset{E_3\ge 0}{\max }\{{\sigma }_3({\theta }_1{E}_1+{\theta }_2{E}_2+{\theta }_3{E}_3+\beta x)-{\displaystyle \frac{{\eta }_3}{2}}{E}_3{}^2\\ +k_3({\mu }_1{E}_1+{\mu }_2{E}_2+{\mu }_3{E}_3-\alpha x)\}\end{array}\right.$$

(6)

where ${\mathit{k}}_{\mathit{i}} = \partial {\mathit{V}}_{\mathit{i}}^{\mathit{N}}/\partial \mathit{x}, \mathit{i} \in \{1, 2, 3\}$.

From the right-hand side of Equation (6), the first-order conditions yield

$$\left\{\begin{array}{l}{E}_1={\displaystyle \frac{{\sigma }_1{\theta }_1+k_1{\mu }_1}{{\eta }_1}}\\ E_2={\displaystyle \frac{{\sigma }_2{\theta }_2+k_2{\mu }_2}{{\eta }_2}}\\ E_3={\displaystyle \frac{{\sigma }_3{\theta }_3+k_3{\mu }_3}{{\eta }_3}}\end{array}\right.$$

(7)

Substituting Equation (7) into Equation (6), we obtain

$$\left\{\begin{array}{l}\rho V_1^N=[x({\sigma }_1\beta -\alpha k_1)+{\displaystyle \frac{{({\sigma }_1{\theta }_1+k_1{\mu }_1)}^2}{2{\eta }_1}}+{\displaystyle \frac{{\sigma }_2{\theta }_2+k_2{\mu }_2}{{\eta }_2}}({\sigma }_1{\theta }_2+k_1{\mu }_2)\\ +{\displaystyle \frac{{\sigma }_3{\theta }_3+k_3{\mu }_3}{{\eta }_3}}({\sigma }_1{\theta }_3+k_1{\mu }_3)]\\ \rho V_2^N=[x({\sigma }_2\beta -\alpha k_2)+{\displaystyle \frac{{\sigma }_1{\theta }_1+k_1{\mu }_1}{{\eta }_1}}({\sigma }_2{\theta }_1+k_2{\mu }_1)+{\displaystyle \frac{{({\sigma }_2{\theta }_2+k_2{\mu }_2)}^2}{2{\eta }_2}}\\ +{\displaystyle \frac{{\sigma }_3{\theta }_3+k_3{\mu }_3}{{\eta }_3}}({\sigma }_2{\theta }_3+k_2{\mu }_3)]\\ \rho V_3^N=[x({\sigma }_3\beta -\alpha k_3)+{\displaystyle \frac{{\sigma }_1{\theta }_1+k_1{\mu }_1}{{\eta }_1}}({\sigma }_3{\theta }_1+k_3{\mu }_1)\\ +{\displaystyle \frac{{\sigma }_2{\theta }_2+k_2{\mu }_2}{{\eta }_2}}({\sigma }_3{\theta }_2+k_3{\mu }_2)+{\displaystyle \frac{{({\sigma }_3{\theta }_3+k_3{\mu }_3)}^2}{2{\eta }_3}}]\end{array}\right.$$

(8)

From Equation (8), it follows that the optimal linear function of $\mathit{x}$ is the solution to the HJB equation, namely

$$\left\{\begin{array}{l}{V}_1^N(x)=K_1^{N}x+B_1^N\\ V_2^N(x)=K_2^{N}x+B_2^N\\ V_3^N(x)=K_3^{N}x+B_3^N\end{array}\right.$$

(9)

Among them, ${\mathit{K}}_1^{\mathit{N}},{ \mathit{B}}_1^{\mathit{N}}, {\mathit{K}}_2^{\mathit{N}}, {\mathit{B}}_2^{\mathit{N}},{ \mathit{K}}_3^{\mathit{N}},{ \mathit{B}}_3^{\mathit{N}}$ are constants. Substituting ${\mathit{V}}_1^{\mathit{N}}\left(\mathit{x}\right),$ ${\mathit{V}}_2^{\mathit{N}}\left(\mathit{x}\right),$ ${\mathit{V}}_3^{\mathit{N}}\left(\mathit{x}\right)$ and their first-order derivatives into Equation (8), and simplifying, yields

$$\left\{\begin{array}{l}\rho (k_1^{N}x+b_1^N)=[x({\sigma }_1\beta -\alpha k_1)+{\displaystyle \frac{{({\sigma }_1{\theta }_1+k_1{\mu }_1)}^2}{2{\eta }_1}}+{\displaystyle \frac{{\sigma }_2{\theta }_2+k_2{\mu }_2}{{\eta }_2}}({\sigma }_1{\theta }_2+k_1{\mu }_2)\\ +{\displaystyle \frac{{\sigma }_3{\theta }_3+k_3{\mu }_3}{{\eta }_3}}({\sigma }_1{\theta }_3+k_1{\mu }_3)]\\ \rho (k_2^{N}x+b_2^N)=[x({\sigma }_2\beta -\alpha k_2)+{\displaystyle \frac{{\sigma }_1{\theta }_1+k_1{\mu }_1}{{\eta }_1}}({\sigma }_2{\theta }_1+k_2{\mu }_1)+{\displaystyle \frac{{({\sigma }_2{\theta }_2+k_2{\mu }_2)}^2}{2{\eta }_2}}\\ +{\displaystyle \frac{{\sigma }_3{\theta }_3+k_3{\mu }_3}{{\eta }_3}}({\sigma }_2{\theta }_3+k_2{\mu }_3)]\\ \rho (k_3^{N}x+b_3^N)=[x({\sigma }_3\beta -\alpha k_3)+{\displaystyle \frac{{\sigma }_1{\theta }_1+k_1{\mu }_1}{{\eta }_1}}({\sigma }_3{\theta }_1+k_3{\mu }_1)\\ +{\displaystyle \frac{{\sigma }_2{\theta }_2+k_2{\mu }_2}{{\eta }_2}}({\sigma }_3{\theta }_2+k_3{\mu }_2)+{\displaystyle \frac{{({\sigma }_3{\theta }_3+k_3{\mu }_3)}^2}{2{\eta }_3}}]\end{array}\right.$$

(10)

According to the previous assumptions, Equation (10) holds for $\mathit{x} \ge 0,$ and thus the values of ${\mathit{K}}_1^{\mathit{N}},{ \mathit{B}}_1^{\mathit{N}},{ \mathit{K}}_2^{\mathit{N}},{ \mathit{B}}_2^{\mathit{N}},{ \mathit{K}}_3^{\mathit{N}},{ \mathit{B}}_3^{\mathit{N}}$ can be obtained as

$$\left\{\begin{array}{l}{K}_1^N={\displaystyle \frac{{\sigma }_1\beta }{\alpha +\rho }};K_2^N={\displaystyle \frac{{\sigma }_2\beta }{\alpha +\rho }};K_3^N={\displaystyle \frac{{\sigma }_3\beta }{\alpha +\rho }}\\ B_1^N={\displaystyle \frac{{\sigma }_1^2{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{2\rho {\eta }_1{(\alpha +\rho )}^2}}+{\displaystyle \frac{{\sigma }_1{\sigma }_2{[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{\rho {\eta }_2{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{{\sigma }_1{\sigma }_3{[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{\rho {\eta }_3{(\alpha +\rho )}^2}}\\ B_2^N={\displaystyle \frac{{\sigma }_1{\sigma }_2{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{\rho {\eta }_1{(\alpha +\rho )}^2}}+{\displaystyle \frac{{\sigma }_2^2{[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{2\rho {\eta }_2{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{{\sigma }_2{\sigma }_3{[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{\rho {\eta }_3{(\alpha +\rho )}^2}}\\ B_3^N={\displaystyle \frac{{\sigma }_1{\sigma }_3{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{\rho {\eta }_1{(\alpha +\rho )}^2}}+{\displaystyle \frac{{\sigma }_2{\sigma }_3{[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{\rho {\eta }_2{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{{\sigma }_3^2{[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{2\rho {\eta }_3{(\alpha +\rho )}^2}}\end{array}\right.$$

(11)

Substituting ${\mathit{k}}_1^{\mathit{N}},{ \mathit{k}}_2^{\mathit{N}},{ \mathit{k}}_3^{\mathit{N}}$ into Equation (7), the optimal strategies of the government, wastewater treatment enterprises, and digital twin platforms are obtained as

$$\left\{\begin{array}{l}{E}_1={\displaystyle \frac{{\sigma }_1[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}{{\eta }_1(\alpha +\rho )}}\\ E_2={\displaystyle \frac{{\sigma }_2[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}{{\eta }_2(\alpha +\rho )}}\\ E_3={\displaystyle \frac{{\sigma }_3[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}{{\eta }_3(\alpha +\rho )}}\end{array}\right.$$

(12)

□

Thus, proposition~1 is proved. Substituting the results into Equation (2), the free trajectory is obtained as

$$\begin{array}{l}\stackrel{·}{x}(t)=A^N-\alpha x(t)\\ x(0)=x_0\ge 0\end{array}$$

(13)

where

$$\begin{array}{l}{A}^N={\mu }_1{E}_1^N+{\mu }_2{E}_2^N+{\mu }_3{E}_3^N={\displaystyle \frac{{\mu }_1{\sigma }_1[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}{{\eta }_1(\alpha +\rho )}}+{\displaystyle \frac{{\mu }_2{\sigma }_2[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}{{\eta }_2(\alpha +\rho )}}\\ +{\displaystyle \frac{{\mu }_3{\sigma }_3[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}{{\eta }_3(\alpha +\rho )}}\end{array}$$

(14)

Solving Equation (12) yields the expression of the intelligent transformation level:

$$x^N={\displaystyle \frac{A^N}{\alpha }}+(x_0-{\displaystyle \frac{A^N}{\alpha }})e^{-\alpha t}$$

(15)

where ${\mathit{A}}^{\mathit{N}}/\alpha$ denotes the steady-state level of intelligent transformation.

Substituting ${\mathit{k}}_1^{\mathit{N}},{ \mathit{b}}_1^{\mathit{N}},{ \mathit{k}}_2^{\mathit{N}},{ \mathit{b}}_2^{\mathit{N}},{ \mathit{k}}_3^{\mathit{N}},{ \mathit{b}}_3^{\mathit{N}}$ into Equation (9), the optimal benefit functions of the government, wastewater treatment enterprises, and digital twin platforms are given as

$$\left\{\begin{array}{l}{V}_1^N(x)={\displaystyle \frac{{\sigma }_1\beta }{\alpha +\rho }}{x}^N+{\displaystyle \frac{{\sigma }_1^2{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{2\rho {\eta }_1{(\alpha +\rho )}^2}}+{\displaystyle \frac{{\sigma }_1{\sigma }_2{[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{\rho {\eta }_2{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{{\sigma }_1{\sigma }_3{[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{\rho {\eta }_3{(\alpha +\rho )}^2}}\\ V_2^N(x)={\displaystyle \frac{{\sigma }_2\beta }{\alpha +\rho }}{x}^N+{\displaystyle \frac{{\sigma }_1{\sigma }_2{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{\rho {\eta }_1{(\alpha +\rho )}^2}}+{\displaystyle \frac{{\sigma }_2^2{[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{2\rho {\eta }_2{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{{\sigma }_2{\sigma }_3{[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{\rho {\eta }_3{(\alpha +\rho )}^2}}\\ V_3^N(x)={\displaystyle \frac{{\sigma }_3\beta }{\alpha +\rho }}{x}^N+{\displaystyle \frac{{\sigma }_1{\sigma }_3{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{\rho {\eta }_1{(\alpha +\rho )}^2}}+{\displaystyle \frac{{\sigma }_2{\sigma }_3{[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{\rho {\eta }_2{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{{\sigma }_3^2{[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{2\rho {\eta }_3{(\alpha +\rho )}^2}}\end{array}\right.$$

(16)

Therefore, under the Nash non-cooperative game framework, the overall payoff is

$$\begin{array}{l}{V}^N(x)=V_1^N(x)+V_2^N(x)+V_3^N(x)\\ ={\displaystyle \frac{\beta }{\alpha +\rho }}{x}^N+{\displaystyle \frac{{\sigma }_1(1+{\sigma }_2+{\sigma }_3){[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{2\rho {\eta }_1{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{{\sigma }_2(1+{\sigma }_1+{\sigma }_3){[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{2\rho {\eta }_2{(\alpha +\rho )}^2}}+{\displaystyle \frac{{\sigma }_3(1+{\sigma }_1+{\sigma }_2){[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{2\rho {\eta }_3{(\alpha +\rho )}^2}}\end{array}$$

(17)

3.4. Stackelberg Game

In the process of intelligent transformation of the sewage treatment industry, the government plays a leading role, while sewage treatment enterprises and digital twin platforms act as driving forces. To encourage more enterprises and platforms to participate in the intelligent transformation of sewage treatment, the government usually provides financial subsidies ${\mathsf{\varpi }}_1$ to sewage treatment enterprises. Since most enterprises lack the necessary conditions for intelligent transformation, they need to rely on technical support from digital twin platforms, for which a technology usage fee ${\mathsf{\varpi }}_2$ must be paid. From a long-term perspective, the strategic interactions among the government, sewage treatment enterprises, and digital twin platforms in intelligent transformation constitute a Stackelberg differential decision-making model.

The decision-making process under this model is as follows: the government determines the subsidy level according to the stage of intelligent transformation of enterprises; digital twin platforms sell part of their technological achievements to enterprises to obtain usage fees; finally, enterprises make decisions based on both subsidies and technology usage fees to maximize their benefits.

The objective functions of the three players are given by

$$\left\{\begin{array}{l}\underset{E_1}{\max }{V}_1^S={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}[{\sigma }_1({\theta }_1{E}_1(t)+{\theta }_2{E}_2(t)+{\theta }_3{E}_3(t)+\beta x(t))-{\displaystyle \frac{{\eta }_1}{2}}{E}_1{\mathit{(t)}}^2-{\mathsf{\varpi }}_1{\displaystyle \frac{{\eta }_2}{2}}{E}_2{\mathit{(t)}}^2-{\mathsf{\varpi }}_2{\displaystyle \frac{{\eta }_3}{2}}{E}_3{\mathit{(t)}}^2]dt\\ \underset{E_2}{\max }{V}_2^S={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}[{\sigma }_2({\theta }_1{E}_1(t)+{\theta }_2{E}_2(t)+{\theta }_3{E}_3(t)+\beta x(t))-{\displaystyle \frac{{\eta }_2}{2}}{E}_2{\mathit{(t)}}^2+{\mathsf{\varpi }}_1{\displaystyle \frac{{\eta }_2}{2}}{E}_2{\mathit{(t)}}^2]dt\\ \underset{E_3}{\max }{V}_3^S={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}[{\sigma }_3({\theta }_1{E}_1(t)+{\theta }_2{E}_2(t)+{\theta }_3{E}_3(t)+\beta x(t))-{\displaystyle \frac{{\eta }_3}{2}}{E}_3{\mathit{(t)}}^2+{\mathsf{\varpi }}_2{\displaystyle \frac{{\eta }_3}{2}}{E}_3{\mathit{(t)}}^2]dt\end{array}\right.$$

(18)

Theorem 2. 

When the government provides subsidies to enterprises and the enterprises pay technology usage fees to the digital twin platforms, the dynamic feedback equilibrium strategies of the government, enterprises, and digital twin platforms are

$$\left\{\begin{array}{l}{E}_1={\displaystyle \frac{{\sigma }_1({\theta }_1(\alpha +\rho )+\beta {\mu }_1)}{(\alpha +\rho ){\eta }_1}}\\ E_2={\displaystyle \frac{(2{\sigma }_1+{\Delta }_2)({\theta }_2(\alpha +\rho )+\beta {\mu }_2)}{(\alpha +\rho )2{\eta }_2}}\\ E_3={\displaystyle \frac{(2{\sigma }_1+{\sigma }_3)({\theta }_3(\alpha +\rho )+\beta {\mu }_3)}{(\alpha +\rho )2{\eta }_3}}\\ {\mathsf{\varpi }}_1={\displaystyle \frac{2{\sigma }_1-{\sigma }_2}{2{\sigma }_1+{\sigma }_2}}\\ {\mathsf{\varpi }}_2={\displaystyle \frac{2{\sigma }_1-{\sigma }_3}{2{\sigma }_1+{\sigma }_3}}\end{array}\right.$$

(19)

Proof. 

Assume that under this condition, the government, enterprises, and platforms achieve optimal payoffs, with each player having continuous and bounded payoff functions ${\mathit{V}}_{\mathit{i}}^{\mathit{S}}\left(\mathit{x}\right), \mathit{i} \in (1, 2, 3)$, which satisfy the HJB equation for any $\mathit{x} \ge 0$. By applying backward induction, the HJB equations for enterprises and platforms can be expressed as

$$\left\{\begin{array}{l}\rho V_2^S(x)=\underset{E_2\ge 0}{\max }\{{\sigma }_2({\theta }_1{E}_1+{\theta }_2{E}_2+{\theta }_3{E}_3+\beta x)-{\displaystyle \frac{{\eta }_2}{2}}{E}_2{}^2+{\mathsf{\varpi }}_1{\displaystyle \frac{{\eta }_2}{2}}{E}_2{}^2\\ +k_2({\mu }_1{E}_1+{\mu }_2{E}_2+{\mu }_3{E}_3-\alpha x)\}\\ \rho V_3^S(x)=\underset{E_3\ge 0}{\max }\{{\sigma }_3({\theta }_1{E}_1+{\theta }_2{E}_2+{\theta }_3{E}_3+\beta x)-{\displaystyle \frac{{\eta }_3}{2}}{E}_3{}^2+{\mathsf{\varpi }}_2{\displaystyle \frac{{\eta }_3}{2}}{E}_3{}^2\\ +k_3({\mu }_1{E}_1+{\mu }_2{E}_2+{\mu }_3{E}_3-\alpha x)\}\end{array}\right.$$

(20)

By solving the first-order conditions of these HJB equations, the optimal efforts ${\mathit{E}}_2$ and ${\mathit{E}}_3$ are obtained as

$$\left\{\begin{array}{l}{E}_2={\displaystyle \frac{{\sigma }_2{\theta }_2+k_2{\mu }_2}{(1-{\mathsf{\varpi }}_1){\eta }_2}}\\ E_3={\displaystyle \frac{{\sigma }_3{\theta }_3+k_3{\mu }_3}{(1-{\mathsf{\varpi }}_2){\eta }_3}}\end{array}\right.$$

(21)

When the government and platforms determine their efforts according to Equation (19), the enterprises then maximize their payoff. The HJB equation for enterprises is given by

$$\begin{array}{l}\rho V_1^S(x)=\underset{E_1\ge 0}{\max }\{{\sigma }_1({\theta }_1{E}_1+{\theta }_2{E}_2+{\theta }_3{E}_3+\beta x)-{\displaystyle \frac{{\eta }_1}{2}}{E}_1{}^2-{\mathsf{\varpi }}_1{\displaystyle \frac{{\eta }_2}{2}}{E}_2{}^2-{\mathsf{\varpi }}_2{\displaystyle \frac{{\eta }_3}{2}}{E}_3{}^2\\ +k_1({\mu }_1{E}_1+{\mu }_2{E}_2+{\mu }_3{E}_3-\alpha x)\}\end{array}$$

(22)

Substituting Equation (19) into Equation (21) and solving the first-order conditions, we obtain

$$\left\{\begin{array}{l}{E}_1={\displaystyle \frac{{\sigma }_1{\theta }_1+k_1{\mu }_1}{{\eta }_1}}\\ {\mathsf{\varpi }}_1={\displaystyle \frac{{\theta }_2(2{\sigma }_1-{\sigma }_2)+{\mu }_2(2k_1-k_2)}{{\theta }_2(2{\sigma }_1+{\sigma }_2)+{\mu }_2(2k_1+k_2)}}\\ {\mathsf{\varpi }}_2={\displaystyle \frac{{\theta }_3(2{\sigma }_1-{\sigma }_3)+{\mu }_3(2k_1-k_3)}{{\theta }_3(2{\sigma }_1+{\sigma }_3)+{\mu }_3(2k_1+k_3)}}\end{array}\right.$$

(23)

Substituting ${\mathit{E}}_1,{ \mathit{E}}_2,{ \mathit{E}}_3,{ \mathsf{\varpi }}_1,{ \mathsf{\varpi }}_2$ into Equations (19) and (20), we obtain

$$\left\{\begin{array}{l}\rho V_1^S(x)=x({\sigma }_1\beta -\alpha k_1)+{\displaystyle \frac{{({\sigma }_1{\theta }_1+k_1{\mu }_1)}^2}{2{\eta }_1}}+{\displaystyle \frac{{[{\theta }_2(2{\sigma }_1+{\sigma }_2)+{\mu }_2(2k_1+k_2)]}^2}{8{\eta }_2}}\\ +{\displaystyle \frac{{[{\theta }_3(2{\sigma }_1+{\sigma }_3)+{\mu }_3(2k_1+k_3)]}^2}{8{\eta }_3}}\\ \rho V_2^S(x)=x({\sigma }_2\beta -\alpha k_2)+{\displaystyle \frac{({\sigma }_2{\theta }_1+k_2{\mu }_1)({\sigma }_1{\theta }_1+k_1{\mu }_1)}{{\eta }_1}}+{\displaystyle \frac{({\sigma }_2{\theta }_2+k_2{\mu }_2)[{\theta }_2(2{\sigma }_1+{\sigma }_2)+{\mu }_2(2k_1+k_2)]}{4{\eta }_2}}\\ +{\displaystyle \frac{({\sigma }_2{\theta }_3+k_2{\mu }_3)[{\theta }_3(2{\sigma }_1+{\sigma }_3)+{\mu }_3(2k_1+k_3)]}{2{\eta }_3}}\\ \rho V_3^S(x)=x({\sigma }_3\beta -\alpha k_3)+{\displaystyle \frac{({\sigma }_3{\theta }_1+k_3{\mu }_1)({\sigma }_1{\theta }_1+k_1{\mu }_1)}{{\eta }_1}}+{\displaystyle \frac{({\sigma }_3{\theta }_2+k_3{\mu }_2)[{\theta }_2(2{\sigma }_1+{\sigma }_2)+{\mu }_2(2k_1+k_2)]}{2{\eta }_2}}\\ +{\displaystyle \frac{({\sigma }_3{\theta }_3+k_3{\mu }_3)[{\theta }_3(2{\sigma }_1+{\sigma }_3)+{\mu }_3(2k_1+k_3)]}{4{\eta }_3}}\end{array}\right.$$

(24)

According to Equation (23), a first-order linear function of $\mathrm{x}$ is the solution to the HJB equation, expressed as

$$\left\{\begin{array}{l}{V}_1^S(x)=k_1^{S}x+b_1^S\\ V_2^S(x)=k_2^{S}x+b_2^S\\ V_3^S(x)=k_3^{S}x+b_3^S\end{array}\right.$$

(25)

where ${\mathit{k}}_1^{\mathit{S}},{ \mathit{b}}_1^{\mathit{S}},{ \mathit{k}}_2^{\mathit{S}},{ \mathit{b}}_2^{\mathit{S}},{ \mathit{k}}_3^{\mathit{S}},{ \mathit{b}}_3^{\mathit{S}}$ are constants. Combining Equations (22) and (24), the variable $\mathit{x}$ can be derived and substituted into Equation (23), which simplifies to

$$\left\{\begin{array}{l}{k}_1^{S}x={\displaystyle \frac{{\sigma }_1\beta }{\alpha +\rho }};k_2^{S}x={\displaystyle \frac{{\sigma }_2\beta }{\alpha +\rho }};k_3^{S}x={\displaystyle \frac{{\sigma }_3\beta }{\alpha +\rho }}\\ \rho ((k_1^{S}x+b_1^S))=({\sigma }_1\beta -\alpha k_1)x+{\displaystyle \frac{{({\sigma }_1{\theta }_1+k_1{\mu }_1)}^2}{2{\eta }_1}}\\ +{\displaystyle \frac{{[{\theta }_2(2{\sigma }_1+{\sigma }_2)+{\mu }_2(2k_1+k_2)]}^2}{8{\eta }_2}}+{\displaystyle \frac{{[{\theta }_3(2{\sigma }_1+{\sigma }_3)+{\mu }_3(2k_1+k_3)]}^2}{8{\eta }_3}}\\ \rho ((k_2^{S}x+b_2^S))=({\sigma }_2\beta -\alpha k_2)x+{\displaystyle \frac{({\sigma }_2{\theta }_1+k_2{\mu }_1)({\sigma }_1{\theta }_1+k_1{\mu }_1)}{{\eta }_1}}\\ +{\displaystyle \frac{({\sigma }_2{\theta }_2+k_2{\mu }_2)[{\theta }_2(2{\sigma }_1+{\sigma }_2)+{\mu }_2(2k_1+k_2)]}{4{\eta }_2}}+{\displaystyle \frac{({\sigma }_2{\theta }_3+k_2{\mu }_3)[{\theta }_3(2{\sigma }_1+{\sigma }_3)+{\mu }_3(2k_1+k_3)]}{2{\eta }_3}}\\ \rho ((k_3^{S}x+b_3^S))=({\sigma }_3\beta -\alpha k_3)x+{\displaystyle \frac{({\sigma }_3{\theta }_1+k_3{\mu }_1)({\sigma }_1{\theta }_1+k_1{\mu }_1)}{{\eta }_1}}\\ +{\displaystyle \frac{({\sigma }_3{\theta }_2+k_3{\mu }_2)[{\theta }_2(2{\sigma }_1+{\sigma }_2)+{\mu }_2(2k_1+k_2)]}{2{\eta }_2}}+{\displaystyle \frac{({\sigma }_3{\theta }_3+k_3{\mu }_3)[{\theta }_3(2{\sigma }_1+{\sigma }_3)+{\mu }_3(2k_1+k_3)]}{4{\eta }_3}}\end{array}\right.$$

(26)

Simplifying further, the constants ${\mathit{k}}_1^{\mathit{S}},{ \mathit{b}}_1^{\mathit{S}},{ \mathit{k}}_2^{\mathit{S}},{ \mathit{b}}_2^{\mathit{S}},{ \mathit{k}}_3^{\mathit{S}},{ \mathit{b}}_3^{\mathit{S}}$ are obtained as

$$\left\{\begin{array}{l}{k}_1^S={\displaystyle \frac{{\sigma }_1\beta }{\alpha +\rho }};k_2^S={\displaystyle \frac{{\sigma }_2\beta }{\alpha +\rho }};k_3^S={\displaystyle \frac{{\sigma }_3\beta }{\alpha +\rho }}\\ b_1^S={\displaystyle \frac{{\sigma }_{{}_1}^2{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{2\rho {\eta }_1{(\alpha +\rho )}^2}}+{\displaystyle \frac{{(2{\sigma }_1+{\sigma }_2)}^2{[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{8\rho {\eta }_2{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{{(2{\sigma }_1+{\sigma }_3)}^2{[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{8\rho {\eta }_3{(\alpha +\rho )}^2}}\\ b_2^S={\displaystyle \frac{{\sigma }_1{\sigma }_2{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{\rho {\eta }_1{(\alpha +\rho )}^2}}+{\displaystyle \frac{{\sigma }_2(2{\sigma }_1+{\sigma }_2){[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{4\rho {\eta }_2{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{{\sigma }_2(2{\sigma }_1+{\sigma }_3){[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{2\rho {\eta }_3{(\alpha +\rho )}^2}}\\ b_3^S={\displaystyle \frac{{\sigma }_1{\sigma }_3{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{\rho {\eta }_1{(\alpha +\rho )}^2}}+{\displaystyle \frac{{\sigma }_3(2{\sigma }_1+{\sigma }_2){[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{2\rho {\eta }_2{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{{\sigma }_3(2{\sigma }_1+{\sigma }_3){[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{4\rho {\eta }_3{(\alpha +\rho )}^2}}\end{array}\right.$$

(27)

Finally, substituting ${\mathit{k}}_1^{\mathit{S}},{ \mathit{k}}_2^{\mathit{S}},{ \mathit{k}}_3^{\mathit{S}}$ into Equations (19) and (21), the optimal strategies of the government, wastewater treatment enterprises, and digital twin platforms, as well as the optimal subsidy levels, are derived as

$$\left\{\begin{array}{l}{E}_1={\displaystyle \frac{{\sigma }_1({\theta }_1(\alpha +\rho )+\beta {\mu }_1)}{(\alpha +\rho ){\eta }_1}}\\ E_2={\displaystyle \frac{(2{\sigma }_1+{\sigma }_2)({\theta }_2(\alpha +\rho )+\beta {\mu }_2)}{(\alpha +\rho )2{\eta }_2}}\\ E_3={\displaystyle \frac{(2{\sigma }_1+{\sigma }_3)({\theta }_3(\alpha +\rho )+\beta {\mu }_3)}{(\alpha +\rho )2{\eta }_3}}\\ {\mathsf{\varpi }}_1={\displaystyle \frac{2{\sigma }_1-{\sigma }_2}{2{\sigma }_1+{\sigma }_2}}\\ {\mathsf{\varpi }}_2={\displaystyle \frac{2{\sigma }_1-{\sigma }_3}{2{\sigma }_1+{\sigma }_3}}\end{array}\right.$$

(28)

□

It can be shown that Theorem 2 holds. Substituting the results into Equation (2), we obtain

$$\begin{array}{l}\stackrel{·}{x}(t)=A^S-\alpha x(t)\\ x(0)=x_0\ge 0\end{array}$$

(29)

Here,

$$\begin{array}{l}{A}^S={\mu }_1{E}_1^S+{\mu }_2{E}_2^S+{\mu }_3{E}_3^S={\displaystyle \frac{{\mu }_1{\sigma }_1[{\theta }_1(\alpha +\rho )+\beta {\mu }_1}{(\alpha +\rho ){\eta }_1}}\\ +{\displaystyle \frac{{\mu }_2(2{\sigma }_1+{\sigma }_2)[{\theta }_2(\alpha +\rho )+\beta {\mu }_2]}{(\alpha +\rho )2{\eta }_2}}+{\displaystyle \frac{{\mu }_3(2{\sigma }_1+{\sigma }_3)[{\theta }_3(\alpha +\rho )+\beta {\mu }_3]}{(\alpha +\rho )2{\eta }_3}}\end{array}$$

(30)

Solving Equation (29), the intelligent transformation level $\mathit{x}\left(\mathit{t}\right)$ is

$$x^S={\displaystyle \frac{A^S}{\alpha }}+(x_0-{\displaystyle \frac{A^S}{\alpha }})e^{-\alpha t}$$

(31)

where ${\mathit{A}}^{\mathit{S}}/\alpha$ is the steady-state level of intelligence. Substituting ${\mathit{k}}_1^{\mathit{S}},{ \mathit{b}}_1^{\mathit{S}},{ \mathit{k}}_2^{\mathit{S}},{ \mathit{b}}_2^{\mathit{S}},{ \mathit{k}}_3^{\mathit{S}},{ \mathit{b}}_3^{\mathit{S}}$ into Equation (22), the final payoff functions of the government, the sewage treatment enterprises, and the digital twin platforms are:

$$\left\{\begin{array}{l}{V}_1^S(x)={\displaystyle \frac{{\sigma }_1\beta }{\alpha +\rho }}{x}^S+{\displaystyle \frac{{\sigma }_{{}_1}^2{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{2\rho {\eta }_1{(\alpha +\rho )}^2}}+{\displaystyle \frac{{(2{\sigma }_1+{\sigma }_2)}^2{[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{8\rho {\eta }_2{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{{(2{\sigma }_1+{\sigma }_3)}^2{[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{8\rho {\eta }_3{(\alpha +\rho )}^2}}\\ V_2^S(x)={\displaystyle \frac{{\sigma }_2\beta }{\alpha +\rho }}{x}^S+{\displaystyle \frac{{\sigma }_1{\sigma }_2{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{\rho {\eta }_1{(\alpha +\rho )}^2}}+{\displaystyle \frac{{\sigma }_2(2{\sigma }_1+{\sigma }_2){[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{4\rho {\eta }_2{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{{\sigma }_2(2{\sigma }_1+{\sigma }_3){[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{2\rho {\eta }_3{(\alpha +\rho )}^2}}\\ V_3^S(x)={\displaystyle \frac{{\sigma }_3\beta }{\alpha +\rho }}{x}^S+{\displaystyle \frac{{\sigma }_1{\sigma }_3{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{\rho {\eta }_1{(\alpha +\rho )}^2}}+{\displaystyle \frac{{\sigma }_3(2{\sigma }_1+{\sigma }_2){[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{2\rho {\eta }_2{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{{\sigma }_3(2{\sigma }_1+{\sigma }_3){[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{4\rho {\eta }_3{(\alpha +\rho )}^2}}\end{array}\right.$$

(32)

Hence, the total system payoff under the Stackelberg game is

$$\begin{array}{l}{V}^S(x)=V_1^S(x)+V_2^S(x)+V_3^S(x)\\ ={\displaystyle \frac{({\sigma }_1+{\sigma }_2+{\sigma }_3)\beta }{\alpha +\rho }}{x}^S+{\displaystyle \frac{{\sigma }_1({\sigma }_1+2{\sigma }_2+2{\sigma }_3){[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{2\rho {\eta }_1{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{(2{\sigma }_1+3{\sigma }_2+4{\sigma }_3)(2{\sigma }_1+{\sigma }_2){[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{8\rho {\eta }_2{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{(2{\sigma }_1+4{\sigma }_2+3{\sigma }_3)(2{\sigma }_1+{\sigma }_3){[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{8\rho {\eta }_3{(\alpha +\rho )}^2}}\end{array}$$

(33)

3.5. Cooperative Game

To further advance the intelligent transformation of the sewage treatment industry and promote the development and utilization of emerging technologies, we also consider a cooperative mode among the government, sewage treatment enterprises, and digital twin platforms. In this mode, the three parties are regarded as an integrated whole, and all aim to enhance the level of intelligence in the industry, which guides their strategic choices. The system’s objective function is

$$\begin{array}{l}\mathrm{\Pi }={\mathrm{\Pi }}_1+{\mathrm{\Pi }}_2+{\mathrm{\Pi }}_3={\int }_0^{\infty }{e}^{-\rho t}[({\theta }_1{E}_1(t)+{\theta }_2{E}_2(t)+{\theta }_3{E}_3(t)+\beta x(t))-{\displaystyle \frac{{\eta }_1}{2}}{E}_1{}^2(t)\\ -{\displaystyle \frac{{\eta }_2}{2}}{E}_2{}^2(t)-{\displaystyle \frac{{\eta }_3}{2}}{E}_3{}^2(t)]dt\end{array}$$

(34)

Theorem 3. 

In the cooperative game, the feedback Nash equilibrium strategies of the three parties are

$$\left\{\begin{array}{l}{E}_1{}^C={\displaystyle \frac{2[{\theta }_1(\rho +\alpha )+{\mu }_1\beta ]}{{\eta }_1(\rho +\alpha )}}\\ E_2{}^C={\displaystyle \frac{2[{\theta }_2(\rho +\alpha )+{\mu }_2\beta ]}{{\eta }_2(\rho +\alpha )}}\\ E_1{}^C={\displaystyle \frac{2[{\theta }_3(\rho +\alpha )+{\mu }_3\beta ]}{{\eta }_3(\rho +\alpha )}}\end{array}\right.$$

(35)

Proof. 

Assume there exists a continuous and bounded differential payoff function ${\mathit{V}}^{\mathit{C}}\left(\mathit{x}\right)$ that, for $\mathit{x} \ge 0,$ satisfies the Hamilton–Jacobi–Bellman equation:

$$\begin{array}{l}\rho V^C(x)=\underset{E_1\ge 0,E_2\ge 0,E_3\ge 0}{\max }[({\theta }_1{E}_1+{\theta }_2{E}_2+{\theta }_3{E}_3+\beta x)-{\displaystyle \frac{{\eta }_1}{2}}{E}_1{}^2-{\displaystyle \frac{{\eta }_2}{2}}{E}_2{}^2-{\displaystyle \frac{{\eta }_3}{2}}{E}_3{}^2\\ +k({\mu }_1{E}_1+{\mu }_2{E}_2+{\mu }_3{E}_3-\alpha x)]\end{array}$$

(36)

Equation (36) is concave in ${\mathit{E}}_1, {\mathit{E}}_2,{ \mathit{E}}_3$. Taking first-order conditions and setting them to zero yields the optimal controls:

$$\left\{\begin{array}{l}{E}_1={\displaystyle \frac{{\theta }_1+k{\mu }_1}{{\eta }_1}}\\ E_2={\displaystyle \frac{{\theta }_2+k{\mu }_2}{{\eta }_2}}\\ E_3={\displaystyle \frac{{\theta }_3+k{\mu }_3}{{\eta }_3}}\end{array}\right.$$

(37)

Substituting Equation (37) into Equation (36) and simplifying gives

$$\rho V^C(x)=(\beta -\alpha k)x+{\displaystyle \frac{{({\theta }_1+{\mu }_{1}k)}^2}{2{\eta }_1}}+{\displaystyle \frac{{({\theta }_2+{\mu }_{2}k)}^2}{2{\eta }_2}}+{\displaystyle \frac{{({\theta }_3+{\mu }_{3}k)}^2}{2{\eta }_3}}$$

(38)

From Equation (38), the optimal linear form in $\mathit{x}$ solves the Hamilton–Jacobi–Bellman equation:

$$V^C(x)=k^{C}x+b^C$$

(39)

where ${\mathit{k}}^{\mathit{C}}$ and ${\mathit{b}}^{\mathit{C}}$ are constants. Substituting ${\mathit{V}}^{\mathit{C}}\left(\mathit{x}\right)$ and its first derivative into the HJB equation and simplifying yields

$$\rho (k^{C}x+b^C)=(\beta -\alpha k^C)x+{\displaystyle \frac{{(2{\theta }_1+{\mu }_1{k}^C)}^2}{2{\eta }_1}}+{\displaystyle \frac{{(2{\theta }_2+{\mu }_2{k}^C)}^2}{2{\eta }_2}}+{\displaystyle \frac{{(2{\theta }_3+{\mu }_3{k}^C)}^2}{2{\eta }_3}}$$

(40)

Since Equation (40) holds for $\mathit{x} \ge 0$, we obtain

$$\begin{array}{l}{k}^C={\displaystyle \frac{\beta }{\alpha +\rho }}\\ b^C={\displaystyle \frac{{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{\rho {\eta }_1{(\alpha +\rho )}^2}}+{\displaystyle \frac{{[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{\rho {\eta }_2{(\alpha +\rho )}^2}}+{\displaystyle \frac{{[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{\rho {\eta }_3{(\alpha +\rho )}^2}}\end{array}$$

(41)

Substituting Equation (41) into Equation (37), the optimal strategies for the government, the sewage treatment enterprises, and the digital twin platforms are

$$\left\{\begin{array}{l}{E}_1{}^C={\displaystyle \frac{[{\theta }_1(\rho +\alpha )+{\mu }_1\beta ]}{{\eta }_1(\rho +\alpha )}}\\ E_2{}^C={\displaystyle \frac{[{\theta }_2(\rho +\alpha )+{\mu }_2\beta ]}{{\eta }_2(\rho +\alpha )}}\\ E_1{}^C={\displaystyle \frac{[{\theta }_3(\rho +\alpha )+{\mu }_3\beta ]}{{\eta }_3(\rho +\alpha )}}\end{array}\right.$$

(42)

□

Thus, Theorem 3 is established. Substituting the results into Equation (2) yields

$$\begin{array}{l}\stackrel{·}{x}(t)=A^C-\alpha x(t)\\ x(0)=x_0\end{array}$$

(43)

where

$$\begin{array}{l}{A}^C={\mu }_1{E}_1(t)+{\mu }_2{E}_2(t)+{\mu }_3{E}_3(t)=E_1{}^C={\displaystyle \frac{{\mu }_1[{\theta }_1(\rho +\alpha )+{\mu }_1\beta ]}{{\eta }_1(\rho +\alpha )}}\\ +{\displaystyle \frac{{\mu }_2[{\theta }_2(\rho +\alpha )+{\mu }_2\beta ]}{{\eta }_2(\rho +\alpha )}}+{\displaystyle \frac{{\mu }_3[{\theta }_3(\rho +\alpha )+{\mu }_3\beta ]}{{\eta }_3(\rho +\alpha )}}\end{array}$$

(44)

Solving Equation (43) gives

$$x^C={\displaystyle \frac{A^C}{\alpha }}+(x_0-{\displaystyle \frac{A^C}{\alpha }})e^{-\alpha t}$$

(45)

Substituting ${\mathit{k}}^{\mathit{C}}$ and ${\mathit{b}}^{\mathit{C}}$ into the value function expression yields the optimal total payoff under the cooperative game:

$$\begin{array}{l}{V}^C(x)={\displaystyle \frac{\beta }{\alpha +\rho }}{x}^C+{\displaystyle \frac{{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{\rho {\eta }_1{(\alpha +\rho )}^2}}+{\displaystyle \frac{{[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{\rho {\eta }_2{(\alpha +\rho )}^2}}\\ +{\displaystyle \frac{{[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{\rho {\eta }_3{(\alpha +\rho )}^2}}\end{array}$$

(46)

4. Comparative Analysis

This study examines the optimal effort strategies and the final payoffs of the government, wastewater treatment enterprises, and the digital twin platform under three conditions: non-cooperation, government subsidies, and cooperation strategies. Relevant conclusions are then drawn.

Theorem 4. 

The comparative analysis of the optimal strategies for the government, wastewater treatment enterprises, and the digital twin platform across the three different game modes is as follows:

$$\left\{\begin{array}{l}{E}_1^C\ge E_1^S=E_1^N\\ E_2^C>E_2^S>E_2^N\\ E_3^C>E_3^S\ge E_3^N\end{array}\right.$$

(47)

Proof. 

Based on Equations (5), (19) and (35), it follows that

$$\left\{\begin{array}{l}{E}_1^N-E_1^S={\displaystyle \frac{{\sigma }_1[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}{{\eta }_1(\alpha +\rho )}}-{\displaystyle \frac{{\sigma }_1[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}{{\eta }_1(\alpha +\rho )}}=0\\ E_1^C-E_1^N=(2-{\sigma }_1){\displaystyle \frac{[{\theta }_1(\rho +\alpha )+{\mu }_1\beta ]}{{\eta }_1(\rho +\alpha )}}>0\end{array}\right.$$

(48)

Therefore, $E_1^C\ge E_1^S=E_1^N$ holds.

Similarly, based on Equations (5), (19) and (35), it follows that

$$\left\{\begin{array}{l}{E}_2^S-E_2^N=2{\sigma }_1{\displaystyle \frac{({\theta }_2(\alpha +\rho )+\beta {\mu }_2)}{(\alpha +\rho )2{\eta }_2}}>0\\ E_2{}^C-E_2{}^S=(2{\sigma }_1+3{\sigma }_2+4{\sigma }_3){\displaystyle \frac{[{\theta }_2(\rho +\alpha )+{\mu }_2\beta ]}{{\eta }_2(\rho +\alpha )}}>0\end{array}\right.$$

(49)

Therefore, $E_2^C>E_2^S>E_2^N$ holds.

Similarly, based on Equations (5), (19) and (35), it follows that

$$\left\{\begin{array}{l}{E}_3^S-E_3^N={\displaystyle \frac{2{\sigma }_1-{\sigma }_3}{2}}({\displaystyle \frac{{\theta }_3(\alpha +\rho )+\beta {\mu }_3}{(\alpha +\rho )2{\eta }_3}})\ge 0\\ E_3^C-E_3^S=(2-{\sigma }_3)({\displaystyle \frac{{\theta }_3(\alpha +\rho )+\beta {\mu }_3}{(\alpha +\rho )2{\eta }_3}})>0\end{array}\right.$$

(50)

Therefore, $E_3^C>E_3^S\ge E_3^N$ holds. □

Corollary 1. 

When the relationship between the government, wastewater treatment enterprises, and the digital twin platform shifts from the Nash non-cooperative game to the Stackelberg model with government subsidies, the government’s optimal effort level remains unchanged. However, the subsidy policy can significantly increase the effort levels of both the wastewater treatment enterprises and the digital twin platform, and the degree of improvement is positively correlated with the subsidy intensity. This indicates that government subsidies can effectively encourage market actors to participate in the intelligent construction of wastewater treatment without increasing the government’s own direct input.

Corollary 2. 

Under the cooperative model, the optimal effort levels of all three parties reach the highest. This shows that a coordinated mechanism driven by government guidance, enterprise implementation, and platform empowerment can overcome interest barriers among the parties. It creates a “policy–technology–market” linkage, thereby maximizing the overall efficiency of the wastewater treatment system. This result provides a theoretical basis for establishing a long-term cooperation mechanism among the three parties.

Theorem 5. 

Under the Nash non-cooperative game, the Stackelberg game with subsidies, and the cooperative game, the comparative results of the industrial intelligence level in the collaborative development of intelligent wastewater treatment systems are as follows: $x^C\ge x^S>x^N$

.

Proof. 

Based on Theorem 4, it follows that

$${\mu }_1{E}_1^C+{\mu }_2{E}_2^C+{\mu }_3{E}_3^C>{\mu }_1{E}_1^S+{\mu }_2{E}_2^S+{\mu }_3{E}_3^S>{\mu }_1{E}_1^N+{\mu }_2{E}_2^N+{\mu }_3{E}_3^N$$

(51)

which means $A^C>A^S>A^N$.

Since ${\displaystyle \frac{dx}{dA}}={\displaystyle \frac{1}{\alpha }}(1-{\mathrm{e}}^{-\alpha t})>0$, and $(\alpha >0)$, and $x$ is an increasing function of A, it follows that $x^C\ge x^S>x^N$ holds. □

Corollary 3. 

By jointly establishing an intelligent transformation center, the three game participants maximize their own effort levels to reduce economic losses during the transformation. At the same time, the synergy effect generates socio-economic benefits greater than the sum of the parts, so that the levels of intelligence under the cooperative model reach the optimum.

Theorem 6. 

The comparative results of the total returns of system efficiency under the three game modes are as follows: $V^C>V^S>V^N$.

Proof. 

Based on Equations (16) and (32), and Theorem 5, it follows that

$$\left\{\begin{array}{l}{V}_1^S-V_1^N=(4{\sigma }_1^2+{\sigma }_2^2+3{\sigma }_1{\sigma }_2){\displaystyle \frac{{[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{\rho {\eta }_2{(\alpha +\rho )}^2}}+(4{\sigma }_1^2+{\sigma }_3^2+3{\sigma }_1{\sigma }_3){\displaystyle \frac{{\sigma }_1{\sigma }_3{[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{\rho {\eta }_3{(\alpha +\rho )}^2}}>0\\ V_2^S-V_2^N={\displaystyle \frac{{\sigma }_2(2{\sigma }_1-{\sigma }_2)}{4}}{\displaystyle \frac{{[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{\rho {\eta }_2{(\alpha +\rho )}^2}}+{\displaystyle \frac{{\sigma }_2(2{\sigma }_1-{\sigma }_3)}{2}}{\displaystyle \frac{{[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{\rho {\eta }_3{(\alpha +\rho )}^2}}>0\\ V_3^S-V_3^N={\displaystyle \frac{{\sigma }_3(2{\sigma }_1-{\sigma }_2)}{4}}{\displaystyle \frac{{[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{\rho {\eta }_2{(\alpha +\rho )}^2}}+{\displaystyle \frac{{\sigma }_3(2{\sigma }_1-{\sigma }_3)}{2}}{\displaystyle \frac{{[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{\rho {\eta }_3{(\alpha +\rho )}^2}}>0\end{array}\right.$$

(52)

According to Equation (52), $V_1^S+V_2^S+V_3^S>V_1^N+V_2^N+V_3^N$ can be obtained. From this it follows that $V^S>V^N$. Combining Equations (33) and (46), and Theorem 5, it can be derived that

$$\begin{array}{l}{V}^C-V^S={\displaystyle \frac{\beta }{\alpha +\rho }}(x^C-x^S)+{\displaystyle \frac{{[{\theta }_1(\alpha +\rho )+{\mu }_1\beta ]}^2}{2\rho {\eta }_1{(\alpha +\rho )}^2}}[2-{\sigma }_1({\sigma }_1+2{\sigma }_2+2{\sigma }_3)];\\ +{\displaystyle \frac{{[{\theta }_2(\alpha +\rho )+{\mu }_2\beta ]}^2}{8\rho {\eta }_2{(\alpha +\rho )}^2}}[8-(2{\sigma }_1+3{\sigma }_2+4{\sigma }_3)(2{\sigma }_1+{\sigma }_2)];\\ +{\displaystyle \frac{{[{\theta }_3(\alpha +\rho )+{\mu }_3\beta ]}^2}{8\rho {\eta }_3{(\alpha +\rho )}^2}}[8-(2{\sigma }_1+4{\sigma }_2+3{\sigma }_3)(2{\sigma }_1+{\sigma }_3)]>0.\end{array}$$

(53)

That is $V^C>V^S>V^N$. □

Corollary 4. 

Within the Stackelberg game framework, the optimal payoffs of the three parties and the total system returns are both significantly higher than those under the Nash non-cooperative game. The core driving mechanism of this difference lies in government subsidies, which create incentives that enable the three parties to achieve a Pareto improvement. In other words, the overall system returns increase without reducing the payoff of any party, confirming the role of government intervention in resolving the dilemma of non-cooperative games.

Corollary 5. 

The cooperative game model performs significantly better in terms of returns and efficiency compared with both the Stackelberg game and the Nash non-cooperative game. This model establishes a coordinated mechanism of “multi-actor capability complementarity and benefit sharing” through resource co-allocation and the integration of production capacity. It breaks the resource constraints and capability boundaries of a single party, enabling the total system returns to reach the Pareto optimal state. This provides a globally optimal organizational reference for the intelligent transformation of the industry.

5. Simulation

In the differential game involving the government, wastewater treatment enterprises, and the digital twin platform under a cooperative model, the equilibrium outcome of the optimal strategies and system performance depends on the parameter characteristics of the model. To ensure the scientific validity and contextual adaptability of the numerical simulation, this study adopts a three-stage approach “theoretical foundation–policy calibration–method optimization” to determine the parameter ranges. First, based on the parameter-setting logic in multi-agent cooperative games proposed by Han et al. [43] and Ortiz-Martínez et al. [44], and by integrating the core dimensions of “technological features–cost structure–policy intensity” in the intelligent transformation of wastewater treatment, the theoretical ranges of parameters are preliminarily defined. Second, according to the mandatory requirements specified in the 14th Five-Year Plan for Smart Water Conservancy Development and its local implementation guidelines, such as energy consumption of intelligent equipment and data-sharing rates, parameter thresholds are adjusted. Furthermore, considering the potential impact of parameters on system performance in intelligent wastewater treatment scenarios, the step sizes of core parameters with significant influence are appropriately narrowed, thereby reserving analytical space to capture marginal effects of minor fluctuations on equilibrium strategies during subsequent sensitivity analysis and ensuring the precision of key factor identification. Finally, regarding the interactions among critical parameters in the model, multiple gradient-based combinations are pre-set to ensure that parameter sets cover the possible ranges of synergistic effects, providing data support for analyzing nonlinear association mechanisms between parameters, so that the numerical simulation results can comprehensively reflect the variations in system performance under different parameter combinations. This paper establishes the baseline parameters of the models as follows: $\alpha =0.05$, $\beta =2.0$, $\rho =0.2$, ${\eta }_1=1.5$, ${\eta }_2=3.0$, ${\eta }_3=1.0$, ${\mu }_1=0.6$, ${\mu }_2=0.9$, ${\mu }_3=1.2$, ${\theta }_1=0.35$, ${\theta }_2=0.18$, ${\theta }_3=0.12$.

To accurately identify the key influencing parameters in the intelligent transformation system for wastewater treatment and to clarify the mechanisms through which these parameters affect system outputs, this study introduces the Sobol global sensitivity analysis method. This method is based on the principle of variance decomposition. By examining the relationship between model input parameters and output variance, it quantitatively determines parameter sensitivity and provides a basis for parameter optimization and decision-making in complex systems.

Assume that the model describing the intelligent transformation system for wastewater treatment is denoted as $y=f(p_1, p_2,\dots , p_k)$. The input parameters are represented by $p_1,p_1,\dots ,p_k$, and the model output is represented by $y$. The output variance $V_{(y)}$ can be decomposed into the sum of the variances of each parameter and their interaction terms.

$$V_{(q)}=\sum _i{V}_i+\sum _{\mathit{i}}\sum _{\mathit{j}>\mathit{i}}{V}_{\mathit{ij}}+\sum _i\sum _{j>\mathit{i}}\sum _{l>j}{V}_{\mathit{ijl}}+\dots +V_{1,2,\dots ,k}.$$

(54)

Among them, $V_i$ denotes the variance caused solely by parameter $p_i$, which characterizes the independent effect of a single parameter on the system output. $V_{ij}$ denotes the variance jointly induced by parameters $p_i$ and $p_j$, which reflects the influence of their interaction. $V_{1,2,\dots ,k}$ denotes the variance term arising from the combined action of all parameters, which represents the overall effect of complex multi-parameter interactions.

To achieve normalized analysis of variance contribution, the above variance decomposition is transformed into a sensitivity index relationship.

$$\sum _{\mathit{i}}{\mathit{S}}_{\mathit{i}}+\sum _{\mathit{i}}\sum _{\mathit{j}>\mathit{i}}{\mathit{S}}_{\mathit{ij}}+\sum _{\mathit{i}}\sum _{\mathit{j}>\mathit{i}}\sum _{\mathit{l}>\mathit{j}}{S}_{\mathit{ijl}}+\dots +S_{1,2,\dots ,k}=1.$$

(55)

Among them, $S_i$ is the first-order sensitivity index. The larger $S_i=V_i/V_{(y)}$ and $S_i$ are, the more sensitive the output result is to parameter $p_i$, which means that the independent effect of a single parameter on the system output is more significant. $S_{ij}$ is the second-order sensitivity index. The higher $S_{ij}$ is, the greater the influence of the joint action of parameters $p_i$ and $p_j$ on the output variance of the model.

In addition, to comprehensively measure the total contribution of parameter $p_i$ to the output variance of the model, the total sensitivity index $S_{Ti}$ is introduced. It considers both the effect of the parameter itself and its interactions with other parameters. The calculation is given as follows:

$$S_{Ti}=1-V_{-i}/V_{(q)}.$$

(56)

In Equation (56), $V_{-i}$ represents the variance obtained from the joint effect of the remaining parameters after excluding parameter $p_i$.Based on the theoretical foundation of the Sobol global sensitivity analysis method, this study applies the method and uses MATLAB 2023a software to compute the parameters of the intelligent transformation system for wastewater treatment. Four key parameters with the strongest sensitivity are identified, as shown in Figure 2 below.

The sensitivity index of parameter $\beta$ is significantly higher than that of other parameters, indicating that system performance is highly sensitive to changes in $\beta$. Its total effect index ($\mathit{S}{\mathit{T}}_{\mathit{i}}$) reaches 0.459, far exceeding the first-order index (${\mathit{S}}_{\mathit{i}}$) of 0.315. This suggests that $\beta$ not only exerts a strong direct influence on the system but also generates synergistic amplification effects through interactions with other parameters, thereby occupying a dominant position in the system parameter structure.

The first-order index of parameter $\alpha$ (0.233) reflects its direct impact when acting independently, whereas its total effect index (0.350) captures both its own and interaction effects. This difference indicates that $\alpha$ makes a significant contribution to the system and enhances its influence through synergistic effects, making it one of the key parameters. Variations in $\alpha$ affect the system through both direct and indirect pathways.

For parameter ${\mu }_3$, the first-order index of 0.151 is lower than that of $\beta$ and $\alpha$, but its total effect index rises to 0.274, implying that ${\mu }_3$ can strengthen its impact through interactions with other parameters. Although its overall influence is relatively weaker, it still plays an important mediating role in specific scenarios such as the mechanism of intelligent transformation.

The sensitivity of parameter ${\eta }_3$ is the lowest among the four, yet its total effect index remains higher than its first-order index, showing that it mainly influences the system indirectly through interactions. While its individual contribution is limited, ${\eta }_3$ may still act as an auxiliary variable under specific parameter combinations.

Based on the Sobol global sensitivity analysis results, this study has identified the key driving parameters influencing system performance and their relative importance. As a representative global sensitivity analysis method, the Sobol approach quantifies both main and interaction effects, thereby overcoming the limitations of traditional local sensitivity analysis that only captures marginal effects of individual parameters. However, two limitations remain: first, the method emphasizes parameter importance ranking but provides insufficient detail on dynamic coupling processes; second, it lacks precision in capturing nonlinear interaction effects when determining the optimal cooperative configuration range of key parameter sets.

To address these limitations and extend the analytical scope, this study introduces the Response Surface Method with Central Composite Design (RSM-CCD). By constructing a second-order response surface model in the parameter space, this approach quantifies the contribution of interaction terms to system outputs and identifies the interaction patterns among key parameters. The combined strategy of “global sensitivity analysis–response surface modeling” enables efficient identification of core parameters through the Sobol method, while the response surface approach captures nonlinear features of parameter interactions. This forms a closed research loop from “key parameter screening” to “cooperative interval optimization,” providing a more operational scientific basis for improving system performance.

An experimental design was constructed using Design-Expert 13 software, with the independent variables—$\alpha$, $\beta$, ${\mu }_3$, and ${\eta }_3$-modeled against the dependent variables of system performance for the intelligent transformation of wastewater treatment. The specific parameter combinations and corresponding system performance values for each experiment are detailed in

Table 1. Specific experimental parameters and corresponding system performance.

Std	Run	α	β	μ3	η3	R1
1	3	0.04	1.6	0.96	0.8	9612
2	8	0.06	1.6	0.96	0.8	10,334.6
3	21	0.04	2.4	0.96	0.8	15,958
4	6	0.06	2.4	0.96	0.8	11,648.9
5	30	0.04	1.6	1.44	0.8	14,060
6	27	0.06	1.6	1.44	0.8	11,999.7
7	19	0.04	2.4	1.44	0.8	28,430
8	29	0.06	2.4	1.44	0.8	15,873
9	20	0.04	1.6	0.96	1.2	8873.3
10	5	0.06	1.6	0.96	1.2	10,345.5
11	7	0.04	2.4	0.96	1.2	12,070
12	1	0.06	2.4	0.96	1.2	8338.1
13	14	0.04	1.6	1.44	1.2	11,172
14	15	0.06	1.6	1.44	1.2	9788.8
15	4	0.04	2.4	1.44	1.2	22,178
16	12	0.06	2.4	1.44	1.2	9921
17	9	0.04	2	1.2	1	27,823
18	18	0.06	2	1.2	1	24,865.6
19	17	0.05	1.6	1.2	1	18,562.8
20	13	0.05	2.4	1.2	1	23,637
21	28	0.05	2	0.96	1	19,527.7
22	22	0.05	2	1.44	1	23,463
23	10	0.05	2	1.2	0.8	23,067
24	25	0.05	2	1.2	1.2	23,956.2
25	24	0.05	2	1.2	1	32,200
26	26	0.05	2	1.2	1	32,200
27	23	0.05	2	1.2	1	32,200
28	11	0.05	2	1.2	1	32,200
20	2	0.05	2	1.2	1	32,200
30	16	0.05	2	1.2	1	32,200

.

Table 2. ANOVA for quadratic model.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	9.051 × 1011	14	9.051 × 1011	165.78	<0.0001	significant
A-α	1.866 × 108	1	1.866 × 108	478.58	<0.0001
B-β	3.592 × 108	1	3.592 × 108	920.97	<0.0001
C-μ3	2.005 × 108	1	2.005 × 108	514.16	<0.0001
D-η3	5.775 × 107	1	5.775 × 107	148.07	<0.0001
AB	2.378 × 107	1	2.378 × 107	60.98	<0.0001
AC	1.316 × 107	1	1.316 × 107	33.75	<0.0001
AD	4.414 × 106	1	4.414 × 106	11.32	0.0043
BC	2.609 × 107	1	2.609 × 107	66.90	<0.0001
BD	8.231 × 106	1	8.231 × 106	21.11	0.0004
CD	8.232 × 106	1	8.232 × 106	21.11	0.0004
A2	1.140 × 106	1	1.140 × 106	2.92	0.1079
B2	4.547 × 105	1	4.547 × 105	1.17	0.2973
C2	2.561 × 105	1	2.561 × 105	0.6566	0.4304
D2	2.832 × 105	1	2.832 × 105	0.7262	0.4075
Residual	5.850 × 106	15	5.850 × 106
Lack of Fit	5.850 × 106	10	5.850 × 106
Pure Error	0.0000	5	0.0000
Cor Total	9.110 × 108	29

presents the results of the regression model ANOVA. The overall significance test indicates that the constructed model provides a significant explanation of the variation in the response value R1 (p < 0.0001, F = 165.78). This result verifies the model’s statistical validity for mapping parameter–response relationships.

At the interaction level, further analysis reveals significant synergistic effects between parameter pairs: $\alpha$–$\beta$, $\alpha$–${\mu }_3$, and $\beta$–${\mu }_3$ (p < 0.0001). This indicates that these parameter pairs exhibit strong synergistic influences on the system response, with their interactions exerting effects on R1 far beyond random error. These interactions can thus be considered core directions for subsequent parameter optimization in regulating interaction effects.

Table 3. Fit statistics.

Std.Dev.	624.49	R2	0.9936
Mean	11,226.84	Adjusted R2	0.9876
C.V%	5.56	Predicted R2	0.9495
		Adeq Precision	58.8089

reports the model fitting statistics, providing further validation of model performance from the perspectives of data dispersion and model adequacy.

Data dispersion: The standard deviation (STD.Dev.) is 624.49, the mean is 11,226.84, and the coefficient of variation (C.V.%) is 5.56%. Since a smaller coefficient of variation indicates lower data dispersion, the relative relationship between the mean and standard deviation confirms the stability of the response value R1 distribution, ensuring a reliable data basis for model fitting.

Model adequacy: The coefficient of determination is ${\mathit{R}}^2 = 0.9936$, with adjusted ${\mathit{R}}^2 = 0.9876$ and predicted ${\mathit{R}}^2 = 0.9495$. The ${\mathit{R}}^2$ value close to 1 demonstrates the strong explanatory power of the model. Both the adjusted ${\mathit{R}}^2$ and predicted ${\mathit{R}}^2$ remain high, indicating that the model not only fits the training data well but also exhibits strong generalization ability.

Predictive accuracy: The adequate precision value reaches 58.8089, far exceeding the threshold of 4. This result indicates that the model can accurately capture system response patterns under parameter interactions, avoiding interference from data fluctuations in analyzing parameter influence mechanisms.

In summary, the model performs excellently in terms of variance significance, model fit, and predictive accuracy, thereby laying a robust foundation for parameter optimization in wastewater treatment intelligent transformation. The model thus serves as a reliable basis for further exploration of parameter interactions and targeted policy design can be conducted.

To more intuitively illustrate the nonlinear effects of key parameter interactions on the system response ${\mathit{R}}_1$, a 3D response surface diagram based on the CCD model was plotted. The interactions $\alpha$–$\beta$, $\alpha$–${\mu }_3$, and $\beta$–${\mu }_3$ were selected as examples for visualization, and the results are shown in Figure 3.

$\alpha$–$\beta$ interaction analysis: Under fixed parameter conditions (${\mu }_3 = 1.2$, ${\eta }_{3 }= 1$), the 3D response surface of $\alpha$ and $\beta$ exhibits a pronounced nonlinear relationship. Specifically, when $\alpha$ increases from 0.04 to 0.06 and $\beta$ from 1.6 to 2.4, the system response ${\mathit{R}}_1$ shows a marked upward trend. The gradient of the surface is relatively steep, and the high-response region expands as the parameter values increase. This indicates that the synergy between $\alpha$ and $\beta$ effectively sustains the stable operation of intelligent technologies, thereby creating favorable conditions for improving benefit conversion rates. When the technological state remains stable, policy guidance and operational optimization measures can exert stronger effects, ultimately enhancing the overall system performance.

$\alpha$–${\mu }_3$ interaction analysis: Under fixed parameter conditions ($\beta = 2$, ${\eta }_3 = 1$), the interaction between $\alpha$ and ${\mu }_3$ presents distinct response characteristics. When $\alpha$ lies within 0.04–0.06 and ${\mu }_3$ within 0.96–1.44, the ${\mathit{R}}_1$ value exhibits nonlinear growth with their synergistic increase. The transition from low- to high-response regions in the surface plot clearly illustrates the strong interaction between the two parameters. This result suggests that the digital twin platform can, through algorithm optimization, real-time diagnostics, and intelligent operation and maintenance, effectively compensate for performance degradation in the process of intelligent transformation, forming a dynamic balance mechanism of “technological decay–platform compensation”.

$\beta$–${\mu }_3$ interaction analysis: Under fixed parameter conditions ($\alpha = 0.05$, ${\eta }_3 = 1$), the response surface of $\beta$ and ${\mu }_3$ displays a symmetrical distribution. When $\beta$ ranges from 1.6 to 2.4 and ${\mu }_3$ from 0.96 to 1.44, the ${\mathit{R}}_1$ value first rises rapidly and then levels off, while the circular contour lines in the surface plot delineate the optimal parameter combination interval ($\beta = 1.8$–2.2, ${\mu }_3 = 1.2$–1.4). This characteristic reveals the synergistic relationship between platform empowerment and the conversion rate of intelligent benefits: within a moderate range, enhancing platform performance can significantly strengthen benefit conversion, whereas once the empowerment surpasses a threshold, diminishing marginal effects emerge. This finding provides a quantitative basis for optimizing the dynamic balance between platform input intensity and benefit growth.

6. Conclusions

The intelligent transformation of the wastewater treatment industry is a key pathway for upgrading modern environmental governance systems and achieving sustainable development, while the construction and optimization of multi-agent collaborative governance mechanisms constitute its core issue. This study focuses on the multi-agent interactions in wastewater treatment intelligent transformation. Based on differential game theory, a tripartite dynamic game model involving government, wastewater treatment enterprises, and digital twin platforms was constructed. By solving equilibrium strategies, analyzing parameter sensitivity, and examining interaction effects, the mechanisms by which different game modes, key parameters, and interactions influence system performance were systematically explored. The main conclusions are as follows:

(1)

Game modes: Different game modes exhibit significant differences in their impact on system performance. In the Nash non-cooperative game, agents act solely in their own interests, leading to dispersed resource allocation and repeated technological investment, hindering governance synergy. The Stackelberg game establishes a hierarchical relationship among agents and partially mitigates disorderly competition, but information asymmetry still induces strategic delays, resulting in limited system improvement. By contrast, the cooperative game fosters information sharing and benefit coordination, enabling the government, enterprises, and digital twin platforms to achieve joint decision-making toward common goals. This avoids the efficiency loss of non-cooperation and the coordination costs of hierarchy, ultimately maximizing both system benefits and governance performance. Thus, cooperation is the optimal choice for maximizing the effectiveness of wastewater treatment intelligent transformation.

(2)

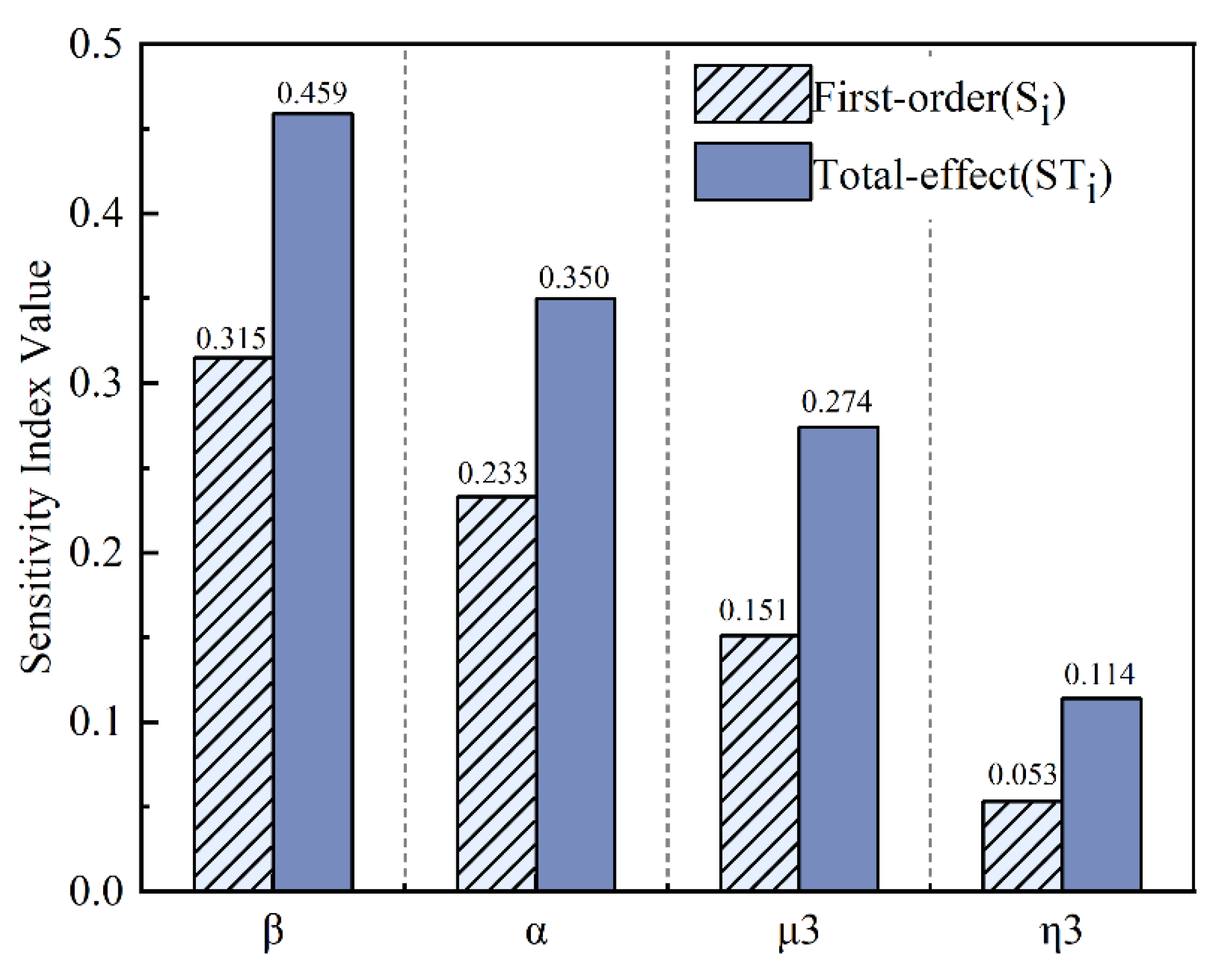
Parameter sensitivity: Parameters show a clear gradient in sensitivity: $\beta$ is the most sensitive, followed by $\alpha$, ${\mu }_3$, and ${\eta }_3$, each exerting distinct mechanisms and ranges of influence. $\beta$ is directly linked to the efficiency of technological investment conversion and serves as the core driver of system performance; $\alpha$ determines the long-term stability of intelligent technologies, influencing sustainability; ${\mu }_3$ enhances intelligent efficiency by integrating technological resources with operational needs; ${\eta }_3$ mainly affects the early stage of transformation, with limited long-term influence. These sensitivity differences imply that differentiated regulation strategies should be adopted according to parameter characteristics.

(3)

Interaction effects: The parameter pairs $\alpha$–$\beta$, $\alpha$–${\mu }_3$, and $\beta$–${\mu }_3$ exhibit significant synergistic effects. The coupling amplification between $\alpha$ and $\beta$ shows that improved technological stability strengthens the marginal contribution of benefit conversion; the dynamic balance between $\alpha$ and ${\mu }_3$ demonstrates that platform capacity can effectively offset the negative impact of technological decay; and the synergistic gain of $\beta$ and ${\mu }_3$ reveals a positive feedback loop that enhances system performance. These multidimensional synergies represent the core pathway for optimizing system effectiveness in intelligent wastewater governance.

Management implications: Based on these findings, three recommendations are proposed:

(1)

The analytical results translate into actionable guidance for public authorities. A pivotal recommendation is the design of an institutional framework that makes multi-agent collaboration the most rational strategic choice. This can be achieved by implementing targeted fiscal instruments like data-sharing subsidies and establishing formal R&D consortia with independent oversight to ensure stability and fair benefit distribution.

(2)

The critical sensitivity of specific parameters further advocates for a dynamic, data-driven regulatory paradigm. Governments should focus on real-time monitoring of ${\mu }_3$ and ${\eta }_3$. A decline in μ₃ warrants policy interventions such as R&D grants to boost innovation effort, while a high ${\eta }_3$ necessitates dynamic subsidies to ensure the platform’s economic viability and continuous service.

(3)

Finally, the identified interaction synergies demand a move beyond siloed policy tools. The interplay between $\alpha$ and $\beta$ is critical. Policies should be designed to counter the natural decay $\alpha$ by amplifying the benefit coefficient $\beta$, for instance, by creating markets for efficiency gains. This ensures that the system’s intelligence level is not only achieved but also effectively utilized and maintained.