Abstract
Few publications have elaborated on the steady-state model, a ‘cybernetic model’ that should not be confused with its namesake in mathematical systems; it is rooted in preceding publications about general systems theories, something that is explored in this paper. First, the origins of homeostasis are briefly addressed as derived from biological concepts. After looking at its legacy the concepts of boundary zones from socio-economic theory, Shannon’s information theory, control mechanisms and engineering principles are added as a multidisciplinary amalgamation to modelling of primary, recurrent processes. The resulting cybernetic steady-state model offers a generic transdisciplinary framework for depicting regulatory and control processes within organisational and engineering systems as well as interaction between agents in networks. In the latter sense, it provides an explanatory concept for self-criticality in complex adaptive systems. Hence, it does not only have a rich heritage but also wide-ranging potential. For example, the steady-state model could be used to support action research and case studies in addition to serving as a reference model for other (business) process modelling techniques. Therefore, the steady-state model offers an enrichment of existing approaches to modelling recurrent processes —not only for operations management; it can also be seen as a more practical extension of Miller’s living systems and Beer’s viable system model making it suitable for a broad range of applications.
Few works, e.g., [1] (pp. xxv–xxviii, 146) [2] (pp. 77–81), have expanded on the so-called steady-state model; this model should not be confused with its namesake in mathematical systems. Whereas it is first mentioned by in ‘t Veld [3] (p. 193), a Dutch take on systems theories mostly based on general systems theory and cybernetics, the model is factually rooted in preceding publications about general systems theory and living systems as a multidisciplinary amalgamation. Thus, this manuscript has two objectives:
- How this specific model can be traced back to earlier thoughts on systems theories, and consequently, how it is a result of combining concepts from biology, control theory, engineering, information theory and systems theories.
- Which potential applications this reference model has with a particular focus on recurring processes such as those found in operations management.
1. Tracing the Steady-State Model Back to Its Roots
Thinking about the steady state of systems and its implications goes back to the time that conceptualisations for systems theories were formalised. To better understand the emergence of the model, it is worthwhile to look at the thoughts of four dominant thinkers of the time on homeostasis, living systems and interactions of systems with their environment: Ludwig von Bertalanffy, James G. Miller, Stafford Beer and Claude E. Shannon.
1.1. Advocating the Steady-State by Ludwig von Bertalanffy
In the context of the general developments of systems theory, the concept of ‘steady state’ as foundation for the steady-state model can be attributed to Ludwig von Bertalanffy [4] (p. 40), though some, such as Gorelik [5], trace it back to Bogdanov’s interpretation of tectology. According to Gorelik [6] (pp. 348, 351), Bogdanov’s tectology advances the notion that systems, called complexes in his writing, are in interaction, and are striving for equilibrium with other complexes, and hitherto, their environments; Bogdanov’s notions came about in the 1920s but were not further advanced due to an early death and political opposition to his ideas. Later, in nascent writings on systems theories, von Bertalanffy advocates the concept of the steady state as similar to maintaining equilibrium (for example, [7] (p. 157)), or just refers to it without further explanation (for instance, [8] (p. 418)). The concept of the steady state implies that a system tries to retain a specific state, as response to perturbations in its environment; this is also called maintaining homeostasis. It should be noted that von Bertalanffy [9] (p. 23) was well aware of its biological roots, though that appeared to be more the background in later writings about general systems theory, e.g., [4]. In most of his writings, though, his approach to the steady state was based on mathematical systems.
Subsequently, this concept of homeostasis by maintaining a steady state articulated by von Bertalanffy is seen by many as the keystone for systems theories. Drack and Schwarz [10] attest to the influence of von Bertalanffy on developments in general systems theory, and Lloyd et al. [11] for conceptualisations of biological systems. Beyond systems theories and biology, Johnson et al. [12] mention the early impact on systems thinking for management, particularly for an organisation maintaining a dynamic equilibrium with its environment; notably, this also appears in the work of Katz and Khan [13] (pp. 14–29) [14] (pp. 353–354). Another paper that advocates systems thinking in management science, including steady-state, dynamic equilibrium and homeostasis, is Kast and Rosenzweig [15] (p. 450), albeit presented in the form of generic reflections. Thinking about the steady state has also influenced some in education, a case in point being Biggs’s [16] work. Furthermore, the notion of steady state appears in geomorphology, e.g., [17], though Chisholm [18] (p. 49) contests the concept of open systems by reducing it to inductive reasoning. Strauss [19] (p. 169) highlights a slightly different point of view when he refers to von Bertalanffy that systems in a steady state might still be away from true equilibrium and call on resources embedded in their environment to return to their true equilibrium; hence, the steady state can also be termed a pseudo-dynamic equilibrium. All this implies that the concept of maintaining a steady state by systems resonates in literature but is restricted to recursive processes since the system does not move to another state with a different equilibrium or structure of the system in principle even though homeostasis is maintained through dynamic processes within the system.
1.2. James G. Miller’s Quest for Pathological Enumeration
Whereas von Bertalanffy has emphasised the steady state as part of the conceptualisation for general systems theory, the approach of Miller [20,21] has been focused on descriptions of living systems in interaction with their environment, which is still to be considered a broad class of systems. In his first conception, Miller [20] (p. 521) distinguishes five levels of hierarchy for systems (cell, organ, individual, group and society) and presents a model of a computer as archetypical [20] (p. 524). In a next stage of development, the conceptualisation of living systems [22] embraces nineteen subsystems within living systems and seven levels of hierarchy; see also François [23] (p. 212). Later, this conceptualisation was extended with a twentieth subsystem, the timer, e.g., Jessie Miller1 and Miller [24] (p. 8), and an eighth level, the community level as noted in Jessie Miller [25] (p. 265). The concept of living systems theory is not only extensive but was considered pathological by Miller and Jessie Miller [26] (p. 246), using their own words, when considering organisations; the maintaining of homeostasis is not explicitly part of living systems theory but present in the way these systems interact with the environment.
The extent of these descriptions, for both subsystems and hierarchical levels, and the interaction of systems with their environments has been well-received. For example, it leads Bailey [27] (p. 45) to laud the concept of living systems for its analytical power. In this spirit, Bailey [28] (pp. 292–296) identifies twenty contributions by living systems theory. The ninth, tenth and nineteenth contributions seem mostly related to maintaining a steady state, although, for Miller [22,29] the maintenance of homeostasis is encapsulated in the transducers for input and output, and the decoder and encoders (for the latter, see Subsection 1.4). It should be noted that in Miller’s original thought, the maintenance of a steady state is related to entropy [22] (p. 203). According to Bailey [28] (p. 295), the concept of joint subsystems was introduced by Miller [30] (p. 32); a joint subsystem is a subsystem that belongs to two systems. However, it is Glassman [31] who introduces the idea that loose coupling of systems is related to stability of systems, before Maturana [32] (p. 320) [33] (pp. 35–36) and even way before Luhmann [34] did reason so for autopoietic systems. Moving back from autopoiesis to living systems theory, the application to organisations and processes is demonstrated by Járos [35], and Járos and Dostal [36]. Furthermore, Nechansky [37] (p. 103) details a schema for living systems based on all twenty subsystems; in this conceptualisation the principles of maintaining homeostasis can be distinguished. Thus, the concept of Miller’s living systems has inspired many to advance theoretical conceptions, including touching on the steady state, albeit implicitly at times inherent to the dominant focus of this perspective on subsystems within a living system.
1.3. Viable System Model by Stafford Beer
The viable system model by Beer [38] (pp. 168, 199) also offers a perspective of maintaining a steady state by its attention to internal processes. According to the summary of thoughts by the Kybernetes Editorial Team [39] (p. 562) from their interview with Stafford Beer, the viable system model builds on the pursuit of fundamental principles of how self-regulatory systems are constructed, particularly derived from the human nervous system, thus building on living systems and cybernetics. It mainly aims at human activity systems, commensurate with what Checkland [40] (pp. 131–132) pursues with soft systems methodology. The core of the viable system model consists of five subsystems, each with particular roles and interactions with the environment. These subsystems of the viable system model interact to maintain homeostasis, albeit that some subsystems concern adaptive processes.
The viable system model found its way into many writings. A notable book is one about images of organisations in which the model features as part of the chapter by Morgan [41] (pp. 73–118) on organisations as brains. Others involved with systems theories have used the conception to link their developments to it. For example, Mlakar and Mulej [42] position the model in the context of what they call dialectical systems thinking; their proposition reflects aspectsystems2 (with focus on specific relationships rather than subsystems that focus on subsets of elements), and is akin to the boundary critique found in [44] and ([45] (p. 254)), and teleological thinking; in this sense, Mlakar’s and Mulej’s proposition does not differ greatly from Churchman’s [46] dialectical inquiring systems method. In addition to these methodological deliberations about systems theories, the viable system model has been contributing to building theoretical conceptions, e.g., [47,48,49,50]; expanding methodologies, for example, [51,52,53,54]; and solving organisational challenges, for instance, [55,56,57], to mention a few of its applications. It should be noted that the application of the viable system model seems mostly directed at organisations and less to other domains of application, such as society, and other disciplines, for example, psychology, even though Beer in an interview sees a far wider range of applications [39].
1.4. Capturing Interaction by Claude E. Shannon
Whereas conceptualisations for systems theories related to the steady state in the previous three strands root in biological notions and to a lesser extent in cybernetics, the contribution of Shannon [58] stems from information and communication technology. His mathematical theory of communication posits that signals from information sources are encoded, processed and decoded, while developing concepts for information entropy, as a measure of uncertainty, randomness and redundancy. The influence of Shannon’s thinking is attested by Weaver’s [59] deliberations, Wyner’s [60] overview, Verdú’s [61] praise and Guizzo’s [62] postgraduate taught dissertation; these give but an impression of the tremendous progress made and the impact of this theory for information and communication technologies. Beyond these technologies it has been extended to epistemology for heterogeneity, e.g., [63,64]; knowledge management, for instance, [65,66]; linguistics, for example, [67,68]; consumer behaviour in marketing with cases in point being [69,70]; and psychology, e.g., [71,72]. In later works, for example [73], Shannon augmented his original thoughts, which started to include steady state, a notion also picked up implicitly by Kalman [74] (p. 485). Other than conceptual approaches in ecology, for instance [75], the concept of steady state related to Shannon’s theory has been used mostly by those who seek mathematical modelling.
1.5. Putting These Four Contributions Together
The notion that the theory of communication seems weakly linked in literature to maintaining the steady state by a system raises the question as to how the theoretical conceptions by Beer, von Bertalanffy, Miller and Shannon are related to each other. In the second Ludwig von Bertalanffy Memorial Lecture, Miller [76] (pp. 220–221) connects his living systems’ approach to von Bertalanffy’s general systems theory explicitly, though implicitly he seems to view his theory as an advancement. In addition, Miller [20] (p. 517) refers to Shannon (and Wiener) in the context of coding, although without including them in the list of references, and subsequently it appears in his diagram [20] (p. 524); in subsequent papers by Miller [21,22] this anomaly persists. Also, Beer [77] (pp. 10–11) refers to the influence of Shannon’s theory of communication on his own ideas; similar to Miller he sometimes refers to von Bertalanffy, though some slight differences of opinion seem to be present as noted in Beer [78] (p. 192). Thus, Beer, von Bertalanffy and Miller were aware of each other’s conceptualisations and Shannon’s contribution to forming their own ideas.
However, it is mostly others who have brought the four conceptualisations together or sought to make connections. For example, Robb [79] mentions the four theoretical contributions in the context of operational research, Duffy [80] makes the case for cybernetics and systems theories being interwoven, and Pierce [81] elaborates on the four conceptualisations from the perspective of investigating problems; however, neither does bring them together in a coherent framework or reference model. Studies in point that focus on connecting a few of these four are Schwaninger [82] (p. 587), who refers to Miller’s concept of living systems and Beer’s viable system model as representing a positivist paradigm for his essay on system dynamics, with Nechansky [83] extending Beer’s viable system model with detailed feedback processes from Miller’s living systems. However, in a preceding publication Nechansky [37] (p. 99) makes no distinction between processes and subsystems, something that may be necessary for developing an adequate reference model for maintaining homeostasis and steady-state behaviour of systems. Some have sought classification, for instance, Adams [84]. Furthermore, Van Gigch and Kramer [85] (p. 185) categorised the living systems theory and viable system model as belonging to the same class ‘living systems theory’, whereas von Bertalanffy’s general systems theory is seen as part of an ‘ontological-theoretical’ strand and Shannon’s theory of communication as part of the ‘conceptual-theoretical’ stream. The classifications and the acknowledgements of their concepts intimate the relevance of Beer, von Bertalanffy, Miller and Shannon’s contributions to operational research and modelling of systems, but that only one study attempts to integrate them is a sign that, for modelling processes to maintain the steady state of systems, beyond mathematical terms, relatively little has been done; something this writing seeks to remedy.
2. Building Blocks of Steady-State Model
The steady-state model—presented in Dekkers [1] (p. xxv–xxviii, 146) and Veeke et al. [2] (pp. 77–81)—builds on the pathological approach, interaction approach and viable system model to describe recurrent processes for maintaining a steady state. It expands the viable system model by separating better transformational processes and control processes, including more explicit boundary zones and focusing on homeostatic processes; the latter as opposed to adaptive processes, which are embedded as System Four and System Five in the viable system model. Moreover, Nechansky’s [83] (p. 69) modelling only contains feedback control mechanisms, whereas from engineering other control mechanisms such as feedforward are known, too. Thus, the steady-state model is informed by the separation between transformational processes and control processes, coding, boundary zones and principal control mechanisms for maintaining homeostasis as pseudo-dynamic equilibrium.
Before moving on to the building blocks of the steady-state model, some foundational concepts of systems theories for further discourse are clarified. The primary process, a generic concept in systems theories, converts input into output (see Figure 1); the primary process is also called transformation. This means that flowing elements as input are converted into a system as output; one could take the sheets of paper holding the individual printed pages that are folded, bound and cut to size into a book as an example. For this to happen, resources are needed for conducting the primary process; in operations and supply chain management, they are also known as transformative resources. In the case of producing a book, these resources are folding machines, nipping presses, book binding and glueing equipment in addition to labour; it may also include the facility in which the book is produced, but such depends mostly on what is investigated. Resources for a specific primary process put together are called a system of resources. Typically, resources are used for the conduct of the primary process within the boundary of the system of resources but can be brought back to their initial state to conduct the process again, keeping in mind wear and tear. Think about employees taking breaks and overnight rests, and machinery being maintained. From a systems-theoretical perspective, a primary process is the interaction between flowing elements and a system of resources, even though the resources have been omitted from further figures for clarity.
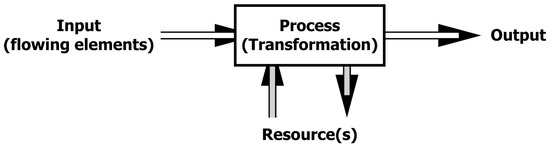
Figure 1.
Primary process with resources.
2.1. Boundary Zones as Central Tenet for Steady-State Model
In order to maintain homeostasis of a system of resources for a primary process, E.J. Miller3 and Rice [86] (p. 9) propose the concept of boundary zones. In this perspective of the (primary) process, boundary zones represent a discontinuity for the input and output in the exchange with the environment by an open system of resources. Again, referring to the example, the sheets of paper for the pages of a book are provided by a supplier with a different primary process and belonging system of resources, and the book is distributed by a publisher with its own specific processes and related system of resources. Hence, the transfer of flowing elements from one system of resources to another can be considered a discontinuity. This reasoning leads to discerning an input boundary zone and an output boundary zone as displayed in Figure 2; the figure also distinguishes a regulatory boundary zone that is described in the next paragraph. Whereas E.J. Miller and Rice arrive at boundary zones from a socio-technical perspective, others, such as Koch [87] (p. 45), approach them from a physiological perspective well before. As discussed before, Shannon’s theory of communication [57] adds encoding and decoding4 to the boundary zones as discontinuity between the system of resources and its environment (see Figure 3), commensurate with Miller [20] (p. 514). In the spirit of the theory of communication, encoding means that the state of the flowing elements as input for a process should match the capabilities of this process; a case in point is the permutation of keyboard characters into binary code as input for a microprocessor. Similarly, decoding makes the output of the primary process suitable for the environment of a system or the subsequent primary process of another system of resources. Blegen [89] (p. 19) also highlights the coding process as part of an organisation’s open systems, although he refers to Katz and Kahn [13] (pp. 22–23) as source for his thought. Note that, in the Zeitgeist of the 1950s and 1960s for an open system (and related processes), it is only possible to sustain homeostasis with energy, for instance, [13] (pp. 23–5) [17] (p. B3); the concept of energy may be substituted by the generic term resources, which could include energy but might also be a wider range of resources (for example, labour and equipment). Building on these thoughts of E.J. Miller and Rice, and Shannon, as recognised by other systems theorists, makes the encoding and decoding an essential part of the primary process for the boundary zones to maintain a steady state for a system of resources.
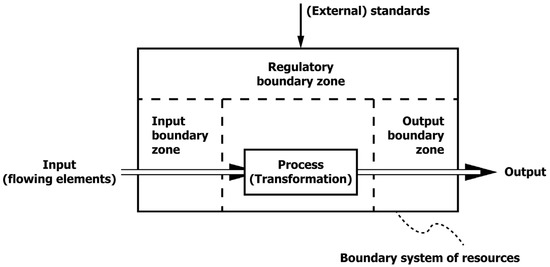
Figure 2.
Boundary zones for a primary process.
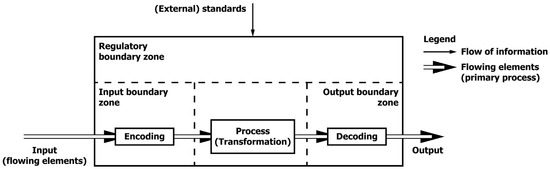
Figure 3.
Boundary zones with encoding for input and decoding for output.
This concept for transitions of input obtained from the environment into output disseminated to the environment also implies that the crossing of these zones leads to regulatory activities as a third zone mentioned by E.J. Miller and Rice [86] (p. 9); see Figure 3. Simon [90] (p. 328) underlines the importance of regulatory activities. These regulatory activities can comprise interventions in the primary process, when the output does not meet standards, revision of those standards and feedback to the environment about the capability of the primary process to maintain its steady state. More details about regulatory activities can be derived from Beer’s [38] viable system model by looking at the interaction between System Two and System Three; System One is equivalent to the primary process in Figure 1 and Figure 2. Within Beer’s model, Systems Four and Five are long-term oriented (and, therefore, might imply a change of structure beyond maintaining homeostasis as such). Also, Blegen [89] (p. 16) mentions so-called self-regulation. This implies that part of these regulatory activities is a feedback loop commensurate with the thoughts about the importance of feedback for maintaining homeostasis, for instance, [8] (p. 421) [12] (pp. 23–25) [89] (p. 15). Hence, Figure 4 extends the previous Figure 3 to include the processes for the regulatory zone; note that, in addition to coding and decoding appearing in the input and output boundary zone, both the initiating and evaluating processes can be considered as coding for the control mechanisms in the spirit of Shannon’s theory of communication.
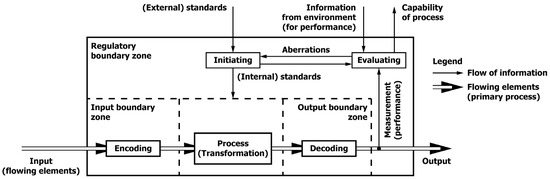
Figure 4.
Processes for regulatory zone.
These regulatory activities are related to three principal control mechanisms, rooted in control theory, cybernetics and engineering. Mostly derived from cybernetics and engineering, feedback is seen as essential to maintaining a steady state, again leaning on the thoughts of von Bertalanffy. Attributing mechanisms for feedback to Ashby and Wiener, Blegen [89] (p. 18) typifies this control process as essential for the stability of a system. In terms of controlling primary processes, feedback mainly intervenes upstream of the point of measurement; based on comparing a parameter of the output with a standard an intervention is generated in either the process itself or the input of the process or the resources used for the process. However, feedback may exhibit instability under certain conditions, a topic not explored here as the focus is on the principle of control mechanisms and not on their (mathematical) optimisation. As a second control mechanism, feedforward is often attributed to MacKay’s [91] contribution to physiology, even though it is also known from control systems, e.g., [92,93]; this control mechanism also appears in Beer [38] (p. 240). A characteristic of feedforward is that the intervention happens downstream of the point of measurement. In Figure 5 feedback and feedforward are depicted by their core processes: measuring, comparing, regulating and intervening. How both control mechanisms complement each other within systems theories is demonstrated by Bogart [94]. In addition to feedback and feedforward, there is a third mechanism that is called ‘completing deficiencies’ here. Its principle can be traced back to Black’s [95] development of the negative feedback amplifier, though he wrote this memoir later than its invention by him in the 1920s. Very different from feedback and feedforward, completing deficiencies means that measuring detects deviations from a standard after the transformation processes, and then the flowing elements are brought up to that standard in a separate, complementary process. In Black’s thoughts, the input serves as the standard, but that might be appropriate for electronics and not necessarily for other disciplines. Alternatively, completing deficiencies could imply that the flowing elements have to be inverted to pass partially or wholly through the transformation process; this approach has been used in the steady-state model. Moreover, the control mechanism for completing deficiencies requires a check on the quality of the flowing elements (or perhaps, system after transformation). And equally, the flowing elements as input may have to be checked against quality standards. In both cases it leads to discarding the flowing elements (or system), unless a process for completing deficiencies is capable of transforming the quality of the flowing elements (or system) to set quality standards. The three control mechanisms—feedback, feedforward and completing deficiencies—and the quality filters have been brought together in Figure 5 as part of the boundary zones.
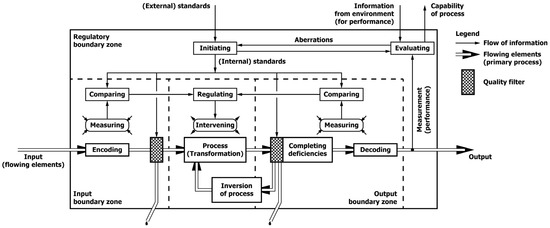
Figure 5.
Boundary zones and control mechanisms.
In addition to the three control processes, from engineering—particularly hydraulics, pneumatics and partially electronics—some additional processes are found in the boundary zones. Referring to the perspective of engineering, Blegen [89] (p. 21) mentions the parallels between hydraulic, mechanical and pneumatic systems as a key notion for generic control mechanisms. Such systems typically contain buffers, (quality) filters as mentioned in the previous paragraph and overflow mechanisms that prevent overload or smooth flows in addition to control mechanisms that ensure a specific output. Buffers dampen out irregularities in the flow of elements (primary process), whereas filters ensure that the quality of the flowing elements matches the capabilities of the primary process. Overflow mechanisms safeguard that the quantity of the flowing elements is compatible with the capacity of the primary process. These three additional mechanisms prevent unsuitable input from entering the system and counteract overload. The necessity for these additional mechanisms has been mentioned by a few but has been incorporated less implicitly in modelling. For example, Katz and Kahn [13] (p. 22) note the rejection and acceptance of materials as an essential process and Miller [29] (p. 165) explicitly refers to storage at the output boundary zone. The same mechanisms in the input boundary zone—buffers, filters and overflow mechanisms—can be used for the output, albeit that the quality filter in the output boundary zone might be related to feedback control processes. Hence, all five concepts—boundary zones, (de/en)coding, regulatory activities, control mechanisms and engineering concepts—have been amalgamated into what one could call the steady-state model as depicted in Figure 6.
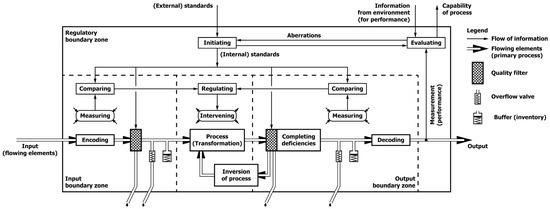
Figure 6.
The steady-state model.
2.2. Potential Limitations
However, this steady-state model only covers maintaining homeostasis for recurrent processes. As can be derived from Beer’s viable system model, this model resembles only Systems One to Three. Structural changes, such as those initiated by System Four and Five, will lead to changes in primary processes, (re-)allocation of resources, control mechanisms and boundary zones. Therefore, so-called adaptive processes require a different approach than covered by the steady-state model; similar to the thoughts of Bogdanov [5] (pp. 162–3) and breakthrough model in Dekkers [1] (pp. 210–215). This is commensurate with Strauss’ [19] (p. 169) notion about the limitations of the steady state; whereas entities might be striving towards maintaining homeostasis during adaptation, so-called adaptive processes are poorly described by the steady-state model. Notwithstanding this limitation, the process in the regulatory boundary zone (see Figure 6) evaluating the performance results in a signal to adaptive processes about the capability of the system of resources to perform the primary process; this is similar to the modelling of System 3 by Nechansky [83] (p. 69). Thus, whereas the steady-state model is limited to maintain homeostasis for recurrent processes, it has a link to adaptive processes.
In addition to being limited to recurrent processes, another limitation is the potential incompatibility for control processes of different aspects to be integrated in one steady-state model. This is illustrated best with an organisation as example. Control processes for operations, quality, logistics and financial management might differ entirely in terms of how they apply control mechanisms and resources they call on; for instance, a quality check from a quality management perspective is a filter based on a standard for requirements for the flowing elements, whereas the same step from a logistic point of view merely is a process with two outputs (accepted versus rejected). Although some features might come together in some persons or departments, it is not hard to imagine how these control mechanisms for different aspects require different processes and resources that may come together at higher levels in the hierarchy for controlling primary processes in which trade-offs may have to be made. Hence, in principle, the use of this steady-state model is limited to one particular aspect for control.
3. Some Applications of the Steady-State Model
Since this generic reference model limits itself to one aspect of primary processes and the related control mechanisms to maintain homeostasis, the question arises how this steady-state model can be used in research and how it can be applied in practice. One could classify the model as a positivist approach; for example, Mangan et al. [96] (p. 568) classify models under this label. Beyond this approach, it can be used for qualitative modelling, in what Eisenhardt and Graebner [97] (p. 26) among others call ‘theory-driven’ case studies; for visualisation in interviews, for instance, Knigge and Cope [98] (p. 2027); and as a representational tool in action research, for example, Dickens and Watkins [99] (p. 129) and Flood [53] (p. 275). These applications also make it suitable for constructivists and for advocates of participatory approaches; for instance, those using the boundary critique such as Ulrich [44] may use the steady-state model for both visualisation and analysis. Hence, this steady-state model can be used in different methodological approaches.
Leaving philosophical streams of thought about research aside, commensurate with Simon’s [89] (pp. 329–330) call for a comprehensive systems framework for teleological systems, the steady-state model offers a generic model for a range of applications; examples are given but not limited to these:
- The integration of separate control mechanisms, regulatory activities and processes for the boundary zones makes the steady-state model suitable as a reference model for technological, biological and social systems (particularly for organisations as entities). This is akin to Miller’s [20,22,29] vision for his living systems theory and Beer’s [39] views on the viable system model. Miller and Jessie Miller [100] (p. 162) present symbols for living systems theory that correspond with the steady-state model, but they have not put them together in a reference model. Moreover, they [26] (pp. 249–252) indicate the application to a hospital, army battalions and IBM Corporation, though without providing models and detail. And, Beer’s [38] (pp. 168, 199) viable system model does not model mechanisms such as feedforward and is less explicit about boundary zones. Thus, compared to these models it offers a different interpretation with regard to control mechanisms and to regulatory activities; hopefully this will be seen as an extension of these reference models instead of a competing conceptualisation.
- Particularly for organisations, this steady-state model can be used for approaches such as business process re-engineering and information systems in general. Dekkers [101] presents six case studies in which the steady-state model has been used for analysis of business processes. For this study, though the focus was on evolutionary processes, the steady-state model served as reference model for analysis, which made it possible to perform a qualitative comparative analysis. Specifically, the steady-state model was used to examine the control processes and the flow of information in the six underlying case studies. Also, Hess and Oesterlee [102] (pp. 81–82) point in this direction when they draw attention to the role of information systems that should be better understood. The steady-state model captures the roles by separating the primary processes from the control processes; the teleonic management framework of Járos and Dostal [36] (pp. 205–209) hints at the same thought. This means that, in the case of a primary process consisting of information, for example, the processing of insurance policies, these two distinct roles of data and information may have to be treated differently by information systems. Some works, for example, Aguilar-Savén [103] (p. 133), Childe et al. [104] and Jansen-Vullers et al. [105], distinguish between processes and their control but mostly in an implicit way. In other publications about information systems and business process re-engineering, such as Kettinger et al. [106], List and Korherr [107], and Scheepers and Scheepers [108], this difference is also absent. The separation of the two processes is important because primary processes can be associated with creating value for customers and control processes with performance management; information systems can embed both processes with their different roles. A distinction between primary and control processes may address the concern of Childe et al. [104] (p. 32) that processes are not well defined, something to which later works, for instance, [109], have not contributed or have left open options for the modelling process, e.g., [110] (p. 44) or resorted to the use of simplified models such as IDEF0 and IDEF3, for example, [111] and [112] (p. 115).
- In this sense, the steady-state model addresses the need set out by Sagasti and Mittrof [113] (pp. 698, 705) for conceptualisation and modelling in operations management research in the context of problem-solving. This potential for conceptual models fits with the call for Mode 2 type of research and action research as outlined by van Aken [114] (p. 31); Mode 2 in the context here is aiming at solving field problems as they are also called, see Meredith [115]. Modelling in operations research seems largely confined to regressions models, for example, [116,117], which only list factors and determinants, or other forms of mathematical modelling, for instance, [118,119,120]. The steady-state model offers a more comprehensive reference model for conceptualisation of processes for operations that could be used to organise factors and determinants a priori in empirical research; outcomes of these studies may then be used for generalisation across studies and for contextual understanding.
- The generic steady-state model can be used for approaches to designing organisational structures. Such an application is found in the case study of an overhaul project of heavy-duty equipment [121]. It links the characteristics of the primary processes and control processes as a base for redesigning organisational structures based on analysis and grouping of resources. From a more generic perspective, the design of an organisational structure may use the steady-state model to group resources for these processes into teams, departments, organisational units, etc., see Dekkers [122] (pp. 429–434); to the same purpose, Emery and Trist [123] (p. 293) use the term differentiation. This notion is merely implicitly present in other works, such as Childe et al. [104] (pp. 28–29), Jang [111] (p. 217), and Melão and Pidd [112] (pp. 112–113, 117–118, 121). Therefore, grouping of processes and resources using the steady-state model as reference model could constitute a systemic approach to analysis and design of organisations.
- Furthermore, the design of collaborative networks might benefit from this steady-state model, especially how boundary zones from two separate actors in such a network are interrelated. Schuh et al. [124] hint in their paper towards this. Moreover, Dekkers and van Luttervelt [125] (pp. 12–13) suggest a reconfiguration model for industrial networks based on the steady-state model; this proposition for reconfiguration uses performance criteria to reposition processes and resources in response to orders and changes in the markets. Also, the regulatory zone could be viewed as a central concept for self-criticality in networks, see Kühnle [126]. Self-criticality is the capability of a system to evaluate its own performance, akin to the concept of teleons as described by Járos and Dostal [36] (pp. 198–199); it was introduced in Figure 4 as the control loop for evaluation in the regulatory boundary zone. In addition, it could be a background model for the integration of suppliers in the boundary control of focal firms, a notion well-embedded in lean production as supplier integration, see Das et al. [127] and Sánchez and Pérez [128] (p. 1444), but as of yet with no explanatory model. Therefore, the steady-state model could be used a reference model for collaborative networks.
- The model can be used for operations research and decision sciences in addition to methods for cybernetics, structuring problems, system dynamics and soft systems methodology that are mentioned by Mingers and White [129] (pp. 1148–1153) for the purpose of advancing investigations into operations research. From this perspective, Veeke et al. [2] (Ch. 11) present the design of a container model based on the steady-state model; simulation was used to define parameters for the design, such as the possibility to share resources (container cranes). Moreover, the model could be used for simulation modelling in both a post-positivist and constructivist tradition for the advancement of theory, see Kabak et al. [130] (p. 707).
These applications only demonstrate the potential of this model, though the focus in the examples was on organisational arrangements. Its origins and its applications are multidisciplinary—Aboelela et al. [131] (p. 339) would call it ‘trans-disciplinary’—whereas those applying it should convert this model to the contingencies of the specific situation.
The steady-state model can be applied recursively. The use of recursion is not restricted to this model, since Beer [38] and Miller [20,22] also incorporated it in their concepts, with Mlakar and Mulej [42] showing its application to hospital services. Moreover, the control processes can be interlaced as echelons of control within levels of recursion. This is not to be confused with the additional Systems 4 and 5 of the viable system model [38] and the complementary breakthrough model [1] (pp. 210–215), which serve a different purpose, namely adaptation. As Beer [38] recognises, a process model for recurrent procedures might also be partly applied to adaptive processes, something not further discussed here.
In addition to research and applications, the steady-state model can be used for teaching purposes in the domains already mentioned and for teaching systems theories in addition to its generic concepts; for the latter, see for example, Banathy and Jenlink [132]. In the context of teaching, Lane [133] (p. 328) makes the case that diagrams are an essential part of systems thinking and implies that this type of visualisation enhances the student learning process. This corresponds with the thoughts of Sagasti and Mittrof [113] (pp. 698, 705) about conceptualisation and modelling for problem solving. This may also apply to action learning, since the steady-state model, as with any other theoretical conception, can be considered part of programmed knowledge; this type of knowledge is seen as part of the action-learning formulae by Marquardt and Waddill [134] (p. 192). It should be noted that popular textbooks represent the primary process from an economic perspective where both flowing elements and resources are considered input as factors (variables); Hill and Hill [135] (pp. 14–15), Jacobs and Chase [136] (p. 15) and Slack et al. [137] (p. 11) are cases in point. Figure 1 is a depiction from the perspective of systems theories and distinguishes between the flowing elements and systems of resources; using this delineation would make the explanation for processes as interaction between flowing elements and systems of resources clearer to what their differing purposes are for operational processes. Hence, the steady-state model based on this representation of primary processes could be used for programmed problem solving, conceptualisation and case studies in teaching, as it offers a more granular and logical explanation for modelling.
4. Application of Steady-State Model to Maintenance
As part of action research into maintenance in the aviation industry, the steady-state model has been used as reference model in three cases. Case A concerns the performance of an airline’s maintenance department, and Cases B and C are on firms that provide overhaul and maintenance services.
4.1. Case A: Maintenance Department
The first example for applying the steady-state model is drawn from a case study into the performance of an airline’s maintenance department. It experienced an increasing number of complaints about the availability of exchange parts for apron and gate-side inspections as well as scheduled maintenance; during the inspections and maintenance of aircraft, parts are replaced with ones that have been refurbished in a repair shop, a unit within the maintenance department. An initial investigation revealed that about 90% of the complaints could be related to this repair shop. Moreover, this first step yielded also a plot on the input and output of the repair shop; see the Z-diagram in Figure 7. The plot shows that over the course of a year both work-in-progress and lead time have increased considerably. This observation led to the conjectures that the increased lead times most likely reduced the availability of exchange parts, and that both the increased lead time and work-in-progress indicate inadequate planning of capacity. Moreover, the airline was also shifting its maintenance policy for exchange parts from ‘hard-time’ replacement (i.e., replacing parts at defined intervals) towards on-condition monitoring and replacement. This change implied that exchange parts would be replaced at lesser predictable intervals, and hence, there would be more variability in demand. Consequently, variability in demand placed greater emphasis on availability of serviceable exchange parts (i.e. parts that are airworthy) that should be reflected in control of operational processes for inventory holding available exchange parts for maintenance and indirectly be connected to control mechanisms for capacity management. Thus, both the analysis of performance and the strategic shift towards on-condition monitoring led to the conjectures that control of the operational processes in the repair shop should be directed at replenishing the inventory of exchange parts available to maintenance (i.e. control of output) and that this mechanism for control should be coupled with capacity management.
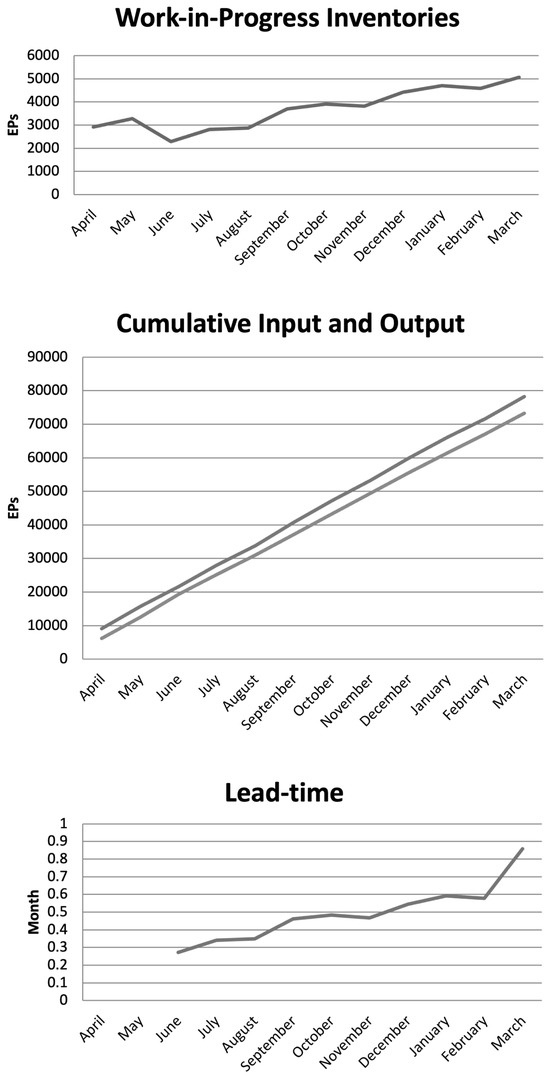
Figure 7.
Z-diagram for performance of repair shop (EP: exchange part).
Taking these conjectures as starting point the internal processes for control were investigated. When so-called unserviceable exchange parts arrived in the repair shop from maintenance processes, they were recorded in a file with their location in storage. Within the repair shop there were specialised groups that took unserviceable parts from this inventory and checked whether the part was still airworthy or needed repair (a part replaced under the hard-time policy for maintenance was not necessarily faulty). If still airworthy, it was placed in the storage of serviceable parts, which is available to maintenance personnel. A sample revealed that about 30% of the unserviceable parts is serviceable. When deemed to be repairable, a group in the repair shop started working on the exchange part, checked it against quality standards and undertook rework, when necessary, before placing it in the storage of serviceable parts; see Figure 8 for the depiction of the primary process. A further investigation revealed that the main mechanism for creating a job list for groups in the repair shop were the inventory levels of unserviceable parts. The list of unserviceable parts in inventory was compared with standards for number of parts to be held in inventory, and those exceeding the standards were taken out of storage, checked and, when faulty, put into repair; see Figure 8 for the control mechanism that generated the job list. This feedforward mechanism was commensurate with a maintenance policy based on hard-time intervals but did not align with control necessary for on-condition monitoring of exchange parts. In addition, the planning of capacity and prioritisation of parts only happened at group level in the repair shop based on the input and repair needed to make exchange parts airworthy. There was no direct link to the availability of serviceable exchange parts, and only when there were calls for urgency, then those exchange parts were treated as rush orders (this process has not been depicted for clarity). Moreover, it remained unclear how the performance of the repair shop was managed. Both the input of unserviceable and output of serviceable exchange parts were registered but this registry was not used for managing the repair shop. Therefore, the investigation confirmed that adequate control mechanisms for the availability of serviceable parts and related capacity management were missing in the repair shop.
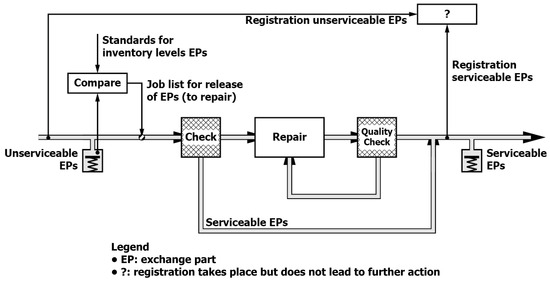
Figure 8.
Process model for repair shop ‘as-is’ (Case A).
As a result of finding inadequate control mechanisms for serviceable exchange parts available to maintenance and capacity management, improved control mechanisms were put forward and implemented; see Figure 9. The first improvement was to set up control for the availability of serviceable exchange parts as feedback for prioritising parts insufficiently held in inventory. The second improvement was adding capacity management to the control mechanisms based on replenishment of unserviceable exchange parts. And, a third improvement was introducing control mechanisms for the performance of the repair shop that was not systematically monitored until then. Using the control mechanisms in Figure 9 as template, improvements were introduced and a backlog cleared; the latter took about three months, and the implementation of control mechanisms for inventory control and capacity management six months as they needed to be integrated with how capacity planning happened at group level. Thus, the introduction of three control mechanisms in the case study incorporating elements aligned with the shift in maintenance policy and effective control of performance was effective.
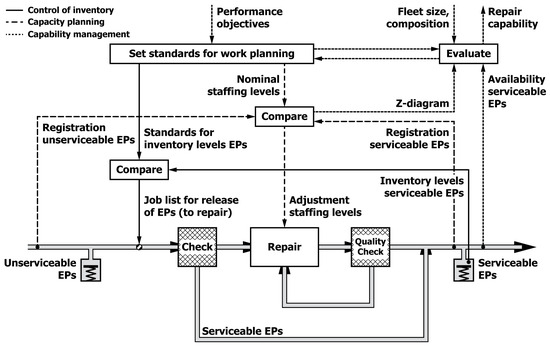
Figure 9.
Process model for repair shop ‘ought-to-be’ (Case A).
Looking at this case and the role of the steady-state model leads to the following observations. First, the steady-state model served as backdrop for modelling the primary and control processes, subsequent analysis and solutions put forward, while keeping in mind that only essential primary processes and control processes relevant to the case have been used for the modelling here. For example, the procurement of additional exchange parts was omitted since this process hardly contributed to the lack of performance. Second, the modelling focused on the aspects of capacity management and ‘order processing’, in accordance with the limitations of the steady-state model. For instance, quality control as another aspect was not included in the model and the two quality checks were only depicted in the primary process as steps for order processing. Were another aspect such as quality control to be included in the analysis, then another model for the control of the primary process focusing on this aspect should have been created. Third, considering the adaptation of control mechanisms to a changing profile of demand, here the availability of serviceable exchange parts on the output side of the repair processes, was an effective way to enhance performance for recurrent processes. This is commensurate with Ashby’s [138] (p. 207) law of requisite variety. These three notions underline the usefulness of the steady-state model as reference model for control of primary processes, albeit limited to one aspect, and its alignment with principles for control.
4.2. Cases B and C: Maintenance Service Providers
Both firms that served as further cases for the application of the steady-state model experienced problems with performance, too, and both encountered similar issues. Case B concerned a provider of overhaul and maintenance for an exchange part, and Case C was part of an original equipment manufacturer of a major exchange part. A key difference between the two cases was that Case B had maintenance departments of airlines, firms that provided overhaul services and firms like Case C as customers, whereas Case C mostly depended on maintenance departments of airlines and less on firms that provided overhaul services. Another relevant dissimilarity related to the customer base was the predictability of exchange parts arriving at the doorstep of the two cases; Case B experienced more variability than Case C. However, it was the difficulty meeting deadlines for the turnaround of exchange parts that spurred investigations.
First, the process for overhauling exchange parts ‘as-is’ was analysed. The processes were depicted using the steady-state model as reference model; see Figure 10 for both Cases B and C since their processes were similar due to the nature of underlying causes for lacking performance. On arrival, exchange parts were encoded and placed in inventory. Encoding here also entailed retrieving service records for the specific exchange part; this was necessary since for exchange parts in the aviation industry manufacturing information and information pertinent to its use are retained, compliant with regulatory requirements. A second reason was minor differences across exchange parts to be accounted for during the repair, i.e. each repair differed in what had to be repaired and how such was done. After job order release, an exchange part was checked and disassembled into its components, which were also checked. One of the outcomes of this process likely was faulty proprietary components that had to be replaced by their respective vendors. It was this process of replacement that caused delays since vendors in both cases were located on different continents and had a multitude of customers; this was reflected in proprietary components taking considerably longer lead times for replacement than often agreed on in purchasing orders. Furthermore, both cases had optimised their internal processes using concepts from lean production, even for the generation of purchase orders for proprietary components. Since control of the performance of vendors could not be ascertained, the question was what principal solutions were at hand to improve performance for the overhaul of exchange parts.
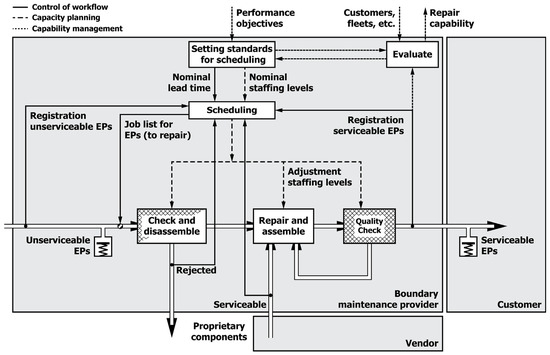
Figure 10.
Process model for maintenance service providers ‘as-is’ (Cases B and C).
Generating the principal solutions following the analysis was the next stage. The first principal solution would be changing the vendor of the proprietary components or bringing the manufacture of these components in-house (akin to moving the discontinuity), but neither was feasible in the circumstances; see Figure 11a for the manufacture of these components in-house. Reasons were economies of scale and limited availability of alternative vendors with the same capabilities. For Case B, the vendor of the exchange part belonged to the same conglomerate, and both were seen as centres of excellence, implying that they had to rely on managing their own resources while there was exchange of technological knowledge. In Case C, the original equipment manufacturer offered maintenance services through this subsidiary when selling exchange parts. Since there was pressure on cost associated with the exchange part, the vendors of proprietary parts were selected based on cost considerations as long as they were certified to comply with regulatory requirements. This means that the first principal solution was not feasible in this cost-dominated industry. The second principal solution was to introduce vendor-managed inventory; see Figure 11b. This would introduce a shift of the discontinuity in the boundary zone from a control perspective and how the primary process is regulated. However, this was also deemed impractical as it relies on sharing information. Most prominently, there were a multitude of airlines and maintenance service providers with specific specifications for the exchange parts leading to complicated information sharing about inventory levels and patterns relevant to maintenance. Moreover, not all customers would be able or willing to provide adequate and reliable information about the use of exchange parts, possibly leading to inconsistent and incoherent decision making. A third principal solution would be to create inventory within Cases B and C; see Figure 11c. Again, this would lead to a high variety of inventory to be maintained and thus increase costs. A fourth principal solution would be to increase the lead times for the repair of exchange parts (as implication of measuring performance and recalibrating standards in the regulatory boundary zone), but it was deemed infeasible and might have invited competition with better offers for maintenance, although competitors would run into the same issues with vendors of proprietary components. Putting this altogether, the four principal solutions for Cases B and C fell short of cost concerns and the impact of variability on managing resources and monitoring of job orders.
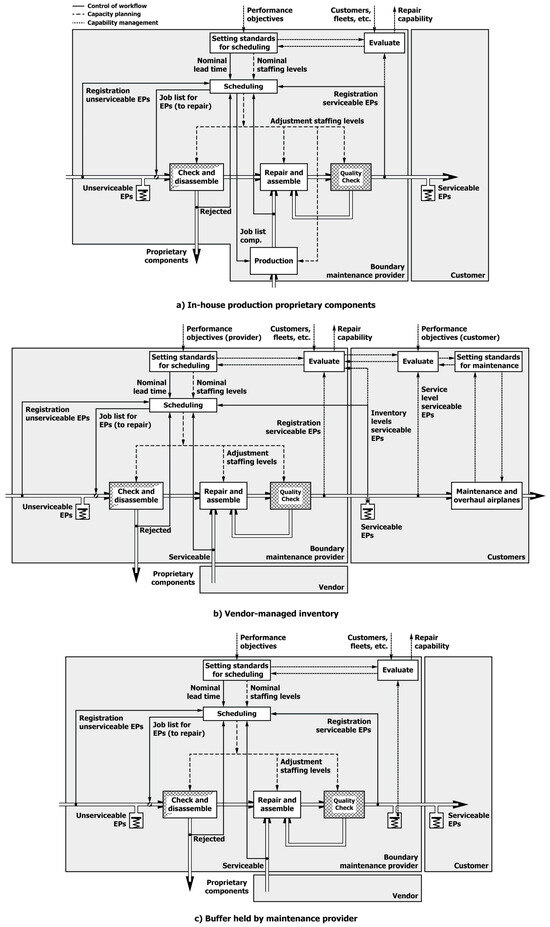
Figure 11.
Principal solutions for maintenance service providers (Cases B and C).
4.3. Use of Steady-State Model for the Three Cases
In all three cases the steady-state model served as reference model for modelling processes in organisations. This was reflected in necessary simplifications that did not affect the analysis and the proposition of solutions; for example, in Cases B and C customs clearance and shipment were not modelled since they had little impact. Across the three cases, the use of the reference model resulted in coherent representation of primary and control processes, regulatory control and boundary zones. In this sense, it fell in line with Bacharach’s [139] (p. 501) criterion of utility for theory, taking here as extending to reference models and conceptualisations; this includes both explanation and prediction. From the perspective of explanation, the steady-state model as reference model served as a ‘scientific model’ in Sagasti and Mitroff’s [113] (p. 699) depiction of the scientific approach to operations research. Concerning prediction as utility, it aligned with van Aken’s [140] call to integrate design science into business and management research; the steady-state model also served as point of departure for defining solutions. In this spirit, Dekkers [141] highlights the relevance of systems theories for integrating design science in this discipline, from both a research and teaching perspective. Consequently, the three cases demonstrated that the steady-state model is well-suited as reference model for diagnosis, pathology as Miller and Jessie Miller call it, and devising solutions, commensurate with prevalent views.
5. Reflecting on Its Contribution
All this means that one of the main applications of the steady-state model will be modelling of business processes in addition to its contribution to systems theories. Both contributions will be discussed in the next subsections.
5.1. Contribution to (Business) Process Modelling in Operations Management
That more modelling techniques for business processes than those derived from systems theories, here the steady-state model as reference model, exist is already evidenced in literature. Aguilar-Savén [103], Barber et al. [142], Hess and Oesterlee [102], and List and Korherr [107] are among those who have provided overviews to compare methods from a specific perspective. Without the intent of adding another comprehensive overview, five techniques, namely ARIS, ASME Process Mapping (aka value stream mapping in lean production, see Salgado and Dekkers [143]), CIMOSA, IDEF and BPMN, are highlighted for the discourse. Keeping in mind that some of the five methods considered are directed at modelling for information systems and data management, the steady-state model as reference model complements these techniques since it is more extensive in terms of its conceptualisation. However, at the more detailed level for application in information systems and data management it does not provide the required information. All this indicates that the steady-state model can be used as a reference model on its own but also complements other process modelling techniques, such as IDEF and BPMN, by its distinction of flowing elements for the primary process and systems of resources enacting this process, a broader range of control mechanisms, and three boundary zones.
This perspective also applies to other methodologies based on systems theories. For example, system dynamics, as a simulation technique developed by Forrester [144], mainly focuses on stock-flow diagrams [144] (p. 142 ff.) and causal-loop diagrams. In this respect, Kabak et al. [130] (p. 707) also point to the utility of the steady-state model as reference model when they review studies using simulation techniques for building theory in operations management. And, de Rosnay [145] (p. 70) uses stock-flow diagrams and causal-loop diagrams to describe organisational processes building on system dynamics, while his model has some characteristics of the steady-state model. In general, modelling with system dynamics leaves open how control mechanisms and interactions with the environment through boundary zones and is subject to interpretation, although Forrester [144] (pp. 51, 112 ff.) limits this interaction to exogenous variables. Furthermore, the approach of soft systems methodology, as advocated by Checkland [146] (pp. 163, 169–177), emphasises modelling of human activity systems but does not have a formal approach to it except for the root definition of a system. This lack of a formal approach is recognised by others, for instance, Bergvall-Kåreborn [147] who proposes a validation technique for Checkland’s soft systems methodology based on Dooyeweerd’s modal aspects. In the same way, the steady-state model as reference model can enhance the modelling of processes, particularly those of human-activity systems as Checkland calls them. Hence, the steady-state model can serve as reference model for both business process modelling and strands within systems theories, exemplified here by system dynamics and soft systems methodology.
5.2. Contribution to Domain of Systems Theories
Moving back from (business) process modelling to what the steady-state model brings to the table for systems theories, it should be noted that the model shares traits with Miller’s concept of living systems and the Beer’s viable system model. It follows the notion that these models should be based on ‘process theory’ [148] (p. 224). However, it goes far beyond Potocan et al.’s [149] position since it merges concepts and modelling from systems theories and cybernetics. In this sense, it combines both a functional and structuralist approach following Jackson’s [150] (pp. S26–S28) descriptions, and should be positioned mostly as ‘unitary’ [151] (pp. 214–215) using his classification; it means that the steady-state model seeks to enhance existing approaches and shares the same objectives as other studies in the domain: the application of systems theories, including cybernetics, for both developing generic concepts and application to real-world problems. In terms of systems theories, it is part of ‘man-made symbols and models’ [152] (p. 570). Compared as a man-made model with Nechansky’s [37] (p. 103) model that amalgamates thinking and concepts from Miller’s [20,30] living systems theory and Beer’s [38] viable system model, the steady-state model in this paper is more detailed and contains a greater variety of control mechanisms. Hence, the steady-state model in the paper could be seen as a comprehensive extension of Miller’s theory of living systems and Beer’s viable system model, and as a more complete alternative to Nechansky’s modelling from a cybernetic point of view.
It should also be noted that in this steady-state model there is a slightly different view on what constitutes input and output. In the more traditional views of the theory of living systems, e.g., Miller [20] (pp. 514–515), and general systems theory, for instance, von Bertalanffy [8]), the interaction with the environment happens primarily through information and energy, and the material flow is often accredited to systems with human interactions; see Laszlo and Krippner [153] for this reasoning. The proposition in this paper is that the primary processes may transform information, energy or matter, but this is separated from information for the process of control. A case in point is order processing in a firm: as information for the primary processes an order holds data about the product specification and as information for the control processes the date of delivery, the costing and data for the quality conformance. This example implies that (process) modelling is an abstraction of reality for generic modelling or problem solving, but not necessarily reality itself in the spirit of Rosenblueth’s and Wiener’s [154] thoughts about models. In this perspective, the steady-state model with its process orientation does not necessarily reflect the physical structure; this structure is determined by how resources for the processes are grouped in (sub)systems. An example is the analysis of order processing by firms, which might include the processes at suppliers when orders are delivered in a make-to-order mode. Therefore, the steady-state model reflects the control that is exerted over the primary process, transforming either of information or energy or materials, but does not directly provide an abstraction of the physical structure, even though the boundary zones suggest so.
In its depiction of those control processes, the model extends beyond feedback as a control mechanism. Many view feedback as the canonical approach to systems for maintaining homeostasis, e.g., Adams [84] (p. 214). Feedback is also a prominent feature of system dynamics, for example, Schwaninger [82] (p. 588), seen as the only relevant control mechanism in this particular approach to systems theory. The model of Brethower and Dams [155] (p. 39) contains two feedback loops; one can be understood as ‘canonical’ feedback and the other as regulatory control. Consequently, not only does the steady-state model include traditional feedback and feedback in the regulatory zone mentioned in literature, but it also incorporates feedforward and completing deficiencies as interrelated control mechanisms that are hardly mentioned in literature on systems theories.
All this leads to the question how the steady-state model is positioned within the development of systems theories. Regarding strands within the development of systems theory, Laszlo and Krippner [153] (pp. 58–59) distinguish between hard systems methodologies, soft system methodologies and mixed methodologies, with the latter seen as an aid to decision making. The steady-state model as reference model represents so-called hard systems methodologies due to its formal approach to modelling the primary and control processes, and the adoption of concepts from biology, engineering, information systems and management science. However, it can also be viewed as aid to decision making. This is similar to reasoning by Minger [156] that soft and hard methods for research into operations management and management science complement each other. Specifically, he [156] (p. 685) refers to the viable system model as informing conceptual models of real-world systems while complementing Checkland’s soft systems methodology. In this sense, the viable system model serves as reference model akin to the intent of the steady-state model. The lack of formal modelling in Checkland’s soft systems methodology, except its acronym CATWOE (customers, actors, transformation, worldview, owners and environment) for the root definition of systems, seems to be abandoned in favour of creating rich pictures as they are called to get stakeholders and actors onboard as illustrated by a figure in Checkland and Poulter [157] (p. 210). How the steady-state model can be used in combination with methods from soft systems approaches is not explored here since this opens a ‘can of worms’ beyond the use of it as a reference model; this could be of interest for an essay.
Another point is that the steady-state model is transdisciplinary, both in its conception and in its applications, which also aligns with Miller’s living systems theory and, to a lesser extent, with Beer’s viable system model. The transdisciplinary nature of these models differs from descriptions by Adams [84] (p. 211) who calls systems theories the foundation for understanding multidisciplinary systems, a somewhat circular way of reasoning if we take second-order models as the paradigm of systems theories, the latter stipulated by Germana [158] (p. 312). However, it fits in with Becht’s [152] (p. 573) conception about the amalgamation of technological and biological concepts, and Schwaninger’s [82] (p. 591) remark about eclecticism as the way forward. Particularly for the steady-state model, building blocks that emerged since the beginning of the 20th century were drawn from a wide variety of disciplines, among them biology, cybernetics, engineering, general systems theory, and information and communication technologies. This is also reflected in the applications of the three models. Besides applications in biology such as Barlow [159] extending mechanisms in the root apex of plants, Miller’s living systems theory informs the architecture for eco-holonic manufacturing systems by Ávila et al. [160], with the regulatory boundary zone in the model for a manufacturing plant [160] (p. 6) being less-systematically structured than in the steady-state model. Another instance is Cowan et al. [161] using living systems theory for functional modelling of artefacts. Furthermore, Beer’s viable system model has been used as reference model for studies into engineering and information systems, with Kawalek and Wastell [162] being an example for the application to the design of information systems and Wilberg et al. [163] for engineering change management; the latter [163] (p. 734) refers to feedback only. Both publications could have benefited from incorporating concepts for regulatory control in boundary zones and more extended control mechanisms, such as using feedforward for capacity planning in the case of Kawalek and Wastell [162]. A final point is that some studies see both the living systems theory and viable system model as cornerstones for education, exemplified by Nehm [164] for education in biology and by Rezk and Gamal [165] for educational institutes. Since the steady-state model can be considered an extension of modelling living systems and the viable system model, the indicative range of applications based on these models attests to the transdisciplinary nature of the steady-state model.
6. Concluding Remarks
Given the wide range of sources that form the background, it is a pity that none of the works about the steady-state model [1] (pp. xxv–xxviii, 146) [2] (pp. 77–81) [3] (p. 193) refer to its transdisciplinary heritage, commensurate with Pouvreau’s [166] (p. 864) wish to keep the legacy for systems theories alive. One should be careful, though, about attributing roots to specific authors. For example, Vallée [167] (p. 854) mentions Leibniz and Descartes as probable originators of feedback mechanisms, based on McCulloch’s work. Also, the general systems theory is related to ancient scholars, among them Heron, Hippocrates, Kepler, Leibniz and (Adam) Smith, according to Schwaninger [82] (p. 584). In this same spirit, Pouvreau [166] (p. 857) mentions d’Arcy Thompson, Donnan, Lotka, Przibram, Rashevsky, Volterra and Woodger as predecessors in thought. Some of these might have influenced indirectly the formation of systems theories because of the broader interests of the conceivers of systems theories; a case in point is the broader perspective of von Bertalanffy, see Drack [168]. In this sense, Jessie Miller [25] (p. 263) mentions that von Bertalanffy saw Lotka as the first to advance a general system law. However, it seems more correct to view as originators those scholars who are closer to the factual conception of systems theories, for example, Bogdanov’s tectology and Hartmann’s ontology and stratifications (referred to by François [23] (p. 204)) as influencing von Bertalanffy and others. According to François [23] (p. 212 ff.), after the 1960s it has become more difficult to discern innovators in the domain of systems theories. While the steady-state model embraces some contributions after the 1960s, it also quite definitely relies on older conceptualisations for systems theories; this proves that even systems theories are continuously in motion, in terms of both building on legacy and introducing new concepts.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
I am very grateful for the notes of Jacques F. Vos, which I was privileged to view; these notes are the inspiration for this writing. And, I thank Andy Furlong for encouraging to put these thoughts on paper.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | To distinguish between James Grier Miller and his wife Jessie L. Miller, the latter is denoted ‘Jessie Miller’ from hereon. |
| 2 | The distinction of aspects in this manner, possibly goes back to the thoughts of Herman Dooyeweerd—a Dutch philosopher—, although he called them ‘modalities’ and ‘modal aspects.’ According to Friesen [43], he came forward with these ideas in 1922. It is not clear how Dooyeweerd’s concept of modal aspects made its way into systems theories, even though the thinking is remarkably similar. |
| 3 | To distinguish E.J. Miller from James G. Miller and his wife Jessie L. Miller, he will be called ‘E.J. Miller’ from hereon. |
| 4 | The interpretation of coding here is seen as separate for primary processes and control processes. For example, Brown [88] (p. 323) sees this all as one type of coding. |
References
- Dekkers, R. Applied Systems Theory; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Veeke, H.P.M.; Ottjes, J.A.; Lodewijks, G. The Delft Systems Approach: Analysis and Design of Industrial Systems; Springer: London, UK, 2008. [Google Scholar]
- in ’t Veld, J. Analyse van Organisatieproblemen: Een Toepassing van Denken in Systemen en Processen; Agon Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- von Bertalanffy, L. General System Theory; George Braziller: New York, NY, USA, 1973. [Google Scholar]
- Gorelik, G. Bogdanov’s Tektologia, General Systems Theory, and Cybernetics. Cybern. Syst. Int. J. 1987, 18, 157–175. [Google Scholar] [CrossRef]
- Gorelik, G. Reemergence of Bogdanov’s Tektology in Soviet Studies of Organization. Acad. Manag. J. 1975, 18, 345–357. [Google Scholar] [CrossRef]
- von Bertalanffy, L. An Outline Of General System Theory. Br. J. Philos. Sci. 1950, 1, 134–165. [Google Scholar] [CrossRef]
- von Bertalanffy, L. The History and Status of General Systems Theory. Acad. Manag. J. 1972, 15, 407–426. [Google Scholar] [CrossRef]
- von Bertalanffy, L. The Theory of Open Systems in Physics and Biology. Science 1950, 111, 23–29. [Google Scholar] [CrossRef]
- Drack, M.; Schwarz, G. Recent Developments in General System Theory. Syst. Res. Behav. Sci. 2010, 27, 601–610. [Google Scholar] [CrossRef]
- Lloyd, D.; Aon, M.A.; Cortassa, S. Why Homeodynamics, Not Homeostasis? Sci. World 2001, 1, 133–145. [Google Scholar] [CrossRef]
- Johnson, R.A.; Kast, F.E.; Rosenzweig, J.E. Systems Theory and Management. Manag. Sci. 1964, 10, 367–384. [Google Scholar] [CrossRef]
- Katz, D.; Kahn, R.L. The Social Psychology of Organizations; John Wiley & Sons: New York, NY, USA, 1966. [Google Scholar]
- Katz, D.; Kahn, R.L. Organizations and the Systems Concept. In Classics of Organization Theory; Shafritz, J.M., Ott, J.S., Jang, Y.S., Eds.; Cengage Learning: Boston, MA, USA, 2015; pp. 347–358. [Google Scholar]
- Kast, F.E.; Rosenzweig, J.E. General Systems Theory: Applications for Organization and Management. Acad. Manag. J. 1972, 15, 447–465. [Google Scholar] [CrossRef]
- Biggs, J.B. From Theory to Practice: A Cognitive Systems Approach. High. Educ. Res. Dev. 1993, 12, 73–85. [Google Scholar] [CrossRef]
- Chorley, R.J. Geomorphology and General Systems Theory; Professional Paper (500-B); U.S. Department of the Interior/U.S. Geological Survey: Washington, DC, USA, 1962. [Google Scholar]
- Chisholm, M. General Systems Theory and Geography. Trans. Inst. Br. Geogr. 1967, 42, 45–52. [Google Scholar] [CrossRef]
- Strauss, D.F.M. The scope and limitations of Von Bertalanffy’s systems theory. South Afr. J. Philos. 2002, 21, 163–179. [Google Scholar] [CrossRef]
- Miller, J.G. Toward a general theory for the behavioral sciences. Am. Psychol. 1955, 10, 513–531. [Google Scholar] [CrossRef]
- Miller, J.G. The nature of living systems. Behav. Sci. 1971, 16, 277–301. [Google Scholar] [CrossRef]
- Miller, J.G. Living systems: Basic concepts. Behav. Sci. 1965, 10, 193–237. [Google Scholar] [CrossRef]
- François, C. Systemics and cybernetics in a historical perspective. Syst. Res. Behav. Sci. 1999, 16, 203–219. [Google Scholar] [CrossRef]
- Miller, J.L.; Miller, J.G. Greater than the sum of its parts. I. subsystems which process both matter-energy and information. Behav. Sci. 1992, 37, 1–9. [Google Scholar] [CrossRef]
- Miller, J.L. A look back at the systems society. Behav. Sci. 1996, 41, 263–269. [Google Scholar] [CrossRef]
- Miller, J.G.; Miller, J.L. A living systems analysis of organizational pathology. Behav. Sci. 1991, 36, 239–252. [Google Scholar] [CrossRef]
- Bailey, K.D. Emergence, Drop-Back and Reductionism in Living Systems Theory. Axiomathes 2005, 15, 29–45. [Google Scholar] [CrossRef]
- Bailey, K.D. Living Systems Theory and Social Entropy Theory. Syst. Res. Behav. Sci. 2006, 23, 291–300. [Google Scholar] [CrossRef]
- Miller, J.G. Living Systems: The Organization. Behav. Sci. 1972, 17, 1–182. [Google Scholar] [CrossRef]
- Miller, J.G. Living Systems; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
- Glassman, R.B. Persistence and loose coupling in living systems. Behav. Sci. 1973, 18, 83–98. [Google Scholar] [CrossRef]
- Maturana, H.R. The Organization of the Living: A Theory of the Living Organization. Int. J. Man-Mach. Stud. 1975, 7, 313–332. [Google Scholar] [CrossRef]
- Maturana, H.R. Biology of Language: The Epistemology of Reality, in Psychology and Biology of Language and Thought: Essays in Honor of Eric Lenneberg; Miller, G.A., Lenneberg, E., Eds.; Academic Press: New York, NY, USA, 1978; pp. 27–63. [Google Scholar]
- Luhmann, N. Die Autopoiesis des Bewußtseins. Soz. Welt 1985, 36, 402–446. Available online: https://www.jstor.org/stable/40877451 (accessed on 8 May 2025).
- Járos, G. Living Systems Theory of James Grier Miller and Teleonics. Syst. Res. Behav. Sci. 2000, 17, 289–300. [Google Scholar] [CrossRef]
- Járos, G.G.; Dostal, E. A Teleonic Management Framework for Organizations. Syst. Pract. Action Res. 1999, 12, 195–217. [Google Scholar] [CrossRef]
- Nechansky, H. The Relationship Between: Miller’s Living Systems Theory and Beer’s Viable Systems Theory. Syst. Res. Behav. Sci. 2010, 27, 97–112. [Google Scholar] [CrossRef]
- Beer, S. Brain of the Firm—The Managerial Cybernetics of Organization; John Wiley & Sons: Chichester, UK, 1972. [Google Scholar]
- Kybernetes’ Editorial Team. Ten pints of Beer: The rationale of Stafford Beer’s cybernetic books (1959-94). Kybernetes 2000, 29, 558–572. [Google Scholar] [CrossRef]
- Checkland, P.B. Science and the Systems Paradigm. Int. J. Gen. Syst. 1976, 3, 127–134. [Google Scholar] [CrossRef]
- Morgan, G. Images of Organization; Sage Publications: Thousand Oaks, CA, USA, 1997. [Google Scholar]
- Mlakar, T.; Mulej, M. On the concept of the “control systems theory” as a new model of systemic consideration. Kybernetes 2008, 37, 215–225. [Google Scholar] [CrossRef]
- Friesen, J.G. Dooyeweerd’s Idea of Modalities: The Pivotal 1922 Article. Philos. Reformata 2016, 81, 113–155. [Google Scholar] [CrossRef]
- Midgley, G.; Munlo, I.; Brown, M. The Theory and Practice of Boundary Critique: Developing Housing Services for Older People. J. Oper. Res. Soc. 1998, 49, 467–478. [Google Scholar] [CrossRef]
- Ulrich, W. Reflective Practice in the Civil Society: The contribution of critically systemic thinking. Reflective Pract. 2000, 1, 247–268. [Google Scholar] [CrossRef]
- Churchman, C.W. The Design of Inquiring Systems: Basic Concepts of Systems and Organization; Basic Books: New York, NY, USA, 1971. [Google Scholar]
- Green, S.G.; Welsh, M.A. Cybernetics and Dependence: Reframing the Control Concept. Acad. Manag. Rev. 1988, 13, 287–301. [Google Scholar] [CrossRef]
- Hedberg, B.L.T.; Bystrom, P.C.; Starbuck, W.H. Camping on Seesaws: Prescriptions for a Self-Designing Organization. Adm. Sci. Q. 1976, 21, 41–65. [Google Scholar] [CrossRef]
- Safayeni, F.; Derbentseva, N.; Cañas, A.J. A theoretical note on concepts and the need for Cyclic Concept Maps. J. Res. Sci. Teach. 2005, 42, 741–766. [Google Scholar] [CrossRef]
- Tsoukas, H. What is Management? An Outline of a Metatheory. Br. J. Manag. 1994, 5, 289–301. [Google Scholar] [CrossRef]
- Ackoff, R.L.; Gharajedaghi, J. Reflections on systems and their models. Syst. Res. 1996, 13, 13–23. [Google Scholar] [CrossRef]
- Checkland, P. OR and the Systems Movement: Mappings and Conflicts. J. Oper. Res. Soc. 1983, 34, 661–675. [Google Scholar] [CrossRef]
- Flood, R.L. The Relationship of ‘Systems Thinking’ to Action Research. Syst. Pract. Action Res. 2010, 23, 269–284. [Google Scholar] [CrossRef]
- Oliga, J.C. Methodological Foundations of Systems Methodologies. Syst. Pract. 1988, 1, 87–112. [Google Scholar] [CrossRef]
- Garud, R.; Kotha, S. Using the Brain as a Metaphor to Model Flexible Production Systems. Acad. Manag. Rev. 1994, 19, 671–698. [Google Scholar] [CrossRef]
- Grandori, A. A Prescriptive Contingency View of Organizational Decision Making. Adm. Sci. Q. 1984, 29, 192–209. [Google Scholar] [CrossRef]
- Rouse, P.; Putterill, M. An integral framework for performance measurement. Manag. Decis. 2003, 41, 791–805. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Weaver, W. Recent Contributions to the Mathematical Theory of Communication. ETC A Rev. Gen. Semant. 1953, 10, 261–281. Available online: https://www.jstor.org/stable/42581364 (accessed on 8 May 2025).
- Wyner, A.D. Recent Results in the Shannon Theory. IEEE Trans. Inf. Theory 1974, 20, 2–10. [Google Scholar] [CrossRef]
- Verdú, S. Fifty Years of Shannon Theory. IEEE Trans. Inf. Theory 1998, 44, 2057–2078. [Google Scholar] [CrossRef]
- Guizzo, E.M. The Essential Message: Claude Shannon and the Making of Information Theory; Department of Humanities, Massachusetts Institute of Technology: Boston, MA, USA, 2003. [Google Scholar]
- Laxton, R.R. The measure of diversity. J. Theor. Biol. 1978, 70, 51–67. [Google Scholar] [CrossRef]
- Maruyama, M. Heterogenistics: An epistemological restructuring of biological and social sciences. Acta Biotheor. 1977, 26, 120–136. [Google Scholar] [CrossRef]
- Liyanage, C.; Elhag, T.; Ballal, T.; Li, Q. Knowledge communication and translation—A knowledge transfer model. J. Knowl. Manag. 2009, 13, 118–131. [Google Scholar] [CrossRef]
- Nonaka, I. A Dynamic Theory of Organizational Knowledge Creation. Organ. Sci. 1994, 5, 14–37. [Google Scholar] [CrossRef]
- Mandelbrot, B. An informational theory of the statistical structure of language. Commun. Theory 1953, 84, 486–502. [Google Scholar]
- Nowak, M.A.; Krakauer, D.C.; Dress, A. An error limit for the evolution of language. Proc. R. Soc. B Biol. Sci. 1999, 266, 2131–2136. [Google Scholar] [CrossRef]
- Malhotra, N.K. Information Load and Consumer Decision Making. J. Consum. Res. 1982, 8, 419–430. [Google Scholar] [CrossRef]
- Swait, J.; Adamowicz, W. Choice Environment, Market Complexity, and Consumer Behavior: A Theoretical and Empirical Approach for Incorporating Decision Complexity into Models of Consumer Choice. Organ. Behav. Hum. Decis. Process. 2001, 86, 141–167. [Google Scholar] [CrossRef]
- Koerner, A.F.; Fitzpatrick, M.A. Toward a Theory of Family Communication. Commun. Theory 2002, 12, 70–91. [Google Scholar] [CrossRef]
- Luce, R.D. Whatever Happened to Information Theory in Psychology? Rev. Gen. Psychol. 2003, 7, 183–188. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication in the Presence of Noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Kalman, R.E. On the General Theory of Control Systems. In First IFAC Congress Automatic Control; Butterworths: Moscow, Russia, 1960. [Google Scholar]
- Müller, F. State-of-the-art in ecosystem theory. Ecol. Model. 1997, 100, 135–161. [Google Scholar] [CrossRef]
- Miller, J.G. Second annual Ludwig von Bertalanffy memorial lecture. Behav. Sci. 1976, 21, 219–227. [Google Scholar] [CrossRef]
- Beer, S. The Viable System Model: Its Provenance, Development, Methodology and Pathology. J. Oper. Res. Soc. 1984, 35, 7–25. [Google Scholar] [CrossRef]
- Beer, S. Death is equifinal: Eighth Annual Ludwig von Bertalanffy Memorial Lecture. Behav. Sci. 1981, 26, 185–196. [Google Scholar] [CrossRef]
- Robb, F.F. Operational Research and General Systems Thinking. Eur. Manag. J. 1986, 4, 55–62. [Google Scholar] [CrossRef]
- Duffy, P.R. Cybernetics. J. Bus. Commun. 1984, 21, 33–41. [Google Scholar] [CrossRef]
- Pierce, L.M. Usefulness of a systems approach for problem conceptualisation and investigation. Nurs. Res. 1972, 21, 509–513. [Google Scholar] [CrossRef]
- Schwaninger, M. System Dynamics and the Evolution of the Systems Movement. Syst. Res. Behav. Sci. 2006, 23, 583–594. [Google Scholar] [CrossRef]
- Nechansky, H. Cybernetics as the science of decision making. Kybernetes 2011, 40, 63–79. [Google Scholar] [CrossRef]
- Adams, K.M. Systems theory: A formal construct for understanding systems. Int. J. Syst. Syst. Eng. 2012, 3, 209–224. [Google Scholar] [CrossRef]
- Van Gigch, J.P.; Kramer, N.J.T.A. A taxonomy of Systems Science. Int. J. Man-Mach. Stud. 1981, 14, 179–191. [Google Scholar] [CrossRef]
- Miller, E.J.; Rice, A.K. Systems of Organisation: Task and Sentinent Systems and Their Boundary Control; Tavistock Institute: London, UK, 1967. [Google Scholar]
- Koch, S. The logical character of the motivation concept. II. Psychol. Rev. 1941, 48, 127–154. [Google Scholar] [CrossRef]
- Brown, W.B. Systems, Boundaries, and Information Flow. Acad. Manag. J. 1966, 9, 318–327. [Google Scholar] [CrossRef]
- Blegen, H.M. The System Approach to the Study of Organizations. Acta Sociol. 1968, 11, 12–30. [Google Scholar] [CrossRef]
- Simon, T.W. Control systems and teleological systems. Behav. Sci. 1975, 20, 325–330. [Google Scholar] [CrossRef]
- MacKay, D.M. Cerebral Organization and the Conscious Control of Action, in Brain and Conscious Experience; Eccles, J.C., Ed.; Springer: Berlin/Heidelberg, Germany, 1965; pp. 422–445. [Google Scholar]
- Lefkowitz, I. Multilevel Approach Applied to Control System Design. J. Basic Eng. 1966, 88, 392–398. [Google Scholar] [CrossRef]
- Morgan, B.S., Jr. The synthesis of linear multivariable systems by state-variable feedback. IEEE Trans. Autom. Control 1964, 9, 405–411. [Google Scholar] [CrossRef]
- Bogart, D.H. Feedback, feedforward, and feedwithin: Strategic information in systems. Behav. Sci. 1980, 25, 237–249. [Google Scholar] [CrossRef]
- Black, H.S. Inventing the negative feedback amplifier: Six years of persistent search helped the author conceive the idea “in a flash” aboard the old Lackawanna Ferry. IEEE Spectr. Mag. 1977, 14, 55–60. [Google Scholar] [CrossRef]
- Mangan, J.; Lalwani, C.; Gardner, B. Combining quantitative and qualitative methodologies in logistics research. Int. J. Phys. Distrib. Logist. Manag. 2004, 34, 565–578. [Google Scholar] [CrossRef]
- Eisenhardt, K.M.; Graebner, M.E. Theory Building from Cases: Opportunities and Challenges. Acad. Manag. J. 2007, 50, 25–32. [Google Scholar] [CrossRef]
- Knigge, L.; Cope, M. Grounded visualization: Integrating the analysis of qualitative and quantitative data through grounded theory and visualization. Environ. Plan. A 2006, 38, 2012–2037. [Google Scholar] [CrossRef]
- Dickens, L.; Watkins, K. Action Research: Rethinking Lewin. Manag. Learn. 1999, 30, 127–140. [Google Scholar] [CrossRef]
- Miller, J.G.; Miller, J.L. Introduction: The nature of living systems. Behav. Sci. 1990, 35, 157–163. [Google Scholar] [CrossRef] [PubMed]
- Dekkers, R. Adapting Organizations: The Instance of Business Process Re-Engineering. Syst. Res. Behav. Sci. 2008, 25, 45–66. [Google Scholar] [CrossRef]
- Hess, T.; Oesterle, H. Methods for Business Process Redesign: Current State and Development Perspectives. Bus. Change Re-Eng. 1996, 3, 73–83. [Google Scholar] [CrossRef]
- Aguilar-Savén, R.S. Business process modelling: Review and framework. Int. J. Prod. Econ. 2004, 90, 129–149. [Google Scholar] [CrossRef]
- Childe, S.J.; Maull, R.S.; Bennett, J. Framework for Understanding Business Process Re-engineering. Int. J. Oper. Prod. Manag. 1994, 14, 22–34. [Google Scholar] [CrossRef]
- Jansen-Vullers, M.H.; van Dorp, C.A.; Beulens, A.J.M. Managing traceability information in manufacture. Int. J. Inf. Manag. 2003, 23, 395–413. [Google Scholar] [CrossRef]
- Kettinger, W.J.; James, T.C.T.; Guha, S. Business Process Change: A Study of Methodologies, Techniques, and Tools. MIS Q. 1997, 21, 55–80. [Google Scholar] [CrossRef]
- List, B.; Korherr, B. An evaluation of conceptual business process modelling languages. In ACM Symposium on Applied Computing; Haddad, H., Ed.; ACM: Dijon, France, 2006; pp. 1532–1539. [Google Scholar]
- Scheepers, H.; Scheepers, R. A process-focused decision framework for analyzing the business value potential of IT investments. Inf. Syst. Front. 2008, 10, 321–330. [Google Scholar] [CrossRef]
- Gunasekaran, A.; Kobu, B. Modelling and analysis of business process reengineering. Int. J. Prod. Res. 2002, 40, 2521–2546. [Google Scholar] [CrossRef]
- Adesola, S.; Baines, T. Developing and evaluating a methodology for business process improvement. Bus. Process Manag. J. 2005, 11, 37–46. [Google Scholar] [CrossRef]
- Jang, K.-J. A model decomposition approach for a manufacturing enterprise in Business Process Reengineering. Int. J. Comput. Integr. Manuf. 2003, 16, 210–218. [Google Scholar] [CrossRef]
- Melão, N.; Pidd, M. A conceptual framework for understanding business processes and business process modelling. Inf. Syst. J. 2000, 10, 105–129. [Google Scholar] [CrossRef]
- Sagasti, F.R.; Mittrof, I.I. Operations Research from the Viewpoint of General Systems Theory. Omega 1973, 1, 695–709. [Google Scholar] [CrossRef]
- van Aken, J.E. Management Research as a Design Science: Articulating the Research Products of Mode 2 Knowledge Production in Management. Br. J. Manag. 2005, 16, 19–36. [Google Scholar] [CrossRef]
- Meredith, J. Building operations management theory through case and field research. J. Oper. Manag. 1998, 16, 441–454. [Google Scholar] [CrossRef]
- Grönroos, C.; Ojasalo, K. Service productivity: Towards a conceptualization of the transformation of inputs into economic results in services. J. Bus. Res. 2004, 57, 414–423. [Google Scholar] [CrossRef]
- Kohlbacher, M.; Gruenwald, S. Process orientation: Conceptualization and measurement. Bus. Process Manag. J. 2011, 17, 267–283. [Google Scholar] [CrossRef]
- Koulouriotis, D.E.; Xanthopoulos, A.S.; Tourassis, V.D. Simulation optimisation of pull control policies for serial manufacturing lines and assembly manufacturing systems using genetic algorithms. Int. J. Prod. Res. 2010, 48, 2887–2912. [Google Scholar] [CrossRef][Green Version]
- Shafer, S.M.; Smunt, T.L. Empirical simulation studies in operations management: Context, trends, and research opportunities. J. Oper. Manag. 2004, 22, 345–354. [Google Scholar] [CrossRef]
- Vlachos, D.; Georgiadis, P.; Iakovou, E. A system dynamics model for dynamic capacity planning of remanufacturing in closed-loop supply chains. Comput. Oper. Res. 2007, 34, 367–394. [Google Scholar] [CrossRef]
- Dekkers, R. Lean Production: Nothing More Than the Learning Curve. In Proceedings of the 23rd EurOMA Conference, Trondheim, Norway, 17–22 June 2016. [Google Scholar]
- Dekkers, R. (R)Evolution, Organizations and the Dynamics of the Environment; Springer: New York, NY, USA, 2005. [Google Scholar]
- Emery, F.E.; Trist, E.L. Socio-technical systems. In Systems Thinking; Emery, F.E., Ed.; Penguin: Middlesex, UK, 1972; pp. 281–296. [Google Scholar]
- Schuh, G.; Sauer, A.; Döring, S. Modeling collaborations as complex systems. In Proceedings of the 4th Industrial Simulation Conference, Palermo, Italy, 5–7 June 2006. [Google Scholar]
- Dekkers, R.; van Luttervelt, C.A. Industrial networks: Capturing changeability? Int. J. Netw. Virtual Organ. 2006, 3, 1–24. [Google Scholar] [CrossRef]
- Kühnle, H. Self-Similarity and Criticality in Dispersed Manufacturing: A Contribution to Production Networks Control. In Dispersed Manufacturing Networks: Challenges for Research and Practice; Dekkers, R., Ed.; Springer: London, UK, 2009; pp. 59–76. [Google Scholar]
- Das, A.; Narasimhan, R.; Talluri, S. Supplier integration—Finding an optimal configuration. J. Oper. Manag. 2006, 24, 563–582. [Google Scholar] [CrossRef]
- Sánchez, A.M.; Pérez, M.P. Lean indicators and manufacturing strategies. Int. J. Oper. Prod. Manag. 2001, 21, 1433–1452. [Google Scholar] [CrossRef]
- Mingers, J.; White, L. A review of the recent contribution of systems thinking to operational research and management science. Eur. J. Oper. Res. 2010, 207, 1147–1161. [Google Scholar] [CrossRef]
- Kabak, K.E.; Hinckeldeyn, J.; Dekkers, R. A systematic literature review into simulation for building operations management theory: Reaching beyond positivism? J. Simul. 2024, 18, 687–715. [Google Scholar] [CrossRef]
- Aboelela, S.W.; Larson, E.; Bakken, S.; Carrasquillo, O.; Formicola, A.; Glied, S.A.; Haas, J.; Gebbie, K.M. Defining Interdisciplinary Research: Conclusions from a Critical Review of the Literature. Health Serv. Res. 2006, 42, 329–346. [Google Scholar] [CrossRef] [PubMed]
- Banathy, B.H.; Jenlink, P.M. Systems Inquiry and Its Application in Education. In Handbook of Research for Educational Communications and Technology; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2004; pp. 37–58. [Google Scholar]
- Lane, A. A Review of Diagramming in Systems Practice and How Technologies Have Supported the Teaching and Learning of Diagramming for Systems Thinking in Practice. Syst. Pract. Action Res. 2013, 26, 319–329. [Google Scholar] [CrossRef]
- Marquardt, M.; Waddill, D. The power of learning in action learning: A conceptual analysis of how the five schools of adult learning theories are incorporated within the practice of action learning. Action Learn. Res. Pract. 2004, 1, 185–202. [Google Scholar] [CrossRef]
- Hill, A.; Hill, T. Essential Operations Management; Palgrave Macmillan: Basingstoke, UK, 2011. [Google Scholar]
- Jacobs, F.R.; Chase, R.B. Operations and Supply Chain Management—Global Edition, 13th ed.; McGraw-Hill/Irwin: New York, NY, USA, 2011. [Google Scholar]
- Slack, N.; Chambers, S.; Johnston, R. Operations Management; Prentice Hall: Harlow, UK, 2010. [Google Scholar]
- Ashby, W.R. An Introduction to Cybernetics; J. Wiley: New York, NY, USA, 1956. [Google Scholar]
- Bacharach, S.B. Organizational Theories: Some Criteria for Evaluation. Acad. Manag. Rev. 1989, 14, 496–515. [Google Scholar] [CrossRef]
- van Aken, J.E. Management Research Based on the Paradigm of the Design Sciences: The Quest for Field-Tested and Grounded Technological Rules. J. Manag. Stud. 2004, 41, 219–246. [Google Scholar] [CrossRef]
- Dekkers, R. Keynote: Why ‘Business and Management Studies’ Do not Get ‘Design and Engineering’? In Building Resilience into Production: Contemporary Challenges for the Future, Proceedings of the 27th International Conference on Production Research, Cluj-Napoca, Romania, 23–28 July 2023; Dragomir, M., Popescu, D., Huang, C.Y., Chiu, S.F., Quezada, L., Eds.; Springer: Cham, Switzerland, 2025; pp. 78–92. [Google Scholar]
- Barber, K.D.; Dewhurst, F.W.; Burns, R.L.D.H.; Rogers, J.B.B. Business-process modelling and simulation for manufacturing management: A practical way forward. Bus. Process Manag. J. 2003, 9, 527–542. [Google Scholar] [CrossRef]
- Salgado, E.G.; Dekkers, R. Lean Product Development: Nothing New Under the Sun? Int. J. Manag. Rev. 2018, 20, 903–933. [Google Scholar] [CrossRef]
- Forrester, J.W. Industrial Dynamics; M.I.T. Press: Cambridge, MA, USA, 1961. [Google Scholar]
- de Rosnay, J. Le Macroscope: Vers Une Vision Globale; Éditions du Seuil: Paris, France, 1975. [Google Scholar]
- Checkland, P. Systems Thinking, Systems Practice; John Wiley & Sons: Chichester, UK, 1981. [Google Scholar]
- Bergvall-Kåreborn, B. Enriching the model-building phase of soft systems methodology. Syst. Res. Behav. Sci. 2002, 19, 27–48. [Google Scholar] [CrossRef]
- Sabelli, H.C. Process theory: A biological model of open systems. In Proceedings of the 35th Annual Meeting of International Society for the Systems Sciences, Ostersund, Sweden, 13–21 June 1991. [Google Scholar]
- Potocan, V.; Mulej, M.; Kajzer, S. Business cybernetics: A provocative suggestion. Kybernetes 2005, 34, 1496–1516. [Google Scholar] [CrossRef]
- Jackson, M.C. Fifty years of systems thinking for management. J. Oper. Res. Soc. 2009, 60, S24–S32. [Google Scholar] [CrossRef]
- Jackson, M.C. Critical systems thinking: Beyond the fragments. Syst. Dyn. Rev. 1994, 10, 213–229. [Google Scholar] [CrossRef]
- Becht, G. Systems Theory, The Key to Holism and Reductionism. BioScience 1974, 24, 569–579. [Google Scholar] [CrossRef]
- Laszlo, A.; Krippner, S. Systems Theories: Their Origins, Foundations, and Development. In Systems Theories and A Priori Aspects of Perception; Jordan, J.S., Ed.; Elsevier Science: Amsterdam, The Netherlands, 1998; pp. 47–74. [Google Scholar]
- Rosenblueth, A.; Wiener, N. The Role of Models in Sciences. Philos. Sci. 1945, 12, 316–321. [Google Scholar] [CrossRef]
- Brethower, D.M.; Dams, P.-C. Systems thinking (and systems doing). Perform. Improv. 1999, 38, 37–50. [Google Scholar] [CrossRef]
- Mingers, J. Variety is the spice of life: Combining soft and hard OR/MS methods. Int. Trans. Oper. Res. 2000, 7, 673–691. [Google Scholar] [CrossRef]
- Checkland, P.; Poulter, J. Soft Systems Methodology. In Systems Approaches to Making Change: A Practical Guide; Reynolds, M., Holwell, S., Eds.; Springer: London, UK, 2020; pp. 201–253. [Google Scholar]
- Germana, J. The Whole and Main Ideas of Systems Science. Syst. Res. Behav. Sci. 2000, 17, 311–313. [Google Scholar] [CrossRef]
- Barlow, P.W. Charles Darwin and the Plant Root Apex: Closing a Gap in Living Systems Theory as Applied to Plants. In Communication in Plants: Neuronal Aspects of Plant Life; Baluška, F., Mancuso, S., Volkmann, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 37–51. [Google Scholar]
- Ávila, M.J.; Martín, A.; Aguayo, F. Metabolism in eco-holonic manufacturing systems based on the living systems theory. In Proceedings of the 9th Manufacturing Engineering Society International Conference, Gijon, Spain, 23–25 June 2021; IOP Publishing: Gijon, Spain. [Google Scholar]
- Cowan, F.S.; Allen, J.K.; Mistree, F. Functional modelling in engineering design: A perspectival approach featuring living systems theory. Syst. Res. Behav. Sci. 2006, 23, 365–381. [Google Scholar] [CrossRef]
- Kawalek, P.; Wastell, D.G. A Case Study Evaluation of the Use of the Viable System Model in Information Systems Development. J. Database Manag. 1999, 10, 24–32. [Google Scholar] [CrossRef]
- Wilberg, J.; Tommelein, I.D.; Elezi, F.; Lindemann, U. Supporting the Implementation of Engineering Change Management with the Viable System Model. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Kowloon Tong, Hong Kong, 9–12 October 2015; IEEE: Hong Kong, China. [Google Scholar]
- Nehm, R.H. Biology education research: Building integrative frameworks for teaching and learning about living systems. Discip. Interdiscip. Sci. Educ. Res. 2019, 1, 15. [Google Scholar] [CrossRef]
- Rezk, S.S.; Gamal, S. The viable system model and its applications in higher education: An overview. Kybernetes 2018, 48, 438–450. [Google Scholar] [CrossRef]
- Pouvreau, D. The project of “general systemology” instigated by Ludwig von Bertalanffy. Kybernetes 2013, 42, 851–868. [Google Scholar] [CrossRef]
- Vallée, R. Cybernetics and systems, from past to future. Kybernetes 2003, 32, 853–857. [Google Scholar] [CrossRef]
- Drack, M. Ludwig von Bertalanffy’s early system approach. Syst. Res. Behav. Sci. 2009, 26, 563–572. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).