Passenger Switch Behavior and Decision Mechanisms in Multimodal Public Transportation Systems
Abstract
1. Introduction
2. Literature Review
3. Related Definitions
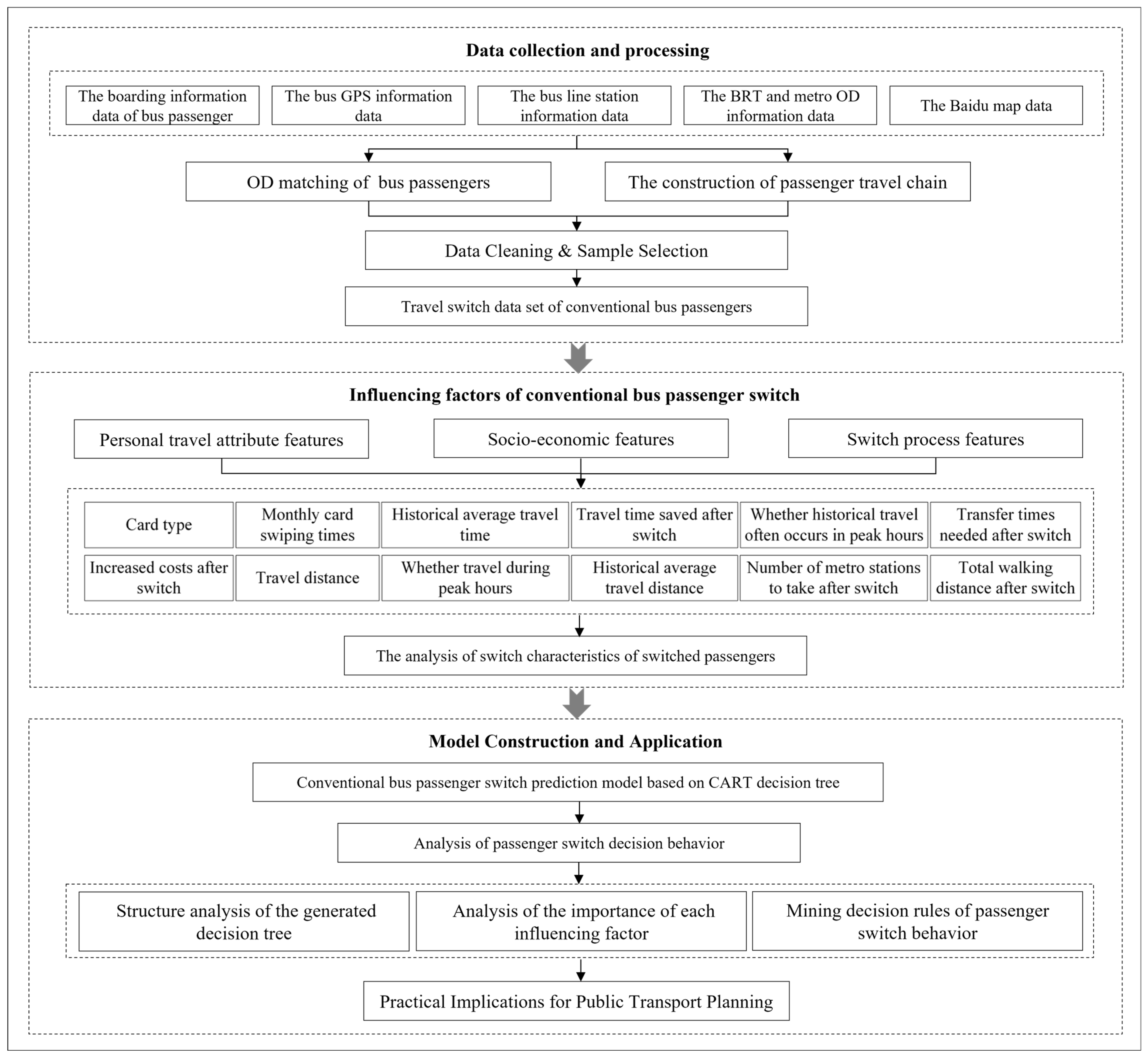
4. Materials and Methods
4.1. Bus Passengers’ Switch Dataset Construction Based on Passenger Swiping-Card Data
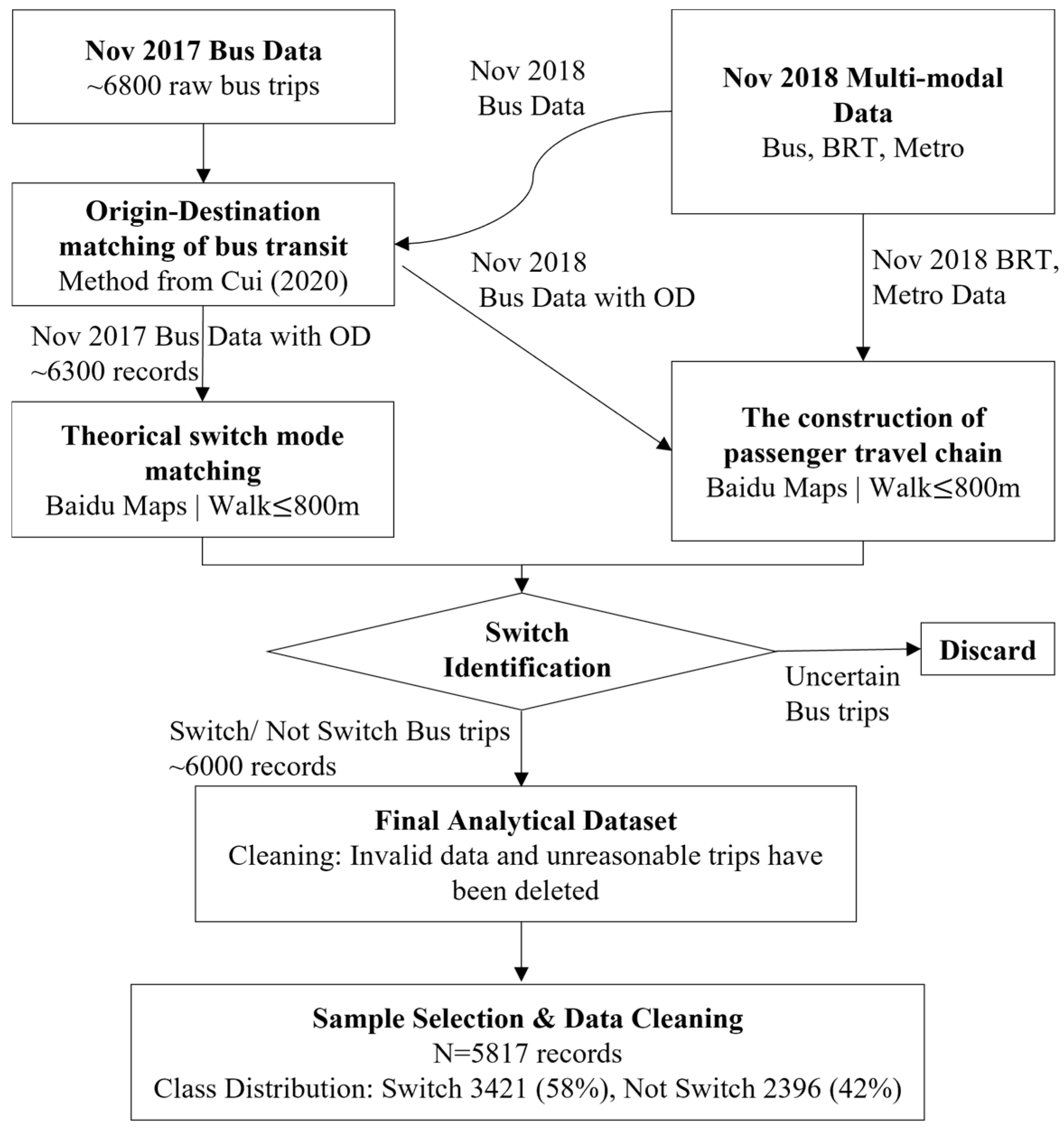
4.1.1. Origin–Destination Matching of Bus Transit
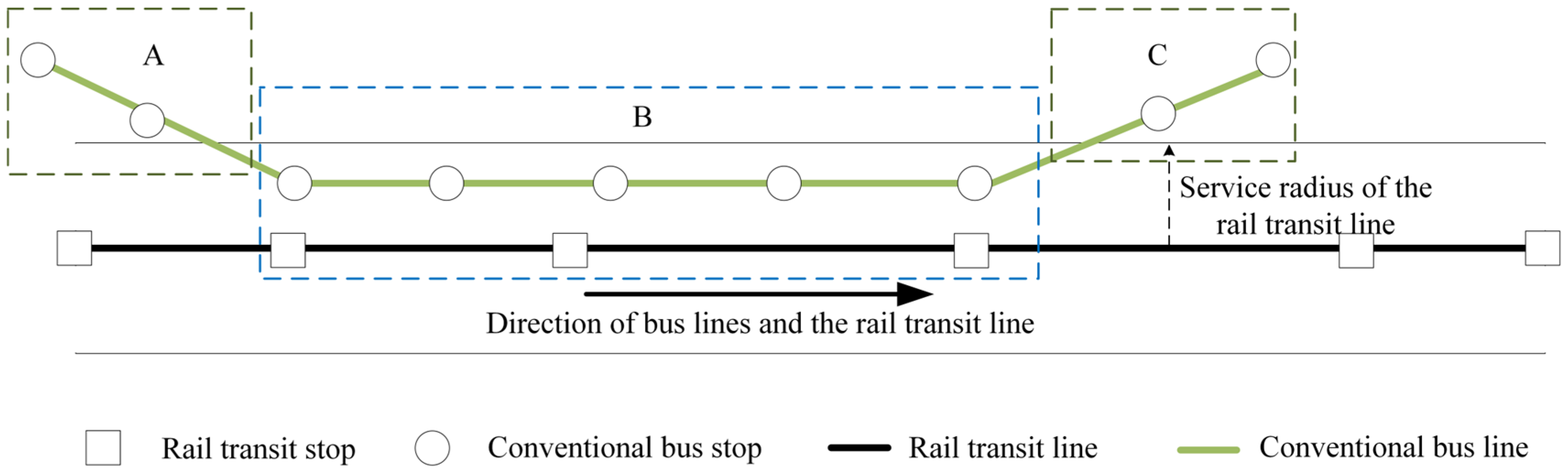
4.1.2. Switch Mode in Theory
4.1.3. Construction of Passenger Trip Chain and Passenger Switch Behavior Recognition
4.1.4. Data Preprocessing: Sample Selection and Cleaning
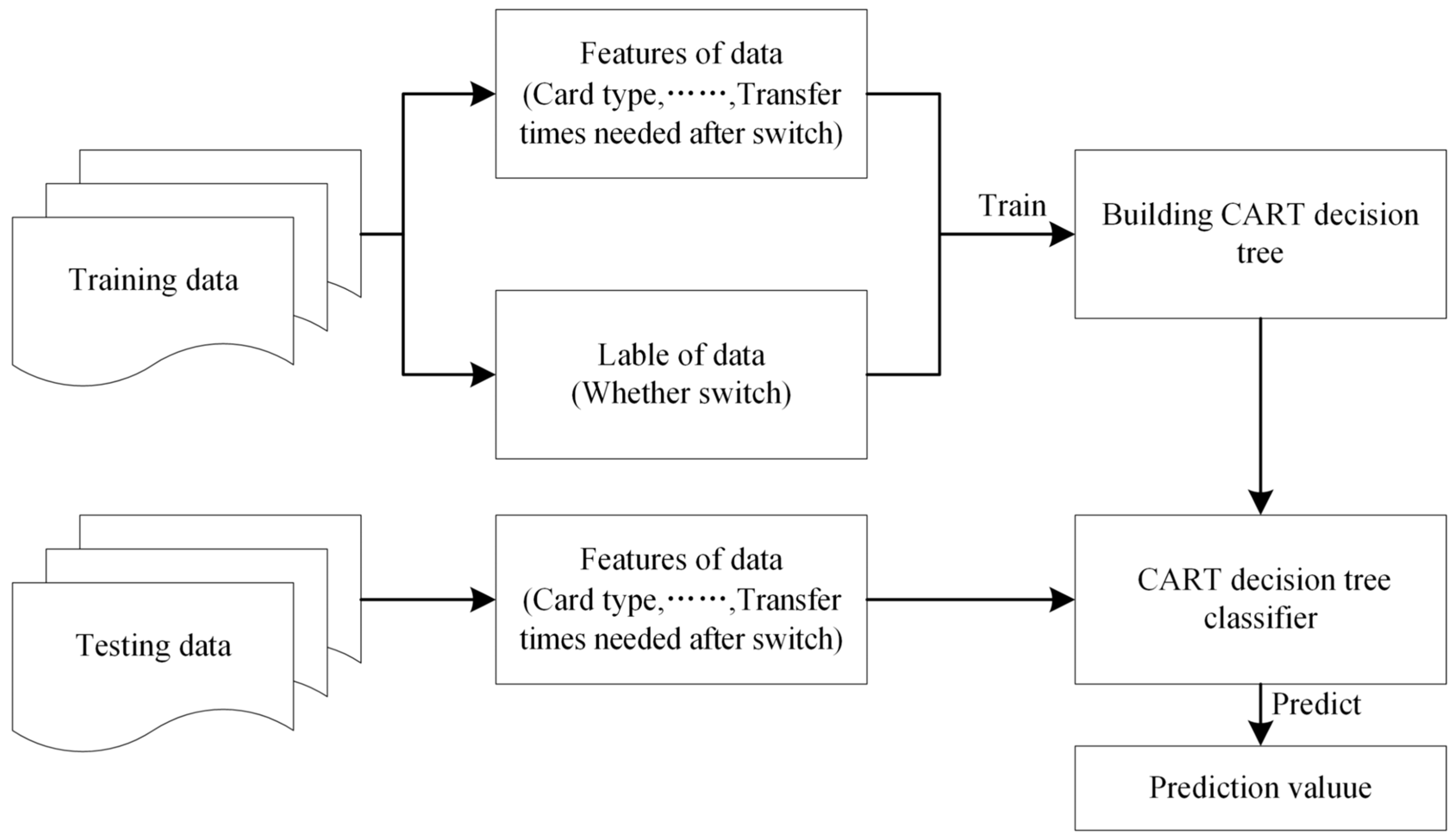
4.2. Predictive Modeling of Switch Behavior
4.2.1. Influencing Factors on the Passengers’ Decision to Switch
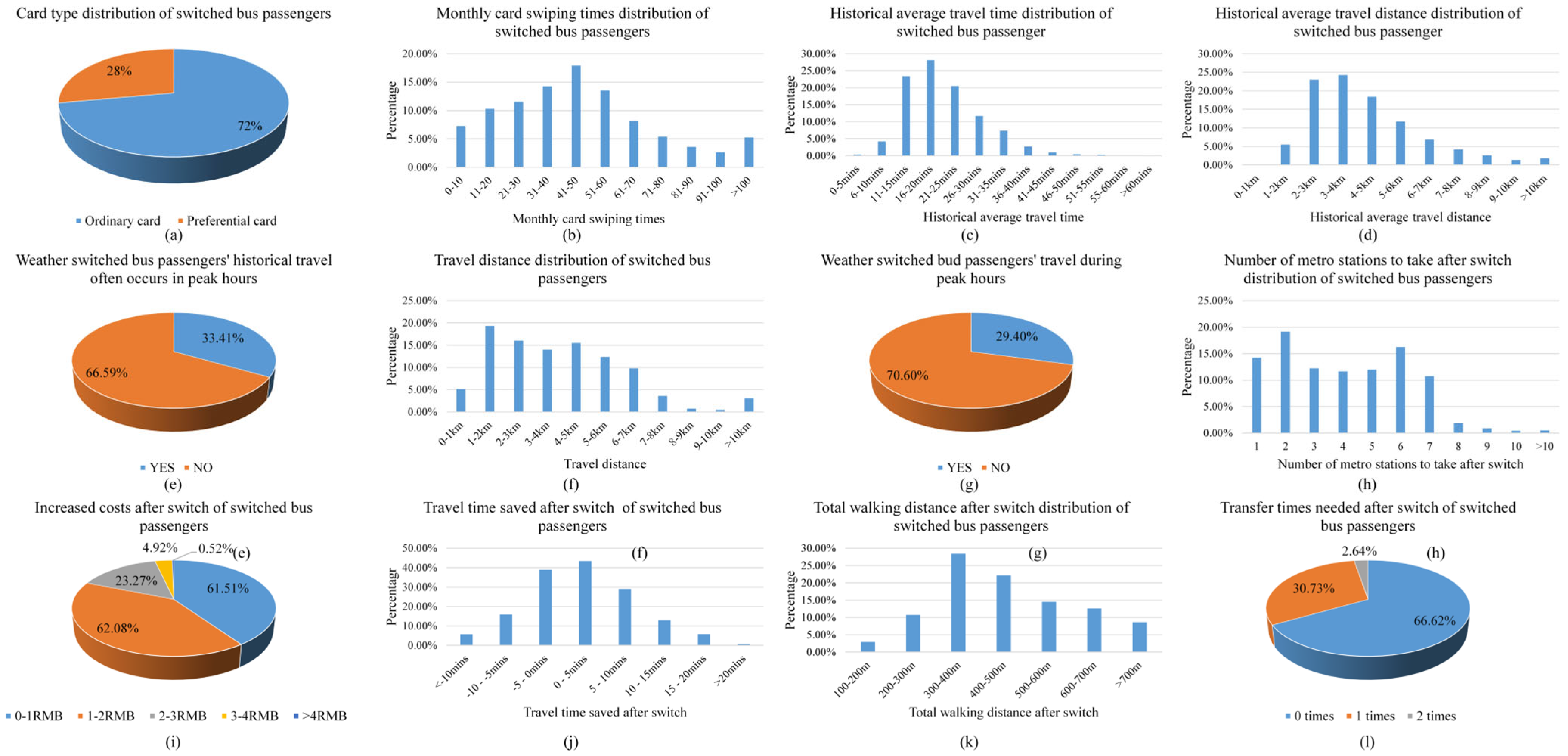
4.2.2. Characteristic Analysis of Switched Bus Passengers
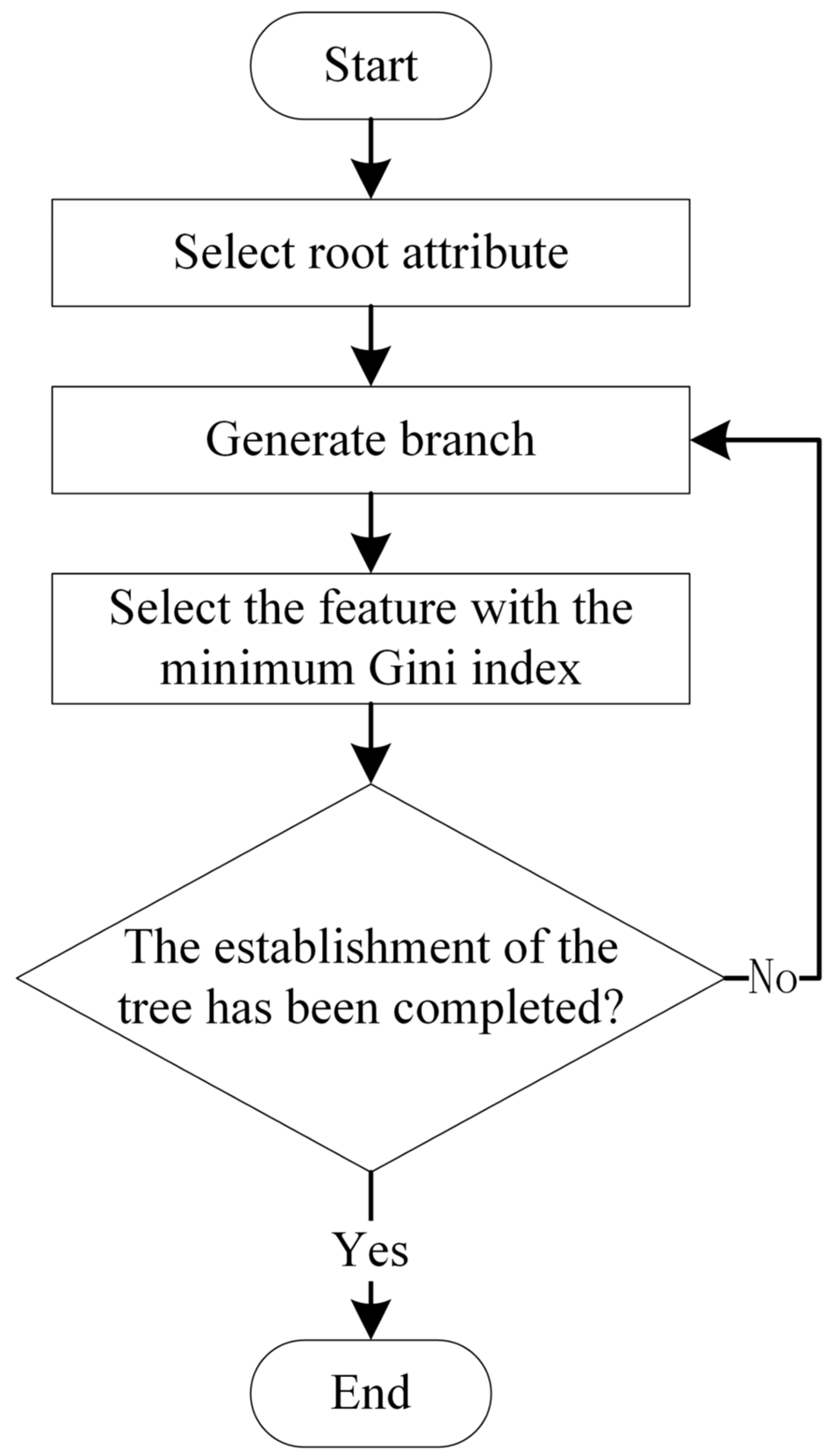
4.2.3. Bus Passengers’ Switch Behavior Model Based on CART Decision Tree
5. Experiment
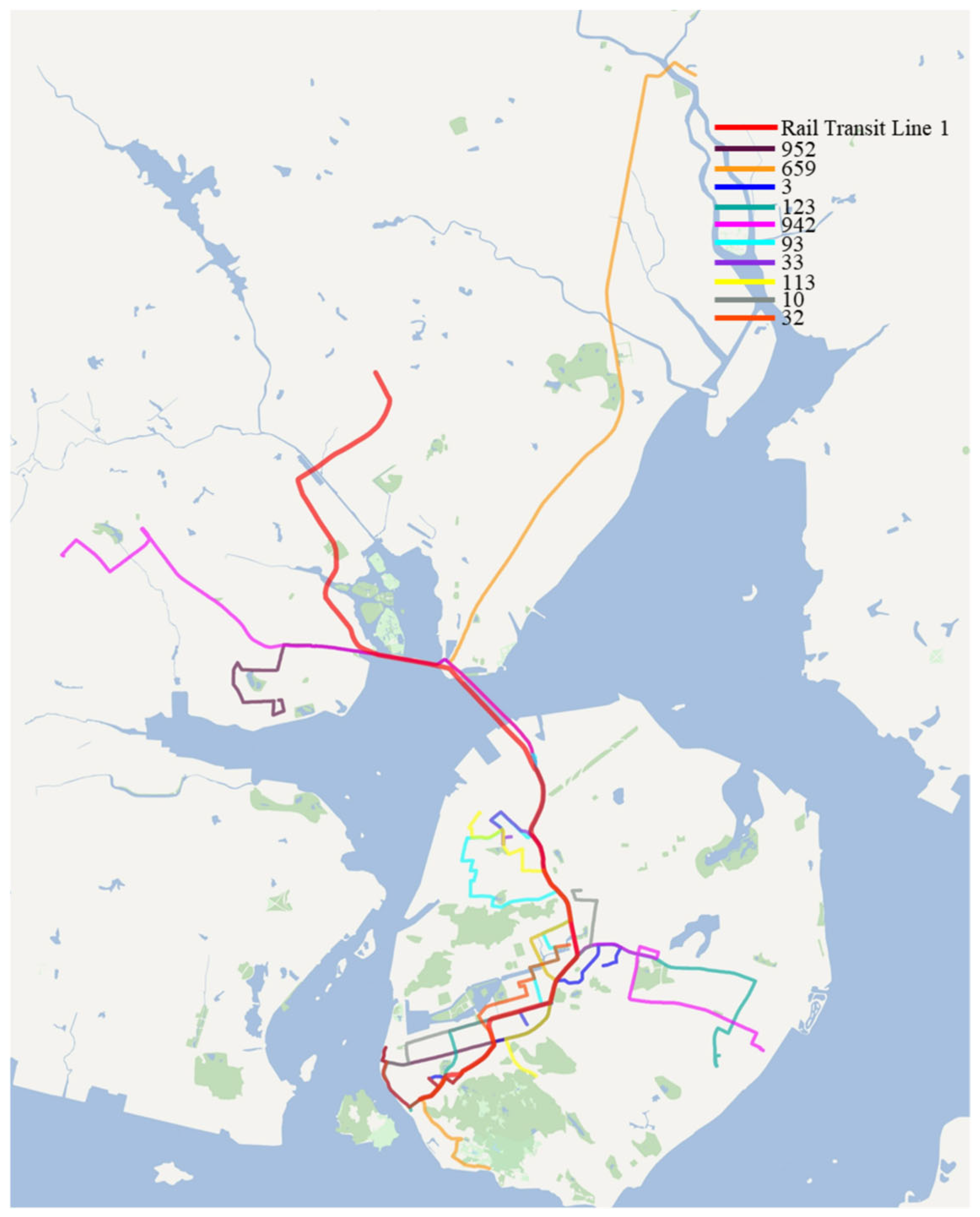
5.1. Study Area and Dataset
5.2. Evaluation Methods and Indicators
5.3. Experimental Setup and Statistical Validation
5.3.1. Parameter Configuration
5.3.2. Model Diagnostics and Statistical Validation
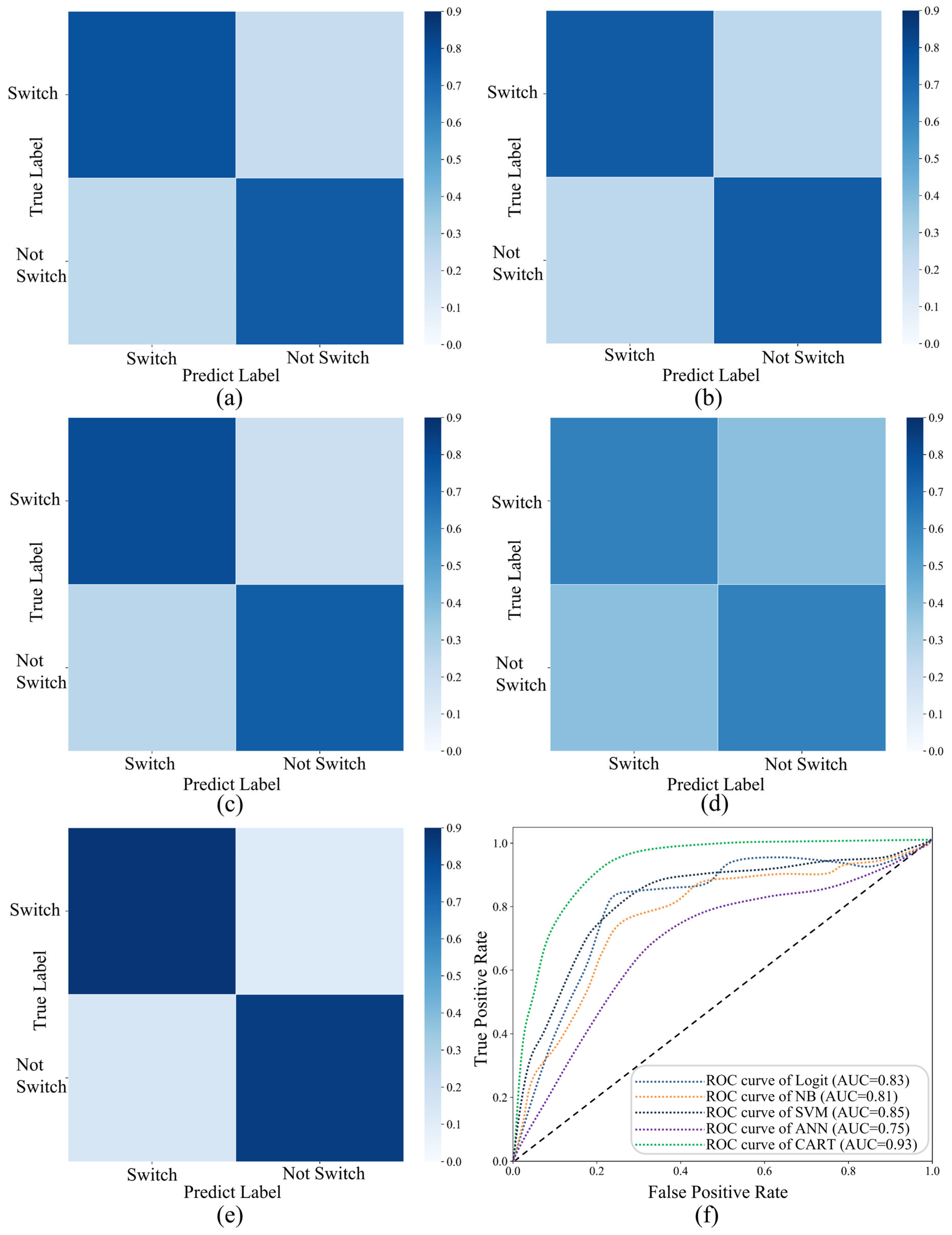
5.4. Experimental Results
5.5. Interpretation of Switching Mechanisms and Practical Implications
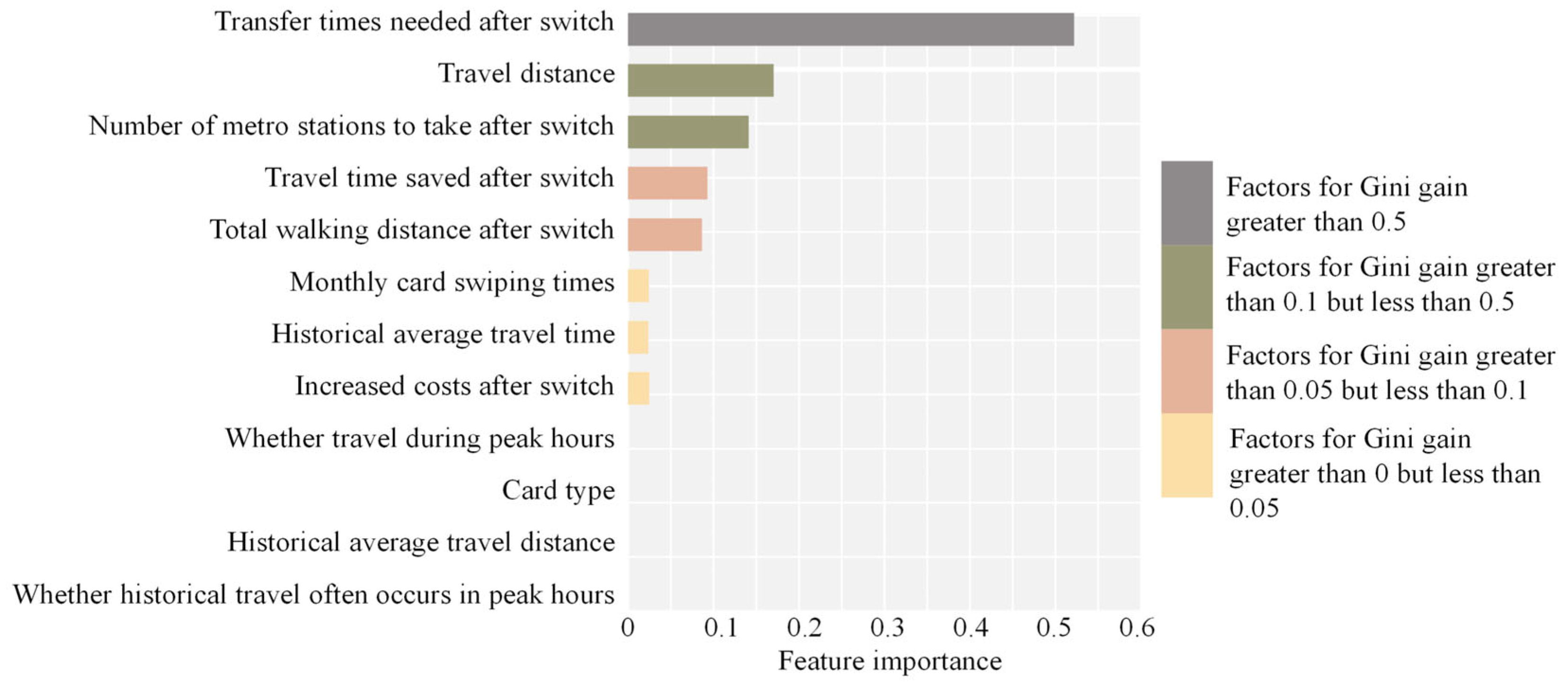
5.5.1. Decision Rules and Factor Importance from the CART Model
5.5.2. Practical Implications for Public Transport Planning
6. Conclusions and Future Work
6.1. Conclusions
6.2. Limitations and Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Juan de Dios, O. Future transportation: Sustainability, complexity and individualization of choices. Commun. Transp. Res. 2021, 1, 100010. [Google Scholar] [CrossRef]
- Guiding Opinions of the State Council on the Priority of Urban Development of Public Transport. Available online: http://www.gov.cn/zwgk/2013-01/05/content_2304962.htm (accessed on 29 December 2012).
- Peled, I.; Lee, K.; Jiang, Y.; Dauwels, J.; Pereira, F.C. On the Quality Requirements of Demand Prediction for Dynamic Public Transport. Commun. Transp. Res. 2020, 1, 100008. [Google Scholar] [CrossRef]
- Sun, G.; Zhao, J.; Webster, C.; Lin, H. New metro system and active travel: A natural experiment. Environ. Int. 2020, 138, 105605. [Google Scholar] [CrossRef]
- Danilevičius, A.; Karpenko, M.; Křivánek, V. Research on the noise pollution from different vehicle categories in the urban area. Transport 2023, 38, 1–11. [Google Scholar] [CrossRef]
- Majumder, S.; Singh, A.; Singh, A.; Karpenko, M.; Sharma, H.K.; Mukhopadhyay, S. On the analytical study of the service quality of Indian Railways under soft-computing paradigm. Transport 2024, 39, 54–63. [Google Scholar] [CrossRef]
- Karpenko, M.; Prentkovskis, O.; Skačkauskas, P. Analysing the impact of electric kick-scooters on drivers: Vibration and frequency transmission during the ride on different types of urban pavements. Eksploat. Niezawodn.-Maint. Reliab. 2025, 27, 1–14. [Google Scholar] [CrossRef]
- Emmanouil, C.; Mohamed, A.; Constantinos, A.; Konstadinos, G. Investigating social media spatiotemporal transferability for transport. Commun. Transp. Res. 2022, 2, 100081. [Google Scholar] [CrossRef]
- Anwar, A.; Oakil, A.T.; Muhsen, A.; Arora, A. What Would it Take for the People of Riyadh City to Shift from Their Cars to the Proposed Metro? Soc. Sci. Res. Netw. 2023, 12, 101008. [Google Scholar] [CrossRef]
- Pan, L.; Waygood, E.; Patterson, Z. Public Transit Itinerary Choice Analysis Considering Various Incentives. Transp. Res. Rec. 2023, 2677, 722–733. [Google Scholar] [CrossRef]
- Elharoun, M.; El-Badawy, S.; Shahdah, U. Artificial Intelligence Techniques for Predicting Individuals’ Mode Choice Behavior in Mansoura City, Egypt. Transp. Res. Rec. 2023, 2677, 605–623. [Google Scholar] [CrossRef]
- Nuzzolo, A.; Comi, A. Advanced public transport and intelligent transport systems: New modelling challenges. Transp. A Transp. Sci. 2016, 12, 674–699. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, Y.; Henrickson, K.; Tang, J.; Wang, Y. Vehicle traffic delay prediction in ferry terminal based on Bayesian multiple models combination method. Transp. A Transp. Sci. 2017, 13, 467–490. [Google Scholar] [CrossRef]
- Yin, H.; Wu, J.; Liu, Z.; Yang, X.; Qu, Y.; Sun, H. Optimizing the release of passenger flow guidance information in urban rail transit network via agent-based simulation. Appl. Math. Model. 2019, 72, 337–355. [Google Scholar] [CrossRef]
- Chen, E.; Luo, Q.; Chen, J.; He, Y. Understanding passenger travel choice behaviours under train delays in urban rail transits: A data-driven approach. Transp. B Transp. Dyn. 2023, 11, 1496–1524. [Google Scholar] [CrossRef]
- Hollander, Y.; Prashker, J.N. The applicability of non-cooperative game theory in transport analysis. Transportation 2006, 33, 481–496. [Google Scholar] [CrossRef]
- Ting, L. Study on Passenger Flow Diversion Between Regular Public Transit and Proposed Rail Transit Based on Discrete Choice Model. Ph.D. Thesis, Chang’an University, Xi’an, China, 2011. [Google Scholar]
- Jiabin, L. Research on the Method of Bus Transit Network Adjustment in the Initial Operation of Urban Rail Transit. Ph.D. Thesis, Southest University, Dhaka, Bangladesh, 2015. [Google Scholar]
- Liang, L.; Wu, J.; Wang, H. Competition Model between Urban Rail and Bus Transit. Urban Mass. Transit. 2009, 7, 30–34. [Google Scholar]
- Wang, K.; Bhat, C.; Ye, X. A multinomial probit analysis of shanghai commute mode choice. Transportation 2022, 50, 1471–1495. [Google Scholar] [CrossRef]
- Harrington, A.; Parolin, B. Factors affecting the use of bus and rail services in a deregulated environment. Transportation 1991, 18, 175–193. [Google Scholar] [CrossRef]
- Murat, Y.S.; Cakici, Z. Comparative Analysis of Public Transport Users’ Perception Targeting Sustainable Transportation. In Engineering Tools and Solutions for Sustainable Transportation Planning; IGI Global: Hershey, PA, USA, 2017; pp. 76–98. [Google Scholar]
- Wang, Y.; Li, L.; Wang, Z.; Lv, T.; Wang, L. Mode Shift Behavior Impacts from the Introduction of Metro Service: Case Study of Xi’an, China. J. Urban Plan. Dev. 2013, 139, 216–225. [Google Scholar] [CrossRef]
- Cats, O. Identifying human mobility patterns using smart card data. Transp. Rev. 2024, 44, 213–243. [Google Scholar] [CrossRef]
- Oliveira, L.K.d.; Isler, C.A.; Balieiro, G.; Carvalho, T.L.L.; Littig, M.A. Bus Line Shift Behaviour: Evidence of Influential Factors based on Smart Card Data. Res. Transp. Bus. Manag. 2024, 52, 101073. [Google Scholar] [CrossRef]
- Ozer, F.C.; Tuydes-Yaman, H.; Dalkic-Melek, G. Increasing the precision of public transit user activity location detection from smart card data analysis via spatial–temporal DBSCAN. Data Knowl. Eng. 2024, 153, 102343. [Google Scholar] [CrossRef]
- Klar, R.; Rubensson, I. Spatio-Temporal Investigation of Public Transport Demand Using Smart Card Data. Appl. Spat. Anal. Policy 2024, 17, 241–268. [Google Scholar] [CrossRef]
- Ruiz, E.; Yushimito, W.F.; Aburto, L.; de la Cruz, R. Predicting passenger satisfaction in public transportation using machine learning models. Transp. Res. Part A Policy Pract. 2024, 181, 103995. [Google Scholar] [CrossRef]
- Nguyen, S.-T.; Moeinaddini, M.; Saadi, I.; Cools, M. Unveiling the drivers of modal switch from motorcycles to public transport in Southeast Asia. Transp. Res. Part F Traffic Psychol. Behav. 2024, 102, 373–391. [Google Scholar] [CrossRef]
- Nguyen-Phuoc, D.Q.; Currie, G.; De Gruyter, C.; Young, W. How do public transport users adjust their travel behaviour if public transport ceases? A qualitative study. Transp. Res. Part F Traffic Psychol. Behav. 2018, 54, 1–14. [Google Scholar] [CrossRef]
- Jian, W.; Liu, X.; Liu, H.; Hu, Y.; Gao, L. The Impacts of the Multiscale Built Environment on Commuting Mode Choice: Spatial Heterogeneity, Moderating Effects, and Implications for Demand Estimation. J. Adv. Transp. 2023, 2023, 9346631. [Google Scholar] [CrossRef]
- Zhou, W.; Li, X.; Shi, Z.; Yang, B.-T.; Chen, D. Impact of Carpooling under Mobile Internet on Travel Mode Choices and Urban Traffic Volume: The Case of China. Sustainability 2023, 15, 6595. [Google Scholar] [CrossRef]
- Deng, Y.J.; Bai, Y.; Cui, L.B.; He, R.J. Travel Mode Choice Behavior for High-Speed Railway Stations Based on Multi-Source Data. Transp. Res. Rec. 2023, 2677, 525–540. [Google Scholar] [CrossRef]
- Ma, S.; Yu, Z.; Liu, C. Nested Logit Joint Model of Travel Mode and Travel Time Choice for Urban Commuting Trips in Xi’an, China. J. Urban Plan. Dev. 2020, 146, 04020020. [Google Scholar] [CrossRef]
- Liu, L.X.; Wang, Y.J.; Hickman, R. How Rail Transit Makes a Difference in People’s Multimodal Travel Behaviours: An Analysis with the XGBoost Method. Land 2023, 12, 675. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, Y. Travel Mode Choice Modeling with Support Vector Machines. Transp. Res. Rec. 2008, 2076, 141–150. [Google Scholar] [CrossRef]
- Mane, A.S.; Sarkar, A.K.; Arkatkar, S.S.; Bhaskar, A. Effect of bus-lane usage by private vehicles on modal shift. Proc. Inst. Civ. Eng.-Transp. 2018, 171, 85–97. [Google Scholar] [CrossRef]
- Pineda-Jaramillo, J.; Arbeláez-Arenas, Ó. Assessing the Performance of Gradient-Boosting Models for Predicting the Travel Mode Choice Using Household Survey Data. J. Urban Plan. Dev. 2022, 148, 04022007. [Google Scholar] [CrossRef]
- Özuysal, M.; Tayfur, G.; Tanyel, S. Passenger flows estimation of light rail transit (LRT) system in Izmir, Turkey using multiple regression and ANN methods. Promet-Traffic Transp. 2012, 24, 1–14. [Google Scholar] [CrossRef]
- Ashik, F.R.; Sreezon, A.I.Z.; Rahman, M.H.; Zafri, N.M.; Labib, S.M. Built environment influences commute mode choice in a global south megacity context: Insights from explainable machine learning approach. J. Transp. Geogr. 2024, 116, 103828. [Google Scholar] [CrossRef]
- Jin, C.-J.; Luo, Y.; Wu, C.; Song, Y.; Li, D. Exploring the Pedestrian Route Choice Behaviors by Machine Learning Models. ISPRS Int. J. Geo-Inf. 2024, 13, 146. [Google Scholar] [CrossRef]
- Yin, G.; Huang, Z.; Fu, C.; Ren, S.; Bao, Y.; Ma, X. Examining active travel behavior through explainable machine learning: Insights from Beijing, China. Transp. Res. Part D Transp. Environ. 2024, 127, 104038. [Google Scholar] [CrossRef]
- Zhao, Y.; Stewart, K. Analyzing travel behavior differences across population groups: An explainable machine learning approach with big mobility data. J. Transp. Geogr. 2025, 128, 104368. [Google Scholar] [CrossRef]
- Tamim Kashifi, M.; Jamal, A.; Samim Kashefi, M.; Almoshaogeh, M.; Masiur Rahman, S. Predicting the travel mode choice with interpretable machine learning techniques: A comparative study. Travel. Behav. Soc. 2022, 29, 279–296. [Google Scholar] [CrossRef]
- Dwivedi, R.; Dave, D.; Naik, H.; Singhal, S.; Omer, R.; Patel, P.; Qian, B.; Wen, Z.; Shah, T.; Morgan, G.; et al. Explainable AI (XAI): Core Ideas, Techniques, and Solutions. ACM Comput. Surv. 2023, 55, 194. [Google Scholar] [CrossRef]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef]
- Islam, M.R.; Ahmed, M.U.; Barua, S.; Begum, S. A Systematic Review of Explainable Artificial Intelligence in Terms of Different Application Domains and Tasks. Appl. Sci. 2022, 12, 1353. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Wadsworth International Group: Monterey, CA, USA, 1984; p. 358. [Google Scholar]
- Hagenauer, J.; Helbich, M. A comparative study of machine learning classifiers for modeling travel mode choice. Expert Syst. Appl. 2017, 78, 273–282. [Google Scholar] [CrossRef]
- Xie, C.; Lu, J.; Parkany, E. Work Travel Mode Choice Modeling with Data Mining: Decision Trees and Neural Networks. Transp. Res. Rec. 2003, 1854, 50–61. [Google Scholar] [CrossRef]
- Ziwei, C.; Cheng, W.; Delei, C.; Lei, L. Alighting stop determination of transit passengers based on expanded history trip records. J. Nanjing Univ. 2020, 56, 227–235. [Google Scholar] [CrossRef]
- Cui, J.; Gao, Y.; Cheng, J.; Shi, L. Study on the Selection Model of Staying Adjustment Bus Lines along Rail Transit. J. Adv. Transp. 2020, 2020, 6385359. [Google Scholar] [CrossRef]
- Board, T.R. Highway Capacity Manual; TRB: Washington, DC, USA, 2000. [Google Scholar]
- Wu, J.; Yang, M.; Rasouli, S.; Cheng, L. Investigating Commuting Time Patterns of Residents Living in Affordable Housing: A Case Study in Nanjing, China. Promet-Traffic Transp. 2019, 31, 423–433. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect Theory: An Analysis of Decision Under Risk. In Handbook of the Fundamentals of Financial Decision Making; World Scientific Handbook in Financial Economics Series; World Scientific: Singapore, 2012; Volume 4, pp. 99–127. [Google Scholar]
- Givoni, M.; Rietveld, P. The access journey to the railway station and its role in passengers’ satisfaction with rail travel. Transp. Policy 2007, 14, 357–365. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, A.; Yeh, A.G.O. The Varying Relationships between Multidimensional Urban Form and Urban Vitality in Chinese Megacities: Insights from a Comparative Analysis. Ann. Am. Assoc. Geogr. 2022, 112, 141–166. [Google Scholar] [CrossRef]
- Mutavdžija, M.; Kovačić, M.; Buntak, K. Moving towards Sustainable Mobility: A Comparative Analysis of Smart Urban Mobility in Croatian Cities. Sustainability 2024, 16, 2004. [Google Scholar] [CrossRef]
| Method Category | Example Models | Typical Data Sources | Interpretability | Predictive Accuracy | Key References |
|---|---|---|---|---|---|
| Traditional Discrete Choice | Logit | Questionnaire (RP/SP) | High | Low | [19,34] |
| Classical Machine Learning | SVM, ANN | Questionnaire, Smart Card | Low to Moderate | Moderate | [36,39] |
| Soft Computing/Advanced ML | Gradient Boosting, Fuzzy Systems | Smart Card, GPS, Sensors | Low to Moderate (model-dependent) | High | [41,42] |
| Our Proposed Method | CART Decision Tree | Smart Card | High | High | This Study |
| Card Number | Date | Bus Line Number | Boarding Time | Boarding Stop | Alighting Time | Alighting Stop | Whether Switch | Switch Mode | Travel Chain After Switch (Line Number: Boarding Station, Alighting Station) |
|---|---|---|---|---|---|---|---|---|---|
| 01**89 | 2017/11/19 | 659 | 20:32:55 | Lvcuobei | 20:48:29 | Jiangjunci | Yes | Rail transit | (rail line 1: Lvcuo, Jiangjunci) |
| 19**65 | 2017/11/12 | 123 | 07:13:32 | Caitang school | 08:18:43 | Fuyoubai jianyuan | No | Bus + Rail transit | (123: Caitang school, Zhiwuyuan)—(rail line 1: Lvcuo, Zhenhailu) |
| 15**37 | 2017/11/30 | 942 | 18:41:01 | Lvcuobei | 19:18:18 | Xingbei xincheng | Yes | Rail transit + Bus | (rail line 1: Lvcuo, Yuanboyuan)—(942: Yuanboyuan, Xingbeixincheng) |
| 82**16 | 2017/11/28 | 659 | 08:10:15 | Yuekouxiaoqu | 09:48:03 | Jinbang park | Yes | Bus + Rail transit + Bus | (659: Yuekouxiaoqu, Zhongpu)—(rail line 1: Gaoqi, Lianban)—(659: Lianbanguomao, Jingbang park) |
| Influencing Factor | Description |
|---|---|
| Card type | Ordinary card: 0, Preferential: 1. |
| Monthly card swiping times | Card swiping times of the passenger in November 2017. |
| Historical average travel time | Historical average travel time of the passenger in November 2017 (measured in minutes). |
| Historical average travel distance | Historical average travel distance of the passenger in November 2017 (measured in meters). |
| Whether historical travel often occurs in peak hours | Whether more than half of the passenger’s trips occurred during peak hours. 1 represents yes, 0 represents no. |
| Travel distance | The travel distance of the OD. |
| Whether travel during peak hours | 1 represents yes, 0 represents no. |
| Number of metro stations to take after switch | The number of metro stations the passenger will take after switching. |
| Increased costs after switch | The increased travel cost of the passenger after switching (measured in RMB). |
| Travel time saved after switch | The saved travel cost of the passenger after switching (measured in minutes). |
| Total walking distance after switch | It includes the walking distance of getting to the station and the walking distance needed for transfer (measured in minutes). |
| Transfer times needed after switch | The needed transfer times of the passenger after switching. |
| Whether switch | 1 represents yes, 0 represents no. |
| Predicted as Positive Value | Predicted as Negative Value | |
|---|---|---|
| Positive true value | True Positives (TP) | False Negatives (FN) |
| Negative true value | False Positives (FP) | True Negatives (TN) |
| Models | Accuracy [95% CI] | Type | Precision [95% CI] | Recall [95% CI] | F1 Score [95% CI] |
|---|---|---|---|---|---|
| Logit | 0.79 [0.76–0.82] | ‘switch’ | 0.78 [0.75–0.81] | 0.82 [0.79–0.85] | 0.80 [0.77–0.83] |
| ‘not switch’ | 0.80 [0.77–0.83] | 0.76 [0.73–0.79] | 0.78 [0.75–0.81] | ||
| average | 0.79 [0.76–0.82] | 0.79 [0.76–0.82] | 0.79 [0.76–0.82] | ||
| NB | 0.78 [0.75–0.81] | ‘switch’ | 0.77 [0.74–0.80] | 0.81 [0.78–0.84] | 0.79 [0.76–0.82] |
| ‘not switch’ | 0.78 [0.75–0.81] | 0.75 [0.72–0.78] | 0.77 [0.74–0.80] | ||
| average | 0.78 [0.75–0.81] | 0.78 [0.75–0.81] | 0.78 [0.75–0.81] | ||
| SVM | 0.80 [0.77–0.83] | ‘switch’ | 0.78 [0.75–0.81] | 0.84 [0.81–0.87] | 0.81 [0.78–0.84] |
| ‘not switch’ | 0.82 [0.79–0.85] | 0.75 [0.72–0.78] | 0.78 [0.75–0.81] | ||
| average | 0.80 [0.77–0.83] | 0.80 [0.77–0.83] | 0.79 [0.76–0.82] | ||
| ANN | 0.70 [0.67–0.73] | ‘switch’ | 0.67 [0.64–0.70] | 0.81 [0.78–0.84] | 0.73 [0.70–0.76] |
| ‘not switch’ | 0.74 [0.71–0.77] | 0.58 [0.55–0.61] | 0.65 [0.62–0.68] | ||
| average | 0.70 [0.67–0.73] | 0.70 [0.67–0.73] | 0.69 [0.66–0.72] | ||
| CART | 0.85 [0.83–0.87] | ‘switch’ | 0.82 [0.79–0.85] | 0.89 [0.87–0.91] | 0.86 [0.84–0.88] |
| ‘not switch’ | 0.87 [0.85–0.89] | 0.80 [0.77–0.83] | 0.83 [0.81–0.85] | ||
| average | 0.85 [0.83–0.87] | 0.85 [0.83–0.87] | 0.84 [0.82–0.86] |
| Comparison | t-Statistic | p-Value | Significance (α = 0.01) |
|---|---|---|---|
| CART vs. Logit | 8.92 | <0.001 | Significant |
| CART vs. SVM | 5.41 | <0.001 | Significant |
| CART vs. ANN | 12.35 | <0.001 | Significant |
| CART vs. NB | 9.18 | <0.001 | Significant |
| SVM vs. Logit | 1.45 | 0.152 | Not Significant |
| Sequence Number | Condition | Result | Accuracy | ||
|---|---|---|---|---|---|
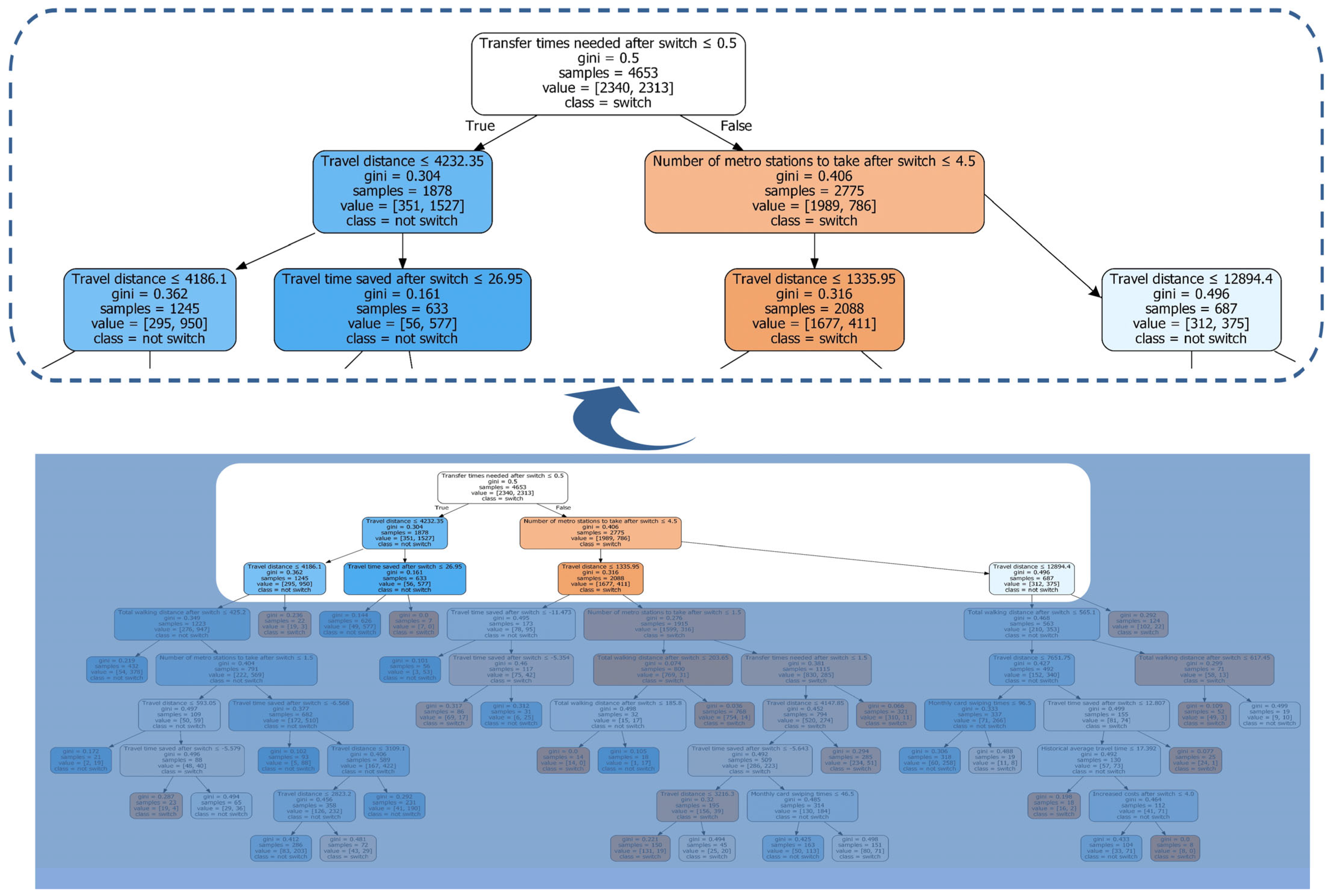
| Rule 1 | IF | Transfer times needed after switch ≤ 0.5 AND Travel distance > 4232.35 AND Travel time saved after switch > 26.95 | THEN | ‘switch’ | 1 |
| Rule 2 | IF | Transfer times needed after switch > 0.5 AND Number of metro stations to take after switch ≤ 1.5 AND Travel distance > 1335.95 AND Total walking distance after switch ≤ 185.8 | THEN | ‘switch’ | 1 |
| Rule 3 | IF | Transfer times needed after switch > 0.5 AND Number of metro stations to take after switch > 4.5 AND (7651.75 < Travel distance ≤ 12,894.4) AND Total walking distance after switch ≤ 565.1 AND Travel time saved after switch ≤ 12.807 AND Historical average travel time > 17.392 AND Increased costs after switch > 4.0 | THEN | ‘switch’ | 1 |
| Rule 4 | IF | (0.5 < Transfer times needed after switch ≤ 1.5) AND (1.5 < Number of metro stations to take after switch ≤ 4.5) AND (1335.95 < Travel distance ≤ 3216.3) AND Travel time saved after switch ≤ −5.643 AND Historical average travel time ≤ 9.182 | THEN | ‘not switch’ | 1 |
| Rule 5 | IF | (0.5 < Transfer times needed after switch ≤ 1.5) AND (1.5 < Number of metro stations to take after switch ≤ 4.5) AND (1335.95 < Travel distance ≤ 3216.3) AND Travel time saved after switch ≤ −5.643 AND Total walking distance after switch ≤ 434.4 | THEN | ‘not switch’ | 1 |
| Rule 6 | IF | Transfer times needed after switch > 0.5 AND Number of metro stations to take after switch ≤ 1.5 AND Travel distance > 1335.95 AND Total walking distance after switch > 203.65 | THEN | ‘switch’ | 0.98 |
| Rule 7 | IF | Transfer times needed after switch > 1.5 AND (1.5 < Number of metro stations to take after switch ≤ 4.5) AND Travel distance > 1335.95 | THEN | ‘switch’ | 0.97 |
| Rule 8 | IF | Transfer times needed after switch > 0.5 AND Number of metro stations to take after switch > 4.5 AND (7651.75 < Travel distance ≤ 12,894.4) AND Total walking distance after switch ≤ 565.1 AND Travel time saved after switch > 12.807 | THEN | ‘switch’ | 0.96 |
| Rule 9 | IF | Transfer times needed after switch ≤ 0.5 AND Travel distance ≤ 4186.1 AND Total walking distance after switch > 425.2 AND Number of metro stations to take after switch > 1.5 AND Travel time saved after switch ≤ −6.568 | THEN | ‘not switch’ | 0.95 |
| Rule 10 | IF | Transfer times needed after switch ≤ 0.5 AND Travel distance > 4232.35 AND Travel time saved after switch ≤ 26.95 | THEN | ‘not switch’ | 0.92 |
| Rule 11 | IF | Transfer times needed after switch > 0.5 AND Number of metro stations to take after switch ≤ 4.5 AND Travel distance ≤ 1335.95 AND Travel time saved after switch ≤ −11.473 | THEN | ‘not switch’ | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Lin, W.; Hu, T.; Cao, Q.; Song, J.; Ren, G.; Wu, C. Passenger Switch Behavior and Decision Mechanisms in Multimodal Public Transportation Systems. Systems 2025, 13, 951. https://doi.org/10.3390/systems13110951
Zhang Z, Lin W, Hu T, Cao Q, Song J, Ren G, Wu C. Passenger Switch Behavior and Decision Mechanisms in Multimodal Public Transportation Systems. Systems. 2025; 13(11):951. https://doi.org/10.3390/systems13110951
Chicago/Turabian StyleZhang, Zhe, Wenxie Lin, Tongyu Hu, Qi Cao, Jianhua Song, Gang Ren, and Changjian Wu. 2025. "Passenger Switch Behavior and Decision Mechanisms in Multimodal Public Transportation Systems" Systems 13, no. 11: 951. https://doi.org/10.3390/systems13110951
APA StyleZhang, Z., Lin, W., Hu, T., Cao, Q., Song, J., Ren, G., & Wu, C. (2025). Passenger Switch Behavior and Decision Mechanisms in Multimodal Public Transportation Systems. Systems, 13(11), 951. https://doi.org/10.3390/systems13110951








