An Analysis of Blockchain Adoption Strategies in a Technology-Supported Supply Chain Considering Government Subsidy
Abstract
1. Introduction
- (1)
- What factors determine whether the manufacturer and retailer should adopt blockchain?
- (2)
- When the blockchain is adopted, how do the prices and profits change, and who should lead the blockchain construction?
- (3)
- When the government utilizes the technology subsidy, what are the corresponding impacts on the manufacturer, retailer, and technical service firm?
2. Literature Review
2.1. The Blockchain Adoption in the Supply Chain
2.2. Government Subsidy Policy
3. Model
3.1. Benchmark: Without Blockchain
3.2. The Manufacturer-Led Blockchain
3.3. The Retailer-Led Blockchain
4. The Effects of Government Subsidy on BT Adoption
4.1. Blockchain Technology Subsidy Under Manufacturer-Led Scenario
4.2. Blockchain Technology Subsidy Under Retailer-Led Scenario
5. Analysis and Discussion
5.1. Comparison of Decision Variables
- (i)
- If and , . If (1) and ; (2) , .
- (ii)
- If and , . If (1) and ; (2) , .
- (iii)
- If and , . If (1) and ; (2) , .
- (iv)
- If and , . If (1) and ; (2) , .
- (v)
- If and , . If (1) and ; (2) , .
- (i)
- ,,, and .
- (ii)
- ,,, and .
5.2. Comparison of Profits
- (i)
- If (1) ; (2) and , . If and , , where .
- (ii)
- If (1) ; (2) and , . If and , , where .
- (i)
- If (1) ; (2) and , . If and , , where .
- (ii)
- If (1) ; (2) and , . If and , , where .
- (i)
- .
- (ii)
- .
- (iii)
- If (1) ; (2) and , . If (1) and ; (2) , .
- (iv)
- If (1) ; (2) and , . If (1) and ; (2) , .
6. Extensions
7. Conclusions and Discussion
- (1)
- For the manufacturer and retailer, blockchain adoption in the supply chain is not always optimal and is contingent on consumers’ acceptance of non-blockchain products and blockchain construction costs. When consumer acceptance of non-blockchain products is low, blockchain effectively mitigates concerns and boosts trust. Conversely, at moderate acceptance levels, high construction costs significantly deter adoption;
- (2)
- The manufacturer and retailer invariably benefit from government subsidies, which lower blockchain construction costs. This enables them to raise product prices and enhance traceability level, thereby boosting profits. Conversely, the technical service firm will only collaborate with the manufacturer or retailer to establish blockchain traceability systems when their cost-bearing ratio is sufficiently low or the construction cost coefficient high;
- (3)
- A win–win situation may exist for the manufacturer, retailer, and technical service firm. Under this scenario, the technical service firm shoulder a smaller proportion of blockchain construction cost. If the manufacturer or retailer aims to shift more blockchain cost onto the service firm, the manufacturer must increase the licensing fee payment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RFID | Radio frequency identification |
| QR | Quick response |
| IoT | Internet of Things |
| IBM | International Business Machines Corporation |
| UK | United Kingdom |
| JD | JD.com, Inc. |
Appendix A
Appendix A.1. Proof of Lemmas 1 and 2
Appendix A.2. Proof of Lemmas 3 and 4
Appendix A.3. Proof of Proposition 1
- (i)
- , , . If and , . If and or , ;
- (ii)
- , , . The result of this equation, , is the same as ;
- (iii)
- . The result of this equation, , is the same as ;
- (iv)
- . The result of this equation, , is the same as ;
- (v)
- , , . The result of this equation, , is the same as .
Appendix A.4. Proof of Proposition 2
- (i)
- , , , , ;
- (ii)
- , , , , .
Appendix A.5. Proof of Proposition 3
Appendix A.6. Proof of Proposition 4
Appendix A.7. Proof of Proposition 5
Appendix A.8. Proof of Proposition 6
Appendix A.9. Proof of Proposition 7
Appendix A.10. Proof of Proposition 8
References
- Wang, Y.; Lin, J.; Choi, T.-M. Gray market and counterfeiting in supply chains: A review of the operations literature and implications to luxury industries. Transp. Res. Part E Logist. Transp. Rev. 2020, 133, 101823. [Google Scholar] [CrossRef]
- Yao, S.; Zhu, K.; Yang, R. Combating counterfeit products: Anti-counterfeiting technology and law enforcement. Prod. Oper. Manag. 2025. [Google Scholar] [CrossRef]
- Babich, V.; Hilary, G. OM Forum—Distributed ledgers and operations: What operations management researchers should know about blockchain technology. Manuf. Serv. Oper. Manag. 2020, 22, 223–240. [Google Scholar] [CrossRef]
- Dai, H.; Tseng, M.M.; Zipkin, P.H. Design of traceability systems for product recall. Int. J. Prod. Res. 2015, 53, 511–531. [Google Scholar] [CrossRef]
- Jin, S.; Zhang, Y.; Xu, Y. Amount of information and the willingness of consumers to pay for food traceability in China. Food Control 2017, 77, 163–170. [Google Scholar] [CrossRef]
- Wu, X.Y.; Fan, Z.P.; Cao, B.B. An analysis of strategies for adopting blockchain technology in the fresh product supply chain. Int. J. Prod. Res. 2023, 61, 3717–3734. [Google Scholar] [CrossRef]
- Wang, J.; Shi, Y.; Zhao, C.; Venkatesh, V.G.; Chen, W. Impact of pricing leadership on blockchain data acquisition efforts in a circular supply chain. Int. J. Prod. Res. 2023, 61, 7248–7262. [Google Scholar] [CrossRef]
- Xu, X.; Chen, J.; Liu, S.; Yu, Y.; Cheng, T.C.E. Should a manufacturer adopt blockchain when its competitor discloses blockchain-enabled product quality information? Int. J. Prod. Res. 2025, 63, 5217–5237. [Google Scholar] [CrossRef]
- Šilenskytė, A.; Butkevičienė, J.; Bartminas, A. Blockchain-based connectivity within digital platforms and ecosystems in international business. J. Int. Manag. 2024, 30, 101109. [Google Scholar] [CrossRef]
- Nestlé Joins WWF’s OpenSC Blockchain for Sustainable Supply Chains. Available online: https://www.ledgerinsights.com/nestle-wwf-opensc-blockchain-sustainable-supply-chains-food-traceability/ (accessed on 9 July 2025).
- Guo, X.; Cheng, L.; Yu, Y. Government subsidy policy for green and efficient raw materials considering farmer heterogeneity. Prod. Oper. Manag. 2022, 31, 4095–4112. [Google Scholar] [CrossRef]
- Bian, J.; Zhang, G.; Zhou, G. Manufacturer vs. consumer subsidy with green technology investment and environmental concern. Eur. J. Oper. Res. 2020, 287, 832–843. [Google Scholar] [CrossRef]
- Blockchain Funding and Investment. Available online: https://digital-strategy.ec.europa.eu/en/policies/blockchain-funding (accessed on 9 July 2025).
- UK Government Invests in TAG TrustNet’s Blockchain Initiative to Make Digital Advertising More Accountable, Responsible and Efficient. Available online: https://www.prnewswire.com/news-releases/uk-government-invests-in-tag-trustnets-blockchain-initiative-to-make-digital-advertising-more-accountable-responsible-and-efficient-301460609.html (accessed on 9 July 2025).
- The Blockchain Industry Demonstrates Robust Growth, Emerging as a New Engine for the Development of the Digital Economy. Available online: http://www.xinhuanet.com/tech/20220624/ef94413abefb4893b72447e2bfe453e9/c.html (accessed on 9 July 2025).
- Thirty-Three Provinces and Cities in China Have Promulgated Special Blockchain Policies, with Some Regions Offering household Registration (Hukou) and One-Million-Yuan Bonuses as Talent Attraction Incentives. Available online: https://finance.sina.com.cn/blockchain/coin/2021-07-13/doc-ikqcfnca6659392.shtml (accessed on 9 July 2025).
- Notice of the Fuzhou Big-Data Development Administration and the Fuzhou Finance Bureau on Issuing Three Measures to Promote the Development of Fuzhou’s Blockchain Industry. Available online: https://sjglj.fuzhou.gov.cn/zwgk/tzgg/202305/t20230511_4601730.htm (accessed on 9 July 2025).
- Pun, H.; Swaminathan, J.M.; Hou, P. Blockchain Adoption for Combating Deceptive Counterfeits. Prod. Oper. Manag. 2021, 30, 864–882. [Google Scholar] [CrossRef]
- Shen, B.; Dong, C.; Minner, S. Combating copycats in the supply chain with permissioned blockchain technology. Prod. Oper. Manag. 2022, 31, 138–154. [Google Scholar] [CrossRef]
- Fang, C.; Chi, M.; Fan, S.; Choi, T.M. Who should invest in blockchain technology under different pricing models in supply chains? Eur. J. Oper. Res. 2024, 319, 777–792. [Google Scholar] [CrossRef]
- Lu, L.; Fang, X.; Gao, S.Y.; Kazaz, B. Converting counterfeiters in emerging markets to authorized suppliers: A new anti-counterfeiting measure. Prod. Oper. Manag. 2025. [Google Scholar] [CrossRef]
- Cai, Y.J.; Choi, T.M.; Zhang, J. Platform supported supply chain operations in the blockchain era: Supply contracting and moral hazards. Decis. Sci. 2021, 52, 866–892. [Google Scholar] [CrossRef]
- Choi, T.-M.; Feng, L.; Li, R. Information disclosure structure in supply chains with rental service platforms in the blockchain technology era. Int. J. Prod. Econ. 2019, 221, 107473. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Y.; Hou, P.; Wang, J. Price signal or blockchain technology? Quality information disclosure in dual-channel supply chains. Eur. J. Oper. Res. 2024, 316, 126–137. [Google Scholar] [CrossRef]
- Franke, B.; Fritz, Q.G.; Stenzel, A. The (limited) power of blockchain networks for information provision. Manag. Sci. 2024, 70, 971–990. [Google Scholar] [CrossRef]
- Fan, Z.P.; Wu, X.Y.; Cao, B.B. Considering the traceability awareness of consumers: Should the supply chain adopt the blockchain technology? Ann. Oper. Res. 2022, 309, 837–860. [Google Scholar] [CrossRef]
- Yang, L.; Ni, Y.; Ng, C.T. Blockchain-enabled traceability and producer’s incentive to outsource delivery. Int. J. Prod. Res. 2023, 61, 3811–3828. [Google Scholar] [CrossRef]
- Tan, Y.; Huang, X.; Li, W. Does blockchain-based traceability system guarantee information authenticity? An evolutionary game approach. Int. J. Prod. Econ. 2023, 264, 108974. [Google Scholar] [CrossRef]
- Naoum-Sawaya, J.; Elhedhli, S.; De Carvalho, P. Strategic blockchain adoption to deter deceptive counterfeiters. Eur. J. Oper. Res. 2023, 311, 373–386. [Google Scholar] [CrossRef]
- Iyengar, G.; Saleh, F.; Sethuraman, J.; Wang, W. Blockchain adoption in a supply chain with manufacturer market power. Manag. Sci. 2024, 70, 6158–6178. [Google Scholar] [CrossRef]
- Alizamir, S.; Iravani, F.; Mamani, H. An Analysis of Price vs. Revenue Protection: Government Subsidies in the Agriculture Industry. Manag. Sci. 2019, 65, 32–49. [Google Scholar] [CrossRef]
- Chen, Y.H.; Chen, M.X.; Mishra, A.K. Subsidies under uncertainty: Modeling of input-and out-put-oriented policies. Econ. Model. 2020, 85, 39–56. [Google Scholar] [CrossRef]
- Fan, T.; Feng, Q.; Li, Y.; Shanthikumar, J.G.; Wu, Y. Output-oriented agricultural subsidy de-sign. Manag. Sci. 2024, 70, 1448–1464. [Google Scholar] [CrossRef]
- Joo, H.Y.; Seo, Y.W.; Min, H. Examining the effects of government intervention on the firm’s environ-mental and technological innovation capabilities and export performance. Int. J. Prod. Res. 2018, 56, 6090–6111. [Google Scholar] [CrossRef]
- Bigerna, S.; Wen, X.; Hagspiel, V.; Kort, P.M. Green electricity investments: Environmental target and the optimal subsidy. Eur. J. Oper. Res. 2019, 279, 635–644. [Google Scholar] [CrossRef]
- Huang, J.; Leng, M.; Liang, L.; Liu, J. Promoting electric automobiles: Supply chain analysis under a government’s subsidy incentive scheme. IIE Trans. 2013, 45, 826–844. [Google Scholar] [CrossRef]
- Yu, Y.; Han, X.; Hu, G. Optimal production for manufacturers considering consumer environmental awareness and green subsidies. Int. J. Prod. Econ. 2016, 182, 397–408. [Google Scholar] [CrossRef]
- Zolfagharinia, H.; Zangiabadi, M.; Hafezi, M. How much is enough? Government subsidies in supporting green product development. Eur. J. Oper. Res. 2023, 309, 1316–1333. [Google Scholar] [CrossRef]
- Jin, W.; Ding, W.; Yang, J. Impact of financial incentives on green manufacturing: Loan guarantee vs. interest subsidy. Eur. J. Oper. Res. 2022, 300, 1067–1080. [Google Scholar] [CrossRef]
- Bai, J.; Hu, S.; Gui, L.; So, K.C.; Ma, Z.J. Optimal subsidy schemes and budget allocations for government subsidized trade-in programs. Prod. Oper. Manag. 2021, 30, 2689–2706. [Google Scholar] [CrossRef]
- Luo, C.; Leng, M.; Huang, J.; Liang, L. Supply chain analysis under a price-discount incentive scheme for electric vehicles. Eur. J. Oper. Res. 2014, 235, 329–333. [Google Scholar] [CrossRef]
- Fan, Z.P.; Cao, Y.; Huang, C.Y.; Li, Y. Pricing strategies of domestic and imported electric vehicle manufacturers and the design of government subsidy and tariff policies. Transp. Res. Part E Logist. Transp. Rev. 2020, 143, 102093. [Google Scholar] [CrossRef]
- Rimba, P.; Tran, A.B.; Weber, I.; Staples, M.; Ponomarev, A.; Xu, X. Quantifying the cost of distrust: Comparing blockchain and cloud services for business process execution. Inf. Syst. Front. 2020, 22, 489–507. [Google Scholar] [CrossRef]
- Zhong, Y.; Yang, T.; Yu, H.; Zhong, S.; Xie, W. Impacts of blockchain technology with government subsidies on a dual-channel supply chain for tracing product information. Transp. Res. Part E Logist. Transp. Rev. 2023, 171, 103032. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, H.; Cao, C.; Tan, Z. Blockchain adoption strategies for combating deficient personal protective equipment in major public health emergencies. Ann. Oper. Res. 2025, 348, 1745–1797. [Google Scholar] [CrossRef]
- Xu, J.; Duan, Y. Pricing and greenness investment for green products with government subsidies: When to apply blockchain technology? Electron. Commer. Res. Appl. 2022, 51, 101108. [Google Scholar] [CrossRef]
- Yenipazarli, A. Incentives for environmental research and development: Consumer preferences, competitive pressure and emissions taxation. Eur. J. Oper. Res. 2019, 276, 757–769. [Google Scholar] [CrossRef]
- Cheng, F.; Chen, T.; Shen, Y.; Jing, X. Impact of green technology improvement and store brand introduction on the sales mode selection. Int. J. Prod. Econ. 2022, 253, 108587. [Google Scholar] [CrossRef]
- Tao, F.; Wang, Y.Y.; Zhu, S.H. Impact of blockchain technology on the optimal pricing and quality decisions of platform supply chains. Int. J. Prod. Res. 2023, 61, 3670–3684. [Google Scholar] [CrossRef]
- Wu, X.; Xiong, J.; Yan, J.; Wang, Y. Perceived quality of traceability information and its effect on purchase intention towards organic food. J. Mark. Manag. 2021, 37, 1267–1286. [Google Scholar] [CrossRef]
- Top 20 Supply Chain Startups That Are Using Blockchain Technology. Available online: https://fortunescrown.com/top-20-supply-chain-startups-that-are-using-blockchain-technology/ (accessed on 9 July 2025).
- Choi, T.M. Blockchain-technology-supported platforms for diamond authentication and certification in luxury supply chains. Transp. Res. Part E Logist. Transp. Rev. 2019, 128, 17–29. [Google Scholar] [CrossRef]
- Blockchain in Retail Industry: Benefits and Use Cases. Available online: https://www.bitdegree.org/crypto/tutorials/blockchain-in-retail (accessed on 9 July 2025).
- Blockchains in Supply Chain Management: A Deeper Look (Part 1). Available online: https://themerkle.com/blockchains-in-supply-chain-management-a-deeper-look-part-1/ (accessed on 9 July 2025).
- Choi, T.M.; Luo, S. Data quality challenges for sustainable fashion supply chain operations in emerging markets: Roles of blockchain, government sponsors and environment taxes. Transp. Res. Part E Logist. Transp. Rev. 2019, 131, 139–152. [Google Scholar] [CrossRef]
- Blockchain Development Cost in 2025: Comprehensive Guide. Available online: https://clutch.co/developers/blockchain/pricing (accessed on 9 July 2025).
- Cao, Y.; Shen, B. Adopting blockchain technology to block less sustainable products’ entry in global trade. Transp. Res. Part E Logist. Transp. Rev. 2022, 161, 102695. [Google Scholar] [CrossRef]
- Exploring Government Funding for Blockchain: Driving Innovation and Transformation. Available online: https://dev.to/vitalisorenko/exploring-government-funding-for-blockchain-driving-innovation-and-transformation-4ica (accessed on 9 July 2025).
- Blockchain for Food: 10 Examples to Know. Available online: https://builtin.com/blockchain/food-safety-supply-chain (accessed on 9 July 2025).
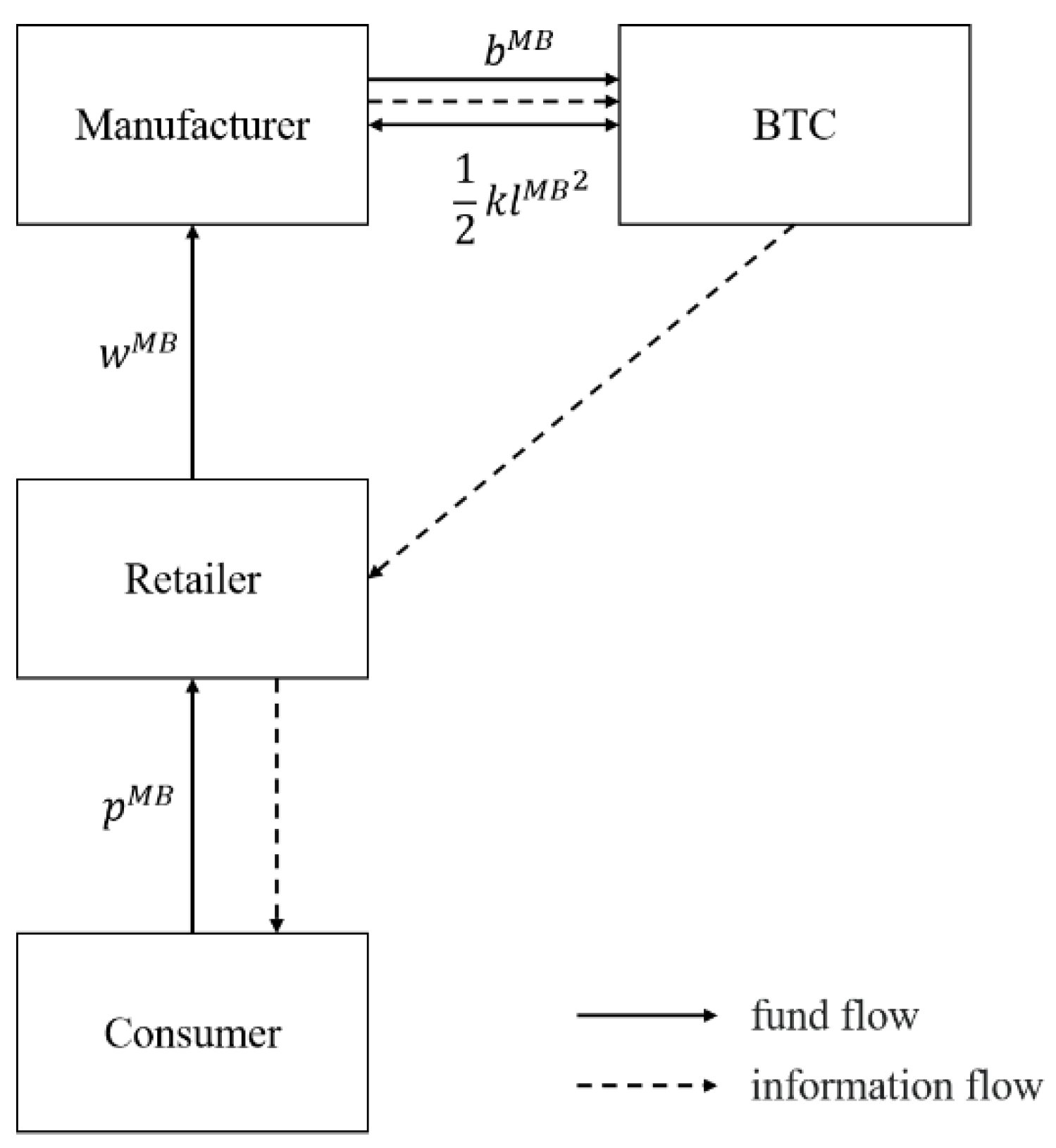
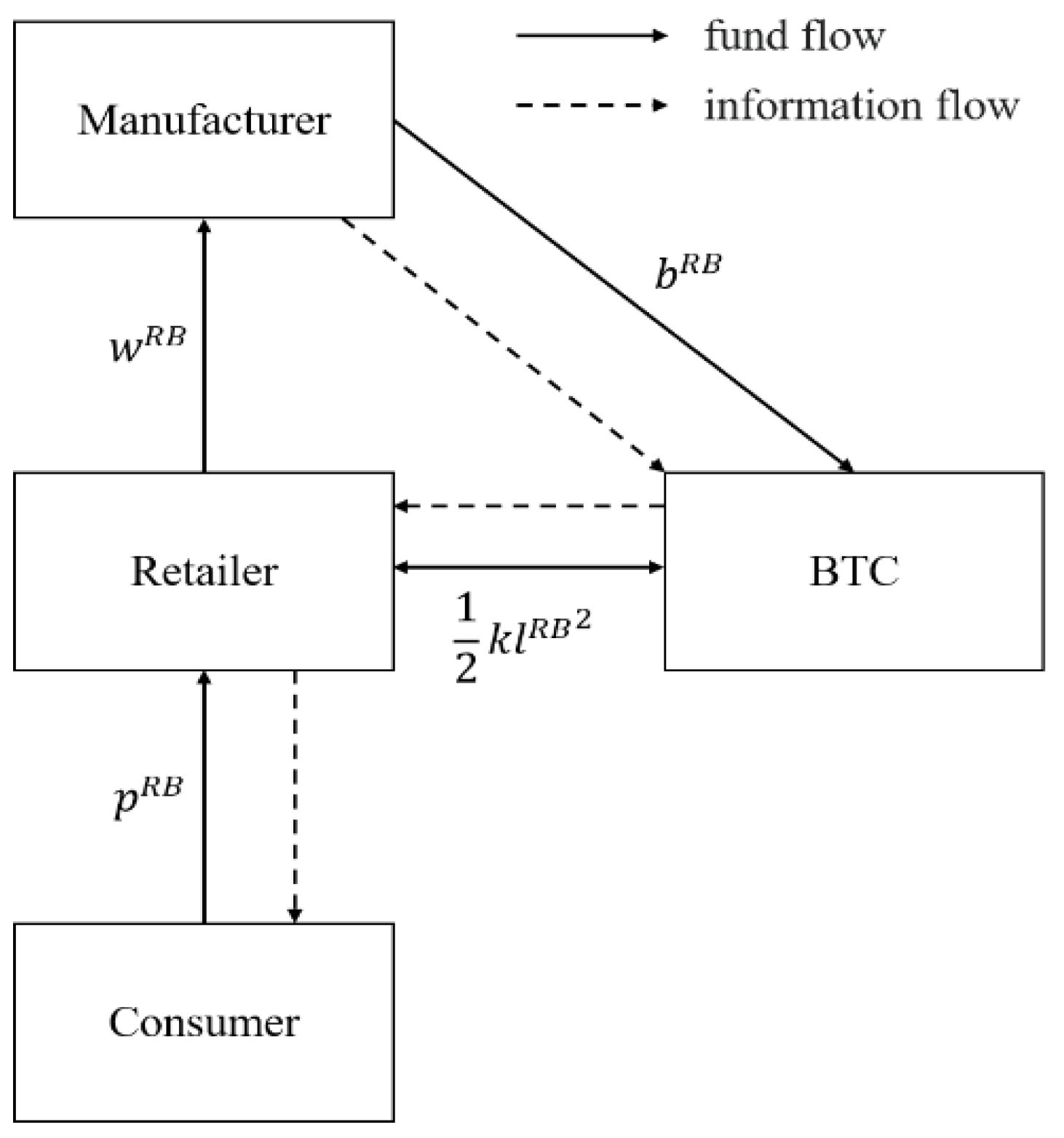


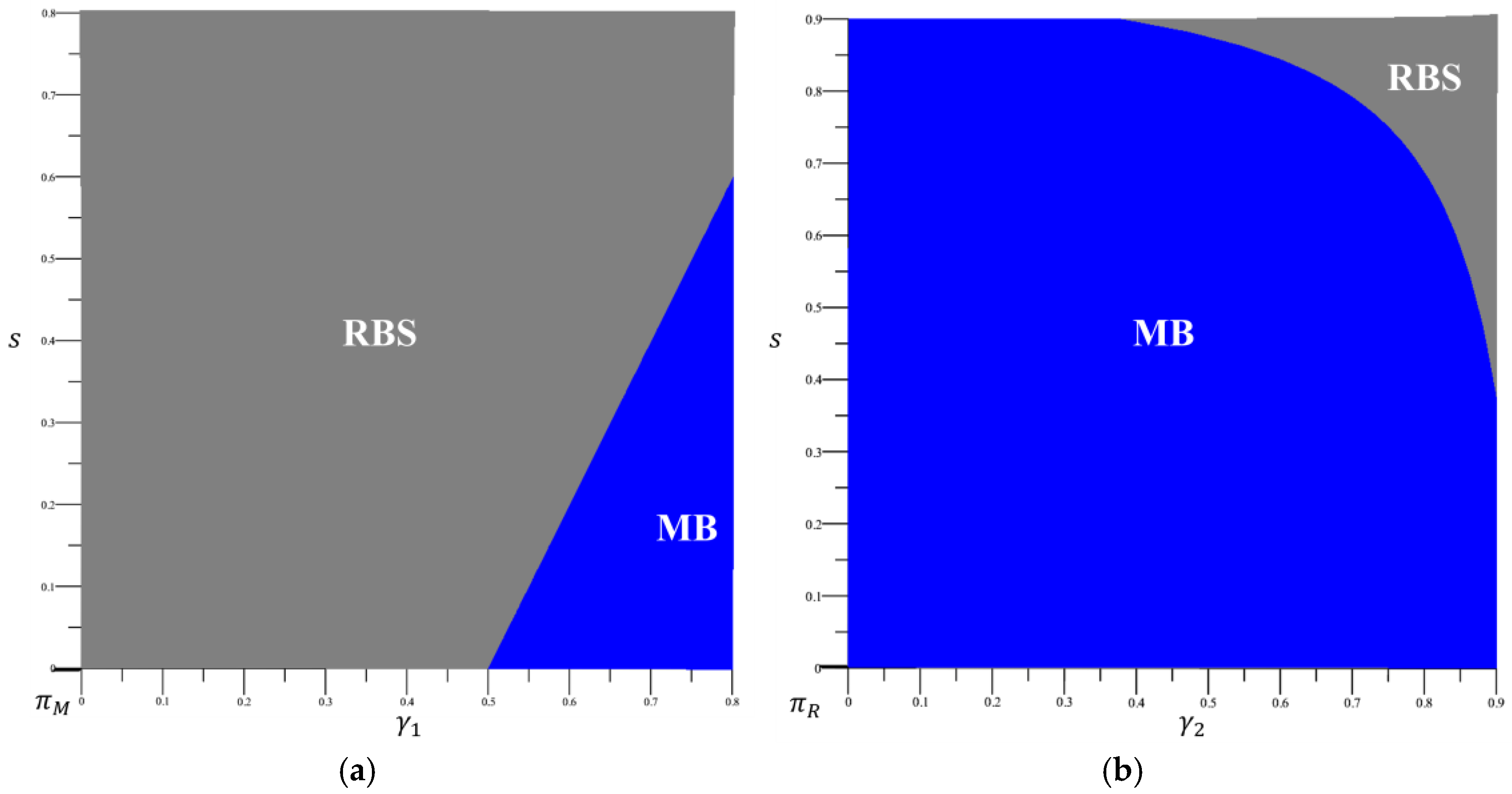
| Main Notations | Descriptions |
|---|---|
| Superscripts for different scenarios, | |
| Manufacturer’s unit product production cost, c | |
| The perceived value of consumers; it follows uniform distribution in | |
| Consumers’ acceptance degree for products, | |
| The consumer’s sensitivity of product’s blockchain traceability level, | |
| The product’s blockchain traceability level (decision variable) | |
| The cost coefficient of blockchain construction, | |
| The unit licensing fee of adopting of blockchain technology (decision variable) | |
| The proportion of blockchain construction costs undertaken by BTC, | |
| Government subsidy ratio for blockchain technology | |
| The retail price of products (decision variable) | |
| The wholesale price of products (decision variable) | |
| The utility of consumers when purchasing the products | |
| The demand of products | |
| The profit of supply chain members |
| Scenario | Wholesale Price | Selling Price | Product Traceability Level | Licensing Fee of Blockchain |
|---|---|---|---|---|
| Scenario | Demand | Manufacturer’s Profit | Retailer’s Profit | BTC’s Profit |
|---|---|---|---|---|
| Scenario | Wholesale Price | Selling Price | Product Traceability Level | Licensing Fee of Blockchain |
|---|---|---|---|---|
| Scenario | Demand | Manufacturer’s Profit | Retailer’s Profit | BTC’s Profit |
|---|---|---|---|---|
| Scenario | Manufacturer’s Profit | Retailer’s Profit | BTC’s Profit |
|---|---|---|---|
| \ | |||
| Scenario | Manufacturer’s Profit | Retailer’s Profit | BTC’s Profit |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, X.; Jiang, Y.; Zhang, W. An Analysis of Blockchain Adoption Strategies in a Technology-Supported Supply Chain Considering Government Subsidy. Systems 2025, 13, 931. https://doi.org/10.3390/systems13110931
Pu X, Jiang Y, Zhang W. An Analysis of Blockchain Adoption Strategies in a Technology-Supported Supply Chain Considering Government Subsidy. Systems. 2025; 13(11):931. https://doi.org/10.3390/systems13110931
Chicago/Turabian StylePu, Xujin, Yukun Jiang, and Wen Zhang. 2025. "An Analysis of Blockchain Adoption Strategies in a Technology-Supported Supply Chain Considering Government Subsidy" Systems 13, no. 11: 931. https://doi.org/10.3390/systems13110931
APA StylePu, X., Jiang, Y., & Zhang, W. (2025). An Analysis of Blockchain Adoption Strategies in a Technology-Supported Supply Chain Considering Government Subsidy. Systems, 13(11), 931. https://doi.org/10.3390/systems13110931






